Electrical Impedance Tomography for Hand Gesture Recognition for HMI Interaction Applications
Abstract
:1. Introduction
2. State of the Art
3. Materials and Method: Experimental Platform
3.1. Measuring System
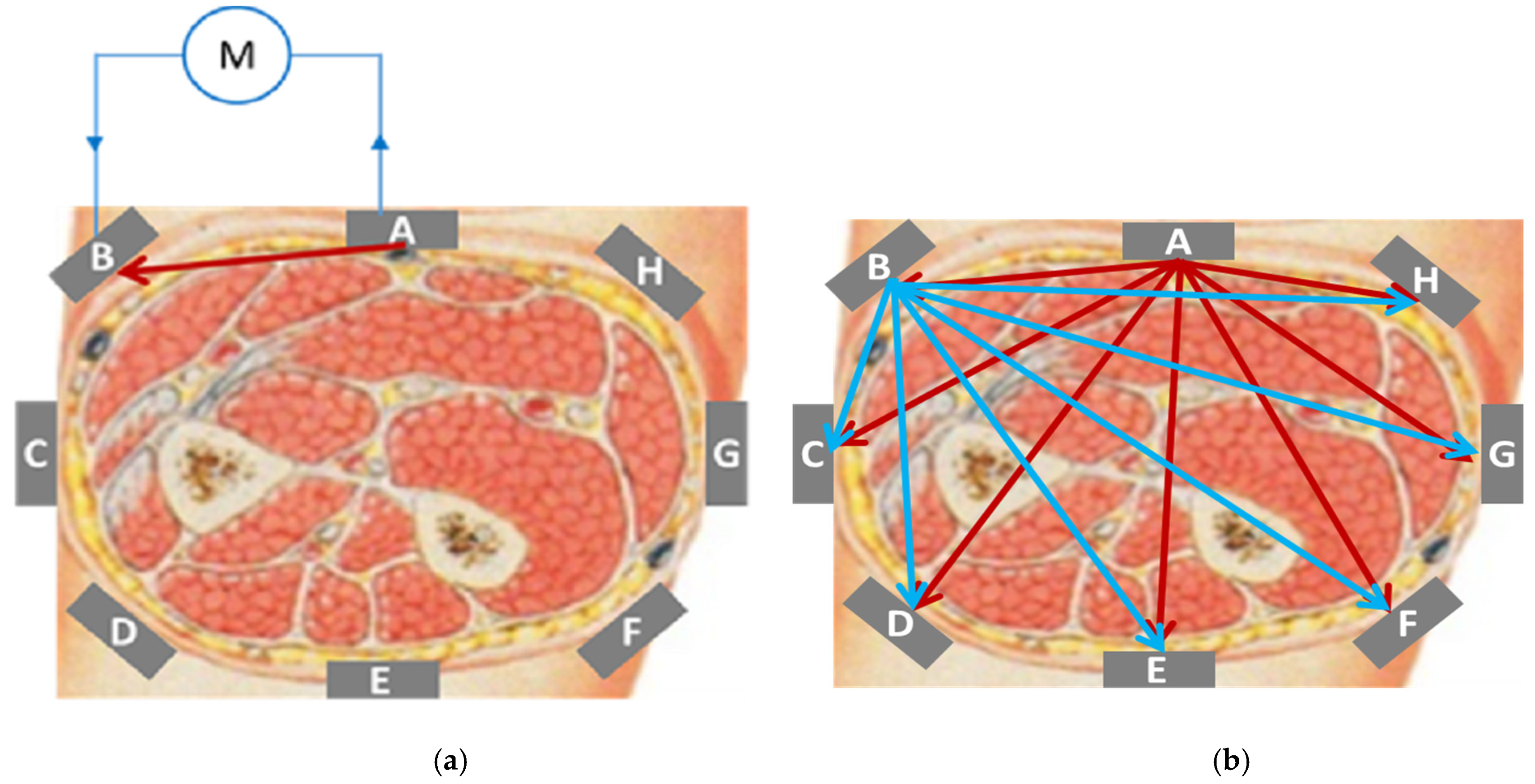
3.1.1. Type of Measurement
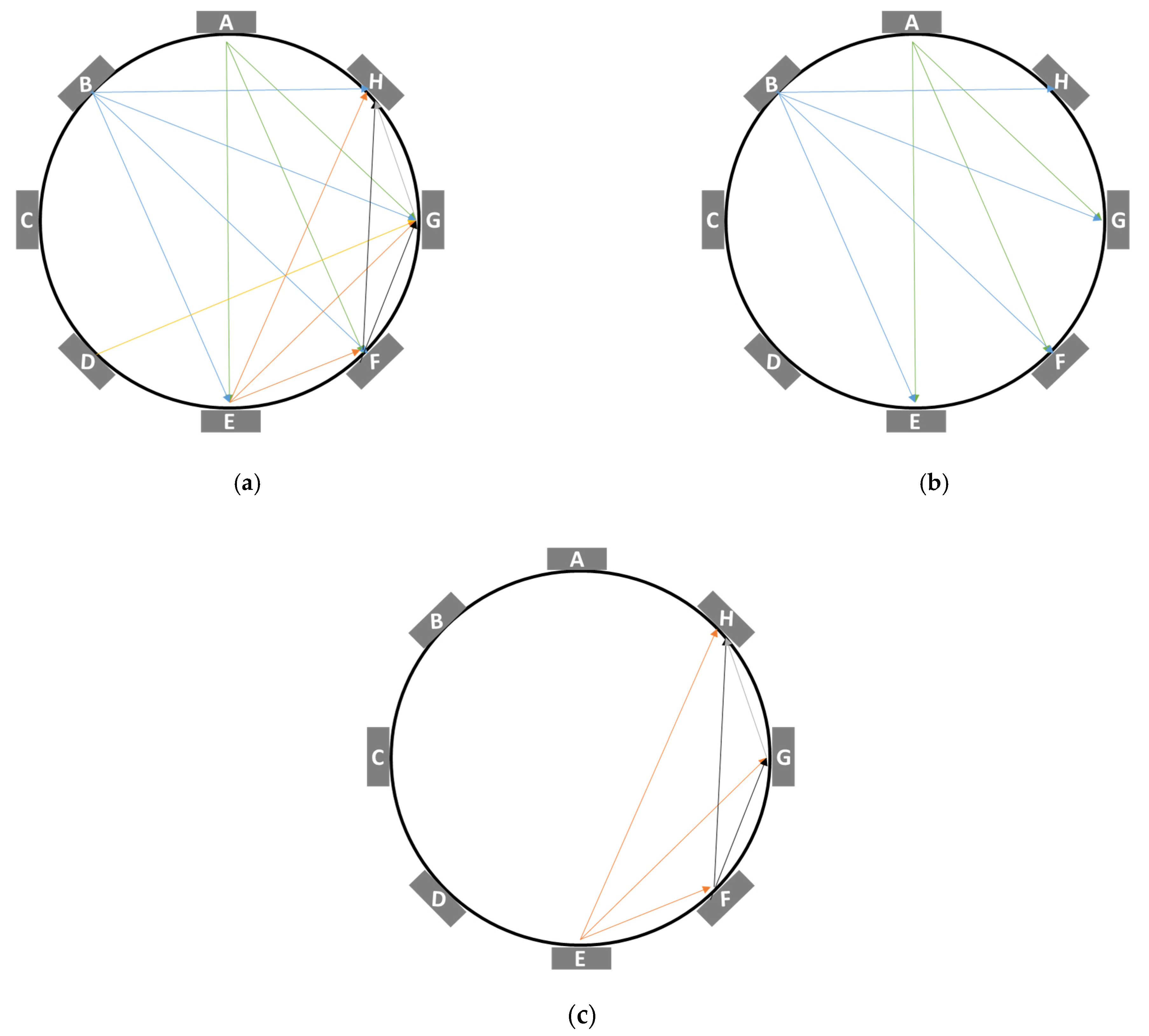
3.1.2. Number of Electrodes and Measurements
3.2. Required Hardware and Software
3.3. Configuration Parameters for Pattern Acquisition
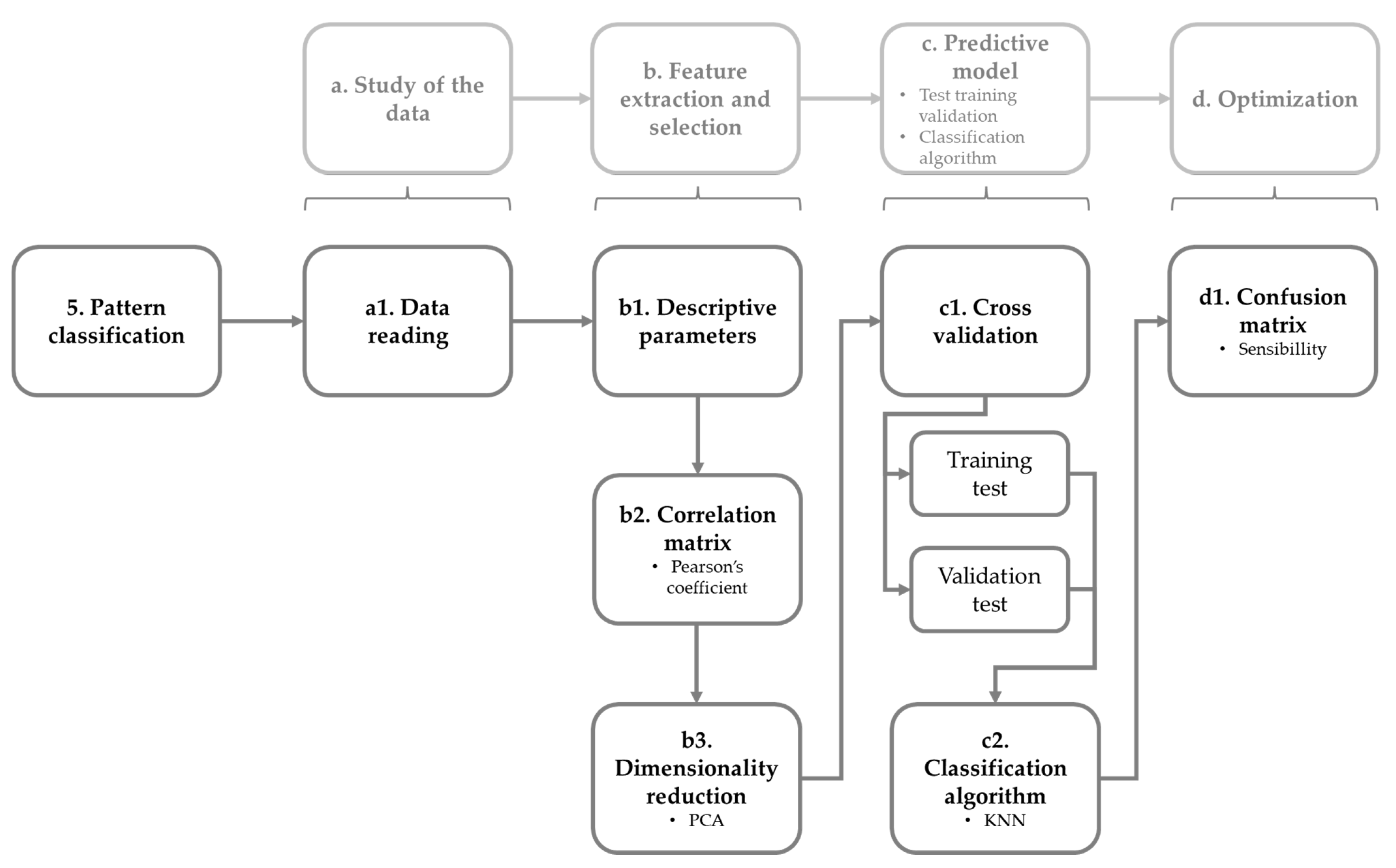
3.4. Pattern Acquisition and Processing
3.5. Pattern Classifier
4. Results
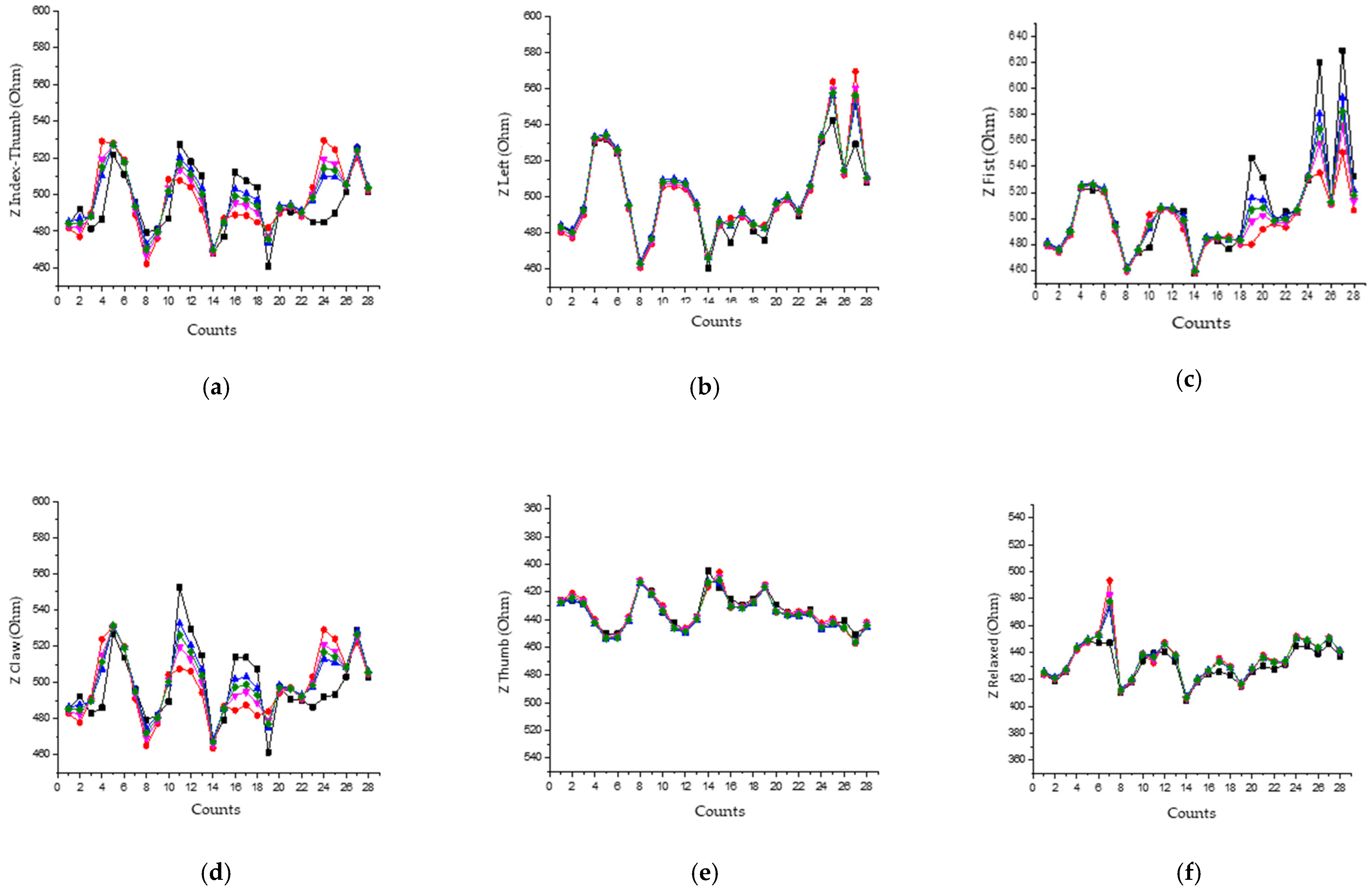
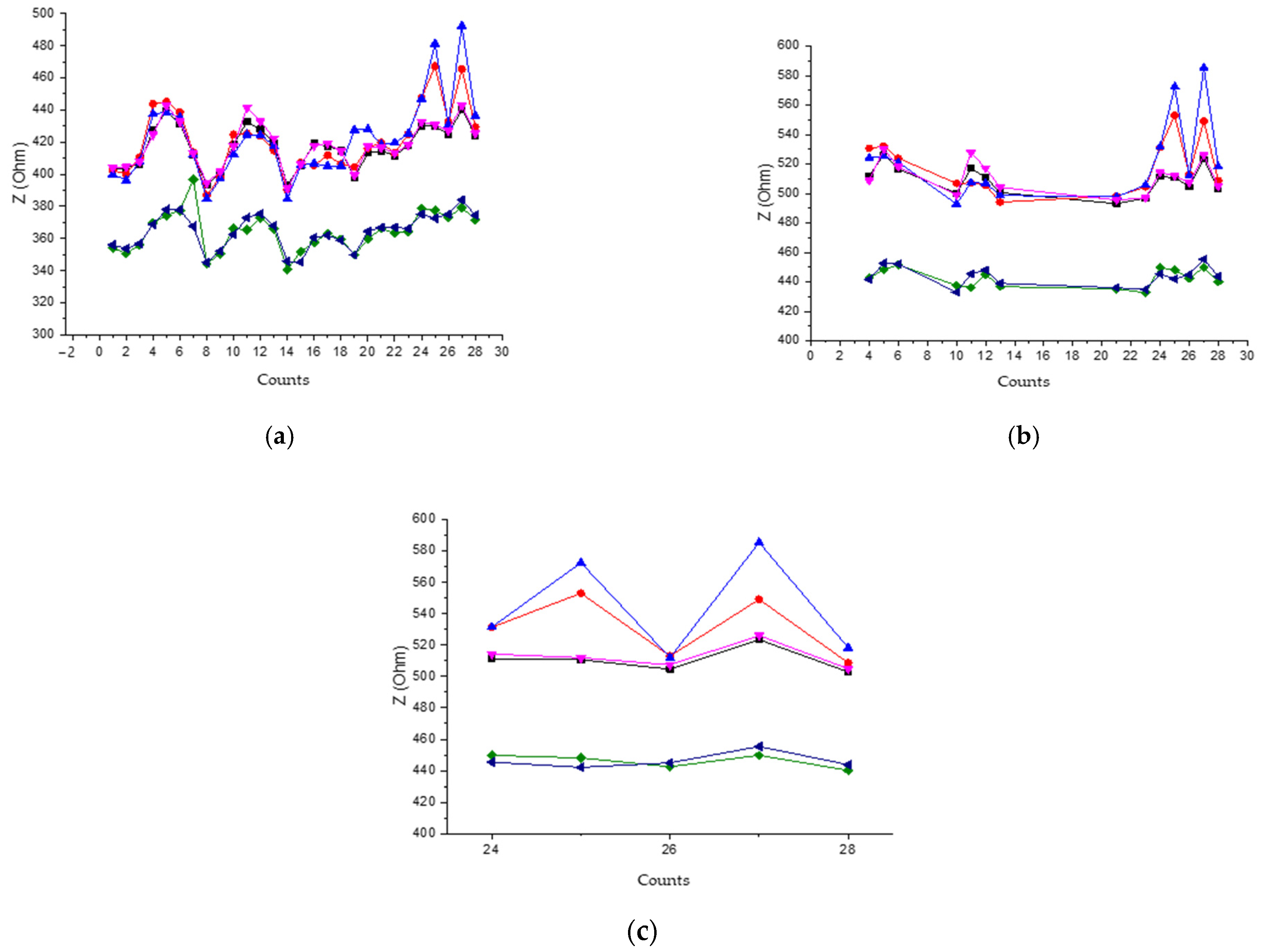
4.1. Experimental Results of Data Reading
Analysis of the Reading of Experimental Results
- The pattern from 28 measurements to 14 measurements will be called “Reduction A”, abbreviated as RedA;
- The pattern from the first 14 measurements to 7 measurements will be called “Reduction B”, abbreviated as RedB;
- The pattern from the last 14 measurements to 5 measurements will be called “Reduction C”, abbreviated as RedC.
4.2. Experimental Results of Feature Extraction and Selection
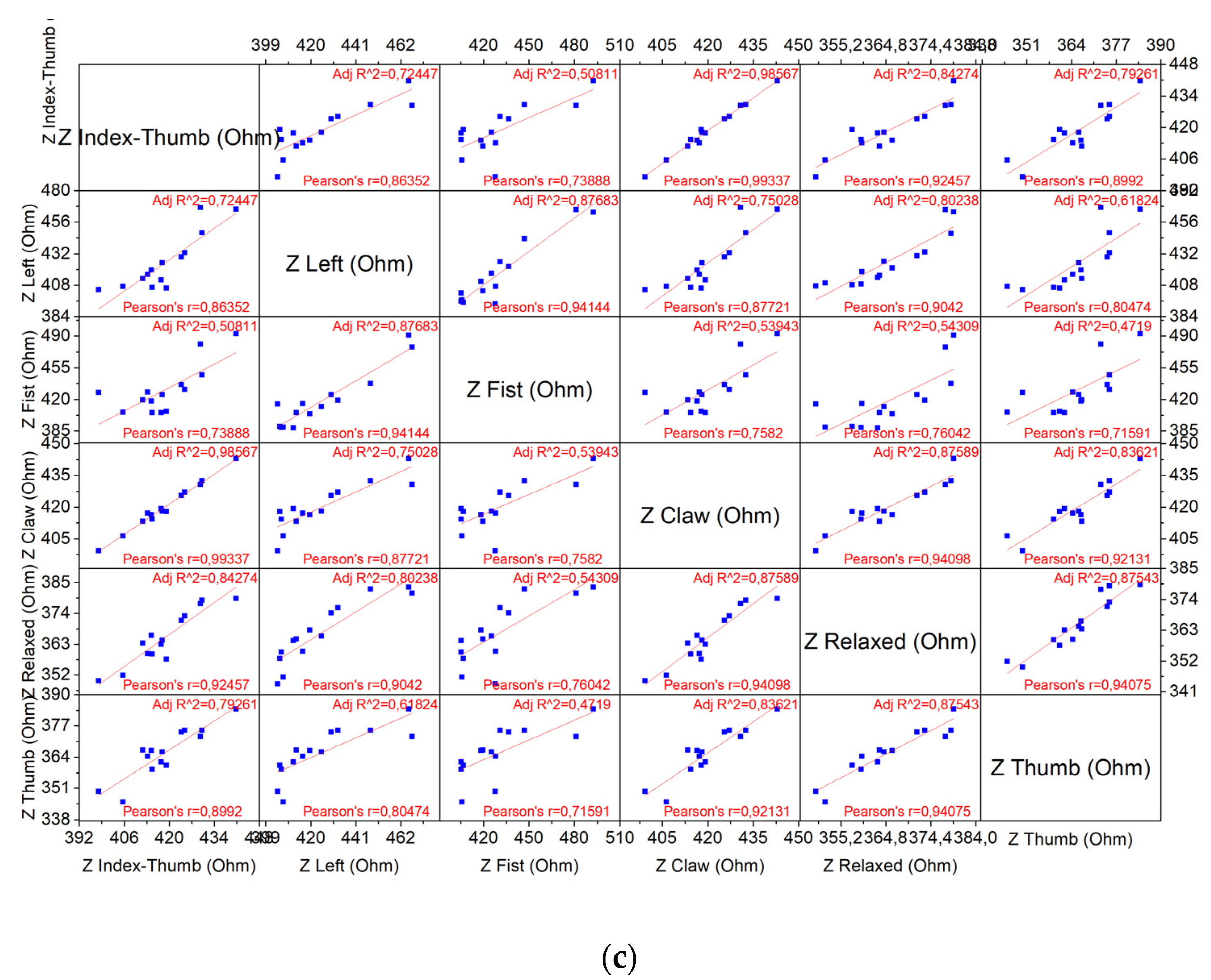
4.2.1. Correlation Matrix Results
- H0 states that the set of measurements obtained by each gesture is linearly independent of each other
- H1 states that the set of measurements obtained by each gesture is linearly dependent on each other
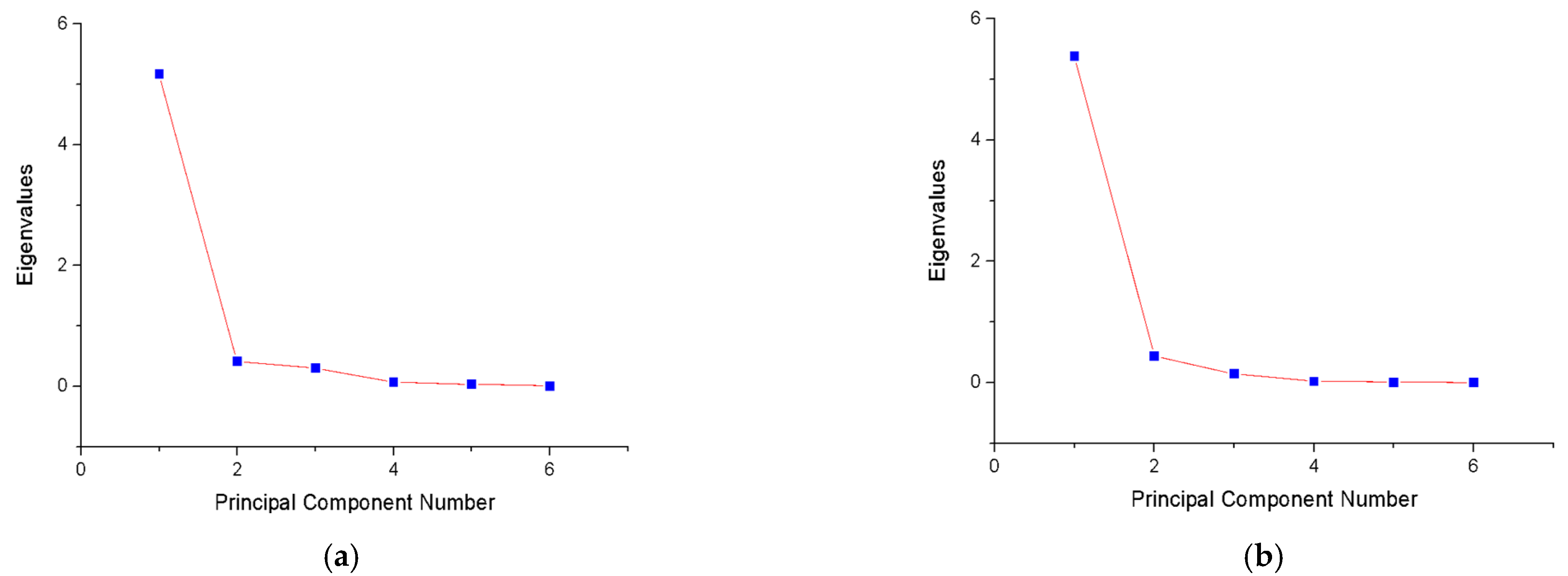
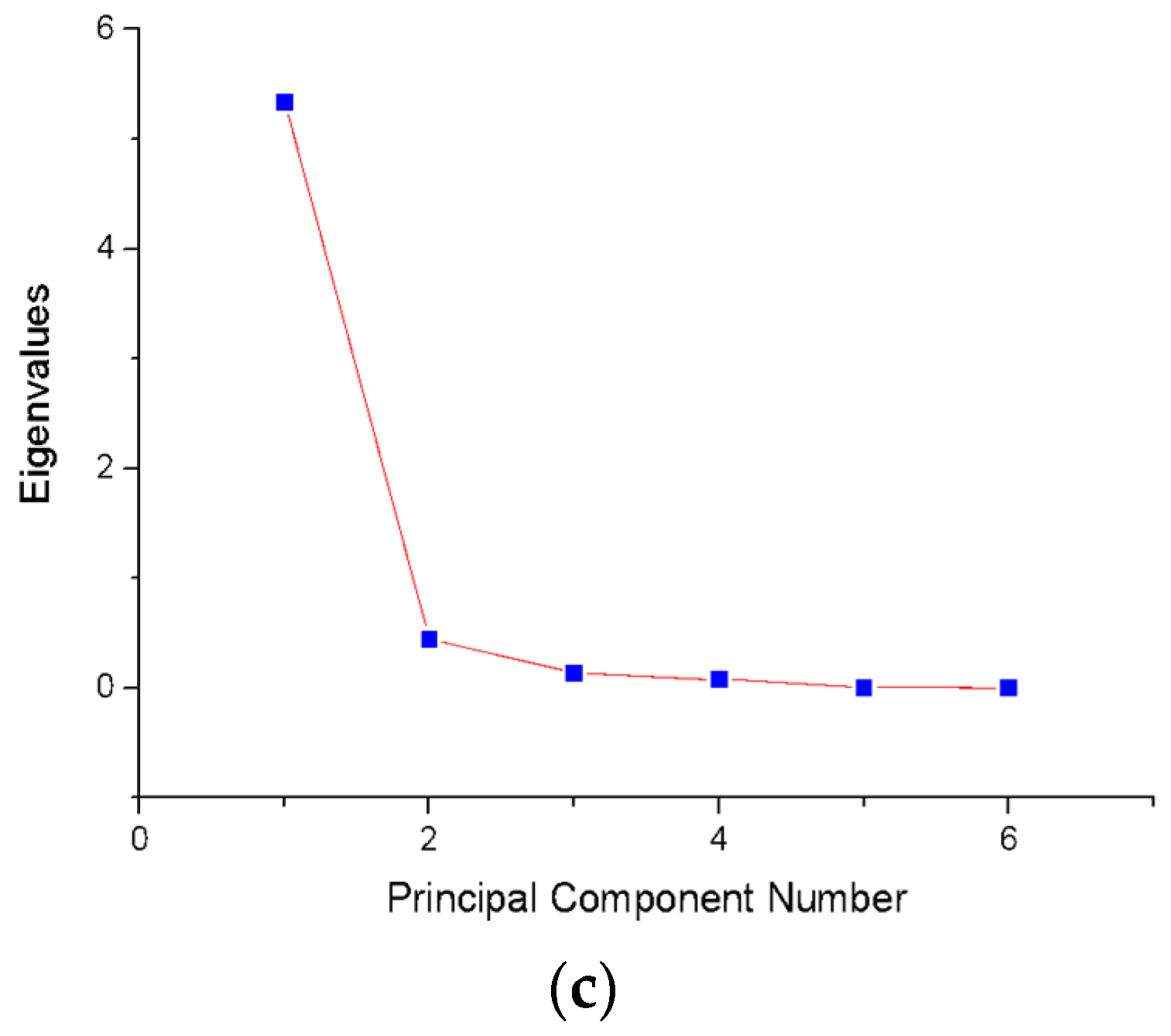
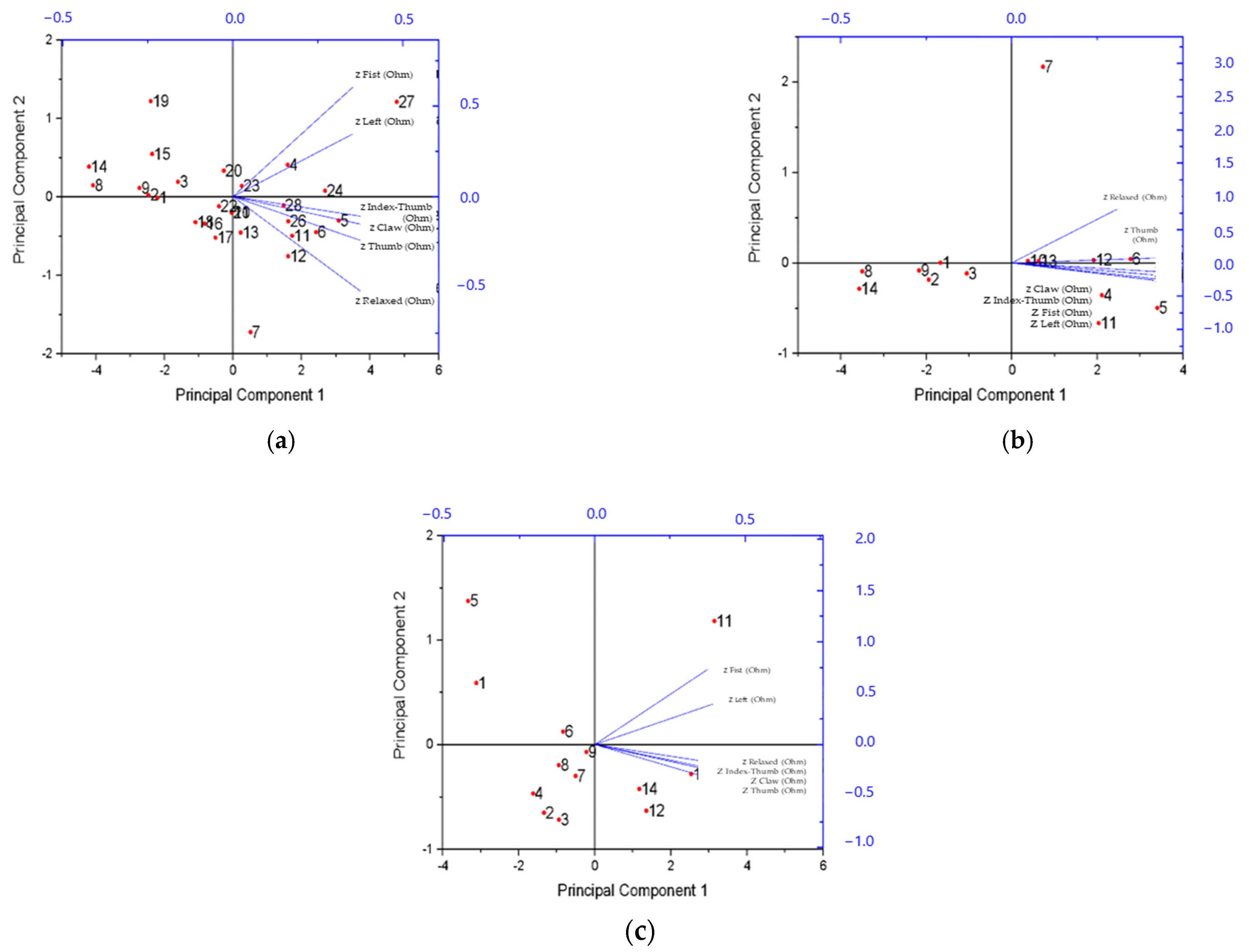
4.2.2. Experimental Results of Dimensionality Reduction by PCA
4.3. Experimental Results of the Predictive Model
Cross-Validation
4.4. Results of the kNN Classification Algorithm and Sensitivity
- Group 1, left gesture and fist;
- Group 2, index-thumb and claw gesture;
- Group 3, thumb gesture and relaxed.
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wu, Y.; Jiang, D.; Liu, X.; Bayford, R.; Demosthenous, A. A Human–Machine Interface Using Electrical Impedance Tomography for Hand Prosthesis Control. IEEE Trans. Biomed. Circuits Syst. 2018, 12, 1322–1333. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ma, G.; Hao, Z.; Wu, X.; Wang, X. An optimal Electrical Impedance Tomography drive pattern for human-computer interaction applications. IEEE Trans. Biomed. Circuits Syst. 2020, 14, 402–411. [Google Scholar] [CrossRef] [PubMed]
- Yao, J.; Chen, H.; Xu, Z.; Huang, J.; Li, J.; Jia, J.; Wu, H. Development of a Wearable Electrical Impedance Tomographic Sensor for Gesture Recognition With Machine Learning. IEEE J. Biomed. Health Inform. 2019, 24, 1550–1556. [Google Scholar] [CrossRef]
- Jiang, D.; Wu, Y.; Demosthenous, A. Hand Gesture Recognition Using Three-Dimensional Electrical Impedance Tomography. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 1554–1558. [Google Scholar] [CrossRef]
- Rezvanigilkilaei, S.; Vefaghnematollahi, S. Using Electrical Impedance Tomography to Control a Robot. Available online: https://publications.waset.org/10003835/using-electrical-impedance-tomography-to-control-a-robot (accessed on 18 June 2022).
- Zhang, Y.; Harrison, C. Tomo: Wearable, Low-Cost Electrical Impedance Tomography for Hand Gesture Recognition. In Proceedings of the 28th Annual ACM Symposium on User Interface Software & Technology, Charlotte, NC, USA, 8–11 November 2015; pp. 167–173. [Google Scholar]
- Dipietro, L.; Sabatini, A.M.; Dario, P. A Survey of Glove-Based Systems and Their Applications. IEEE Trans. Syst. Man Cybern. Part C (Appl. Rev.) 2008, 38, 461–482. [Google Scholar] [CrossRef]
- Kumuda, S.; Mane, P.K. Smart Assistant for Deaf and Dumb Using Flexible Resistive Sensor: Implemented on LabVIEW Platform. In Proceedings of the 2020 International Conference on Inventive Computation Technologies (ICICT), Coimbatore, India, 26–28 February 2020; pp. 994–1000. [Google Scholar] [CrossRef]
- Chen, Y.; Liang, X.; Assaad, M.; Heidari, H. Wearable Resistive-based Gesture-Sensing Interface Bracelet. In Proceedings of the 2019 UK/China Emerging Technologies (UCET), Glasgow, UK, 21–22 August 2019; pp. 1–4. [Google Scholar] [CrossRef] [Green Version]
- Stowe, S.; Adler, A. The Effect of Internal Electrodes on Electrical Impedance Tomography Sensitivity. In Proceedings of the 2020 42nd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Montreal, QC, Canada, 20–24 July 2020; Volume 2020, pp. 1457–1460. [Google Scholar] [CrossRef]
- Grimnes, S.; Martinsen, O.G. Bioimpedance and Bioelectricity Basics, 3rd ed.; Elsevier: London, UK, 2014; Chapter 3. [Google Scholar]
- Bronzino, J.D.; Peterson, D.R. Medical Devices and Human Engineering, 1st ed.; Bronz, J.D., Ed.; CRC Press: Boca Raton, FL, USA, 2014; Chapter 10. [Google Scholar]
- Singh, H.P.; Kumar, P. Developments in the human machine interface technologies and their applications: A review. J. Med. Eng. Technol. 2021, 45, 552–573. [Google Scholar] [CrossRef] [PubMed]
- Rosell Ferrer, F.X. Tomografía de Impedancia Eléctrica Para Aplicaciones Médicas. Ph.D. Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, 1989. [Google Scholar]
- Gabriel, C.; Gabriel, S.; Corthout, E. The dielectric properties of biological tissues: I. Literature survey. Phys. Med. Biol. 1996, 41, 2231–2249. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barnes, F.S.; Greenebaum, B.; Greenebaum, B. Handbook of Biological Effects of Electromagnetic Fields—Two Volume Set; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Nordenström, B. Biologically Closed Electric Circuits: Clinical, Experimental and Theoretical Evidence for an Additional Circulatory System; Princeton University Press: Princeton, NJ, USA, 1983. [Google Scholar]
- Rigaud, B.; Morucci, J.P. Bioelectrical impedance techniques in medicine. Part III: Impedance imaging. First section: General concepts and hardware. Crit. Rev. Biomed. Eng. 1996, 24, 467–597. [Google Scholar] [CrossRef]
- Ackmann, J.J.; Seitz, M.A. Methods of complex impedance measurements in biologic tissue. Crit. Rev. Biomed. Eng. 1984, 11, 281–311. [Google Scholar] [PubMed]
- Cömert, A. The Assessment and Reduction of Motion Artifact in Dry Contact Biopotential Electrodes. Ph.D. Thesis, Tampere University of Technology, Tampere, Finland, 2015. [Google Scholar]
- Holder, D.S. Electrical Impedance Tomography, 1st ed.; Institute of Physics Publishing: Bristol, PA, USA, 2005; Article number 27. [Google Scholar] [CrossRef] [Green Version]
- Gupta, A.K. Application Report Respiration Rate Measurement Based on Impedance Pneumography. Texas Instruments. Application Report, 2011. Available online: https://www.semanticscholar.org/paper/Respiration-Rate-Measurement-Based-on-Impedance-Gupta/c761bc3d0abf54c4d042d9670808344248b7edc3 (accessed on 28 May 2022).
- Yufera, A.; Rueda, A. A method for bioimpedance measure with four- and two-electrode sensor systems. In Proceedings of the 2008 30th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Vancouver, BC, Canada, 20–25 August 2008; Volume 2008, pp. 2318–2321. [Google Scholar] [CrossRef]
- Webster, J.G. Medical Instrumentation: Application and Design, 5th ed.; John Wiley & Sons: New York, NY, USA, 2020. [Google Scholar]
- Chong, Y.L.; Chin, R.K.Y. An Investigation of the Effect of Different Number of Electrodes on EIT Reconstructed Images. In Proceedings of the 2020 IEEE 2nd International Conference on Artificial Intelligence in Engineering and Technology (IICAIET), Kota Kinabalu, Malaysia, 26–27 September 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Mikulka, J.; Dusek, J.; Dedkova, J.; Pařílková, J.; Munsterova, Z. A Fast and Low-cost Measuring System for Electrical Impedance Tomography. In Proceedings of the 2019 PhotonIcs & Electromagnetics Research Symposium—Spring (PIERS-Spring), Rome, Italy, 17–20 June 2019; pp. 3751–3755. [Google Scholar] [CrossRef]
- Ito, T.; Kaneda, N.; Higuchi, Y. Simulation based prior evaluation of 3-D EIT system with a small number of electrodes. In Proceedings of the 2017 56th Annual Conference of the Society of Instrument and Control Engineers of Japan (SICE), Kanazawa, Japan, 19–22 September 2017; pp. 912–915. [Google Scholar] [CrossRef]
- Bagdalkar, P.; Ali, L. Interfacing of light sensor with FPGA using I2C bus. In Proceedings of the 2020 6th International Conference on Advanced Computing and Communication Systems (ICACCS), Coimbatore, India, 6–7 March 2020; pp. 843–846. [Google Scholar] [CrossRef]
- Liu, S.; Cao, R.; Huang, Y.; Ouypornkochagorn, T.; Jia, J. Time Sequence Learning for Electrical Impedance Tomography Using Bayesian Spatiotemporal Priors. IEEE Trans. Instrum. Meas. 2020, 69, 6045–6057. [Google Scholar] [CrossRef] [Green Version]
- Nansheng, P.; Yingling, S.; Changming, J. Research on comprehensive bid evaluation of construction project based on the principal component analysis. In Proceedings of the 2008 4th International Conference on Wireless Communications, Networking and Mobile Computing, Dalian, China, 12–14 October 2008. [Google Scholar]
- Sun, S.; Huang, R. An adaptive k-nearest neighbor algorithm. In Proceedings of the 2010 Seventh International Conference on Fuzzy Systems and Knowledge Discovery, Yantai, China, 10–12 August 2010; Volume 1, pp. 91–94. [Google Scholar] [CrossRef]
- Barreiro, M.; Sánchez, P.; Vera, J.; Viera, M.; Morales, I.; Dell´osa, A.H.; Bertemes-Filho, P.; Simini, F. Multiplexing Error and Noise Reduction in Electrical Impedance Tomography Imaging. Front. Electron. 2022, 3, 848618. [Google Scholar] [CrossRef]

| Parameter | Value |
|---|---|
| Start frequency | 50 kHz |
| Delta frequency | 500 Hz |
| Increment number | 100 |
| Final frequency | 100 kHz |
| Parameter | Value |
|---|---|
| System clock | External clock |
| Output excitation | 1 VPP |
| PGA control | Gain = 1 |
| Calibration impedance | R1 = 2 kΩ |
| Component (PCi) | Eigenvalue | Variance (%) | Accumulated |
|---|---|---|---|
| 1 | 5.178 | 86.29% | 86.29% |
| 2 | 0.413 | 6.89% | 93.18% |
| 3 | 0.301 | 5.03% | 98.20% |
| 4 | 0.0681 | 1.14% | 99.34% |
| 5 | 0.0333 | 0.55% | 99.89% |
| 6 | 0.00654 | 0.11% | 100.00% |
| Component (PCi) | Eigenvalue | Variance (%) | Accumulated |
|---|---|---|---|
| 1 | 5.387 | 89.79% | 89.79% |
| 2 | 0.436 | 7.27% | 97.06% |
| 3 | 0.145 | 2.43% | 99.49% |
| 4 | 0.0215 | 0.36% | 99.85% |
| 5 | 0.00817 | 0.14% | 99.98% |
| 6 | 9.22 × 10−4 | 0.02% | 100.00% |
| Component (PCi) | Eigenvalue | Variance (%) | Accumulated |
|---|---|---|---|
| 1 | 5.3359 | 88.93% | 88.93% |
| 2 | 0.447 | 7.46% | 96.39% |
| 3 | 0.130 | 2.17% | 98.56% |
| 4 | 0.0773 | 1.29% | 99.85% |
| 5 | 0.00479 | 0.08% | 99.93% |
| 6 | 4.02 × 10−3 | 0.07% | 100.00% |
| Measurements | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RedA | 4 AE | 5 AF | 6 AG | 10 BE | 11 BF | 12 BG | 13 BH | 21 DG | 23 EF | 24 EG | 25 EH | 26 FG | 27 FH | 28 GH |
| RedB | 4 AE | 5 AF | 6 AG | 10 BE | 11 BF | 12 BG | 13 BH | - | - | - | - | - | - | - |
| RedC | - | - | - | - | - | - | - | - | - | 24 EG | 25 EH | 26 FG | 27 FH | 28 GH |
| Iteration K | Gesture | Error, RedA | Error, RedB | Error, RedC |
|---|---|---|---|---|
| K = 2 | Z Index-Thumb (Ω) | 0.930 | 0.432 | 0.874 |
| Z Left (Ω) | 0.955 | 0.443 | 0.897 | |
| Z Fist (Ω) | 0.953 | 0.442 | 0.895 | |
| Z Claw (Ω) | 0.934 | 0.433 | 0.877 | |
| Z Relaxed (Ω) | 0.779 | 0.361 | 0.732 | |
| Z Thumb (Ω) | 0.958 | 0.444 | 0.900 | |
| K = 3 | Z Index-Thumb (Ω) | 0.861 | 0.403 | 0.823 |
| Z Left (Ω) | 0.863 | 0.403 | 0.822 | |
| Z Fist (Ω) | 0.861 | 0.402 | 0.819 | |
| Z Claw (Ω) | 0.858 | 0.399 | 0.813 | |
| Z Relaxed (Ω) | 0.836 | 0.389 | 0.790 | |
| Z Thumb (Ω) | 0.858 | 0.399 | 0.809 | |
| K = 4 | Z Index-Thumb (Ω) | 0.846 | 0.392 | 0.795 |
| Z Left (Ω) | 0.868 | 0.403 | 0.815 | |
| Z Fist (Ω) | 0.866 | 0.402 | 0.814 | |
| Z Claw (Ω) | 0.849 | 0.394 | 0.798 | |
| Z Relaxed (Ω) | 0.708 | 0.328 | 0.665 | |
| Z Thumb (Ω) | 0.870 | 0.404 | 0.818 | |
| K = 5 | Z Index-Thumb (Ω) | 0.872 | 0.405 | 0.819 |
| Z Left (Ω) | 0.895 | 0.415 | 0.841 | |
| Z Fist (Ω) | 0.893 | 0.414 | 0.839 | |
| Z Claw (Ω) | 0.875 | 0.406 | 0.822 | |
| Z Relaxed (Ω) | 0.730 | 0.339 | 0.686 | |
| Z Thumb (Ω) | 0.897 | 0.416 | 0.843 | |
| K = 6 | Z Index-Thumb (Ω) | 0.846 | 0.392 | 0.795 |
| Z Left (Ω) | 0.868 | 0.403 | 0.815 | |
| Z Fist (Ω) | 0.866 | 0.402 | 0.814 | |
| Z Claw (Ω) | 0.849 | 0.394 | 0.798 | |
| Z Relaxed (Ω) | 0.708 | 0.328 | 0.665 | |
| Z Thumb (Ω) | 0.870 | 0.404 | 0.818 |
| Z Index- Thumb (Ω) | Z Left (Ω) | Z Fist (Ω) | Z Claw (Ω) | Z Relaxed (Ω) | Z Thumb (Ω) | ||
|---|---|---|---|---|---|---|---|
| Red. A | x | 416.82 | 420.37 | 421.56 | 418.29 | 364.31 | 364.38 |
| δ | 13.09 | 20.38 | 24.48 | 14.08 | 12.39 | 10.79 | |
| Red. B | x | 414.98 | 415.59 | 412.44 | 416.54 | 363.20 | 362.90 |
| δ | 15.24 | 18.93 | 18.31 | 16.79 | 15.01 | 11.39 | |
| Red. C | x | 418.67 | 425.15 | 430.68 | 420.05 | 365.41 | 365.86 |
| δ | 10.80 | 21.32 | 27.02 | 11.10 | 9.53 | 10.37 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vaquero-Gallardo, N.; Martínez-García, H. Electrical Impedance Tomography for Hand Gesture Recognition for HMI Interaction Applications. J. Low Power Electron. Appl. 2022, 12, 41. https://doi.org/10.3390/jlpea12030041
Vaquero-Gallardo N, Martínez-García H. Electrical Impedance Tomography for Hand Gesture Recognition for HMI Interaction Applications. Journal of Low Power Electronics and Applications. 2022; 12(3):41. https://doi.org/10.3390/jlpea12030041
Chicago/Turabian StyleVaquero-Gallardo, Noelia, and Herminio Martínez-García. 2022. "Electrical Impedance Tomography for Hand Gesture Recognition for HMI Interaction Applications" Journal of Low Power Electronics and Applications 12, no. 3: 41. https://doi.org/10.3390/jlpea12030041
APA StyleVaquero-Gallardo, N., & Martínez-García, H. (2022). Electrical Impedance Tomography for Hand Gesture Recognition for HMI Interaction Applications. Journal of Low Power Electronics and Applications, 12(3), 41. https://doi.org/10.3390/jlpea12030041







