A Network Simulator for the Estimation of Bandwidth Load and Latency Created by Heterogeneous Spiking Neural Networks on Neuromorphic Computing Communication Networks †
Abstract
:1. Introduction
2. Background and Motivation
2.1. Neuromorphic Computing Systems
2.1.1. Neural and Synaptic Modeling by the CUs
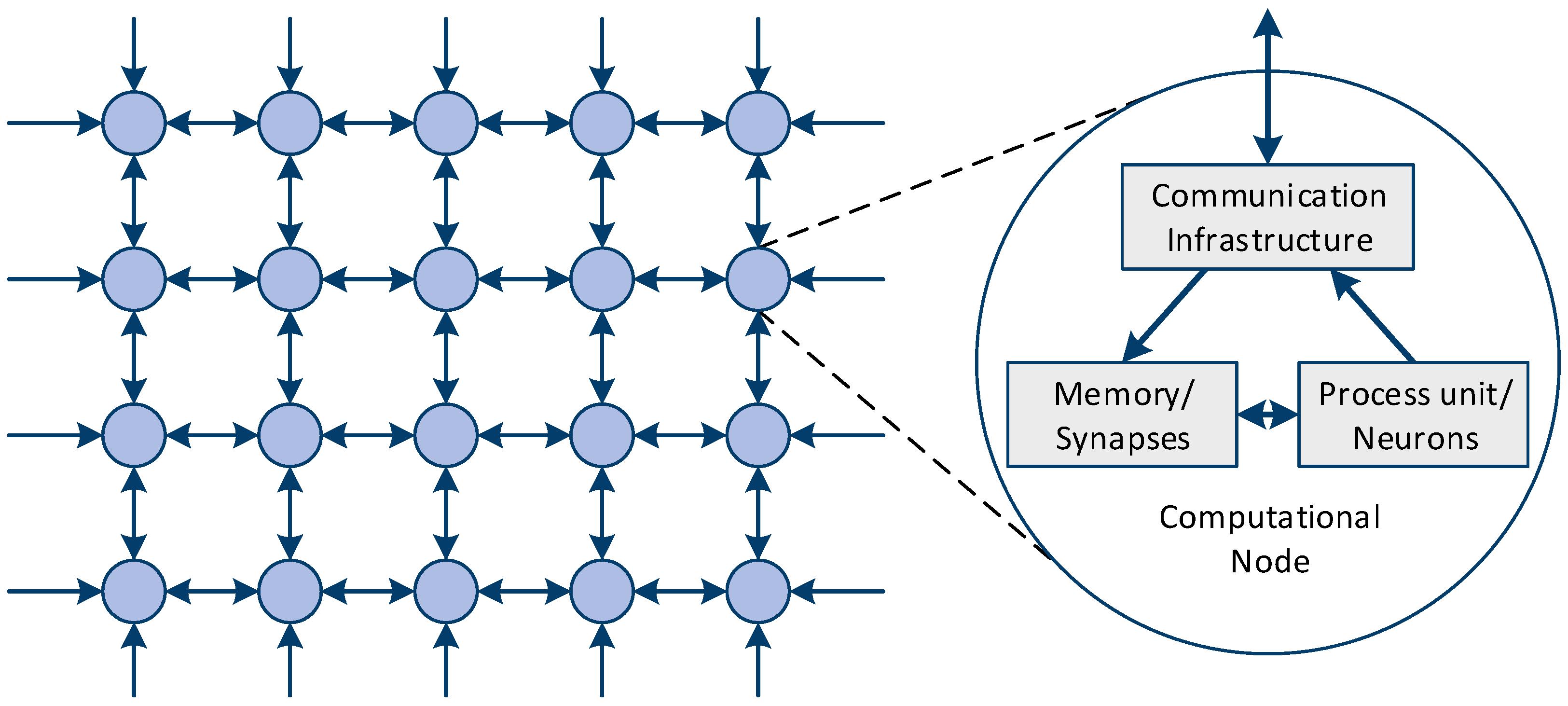
2.1.2. Interconnect Design and Spike Communication
2.2. Motivation and Comparable Work
3. Neuromorphic Communication Network Simulator
3.1. High-Level Simulator Description
3.2. Neural Network Generation
- Netlist-based simulation.
- Connectivity matrix simulation.
- Location-based connectivity simulation.
3.2.1. Netlist-Based Simulation
3.2.2. Connectivity Matrix Simulation
3.2.3. Location Based Connectivity
3.3. Neuron Mapping
4. Results
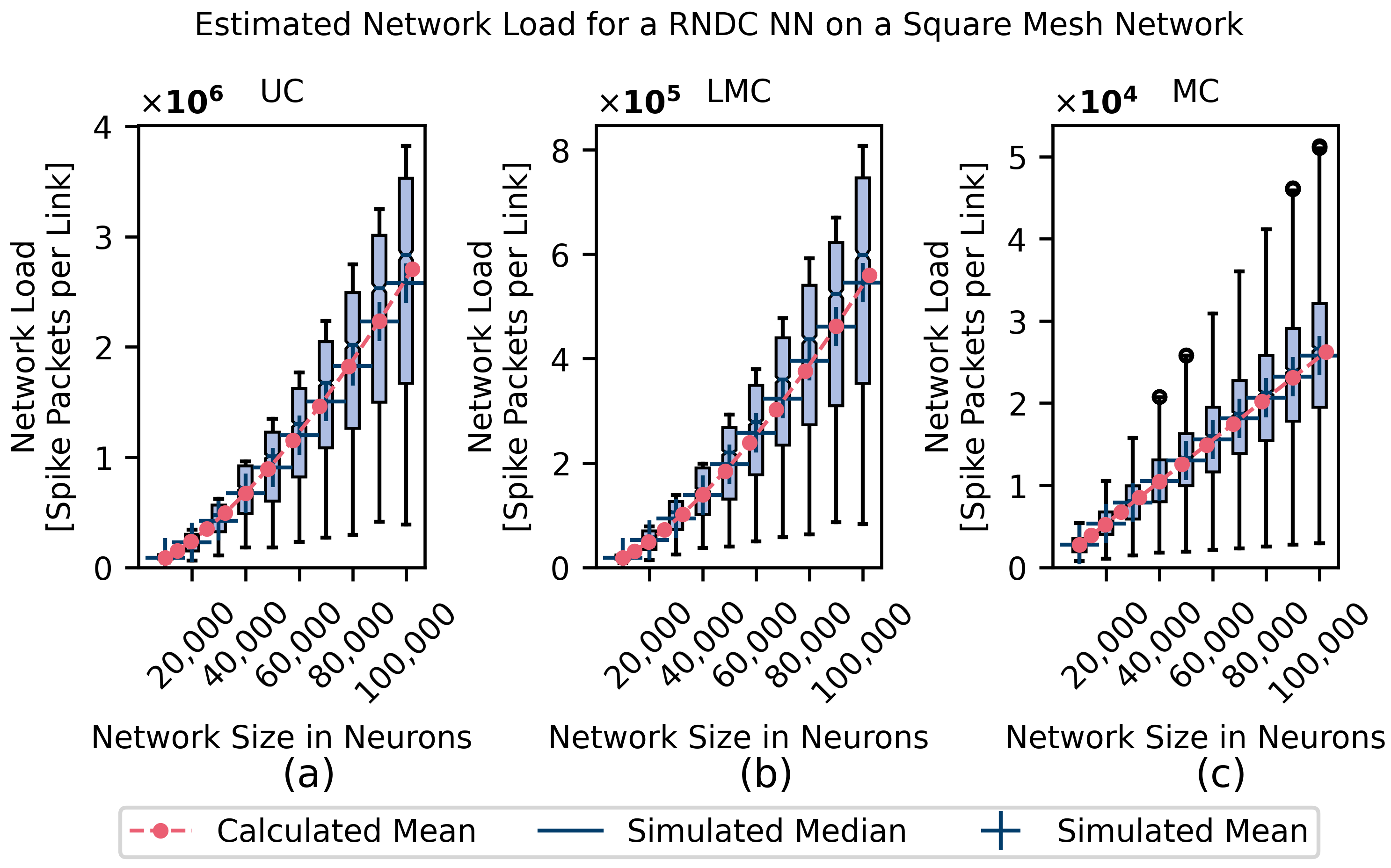
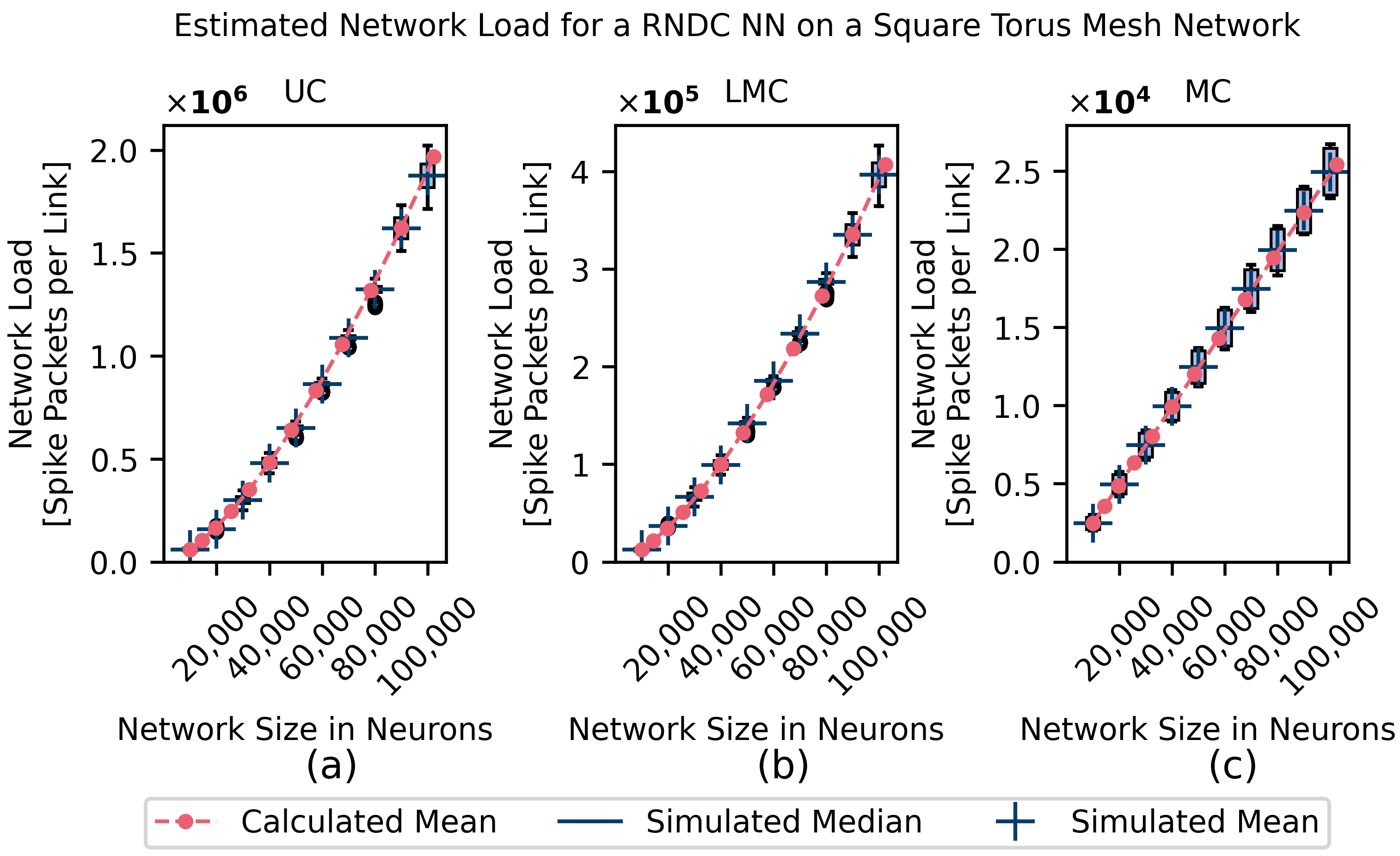
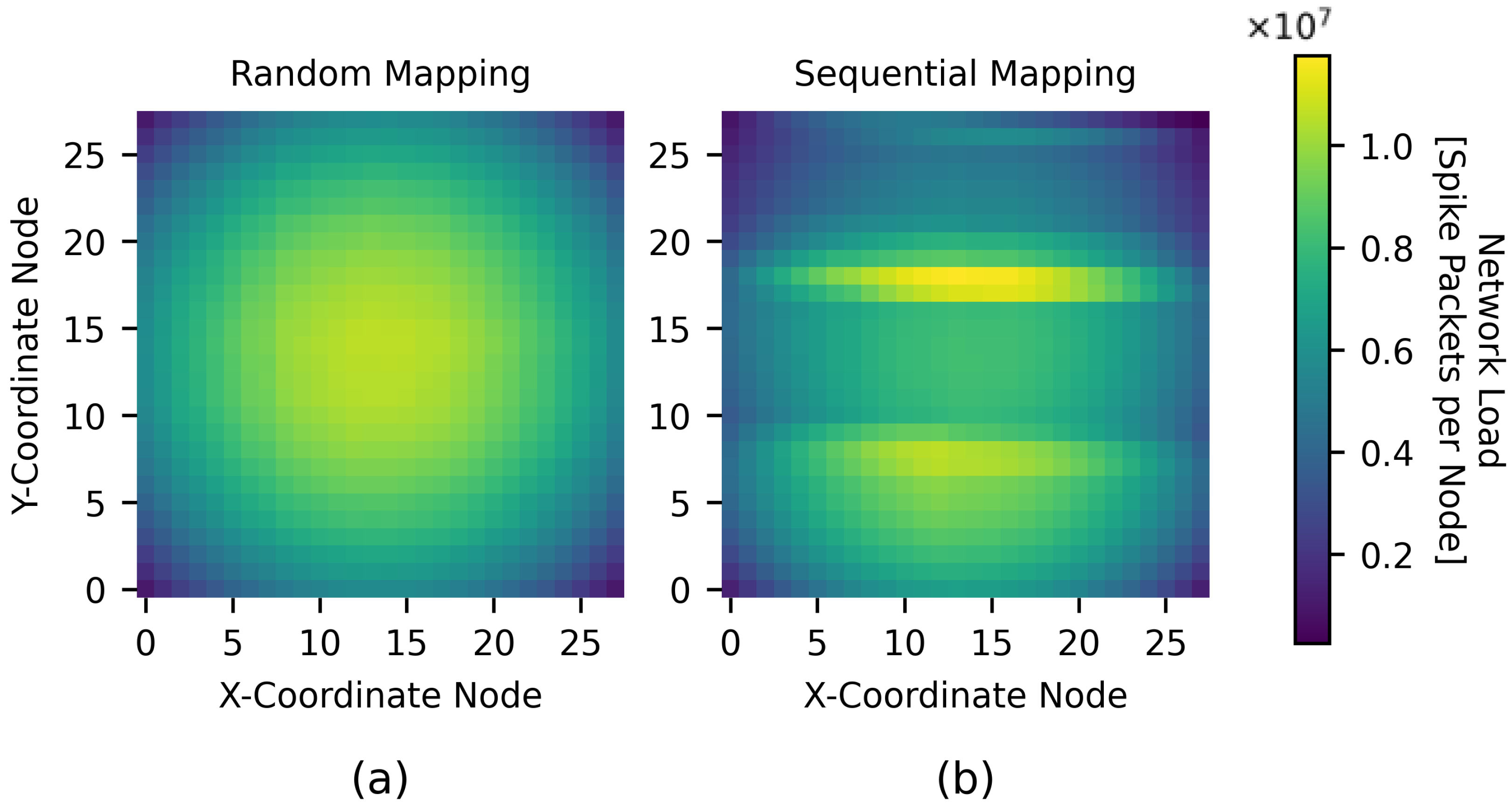
4.1. Homogeneous Connectivity Model Simulations
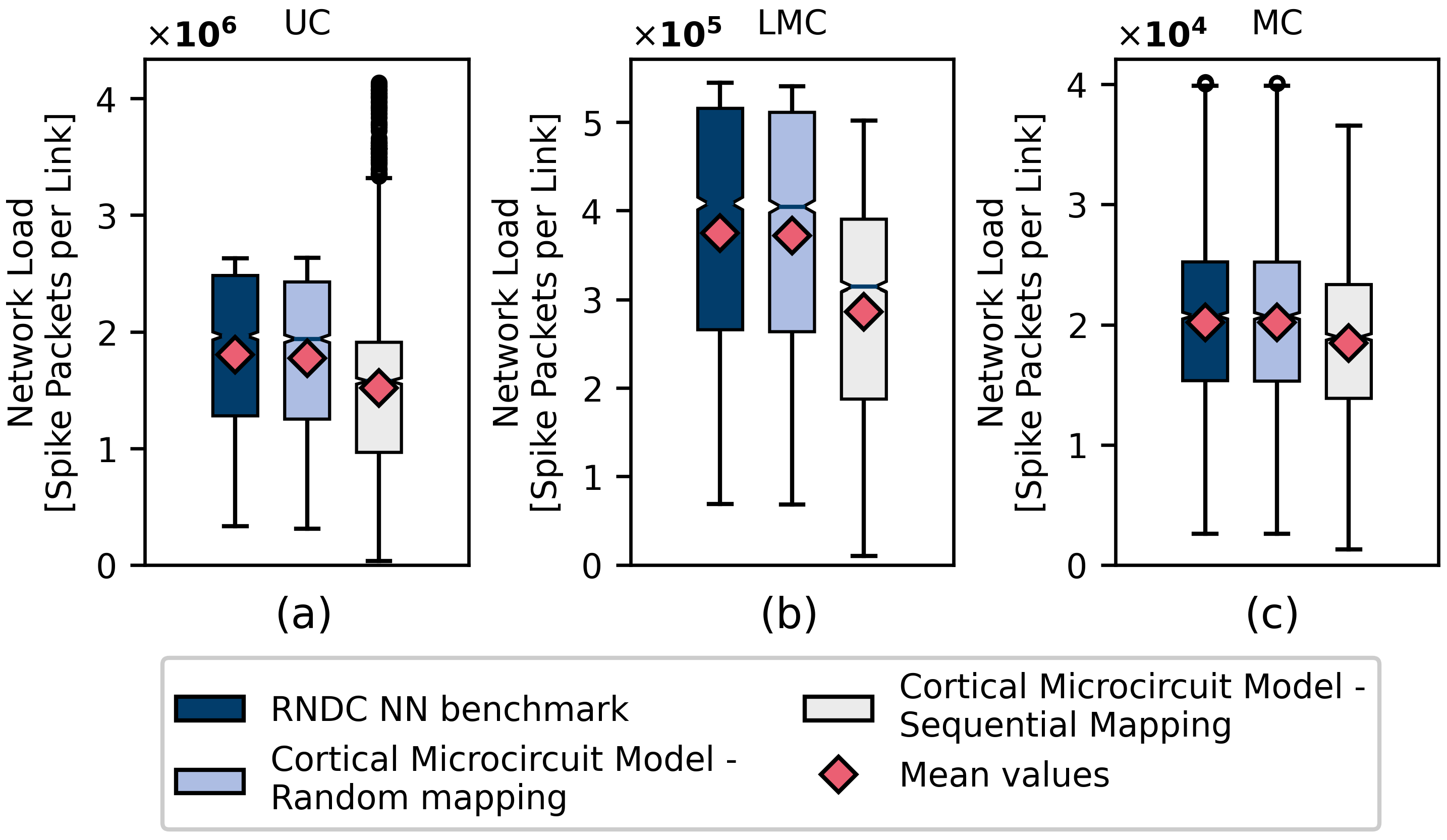
4.2. Heterogeneous Connectivity Model Simulations
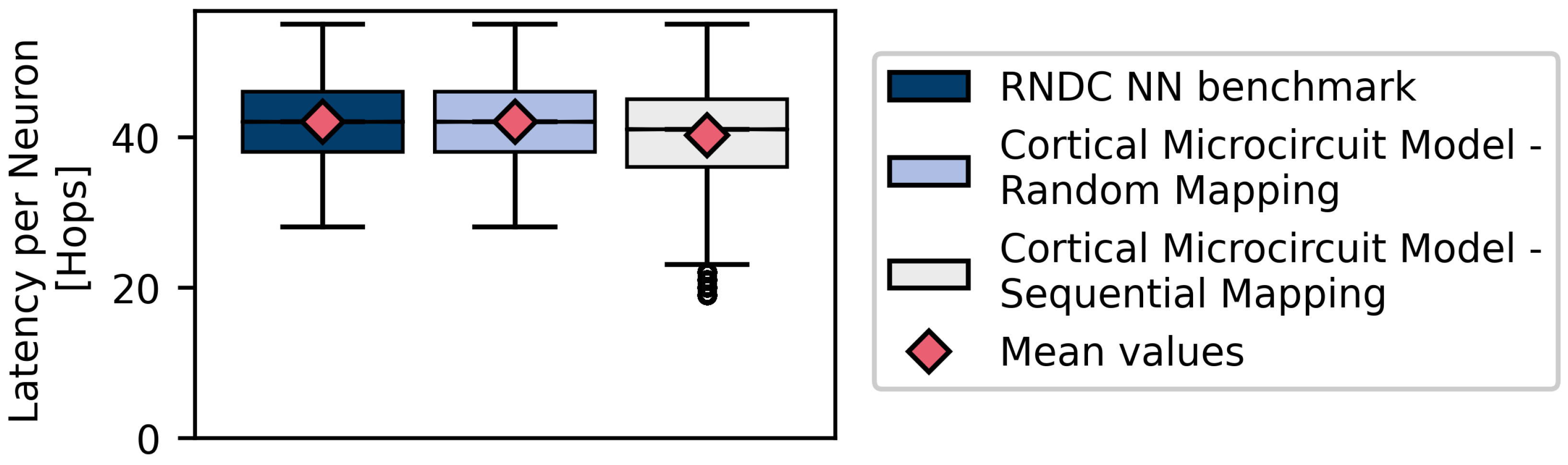
4.2.1. Cortical Microcircuit Model
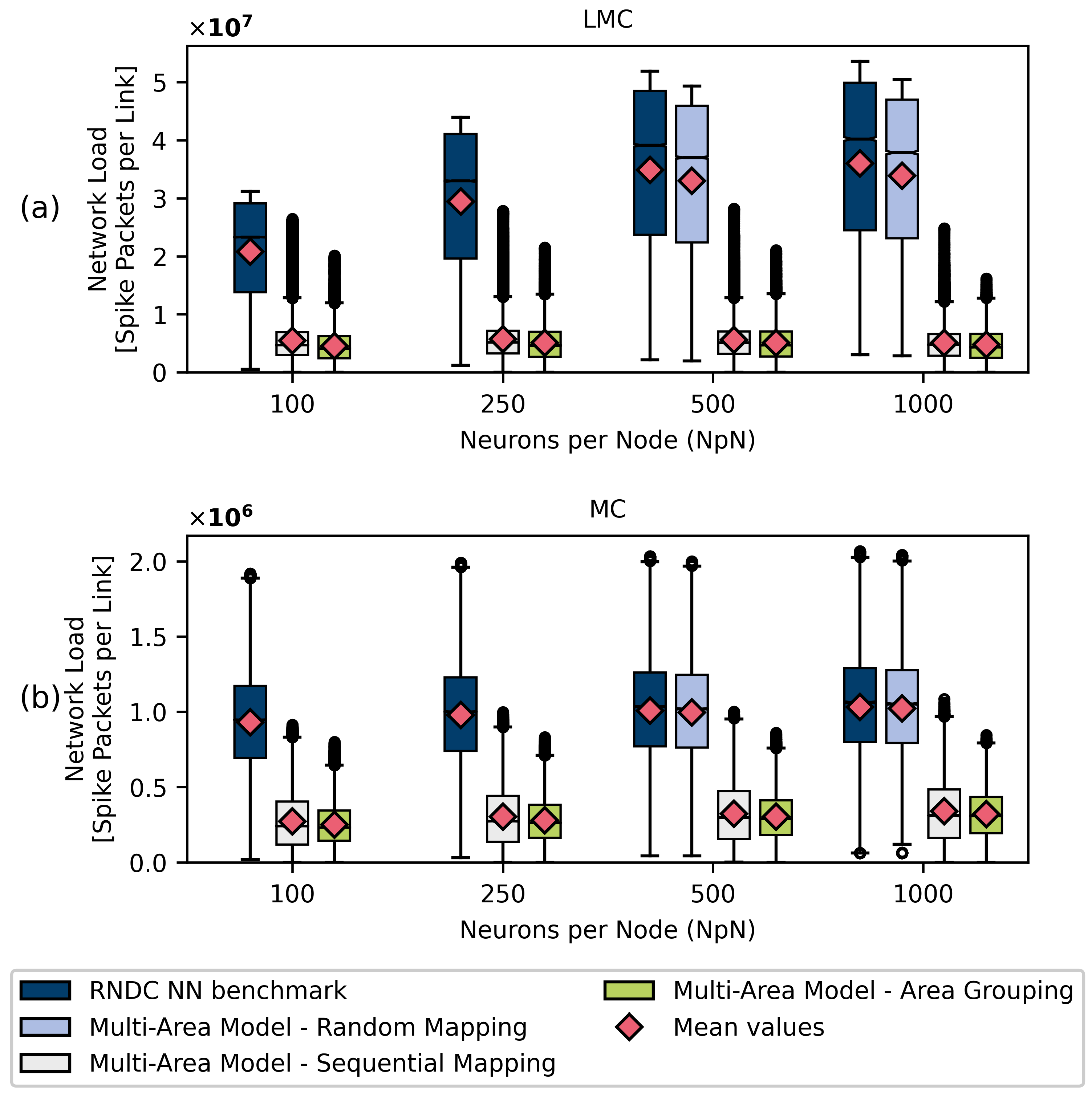
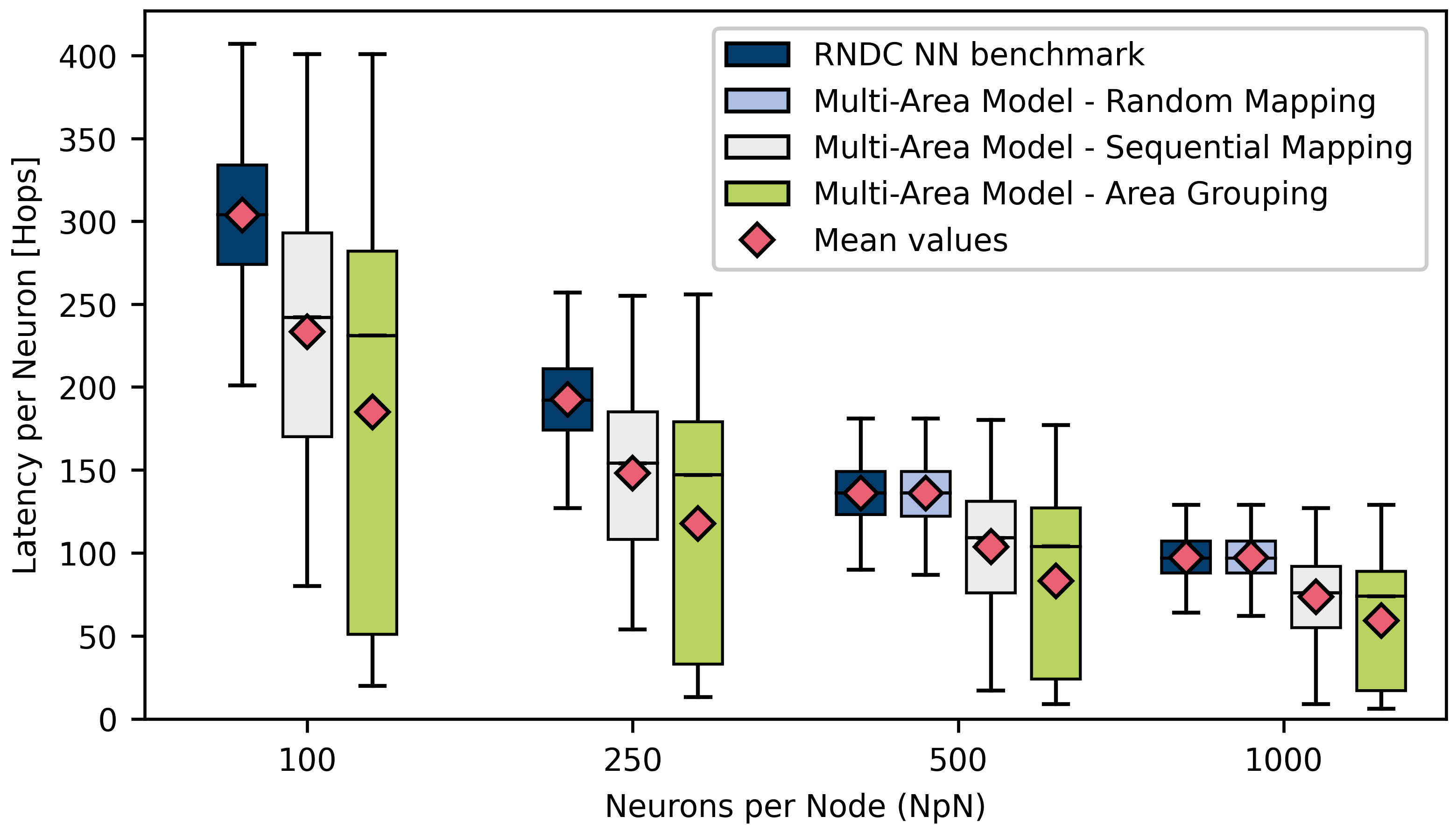
4.2.2. Multi-Area Model
5. Summary and Future Work
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ACA | Advanced Computing Architectures |
| AER | Address event representation |
| BC | Broadcast |
| BNN | Biological neural network |
| CAM | Content addressable memory |
| CM | Connectivity matrix |
| CU | Computational unit |
| FR | Firing rate |
| LDFR | Longest dimension first routing |
| LMC | Local multicast |
| LUT | Lookup table |
| MC | Multicast |
| NC | Neuromorphic computing |
| NN | Neural network |
| NpN | Neurons per node |
| RNDC NN | Randomly connected neural network |
| SpN | Synapses per neuron |
| UC | Unicast |
| VLSI | Very large scale integration |
References
- Akopyan, F.; Sawada, J.; Cassidy, A.; Alvarez-Icaza, R.; Arthur, J.; Merolla, P.; Imam, N.; Nakamura, Y.; Datta, P.; Nam, G.-J.; et al. TrueNorth: Design and Tool Flow of a 65 MW 1 Million Neuron Programmable Neurosynaptic Chip. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2015, 34, 1537–1557. [Google Scholar] [CrossRef]
- Furber, S.B.; Galluppi, F.; Temple, S.; Plana, L.A. The SpiNNaker Project. Proc. IEEE 2014, 102, 652–665. [Google Scholar] [CrossRef]
- Schemmel, J.; Briiderle, D.; Griibl, A.; Hock, M.; Meier, K.; Millner, S. A Wafer-Scale Neuromorphic Hardware System for Large-Scale Neural Modeling. In Proceedings of the 2010 IEEE International Symposium on Circuits and Systems, Paris, France, 30 May–2 June 2010; pp. 1947–1950. [Google Scholar]
- Benjamin, B.V.; Gao, P.; McQuinn, E.; Choudhary, S.; Chandrasekaran, A.R.; Bussat, J.-M.; Alvarez-Icaza, R.; Arthur, J.V.; Merolla, P.A.; Boahen, K. Neurogrid: A Mixed-Analog-Digital Multichip System for Large-Scale Neural Simulations. Proc. IEEE 2014, 102, 699–716. [Google Scholar] [CrossRef]
- Meier, K. A Mixed-Signal Universal Neuromorphic Computing System. In Proceedings of the 2015 IEEE International Electron Devices Meeting (IEDM), Washington, DC, USA, 7–9 December 2015; pp. 4–6. [Google Scholar]
- Forschungszentrum Jülich. Advanced Computing Architectures (ACA) towards Multi-Scale Natural-Density Neuromorphic Computing. Available online: https://www.fz-juelich.de/aca/EN/Home/home_node.html (accessed on 31 January 2022).
- Kleijnen, R.; Robens, M.; Schiek, M.; van Waasen, S. A Network Simulator for the Estimation of Bandwidth Load and Latency Created by Heterogeneous Spiking Neural Networks on Neuromorphic Computing Communication Networks. In Proceedings of the 2021 IEEE 14th International Symposium on Embedded Multicore/Many-core Systems-on-Chip (MCSoC), Singapore, 20–23 December 2021; pp. 320–327. [Google Scholar] [CrossRef]
- Schmidt, M.; Bakker, R.; Hilgetag, C.C.; Diesmann, M.; van Albada, S.J. Multi-Scale Account of the Network Structure of Macaque Visual Cortex. Brain Struct. Funct. 2018, 223, 1409–1435. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Young, A.R.; Dean, M.E.; Plank, J.S.; Rose, G.S. A Review of Spiking Neuromorphic Hardware Communication Systems. IEEE Access 2019, 7, 135606–135620. [Google Scholar] [CrossRef]
- Thakur, C.S.; Molin, J.L.; Cauwenberghs, G.; Indiveri, G.; Kumar, K.; Qiao, N.; Schemmel, J.; Wang, R.; Chicca, E.; Olson Hasler, J.; et al. Large-Scale Neuromorphic Spiking Array Processors: A Quest to Mimic the Brain. Front. Neurosci. 2018, 12, 891. [Google Scholar] [CrossRef] [PubMed]
- Vainbrand, D.; Ginosar, R. Scalable Network-on-Chip Architecture for Configurable Neural Networks. Microprocessors and Microsystems 2011, 35, 152–166. [Google Scholar] [CrossRef]
- Kauth, K.; Stadtmann, T.; Brandhofer, R.; Sobhani, V.; Gemmeke, T. Communication Architecture Enabling 100x Accelerated Simulation of Biological Neural Networks. In Proceedings of the Workshop on System-Level Interconnect: Problems and Pathfinding Workshop, San Diego, CA, USA, 5 November 2020; pp. 1–8. [Google Scholar]
- Potjans, T.C.; Diesmann, M. The Cell-Type Specific Cortical Microcircuit: Relating Structure and Activity in a Full-Scale Spiking Network Model. Cereb. Cortex 2014, 24, 785–806. [Google Scholar] [CrossRef] [PubMed]
- Navaridas, J.; Luján, M.; Plana, L.A.; Temple, S.; Furber, S.B. SpiNNaker: Enhanced Multicast Routing. Parallel Comput. 2015, 45, 49–66. [Google Scholar] [CrossRef]
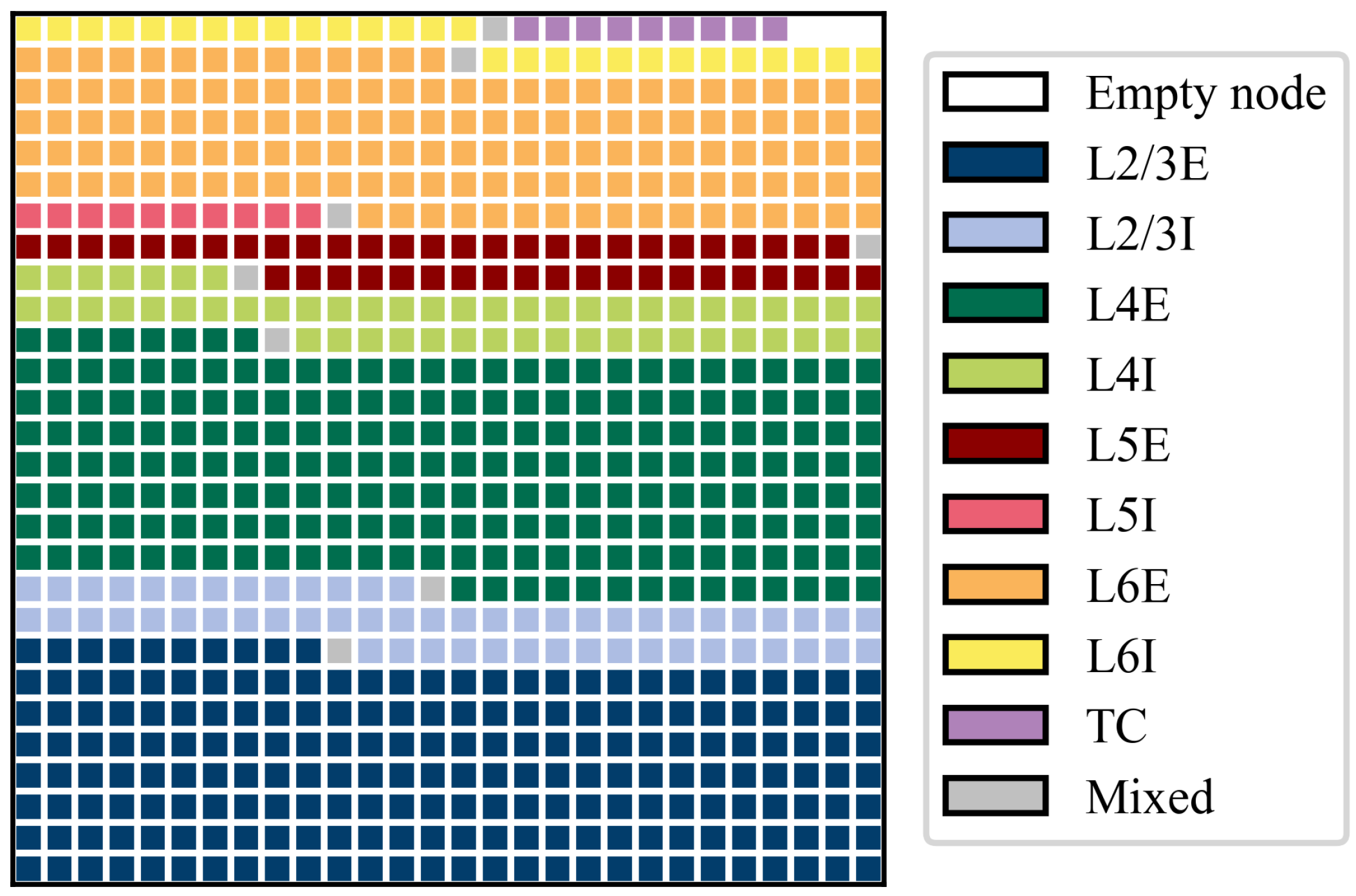
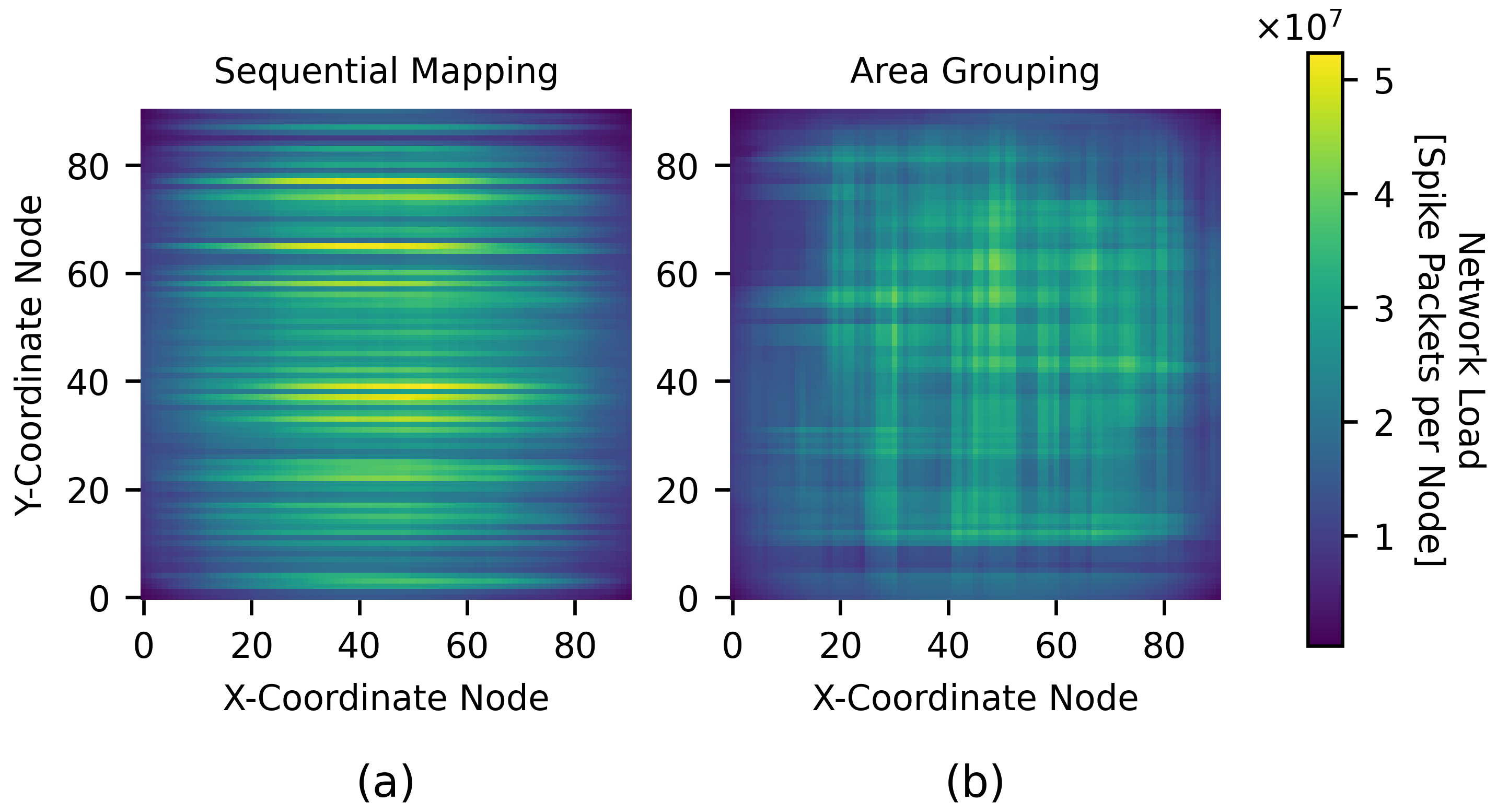
| Source Population (X) | Number of Neurons | Target Population (Y) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| L2/3E | L2/3I | L4E | L4I | L5E | L5I | L6E | L6I | ||
| L2/3E | 20,683 | 0.1009 | 0.1346 | 0.0077 | 0.0691 | 0.1004 | 0.0548 | 0.0156 | 0.0364 |
| L2/3I | 5834 | 0.1689 | 0.1371 | 0.0059 | 0.0029 | 0.0622 | 0.0269 | 0.0066 | 0.0010 |
| L4E | 21,915 | 0.0437 | 0.0316 | 0.0497 | 0.0794 | 0.0505 | 0.0257 | 0.0211 | 0.0034 |
| L4I | 5479 | 0.0818 | 0.0515 | 0.1350 | 0.1597 | 0.0057 | 0.0022 | 0.0166 | 0.0005 |
| L5E | 4850 | 0.0323 | 0.0755 | 0.0067 | 0.0033 | 0.0831 | 0.0600 | 0.0572 | 0.0277 |
| L5I | 1065 | 0.0 | 0.0 | 0.0003 | 0.0 | 0.3726 | 0.3158 | 0.0197 | 0.0080 |
| L6E | 14,395 | 0.0076 | 0.0042 | 0.0453 | 0.1057 | 0.0204 | 0.0086 | 0.0396 | 0.0658 |
| L6I | 2948 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.2252 | 0.1443 |
| TC | 902 | 0.0 | 0.0 | 0.0983 | 0.0619 | 0.0 | 0.0 | 0.0512 | 0.0196 |
| Neurons per Node | |||||
|---|---|---|---|---|---|
| 100 | 250 | 500 | 1000 | ||
| RNDC Benchmark | Average | 303.808 | 192.428 | 135.945 | 97.2743 |
| Maximum | 407 | 257 | 181 | 129 | |
| Randomly Mapped | Average | 135.828 | 97.2132 | ||
| Multi-Area Model | Maximum | 181 | 129 | ||
| Sequentially Mapped | Average | 233.358 | 147.889 | 103.895 | 73.5825 |
| Multi-Area Model | Maximum | 401 | 255 | 180 | 127 |
| Grouped Areas | Average | 184.783 | 117.5 | 83.3113 | 59.1662 |
| Multi-Area Model | Maximum | 401 | 256 | 177 | 129 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kleijnen, R.; Robens, M.; Schiek, M.; van Waasen, S. A Network Simulator for the Estimation of Bandwidth Load and Latency Created by Heterogeneous Spiking Neural Networks on Neuromorphic Computing Communication Networks. J. Low Power Electron. Appl. 2022, 12, 23. https://doi.org/10.3390/jlpea12020023
Kleijnen R, Robens M, Schiek M, van Waasen S. A Network Simulator for the Estimation of Bandwidth Load and Latency Created by Heterogeneous Spiking Neural Networks on Neuromorphic Computing Communication Networks. Journal of Low Power Electronics and Applications. 2022; 12(2):23. https://doi.org/10.3390/jlpea12020023
Chicago/Turabian StyleKleijnen, Robert, Markus Robens, Michael Schiek, and Stefan van Waasen. 2022. "A Network Simulator for the Estimation of Bandwidth Load and Latency Created by Heterogeneous Spiking Neural Networks on Neuromorphic Computing Communication Networks" Journal of Low Power Electronics and Applications 12, no. 2: 23. https://doi.org/10.3390/jlpea12020023
APA StyleKleijnen, R., Robens, M., Schiek, M., & van Waasen, S. (2022). A Network Simulator for the Estimation of Bandwidth Load and Latency Created by Heterogeneous Spiking Neural Networks on Neuromorphic Computing Communication Networks. Journal of Low Power Electronics and Applications, 12(2), 23. https://doi.org/10.3390/jlpea12020023







