A Case for Security-Aware Design-Space Exploration of Embedded Systems
Abstract
1. Introduction
2. Design-Space Exploration
2.1. Multi-Objective Optimization
2.2. Search for Pareto Optimal Solutions
- The evaluation of a single design point using the fitness function(s) regarding all the objectives in question like system performance, power/energy consumption and so on. These evaluations are usually based on measurements using real systems or predictions from either analytical models or simulation models [2].
- The search strategy for navigating through and covering the design space during the DSE process. Such search strategies can be based on exact, but typically unscalable, methods that guarantee finding the optimal solution(s). These exact methods can, for example, be implemented using integer linear programming (ILP) solutions (e.g., References [6,7]) or branch & bound algorithms (e.g., Reference [8]). Alternatively, so-called meta-heurisics, such as genetic algorithms (GA) or simulated annealing, can be used to search the design space for optimal solutions. They only perform a finite number of design point evaluations, and can thus handle larger design spaces. However, there is no guarantee that the global optimum will be found using meta-heuristics, and therefore the result can be a local optimum within the design space. GA-based DSE has been widely studied in the domain of system-level embedded design (e.g., References [9,10,11,12]) and has demonstrated to yield good results.
3. Towards Security-Aware, System-Level DSE
3.1. Assumptions
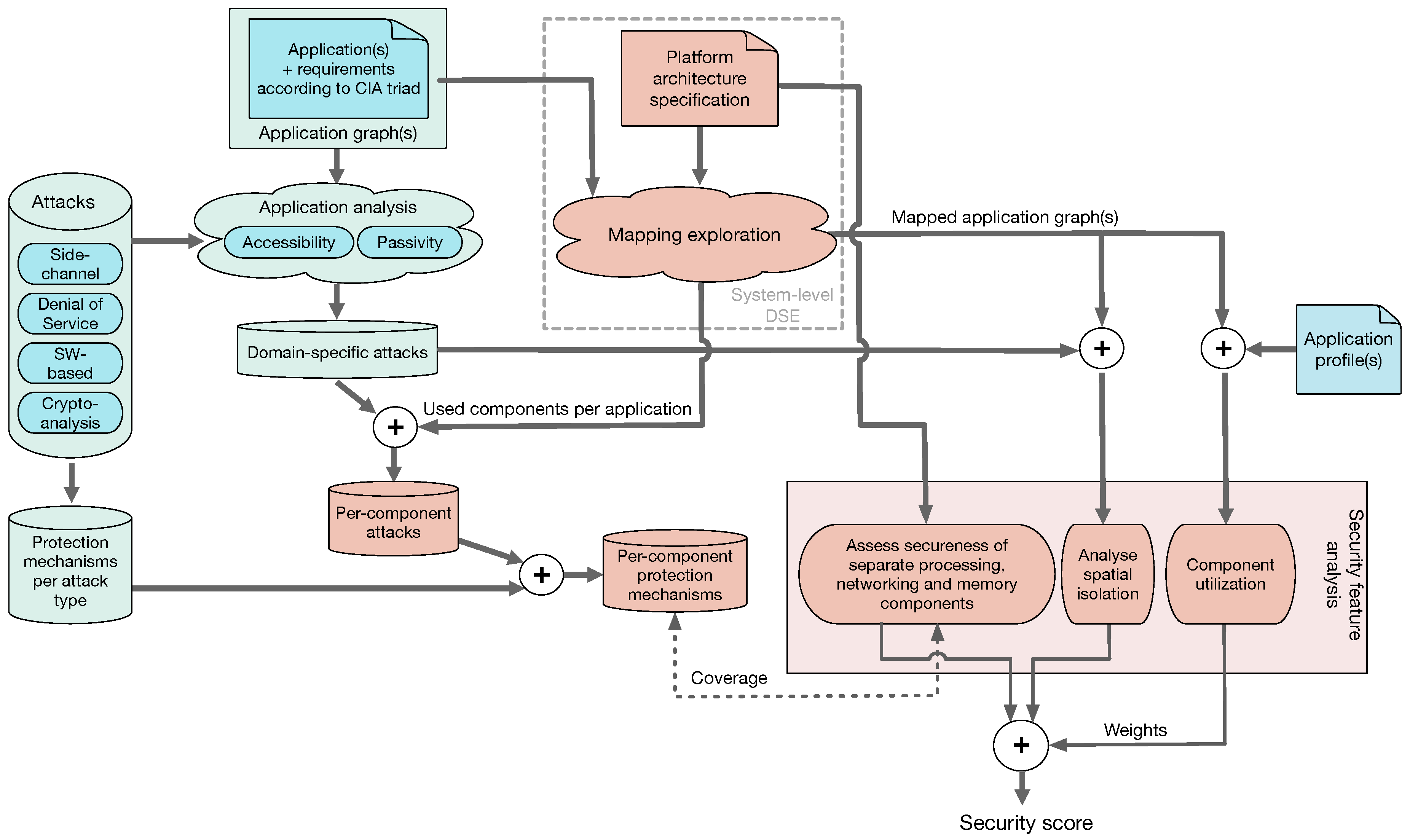
3.2. A Multifaceted, Scoring-Based Methodology for Secureness Quantification
3.3. Scoring the Security of Design Instances
4. Related Work
5. Conclusions
Funding
Conflicts of Interest
References
- Keutzer, K.; Newton, A.; Rabaey, J.; Sangiovanni-Vincentelli, A. System-level design: Orthogonalization of concerns and platform-based design. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2000, 19, 1523–1543. [Google Scholar] [CrossRef]
- Pimentel, A.D. Exploring Exploration: A Tutorial Introduction to Embedded Systems Design Space Exploration. IEEE Des. Test 2017, 34, 77–90. [Google Scholar] [CrossRef]
- Singh, A.K.; Shafique, M.; Kumar, A.; Henkel, J. Mapping on multi/many-core systems: Survey of current and emerging trends. In Proceedings of the 2013 50th ACM/EDAC/IEEE Design Automation Conference (DAC), Austin, TX, USA, 29 May–7 June 2013; pp. 1–10. [Google Scholar]
- Ravi, S.; Raghunathan, A.; Kocher, P.; Hattangady, S. Security in embedded systems: Design challenges. ACM Trans. Embed. Comput. Syst. (TECS) 2004, 4, 461–491. [Google Scholar] [CrossRef]
- Gries, M. Methods for evaluating and covering the design space during early design development. Integration 2004, 38, 131–183. [Google Scholar] [CrossRef]
- Niemann, R.; Marwedel, P. An Algorithm for Hardware/Software Partitioning Using Mixed Integer Linear Programming. Des. Autom. Embed. Syst. 1997, 2, 165–193. [Google Scholar] [CrossRef]
- Lukasiewycz, M.; Glass, M.; Haubelt, C.; Teich, J. Efficient symbolic multi-objective design space exploration. In Proceedings of the 2008 Asia and South Pacific Design Automation Conference, Seoul, Korea, 21–24 March 2008; pp. 691–696. [Google Scholar]
- Padmanabhan, S.; Chen, Y.; Chamberlain, R.D. Optimal design-space exploration of streaming applications. In Proceedings of the ASAP 2011-22nd IEEE International Conference on Application-specific Systems, Architectures and Processors, Santa Monica, CA, USA, 11–14 September 2011; pp. 227–230. [Google Scholar]
- Palesi, M.; Givargis, T. Multi-objective Design Space Exploration Using Genetic Algorithms. In Proceedings of the CODES02: 10th International Symposium on Hardware/Software Codesign, Estes Park, CO, USA, 6–8 May 2002; pp. 67–72. [Google Scholar]
- Erbas, C.; Cerav-Erbas, S.; Pimentel, A.D. Multiobjective Optimization and Evolutionary Algorithms for the Application Mapping Problem in Multiprocessor System-on-Chip Design. IEEE Trans. Evol. Comput. 2006, 10, 358–374. [Google Scholar] [CrossRef]
- Thompson, M.; Pimentel, A.D. Exploiting Domain Knowledge in System-level MPSoC Design Space Exploration. J. Syst. Archit. 2013, 59, 351–360. [Google Scholar] [CrossRef]
- Quan, W.; Pimentel, A.D. Towards Exploring Vast MPSoC Mapping Design Spaces using a Bias-Elitist Evolutionary Approach. In Proceedings of the 2014 17th Euromicro Conference on Digital System Design, Verona, Italy, 27–29 August 2014; pp. 655–658. [Google Scholar]
- Ravi, S.; Raghunathan, A.; Chakradhar, S. Tamper resistance mechanisms for secure embedded systems. In Proceedings of the 17th International Conference on VLSI Design. Proceedings, Mumbai, India, 9 January 2004; pp. 605–611. [Google Scholar] [CrossRef]
- Yang, B.; Wu, K.; Karri, R. Scan based side channel attack on dedicated hardware implementations of Data Encryption Standard. In Proceedings of the 2004 International Conferce on Test, Charlotte, NC, USA, 26–28 October 2004; pp. 339–344. [Google Scholar] [CrossRef]
- Papp, D.; Ma, Z.; Buttyan, L. Embedded systems security: Threats, vulnerabilities, and attack taxonomy. In Proceedings of the 2015 13th Annual Conference on Privacy, Security and Trust (PST), Izmir, Turkey, 21–23 July 2015; pp. 145–152. [Google Scholar] [CrossRef]
- Koopman, P. Embedded systems security. IEEE Comput. 2004, 37, 145–152. [Google Scholar] [CrossRef]
- Swenson, C. Modern Cryptanalysis: Techniques for Advanced Code Breaking; Wiley Publishing: Hoboken, NJ, USA, 2008. [Google Scholar]
- Pimentel, A.D.; Erbas, C.; Polstra, S. A Systematic Approach to Exploring Embedded System Architectures at Multiple Abstraction Levels. IEEE Trans. Comput. 2006, 55, 99–112. [Google Scholar] [CrossRef]
- Erbas, C.; Pimentel, A.D.; Thompson, M.; Polstra, S. A Framework for System-level Modeling and Simulation of Embedded Systems Architectures. EURASIP J. Embed. Syst. 2007, 2007, 082123. [Google Scholar] [CrossRef]
- Mohanty, S.; Prasanna, V.K.; Neema, S.; Davis, J. Rapid Design Space Exploration of Heterogeneous Embedded Systems Using Symbolic Search and Multi-granular Simulation. ACM SIGPLAN Not. 2002, 37, 18–27. [Google Scholar] [CrossRef]
- Mariani, G.; Brankovic, A.; Palermo, G.; Jovic, J.; Zaccaria, V.; Silvano, C. A correlation-based design space exploration methodology for multi-processor systems-on-chip. In Proceedings of the Proc. of the Design Automation Conference (DAC), Anaheim, CA, USA, 13–18 June 2010; pp. 120–125. [Google Scholar]
- Jia, Z.J.; Bautista, T.; Núñez, A.; Thompson, M.; Pimentel, A.D. A System-level Infrastructure for Multi-dimensional MP-SoC Design Space Co-exploration. ACM Trans. Embed. Comput. Syst. 2013, 13, 1–26. [Google Scholar] [CrossRef]
- Whitman, M.E.; Mattord, H.J. Principles of Information Security, 4th ed.; Course Technology Press: Boston, MA, USA, 2011. [Google Scholar]
- Benini, L.; Macii, A.; Macii, E.; Omerbegovic, E.; Pro, F.; Poncino, M. Energy-Aware Design Techniques for Differential Power Analysis Protection. In Proceedings of the 40th Annual Design Automation Conference (DAC), Anaheim, CA, USA, 2–6 June 2003; pp. 36–41. [Google Scholar]
- Lin, C.W.; Zheng, B.; Zhu, Q.; Sangiovanni-Vincentelli, A. Security-Aware Design Methodology and Optimization for Automotive Systems. ACM Trans. Des. Autom. Electron. Syst. 2015, 21, 1–26. [Google Scholar] [CrossRef]
- Weichslgartner, A.; Wildermann, S.; Götzfried, J.; Freiling, F.; Glaundefined, M.; Teich, J. Design-Time/Run-Time Mapping of Security-Critical Applications in Heterogeneous MPSoCs. In Proceedings of the 19th International Workshop on Software and Compilers for Embedded Systems (SCOPES), Sankt Goar, Germany, 23–25 May 2016; pp. 153–162. [Google Scholar]
- Stierand, I.; Malipatlolla, S.; Fröschle, S.; Stühring, A.; Henkler, S. Integrating the Security Aspect into Design Space Exploration of Embedded Systems. In Proceedings of the IEEE International Symposium on Software Reliability Engineering Workshops, Naples, Italy, 3–6 November 2014; pp. 371–376. [Google Scholar]
- Tan, B.; Biglari-Abhari, M.; Salcic, Z. An Automated Security-Aware Approach for Design of Embedded Systems on MPSoC. ACM Trans. Embed. Comput. Syst. 2017, 16, 1–20. [Google Scholar] [CrossRef]
- Rocchetto, M.; Ferrari, A.; Senni, V. Challenges and Opportunities for Model-Based Security Risk Assessment of Cyber-Physical Systems. In Resilience of Cyber-Physical Systems. Advanced Sciences and Technologies for Security Applications; Flammini, F., Ed.; Springer: Berlin, Germany, 2019. [Google Scholar]
- Asif, W.; Ray, I.G.; Rajarajan, M. An Attack Tree Based Risk Evaluation Approach for the Internet of Things. In Proceedings of the 8th International Conference on the Internet of Things, Santa Barbara, CA, USA, 15–18 October 2018. [Google Scholar]
- Ferrante, A.; Milosevic, J.; Janjšević, M. A security-enhanced design methodology for embedded systems. In Proceedings of the 2013 International Conference on Security and Cryptography (SECRYPT), Reykjavik, Iceland, 29–31 July 2013; pp. 1–12. [Google Scholar]
- Ferrante, A.; Kaitovic, I.; Milosevic, J. Modelling Requirements for Security-Enhanced Design of Embedded Systems. In Proceedings of the International Conference on Security and Cryptography (SECRYPT), Vienna, Austria, 28–30 August 2014; pp. 315–320. [Google Scholar]
- Gressl, L.; Steger, C.; Neffe, U. Security Driven Design Space Exploration for Embedded Systems. In Proceedings of the 2019 Forum for Specification and Design Languages (FDL), Southampton, UK, 2–4 September 2019; pp. 1–8. [Google Scholar]

| Attack | Sub-Type | Access Level | Passivity |
|---|---|---|---|
| Side-channel | Power analysis | Physical | Passive |
| Timing attack | Virtual | Passive | |
| Scan attack | Physical | Active | |
| Fault Analysis | Physical & Virtual | Passive & Active | |
| Electromagnetic Analysis | Physical | Passive | |
| Denial of Service | Virtual | Active | |
| Software | Buffer overflow | Virtual | Active |
| Cryptanalysis | None | Passive |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pimentel, A.D. A Case for Security-Aware Design-Space Exploration of Embedded Systems. J. Low Power Electron. Appl. 2020, 10, 22. https://doi.org/10.3390/jlpea10030022
Pimentel AD. A Case for Security-Aware Design-Space Exploration of Embedded Systems. Journal of Low Power Electronics and Applications. 2020; 10(3):22. https://doi.org/10.3390/jlpea10030022
Chicago/Turabian StylePimentel, Andy D. 2020. "A Case for Security-Aware Design-Space Exploration of Embedded Systems" Journal of Low Power Electronics and Applications 10, no. 3: 22. https://doi.org/10.3390/jlpea10030022
APA StylePimentel, A. D. (2020). A Case for Security-Aware Design-Space Exploration of Embedded Systems. Journal of Low Power Electronics and Applications, 10(3), 22. https://doi.org/10.3390/jlpea10030022




