A Hybrid Wavelet Analysis-Based New Information Priority Nonhomogeneous Discrete Grey Model with SCA Optimization for Language Service Demand Forecasting
Abstract
1. Introduction
- Wavelet-based time-series denoising is employed as a preprocessing step to extract the intrinsic signal and suppress stochastic fluctuations in the raw data, significantly improving the quality of the input series for grey modeling.
- A novel grey forecasting model, termed the new information priority nonhomogeneous discrete grey model (NIPNDGM) with wavelet analysis, is developed by incorporating the new information priority accumulation operator into the traditional nonhomogeneous discrete grey model. This is the first attempt to combine these two components, enhancing the model’s ability to adapt to recent data trends and capture short-term nonlinear dynamics.
- To address the parameter estimation challenges introduced by the nonlinear nature of the accumulation operator, this study adopts the SCA for automatic parameter optimization. This metaheuristic algorithm ensures global search capability and efficient convergence, enabling the model to achieve high prediction accuracy.
- The proposed hybrid SCA–WA–NIPNDGM is empirically validated on the time series of translation company counts across three representative industries: manufacturing; water conservancy, environmental, and public facilities management; and wholesale and retail. This is the first time it has been applied in the language service industry, and this application provides insight into the sectoral dynamics of language service demand, offering valuable evidence for regional language service planning and targeted policy support.
2. New Information Priority Nonhomogeneous Discrete Grey Model with Wavelet Analysis
2.1. Wavelet Analysis for Data Preprocessing
2.2. New Information Priority Nonhomogeneous Discrete Grey Model
3. Hyperparameter Optimization Using the Sine Cosine Algorithm
3.1. Optimization Process Using the Sine Cosine Algorithm
3.2. The Sine Cosine Algorithm
| Algorithm 1: Hyperparameter optimization of the WA–NIPNDGM using the SCA |
 |
4. Applications
4.1. Data Collection
4.2. Benchmark Models and Algorithms for Comparisons and Evaluation Metrics
4.3. Forecasting Results and Analysis
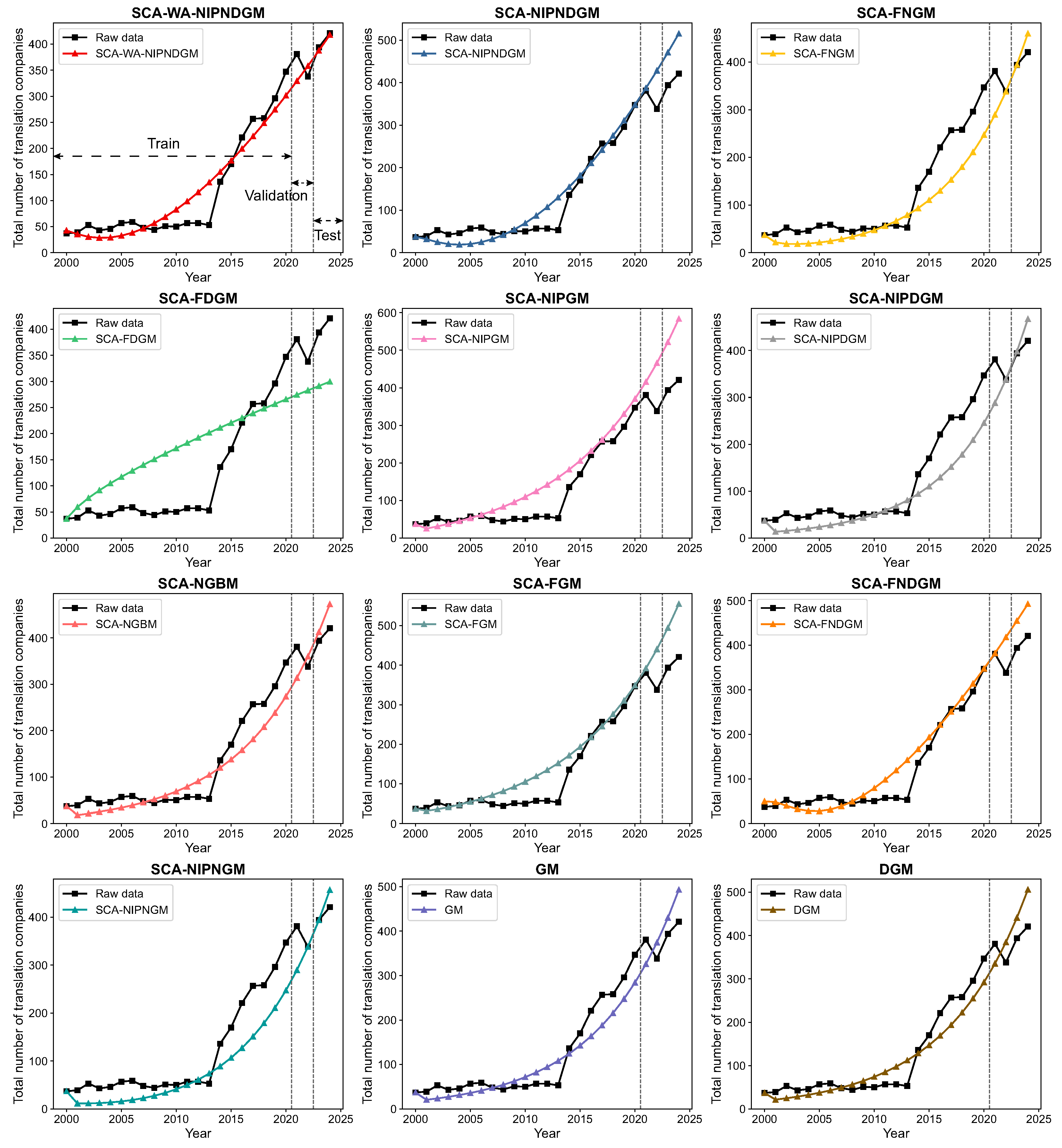
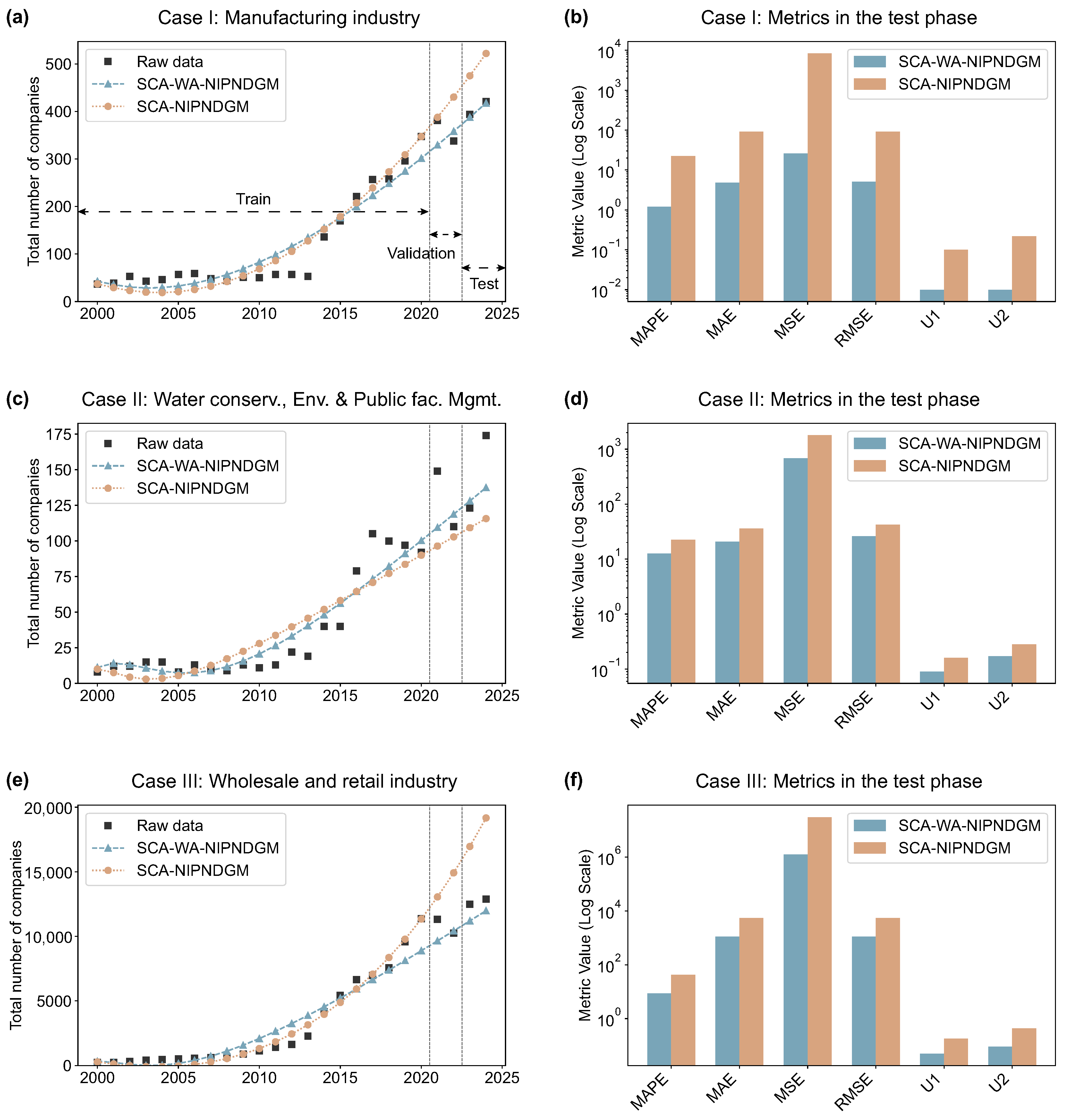
4.3.1. Case I: Prediction of the Total Number of Translation Companies in the Manufacturing Sector in China
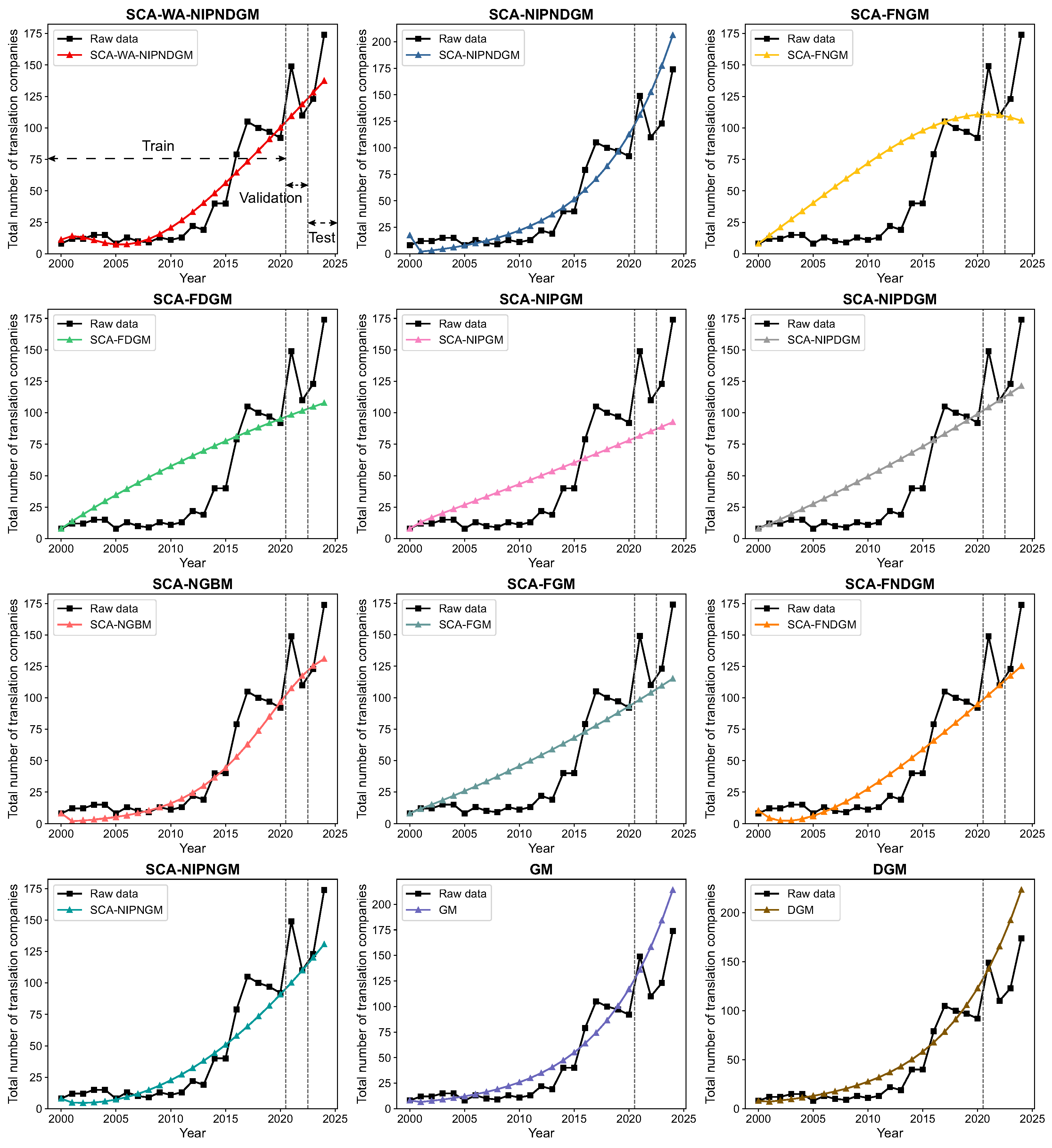
4.3.2. Case II: Prediction of Total Number of Translation Companies in the Water Conservancy, Environmental, and Public Facilities Management Sector in China
4.3.3. Case III: Prediction of the Total Number of Translation Companies in the Wholesale and Retail Sector in China
5. Discussion
5.1. Effectiveness of Integrating Wavelet Analysis in Enhancing NIPNDGM Forecasting Accuracy
5.2. Policy Implications for the Development of China’s Language Service Industry
- The lack of standardized data at both regional and sectoral levels remains a major obstacle to accurate forecasting in the language service industry. Establishing a unified statistical reporting standard, alongside secure and accessible data repositories, would enhance the reliability and geographic coverage of analyses.
- Government and industry associations should establish a unified statistical framework and create secure, high-quality language data repositories. This dual initiative would support accurate policymaking and enable Chinese enterprises to safely train domain-specific AI models, thereby enhancing global competitiveness.
- To support the small and medium-sized enterprises that constitute the majority of firms in the industry, policies should facilitate the ethical and effective adoption of AI through targeted measures. These include subsidies for privacy-compliant tools, AI literacy workshops, and funding for secure, pre-trained models to help these enterprises meet modern trade demands while mitigating data security risks.
- To ensure responsible innovation, industry associations, with governmental support, should develop a dedicated AI governance framework. This framework must establish a clear ethical code of conduct addressing data privacy, transparency, accountability for AI output, and intellectual property rights, thereby fostering trust and sustainable industry growth.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, J. Exploring Chinese Economic Discourse and Translation Strategies in the Era of AI: A Digital-Tech Approach. Commun. Across Borders Transl. Interpret. 2024, 4, 13–19. [Google Scholar]
- Gao, Y.; La, T. A Frontier Exploration of Translation Industry Research in the Age of Artificial Intelligence. J. Humanit. Arts Soc. Sci. 2024, 8, 2852–2862. [Google Scholar] [CrossRef]
- Kunkel, S.; Matthess, M.; Xue, B.; Beier, G. Industry 4.0 in sustainable supply chain collaboration: Insights from an interview study with international buying firms and Chinese suppliers in the electronics industry. Resour. Conserv. Recycl. 2022, 182, 106274. [Google Scholar] [CrossRef]
- Huang, X. The roles of competition on innovation efficiency and firm performance: Evidence from the Chinese manufacturing industry. Eur. Res. Manag. Bus. Econ. 2023, 29, 100201. [Google Scholar] [CrossRef]
- Tang, W.; Li, G. Enhancing competitiveness in cross-border e-commerce through knowledge-based consumer perception theory: An exploration of translation ability. J. Knowl. Econ. 2024, 15, 14935–14968. [Google Scholar] [CrossRef]
- Zhao, Y.; Huang, S.; Wang, X.; Shi, J.; Yao, S. Energy management with adaptive moving average filter and deep deterministic policy gradient reinforcement learning for fuel cell hybrid electric vehicles. Energy 2024, 312, 133395. [Google Scholar] [CrossRef]
- Le, T.T.; Abed-Meraim, K.; Trung, N.L.; Ravier, P.; Buttelli, O.; Holobar, A. Tensor-based higher-order multivariate singular spectrum analysis and applications to multichannel biomedical signal analysis. Signal Process. 2026, 238, 110113. [Google Scholar] [CrossRef]
- Yang, W.; Zhang, H.; Wang, J.; Hao, Y. A new perspective on non-ferrous metal price forecasting: An interpretable two-stage ensemble learning-based interval-valued forecasting system. Adv. Eng. Inform. 2025, 65, 103267. [Google Scholar] [CrossRef]
- Moni, M.; Sreeraj; Sankararaman, S. Unveiling the interdependency of cryptocurrency and Indian stocks through wavelet and nonlinear time series analysis: An Econophysics approach. Phys. Stat. Mech. Its Appl. 2025, 670, 130643. [Google Scholar] [CrossRef]
- Deng, J.-L. Control problems of grey systems. Syst. Control Lett. 1982, 1, 288–294. [Google Scholar] [CrossRef]
- Wu, W.; Ma, X.; Zhang, Y.; Li, W.; Wang, Y. A novel conformable fractional non-homogeneous grey model for forecasting carbon dioxide emissions of BRICS countries. Sci. Total Environ. 2020, 707, 135447. [Google Scholar] [CrossRef] [PubMed]
- Xiang, X.; Ma, X.; Ma, M.; Wu, W.; Yu, L. Research and application of novel Euler polynomial-driven grey model for short-term PM10 forecasting. Grey Syst. Theory Appl. 2021, 11, 498–517. [Google Scholar] [CrossRef]
- Liu, L.; Chen, Y.; Wu, L. The damping accumulated grey model and its application. Commun. Nonlinear Sci. Numer. Simul. 2021, 95, 105665. [Google Scholar] [CrossRef]
- Saxena, A. Optimized Fractional Overhead Power Term Polynomial Grey Model (OFOPGM) for market clearing price prediction. Electr. Power Syst. Res. 2023, 214, 108800. [Google Scholar] [CrossRef]
- Xie, N.; Liu, S. Research on Discrete Grey Model and Its Mechanism. In Proceedings of the 2005 IEEE International Conference on Systems, Man and Cybernetics, Waikoloa, HI, USA, 12 October 2005; Volume 1, pp. 606–610. [Google Scholar]
- Xie, N.; Liu, S. Interval grey number sequence prediction by using non-homogenous exponential discrete grey forecasting model. J. Syst. Eng. Electron. 2015, 26, 96–102. [Google Scholar] [CrossRef]
- Xie, N.; Wang, R.; Chen, N. Measurement of shock effect following change of one-child policy based on grey forecasting approach. Kybernetes 2018, 47, 559–586. [Google Scholar] [CrossRef]
- Liu, L.; Wu, L. Forecasting the renewable energy consumption of the European countries by an adjacent non-homogeneous grey model. Appl. Math. Model. 2021, 89, 1932–1948. [Google Scholar] [CrossRef]
- Zhou, W.; Ding, S. A novel discrete grey seasonal model and its applications. Commun. Nonlinear Sci. Numer. Simul. 2021, 93, 105493. [Google Scholar] [CrossRef]
- Ding, S.; Li, R.; Tao, Z. A novel adaptive discrete grey model with time-varying parameters for long-term photovoltaic power generation forecasting. Energy Convers. Manag. 2021, 227, 113644. [Google Scholar] [CrossRef]
- Qian, W.; Sui, A. A novel structural adaptive discrete grey prediction model and its application in forecasting renewable energy generation. Expert Syst. Appl. 2021, 186, 115761. [Google Scholar] [CrossRef]
- Zhou, W.; Zeng, B.; Wu, Y.; Wang, J.; Li, H.; Zhang, Z. Application of the three-parameter discrete direct grey model to forecast Chinas natural gas consumption. Soft Comput. 2023, 27, 3213–3228. [Google Scholar] [CrossRef]
- Wu, L.; Liu, S.; Yao, L.; Yan, S.; Liu, D. Grey system model with the fractional order accumulation. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 1775–1785. [Google Scholar] [CrossRef]
- Wu, L.F.; Liu, S.F.; Cui, W.; Liu, D.L.; Yao, T.X. Non-homogenous discrete grey model with fractional-order accumulation. Neural Comput. Appl. 2014, 25, 1215–1221. [Google Scholar] [CrossRef]
- Hao, Y.; Wang, X.; Wang, J.; Yang, W. A new perspective of wind speed forecasting: Multi-objective and model selection-based ensemble interval-valued wind speed forecasting system. Energy Convers. Manag. 2024, 299, 117868. [Google Scholar] [CrossRef]
- Chen, Y.; Wu, L.; Liu, L.; Zhang, K. Fractional Hausdorff grey model and its properties. Chaos Solitons Fractals 2020, 138, 109915. [Google Scholar] [CrossRef]
- Zhu, H.; Liu, C.; Wu, W.Z.; Xie, W.; Lao, T. Weakened fractional-order accumulation operator for ill-conditioned discrete grey system models. Appl. Math. Model. 2022, 111, 349–362. [Google Scholar] [CrossRef]
- Ma, X.; He, Q.; Li, W.; Wu, W. Time-delayed fractional grey Bernoulli model with independent fractional orders for fossil energy consumption forecasting. Eng. Appl. Artif. Intell. 2025, 155, 110942. [Google Scholar] [CrossRef]
- Ma, X.; Yuan, H.; Ma, M.; Wu, L. A novel fractional Bessel grey system model optimized by Salp Swarm Algorithm for renewable energy generation forecasting in developed countries of Europe and North America. Comput. Appl. Math. 2025, 44, 98. [Google Scholar] [CrossRef]
- Zhou, W.; Zhang, H.; Dang, Y.; Wang, Z. New information priority accumulated grey discrete model and its application. Chin. J. Manag. Sci. 2017, 25, 140–148. [Google Scholar]
- Wang, Y.; Yang, Z.; Zhou, Y.; Liu, H.; Yang, R.; Sun, L.; Sapnken, F.E.; Narayanan, G. A novel structure adaptive new information priority grey Bernoulli model and its application in China’s renewable energy production. Renew. Energy 2025, 239, 122052. [Google Scholar] [CrossRef]
- Guo, X.; Dang, Y.; Ding, S.; Cai, Z.; Li, Y. A new information priority grey prediction model for forecasting wind electricity generation with targeted regional hierarchy. Expert Syst. Appl. 2024, 252, 124199. [Google Scholar] [CrossRef]
- He, X.; Wang, Y.; Zhang, Y.; Ma, X.; Wu, W.; Zhang, L. A novel structure adaptive new information priority discrete grey prediction model and its application in renewable energy generation forecasting. Appl. Energy 2022, 325, 119854. [Google Scholar] [CrossRef]
- Li, K.; Xiong, P.; Wu, Y.; Dong, Y. Forecasting greenhouse gas emissions with the new information priority generalized accumulative grey model. Sci. Total Environ. 2022, 807, 150859. [Google Scholar] [CrossRef]
- Pollini, N. A multi-objective gradient-based approach for prestress and size optimization of cable domes. Int. J. Solids Struct. 2025, 320, 113476. [Google Scholar] [CrossRef]
- Wan, Z.; Zhang, J.; Sun, X.; Zhang, Z. Efficient deterministic algorithms for maximizing symmetric submodular functions. Theor. Comput. Sci. 2025, 1046, 115312. [Google Scholar] [CrossRef]
- Yousif, A. An Adaptive Firefly Algorithm for Dependent Task Scheduling in IoT-Fog Computing. Cmes Comput. Model. Eng. Sci. 2025, 142, 2869–2892. [Google Scholar] [CrossRef]
- Masood, M.; Fouad, M.M.; Kamal, R.; Aurangzeb, K.; Aslam, S.; Ullah, Z.; Glesk, I. Enhanced optimisation of MPLS network traffic using a novel adjustable Bat algorithm with loudness optimizer. Results Eng. 2025, 26, 104774. [Google Scholar] [CrossRef]
- Sowmiya, M.; Banu Rekha, B.; Malar, E. Optimized heart disease prediction model using a meta-heuristic feature selection with improved binary salp swarm algorithm and stacking classifier. Comput. Biol. Med. 2025, 191, 110171. [Google Scholar] [CrossRef]
- Hu, G.; Wang, S.; Shu, B.; Wei, G. AEPSO: An adaptive learning particle swarm optimization for solving the hyperparameters of dynamic periodic regulation grey model. Expert Syst. Appl. 2025, 283, 127578. [Google Scholar] [CrossRef]
- Manafi, E.; Domenech, B.; Tavakkoli-Moghaddam, R.; Ranaboldo, M. A self-learning whale optimization algorithm based on reinforcement learning for a dual-resource flexible job shop scheduling problem. Appl. Soft Comput. 2025, 180, 113436. [Google Scholar] [CrossRef]
- Agrawal, S.P.; Jangir, P.; Abualigah, L.; Pandya, S.B.; Parmar, A.; Ezugwu, A.E.; Arpita; Smerat, A. The quick crisscross sine cosine algorithm for optimal FACTS placement in uncertain wind integrated scenario based power systems. Results Eng. 2025, 25, 103703. [Google Scholar] [CrossRef]
- He, Q.; Ma, X.; Zhang, L.; Li, W.; Li, T. The nonlinear multi-variable grey Bernoulli model and its applications. Appl. Math. Model. 2024, 134, 635–655. [Google Scholar] [CrossRef]
- Lee, G.; Gommers, R.; Waselewski, F.; Wohlfahrt, K.; O’Leary, A. PyWavelets: A Python package for wavelet analysis. J. Open Source Softw. 2019, 4, 1237. [Google Scholar] [CrossRef]
- Mallat, S. A theory for multiresolution signal decomposition: The wavelet representation. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 674–693. [Google Scholar] [CrossRef]
- Donoho, D.L. De-noising by soft-thresholding. IEEE Trans. Inf. Theory 2002, 41, 613–627. [Google Scholar] [CrossRef]
- Xie, N.M.; Liu, S.F. Discrete grey forecasting model and its optimization. Appl. Math. Model. 2009, 33, 1173–1186. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A Sine Cosine Algorithm for solving optimization problems. Knowl.-Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Duan, H.; Lei, G.R.; Shao, K. Forecasting crude oil consumption in China using a grey prediction model with an optimal fractional-order accumulating operator. Complexity 2018, 2018, 3869619. [Google Scholar] [CrossRef]
- Wu, L.; Liu, S.; Chen, H.; Zhang, N. Using a novel grey system model to forecast natural gas consumption in China. Math. Probl. Eng. 2015, 2015, 686501. [Google Scholar] [CrossRef]
- Chen, C.I.; Chen, H.L.; Chen, S.P. Forecasting of foreign exchange rates of Taiwan’s major trading partners by novel nonlinear Grey Bernoulli model NGBM (1, 1). Commun. Nonlinear Sci. Numer. Simul. 2008, 13, 1194–1204. [Google Scholar] [CrossRef]
- Cui, J.; Dang, Y.; Liu, S. Novel grey forecasting model and its modeling mechanism. Control Decis. 2009, 24, 1702–1706. [Google Scholar]
- Yang, X.S. Nature-Inspired Metaheuristic Algorithms; Luniver Press: Bristol, UK, 2010. [Google Scholar]
- Yang, X.S. A New Metaheuristic Bat-Inspired Algorithm. In Nature Inspired Cooperative Strategies for Optimization (NICSO 2010); González, J.R., Pelta, D.A., Cruz, C., Terrazas, G., Krasnogor, N., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 65–74. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Cui, Y.; Jia, L.; Fan, W. Estimation of actual evapotranspiration and its components in an irrigated area by integrating the Shuttleworth-Wallace and surface temperature-vegetation index schemes using the particle swarm optimization algorithm. Agric. For. Meteorol. 2021, 307, 108488. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Siu, S.C. ChatGPT and GPT-4 for professional translators: Exploring the potential of large language models in translation. SSRN Electron. J. 2023. [Google Scholar] [CrossRef]


| Model | Model Abbreviation | Reference |
|---|---|---|
| New Information Priority Nonhomogeneous Discrete Grey Model | NIPNDGM | - |
| Fractional-Order Nonhomogeneous Grey Model | FNGM | [49] |
| Fractional-Order Discrete Grey Model | FDGM | [24] |
| New Information Priority Grey Model | NIPGM | [50] |
| New Information Priority Discrete Grey Model | NIPDGM | [30] |
| Nonhomogeneous Grey Bernoulli Model | NGBM | [51] |
| Fractional-Order Grey Model | FGM | [23] |
| Fractional-Order Nonhomogeneous Discrete Grey Model | FNDGM | [24] |
| New Information Priority Nonhomogeneous Grey Model | NIPNGM | [52] |
| Grey Model | GM | [10] |
| Discrete Grey Model | DGM | [47] |
| Model | Model Abbreviation | Reference |
|---|---|---|
| Sine Cosine Algorithm | SCA | [48] |
| Firefly Algorithm (with wavelet analysis) | FFA | [53] |
| Bat Algorithm | BAT | [54] |
| Salp Swarm Algorithm | SSA | [55] |
| Particle Swarm Optimization | PSO | [56] |
| Whale Optimization Algorithm | WOA | [57] |
| Metrics | Abbreviation | Expression |
|---|---|---|
| Mean Absolute Percentage Error | MAPE | |
| Mean Absolute Error | MAE | |
| Mean Squared Error | MSE | |
| Root Mean Square Error | RMSE | |
| Theil U Statistic 1 | U1 | |
| Theil U Statistic 2 | U2 |
| Metrics | SCA-WA-NIPNDGM | SCA-NIPNDGM | SCA-FNGM | SCA-FDGM | SCA-NIPGM | SCA-NIPDGM | SCA-NGBM | SCA-FGM | SCA-FNDGM | SCA-NIPNGM | GM | DGM | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Optimal Hyperparameters | – | – | |||||||||||
| Validation | MAPE | 9.75 | 14.14 | 12.04 | 22.17 | 23.50 | 12.26 | 12.05 | 16.60 | 11.97 | 12.00 | – | – |
| MAE | 35.86 | 48.14 | 45.86 | 80.95 | 81.40 | 46.68 | 44.52 | 56.73 | 40.53 | 45.71 | – | – | |
| MSE | 1534.43 | 4081.80 | 4203.52 | 7216.20 | 8793.24 | 4300.66 | 2493.36 | 5301.89 | 3195.69 | 4178.34 | – | – | |
| RMSE | 39.17 | 63.89 | 64.83 | 84.95 | 93.77 | 65.58 | 49.93 | 72.81 | 56.53 | 64.64 | – | – | |
| U1 | 0.06 | 0.08 | 0.10 | 0.13 | 0.12 | 0.10 | 0.07 | 0.09 | 0.07 | 0.10 | – | – | |
| U2 | 0.11 | 0.18 | 0.18 | 0.24 | 0.26 | 0.18 | 0.14 | 0.20 | 0.16 | 0.18 | – | – | |
| Test | MAPE | 1.20 | 20.99 | 4.69 | 27.46 | 35.55 | 6.01 | 8.56 | 28.68 | 16.25 | 4.33 | 13.11 | 16.07 |
| MAE | 4.84 | 85.72 | 19.72 | 112.08 | 145.29 | 25.16 | 35.38 | 117.31 | 66.34 | 18.22 | 53.95 | 66.02 | |
| MSE | 25.95 | 7425.18 | 758.35 | 12,648.40 | 21,417.47 | 1087.78 | 1531.57 | 14,045.38 | 4431.54 | 644.66 | 3243.97 | 4716.84 | |
| RMSE | 5.09 | 86.17 | 27.54 | 112.47 | 146.35 | 32.98 | 39.14 | 118.51 | 66.57 | 25.39 | 56.96 | 68.68 | |
| U1 | 0.01 | 0.10 | 0.03 | 0.16 | 0.15 | 0.04 | 0.05 | 0.13 | 0.08 | 0.03 | 0.07 | 0.08 | |
| U2 | 0.01 | 0.21 | 0.07 | 0.28 | 0.36 | 0.08 | 0.10 | 0.29 | 0.16 | 0.06 | 0.14 | 0.17 |
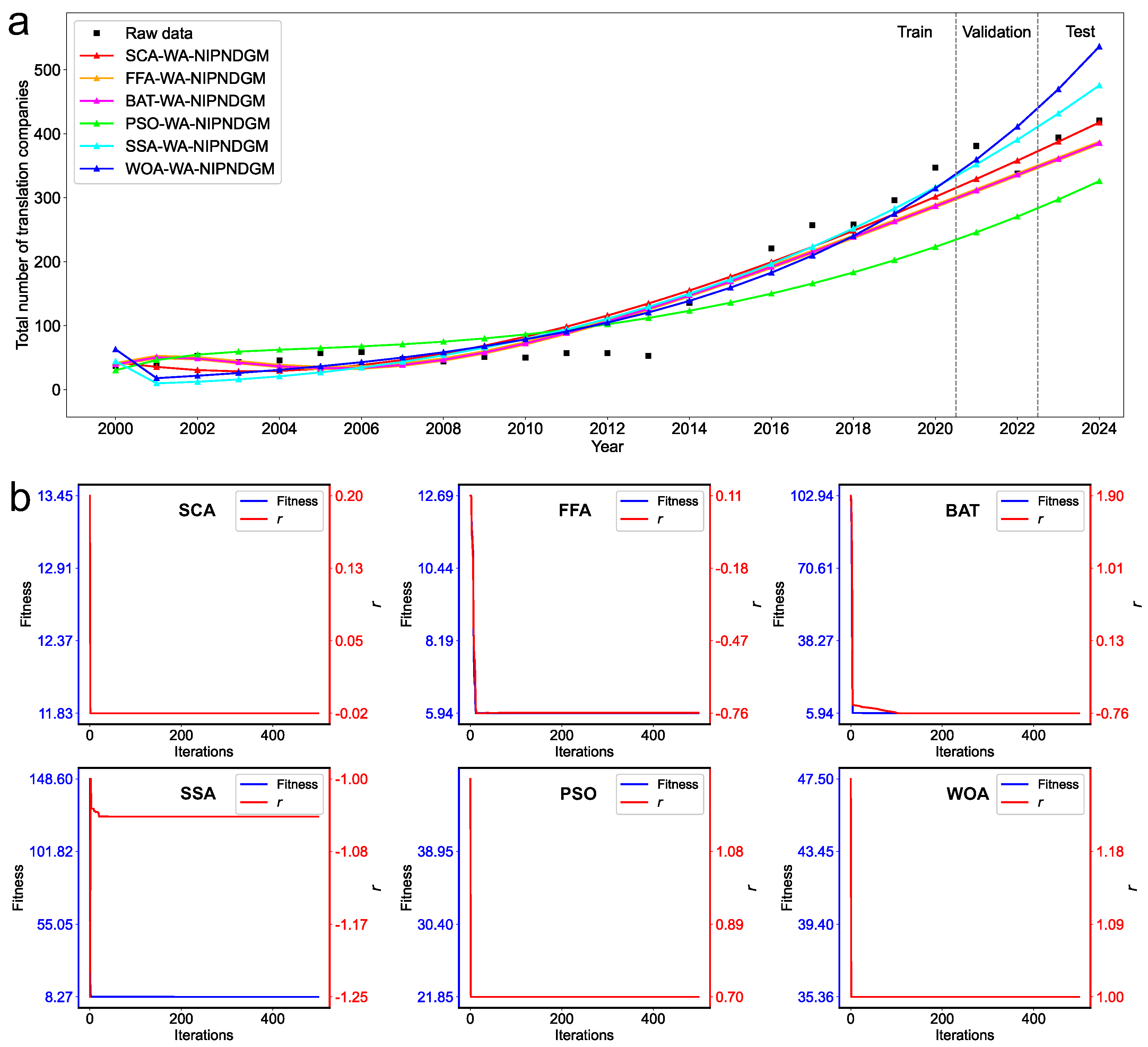
| Metrics | SCA–WA–NIPNDGM | FFA–WA–NIPNDGM | BAT–WA–NIPNDGM | PSO–WA–NIPNDGM | SSA–WA–NIPNDGM | WOA–WA–NIPNDGM | |
|---|---|---|---|---|---|---|---|
| Optimal Hyperparameters | |||||||
| Validation | MAPE | 9.75 | 9.38 | 9.38 | 27.71 | 11.56 | 13.61 |
| MAE | 35.86 | 35.61 | 35.61 | 101.29 | 40.71 | 47.21 | |
| MSE | 1534.43 | 2410.64 | 2410.65 | 11,403.36 | 1798.16 | 2901.04 | |
| RMSE | 39.17 | 49.10 | 49.10 | 106.79 | 42.40 | 53.86 | |
| U1 | 0.06 | 0.07 | 0.07 | 0.17 | 0.06 | 0.07 | |
| U2 | 0.11 | 0.14 | 0.14 | 0.30 | 0.12 | 0.15 | |
| Test | MAPE | 1.20 | 8.39 | 8.39 | 23.57 | 11.27 | 23.33 |
| MAE | 4.84 | 34.20 | 34.20 | 95.90 | 46.15 | 95.61 | |
| MSE | 25.95 | 1170.53 | 1170.53 | 9196.86 | 2201.10 | 9536.34 | |
| RMSE | 5.09 | 34.21 | 34.21 | 95.90 | 46.92 | 97.65 | |
| U1 | 0.01 | 0.04 | 0.04 | 0.13 | 0.05 | 0.11 | |
| U2 | 0.01 | 0.08 | 0.08 | 0.24 | 0.12 | 0.24 |
| Metrics | SCA-WA-NIPNDGM | SCA-NIPNDGM | SCA-FNGM | SCA-FDGM | SCA-NIPGM | SCA-NIPDGM | SCA-NGBM | SCA-FGM | SCA-FNDGM | SCA-NIPNGM | GM | DGM | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Optimal Hyperparameters | – | – | |||||||||||
| Validation | MAPE | 17.24 | 25.36 | 12.88 | 20.80 | 33.85 | 14.94 | 17.31 | 19.68 | 15.63 | 16.37 | – | – |
| MAE | 24.14 | 30.25 | 19.16 | 29.50 | 46.06 | 22.26 | 24.45 | 28.26 | 23.29 | 24.40 | – | – | |
| MSE | 819.43 | 1065.70 | 729.44 | 1315.49 | 2575.48 | 991.41 | 883.48 | 1292.29 | 1084.39 | 1190.49 | – | – | |
| RMSE | 28.63 | 32.65 | 27.01 | 36.27 | 50.75 | 31.49 | 29.72 | 35.95 | 32.93 | 34.50 | – | – | |
| U1 | 0.12 | 0.12 | 0.11 | 0.16 | 0.24 | 0.13 | 0.12 | 0.15 | 0.14 | 0.15 | – | – | |
| U2 | 0.22 | 0.25 | 0.21 | 0.28 | 0.39 | 0.24 | 0.23 | 0.27 | 0.25 | 0.26 | – | – | |
| Test | MAPE | 12.57 | 31.38 | 25.55 | 26.45 | 37.25 | 18.13 | 13.39 | 22.39 | 16.19 | 13.52 | 36.37 | 42.40 |
| MAE | 20.81 | 43.32 | 41.44 | 42.24 | 57.74 | 30.01 | 22.76 | 36.15 | 27.06 | 22.96 | 50.62 | 59.40 | |
| MSE | 680.86 | 1999.51 | 2440.26 | 2358.57 | 3894.24 | 1413.45 | 925.61 | 1821.10 | 1201.65 | 934.19 | 2672.01 | 3628.01 | |
| RMSE | 26.09 | 44.72 | 49.40 | 48.57 | 62.40 | 37.60 | 30.42 | 42.67 | 34.66 | 30.56 | 51.69 | 60.23 | |
| U1 | 0.09 | 0.13 | 0.19 | 0.19 | 0.26 | 0.14 | 0.11 | 0.16 | 0.13 | 0.11 | 0.15 | 0.17 | |
| U2 | 0.17 | 0.30 | 0.33 | 0.32 | 0.41 | 0.25 | 0.20 | 0.28 | 0.23 | 0.20 | 0.34 | 0.40 |
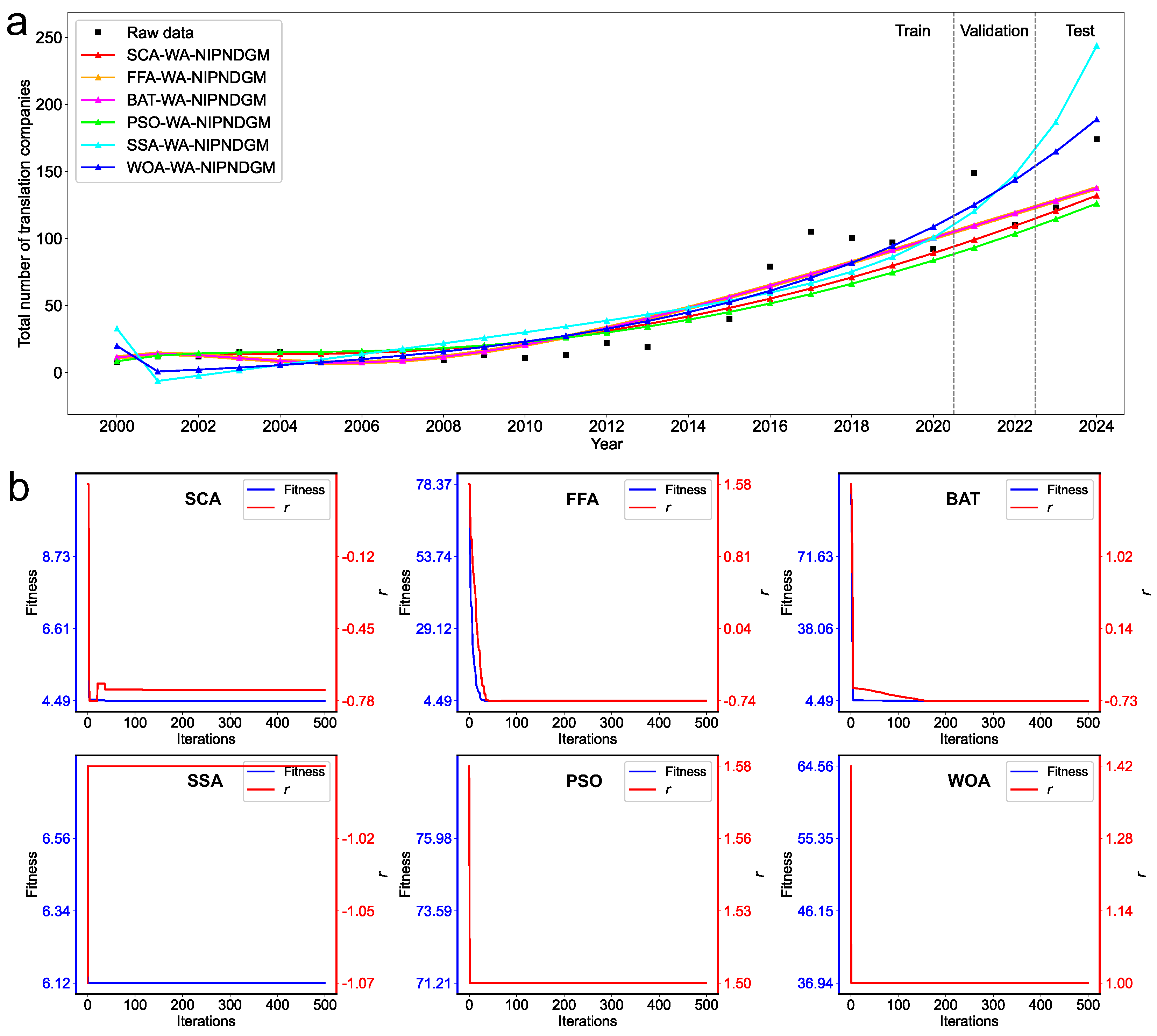
| Metrics | SCA–WA–NIPNDGM | FFA–WA–NIPNDGM | BAT–WA–NIPNDGM | PSO–WA–NIPNDGM | SSA–WA–NIPNDGM | WOA–WA–NIPNDGM | |
|---|---|---|---|---|---|---|---|
| Optimal Hyperparameters | |||||||
| Validation | MAPE | 17.24 | 17.24 | 17.24 | 21.69 | 26.78 | 23.31 |
| MAE | 24.14 | 24.14 | 24.14 | 31.17 | 33.23 | 28.79 | |
| MSE | 819.43 | 819.46 | 819.46 | 1578.76 | 1123.54 | 851.45 | |
| RMSE | 28.63 | 28.63 | 28.63 | 39.73 | 33.52 | 29.18 | |
| U1 | 0.12 | 0.12 | 0.12 | 0.17 | 0.13 | 0.11 | |
| U2 | 0.22 | 0.22 | 0.22 | 0.30 | 0.26 | 0.22 | |
| Test | MAPE | 12.57 | 12.57 | 12.57 | 17.28 | 45.97 | 21.19 |
| MAE | 20.81 | 20.81 | 20.81 | 28.29 | 66.75 | 28.23 | |
| MSE | 680.86 | 680.87 | 680.87 | 1188.60 | 4464.40 | 978.39 | |
| RMSE | 26.09 | 26.09 | 26.09 | 34.48 | 66.82 | 31.28 | |
| U1 | 0.09 | 0.09 | 0.09 | 0.13 | 0.18 | 0.10 | |
| U2 | 0.17 | 0.17 | 0.17 | 0.23 | 0.44 | 0.21 |
| Metrics | SCA-WA- NIPNDGM | SCA- NIPNDGM | SCA-FNGM | SCA-FDGM | SCA-NIPGM | SCA- NIPDGM | SCA-NGBM | SCA-FGM | SCA- FNDGM | SCA- NIPNGM | GM | DGM | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Optimal Hyperparameters | – | – | |||||||||||
| Validation | MAPE | 8.25 | 30.14 | 14.53 | 28.14 | 105.50 | 137.79 | 19.03 | 105.50 | 28.93 | 14.38 | – | – |
| MAE | 924.62 | 3166.93 | 1514.26 | 3063.21 | 11,233.73 | 14,666.15 | 1983.73 | 11,233.73 | 3048.40 | 1537.65 | – | – | |
| MSE | 1,410,678.91 | 12,301,540.50 | 3,266,074.76 | 9,896,587.21 | 131,507,197.91 | 224,895,250.09 | 5,563,864.46 | 131,507,197.91 | 10,920,063.24 | 2,401,966.12 | – | – | |
| RMSE | 1187.72 | 3507.36 | 1807.23 | 3145.88 | 11,467.66 | 14,996.51 | 2358.78 | 11,467.66 | 3304.55 | 1549.83 | – | – | |
| U1 | 0.06 | 0.14 | 0.08 | 0.17 | 0.35 | 0.41 | 0.10 | 0.35 | 0.13 | 0.07 | – | – | |
| U2 | 0.11 | 0.32 | 0.17 | 0.29 | 1.06 | 1.39 | 0.22 | 1.06 | 0.31 | 0.14 | – | – | |
| Test | MAPE | 8.65 | 43.60 | 28.34 | 33.55 | 139.08 | 201.45 | 22.23 | 139.08 | 33.21 | 24.01 | 139.08 | 142.15 |
| MAE | 1,093.84 | 5546.53 | 3612.28 | 4255.84 | 17,678.74 | 25,613.66 | 2826.71 | 17,678.74 | 4221.93 | 3065.44 | 17,678.74 | 18,067.92 | |
| MSE | 1,233,627.24 | 31,720,758.63 | 14,262,323.42 | 18,112,584.96 | 317,540,349.69 | 669,762,605.35 | 8,167,951.04 | 317,540,349.69 | 18,187,814.13 | 10,853,911.35 | 317,540,349.69 | 331,527,111.44 | |
| RMSE | 1110.69 | 5632.12 | 3776.55 | 4255.89 | 17,819.66 | 25,879.77 | 2857.96 | 17,819.66 | 4264.72 | 3294.53 | 17,819.66 | 18,207.89 | |
| U1 | 0.05 | 0.18 | 0.13 | 0.20 | 0.41 | 0.51 | 0.10 | 0.41 | 0.14 | 0.12 | 0.41 | 0.42 | |
| U2 | 0.09 | 0.44 | 0.30 | 0.34 | 1.40 | 2.04 | 0.23 | 1.40 | 0.34 | 0.26 | 1.40 | 1.43 |
| Metrics | SCA–WA–NIPNDGM | FFA–WA–NIPNDGM | BAT–WA–NIPNDGM | PSO–WA–NIPNDGM | SSA–WA–NIPNDGM | WOA–WA–NIPNDGM | |
|---|---|---|---|---|---|---|---|
| Optimal Hyperparameters | |||||||
| Validation | MAPE | 8.25 | 12.02 | 12.02 | 12.52 | 10.70 | 12.52 |
| MAE | 924.62 | 1337.29 | 1337.29 | 1293.50 | 1119.83 | 1293.50 | |
| MSE | 141,0678.91 | 2,590,496.67 | 2,590,498.27 | 2,793,197.56 | 1,635,935.15 | 2,793,197.56 | |
| RMSE | 1187.72 | 1609.50 | 1609.50 | 1671.29 | 1279.04 | 1671.29 | |
| U1 | 0.06 | 0.08 | 0.08 | 0.07 | 0.06 | 0.07 | |
| U2 | 0.11 | 0.15 | 0.15 | 0.15 | 0.12 | 0.15 | |
| Test | MAPE | 8.65 | 14.25 | 14.25 | 19.86 | 9.09 | 19.86 |
| MAE | 1093.84 | 1805.73 | 1805.73 | 2531.30 | 1160.04 | 2531.30 | |
| MSE | 1,233,627.24 | 3,286,812.38 | 3,286,814.40 | 6,954,678.80 | 1,541,997.90 | 6,954,678.80 | |
| RMSE | 1110.69 | 1812.96 | 1812.96 | 2637.17 | 1241.77 | 2637.17 | |
| U1 | 0.05 | 0.08 | 0.08 | 0.09 | 0.05 | 0.09 | |
| U2 | 0.09 | 0.14 | 0.14 | 0.21 | 0.10 | 0.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Ma, X. A Hybrid Wavelet Analysis-Based New Information Priority Nonhomogeneous Discrete Grey Model with SCA Optimization for Language Service Demand Forecasting. Systems 2025, 13, 768. https://doi.org/10.3390/systems13090768
Li X, Ma X. A Hybrid Wavelet Analysis-Based New Information Priority Nonhomogeneous Discrete Grey Model with SCA Optimization for Language Service Demand Forecasting. Systems. 2025; 13(9):768. https://doi.org/10.3390/systems13090768
Chicago/Turabian StyleLi, Xixi, and Xin Ma. 2025. "A Hybrid Wavelet Analysis-Based New Information Priority Nonhomogeneous Discrete Grey Model with SCA Optimization for Language Service Demand Forecasting" Systems 13, no. 9: 768. https://doi.org/10.3390/systems13090768
APA StyleLi, X., & Ma, X. (2025). A Hybrid Wavelet Analysis-Based New Information Priority Nonhomogeneous Discrete Grey Model with SCA Optimization for Language Service Demand Forecasting. Systems, 13(9), 768. https://doi.org/10.3390/systems13090768






