Integrated Operations Scheduling and Resource Allocation at Heavy Haul Railway Port Stations: A Collaborative Dual-Agent Actor–Critic Reinforcement Learning Framework
Abstract
1. Introduction
1.1. Literature Review
1.2. Contributions
2. Problem Description and Assumptions
2.1. Problem Description
2.2. Assumptions
3. Model Formulation
3.1. Objective Function
3.2. Constraints
- (1)
- Assignment of Unit Trains
- (2)
- Utilization of Shunting Engines
- (3)
- Sequence of Operations
- (4)
- Combination of Unit Trains
4. Dual-Agent Advantage Actor–Critic with Pareto Reward Shaping
4.1. Markov Decision Process
4.2. State Representation
4.3. Action Space
4.4. Reward Function
4.4.1. Local Reward for the Train Agent
| Algorithm 1 Step rewards for the train agent |
| do 2: if 1st shunting operation then |
| ; |
| ; |
| ; |
| ; |
| ; 8: end |
| 9: if 2nd shunting operation then |
| ; |
| ; |
| ; |
| 13: end 14: if 3rd shunting operation then 15: ; 16: ; 17: ; 18: end 19: end |
| Algorithm 2 Terminal rewards for the train agent |
| , with the window size = 2, slide step size = 1 |
| do 2: ; |
| 3: Update the remaining unassigned trains after calculate combination of outbound train types; |
| do |
| ;
6: ; |
| 7: end |
| then |
| 9: Select the combination plan of outbound train ; |
| 10: for unit trains assigned to outbound train do |
| ; |
| 12: end |
| 13: Update the remaining unassigned trains after determining combination of outbound train ; |
| 14: end 15: then 16: with the maximum ; 17: do 18: ; 19: end 20:; 21: end 22: end |
4.4.2. Local Reward for the Shunting Agent
4.4.3. Pareto Reward Shaping
4.5. Algorithm Framework
5. Case Study
5.1. Background and Parameters
5.2. Results and Analysis
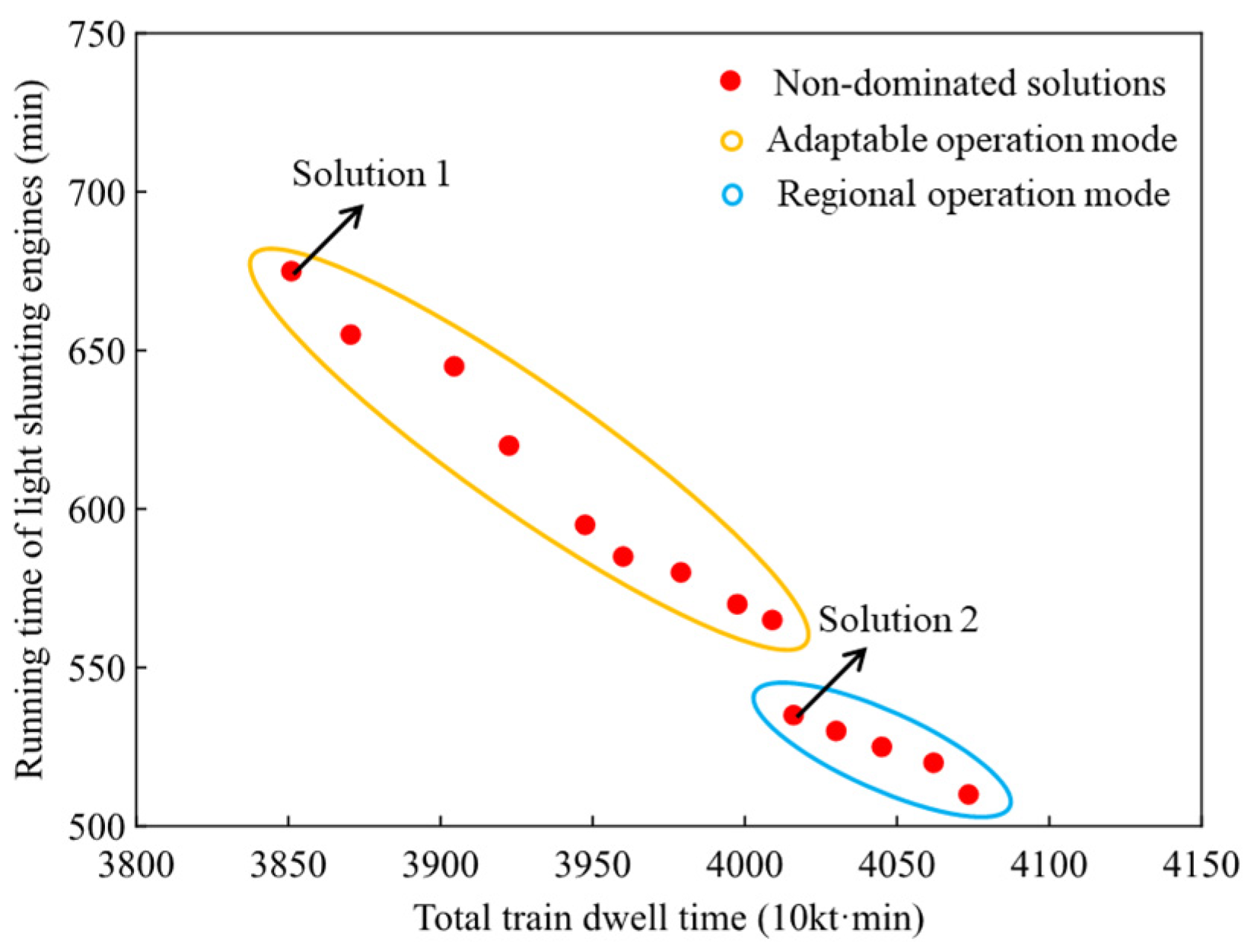
5.2.1. Computational Results
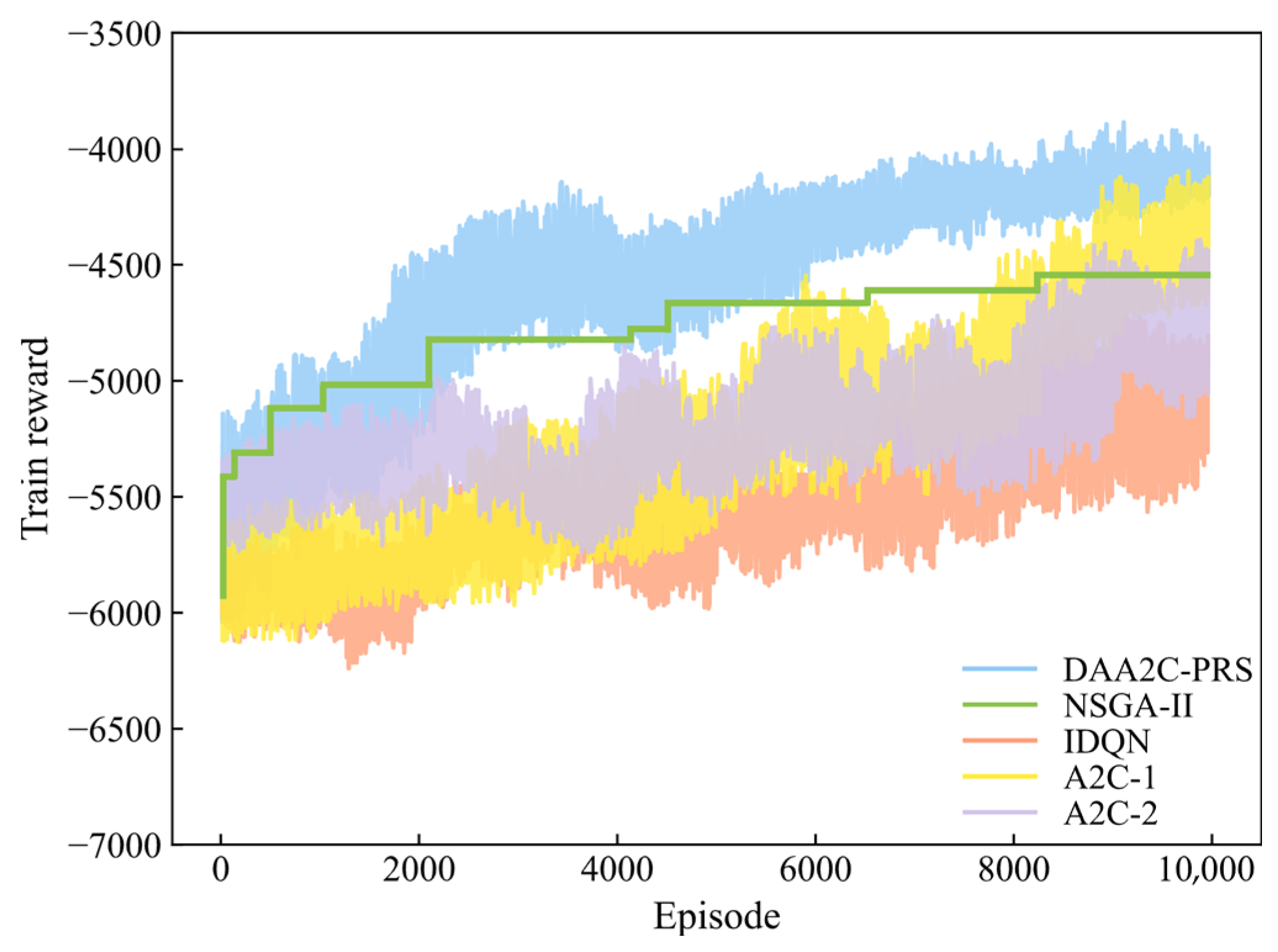
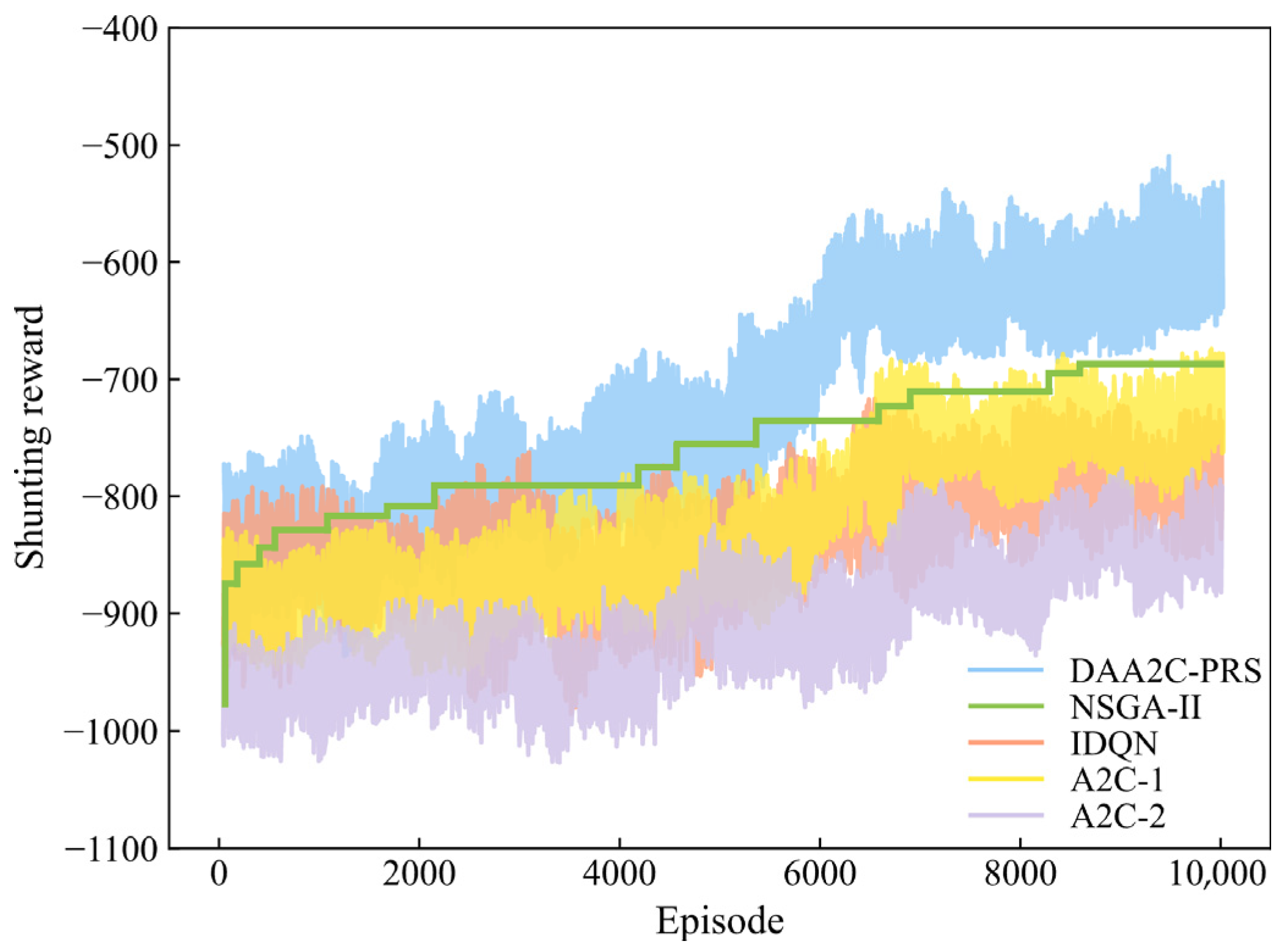
5.2.2. Algorithm Evaluation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jing, Y.; Zhang, Z. A Study on Car Flow Organization in the Loading End of Heavy Haul Railway Based on Immune Clonal Selection Algorithm. Neural Comput. Appl. 2019, 31, 1455–1465. [Google Scholar] [CrossRef]
- Esteso, A.; Peidro, D.; Mula, J.; Diaz-Madronero, M. Reinforcement Learning Applied to Production Planning and Control. Int. J. Prod. Res. 2023, 61, 5772–5789. [Google Scholar] [CrossRef]
- Zhou, H.; Zhou, L.; Guo, B.; Bai, Z.; Wang, Z.; Yang, L. A Scheduling Approach for the Combination Scheme and Train Timetable of a Heavy-Haul Railway. Mathematics 2021, 9, 3068. [Google Scholar] [CrossRef]
- Wang, D.; Zhao, J.; Peng, Q. Optimizing the Loaded Train Combination Problem at a Heavy-Haul Marshalling Station. Transp. Res. Part E Logist. Transp. Rev. 2022, 162, 102717. [Google Scholar] [CrossRef]
- Chen, W.; Zhuo, Q.; Zhang, L. Modeling and Heuristically Solving Group Train Operation Scheduling for Heavy-Haul Railway Transportation. Mathematics 2023, 11, 2489. [Google Scholar] [CrossRef]
- Zhuo, Q.; Chen, W.; Yuan, Z. Optimizing Mixed Group Train Operation for Heavy-Haul Railway Transportation: A Case Study in China. Mathematics 2023, 11, 4712. [Google Scholar] [CrossRef]
- Tian, A.-Q.; Wang, X.-Y.; Xu, H.; Pan, J.-S.; Snasel, V.; Lv, H.-X. Multi-Objective Optimization Model for Railway Heavy-Haul Traffic: Addressing Carbon Emissions Reduction and Transport Efficiency Improvement. Energy 2024, 294, 130927. [Google Scholar] [CrossRef]
- Boysen, N.; Fliedner, M.; Jaehn, F.; Pesch, E. Shunting Yard Operations: Theoretical Aspects and Applications. Eur. J. Oper. Res. 2012, 220, 1–14. [Google Scholar] [CrossRef]
- Zhao, J.; Xiang, J.; Peng, Q. Routing and Scheduling of Trains and Engines in a Railway Marshalling Station Yard. Transp. Res. Part C Emerg. Technol. 2024, 167, 104826. [Google Scholar] [CrossRef]
- Adlbrecht, J.-A.; Hüttler, B.; Zazgornik, J.; Gronalt, M. The Train Marshalling by a Single Shunting Engine Problem. Transp. Res. Part C Emerg. Technol. 2015, 58, 56–72. [Google Scholar] [CrossRef]
- Deleplanque, S.; Hosteins, P.; Pellegrini, P.; Rodriguez, J. Train Management in Freight Shunting Yards: Formalisation and Literature Review. IET Intell. Transp. Syst. 2022, 16, 1286–1305. [Google Scholar] [CrossRef]
- Yu, F.; Zhang, C.; Yao, H.; Yang, Y. Coordinated Scheduling Problems for Sustainable Production of Container Terminals: A Literature Review. Ann. Oper. Res. 2024, 332, 1013–1034. [Google Scholar] [CrossRef]
- Kizilay, D.; Eliiyi, D.T. A Comprehensive Review of Quay Crane Scheduling, Yard Operations and Integrations Thereof in Container Terminals. Flex. Serv. Manuf. J. 2021, 33, 1–42. [Google Scholar] [CrossRef]
- Jonker, T.; Duinkerken, M.B.; Yorke-Smith, N.; de Waal, A.; Negenborn, R.R. Coordinated Optimization of Equipment Operations in a Container Terminal. Flex. Serv. Manuf. J. 2021, 33, 281–311. [Google Scholar] [CrossRef]
- Azab, A.; Morita, H. Coordinating Truck Appointments with Container Relocations and Retrievals in Container Terminals under Partial Appointments Information. Transp. Res. Part E Logist. Transp. Rev. 2022, 160, 102673. [Google Scholar] [CrossRef]
- Yue, L.-J.; Fan, H.-M.; Fan, H. Blocks Allocation and Handling Equipment Scheduling in Automatic Container Terminals. Transp. Res. Part C-Emerg. Technol. 2023, 153, 104228. [Google Scholar] [CrossRef]
- Yang, Y.; Liang, J.; Feng, J. Simulation and Optimization of Automated Guided Vehicle Charging Strategy for U-Shaped Automated Container Terminal Based on Improved Proximal Policy Optimization. Systems 2024, 12, 472. [Google Scholar] [CrossRef]
- Liu, C. Iterative Heuristic for Simultaneous Allocations of Berths, Quay Cranes, and Yards under Practical Situations. Transp. Res. Part E Logist. Transp. Rev. 2020, 133, 101814. [Google Scholar] [CrossRef]
- Rosca, E.; Rusca, F.; Carlan, V.; Stefanov, O.; Dinu, O.; Rusca, A. Assessing the Influence of Equipment Reliability over the Activity Inside Maritime Container Terminals Through Discrete-Event Simulation. Systems 2025, 13, 213. [Google Scholar] [CrossRef]
- Menezes, G.C.; Mateus, G.R.; Ravetti, M.G. A Hierarchical Approach to Solve a Production Planning and Scheduling Problem in Bulk Cargo Terminal. Comput. Ind. Eng. 2016, 97, 1–14. [Google Scholar] [CrossRef]
- Unsal, O.; Oguz, C. An Exact Algorithm for Integrated Planning of Operations in Dry Bulk Terminals. Transp. Res. Part E Logist. Transp. Rev. 2019, 126, 103–121. [Google Scholar] [CrossRef]
- Kayhan, B.M.; Yildiz, G. Reinforcement Learning Applications to Machine Scheduling Problems: A Comprehensive Literature Review. J. Intell. Manuf. 2023, 34, 905–929. [Google Scholar] [CrossRef]
- Yuan, E.; Cheng, S.; Wang, L.; Song, S.; Wu, F. Solving Job Shop Scheduling Problems via Deep Reinforcement Learning. Appl. soft Comput. 2023, 143, 110436. [Google Scholar] [CrossRef]
- Lei, K.; Guo, P.; Wang, Y.; Zhang, J.; Meng, X.; Qian, L. Large-Scale Dynamic Scheduling for Flexible Job-Shop With Random Arrivals of New Jobs by Hierarchical Reinforcement Learning. IEEE Trans. Ind. Inform. 2024, 20, 1007–1018. [Google Scholar] [CrossRef]
- Luo, S. Dynamic Scheduling for Flexible Job Shop with New Job Insertions by Deep Reinforcement Learning. Appl. Soft Comput. 2020, 91, 106208. [Google Scholar] [CrossRef]
- Huang, J.; Huang, S.; Moghaddam, S.K.; Lu, Y.; Wang, G.; Yan, Y.; Shi, X. Deep Reinforcement Learning-Based Dynamic Reconfiguration Planning for Digital Twin-Driven Smart Manufacturing Systems With Reconfigurable Machine Tools. IEEE Trans. Ind. Inform. 2024, 20, 13135–13146. [Google Scholar] [CrossRef]
- Liu, C.; Xu, X.; Hu, D. Multiobjective Reinforcement Learning: A Comprehensive Overview. IEEE Trans. Syst. Man Cybern.-Syst. 2015, 45, 385–398. [Google Scholar]
- Wang, M.; Zhang, J.; Zhang, P.; Cui, L.; Zhang, G. Independent Double DQN-Based Multi-Agent Reinforcement Learning Approach for Online Two-Stage Hybrid Flow Shop Scheduling with Batch Machines. J. Manuf. Syst. 2022, 65, 694–708. [Google Scholar] [CrossRef]
- Lowe, R.; WU, Y.; Tamar, A.; Harb, J.; Abbeel, P.; Mordatch, I. Multi-Agent Actor-Critic for Mixed Cooperative-Competitive Environments. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Wang, Z.; Yang, K.; Li, L.; Lu, Y.; Tao, Y. Traffic Signal Priority Control Based on Shared Experience Multi-Agent Deep Reinforcement Learning. IET Intell. Transp. Syst. 2023, 17, 1363–1379. [Google Scholar] [CrossRef]
- Li, W.; Ni, S. Train Timetabling with the General Learning Environment and Multi-Agent Deep Reinforcement Learning. Transp. Res. Part B Methodol. 2022, 157, 230–251. [Google Scholar] [CrossRef]
- Ying, C.; Chow, A.H.F.; Nguyen, H.T.M.; Chin, K.-S. Multi-Agent Deep Reinforcement Learning for Adaptive Coordinated Metro Service Operations with Flexible Train Composition. Transp. Res. Part B Methodol. 2022, 161, 36–59. [Google Scholar] [CrossRef]
- Rusca, A.; Popa, M.; Rosca, E.; Rosca, M.; Dragu, V.; Rusca, F. Simulation Model for Port Shunting Yards. IOP Conf. Ser. Mater. Sci. Eng. 2016, 145, 082003. [Google Scholar] [CrossRef]
- Mannion, P.; Devlin, S.; Mason, K.; Duggan, J.; Howley, E. Policy Invariance under Reward Transformations for Multi-Objective Reinforcement Learning. Neurocomputing 2017, 263, 60–73. [Google Scholar] [CrossRef]
- Han, B.-A.; Yang, J.-J. Research on Adaptive Job Shop Scheduling Problems Based on Dueling Double DQN. IEEE Access 2020, 8, 186474–186495. [Google Scholar] [CrossRef]
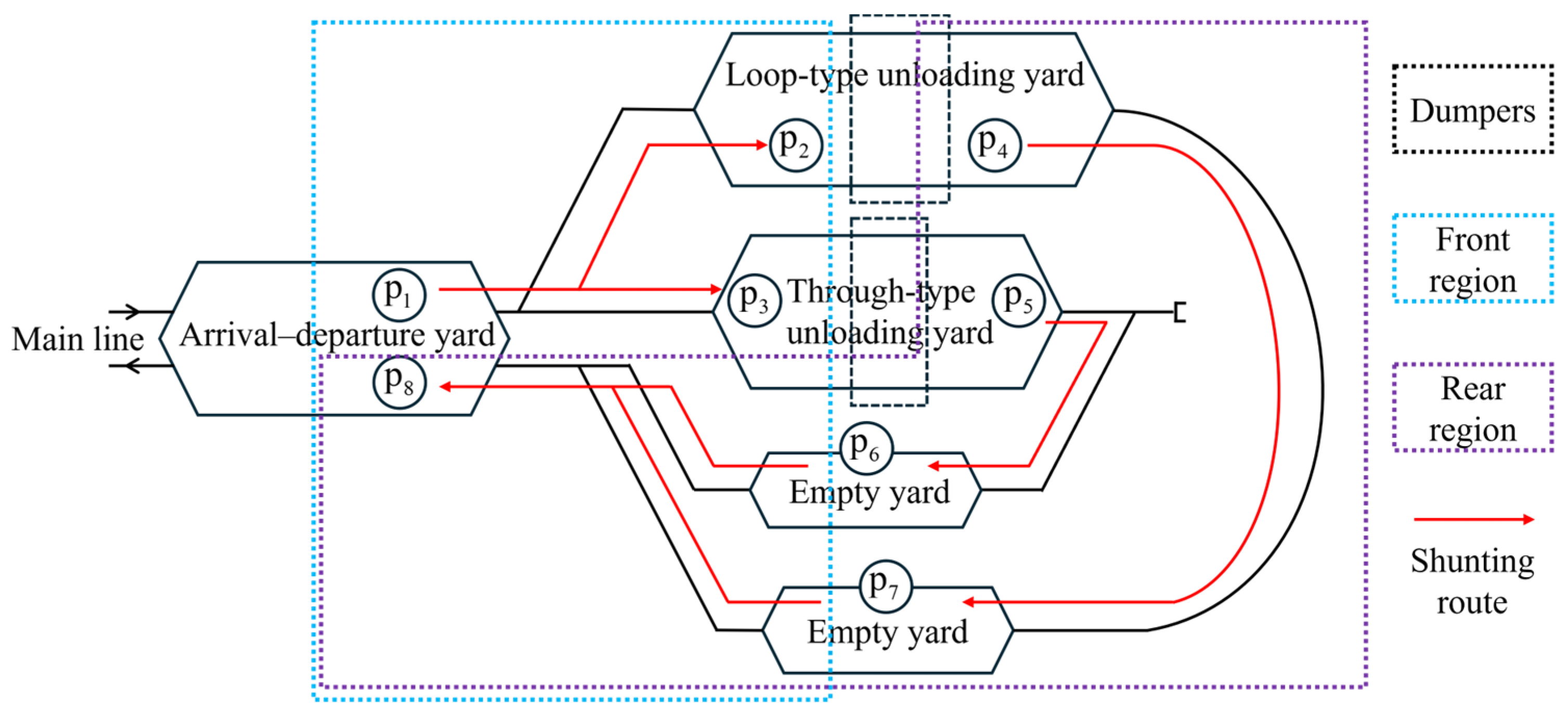
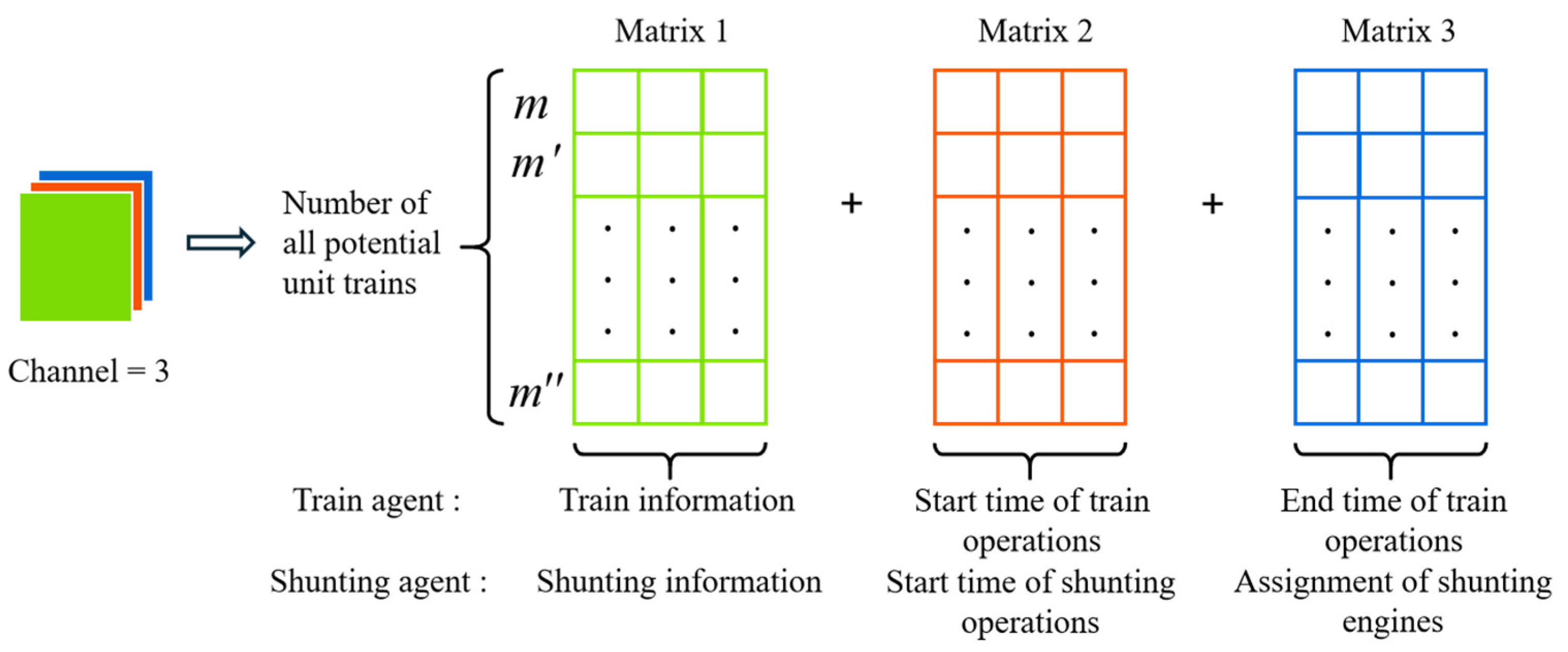


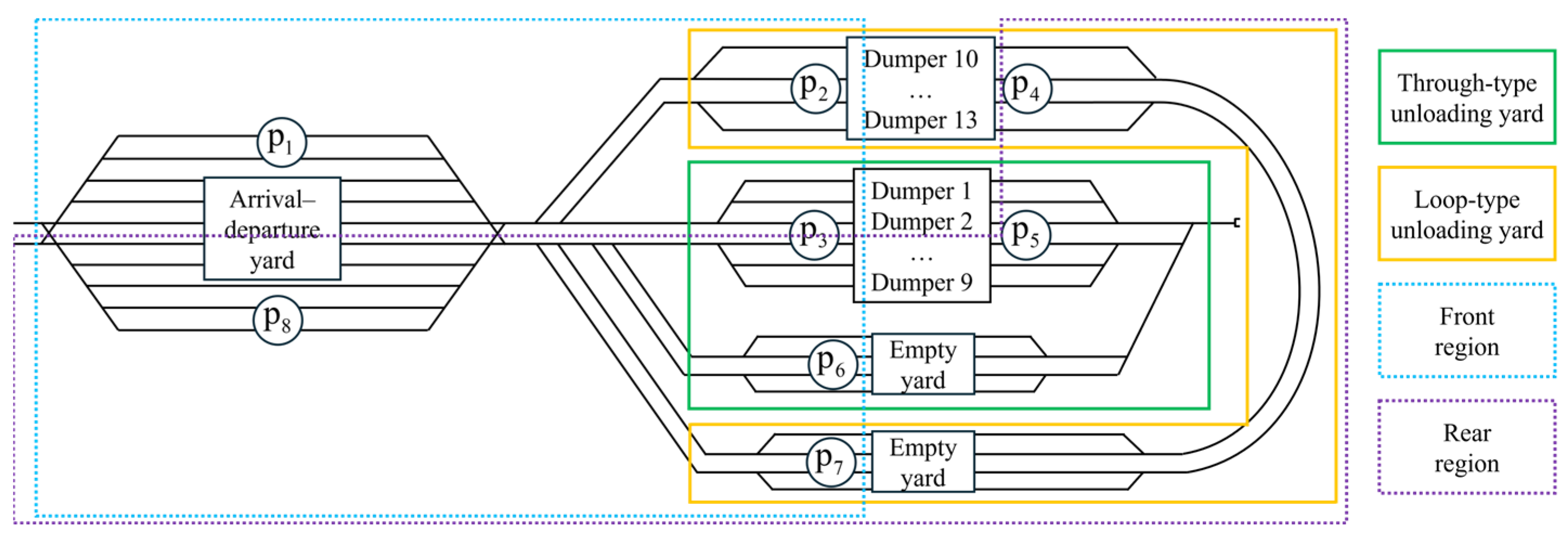
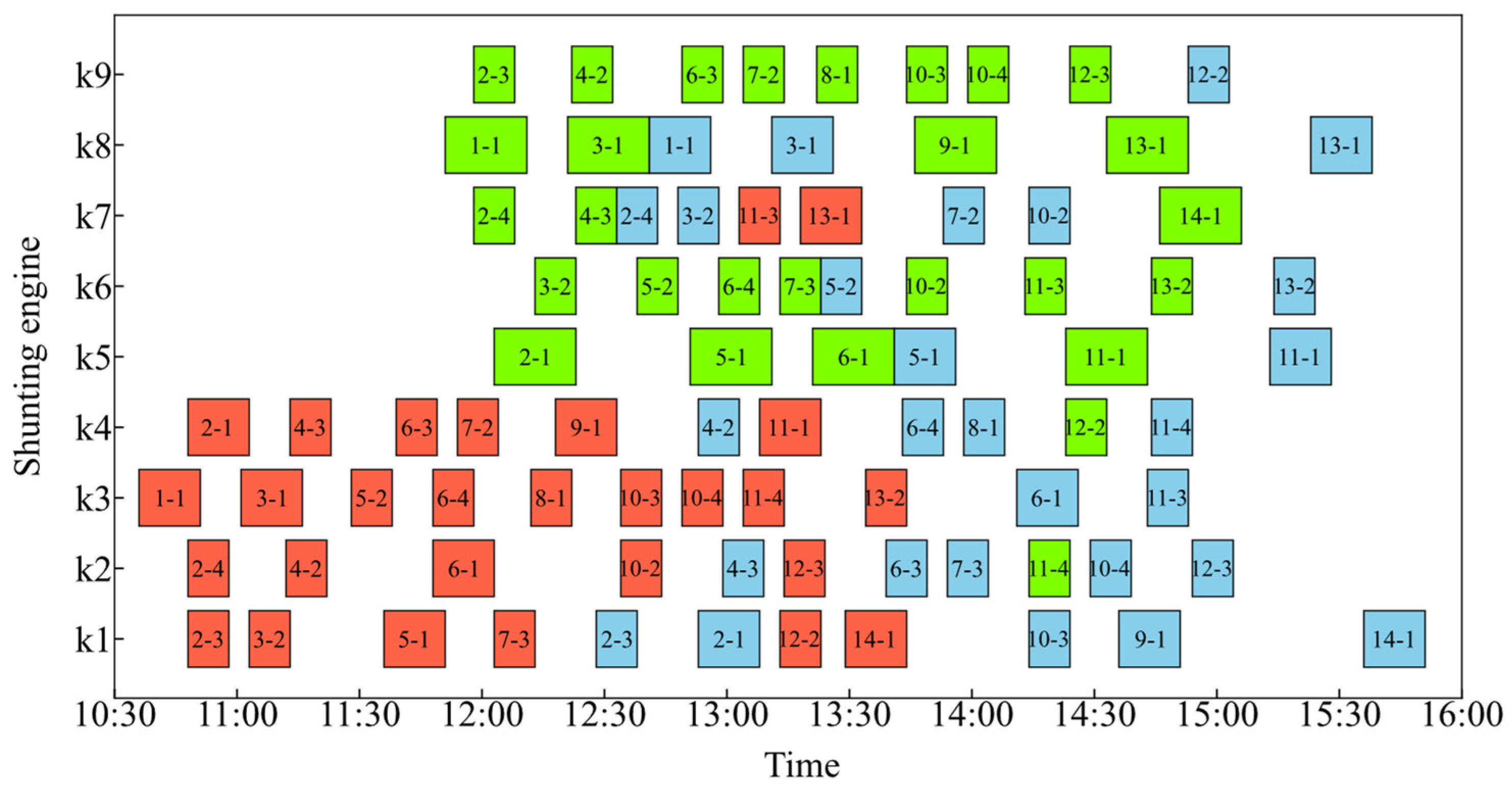
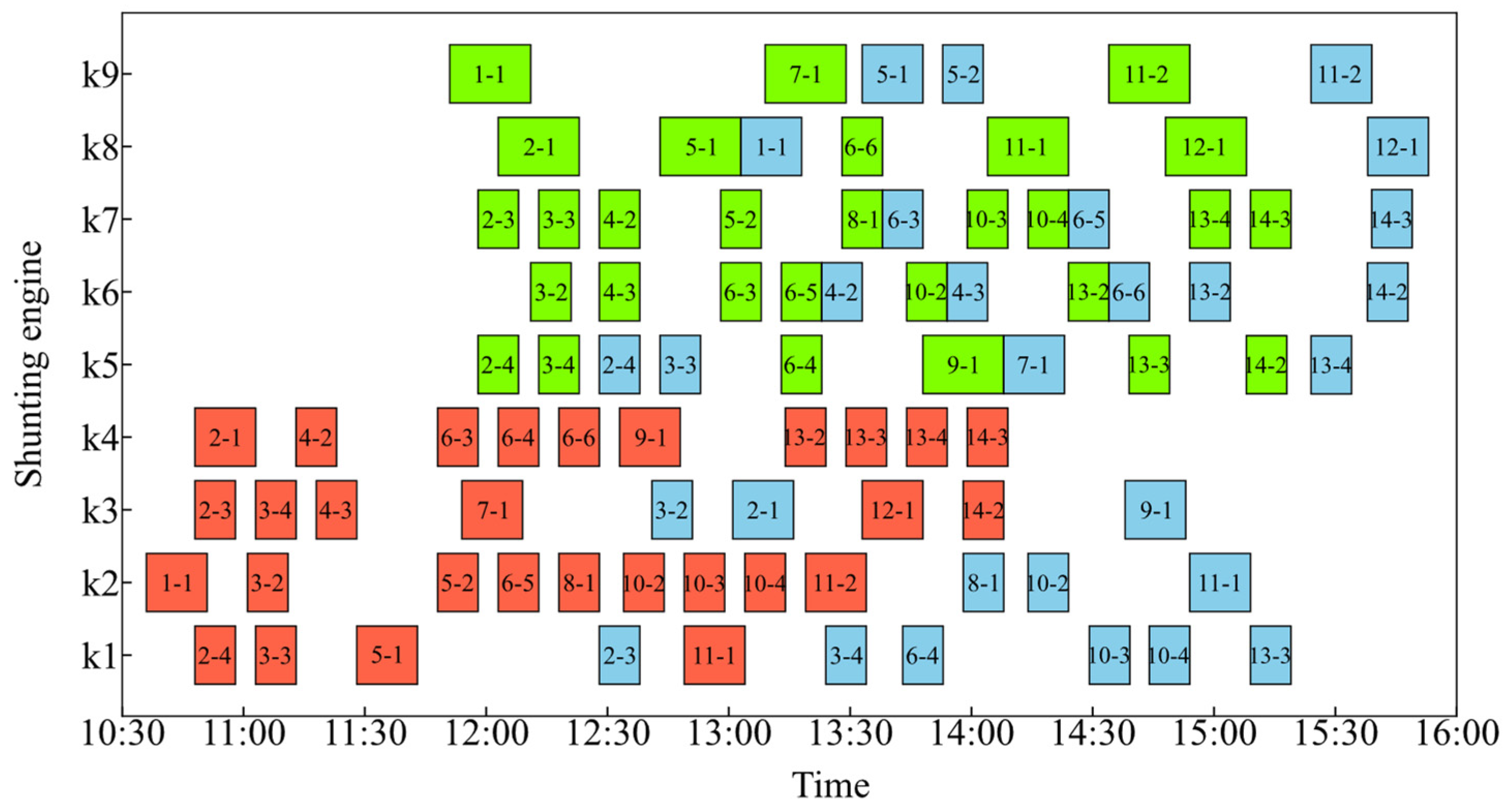

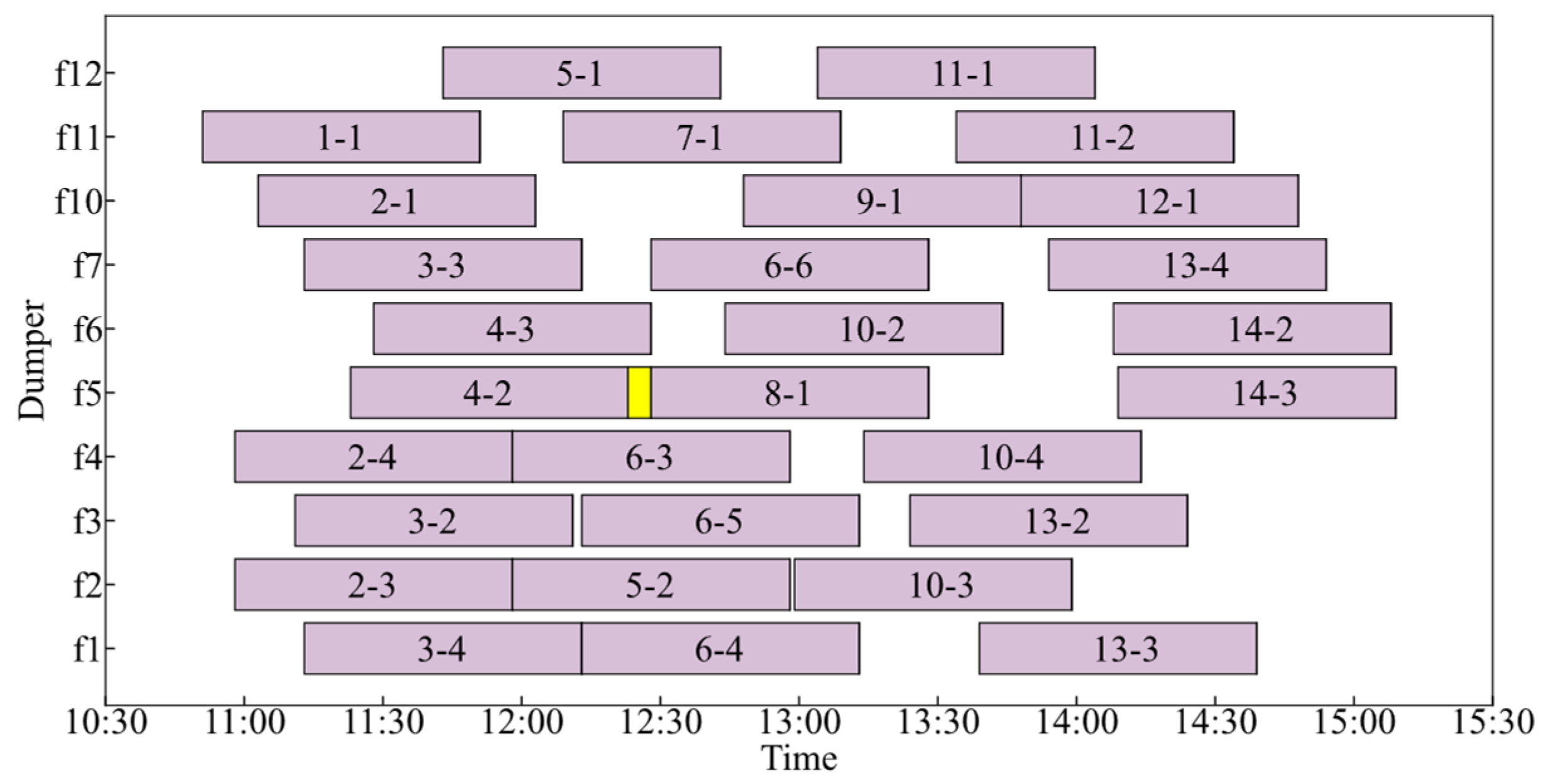
| Weight of Inbound Trains | Options for Splitting Plans |
|---|---|
| 5 kt | (1) 5 kt unit train |
| 10 kt | (1) 10 kt unit train |
| (2) 5 kt unit train + 5 kt unit train | |
| 15 kt | (1) 10 kt unit train + 5 kt unit train |
| (2) 5 kt unit train + 5 kt unit train + 5 kt unit train | |
| 20 kt | (1) 10 kt unit train + 10 kt unit train |
| (2) 10 kt unit train + 5 kt unit train + 5 kt unit train | |
| (3) 5 kt unit train + 5 kt unit train + 5 kt unit train + 5 kt unit train |
| Symbols | Descriptions |
|---|---|
| . | |
| Set of all potential unit trains in inbound train . | |
| Set of dumpers correspond to unit train in inbound train . | |
| . | |
| Set of operation locations, indexed by . | |
| Set of start locations of the shunting operation for unit train in inbound train . | |
| The end location corresponds to the start location of the shunting operation. | |
| Weight and formation of unit train in inbound train , . | |
| The start time and end time of the scheduling period. | |
| Index of discretized times within the scheduling period. | |
| Arrival time of inbound train . | |
| Arrival inspection and splitting time of inbound train . | |
| Shunting operation time of unit train in inbound train at shunting operation location . | |
| Running time of shunting engine from the end location of last operation to the start location of the next operation. | |
| Unloading time of unit train in inbound train . | |
| Coal cleaning time of unit train in inbound train . | |
| Set of outbound trains, indexed by . | |
| Departure time of outbound train . | |
| Combination and departure inspection time of outbound train . | |
| Set of types of railcars, indexed by . | |
| Type of railcars in inbound train . | |
| Set of weight and composition of trains, indexed by . | |
| Composition of inbound train . | |
| A maximum positive constant. |
| Variables | Descriptions |
|---|---|
| Binary variable, 1 if inbound train split into unit train , 0 otherwise. | |
| Binary variable, 1 if unit train in inbound train is assigned to dumper , 0 otherwise. | |
| Binary variable, 1 if unit train in inbound train starts shunting operation at location by shunting engine at time , 0 otherwise. | |
| Binary variable, 1 if shunting operation at location by shunting engine for unit train in inbound train by shunting engine , 0 otherwise. | |
| Binary variable, 1 if unit train in inbound train unloads at dumper , 0 otherwise. | |
| Binary variable, 1 if unit train in inbound train is assigned to outbound train , 0 otherwise. | |
| Binary variable, 1 if type of railcars in outbound train is , 0 otherwise. | |
| Binary variable, 1 if composition of outbound train is , 0 otherwise. | |
| Nonnegative integer variable, unit train in inbound train starts shunting operation time at location by shunting engine . | |
| Nonnegative integer variable, unit train in inbound train starts shunting operation time at location . | |
| Nonnegative integer variable, unit train in inbound train starts unloading operation time. |
| Rules | Descriptions |
|---|---|
| Sequence 1 | Select the unit train with the maximum number of remaining shunting operations. |
| Sequence 2 | Select the unit train with the minimum number of remaining shunting operations. |
| Sequence 3 | Select the unit train that completes unloading operations earliest. |
| Composition 1 | Select the unit train composition with greater capacity in the unloading system. |
| Composition 2 | Select the unit train composition with relatively idle resources in the unloading system. |
| Type 1 | Select the unit train type with the maximum number of types at the station currently. |
| Type 2 | Select the unit train type with the same type of outbound trains waiting for departure. |
| Rules | Descriptions |
|---|---|
| Regional 1 | Select the shunting engine with the earliest available time in the specific region. |
| Regional 2 | Select the shunting engine with the shortest running time to the start location in the specific region. |
| Cross-regional 1 | Select the shunting engine with the earliest available time among regions. |
| Cross-regional 2 | Select the shunting engine with the shortest running time to the start location among regions. |
| Symbols | Descriptions |
|---|---|
| The shunting engines corresponding to the 1st, 2nd, and 3rd shunting operations for the unit train are determined by the shunting agent. | |
| . | |
| . | |
| The selected dumper. | |
| The earliest available time of unloading track in front of and behind the dumper . | |
| The step rewards obtained by the train agent for the 1st, 2nd, and 3rd operations of unit train . | |
| Maximum combination of outbound train with type . | |
| Type of outbound train . | |
| Departure time of unit train . | |
| . | |
| . | |
| The terminal reward of the train agent. | |
| The step rewards obtained by the shunting agent. | |
| Pareto reward. | |
| Weight factor. | |
| Scaling factor of the train agent. | |
| Scaling factor of the shunting agent. | |
| Number of cross-regional operations. | |
| The cumulative reward of the train agent. | |
| The cumulative reward of the shunting agent. |
| Number of Cross-Regional Operations | Terminal Penalty |
|---|---|
| Other |
| Shunting Operation | Operation Time (min) | |
|---|---|---|
| 5 kt Unit Train | 10 kt Unit Train | |
| Arrival yard to unloading yard | ) | ) |
| Unloading yard to empty yard | ) | ) |
| Empty yard to departure yard | ) | ) |
| No. | Inbound Train Number | Arrival Time | Weight | Type | Candidate Set of Unit Train | |
|---|---|---|---|---|---|---|
| 10 kt | 5 kt | |||||
| 1 | 16,165 | 10:06 | 10 kt | C64 | 1-1 | 1-2, 1-3 |
| 2 | 28,053 | 10:18 | 20 kt | C80 | 2-1, 2-2 | 2-3, 2-4, 2-5, 2-6 |
| 3 | 16,749 | 10:29 | 15 kt | C70 | 3-1 | 3-2, 3-3, 3-4 |
| 4 | 15,683 | 10:42 | 10 kt | C64 | 4-1 | 4-2, 4-3 |
| 5 | 16,827 | 10:58 | 15 kt | C80 | 5-1 | 5-2, 5-3, 5-4 |
| 6 | 27,141 | 11:09 | 20 kt | C70 | 6-1, 6-2 | 6-3, 6-4, 6-5, 6-6 |
| 7 | 16,177 | 11:24 | 10 kt | C64 | 7-1 | 7-2, 7-3 |
| 8 | 6503 | 11:34 | 5 kt | C64 | - | 8-1 |
| 9 | 15,729 | 11:48 | 10 kt | C70 | 9-1 | 9-2, 9-3 |
| 10 | 16,845 | 12:04 | 15 kt | C80 | 10-1 | 10-2, 10-3, 10-4 |
| 11 | 28,103 | 12:19 | 20 kt | C80 | 11-1, 11-2 | 11-3, 11-4, 11-5, 11-6 |
| 12 | 15,741 | 12:31 | 10 kt | C70 | 12-1 | 12-2, 12-3 |
| 13 | 16,867 | 12:44 | 15 kt | C80 | 13-1 | 13-2, 13-3, 13-4 |
| 14 | 15,779 | 12:59 | 10 kt | C70 | 14-1 | 14-2, 14-3 |
| No. | Departure Time | Solution 1 | Solution 2 | ||||
|---|---|---|---|---|---|---|---|
| Type | Formation | Combination | Type | Formation | Combination | ||
| 1 | 13:40 | C60 | 20 kt | 1-1, 4-2, 4-3 | C70 | 10 kt | 3-2, 3-3 |
| 2 | 13:55 | C80 | 20 kt | 2-1, 2-3, 2-4 | C80 | 20 kt | 2-1, 2-3, 2-4 |
| 3 | 14:08 | C70 | 15 kt | 3-1, 3-2 | C60 | 15 kt | 1-1, 4-2 |
| 4 | 14:27 | C80 | 15 kt | 5-1, 5-2 | C70 | 15 kt | 3-4, 6-3, 6-4 |
| 5 | 14:42 | C60 | 15 kt | 7-2, 7-3, 8-1 | C80 | 15 kt | 5-1, 5-2 |
| 6 | 14:56 | C70 | 20 kt | 6-1, 6-3, 6-4 | C60 | 20 kt | 4-3, 7-1, 8-1 |
| 7 | 15:12 | C80 | 15 kt | 10-2, 10-3, 10-4 | C80 | 10 kt | 10-2, 10-3 |
| 8 | 15:29 | C80 | 10 kt | 11-3, 11-4 | C70 | 20 kt | 6-5, 6-6, 9-1 |
| 9 | 15:43 | C70 | 20 kt | 9-1, 12-2, 12-3 | C80 | 20 kt | 10-4, 11-1, 13-2 |
| 10 | 16:04 | C80 | 15 kt | 11-1, 13-2 | C80 | 10 kt | 13-3, 13-4 |
| 11 | 16:14 | C80 | 10 kt | 13-1 | C80 | 10 kt | 11-2 |
| 12 | 16:22 | C70 | 10 kt | 14-1 | C70 | 10 kt | 14-2, 14-3 |
| 13 | 16:34 | - | - | - | C70 | 10 kt | 12-1 |
| Horizons | Numbers of Inbound Trains | min) | ||||
|---|---|---|---|---|---|---|
| DAA2C-PRS | NSGA-II | IDQN | A2C-1 | A2C-2 | ||
| 3 h | 13 | (3690.5; 580) | (3925; 610) | (3904; 610) | (3841.5; 585) | (3836; 600) |
| 14 | (3851; 675) | (4562.5; 690) | (4636; 760) | (4092.5; 725) | (4394; 835) | |
| 15 | (4076; 695) | (4503; 720) | (4727.5; 805) | (4568; 735) | (4610.5; 840) | |
| 6 h | 26 | (7621; 1285) | (7910.5; 1360) | (7828; 1390) | (7885.5; 1395) | (7846; 1395) |
| 28 | (7964; 1400) | (8406.5; 1520) | (8640.5; 1605) | (8587.5; 1630) | (8651.5; 1705) | |
| 30 | (8430.5; 1615) | (8991.5; 1805) | (9289; 1755) | (9276; 1790) | (9195; 1840) | |
| 12 h | 52 | (15,943; 2615) | (16,775; 2885) | (16,796.5; 2905) | (16,642; 2890) | (16,581; 2920) |
| 56 | (16,789.5; 2955) | (17,542.5; 3105) | (17,602; 3220) | (17,324; 3215) | (17,751.5; 3195) | |
| 60 | (18,196.5; 3140) | (19,268; 3305) | (19,317.5; 3375) | (19,244.5; 3365) | (19,405; 3410) | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; He, S.; Long, Z.; Tang, H. Integrated Operations Scheduling and Resource Allocation at Heavy Haul Railway Port Stations: A Collaborative Dual-Agent Actor–Critic Reinforcement Learning Framework. Systems 2025, 13, 762. https://doi.org/10.3390/systems13090762
Wu Y, He S, Long Z, Tang H. Integrated Operations Scheduling and Resource Allocation at Heavy Haul Railway Port Stations: A Collaborative Dual-Agent Actor–Critic Reinforcement Learning Framework. Systems. 2025; 13(9):762. https://doi.org/10.3390/systems13090762
Chicago/Turabian StyleWu, Yidi, Shiwei He, Zeyu Long, and Haozhou Tang. 2025. "Integrated Operations Scheduling and Resource Allocation at Heavy Haul Railway Port Stations: A Collaborative Dual-Agent Actor–Critic Reinforcement Learning Framework" Systems 13, no. 9: 762. https://doi.org/10.3390/systems13090762
APA StyleWu, Y., He, S., Long, Z., & Tang, H. (2025). Integrated Operations Scheduling and Resource Allocation at Heavy Haul Railway Port Stations: A Collaborative Dual-Agent Actor–Critic Reinforcement Learning Framework. Systems, 13(9), 762. https://doi.org/10.3390/systems13090762






