Abstract
Pre-disaster and post-disaster allocation strategies are widely investigated as the single optimization problem in humanitarian supply chain management, while integrated decisions including the above two problems are seldom discussed in the existing literature. Here, this paper proposes a mixed-integer programming model to determine these decisions, including the location of central warehouses and emergency storage points and the quantities of relief items pre-deployed and distributed. Specially, two preferences regarding costs and cost-resilience are considered, and a comparison of two models concerning the above preferences is performed. The results are as follows: (i) When the impact of disasters is at a relatively low or moderate level, the cost-oriented model can reduce the government’s financial burden and increase the coverage of relief items. However, when the severity of the disaster is high, the cost resilience-oriented model can respond to the needs of victims within the shortest time, although these needs cannot be completely met. (ii) Increasing the initial inventory level of emergency storage points and enhancing the victims’ tolerance time through social support can effectively reduce the total costs, while increasing the transportation speed can effectively reduce the response delay time. (iii) Adjusting the unit penalty cost can make the total penalty costs and transportation costs decline within a certain range, but such an adjustment has no influence on the response delay time. This paper not only proposes an integrated framework for pre- and post-disaster allocation decisions but also highlights the importance of incorporating resilience into relief item allocation in disaster contexts.
1. Introduction
Over the past few decades, the frequency of natural disasters such as earthquakes, floods, storms, or droughts has significantly increased, causing a large number of casualties and huge economic losses [1]. For instance, the economic losses caused by global natural disasters in 2024 reached at least USD 368 billion [2]. After the occurrence of disasters, it is vital to organize relief items (e.g., food, water, and medical supplies) and promptly transport them to the affected area. Timely assistance relies on two critical aspects, including pre-disaster allocation (also called pre-positioning strategy) and post-disaster allocation of relief items. Pre-positioning refers to the location of strategic warehouses and the storage of a reasonable amount of relief items prior to disasters [3]. The post-disaster allocation addresses the question regarding how to reasonably allocate the pre-deployed items to demand points [4]. It can be seen that pre-disaster allocation is the foundation for rapid response after disasters, while post-disaster allocation relies on the rational layout of pre-positioned resources. In addition, there is a trade-off relationship between pre-positioning costs (e.g., warehousing and maintenance for relief items) and post-disaster allocation costs (e.g., transportation and penalties for unmet demand). Isolated optimization of the pre-positioning decision may lead to a sharp increase in post-disaster allocation costs, while focusing only on the post-disaster allocation decision may increase the risk of loss of life due to insufficient relief items [5]. In this context, the integration of pre-disaster and post-disaster allocation is of great significance for saving lives and reducing costs.
The traditional optimization problem of pre- and post-disaster allocation is related to the minimization of total costs due to limited financial support, disregard for the consequences of disasters, and the ease of characterizing economic goals [6]. However, cost savings are certainly not the primary consideration in humanitarian logistics, which has led to an increasing number of scholars exploring additional goals. In recent years, resilience has received growing attention; this specifically refers to the ability of affected areas to mitigate the impact of disasters, accelerate recovery, and reduce future vulnerability. In humanitarian supply chains, this ability is reflected in how relief items in adequate quantities can be delivered quickly to victims. As Mitsotakis and Kassaras [6] state, decision-makers should make an initial response within the first 72 h after a disaster, and the first 12 h are the most critical period, known as the Standard Response Time [7]. During this period, humanitarian organizations should quickly assess the disaster situation and promptly deliver relief items to the areas in need within this time frame. Thus, the minimization of the response delay time is a critical indicator of the effectiveness of the disaster response. Consequently, how to balance the trade-off relationship between cost minimization and the achievement of resilience measured by the response delay time is an important decision-making issue in humanitarian supply chains.
Based on the aforementioned statements, three research questions are summarized, as follows: (i). How can we formulate a mathematical model to capture the pre- and post-allocation strategy in the presence of resilience? (ii) Is the cost resilience-oriented model superior to the cost-oriented model both in regard to cost reductions and the rapid satisfaction of victims’ needs? (iii) When resilience is taken into account, what factors influence pre- and post-disaster allocation strategies? Furthermore, how should decision-makers select the most appropriate strategy across various disaster scenarios?
To address the above questions, three main tasks are implemented here. Firstly, the response delay time, which is measured by the difference between the victims’ tolerance time and the transportation time of relief items and is used to examine resilience. A pre- and post-allocation strategy is formulated as a mixed integral programming model that integrates the location of central warehouses and emergency storage points, the quantities of relief items pre-deployed in these warehouses, the plan for allocating these items from the central warehouse (emergency storage points) to the emergency storage points (demand points), the severity of disasters, and the different types of relief items, so as to minimize total costs and the response delay time. Secondly, we aimed to explore whether the cost resilience-oriented model is always superior to the cost-oriented model in terms of cost reduction and in meeting the needs of victims. This paper established two models, one with the goal of minimizing total costs, and the other with the goal of minimizing both costs and resilience simultaneously. Computational experiments based on a case study of Xiangtan City were implemented to validate the effectiveness of the proposed model, and the results were calculated using CPLEX solver. Furthermore, this paper set up multiple disaster scenarios (e.g., mild, moderate, and severe) in the computational experiment and compared the costs (e.g., deployment cost, storage cost, transportation cost, and penalty cost), as well as the time to meet the demands under different scenarios, in order to provide decision support for managers. Thirdly, sensitive analyses were employed to test the effects of various factors (e.g., initial inventory level of emergency storage points, victims’ tolerance time, transportation speed of vehicles, unit penalty cost, and disaster severity probability) on the computational results.
The rest of this paper is organized as follows. Section 2 presents a critical literature review. Section 3 proposes the cost- and the cost resilience-oriented model. Section 4 takes the operations of the flood disaster in Xiangtan City, China, as an example to validate the effectiveness of the proposed model. Section 5 summarizes the main findings, theoretical contributions, managerial insights, limitations, and future directions.
2. Literature Review
This section reviews the related literature focusing on the two streams including (i) pre- and post-disaster allocation decisions of relief items, and (ii) resilience and its measurement.
2.1. Pre- and Post-Disaster Allocation Decisions of Relief Items
In the field of humanitarian operations management, pre- and post-disaster allocation decisions were usually studied independently by scholars, with relatively few studies integrating these two issues into a unified analytic framework. In addition, given that these two issues involve critical decisions such as determining inventory levels, selecting facility locations (e.g., central warehouses and emergency storage points), defining distribution quantities, and choosing transportation routes, mathematical optimization methods are widely used in this field [8].
Regarding the pre-disaster allocation strategy, Rawls and Turnquist [9] considered three types of relief items including food, water, and medical supplies, and they proposed a two-stage stochastic mixed-integer programming model to determine the optimal locations and quantities of various emergency supplies to be pre-deployed in the event of a hurricane disaster, so as to minimize expected total costs. Torabi et al. [3] established a two-stage scenario-based hybrid fuzzy-stochastic programming model to investigate the interrelationship among the optimal quantities of pre-deployed relief items, pre-disaster contractual agreements, and post-disaster procurement quantities in the context of an earthquake disaster. Hu and Dong [10] developed a two-stage stochastic mixed-integer programming model to explore the question of supplier selection with the consideration of cost reduction. Turkes et al. [11] established a two-stage stochastic mixed-integer programming model to examine the facility location problem under stochastic capacity constraints across different types and scales of disasters, with the aim of minimizing both unmet demand and response time. Liu et al. [12] established a two-stage stochastic programming model to investigate the pre-deployment of medical resources as well as patient admission and transfer decisions, with the consideration of uncertain demand and random resource consumption. Furthermore, they integrated an AI algorithm based on K-means clustering to address the above problem, which significantly reduced the computational time without compromising solution quality. Desai et al. [13] established a deep-embedded clustering-based approach to predict the optimal pre-deployment locations of ambulances, taking into account the complexities of the transportation system. Moreover, they verified the superiority of the AI-based method by comparing it with traditional clustering algorithms.
Regarding the post-disaster allocation decision, Pradhananga et al. [14] developed a scenario-based two-stage stochastic programming model to address the integrated emergency preparedness and response planning problem under hurricane disasters. Mahtab et al. [15] proposed a robust stochastic mixed-integer programming model to formulate the rescue material distribution plan under flood disasters, considering three types of relief items (e.g., food, water, and medical supplies), with the objectives of minimizing total costs and improving the fairness of relief distribution. Cao et al. [16] constructed a fuzzy three-objective bi-level integer programming model to investigate the optimization problem of multi-stage post-disaster relief distribution under earthquake disasters, aiming to minimize the unmet demand rate, potential environmental risks, and emergency costs. Considering regional variations in disaster impact, Fan et al. [17] developed a dynamic mathematical programming model to optimize post-disaster resource allocation strategies. The model aimed to simultaneously minimize operational costs, reduce the suffering of affected populations, and enhance the fairness of resource distribution. The study incorporated the Q-learning algorithm and demonstrated the effectiveness of deep reinforcement learning in addressing large-scale emergency resource allocation problems.
Regarding the integrated decision including pre- and post-disaster allocation issues, Rezaei-Malek et al. [18] established a two-stage stochastic nonlinear mixed-integer mathematical model for disaster management and pre-positioning of relief items, with the objectives of minimizing total costs, maximizing the weighted utility level of time, demand, and priority, and minimizing the difference in utility levels across demand points. The model focused on the pre-disaster storage and post-disaster allocation of non-perishable items, such as food, medical supplies, clothing, blankets, and tents. Tofighi et al. [19] formulated a novel two-stage scenario-based mixed-uncertainty stochastic programming model aimed at minimizing total costs, total allocation time, and the maximum weighted travel time between distribution centers and demand points. The model analyzed the storage and allocation of essential items such as water, food, healthcare supplies, clothing, and shelters. Amani et al. [20] proposed a data-driven hybrid scenario-based robust optimization model to allocate the relief items in both pre- and post-disaster phases. Specifically, a machine learning technique was employed to cluster casualties based on their locations and the severity of the disaster. Subsequently, an uncertainty technique was applied to characterize key parameters in the hybrid robust optimization model, such as the probability of facility disruption, the number of injured individuals, transportation time, and relief demand. Finally, the epsilon-constraint technique was utilized to solve the proposed bi-objective model. Ehsani et al. [21] investigated an IoT-based humanitarian supply chain network to dynamically collect disaster-related information and enable timely decision-making regarding medical resources allocation. The LP-metric method was applied to solve the proposed model.
2.2. Resilience and Its Measurement
The concept of resilience originated in the ecological field, and it is defined as “a measure of the persistence of systems and their ability to absorb change and disturbance and still maintain the same relationships between populations or state variables” [22]. Along with the annual increase in the frequency of disasters and the severity of their consequences, resilience has increasingly drawn the attention of scholars in the field of disaster management [23]. Although there is no unified understanding of disaster resilience in recent years, the three core capabilities of maintenance, recovery, and transformation are widely recognized as the key components of this concept [24]. Measuring these capacities remain a challenging yet essential task in this field.
Recent studies on resilience measurement have primarily focused on four distinct dimensions. Firstly, resilience can be assessed by calculating the integral area between the baseline performance and the actual performance curve. For example, Ouyan et al. [25] evaluated urban infrastructure resilience by computing the average ratio of the area between the actual performance curve and the time axis to the area between the target performance curve and the time axis. Secondly, attention is given to the time-series characteristics during the system recovery process, which can also be interpreted as the dynamic evolution of the recovery rate. For instance, Almoghathawi et al. [26] innovatively put forward a time-varying function to model network resilience. Specifically, they characterized the resilience of interconnected infrastructure in disaster contexts by the ratio of recovery speed to the degree of loss. Similarly, Zobel [27] employed the cumulative loss percentage within a defined time window as a measurement criterion. Thirdly, resilience can be computed based on the degree of deviation of the system’s function from its baseline state. For example, Hosseini et al. [28] quantified resilience as the rate of change over time of the difference between actual and expected performance levels. Jin et al. [29] defined resilience from a network perspective as the percentage of real-world demands (e.g., travel demands or material supply demands) that a network (e.g., transportation network or supply chain network) can fulfill. Fourthly, beyond the above-mentioned approaches, some scholars have integrated multiple methodologies and proposed hybrid resilience measurement frameworks that incorporate diverse dimensions. For example, Chang and Shinozuka [30] defined resilience as the probability that the initial performance loss after a disruption is below an acceptable threshold and the time required for complete recovery is within an acceptable limit.
2.3. Summary of Recent Studies
Based on the literature review and Table 1, some observations are concluded as follows.

Table 1.
Summary of the existing literature.
- (i)
- Most existing studies focus on optimizing isolated decision-making problems, such as pre- or post-disaster resource allocation, with limited attention paid to integrated strategies. Furthermore, a majority of current studies adopt a two-tier network structure and concentrate on the management of a single category of relief items, which to some extent reduces the applicability of decision-making models in real-world management practices. In the study of the optimization of pre-deployment of relief items, incorporating additional levels into the supply chain network structure can provide a more realistic representation of the problem. One possible extension is to consider multiple warehouses with different capacities, such as setting up a central warehouse at a distant location and local emergency storage points near demand points. Under this setting, decisions concerning facility location, inventory management, and distribution across different levels must be coordinated, thereby improving the overall performance of the logistics system. Additionally, different types of relief items exhibit distinct characteristics and management requirements. Investigating the classification of relief items can facilitate a deeper understanding of management strategies related to procurement, storage, and distribution.
- (ii)
- Currently, cost minimization remains the most commonly used objective function in optimization models. However, an increasing number of scholars have recognized that relying solely on cost minimization as the primary objective in the context of humanitarian relief operations is insufficiently comprehensive. In recent years, resilience has garnered increasing attention from researchers and has been applied in the domains of key infrastructure, supply chain networks, and ecosystems. In the field of supply chain management, resilience is typically characterized by the degree to which system functionality deviates from a benchmark state. When extended to humanitarian supply chains, rapid supply of relief items can significantly enhance rescue efficiency, alleviate the anxiety of victims, and thereby facilitate the restoration of societal stability. Conversely, when relief items cannot be delivered immediately, prolonged delay increases the likelihood of societal instability. Furthermore, considering data availability, this paper adopts response delay time as an indicator to quantify resilience.
- (iii)
- Existing research on the pre- and post-disaster allocation of relief items primarily focuses on public health events, earthquakes, or hurricanes as case backgrounds for discussion. However, the greenhouse effect has contributed to an increase in extreme rainfall events globally, making flood disasters a significant threat to sustainable global development. Effectively pre-positioning an appropriate quantity of relief items and ensuring their efficient distribution to affected populations represent crucial strategies for minimizing economic losses and reducing human casualties. Building upon this context, this paper addresses the challenges associated with the pre-positioning and allocation of relief items in flood disaster scenarios.
3. The Pre- and Post-Disaster Allocation Model of Relief Items Concerning Resilience
3.1. Problem Description
This paper formulates a three-tier supply chain structure consisting of central warehouses, emergency storage points, and demand points. At the stage of preparedness, practitioners should address key issues, such as the location of central warehouses (typically established within existing infrastructures, such as schools, hospitals, and churches) and emergency storage points (usually locates near potential demand points), and the quantities of relief items to be pre-positioned at each level. Generally, central warehouses store a large amount of relief items to meet long-term needs following a disaster, while emergency storage points maintain smaller inventories to temporarily deal with the sudden situation. Given the scattered characteristics of the affected areas (also referred to as demand points), relief items in the central warehouse are first transported to emergency storage points. Then, emergency storage points distribute the appropriate amount of relief items to demand points based on the severity of the disaster. Therefore, after the occurrence of a disaster, the quantities of relief items to be transported from central warehouses to emergency storage points and the quantities of relief items to be distributed from emergency storage points to demand points should be determined by decision makers. The supply chain network for the pre- and post-disaster allocation strategy is presented in Figure 1. Given the limitations of financial budgets, cost minimization is prioritized as the foundational objective in the basic model presented in Section 3.3. Furthermore, to integrate resilience (e.g., minimize the response delay time) into the decision-making process, a cost resilience-oriented model is proposed in Section 3.4.
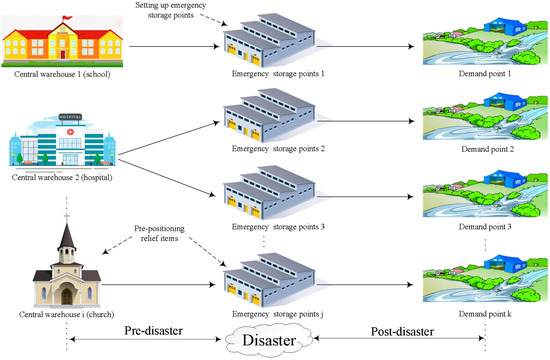
Figure 1.
Supply chain network for pre-positioning and allocation strategies.
Let , , denote the sets of locations of central warehouses, emergency storage points, and demand points, indexed by , , , respectively. In practice, central warehouses are typically located in three categories of existing infrastructures (e.g., schools, hospitals, and churches), and emergency storage points can be divided into a small type and a large type. Let and represent the sets of candidate types for central warehouses and emergency storage points, indexed by , , respectively. Denoting the capacity of a type central warehouse at location , the capacity of a type emergency storage point at location as , , respectively. Denoting the fixed cost of establishing a type emergency storage point at location as .
After the occurrence of disasters, the relief items required by victims can be divided into different types, such as life essentials (e.g., food and water), medical kits, and rescue equipment. Let the sets represent all types of relief items, indexed by . The costs related to each type of relief item include the pre-positioning cost , the management cost paid for central warehouses , the penalty cost for unmet demand , and the unit-distance transportation cost . For the calculation of transportation costs, let the distance from to and the distance from to be denoted as and , respectively.
The uncertainty of disasters is captured by a set of scenarios , indexed by . Let denote the probability of scenario . is the severity of a disaster at demand point . denotes the amount of type of relief item required by demand point under scenario . Given the complexity of disasters, the maximum tolerable time of victims across different demand points is different. Let denote the maximum tolerance time of victims at demand point under scenarios . is the average transportation speed of vehicles. is a huge positive number.
Decision variables are classified into two stages including pre-disaster preparedness and post-disaster response. The pre-disaster decision variables include , , , and , while the post-disaster decision variables consist of and . Specifically, the binary decision variables and are used to decide the questions regarding whether a type central warehouse is pre-deployed at location and whether a type emergency storage point is established at location , respectively. Non-negative continuous variables , , , represent the quantities of a type relief item pre-stocked in a type central warehouse at location , the quantities of a type relief item pre-stocked in a type emergency storage point at location , the quantities of a type relief item delivered from a central warehouse at location to an emergency storage point at location under scenario , and the quantities of a type relief item delivered from an emergency storage point at location to a demand point at location under scenario , respectively. and are set as auxiliary variables. determines whether the quantities of relief items pre-deployed at an emergency storage point at location can fully meet the demand at demand point under scenario . represents the unmet demand of a type relief item at demand point under scenario .
After the occurrence of a disaster, relief items pre-deployed at the emergency storage points are first distributed to demand points. If the quantities of relief items at these emergency storage points are sufficient to meet the demand, there is no need to transfer additional items from central warehouses. In this case, the transportation distance is the distance between the emergency storage points and demand points. Conversely, if the relief items at an emergency storage point cannot meet the demand at a demand point, the transportation distance includes two parts including the distance between emergency storage points and demand points, and the distance between central warehouses and emergency storage points. indicates that relief items were not delivered on time, whereas indicates the timely delivery of relief items. Here, .
3.2. Notations
For the convenience of readers, the following Table 2 summarizes the parameters.

Table 2.
Parameter settings.
3.3. Model 1: Cost-Oriented Model
The subsection proposes a cost-oriented model that the economic aspect is preferentially considered by decision makers. Also, this model is widely used in practical applications.
s.t.
Equation (1) focuses on the minimization of total costs, which include the fixed cost for the pre-disaster deployment at emergency storage points (Part 1), the cost for pre-positioning relief items at central warehouses and the corresponding management cost (Part 2), the cost for pre-positioning relief items at emergency storage points (Part 3), the penalty cost for unmet demand (Part 4), and the transportation cost for the delivery of relief items (final part).
Constraint (2) ensures that the quantity of a type relief item distributed to all emergency storage points does not exceed the pre-positioned quantity at central warehouses. Constraint (3) states that the sum of a type relief item delivered to demand points, and the unmet demand equals the total demand of a type relief item at a demand point. Constraint (4) specifies that the quantity of relief items pre-deployed at central warehouses must not exceed their maximum capacities. Constraint (5) mandates that the volume of relief items distributed from central warehouses to emergency storage points does not exceed the capacities of the established emergency storage points. Constraint (6) ensures that the quantity of relief items pre-positioned at emergency storage points does not exceed their respective capacities. Constraint (7) ensures that in any scenario , each emergency storage point can only fully satisfy the demand of one demand point . Constraint (8) specifies that transportation times across disaster scenarios must not exceed the maximum tolerable time of victims under different disaster severities. Constraint (9) enforces that relief items must be distributed only from the selected central warehouses. Constraint (10) restricts the distribution of relief items to only the established emergency storage points. Constraint (11) limits that only one type of central warehouse can be located in the candidate position. Constraint (12) limits the maximum number of different types of central warehouses that can be established. Constraint (13) requires that the number of a type relief item distributed from central warehouses to emergency storage points should not be less than the quantity distributed from storage points to demand points minus a type relief item pre-positioned at an emergency storage point at location under scenario . Constraint (14) ensures that relief items are pre-deployed in the central warehouse. Constraint (15) ensures the fair access to relief items for the most vulnerable populations, which is captured by a minimum allocation based on the severity of the disaster. Finally, constraints (16)–(22) define all binary and non-negative continuous decision variables.
3.4. Model 2: Cost Resilience-Oriented Model
Recently, resilience characterized by response delay time is important in disaster operations decision-making. Here, the minimization of response delay time is highlighted to mitigate the negative impact on victims. The achievement of this objective typically leads to an increase in total costs, primarily due to the need for additional transportation vehicles and expenses associated with the deployment of sufficient relief items. Therefore, the second model is to examine the trade-off between minimizing response delay time and controlling total costs.
s.t.
Constraints (2)–(7) and (9)–(22)
Equation (23) aims to optimize the model from two perspectives including the minimization of total costs and the minimization of response delay time. The function describing the economic impact is identical to the one presented in Equation (1). The objective function (24) emphasizes the resilience of relief items by incorporating response delay time. When the transportation time exceeds the maximum tolerance time, it indicates that the demand has not been met in a timely manner. The difference between the transportation time and the maximum tolerance time represents the response delay time. The constraints and decision variables of this model are the same as those of the cost-oriented model.
4. Case Study
4.1. Case Study on Xiangtan During the Flood Disaster
This section presents a case study of the flood disaster in Xiangtan to validate the effectiveness of the proposed model. Xiangtan City is located in the central region of Hunan Province, China, and its water system is primarily composed of the Xiangjiang River, as well as the Lian and Juan Rivers. The terrain of the entire city, structured with “four mountains, one river and two waterways” as the framework, forms a hilly basin opening towards the northeast. Frequent rainstorms make floods the most prone natural disaster in Xiangtan. This article takes two main districts in Xiangtan, namely Yuhu and Yuetang district, as the research area. Flood events in these areas were documented by citizens through short-video platforms such as Douyin and Xiaohongshu. These areas include Yaowan (Tangxingsi Community), Xiangtan Railway Station (Railway Station Community), the dormitory of the Municipal Highway Bureau (Community of Yuntang Street Park), Shaoshan Road Community, the Sports Center (Sanjiaoping Community), Xiangtan University (Xiangda Community), the underground commercial street on the west bank (Chezhan Road Community), Jiuhua Lake Park (Heshan Community of Jiuhua Street), Bubugao New World (Hongqi Community of Jiuhua Street), Tianyuan Yucheng (Letang Community of Heping Street), Wulidui Community, Shaziling Community, and Xiacheng Village of Xiacheng Street, as depicted in Figure 2. These locations sourced from social media were cross-validated by official news reports or community announcements. These areas might potentially become demand points. Emergency storage points are established near demand points or on the affiliated streets, while the central warehouse is selected from schools, hospitals, and churches based on available financial budgets.

Figure 2.
The records of flood disasters in Xiangtan.
Figure 3 presents the layout of potential emergency storage points (marked by red dots) and central warehouses (marked by blue dots) in Xiangtan. Based on Figure 2, flood-prone areas have been recognized as potential demand points, and potential emergency storage sites are established near these demand points. The locations of emergency storage points are as follows. Location 1 is Yaowan Sub-district, Location 2 is Xiangtan Station, Location 3 is Park Community, Location 4 is Shaoshan Road Community, Location 5 is Sports Center, Location 6 is Xiangtan University, Location 7 is Chezhan Road Community, Location 8 is Heshan Community, Location 9 is Hongqi Community, Location 10 is Letang Community, Location 11 is Wulidui Sub-district, Location 12 is Shaziling Community, and Location 13 is Xiacheng Sub-district. This paper proposes that any area within a 1.5-km radius containing a school, a hospital, and a church may qualify as a candidate for a central warehouse. Specifically, area A includes Xianggang No. 3 School, a hospital combining traditional Chinese and Western medicine, and Yuetang District High-tech Christian Church. Area B encompasses Fengcheping Square School in Yuhua District, Xiangtan Kelin Hospital, and Nanpanling Church. Area C features Jinting School, Xiangtan Traditional Chinese Medicine Hospital, and Christian Church. Area D comprises Xiangtan No. 4 Middle School, Xiangtan Central Hospital, and Christian Church of Gratitude. Lastly, area E contains Shuguang Middle School, Xiangtan Legal and Inspection Hospital, and Xiangtan Christian Church. Consequently, areas A, B, C, D, and E are all viable candidates for central warehouses.
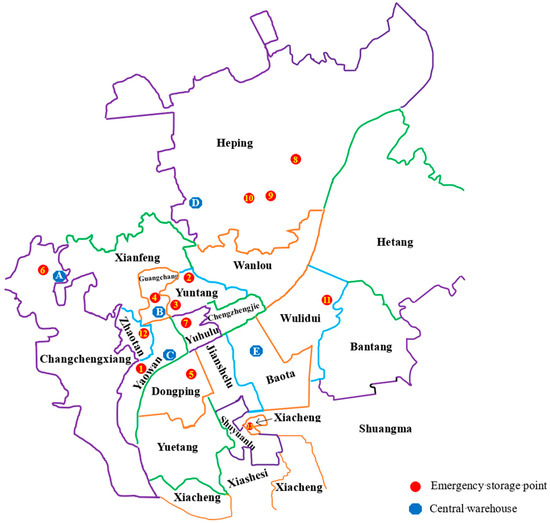
Figure 3.
Layout of potential emergency storage points and central warehouses in Xiangtan.
Three types of central warehouses located in schools, hospitals, and churches are considered, and the corresponding capacities of such central warehouses are set as 20,000, 30,000, and 50,000, respectively. Two types of emergency storage points (e.g., small and large) with capacities of 5000 and 10,000 are defined. Based on the economic development level of Xiangtan City, the construction costs for these two types of emergency storage points are set as 5000 and 8000. The cost for pre-positioning is estimated based on the procurement cost of specific relief items, and the unit penalty cost is assumed to be 10 times the pre-positioning cost [1]. The distances presented in Appendix A and Appendix B, including the distance between central warehouses and emergency storage points and the distance between emergency storage points and demand points, are obtained using Gaode Map. The transportation speed of vehicles is set according to the average speed on urban roads in busy time, which is 30 km per hour. Three severities of scenarios including the mild scenario (), the moderate scenario (), and the severe scenario () are defined. The probabilities for occurrence for these scenarios are 0.5, 0.4, and 0.1, respectively. is relatively large number, and it is set to 99,999. Table 3 presents the cost parameter associated with different types of relief items, including the pre-positioning cost , the penalty cost of unmet demand , the transportation cost for unit distance , and the management cost .

Table 3.
The costs associated with different types of relief items.
Table 4 presents demand points, the maximum tolerance time , the severity of the disaster in affected areas , the demand for different relief items , and the penalty cost of unmet demand under different scenarios.

Table 4.
Parameter settings related to different disaster scenarios.
For the cost-oriented model, the branch-and-bound algorithm embedded in CPLEX solver is employed to calculate the optimal solutions. For the cost resilience-oriented model, the linear weighted sum method is used to solve the model. In detail, this paper first solves a single-objective mixed-integer programming model aimed at minimizing total costs (), which is denoted by the objective function in Equation (23) and constraints (2)–(7) and (9)–(22). Accordingly, the maximum and minimum cost objectives are denoted as and . Secondly, a similar approach is used to resolve another single-objective mixed-integer programming model focused on minimizing response delay time (), which is represented by the objective function in Equation (24) and constraints (2)–(7) and (9)–(22). Consequently, the maximum and minimum resilience objectives are denoted as and . Thirdly, as previously outlined, a linear weighted model is used to transform a multi-objective optimization model into a single-objective one. Specially, the transformed objective is presented as follows:
Specifically, and indicate the importance of total costs and the resilience aspect. In this paper, it is assumed that the importance of economic efficiency and resilience is equal, which implies . Based on the parameter settings, some observations derived from the results of different models are discussed as follows.
4.2. Computational Results
The pre-positioning strategies of the two models under different scenarios are illustrated in Figure 4. Area B is selected as the central warehouse in both models. Furthermore, there is no difference in the quantities pre-deployed at the central warehouse across the two models, which can be discovered in Figure 4.
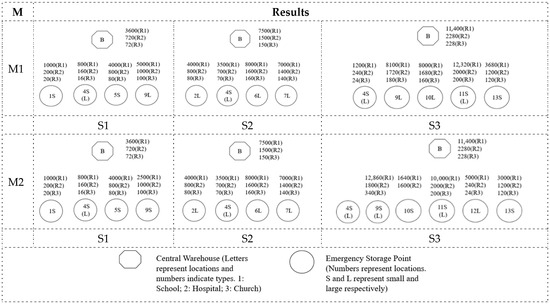
Figure 4.
Pre-disaster allocation decisions of relief items obtained by the proposed two models. M indicates the model proposed in Section 3.
Regarding the locations of emergency storage points, there are notable differences in both location decisions and the quantities of pre-deployed relief items. Specifically, under the slight scenario (S1), the two models are consistent in terms of location selection, but Model 2 only stores 2500 units of R1-type relief items at the emergency storage point 9. This quantity is insufficient to meet the actual demand, whereas Model 1 fully satisfies the demand. Under the moderate scenario (S2), the decision-making strategies of the two models are completely consistent. Under the severe scenario (S3), the strategies derived from the two models are significantly different. Particularly, given the short distance (e.g., 0.1 km) between the emergency storage point 4 and the central warehouse B, Model 2 does not pre-store any relief items at the location 4. Instead, it opts for direct post-disaster distribution of relief items from the central warehouse B to this point.
Table 5 displays the comparative results of the two models in terms of total costs and response delay time under different scenarios.

Table 5.
Comparison of the related costs and response delay time of two models under different scenarios.
Some observations are concluded as follows.
- (i)
- When the severity of a disaster is relatively slight, the establishment of a large-scale emergency storage point at location 9 results in higher setup costs for Model 1 compared to Model 2. Meanwhile, the pre-positioning of 2500 units of life essentials at this location reduces the pre-positioning cost for Model 2 relative to Model 1. However, it also incurs a penalty cost of CNY 125,000 for Model 2. This outcome might be attributed to the fact that Model 2 prioritizes meeting demands across all affected areas yet fails to fully meet localized needs. These findings suggests that in a slight scenario, the cost-oriented model can better achieve the goals of cost reduction and broader coverage of relief items.
- (ii)
- When the severity of a disaster is moderate, establishment cost, pre-positioning cost, management cost, and penalty cost are identical between the two models. In terms of response delay time, Model 2 shows superior performance with a value of 0.88. However, this superiority leads to a higher transportation cost (231,744), compared to Model 1. In this case, decision makers need to evaluate the available financial budget to determine the most appropriate course of action.
- (iii)
- When the severity of a disaster is high, the total costs of Model 2 are significantly higher than those of Model 1. However, the response time delay of Model 2 is considerably lower compared to Model 1. In addition, Model 2 incurs a higher penalty cost, as it prioritizes the timeliness of relief item delivery over fully meeting the demand. This strategy can better mitigate the anxiety of victims in this context [44].
Table 6 and Table 7 display the distribution strategy from the central warehouse B to each emergency storage point and the distribution scheme from emergency storage points to demand points, respectively.

Table 6.
The quantities of relief items distributed from central warehouse B to each emergency storage point.

Table 7.
The quantities of relief items distributed from emergency storage points to demand points.
Some observations are concluded based on the above results.
- (i)
- The results of Model 1 and Model 2 are identical in terms of the distribution scheme from central warehouse B to the emergency storage points. However, notable differences exist between the two models regarding the distribution scheme from emergency storage points to demand points, particularly under high-severity scenarios.
- (ii)
- When the severity of a disaster is high, both models choose location 4 as the transfer station and transport relief items to location 12. However, to deliver life essentials to location 12 more quickly, Model 2 chooses to establish a local emergency storage point and stores 5000 units of life essentials. Model 1 performs better in terms of demand fulfillment. For instance, locations 10 and 13 can receive larger quantities of relief items (e.g., 8000 and 6000 units, respectively). Unfortunately, this outcome requires a higher tolerance time among the affected people.
The main differences between the cost- and cost resilience-oriented models are reflected in various cost and response delay times. Table 8, Table 9 and Table 10 apply the paired-samples t-test test the robustness of the observed differences under different scenarios (i.e., slight, moderate, and severe). For each scenario, this paper generates 30 groups of input data. Since the inherent uncertainty of disasters complicates the accurate estimation of demand locations and the corresponding demand, this paper adjusts these two parameters to test the robustness of the observed results. The parameter setting of input data can be found in Appendix C.

Table 8.
The robustness of the observed differences between cost-oriented and cost resilience-oriented models under the slight scenario.

Table 9.
The robustness of the observed differences between cost-oriented and cost resilience-oriented models under the moderate scenario.

Table 10.
The robustness of the observed differences between cost-oriented and cost resilience-oriented models under the severe scenario.
Table 8, Table 9 and Table 10 confirm the robustness of the above results. Generally speaking, the cost-oriented model is capable of achieving significant financial savings under slight or moderate scenarios. When the severity of a disaster is high, the cost resilience-oriented model can deliver relief items to affected populations more rapidly, although the corresponding cost is much higher than that of the cost-oriented model. Similarly, Cai et al. [45] addressed the issue of medical supplies distribution by converting the delayed response time into deprivation costs. By comparing the results of the BM model (which considers only logistics costs) and the DF model (which incorporates both logistics costs and deprivation costs), they also found that although the DF model incurred higher overall costs, it significantly reduced total response delay time and improved social welfare.
4.3. The Impact of the Initial Inventory Level of Emergency Storage Points on Results
The initial level inventory of emergency storage points may influence the pre-deployment and post-disaster allocation decisions [14]. When the initial inventory level is low, relief items are primarily pre-deployed at central warehouses, which results in a significant increase in management and distribution costs. Conversely, when the initial inventory level is high, relief items are easily distributed from emergency storage points to demand points. However, due to the high uncertainty of disasters, this may lead to either an oversupply or a severe shortage of relief items. Therefore, this subsection analyzes the impact of the initial inventory level of emergency storage points on the computational results of different models. Parameter setting that captures the severe scenario is used here. Figure 5 presents the impact on penalty costs and transportation costs.
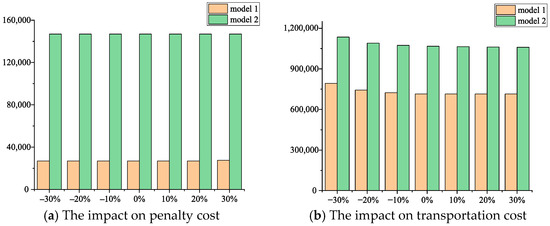
Figure 5.
The impact of initial inventory level on various costs.
From Figure 5a, the penalty cost is almost unaffected by the initial inventory level of emergency storage points. From Figure 5b, as the initial inventory level increases, the transportation cost exhibits a downward trend, with a more pronounced decline observed in Model 1, especially when the initial inventory level is relatively low (from 70% to 100%). A similar result was also discovered by Celik et al. [46].
Figure 6 displays the impact on response delay time. It is observed that the response time remains unchanged with the increase in initial inventory levels in both models. According to the model formulation, the response delay time is determined by the post-disaster allocation strategy, whereas the initial inventory level primarily influences pre-positioning decisions (e.g., management expenses or deployment costs).
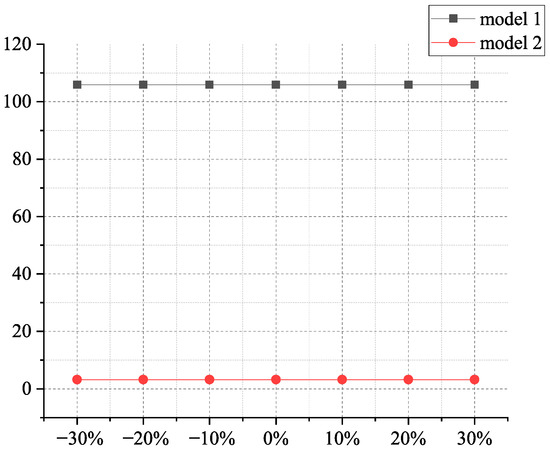
Figure 6.
The impact of initial inventory level on response delay time.
4.4. The Impact of Victims’ Tolerance Time on Results
Recently, a limited number of studies have attempted to integrate victims’ psychology into disaster operations management [47]. As Rabiei et al. [48] portrayed, perceived social supports can alleviate fear of disasters, thereby reducing victims’ anxiety and increasing their tolerance for waiting for emergency rescue. Therefore, this paper suggests that the care and concern demonstrated by community or society towards victims can prolong their tolerance for the shortage of relief items. Figure 7 presents the impact of victims’ tolerance time on penalty costs and transportation costs.
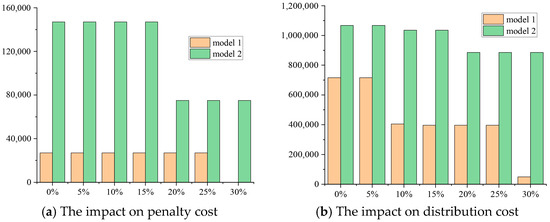
Figure 7.
The impact of residents’ tolerance time on various costs.
From Figure 7, the penalty costs and transportation costs of Model 2 are significantly higher than those of Model 1. This is because Model 2 focuses on the optimization of rapid response to victims’ immediate demands rather than fully satisfying the total quantity of relief items required. Furthermore, it is found that an increase in tolerance time has a great influence on the reduction in total costs. Specifically, when the tolerance time increases sufficiently (reaching 30%), both the penalty costs and the transportation costs significantly reduce. Cai et al. [45] found that the reduction in total costs was most significant when the latest delivery time exceeded the expected time by no more than 30 min. Meanwhile, as the latest delivery time increased, the average total delay time for material delivery gradually decreased to 30 min, and in 80% of the scenarios, the total delivery time delay was improved by 90%.
Figure 8 shows the impact on response delay time. In Model 1, the delay time increases (from 105.87 to 137.16) as the victims’ tolerance time increases, whereas in Model 2, the delay time decreases. This result indicates that the cost-oriented model is extremely unsuitable for emergency rescue activities, especially under high-severity disaster conditions. In other words, as victims’ tolerance for unmet needs increases, this leniency may lead relief item providers to increasingly ignore victims’ emotions and needs, thereby leading to a large-scale shortage of relief supplies. A similar finding was reported by [49].
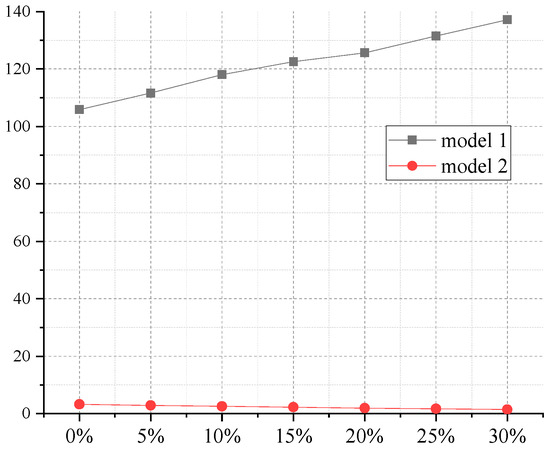
Figure 8.
The impact of residents’ tolerance time on response delay time.
4.5. The Impact of Transportation Speed on Results
Relief allocation is carried out through the existing transportation network. Even under normal conditions, traffic congestion can reduce transportation speed. Following a disaster, various factors, such as damaged infrastructures, changed traffic patterns, and emergency traffic control, can exacerbate traffic congestion [50]. Conversely, if roads are not affected by disasters, decision makers may increase transportation speed to reduce travel time. Therefore, this subsection conducts a sensitivity analysis to examine the impact of transportation speed on computational results. Figure 9 presents the impact on penalty costs and transportation costs.
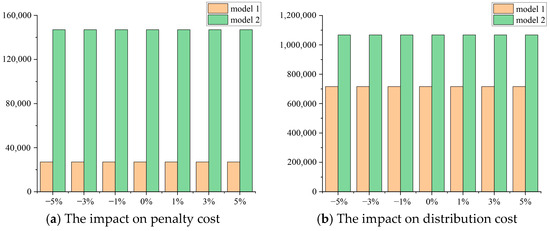
Figure 9.
The impact of transportation speed on various costs.
From Figure 9, the results show that when transportation speed increases from −5% to 5%, both penalty costs and transportation costs remain unchanged. A possible reason is that these costs are solely dependent on the distances between locations. Hu and Dong [10] pointed out that penalty costs were only related to the integrity of delivered relief items, and transportation costs were only associated with transportation distance. Therefore, neither penalty costs nor transportation costs have a direct relationship with transportation speed, which supports the findings of this paper.
Figure 10 demonstrates the impact on response delay time. In Model 1, when the range of transportation speed is changed from −5% to 0%, the delay time first decreases and then increases, with an inflection point at −3%. Otherwise, when the speed range is from 0% to 5%, the delay time initially increases and then decreases, with an inflection point at 3%. This suggests the existence of an optimal transportation speed range that influences delay time. Decision makers should evaluate the extent and nature of transportation speed’s impact on operational costs. In Model 2, the response delay time consistently decreases as transportation speed increases. Specifically, when the transportation speed varies from −5% to 5%, the decline rate is 29.4%. This result indicates that in Model 2, the faster the transportation speed, the more conducive it is to reduce response delay time. Yilmaz et al. [51] pointed out that most countries face the problem of partial or complete infrastructure damage following severe disasters. Debris from damaged buildings can slow down the speed of vehicles, increasing the total travel time of the optimal route from 635.2 s to 2788.9 s. It is evident that the reduced vehicle speed prolongs total travel time, which is consistent with the findings of this paper.
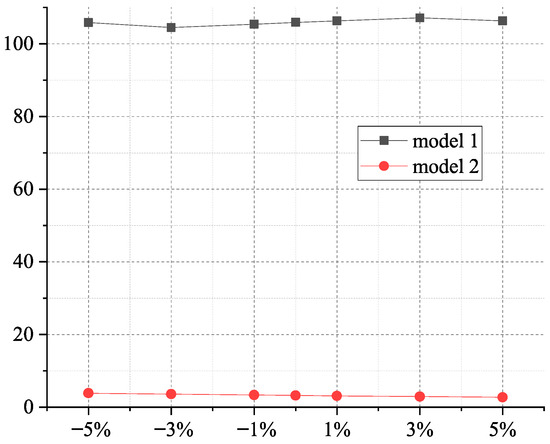
Figure 10.
The impact of transportation speed on response delay time.
4.6. The Impact of Unit Penalty Cost
The unit penalty cost has a significant impact on unmet demand. When the unit penalty cost is low, it reduces the incentive to fulfill demand, resulting in a substantial increase in unmet demand rate. Conversely, when the unit penalty cost is high, the emergency management department tends to deploy more relief items to satisfy a greater portion of the demand [10]. An excessively high unit penalty cost may lead to an increase in total costs, which in turn diminishes the motivation of emergency management department to meet demand in a timely manner. Therefore, it is necessary to determine an appropriate unit penalty cost that balances total costs, response time, and demand coverage. Thus, this subsection discusses the impact of unit penalty cost on computational results. Figure 11 shows the impact on total penalty costs and transportation cost.
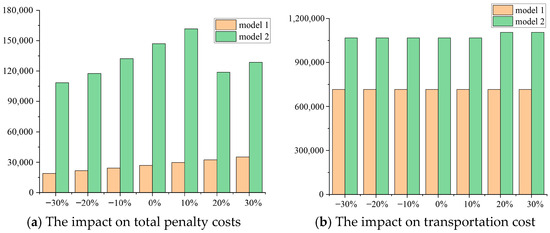
Figure 11.
The impact of the unit penalty cost on various costs.
From Figure 11a, in Model 1, the total penalty cost is always increasing as the unit penalty cost grows. In Model 2, when the variation in the unit penalty cost falls within the interval [−30%, 10%], the total penalty cost increases as the unit penalty cost rises. When the variation is within [20%, 30%], the total penalty cost first decreases and then increases, which fully confirms the existence of an optimal penalty cost threshold as previously discussed.
From Figure 11b, in terms of transportation costs, both Model 1 and Model 2 show the same trend. Specifically, when the unit penalty cost ranges from −30% to 20%, transportation costs show a relatively gentle upward trend as the unit penalty cost increases. The findings of Hu et al. [52] supported the above results. More precisely, when the unit penalty cost increases from −25% to 25%, the economic costs of the post-disaster allocation model (e.g., transportation costs, procurement costs) show a relatively gentle upward trend. When the unit penalty cost changes from +25% to +50%, the cost of the model increases significantly (approximately 2.2 times compared to the benchmark), but the total penalty cost decreases by 5%. It can be seen that the adjustment of the unit penalty cost may lead to a trade-off between total costs and the total penalty cost.
Furthermore, by comparing Figure 11a and Figure 11b, it can be found that although increasing the unit penalty cost can reduce the total penalty cost, the corresponding rise in transportation costs imposes greater economic pressure on relief item providers, thereby reducing their motivations for timely delivery. In this case, decision makers need to strike a balance between total penalty cost and transportation costs, which are in a trade-off relationship.
Figure 12 shows the impact on response delay time, and the results show that the unit penalty cost has no impact on response delay time.
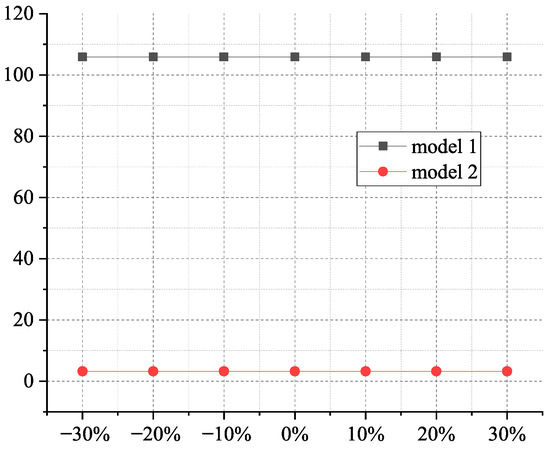
Figure 12.
The impact of unit penalty cost on response delay time.
4.7. The Impact of Disaster Severity Probability
The severity of demand points is a critical factor to be considered in emergency rescue operations. This not only reflects the principle of fairness but also demonstrates a commitment to humanitarian care. However, when the aforementioned demands need to be prioritized, the transportation cost associated with emergency material dispatch increases significantly. Figure 13a shows that disaster severity probability has no influence on penalty costs in Model 1, since the cost-oriented model is able to completely allocate relief items under conditions of sufficient financial budget and without consideration of victims’ waiting time. For the cost resilience-oriented model, total penalty costs decrease with the growth in disaster severity probability. This is attributed to the fact that with higher disaster severity, more emergency storage points are established near demand points to better meet the needs of disaster victims, thereby reducing the unmet demand rate. Figure 13b indicates that transportation costs continuously increase as the severity of the disaster intensifies, and this increase is more pronounced in Model 2. This outcome is intuitive, but the significant difference in transportation costs is a key consideration for managers when implementing specific allocation strategies.
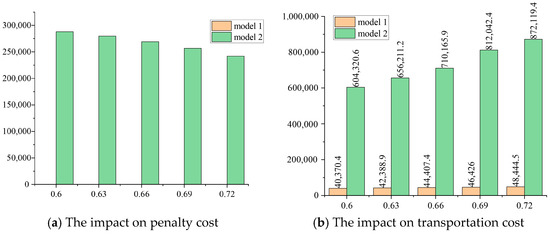
Figure 13.
The impact of disaster severity probability on various costs.
Figure 13 demonstrates that as the disaster severity probability increases, the total penalty cost is constantly decreasing, which confirms the constraining effect of the penalty cost on relief item providers. On the contrary, if there is no penalty cost, enterprises will prioritize providing to regions with higher bids. This strategy is unreasonable in humanitarian operations. Hu and Dong [10] discovered that suppliers typically prioritize high-risk areas, which may result in delayed responses to low-risk regions.
Figure 14 shows that as disaster severity increases, the response delay time of Model 1 gradually decreases, and the decline is quite significant. This is because under more severe disaster conditions, both society and relief item providers exhibit heightened awareness and responsiveness, leading to prioritized and concentrated delivery of sufficient relief items to affected areas [16]. In contrast, the severity of disasters has no significant influence on response delay time in Model 2, which clearly highlights the unique value of the cost resilience-oriented model in managing severe disaster scenarios.
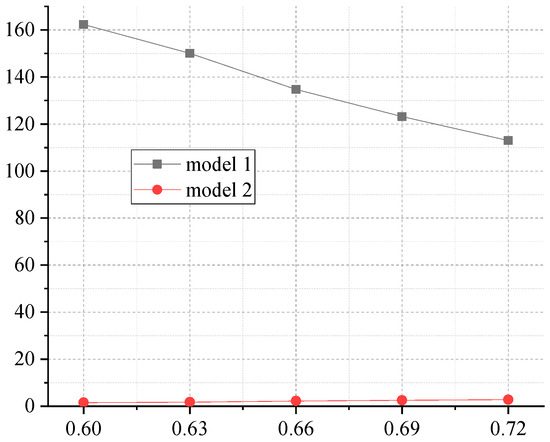
Figure 14.
The impact of disaster severity probability on response delay time.
5. Conclusions
5.1. Main Findings
This paper focuses on the integrated optimization problem related to allocation strategies of relief items in both pre-disaster and post-disaster phases, aiming to save lives and reduce the suffering of victims. The above problem is formulated as a mixed integer programming model that considers three types of relief items, victims’ tolerance time, disaster severity, and various scenarios and their corresponding probabilities. The model determines key decisions such as the location of central warehouses and emergency storage points, the pre-deployed quantities of relief items, and the distribution quantities during the response phase. To highlight the importance of resilience, this paper establishes two models including a cost-oriented model (Model 1) and a cost resilience-oriented model (Model 2). A real-world case study based on the emergency response practices of Xiangtan, China, is conducted to validate the effectiveness of the proposed models. Further, a comparison analysis between two models is carried out, and sensitive analyses are employed to test the impact of factors (e.g., initial inventory level of emergency storage points, victims’ tolerance time, transportation speed, unit penalty cost, and disaster severity probability) on the computational results. The main findings are summarized as follows.
- (i)
- Model 1 demonstrates superior performance in cost control and improving the coverage of relief items. Model 2 excels in reducing the waiting time, although Model 2 may not guarantee full and timely satisfaction of all demand in disaster-affected areas.
- (ii)
- The initial inventory level of emergency storage points primarily influences post-disaster allocation decisions, with the most significant impact on transportation costs. Increasing the initial inventory can significantly reduce transportation costs, but may lead to higher inventory costs, thereby increasing the financial burden on the government. In addition, the uncertainty of disaster occurrences complicates pre-positioning decisions. Storing large quantities of unused relief items over long periods without a disaster may raise public concerns and scrutiny.
- (iii)
- When the victims’ tolerance time is extended through social support mechanisms, decision-making strategies that focus solely on economic goals may excessively prioritize cost minimization, which is unfavorable for accelerating rescue efforts and reducing the harm to victims. In contrast, Model 2 can effectively balance cost reduction with minimizing victim suffering.
- (iv)
- Transportation speed has no impact on cost control but significantly affects response delay time. Specifically, as transportation speed increases, the cost-resilience balanced model can continuously reduce response time, whereas the cost-oriented model only shows a downward trend within a time window.
- (v)
- Unit penalty cost influences both total penalty cost and transportation costs, although its effect is more pronounced within a specific threshold range.
5.2. Theoretical Contributions
Several theoretical contributions are summarized as follows. Firstly, while most scholars have studied pre-positioning and post-disaster allocation decisions as independent optimization problems [15,41,43], this paper focuses on the joint decision-making from an integrated perspective, establishing a clear linkage between the two stages.
Secondly, driven by commercial supply chain practices, cost minimization is a commonly used decision-making objective, offering advantages in reducing expenditures and expanding the coverage of relief items. However, in disaster contexts, prioritizing the urgent needs of victims for relief items becomes a more critical objective, especially in the case of extreme disasters. To address this, this paper proposes two models (e.g., a cost-oriented model and a cost resilience-oriented model) to discuss their applicability across different scenarios. This approach not only affirms the practices of predecessors but also better improves their research results. Moreover, previous studies on disaster response optimization have primarily focused on public health events, earthquakes, and hurricanes, with less attention paid to flood disasters. This study contributes to the literature by expanding the application scope to include flood-related scenarios.
Thirdly, although lots of existing studies have examined the impact of disaster scenarios on decision-making, they typically focus only on the probability of occurrence and seldom consider the varying severity levels of the same disaster type across different regions. This paper explicitly considers regional severity differences into the model and further demonstrates the superior performance of the cost resilience-oriented model in such contexts.
5.3. Managerial Insights
Managerial insights are concluded as follows. Firstly, it is found that when the initial inventory level at emergency storage points exceeds 70%, the marginal improvement in cost reduction becomes minimal. This suggests that managers should estimate the initial inventory level for each emergency storage point based on historical data. In addition, a “gradient-based” pre-storage plan should be implemented across the entire region. In detail, relief items should be fully deployed in disaster-prone areas, while the pre-storage quantity in areas with fewer disasters should be reduced, with the exact quantities determined through model-based decision-making. Secondly, managers should pay attention to the psychological comfort of victims, which plays a significant role in extending rescue time and enhancing rescue effectiveness. In the case of severe disasters, the cost resilience-oriented model (Model 2) demonstrates greater effectiveness in cost reduction and minimizing casualties. Thirdly, increasing transportation speed can reduce response delay time. Under a limited government budget, this paper proposes adjusting transportation speed to achieve the desired response efficiency. When budgetary resources are sufficient, developing a high-speed transportation network (e.g., deploying emergency corridors for drones) can further enhance emergency management performance.
For the implementation of the proposed model, several challenges must be considered and addressed. Firstly, regarding data availability, the input data of the proposed model, such as potential demand points, severity levels of demand points, dynamic demands of disaster-stricken regions, or the real-time status of roads or transportation networks, are relatively difficult to obtain quickly. In addition, the demand from affected areas evolves dynamically as the disaster unfolds, making accurate and timely data collection challenging [12]. Fortunately, this paper can prioritize the delivery of relief items to high-risk areas based on the severity of the disaster. After the initial distribution, updated demand information can be collected and used to guide the subsequent reallocation of relief items.
Secondly, legal constraints, such as cross-regional relief distribution, the responsibilities of different departments, compulsory requisition and compensation procedures during emergencies, pre-positioning regulations, and accountability for the consequences of suboptimal allocation decisions, should be considered during the implementation of the proposed model [16].
Thirdly, political coordination is hard to be achieved due to the differences in objectives, regulations, and priorities [53]. For example, the question regarding how to establish a temporary central organization (in China, such an organization is called a command center) to coordinate actions among various regions, different levels (e.g., village, town, city, and province in China), and diverse departments (e.g., meteorological, public security, transportation, fire and rescue, as well as natural resources management) is hard to be addressed, especially when these organizations have no prior coordination experience. Additionally, public–private coordination (e.g., third-party logistics companies, churches, and schools sponsored by private organizations) should be also considered as potential challenges since private organizations typically prioritize profit maximization.
5.4. Limitations and Future Directions
Limitations and future directions are summarized in the following aspects.
Firstly, although this paper has taken into account the uncertainty of disaster scenarios, it remains valuable to integrate more complex sources of uncertainty into the joint decision-making framework for pre- and post-disaster resource allocation. Robust or distributionally robust optimization is recommended for future research. For instance, ambiguity sets combined with historical data can be used to characterize demand patterns and the probability distribution of disaster severity [54]. The distributionally robust optimization model can then be transformed into a worst-case formulation, with solutions derived using improved algorithmic techniques.
Secondly, this paper characterizes disaster resilience by response delay time. Although resilience concept is hard to be captured using mathematical model method [55], the hybrid methods (e.g., complex network theory) are also recommended for future research in humanitarian supply chain network design [56]. For example, the density of network is able to discuss the redundancy of humanitarian supply chain networks.
Thirdly, although the commercial solver CPLEX is able to solve the results of cases in this paper, it is hard to address the large-scale cases due to the vast solution space. Therefore, in the future, it is necessary to combine multiple solution approaches (e.g., heuristics, metaheuristics, and hybrid methods) into complex disaster environments, thus expanding the scalability of the proposed model.
Fourthly, using social media data to identity potential demand points is an innovative approach. However, key limitations include the ignorance of heavily affected areas with no social media users or poor network connectivity, as well as the exaggeration of the severity of disasters. Additionally, the data used in this study require long-term accumulation from different sources. Future research should consider combining digital technologies (e.g., Internet of Things, digital twin, and blockchain) to collect richer and more timely data, thereby improving the accuracy of model predictions [57,58]. In particular, to capture the dynamic and real-time information in digital environments, optimization models with a sliding time window approach are recommended [59].
Author Contributions
Conceptualization, F.Z., C.C. and X.L.; methodology, Y.L. and H.Y.; software, Y.L.; validation, F.Z., C.C. and H.Y.; formal analysis, F.Z. and Y.L.; investigation, Y.L. and F.Z.; resources, F.Z. and Y.L.; data curation, F.Z. and Y.L.; writing—original draft preparation, Y.L. and F.Z.; writing—review and editing, F.Z., H.Y., C.C. and X.L.; visualization, Y.L. and F.Z.; supervision, F.Z., C.C. and X.L.; project administration, F.Z., C.C. and X.L.; funding acquisition, F.Z., C.C. and X.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by the National Natural Science Foundation of China Grant No. 72404237 and 72374036; the Chongqing Social Science Planning Project on the Theoretical System of Socialism with Chinese Characteristics Grant No. 2024ZTZD15; the Natural Science Foundation of Chongqing, China Grant No. CSTB2025NSCQ-GPX0138; the Science and Technology Research Program of Chongqing Municipal Education Commission, China Grant No. KJZD-K202500801; the National Social Science Fund of China Grant No. 22BGL243; the MOE Layout Foundation of Humanities and Social Sciences Grant No. 23YJC630225; the Natural Science Foundation of Hunan Province Grant No. 2025JJ60233; the Excellent Youth Project of the Education Department of Hunan Province Grant No. 23B0145; the Social Science Planning Project in Chongqing Grant No. 2023BS037.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Correction Statement
This article has been republished with a minor correction to the Data Availability Statement. This change does not affect the scientific content of the article.
Appendix A

Table A1.
The distances between central warehouses and the emergency storage points.
Table A1.
The distances between central warehouses and the emergency storage points.
| Dij | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 9 | 6.7 | 5.9 | 6.1 | 2 | 13 | 5.2 | 14 | 12 | 12 | 6.8 | 8.1 | 2.9 |
| B | 2.8 | 2.5 | 1.3 | 0.1 | 4.2 | 5.5 | 2.2 | 11 | 8.4 | 8.9 | 9.2 | 2.7 | 6.9 |
| C | 1.7 | 3.6 | 2.8 | 2.6 | 3.2 | 7.8 | 1.4 | 11 | 8 | 8.3 | 9 | 3 | 6.1 |
| D | 4.6 | 1.5 | 1.8 | 2.6 | 3.9 | 7.8 | 1.4 | 7.9 | 5.3 | 5.6 | 7 | 4.5 | 6.6 |
| E | 4.6 | 2.4 | 3.2 | 3.4 | 3.9 | 8.4 | 2.1 | 7.7 | 5.6 | 5.9 | 6.9 | 5.9 | 6.6 |
Appendix B

Table A2.
The distances between emergency storage points and demand points.
Table A2.
The distances between emergency storage points and demand points.
| Djk | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Yaowan (1) | 1.1 | 4.5 | 4 | 2.9 | 8.5 | 5.7 | 3.8 | 11 | 9.6 | 10 | 8.3 | 3.5 | 12 |
| Xiangtan Railway Station (2) | 4.3 | 1.4 | 1.7 | 2.5 | 4.9 | 7.4 | 2.5 | 7.9 | 5.5 | 6.6 | 4.3 | 5 | 8.5 |
| Municipal Highway Bureau (3) | 3.5 | 2.1 | 0.5 | 1.2 | 4.1 | 6.3 | 1.7 | 9.4 | 6.6 | 6.3 | 5.8 | 4 | 8.3 |
| Shaoshan Road Community (4) | 3.3 | 2.4 | 1.2 | 0.5 | 4.4 | 5.9 | 1.9 | 11 | 7.7 | 7.4 | 6.5 | 3.5 | 8.5 |
| Sports Center (5) | 3.8 | 3.8 | 3.6 | 4.1 | 0.5 | 13 | 2.9 | 12 | 9.8 | 9.9 | 4.3 | 7.8 | 4.9 |
| Xiangtan University (6) | 7.3 | 7.7 | 6.9 | 5.4 | 13 | 0.5 | 8.1 | 12 | 8.4 | 7.9 | 11 | 5.2 | 16 |
| Hexi Underground Commercial Street (7) | 2.7 | 1.2 | 2.2 | 2.2 | 3.3 | 6.7 | 1 | 9.6 | 6.2 | 7.8 | 5 | 4.1 | 7.5 |
| Jiuhua Lake Park (8) | 11 | 8 | 10 | 11 | 14 | 11 | 9.4 | 3.2 | 4.2 | 4.1 | 7.9 | 13 | 20 |
| Bubugao New World (9) | 9.2 | 5.4 | 7.6 | 8.3 | 13 | 8.6 | 6.8 | 2.9 | 2.4 | 1.7 | 6.4 | 9.4 | 11 |
| Tianyuan Yucheng (10) | 9.5 | 5.7 | 7.9 | 8.7 | 13 | 9 | 7.1 | 3.3 | 2.7 | 1.9 | 6.7 | 9.7 | 11 |
| Wulidui Community (11) | 9.4 | 7.1 | 8.5 | 9.7 | 6.2 | 14 | 8.5 | 9.9 | 8.8 | 10 | 2.2 | 12 | 5.8 |
| Shaziling Community (12) | 3.5 | 4.4 | 3.9 | 2.8 | 7.3 | 4.5 | 4.1 | 13 | 11 | 10 | 9.7 | 0.5 | 12 |
| Xiacheng Village (13) | 6.6 | 6.5 | 6.3 | 6.8 | 3.5 | 15 | 5.6 | 13 | 11 | 13 | 5.5 | 9.6 | 2.6 |
Appendix C

Table A3.
Parameter settings under the slight scenario.
Table A3.
Parameter settings under the slight scenario.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| DP | 1, 5, 6, 7 | 1, 5, 7, 8 | 1, 5, 8, 9 | 1, 5, 9, 10 | 1, 5, 10, 11 | 1, 5, 11, 12 | 1, 5, 12, 13 | 1, 6, 7, 8 | 1, 6, 8, 9 | 1, 6, 9, 10 |
| 2, 2, 2, 2 | 1, 1, 1, 1 | 0.67, 0.67, 0.67, 0.67 | 0.5, 0.5, 0.5, 0.5 | 0.4, 0.4, 0.4, 0.4 | 2, 2, 1, 1 | 2, 1, 0.67, 0.5 | 1, 1, 0.67, 0.5 | 0.67, 1, 0.67, 0.5 | 0.5, 1, 0.67, 0.5 | |
| 0.1, 0.1, 0.1, 0.1 | 0.2, 0.2, 0.2, 0.2 | 0.3, 0.3, 0.3, 0.3 | 0.4, 0.4, 0.4, 0.4 | 0.5, 0.5, 0.5, 0.5 | 0.1, 0.1, 0.2, 0.2 | 0.1, 0.2, 0.3, 0.4 | 0.2, 0.2, 0.3, 0.4 | 0.3, 0.2, 0.3, 0.4 | 0.4, 0.2, 0.3, 0.4 | |
| R1 | 1000, 1000, 1000, 1000 | 2000, 2000, 2000, 2000 | 3000, 3000, 3000, 3000 | 4000, 4000, 4000, 4000 | 5000, 5000, 5000, 5000 | 1000, 1000, 2000, 2000 | 1000, 2000, 3000, 4000 | 2000, 2000, 3000, 4000 | 3000, 2000, 3000, 4000 | 4000, 2000, 3000, 4000 |
| R2 | 200, 200, 200, 200 | 400, 400, 400, 400 | 600, 600, 600, 600 | 800, 800, 800, 800 | 1000, 1000, 1000, 1000 | 200, 200, 400, 400 | 200, 400, 600, 800 | 400, 400, 600, 800 | 600, 400, 600, 800 | 800, 400, 600, 800 |
| R3 | 20, 20, 20, 20 | 40, 40, 40, 40 | 60, 60, 60, 60 | 80, 80, 80, 80 | 100, 100, 100, 100 | 20, 20, 40, 40 | 20, 40, 60, 80 | 40, 40, 60, 80 | 60, 40, 60, 80 | 80, 40, 60, 80 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
| DP | 1, 6, 10, 11 | 1, 6, 11, 12 | 1, 6, 12, 13 | 1, 7, 8, 9 | 1, 7, 9, 10 | 1, 7, 10, 11 | 1, 7, 11, 12 | 1, 7, 12, 13 | 1, 8, 9, 10 | 1, 8, 10, 11 |
| 0.4, 1, 0.67, 0.5 | 2, 0.67, 0.67, 0.5 | 2, 0.5, 0.67, 0.5 | 2, 0.4, 0.67, 0.5 | 2, 1, 0.5, 0.5 | 2, 1, 0.4, 0.5 | 2, 1, 0.67, 0.4 | 1, 0.67, 0.5, 0.4 | 0.67, 0.67, 0.5, 0.4 | 0.5, 0.67, 0.5, 0.4 | |
| 0.5, 0.2, 0.3, 0.4 | 0.1, 0.3, 0.3, 0.4 | 0.1, 0.4, 0.3, 0.4 | 0.1, 0.5, 0.3, 0.4 | 0.1, 0.2, 0.4, 0.4 | 0.1, 0.2, 0.5, 0.4 | 0.1, 0.2, 0.3, 0.5 | 0.2, 0.3, 0.4, 0.5 | 0.3, 0.3, 0.4, 0.5 | 0.4, 0.3, 0.4, 0.5 | |
| R1 | 5000, 2000, 3000, 4000 | 1000, 3000, 3000, 4000 | 1000, 3000, 3000, 4000 | 1000, 5000, 3000, 4000 | 1000, 2000, 4000, 4000 | 1000, 2000, 5000, 4000 | 1000, 2000, 3000, 5000 | 2000, 3000, 4000, 5000 | 3000, 3000, 4000, 5000 | 4000, 3000, 4000, 5000 |
| R2 | 1000, 400, 600, 800 | 200, 600, 600, 800 | 200, 800, 600, 800 | 200, 1000, 600, 800 | 200, 400, 800, 800 | 200, 400, 1000, 800 | 200, 400, 600, 1000 | 400, 600, 800, 1000 | 600, 600, 800, 1000 | 800, 600, 800, 1000 |
| R3 | 100, 40, 60, 80 | 20, 60, 60, 80 | 20, 80, 60, 80 | 20, 100, 60, 80 | 20, 40, 80, 80 | 20, 40, 100, 80 | 20, 40, 60, 100 | 40, 60, 80, 100 | 60, 60, 80, 100 | 80, 60, 80, 100 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | |
| DP | 1, 8, 11, 12 | 1, 8, 12, 13 | 1, 9, 10, 11 | 1, 9, 11, 12 | 1, 9, 12, 13 | 1, 10, 11, 12 | 1, 10, 12, 13 | 2, 3, 5, 6 | 2, 3, 5, 7 | 2, 3, 5, 8 |
| 0.4, 0.67, 0.5, 0.4 | 1, 0.5, 0.5, 0.4 | 1, 0.4, 0.5, 0.4 | 1, 0.67, 0.4, 0.4 | 0.67, 1, 0.5, 0.4 | 0.67, 1, 0.4, 0.4 | 0.5, 0.67, 1, 0.67 | 0.4, 0.4, 0.5, 0.67 | 0.4, 0.4, 0.67, 0.67 | 0.4, 0.4, 0.5, 0.5 | |
| 0.5, 0.3, 0.4, 0.5 | 0.2, 0.4, 0.4, 0.5 | 0.2, 0.5, 0.4, 0.5 | 0.2, 0.3, 0.5, 0.5 | 0.3, 0.2, 0.4, 0.5 | 0.3, 0.2, 0.5, 0.5 | 0.4, 0.3, 0.2, 0.3 | 0.5, 0.5, 0.4, 0.3 | 0.5, 0.5, 0.3, 0.3 | 0.5, 0.5, 0.4, 0.4 | |
| R1 | 5000, 3000, 4000, 5000 | 2000, 4000, 4000, 5000 | 2000, 5000, 4000, 5000 | 2000, 3000, 5000, 5000 | 3000, 2000, 4000, 5000 | 3000, 2000, 5000, 5000 | 4000, 3000, 2000, 3000 | 5000, 5000, 4000, 3000 | 5000, 5000, 3000, 3000 | 5000, 5000, 4000, 4000 |
| R2 | 1000, 600, 800, 1000 | 400, 800, 800, 1000 | 400, 1000, 800, 1000 | 400, 600, 1000, 1000 | 600, 400, 800, 1000 | 600, 400, 1000, 1000 | 800, 600, 400, 600 | 1000, 1000, 800, 600 | 1000, 1000, 600, 600 | 1000, 1000, 800, 800 |
| R3 | 100, 60, 80, 100 | 40, 80. 80, 100 | 40, 100, 80, 100 | 40, 60, 100, 100 | 60, 40, 80, 100 | 60, 40, 100, 100 | 80, 60, 40, 60 | 100, 100, 80, 60 | 100, 100, 60, 60 | 100, 100, 80, 80 |

Table A4.
Parameter settings under the moderate scenario.
Table A4.
Parameter settings under the moderate scenario.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| DP | 1, 2, 3, 4 | 2, 3, 4, 5 | 3, 4, 5, 6 | 4, 5, 6, 7 | 5, 6, 7, 8 | 6, 7, 8, 9 | 7, 8, 9, 10 | 8, 9, 10, 11 | 9, 10, 11, 12 | 10, 11, 12, 13 |
| 0.5, 0.5, 0.5, 0.5 | 0.4, 0.4, 0.4, 0.4 | 0.36, 0.36, 0.36, 0.36 | 0.33, 0.33, 0.33, 0.33 | 0.5, 0.4, 0.5, 0.5 | 0.5, 0.36, 0.5, 0.5 | 0.5, 0.33, 0.5, 0.5 | 0.5, 0.5, 0.4, 0.36 | 0.5, 0.5, 0.36, 0.36 | 0.5, 0.5, 0.33, 0.36 | |
| 0.4, 0.4, 0.4, 0.4 | 0.5, 0.5, 0.5, 0.5 | 0.55, 0.55, 0.55, 0.55 | 0.6, 0.6, 0.6, 0.6 | 0.4, 0.5, 0.4, 0.4 | 0.4, 0.55, 0.4, 0.4 | 0.4, 0.6, 0.4, 0.4 | 0.4, 0.4, 0.5, 0.55 | 0.4, 0.4, 0.55, 0.55 | 0.4, 0.4, 0.6, 0.55 | |
| R1 | 4000, 4000, 4000, 4000 | 5000, 5000, 5000, 5000 | 5500, 5500, 5500, 5500 | 6000, 6000, 6000, 6000 | 4000, 5000, 4000, 4000 | 4000, 5500, 4000, 4000 | 4000, 6000, 4000, 4000 | 4000, 4000, 5000, 5500 | 4000, 4000, 5500, 5500 | 4000, 4000, 6000, 5500 |
| R2 | 800, 800, 800, 800 | 1000, 1000, 1000, 1000 | 1100, 1100, 1100, 1100 | 1200, 1200, 1200, 1200 | 800, 1000, 800, 800 | 800, 1100, 800, 800 | 800, 1200, 800, 800 | 800, 800, 1000, 1100 | 800, 800, 1100, 1100 | 800, 800, 1200, 1100 |
| R3 | 80, 80, 80, 80 | 100, 100, 100, 100 | 110, 110, 110, 110 | 120, 120, 120, 120 | 80, 100, 80, 80 | 80, 110, 80, 80 | 80, 120, 80, 80 | 80, 80, 100, 110 | 80, 80, 110, 110 | 80, 80, 120, 110 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
| DP | 1, 2, 4, 5 | 1, 2, 5, 6 | 1, 2, 6, 7 | 1, 2, 7, 8, | 1, 2, 8, 9 | 1, 2, 9, 10 | 1, 2, 10, 11 | 1, 2, 11, 12 | 1, 2, 12, 13 | 1, 3, 4, 5 |
| 0.5, 0.5, 0.4, 0.33 | 0.5, 0.4, 0.36, 0.33 | 0.4, 0.36, 0.36, 0.33 | 0.5, 0.33, 0.36, 0.33 | 0.5, 0.4, 0.33, 0.33 | 0.4, 0.4, 0.36, 0.33 | 0.36, 0.4, 0.36, 0.33 | 0.33, 0.4, 0.36, 0.33 | 0.4, 0.36, 0.36, 0.33 | 0.4, 0.33, 0.36, 0.33 | |
| 0.4, 0.4, 0.5, 0.6 | 0.4, 0.5, 0.55, 0.6 | 0.5, 0.55, 0.55, 0.6 | 0.4, 0.6, 0.55, 0.6 | 0.4, 0.5, 0.6, 0.6 | 0.5, 0.5, 0.55, 0.6 | 0.55, 0.5, 0.55, 0.6 | 0.6, 0.5, 0.55, 0.6 | 0.5, 0.55, 0.55, 0.6 | 0.5, 0.6, 0.55, 0.6 | |
| R1 | 4000, 4000, 5000, 6000 | 4000, 5000, 5500, 6000 | 5000, 5500, 5500, 6000 | 4000, 6000, 5500, 6000 | 4000, 5000, 6000, 6000 | 5000, 5000, 5500, 6000 | 5500, 5000, 5500, 6000 | 6000, 5000, 5500, 6000 | 5000, 5500, 5500, 6000 | 5000, 6000, 5500, 6000 |
| R2 | 800, 800, 100, 1200 | 800, 1000, 1100, 1200 | 1000, 1100, 1100, 1200 | 800, 1200, 1100, 1200 | 800, 1000, 1200, 1200 | 1000, 1000, 1100, 1200 | 1100, 1000, 1100, 1200 | 1200, 1000, 1100, 1200 | 1000, 1100, 1100, 1200 | 1000, 1200, 1100, 1200 |
| R3 | 80, 80, 100, 120 | 80, 100, 110, 120 | 100, 110, 110, 120 | 80, 120, 110, 120 | 80, 100, 120, 120 | 100, 100, 110, 120 | 110, 100, 110, 120 | 120, 100, 110, 120 | 100, 110, 110, 120 | 100, 120, 110, 120 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | |
| DP | 1, 4, 6, 7 | 1, 3, 5, 6 | 1, 3, 6, 7 | 1, 3, 7, 8 | 1, 3, 8, 9 | 1, 3, 9, 10 | 1, 3, 10, 11 | 1, 3, 11, 12 | 1, 3, 12, 13 | 1, 4, 5, 6 |
| 0.4, 0.4, 0.33, 0.33 | 0.36, 0.5, 0.4, 0.33 | 0.36, 0.4, 0.4, 0.33 | 0.36, 0.36, 0.4, 0.33 | 0.36, 0.33, 0.4, 0.33 | 0.33, 0.36, 0.36, 0.36 | 0.33, 0.4, 0.4, 0.4 | 0.33, 0.5, 0.5, 0.5 | 0.33, 0.36, 0.36, 0.4 | 0.33, 0.36, 0.4, 0.5 | |
| 0.5, 0.5, 0.6, 0.6 | 0.55, 0.4, 0.5, 0.6 | 0.55, 0.5, 0.5, 0.6 | 0.55, 0.55, 0.5, 0.6 | 0.55, 0.6, 0.5, 0.6 | 0.6, 0.55, 0.55, 0.55 | 0.6, 0.5, 0.5, 0., 5 | 0.6, 0.4, 0.4, 0.4 | 0.6, 0.55, 0.55, 0.5 | 0.6, 0.55, 0.5, 0.4 | |
| R1 | 5000, 5000, 6000, 6000 | 5500, 4000, 5000, 6000 | 5500, 5000, 5000, 6000 | 5500, 5500, 5000, 6000 | 5500, 6000, 5000, 6000 | 6000, 5500, 5500, 5500 | 6000, 5000, 5000, 5000 | 6000, 4000, 4000, 4000, | 6000, 5500, 5500, 5000 | 6000, 5500, 5000, 4000 |
| R2 | 1000, 1000, 1200, 1200 | 1100, 800, 1000, 1200 | 1100, 1000, 1000, 1200 | 1100, 1100, 1000, 1200 | 1100, 1200, 1000, 1200 | 1200, 1100, 1100, 1100 | 1200, 1000, 1000, 1000 | 1200, 800, 800, 800 | 1200, 1100, 1100, 1000 | 1200, 1100, 1000, 800 |
| R3 | 100, 100, 120, 120 | 110, 80, 100, 120 | 110, 100, 100, 120 | 110, 110, 100, 120 | 110, 120, 100, 120 | 120, 110, 110, 110 | 120, 100, 100, 100 | 120, 80, 80, 80 | 120, 110, 110, 100 | 120, 110, 100, 80 |

Table A5.
Parameter settings under the severe scenario.
Table A5.
Parameter settings under the severe scenario.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| DP | 1, 2, 7, 8, 9 | 1, 2, 8, 9, 10 | 1, 2, 9, 10, 11 | 1, 2, 10, 11, 12 | 1, 2, 11, 12, 13 | 1, 3, 5, 6, 7 | 1, 3, 6, 7, 8 | 1, 3, 7, 8, 9 | 1, 3, 8, 9, 10 | 1, 3, 9, 10, 11 |
| 0.33, 0.33, 0.33, 0.33, 0.33 | 0.29, 0.29, 0.29, 0.29, 0.29 | 0.29, 0.33, 0.33, 0.33, 0.33 | 0.29, 0.29, 0.33, 0.33, 0.33 | 0.29, 0.29, 0.29, 0.33, 0.33 | 0.29, 0.29, 0.29, 0.29, 0.33 | 0.33, 0.29, 0.29, 0.29, 0.29 | 0.33, 0.33, 0.29, 0.29, 0.29 | 0.33, 0.33, 0.33, 0.29, 0.29 | 0.33, 0.33, 0.33, 0.33, 0.29 | |
| 0.6, 0.6, 0.6, 0.6, 0.6 | 0.7, 0.7, 0.7, 0.7, 0.7 | 0.7, 0.6, 0.6, 0.6, 0.6 | 0.7, 0.7, 0.6, 0.6, 0.6 | 0.7, 0.7, 0.7, 0.6, 0.6 | 0.7, 0.7, 0.7, 0.7, 0.6 | 0.6, 0.7, 0.7, 0.7, 0.7 | 0.6, 0.6, 0.7, 0.7, 0.7 | 0.6, 0.6, 0.6, 0.7, 0.7 | 0.6, 0.6, 0.6, 0.6, 0.7 | |
| R1 | 6000, 6000, 6000, 6000, 6000 | 7000, 7000, 7000, 7000, 7000 | 7000, 6000, 6000, 6000, 6000 | 7000, 7000, 6000, 6000, 6000 | 7000, 7000, 7000, 6000, 6000 | 7000, 7000, 7000, 7000, 6000 | 6000, 7000, 7000, 7000, 7000 | 6000, 6000, 7000, 7000, 7000 | 6000, 6000, 6000, 7000, 7000 | 6000, 6000, 6000, 6000, 7000 |
| R2 | 1200, 1200, 1200, 1200, 1200 | 1400, 1400, 1400, 1400, 1400 | 1400, 1200, 1200, 1200, 1200 | 1400, 1400, 1200, 1200, 1200 | 1400, 1400, 1400, 1200, 1200 | 1400, 1400, 1400, 1400, 1200 | 1200, 1400, 1400, 1400, 1400 | 1200, 1200, 1400, 1400, 1400 | 1200, 1200, 1200, 1400, 1400 | 1200, 1200, 1200, 1200, 1400 |
| R3 | 120, 120, 120, 120, 120 | 140, 140, 140, 140, 140 | 140, 120, 120, 120, 120 | 140, 140, 120, 120, 120 | 140, 140, 140, 120, 120 | 140, 140, 140, 140, 120 | 120, 140, 140, 140, 140 | 120, 120, 140, 140, 140 | 120, 120, 120, 140, 140 | 120, 120, 120, 120, 140 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
| DP | 1, 2, 4, 5, 6 | 1, 2, 5, 6, 7 | 1, 2, 6, 7, 8 | 1, 5, 6, 7, 8 | 1, 6, 7, 8, 9 | 1, 7, 8, 9, 10 | 1, 8, 9, 10, 11 | 1, 9, 10, 11, 12 | 5, 6, 7, 8, 9 | 1, 2, 3, 4, 5 |
| 0.32, 0.32, 0.32, 0.32, 0.32 | 0.3, 0.3, 0.3, 0.3, 0.3 | 0.29, 0.29, 0.29, 0.29, 0.29 | 0.28, 0.28, 0.28, 0.28, 0.28 | 0.33, 0.32, 0.3, 0.29, 0.28 | 0.32, 0.32, 0.3, 0.29, 0.28 | 0.3, 0.32, 0.3, 0.29, 0.28 | 0.29, 0.32, 0.3, 0.29, 0.28 | 0.28, 0.32, 0.3, 0.29, 0.28 | 0.33, 0.3, 0.3, 0.29, 0.28 | |
| 0.63, 0.63, 0.63, 0.63, 0.63 | 0.66, 0.66, 0.66, 0.66, 0.66 | 0.69, 0.69, 0.69, 0.69, 0.69 | 0.72, 0.72, 0.72, 0.72, 0.72 | 0.6, 0.63, 0.66, 0.69, 0.72 | 0.63, 0.63, 0.66, 0.69, 0.72 | 0.66, 0.63, 0.66, 0.69, 0.72 | 0.69, 0.63, 0.66, 0.69, 0.72 | 0.72, 0.63, 0.66, 0.69, 0.72 | 0.6, 0.66, 0.66, 0.69, 0.72 | |
| R1 | 6300, 6300, 6300, 6300, 6300 | 6600, 6600, 6600, 6600, 6600 | 6900, 6900, 6900, 6900, 6900 | 7200, 7200, 7200, 7200, 7200 | 6000, 6300, 6600, 6900, 7200 | 6300, 6300, 6600, 6900, 7200 | 6600, 6300, 6600, 6900, 7200 | 6900, 6300, 6600, 6900, 7200 | 7200, 6300, 6600, 6900, 7200 | 6000, 6600, 6600, 6900, 7200 |
| R2 | 1260, 1260, 1260, 1260, 1260 | 1320, 1320, 1320, 1320, 1320 | 1380, 1380, 1380, 1380, 1380 | 1440, 1440, 1440, 1440, 1440 | 1200, 1260, 1320, 1380, 1440 | 1260, 1260, 1320, 1380, 1440 | 1320, 1260, 1320, 1380, 1440 | 1380, 1260, 1320, 1380, 1440 | 1440, 1260, 1320, 1380, 1440 | 1200, 1320, 1320, 1380, 1440 |
| R3 | 126, 126, 126, 126, 126 | 132, 132, 132, 132, 132 | 138, 138, 138, 138, 138 | 144, 144, 144, 144, 144 | 120, 126, 132, 138, 144 | 126, 126, 132, 138, 144 | 132, 126, 132, 138, 144 | 138, 126, 132, 138, 144 | 144, 126, 132, 138, 144 | 120, 132, 132, 138, 144 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | |
| DP | 2, 3, 4, 5, 6 | 3, 4, 5, 6, 7 | 4, 5, 6, 7, 8 | 5, 6, 7, 8, 9 | 6, 7, 8, 9, 10 | 7, 8, 9, 10, 11 | 8, 9, 10, 11, 12 | 9, 10, 11, 12, 13 | 1, 3, 4, 5, 6 | 1, 4, 5, 6, 7 |
| 0.33, 0.29, 0.3, 0.29, 0.28 | 0.28, 0.28, 0.3, 0.29, 0.28 | 0.33, 0.32, 0.29, 0.29, 0.28 | 0.33, 0.32, 0.28, 0.29, 0.28 | 0.33, 0.32, 0.3, 0.28, 0.28 | 0.33, 0.33, 0.32, 0.32, 0.3 | 0.33, 0.33, 0.32, 0.3, 0.29 | 0.33, 0.33, 0.32, 0.29, 0.28 | 0.33, 0.32, 0.32, 0.32, 0.3 | 0.33, 0.32, 0.3, 0.29, 0.3 | |
| 0.6, 0.69, 0.66, 0.69, 0.72 | 0.72, 0.72, 0.66, 0.69, 0.72 | 0.6, 0.63, 0.69, 0.69, 0.72 | 0.6, 0.63, 0.72, 0.69, 0.72 | 0.6, 0.63, 0.66, 0.72, 0.72 | 0.6, 0.6, 0.63, 0.63, 0.66 | 0.6, 0.6, 0.63, 0.66, 0.69 | 0.6, 0.6, 0.63, 0.69, 0.72 | 0.6, 0.63, 0.63, 0.63, 0.66 | 0.6, 0.63, 0.66, 0.69, 0.66 | |
| R1 | 6000, 6900, 6600, 6900, 7200 | 7200, 7200, 6600, 6900, 7200 | 6000, 6300, 6900, 6900, 7200 | 6000, 6300, 7200, 6900, 7200 | 6000, 6300, 6600, 7200, 7200 | 6000, 6000, 6300, 6300, 6600 | 6000, 6000, 6300, 6600, 6900 | 6000, 6000, 6300, 6900, 7200 | 6000, 6300, 6300, 6300, 6600 | 6000, 6300, 6600, 6900, 6600 |
| R2 | 1200, 1380, 1320, 1380, 1440 | 1440, 1440, 1320, 1380, 1440 | 1200, 1260, 1380, 1380, 1440 | 1200, 1260, 1440, 1380, 1440 | 1200, 1260, 1320, 1440, 1440 | 1200, 1200, 1260, 1260, 1320 | 1200, 1200, 1260, 1320, 1380 | 1200, 1200, 1260, 1380, 1440 | 1200, 1260, 1260, 1260, 1320 | 1200, 1260, 1320, 1380, 1320 |
| R3 | 120, 138, 132, 138, 144 | 144, 144, 132, 138, 144 | 120, 126, 138, 138, 144 | 120, 126, 144, 138, 144 | 120, 126, 132, 144, 144 | 120, 120, 126, 126, 132 | 120, 120, 126, 132, 138 | 120, 120, 126, 138, 144 | 120, 126, 126, 126, 132 | 120, 126, 132, 138, 132 |
References
- Yang, W.J.; Caunhye, A.M.; Zhuo, M.L.; Wang, Q. Integrated planning of emergency supply pre-positioning and victim evacuation. Socio-Econ. Plan. Sci. 2024, 95, 101965. [Google Scholar] [CrossRef]
- Aon Corporate. Climate and Catastrophe Insight. 2025. Available online: https://www.aon.com/en/insights/reports/climate-and-catastrophe-report (accessed on 2 August 2025).
- Torabi, S.A.; Shokr, I.; Tofighi, S.; Heydari, J. Integrated relief pre-positioning and procurement planning in humanitarian supply chains. Transp. Res. Part E Logist. Transp. Rev. 2018, 113, 123–146. [Google Scholar] [CrossRef]
- Rawls, C.G.; Turnquist, M.A. Pre-positioning and dynamic delivery planning for short-term response following a natural disaster. Socio-Econ. Plan. Sci. 2012, 46, 46–54. [Google Scholar] [CrossRef]
- Wang, Q.Y.; Liu, Z.M.; Jiang, P.; Luo, L. A stochastic programming model for emergency supplies pre-positioning, transshipment and procurement in a regional healthcare coalition. Socio-Econ. Plan. Sci. 2022, 82, 101279. [Google Scholar] [CrossRef]
- Mohammadi, R.; Ghomi, S.M.T.F.; Jolai, F. Prepositioning emergency earthquake response supplies: A new multi-objective particle swarm optimization algorithm. Appl. Math. Model. 2016, 40, 5183–5199. [Google Scholar] [CrossRef]
- Mitsotakis, A.; Kassaras, G. Managing Disaster in the Ionian Sea: Planning and Optimizing Logistics for Disaster Relief Operations for the Island of Kefalonia; DTIC Document: Fort Belvoir, VA, USA, 2010. [Google Scholar]
- Cao, C.J.; Liu, J.H.; Liu, W.H.; Chou, M.C.; Zhang, F.; Zhang, Y. Location and transportation joint decisions for infectious medical waste in sustainable supply chains during a pandemic: A bi-level optimization approach. Ann. Oper. Res. 2025, 1–49. [Google Scholar] [CrossRef]
- Rawls, C.G.; Turnquist, M.A. Pre-positioning of emergency supplies for disaster response. Transp. Res. Part B Methodol. 2010, 44, 521–534. [Google Scholar] [CrossRef]
- Hu, S.; Dong, Z.S. Supplier selection and pre-positioning strategy in humanitarian relief. Omega 2019, 83, 287–298. [Google Scholar] [CrossRef]
- Turkes, R.; Sörensen, K.; Cuervo, D.P. A matheuristic for the stochastic facility location problem. J. Heuristics 2021, 27, 649–694. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, J.H.; Chan, F.T.S. AI-enhanced robust method for integrated healthcare resource pre-positioning and patient scheduling. Int. J. Prod. Res. 2025, 63, 729–757. [Google Scholar] [CrossRef]
- Desai, D.D.; Dey, J.; Satapathy, S.K.; Mishra, S.; Mohanty, S.N.; Mishra, P.; Panda, S.K. Optimal ambulance positioning for road accidents with deep embedded clustering. IEEE Access 2023, 11, 59917–59934. [Google Scholar] [CrossRef]
- Pradhananga, R.; Mutlu, F.; Pokharel, S.; Seth, D. An integrated resource allocation and distribution model for pre-disaster planning. Comput. Ind. Eng. 2016, 91, 229–238. [Google Scholar] [CrossRef]
- Mahtab, Z.; Azeem, A.; Ali, S.M.; Paul, S.K.; Fathollahi-Fard, A.M. Multi-objective robust-stochastic optimisation of relief goods distribution under uncertainty: A real-life case study. Int. J. Syst. Sci. Oper. Logist. 2022, 9, 241–262. [Google Scholar] [CrossRef]
- Cao, C.J.; Liu, Y.; Tang, O.; Gao, X. A fuzzy bi-level optimization model for multi-period post-disaster relief distribution in sustainable humanitarian supply chains. Int. J. Prod. Econ. 2021, 235, 108081. [Google Scholar] [CrossRef]
- Fan, J.C.; Chang, X.L.; Misic, J.; Mišić, V.B.; Kang, H. DHL: Deep reinforcement learning-based approach for emergency supply distribution in humanitarian logistics. Peer Peer Netw. Appl. 2022, 15, 2376–2389. [Google Scholar] [CrossRef]
- Rezaei-Malek, M.; Tavakkoli-Moghaddam, R.; Cheikhrouhou, N.; Taheri-Moghaddam, A. An approximation approach to a trade-off among efficiency, efficacy, and balance for relief pre-positioning in disaster management. Transp. Res. Part E Logist. Transp. Rev. 2016, 93, 485–509. [Google Scholar] [CrossRef]
- Tofighi, S.; Torabi, S.A.; Mansouri, S.A. Humanitarian logistics network design under mixed uncertainty. Eur. J. Oper. Res. 2016, 250, 239–250. [Google Scholar] [CrossRef]
- Amani, M.A.; Sarkodie, S.A.; Sheu, J.B.; Nasiri, M.M.; Tavakkoli-Moghaddam, R. A data-driven hybrid scenario-based robust optimization method for relief logistics network design. Transp. Res. Part E Logist. Transp. Rev. 2025, 194, 103931. [Google Scholar] [CrossRef]
- Ehsani, B.; Karimi, H.; Bakhshi, A.; Aghsami, A.; Rabbani, M. Designing humanitarian logistics network for managing epidemic outbreaks in disasters using Internet-of-Things. A case study: An earthquake in Salas-e-Babajani city. Comput. Ind. Eng. 2023, 175, 108821. [Google Scholar] [CrossRef]
- Cutter, S.L.; Barnes, L.; Berry, M.; Burton, C.; Evans, E.; Tate, E.; Webb, J. A place-based model for understanding community resilience to natural disasters. Glob. Environ. Change 2008, 18, 598–606. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, X.Q.; Xie, Y.K.; Gou, Q.; Li, R.; Qiu, Y.; Hu, Y.; Huang, B. Assessment and Improvement of Urban Resilience to Flooding at a Subdistrict Level Using Multi-Source Geospatial Data: Jakarta as a Case Study. Remote Sens. 2022, 14, 2010. [Google Scholar] [CrossRef]
- Shiozaki, Y.; Nagamatsu, S.; Sato, K.; Bhattacharya, Y. A systematic literature review of empirical validation of disaster resilience indicators. Int. J. Disaster Risk Reduct. 2024, 111, 104681. [Google Scholar] [CrossRef]
- Ouyan, M.; Duenas-Osorio, L.; Min, X. A three-stage resilience analysis framework for urban infrastructure systems. Struct. Saf. 2012, 36, 23–31. [Google Scholar] [CrossRef]
- Almoghathawi, Y.; Barker, K.; Albert, L.A. Resilience-driven restoration model for interdependent infrastructure networks. Reliab. Eng. Syst. Saf. 2019, 185, 12–23. [Google Scholar] [CrossRef]
- Zobel, C.W. Representing perceived tradeoffs in defining disaster resilience. Decis. Support Syst. 2011, 50, 394–403. [Google Scholar] [CrossRef]
- Hosseini, S.; Barker, K.; Ramirez-Marquez, J.E. A review of definitions and measures of system resilience. Reliab. Eng. Syst. Saf. 2016, 145, 47–61. [Google Scholar] [CrossRef]
- Jin, J.G.; Tang, L.C.; Sun, L.J.; Lee, D.-H. Enhancing metro network resilience via localized integration with bus services. Transp. Res. Part E Logist. Transp. Rev. 2014, 63, 17–30. [Google Scholar] [CrossRef]
- Chang, S.E.; Shinozuka, M. Measuring improvements in the disaster resilience of communities. Earth Spectra 2004, 20, 739–755. [Google Scholar] [CrossRef]
- Javid, A.A.; Azad, N. Incorporating location, routing and inventory decisions in supply chain network design. Transp. Res. Part E Logist. Transp. Rev. 2010, 46, 582–597. [Google Scholar] [CrossRef]
- Park, S.; Lee, T.E.; Sung, C.S. A three-level supply chain network design model with risk-pooling and lead times. Transp. Res. Part E Logist. Transp. Rev. 2010, 46, 563–581. [Google Scholar] [CrossRef]
- Carvalho, H.; Barroso, A.P.; Machado, V.H.; Azevedo, S.; Cruz Machado, V. Supply chain redesign for resilience using simulation. Comput. Ind. Eng. 2012, 62, 329–341. [Google Scholar] [CrossRef]
- Condeixa, L.D.; Leiras, A.; Oliveira, F.; de Brito, I. Disaster relief supply pre-positioning optimization: A risk analysis via shortage mitigation. Int. J. Disaster Risk Reduct. 2017, 25, 238–247. [Google Scholar] [CrossRef]
- Zheng, Y.J.; Wang, Y.; Ling, H.F.; Xue, Y.; Chen, S.Y. Integrated civilian–military pre-positioning of emergency supplies: A multi-objective optimization approach. Appl. Soft Comput. 2017, 58, 732–741. [Google Scholar] [CrossRef]
- Fang, Y.P.; Sansavini, G. Optimum post-disruption restoration under uncertainty for enhancing critical infrastructure resilience. Reliab. Eng. Syst. Saf. 2019, 185, 1–11. [Google Scholar] [CrossRef]
- Turkeš, R.; Cuervo, D.P.; Sörensen, K. Pre-positioning of emergency supplies: Does putting a price on human life help to save lives? Ann. Oper. Res. 2019, 283, 865–895. [Google Scholar] [CrossRef]
- Alkhaleel, B.A.; Liao, H.T.; Sullivan, K.M. Risk and resilience-based optimal post-disruption restoration for critical infrastructures under uncertainty. Eur. J. Oper. Res. 2022, 296, 174–202. [Google Scholar] [CrossRef]
- Zhang, G.W.; Jia, N.; Zhu, N.; He, L.; Adulyasak, Y. Humanitarian transportation network design via two-stage distributionally robust optimization. Transp. Res. Part B Methodol. 2023, 176, 102805. [Google Scholar] [CrossRef]
- Che, A.; Li, J.; Chu, F.; Chu, C. Optimizing emergency supply pre-positioning for disaster relief: A two-stage distributionally robust approach. Comput. Oper. Res. 2024, 166, 106607. [Google Scholar] [CrossRef]
- Oksuz, M.K.; Satoglu, S.I. Integrated optimization of facility location, casualty allocation and medical staff planning for post-disaster emergency response. J. Humanit. Logist. Supply Chain Manag. 2024, 14, 285–303. [Google Scholar] [CrossRef]
- Sun, P.; Zhao, D.P.; Chen, Q.X.; Yu, X.; Zhu, N. Distributionally robust optimization for pre-disaster facility location problem with 3D printing. Transp. Res. Part E Logist. Transp. Rev. 2025, 193, 103844. [Google Scholar] [CrossRef]
- Yu, X.Y.; Chen, J.; Zhu, N.; Ma, S.; Peng, B. A robust stochastic approach to relief pre-positioning for earthquake response under event-wise uncertainties. Transp. Res. Part E Logist. Transp. Rev. 2025, 198, 104054. [Google Scholar] [CrossRef]
- Hu, Z.H.; Sheu, J.B. Post-disaster debris reverse logistics management under psychological cost minimization. Transp. Res. Part B Methodol. 2013, 55, 118–141. [Google Scholar] [CrossRef]
- Cai, T.Y.; Ye, Y.S.; Yan, H. Optimizing social costs in post-pandemic humanitarian distribution models. Transp. Lett. Int. J. Transp. Res. 2025, 17, 628–638. [Google Scholar] [CrossRef]
- Celik, E.; Aydin, N.; Gumus, A.T. A stochastic location and allocation model for critical items to response large-scale emergencies: A case of Turkey. Int. J. Optim. Control Theor. Appl. 2017, 7, 1–15. [Google Scholar] [CrossRef]
- Prewitt, D.J.O. Role of Psycho-social Support Programmes following Natural Disasters. Disaster Adv. 2008, 1, 18–24. [Google Scholar]
- Rabiei, A.; Nakhaee, N.; Pourhosseini, S.S. Shortcomings in Dealing with Psychological Effects of Natural Disasters in Iran. Iran. J. Public Health 2014, 43, 1132–1138. [Google Scholar] [PubMed]
- Tzeng, G.H.; Cheng, H.J.; Huang, T.D. Multi-objective optimal planning for designing relief delivery systems. Transp. Res. Part E Logist. Transp. Rev. 2007, 43, 673–686. [Google Scholar] [CrossRef]
- Wang, Q.Y.; Nie, X.F. A stochastic programming model for emergency supply planning considering transportation network mitigation and traffic congestion. Socio-Econ. Plan. Sci. 2022, 79, 101119. [Google Scholar] [CrossRef]
- Yilmaz, Z.; Aydemir-Karadag, A.; Erol, S. Finding optimal depots and routes in sudden-onset disasters: An earthquake case for Erzincan. Transp. J. 2019, 58, 168–196. [Google Scholar] [CrossRef]
- Hu, S.L.; Hu, Q.M.; Tao, S.; Dong, Z.S. A multi-stage stochastic programming approach for pre-positioning of relief supplies considering returns. Socio-Econ. Plan. Sci. 2023, 88, 101617. [Google Scholar] [CrossRef]
- Zhang, F.S.; Huang, H.; Cao, C.J.; Yang, Q. Coordination mechanism of integrative humanitarian-business partnership for relief supplies with the consideration of public engagement amidst the Coronavirus Disease 2019 pandemic. Ann. Oper. Res. 2024, 341, 1339. [Google Scholar] [CrossRef]
- Yang, Y.; Yin, Y.; Wang, D.; Ignatius, J.; Cheng, T.; Dhamotharan, L. Distributionally robust multi-period location-allocation with multiple resources and capacity levels in humanitarian logistics. Eur. J. Oper. Res. 2023, 305, 1042–1062. [Google Scholar] [CrossRef]
- Bruckler, M.; Wietschel, L.; Messmann, L.; Thorenz, A.; Tuma, A. Review of metrics to assess resilience capacities and actions for supply chain resilience. Comput. Ind. Eng. 2024, 192, 110176. [Google Scholar] [CrossRef]
- Kumar, D.; Soni, G.; Rathore, A.P.S.; Kazancoglu, Y. Modelling and analysis of resilience and reliability in pharmaceutical supply chains. Comput. Ind. Eng. 2025, 200, 109194. [Google Scholar] [CrossRef]
- Cao, C.; Li, J.; Liu, J.; Liu, J.; Qiu, H.; Zhen, J. Sustainable development-oriented location-transportation integrated optimization problem regarding multi-period multi-type disaster medical waste during COVID-19 pandemic. Ann. Oper. Res. 2024, 335, 1401–1447. [Google Scholar] [CrossRef]
- Cao, C.; He, Y.; Liu, Y.; Huang, H.; Zhang, F. Blockchain technology adoption mechanism for semiconductor chip supply chains considering information disclosure under cost-sharing contract. Int. J. Prod. Econ. 2025, 282, 109496. [Google Scholar] [CrossRef]
- Mishra, B.K.; Dahal, K.; Pervez, Z. Dynamic relief items distribution model with sliding time window in the post-disaster environment. Appl. Sci. 2022, 12, 8358. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).