An Optimization Model of Coupled Medical Material Dispatching Inside and Outside Epidemic Areas Considering Comprehensive Satisfaction
Abstract
1. Introduction
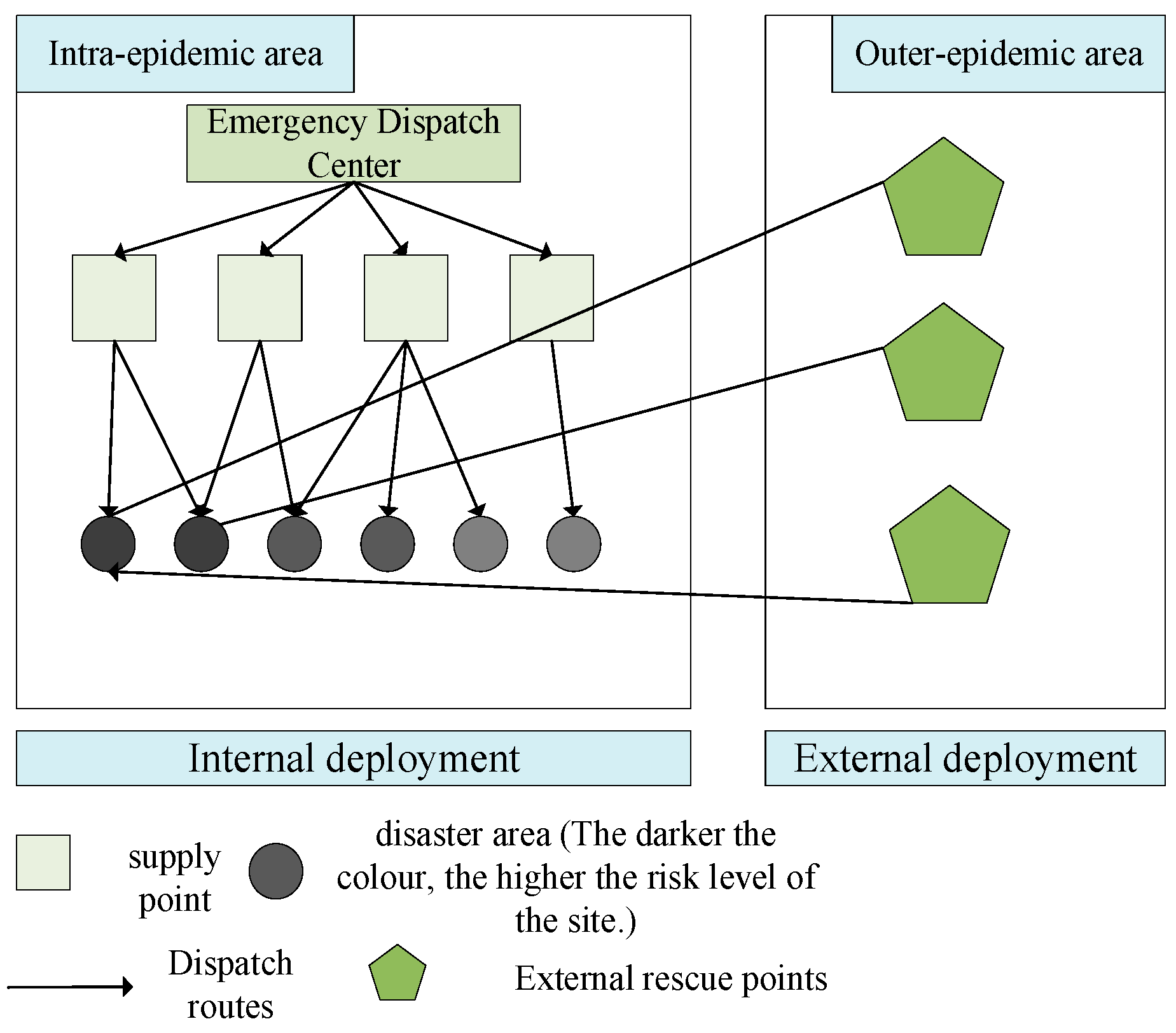
2. Coupled Medical Material Dispatching Model for the Internal and External Infected Area Considering Comprehensive Satisfaction
2.1. Problem Description
2.2. Epidemic Spreading Model
- (1)
- The population within the infected region at time t is divided into four categories, namely the susceptible population S(t), the non-infectious incubator population E(t), the infected population with disease flare-ups I(t), and the recovered population with acquired immunity R(t), and the four categories are homogeneously mixed.
- (2)
- The infected region is considered closed, disregarding population movements, births and deaths, and the total population is held constant, namely, .
- (3)
- At moment t, the incubators are transformed into infected people in a certain proportion and their number is proportional to the number of incubators, noting the proportion as .
- (4)
- is the recovery rate, which is the probability that an infected person is successfully cured and transformed into a recovered person after treatment.
2.3. Demand Forecast for Emergency Supplies
2.4. Consideration of the Urgency of the Demand for Internal and External Coupling
2.4.1. Internal and External Dispatching Degree
- (1)
- Calculation of internal and external dispatching degree
- (2)
- Application of internal and external dispatching degree
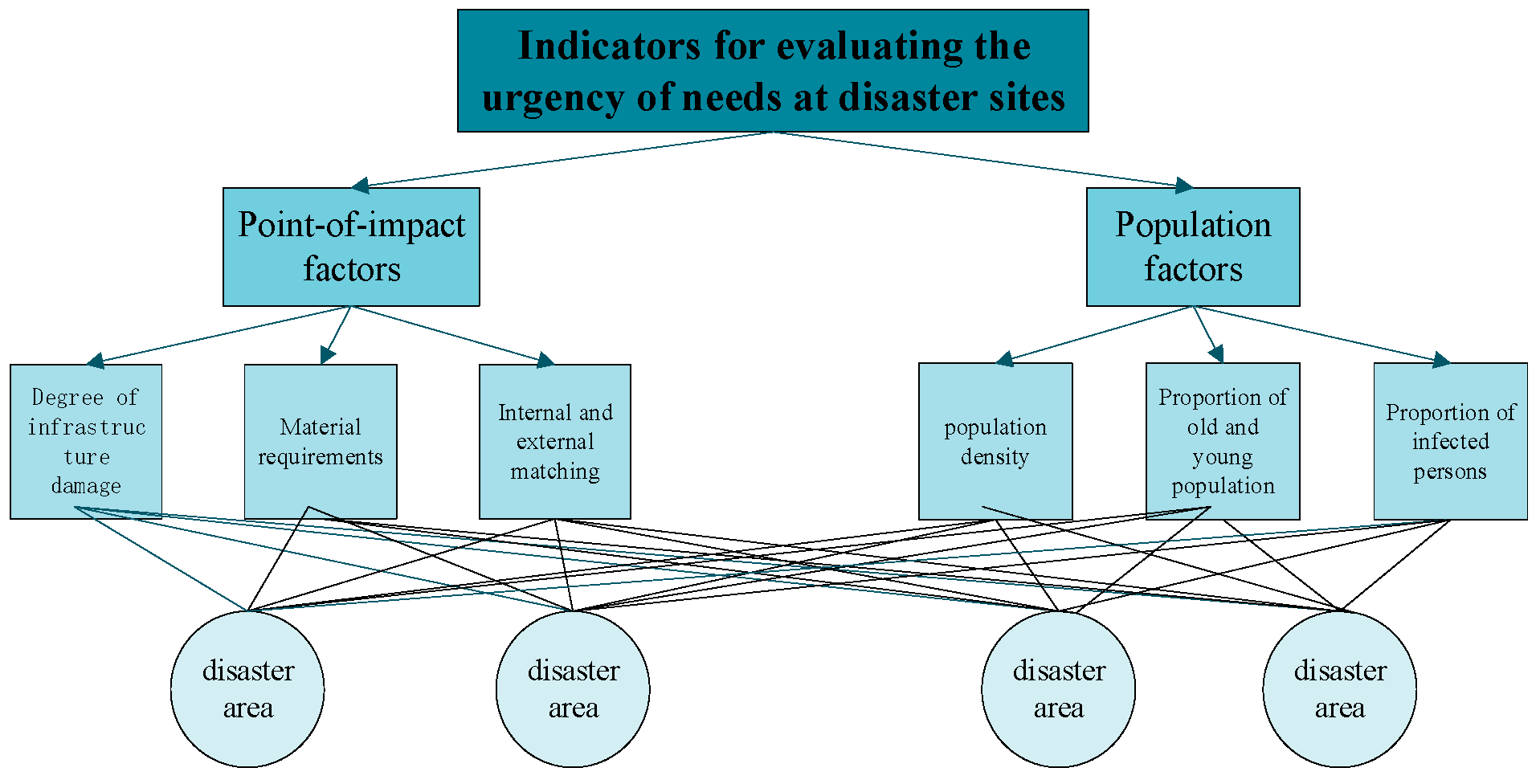
2.4.2. Demand Urgency Factors
2.4.3. Calculation of Demand Urgency
2.5. Material Dispatching Model
- (1)
- The number of emergency supplies dispatched to disaster point k must not exceed their demand: ;
- (2)
- The total number of emergency supplies dispatched is not greater than the total supply: , where is the number of emergency supplies available at distribution center i;
- (3)
- Ensure that limited emergency supplies are fully distributed: ;
- (4)
- A 0 to 1 decision variable indicates whether distribution center i dispatches to disaster point k or not: ;
- (5)
- At least one distribution center i dispatches supplies to disaster point k: ;
- (6)
- A distribution center i dispatches supplies to at least one disaster point k: ;
- (7)
- Demand satisfaction at disaster point k is not less than 10 per cent, with demand satisfaction equal to supply divided by demand: ;
- (8)
- The range of values of each variable is .
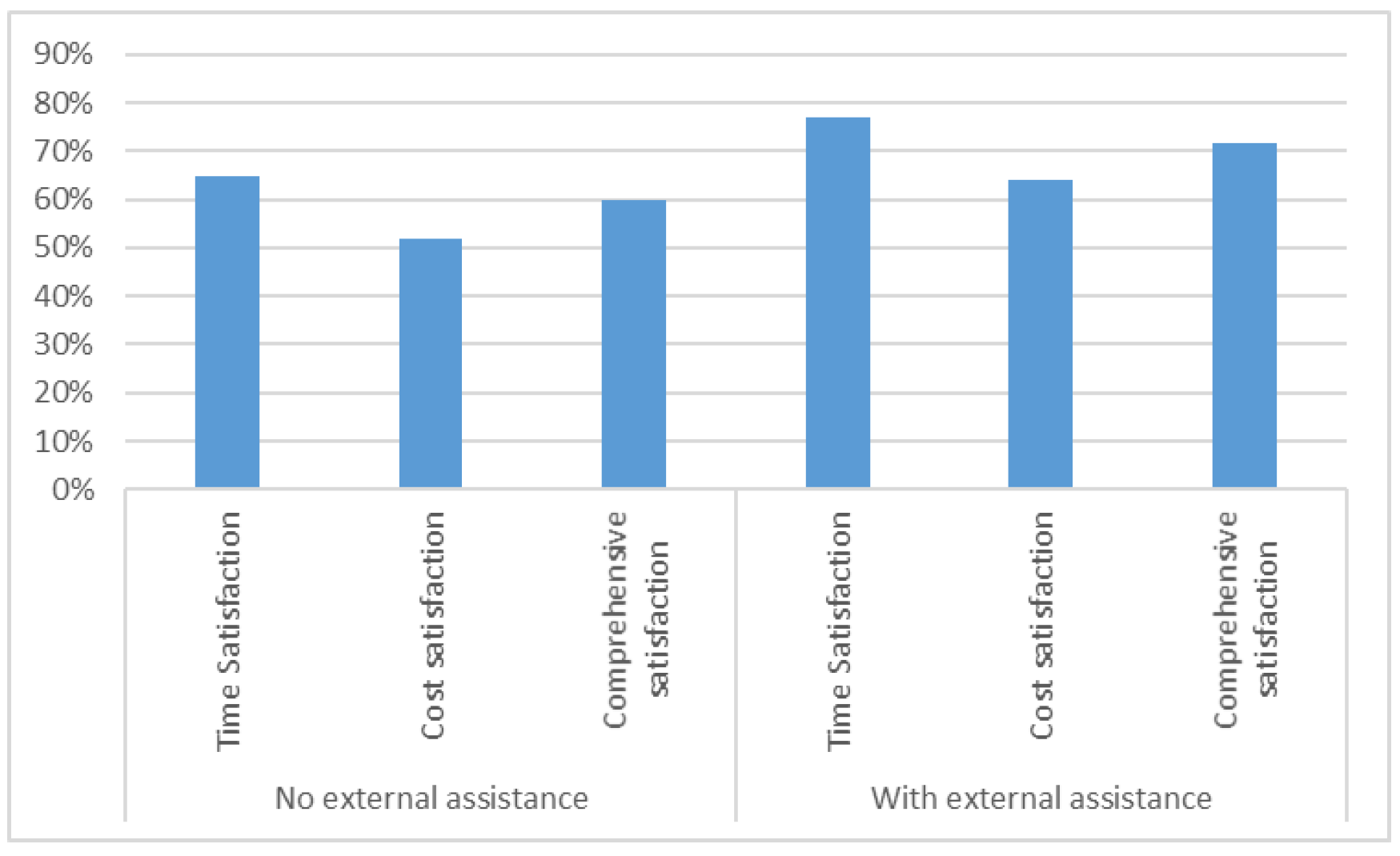
2.6. Comprehensive Satisfaction
- (1)
- Time satisfaction:
- (2)
- Cost satisfaction:
3. Numerical Experiments
3.1. Prediction of the Number of Infected People
3.2. Epidemic Medical Material Demand Prediction
3.3. Measurement of the Urgency of Demand
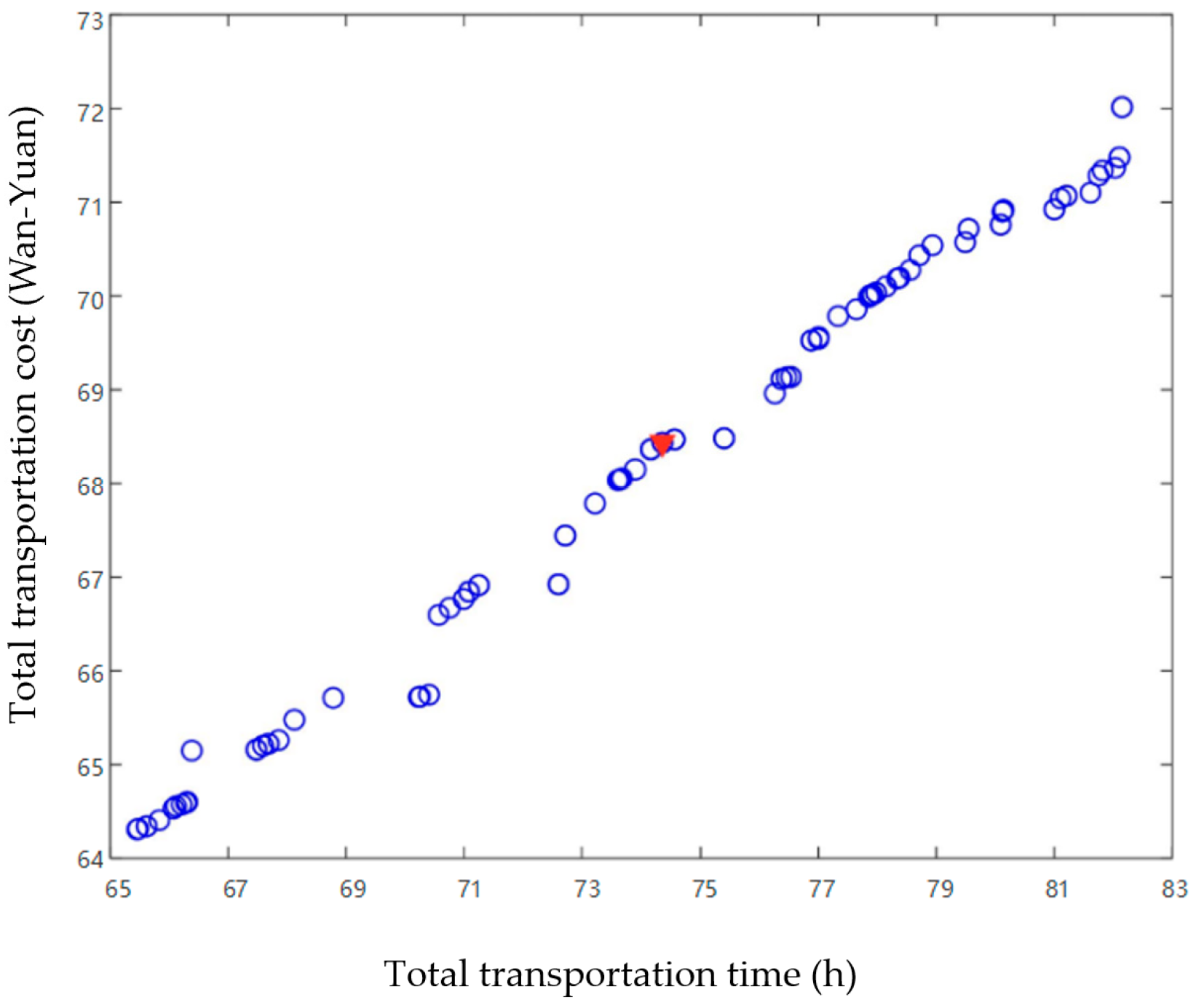
3.4. Emergency Material Dispatching Model Solutions
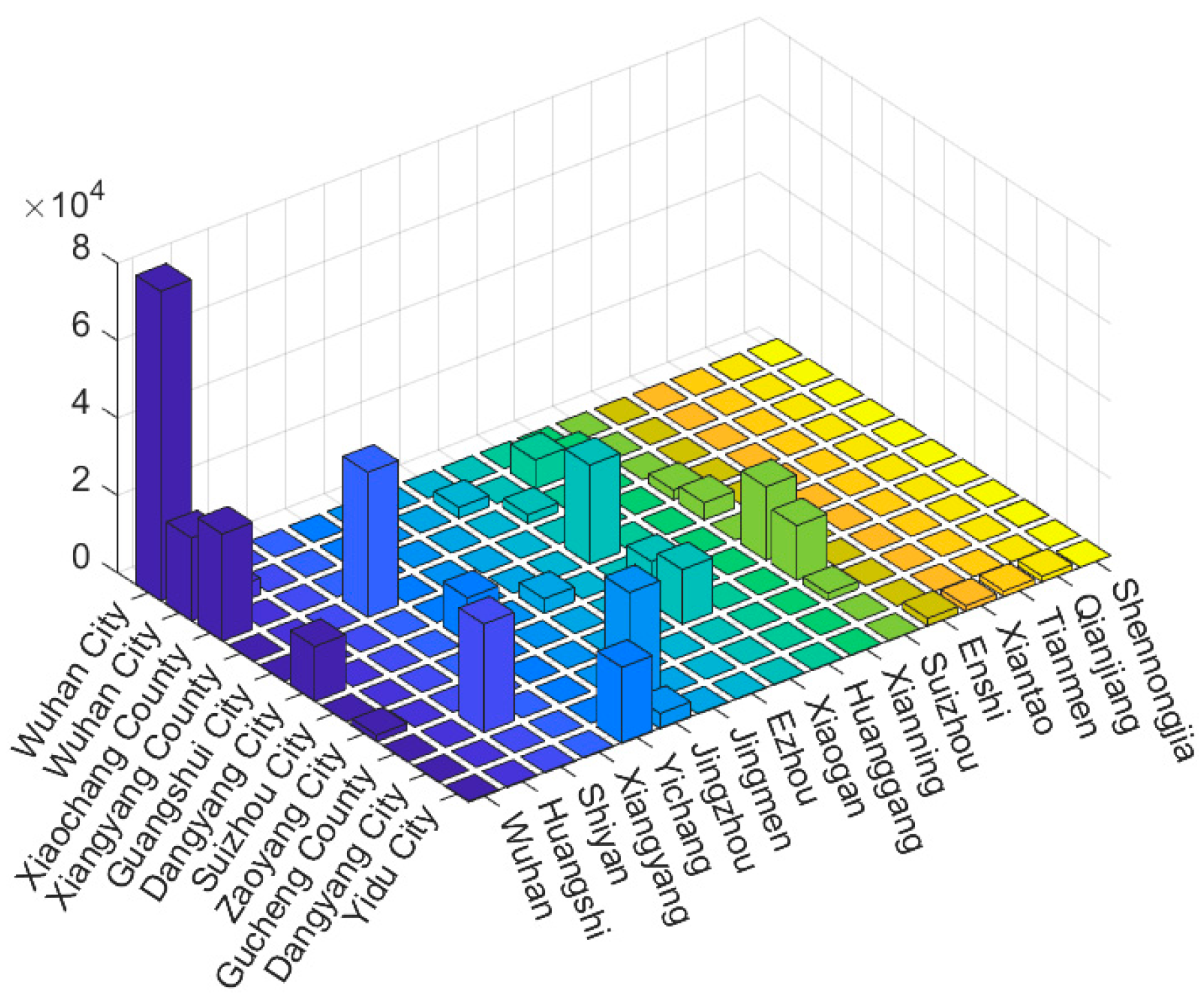
3.5. Analysis of Emergency Material Dispatching Results
4. Conclusions and Discussion
- (1)
- When dispatching materials during public health incidents like epidemics, subdividing the infected population and predicting the number of infections using the SEIR model allows for a more scientific prediction of material needs, thereby more effectively responding to the actual epidemic material dispatch.
- (2)
- Introducing external rescue when there is a shortage of materials within the affected area can significantly improve the satisfaction of demand in the affected area and enhance the effectiveness of the rescue efforts.
- (3)
- By calculating the internal and external matching degree, it is possible to clarify the matching degree between the affected area and the external rescue points, improving the specificity of the rescue while reducing rescue costs.
Author Contributions
Funding
Conflicts of Interest
References
- Ropke, S.; Pisinger, D. An Adaptive Large Neighborhood Search Heuristic for the Pickup and Delivery Problem with Time Windows. Transp. Sci. 2006, 40, 455–472. [Google Scholar] [CrossRef]
- Dasaklis, T.K.; Rachaniotis, N.P.; Pappis, C.P. Emergency supply chain management for controlling a smallpox outbreak: The case for regional mass vaccination. Int. J. Syst. Sci. Oper. Logist. 2017, 4, 27–40. [Google Scholar] [CrossRef]
- Chen, H.; Guo, Y.; Lin, X.; Qi, X. Study on regional differences and causes of emergency logistics responsiveness under the impact of public emergencies—Findings from Chinese samples. Front. Public Health 2024, 12, 1508467. [Google Scholar] [CrossRef] [PubMed]
- Yin, Z.; Yin, Z.; Ye, J.; Liu, R. Optimization of emergency logistics delivery path based on guided local search algorithm. J. Comput. Methods Sci. Eng. 2024, 24, 1889–1902. [Google Scholar] [CrossRef]
- Tan, K.; Liu, W.; Xu, F.; Li, C. Optimization model and algorithm of logistics vehicle routing problem under major emergency. Mathematics 2023, 11, 1274. [Google Scholar] [CrossRef]
- Wu, J.; Wang, X.Y.; Tian, A.Q.; Du, Z.G.; Yang, Z.J. A hybrid meta-heuristic approach for emergency logistics distribution under uncertain demand. IEEE Access 2024, 12, 135701–135729. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, X.; Wang, L. Deep reinforcement learning-based rescue resource distribution scheduling of storm surge inundation emergency logistics. IEEE Trans. Ind. Inform. 2023, 19, 10004–10013. [Google Scholar] [CrossRef]
- Fan, J.; Chang, X.; Mišić, J.; Mišić, V.B.; Kang, H. DHL: Deep reinforcement learning-based approach for emergency supply distribution in humanitarian logistics. Peer—Peer Netw. Appl. 2022, 15, 2376–2389. [Google Scholar] [CrossRef]
- Sun, H.; Cai, Q. Emergency logistics siting-path question for engineering construction projects based on quantum particle swarm algorithm. J. Comput. Methods Sci. Eng. 2024, 24, 1993–2005. [Google Scholar] [CrossRef]
- Yan, T.; Lu, F.; Wang, S.; Wang, L.; Bi, H. A hybrid metaheuristic algorithm for the multi-objective location-routing problem in the early post-disaster stage. J. Ind. Manag. Optim. 2023, 19, 4663–4691. [Google Scholar] [CrossRef]
- Ge, J.; Li, X.; Wu, Z.; Sun, Y.; Kanrak, M. The distribution of emergency logistics centers under the covid-19 lockdown: The case of yangtze river delta area. Sustainability 2022, 14, 10594. [Google Scholar] [CrossRef]
- Eshghi, A.; Tavakkoli-Moghaddam, R.; Ebrahimnejad, S.; Ghezavati, V. Multi-objective robust mathematical modeling of emergency relief in disaster under uncertainty. Sci. Iran. 2022, 29, 2670–2695. [Google Scholar] [CrossRef]
- Li, T. Emergency logistics resource scheduling algorithm in cloud computing environment. Phys. Commun. 2024, 64, 102340. [Google Scholar] [CrossRef]
- Lei, Y.; Zhang, G.; Lu, S.; Qian, J. Revealing the generation mechanism of cross-regional emergency cooperation during accidents and disasters rescue. Saf. Sci. 2023, 163, 106140. [Google Scholar] [CrossRef]
- Zhu, J.; Shi, Y.; Venkatesh, V.G.; Islam, S.; Hou, Z.; Arisian, S. Dynamic collaborative optimization for disaster relief supply chains under information ambiguity. Ann. Oper. Res. 2024, 335, 1303–1329. [Google Scholar] [CrossRef]
- Ding, Z.; Xu, X.; Jiang, S.; Yan, J.; Han, Y. Emergency logistics scheduling with multiple supply-demand points based on grey interval. J. Saf. Sci. Resil. 2022, 3, 179–188. [Google Scholar] [CrossRef]
- Guo, J.; Liu, H.; Liu, T.; Song, G.; Guo, B. The multi-objective shortest path problem with multimodal transportation for emergency logistics. Mathematics 2024, 12, 2615. [Google Scholar] [CrossRef]
- Xu, Z.; Zheng, C.; Zheng, S.; Ma, G.; Chen, Z. Multimodal transportation route optimization of emergency supplies under uncertain conditions. Sustainability 2024, 16, 10905. [Google Scholar] [CrossRef]
- Ye, J.; Jiang, W.; Yang, X.; Hong, B. Emergency materials response framework for petrochemical enterprises based on multi-objective optimization. Energy 2023, 269, 126670. [Google Scholar] [CrossRef]
- Hu, Y.; Liu, Q.; Li, S.; Wu, W. Robust emergency logistics network design for pandemic emergencies under demand uncertainty. Transp. Res. Part E 2025, 196, 103957. [Google Scholar] [CrossRef]
- Wang, F.; Ge, X.; Li, Y.; Zheng, J.; Zheng, W. Optimising the distribution of multi-cycle emergency supplies after a disaster. Sustainability 2023, 15, 902. [Google Scholar] [CrossRef]
- Liu, J.; Dong, C. Understanding the complex adaptive characteristics of cross-regional emergency collaboration in China: A stochastic evolutionary game approach. Fractal Fract. 2024, 8, 98. [Google Scholar] [CrossRef]

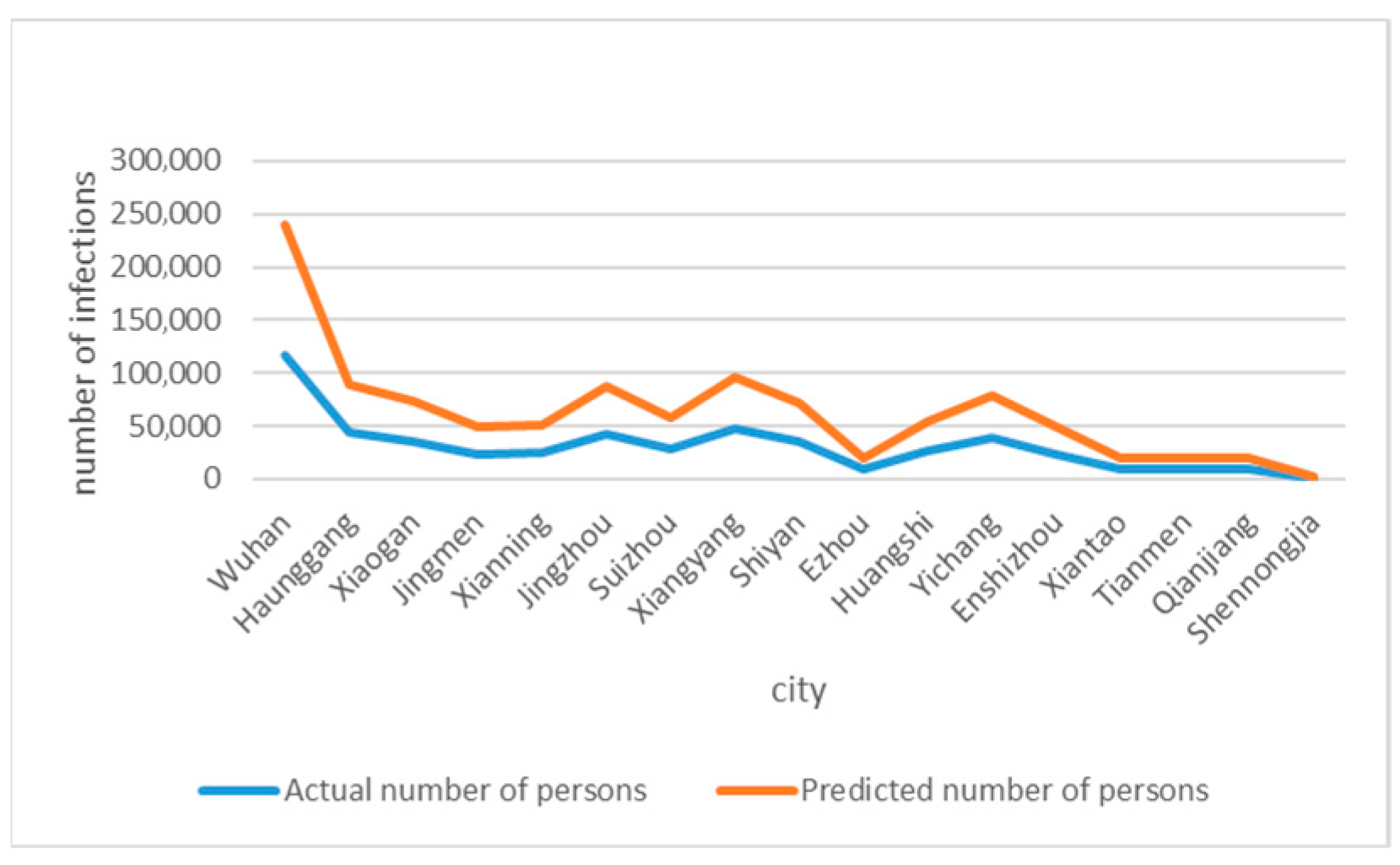
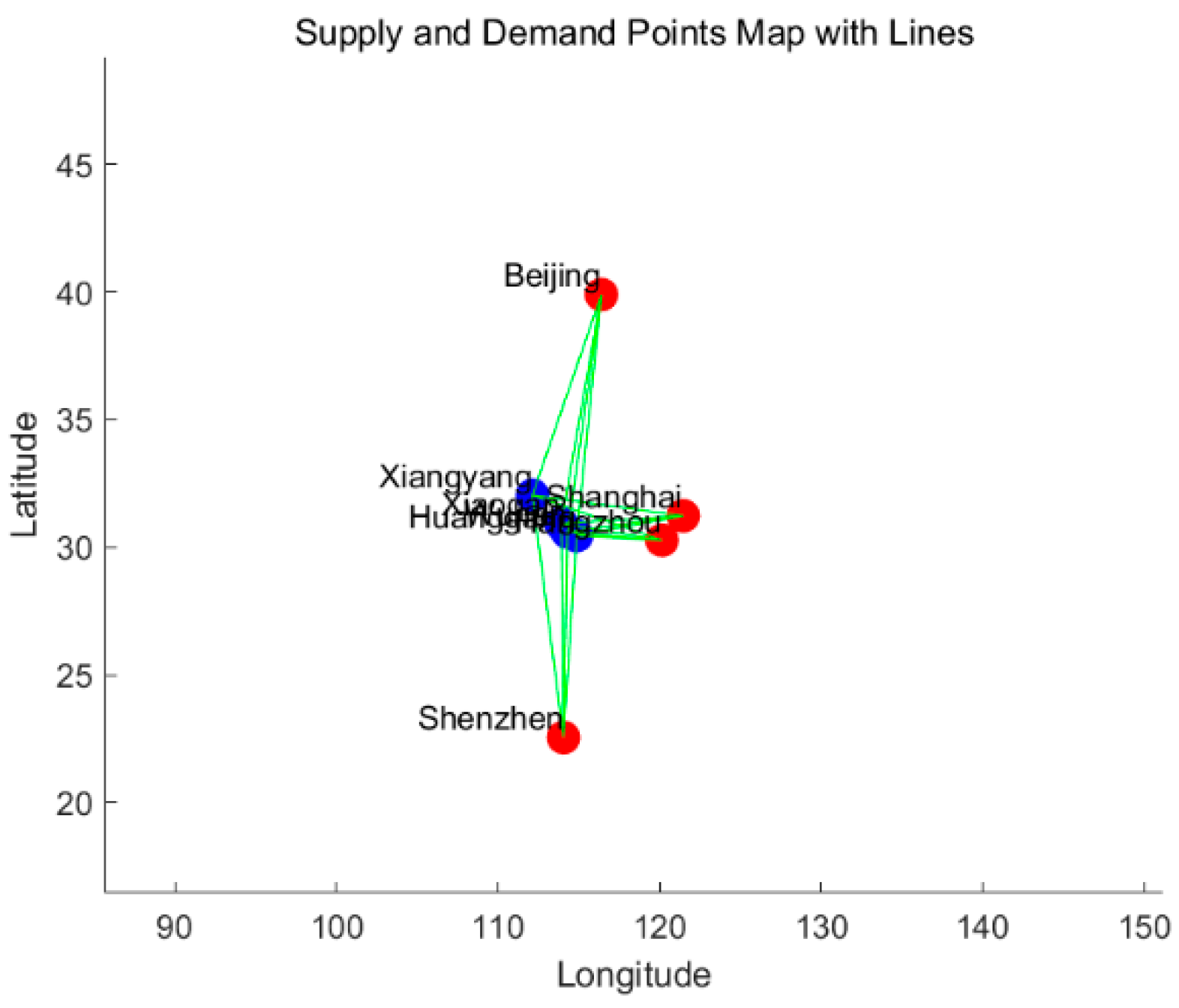
| City | Number of Infections |
|---|---|
| Wuhan | 117,100 |
| Huanggang | 43,919 |
| Xiaogan | 35,384 |
| Jingmen | 23,714 |
| Xianning | 24,560 |
| Jingzhou | 42,422 |
| Suizhou | 27,997 |
| Xiangyang | 46,804 |
| Shiyan | 35,038 |
| Ezhou | 9429 |
| Huangshi | 26,806 |
| Yichang | 39,069 |
| Enshi | 23,800 |
| Xiantao | 9062 |
| Tianmen | 9190 |
| Qianjiang | 9392 |
| Shennongjia | 799 |
| City | Epidemic Level |
|---|---|
| Wuhan | High-risk |
| Huanggang | High-risk |
| Xiaogan | High-risk |
| Jingmen | High-risk |
| Xianning | Medium-risk |
| Jingzhou | Medium-risk |
| Suizhou | Medium-risk |
| Xiangyang | Medium-risk |
| Shiyan | Medium-risk |
| Ezhou | Medium-risk |
| Huangshi | Medium-risk |
| Yichang | Medium-risk |
| Enshi | Medium-risk |
| Xiantao | Medium-risk |
| Tianmen | Medium-risk |
| Qianjiang | Low-risk |
| Shennongjia | Low-risk |
| City | Number of Infections |
|---|---|
| Wuhan | 175,650 |
| Huanggang | 35,135.2 |
| Xiaogan | 53,076 |
| Jingmen | 18,971.2 |
| Xianning | 19,648 |
| Jingzhou | 33,937.6 |
| Suizhou | 41,995.5 |
| Xiangyang | 37,443 |
| Shiyan | 28,030 |
| Ezhou | 14,143 |
| Huangshi | 21,444 |
| Yichang | 31,255 |
| Enshi | 11,900 |
| Xiantao | 7249 |
| Tianmen | 7352 |
| Qianjiang | 7513 |
| Shennongjia | 399 |
| Disaster Area | Number of Infected Persons | Material Shortages | Distance | |||
|---|---|---|---|---|---|---|
| Beijing | Shanghai | Hangzhou | Shenzhen | |||
| Wuhan | 117,100 | 52,695 | 1149 | 801 | 722 | 1092 |
| Huangshi | 26,806 | 5872 | 1181 | 756 | 682 | 1001 |
| Shiyan | 35,038 | 7607 | 1158 | 1176 | 1143 | 1448 |
| Xiangyang | 46,804 | 10,632 | 1058 | 1076 | 1000 | 1277 |
| Yichang | 39,069 | 8460 | 1294 | 1108 | 1056 | 1149 |
| Jingzhou | 42,422 | 9974 | 1251 | 1016 | 959 | 1072 |
| Jingmen | 23,714 | 2975 | 1179 | 1012 | 938 | 1160 |
| Ezhou | 9429 | 1248 | 1150 | 773 | 678 | 1014 |
| Xiaogan | 35,384 | 15,285 | 1127 | 834 | 762 | 1102 |
| Huanggang | 43,919 | 10,400 | 1143 | 743 | 669 | 1028 |
| Xianning | 24,560 | 4065 | 1252 | 832 | 727 | 994 |
| Suizhou | 27,997 | 12,559 | 1053 | 911 | 857 | 1196 |
| Enshi | 23,800 | 3380 | 1514 | 1317 | 1267 | 1326 |
| Xiantao | 9062 | 2 | 1233 | 897 | 834 | 1060 |
| Tianmen | 9190 | 4 | 1180 | 913 | 839 | 1059 |
| Qianjiang | 9392 | 4 | 1224 | 951 | 894 | 1047 |
| Shennongjia | 799 | 0 | 1227 | 1197 | 1134 | 1339 |
| Disaster Area | Degree |
|---|---|
| Wuhan | 1.0000 |
| Huangshi | 0.1989 |
| Shiyan | 0.2625 |
| Xiangyang | 0.3541 |
| Yichang | 0.2931 |
| Jingzhou | 0.3217 |
| Jingmen | 0.1667 |
| Ezhou | 0.0626 |
| Xiaogan | 0.2953 |
| Huanggang | 0.3331 |
| Xianning | 0.1765 |
| Suizhou | 0.2344 |
| Enshi | 0.1697 |
| Xiantao | 0.0553 |
| Tianmen | 0.0562 |
| Qianjiang | 0.0576 |
| Shennongjia | 0 |
| Disaster Area | Number | Evaluation Indicators | |||||
|---|---|---|---|---|---|---|---|
| Population Density (person/km2) | Infected Person/% | Ratio of Old to Young/% | Emergency Material Requirements/Set | Degree of Infrastructure Damage | Internal and External Dispatch | ||
| Wuhan | Y1 | 1308.44 | 46.0052 | 31.41 | 175,650 | 0 | 1.0000 |
| Huangshi | Y7 | 540.13 | 2.9883 | 34.28 | 21,444.8 | 0 | 0.1989 |
| Shiyan | Y12 | 143.58 | 2.2904 | 31.27 | 28,030.4 | 0 | 0.2625 |
| Xiangyang | Y4 | 287.92 | 4.9029 | 34.17 | 37,443.2 | 0 | 0.3541 |
| Yichang | Y9 | 194.91 | 3.5072 | 33.38 | 31,255.2 | 0 | 0.2931 |
| Jingzhou | Y5 | 391.10 | 4.4645 | 32.69 | 33,937.6 | 0 | 0.3217 |
| Jingmen | Y10 | 233.59 | 3.0867 | 29.07 | 18,971.2 | 0 | 0.1667 |
| Ezhou | Y8 | 663.97 | 2.7378 | 33.63 | 14,143.5 | 0 | 0.0626 |
| Xiaogan | Y2 | 552.67 | 8.2133 | 34.11 | 53,076 | 0 | 0.2953 |
| Huanggang | Y3 | 362.78 | 11.1479 | 34.31 | 35,135.2 | 0 | 0.3331 |
| Xianning | Y11 | 261.32 | 2.6483 | 36.36 | 19,648 | 0 | 0.1765 |
| Suizhou | Y6 | 231.02 | 4.0977 | 32.60 | 41,995.5 | 0 | 0.2344 |
| Enshi | Y16 | 140.60 | 0.9931 | 36.79 | 11,900 | 0 | 0.1697 |
| Xiantao | Y13 | 449.21 | 1.5120 | 32.82 | 7249.6 | 0 | 0.0553 |
| Tianmen | Y14 | 475.74 | 1.0289 | 32.58 | 7352 | 0 | 0.0562 |
| Qianjiang | Y15 | 482.09 | 0.3131 | 27.95 | 7513.6 | 0 | 0.0576 |
| Shennongjia | Y17 | 23.39 | 0.0626 | 35.94 | 399.5 | 0 | 0 |
| Disaster Area | Number | Score | Disaster Risk Value Ranking Results | Disaster Risk Level |
|---|---|---|---|---|
| Wuhan | Y1 | 100 | 1 | Class Ⅰ |
| Huangshi | Y7 | 11.7955 | 7 | Class II |
| Shiyan | Y12 | 8.6791 | 12 | Class II |
| Xiangyang | Y4 | 14.8797 | 4 | Class II |
| Yichang | Y9 | 11.2302 | 9 | Class II |
| Jingzhou | Y5 | 14.5858 | 5 | Class II |
| Jingmen | Y10 | 8.8723 | 10 | Class II |
| Ezhou | Y8 | 11.2542 | 8 | Class II |
| Xiaogan | Y2 | 24.0761 | 2 | Class Ⅰ |
| Huanggang | Y3 | 23.0582 | 3 | Class II |
| Xianning | Y11 | 8.6786 | 11 | Class II |
| Suizhou | Y6 | 14.1645 | 6 | Class II |
| Enshi | Y16 | 4.1921 | 16 | Class III |
| Xiantao | Y13 | 6.6611 | 13 | Class II |
| Tianmen | Y14 | 6.2900 | 14 | Class II |
| Qianjiang | Y15 | 5.4555 | 15 | Class III |
| Shennongjia | Y17 | 0 | 17 | Class III |
| Wuhan (1) | Wuhan (2) | Xiaochang | Xiangyang | Guangshui | Dangyang (1) | Suizhou | Zaoyang | Gucheng | Dangyang (2) | Yidu |
|---|---|---|---|---|---|---|---|---|---|---|
| 80,000 | 40,000 | 30,000 | 40,000 | 30,000 | 30,000 | 30,000 | 30,000 | 30,000 | 30,000 | 30,000 |
| Beijing | Shanghai | Hangzhou | Shenzhou |
|---|---|---|---|
| 25,000 | 25,000 | 25,000 | 25,000 |
| City | Predicted Need |
|---|---|
| Wuhan | 175,650 |
| Huangshi | 35,135.2 |
| Shiyan | 53,076 |
| Xiangyang | 18,971.2 |
| Yichang | 19,648 |
| Jingzhou | 33,937.6 |
| Jingmen | 41,995.5 |
| Ezhou | 37,443 |
| Xiaogan | 28,030 |
| Huanggang | 14,143 |
| Xianning | 21,444 |
| Suizhou | 31,255 |
| Enshi | 11,900 |
| Xiantao | 7249 |
| Tianmen | 7352 |
| Qianjiang | 7513 |
| Shennongjia | 399 |
| Supply/Need | Wuhan (1) | Wuhan (2) | Xiaochang | Xiangyang | Guangshui | Dangyang (1) | Suizhou | Zaoyang | Gucheng | Dangyang (2) | Yidu |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Wuhan | 3 | 24 | 93 | 323 | 145 | 270 | 171 | 246 | 355 | 286 | 309 |
| Huangshi | 102 | 76 | 167 | 397 | 221 | 330 | 245 | 320 | 429 | 345 | 387 |
| Shiyan | 62 | 88 | 40 | 265 | 90 | 262 | 115 | 190 | 299 | 273 | 325 |
| Xiangyang | 240 | 224 | 216 | 139 | 261 | 61 | 218 | 192 | 203 | 76 | 123 |
| Yichang | 112 | 94 | 175 | 405 | 228 | 336 | 253 | 328 | 437 | 336 | 328 |
| Jingzhou | 225 | 213 | 253 | 216 | 298 | 114 | 266 | 251 | 280 | 108 | 97 |
| Jingmen | 158 | 170 | 92 | 179 | 63 | 263 | 4 | 91 | 200 | 256 | 318 |
| Ezhou | 298 | 309 | 244 | 21 | 211 | 188 | 156 | 81 | 66 | 180 | 251 |
| Xiaogan | 449 | 441 | 376 | 179 | 343 | 312 | 289 | 212 | 101 | 302 | 352 |
| Huanggang | 75 | 82 | 177 | 390 | 230 | 350 | 256 | 313 | 422 | 365 | 381 |
| Xianning | 94 | 102 | 201 | 416 | 253 | 393 | 279 | 354 | 448 | 377 | 407 |
| Suizhou | 321 | 313 | 322 | 264 | 367 | 69 | 324 | 298 | 296 | 74 | 53 |
| Enshi | 503 | 521 | 515 | 457 | 560 | 256 | 517 | 491 | 489 | 270 | 246 |
| Xiantao | 103 | 121 | 151 | 322 | 191 | 234 | 190 | 264 | 373 | 241 | 217 |
| Tianmen | 134 | 143 | 118 | 274 | 230 | 191 | 198 | 254 | 338 | 189 | 164 |
| Qianjiang | 157 | 167 | 185 | 274 | 230 | 181 | 198 | 254 | 338 | 189 | 164 |
| Shennongjia | 483 | 472 | 407 | 237 | 374 | 203 | 326 | 300 | 192 | 206 | 256 |
| Supply/Need | Wuhan (1) | Wuhan (2) | Xiaochang | Xiangyang | Guangshui | Dangyang (1) | Suizhou | Zaoyang | Gucheng | Dangyang (2) | Yidu |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Wuhan | 80,000 | 21,444 | 27,662 | 0 | 0 | 14,209 | 0 | 1713 | 0 | 0 | 0 |
| Huangshi | 0 | 4289 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Shiyan | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 28,030 | 0 | 0 |
| Xiangyang | 0 | 0 | 0 | 37,443.2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Yichang | 0 | 0 | 0 | 0 | 0 | 11,607 | 0 | 0 | 0 | 0 | 19,648 |
| Jingzhou | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 30,000 | 3937 |
| Jingmen | 0 | 0 | 0 | 0 | 0 | 3794 | 0 | 0 | 0 | 0 | 0 |
| Ezhou | 0 | 3755 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Xiaogan | 0 | 0 | 2338 | 0 | 25,565 | 0 | 11,028 | 14,143 | 0 | 0 | 0 |
| Huanggang | 0 | 7507 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Xianning | 0 | 3929 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Suizhou | 0 | 0 | 0 | 2556 | 4434 | 0 | 18,971 | 14,143 | 1889 | 0 | 0 |
| Enshi | 0 | 0 | 0 | 0 | 0 | 388 | 0 | 0 | 0 | 0 | 1991 |
| Xiantao | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1449 |
| Tianmen | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1470 |
| Qianjiang | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1502 |
| Shennongjia | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 80 | 0 | 0 |
| Supply/Need | Beijing | Shanghai | Hangzhou | Shenzhen |
|---|---|---|---|---|
| Wuhan | 7505 | 7497 | 7495 | 7503 |
| Xiangyang | 6248 | 6249 | 6246 | 6256 |
| Xiaogan | 5007 | 4995 | 4992 | 5006 |
| Huanggang | 6260 | 6244 | 6241 | 6255 |
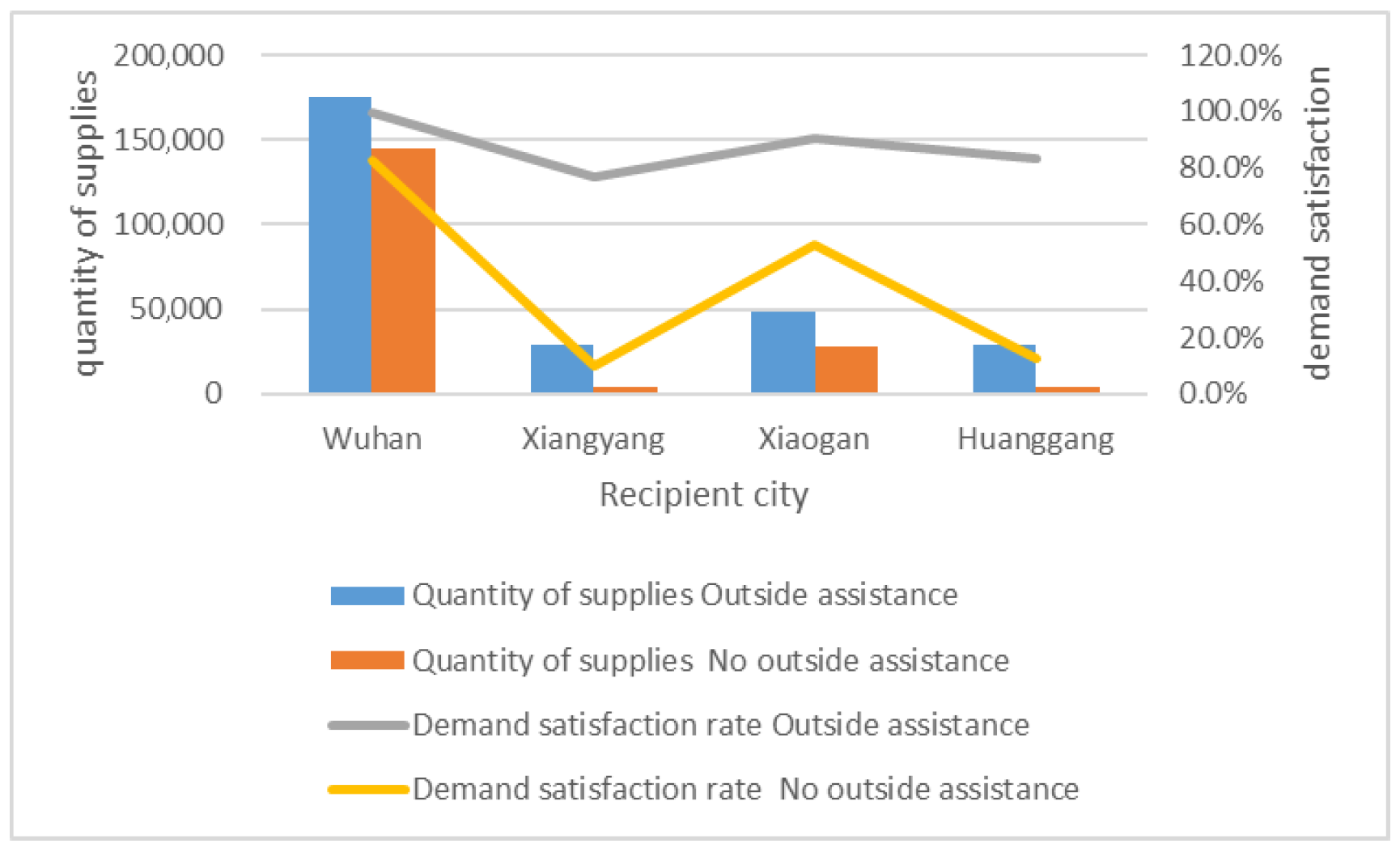
| Need | Demand Point Base Data | No Consideration of External Rescue | Consideration of External Rescue | |||||
|---|---|---|---|---|---|---|---|---|
| Wuhan | Material needs | Internal and external dispatch | Quantity of material acquired | Demand shortfall | Demand satisfaction | Material needs | Demand shortfall | Demand satisfaction |
| Xiaogan | 175,650 | 1 | 145,028 | 30,622 | 82.6% | 175,028 | 622 | 99.6% |
| Huanggang | 53,076 | 0.30 | 28,030 | 25,046 | 52.8% | 48,030 | 5046 | 90.5% |
| Xiangyang | 35,135 | 0.33 | 4289 | 30,846 | 12.2% | 29,289 | 5847 | 83.4% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Ye, X.; Pei, S.; Yan, X.; Wang, T.; Chen, J.; Zheng, P.; Cheng, R. An Optimization Model of Coupled Medical Material Dispatching Inside and Outside Epidemic Areas Considering Comprehensive Satisfaction. Systems 2025, 13, 714. https://doi.org/10.3390/systems13080714
Yang J, Ye X, Pei S, Yan X, Wang T, Chen J, Zheng P, Cheng R. An Optimization Model of Coupled Medical Material Dispatching Inside and Outside Epidemic Areas Considering Comprehensive Satisfaction. Systems. 2025; 13(8):714. https://doi.org/10.3390/systems13080714
Chicago/Turabian StyleYang, Jun, Xiaofei Ye, Shuyi Pei, Xingchen Yan, Tao Wang, Jun Chen, Pengjun Zheng, and Rongjun Cheng. 2025. "An Optimization Model of Coupled Medical Material Dispatching Inside and Outside Epidemic Areas Considering Comprehensive Satisfaction" Systems 13, no. 8: 714. https://doi.org/10.3390/systems13080714
APA StyleYang, J., Ye, X., Pei, S., Yan, X., Wang, T., Chen, J., Zheng, P., & Cheng, R. (2025). An Optimization Model of Coupled Medical Material Dispatching Inside and Outside Epidemic Areas Considering Comprehensive Satisfaction. Systems, 13(8), 714. https://doi.org/10.3390/systems13080714









