A Quasi-Bonjean Method for Computing Performance Elements of Ships Under Arbitrary Attitudes
Abstract
1. Introduction
2. Related Works
2.1. Ship NURBS Surface Modeling
2.2. Ship Performance Elements
3. Preliminary
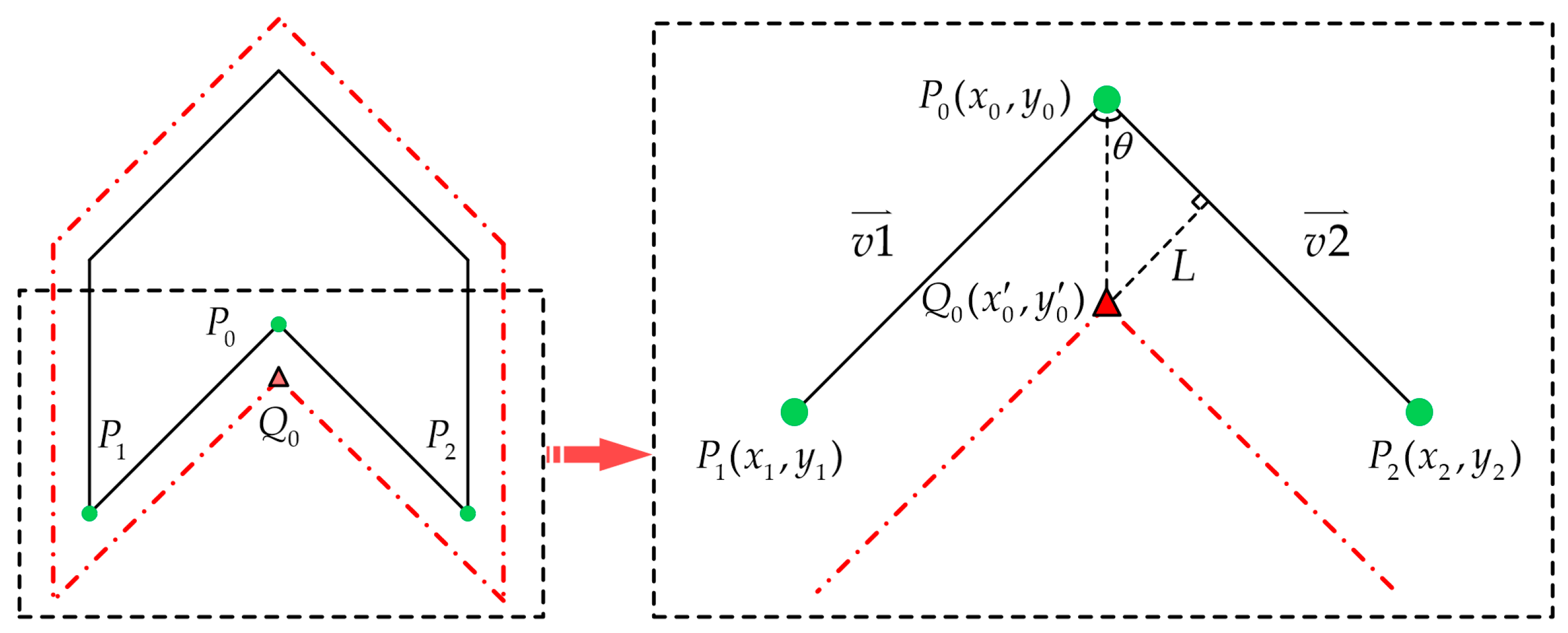
3.1. Point Inversion of NURBS Curve
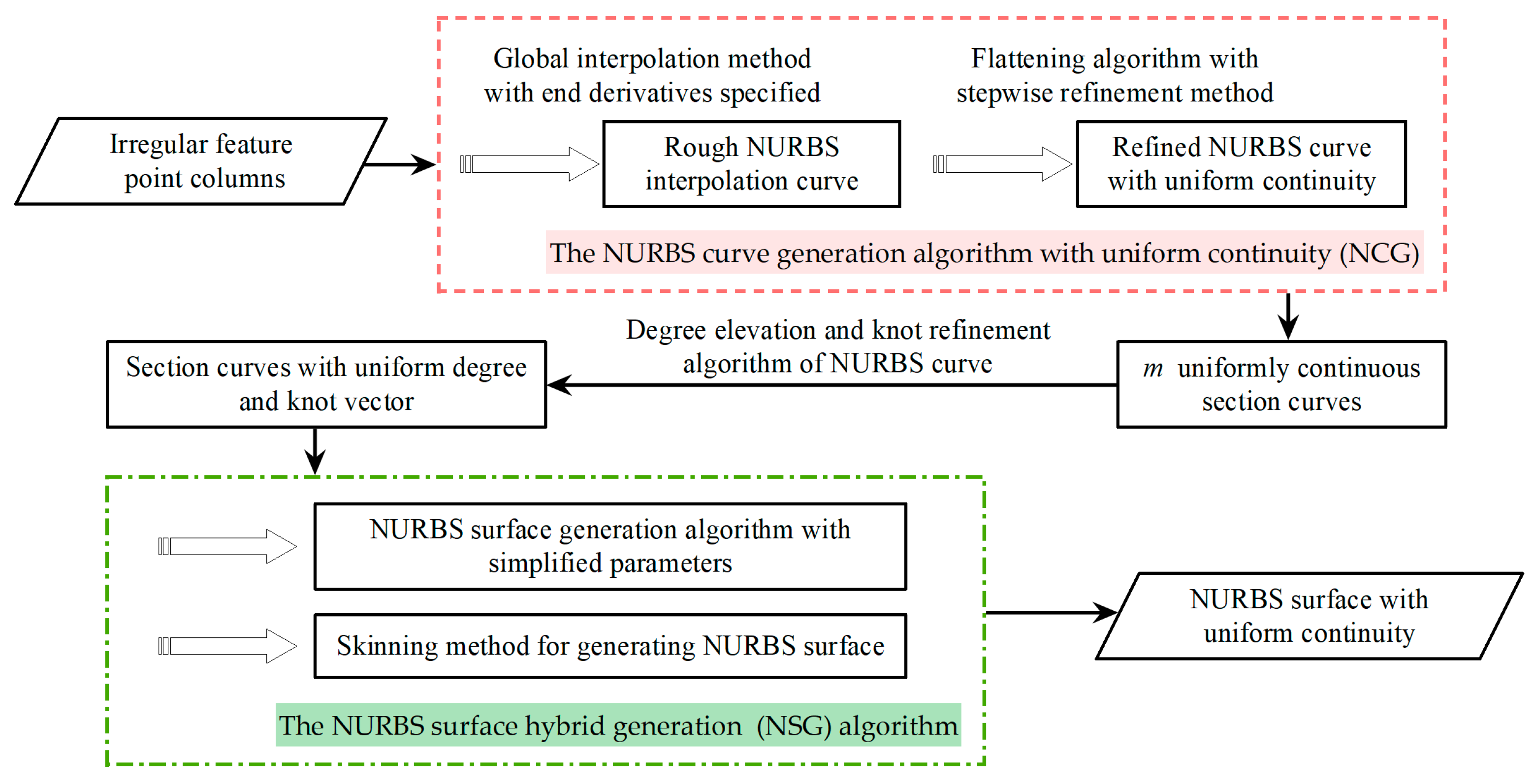
3.2. Rapid Reconstruction of NURBS Surface
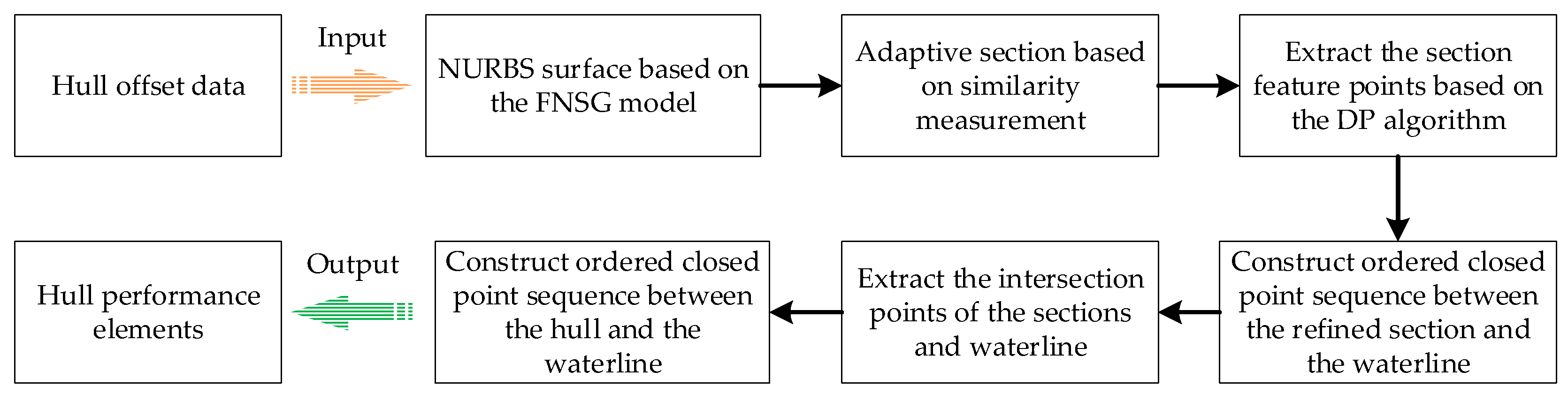
4. Methodology
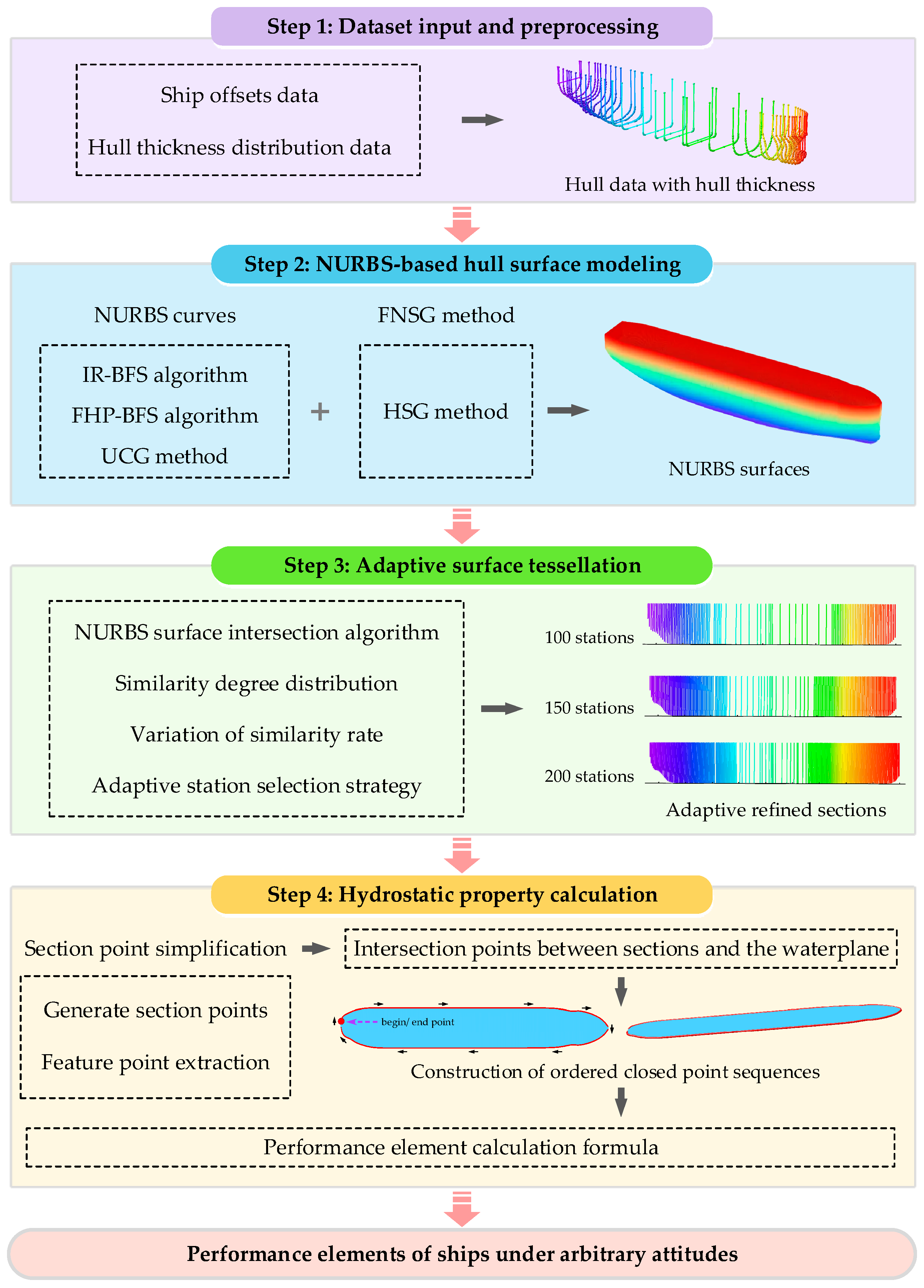
4.1. Framework of QB Method
- Step 1: Dataset input and preprocessing: This step constructs hull surface data considering shell thickness based on the initial design offsets and shell thickness distribution.
- Step 2: NURBS-based hull surface modeling: This step constructs NURBS surface models based on the hull surface data.
- Step 3: Adaptive Surface Tessellation (AST) method: This step generates multi-station sections via NURBS surface intersection algorithm and then applies adaptive refinement algorithm to create simplified sections that maximally preserve longitudinal distribution characteristics while minimizing section quantity.
- Step 4: Hydrostatic property calculation: This step calculates hull performance elements in arbitrary attitudes by constructing ordered closed point sequences of submerged hull geometry.
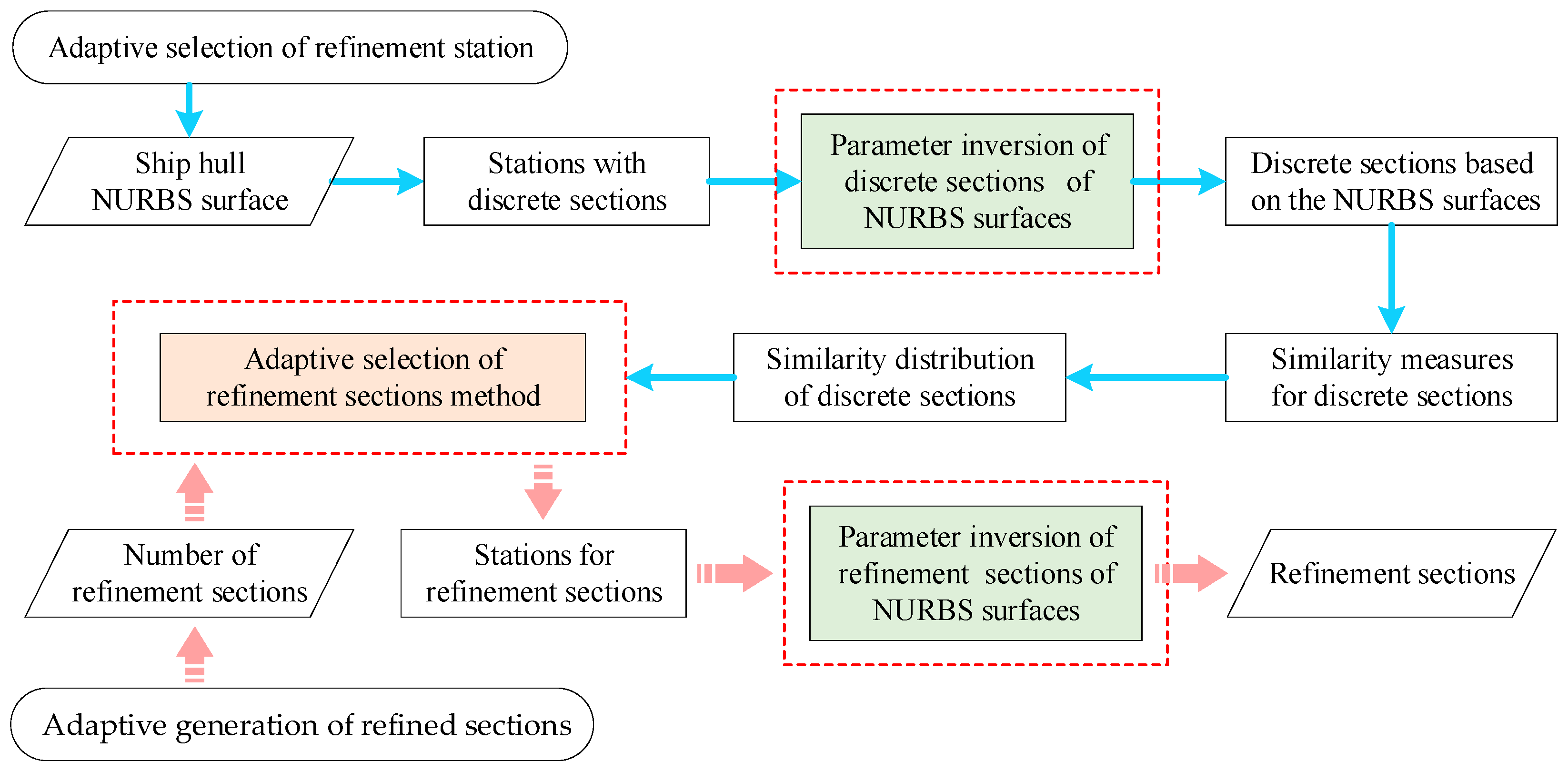
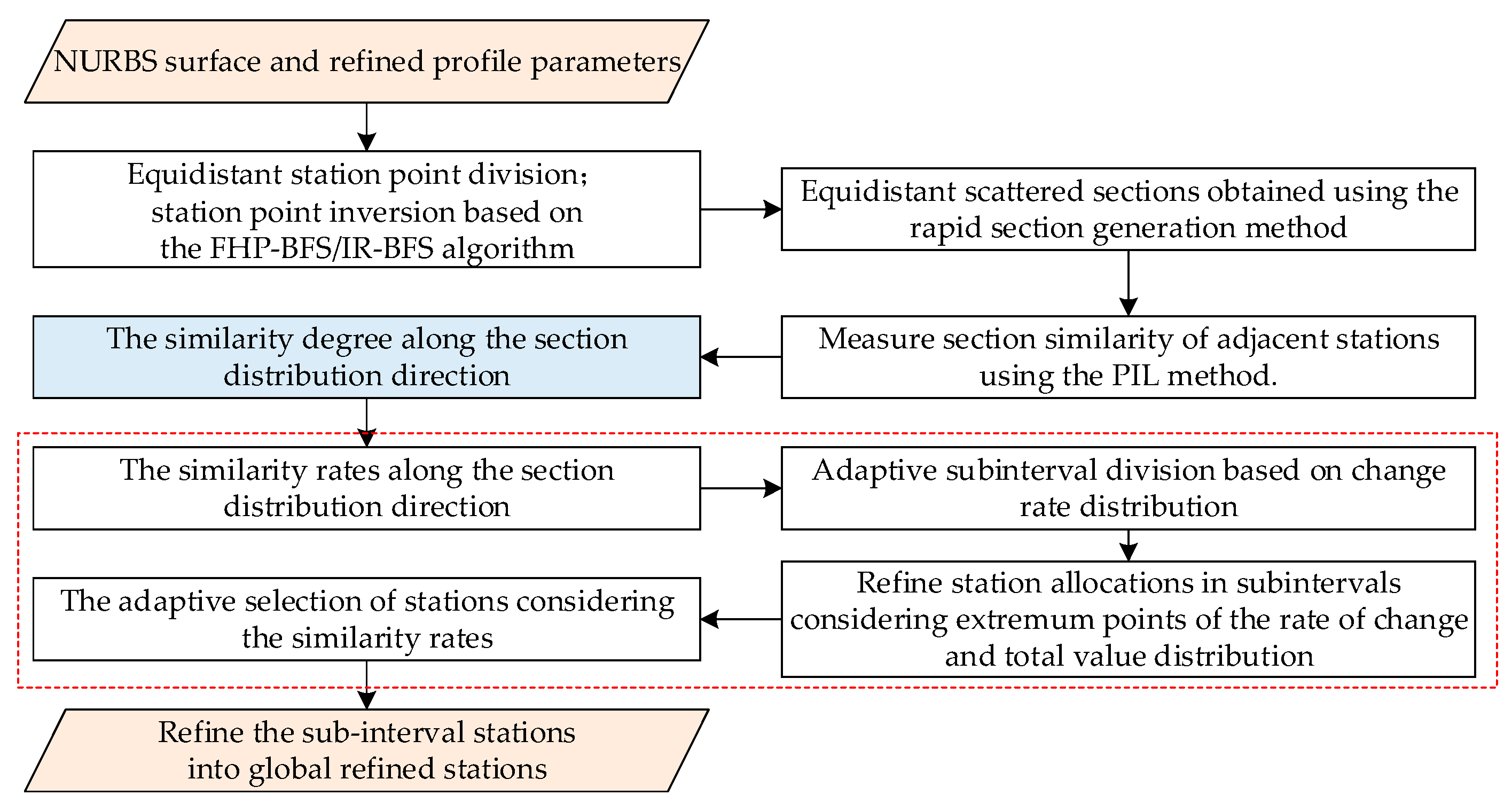
4.2. AST Method
4.2.1. Selection of Similarity Measurement Elements
4.2.2. Similarity Measurement Method
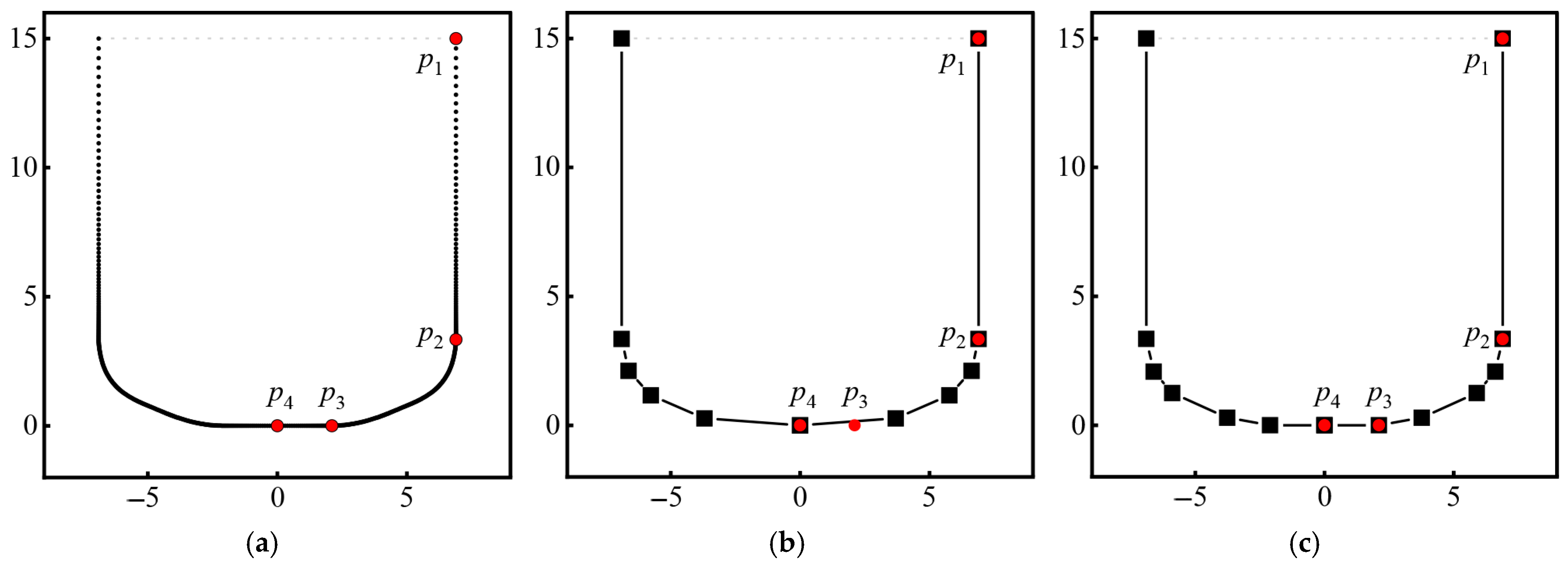
4.2.3. Adaptive Station Selection Strategy
4.3. Performance Elements Calculation Method
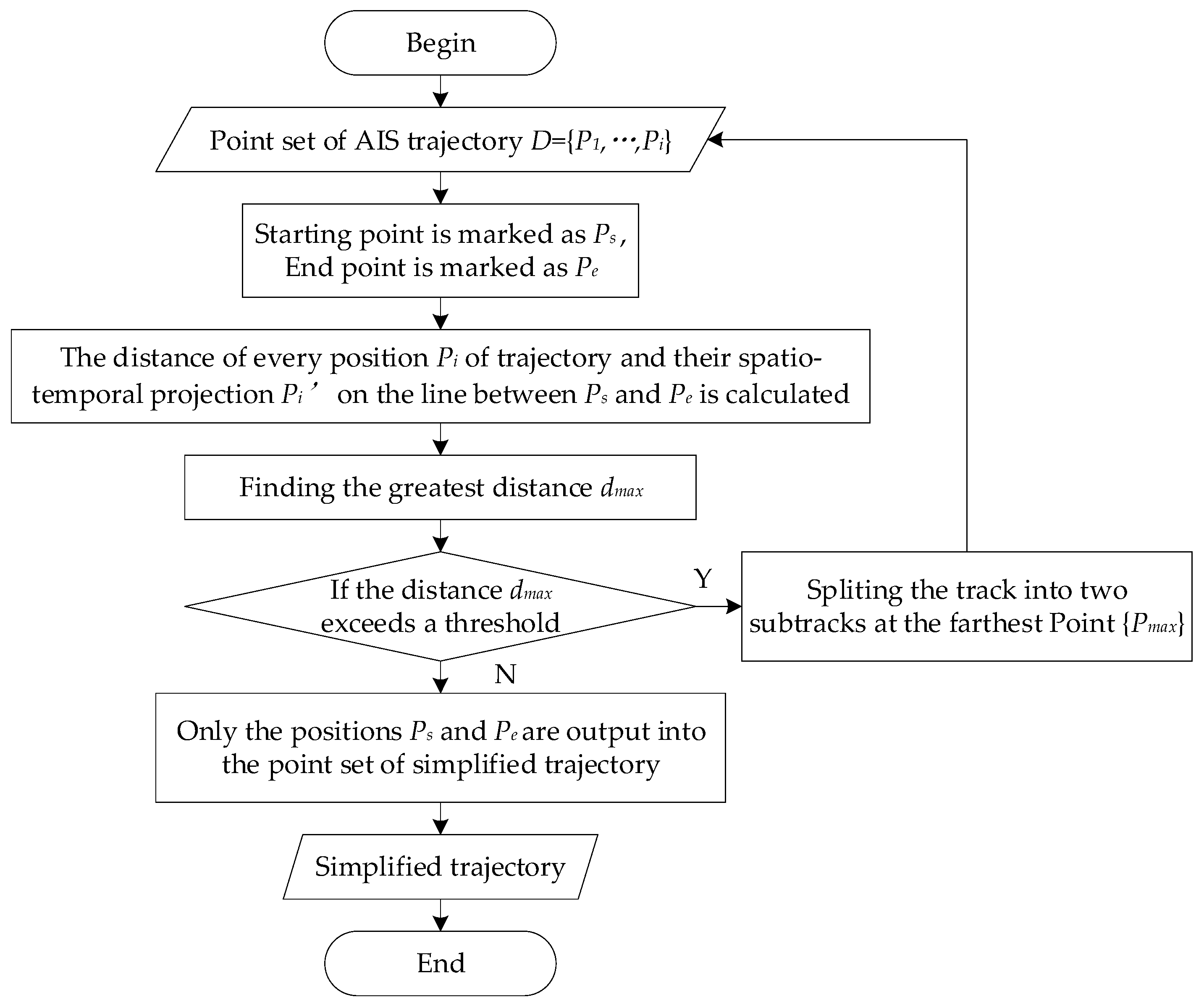
4.3.1. Extraction Algorithm of Section Feature Points
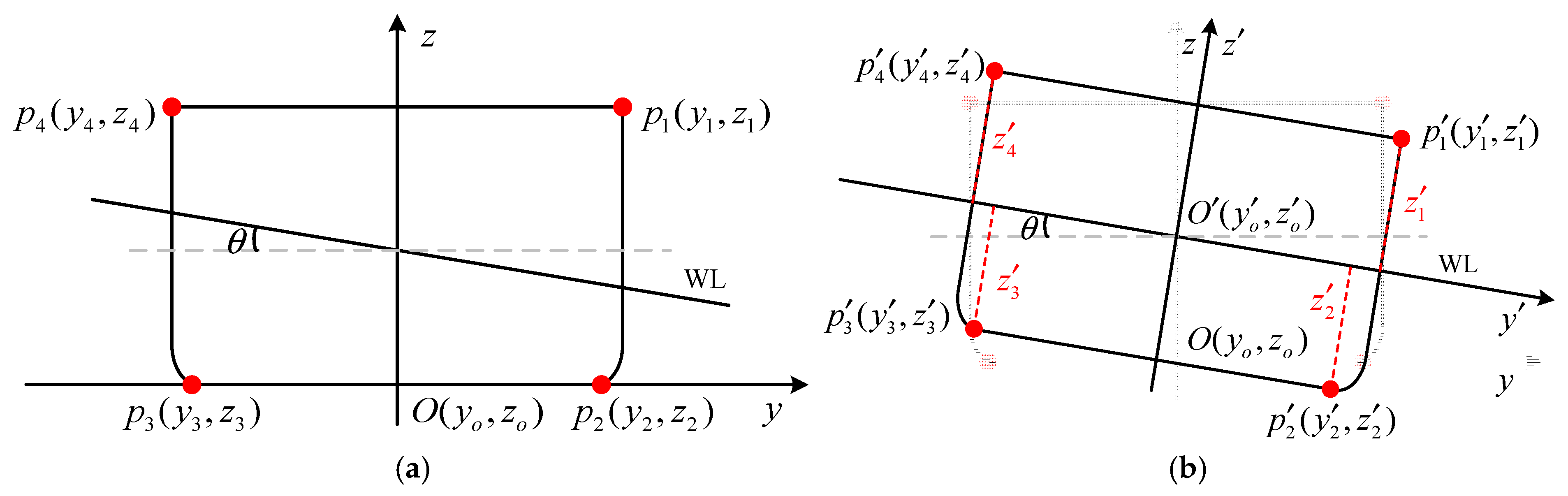
4.3.2. Fast Intersection Judgment Method
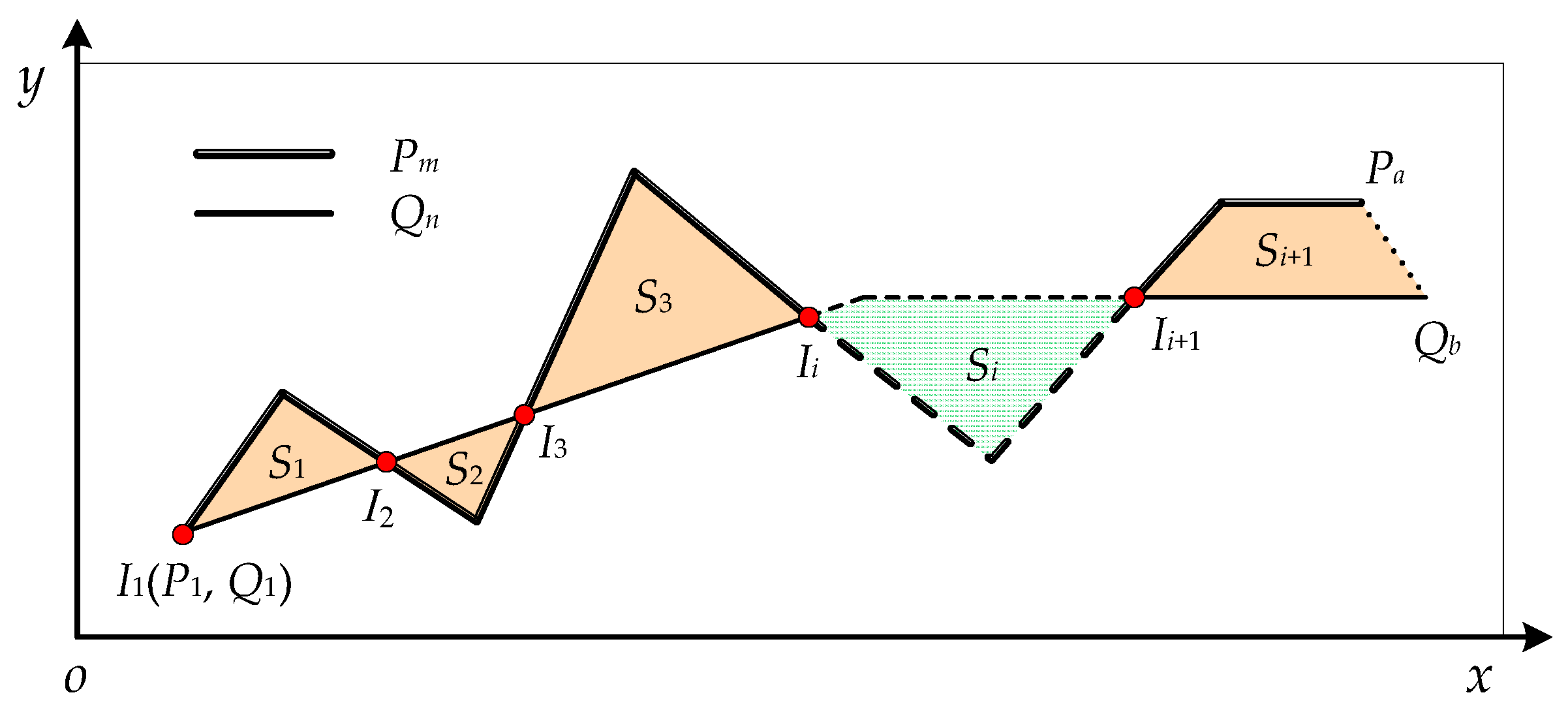
4.3.3. Construction of Ordered Closed Point Sequence
5. Results and Discussions
5.1. Datasets and Setting
5.1.1. Dataset Introduction
5.1.2. Tolerance Criteria
5.1.3. Dataset Preprocessing
5.2. Analysis of Experimental Process
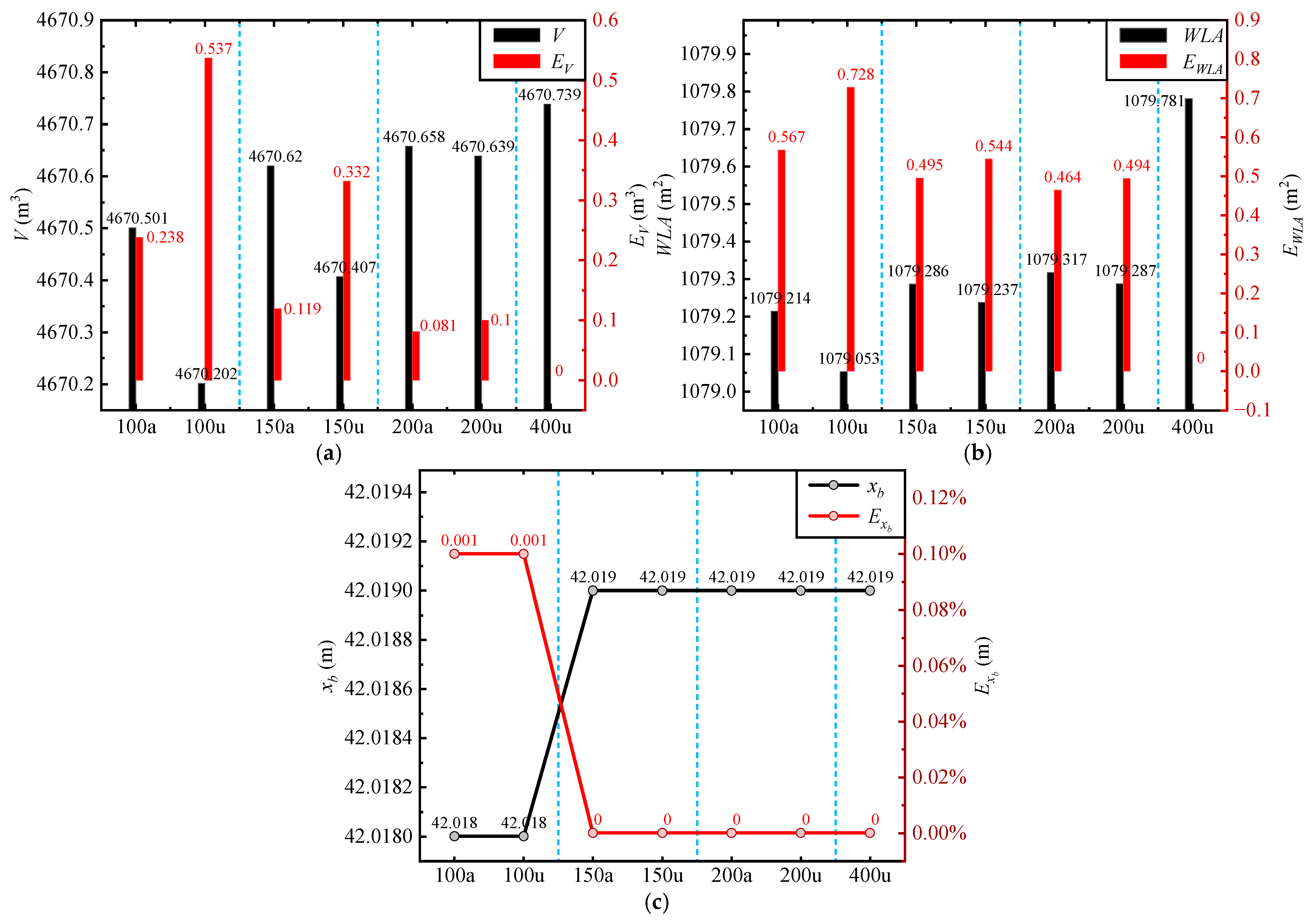
5.3. Validation of AST Method Accuracy
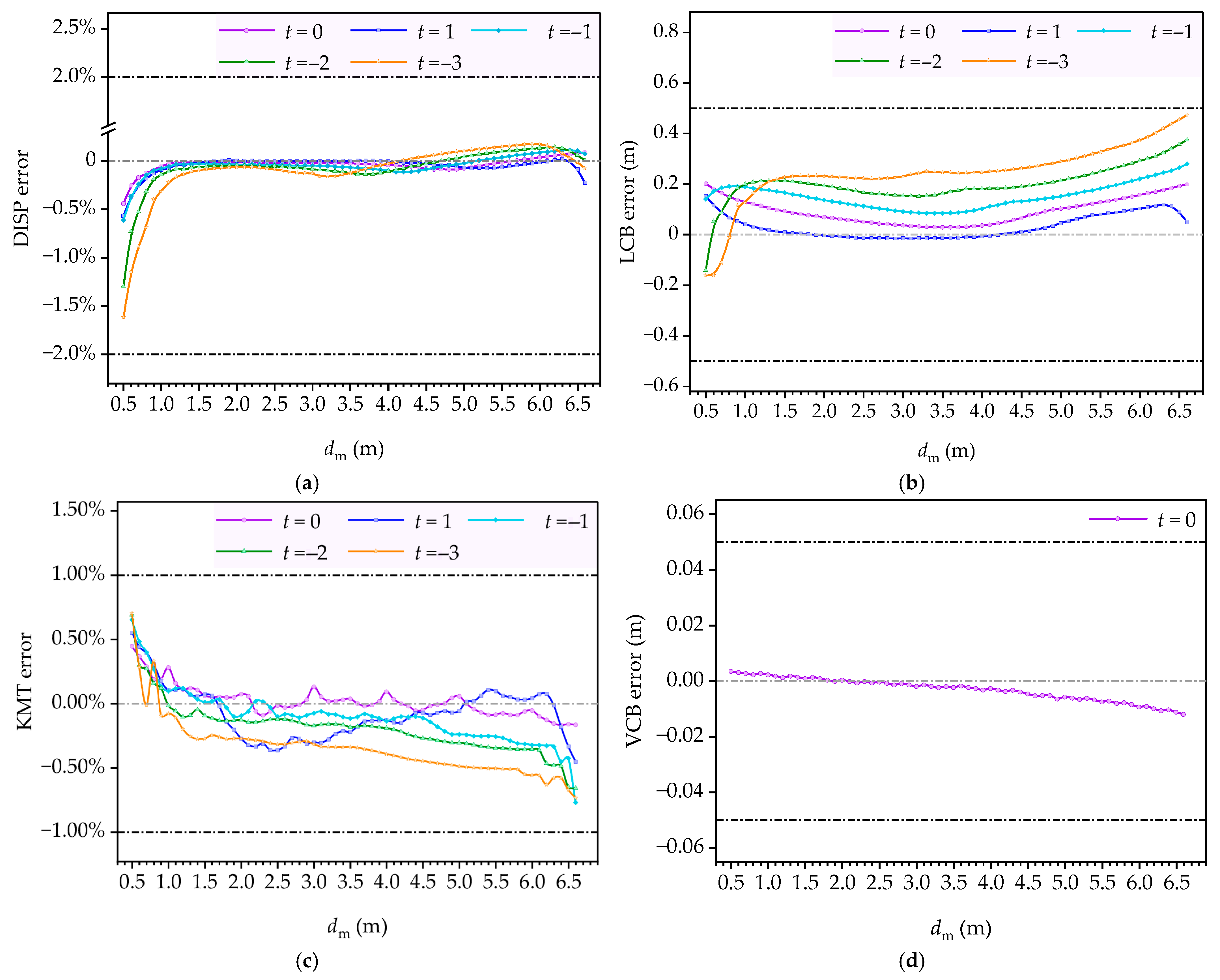
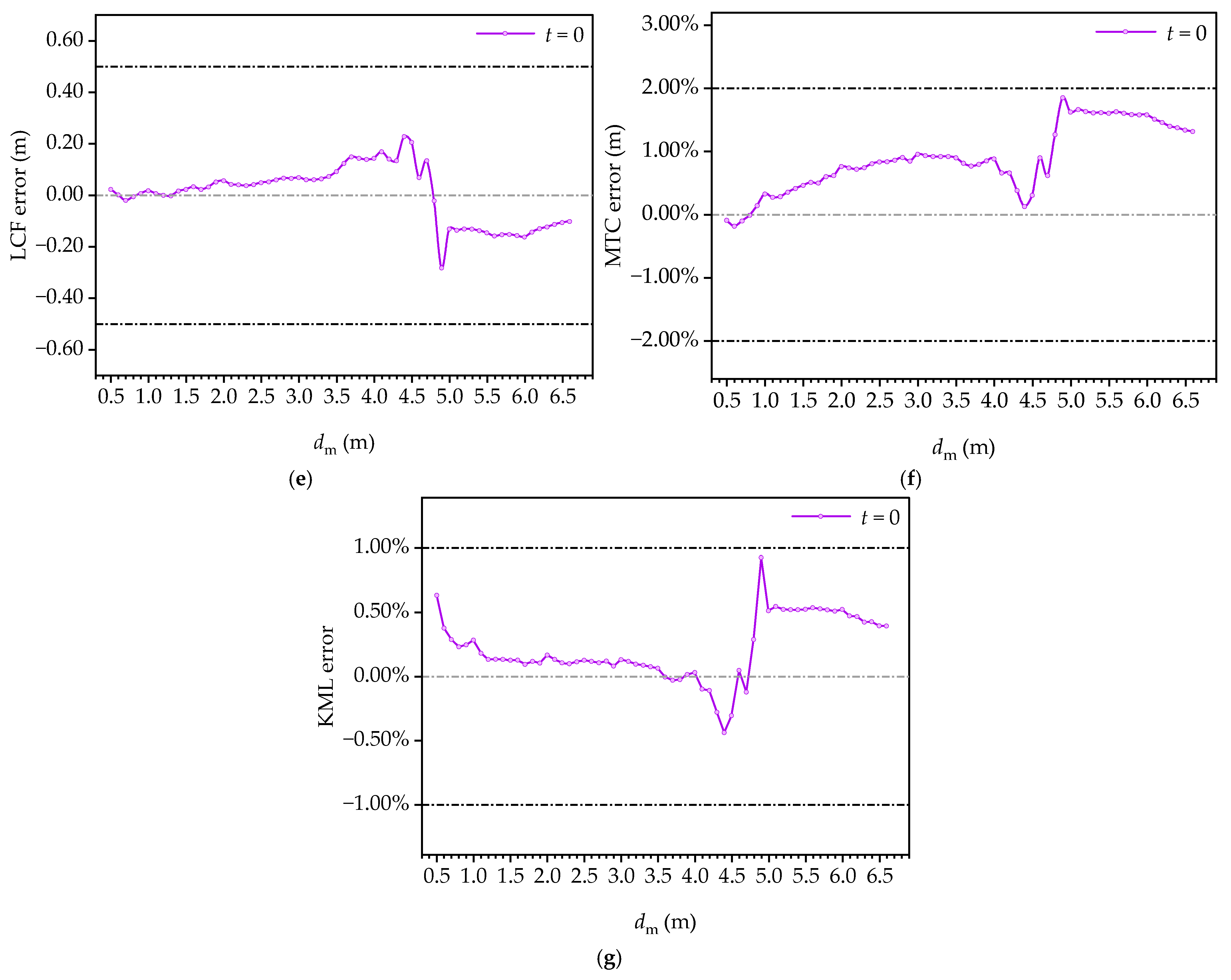
5.4. Validation of QB Method Accuracy
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| IMO | International Maritime Organization |
| SGISc | Second-Generation Intact Stability Criteria |
| QB | Quasi-Bonjean |
| AST | Adaptive Surface Tessellation |
| NURBS | Non-Uniform Rational B-Spline |
| IR- BFS | Interval Refinement and Bi-Section Feedback Search |
| FHP-BFS | Fast High-Precision Bi-Section Feedback Search |
| NCG | NURBS Curve Generation with Uniform Continuity |
| FNSG | Fast NURBS Surface Generation with Uniform Continuity |
| NSG | NURBS Surface Hybrid Generation |
| LIP | Locality In-Between Polylines |
| DP | Douglas–Peucker |
| IACS | International Association of Classification Societies |
| LCB | Longitudinal Center of Buoyancy |
| VCB | Vertical Center of Buoyancy |
| TCB | Transverse Center of Buoyancy |
| LCF | Longitudinal Center of Floatation |
| MTC | Moment to Trim One Centimeter |
| KMT | Transverse Metacenter above Base Line |
| KML | Longitudinal Metacenter above Base Line |
Appendix A
| dm | DISP (Vb) | DISP (Vc) | Error | dm | DISP (Vb) | DISP (Vc) | Error | dm | DISP (Vb) | DISP (Vc) | Error |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.5 | 365.3 | 366.908 | −0.440% | 2.6 | 2294.7 | 2295.246 | −0.024% | 4.7 | 4493.7 | 4497.521 | −0.085% |
| 0.6 | 445.7 | 446.838 | −0.255% | 2.7 | 2395.0 | 2395.581 | −0.024% | 4.8 | 4603.2 | 4607.233 | −0.088% |
| 0.7 | 527.9 | 528.804 | −0.171% | 2.8 | 2495.8 | 2496.439 | −0.026% | 4.9 | 4713.5 | 4717.638 | −0.088% |
| 0.8 | 611.7 | 612.469 | −0.126% | 2.9 | 2597.1 | 2597.698 | −0.023% | 5.0 | 4825.0 | 4828.588 | −0.074% |
| … | … | … | … | … | … | … | … | … | … | … | … |
| 2.2 | 1899.5 | 1899.722 | −0.012% | 4.3 | 4061.5 | 4063.734 | −0.055% | 6.3 | 6313.4 | 6309.220 | 0.066% |
| 2.3 | 1997.4 | 1997.768 | −0.018% | 4.4 | 4168.7 | 4171.433 | −0.066% | 6.4 | 6430.3 | 6425.556 | 0.074% |
| 2.4 | 2095.9 | 2096.317 | −0.020% | 4.5 | 4276.4 | 4279.661 | −0.076% | 6.5 | 6547.5 | 6542.175 | 0.081% |
| 2.5 | 2195.0 | 2195.450 | −0.021% | 4.6 | 4384.5 | 4388.353 | −0.088% | 6.6 | 6664.9 | 6658.961 | 0.089% |
| dm | DISP (Vb) | DISP (Vc) | Error | Tm | DISP (Vb) | DISP (Vc) | Error | dm | DISP (Vb) | DISP (Vc) | Error |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.5 | 387.3 | 389.505 | −0.569% | 2.6 | 2314.8 | 2314.915 | −0.005% | 4.7 | 4482.3 | 4484.127 | −0.041% |
| 0.6 | 467.6 | 469.316 | −0.367% | 2.7 | 2414.3 | 2414.376 | −0.003% | 4.8 | 4589.8 | 4591.958 | −0.047% |
| 0.7 | 549.9 | 551.338 | −0.262% | 2.8 | 2514.2 | 2514.282 | −0.003% | 4.9 | 4697.9 | 4700.433 | −0.054% |
| 0.8 | 634.0 | 635.148 | −0.181% | 2.9 | 2614.5 | 2614.512 | 0.000% | 5.0 | 4806.2 | 4809.447 | −0.068% |
| … | … | … | … | … | … | … | … | … | … | … | … |
| 2.2 | 1922.2 | 1922.118 | 0.004% | 4.3 | 4057.0 | 4057.792 | −0.020% | 6.3 | 6278.1 | 6276.946 | 0.018% |
| 2.3 | 2019.6 | 2019.600 | 0.000% | 4.4 | 4162.6 | 4163.611 | −0.024% | 6.4 | 6392.9 | 6393.054 | −0.002% |
| 2.4 | 2117.5 | 2117.505 | 0.000% | 4.5 | 4268.8 | 4269.982 | −0.028% | 6.5 | 6504.0 | 6509.496 | −0.085% |
| 2.5 | 2215.9 | 2215.916 | −0.001% | 4.6 | 4375.2 | 4376.819 | −0.037% | 6.6 | 6611.3 | 6626.156 | −0.225% |
| dm | DISP (Vb) | DISP (Vc) | Error | Tm | DISP (Vb) | DISP (Vc) | Error | dm | DISP (Vb) | DISP (Vc) | Error |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.5 | 363.3 | 365.539 | −0.616% | 2.6 | 2282.7 | 2283.683 | −0.043% | 4.7 | 4519.4 | 4521.932 | −0.056% |
| 0.6 | 441.9 | 443.526 | −0.368% | 2.7 | 2383.6 | 2384.688 | −0.046% | 4.8 | 4632.0 | 4634.029 | −0.044% |
| 0.7 | 522.6 | 523.855 | −0.240% | 2.8 | 2485.1 | 2486.301 | −0.048% | 4.9 | 4744.9 | 4746.446 | −0.033% |
| 0.8 | 605.2 | 606.085 | −0.146% | 2.9 | 2587.2 | 2588.406 | −0.047% | 5.0 | 4858.0 | 4859.107 | −0.023% |
| … | … | … | … | … | … | … | … | … | … | … | … |
| 2.2 | 1885.7 | 1886.343 | −0.034% | 4.3 | 4072.8 | 4077.289 | −0.110% | 6.3 | 6355.0 | 6348.059 | 0.109% |
| 2.3 | 1983.9 | 1984.710 | −0.041% | 4.4 | 4183.3 | 4187.685 | −0.105% | 6.4 | 6471.9 | 6464.483 | 0.115% |
| 2.4 | 2082.8 | 2083.671 | −0.042% | 4.5 | 4295.0 | 4298.691 | −0.086% | 6.5 | 6588.0 | 6581.138 | 0.104% |
| 2.5 | 2182.5 | 2183.303 | −0.037% | 4.6 | 4407.0 | 4410.137 | −0.071% | 6.6 | 6702.7 | 6697.916 | 0.071% |
| dm | DISP (Vb) | DISP (Vc) | Error | dm | DISP (Vb) | DISP (Vc) | Error | dm | DISP (Vb) | DISP (Vc) | Error |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.5 | 388.7 | 393.746 | −1.298% | 2.6 | 2280.7 | 2282.111 | −0.062% | 4.7 | 4553.4 | 4553.314 | 0.002% |
| 0.6 | 461.1 | 464.468 | −0.730% | 2.7 | 2382.0 | 2383.645 | −0.069% | 4.8 | 4667.8 | 4667.028 | 0.017% |
| 0.7 | 536.7 | 539.514 | −0.524% | 2.8 | 2484.1 | 2485.899 | −0.072% | 4.9 | 4782.4 | 4781.060 | 0.028% |
| 0.8 | 616.0 | 617.933 | −0.314% | 2.9 | 2586.7 | 2588.752 | −0.079% | 5.0 | 4897.3 | 4895.267 | 0.042% |
| … | … | … | … | … | … | … | … | … | … | … | … |
| 2.2 | 1882.8 | 1883.778 | −0.052% | 4.3 | 4098.9 | 4101.364 | −0.060% | 6.3 | 6400.5 | 6392.061 | 0.132% |
| 2.3 | 1981.0 | 1982.226 | −0.062% | 4.4 | 4212.0 | 4213.785 | −0.042% | 6.4 | 6515.1 | 6508.494 | 0.101% |
| 2.4 | 2080.1 | 2081.379 | −0.062% | 4.5 | 4325.4 | 4326.661 | −0.029% | 6.5 | 6629.0 | 6625.132 | 0.058% |
| 2.5 | 2180.1 | 2181.315 | −0.056% | 4.6 | 4439.2 | 4439.854 | −0.015% | 6.6 | 6742.3 | 6741.884 | 0.006% |
| dm | DISP (Vb) | DISP (Vc) | Error | dm | DISP (Vb) | DISP (Vc) | Error | dm | DISP (Vb) | DISP (Vc) | Error |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.5 | 443.9 | 451.088 | −1.619% | 2.6 | 2290.5 | 2292.795 | −0.100% | 4.7 | 4593.2 | 4589.837 | 0.073% |
| 0.6 | 509.6 | 515.439 | −1.146% | 2.7 | 2392.1 | 2394.771 | −0.112% | 4.8 | 4708.5 | 4704.474 | 0.086% |
| 0.7 | 578.7 | 583.845 | −0.889% | 2.8 | 2494.6 | 2497.616 | −0.121% | 4.9 | 4824.0 | 4819.412 | 0.095% |
| 0.8 | 651.4 | 655.891 | −0.689% | 2.9 | 2598.0 | 2601.222 | −0.124% | 5.0 | 4939.6 | 4934.508 | 0.103% |
| … | … | … | … | … | … | … | … | … | … | … | … |
| 2.2 | 1892.9 | 1894.077 | −0.062% | 4.3 | 4134.8 | 4133.911 | 0.022% | 6.3 | 6445.4 | 6440.173 | 0.081% |
| 2.3 | 1991.0 | 1992.413 | −0.071% | 4.4 | 4249.0 | 4247.382 | 0.038% | 6.4 | 6558.6 | 6556.677 | 0.029% |
| 2.4 | 2089.9 | 2091.593 | −0.081% | 4.5 | 4363.4 | 4361.267 | 0.049% | 6.5 | 6672.6 | 6673.327 | −0.011% |
| 2.5 | 2189.8 | 2191.693 | −0.086% | 4.6 | 4478.2 | 4475.434 | 0.062% | 6.6 | 6785.0 | 6790.015 | −0.074% |
| dm | LCB (Vb) | LCB (Vc) | Error | dm | LCB (Vb) | LCB (Vc) | Error | dm | LCB (Vb) | LCB (Vc) | Error |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.5 | 1.196 | 0.994 | 0.202 | 2.6 | 1.559 | 1.511 | 0.048 | 4.7 | 0.922 | 0.840 | 0.082 |
| 0.6 | 1.223 | 1.041 | 0.182 | 2.7 | 1.551 | 1.507 | 0.044 | 4.8 | 0.866 | 0.774 | 0.092 |
| 0.7 | 1.249 | 1.085 | 0.164 | 2.8 | 1.542 | 1.500 | 0.042 | 4.9 | 0.805 | 0.705 | 0.100 |
| 0.8 | 1.276 | 1.127 | 0.149 | 2.9 | 1.530 | 1.491 | 0.039 | 5.0 | 0.738 | 0.635 | 0.103 |
| … | … | … | … | … | … | … | … | … | … | … | … |
| 2.2 | 1.562 | 1.500 | 0.062 | 4.3 | 1.126 | 1.077 | 0.049 | 6.3 | −0.067 | −0.244 | 0.177 |
| 2.3 | 1.565 | 1.507 | 0.058 | 4.4 | 1.079 | 1.022 | 0.057 | 6.4 | −0.118 | −0.303 | 0.185 |
| 2.4 | 1.566 | 1.511 | 0.055 | 4.5 | 1.030 | 0.964 | 0.066 | 6.5 | −0.167 | −0.359 | 0.192 |
| 2.5 | 1.563 | 1.513 | 0.051 | 4.6 | 0.980 | 0.903 | 0.077 | 6.6 | −0.215 | −0.414 | 0.199 |
| dm | LCB (Vb) | LCB (Vc) | Error | dm | LCB (Vb) | LCB (Vc) | Error | dm | LCB (Vb) | LCB (Vc) | Error |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.5 | 9.214 | 9.061 | 0.153 | 2.6 | 3.765 | 3.779 | −0.014 | 4.7 | 2.322 | 2.301 | 0.021 |
| 0.6 | 8.215 | 8.099 | 0.116 | 2.7 | 3.693 | 3.707 | −0.014 | 4.8 | 2.254 | 2.227 | 0.027 |
| 0.7 | 7.465 | 7.377 | 0.088 | 2.8 | 3.623 | 3.637 | −0.014 | 4.9 | 2.187 | 2.152 | 0.035 |
| 0.8 | 6.884 | 6.816 | 0.068 | 2.9 | 3.553 | 3.568 | −0.015 | 5.0 | 2.122 | 2.076 | 0.046 |
| … | … | … | … | … | … | … | … | … | … | … | … |
| 2.2 | 4.080 | 4.088 | −0.008 | 4.3 | 2.596 | 2.593 | 0.003 | 6.3 | 1.196 | 1.077 | 0.119 |
| 2.3 | 3.996 | 4.006 | −0.010 | 4.4 | 2.527 | 2.520 | 0.007 | 6.4 | 1.120 | 1.007 | 0.114 |
| 2.4 | 3.916 | 3.927 | −0.011 | 4.5 | 2.458 | 2.447 | 0.011 | 6.5 | 1.027 | 0.938 | 0.089 |
| 2.5 | 3.839 | 3.852 | −0.013 | 4.6 | 2.390 | 2.374 | 0.016 | 6.6 | 0.921 | 0.871 | 0.051 |
| dm | LCB (Vb) | LCB (Vc) | Error | dm | LCB (Vb) | LCB (Vc) | Error | dm | LCB (Vb) | LCB (Vc) | Error |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.5 | −6.967 | −7.108 | 0.141 | 2.6 | −0.717 | −0.825 | 0.108 | 4.7 | −0.599 | −0.738 | 0.139 |
| 0.6 | −5.860 | −6.033 | 0.173 | 2.7 | −0.661 | −0.765 | 0.104 | 4.8 | −0.645 | −0.788 | 0.143 |
| 0.7 | −5.026 | −5.212 | 0.186 | 2.8 | −0.611 | −0.710 | 0.099 | 4.9 | −0.693 | −0.840 | 0.147 |
| 0.8 | −4.371 | −4.562 | 0.191 | 2.9 | −0.568 | −0.663 | 0.095 | 5.0 | −0.742 | −0.894 | 0.152 |
| … | … | … | … | … | … | … | … | … | … | … | … |
| 2.2 | −1.020 | −1.147 | 0.127 | 4.3 | −0.449 | −0.574 | 0.125 | 6.3 | −1.321 | −1.566 | 0.245 |
| 2.3 | −0.932 | −1.053 | 0.121 | 4.4 | −0.478 | −0.609 | 0.131 | 6.4 | −1.357 | −1.610 | 0.253 |
| 2.4 | −0.852 | −0.969 | 0.117 | 4.5 | −0.516 | −0.648 | 0.132 | 6.5 | −1.388 | −1.653 | 0.265 |
| 2.5 | −0.780 | −0.893 | 0.113 | 4.6 | −0.556 | −0.691 | 0.135 | 6.6 | −1.414 | −1.694 | 0.280 |
| dm | LCB (Vb) | LCB (Vc) | Error | dm | LCB (Vb) | LCB (Vc) | Error | dm | LCB (Vb) | LCB (Vc) | Error |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.5 | −12.765 | −12.623 | −0.142 | 2.6 | −3.031 | −3.194 | 0.163 | 4.7 | −2.224 | −2.422 | 0.198 |
| 0.6 | −11.457 | −11.509 | 0.052 | 2.7 | −2.914 | −3.075 | 0.161 | 4.8 | −2.240 | −2.443 | 0.203 |
| 0.7 | −10.392 | −10.480 | 0.088 | 2.8 | −2.808 | −2.966 | 0.158 | 4.9 | −2.257 | −2.465 | 0.208 |
| 0.8 | −9.401 | −9.550 | 0.149 | 2.9 | −2.711 | −2.867 | 0.156 | 5.0 | −2.275 | −2.489 | 0.214 |
| … | … | … | … | … | … | … | … | … | … | … | … |
| 2.2 | −3.612 | −3.795 | 0.183 | 4.3 | −2.179 | −2.363 | 0.184 | 6.3 | −2.558 | −2.881 | 0.323 |
| 2.3 | −3.447 | −3.625 | 0.178 | 4.4 | −2.187 | −2.374 | 0.187 | 6.4 | −2.571 | −2.910 | 0.339 |
| 2.4 | −3.296 | −3.468 | 0.172 | 4.5 | −2.198 | −2.387 | 0.189 | 6.5 | −2.581 | −2.938 | 0.357 |
| 2.5 | −3.158 | −3.325 | 0.167 | 4.6 | −2.210 | −2.404 | 0.194 | 6.6 | −2.590 | −2.964 | 0.374 |
| dm | LCB (Vb) | LCB (Vc) | Error | dm | LCB (Vb) | LCB (Vc) | Error | dm | LCB (Vb) | LCB (Vc) | Error |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.5 | −15.613 | −15.452 | −0.162 | 2.6 | −5.339 | −5.561 | 0.222 | 4.7 | −3.883 | −4.155 | 0.272 |
| 0.6 | −14.705 | −14.545 | −0.161 | 2.7 | −5.173 | −5.395 | 0.222 | 4.8 | −3.866 | −4.143 | 0.277 |
| 0.7 | −13.825 | −13.713 | −0.112 | 2.8 | −5.019 | −5.243 | 0.224 | 4.9 | −3.852 | −4.134 | 0.282 |
| 0.8 | −12.952 | −12.941 | −0.011 | 2.9 | −4.879 | −5.105 | 0.226 | 5.0 | −3.838 | −4.127 | 0.289 |
| … | … | … | … | … | … | … | … | … | … | … | … |
| 2.2 | −6.157 | −6.385 | 0.228 | 4.3 | −3.968 | −4.223 | 0.255 | 6.3 | −3.766 | −4.185 | 0.419 |
| 2.3 | −5.927 | −6.153 | 0.226 | 4.4 | −3.943 | −4.202 | 0.259 | 6.4 | −3.759 | −4.197 | 0.438 |
| 2.4 | −5.714 | −5.939 | 0.225 | 4.5 | −3.921 | −4.184 | 0.263 | 6.5 | −3.754 | −4.209 | 0.455 |
| 2.5 | −5.519 | −5.742 | 0.223 | 4.6 | −3.901 | −4.168 | 0.267 | 6.6 | −3.748 | −4.221 | 0.473 |
| dm | VCB (Vb) | VCB (Vc) | Error | dm | VCB (Vb) | VCB (Vc) | Error | dm | VCB (Vb) | VCB (Vc) | Error |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.5 | 0.261 | 0.258 | 0.003 | 2.6 | 1.380 | 1.381 | −0.001 | 4.7 | 2.500 | 2.505 | −0.005 |
| 0.6 | 0.314 | 0.311 | 0.003 | 2.7 | 1.433 | 1.435 | −0.002 | 4.8 | 2.554 | 2.559 | −0.005 |
| 0.7 | 0.367 | 0.364 | 0.003 | 2.8 | 1.487 | 1.488 | −0.001 | 4.9 | 2.607 | 2.614 | −0.006 |
| 0.8 | 0.420 | 0.418 | 0.002 | 2.9 | 1.540 | 1.542 | −0.002 | 5.0 | 2.662 | 2.668 | −0.006 |
| … | … | … | … | … | … | … | … | … | … | … | … |
| 2.2 | 1.166 | 1.167 | −0.001 | 4.3 | 2.287 | 2.290 | −0.003 | 6.3 | 3.368 | 3.379 | −0.011 |
| 2.3 | 1.220 | 1.220 | 0.000 | 4.4 | 2.340 | 2.344 | −0.004 | 6.4 | 3.423 | 3.434 | −0.011 |
| 2.4 | 1.273 | 1.274 | −0.001 | 4.5 | 2.393 | 2.398 | −0.005 | 6.5 | 3.477 | 3.488 | −0.011 |
| 2.5 | 1.327 | 1.327 | 0.000 | 4.6 | 2.446 | 2.451 | −0.005 | 6.6 | 3.531 | 3.543 | −0.012 |
References
- Wang, B.; Liu, Y.; Dai, W.; Li, J. Incremental route planning based on daily risk assessment for arctic navigation. Ocean Eng. 2025, 320, 120294. [Google Scholar] [CrossRef]
- Yao, S.; Wu, Q.; Kang, Q.; Chen, Y.W.; Lu, Y. An interpretable XGBboost-based approach for arctic navigation risk assessment. Risk Anal. 2024, 44, 459–476. [Google Scholar] [CrossRef]
- Shu, Y.; Zhu, Y.; Xu, F.; Gan, L.; Lee, P.; Yin, J.; Chen, J. Path planning for ships assisted by the icebreaker in ice-covered waters in the Northern Sea Route based on optimal control. Ocean Eng. 2023, 267, 113182. [Google Scholar] [CrossRef]
- Shu, Y.; Huang, F.; Wu, J.; Chen, J.; Song, L.; Gan, L. Research on Ship Following Behavior Based on Data Mining in Arctic Waters. IEEE Trans. Intell. Transp. Syst. 2025, 26, 6778–6788. [Google Scholar] [CrossRef]
- Shu, Y.; Cui, H.; Song, L.; Gan, L.; Xu, S.; Wu, J.; Zheng, C. Influence of sea ice on ship routes and speed along the Arctic Northeast Passage. Ocean Coast. Manag. 2024, 256, 107320. [Google Scholar] [CrossRef]
- Jin, L.; Li, P.; Wang, Y.; Yang, Z. Risk analysis of Arctic navigation using text mining (TM) and improved association rule mining (ARM) methods. Reg. Stud. Mar. Sci. 2025, 81, 103990. [Google Scholar] [CrossRef]
- IMO. Finalization of Second-Generation Intact Stability Criteria; IMO: London, UK, 2019. [Google Scholar]
- Nicola, P.; Goran, P.; Paola, G. An insight on the post-processing procedure of the Direct Stability Assessment within SGISC. Ocean Eng. 2024, 305, 117982. [Google Scholar] [CrossRef]
- Petacco, N.; Gualeni, P. IMO second generation intact stability criteria: General overview and focus on operational measures. J. Mar. Sci. Eng. 2020, 8, 494. [Google Scholar] [CrossRef]
- Lin, Y.; Shou, K.; Huang, L. The initial study of LLS-based binocular stereo-vision system on underwater 3D image reconstruction in the laboratory. J. Mar. Sci. Technol. 2017, 22, 513–532. [Google Scholar] [CrossRef]
- Kim, D.; Yeo, D. Estimation of drafts and metacentric heights of small fishing vessels according to loading conditions. Int. J. Nav. Archit. Ocean Eng. 2019, 12, 199–212. [Google Scholar] [CrossRef]
- Lee, D.; Lim, C.; Oh, S.; Kim, M.; Park, J.; Shin, S. Predictive model for hydrostatic curves of chine-type small ships based on deep learning. J. Mar. Sci. Eng. 2024, 12, 180. [Google Scholar] [CrossRef]
- Pérez, F.; Suárez, J.; Fernández, L. Automatic surface modelling of a ship hull. Comput.-Aided Des. 2006, 38, 584–594. [Google Scholar] [CrossRef]
- Adarsh, K.; Sara, M. Accurate GPU-accelerated surface integrals for moment computation. Comput. Aided Des. 2011, 43, 1284–1295. [Google Scholar] [CrossRef]
- Ingrassia, T.; Mancuso, A.; Nigrelli, V.; Saporito, A.; Tumino, D. Parametric hull design with rational Bézier curves and estimation of performances. J. Mar. Sci. Eng. 2021, 9, 360. [Google Scholar] [CrossRef]
- Jiang, X.; Lin, Y. Reparameterization of B-spline surface and its application in ship hull modeling. Ocean Eng. 2023, 286, 115535. [Google Scholar] [CrossRef]
- Zhu, K.; Shi, G.; Liu, J.; Shi, J.; Wang, Y.; Jiang, X. Fast NURBS skinning algorithm and ship hull section refinement model. In Proceedings of the 2023 7th International Conference on Machine Learning and Soft Computing, Chongqing, China, 5–7 January 2023; pp. 26–33. [Google Scholar] [CrossRef]
- Lee, K.; Cho, D.; Kim, T. Interpolation of the irregular curve network of ship hull form using subdivision surfaces. Comput.-Aided Des. Appl. 2004, 1, 17–23. [Google Scholar] [CrossRef]
- Greshake, S.; Bronsart, R. Using subdivision surfaces to address the limitations of B-spline surfaces in ship hull form modeling. In Proceedings of the International Symposium on Practical Design of Ships and other Floating Structures, Copenhagen, Denmark, 4–8 September 2016. [Google Scholar]
- Coppedé, A.; Vernengo, G.; Villa, D. A combined approach based on subdivision surface and free form deformation for smart ship hull form design and variation. Ship Offshore Struct. 2018, 13, 769–778. [Google Scholar] [CrossRef]
- Greshake, S. Generalized B-Spline Surfaces for Ship Hull form Representation and Modeling. Ph.D. Thesis, University of Rostock, Rostock, Germany, 2021. [Google Scholar]
- Pérez, F.; Calderon, J. A parametric methodology for the preliminary design of SWATH hulls. Ocean Eng. 2020, 197, 106823. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, N.; Gu, X.; Shi, Q. Geometric space construction method combined of a spline-skinning based geometric variation method and PCA dimensionality reduction for ship hull form optimization. Ocean Eng. 2024, 302, 117604. [Google Scholar] [CrossRef]
- Kim, J.-H.; Roh, M.-I.; Yeo, I.-C. A method for generating multiple hull forms at once using MLP (Multi-Layer Perceptron). Ocean Eng. 2025, 324, 120659. [Google Scholar] [CrossRef]
- Khan, S.; Goucher-Lambert, K.; Kostas, K.; Kaklis, P. ShipHullGAN: A generic parametric modeller for ship hull design using deep convolutional generative model. Comput. Methods Appl. Mech. Eng. 2023, 411, 116051. [Google Scholar] [CrossRef]
- Sarioz, E. An optimization approach for fairing of ship hull forms. Ocean Eng. 2006, 33, 2105–2118. [Google Scholar] [CrossRef]
- Luong, Q.P.; Nam, J.H. Surface modification by superimposing piecewise shape function satisfying hull variation given by arbitrary characteristic curve on surface. J. Comput. Des. Eng. 2021, 8, 1125–1140. [Google Scholar] [CrossRef]
- Luong, Q.P.; Nam, J.H.; Le, T.H. An approach for multi-patch surface modification with a curve constraint satisfying convergent G1 continuity. J. Comput. Des. Eng. 2022, 9, 2073–2088. [Google Scholar] [CrossRef]
- Nam, J.H.; Bang, N.S. A curve based hull form variation with geometric constraints of area and centroid. Ocean Eng. 2017, 133, 1–8. [Google Scholar] [CrossRef]
- Son, E.Y.; Oh, S.J. Entrance and run angle variations of hull form preserving the prismatic coefficient. Int. J. Nav. Archit. Ocean Eng. 2023, 15, 100519. [Google Scholar] [CrossRef]
- Liu, X.; Zhao, W.; Wan, D. Multi-fidelity Co-Kriging surrogate model for ship hull form optimization. Ocean Eng. 2022, 243, 110239. [Google Scholar] [CrossRef]
- Liu, X.; Wan, D.; Lei, L. Multi-fidelity model and reduced-order method for comprehensive hydrodynamic performance optimization and prediction of JBC ship. Ocean Eng. 2023, 267, 113321. [Google Scholar] [CrossRef]
- DeBoer, A.; Vander, S.; Bijl, H. Mesh deformation based on radial basis function interpolation. Comput. Struct. 2007, 85, 784–795. [Google Scholar] [CrossRef]
- Kim, H.; Yang, C. A new surface modification approach for CFD-based hull form optimization. J. Hydrodyn. 2010, 22, 503–508. [Google Scholar] [CrossRef]
- Nazemian, A.; Ghadimi, P. Shape optimisation of trimaran ship hull using CFD based simulation and adjoint solver. Ships Offshore Struct. 2022, 17, 359–373. [Google Scholar] [CrossRef]
- Ouyang, X.; Chang, H.; Feng, B.; Liu, Z.; Zhan, C.; Cheng, X. Application of an improved maximum entropy sampling method in hull form optimization. Ocean Eng. 2023, 270, 112702. [Google Scholar] [CrossRef]
- Ichinose, Y. Method involving shape-morphing of multiple hull forms aimed at organizing and visualizing the propulsive performance of optimal ship designs. Ocean Eng. 2022, 263, 112355. [Google Scholar] [CrossRef]
- Zhu, K.; Shi, G.; Liu, J. Improved flattening algorithm for NURBS curve based on bisection feedback search algorithm and interval reformation method. Ocean Eng. 2022, 247, 110635. [Google Scholar] [CrossRef]
- Zhu, K.; Shi, G.; Liu, J.; Shi, J. Fast High-Precision Bisection Feedback Search Algorithm and Its Application in Flattening the NURBS Curve. J. Mar. Sci. Eng. 2022, 10, 1851. [Google Scholar] [CrossRef]
- Zhu, K.; Shi, G.; Liu, J.; Shi, J. Fast Reconstruction Model of the Ship Hull NURBS Surface with Uniform Continuity for Calculating the Hydrostatic Elements. J. Mar. Sci. Eng. 2023, 11, 1816. [Google Scholar] [CrossRef]
- Bae, S.H.; Shin, H.; Jung, W.H.; Choi, B.K. Parametric-surface adaptive tessellation based on degree reduction. Comput. Graph. 2002, 26, 5. [Google Scholar] [CrossRef]
- Espino, F.; Bo, M.; Amor, M.; Bruguera, J. Adaptive tessellation of NURBS surfaces. J. WSCG 2003, 11, 1–8. [Google Scholar]
- Munakata, S.; Takagaki, K.; Umeda, N.; Koike, H.; Sakai, M.; Maki, A. An investigation into false-negative cases for low-freeboard ships in the vulnerability criteria of dead ship stability. Ocean Eng. 2022, 266, 113130. [Google Scholar] [CrossRef]
- Park, K.S.; Park, H.C.; Lee, C.H. Consideration of Second Intact Stability Criteria. Spec. Issue Soc. Nav. Archit. Korea 2017, 10, 19–27. [Google Scholar]
- Markus, T.; Pekka, R.; Daniel, L. On the consistency of the level 1 and 2 vulnerability criteria in the Second Generation Intact Stability. In Proceedings of the 16th International Ship Stability Workshop, Belgrade, Serbia, 5–7 June 2017; Volume 5, pp. 1–6. [Google Scholar]
- Kim, K.B. Estimating System of Pure-Loss of Stability Based on Artificial Neural Network for IMO 2nd Generation Intact Stability Criteria. Master’s Thesis, Korea Maritime & Ocean University, Busan, Republic of Korea, 2020. [Google Scholar]
- Petacco, N.; Pitardi, D.; Podenzana, C.; Gualeni, P. Application of the IMO second generation intact stability criteria to a ballast-free containership. J. Mar. Sci. Eng. 2021, 9, 1416. [Google Scholar] [CrossRef]
- Shin, D.M.; Chung, J.H. Application of dead ship condition based on IMO second-generation intact stability criteria for 13K oil chemical tanker. Ocean Eng. 2021, 238, 109776. [Google Scholar] [CrossRef]
- Shin, D.M.; Moon, B.Y. Assessment of excessive acceleration of the IMO second generation intact stability criteria for the tanker. J. Mar. Sci. Eng. 2022, 10, 229. [Google Scholar] [CrossRef]
- Shin, D.M.; Moon, B.Y.; Chung, J.H. Application of surf-riding and broaching mode based on IMO second-generation intact stability criteria for previous ships. Int. J. Nav. Archit. Ocean Eng. 2021, 13, 545–553. [Google Scholar] [CrossRef]
- Marlantes, K.E.; Kim, S.; Hurt, L.A. Implementation of the IMO second generation intact stability guidelines. J. Mar. Sci. Eng. 2022, 10, 41. [Google Scholar] [CrossRef]
- Petacco, N. An alternative methodology for the simplified operational guidance in the framework of second generation intact stability criteria. Ocean Eng. 2022, 266, 112665. [Google Scholar] [CrossRef]
- Bulian, G.; Orlandi, A. Effect of environmental data uncertainty in the framework of second generation intact stability criteria. Ocean Eng. 2022, 253, 111253. [Google Scholar] [CrossRef]
- Kwang-phil, P.; Jahun, K.; Jaeyong, L.; Namkug, K. Real-time ship stability evaluation program through deterministic method based on second-generation intact stability. Int. J. Nav. Archit. Ocean Eng. 2023, 15, 100526. [Google Scholar] [CrossRef]
- Shin, D.; Lee, S.; Sung, Y.; Jeong, H.; Moon, B. Assessment of Dead Ship Condition by the IMO Second Generation Intact Stability Criteria for 5000HP Tug Boat. J. Ship Prod. Des. 2024, 40, 185–193. [Google Scholar] [CrossRef]
- International Code for Ships Operating in Polar Waters (Polar Code). Available online: https://www.imo.org/en/ourwork/safety/pages/polar-code.aspx#:~:text=The%20Polar%20Code%20covers%20the%20full%20range%20of,in%20the%20inhospitable%20waters%20surrounding%20the%20two%20poles (accessed on 6 July 2025).
- Bonath, V.; Zhaka, V.; Sand, B. Field measurements on the behavior of brash ice. In Proceedings of the 25th International Conference on Port and Ocean Engineering Under Arctic Conditions, Delft, The Netherlands, 9–13 June 2019. [Google Scholar]
- Jeong, S.Y.; Choi, K.; Kim, H.S. Investigation of ship resistance characteristics under pack ice conditions. Ocean Eng. 2021, 219, 108264. [Google Scholar] [CrossRef]
- Matala, R. Investigation of model-scale brash ice properties. Ocean Eng. 2021, 225, 108539. [Google Scholar] [CrossRef]
- Matala, R.; Suominen, M. Scaling principles for model testing in old brash ice channel. Cold Reg. Sci. Technol. 2023, 210, 103857. [Google Scholar] [CrossRef]
- Kim, J.H.; Kim, Y.; Kim, H.S.; Jeong, S.Y. Numerical simulation of ice impacts on ship hulls in broken ice fields. Ocean Eng. 2019, 182, 211–221. [Google Scholar] [CrossRef]
- Luo, W.; Jiang, D.; Wu, T.; Guo, C.; Wang, C.; Deng, R.; Dai, S. Numerical simulation of an ice-strengthened bulk carrier in brash ice channel. Ocean Eng. 2020, 196, 106830. [Google Scholar] [CrossRef]
- Zong, Z.; Zhou, L. A theoretical investigation of ship ice resistance in waters covered with ice floes. Ocean Eng. 2019, 186, 106114. [Google Scholar] [CrossRef]
- Spencer, D.; Jones, S.J. Model-scale/full-scale correlation in open water and ice for Canadian coast guard “R-class” icebreakers. J. Ship Res. 2001, 45, 249–261. [Google Scholar] [CrossRef]
- Dobrodeev, A.; Sazonov, K. Ice resistance of ships in brash ice channel: Calculation method. Trans. Krylov State Res. Cent. 2019, 3, 11–21. [Google Scholar] [CrossRef]
- Colbourne, D. Scaling pack ice and iceberg loads on moored ship shapes. Ocean Eng. Int. 2000, 4, 39–45. [Google Scholar]
- Huang, L.; Li, Z.; Ryan, C.; Ringsberg, J.W.; Pena, B.; Li, M.; Ding, L.; Thomas, G. Ship resistance when operating in floating ice floes: Derivation, validation, and application of an empirical equation. Mar. Struct. 2021, 79, 103057. [Google Scholar] [CrossRef]
- Karulina, M.M.; Karulin, E.B.; Tarovik, O.V. Extension of FSICR method for calculation of ship resistance in brash ice channel. In Proceedings of the 25th International Conference on Port and Ocean Engineering under Arctic Conditions, Delft, The Netherlands, 9–13 June 2019. [Google Scholar]
- Matala, R.; Suominen, M. Impact of new bow shapes on FSICR power requirements. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Melbourne, Australia, 11–16 June 2023. [Google Scholar] [CrossRef]
- Barequet, G.; Goryachev, A. Offset polygon and annulus placement problems. Comput. Geom. 2014, 47, 407–434. [Google Scholar] [CrossRef]
- Li, J.; Cheng, R. A real-time adaptive signal control method for multi-intersections in mixed connected vehicle environments. J. Zhejiang Univ. Sci. A, 2025; in press. [Google Scholar] [CrossRef]
- Zhao, L.; Shi, G. A trajectory clustering method based on Douglas-Peucker compression and density for marine traffic pattern recognition. Ocean Eng. 2019, 172, 456–467. [Google Scholar] [CrossRef]
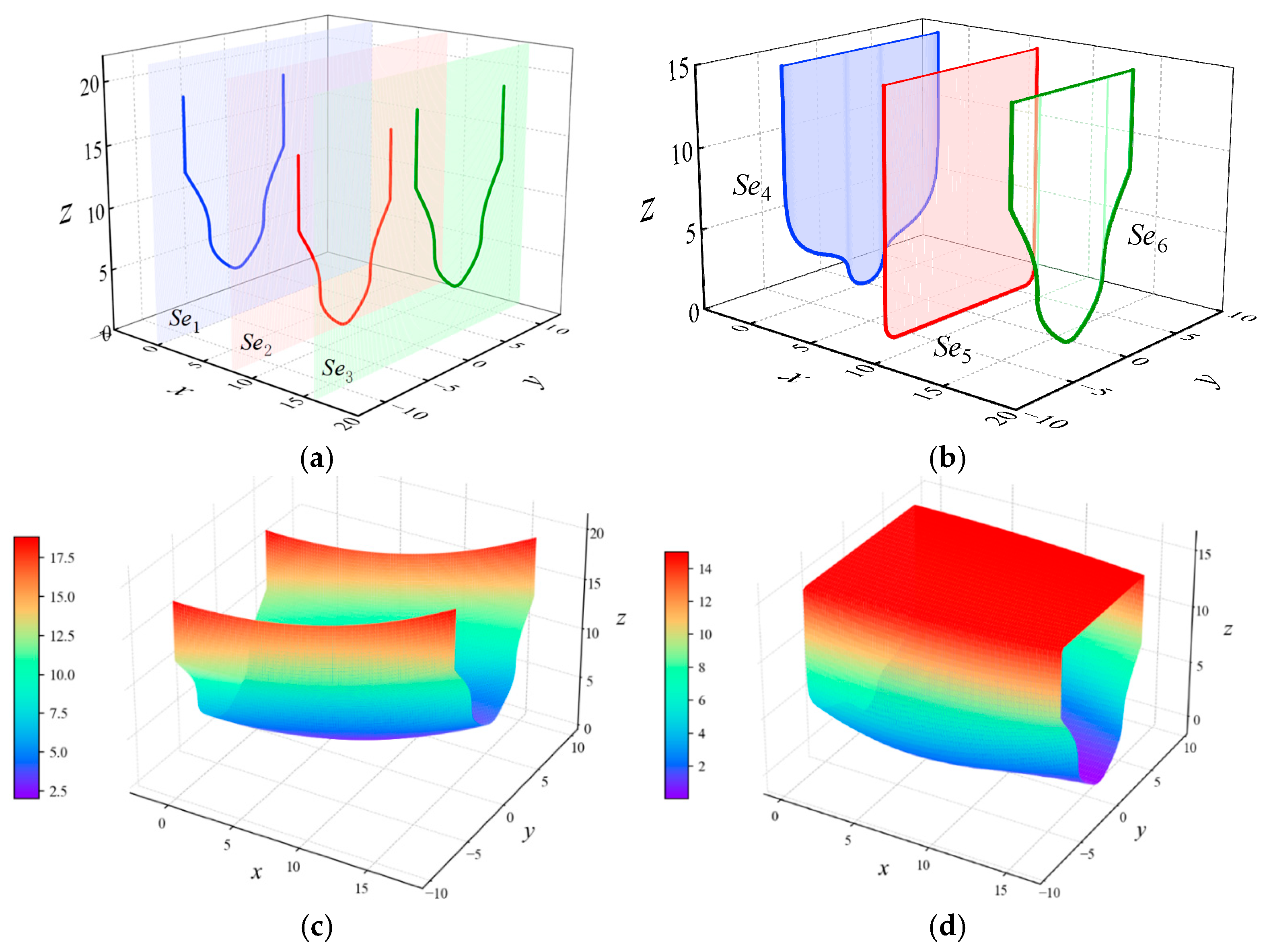
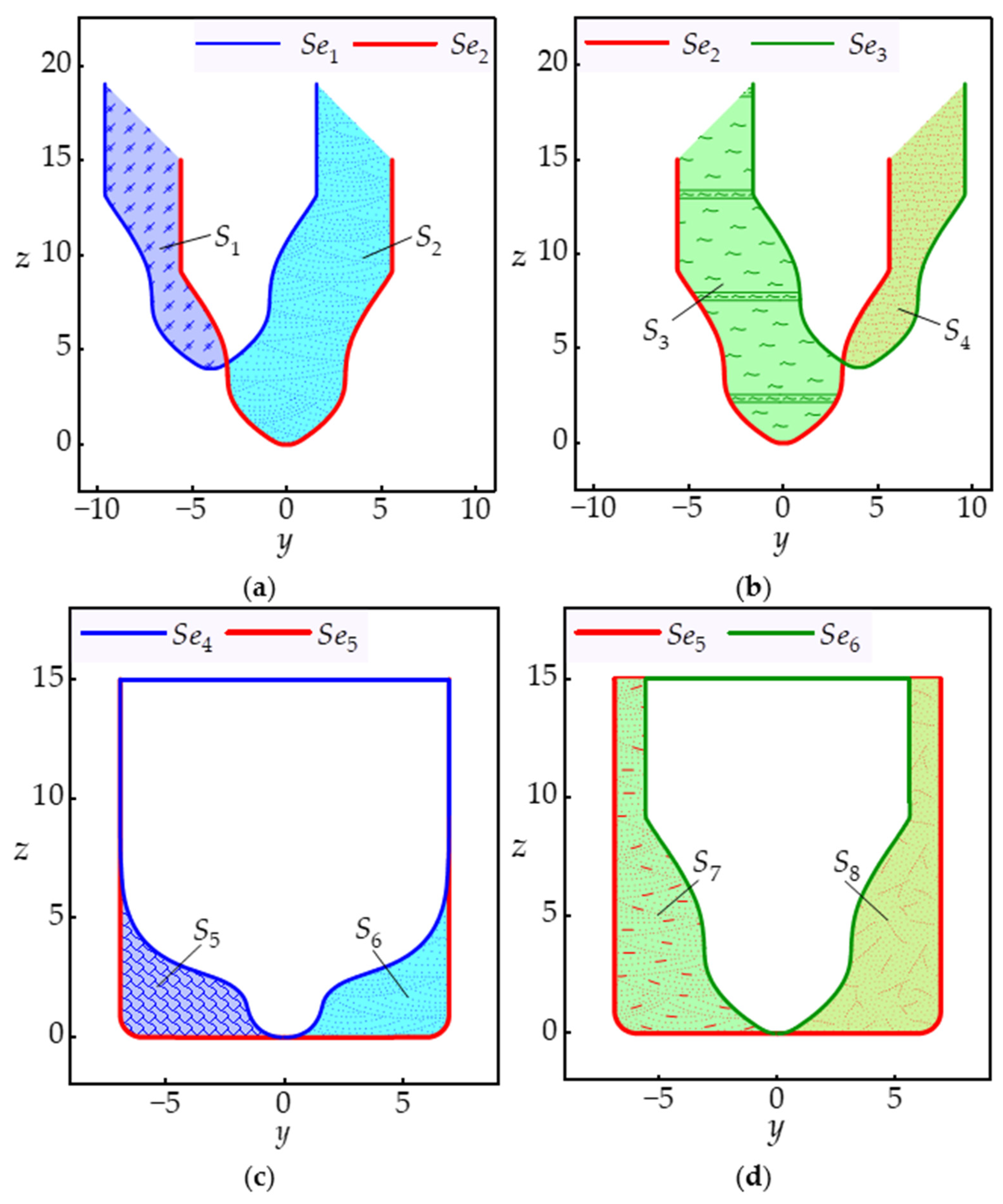
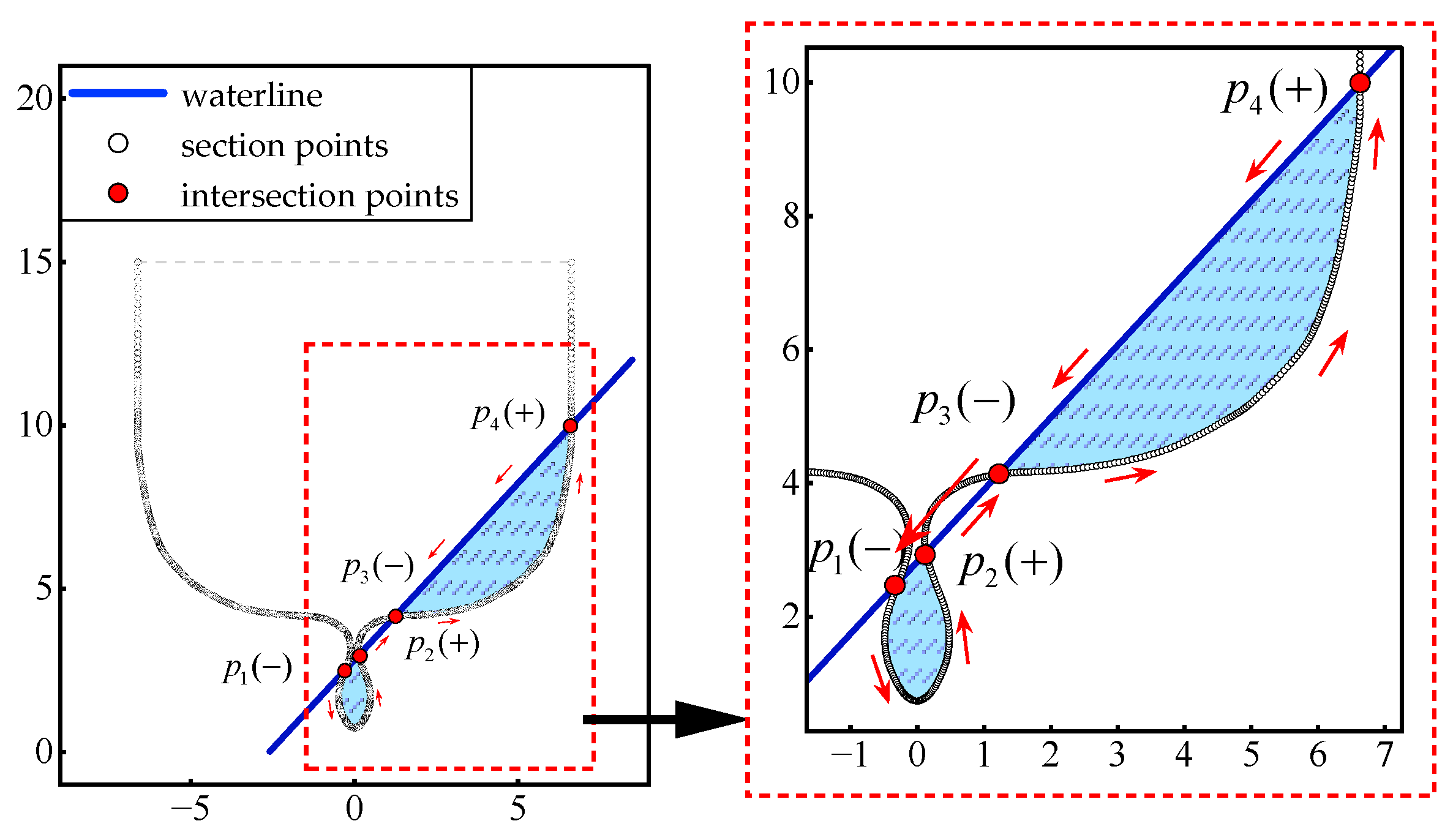
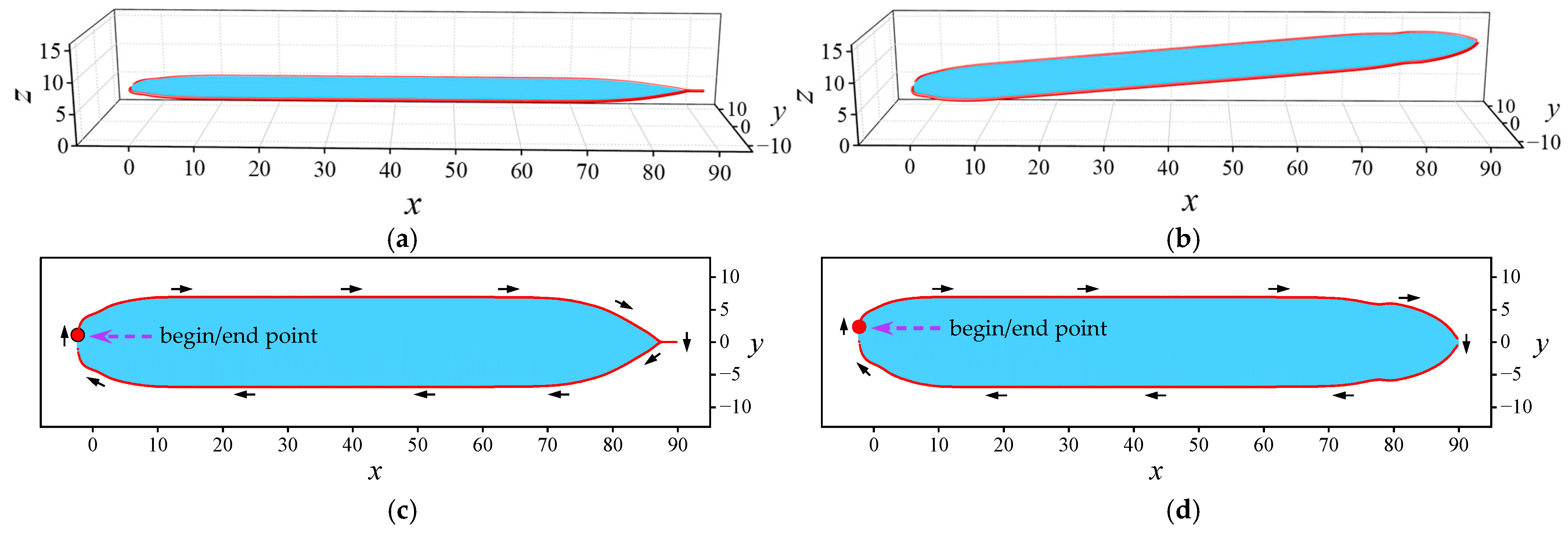
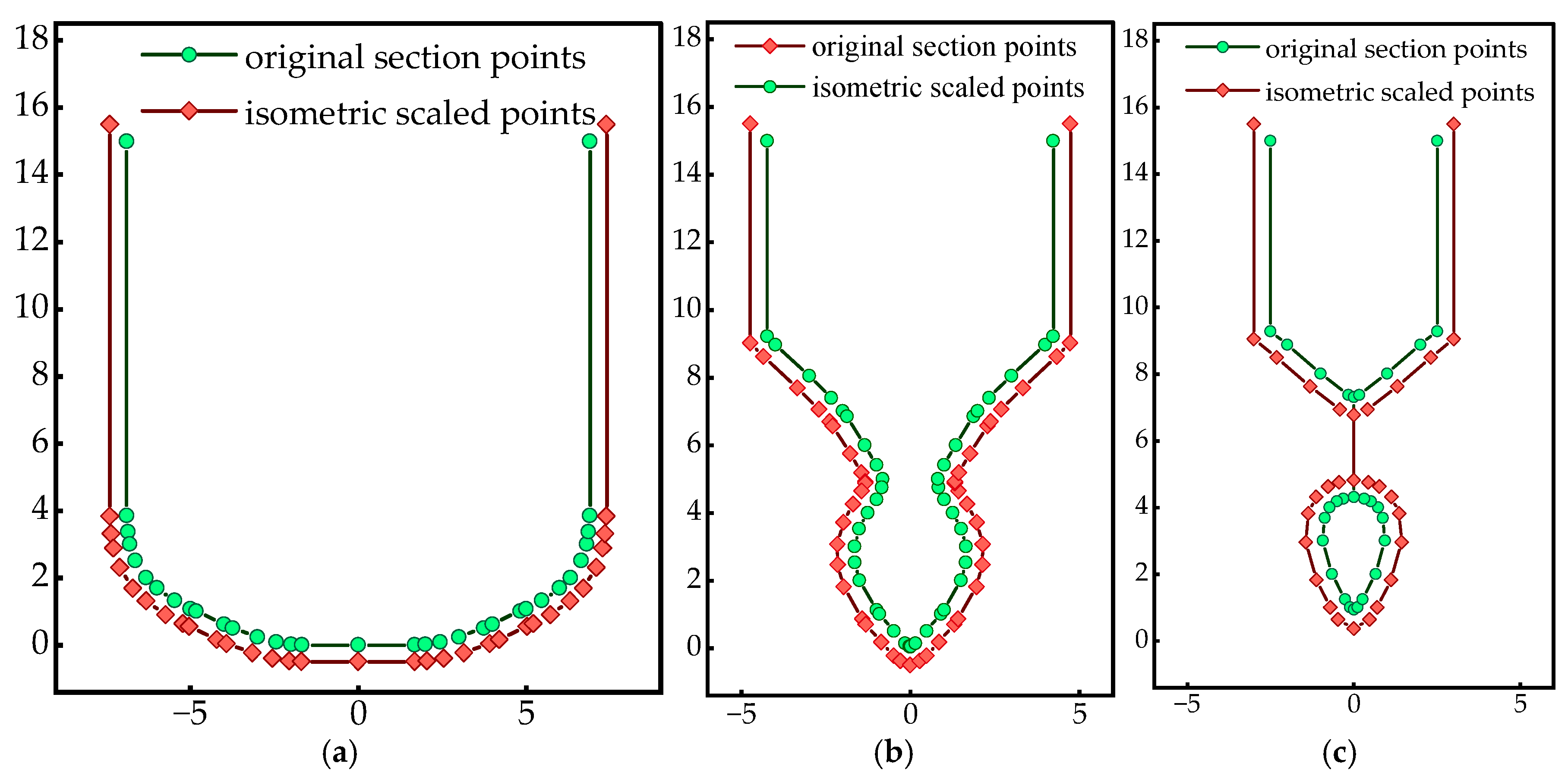
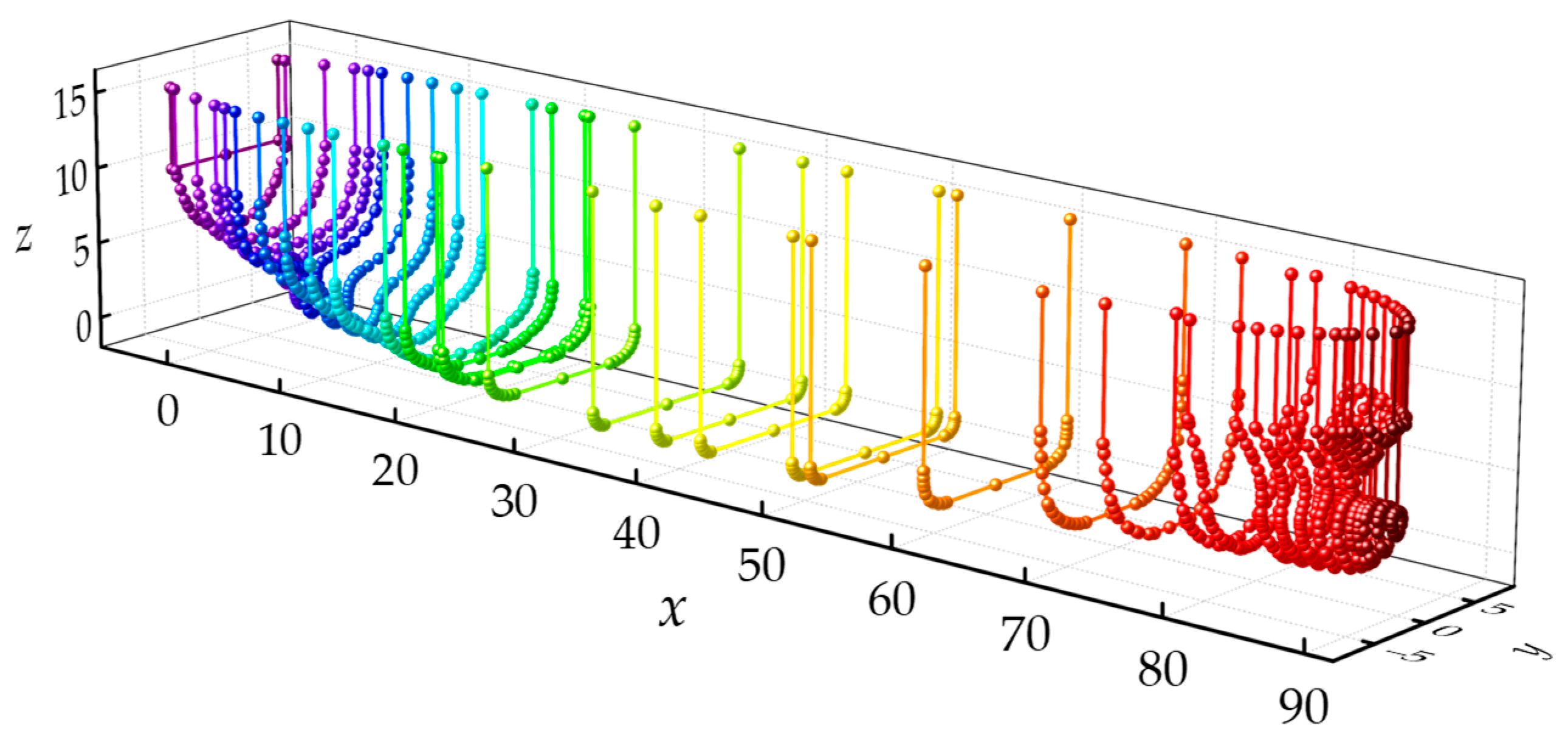
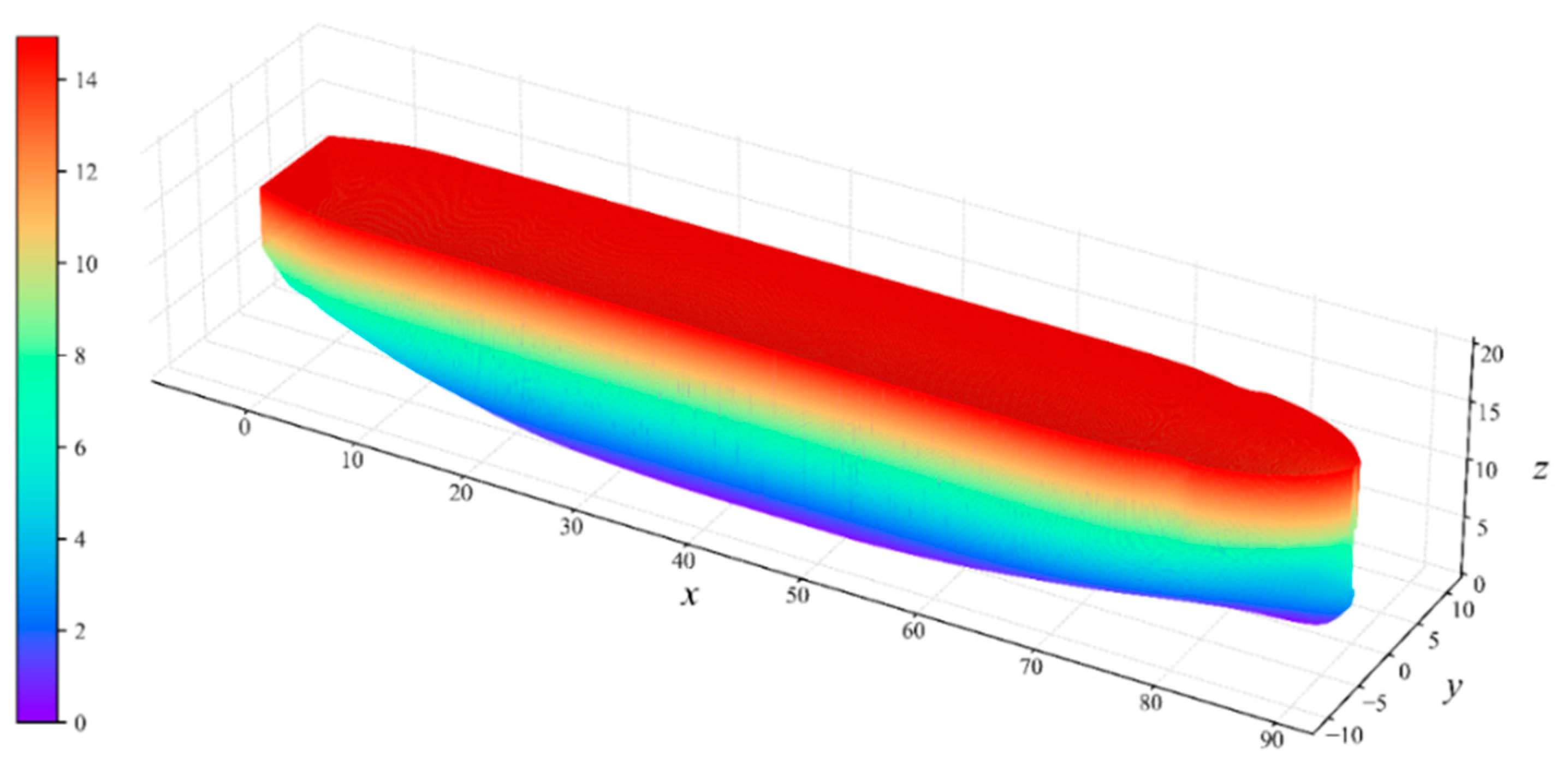

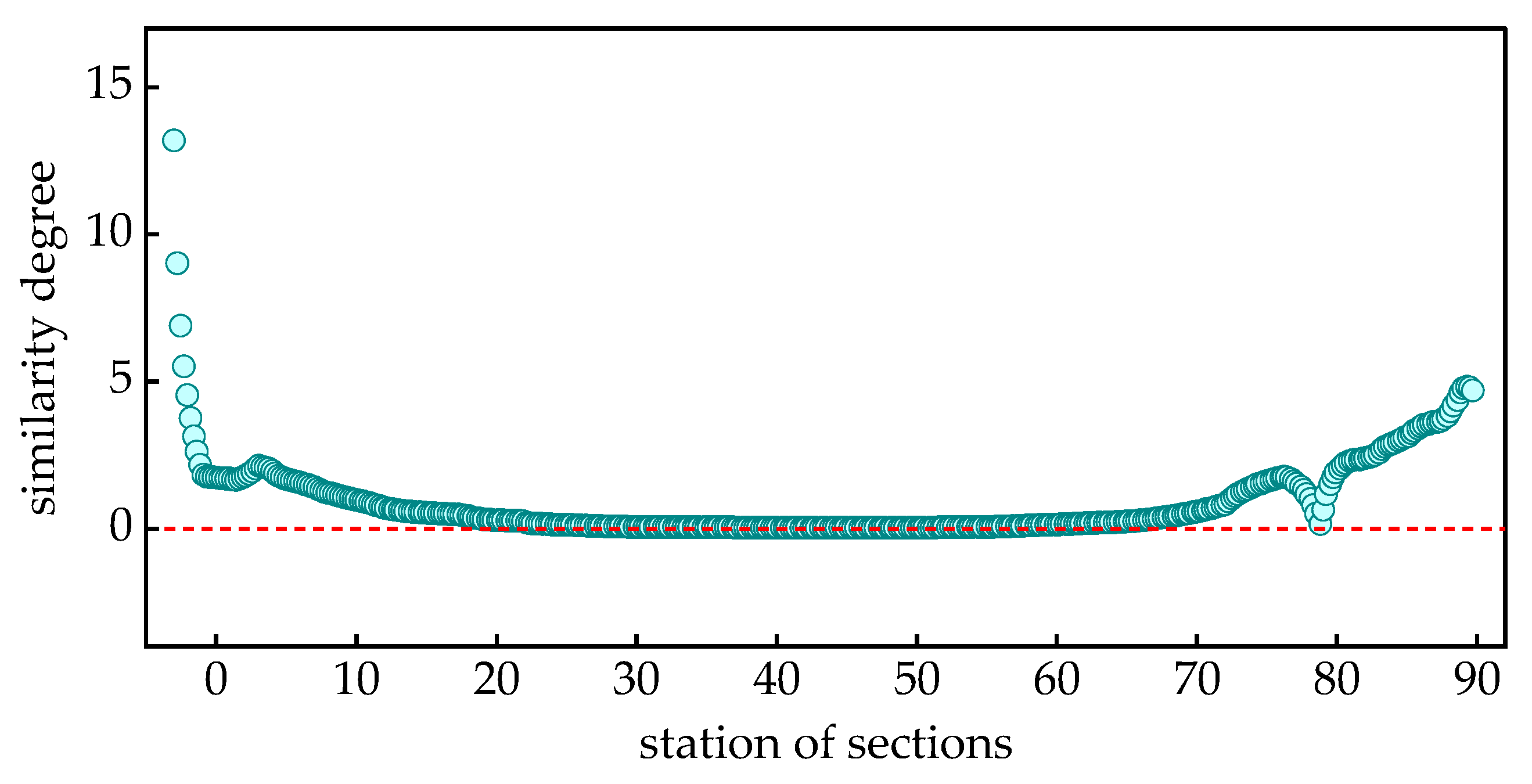
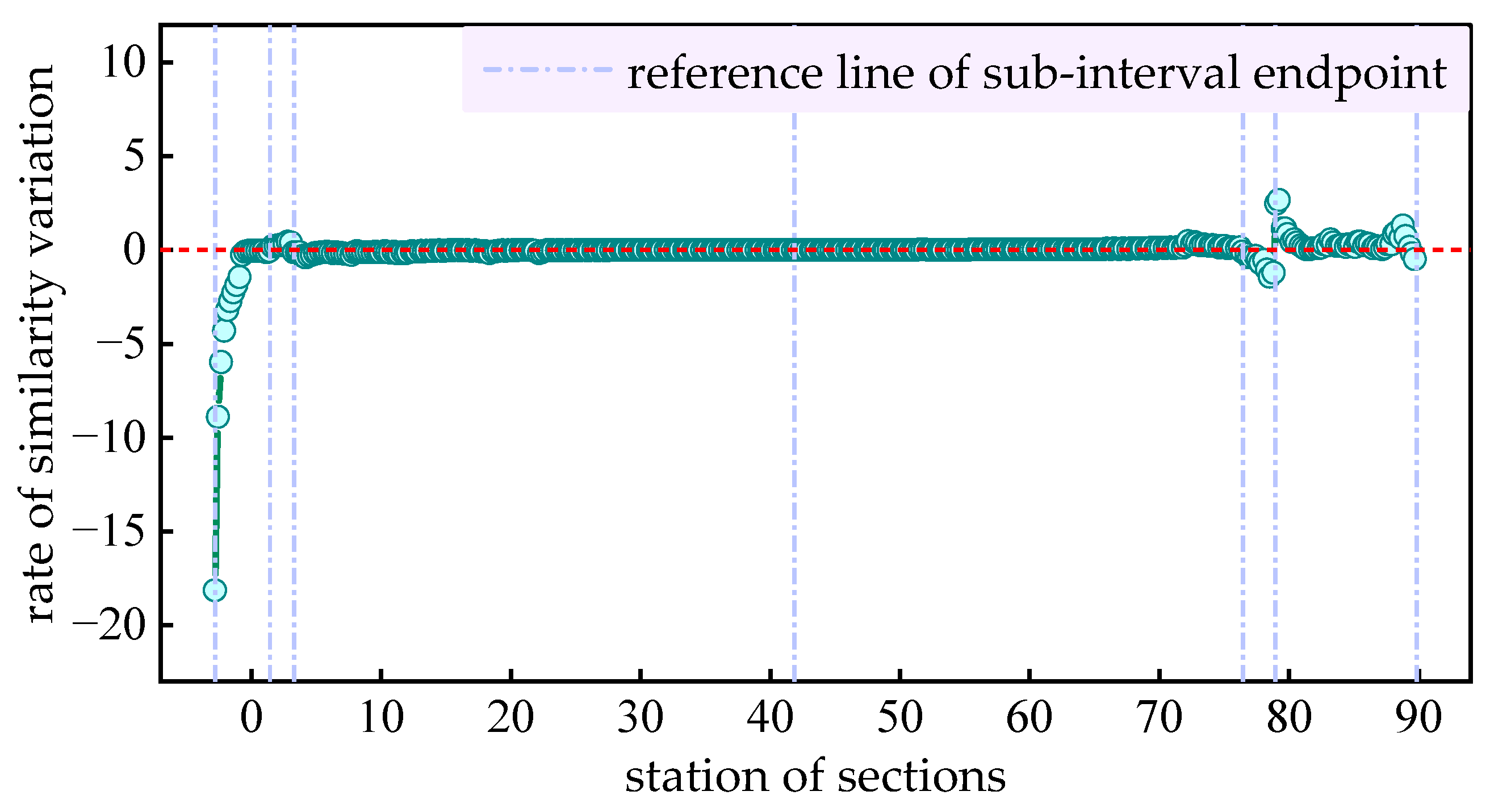
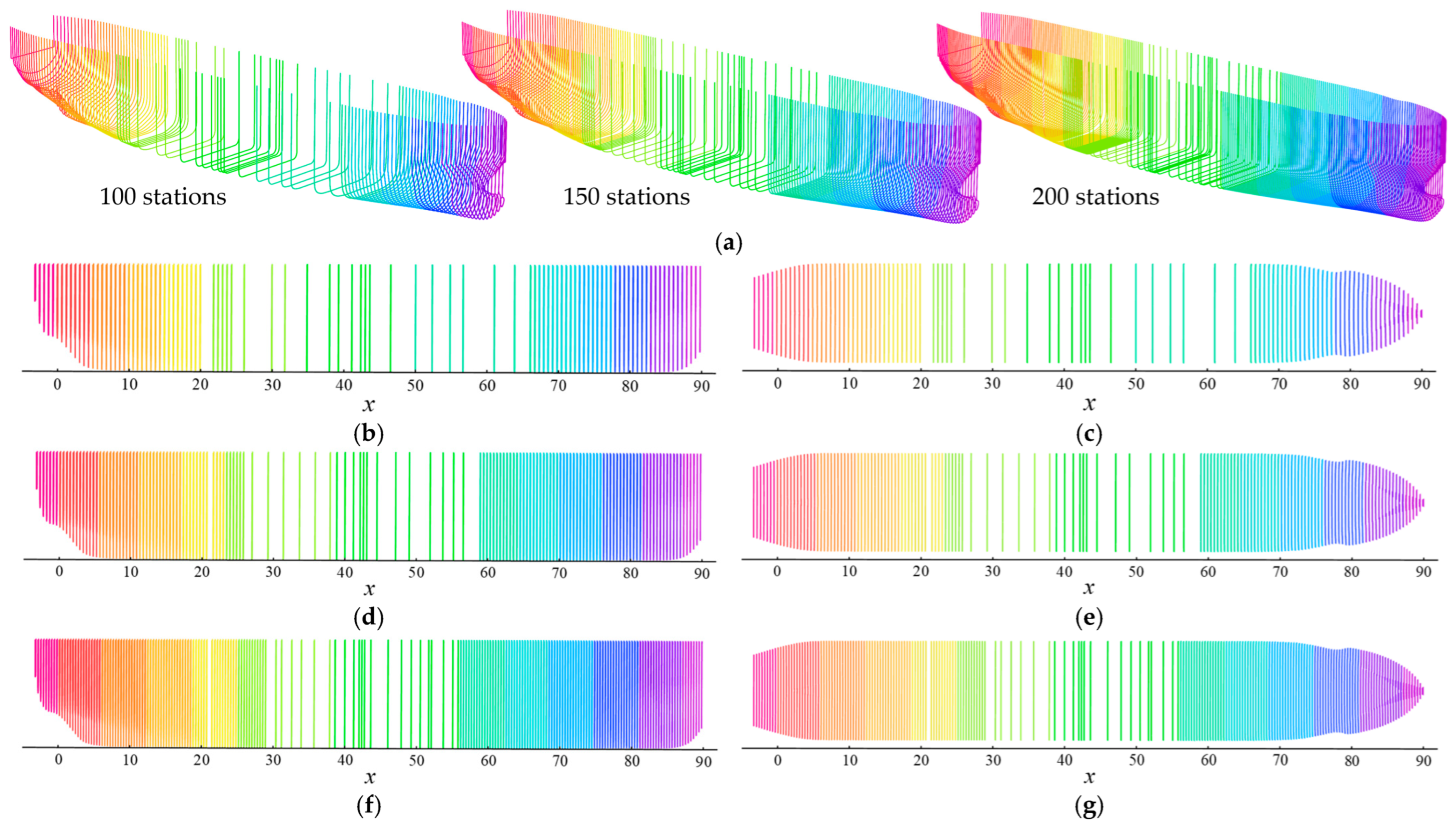
| x (the 8th Station) | x (the 8th Station) | x (the 28th Station) | ||||||
|---|---|---|---|---|---|---|---|---|
| Index | y | z | Index | y | z | Index | y | z |
| 1 | 0.000 | 0.000 | 1 | 0.000 | 0.000 | 1 | 0.000 | 0.000 |
| 2 | 0.240 | 0.000 | 2 | 5.977 | 0.000 | 2 | 0.000 | 0.035 |
| 3 | 0.471 | 0.035 | 3 | 6.000 | 0.000 | 3 | 0.034 | 0.155 |
| 4 | 0.734 | 0.118 | 4 | 6.283 | 0.051 | … | … | … |
| … | … | … | 5 | 6.476 | 0.142 | 13 | 2.012 | 3.000 |
| 22 | 6.691 | 5.532 | 6 | 6.636 | 0.272 | 14 | 2.000 | 3.188 |
| 23 | 6.788 | 6.000 | 7 | 6.802 | 0.500 | … | … | … |
| 24 | 6.868 | 6.902 | 8 | 6.874 | 0.694 | 25 | 4.000 | 8.432 |
| 25 | 6.900 | 7.578 | 9 | 6.900 | 0.934 | 26 | 4.721 | 9.194 |
| 26 | 6.900 | 15.000 | 10 | 6.900 | 15.000 | 27 | 4.721 | 15.000 |
| Elements | Acceptable Tolerance 1 | Acceptable Tolerance 2 |
|---|---|---|
| DISP | 2% | - |
| LCB | 1% | 50 cm |
| VCB | 1% | 5 cm |
| LCF | 1% | 50 cm |
| MTC | 2% | - |
| KMT | 1% | 5 cm |
| KML | 1% | 50 cm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, K.; Liu, J.; Zhang, Y. A Quasi-Bonjean Method for Computing Performance Elements of Ships Under Arbitrary Attitudes. Systems 2025, 13, 571. https://doi.org/10.3390/systems13070571
Zhu K, Liu J, Zhang Y. A Quasi-Bonjean Method for Computing Performance Elements of Ships Under Arbitrary Attitudes. Systems. 2025; 13(7):571. https://doi.org/10.3390/systems13070571
Chicago/Turabian StyleZhu, Kaige, Jiao Liu, and Yuanqiang Zhang. 2025. "A Quasi-Bonjean Method for Computing Performance Elements of Ships Under Arbitrary Attitudes" Systems 13, no. 7: 571. https://doi.org/10.3390/systems13070571
APA StyleZhu, K., Liu, J., & Zhang, Y. (2025). A Quasi-Bonjean Method for Computing Performance Elements of Ships Under Arbitrary Attitudes. Systems, 13(7), 571. https://doi.org/10.3390/systems13070571





