City-Level Road Traffic CO2 Emission Modeling with a Spatial Random Forest Method
Abstract
1. Introduction
2. Literature Review
2.1. Road Traffic CO2 Emissions
2.2. Analytic Methods for Emission Modeling
2.3. Research Objectives
3. Methodology
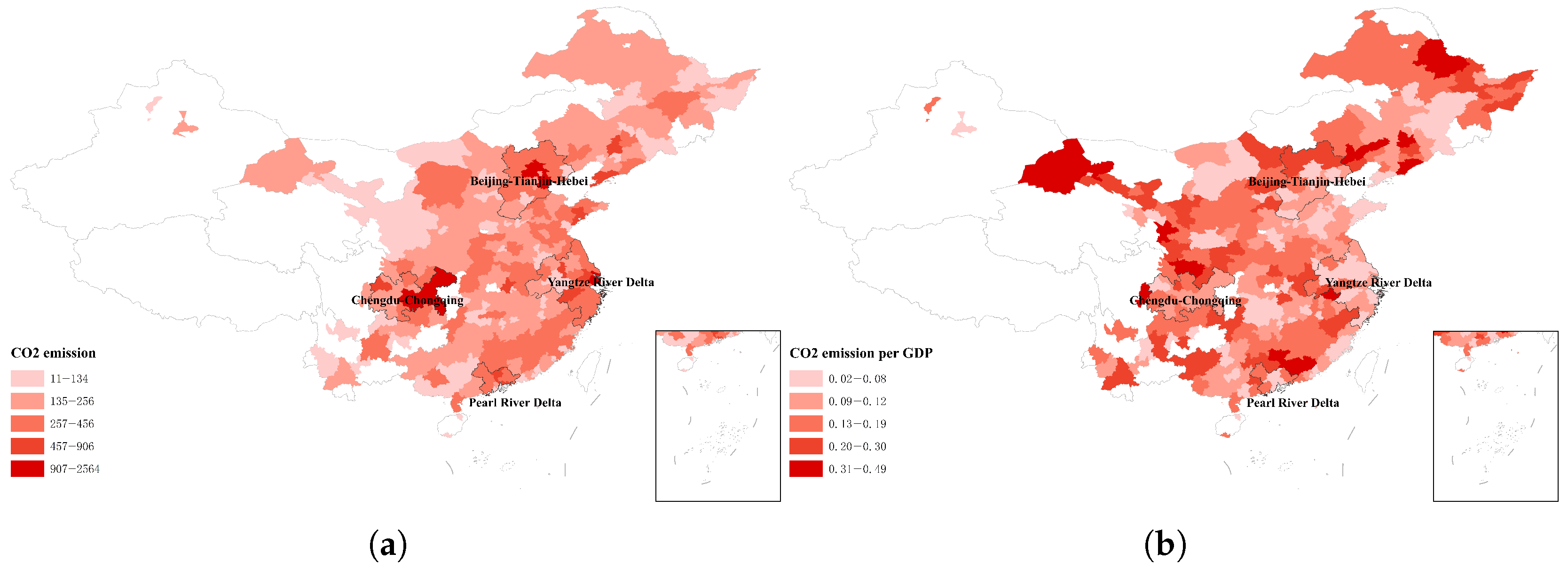
3.1. Data Source
3.2. Methods
3.2.1. Geographically Weighted Regression
3.2.2. Random Forests
3.2.3. Spatial Random Forests
3.3. Performance Measures
4. Empirical Results and Discussion
4.1. GWR Results
4.1.1. General Results
4.1.2. Spatial Distribution of Regression Coefficients
4.2. GWRF Results
4.2.1. Comparison of Predictive Performance
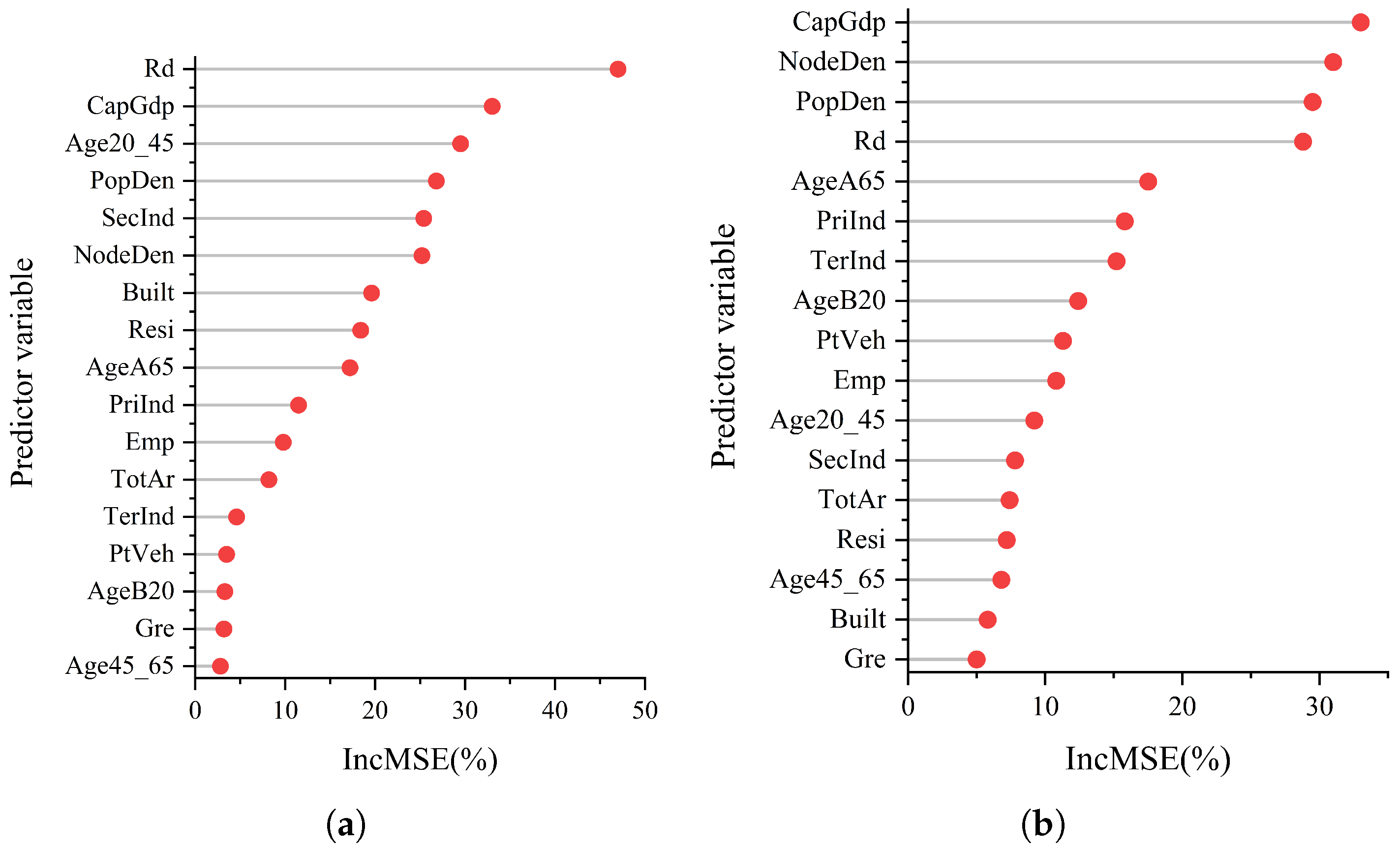
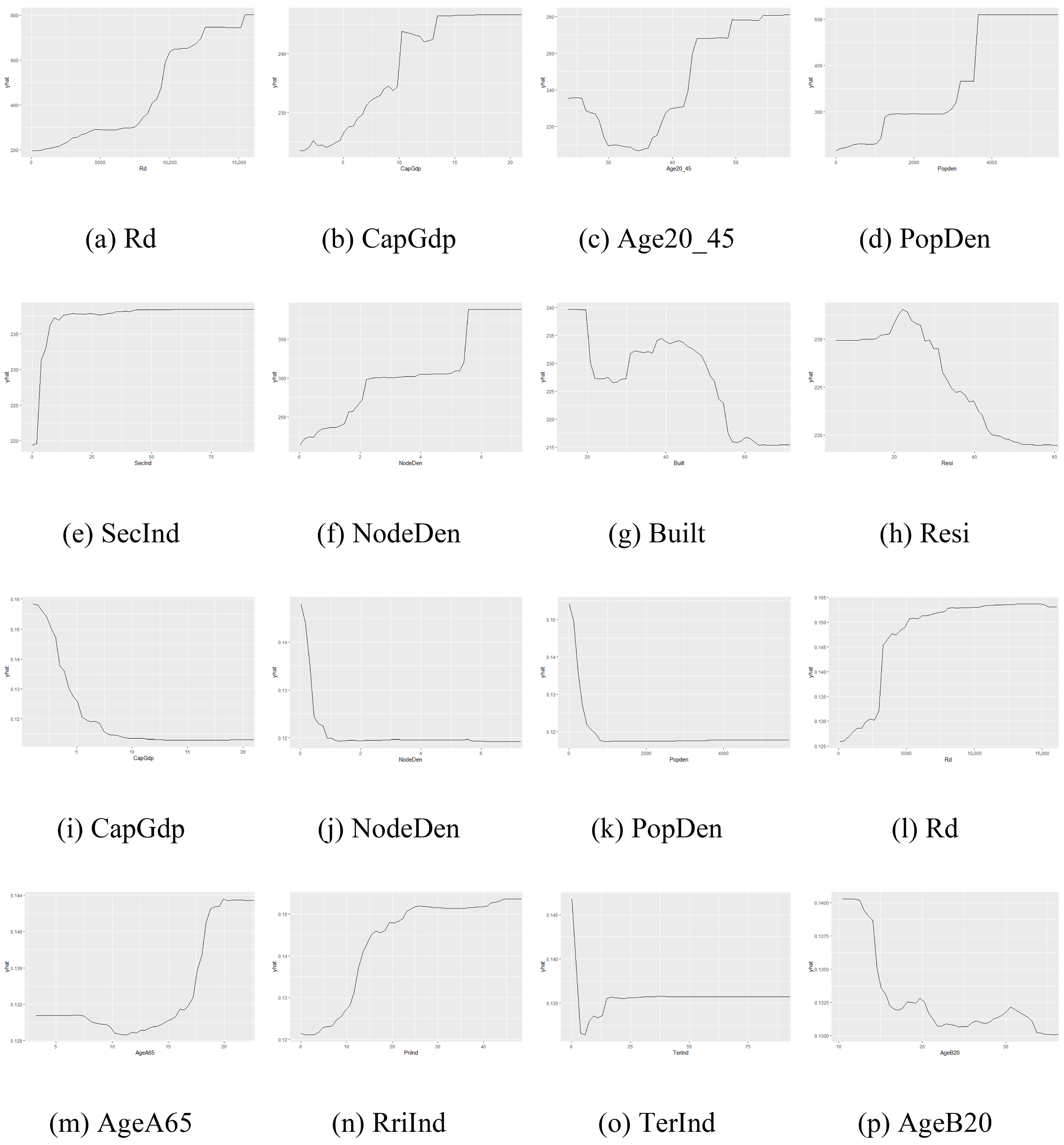
4.2.2. Explanatory Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Statista. Transportation Emissions Worldwide. 2025. Available online: https://www.statista.com/topics/7476/transportation-emissions-worldwide (accessed on 13 April 2025).
- Wang, W.; Zhang, M.; Zhou, M. Using LMDI method to analyze transport sector CO2 emissions in China. Energy 2011, 36, 5909–5915. [Google Scholar] [CrossRef]
- Krause, J.; Small, M.J.; Haas, A.; Jaeger, C.C. An expert-based bayesian assessment of 2030 German new vehicle CO2 emissions and related costs. Transp. Policy 2016, 52, 197–208. [Google Scholar] [CrossRef]
- Oduro, S.; Ha, Q.; Duc, H. Vehicular emissions prediction with CART-BMARS hybrid models. Transp. Res. Part D Transp. Environ. 2016, 49, 188–202. [Google Scholar] [CrossRef]
- Grote, M.; Williams, I.; Preston, J.; Kemp, S. A practical model for predicting road traffic carbon dioxide emissions using Inductive Loop Detector data. Transp. Res. Part D Transp. Environ. 2018, 63, 809–825. [Google Scholar] [CrossRef]
- Fu, M.; Kelly, J.A.; Clinch, J.P. Estimating annual average daily traffic and transport emissions for a national road network: A bottom-up methodology for both nationally-aggregated and spatially-disaggregated results. J. Transp. Geogr. 2017, 58, 186–195. [Google Scholar] [CrossRef]
- Chuai, X.; Feng, J. High resolution carbon emissions simulation and spatial heterogeneity analysis based on big data in Nanjing City, China. Sci. Total Environ. 2019, 686, 828–837. [Google Scholar] [CrossRef]
- Li, Y.; Li, T.; Lu, S. Forecast of urban traffic carbon emission and analysis of influencing factors. Energy Effic. 2021, 14, 84. [Google Scholar] [CrossRef]
- Zhou, X.; Wang, H.; Huang, Z.; Bao, Y.; Zhou, G.; Liu, Y. Identifying spatiotemporal characteristics and driving factors for road traffic CO2 emissions. Sci. Total Environ. 2022, 834, 155270. [Google Scholar] [CrossRef]
- Wu, J.; Jia, P.; Feng, T.; Li, H.; Kuang, H. Spatiotemporal analysis of built environment restrained traffic carbon emissions and policy implications. Transp. Res. Part D Transp. Environ. 2023, 121, 103839. [Google Scholar] [CrossRef]
- Büchs, M.; Schnepf, S.V. Who emits most? Associations between socio-economic factors and UK households’ home energy, transport, indirect and total CO2 emissions. Ecol. Econ. 2013, 90, 114–123. [Google Scholar] [CrossRef]
- Wang, S.; Liu, X.; Zhou, C.; Hu, J.; Ou, J. Examining the impacts of socioeconomic factors, urban form, and transportation networks on CO2 emissions in China’s megacities. Appl. Energy 2017, 185, 189–200. [Google Scholar] [CrossRef]
- Eschmann, J.; Mueller, K.; Oesingmann, K.; Ennen, D. The economic implications of carbon neutrality ambitions in extra-European freight transport. Transp. Res. Part D Transp. Environ. 2025, 146, 104812. [Google Scholar] [CrossRef]
- Liu, X.; Wang, M.; Qiang, W.; Wu, K.; Wang, X. Urban form, shrinking cities, and residential carbon emissions: Evidence from Chinese city-regions. Appl. Energy 2020, 261, 114409. [Google Scholar] [CrossRef]
- Xie, R.; Fang, J.; Liu, C. The effects of transportation infrastructure on urban carbon emissions. Appl. Energy 2017, 196, 199–207. [Google Scholar] [CrossRef]
- Xu, C.; Zhao, J.; Liu, P. A geographically weighted regression approach to investigate the effects of traffic conditions and road characteristics on air pollutant emissions. J. Clean. Prod. 2019, 239, 118084. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, H.; Li, S.; Liu, Y. How road network transformation may be associated with reduced carbon emissions: An exploratory analysis of 19 major Chinese cities. Sustain. Cities Soc. 2023, 95, 104575. [Google Scholar] [CrossRef]
- Song, L.; Cheng, H.; Wang, J.; Yu, S.; Du, Y. Geometric and operational optimization at reversible unconventional arterial intersection reducing traffic emissions. Transp. Res. Part D Transp. Environ. 2025, 141, 104656. [Google Scholar] [CrossRef]
- Shen, Y.S.; Lin, Y.C.; Cui, S.; Li, Y.; Zhai, X. Crucial factors of the built environment for mitigating carbon emissions. Sci. Total Environ. 2022, 806, 150864. [Google Scholar] [CrossRef]
- Wang, S.; Hu, M.; Li, J.; Liu, G.; Hu, W.; Qi, J.; Huang, J.; Liu, Z.; Wang, H.; Han, B. An interpretable spatially weighted machine learning approach for revealing spatial nonstationarity impacts of the built environment on air pollution. Build. Environ. 2025, 280, 113150. [Google Scholar] [CrossRef]
- Pallavidino, L.; Prandi, R.; Bertello, A.; Bracco, E.; Pavone, F. Compilation of a road transport emission inventory for the Province of Turin: Advantages and key factors of a bottom–up approach. Atmos. Pollut. Res. 2014, 5, 648–655. [Google Scholar] [CrossRef]
- Puliafito, S.E.; Allende, D.; Pinto, S.; Castesana, P. High resolution inventory of GHG emissions of the road transport sector in Argentina. Atmos. Environ. 2015, 101, 303–311. [Google Scholar] [CrossRef]
- Handy, S.L.; Boarnet, M.G.; Ewing, R.; Killingsworth, R.E. How the built environment affects physical activity. Am. J. Prev. Med. 2002, 23, 64–73. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Xi, F.; Yin, Y.; Wang, J.; Bing, L. Industrial total factor CO2 emission performance assessment of Chinese heavy industrial province. Energy Effic. 2019, 13, 177–192. [Google Scholar] [CrossRef]
- Zhao, W.; Niu, D. Prediction of CO2 Emission in China’s Power Generation Industry with Gauss Optimized Cuckoo Search Algorithm and Wavelet Neural Network Based on STIRPAT model with Ridge Regression. Sustainability 2017, 9, 2377. [Google Scholar] [CrossRef]
- Sun, W.; Jin, H.; Wang, X. Predicting and Analyzing CO2 Emissions Based on an Improved Least Squares Support Vector Machine. Pol. J. Environ. Stud. 2019, 28, 4391–4401. [Google Scholar] [CrossRef]
- Khajavi, H.; Rastgoo, A. Predicting the carbon dioxide emission caused by road transport using a Random Forest (RF) model combined by Meta-Heuristic Algorithms. Sustain. Cities Soc. 2023, 93, 104503. [Google Scholar] [CrossRef]
- Georganos, S.; Grippa, T.; Niang Gadiaga, A.; Linard, C.; Lennert, M.; Vanhuysse, S.; Mboga, N.; Wolff, E.; Kalogirou, S. Geographical random forests: A spatial extension of the random forest algorithm to address spatial heterogeneity in remote sensing and population modelling. Geocarto Int. 2019, 36, 121–136. [Google Scholar] [CrossRef]
- Grekousis, G.; Feng, Z.; Marakakis, I.; Lu, Y.; Wang, R. Ranking the importance of demographic, socioeconomic, and underlying health factors on US COVID-19 deaths: A geographical random forest approach. Health Place 2022, 74, 102744. [Google Scholar] [CrossRef]
- Wu, D.; Zhang, Y.; Xiang, Q. Geographically weighted random forests for macro-level crash frequency prediction. Accid. Anal. Prev. 2024, 194, 107370. [Google Scholar] [CrossRef]
- Yazdian, H.; Salmani-Dehaghi, N.; Alijanian, M. A spatially promoted SVM model for GRACE downscaling: Using ground and satellite-based datasets. J. Hydrol. 2023, 626, 130214. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, X.; Zeng, P.; Chen, X. Centrality Characteristics of Road Network Patterns of Traffic Analysis Zones. Transp. Res. Rec. J. Transp. Res. Board 2011, 2256, 16–24. [Google Scholar] [CrossRef]
- Hadayeghi, A.; Shalaby, A.S.; Persaud, B.N. Development of planning level transportation safety tools using Geographically Weighted Poisson Regression. Accid. Anal. Prev. 2010, 42, 676–688. [Google Scholar] [CrossRef]
- Bao, J.; Liu, P.; Qin, X.; Zhou, H. Understanding the effects of trip patterns on spatially aggregated crashes with large-scale taxi GPS data. Accid. Anal. Prev. 2018, 120, 281–294. [Google Scholar] [CrossRef]
- Lu, B.; Harris, P.; Charlton, M.; Brunsdon, C.; Nakaya, T. GWmodel: Geographically-Weighted Models. 2013. Available online: https://doi.org/10.32614/cran.package.gwmodel (accessed on 13 April 2025).
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Janitza, S.; Hornung, R. On the overestimation of random forest’s out-of-bag error. PLoS ONE 2018, 13, e0201904. [Google Scholar] [CrossRef]
- Probst, P.; Wright, M.N.; Boulesteix, A. Hyperparameters and tuning strategies for random forest. WIREs Data Min. Knowl. Discov. 2019, 9, e1301. [Google Scholar] [CrossRef]
- Brunsdon, C.; Fotheringham, S.; Charlton, M. Geographically Weighted Regression. J. R. Stat. Soc. Ser. D 1998, 47, 431–443. [Google Scholar] [CrossRef]
- Kalogirou, S.; Georganos, S. SpatialML: Spatial Machine Learning. 2019. Available online: https://doi.org/10.32614/cran.package.spatialml (accessed on 13 April 2025).
- Marshall, W.E.; Garrick, N.W. Effect of Street Network Design on Walking and Biking. Transp. Res. Rec. J. Transp. Res. Board 2010, 2198, 103–115. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, H.; Qiu, H. Population aging reduces carbon emissions: Evidence from China’s latest three censuses. Appl. Energy 2023, 351, 121799. [Google Scholar] [CrossRef]
- Cervero, R.; Sarmiento, O.L.; Jacoby, E.; Gomez, L.F.; Neiman, A. Influences of Built Environments on Walking and Cycling: Lessons from Bogotá. Int. J. Sustain. Transp. 2009, 3, 203–226. [Google Scholar] [CrossRef]
- Gu, Y.; Liu, D.; Arvin, R.; Khattak, A.J.; Han, L.D. Predicting intersection crash frequency using connected vehicle data: A framework for geographical random forest. Accid. Anal. Prev. 2023, 179, 106880. [Google Scholar] [CrossRef] [PubMed]
- Greenwell, B.M. pdp: Partial Dependence Plots. 2016. Available online: https://cran.r-project.org/web/packages/pdp/index.html (accessed on 13 April 2025).
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]




| Category | Independent Variables | References |
|---|---|---|
| Demographic and socioeconomic features | Population, age structure, GDP, employment rate, industrialization level, private car ownership | Büchs and Schnepf (2013) [11]; Wang et al. (2017) [12]; Eschmann et al. (2025) [13] |
| Road network features | Road network density, road network topology structure | Liu et al. (2020) [14]; Xie et al. (2017) [15]; Xu et al. (2019) [16]; Zhang et al. (2023) [17]; Song et al. (2025) [18] |
| Built environment features | Urban form, land use patterns, urban transportation systems | Shen et al. (2022) [19]; Zhou et al. (2022) [9]; Wang et al. (2025) [20] |
| Variables | Abbreviation | Min | Max | Mean | S.D. |
|---|---|---|---|---|---|
| Dependent variables | |||||
| CO2 emissions ( t) | Emi | 11 | 2564 | 226.73 | 235.47 |
| CO2 emissions per GDP (t/ RMB) | GdpEmi | 0.02 | 0.49 | 0.13 | 0.08 |
| Socio-demographic | |||||
| Population density (person/km2 ) | PopDen | 5.77 | 5698.55 | 467.54 | 548.41 |
| Per capita GDP ( RMB) | CapGdp | 1.1 | 21 | 5.14 | 3.09 |
| Employment rate (%) | Emp | 50.27 | 99.79 | 97.21 | 3.35 |
| Primary industry (%) | PriInd | 0.04 | 48.32 | 12.38 | 7.91 |
| Secondary industry (%) | SecInd | 15.17 | 71.45 | 46.57 | 9.56 |
| Tertiary Industry (%) | TerInd | 24.17 | 79.65 | 41.05 | 8.7 |
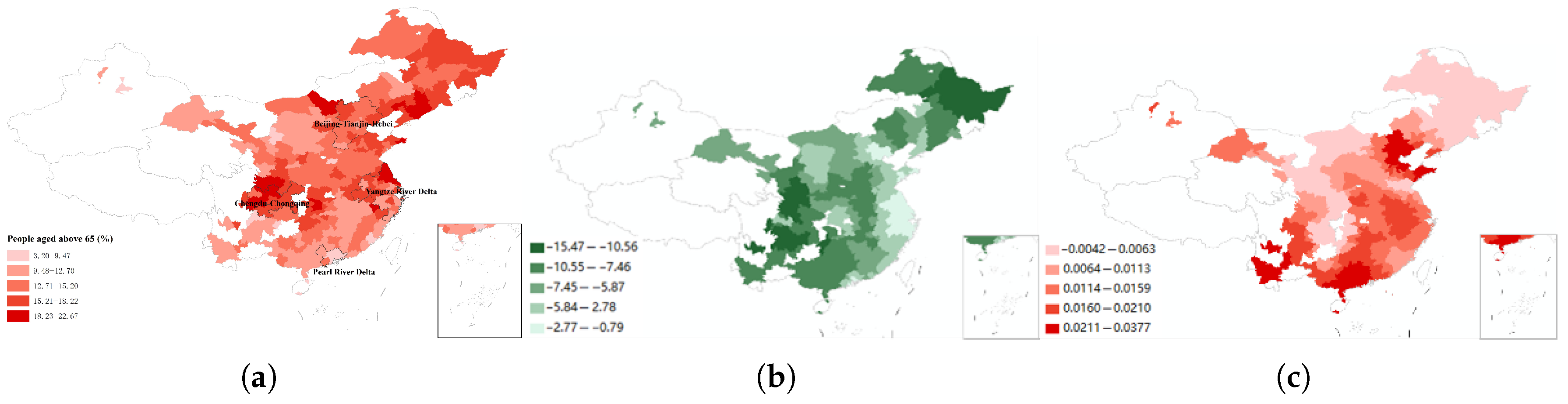
| People aged below 20 (%) | AgeB20 | 10.45 | 36.26 | 22.69 | 5.51 |
| People aged 20 to 45 (%) | Age20_45 | 23.66 | 58.47 | 32.54 | 5.05 |
| People aged 45 to 65 (%) | Age45_65 | 19.56 | 45.44 | 30.65 | 4.53 |
| People aged above 65 (%) | AgeA65 | 3.2 | 22.67 | 14.12 | 3.13 |
| Road network | |||||
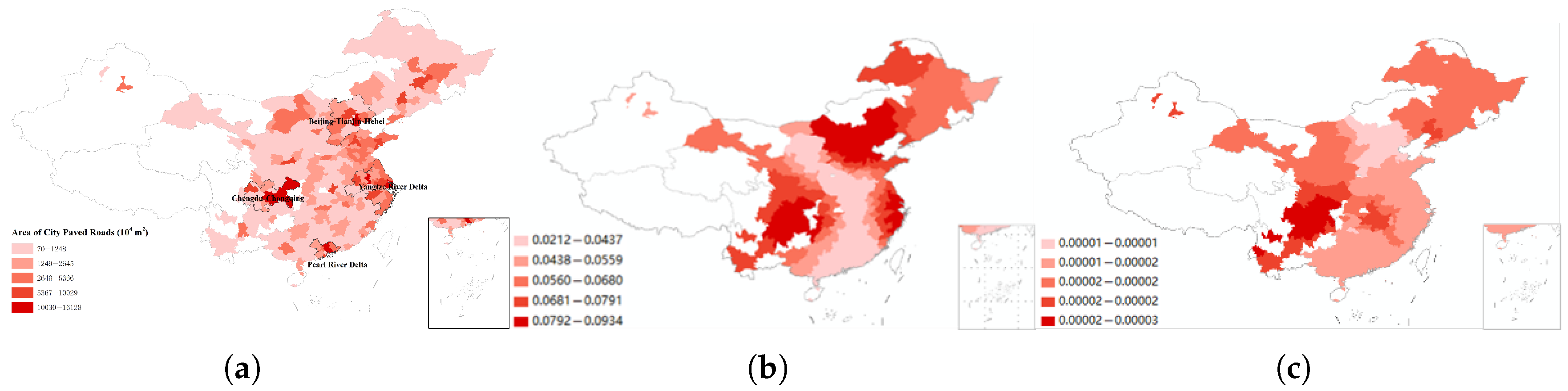
| Paved roads ( m2) | Rd | 70 | 16,128 | 1968.91 | 2507.19 |
| Node density (points/km2) | NodeDen | 0.01 | 7.32 | 0.67 | 1.11 |
| Built environment | |||||
| Total urban area (km2) | TotAr | 1201 | 252,777 | 16,691.69 | 21,823.97 |
| Built districts area (%) | Built | 0.03 | 45.07 | 1.83 | 3.9 |
| Residential land area (%) | Resi | 5.51 | 60.87 | 31.22 | 7.97 |
| Urban green land area (%) | Gre | 2.71 | 51.44 | 38.45 | 7.34 |
| Public transportation vehicles per population | PtVeh | 1.04 | 225.5 | 9.61 | 15 |
| Variable | Model 1 Emission Model | Model 2 Efficiency Model | ||
|---|---|---|---|---|
| Estimate | Std.Error | Estimate | Std.Error | |
| Intercept | 5.15 × 102 | 9.17 × 101 | 3.34 × 10−1 | 8.88 × 10−2 |
| Popden | 9.23 × 10−2 | 2.82 × 10−2 | −1.01 × 10−4 | 1.76 × 10−5 |
| Emp | 3.20 × 10−1 | 1.42 × 10−1 | - | - |
| CapGdp | 7.90 | 8.99 × 10−1 | −1.64 × 10−2 | 2.58 × 10−3 |
| Age20_45 | 7.76 | 1.13 | - | - |
| AgeA65 | −6.15 | 2.45 | 1.34 × 10−3 | 6.06 × 10−4 |
| SecInd | 2.34 | 6.47 × 10−1 | - | - |
| TerInd | - | - | −1.78 × 10−3 | 8.34 × 10−4 |
| Rd | 6.59 × 10−2 | 6.45 × 10−3 | 2.01 × 10−5 | 5.56 × 10−6 |
| Nodeden | 1.54 × 102 | 4.18 × 101 | −5.49 × 10−2 | 7.61 × 10−3 |
| TotAr | 5.57 × 10−4 | 2.51 × 10−4 | - | - |
| Built | −1.39 | 4.32 × 10−1 | - | - |
| Resi | −1.11 | 4.21 × 10−1 | - | - |
| PtVeh | - | - | −1.05 × 10−2 | 5.00 × 10−3 |
| Metric | GWR | RF | Spatial SVM | GWRF |
|---|---|---|---|---|
| RMSE | 1.652 | 1.323 | 1.258 | 1.146 |
| MAPE | 0.175 | 0.134 | 0.122 | 0.118 |
| R2 | 0.636 | 0.832 | 0.861 | 0.874 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, H.; Wu, D.; Zhang, Y. City-Level Road Traffic CO2 Emission Modeling with a Spatial Random Forest Method. Systems 2025, 13, 632. https://doi.org/10.3390/systems13080632
Jin H, Wu D, Zhang Y. City-Level Road Traffic CO2 Emission Modeling with a Spatial Random Forest Method. Systems. 2025; 13(8):632. https://doi.org/10.3390/systems13080632
Chicago/Turabian StyleJin, Hansheng, Dongyu Wu, and Yingheng Zhang. 2025. "City-Level Road Traffic CO2 Emission Modeling with a Spatial Random Forest Method" Systems 13, no. 8: 632. https://doi.org/10.3390/systems13080632
APA StyleJin, H., Wu, D., & Zhang, Y. (2025). City-Level Road Traffic CO2 Emission Modeling with a Spatial Random Forest Method. Systems, 13(8), 632. https://doi.org/10.3390/systems13080632





