Distributed Trajectory Optimization for Connected and Automated Vehicle Platoons Considering Safe Inter-Vehicle Following Gaps
Abstract
1. Introduction
2. Model Formulation
2.1. Problem Statement
2.2. Control and State Variables
2.3. System Dynamics
2.4. Objective Function
2.5. Controller Constraints
3. Solution Method
3.1. Linearization
3.2. Centralized Method
3.3. Distributed Method
3.3.1. Dual Problem
3.3.2. Distributed Optimization
| Algorithm 1: Distributed optimization method |
Initialization: 1: 2: 3: Iteration: 4: while do: 5: Initialize for 6: for each do: 7: Calculate Equation (18) 8: Calculate Equation (19) 9: end for 10: 11: end while Return: |
4. Simulation and Results
4.1. Experiment Design
4.2. Simulation Results of Distributed and Centralized Methods
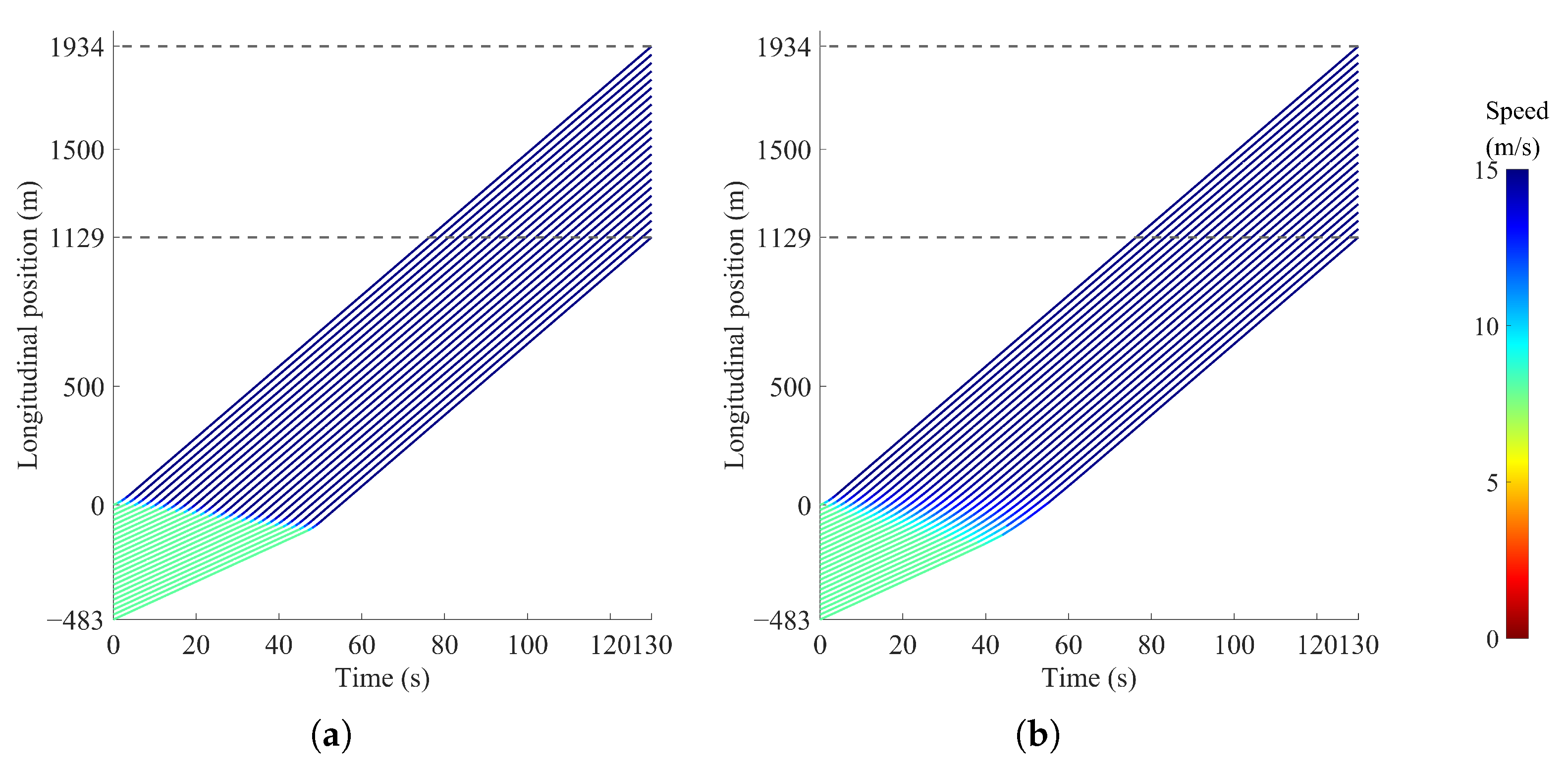
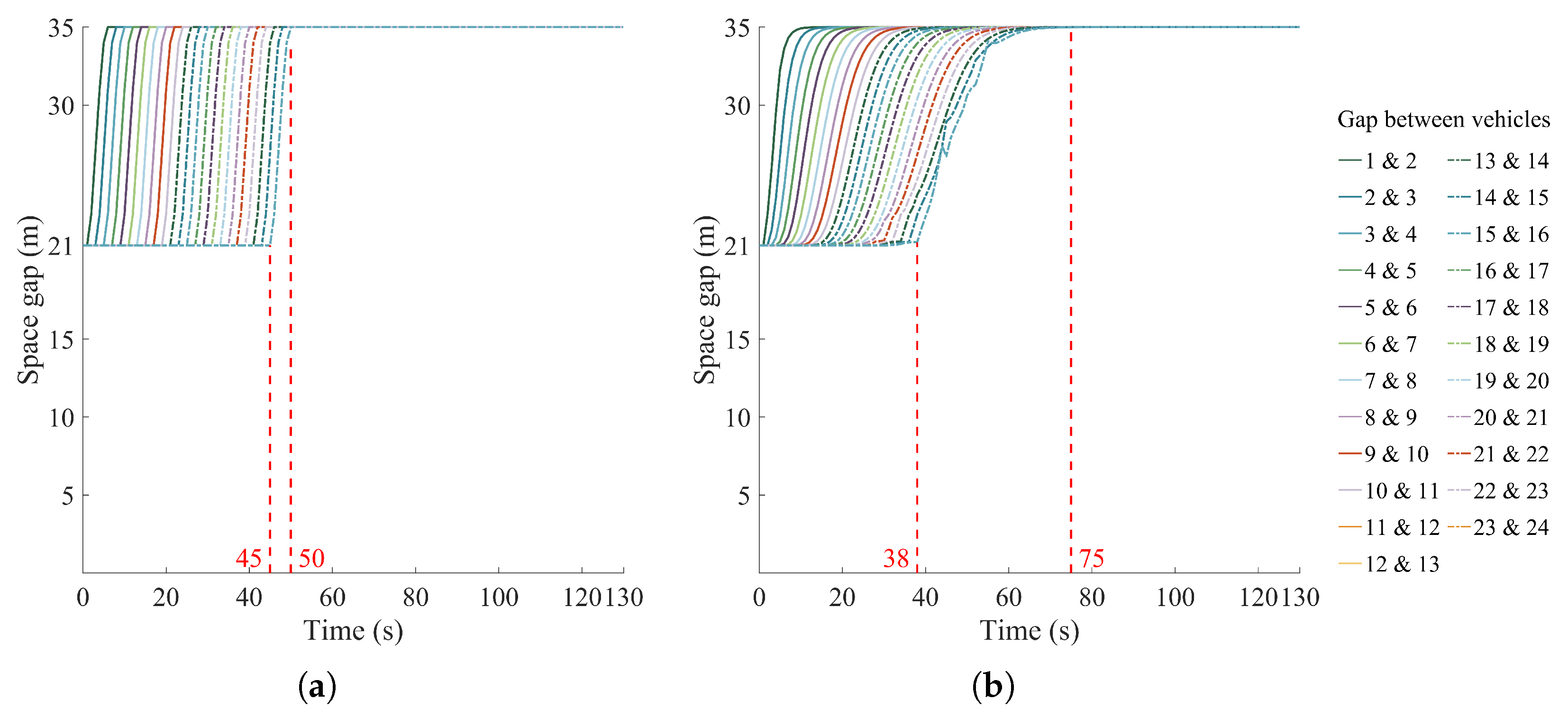
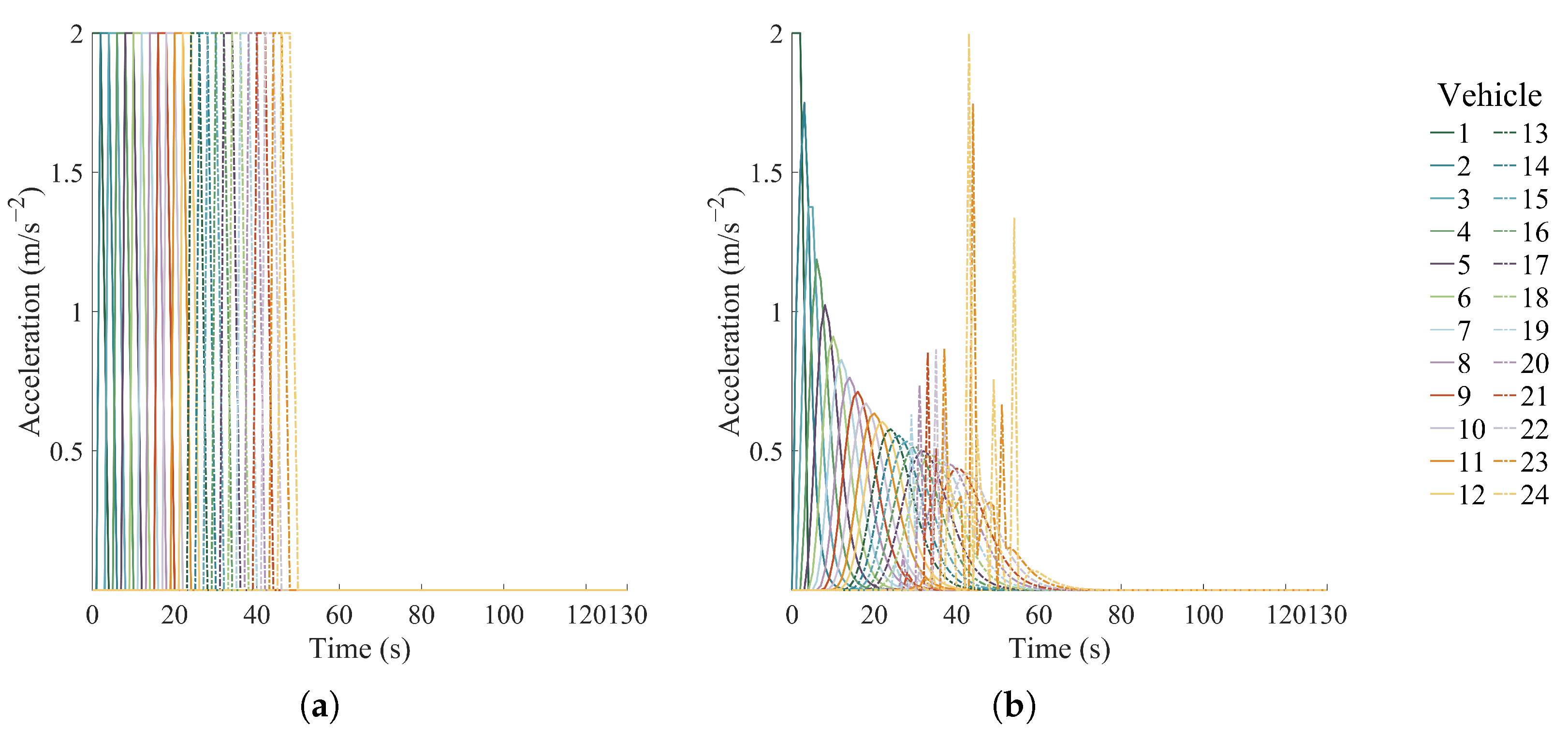
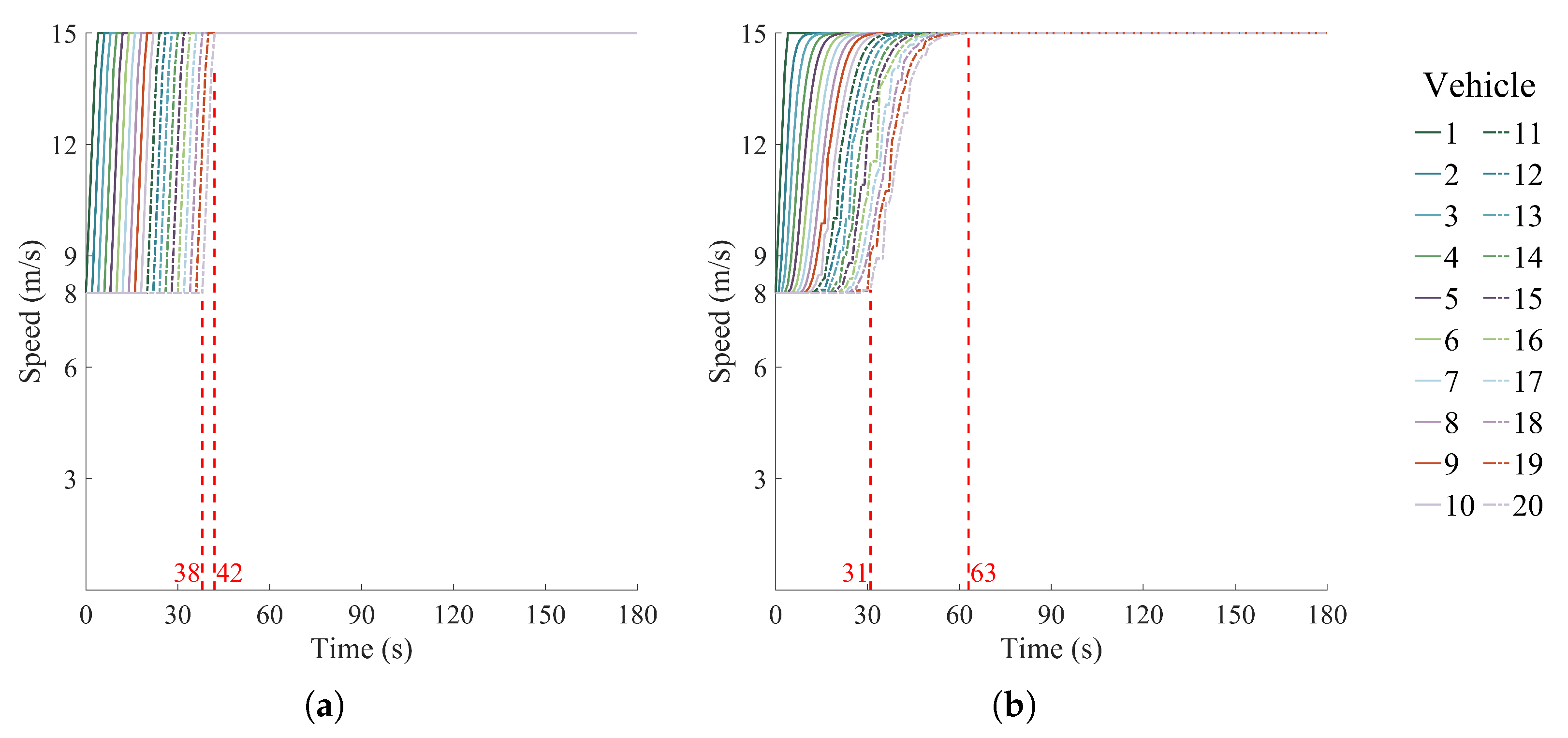
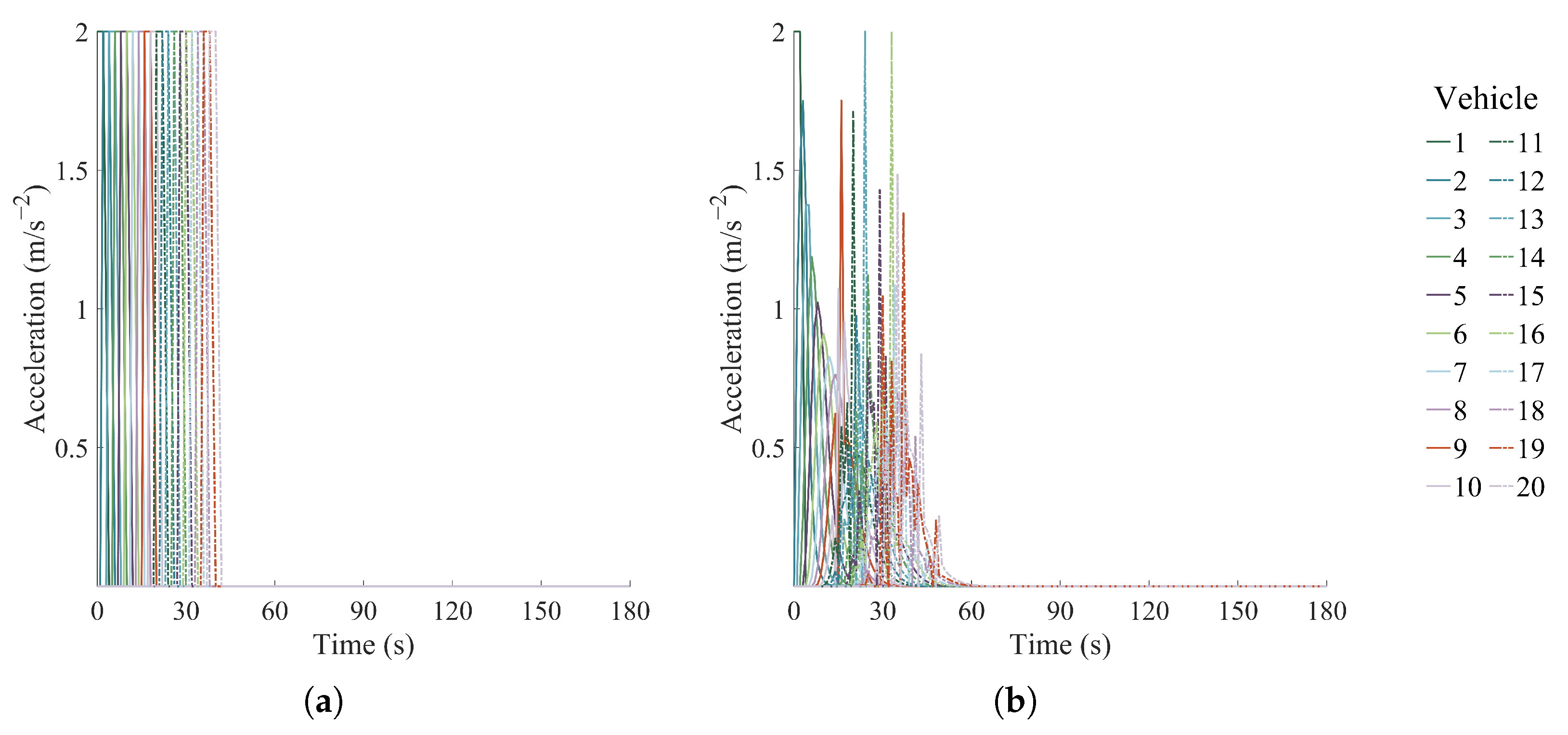
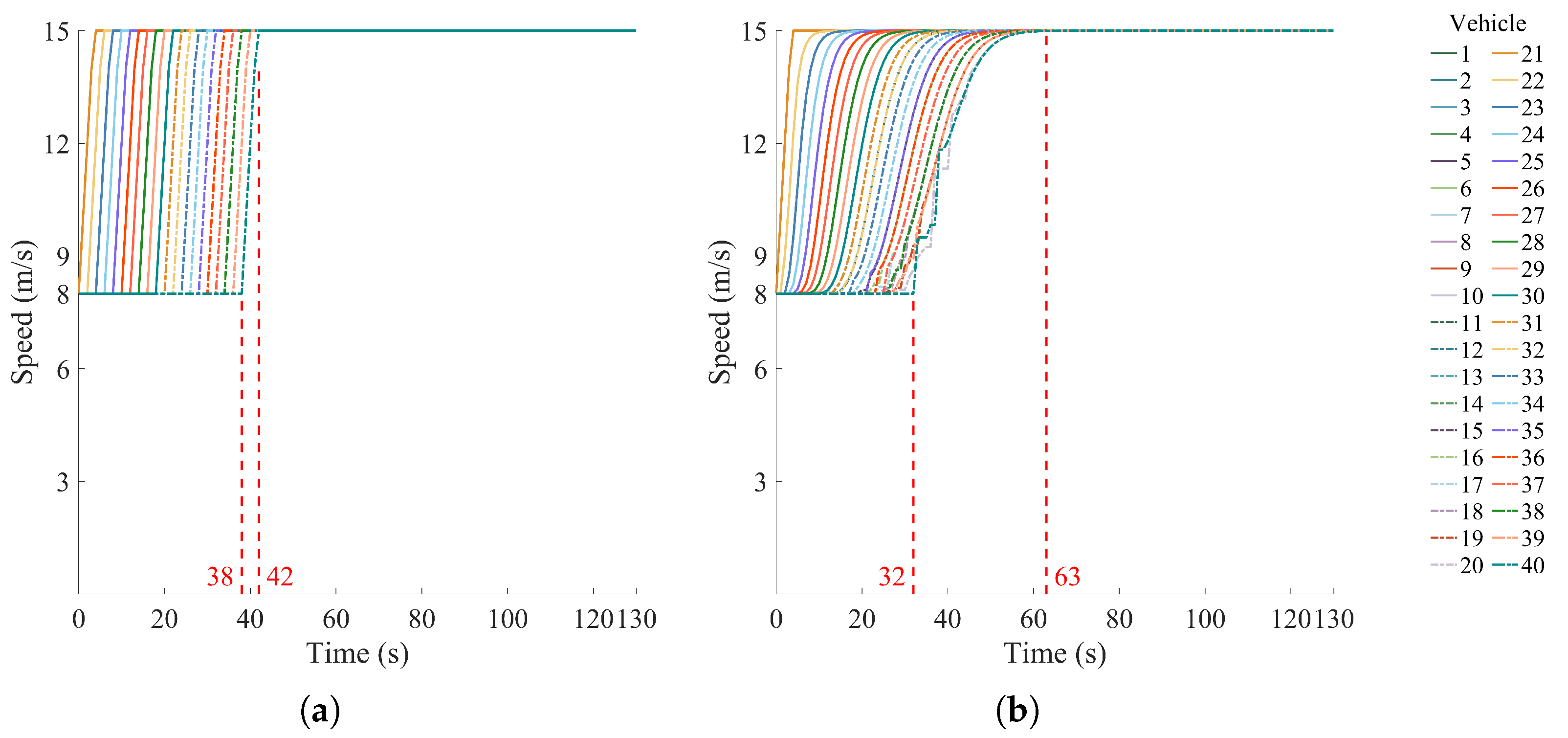
4.2.1. Single-Platoon Scenario 1
4.2.2. Single-Platoon Scenario 2 with Different Simulation Horizon
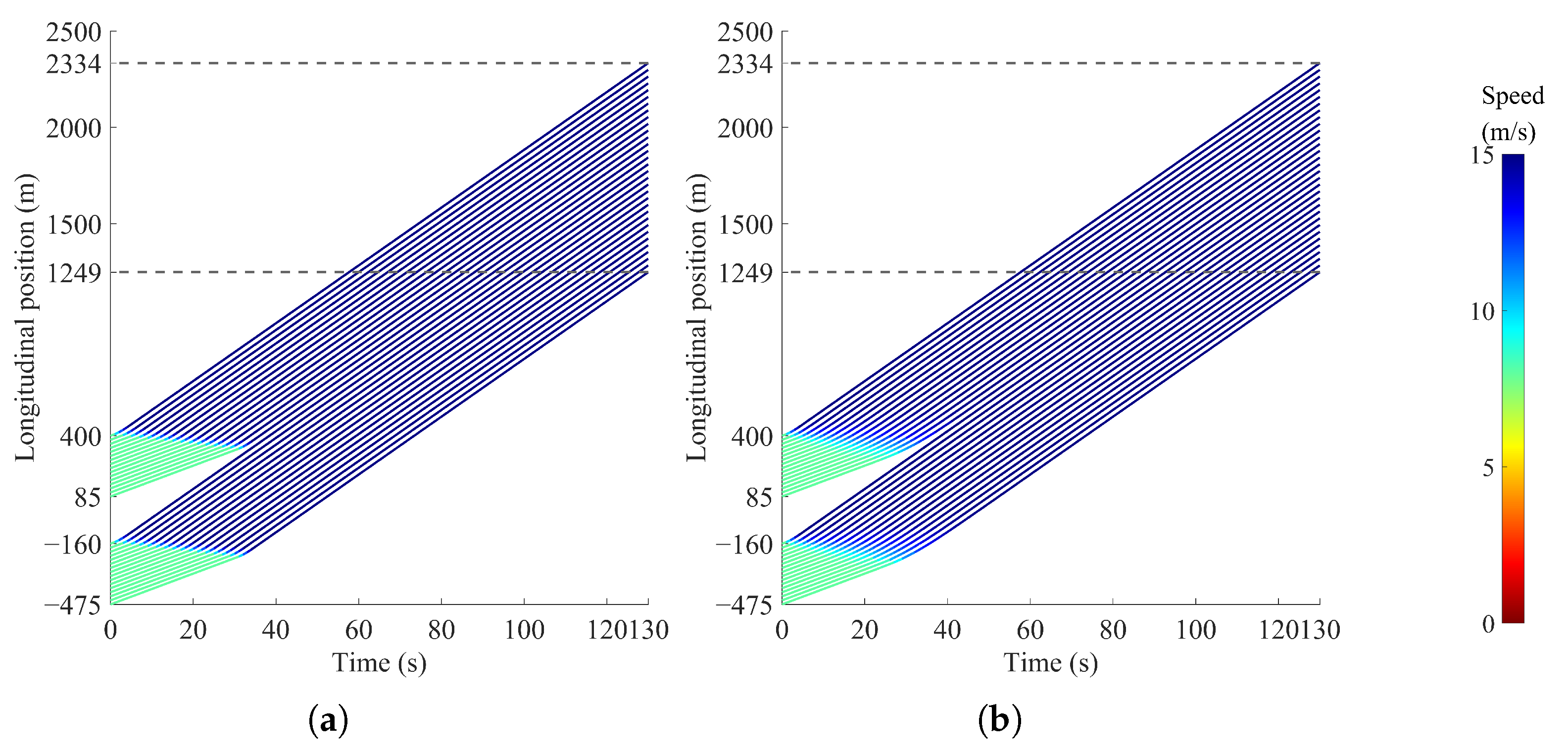
4.2.3. Multi-Platoon Scenario 3
4.2.4. Platoon-Merging Scenario 4
5. Discussion
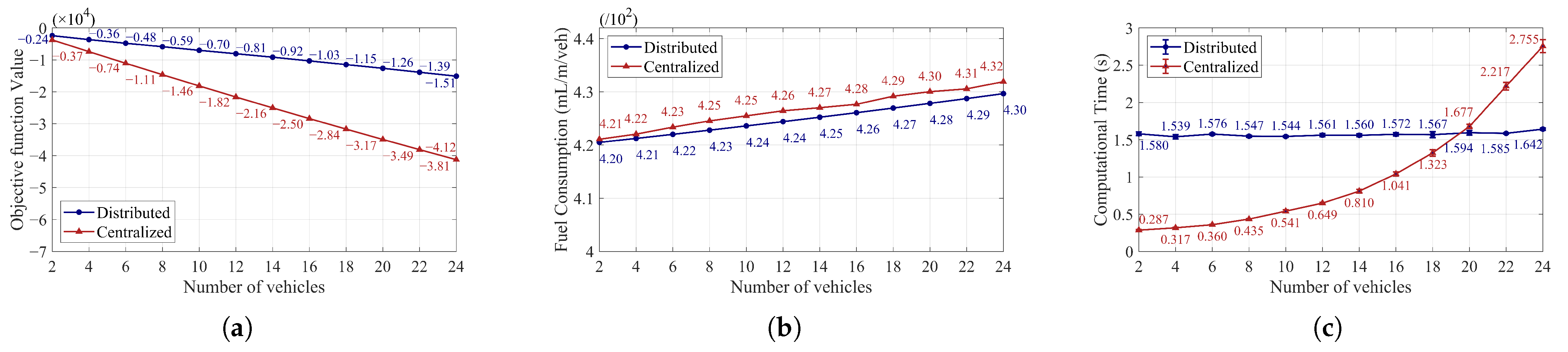
5.1. Impact of Vehicle Number in the Single-Platoon Scenario 1
5.2. Impact of Simulation Horizon Length in the Single-Platoon Scenario 2
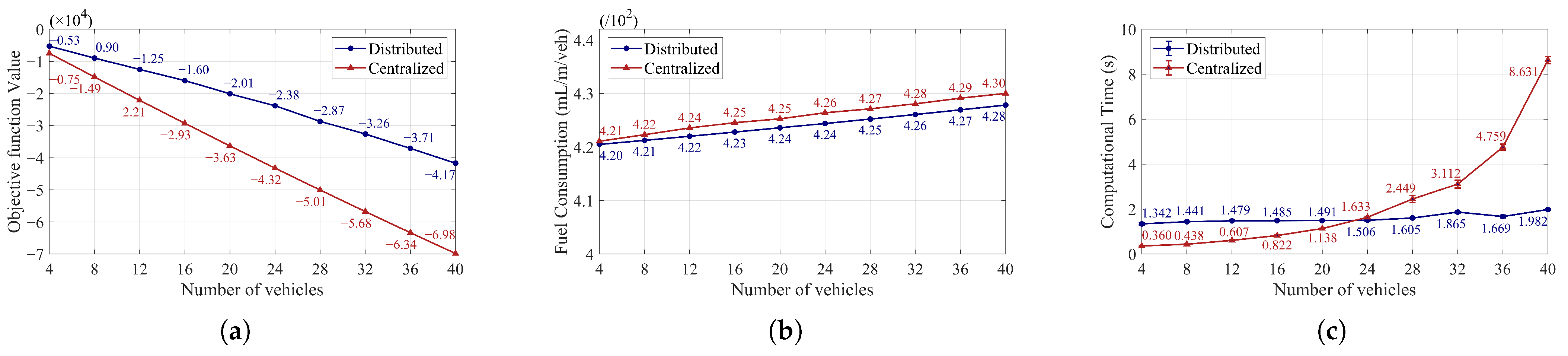
5.3. Impact of Vehicle Number in the Multi-Platoon Scenario 3
5.4. Control Performance Comparison Between the Single-Platoon Scenario 1 and Multi-Platoon Scenario 3
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Han, Y.; Wang, M.; Leclercq, L. Leveraging reinforcement learning for dynamic traffic control: A survey and challenges for field implementation. Commun. Transp. Res. 2023, 3, 100104. [Google Scholar] [CrossRef]
- He, X.; Liu, H.X.; Liu, X. Optimal vehicle speed trajectory on a signalized arterial with consideration of queue. Transp. Res. Part C Emerg. Technol. 2015, 61, 106–120. [Google Scholar] [CrossRef]
- Yang, K.; Guler, S.I.; Menendez, M. Isolated intersection control for various levels of vehicle technology: Conventional, connected, and automated vehicles. Transp. Res. Part C Emerg. Technol. 2016, 72, 109–129. [Google Scholar] [CrossRef]
- Zhou, Q.; Zhou, B.; Hu, S.; Roncoli, C.; Wang, Y.; Hu, J.; Lu, G. A safety-enhanced eco-driving strategy for connected and autonomous vehicles: A hierarchical and distributed framework. Transp. Res. Part C Emerg. Technol. 2023, 156, 104320. [Google Scholar] [CrossRef]
- Stebbins, S.; Hickman, M.; Kim, J.; Vu, H.L. Characterising green light optimal speed advisory trajectories for platoon-based optimisation. Transp. Res. Part C Emerg. Technol. 2017, 82, 43–62. [Google Scholar] [CrossRef]
- Typaldos, P.; Papageorgiou, M. Modified dynamic programming algorithms for GLOSA systems with stochastic signal switching times. Transp. Res. Part C Emerg. Technol. 2023, 157, 104364. [Google Scholar] [CrossRef]
- Yang, Z.; Zheng, Z.; Kim, J.; Rakha, H. Eco-driving strategies using reinforcement learning for mixed traffic in the vicinity of signalized intersections. Transp. Res. Part C Emerg. Technol. 2024, 165, 104683. [Google Scholar] [CrossRef]
- Zhou, F.; Li, X.; Ma, J. Parsimonious shooting heuristic for trajectory design of connected automated traffic part I: Theoretical analysis with generalized time geography. Transp. Res. Part B Methodol. 2017, 95, 394–420. [Google Scholar] [CrossRef]
- Ma, J.; Li, X.; Zhou, F.; Hu, J.; Park, B.B. Parsimonious shooting heuristic for trajectory design of connected automated traffic part II: Computational issues and optimization. Transp. Res. Part B Methodol. 2017, 95, 421–441. [Google Scholar] [CrossRef]
- Yang, H.; Rakha, H.; Ala, M.V. Eco-cooperative adaptive cruise control at signalized intersections considering queue effects. IEEE Trans. Intell. Transp. Syst. 2016, 18, 1575–1585. [Google Scholar] [CrossRef]
- Yang, X.T.; Huang, K.; Zhang, Z.; Zhang, Z.A.; Lin, F. Eco-driving system for connected automated vehicles: Multi-objective trajectory optimization. IEEE Trans. Intell. Transp. Syst. 2020, 22, 7837–7849. [Google Scholar] [CrossRef]
- Nguyen, C.H.; Hoang, N.H.; Lee, S.; Vu, H.L. A system optimal speed advisory framework for a network of connected and autonomous vehicles. IEEE Trans. Intell. Transp. Syst. 2021, 23, 5727–5739. [Google Scholar] [CrossRef]
- Hoang, A.T.; Nguyen, C.H.; Ngoduy, D.; Vu, H.L. Optimal trajectory planning framework for a mixed traffic network. In Proceedings of the 2022 IEEE 25th International Conference on Intelligent Transportation Systems (ITSC), Macau, China, 8–12 October 2022; pp. 2756–2762. [Google Scholar]
- Wang, Y.; Li, J.; Ke, T.; Ke, Z.; Jiang, J.; Xu, S.; Wang, J. A homogeneous multi-vehicle cooperative group decision-making method in complicated mixed traffic scenarios. Transp. Res. Part C Emerg. Technol. 2024, 167, 104833. [Google Scholar] [CrossRef]
- Ma, M.; Li, Z. A speed-maximization trajectory optimization model on a reservation-based intersection control system. Transp. Res. Part C Emerg. Technol. 2023, 154, 104266. [Google Scholar] [CrossRef]
- Yao, H.; Li, X. Decentralized control of connected automated vehicle trajectories in mixed traffic at an isolated signalized intersection. Transp. Res. Part C Emerg. Technol. 2020, 121, 102846. [Google Scholar] [CrossRef]
- Yao, S.; Zhou, Y.; Friedrich, B.; Ahn, S. Planning trajectories for connected and automated vehicle platoon on curved roads: A two-dimensional cooperative approach. Transp. Res. Part C Emerg. Technol. 2024, 165, 104718. [Google Scholar] [CrossRef]
- Ma, C.; Yu, C.; Yang, X. Trajectory planning for connected and automated vehicles at isolated signalized intersections under mixed traffic environment. Transp. Res. Part C Emerg. Technol. 2021, 130, 103309. [Google Scholar] [CrossRef]
- Zou, Y.; Zheng, F.; Liu, C.; Liu, X. Integrated optimization of traffic signals and vehicle trajectories for mixed traffic at signalized intersections: A two-level hierarchical control framework. Transp. Res. Part C Emerg. Technol. 2024, 169, 104884. [Google Scholar] [CrossRef]
- Wang, J.; Lian, Y.; Jiang, Y.; Xu, Q.; Li, K.; Jones, C.N. Distributed data-driven predictive control for cooperatively smoothing mixed traffic flow. Transp. Res. Part C Emerg. Technol. 2023, 155, 104274. [Google Scholar] [CrossRef]
- Wang, Q.; Gong, Y.; Yang, X. Connected automated vehicle trajectory optimization along signalized arterial: A decentralized approach under mixed traffic environment. Transp. Res. Part C Emerg. Technol. 2022, 145, 103918. [Google Scholar] [CrossRef]
- Mohebifard, R.; Hajbabaie, A. Connected automated vehicle control in single lane roundabouts. Transp. Res. Part C Emerg. Technol. 2021, 131, 103308. [Google Scholar] [CrossRef]
- Lei, Y.Z.; Cheng, Y.; Yang, X.T. An optimization-free approximation Framework for Connected and Automated Vehicles Eco-Trajectory Planning Under limited computing capacity. Transp. Res. Part C Emerg. Technol. 2025, 171, 104949. [Google Scholar] [CrossRef]
- Falsone, A.; Margellos, K.; Garatti, S.; Prandini, M. Dual decomposition for multi-agent distributed optimization with coupling constraints. Automatica 2017, 84, 149–158. [Google Scholar] [CrossRef]
- Falsone, A.; Margellos, K.; Prandini, M. A decentralized approach to multi-agent MILPs: Finite-time feasibility and performance guarantees. Automatica 2019, 103, 141–150. [Google Scholar] [CrossRef]
- Falsone, A.; Margellos, K.; Prandini, M. A distributed iterative algorithm for multi-agent MILPs: Finite-time feasibility and performance characterization. IEEE Control. Syst. Lett. 2018, 2, 563–568. [Google Scholar] [CrossRef]
- Zhou, J.; Zhu, F. Analytical analysis of the effect of maximum platoon size of connected and automated vehicles. Transp. Res. Part C Emerg. Technol. 2021, 122, 102882. [Google Scholar] [CrossRef]
- Li, S.; Zheng, H.; Wang, J.; Chen, C.; Xu, Q.; Wang, J.; Li, K. Influence of information flow topology and maximum platoon size on mixed traffic stability. Transp. Res. Part C Emerg. Technol. 2025, 171, 104950. [Google Scholar] [CrossRef]
- Sánchez, M.M.; van der Ploeg, C.; Smit, R.; Elfring, J.; Silvas, E.; van de Molengraft, R. Prediction horizon requirements for automated driving: Optimizing safety, comfort, and efficiency. In Proceedings of the 2024 IEEE Intelligent Vehicles Symposium (IV), Jeju Island, Republic of Korea, 2–5 June 2024; pp. 2575–2582. [Google Scholar]
- Bai, T.; Johansson, A.; Johansson, K.H.; Mårtensson, J. Large-scale multi-fleet platoon coordination: A dynamic programming approach. IEEE Trans. Intell. Transp. Syst. 2023, 24, 14427–14442. [Google Scholar] [CrossRef]
- Zhao, W.; Yildirimoglu, M. A scalable macro–micro approach for cooperative platoon merging in mixed traffic flows. Transp. Res. Part C Emerg. Technol. 2024, 169, 104859. [Google Scholar] [CrossRef]
- Kamal, M.A.S.; Mukai, M.; Murata, J.; Kawabe, T. Model predictive control of vehicles on urban roads for improved fuel economy. IEEE Trans. Control. Syst. Technol. 2012, 21, 831–841. [Google Scholar] [CrossRef]





| Scenario | Platoon Setting | Vehicle Number | Simulation Horizon (s) | Initial Platoon Leader Position (m) | Objective |
|---|---|---|---|---|---|
| 1 | Single | 2, 4, …, 24 | 130 | 0 | Test the impact of different single-platoon vehicle numbers |
| 2 | Single | 20 | 110, 120, …, 200 | 0 | Test the impact of different simulation horizons |
| 3 | Multiple | 4, 8, …, 40 | 130 | 400 | Test the impact of different total vehicle numbers in multi-platoons |
| 4 | Multiple | 32 | 130 | 400 | Validate the control performance in platoon merging |
| Notation | Description | Value | Unit |
|---|---|---|---|
| Time step | 1 | s | |
| K | Simulation horizon in scenarios 1 to 4 | 130, 110 to 200, 130, 130 | s |
| N | Total number of vehicles in scenarios 1 to 4 | 2 to 24, 20, 4 to 40, 32 | veh |
| Ride comfort weight coefficient | 10 | s | |
| Delay weight coefficient | 1 | - | |
| Minimum acceleration | −5 | m/ | |
| Maximum acceleration | 2 | m/ | |
| Maximum speed | 15 | m/s | |
| Length of vehicle i | 3 | m | |
| Minimum safe time gap | 2 | s | |
| Minimum space gap at standstill | 2 | m | |
| – | Initial position | 0, 400 | m |
| – | Initial inter-vehicle gap | 21 | m |
| – | Initial speed | 8 | m/s |
| – | Inter-platoon gap in scenarios 3 and 4 | 400, 245 | m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, M.; Gao, Y.; Zeng, Y.; Hao, R. Distributed Trajectory Optimization for Connected and Automated Vehicle Platoons Considering Safe Inter-Vehicle Following Gaps. Systems 2025, 13, 483. https://doi.org/10.3390/systems13060483
Liu M, Gao Y, Zeng Y, Hao R. Distributed Trajectory Optimization for Connected and Automated Vehicle Platoons Considering Safe Inter-Vehicle Following Gaps. Systems. 2025; 13(6):483. https://doi.org/10.3390/systems13060483
Chicago/Turabian StyleLiu, Meiqi, Ying Gao, Yikai Zeng, and Ruochen Hao. 2025. "Distributed Trajectory Optimization for Connected and Automated Vehicle Platoons Considering Safe Inter-Vehicle Following Gaps" Systems 13, no. 6: 483. https://doi.org/10.3390/systems13060483
APA StyleLiu, M., Gao, Y., Zeng, Y., & Hao, R. (2025). Distributed Trajectory Optimization for Connected and Automated Vehicle Platoons Considering Safe Inter-Vehicle Following Gaps. Systems, 13(6), 483. https://doi.org/10.3390/systems13060483






