Abstract
Intelligent and information systems in transportation record and accumulate large volumes of raw data on dynamic transportation processes. However, these data are not fully utilized for forecasting, real-time planning, and transportation management. Spatio-temporal graphs allow describing simultaneously both the structure of transportation systems of different modes of transportation and the dynamics of transportation flows. Optimization of such graphs makes it possible to justify management decisions in real time, as well as to forecast the parameters of traffic flows and transportation processes. The purpose of the study is to identify trends in the use of spatio-temporal graphs for solving various problems in transportation, as well as the most common methods of optimization of such graphs. The sample papers studied include 114 publications from the Scopus database over 25 years, from 1999 to 2024. First, a bibliometric analysis was conducted to establish the increase in the number of publications, journals, countries, institutions, subject areas, articles, authors, and keyword matches, to understand the amount of literature generated. Secondly, a literature review was conducted based on content analysis to predict future research directions in the field. We have found that the development of deep learning methods and approaches for designing graph neural networks based on spatio-temporal graphs is a promising direction. Such methods are mostly used to solve the tasks of real-time control of urban transportation systems. There are fewer publications in areas that require in-depth knowledge of transportation technology, such as air, sea, and rail transportation. This study contributes to the expansion of scientific knowledge about methods of spatio-temporal optimization of transport systems based on bibliometric analysis.
1. Introduction
The tasks of transportation systems management are the most complex in science and have become especially relevant under conditions of increasing uncertainty in the external environment and increasing complexity of transportation systems themselves [1]. Improvements in information technologies [2], the intensive spread of Industry 4.0 [3], and Internet of Things concepts [4] have formed prerequisites for obtaining large amounts of dynamic, reliable data on the parameters of transportation systems [5], as well as for employing these data to facilitate management decision-making in real time. The dimensionality of operational management tasks within the transport sector is expanding in response to the necessity for the analysis of substantial volumes of detailed current data [6]. An examination of scientific literature has facilitated the categorization of five distinct groups of methods for addressing these challenges: mathematical programming methods, simulation modeling, heuristic methods, analytical models, and combined (hybrid) methods.
In the domain of mathematical programming, numerous single-objective and multi-objective methodologies exist for addressing optimization problems. These methodologies have been extensively utilized in the optimization of traffic flow parameters [7]. Various approaches are employed to account for spatial and temporal dependencies within these methodologies. A distinct category encompasses methods derived from control theory and dynamic programming [8]. Methods based on dynamic programming effectively consider intricate spatial and temporal dependencies. The dynamic optimization of traffic flow parameters, facilitated by the utilization of substantial volumes of spatio-temporal data collected in real time, results in an escalation in the dimensionality of the optimization problem.
The insufficient development of mathematical programming methods and analytical models based on large volumes of real-time data limits the accuracy of their results and reduces management efficiency. Analytical models [9] are employed to address large-scale management problems that incorporate multiple criteria. A promising avenue for the advancement of these models involves multicriteria analysis methods for decision-making in management. The primary factor constraining the application of these methods in the operational management of transport systems is their limited accuracy in accounting for frequent interactions and fluctuations in the state of control objects.
Heuristic methods and artificial intelligence methodologies facilitate the resolution of large-scale problems within constrained timeframes and with requisite accuracy [10]. The primary focus of development for these methods, in the context of transport systems, is the advancement of novel adaptive algorithms and techniques for the formation of neural networks, with the objective of enhancing the precision of monitoring the positions of individual components within traffic flow, followed by the optimization of transport system parameters in real time.
The simulation modeling method is an alternative approach for forecasting transportation flows and developing plans for the structural development of transportation systems [11]. This method is primarily used for justifying infrastructure projects or making decisions at the strategic management level. The main limitations of this method include the complexity of accurately describing real-world systems and the significant time required to build and validate the simulation model [7]. Nevertheless, the combination of different simulation modeling paradigms with optimization models in modern software tools enables the use of this method for constructing synchronized simulation models of transportation systems [12].
Metaheuristic strategies are also used to select optimal solutions based on predictive scenarios [13]. However, the computational efficiency of metaheuristic algorithms decreases as the structure of the optimized system becomes more complex or as the topology of the solution space for possible decision sequences becomes more intricate [14].
A key research trend in recent years in the field of forecasting and optimal management of transportation systems has been the combination of the above methods. The results of such studies include, for example, combined simulation-analytical models, hybrid multi-criteria models, hybrid neural networks, and deep learning structures [15]. A promising development in this area, in our view, is the use of graph theory methods to describe the structure, topology, and temporal changes of transportation systems, as well as management decision options, followed by the application of the discussed optimization and forecasting methods [15].
In transportation systems, the structure of space topology dynamically depends both on the parameters of transportation flows [16] and the individual elements of these flows. A promising way to overcome these limitations is to combine graph theory and optimization methods. Currently, there is an intensive improvement of graph theory in the direction of creating new methods of optimization for solving a wide range of applied problems [17]. However, the use of traditional methods of describing the space of complex topology using graphs has limitations. These relate to two main factors—peculiarities of the topology of transport systems, especially railway transport systems, and variability of parameters of transport flows in a broad sense. The complex and specific topology of transportation systems, especially in railway transport, requires the use of additional constraints in the process of solving optimization problems on spatial graphs. An alternative solution is the creation of specialized spatial graphs through various transformations of the original graphs. The factor of traffic flow dynamics affects the dimensionality of temporal graphs, complicating the use of such graphs for solving optimization and forecasting issues with most known methods.
The problem of improving the accuracy of system state prediction based on the development of graph structure optimization methods has only been considered in a discrete formulation until recently. The result of this approach is the multivariate structure of graphs used to describe complex transportation systems. Most of the known algorithms for predicting the state of transportation systems are based on heuristic and meta-heuristic methods [18]. These algorithms are characterized by insufficient accuracy in predicting the state of complex transport systems [19].
The use of combined spatio-temporal graphs potentially enables the creation of more accurate and computationally efficient methods of describing and predicting the state of complex transportation systems [20]. The need to expand the understanding of the state of research in the use of spatio-temporal graph optimization methods in transportation, and the prospects for the development of these methods as applied to complex control problems, necessitated a systematic literature review.
We searched for review articles in the Scopus database to identify previous similar studies. The keywords “Spatio-Temporal graph” AND “Review” were used for the query. As a result, 36 review articles were found. Most existing literature reviews focused on a specific scientific field, especially in areas related to the use of the “Spatio-Temporal graph” in neuroscience, medicine, biochemistry, genetics and molecular biology, and computer science. The results of the review article analysis show that spatio-temporal graphs are actively used to solve a wide range of applied problems related to optimizing parameters and forecasting the state of complex dynamic systems. Out of 36 articles, only one article is related to the topic of this study, and it is a review of machine learning-based traffic prediction methods [21]. The value of this study lies in summarizing research on the use of spatio-temporal graphs in transportation systems to address relevant and widespread problems of forecasting their state and optimizing transportation flow parameters in real time. Therefore, this study uses a systematic literature review methodology to synthesize graph theory research as applied to transportation systems of different modes and varying complexity.
This paper aims to fill the gap in the analysis of scientific papers on the use of spatio-temporal optimization methods for transportation systems by conducting a systematic literature review of a 25-year period from 1999 to 2024. The main scientific contributions of this paper are as follows:
1. The formulation of a comprehensive view of the research environment that links spatio-temporal graphs, optimization methods, and transport systems of different modes of transport.
2. The identification of the main tasks and methods of spatio-temporal optimization of transport systems based on bibliometric and content analysis of scientific publications.
3. The identification of future research directions in spatio-temporal optimization of transport systems to fill the research gap.
To comprehensively evaluate and analyze the existing research, identify the tasks and areas of application of the “Spatio-Temporal graph” in transportation, as well as to identify promising directions for the development of the “Spatio-Temporal graph” in the future, we formulated the following questions.
1. What quantitative and qualitative changes have been observed in publications on the application of the “Spatio-Temporal graph” in transportation systems?
2. Which authors and organizations, and from which countries, contributed to the development of scientific knowledge in the field of “Spatio-Temporal graph” application to transport systems?
3. What are the most cited publications, and which scientific journals publish research on the use of the “Spatio-Temporal graph” in transportation systems most frequently?
4. What problems and methods of spatio-temporal optimization of transport systems are relevant and promising?
This article consists of four sections. After the “Introduction” section, the “Research Method” section presents a description of the research methodology. The “Analysis Results” section contains the results of bibliometric analysis and content analysis of publications from the Scopus database, as well as the systematization of spatio-temporal optimization problems and methods as applied to transport systems. Finally, the “Conclusion” section summarizes the results of the study and points out its limitations.
2. Research Method
A systematic literature review aims to identify, evaluate, interpret, and categorize research papers addressing one or more research questions and topics. The main steps of the systematic review methodology in this study are as follows [22]:
1. Defining the research questions: formulating the research questions that need to be answered.
2. Literature search and selection: developing a strategy for finding documents using different combinations of keywords to get the most comprehensive overview of the research area, and setting up filters to obtain the most relevant sample of articles.
3. Bibliometric analysis: presenting quantitative analysis and data visualization of the selected sample of articles to understand the key characteristics of the study area, including publication, journal, and citation trends, collaboration, and keyword focus.
4. Content analysis: analyzing the content of the articles selected in the second step to understand the content of current and prospective research.
In this study, the Scopus database was used to analyze research trends in the literature on the application of spatio-temporal optimization methods for solving relevant problems in the operation of various transportation systems. The Scopus database covers a large volume of scientific publications, which provides a rich and diverse dataset for a systematic literature review and reliable analysis results.
We used the following rules to collect relevant literature:
- The papers should contain the keywords “Spatio-Temporal graph” and “Transport systems”. The filter [Article title, Abstract, Keywords] was used as a criterion for selecting publications.
- Papers should be indexed in the Scopus database and should include articles in peer-reviewed English language journals, conference proceedings, and book chapters on the field under study.
Spreadsheets were used to perform statistical analysis of publication search results, and VOSviewer [23] was used to visually represent and analyze the keyword network.
Figure 1 presents the scheme of the research methodology. The PRISMA flow diagram [24] approach was used to determine the number of papers selected for analysis, accounting for the exclusion of duplicates and papers not relevant to the field of study. At the “Identification” stage, we selected 184 papers according to the given query combinations: “spatiotemporal” AND “transport systems” (98 papers); “spatio-temporal” AND “transport systems” (86 papers). In the “Screening” stage, we excluded 37 publications that were duplicated from the analysis. An additional 26 papers were excluded based on the results of the abstract analysis as not relevant to the field of study. Thus, the total number of selected papers for bibliometric analysis and content analysis was 114.
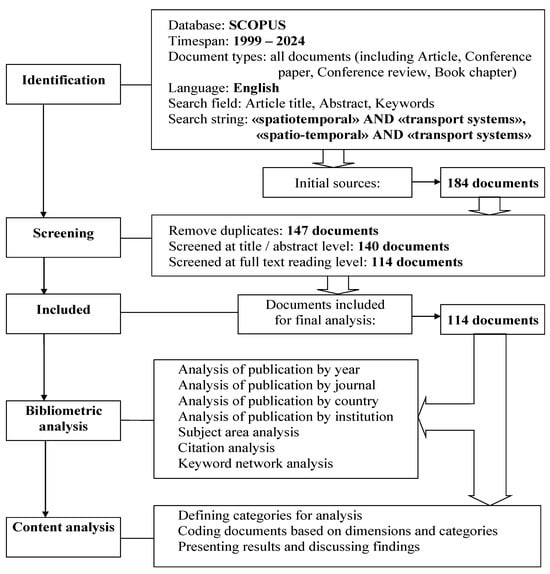
Figure 1.
The PRISMA flow diagram.
3. Results
Studies on the use of spatio-temporal graphs for transportation systems of various complexities appeared in the late 1990s and became most prominent in the past five years—this period accounts for about 89% of indexed papers. Figure 2 shows the trend in the number of scientific papers indexed in the Scopus database from 1999 to 2024. Since 2019, there has been a significant increase in the number of publications, which shows the increasing interest of researchers in the use of spatio-temporal graphs to describe and model the operation of various transportation systems.
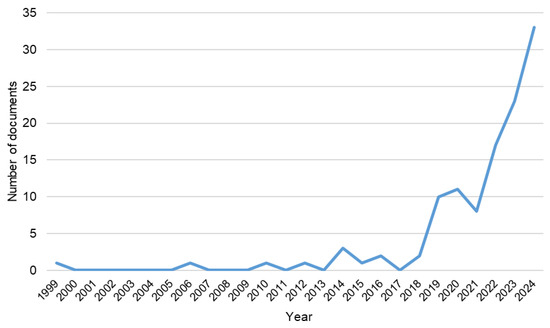
Figure 2.
Distribution of papers on the researched subject in the Scopus database from 1999 to 2024 by year.
Most papers (about 93%) were published in English, and up to 80% of papers were published articles in scientific journals (Figure 3).
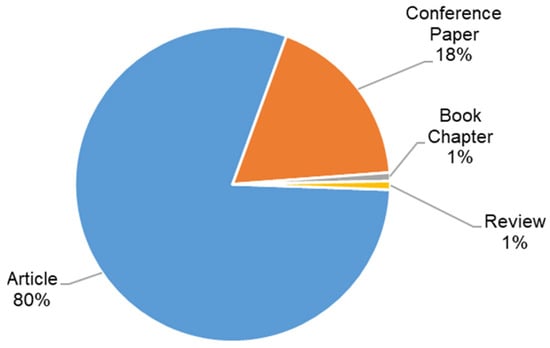
Figure 3.
Distribution of papers by type.
Analysis of the distribution of papers across scientific journals shows broad coverage of various resources indexed in the Scopus database. The list of journals includes 63 titles. The top five journals by number of publications were Transportation Research Part C: Emerging Technologies (11 papers), IEEE Transactions on Intelligent Transportation Systems (7 papers), IEEE Access (5 papers), Sustainability (Switzerland) (4 papers), and Computers Environment and Urban Systems (3 papers). No more than three articles were published in 15 journals. We found only one paper in 43 journals. The number of these journals is shown in the “Other sources” column in Figure 4. The other columns of the diagram in this figure correspond to journals with more than two publications.
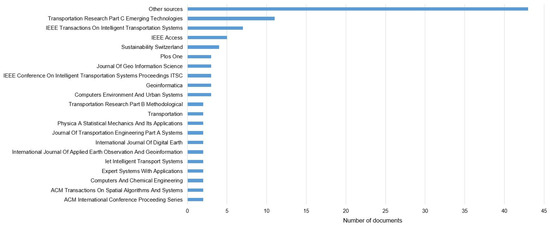
Figure 4.
Distribution of papers by journals.
Figure 5 shows the distribution of publications by different branches of knowledge or subject areas. The topics of the articles are related to many subject areas, ranging from computer science, engineering, and social sciences to mining sciences. The diversity of subject areas indicates not only the importance of the topic under study but also the interdisciplinary nature of the issues related to the use of spatio-temporal graph methods for the optimization of transport systems.
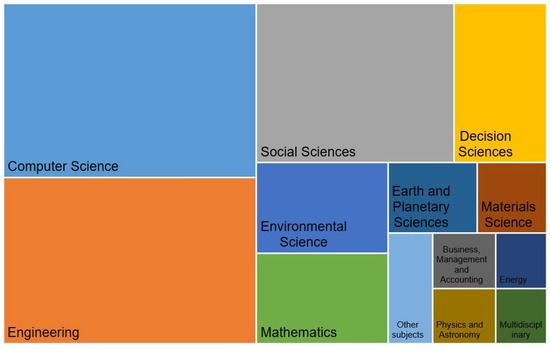
Figure 5.
Distribution of papers by fields of knowledge.
Figure 6 shows the distribution of the analyzed publications across the countries to which the authors were affiliated. The leader in the number of publications is China (66 papers). In addition to China, the top five countries by publications are the USA (17 papers), Hong Kong (12 papers), the United Kingdom (8 papers), and South Korea (6 papers). One publication per country was found in 17 countries, including Austria, Brazil, Canada, Egypt, Indonesia, Netherlands, Norway, Poland, Portugal, Qatar, the Russian Federation, Saudi Arabia, Slovakia, Spain, Sweden, Switzerland, and Taiwan. The Scopus database did not identify publications on the subject of the study from the countries of Central, Eastern, and Southern Africa, Central Asia, or South America, with the exception of Brazil.
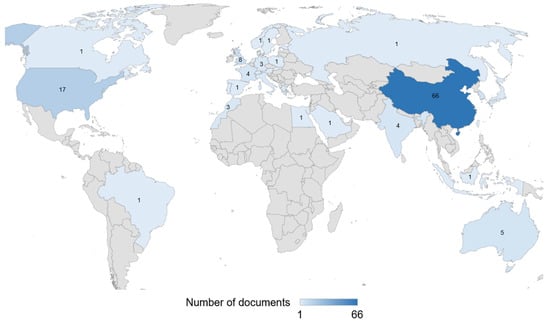
Figure 6.
Distribution of papers by country.
The leading organizations with which authors with the largest number of scientific articles on the research topic are the Chinese Academy of Sciences (seven papers), Hong Kong University of Science and Technology (six papers), The Hong Kong Polytechnic University (six papers), Beijing Jiaotong University (five papers), and The University of Hong Kong (four papers). In total, the analysis identified 160 organizations from 34 countries.
Analysis of publication citations indicated that the first citation appeared in 1999, and the total number of citations reached 1728 at the time of the study. A total of 87 papers out of 114 were cited in the Scopus database at least once, which is 76% (Figure 7).
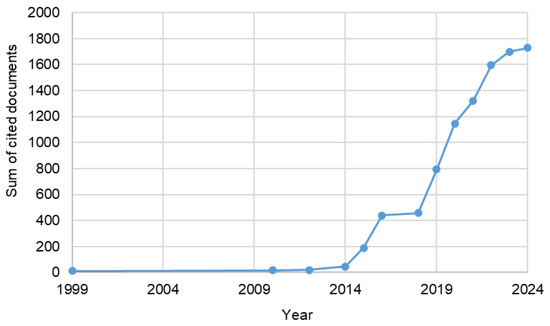
Figure 7.
Number of citations cumulatively by year.
The most cited papers at the time of the study are presented in Table 1. Researchers have focused primarily on areas related to modeling and control of traffic in urban networks [25], bike sharing systems [26,27], traffic speed prediction in Intelligent Transportation Systems [28], and forecasting the demand for urban taxi rides within an online car-hailing system [29].

Table 1.
Top 5 most cited papers.
Keyword analysis was performed by dividing the papers by year of publication into two periods—from 1999 to 2018 and from 2019 to 2024. This division is justified by the sharp increase in the number of publications starting from 2019. In the papers from the first period, 194 keywords were identified. The keywords are grouped into three clusters: red, blue, and green (Figure 8), each represented by four main areas with high linkage strength.

Figure 8.
Most frequently used keywords in papers published between 1999 and 2018.
The red cluster reflects the relevance of issues related to “complex network” formation. Research topics are devoted to the assessment of air network development in China, and to modeling and traffic management in urban networks. The blue cluster covers problems related to “travel time”. The subject matter of these works includes the estimation of vehicle travel time, passenger departure time, modeling of road users’ behavior, and estimation of probable spatial and temporal travel paths. These studies cover both air and urban modes of transport. The green cluster, “transportation”, reflects the solution of problems related to the transportation of dangerous goods, route selection in multimodal transport systems, and modeling the location of transport hubs.
In papers published during the second analysis period, from 2019 to 2024, 1318 keywords were identified. In the subsequent analysis, all keywords were grouped into four clusters comprising 29 main areas (Figure 9). The red cluster includes nine domains—graph, data, approach, algorithm, graphic method, public transportation, demand prediction, bicycle, and COVID-19. The green cluster includes nine areas—street, road, motor transportation, road network, traffic prediction, travel time, and spatio-temporal data. The blue cluster includes eight areas—graph convolutional network, spatio, convolutional network, traffic flow prediction, traffic forecasting, intelligent transportation systems, and intelligent vehicle highway system. The yellow cluster includes three areas—transportation systems, traffic management, and China.
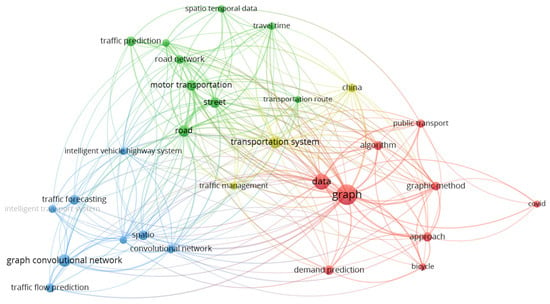
Figure 9.
Most frequently used keywords in papers published between 2019 and 2024.
The results of keyword analysis in the 114 selected papers revealed 506 words (Figure 10).

Figure 10.
Frequency of keywords in the selected research papers.
The keywords “spatio-temporal graph”, “neural networks”, “machine learning”, “deep learning”, “forecasting”, “analysis”, “traffic flow”, “spatio-temporal data”, and “transportation system” are the most frequently used. Thus, a formal analysis of keyword frequency shows a clear interest among scientists in using neural networks and machine learning methods combined with spatio-temporal graphs to address various problems in transportation systems. A set of key terms including “optimization”, “dynamic optimization”, “hybrid methods”, “spatio-temporal graph neural networks”, “combined model” or “hybrid model”, “deep learning”, and “hybrid neural network” holds promise for further detailing research publications on the use of spatio-temporal graphs in transportation.
In addition to the keyword analysis, all papers were grouped by areas of application of the spatio-temporal graph as applied to different modes of transportation or transportation systems (Table 2). Despite the interdisciplinary nature of most publications on each mode of transportation, specific areas of application can be attributed to individual elements of transportation systems—transport communications and infrastructure, vehicles, road users, control systems, information-telecommunication systems, etc.

Table 2.
Distribution of papers by mode of transport and subject areas.
In recent years, there has been increased interest among researchers in using various spatio-temporal optimization methods in real-time transportation applications. Such methods are applied to traffic forecasting (34 papers) and passenger flow forecasting (5 papers), route and trip planning (13 papers), vehicle allocation (demand forecasting), vehicle sharing forecasting (29 papers), and monitoring the use of transport infrastructure by different modes of transport (33 papers).
Based on the results of the content analysis of publications, we arranged the methods of spatio-temporal optimization into groups and subgroups (Table 3). The most frequently used methods for spatio-temporal graph optimization are mathematical programming methods (linear programming, multi-criteria analysis, dynamic programming), graph theory (simple graph, dynamic graphs and methods for generalizing their structure, spatio-temporal graphs and methods for their formation, biological graphs), and heuristic methods (heuristic strategies, feedforward neural networks, convolutional neural networks (CNNs), graph convolutional neural networks (GCNs), graph neural networks (GNNs), and other methods).

Table 3.
Distribution of studies by method of transport systems spatio-temporal optimization.
The results of the extended analysis of the advantages and limitations of current methods for spatio-temporal optimization of transport systems are presented in Table 4.

Table 4.
Advantages and limitations of spatio-temporal optimization methods for transport systems.
Content analysis has shown the greatest number of uses of heuristic methods of spatio-temporal optimization for solving real-time decision support problems (90 publications). Neural networks, along with machine and deep learning methods (73 publications), are used to account for spatio-temporal dependencies in complex transportation systems with a high degree of accuracy. A promising direction is the use of graph neural networks (16 publications) and methods for their training. A distinctive feature of graph neural networks is the possibility of using a spatio-temporal graph without additional transformations. Machine learning methods (19 publications) and methods of their combination (deep learning methods, 11 publications) are used for training such neural networks.
The results of the paper analysis show the interest of researchers in combining graphs with methods of mathematical statistics and analysis, optimization, numerical methods, probability theory, and multicriteria analysis for training neural networks. The basis of such deep learning methods is the transformation of data on transportation system parameters into spatio-temporal estimates of the graph, and their use in solving problems of spatio-temporal optimization. This optimization is based on the formalization of spatial and temporal data in the form of graphs. We identified 16 different methods of graph theory and 11 methods of mathematical programming for forming spatial and temporal estimates of a graph and for optimizing it (Figure 11).
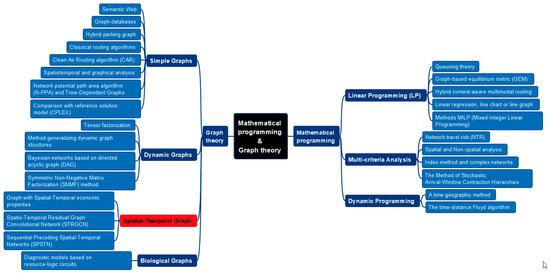
Figure 11.
Methods of mathematical programming and graph theory for solving spatio-temporal optimization problems in transportation systems.
The operation of a complex transportation system is accompanied by a large volume of spatial and temporal data about its state. The need to improve the accuracy of describing such spatial and temporal dependencies leads to an increase in the dimensionality of optimization and forecasting problems for the state of the transportation system. Artificial neural networks are used to reduce the optimization space (Figure 12).
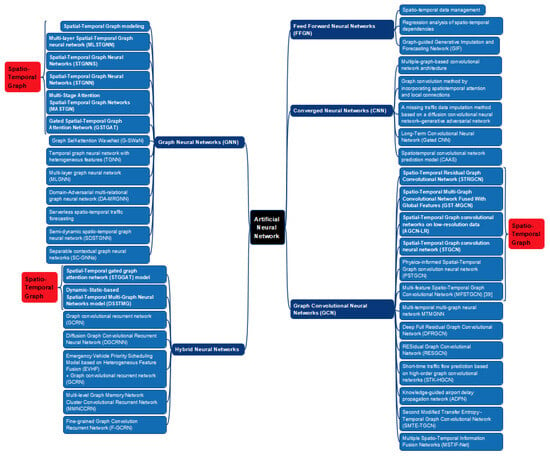
Figure 12.
Artificial neural networks in spatio-temporal optimization problems of transportation systems.
Graph theory and mathematical programming methods form the basis for creating and training feedforward neural networks (3 methods), convolutional neural networks (5 methods), graph neural networks (13 methods), graph convolutional neural networks (13 methods), and merged neural networks (hybrid neural networks, 7 methods) to recognize complex spatial and temporal dependencies. A total of 30 machine learning methods were been identified when using such neural networks. These methods account for spatial and temporal dependencies in different ways (Figure 13).
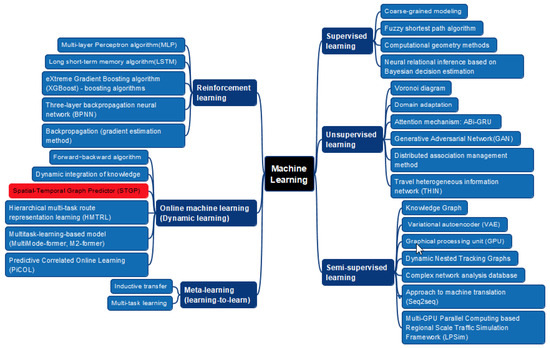
Figure 13.
Machine learning methods in spatio-temporal optimization problems of transportation systems.
Most of the mentioned machine learning methods use either spatial or temporal data separately. We found only one machine learning method that allows for the integrated use of both spatial and temporal data to form a predictor for the objective function [132]. However, the high uncertainty of spatial and temporal data requires frequent adjustments of the predictor in the machine learning algorithm. This is the main limitation of using machine learning methods, as the predictor cannot be changed during the calculation process. Deep learning methods or deep (multilayer) neural networks are more effective for the integrated use of stochastic spatial and temporal data (Figure 14).
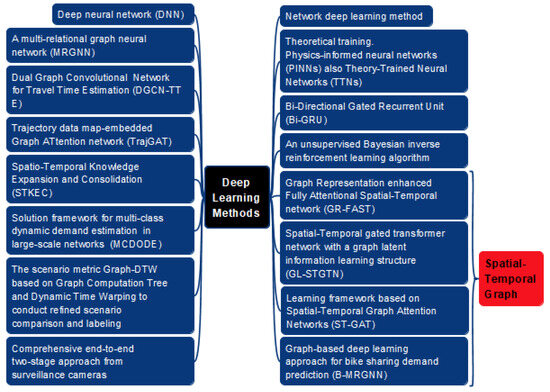
Figure 14.
Deep learning methods in spatio-temporal optimization problems of transportation systems.
The creation and training of deep or multilayer neural networks for forecasting the state of transportation systems is an especially challenging task. The complexity is due to the frequent changes and large volume of spatial and temporal data collected and analyzed. The need to account for such data changes leads to an increase in the dimensionality of the problem. Four deep learning methods that use a spatio-temporal graph to reduce the problem’s dimensionality have been identified [28,67,91,120].
Further analysis of research on the use of spatio-temporal graphs for forecasting and managing transportation systems revealed a promising direction for overcoming the identified challenges and limitations. This direction involves developing methods for constructing a spatio-temporal graph of the transportation system’s state, in combination with methods for its optimization, as well as methods for creating and training artificial neural networks (Figure 15).
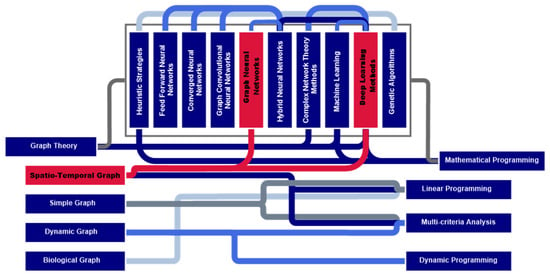
Figure 15.
Possible combinations of identified methods for spatio-temporal optimization of transportation systems.
Such combinations are found in publications on graph theory (three publications) [58,89,124], graph neural networks (eight publications) [42,61,84,95,97,99,109,113], graph convolutional neural networks (six publications) [55,60,96,105,110,119], hybrid neural networks (two publications) [44,121], the dynamic machine learning method (one publication) [132], deep neural networks, and deep learning methods (four publications) [28,67,91,120].
We identify a separate subgroup within graph theory that focuses on methods for constructing and optimizing spatio-temporal graphs, which serve as the foundation for developing and utilizing deep spatio-temporal graph neural networks [139]. Surprisingly, we could not find any publications on combining the popular simulation modeling methods either for training neural networks or for solving spatio-temporal optimization problems.
Most of the publications reflect the use and development of spatio-temporal optimization methods for solving problems of both real-time management of urban transport systems and planning tasks. The smallest number of publications was found in the areas of rail, sea, and air transportation. In our opinion, this is due to the need to consider the specific management and technology of the transportation process when using spatio-temporal optimization methods. When applying optimization methods to simple graphs, the formation of a vehicle route may include turning at points in the transport infrastructure where this is prohibited by traffic safety rules or infeasible according to the technology of operation. For such conditions, specialized graph structures like linear (edge) or two-vertex graphs are used. The result of using such graphs is the blocking of vehicle turns based on the introduction of additional rules and exceptions. For example, when using methods of spatio-temporal optimization of railway transport systems, it is necessary to consider the specifics of train shunting. The result of solving the problems of train shunting is significantly affected by changes in the direction of trains when following shunting routes, the structure of trains, timetables, and loading and unloading schedules of cars. These factors determine the method of spatio-temporal graph formation. On the one hand, the accuracy of data conversion into spatio-temporal graph estimates depends on the correct description of the transportation process technology. This requires the use of specialized graph structures: line graph (edge graph), two-vertex graph with connected bijective vertices, and two-vertex graph with separated bijective vertices and edges [140]. On the other hand, the management process in railway transportation is accompanied by many variations in managerial decisions related to train shunting. Depending on the choice of a certain variant of such a sequence, different changes in the spatio-temporal state of the railway transportation system are observed. Therefore, it is necessary to use technologically informed spatio-temporal graphs when making managerial decisions.
4. Conclusions
Recently, within the field of transport systems management, there has been growing interest in the use of various methods of spatio-temporal optimization in real time to solve problems such as forecasting traffic and passenger flows, planning routes and trips, distribution of vehicles, forecasting the joint use of vehicles, and monitoring the use of transport infrastructure by different types of transport. The main groups and subgroups of spatio-temporal optimization methods identified for solving such problems include the following: mathematical programming (linear programming (LP), multi-criteria analysis, dynamic programming); graph theory (simple graphs, dynamic graphs, spatio-temporal graph, biological graphs); heuristic methods (heuristic strategies, feedforward neural networks (FFGN), converged neural networks (CNN), graph convolutional neural networks (GCN), graph neural networks (GNN), hybrid neural networks, complex network theory methods, machine learning, deep learning methods, genetic algorithms). The main advantages and disadvantages of the identified methods regarding complex spatial and temporal dependencies are presented. A more detailed analysis of each spatio-temporal optimization method individually is part of future research.
The results of the conducted systematic literature review of publications show the intensive development of spatio-temporal optimization methods based on the use of spatio-temporal graphs for predicting changes in spatial topology structures depending on the parameters of transport flows.
The results of the analysis also highlight the interest of researchers in combining graphs with methods of mathematical statistics and analysis, optimization, numerical methods, probability theory, and multicriteria analysis for training neural networks. The basis of such deep learning methods is the transformation of transportation system parameter data into spatio-temporal estimates on a graph and their use in solving problems of spatio-temporal optimization.
Particular interest has been observed in the use of spatio-temporal graphs within heuristic methods. A promising direction is the development of deep learning methods and methods of forming graph neural networks based on the use of spatio-temporal graphs. These methods are most often used to solve problems related to the real-time control of urban transportation systems.
The fewest publications were found in fields requiring in-depth knowledge of transportation technology, such as air, sea, and railway transport. This is because the result of spatial and temporal optimization, and consequently, the forecast values of transport system parameters depend on the correctness and detail of the description of the specifics and technology of a particular transportation process. A multitude of specific constraints and requirements related to transportation safety and operating technology must be monitored in transportation management in these modes of transportation. On the other hand, the management process is accompanied by changes in the spatio-temporal state of the transportation system. These features of transportation systems require, in our opinion, the use of specific graphs such as, for example, line graphs (edge graphs), two-vertex graphs with connected bijective vertices, and two-vertex graphs with separated bijective vertices and edges.
The systematic review allowed us to identify both missing areas and prospects for research on the use of spatio-temporal optimization of transport systems. Such research should be focused on the development of deep learning algorithms of graph neural networks for predicting the parameters of transportation systems by determining the optimal sequences of changes in their state.
The improvement of deep learning methods for graph neural networks is a promising area of research. We highlight the high potential of methods for dynamic optimization of spatio-temporal graphs and the use of optimization results to train graph neural networks for predicting the state of transportation systems. The results of experiments on highly detailed simulation models can be used for training graph neural networks. These approaches, in our opinion, will expand the adaptability of the use of graph neural networks for transportation system state prediction. The most promising types of transport for the application of spatio-temporal optimization methods are railway, air, and sea transport systems.
The main limitations of our study are as follows:
- Only the Scopus database was used for analysis.
- The filter [Article title, Abstract, Keywords] was applied as a search criterion.
- Only specific keyword combinations (“spatiotemporal”, “spatio-temporal”, “transport systems”) were used, which limited the depth of analysis and provided only an initial understanding of the use of spatio-temporal graphs in transportation.
- Open-source software with functional limitations was used for bibliometric analysis.
These limitations prevented a more detailed analysis and investigation of the specific problems associated with the use of spatio-temporal graphs in transportation systems. The authors intend to eliminate these limitations in future studies. The directions of our future research, considering the study’s limitations, include the following:
- Utilizing additional databases for searching scientific publications, such as Web of Science.
- Enhancing the methodology for analyzing publications by incorporating more complex and statistically oriented text analysis methods (e.g., topic modeling, word embeddings, etc.).
- Applying additional search filters for articles and exploring alternative keywords and their combinations. The results of this study indicate that relevant keywords may include “optimization”, “dynamic optimization”, “hybrid methods”, “spatio-temporal graph neural networks”, “combined model” or “hybrid model”, “deep learning”, and “hybrid neural network”.
- Implementing specialized software tools to support deeper analysis and provide a more reliable statistical foundation for research.
Author Contributions
Conceptualization, A.R. and N.O.; methodology, A.R., N.O. and P.M.; software, N.O. and P.M.; validation, N.O., A.R. and P.M.; formal analysis, N.O. and P.M.; investigation, N.O. and P.M.; resources, A.R.; data curation, N.O. and P.M.; writing—original draft preparation, N.O. and P.M.; writing—review and editing, A.R.; visualization, N.O. and P.M.; supervision, A.R.; project administration, A.R.; funding acquisition, N.O. and A.R. All authors have read and agreed to the published version of the manuscript.
Funding
The work was carried out with the financial support of the Russian Science Foundation No. 23-11-00164, https://rscf.ru/project/23-11-00164/ (accessed on 20 February 2024).
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Rakhmangulov, A.N.; Kornilov, S.N.; Kolga, A.D. Timeliness of Freight Traffic in Transport Technological Systems. Vestn. Nosov Magnitogorsk State Tech. Univ. 2014, 45, 115–121. [Google Scholar]
- Rakhmangulov, A.; Sładkowski, A.; Osintsev, N. Design of an ITS for industrial enterprises. In Intelligent Transportation Systems—Problems and Perspectives; Sładkowski, A., Pamuła, W., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 161–215. ISBN 978-3-319-19149-2. [Google Scholar]
- Laiton-Bonadiez, C.; Branch-Bedoya, J.W.; Zapata-Cortes, J.; Paipa-Sanabria, E.; Arango-Serna, M. Industry 4.0 technologies applied to the rail transportation industry: A systematic review. Sensors 2022, 22, 2491. [Google Scholar] [CrossRef] [PubMed]
- Kljaić, Z.; Pavković, D.; Cipek, M.; Trstenjak, M.; Mlinarić, T.J.; Nikšić, M. An overview of current challenges and emerging technologies to facilitate increased energy efficiency, safety, and sustainability of railway transport. Future Internet 2023, 15, 347. [Google Scholar] [CrossRef]
- Jin, G.; Liang, Y.; Fang, Y.; Shao, Z.; Huang, J.; Zhang, J.; Zheng, Y. Spatio-Temporal Graph Neural Networks for Predictive Learning in Urban Computing: A Survey; Institute of Electrical and Electronics Engineers: New York, NY, USA, 2023. [Google Scholar]
- Anda, C.; Erath, A.; Fourie, P.J. Transport modelling in the age of big data. Int. J. Urban Sci. 2017, 21, 19–42. [Google Scholar] [CrossRef]
- van Nes, R.; de Jong, G. Transport models. In Standard Transport Appraisal Methods; Elsevier: Amsterdam, The Netherlands, 2020; pp. 101–128. ISBN 9780128208212. [Google Scholar]
- Jain, S.K.; Singh, V.P. Systems analysis techniques. In Water Resources Systems Planning and Management; Elsevier: Amsterdam, The Netherlands, 2003; pp. 279–350. ISBN 9780444514295. [Google Scholar]
- Terentyev, A.; Marusin, A.; Evtyukov, S.; Marusin, A.; Shevtsova, A.; Zelenov, V. Analytical model for information flow management in intelligent transport systems. Mathematics 2023, 11, 3371. [Google Scholar] [CrossRef]
- Ali, M. Discrete choice models and artificial intelligence techniques for predicting the determinants of transport mode choice—A systematic review. Comput. Mater. Contin. 2024, 81, 2161–2194. [Google Scholar] [CrossRef]
- Pouryousef, H.; Lautala, P.; White, T. Railroad capacity tools and methodologies in the U.S. and Europe. J. Mod. Transp. 2015, 23, 30–42. [Google Scholar] [CrossRef]
- Mancera, A.; Bruckman, D.; Weidmann, U. Single wagonload production schemes improvements using GüterSim (Agent-based simulation tool). Transp. Res. Procedia 2015, 10, 615–624. [Google Scholar] [CrossRef]
- Bueno-Ferrer, Á.; de Pablo Valenciano, J.; de Burgos Jiménez, J. Unveiling the potential of metaheuristics in transportation: A path towards efficiency, optimization, and intelligent management. Infrastructures 2025, 10, 4. [Google Scholar] [CrossRef]
- Colombaroni, C.; Fusco, G.; Isaenko, N. Meta-heuristic aggregate calibration of transport models exploiting data collected in mobility. Case Stud. Transp. Policy 2023, 13, 101039. [Google Scholar] [CrossRef]
- Dou, Z.; Guo, D. DPSTCN: Dynamic Pattern-Aware Spatio-Temporal Convolutional Networks for Traffic Flow Forecasting. IJGI 2025, 14, 10. [Google Scholar] [CrossRef]
- Rakhmangulov, A.; Sładkowski, A.; Osintsev, N.; Mishkurov, P.; Muravev, D. Dynamic Optimization of Railcar Traffic Volumes at Railway Nodes. In Rail Transport—Systems Approach; Sładkowski, A., Ed.; Springer International Publishing: Cham, Switzerland, 2017; pp. 405–456. ISBN 978-3-319-51501-4. [Google Scholar]
- Cheramangalath, U.; Nasre, R.; Srikant, Y.N. Distributed Graph Analytics; Springer International Publishing: Cham, Switzerland, 2020; ISBN 978-3-030-41885-4. [Google Scholar]
- Mahmudy, W.F.; Widodo, A.W.; Haikal, A.H. Challenges and opportunities for applying meta-heuristic methods in vehicle routing problems: A review. Eng. Proc. 2024, 63, 12. [Google Scholar] [CrossRef]
- Murrar, S.; Alhaj, F.M.; Qutqut, M. Machine learning algorithms for transportation mode pprediction: A comparative analysis. Informatica 2024, 48, 6. [Google Scholar] [CrossRef]
- Zhao, S.; Xing, S.; Mao, G. An attention and wavelet based spatial-temporal graph neural network for traffic flow and speed prediction. Mathematics 2022, 10, 3507. [Google Scholar] [CrossRef]
- Cui, J.-X.; Yao, J.; Zhao, B.-Y. Review on short-term traffic flow prediction methods based on deep learning. J. Traffic Transp. Eng. 2024, 24, 50–64. [Google Scholar] [CrossRef]
- Sun, X.; Yu, H.; Solvang, W.D.; Wang, Y.; Wang, K. The application of Industry 4.0 technologies in sustainable logistics: A systematic literature review (2012-2020) to explore future research opportunities. Environ. Sci. Pollut. Res. Int. 2022, 29, 9560–9591. [Google Scholar] [CrossRef] [PubMed]
- VOSviewer. Available online: https://www.vosviewer.com/ (accessed on 20 February 2025).
- PRISMA. Available online: https://www.prisma.io/ (accessed on 8 December 2024).
- Saeedmanesh, M.; Geroliminis, N. Clustering of heterogeneous networks with directional flows based on “Snake” similarities. Transp. Res. Part B Methodol. 2016, 91, 250–269. [Google Scholar] [CrossRef]
- Zhou, X. Understanding spatiotemporal patterns of biking behavior by analyzing massive bike sharing data in Chicago. PLoS ONE 2015, 10, e0137922. [Google Scholar] [CrossRef]
- Yang, Y.; Heppenstall, A.; Turner, A.; Comber, A. A spatiotemporal and graph-based analysis of dockless bike sharing patterns to understand urban flows over the last mile. Comput. Environ. Urban Syst. 2019, 77, 101361. [Google Scholar] [CrossRef]
- Zhang, C.; Yu, J.J.Q.; Liu, Y. Spatial-Temporal Graph Attention Networks: A Deep Learning Approach for Traffic Forecasting. IEEE Access 2019, 7, 166246–166256. [Google Scholar] [CrossRef]
- Jin, G.; Cui, Y.; Zeng, L.; Tang, H.; Feng, Y.; Huang, J. Urban ride-hailing demand prediction with multiple spatio-temporal information fusion network. Transp. Res. Part C Emerg. Technol. 2020, 117, 102665. [Google Scholar] [CrossRef]
- Rathore, M.M.; Attique Shah, S.; Awad, A.; Shukla, D.; Vimal, S.; Paul, A. A cyber-physical system and graph-based approach for transportation management in smart cities. Sustainability 2021, 13, 7606. [Google Scholar] [CrossRef]
- Qin, K.; Xu, Y.; Kang, C.; Kwan, M.-P. A graph convolutional network model for evaluating potential congestion spots based on local urban built environments. Trans. GIS 2020, 24, 1382–1401. [Google Scholar] [CrossRef]
- Kyriakou, K.; Lakakis, K.; Savvaidis, P.; Basbas, S. Analysis of spatiotemporal data to predict traffic conditions aiming at a smart navigation system for sustainable urban mobility. Arch. Transp. 2019, 52, 27–46. [Google Scholar] [CrossRef]
- Furno, A.; Faouzi, N.-E.E.; Sharma, R.; Zimeo, E. Graph-based ahead monitoring of vulnerabilities in large dynamic transportation networks. PLoS ONE 2021, 16, e0248764. [Google Scholar] [CrossRef]
- Zhao, P.; Liu, X.; Shen, J.; Chen, M. A network distance and graph-partitioning-based clustering method for improving the accuracy of urban hotspot detection. Geocarto Int. 2019, 34, 293–315. [Google Scholar] [CrossRef]
- Myrovali, G.; Karakasidis, T.; Charakopoulos, A.; Tzenos, P.; Morfoulaki, M.; Aifadopoulou, G. Exploiting the knowledge of dynamics, correlations and causalities in the performance of different road paths for enhancing urban transport management. In Decision Support Systems IX: Main Developments and Future Trends; Freitas, P.S.A., Dargam, F., Moreno, J.M., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 28–40. ISBN 978-3-030-18818-4. [Google Scholar]
- Tygesen, M.N.; Pereira, F.C.; Rodrigues, F. Unboxing the graph: Towards interpretable graph neural networks for transport prediction through neural relational inference. Transp. Res. Part C Emerg. Technol. 2023, 146, 103946. [Google Scholar] [CrossRef]
- Tang, H.; Wu, Y.; Guo, Z. Graph multi-attention network-based taxi demand prediction. In 2022 4th International Conference on Data-Driven Optimization of Complex Systems (DOCS), Proceedings of the 2022 4th International Conference on Data-Driven Optimization of Complex Systems (DOCS), Chengdu, China, 28–30 October 2022; Institute of Electrical and Electronics Engineers: New York, NY, USA, 2022; pp. 1–6. ISBN 978-1-6654-5982-2. [Google Scholar]
- Lyu, C.; Wu, X.; Liu, Y.; Liu, Z. A partial-fréchet-distance-based framework for bus route identification. IEEE Trans. Intell. Transp. Syst. 2022, 23, 9275–9280. [Google Scholar] [CrossRef]
- Lee, K.; Park, J.S.; Goh, S.; Choi, M. Accessibility measurement in transportation networks and application to the Seoul bus system. Geogr. Anal. 2019, 51, 339–353. [Google Scholar] [CrossRef]
- Hou, M.; Xia, F.; Chen, X.; Saikrishna, V.; Chen, H. Adaptive spatio-temporal graph learning for bus station profiling. ACM Trans. Spat. Algorithms Syst. 2024, 10, 25. [Google Scholar] [CrossRef]
- Xiao, S.; Shi, Q.; Shao, L.; Du, B.; Wang, Y.; Shen, Q.; Zeng, W. MetroBUX: A Topology-Based Visual Analytics for Bus Operational Uncertainty EXploration. IEEE Trans. Intell. Transp. Syst. 2024, 25, 5525–5538. [Google Scholar] [CrossRef]
- Peng, J.; Zhang, G.; Wang, T.; Wang, P.; Zhang, T. A trajectory-driven multi-layer spatiotemporal graph neural network for predicting short-term urban traffic state. J. Geo-Inf. Sci. 2024, 26, 2300–2315. [Google Scholar] [CrossRef]
- Li, W.; Liu, C.; Wang, T.; Ji, Y. An innovative supervised learning structure for trajectory reconstruction of sparse LPR data. Transportation 2024, 51, 73–97. [Google Scholar] [CrossRef]
- Tang, J.; Zeng, J. Spatiotemporal gated graph attention network for urban traffic flow prediction based on license plate recognition data. Comput. Aided Civil Infrastruct. Eng. 2022, 37, 3–23. [Google Scholar] [CrossRef]
- Chen, Y.; He, Z. Vehicle identity recovery for automatic number plate recognition data via heterogeneous network embedding. Sustainability 2020, 12, 3074. [Google Scholar] [CrossRef]
- Zhao, X.; Zhang, M. Enhancing predictive models for on-street parking occupancy: Integrating adaptive GCN and GRU with household categories and POI factors. Mathematics 2024, 12, 2823. [Google Scholar] [CrossRef]
- Chen, T.; Sun, C. An optimization design of hybrid parking lots in an automated environment. Sustainability 2023, 15, 15475. [Google Scholar] [CrossRef]
- Ma, W.; Pi, X.; Qian, S. Estimating multi-class dynamic origin-destination demand through a forward-backward algorithm on computational graphs. Transp. Res. Part C Emerg. Technol. 2020, 119, 102747. [Google Scholar] [CrossRef]
- Boulmakoul, A.; Karim, L.; Laarabi, M.H.; Sacile, R.; Garbolino, E. MongoDB-hadoop distributed and scalable framework for spatio-temporal hazardous materials data warehousing. In The 7th International Congress on Environmental Modelling and Software, Proceedings of the 7th International Congress on Environmental Modeling and Software (iEMSs), San Diego, CA, USA, 15–19 June 2014; iEMSs: San Diego, CA, USA, 2014; pp. 2255–2262. [Google Scholar]
- Mimeur, C.; Thévenin, T. Diachronic analysis of the growth of the French railway network between 1860 and 1930: Connectionist expansion and hierarchical selection? Flux 2021, 122, 69–87. [Google Scholar] [CrossRef]
- Guo, Y.; Zhu, Q.; Ding, Y.; Li, Y.; Wu, H.; He, Y.; Li, Z.; Li, H.; Zhang, L.; Zhao, Y.; et al. Efficient distributed association management method of data, model, and knowledge for digital twin railway. Int. J. Digit. Earth 2024, 17, 2340089. [Google Scholar] [CrossRef]
- Li, H.; Zhu, Q.; Zhang, L.; Ding, Y.; Guo, Y.; Wu, H.; Wang, Q.; Zhou, R.; Liu, M.; Zhou, Y. Integrated representation of geospatial data, model, and knowledge for digital twin railway. Int. J. Digit. Earth 2022, 15, 1657–1675. [Google Scholar] [CrossRef]
- Wang, C. Identification of inter-urban container transport hubs and their spatial characteristics: A case study of railway transportation in China. Acta Geogr. Sin. 2010, 25, 1275–1286. [Google Scholar]
- Zhang, Q.; Ma, Z.; Zhang, P.; Jenelius, E. Mobility knowledge graph: Review and its application in public transport. Transportation 2023, 40, 1–27. [Google Scholar] [CrossRef]
- Heglund, J.S.; Taleongpong, P.; Hu, S.; Tran, H.T. Railway delay prediction with spatial-temporal graph convolutional networks. In 2020 IEEE 23rd International Conference on Intelligent Transportation Systems (ITSC), Proceedings of the 2020 IEEE 23rd International Conference on Intelligent Transportation Systems (ITSC), Rhodes, Greece, 20–23 September 2020; Institute of Electrical and Electronics Engineers: New York, NY, USA, 2020; pp. 1–6. ISBN 978-1-7281-4149-7. [Google Scholar]
- Zou, L.; Wang, Z.; Guo, R. Real-time prediction of transit origin–destination flows during underground incidents. Transp. Res. Part C Emerg. Technol. 2024, 163, 104622. [Google Scholar] [CrossRef]
- Wang, Q.; He, R.; Zhu, C.; Rao, H. Short-time passenger flow prediction of new urban rail transit based on graph convolutional neural network. IAENG Int. J. Comput. Sci. 2024, 51, 1612–1626. [Google Scholar]
- Fu, J.; Zhong, L.; Li, C.; Li, H.; Kong, C.; Shao, J. SPSTN: Sequential Precoding Spatial-Temporal Networks for Railway Delay Prediction. In Web and Big Data; Li, B., Yue, L., Tao, C., Han, X., Calvanese, D., Amagasa, T., Eds.; Springer Nature: Cham, Switzerland, 2023; pp. 451–458. ISBN 978-3-031-25157-3. [Google Scholar]
- Rahmawan Destyanto, A.; Huang, Y.; Verbraeck, A. Examining the spatiotemporal changing pattern of freight maritime transport networks in Indonesia during COVID-19 outbreaks. In 4th Asia Pacific Conference on Research in Industrial and Systems Engineering 2021, Proceedings of the APCORISE 2021: 4th Asia Pacific Conference on Research in Industrial and Systems Engineering 2021, Depok Indonesia, 25 May 2021; Ardi, R., Moeis, A.O., Eds.; ACM: New York, NY, USA, 2021; pp. 590–597. ISBN 9781450390385. [Google Scholar]
- Dong, W.; Zhang, L.; Jin, Z.; Sun, W.; Gao, J. Prediction of the waterborne navigation density based on the multi-feature spatio-temporal graph convolution network. Chin. J. Internet Things 2020, 4, 78–85. [Google Scholar] [CrossRef]
- Li, L.; Pan, M.; Liu, Z.; Sun, H.; Zhang, R. Semi-dynamic spatial–temporal graph neural network for traffic state prediction in waterways. Ocean Eng. 2024, 293, 116685. [Google Scholar] [CrossRef]
- Bakdi, A.; Glad, I.K.; Vanem, E. Testbed scenario design exploiting traffic big data for autonomous ship trials under multiple conflicts with collision/grounding risks and spatiooral dependencies. IEEE Trans. Intell. Transp. Syst. 2021, 22, 7914–7930. [Google Scholar] [CrossRef]
- Wang, J.-E.; Mo, H.-H. Complex evolution process of China’s air transport network. J. Transp. Syst. Eng. Inf. Technol. 2014, 14, 71–80. [Google Scholar]
- Wan, J.; Zhang, H.; Zhang, Q.; Li, M.Z.; Xu, Y. Deep learning framework for forecasting en route airspace emissions considering temporal-spatial correlation. Sci. Total Environ. 2023, 905, 166986. [Google Scholar] [CrossRef]
- Lehner, S.; Kölker, K.; Lütjens, K. Evaluating temporal integration of European air transport. In ICAS 2014, Proceedings of the 29th Congress of the International Council of the Aeronautical Sciences St. Peterburg, Russia 7–12 September 2014; CD-ROM Proceedings; International Council of the Aeronautical Sciences: Bonn, Germany, 2014; ISBN 3932182804. [Google Scholar]
- Sun, M.; Tian, Y.; Wang, X.; Huang, X.; Li, Q.; Li, Z.; Li, J. Transport causality knowledge-guided GCN for propagated delay prediction in airport delay propagation networks. Expert Syst. Appl. 2024, 240, 122426. [Google Scholar] [CrossRef]
- Liang, Y.; Huang, G.; Zhao, Z. Bike sharing demand prediction based on knowledge sharing across modes: A graph-based deep learning approach. In 2022 IEEE 25th International Conference on Intelligent Transportation Systems (ITSC), Proceedings of the 2022 IEEE 25th International Conference on Intelligent Transportation Systems (ITSC), Macau, China, 8–12 October 2022; IEEE: New York, NY, USA, 2022; pp. 857–862. ISBN 978-1-6654-6880-0. [Google Scholar]
- Yang, X.; He, S.; Shin, K.G.; Tabatabaie, M.; Dai, J. Cross-modality and equity-aware graph pooling fusion: A bike mobility prediction study. IEEE Trans. Big Data 2024, 11, 286–302. [Google Scholar] [CrossRef]
- Liang, Y.; Huang, G.; Zhao, Z. Cross-mode knowledge adaptation for bike sharing demand prediction using domain-adversarial graph neural networks. IEEE Trans. Intell. Transp. Syst. 2024, 25, 3642–3653. [Google Scholar] [CrossRef]
- Xu, X.; Wang, J.; Poslad, S.; Rui, X.; Zhang, G.; Fan, Y. Exploring intra-urban human mobility and daily activity patterns from the lens of dockless bike-sharing: A case study of Beijing, China. Int. J. Appl. Earth Obs. Geoinf. 2023, 122, 103442. [Google Scholar] [CrossRef]
- Kim, T.S.; Lee, W.K.; Sohn, S.Y. Graph convolutional network approach applied to predict hourly bike-sharing demands considering spatial, temporal, and global effects. PLoS ONE 2019, 14, e0220782. [Google Scholar] [CrossRef]
- Qin, T.; Liu, T.; Wu, H.; Tong, W.; Zhao, S. RESGCN: RESidual Graph Convolutional Network based free dock prediction in bike sharing system. In 2020 21st IEEE International Conference on Mobile Data Management (MDM), Proceedings of the 2020 21st IEEE International Conference on Mobile Data Management (MDM), Versailles, France, 30 Jun–3 July 2020; IEEE: New York, NY, USA, 2020; pp. 210–217. ISBN 978-1-7281-4663-8. [Google Scholar]
- Song, J.; Zhang, L.; Qin, Z.; Ramli, M.A. Spatiotemporal evolving patterns of bike-share mobility networks and their associations with land-use conditions before and after the COVID-19 outbreak. Physica A 2022, 592, 126819. [Google Scholar] [CrossRef] [PubMed]
- Kubaľák, S.; Kalašová, A.; Hájnik, A. The bike-sharing system in slovakia and the impact of COVID-19 on this shared mobility service in a selected city. Sustainability 2021, 13, 6544. [Google Scholar] [CrossRef]
- Yang, Y.; Heppenstall, A.; Turner, A.; Comber, A. Using graph structural information about flows to enhance short-term demand prediction in bike-sharing systems. Comput. Environ. Urban Syst. 2020, 83, 101521. [Google Scholar] [CrossRef]
- Wang, Y.-J.; Kuo, Y.-H.; Huang, G.Q.; Gu, W.; Hu, Y. Dynamic demand-driven bike station clustering. Transp. Res. Part E Logist. Transp. Rev. 2022, 160, 102656. [Google Scholar] [CrossRef]
- Tian, Z.; Zhou, J.; Tian, L.; Wang, D.Z. Dynamic spatio-temporal interactive clustering strategy for free-floating bike-sharing. Transp. Res. Part B Methodol. 2024, 179, 102872. [Google Scholar] [CrossRef]
- Kopsidas, A.; Kepaptsoglou, K. Identification of critical stations in a Metro System: A substitute complex network analysis. Phys. A Stat. Mech. Its Appl. 2022, 596, 127123. [Google Scholar] [CrossRef]
- Du, Y.; Jiang, R.; Deng, J.; Li, Y.; Xie, Y.; Wang, Z.; Zhou, Y.; Song, X.; Shang, J.S. MTMGNN: Multi-time multi-graph neural network for metro passenger flow prediction. GeoInformatica 2023, 27, 77–105. [Google Scholar] [CrossRef]
- Chang, X.; Wu, J.; Yu, J.; Liu, T.; Yan, X.; Lee, D.-H. Addressing COVID-induced changes in spatiotemporal travel mobility and community structure utilizing trip data: An innovative graph-based deep learning approach. Transp. Res. Part A Policy Pract. 2024, 180, 103973. [Google Scholar] [CrossRef]
- Mahajan, S.; Tang, Y.-S.; Wu, D.-Y.; Tsai, T.-C.; Chen, L.-J. CAR: The Clean Air Routing algorithm for path navigation with minimal PM2.5 exposure on the move. IEEE Access 2019, 7, 147373–147382. [Google Scholar] [CrossRef]
- Rodrigues, D.O.; Fernandes, J.T.; Curado, M.; Villas, L.A. Hybrid context-aware multimodal routing. In 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; IEEE: New York, NY, USA, 2018; pp. 2250–2255. ISBN 978-1-7281-0321-1. [Google Scholar]
- Liu, H.; Han, J.; Fu, Y.; Zhou, J.; Lu, X.; Xiong, H. Multi-modal transportation recommendation with unified route representation learning. Proc. VLDB Endow. 2020, 14, 342–350. [Google Scholar] [CrossRef]
- Liu, H.; Han, J.; Fu, Y.; Li, Y.; Chen, K.; Xiong, H. Unified route representation learning for multi-modal transportation recommendation with spatiotemporal pre-training. VLDB J. 2023, 32, 325–342. [Google Scholar] [CrossRef]
- Li, C.; Liu, W. Multimodal transport demand forecasting via federated learning. IEEE Trans. Intell. Transp. Syst. 2024, 25, 4009–4020. [Google Scholar] [CrossRef]
- Li, C.; Liu, W.; Yang, H. Simultaneous multimodal demand imputation and forecasting via graph-guided generative network. In Proceedings of the 27th International Conference of Hong Kong Society for Transportation Studies: Transport and Equity, HKSTS 2023, Hong Kong, China, 12 November–12 December 2023; pp. 509–517. [Google Scholar]
- Shao, Y.; Ma, J.; Zavala, V.M. A spatial superstructure approach to the optimal design of modular processes and supply chains. Comput. Chem. Eng. 2023, 170, 108102. [Google Scholar] [CrossRef]
- Fang, K.; Fan, J.; Yu, B. A trip-based network travel risk: Definition and prediction. Ann. Oper. Res. 2022, 343, 1069–1094. [Google Scholar] [CrossRef]
- Tominac, P.A.; Zhang, W.; Zavala, V.M. Spatio-temporal economic properties of multi-product supply chains. Comput. Chem. Eng. 2022, 159, 107666. [Google Scholar] [CrossRef]
- Feng, S.; Wei, S.; Zhang, J.; Li, Y.; Ke, J.; Chen, G.; Zheng, Y.; Yang, H. A macro–micro spatio-temporal neural network for traffic prediction. Transp. Res. Part C Emerg. Technol. 2023, 156, 104331. [Google Scholar] [CrossRef]
- Li, G.; Wang, J.; Zhao, Z.; Chen, Y.; Tang, L.; Li, Q. Advancing complex urban traffic forecasting: A fully attentional spatial-temporal network enhanced by graph representation. Int. J. Appl. Earth Obs. Geoinf. 2024, 134, 104237. [Google Scholar] [CrossRef]
- Prabowo, A.; Shao, W.; Xue, H.; Koniusz, P.; Salim, F.D. Because every sensor is unique, so is every pair: Handling dynamicity in traffic forecasting. In IoTDI ‘23: International Conference on Internet-of-Things Design and Implementation, Proceedings of the 8th ACM/IEEE Conference on Internet of Things Design and Implementation, San Antonio TX USA, 9–12 May 2023; ACM: New York, NY, USA, 2023; pp. 93–104. ISBN 9798400700378. [Google Scholar]
- Oakley, J.; Conlan, C.; Demirci, G.V.; Sfyridis, A.; Ferhatosmanoglu, H. Foresight plus: Serverless spatio-temporal traffic forecasting. GeoInformatica 2024, 28, 649–677. [Google Scholar] [CrossRef]
- Sun, L.; Dai, W.; Muhammad, G. Multi-level graph memory network cluster convolutional recurrent network for traffic forecasting. Inf. Fusion 2024, 105, 102214. [Google Scholar] [CrossRef]
- Yin, X.; Wu, G.; Wei, J.; Shen, Y.; Qi, H.; Yin, B. Multi-stage attention spatial-temporal graph networks for traffic prediction. Neurocomputing 2021, 428, 42–53. [Google Scholar] [CrossRef]
- Shi, Z.; Chen, Y.; Liu, J.; Fan, D.; Liang, C. Physics-informed spatiotemporal learning framework for urban traffic state estimation. J. Transp. Eng. Part A Syst. 2023, 149, 04023056. [Google Scholar] [CrossRef]
- Shirakami, R.; Kitahara, T.; Takeuchi, K.; Kashima, H. Queue length prediction using traffic-theory-based deep learning. Trans. Jpn. Soc. Artif. Intell. 2024, 39, 1–12. [Google Scholar] [CrossRef]
- Wang, Q.; He, R.; Zhu, C.; Rao, H. Short-time traffic flow prediction based on high-order graph convolutional networks. Int. J. Comput. Sci. 2024, 51, 1612–1626. [Google Scholar]
- Rao, K.V.; Selvakumar, R.K. Spatiotemporal graph neural networks for traffic forecasting: A comparative analysis. In Advanced Engineering Optimization Through Intelligent Techniques; Venkata Rao, R., Taler, J., Eds.; Springer Nature: Singapore, 2024; pp. 451–463. ISBN 978-981-97-4653-8. [Google Scholar]
- Ku, Y.; Wang, Y.; Liu, Q.; Yang, Y.; Peng, L. TEDGCN: Asymmetric spatiotemporal GNN for heterogeneous traffic prediction. In 2023 IEEE 26th International Conference on Intelligent Transportation Systems (ITSC), Proceedings of the 2023 IEEE 26th International Conference on Intelligent Transportation Systems (ITSC), Bilbao, Spain, 24–28 September 2023; IEEE: New York, NY, USA, 2023; pp. 1052–1057. ISBN 979-8-3503-9946-2. [Google Scholar]
- Wang, B.; Zhang, Y.; Shi, J.; Wang, P.; Wang, X.; Bai, L.; Wang, Y. Knowledge expansion and consolidation for continual traffic prediction with expanding graphs. IEEE Trans. Intell. Transp. Syst. 2023, 24, 7190–7201. [Google Scholar] [CrossRef]
- Cheng, S.; Xie, B.; Bie, Y.; Zhang, Y.; Zhang, S. Measure dynamic individual spatial-temporal accessibility by public transit: Integrating time-table and passenger departure time. J. Transp. Geogr. 2018, 66, 235–247. [Google Scholar] [CrossRef]
- Zhang, C.; Zhou, L.; Xiao, X.; Xu, D. A missing traffic data imputation method based on a diffusion convolutional neural network–generative adversarial network. Sensors 2023, 23, 9601. [Google Scholar] [CrossRef] [PubMed]
- Tang, J.; Song, Y.; Miller, H.J.; Zhou, X. Estimating the most likely space–time paths, dwell times and path uncertainties from vehicle trajectory data: A time geographic method. Transp. Res. Part C Emerg. Technol. 2016, 66, 176–194. [Google Scholar] [CrossRef]
- Li, X.; Wang, H.; Quan, W.; Wang, J.; An, P.; Sun, P.; Sui, Y. Spatial-temporal graph-enabled convolutional neural network-based approach for traffic networkwide travel time. J. Transp. Eng. Part A Syst. 2022, 148, 04022016. [Google Scholar] [CrossRef]
- Zhao, C.; Song, A.; Du, Y.; Yang, B. TrajGAT: A map-embedded graph attention network for real-time vehicle trajectory imputation of roadside perception. Transp. Res. Part C Emerg. Technol. 2022, 142, 103787. [Google Scholar] [CrossRef]
- Soltani Naveh, K.; Kim, J. Urban trajectory analytics: Day-of-week movement pattern mining using tensor factorization. IEEE Trans. Intell. Transp. Syst. 2019, 20, 2540–2549. [Google Scholar] [CrossRef]
- Zhang, L.; Guo, Q.; Li, D.; Pan, J.; Wei, C.; Lin, J. Forecasting traffic speed using spatio-temporal hybrid dilated graph convolutional network. Proc. Inst. Civil Eng. Transp. 2024, 177, 80–89. [Google Scholar] [CrossRef]
- Yao, S.; Zhang, H.; Wang, C.; Zeng, D.; Ye, M. GSTGAT: Gated spatiotemporal graph attention network for traffic demand forecasting. IET Intell. Transp. Syst. 2024, 18, 258–268. [Google Scholar] [CrossRef]
- Huang, X.; Mao, Z. Prediction of passenger demand for online car-hailing based on spatio-temporal multigraph convolution network. J. Geo-Inf. Sci. 2023, 25, 311–323. [Google Scholar] [CrossRef]
- Jiang, X.; Sengupta, R.; Demmel, J.; Williams, S. Large scale multi-GPU based parallel traffic simulation for accelerated traffic assignment and propagation. Transp. Res. Part C Emerg. Technol. 2024, 169, 104873. [Google Scholar] [CrossRef]
- Jin, G.; Sha, H.; Zhang, J.; Huang, J. Travel time estimation method based on dual graph convolutional networks via joint modeling of road segments and intersections. J. Geo-Inf. Sci. 2023, 25, 1500–1513. [Google Scholar] [CrossRef]
- Wei, S.; Shen, S.; Liu, D.; Song, Y.; Gao, R.; Wang, C. Coordinate attention enhanced adaptive spatiotemporal convolutional networks for traffic flow forecasting. IEEE Access 2024, 12, 140611–140627. [Google Scholar] [CrossRef]
- Xie, Y.; Jin, C. Evaluations of multi-step traffic flow prediction models based on graph neural networks. In 2024 6th International Conference on Communications, Information System and Computer Engineering (CISCE), Proceedings of the 2024 6th International Conference on Communications, Information System and Computer Engineering (CISCE), Guangzhou, China, 10–12 May 2024; IEEE: New York, NY, USA, 2024; pp. 1100–1104. ISBN 979-8-3503-5317-4. [Google Scholar]
- Feng, J.; Guo, G.; Wang, J.; Liu, X.; Liu, Z.; Ding, Y. EVHF-GCN: An emergency vehicle priority scheduling model based on heterogeneous feature fusion with graph convolutional networks. IEEE Access 2024, 12, 4166–4177. [Google Scholar] [CrossRef]
- Liu, L.; Wang, F.; Liu, H.; Zhu, S.; Wang, Y. HD-Net: A hybrid dynamic spatio-temporal network for traffic flow prediction. IET Intell. Transp. Syst. 2024, 18, 672–690. [Google Scholar] [CrossRef]
- Han, X.; Zhu, G.; Zhao, L.; Du, R.; Wang, Y.; Chen, Z.; Liu, Y.; He, S. Ollivier–Ricci curvature based spatio-temporal graph neural networks for traffic flow forecasting. Symmetry 2023, 15, 995. [Google Scholar] [CrossRef]
- Feng, Y.; Zhao, Y.; Zhang, X.; Batista, S.F.A.; Demiris, Y.; Angeloudis, P. Predicting spatio-temporal traffic flow: A comprehensive end-to-end approach from surveillance cameras. Transp. B Transp. Dyn. 2024, 12, 2380915. [Google Scholar] [CrossRef]
- Zhang, Q.; Tan, M.; Li, C.; Xia, H.; Chang, W.; Li, M. Spatio-temporal residual graph convolutional network for short-term traffic flow prediction. IEEE Access 2023, 11, 84187–84199. [Google Scholar] [CrossRef]
- Li, Z.; Zhou, J.; Lin, Z.; Zhou, T. Dynamic spatial aware graph transformer for spatiotemporal traffic flow forecasting. Knowl.-Based Syst. 2024, 297, 111946. [Google Scholar] [CrossRef]
- Ma, J.; Gu, J.; Zhou, Q.; Wang, Q.; Sun, M. Dynamic-static-based spatiotemporal multi-graph neural networks for passenger flow prediction. In 2020 IEEE 26th International Conference on Parallel and Distributed Systems (ICPADS), Proceedings of the 2020 IEEE 26th International Conference on Parallel and Distributed Systems (ICPADS), Hong Kong, China 2–4 December 2020; IEEE: New York, NY, USA, 2020; pp. 673–678. ISBN 978-1-7281-9074-7. [Google Scholar]
- Hu, S.; Weng, J.; Liang, Q.; Zhou, W.; Wang, P. Individual travel knowledge graph-based public transport commuter identification: A mixed data learning approach. J. Adv. Transp. 2022, 2022, 2012579. [Google Scholar] [CrossRef]
- Mützel, C.M.; Scheiner, J. Investigating spatio-temporal mobility patterns and changes in metro usage under the impact of COVID-19 using Taipei Metro smart card data. Public Transp. 2022, 14, 343–366. [Google Scholar] [CrossRef]
- Sastry, S. Coordinated conveying. In 2019 IEEE 22nd International Symposium on Real-Time Distributed Computing (ISORC), Proceedings of the 2019 IEEE 22nd International Symposium on Real-Time Distributed Computing (ISORC), Valencia, Spain, 7–9 May 2019; IEEE: New York, NY, USA, 2019; pp. 61–68. ISBN 978-1-7281-0151-4. [Google Scholar]
- Muthugama, L.; Xie, H.; Tanin, E.; Karunasekera, S. Real-time road safety optimization through network-level data management. GeoInformatica 2023, 27, 491–523. [Google Scholar] [CrossRef]
- Lee, J.; Lee, S. Separable contextual graph neural networks to identify tailgating-oriented traffic congestion. Expert Syst. Appl. 2024, 254, 124354. [Google Scholar] [CrossRef]
- Wang, H.-W.; Peng, Z.-R.; Wang, D.; Meng, Y.; Wu, T.; Sun, W.; Lu, Q.-C. Evaluation and prediction of transportation resilience under extreme weather events: A diffusion graph convolutional approach. Transp. Res. Part C Emerg. Technol. 2020, 115, 102619. [Google Scholar] [CrossRef]
- Gora, P.; Bogucki, D.; Bolum, M.L. Explainability of surrogate models for traffic signal control. In Explainable Artificial Intelligence for Intelligent Transportation Systems; Adadi, A., Bouhoute, A., Eds.; CRC Press: Boca Raton, FL, USA, 2023; pp. 135–152. ISBN 9781003324140. [Google Scholar]
- Boulmakoul, A.; Laurini, R.; Servigne, S.; Idrissi, M. First specifications of a telegeomonitoring system for the transportation of hazardous materials. Comput. Environ. Urban Syst. 1999, 23, 259–270. [Google Scholar] [CrossRef]
- Boulmakoul, A.; Bouziri, A.E. Mobile object framework and fuzzy graph modelling to boost HazMat telegeomonitoring. In Transport of Dangerous Goods; Garbolino, E., Tkiouat, M., Yankevich, N., Lachtar, D., Eds.; Springer: Dordrecht, The Netherlands, 2012; pp. 119–149. ISBN 978-94-007-2683-3. [Google Scholar]
- Zhou, F.; Luo, S.; Qie, X.; Ye, J.; Zhu, H. Graph-based equilibrium metrics for dynamic supply–demand systems with applications to ride-sourcing platforms. J. Am. Stat. Assoc. 2021, 116, 1688–1699. [Google Scholar] [CrossRef]
- Li, T.; Bian, Z.; Lei, H.; Zuo, F.; Yang, Y.-T.; Zhu, Q.; Li, Z.; Ozbay, K. Multi-level traffic-responsive tilt camera surveillance through predictive correlated online learning. Transp. Res. Part C Emerg. Technol. 2024, 167, 104804. [Google Scholar] [CrossRef]
- Rani, B.K.; Rao, M.V.; Patra, R.K.; Srinivas, K.; Madhukar, G. Vehicle type classification using graph ant colony optimizer based stack autoencoder model. Multimed. Tools Appl. 2022, 81, 42163–42182. [Google Scholar] [CrossRef]
- Chang, C.; Zhang, J.; Ge, J.; Zhang, Z.; Wei, J.; Li, L.; Wang, F.-Y. VistaScenario: Interaction scenario engineering for vehicles with intelligent systems for transport automation. IEEE Trans. Intell. Veh. 2024, 1–17. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, J.; Yang, L.; Gao, Z. Network-wide short-term inflow prediction of the multi-traffic modes system: An adaptive multi-graph convolution and attention mechanism based multitask-learning model. Transp. Res. Part C Emerg. Technol. 2024, 158, 104428. [Google Scholar] [CrossRef]
- Nikishchenkov, S. Complex of diagnostic models of reconfigurable multioperational transport processes. Transp. Res. Procedia 2022, 61, 340–346. [Google Scholar] [CrossRef]
- Pedersen, S.A.; Yang, B.; Jensen, C.S.; Møller, J. Stochastic routing with arrival windows. ACM Trans. Spat. Algorithms Syst. 2023, 9, 30. [Google Scholar] [CrossRef]
- Ganapathy, J.; García Márquez, F.P.; Ragavendra Prasad, M. Routing vehicles on highways by augmenting traffic flow network: A review on speed up techniques. In International Conference on Intelligent Emerging Methods of Artificial Intelligence & Cloud Computing; García Márquez, F.P., Ed.; Springer: Cham, Switzerland, 2022; pp. 96–105. ISBN 978-3-030-92904-6. [Google Scholar]
- Zou, G.; Lai, Z.; Wang, T.; Liu, Z.; Li, Y. MT-STNet: A novel multi-task spatiotemporal network for highway traffic flow prediction. IEEE Trans. Intell. Transp. Syst. 2024, 25, 8221–8236. [Google Scholar] [CrossRef]
- Mishkurov, P.N.; Rakhmangulov, A.N.; Friedrichson, O.V. Methodology of forming the transport network of a railway station. Herald Ural State Univ. Railw. Transp. 2021, 3, 50–64. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).