Abstract
Crowdshipping establishes a short-term connection between shippers and individual carriers, bridging the service requirements in last-mile logistics. From the perspective of a carrier operating multiple vehicles, this study considers the challenge of maximizing profits by optimizing bid strategies for delivery prices and transportation conditions in the context of bid-based crowdshipping services. We considered two types of bid strategies: a price bid that adjusts the RFQ freight charge and a multi-attribute bid that scores both price and service quality. We formulated the problem as a Markov decision process (MDP) to represent uncertain and sequential decision-making procedures. Furthermore, given the complexity of the newly proposed problem, which involves multiple vehicles, route optimizations, and multiple attributes of bids, we employed a reinforcement learning (RL) approach that learns an optimal bid strategy. Finally, numerical experiments are conducted to illustrate the superiority of the bid strategy learned by RL and to analyze the behavior of the bid strategy. A numerical analysis shows that the bid strategies learned by RL provide more rewards and lower costs than other benchmark strategies. In addition, a comparison of price-based and multi-attribute strategies reveals that the choice of appropriate strategies is situation-dependent.
1. Introduction
The importance of last-mile logistics has increased with rapid growth in e-commerce. Last-mile delivery is the last step of the distribution process, in which an item is sent out for final delivery to the customer. Well-managed last-mile delivery is essential for e-commerce, as it enhances customer satisfaction, provides a competitive edge, and improves cost efficiency. In addition, last-mile delivery is the most challenging part of the entire distribution process, incurring the highest costs and increasing customer expectations for quick and flexible delivery services.
Crowdshipping is emerging as a popular alternative to last-mile delivery. Unlike traditional systems, in which shippers directly make long-term contracts with carriers who own trucks and human resources for delivery, crowdshipping establishes a short-term connection between shippers and individual carriers through an online platform service known as a crowdshipping marketplace [1]. Large carriers in traditional systems have successfully lowered delivery costs by taking advantage of economies of scale; however, they cannot satisfy various customer needs. In the spot market, crowdshipping solves such problems by utilizing crowds of individuals that allow shippers to efficiently find an available carrier and carriers to provide quick and flexible services while lowering delivery costs [2]. There have been many crowd-delivery platforms launched in the market since the 2010s. These crowd-delivery platforms have implemented crowdsourcing services for the last-mile segment and continue to experience sustained market growth as innovative services leverage the latest digital information technologies.
Crowdshipping services generally consist of five stages [3]: (1) a shipper post-delivery request (request for quote, RFQ) on the platform, (2) crowd carriers participating in the bidding, (3) bids are evaluated and awarded through the platform, (4) carriers pick up and deliver the requests, and (5) settlement (Figure 1). Among these five stages, the bidding and awarding process based on the pricing policy is the most critical step in determining the characteristics of crowdshipping services. Pourrahmani and Jaller [4] classified crowdsourcing pricing policies into three types: (1) a flat rate payment, (2) fixed price plus additional fees, and (3) bid-based pricing. Lafkihi et al. [5] suggested maintaining a simple fixed pricing policy to attract market participation during the early stages of crowdshipping services. However, bid-based pricing policies are worth considering after achieving economies of scale, given the limitations of fixed pricing policies in reflecting diverse needs, such as distance, route, characteristics of delivered products, and delivery time. Among the various research topics related to online platform environments, where multiple crowd carriers compete in response to shippers’ delivery requirements, developing optimal bidding strategies is significantly focused.
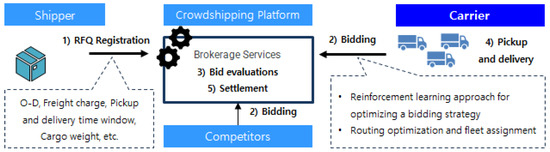
Figure 1.
Service flow of a crowdshipping platform.
Bid-based pricing involves crowd carrier bidding based on the shipper’s request conditions with platform matching to consider multiple bidding conditions. Here, carriers decide to maximize their profits by bidding with conditions superior to those of competitors and increase their chances of winning contracts. According to Lafkihi et al. [5], 83% of academic studies on pricing decisions for delivery services focus on auction mechanisms that rely on bidding and awarding strategies, including optimization [6,7] and game-theoretic approaches [8,9]. Nonetheless, despite earlier work, research on pricing methods is still in its early stages, and studies on carriers’ pricing strategies and optimal algorithms remain limited.
Notably, research has expanded traditional deterministic optimization models to probabilistic optimization models to solve the optimal bidding decision problem from the carrier’s perspective [10,11,12]. However, these studies generally target fixed truckload (TL) routes and multiperiod demands, making them less suitable for the last-mile delivery sector, a key application area for crowd delivery.
Pourrahmani and Jaller [4] conducted a comprehensive literature review of crowd delivery. Their review highlighted the need for advanced models and algorithms to facilitate connections between shippers and crowd carriers, particularly emphasizing the use of artificial intelligence techniques to address uncertain and dynamic business environments. In the context of bidding strategy development for carriers, recent research employing artificial intelligence (AI) techniques, such as reinforcement learning (RL), has been actively explored [13,14,15,16,17,18].
Kang [13] and Kang et al. [14] applied RL techniques to derive order-acceptance policies to maximize the expected revenue of a single delivery truck. However, these studies focused solely on optimal order management policies without proposing specific bidding strategies. Guo et al. [15] proposed the use of a deep Q-network (DQN) model, a representative technique of deep RL (DRL), to develop bidding strategies for auction-based logistics service platforms aimed at connecting shippers and carriers. Nonetheless, this study considered only a single vehicle and a single attribute (i.e., price) and used simple simulations to account for route changes and cost increases due to new orders, rather than optimizing transportation routes, which is critical for bidding price determination. Xiao et al. [17] demonstrated through numerical experiments that multi-attribute bidding on auction-based crowd delivery platforms is superior to single-attribute bidding or fixed-rate policies in terms of social welfare. In response to the importance of multi-attribute bidding strategies, Li et al. [18] examined the development of multi-attribute bidding strategies for carriers on crowd-delivery platforms. However, Li et al. [18] proposed a tree search-based sequential heuristic algorithm for multi-attribute bidding strategy development without considering the optimization of bidding strategies.
This study aimed to move beyond the simplistic and restrictive assumptions addressed in previous research to develop a more realistic and detailed model. To achieve this, we extend the research of Guo et al. [15] and Li et al. [18] by proposing an AI model (i.e., RL and route optimization) to optimize multi-attribute bidding strategies for carriers operating multiple vehicles. Referencing Guo et al. [15], this study integrates RL with route optimization models to establish optimal bidding strategies in dynamic environments while considering existing transportation routes. Additionally, it incorporates procedures for developing multi-attribute bidding strategies into the RL model, as demonstrated by Li et al. [18].
This study addresses a significant practical challenge for carriers operating within the increasing bid-based crowdshipping market. In this competitive environment, carriers must strategically determine their bids, balancing potential profit with the likelihood of winning contracts. The ability to satisfy service quality requirements, particularly meeting tight pickup and delivery time windows, is not merely a preference but a crucial factor directly impacting profitability due to associated penalties. Furthermore, carriers often manage multiple vehicles, requiring complex coordination and dynamic decision-making as new requests arrive sequentially and operations unfold. Traditional deterministic or simpler probabilistic models are often insufficient to capture the dynamic, uncertain, and multi-faceted nature of this problem. By developing a RL model integrated with route optimization, our research provides a sophisticated approach for carriers to learn optimal dynamic bidding strategies that account for multiple vehicles and prioritize both price and service quality, thereby offering a practical tool to enhance operational efficiency and profitability in real-world crowdshipping operations. This focus on a carrier’s dynamic operational strategy in a competitive, quality-sensitive environment highlights the immediate applicability and practical value of our research.
This study considers the problem of maximizing profits by optimizing bidding strategies for delivery prices and transportation conditions from the perspective of a carrier operating multiple vehicles on a bid-based crowdshipping platform with multiple competing companies. Specifically, the bidding strategy developed in this study, which considers multiple attributes, provides various pricing alternatives for delivery conditions on a bidding-based crowdshipping platform. This approach offers new business value and opportunities by satisfying the needs of shippers and carriers.
Given the complexity of the newly proposed problem, which involves multiple vehicles, route optimizations, and multi-attributes of bids, advanced RL techniques capable of handling large-scale problems are required. By employing RL techniques, the model introduces flexibility to account for transportation history and future uncertainties. We developed solutions based on RL and optimal control theory to overcome the limitations of the existing research (e.g., single vehicles, consideration of only a single attribute such as price, and insufficient consideration of dynamic environments).
Compared with the existing research, this study considers three innovative features: a model considering multiple vehicles, a model considering multi-attribute bidding strategies, and solving dynamic decision-making problems using AI techniques.
Our specific innovative contributions over existing research are summarized as follows:
- -
- The model accounts for a carrier operating a fleet of multiple vehicles, which is a more realistic representation than models focusing on a single vehicle.
- -
- The research models and optimizes bids that consider not just price but also service quality, such as flexibility in pickup and delivery times, allowing for more nuanced strategic decision-making.
- -
- We solve dynamic decision-making problems using AI technique such as RL and integrates it with route optimization to address the complex, uncertain, and sequential nature of carrier bidding in this dynamic environment, overcoming limitations of deterministic or simpler probabilistic models.
The remainder of this study is organized as follows. Section 2 begins with the problem description and its formulation as an MDP model. Section 3 presents the RL-based solution approach. Section 4 presents the numerical tests and shows the value of the proposed bidding strategy. Finally, Section 5 concludes the study by summarizing the key findings.
2. Problem Description
In this study, we considered a crowdshipping platform involving multiple shippers and carriers. Any shipper can register an RFQ on the platform, and each carrier participates in the bidding process by considering the state of its multiple operating vehicles. An RFQ includes information such as origin–destination (O–D) locations, time windows defining the upper and lower bounds for pickup and delivery times, cargo weight, and freight charge, which are calculated per km. As multiple shippers register RFQs on crowdshipping platforms, RFQs are registered at arbitrary time intervals.
Let and denote the desired pickup and delivery times, respectively. If the current time is t, then the pickup request period is () = (), where and are the time allowance and window for pickup at the origin, respectively. RFQ requests carriers to deliver an order within a period between (, ) = (, , where and are the time allowance and window for delivery to the destination, respectively. Here, is longer than the average travel time between pickup and delivery locations, assuming the vehicle moves at a constant speed along the Euclidean distance between the two points. We randomly generate , , , the freight charge, and cargo weights presented by the shippers in the RFQ from uniform distributions.
Upon the arrival of a new RFQ on the crowdshipping platform, carriers respond to the RFQ by participating in the bidding process. In this context, carriers must establish a bidding policy that maximizes both the chance of winning the bid and the resulting profit, considering their competitors.
The bid price is the amount the carrier is willing to pay for the RFQ. A carrier determines its bid price by adding a margin or discount to the freight charge provided in the RFQ, considering the cost of delivering freight to the destination and the probability of winning the bid [11,19]. Let p and a represent the freight charge and carrier margin or discount of the RFQ, respectively. Subsequently, the carrier’s bid price becomes . If the delivery cost exceeds the bid price, the carrier expects a negative profit. Conversely, the carrier may achieve a profit if the delivery cost is less than the bid price. The carrier should satisfy the pickup and delivery time windows, which represent the service quality level that the carrier is willing to provide. Referring to Zhang et al. [20], if the carrier fails to meet the pickup and delivery time windows, profit is penalized. Let us define as the carrier’s delivery cost for vehicle j. If the time differences between the proposed pickup and delivery times of shippers and carriers are and , respectively, the carrier’s profit becomes Equation (1), reflecting the unit penalty costs and .
In this problem, carriers should dynamically consider the operating conditions of their vehicles in an environment in which multiple RFQs arise sequentially to generate optimal bids. Therefore, a carrier’s decision-making problem is defined as a typical sequential decision-making problem. In the next section, we formulate the problem as a Markov decision process (MDP).
2.1. MDP Model: Price-Based Strategy
This section provides an MDP model that represents the decision-making process of a carrier with the notations presented in Table 1; however, we arbitrarily drop the indices for simplicity. The carrier observes the state when ith RFQ is registered on the platform. State s is composed of the cumulative odds of winning up to ith RFQ, denoted by , the most recently registered on the crowdshipping platform, and the status of multiple vehicles operated by the carrier. That is, . The component includes and that represent the desired pickup and delivery times, respectively, with an allowable time window of . Additionally, is the load amount and denotes the prices associated with the RFQ. The vehicle status reflects its remaining capacity when the ith RFQ is registered, whereas and represent the earliness or tardiness at the origin (O) and destination (d), respectively.

Table 1.
Notation summary.
Action is the margin or discount added to the freight charge provided in the ith RFQ. The delivery cost of vehicle j for ith RFQ, , is calculated by considering the unit delivery cost c (in currency per unit-km) over the travel distance. Here, the travel distance includes empty travel and the distance between the origin and destination. Let us assume a vehicle j travels a distance of for ith RFQ. Subsequently, the delivery cost becomes . The travel distance is obtained using a simulator.
We define the reward for a given state-action combination as the carrier’s profit, depending on whether the bid is successful. If the carrier wins the bid, the immediate reward is a profit, as shown in Equation (1). Conversely, if the bid is lost because of the competitor’s lower price, we consider regret as an immediate reward. The crowdshipping platform evaluates the bids with respect to the bid price under a price-based strategy. In other words, the carrier that offers the lowest bid price wins the bid.
Equation (2) represents the immediate reward for a given state and action , where is the competitor’s bid price.
We aim to determine the optimal bidding policy that maximizes the total discounted reward as shown in Equation (3).
where and are the discount rate and optimal total discounted reward, respectively, over I number of RFQs.
Finally, the state transition is a stochastic process influenced by vehicle operations and RFQs generation. For instance, the vehicle state is regularly updated in the simulator considering the travel time.
2.2. The MDP Model: Multi-Attribute Strategy
We extend the price-based strategy into a multi-attribute model by allowing the model to evaluate the bid based not only on the bid price but also on service quality (Figure 2). To accommodate the multi-attribute strategy, we modified the action and reward of the MDP model given in Section 2.1.
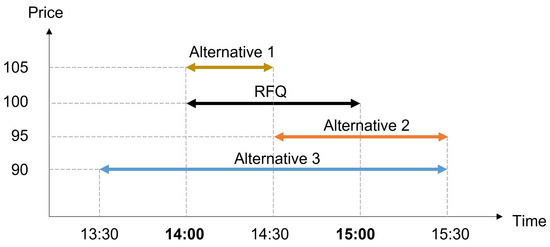
Figure 2.
Example of actions under multi-attribute strategy. When a RFQ requires parcel delivery to be completed within a specific time window and the expected price is $100, there can be various alternatives that consider different levels of service quality (i.e., earliness/tardiness) and price.
The action is tuple , where is the service quality level representing the time that deviates from the desired pickup and delivery times. For example, assume that an RFQ requires carriers to complete delivery within ( and ). Given the status of the operating vehicles, the carrier evaluates the expected tardiness when accepting the RFQ. Subsequently, the service quality level becomes .
Unlike the price-based strategy, the multi-attribute-based strategy requires a crowdshipping platform to evaluate bids based on both the bid price and service quality. We constructed an evaluation function that transforms the multi-attribute bid into a single-valued cost, and the system chooses the one with the lowest cost. Let and denote the costs to the carrier and the competitor, respectively, where and . Equation (4) represents immediate rewards.
3. Solution Approach
3.1. Deep Reinforcement Learning
The proposed MDP models are ambiguous because of the stochastic nature of trucking operations and large models that incur dimensionality problems. To address these issues, we use a model-free RL method that is reasonably scalable and learns an optimal policy with no assumptions about the system. Figure 3 illustrates a brief framework of RL, containing two elements: RL agent and the environment.
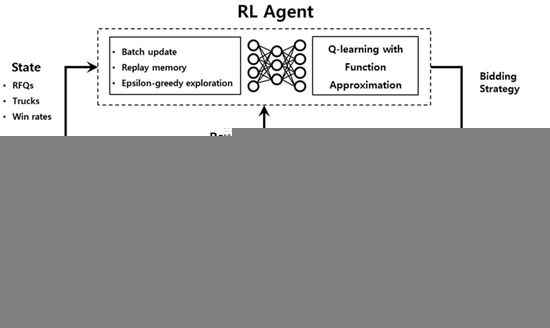
Figure 3.
RL framework.
We designed the RL agent based on DQN, which is a Q-learning-based algorithm that updates the Q-function using temporal difference (TD) errors (Equation (5)).
where is the Q-function, is the learning rate, and is the discount factor. The DQN method uses deep neural networks to approximate Q functions , where are the weights in the deep neural networks. The RL agent uses to determine the best bid strategy for a given observation of the current state s. In other words, .
The system environment receives the action and simulates state transitions, such as vehicle movements, load allocations, and bid evaluations. The environment finally returns immediate rewards after observing system transitions.
3.2. Environment Simulator
In this study, the simulator provided the necessary information for generating state transitions and reward signals using the RL algorithm. The simulator includes the following elements:
3.2.1. RFQ Generation Process
A set of RFQs was generated for each episode. Each RFQ was then assumed to arrive sequentially, with its arrival process following a Poisson distribution over a time horizon. RFQs are generated using the following information: (1) OD locations, (2) pickup and delivery request times along the time window, (3) parcel load to be delivered, and (4) base price, which considers the estimated traveling distance with some variations. The OD locations of RFQs were generated at random points within a range, and the pickup and delivery request times were generated as arbitrary points and intervals from the current time.
3.2.2. Fleet Operations
This study implemented a simulator to extend the MDP model to an RL model as a transportation management system (TMS). The TMS is responsible for optimization models that include transport route optimization for multiple vehicles owned by the carrier, vehicle assignment for new orders, route optimization, and estimation of costs and transport conditions. Specifically, the TMS solves the vehicle routing problem from the perspective of minimizing vehicle speed and fuel consumption using the greening via the energy and emissions in transportation (GEET) algorithm [21]. The GEET algorithm is an extension of the distributed arrival time control (DATC) system [21,22], which converts a combinatorial scheduling challenge involving discrete events in manufacturing into a continuous-time feedback control problem in the vector space. DATC functions as an iterative algorithm, obtaining feedback through simulations conducted on a single computer or across multiple computers in parallel. Specifically, the distributed arrival time controller for each job (in our case, delivery jobs) uses a local control law and local feedback to adjust the arrival time of a job in a queue. This eliminates the need for assumptions about job parameters, such as the number of jobs, delivery sequences, or transportation times, enabling high levels of local autonomy and decentralized control while relying on minimal global information. Consequently, this approach is effective for designing a highly autonomous transportation system with many uncertainties in delivery demands and road conditions.
The TMS is invoked in the following situations within the RL algorithm: (1) When an RFQ is generated, the expected vehicle travel distance (including the empty travel distance and OD transport distance), expected earliness/tardiness values, and remaining capacity when the received RFQ order is hypothetically assigned to each vehicle. (2) When a bid is won, reflect the corresponding RFQ order in the system and execute it.
The TMS simulator was implemented in C++ owing to algorithm speed issues and was provided as a DLL file. Within the RL algorithm, this is utilized by invoking it through wrapper functions.
3.2.3. Competitors and Bid Evaluations
The crowshipping platform evaluates and compares carriers’ bids while satisfying time windows as close as desired. The RL algorithm suggests a bidding price and/or service quality (i.e., additional delivery delay) based on its current strategy, whereas the competitor’s bidding price is randomly determined within a certain range of the base price. A carrier wins the bid over other competitors if it offers the lowest bid price and complies with the pickup and delivery periods. Given the nature of a crowdshipping platform involving multiple carriers, carriers may have the same price. In such cases, the bidding result is achieved with a 50% chance. Once the bidding process is complete and the bid is won, the simulator calculates the reward by considering the winning bid price, transportation cost, and penalties for earliness or tardiness. If the bid is lost, the difference between the submitted bid price and the competitor’s price is considered regret and is then treated as a negative reward (Equations (2) and (4)).
4. Numerical Experiments
In this section, we describe the extensive numerical tests conducted to verify the performance of the proposed RL model. First, we compare the price-based and multi-attribute strategies according to their response to RFQs. Additional tests evaluate the performance according to changes in demand characteristics, which are key components of the crowdshipping platform service.
4.1. Experiment Design
In this study, a test problem was developed by referring to the literature (Kang et al. [14], Min and Kang [16]) with additional modifications to several factors. Shippers generate and register RFQs on the platform at varying time intervals, where the time interval follows an exponential distribution with the parameter . We varied the mean interval from 5 to 60. The O-D locations of RFQs were randomly generated within a 30 km × 30 km area, and the O-D distance was at least 5 km. The time window size at the O-D locations was 30 min (i.e., = 30). The delivery load was uniformly generated between 50 and 100, and the basic freight fare was 4000/unit-km. The vehicles were assumed to travel at a constant speed of 20 km/h. Finally, the unit costs for earliness and tardiness were 0.1 and 0.2, respectively (i.e., , ).
Evaluating performance based on environmental factors requires detailed planning for numerical experiments. The effects of the proposed RL model are verified by addressing the following research questions: The first research question aims to compare how an RL agent behaves under price-based and multi-attribute strategies. In addition, we evaluated whether the RL agent could win bids against competitors. For this purpose, we conducted extensive numerical tests and measured the average reward, including revenue and cost details, and the odds of winning achieved by the RL agent. Second, we evaluated performance according to changes in demand, such as the mean inter-arrival time of RFQs. The additional research question aims to test the hypothesis that the two strategies differ when the demand rate is low or high.
Before evaluating the influence of environmental factors on performance, preliminary numerical tests were conducted to analyze the learning behavior of the RL agent. In general, if the RL agent learns appropriately in response to an uncertain environment, the reward and loss function values are expected to converge as the number of learning episodes increases. The learning behavior of the RL agent is highly sensitive to the parameters that constitute the RL model, along with the appropriateness of the MDP model. We tuned the hyperparameters of the DQN algorithm by running preliminary tests. Table 2 summarizes the resulting values.

Table 2.
Hyperparameters of DQN.
We conducted a set of preliminary tests to determine the sufficient number of episodes to train the model. Figure 4 illustrates the trajectory of MSE loss and reward, which indicates that the model converges sufficiently when the number of episodes exceeds 15,000. Therefore, we trained the RL model with 15,000 episodes for further analysis.
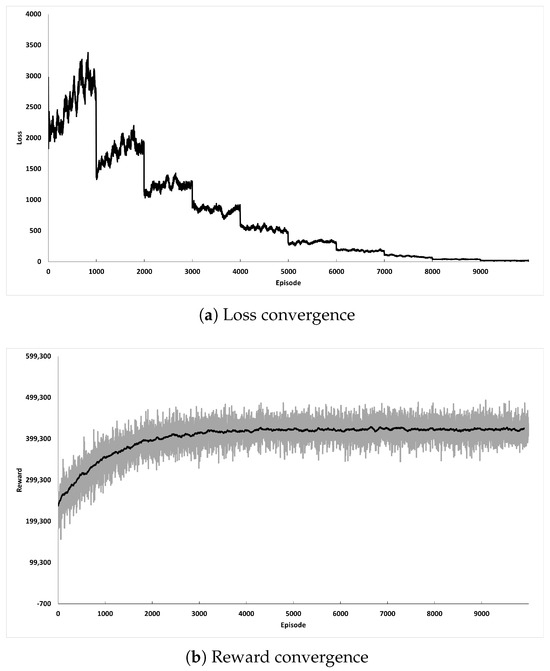
Figure 4.
Convergence of the proposed RL model.
For testing purposes, we ran separate simulations using a pre-trained RL agent and other benchmark bidding strategies. The test was repeated 100 times for each scenario to obtain statistical validation. Each test randomly generated 200 RFQs and collected detailed information such as rewards, transportation costs, and odds of winning.
4.2. Effects of Price-Based Strategy
Table 3 presents the performance of the price-based strategy compared with other benchmark scenarios. Here, the propsed RL defines an action as . For the benchmark scenarios, we similarly consider five fixed bidding strategies in which the price margin is set at −10%, −5%, 0%, 5%, and 10% relative to the baseline price. In addition, we varied the interarrival times between RFQs 5, 10, 15, 30, and 60.

Table 3.
Performance of RL: single-attribute strategy.
Overall, regardless of the mean interarrival time (), the proposed RL produces a policy that is on par with or better than that of the other benchmark scenarios. In particular, when the mean inter-arrival time is short (e.g., is 5), the RL agent significantly outperforms the other strategies. This is because, when the demand inter-arrival time is short, a large volume of orders has already been received, removing the necessity to continually lower prices to secure bids or to use an excessively cautious pricing approach. Under these conditions, a resourceful and efficient bidding strategy is more suitable, and the RL approach is effective in addressing this situation.
However, when the mean interarrival time increases, accepting the majority of orders generally becomes advantageous. Consequently, the win rate approaches 100%, and the RL shows a similar pattern. In particular, at a mean interarrival time of 60, RL bids for all orders at the lowest price to achieve a 100% win rate, which is essentially the same approach as maintaining a fixed 10% margin.
In conclusion, the RL-based strategy proved its value when the demand interarrival times were short, requiring a more sophisticated and dynamic bidding approach. However, when the inter-arrival times were longer, the performance of RL strategies aligned closely with that of simple price-lowering strategies.
4.3. Effects of Multi-Attribute Strategy
In this section, we present the results of the numerical analysis for a multi-attribute strategy that considers not only the bidding price but also the service quality. We compared the RL approach under the multi-attribute strategy with other benchmark strategies, where the bidding price and service quality were fixed for every RFQ. Here, we define the action of service quality as in addition to the price action .
Table 4 summarizes the numerical test results. In Table 4, the action is a tuple representing the bidding price () and delivery time allowance (). For example, ‘Action(0,1)’ means 10% discount added to the basic freight charge ( = 0 is −10% fixed margin) and a delay of 10 min in delivery ().

Table 4.
Performance of the multi-attribute strategy ().
The numerical analysis shows that the RL proposed under the multi-attribute strategy is at least as good as the other fixed strategies. Although no significant difference exists in the mean reward, the RL agent increases the reward by 2.3% while attaining a similar transportation cost compared to the best-fixed strategy of ‘Action(1,1)’. We observed a larger performance gap when deviating from the best-fixed strategy ‘Action(1,1)’ or ‘Action(1,3)’.
The reward is more sensitive to the bidding price than to service quality. In Table 4, the reward changes by 8% when we change the action of service quality () from zero to three. However, the reward of more than 100% changed significantly when the bidding price changed from zero to 2.
The numerical tests reveal that the RL agent learns a policy that improves the reward and odds of winning without significantly increasing the transportation cost. The effectiveness of RL can be explained by investigating how an agent behaves in response to a state. Figure 5 illustrates the actions selected for each RFQ and corresponding states. The RL agent discounts the price when the trucks have sufficient capacity to increase the probability of winning the bid. By contrast, the discount rate decreases (i.e., the chosen action increases from zero to one) as the trucks highly utilize the capacity.
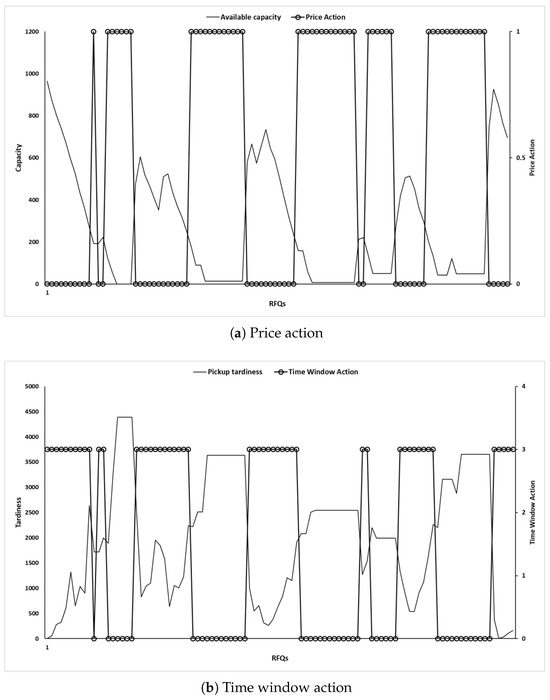
Figure 5.
Action behavior of multi-attribute strategy.
We observed that an action representing service quality () is related to the extent of tardiness. Figure 5b shows that the RL agent chooses an action of zero (i.e., no additional allowance for delays in pickup and delivery) when the amount of tardiness is large.
Moreover, we varied the mean inter-arrival time between two consecutive RFQs (i.e., ) from 5 to 60 and evaluated the effect of demand strength on performance. Table 5 summarizes the results and presents interesting findings. First, we observe that the multi-attribute strategy is at least as effective as the price-based strategy for all values. In particular, the multi-attribute strategy performs better, showing significant differences in rewards between the two strategies when (i.e., the mean interval between two consecutive RFQs) is between 10 and 15.

Table 5.
Performance comparisons.
The two strategies become statistically insignificant when is either very large (e.g., is over 20) or small (e.g., is 5). Regardless of strategy, the RL agent wins against the competitor for a large ; thus, the chance of winning the bid is close to 100% (see Table 3). Therefore, the average reward converges as increases, and no further improvement is expected (Figure 6).
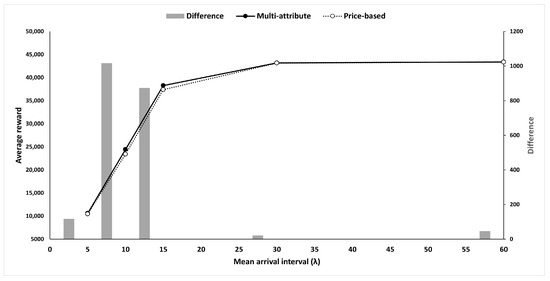
Figure 6.
Reward comparison.
When is 5, implying that RFQs arrive frequently, vehicles are expected to be highly utilized. Therefore, adjusting the time windows has little chance, and the price-based strategy may provide a similar performance.
5. Conclusions
In a bid-based crowdshipping platform, optimizing the bidding strategy is important for the carrier to maximize its profit over competing carriers. A carrier should optimize its bidding strategy, which consists of the price and level of service quality, considering the shipper’s RFQ, fleet operations, and market situations. This study formulated the problem as a sequential decision-making problem by employing an MDP framework. The formulation also accommodates two major bidding strategies: a price-based strategy and a multi-attribute strategy. To overcome the drawbacks of undefined MDP elements and dimensionality, we proposed an RL-based approach.
Extensive numerical experiments have yielded several interesting results.
- -
- Both the price-based and multi-attribute bidding strategies learned by the proposed RL approach perform at least as well as other fixed strategies for all test scenarios. In particular, the RL agent outperforms other benchmarks when the demand interval (i.e., ) is small enough.
- -
- The RL agent learns the bidding strategies that are adaptive to the state of vehicles. The RL agent increases or decreases the bid price according to the available remaining capacity of vehicles. In addition, the service quality is sensitive to the amount of tardiness.
- -
- Notably, the comparison of two bidding strategies reveals that the choice of appropriate strategy is situation-dependent. The price-based strategy provides similar performance when the demand interval is extremely small or large, but the multi-attribute strategy yields better performance for test scenarios with moderate demand. If vehicles have some free time after delivery, the RL agent can accept an additional delay in the next pickup and/or delivery. Therefore, the multi-attribute strategy may achieve better performance.
These findings offer valuable managerial insights for carriers operating in bid-based crowdshipping platforms. Firstly, the consistent superiority of the RL approach over fixed strategies, especially in high-demand scenarios, must be beneficial for carriers to adopt dynamic and adaptive bidding mechanisms. Relying on static rules (e.g., fixed discount/margin strategy) can lead to suboptimal performance, particularly when the market is volatile or busy. Secondly, the RL agent’s behavior demonstrates that optimal bidding is highly contingent on the carrier’s internal state, such as vehicle capacity and current schedules. Managers should develop systems that allow their bidding strategy to dynamically adjust price margins based on vehicle availability and potential service quality deviations such as earliness/tardiness, utilizing operational data to inform real-time decisions. Finally, our comparison of strategies highlights that the choice between competing primarily on price or leveraging service quality as a bidding attribute is a strategic decision dependent on market conditions. Under moderate demand, where there is operational flexibility, multi-attribute bidding can yield superior results, suggesting carriers should build the capability to offer and strategically price varied service levels. Consequently, these results indicate that investing in sophisticated, data-driven decision-making tools, such as the proposed RL model, can significantly enhance a carrier’s profitability and competitiveness in the dynamic crowdshipping environment.
Several possible directions exist for future research in this field. The current definition of action should be extended to include more bidding strategies. For example, the proposed model only considers price and service quality; however, considering a situation in which partial delivery is allowed would be interesting, so the quantity of delivery becomes an element of action. Second, additional numerical tests can be conducted for various market situations. For example, considering whether the RL model is effective even if competitors propose a bid with a very competitive price or service quality would be interesting. We expect the agent to learn about the market properly and optimize its actions. From a methodological perspective, trying various RL approaches (e.g., Actor-Critic) is worthwhile to achieve better computational performance and solution quality.
Author Contributions
Study conception and design: D.M. and Y.K.; coding and experiment: D.M., S.L. and Y.K.; analysis and interpretation of results: D.M. and Y.K.; draft manuscript preparation: D.M., S.L. and Y.K. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Jungseok Logistics Foundation.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
No potential conflict of interest was reported by the author(s).
References
- Castillo, V.E.; Bell, J.E.; Rose, W.J.; Rodrigues, A.M. Crowdsourcing last mile delivery: Strategic implications and future research directions. J. Bus. Logist. 2018, 39, 7–25. [Google Scholar] [CrossRef]
- Gartner. Adopt Crowdsourcing Last-Mile Platforms as a Key Component of Your Logistics Strategy. 2021. Available online: https://www.gartner.com/en/documents/4008043 (accessed on 1 December 2023).
- Ermagun, A.; Stathopoulos, A. Crowd-shipping delivery performance from bidding to delivering. Res. Transp. Bus. Manag. 2021, 41, 100614. [Google Scholar] [CrossRef]
- Pourrahmani, E.; Jaller, M. Crowdshipping in last mile deliveries: Operational challenges and research opportunities. Socio-Econ. Plan. Sci. 2021, 78, 101063. [Google Scholar] [CrossRef]
- Lafkihi, M.; Pan, S.; Ballot, E. Freight transportation service procurement: A literature review and future research opportunities in omnichannel E-commerce. Transp. Res. Part E Logist. Transp. Rev. 2019, 125, 348–365. [Google Scholar] [CrossRef]
- Oyama, Y.; Akamatsu, T. A market-based efficient matching mechanism for crowdsourced delivery systems with demand/supply elasticities. Transp. Res. Part C Emerg. Technol. 2025, 174, 105110. [Google Scholar] [CrossRef]
- Peng, S.; Park, W.Y.; Eltoukhy, A.E.; Xu, M. Outsourcing service price for crowd-shipping based on on-demand mobility services. Transp. Res. Part E Logist. Transp. Rev. 2024, 183, 103451. [Google Scholar] [CrossRef]
- Xiao, H.; Xu, M.; Wang, S. A game-theoretic model for crowd-shipping operations with profit improvement strategies. Int. J. Prod. Econ. 2023, 262, 108914. [Google Scholar] [CrossRef]
- Xiao, H.; Xu, M.; Wang, S. Crowd-shipping as a Service: Game-based operating strategy design and analysis. Transp. Res. Part B Methodol. 2023, 176, 102802. [Google Scholar] [CrossRef]
- Hammami, F.; Rekik, M.; Coelho, L.C. Exact and hybrid heuristic methods to solve the combinatorial bid construction problem with stochastic prices in truckload transportation services procurement auctions. Transp. Res. Part B Methodol. 2021, 149, 204–229. [Google Scholar] [CrossRef]
- Kuyzu, G.; Akyol, Ç.G.; Ergun, Ö.; Savelsbergh, M. Bid price optimization for truckload carriers in simultaneous transportation procurement auctions. Transp. Res. Part B Methodol. 2015, 73, 34–58. [Google Scholar] [CrossRef]
- Lyu, K.; Chen, H.; Che, A. A bid generation problem in truckload transportation service procurement considering multiple periods and uncertainty: Model and benders decomposition approach. IEEE Trans. Intell. Transp. Syst. 2021, 23, 9157–9170. [Google Scholar] [CrossRef]
- Kang, Y. An order control policy in crowdsourced parcel pickup and delivery service. In Proceedings of the Advances in Production Management Systems. Smart Manufacturing for Industry 4.0: IFIP WG 5.7 International Conference, APMS 2018, Seoul, Republic of Korea, 26–30 August 2018; Proceedings, Part II; Springer: Cham, Switzerland; pp. 164–171.
- Kang, Y.; Lee, S.; Do Chung, B. Learning-based logistics planning and scheduling for crowdsourced parcel delivery. Comput. Ind. Eng. 2019, 132, 271–279. [Google Scholar] [CrossRef]
- Guo, C.; Thompson, R.G.; Foliente, G.; Peng, X. Reinforcement learning enabled dynamic bidding strategy for instant delivery trading. Comput. Ind. Eng. 2021, 160, 107596. [Google Scholar] [CrossRef]
- Min, D.; Kang, Y. A learning-based approach for dynamic freight brokerages with transfer and territory-based assignment. Comput. Ind. Eng. 2021, 153, 107042. [Google Scholar] [CrossRef]
- Xiao, F.; Wang, H.; Guo, S.; Guan, X.; Liu, B. Efficient and truthful multi-attribute auctions for crowdsourced delivery. Int. J. Prod. Econ. 2021, 240, 108233. [Google Scholar] [CrossRef]
- Li, Y.; Li, Y.; Peng, Y.; Fu, X.; Xu, J.; Xu, M. Auction-based crowdsourced first and last mile logistics. IEEE Trans. Mob. Comput. 2022, 23, 180–193. [Google Scholar] [CrossRef]
- Song, J.; Regan, A. Combinatorial auctions for transportation service procurement: The carrier perspective. Transp. Res. Rec. 2003, 1833, 40–46. [Google Scholar] [CrossRef]
- Zhang, J.; Xiang, J.; Cheng, T.E.; Hua, G.; Chen, C. An optimal efficient multi-attribute auction for transportation procurement with carriers having multi-unit supplies. Omega 2019, 83, 249–260. [Google Scholar] [CrossRef]
- Lee, S.; Prabhu, V.V. A dynamic algorithm for distributed feedback control for manufacturing production, capacity, and maintenance. IEEE Trans. Autom. Sci. Eng. 2014, 12, 628–641. [Google Scholar] [CrossRef]
- Duffie, N.A.; Prabhu, V.V. Real-time distributed scheduling of heterarchical manufacturing systems. J. Manuf. Syst. 1994, 13, 94–107. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).