Abstract
Empirical studies have suggested that travelers’ risk attitudes affect their choice behavior when travel conditions are stochastic. By considering the travelers’ risk attitudes, we extend the classical two-route model, in which road capacities vary due to such shocks as bad weather, accidents, and special events. Two information regimes have been investigated. In the zero-information regime, we postulate that travelers acquire the variability in route travel time based on past experiences and choose the route to minimize the travel time budget. In the full-information regime, travelers have pre-trip information of the road capacities and thus choose the route to minimize the travel time. User equilibrium states of the two regimes have been analyzed, based on the canonical BPR travel time function with power coefficient . In the special case , the closed form solutions have been derived. Three cases and eleven subcases have been classified concerning the dependence of expected total travel times on the risk attitude in the zero-information regime. In the general condition , although we are not able to derive the closed form solutions, we proved that the results are qualitatively unchanged. We have studied the benefit gains/losses by shifting from the zero-information to the full-information regime. The circumstance under which pre-trip information is beneficial has been identified. A numerical analysis is conducted to further illustrate the theoretical findings.
1. Introduction
Transportation system dynamics are fundamentally shaped by traffic demand and travelers’ choice behavior, encompassing transportation mode selection, departure scheduling, and route planning. This intrinsic relationship underscores the critical importance of understanding commuter behavioral mechanisms for effective system management and optimization. Among numerous behavioral determinants, the role of information provision has emerged as a pivotal research focus in transportation studies.
Historically, traffic information dissemination relied on conventional media channels, including print publications, broadcast systems, and dynamic signage. The technological evolution has witnessed the proliferation of Advanced Traveler Information Systems (ATISs) [1,2,3,4,5,6,7], integrating multimodal data streams through digital platforms such as navigation applications, mobile devices, and personalized travel assistants [8,9,10,11]. Such real-time data provisions empower travelers to optimize their mobility strategies across multiple dimensions—from parking location selection to itinerary customization—aimed at minimizing individual travel disutility [12,13,14,15,16,17,18,19]. While empirical evidence suggests potential societal benefits through enhanced network efficiency [20,21,22,23], contrasting findings reveal an “information paradox”, where excessive information provision paradoxically degrades system performance. This counterintuitive phenomenon manifests through three primary mechanisms: concentration, overreaction, and oversaturation [13]. Notably, Emmerink et al. demonstrated how amplified congestion levels could emerge from disproportionate user reactions to traffic alerts [24]. Subsequent studies by Verhoef et al. and Emmerink et al. further identified scenarios where expanded informational access precipitated network-wide performance deterioration [25,26]. Acemoglu et al. found that the informational Braess’s Paradox can occur in a network congestion game, where commuters with access to information about alternative routes paradoxically experience worse outcomes than those lacking such information [27].
In particular, Lindsey et al. conducted seminal research on the classical “two-route network”, analyzing pre-trip information efficacy under stochastic travel conditions [28]. Their model compares two information regimes: zero-information and full-information regimes. In the zero-information regime, travelers only know the unconditional probability distribution of traffic conditions on the two routes, while in the other regime, they are provided the road conditions before choosing a route. Travelers are assumed to be risk-neutral with respect to travel times, so that they prefer the route with a lower expected travel cost in their model. They found that information can have a negative impact on social welfare when travel cost functions on the two routes are quadratic. By contrast, when capacities vary independently and travel cost functions are linear, pre-trip information is always welfare-improving. Complementary experimental work by Rapoport et al. validated these theoretical predictions through observed behavioral patterns [6].
However, emerging empirical evidence challenges the risk-neutrality assumption, highlighting the significant role of risk perception in shaping travelers’ route selection strategies [29,30]. In response to these behavioral observations, transportation researchers have developed sophisticated equilibrium models to analyze risk-adaptive behaviors in network performance scenarios [31,32,33,34,35]. Lo et al. introduced an innovative travel time budget (TTB) framework that incorporates historical variability data into commuters’ decision-making processes, formulating a multi-class equilibrium model to simulate the route choice behaviors of risk-averse travelers [36,37]. Parallel developments include Yin et al.’s expected disutility paradigm that quantifies risk-taking behavior [38]. Recent theoretical advancements by Tan et al. have systematically compared the Pareto efficiency of various reliability-based equilibrium states, employing statistical descriptors of the central tendency and dispersion for network performance assessment [39]. Li studied heterogeneous risk preferences through a revealed preference analysis. They found differences in the willingness to pay for time savings and reduced travel time variability [40].
As mentioned above, most scholars have employed equilibrium analysis and empirical research methods to analyze risk-adaptive behaviors in network performance scenarios. However, there is still a lack of detailed theoretical analysis on the impact of pre-trip information and travelers’ risk attitudes on travel choice behaviors.
In this study, we extend the model proposed by Lindsey et al. to consider travelers’ risk attitudes. We postulate that travelers acquire the variability in route travel time based on past experiences and choose the route to minimize the travel time budget in the zero-information regime. We study the welfare gains or losses by shifting from the zero-information to the full-information regime. Using the canonical BPR travel time function with power coefficient p, user equilibrium states of the two regimes are analyzed. In the special case p = 1, the closed form solutions have been derived. Three cases and eleven subcases have been classified concerning the dependence of expected total travel times on the risk attitude in the zero-information regime. In the general condition p > 0, the travel time function is not linear. Although we are not able to derive the closed form solutions, we proved that the results are qualitatively unchanged. We have studied the benefit gains/losses by shifting from the zero-information to the full-information regime. The circumstance under which pre-trip information is beneficial has been identified. Finally, a numerical analysis is conducted to further illustrate the theoretical findings.
The rest of this paper is organized as follows. Section 2 gives a brief introduction to the model. Section 3 derives the closed form user equilibrium solutions in the special case p = 1 and discusses the general condition p > 0. Section 4 studies welfare gains or losses from information. The numerical examples are presented in Section 5 to further illustrate the theoretical findings. The conclusion is given in Section 6.
2. The Model
The notations used in the paper are listed in Table 1.

Table 1.
Notational glossary.
Consider the classical “two-route network” model as shown in Figure 1, in which a single origin (O) is connected to a single destination (D) by two routes. The traffic demand is fixed at . Assuming constant demand in a commuting corridor is justified, as we consider a long-run equilibrium, and the volume of daily commuters generally exhibits minimal fluctuation over a long period. Travel conditions on each route vary from day to day because of bad weather, accidents, roadwork, or other shocks. The state of the route, denoted as , is random and drawn from the set , where and represent the good (normal) and bad (incident) conditions, respectively. The traffic demand on route is denoted as . The travel time on route when it is in state is assumed to follow the canonical U.S. Bureau of Public Roads form [41],
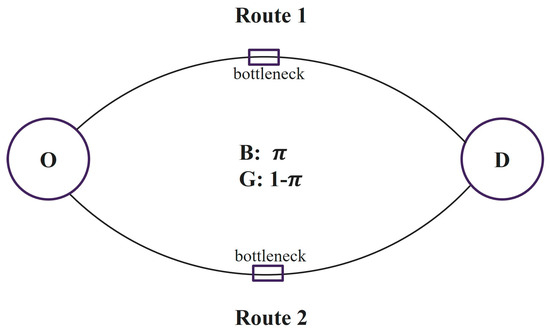
Figure 1.
The classical “two-route network”. The probability of a bad condition () occurring is , and the probability of a good condition () occurring is on each route.
Let denote the free-flow travel time on route . Parameter represents the stochastic congestion coefficient on route , and is the power coefficient. For simplicity, we do not consider the situation that can also change in a stochastic way.
Following existing studies, we adopt the following assumptions in our model:
Assumption 1.
Travel conditions on each route are either good () or bad (), with .
In contrast to the deterministic bottleneck model, we consider a bottleneck capacity by two distinct operational states: good () and bad (), varying from day to day due to random factors (e.g., traffic incidents, construction activities), with probabilities for the bad state and for the good state. The assumed binary capacity model is practical. For instance, a two-lane road operates at full capacity without accidents but loses half its capacity if a lane is blocked by an accident.
Assumption 2.
Without loss of generality, assume .
Assumption 3.
The congestion coefficients and are statistically independent.
Th ratio quantifies the congestion elasticity, indicating the proportional increase in congestion due to incidents relative to baseline conditions. Assumption 2 indicates that route 1 exhibits less significant congestion growth compared to route 2 under the same incident severity. This higher reliability may stem from road designs, such as emergency shoulders or parallel arterials, which reduce by limiting bottleneck formations. Assumption 3 guarantees that special incidents occur stochastically on each route. When a pair of routes are geographically separated and disruptions like accidents occur on one of the two routes, the capacity of the other route can remain the designed capacity. Such a separation allows parameters and to exhibit statistical independence.
Route capacity degradations can cause route travel time variability. Travelers do not know their exact a priori travel time without pre-trip information. As Lo et al. proposed, in the presence of travel condition variations, to hedge against uncertainty, travelers generally add or deduct a travel time margin to the expected trip time to form their travel time budget [3]. The travel time budget depends on the risk attitudes of the travelers and also on the trip purposes. For trips that have a high penalty for lateness, such as trips to job interviews or trips to the airport to catch a flight, one can expect that travelers can be risk-averse and reserve a larger travel time budget. The travel time budget is defined as
Mathematically, the travel time budget on route , , can be expressed as
where is the random variable of travel time on route ; and are the mean and variance of , respectively; and is the risk-preference coefficient. The risk-averse travelers with will reserve a relatively large travel time budget; the risk-preferred travelers with will reserve a relatively small travel time budget. For , travelers are risk-neutral.
3. User Equilibrium
In this section, two information regimes are considered: zero-information () and full-information () regimes. Travelers are assumed to adopt pure strategies and follow the user equilibrium (UE) principle so that they choose a route deterministically. Three scenarios (A–C) and seven situations (i–vii) are studied in this section.
3.1. User Equilibrium in the Zero-Information Regime
In the zero-information regime, travelers only know the unconditional probability distribution of conditions on the route (i.e., the probability of a bad condition () occurring is , and the probability of a good condition () occurring is ), but do not know the specific congestion state of the two routes on each day. Travelers are assumed to prefer the route with lower travel time budget. Let denote the traffic demand on route in the zero-information regime. The expected travel time on route can be written as
in which . Then, the expected total travel time on the network can be calculated
Similarly, the expectation of can be written as
Thus, the variance in travel time can be obtained,
The travel time budget of route , is a function of , and can be written as
in which .
Let denote a composite function of and ; then, the following can be obtained:
The user equilibrium (UE) is realized when the travel time budget on the two routes is equal, i.e.,
3.1.1. Three Scenarios Under
Given , one can see that the function of versus is a linear function. Equation (8) can be simplified into
Then, the equation has a unique solution, unless . In this case, the solution can be denoted as
Note that from Equation (13), one can easily derive that the solution is a constant when , no matter which situation it is. We denote it as ,
and it is obvious that .
As a result, there are three scenarios under , i.e., scenario A–C, which are classified based on the relationship between and . Under each scenario, there are different possible UE patterns, denoted as pattern ij, where i = A, B, C and j = 1, 2 …, which are classified due to the possibilities of .
- Scenario A:
We can derive that scenario A exists when
by solving . In this scenario, functions and are parallel (or identical) to each other. One has by substituting into . One can easily derive that since (Assumption 2). As a result, in this scenario, there are three possible UE patterns, as shown in Figure 2 and Table 2.
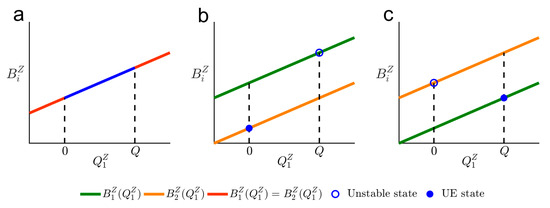
Figure 2.
Equilibrium state in scenario A. (a) , (b) , (c) .

Table 2.
Three possible UE patterns in scenario A.
- 2.
- Scenario B: and
By solving and , we can derive that scenario B exists when . Here, and can be obtained by solving and , separately,
In this scenario, the equation has a unique solution, , as shown in Equation (13). Substituting into , one has . Since is an increasing function of , one has in scenario B. Accordingly, . Therefore, the slopes of functions and have the same sign. As a result, in this scenario, there are six possible patterns, as shown in Figure 3 and Table 3.
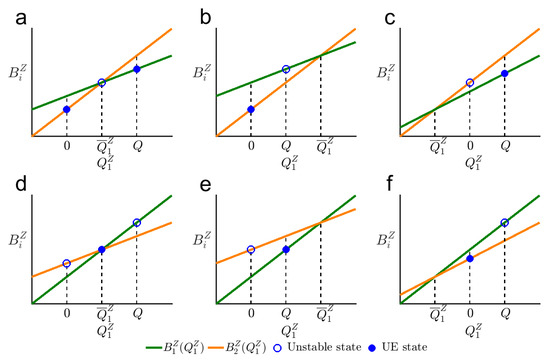
Figure 3.
Equilibrium state in scenario B. (a–c) , (d–f) .

Table 3.
Six possible UE patterns in scenario B.
- 3.
- Scenario C: and
Obviously, scenario C exists when or . In this scenario, the equation has a unique solution, as shown in Equation (13), and the slopes of functions and have a different sign. As a result, in this scenario, there are six possible UE patterns, as shown in Figure 4 and Table 4.
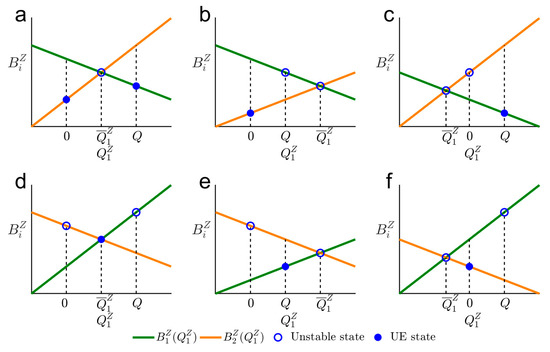
Figure 4.
Equilibrium state in scenario C. (a–c) , (d–f) .

Table 4.
Six possible UE patterns in scenario C.
3.1.2. Closed Form UE Solutions Under
In this section, we first discuss the relation between and in the zero-information regime based on the above patterns in the three scenarios. By setting and , respectively, we obtain two thresholds:
Note that when , and when . Here,
by solving . Due to Assumption 2, it is obvious that . Moreover, the other two thresholds of can be obtained by solving and , respectively,
In the special case , in Equation (13) is a constant no matter what the risk attitude is (see Figure 5c). We denote the constant as ,
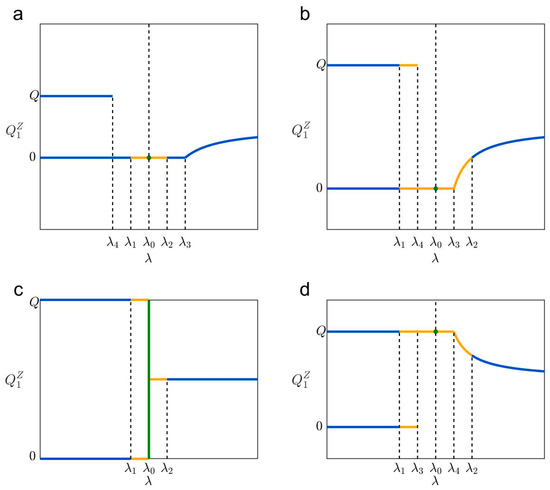
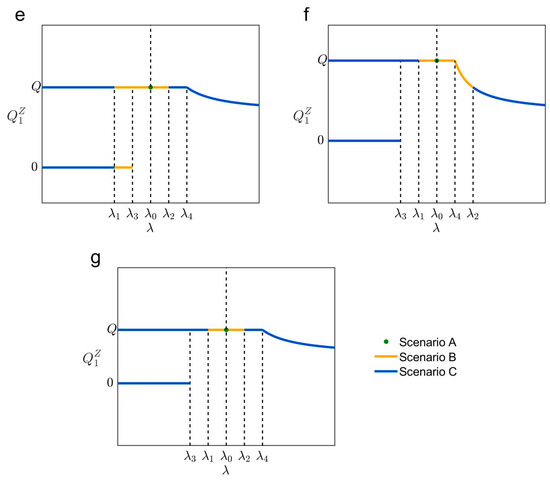
Figure 5.
Relation between and in the seven possible situations in the zero-information regime. (a–g) Situations (i)–(vii).
If , the function (13) of versus is a hyperbolic curve. When , the function is an increasing one for the two branches (see Figure 5a,b); when , the function is a decreasing one for the two branches (see Figure 5d–g). Note that the two branches are separated by . From Equation (13), can be less than 0 or larger than ; however, should be met.
According to the above analysis, under UE, seven situations are given based on the relationship of and , and different scenarios may belong to one of the situations.
- 1.
- Situations (i) and (ii)
When , situations (i) and (ii) can exist. In the two situations, when , pattern A2 exists, in which all travelers choose route 2 under UE.
- Situation (i) corresponds to and (see Figure 5a). In this situation, patterns C1, C2, B2, B6, C6, and C4 exist when the risk attitude belongs to , , , , , and , respectively.
- Situation (ii) corresponds to and (see Figure 5b). In this situation, patterns C1, B1, B2, B6, B4, and C4 exist when belongs to , , , , , and , respectively.
- Note that when , , and cannot be not met simultaneously, and cannot be not met simultaneously, either.
- 2.
- Situation (iii)
When , one has situation (iii). In this situation, when , pattern A1 exists, in which is not uniquely determined under UE, which can be any value between 0 and (). Moreover, patterns C1, B1, B4, and C4 exist when belongs to , , , and , respectively (see Figure 5c).
- 3.
- Situations (iv)–(vii)
When , situations (iv), (v), or (vi), and (vii) can exist. In the four situations, when , pattern A3 exists, in which all travelers choose route 1 under UE.
- Situation (iv) corresponds to and (see Figure 5d). In this situation, patterns C1, B1, B3, B5, B4, and C4 exist when belongs to , , , , , and , respectively.
- Situation (v) corresponds to and (see Figure 5e). In this situation, patterns C1, B1, B3, B5, C5, and C4 exist when belongs to , , , , , and , respectively.
- Situation (vi) corresponds to and (see Figure 5f). In this situation, patterns C1, C3, B3, B5, B4, and C4 exist when belongs to , , , , , and , respectively.
- Situation (vii) corresponds to and (see Figure 5g). In this situation, patterns C1, C3, B3, B5, C5, and C4 exist when belongs to , , , , , and , respectively.
The boundary conditions for the seven possible situations are shown in Table 5. One can see that the existence conditions of situation (vi) and (v) are mutually exclusive. In other words, with other parameters fixed, when increases from to +, while situations (i)–(iv) and (vii) can always be observed, either situation (v) or situation (vi) can emerge.

Table 5.
Boundary conditions for seven possible situations in the zero-information regime under .
If we only concern the relation between and , and do not care for the specific scenario, then the seven situations can be attributed to three cases.
Case 1 includes situation (i) and (ii), in which or when ; when ; and when .
Case 2 includes situation (iii), in which or when ; when ; and when .
Case 3 includes situation (iv)-(vii), in which or when ; when ; and when .
Now we investigate the relation between and based on the three cases. Note that from Equation (5), the expected total travel time, , is a quadratic function of under , and reaches a minimum value when
which corresponds to
Obviously, may be less than 0 or greater than ; however, should be met. Substituting , and into Equation (5), respectively, one has three critical values of expected total travel time,
By setting , one has
Moreover, based on the three critical values, we have the following thresholds of risk coefficient ,
by solving , , and , respectively.
As a result, the three cases can be classified into eleven subcases (see Figure 6, Figure 7 and Figure 8 and Table 6).
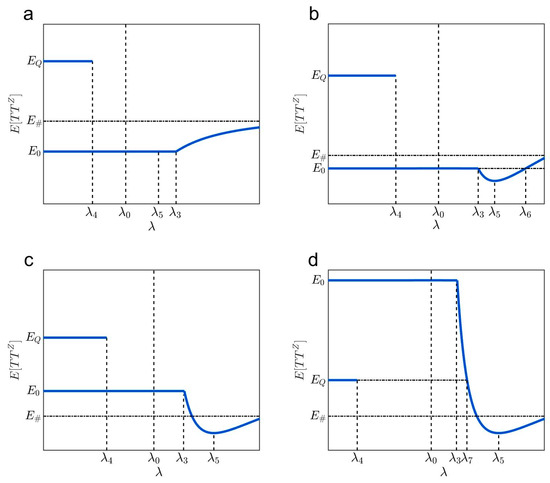
Figure 6.
Expected total travel time in (a–d) cases 1a–1d.
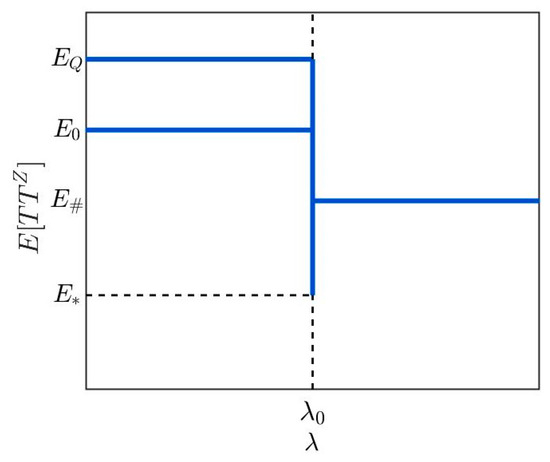
Figure 7.
Expected total travel time in case 2.
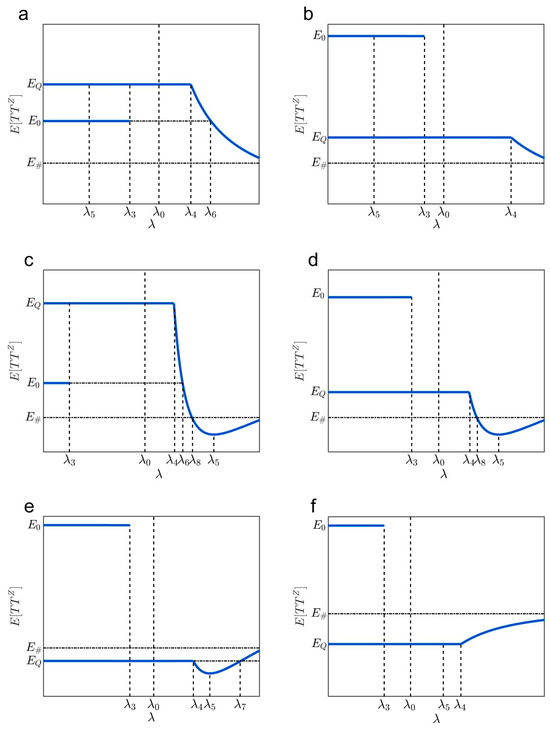
Figure 8.
Expected total travel time in (a–f) cases 3a–3f.

Table 6.
Boundary conditions for 11 subcases in the zero-information regime under .
- Case 1 in Figure 6a–d: When , case 1 exists. One can easily prove that and are always met in case 1. Case 1 can be further classified into cases 1a–1d.
In case 1a, and . In this subcase, increases with when ; there are two possible UE states when , and is a constant when (see Figure 6a).
In case 1b–1d, . The three subcases correspond to , , and , respectively. In the three subcases, increases with when and decreases with when ; there are two possible UE states when , and is a constant when ; reaches the minimum value when (see Figure 6b–d).
- Case 2 in Figure 7: When , case 2 exists. One can easily prove that and are always met in case 2. In this case, there are two possible UE states when ; the expected total travel time is not uniquely determined when , which can be any value between and . Here,which denotes the minimum value of the expected total travel time. Note that is met due to . Finally, is a constant no matter what the risk attitude is when , which can be calculated,
- Case 3 in Figure 8a–f: When , case 3 exists. One can easily prove that and are always met in case 3. Case 3 can be further classified into cases 3a–3f.
In case 3a and case 3b, . The two subcases correspond to and , respectively (see Figure 8a,b). In the two subcases, decreases with when ; there are two possible UE states when , and is a constant when .
In case 3c–3e, . The three subcases correspond to , , and , respectively (see Figure 8c–e). In the three subcases, decreases with when , and increases with when ; there are two possible UE states when , and is a constant when ; reaches the minimum value when .
In case 3f, and (see Figure 8f). increases with when ; there are two possible UE states when , and is a constant when .
Actually, with other parameters fixed, not all 11 subcases can be observed when increases from to +. For example, when , case 3a and case 3c do not exist; when , case 1d and case 3c do not exist; and when , case 1d and case 3b do not exist (see Table 6). This will be further illustrated in numerical examples in Section 5.
3.1.3. General Results Under
In the zero-information regime, we have derived the closed form solutions under in the above subsection. However, the equation does not have closed form solutions for arbitrary ( and ) if the free-flow travel times are different (i.e., ). Nevertheless, we can prove that the results are qualitatively unchanged.
For arbitrary (), denote the solution of equation for a given as , and assume that the slopes of functions and under the solution are
It is obvious that the state is not a UE state when or , because should be met. Based on the definition of the UE principle, we have the following property.
Property 1.
Assume that the state satisfies . Then the following is obtained:
- (a)
- when , if the functions and are identical, the state is a UE state; otherwise, the two functions are a tangent at , which is not a UE state, unless (if is above ) or (if is below );
- (b)
- when , the state is not a UE state;
- (c)
- when , the state is a UE state.
By substituting and into equation , respectively, one has
By solving , one has
As a result, we have the following propositions.
Proposition 1.
When , the traffic demand under UE is a constant no matter what is.
Proof.
Substituting into the UE condition , one can easily derive that the solution is
which is a constant independent of . When , one has . Moreover, is always met, provided . Thus, . Thereby, the solution is unique. According to Property 1(c), the state is a unique UE state. □
Proposition 2.
- (a)
- when , there are two possible UE states ( or ) when . Otherwise, a unique UE state exists: when ; and increases with when ;
- (b)
- when , there are two possible UE states ( or ) when ; the UE traffic demand is not uniquely determined, which can be any value between 0 and () when ; the UE traffic demand is a constant when ;
- (c)
- when , there are two possible UE states ( or ) when . Otherwise, a unique UE state exists: when ; ; and decreases with when .
Proof.
The proof of the proposition can be found in Appendix A1. □
Proposition 3.
The function of versus has at most one extreme point.
Proof.
The proof of the proposition can be found in Appendix A2. □
Proposition 2 is consistent with the three cases of the relation between and under . The result of Proposition 3 is consistent with that of the 11 subcases under , in which there is no extreme point in cases 1a, 2, 3a, 3b and 3f, and one extreme point exists at in other cases. Given the three propositions, one can conclude that the results under the general condition () are qualitatively unchanged as that under .
3.2. User Equilibrium in the Full-Information Regime
In the full-information regime, travelers can be informed about the accurate travel conditions before choosing a route and thus choose the route to minimize the travel time. Given Assumption 3, there are four possible combinations for the system: , , , and , where the first letter refers to the condition of route 1, and the second refers to the condition of route 2 as shown in Figure 9. Accordingly, there are four possible UE usage levels of route : , , , and . The expected total travel time on the network can be calculated by
in which denotes the total travel time on the network when route 1 is in state and route 2 is in state , ,
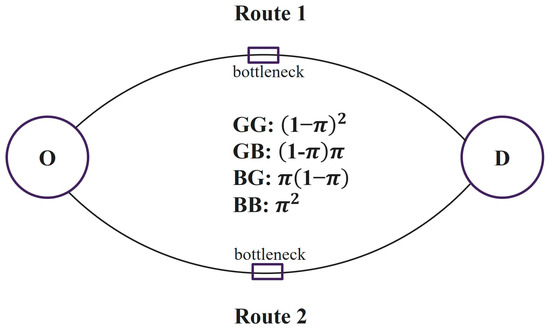
Figure 9.
The classical “two-route network”. The probabilities of the four states combinations , , , and occurring on the two routes are , , , and , respectively.
With full information, the UE division of traffic between routes is realized when the travel time is equal, i.e., ; here,
Given , substituting Equation (1) into , the UE traffic demand on route 1 can be obtained,
and one has .
In the full-information regime, for arbitrary (), denote the solution of as ; then, we have the following proposition.
Proposition 4.
In the full-information regime, there is a unique UE state for each combination , and
- (a)
- when , all travelers choose route 2 under UE (i.e., );
- (b)
- when , the UE state is ();
- (c)
- when , all travelers choose route 1 under UE (i.e., ).
Proof.
The proof of the proposition can be found in Appendix A3. □
4. Welfare Gains or Losses from Information
In this section, we study the welfare gains/losses from pre-trip information. We compare the expected total travel time between the zero-information and full-information regimes. The welfare gains/losses under equilibrium by shifting from the zero-information to full-information regimes are
Welfare improvement is defined as . corresponds to the information paradox.
Proposition 5.
For the general condition (), full information is always welfare-improving under the UE state or .
Proof.
The proof of the proposition can be found in Appendix A4. □
Proposition 5 indicates that providing pre-trip information is of vital importance to avoid the overuse of one route that arises from uncertainty. In the zero-information regime, if most travelers are risk-averse, they may all end up choosing the same route. This is an outcome we obviously wish to avoid. This homogeneity occurs because risk-averse travelers tend to be more cautious, and they allocate more time to travel and prefer stable, predictable routes over accident-prone, unreliable ones. To mitigate this inefficiency, it is prudent to provide accurate pre-trip information via intelligent transportation systems, diverting a portion of travelers to less-used routes. Such strategic guidance can significantly enhance the transportation network’s operational efficiency and improve overall travel quality. Based on proposition 5, we have the following corollaries.
Corollary 1.
In case 1a and case 3f, full information is always welfare-improving.
Proof.
In case 1a, the minimum of is achieved when . In case 3f, the minimum of is achieved when . According to proposition 5, one has . □
By denoting and as the two critical values of by solving and under , respectively, we have the following corollary.
Corollary 2.
Full information is welfare-improving, if one of the following cases occurs in the zero-information regime:
- (a)
- when in either case 1c or case 2;
- (b)
- when in either case 3b or case 3d;
- (c)
- when in either case 3a or case 3c;
- (d)
- when in case 1d;
- (e)
- when or in case 1b;
- (f)
- when or in case 3e.
Proof.
In the above-mentioned range of , is not smaller than either or . According to Proposition 5, one has . □
Since risk attitudes affect travelers’ route choice behavior and therefore welfare gain, next, we compare the welfare gain of risk-neutral travelers with that of risk-preferred ones and risk-averse ones. Since there is no closed form solution in the general condition (), we focus on the special condition ().
Proposition 6.
In case 1a and case 3f, risk-neutral travelers obtain no more welfare gains than risk-preferred ones or risk-averse ones.
Proof.
In case 1a, from , one can derive . In case 3f, from , one can derive . Since reaches the minimum when in case 1a and when in case 3f, risk-neutral travelers can obtain a minimum welfare gain. □
Proposition 7.
In case 2, risk-neutral travelers obtain no more welfare gains than risk-preferred ones with risk attitude .
Proof.
In case 2, (see Figure 7). Thus, risk-neutral travelers obtain no more welfare gains than risk-preferred ones with risk attitude . □
Proposition 8.
- (a)
- In case 3a and case 3c, risk-neutral travelers obtain no more welfare gains than risk-preferred ones with risk attitude ;
- (b)
- In case 1d, risk-neutral travelers obtain no more welfare gains than risk-preferred ones with risk attitude .
Proof.
In case 3a and case 3c, from , one can derive . Thus, one can easily prove that is always met in the two cases. Therefore, risk-neutral travelers obtain no more welfare gains than risk-preferred ones with risk attitude (see Figure 8a,c).
In case 1d, from , one can derive . Thus, one can easily prove that is always met in this case. Therefore, risk-neutral travelers obtain no more welfare gains than risk-preferred ones with risk attitude (see Figure 6d). □
Proposition 9.
- (a)
- In case 1b, risk-neutral travelers obtain no more welfare gains than risk-averse ones with risk attitude ;
- (b)
- In case 3e, risk-neutral travelers obtain no more welfare gains than risk-averse ones with risk attitude .
Proof.
In case 1b, from , one can derive . Thus, one can easily prove that is always met in this case. Therefore, risk-neutral travelers obtain no more welfare gains than risk-averse ones with risk attitude (see Figure 6b).
In case 3e, from , one can derive . Thus, one can easily prove that is always met in this case. Therefore, risk-neutral travelers obtain no more welfare gains than risk-averse ones with risk attitude (see Figure 8e). □
Proposition 10.
- (a)
- In case 3c and case 3d, risk-neutral travelers obtain more welfare gains than risk-averse ones with risk attitude ;
- (b)
- In case 3e, risk-neutral travelers obtain more welfare gains than risk-averse ones with risk attitude .
Proof.
In case 3c and case 3d, from , one can derive . Thus, one can easily prove that is always met in these two cases (see Figure 8c,d). Therefore, risk-neutral travelers obtain more welfare gains than risk-averse ones with risk attitude .
In case 3e, from , one can derive . Thus, one can easily prove that is always met in this case (see Figure 8e). Therefore, risk-neutral travelers obtain more welfare gains than risk-averse ones with risk attitude . □
Propositions 6–10 indicate that risk-neutral travelers sometimes obtain less (or larger) welfare gains. The assumption that travelers are risk-neutral may underestimate or overestimate the benefit gains or losses of the information. As demonstrated in Propositions 6–9, risk-preferred and risk-averse travelers may exhibit a stronger preference for choosing specific routes compared to risk-neutral travelers. This route selection behavior could increase the total system travel cost due to congestion on preferred routes. Such scenarios are more likely to occur when a route exhibits higher elasticity in its capacity response to demand fluctuations. Under these circumstances, providing pre-trip information proves more advantageous for risk-preferred and risk-averse travelers. Conversely, when two routes maintain comparable and stable capacities, the situation described in Proposition 10 becomes more prevalent. In this case, providing pre-trip information yields greater benefits if all travelers are risk-neutral.
5. Numerical Analysis
In this section, we present the results of the numerical analysis to illustrate further the effects of pre-trip information on system efficiency under varying risk-preference coefficients.
5.1. The Effect of Pre-Trip Information in the General Condition
Firstly, we consider UE states and in the general condition. Figure 10 shows examples of welfare gains by shifting from zero information to full information in the two UE states. One can see that providing pre-trip information is always welfare-improving (). Moreover, we can see that providing pre-trip information can gain more benefits when increases/decreases for /. This is in consistent with Proposition 5. In real-world traffic scenarios, we often encounter situations where two alternative routes between an origin and destination (OD) offer similar travel times. One route is a longer-distance highway with higher speeds, while the other is a shorter urban arterial road featuring more traffic lights and lower speeds. Without traffic information, most travelers may prefer the highway for its perceived smoother flow. However, increased highway traffic could lead to significant travel time delays, which should be prevented. A judicious solution involves providing pre-trip information to divert a portion of travelers to urban arterial roads, thereby effectively minimizing total system travel costs.
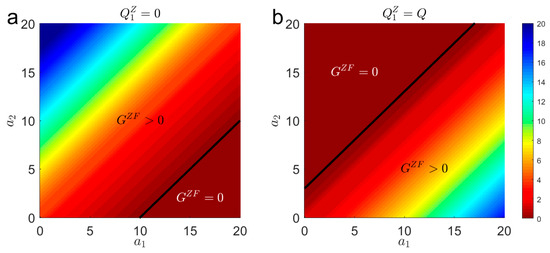
Figure 10.
Benefit gains from full information. (a) , (b) . The black line separates from . The parameters are set as , , , , , , and .
Figure 11 shows benefit gains/losses from pre-trip information under different . For the specific parameters, case 3a and case 3c do not exist when increases from to +. In Figure 11a–d,f–i, there are two UE states (the welfare gains or corresponding to UE state or in the zero-information regime) when (); the welfare gains correspond to UE state when (); and a unique UE state exists when (). This is in consistent with Proposition 2. Furthermore, the minimum value is observed at in cases 1b, 1c, 1d, 3d, and 3e. This is in consistent with Proposition 3.
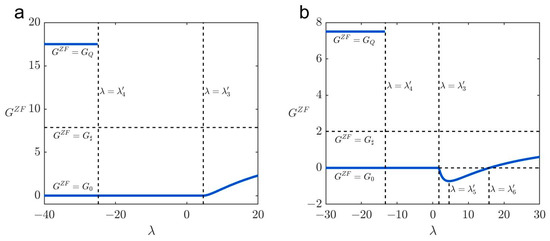
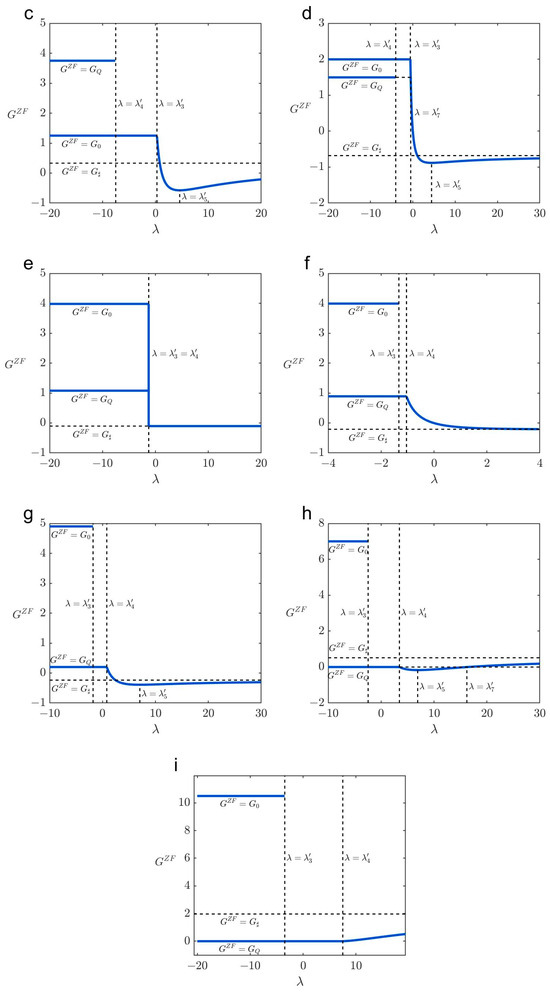
Figure 11.
Benefit gains/losses from full information under different . (a–d) Cases 1a–1d, (e) case 2, (f) case 3b, and (g–i) cases 3d–3f. The parameters are set as , , , , , , and . In (a) , ; (b) , ; (c) , ; (d) , ; (e) , ; (f) , ; (g) , ; (h) , ; and (i) , . , , and correspond to the welfare gains/losses under UE states , , and in the zero-information regime.
Moreover, from Figure 11a,i, one can see that pre-trip information is always beneficial () in case 1a and 3f. This is in consistent with Corollary 1. Providing pre-trip information is welfare-improving when in case 1c and case 2; when in case 3b and case 3d; when in case 1d; when or in case 1b; and when or in case 3e. This is in consistent with Corollary 2. Under other circumstances, providing pre-trip information may have either positive or negative impact on improving the welfare gains, which depends on the parameters.
5.2. The Effect of Pre-Trip Information in the Special Case
The Figure 12 plots show the benefit gains from pre-trip information under different in the special case . For the specific parameters, (i) case 1d and case 3b do not exist when increases from to +; and (ii) providing pre-trip information is always welfare-improving.
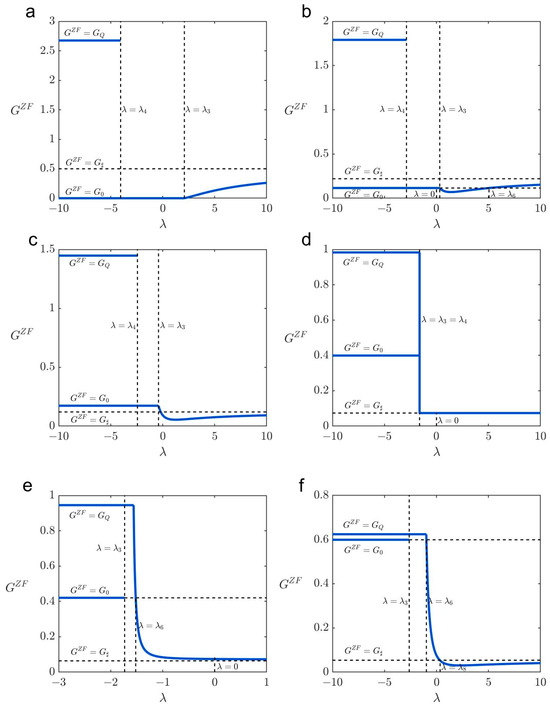
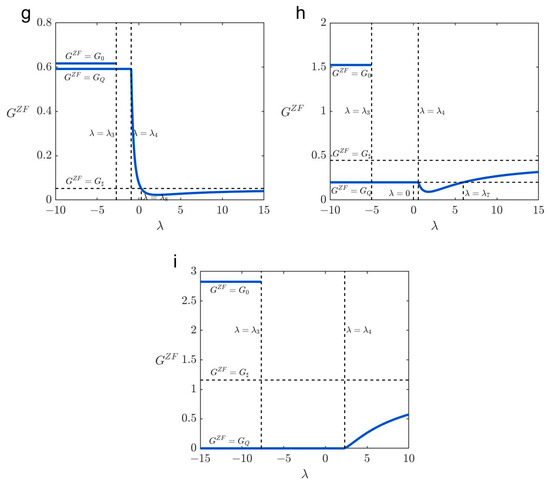
Figure 12.
Benefit gains from full information under different . (a–c) Cases 1a–1c, (d) case 2, (e) case 3a, and (f–i) cases 3c–3f. The parameters are set as , , , , , , and . In (a) , ; (b) , ; (c) , ; (d) , ; (e) , ; (f) , ; (g) , ; (h) , ; and (i) , .
From Figure 12a,h, one can see that risk-neutral travelers () obtain no more benefit gains than risk-preferred ones () or risk-averse ones () in case 1a or 3f. This is in consistent with Proposition 6. Moreover, risk-neutral travelers obtain no more welfare gains than risk-preferred ones with risk attitude (i) in case 2; (ii) in case 3a and case 3c, or risk-averse ones with risk attitude (iii) in case 1b; (iv) in case 3e. This is consistent with Proposition 7–9. Nevertheless, risk-neutral travelers obtain more welfare gains than risk-averse ones with risk attitude (v) in case 3c and case 3d; (vi) in case 3e. This is consistent with Proposition 10.
5.3. The Effect of Pre-Trip Information on Different Routes
Figure 13 shows two examples of benefit gains/losses from pre-trip information on different routes. In example 1 (Figure 13a), given , full information is always welfare-improving on the network () (see Figure 13a). While providing pre-trip information is welfare-improving on both routes when , information is welfare-improving on route 2 (route 1) and welfare-reducing on route 1 (route 2) when (). In example 2, the free-flow travel costs are significantly larger on route 2 () than those on route 1 (). Unfortunately, a counterintuitive information paradox occurs when travelers are risk-averse with the risk-preference coefficient (see Figure 13b). In this example, providing information exerts adverse effects. This result suggests that we should not blindly provide pre-trip information to travelers. Instead, it is crucial to comprehensively consider factors such as free-flow travel costs, the reliability of different routes, and travelers’ risk attitudes when deciding whether to disseminate information.
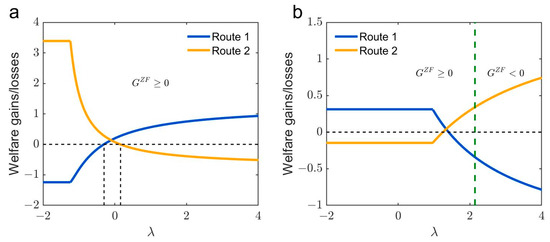
Figure 13.
Benefit gains/losses from full information on different routes. (a) and (b) . The parameters are set as , , , , , and . In (a) and ; (b) and . The dashed green line separates from .
6. Conclusions and Discussion
In this study, we extended the classical two-route network model proposed by Lindsey et al. [28] and considered travelers’ risk attitudes. The travel time variability due to stochastic network link capacity variations has been taken into account. We postulated that travelers acquire the variability in route travel time based on past experiences and factor such variability into their route choice consideration in the form of a “travel time budget”. Two information regimes, zero-information and full-information regimes, were considered. Commuters only know the unconditional probability distribution of conditions on the two routes in the zero-information regime, while they are provided the road conditions before choosing a route in the full-information regime.
User equilibrium states of the two regimes have been analyzed. In the special case , the closed form solutions have been derived. Three cases and eleven subcases have been classified concerning the dependence of expected total travel times on the risk attitude in the zero-information regime. In the general condition , although we are not able to derive the closed form solutions, we proved that the results are qualitatively unchanged.
We have studied the benefit gains/losses by shifting from the zero-information to the full-information regime. The circumstance under which pre-trip information is beneficial has been identified. We also demonstrated that risk-averse (risk-preferred) travelers might obtain more/less welfare than risk-neutral ones. Thus, the assumption that travelers are risk-neutral may underestimate or overestimate the benefit gains/losses of the information. Finally, a numerical analysis was conducted to further illustrate the benefits of information under the general conditions, which also demonstrated that while the network welfare improves/reduces, welfare on one of the routes may reduce/improve. Counterintuitively, the information paradox is more likely to occur when risk-averse travelers confront routes with substantial disparities in free-flow travel costs. Therefore, it is crucial to comprehensively consider factors such as free-flow travel costs, the reliability of different routes, and travelers’ risk attitudes when formulating traffic information dissemination strategies.
Our study has several limitations that could provide opportunities for future research. With pre-trip information, travelers might adjust their decisions from multiple aspects, e.g., travel route, departure time, travel mode, and destination. Our model only considers route choices based on the classical “two-route network”. Thus, the first extension would be to incorporate simultaneous multi-dimensional decision-making. Analyzing how travelers prioritize goals in multi-OD complex networks could deepen our understanding of pre-trip information’s impact on transportation efficiency. Second, our model features two polar information regimes. Full information is an idealization that is practically unattainable. Information on travel conditions may be imperfect and collected with delays, which should be considered in further work. Third, we assume a constant demand in commuting corridors. Yet, in emerging residential areas, dynamic demand fluctuations may significantly influence travel behavior, necessitating further exploration. Fourth, the model simplifies route states to binary conditions (good/bad). Extending this to multi-state stochastic scenarios would clarify how risk attitudes and information interact under realistic variability. Finally, we treat travelers as homogeneous. Future work should examine heterogeneous populations with diverse risk preferences to better reflect real-world decision dynamics.
Author Contributions
Methodology, Y.Y.; software, Y.Y.; investigation, H.L. and J.C.; data curation, Y.L.; writing-original draft preparation, Y.Y.; writing-review and editing, S.Z.; funding acquisition, S.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China under grant no. 72288101, the Beijing-Tianjin-Hebei Basic Research Cooperation Project under grant no. G2024210009, the National Natural Science Foundation of Ningbo under grant no. 2024J191, and the Fundamental Research Funds for the Central Universities under grant no. 2024XKRC031.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Appendix A.1. Proof of Proposition 2
Firstly, we derive the monotonicity of with respect to as follows.
Let and denote the partial derivative of with respect to and , respectively. Consider any two solutions of the equation , denoted as and . Via Taylor expansion, one has
in which is a second-order infinitesimal. Let and , we can derive
Next, we calculate and , which can be formulated as
and
Thus,
It is obvious that 0, provided . Therefore,
- (a)
- The function is an increasing one of . Substituting into the equation , one has
Note that . Substituting and into , one has and , respectively. Therefore, there is unique value that makes . As a result, is a decreasing function of when and an increasing function when .
- (b)
- The function is an increasing one of . By solving , one has . Substituting and into , one has and , respectively. Therefore, is a decreasing function of when and an increasing function when .
Note that the function with respect to is discontinuous at . At the discontinuity, one has , so that . As a result, the monotonicity of the two branches separated by is the same, provided . Moreover, because , one has when and when . As a result, three possible cases need to be classified.
- (1)
- . In this case, one has . When , one has , in which and , so that . When , one has , in which and , so that . Therefore, the function is an increasing one of for the two branches. Moreover, when (or ), one has (or ), because the function is continuous, except at . As a result, three possible subcases need to be classified.
- -
- When , one can easily prove that is always met; thereby, is a UE state. However, according to Property 1(b), the solution is not a UE state, because is always met when ;
- -
- When , one can easily prove that is always met. Thereby, is a UE state;
- -
- When , it is obvious that or is not a UE state; however, according to Property 1(c), the solution is a UE state, because is always met when .
This completes the proof of Proposition 2(a).
- (2)
- . In this case, one has . It is straightforward to prove that is always met, so that for an arbitrary , in which is a constant (), no matter what the risk attitude is. As a result, three possible subcases need to be classified.
- -
- . According to Property 1(b), the solution is not a UE state because ; similar to the analysis above, there are two possible UE states, or ;
- -
- . According to Property 1(c), the solution is a UE state, because ;
- -
- . In this subcase, is always met when . Substituting into , one has . Thus, we have , because . As a result, the functions and are identical. According to Property 1(a), is not uniquely determined, which can be any value between 0 and ().
This completes the proof of Proposition 2(b).
- (3)
- . In this case, one has . When , one has , in which and , so that . When , one has , in which and , so that . Therefore, the function is a decreasing one of for the two branches. Moreover, when (or ), one has (or ), because the function is continuous except at . Similar to the analysis above, three possible subcases need to be classified:
- -
- when , one can easily prove that is always met. Thus, is a UE state; however, according to Property 1(b), the solution is not a UE state, because is always met when ;
- -
- when , one can easily prove that is always met. Thus, is a UE state;
- -
- when , it is obvious that or is not a UE state; however, according to Property 1(c), the solution is a UE state because is always met when .
This completes the proof of Proposition 2(c). □
Appendix A.2. Proof of Proposition 3
Based on Proposition 2, there is no extreme point when , because or is the possible UE state under this case. The UE traffic demand versus is a decreasing (an increasing) function when . If the function versus is also a decreasing (an increasing) function, then the function with respect to has no extreme point.
Next, we study the monotonicity of the function with respect to . The first and second-order derivative of with respect to are
Since is always met, one has , so that is an increasing function of : the minimum of is and the maximum is . The function is an increasing (or a decreasing) function of when (or ). There is no extreme point for function versus under this case. However, a unique extreme point exists when , in which firstly decreases and then increases with . □
Appendix A.3. Proof of Proposition 4
It is obvious that the solution or is not a UE state, because should be met. As a result, three cases need to be classified:
- (1)
- when , it is clear that is a UE state and is not a UE state. Substituting and into Equation (34), one has
This goes against the UE principle . Therefore, is a unique UE state.
- (2)
- when , it is clear that is a UE state and is not a UE state. Substituting and into Equation (34), one has
This goes against the UE principle . Therefore, is a unique UE state.
- (3)
- when , it is clear that neither nor is a UE state. Assume that the slopes of functions and under the solution are
Substituting and into the above equations, one has and . According to Property 1(c), is a UE state. Next, we prove that the solution is unique. The derivative of with respect to is
Thus, is an increasing function of . Therefore, there is a unique that meets , and is a unique UE state. □
Appendix A.4. Proof of Proposition 5
Assuming , from Equation (5), one has
- (a)
- If , together with (Assumption 1), one can easily derive that all travelers choose route 1 under UE, i.e., . Substituting into Equation (32), one has
Since one has
- (b)
- If , then one has and . Substituting into Equation (32), one has
Then, one has
- (c)
- If , then one has . Substituting into Equation (32), one has
Therefore, one has .
When , the proposition can be proved in a similar way and is omitted here. □
References
- Levinson, D. The value of advanced traveler information systems for route choice. Transp. Res. Part C Emerg. Technol. 2003, 11, 75–87. [Google Scholar] [CrossRef]
- Luo, X.; Liu, Y.; Yu, Y. Dynamic bus dispatching using multiple types of real-time information. Transp. B Transp. Dyn. 2019, 7, 519–545. [Google Scholar] [CrossRef]
- Mori, U.; Mendiburu, A.; Alvarez, M.; Lozano, J.A. A review of travel time estimation and forecasting for advanced traveler information systems. Transp. A Transp. Sci. 2015, 11, 119–157. [Google Scholar]
- Neil, L.; Richard, H.; Jeff, H. Driver opinion of message requirements for advanced traveler information systems. Plant Physiol. 1970, 45, 576–578. [Google Scholar]
- Perez, W.A.; Mast, T.M. Human factors and advanced traveler information systems (ATIS). Proc. Hum. Factors Ergon. Soc. Annu. Meet. 1992, 36, 1073–1077. [Google Scholar] [CrossRef]
- Rapoport, A.; Gisches, E.J.; Daniel, T.; Lindsey, R. Pre-trip information and route-choice decisions with stochastic travel conditions: Experiment. Transp. Res. Part B Methodol. 2014, 68, 154–172. [Google Scholar] [CrossRef]
- Sen, S.; Pillai, R.; Joshi, S.; Rathi, A.K. A mean-variance model for route guidance in advanced traveler information systems. Transp. Sci. 2001, 35, 37–49. [Google Scholar] [CrossRef]
- Emmerink, R.H.M.; Nijkamp, P.; Rietveld, P.; Van Ommeren, J.N. Variable message signs and radio traffic information: An integrated empirical analysis of drivers’ route choice behavior. Transp. Res. Part A Policy Pract. 1996, 30, 135–153. [Google Scholar] [CrossRef]
- Li, M.; Lin, X.; He, F.; Jiang, H. Optimal locations and travel time display for variable message signs. Transp. Res. Part C Emerg. Technol. 2016, 69, 418–435. [Google Scholar] [CrossRef]
- Wang, C.; David, B.; Chalon, R. Dynamic road lane management study. Transp. Res. Part E Logist. Transp. Rev. 2016, 89, 272–287. [Google Scholar] [CrossRef]
- Yu, Y.; Machemehl, R.B.; Xie, C. Demand-responsive transit circulator service network design. Transp. Res. Part E Logist. Transp. Rev. 2015, 76, 160–175. [Google Scholar] [CrossRef]
- Ahmed, A.; Ngoduy, D.; Watling, D. Prediction of traveller information and route choice based on real-time estimated traffic state. Transp. B Transp. Dyn. 2016, 4, 23–47. [Google Scholar] [CrossRef]
- Ben-Elia, E.; Avineri, E. Response to travel information: A behavioral review. Transp. Rev. 2015, 35, 352–377. [Google Scholar] [CrossRef]
- Chorus, C.G.; Eric JE, M.; van Wee, B. Travel information as an instrument to change car drivers’ travel choices: A literature review. Eur. J. Transp. Infrastruct. Res. 2006, 6, 335–364. [Google Scholar]
- Chorus, C.G.; Arentze, T.A.; Timmermans, H.J.P. Traveler compliance with advice: A Bayesian utilitarian perspective. Transp. Res. Part E Logist. Transp. Rev. 2009, 45, 486–500. [Google Scholar] [CrossRef]
- Golob, T.F.; Regan, A.C. The perceived usefulness of different sources of traffic information to trucking operations. Transp. Res. Part E Logist. Transp. Rev. 2002, 38, 97–116. [Google Scholar] [CrossRef]
- Los, J.; Schulte, F.; Spaan, M.T.J. The Value of Information Sharing for Platform-Based Collaborative Vehicle Routing. Transp. Res. Part E Logist. Transp. Rev. 2020, 141, 102011. [Google Scholar] [CrossRef]
- Wepulanon, P.; Sumalee, A.; Lam, W.H.K. A real-time bus arrival time information system using crowdsourced smartphone data: A novel framework and simulation experiments. Transp. B 2017, 6, 34–53. [Google Scholar] [CrossRef]
- Zhu, Z.; Li, X.W.; Liu, W.; Yang, H. Day-to-day evolution of departure time choice in stochastic capacity bottleneck models with bounded rationality and various information perceptions. Transp. Res. Part E Logist. Transp. Rev. 2019, 131, 168–192. [Google Scholar] [CrossRef]
- Ben-Elia, E.; Pace, R.D.; Bifuico, G.N. The impact of travel information’s accuracy on route-choice. Transp. Res. Part C Emerg. Technol. 2013, 26, 146–159. [Google Scholar] [CrossRef]
- Engelson, L.; Fosgerau, M. Scheduling preferences and the value of travel time information. Transp. Res. Part B Methodol. 2020, 134, 256–265. [Google Scholar] [CrossRef]
- Khattak, A.J.; Yim, Y.; Prokopy, L.S. Willingness to pay for travel information. Transp. Res. Part C Emerg. Technol. 2003, 11, 137–159. [Google Scholar] [CrossRef]
- Mahmassani, H.S.; Chee, C.T. Availability of information and dynamics of departure time choices: Experimental investigation. Transp. Res. Rec. J. Transp. Res. Board 1986, 1085, 33–49. [Google Scholar]
- Emmerink, R.H.M.; Kay, W.A.; Peter, N.; Piet, R. The potential of information provision in a simulated road transport network with non-recurrent congestion. Transp. Res. Part C Emerg. Technol. 1995, 3, 293–309. [Google Scholar] [CrossRef]
- Acemoglu, D.; Makhdoumi, A.; Malekian, A.; Ozdaglar, A. Informational braess’ paradox: The effect of information on traffic congestion. Oper. Res. 2016, 66, 893–917. [Google Scholar] [CrossRef]
- Emmerink, R.H.M.; Verhoef, E.T.; Nijkamp, P.; Rietveld, P. Information policy in road transport with elastic demand: Some welfare economic considerations. Eur. Econ. Rev. 1998, 42, 71–95. [Google Scholar] [CrossRef]
- Verhoef, E.T.; Emmerink, R.H.M.; Nijkamp, P.; Rietveld, P. Information provision, flat and fine congestion tolling and the efficiency of road usage. Reg. Sci. Urban Econ. 1996, 26, 505–529. [Google Scholar] [CrossRef]
- Lindsey, R.; Daniel, T.; Gisches, E.J.; Rapoport, A. Pre-trip information and route-choice decisions with stochastic travel conditions: Theory. Transp. Res. Part B Methodol. 2014, 67, 187–207. [Google Scholar] [CrossRef]
- Abdel-Aty, M.A.; Kitamura, R.; Jovanis, P.P. Investigating effect of travel time variability on route choice using repeated-measurement stated preference data. Transp. Res. Rec. 1995, 1493, 39–45. [Google Scholar]
- Jackson, W.B.; Jucker, J.V. An empirical study of travel time variability and travel choice behavior. Transp. Sci. 1982, 16, 460–475. [Google Scholar] [CrossRef]
- Chen, A.; Zhou, Z. The α-reliable mean-excess traffic equilibrium model with stochastic travel times. Transp. Res. Part B Methodol. 2010, 44, 493–513. [Google Scholar] [CrossRef]
- Chen, A.; Zhou, Z.; Lam, W.H.K. Modeling stochastic perception error in the mean-excess traffic equilibrium model. Transp. Res. Part B Methodol. 2011, 45, 1619–1640. [Google Scholar] [CrossRef]
- Xu, X.; Chen, A.; Cheng, L. Assessing the effects of stochastic perception error under travel time variability. Transportation 2013, 40, 525–548. [Google Scholar] [CrossRef]
- Xu, X.; Chen, A.; Cheng, L.; Lo, H.K. Modeling distribution tail in network performance assessment: A mean-excess total travel time risk measure and analytical estimation method. Transp. Res. Part B Methodol. 2014, 66, 32–49. [Google Scholar] [CrossRef]
- Zhou, Z.; Chen, A. Comparative analysis of three user equilibrium models under stochastic demand. J. Adv. Transp. 2008, 42, 239–263. [Google Scholar] [CrossRef]
- Lo, H.K.; Tung, Y.K. Network with degradable links: Capacity analysis and design. Transp. Res. Part B Methodol. 2003, 37, 345–363. [Google Scholar] [CrossRef]
- Lo, H.K.; Luo, X.W.; Siu, B.W.Y. Degradable transport network: Travel time budget of travelers with heterogeneous risk aversion. Transp. Res. Part B Methodol. 2006, 40, 792–806. [Google Scholar] [CrossRef]
- Yin, Y.; Lam, W.H.K.; Ieda, H. New technology and the modeling of risk-taking behavior in congested road networks. Transp. Res. Part C 2004, 12, 171–192. [Google Scholar] [CrossRef]
- Tan, Z.; Yang, H.; Guo, R. Pareto efficiency of reliability-based traffic equilibria and risk-taking behavior of travelers. Transp. Res. Part B Methodol. 2014, 66, 16–31. [Google Scholar] [CrossRef]
- Li, Z. Unobserved and observed heterogeneity in risk attitudes: Implications for valuing travel time savings and travel time variability. Transp. Res. Part E Logist. Transp. Rev. 2018, 112, 12–18. [Google Scholar] [CrossRef]
- U.S. Bureau of Public Roads. Traffic Assignment Manual; U.S. Bureau of Public Roads: Washington, DC, USA, 1964.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).