Dynamic Governance of China’s Copper Supply Chain: A Stochastic Differential Game Approach

Abstract

As global copper demand continues to grow, China, being the largest copper consumer, faces increasingly complex challenges in ensuring the security of its supply chain. However, a substantive gap remains: prevailing assessments rely on static index systems and discrete scenario analyses that seldom model uncertainty-driven, continuous-time strategic interactions, leaving the conditions for self-enforcing cooperation and the attendant policy trade-offs insufficiently identified. This study models the interaction between Chinese copper importers and foreign suppliers as a continuous-time stochastic differential game, with feedback Nash equilibria derived from a Hamilton–Jacobi–Bellman system. The supply security utility is specified as a diffusion process perturbed by Brownian shocks, while regulatory intensity and profit-sharing are treated as structural parameters shaping its drift and volatility—thereby delineating the parameter region for self-enforcing cooperation and clarifying how sudden disturbances reconfigure equilibrium security. The research findings reveal the following: (i) the mean and variance of supply security utility progressively strengthen over time under the influence of both parties’ maintenance efforts, while stochastic disturbances causing actual fluctuations remain controllable within the contract period; (ii) spontaneous cooperation can be achieved under scenarios featuring strong regulation of domestic importers, weak regulation of foreign suppliers, and a profit distribution ratio slightly favoring foreign suppliers, thereby reducing regulatory costs; this asymmetry is beneficial because stricter oversight of domestic importers curbs the primary deviation risk, lighter oversight of foreign suppliers avoids cross-border enforcement frictions, and a modest supplier-favored profit-sharing ratio sustains participation—together expanding the self-enforcing cooperation set; (iii) sudden events exert only short-term impacts on supply security with controllable long-term effects; however, an excessively stringent regulatory environment can paradoxically reduce long-term supply security. Security effort levels demonstrate positive correlation with supply security, while regulatory intensity must be maintained within a moderate range to balance incentives and constraints.

1. Introduction

Amid accelerating global energy transition and digital transformation, copper, as a critical strategic resource underpinning clean energy technologies, smart grids, and advanced manufacturing, is undergoing profound restructuring in its supply–demand dynamics [1]. Over the past decade, global copper demand has surged by over 30%, with the International Energy Agency forecasting that clean energy applications will double copper requirements by 2040 to achieve carbon neutrality targets [2]. China, accounting for over 50% of global copper consumption yet possessing merely 3% of worldwide copper reserves, maintains long-term import dependence exceeding 75% due to acute disparities between resource endowment and consumption scale. However, escalating geopolitical conflicts, resurgent resource nationalism, and pervasive opportunism in cross-border supply chains have compounded moral hazards and information asymmetries, threatening China’s copper supply chain security [3]. This situation creates a complex strategic environment where firms must simultaneously compete for value while cooperating to ensure the stability of the entire supply chain—a dynamic known as coopetition. Recent studies highlight that such coopetitive relationships are critical for building startup resilience, particularly through the development of network-building and resource integration capabilities within a broader entrepreneurial ecosystem [4]. The challenge, therefore, is not merely to mitigate risk but to design governance mechanisms that foster this productive form of coopetition. How to balance supervision cost and cooperation incentive through mechanism design, and achieve long-term stability of supply chain security in a dynamic game, has become a major practical problem related to national resource security and industrial competitiveness.

In recent years, research on copper has moved beyond single-dimension analyses of price and quantity volatility toward an integrated governance orientation that jointly considers import concentration, technological substitutability, and recycling. First, in supply chain risk measurement, prior work integrates the probability of external disruption, economic exposure, and absorptive capacity into a unified criticality index, thereby establishing a comparable and trackable assessment paradigm that serves as a methodological baseline for profiling risks across minerals and along industrial chains [5]. Building on this, copper studies have advanced from single-indicator vulnerability to a joint depiction of network-system-scenario dynamics: on the one hand, by constructing multi-layer trade networks of primary and secondary resources to reveal structural heterogeneity and co-movement between upstream/downstream segments and the recycling end, and to test how policies perturb and re-balance the composite system [6]; on the other hand, by leveraging mechanisms in multi-layer networks-such as cascading failures and the “strengthening” role of weak layers-to map cross-layer transmission chains and directed diffusion, showing that upstream hub nodes can generate pronounced amplification and threshold effects under particular scenarios [7]. In short, the differential game complements multi-layer network evidence by endogenizing the parties’ incentives and mapping network shocks into feedback Nash paths of supply-security utility, which identifies self-enforcing cooperation thresholds under regulatory intensity and profit distribution parameters. From the perspective of market transmission and price formation, the relational structure of the industrial chain significantly shapes the level and strength of copper-price pass-through, underscoring the foundational role of network identification in supply chain security governance [8]. Meanwhile, dynamic analyses of global copper flows uncover the temporal coupling and long-run constraints linking stocks, recycling, and re-use, implying that circularity indicators (e.g., recovery rates) should be embedded in medium- to long-term security assessments [9]. Evidence for China further shows that provincial material footprints of copper-embedded in domestic and international trade exhibit structural differences and temporal shifts, reflecting the evolving exposure and spatial distribution of the chain; accordingly, early warning systems should embed both time and scenario dimensions [10]. In addition, during crises, directional volatility, connectedness and structural breaks between metal and energy markets can amplify price and inventory fluctuations through financial-commodity channels, altering the propagation of supply-side pressures and necessitating explicit treatment of the persistence and spillovers of market-driven shocks in supply chain security analysis [11].

On methodology, research on dynamic interactions in resources and the environment has shifted from static-equilibrium treatments to continuous-time frameworks. Differential games and stochastic optimal control permit multi-agent behaviour to be modelled within a unified system of strategic interaction, state evolution, and exogenous shocks; in particular, stochastic differential games, by incorporating Brownian perturbations, feedback strategies, and random horizons, can simultaneously address uncertainty and asymmetric information while delivering equilibrium concepts and stability conditions consistent with game-theoretic foundations [12]. By contrast, many quantitative studies of copper import security still rely on static-weight index systems or discrete scenario simulations. Although these approaches are policy-relevant and data-granular-useful for identifying vulnerable links, proposing substitutions, and producing risk forecasts, they do not provide a unified dynamic-uncertainty framework to analyze (i) the co-evolution, in continuous time, of regulatory intensity, cooperative effort, and external shocks; (ii) self-enforcing cooperation thresholds under asymmetric regulation and revenue-sharing rules; or (iii) the impact of shock persistence on long-run stability.

Synthesising the above strands, structural facts, and network-based evidence on copper supply chain risk and resilience have become clearer: multi-layer network models capture the coupling between primary and secondary systems [6]; multi-layer theory identifies cross-layer propagation and cascading amplification [7]; the industrial-chain relational structure links network topology to market price transmission [8]. At the same time, cross-market connectedness indicates that risks arise not only from physical supply–demand and geopolitics but are also amplified and redirected by financial channels [11]. However, studies that integrate regulator-firm strategic interaction, firms’ effort choices, and the persistence of exogenous shocks within a single continuous-time framework remain scarce, especially under a game between importers and foreign suppliers, with the regulator’s actions treated as exogenous parameters that can identify the self-enforcing cooperation threshold and the trade-off between long-run stability and stochastic disturbances.

Relative to multi-layer trade-network models—which illuminate structural heterogeneity, path dependence, and co-movement across upstream, downstream, and recycling layers—a stochastic differential game offers a complementary, mechanism-based lens with clear methodological advantages. First, it micro-grounds observed linkages in incentive-compatible interaction between domestic importers and foreign suppliers, yielding equilibrium behaviour rather than reduced-form associations. Second, it treats regulatory intensity and profit distribution as structural primitives that determine continuous-time adjustment paths. Third, by embedding uncertainty through diffusion dynamics and feedback strategies, it produces testable stability domains and cooperation thresholds, along with diagnostics on shock persistence, that network model typically do not identify. In this sense, the differential-game perspective does not displace network analysis; it supplies the equilibrium mechanism and policy calculus that the latter abstracts from.

In response to these issues, this paper innovatively develops a stochastic differential game model that transcends the limitations of conventional static analysis and, within a unified dynamic-uncertainty framework, reveals three core mechanisms: (i) by treating regulatory intensity, cooperative effort, and random disturbances as coupled endogenous-exogenous drivers, it derives the co-evolution laws of the mean and variance of supply chain security across parameter regions; (ii) it delineates the minimal feasible set for asymmetric regulation and revenue sharing and the constraints on steady-state variance, thereby identifying the threshold conditions for self-enforcing cross-border cooperation; and (iii) it quantifies the persistence of external shocks and demonstrates the role of regulation in shaping long-run stability. The findings provide a tractable theoretical instrument for addressing the “high regulatory cost-low cooperation efficiency” dilemma and aim to contribute to the safeguarding of critical mineral resource security.

The rest of this paper is organized as follows: Section 2 introduces core parameters, including regulatory intensity, incentive mechanisms, and safety utility, and develops a differential game model. Section 3 and Section 4 presents an analysis and discussion of the results to assess the variations in safety utility and the impact of different factors on its performance. Section 5 conducts simulation analysis. Section 6 concludes the paper and provides policy recommendations. Section 7 discusses the research limitations and future research directions.

2. Methods

2.1. Related Parameters

2.1.1. The Effort Costs Quadratic Equation of Governments and Enterprises

Consistent with previous studies [13], we assumed the effort costs of domestic importers and foreign suppliers are quadratic forms and satisfy the following equations.

$$C\left(t\right)={\displaystyle \frac{\eta I^2\left(t\right)}{2}}$$

(1)

$$C_E\left(t\right)={\displaystyle \frac{{\eta }_E{E}^2\left(t\right)}{2}}$$

(2)

where $\eta$ and ${\eta }_E$ represent the cost coefficients of domestic importers and foreign suppliers’ effort levels, respectively. The cost coefficients measure how costly it is to raise the effort level by one unit; a larger coefficient implies a faster increase in marginal cost. $I\left(t\right)$ and $E\left(t\right)$ are the safety effort levels of domestic importers and foreign suppliers at time t, respectively. “Safety efforts” refer to observable or contractible actions undertaken by domestic importers and foreign suppliers to improve copper supply chain security and reduce breach and disruption risks. In practice, these actions include, for example, compliance and quality assurance, due diligence on counterparties, inventory buffering and logistics redundancy, process safety and traceability, and information-sharing for shipment and documentation. In the model, they are time-dependent, non-negative intensities—the higher the intensity, the greater the deterministic improvement (drift) in the supply-security utility in Equation (3), albeit at increasing costs as specified by Equations (1) and (2).

2.1.2. Profit Distribution Ratio and Chinese Government Subsidies

It is assumed that the distribution of the revenue obtained from copper import trade is negotiated between the domestic importers and the foreign suppliers. The domestic importers receive a proportion of the revenue, denoted by $\alpha$, while the foreign suppliers receive the remaining proportion, which is $1-\alpha$.

To ensure copper supply chain security and meet domestic demand, the Chinese government provides subsidies to cover costs incurred by domestic importers and foreign suppliers during trade transactions, such as tax incentives, with subsidy rates of ${\epsilon }_I$ and ${\epsilon }_E$, respectively, where $0<{\epsilon }_I<1$ and $0<{\epsilon }_E<1$. The subsidy rate for domestic importers and for foreign suppliers is understood as the share of verified safety-effort expenditure that is reimbursed by the regulator. A higher subsidy rate reduces the private cost of undertaking such efforts but does not change their physical effectiveness in improving supply security. Disbursement is made ex post against audited documentation and is conditional on compliance.

2.1.3. Supply Security Utility

For both parties involved in multinational supply, when contract costs are high or when there is a long-term cooperation foundation between the parties, the supply chain exhibits greater resilience, thereby ensuring its supply security. Therefore, it is assumed that the dynamic changes in copper supply security utility consist of two parts: first, the security efforts made by the domestic importer and foreign supplier to establish long-term cooperation, as well as the natural decay of supply security utility during this process; second, the decay of supply security utility caused by uncontrollable factors such as natural disasters, economic fluctuations, and geopolitical relations. In practical applications, stochastic processes driven by random factors are typically approximated by Brownian motion, whose increments follow a normal distribution [14]. Therefore, this paper introduces the Brownian process to reflect the random disturbances encountered during the decision-making process of the agents, analyses the behaviour decisions of the domestic importer and foreign supplier, and discusses the changes in system stability under random disturbances. The copper supply security utility function is then expressed as follows:

$$d\dot{U}\left(t\right)=\left({\lambda }_{1}I\left(t\right)+{\lambda }_{2}E\left(t\right)-\xi U\left(t\right)\right)dt+\sigma \sqrt{U\left(t\right)}dz\left(t\right)$$

(3)

where $U\left(t\right)$ represents the copper supply security utility; ${\lambda }_1$ and ${\lambda }_2$ represent the coefficients of the impact of the domestic importers and foreign suppliers’ security effort levels on the supply security utility; $\xi$ represents the decay rate of the supply security utility; $\sigma \left(U\left(t\right)\right)$ represents the random disturbance term; and $dz\left(t\right)$ represents Gaussian white noise, which follows a normal distribution.

2.1.4. Demand Function

$$Q\left(t\right)=q_0-\beta p\left(t\right)+\gamma U\left(t\right)$$

(4)

where $Q\left(t\right)$ represents the copper demand of the domestic importers at time $t$, $Q\left(t\right)>0$; $q_0$ represents the initial copper demand of the domestic importers; $\beta$ represents the price elasticity of the domestic importers’ copper demand; $p\left(t\right)$ represents the copper price at time $t$; and $\gamma$ represents the efficiency coefficient of the copper supply security utility on copper demand.

2.1.5. Chinese Government Supervision

The Chinese government regulates domestic importers, assuming the regulatory intensity is $\theta$. In the event of a breach, there is a probability of being detected, denoted as $P\left(\theta \right)$, $P^{\prime }\left(\theta \right)>0$, and a penalty of $\tau P\left(\theta \right)\left(I\left(0\right)-I\left(t\right)\right)$ will be paid, where $\tau$ represents the penalty coefficient for the domestic importers’ breach, and $I\left(0\right)$ is the minimum security effort level agreed upon by the domestic importers and foreign suppliers in their contract. In the absence of a breach, $I\left(t\right)\ge I\left(0\right)$; when the domestic importers breach the contract to pursue additional personal gains, $I\left(t\right)$ is much smaller than $I\left(0\right)$. If the breach is not detected by the Chinese government promptly, the gain obtained is denoted as $\omega \left(1-P\left(\theta \right)\right)\left(I\left(0\right)-I\left(t\right)\right)$, where $\omega$ is the payoff coefficient for the domestic importers.

Similarly, the foreign suppliers’ breach will be detected with a probability of $P\left({\theta }_E\right)$ (where $P^{\prime }\left({\theta }_E\right)>0$), and a penalty of ${\tau }_{E}P\left({\theta }_E\right)\left(E\left(0\right)-E\left(t\right)\right)$ will be paid, where ${\tau }_E$ represents the breach penalty coefficient for the foreign suppliers, and $E\left(0\right)$ is the minimum security effort level agreed upon by the foreign suppliers and the domestic importers in their contract. If the breach is not detected by the Chinese government on time, the gain obtained is denoted as ${\omega }_E\left(1-P\left({\theta }_E\right)\right)\left(E\left(0\right)-E\left(t\right)\right)$, where ${\omega }_E$ is the payoff coefficient for the foreign supplier.

2.2. The Model

2.2.1. Model Description

Both the domestic importers and the foreign suppliers aim to maximise their expected payoffs. Due to the insufficient domestic copper supply to meet domestic consumption demand, China relies heavily on imports. In this process, we model a Stackelberg game in which foreign suppliers act as leaders and domestic importers act as followers. This timing choice reflects the institutional features of the copper-concentrate trade: annual benchmark and term negotiations are typically anchored by upstream mining firms and then followed by smelter/importer procurement decisions [15,16]. It also aligns with evidence that metals markets can exhibit supply-side pricing power and strategic supply management, consistent with leader behaviour on the upstream side [17]. Moreover, network structure in the copper trade—particularly upstream concentration and centrality—has been shown to shape price formation, reinforcing the plausibility of supplier leadership in equilibrium [8]. Finally, the irreversibility and long lead times of mining capacity provide upstream actors with commitment advantages over short-horizon smelting adjustments, a classic rationale for Stackelberg leadership [18].

Specifically, in the first stage, foreign suppliers publicly post contract terms for concentrate deliveries over the planning horizon, including volumes, shipment windows, and quality or traceability clauses. This mirrors the benchmark and term contracting protocol documented for the copper-concentrate trade [15]. In the second stage, domestic importers observe the posted terms and choose procurement and operational decisions that maximize expected payoffs under uncertainty. Payoffs are realized after exogenous shocks within the contract period. The first move creates a commitment effect. By fixing observable terms in advance, the leader reshapes the follower’s best-response set and selects a favorable point on the reaction curve. This is the canonical Stackelberg advantage in dynamic settings [19].

2.2.2. Objective Functions for Domestic Importers and Foreign Suppliers

The domestic importers obtain a payoff $\alpha p\left(t\right)\left(q_0-\beta p\left(t\right)+\gamma U\left(t\right)\right)$ from copper import trade, with the trade cost of $\left(1-\epsilon \right)C\left(t\right)$ after government subsidies. If the domestic importers breach the contract, there is a probability of $P\left(\theta \right)$ being detected by the Chinese government, in which case a penalty of $\tau P\left(\theta \right)\left(I\left(0\right)-I\left(t\right)\right)$ must be paid. If the breach is not detected, the potential payoff is $\left(1-P\left(\theta \right)\right)\omega \left(I\left(0\right)-I\left(t\right)\right)$. $\rho$ is the discount factor. Therefore, the objective function of the domestic importers is:

$${\pi }_I=\underset{I\left(t\right)}{max}E\left\{{\int }_0^T{e}^{-\rho t}\left[\begin{array}{c}\left(\alpha p\left(t\right)\left(q_0-\beta p\left(t\right)+\gamma U\left(t\right)\right)\right)-\left(1-\epsilon \right)C\left(t\right)-\hfill \\ \tau P\left(\theta \right)\left(I\left(0\right)-I\left(t\right)\right)+\left(1-P\left(\theta \right)\right)\omega \left(I\left(0\right)-I\left(t\right)\right)\hfill \end{array}\right]dt\right\}$$

(5)

Similarly, the foreign suppliers obtain a payoff $\left(1-\alpha \right)p\left(t\right)\left(q_0-\beta p\left(t\right)+\gamma U\left(t\right)\right)$ from copper import trade, with the trade cost of $\left(1-{\epsilon }_E\right)C_E\left(t\right)$ after government subsidies. If the foreign suppliers breach the contract, there is a probability of $P\left({\theta }_E\right)$ being detected by the Chinese government, in which case a penalty of ${\tau }_{E}P\left({\theta }_E\right)\left(E\left(0\right)-E\left(t\right)\right)$ must be paid. If the breach is not detected, the potential payoff is $\left(1-P\left({\theta }_E\right)\right){\omega }_E\left(E\left(0\right)-E\left(t\right)\right)$. $\rho$ is the discount factor. Therefore, the objective function of the foreign suppliers is:

$${\pi }_E=\underset{E\left(t\right)}{max}E\left\{{\int }_0^T{e}^{-\rho t}\left[\begin{array}{c}\left(\left(1-\alpha \right)p\left(t\right)\left(q_0-\beta p\left(t\right)+\gamma U\left(t\right)\right)\right)-\left(1-{\epsilon }_E\right)C_E\left(t\right)-\hfill \\ {\tau }_{E}P\left({\theta }_E\right)\left(E\left(0\right)-E\left(t\right)\right)+\left(1-P\left({\theta }_E\right)\right){\omega }_E\left(E\left(0\right)-E\left(t\right)\right)\hfill \end{array}\right]dt\right\}$$

(6)

For convenience of notation, the time unit will be omitted in the following text.

3. Results

3.1. Optimal Strategy Solution

Building on the Stackelberg timing in Section 2.2 and the payoff functionals specified for domestic importers and foreign suppliers, we derive a feedback Nash solution on the planning horizon by solving the coupled Hamilton-Jacobi-Bellman system.

Proposition 1.

The feedback Nash equilibrium result of the non-cooperative Stackelberg game model, composed of Equations (5) and (6) within the time interval $\left[0,T\right]$ is as follows.

The optimal security effort level for the domestic importers is:

$$I^{*}={\displaystyle \frac{\Lambda \left(\rho +\xi \right)-{\lambda }_1\alpha p\gamma }{\left(1-\epsilon \right)\eta \left(\rho +\xi \right)}}$$

(7)

where $\Lambda =\left(1-P\left(\theta \right)\right)\omega -\tau P\left(\theta \right)$.

The optimal security effort level for the foreign suppliers is:

$$E^{*}={\displaystyle \frac{{\Lambda }_E\left(\rho +\xi \right)-{\lambda }_2\left(1-\alpha \right)p\gamma }{\left(1-{\epsilon }_E\right){\eta }_E\left(\rho +\xi \right)}}$$

(8)

where ${\Lambda }_E=\left(1-P\left({\theta }_E\right)\right){\omega }_E-{\tau }_{E}P\left({\theta }_E\right)$.

The optimal trajectory of supply security utility is:

$$d{U}^{*}=\left({\lambda }_1{I}^{*}+{\lambda }_2{E}^{*}-\xi U^{*}\right)dt+\sigma \sqrt{U^{*}}dz$$

(9)

Proof of Proposition 1. 

The following Hamilton–Jacobi–Bellman (HJB) equation characterises the optimal value functions of domestic importers and foreign suppliers:

$$\rho V_I=\underset{I\ge 0}{max}\left\{\begin{array}{c}\alpha p\left(q_0-\beta p+\gamma U\right)+\left(1-\epsilon \right)C-\tau P\left(\theta \right)\left(I_0-I\right)\\ +\left(1-P\left(\theta \right)\right)\omega \left(I_0-I\right)+{V_I}^{\prime }\left({\lambda }_{1}I+{\lambda }_{2}E-\xi U\right)+{\displaystyle \frac{1}{2}}{\sigma }^{2}U{V_I}^{″}\end{array}\right\}$$

(10)

$$\rho V_E=\underset{E\ge 0}{max}\left\{\begin{array}{c}\left(1-\alpha \right)p\left(q_0-\beta p+\gamma U\right)+\left(1-{\epsilon }_E\right)C_E-{\tau }_{E}P\left({\theta }_E\right)\left(E_0-E\right)\\ +\left(1-P\left({\theta }_E\right)\right){\omega }_E\left(E_0-E\right)+{V_E}^{\prime }\left({\lambda }_{1}I+{\lambda }_{2}E-\xi U\right)+{\displaystyle \frac{1}{2}}{\sigma }^{2}U{V_E}^{″}\end{array}\right\}$$

(11)

By taking the partial derivative with respect to the decision variable.

$$I^{*}={\displaystyle \frac{\Lambda -{\lambda }_1{V_I}^{\prime }}{\left(1-\epsilon \right)\eta }}$$

(12)

$$E^{*}={\displaystyle \frac{{\Lambda }_E-{\lambda }_2{V_E}^{\prime }}{\left(1-{\epsilon }_E\right){\eta }_E}}$$

(13)

The linear optimal functions of security effort levels for domestic importers and foreign suppliers, which are solutions to the HJB equation, can be expressed as Equation (14) based on their structural form, and the following results can be derived: ${V_I}^{\prime }=s_1$, ${V_E}^{\prime }=s_2$.

$$\left\{\begin{array}{c}{V}_I\left(U\right)=s_{1}U+d_1\\ V_E\left(U\right)=s_{2}U+d_2\end{array}\right.$$

(14)

By substituting Equations (12)–(14) into Equations (10) and (11), the following can be derived:

$$\rho \left(s_{1}U+d_1\right)=\left\{\begin{array}{c}\alpha p\left(q_0-\beta p+\gamma U\right)+\left(1-\epsilon \right)C-\tau P\left(\theta \right)\left(I_0-{\displaystyle \frac{\Lambda -{\lambda }_1{s}_1}{\left(1-\epsilon \right)\eta }}\right)\\ +\left(1-P\left(\theta \right)\right)\omega \left(I_0-{\displaystyle \frac{\Lambda -{\lambda }_1{s}_1}{\left(1-\epsilon \right)\eta }}\right)+s_1\left({\lambda }_1{\displaystyle \frac{\Lambda -{\lambda }_1{s}_1}{\left(1-\epsilon \right)\eta }}+{\lambda }_2{\displaystyle \frac{{\Lambda }_E-{\lambda }_2{s}_2}{\left(1-{\epsilon }_E\right){\eta }_E}}-\xi U\right)\end{array}\right\}$$

(15)

$$\rho \left(s_{2}U+d_2\right)=\left\{\begin{array}{c}\left(1-\alpha \right)p\left(q_0-\beta p+\gamma U\right)+\left(1-{\epsilon }_E\right)C_E-{\tau }_{E}P\left({\theta }_E\right)\left(E_0-{\displaystyle \frac{{\Lambda }_E-{\lambda }_2{s}_2}{\left(1-{\epsilon }_E\right){\eta }_E}}\right)\\ +\left(1-P\left({\theta }_E\right)\right){\omega }_E\left(E_0-{\displaystyle \frac{{\Lambda }_E-{\lambda }_2{s}_2}{\left(1-{\epsilon }_E\right){\eta }_E}}\right)+s_2\left({\lambda }_1{\displaystyle \frac{\Lambda -{\lambda }_1{s}_1}{\left(1-\epsilon \right)\eta }}+{\lambda }_2{\displaystyle \frac{{\Lambda }_E-{\lambda }_2{s}_2}{\left(1-{\epsilon }_E\right){\eta }_E}}-\xi U\right)\end{array}\right\}$$

(16)

It can be derived that,

$$s_1={\displaystyle \frac{\alpha p\gamma }{\rho +\xi }},s_2={\displaystyle \frac{\left(1-\alpha \right)p\gamma }{\rho +\xi }},I^{*}={\displaystyle \frac{\Lambda \left(\rho +\xi \right)-{\lambda }_1\alpha p\gamma }{\left(1-\epsilon \right)\eta \left(\rho +\xi \right)}},E^{*}={\displaystyle \frac{{\Lambda }_E\left(\rho +\xi \right)-{\lambda }_2\left(1-\alpha \right)p\gamma }{\left(1-{\epsilon }_E\right){\eta }_E\left(\rho +\xi \right)}}.\square$$

3.2. Analysis of the Evolutionary Characteristics of Supply Security Utility

To investigate the impact of optimal security effort levels between domestic importers and foreign suppliers on supply security utility, this paper conducts a statistical analysis of supply security utility.

Proposition 2. 

The expected value of supply security utility is:

$$E\left(U^{*}\right)={\displaystyle \frac{\Omega }{\xi }}+e^{-\xi t}\left(U_0-{\displaystyle \frac{\Omega }{\xi }}\right)$$

(17)

where $\Omega ={\lambda }_1{I}^{*}+{\lambda }_2{E}^{*}$.

The variance of supply security utility is:

$$D\left(U^{*}\right)=e^{-2\xi t}{\left(U_0-{\displaystyle \frac{\Omega }{\xi }}+e^{\xi t}{\displaystyle \frac{\Omega }{\xi }}\right)}^2-{\displaystyle \frac{e^{-\xi t}\left(\Omega -\xi U_0\right)\left(2\Omega +{\sigma }^2\right)}{{\xi }^2}}-e^{-2\xi t}\left(U_0^2+{\displaystyle \frac{2\left(2\Omega +{\sigma }^2\right)\left(\Omega -\xi U_0\right)-\Omega \left(2\Omega +{\sigma }^2\right)}{2{\xi }^2}}\right)+{\displaystyle \frac{\Omega \left(2\Omega +{\sigma }^2\right)}{2{\xi }^2}}$$

(18)

As a random variable, the supply security utility fluctuates around its expected value. For participating entities such as domestic importers and foreign suppliers, it is challenging to obtain a deterministic value of supply security utility at any given moment. However, they can assess and delineate the range of supply security utility through confidence intervals. At the 95% confidence level, the confidence interval for supply security utility is $\left(E\left(U^{*}\right)-1.96\sqrt{D\left(U^{*}\right)}, E\left(U^{*}\right)+1.96\sqrt{D\left(U^{*}\right)}\right)$.

Furthermore, Equations (19) and (20) reveal that over time, the mean and variance of supply security utility are increasingly influenced by the security effort levels of domestic importers and foreign suppliers. From the perspective of dynamic evolution characteristics, it can be inferred that the actual level of supply security utility may deviate from its expected value due to stochastic factors. However, within the contractual period, the actual utility fluctuates around the expected value in a controlled manner within specified bounds. These fluctuations remain manageable, enabling participating entities to reasonably interpret the anticipated state and make informed decisions based on these expectations.

$$\underset{t\to \infty }{lim}E\left(U\left(t\right)\right)={\displaystyle \frac{{\lambda }_{1}I+{\lambda }_{2}E}{\xi }}$$

(19)

$$\underset{t\to \infty }{lim}D\left(U\left(t\right)\right)={\left({\displaystyle \frac{{\lambda }_{1}I+{\lambda }_{2}E}{\xi }}\right)}^2+{\displaystyle \frac{{\sigma }^2}{2{\xi }^2}}$$

(20)

For further analysis, Equation (18) can be expressed in the following form:

$$D\left(U^{*}\right)={\displaystyle \frac{2-4e^{-\xi t}}{{\xi }^2}}{\Omega }^2+\left({\displaystyle \frac{4e^{-\xi t}{U}_0}{\xi }}+{\displaystyle \frac{{\sigma }^2\left(1-e^{-\xi t}-e^{-2\xi t}\right)}{2{\xi }^2}}\right)\Omega +{\displaystyle \frac{U_0{\sigma }^2\left(e^{-\xi t}+e^{-2\xi t}\right)}{\xi }}$$

(21)

It can be observed that when $t<t_0={\displaystyle \frac{\mathit{ln}2}{\xi }}$, indicating an inverted U-shaped relationship between $\Omega$ and $D\left(U^{*}\right)$. Under this condition, the extreme point of ${\Omega }_0={\displaystyle \frac{8\xi e^{-\xi t}{U}_0+{\sigma }^2\left(1-e^{-\xi t}-e^{-2\xi t}\right)}{16e^{-\xi t}-8}}$ can be derived. Furthermore, $\Omega$ and $D\left(U^{*}\right)$ are positively correlated when $\Omega <{\Omega }_0$, $\Omega$ and $D\left(U^{*}\right)$ are negatively correlated when $\Omega <{\Omega }_0$. This observation indicates that during the initial stages of contract execution, the supply security utility exhibits heightened sensitivity to external factors, primarily due to insufficient mutual trust between domestic importers and foreign suppliers. As collaboration deepens and both parties invest sustained safety efforts, the uncertainty and instability gradually diminish beyond a critical threshold.

When $t>t_0$, $\Omega$ and $D\left(U^{*}\right)$ exhibit a U-shaped relationship with the extremum point ${\Omega }_0$ as the threshold. This phenomenon suggests that long-term collaboration enhances supply stability and resilience by incentivising security efforts from both domestic importers and foreign suppliers. However, uncertainties in international trade processes-such as information asymmetry, moral hazard, and external risks-persist. Over time, these factors may amplify the uncertainties.

Proof of Proposition 2. 

By substituting Equations (7) and (8) into Equation (3), the following result can be derived:

$$d\dot{U}\left(t\right)=\left(\Omega -\xi U\left(t\right)\right)dt+\sigma \sqrt{U\left(t\right)}dz\left(t\right),U\left(0\right)=U_0\ge 0$$

(22)

Rewrite it in the form of a stochastic integral as follows:

$$U\left(t\right)=U_0+{\int }_0^t\left(\Omega -\xi U\left(v\right)\right)dv+{\int }_0^t\sigma \sqrt{U\left(v\right)}dz\left(v\right)$$

(23)

Taking expectations on both sides and utilising the zero-expectation property of the Wiener process,

$$E\left(U\left(t\right)\right)=U_0+{\int }_0^t\left(\Omega -\xi E\left(U\left(v\right)\right)\right)dv$$

(24)

Taking the derivative of its expectation yields:

$$E\left(U^{\prime }\left(t\right)\right)=\Omega -\xi E\left(U\left(t\right)\right)$$

(25)

To solve for the variance, define a stochastic process $M\left(t\right)=f\left(t,U\left(t\right)\right)=U^2\left(t\right)$. According to Itô’s lemma, the variation process of supply security utility is derived as follows:

$$E\left(U\left(t\right)\right)={\displaystyle \frac{\Omega }{\xi }}+e^{-\xi t}\left(U_0-{\displaystyle \frac{\Omega }{\xi }}\right)$$

(26)

Integrating both sides and taking expectations while applying the zero-expectation property of the Wiener process, we obtain:

$$d{U}^2\left(t\right)=\left[-2\xi U^2\left(t\right)+\left(2\Omega +{\sigma }^2\right)U\left(t\right)\right]dt+2\sigma U\left(t\right)\sqrt{U\left(t\right)}dz\left(t\right)$$

(27)

Substituting Equation (26) into Equation (28) yields:

$$E\left(U^2\left(t\right)\right)=U_0^2+{\int }_0^t\left[-2\xi E\left(U^2\left(v\right)\right)+\left(2\Omega +{\sigma }^2\right)E\left(U\left(v\right)\right)\right]dv$$

(28)

Given $E\left(U^2\left(0\right)\right)=U_0^2$, taking the derivative of Equation (29) gives:

$$\begin{array}{c}E\left(U^2\left(t\right)\right)={\displaystyle \frac{\Omega \left(2\Omega +{\sigma }^2\right)}{2{\xi }^2}}-{\displaystyle \frac{e^{-\xi t}\left(2\Omega +{\sigma }^2\right)\left(\Omega -\xi U_0\right)}{{\xi }^2}}\\ +e^{-2\xi t}\left(U_0^2+{\displaystyle \frac{2\left(2\Omega +{\sigma }^2\right)\left(\Omega -\xi U_0\right)-\Omega \left(2\Omega +{\sigma }^2\right)}{2{\xi }^2}}\right)\end{array}$$

(29)

Using $D\left(U\left(t\right)\right)=E\left(U^2\left(t\right)\right)-E^2\left(U\left(t\right)\right)$, we can derive:

$$\begin{array}{c}D\left(U\left(t\right)\right)=e^{-2\xi t}{\left(U_0-{\displaystyle \frac{\Omega }{\xi }}+e^{-\xi t}{\displaystyle \frac{\Omega }{\xi }}\right)}^2-{\displaystyle \frac{e^{-\xi t}\left(\Omega -\xi U_0\right)\left(2\Omega +{\sigma }^2\right)}{{\xi }^2}}\\ -e^{-2\xi t}\left(U_0^2+{\displaystyle \frac{2\left(2\Omega +{\sigma }^2\right)\left(\Omega -\xi U_0\right)-\Omega \left(2\Omega +{\sigma }^2\right)}{2{\xi }^2}}\right)+{\displaystyle \frac{\Omega \left(2\Omega +{\sigma }^2\right)}{2{\xi }^2}}.\square \end{array}$$

(30)

4. Discussion

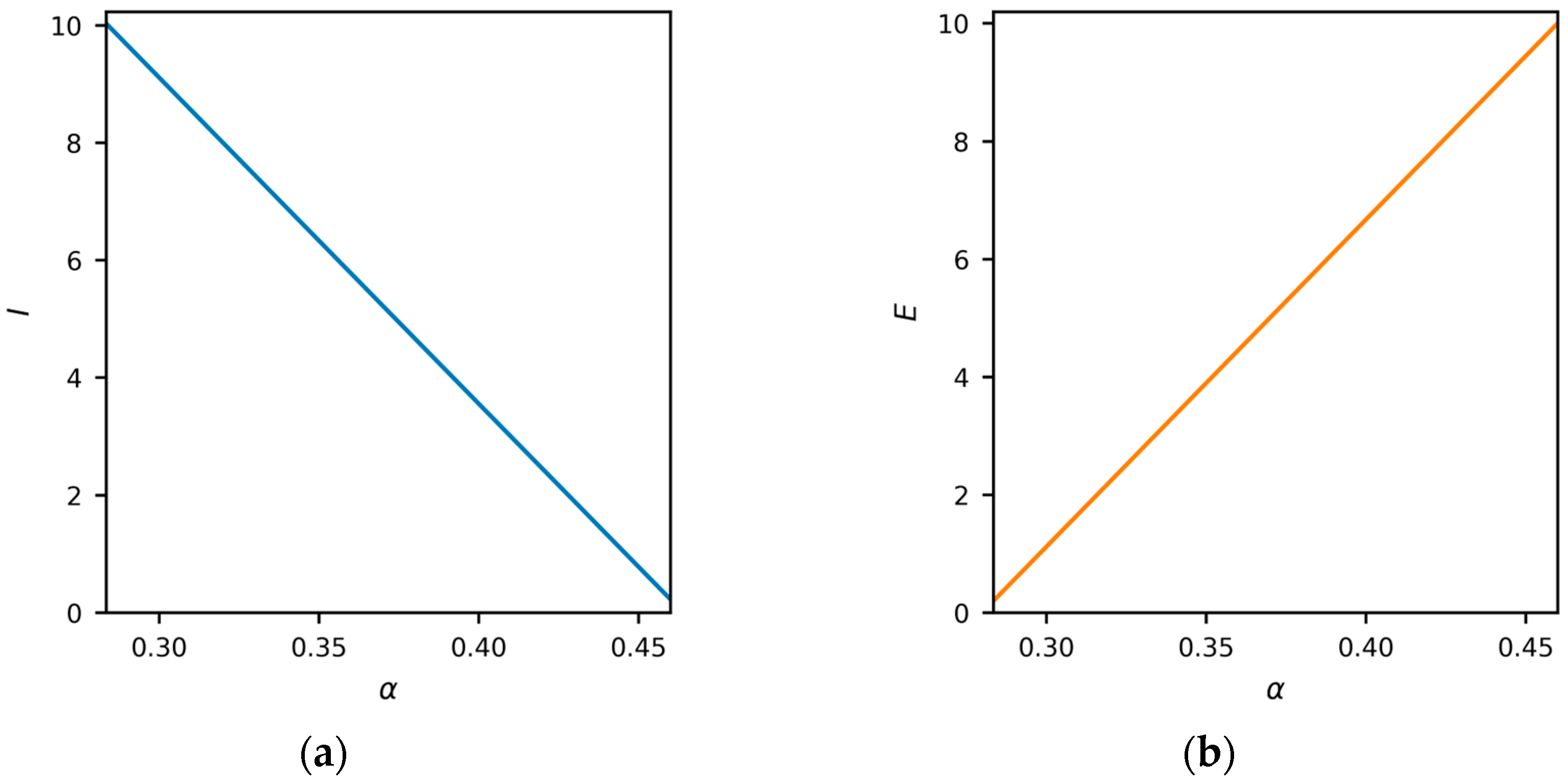
From Equation (7), when term $\Lambda$ dominates, the domestic importers’ optimal security effort level is positively related to the breach benefit coefficient $\omega$, but negatively related to the probability of breach detection $P\left(\theta \right)$ and the breach penalty coefficient $\tau$. When the denominator dominates, the optimal security effort is positively related to the subsidy rate $\epsilon$ and negatively related to the supply security utility decay rate $\xi$. Taken together, the greater the gains domestic importers obtain from trade, the greater the security effort they will exert.

For further analysis, when international market supply sources are stable, the discount rate $\rho$ and supply security utility decay rate $\xi$ increase. In extreme cases where ${\displaystyle \frac{\Lambda }{\left(1-\epsilon \right)\eta }}\gg {\displaystyle \frac{{\lambda }_1\alpha p\gamma }{\left(1-\epsilon \right)\eta \left(\rho +\xi \right)}}$, factors such as the profit-sharing ratio $\alpha$ and copper price $p$ cease to play pivotal roles in domestic importers’ decision-making. Firms prioritise short-term economic gains, with the dominant influencing factors shifting to the probability of breach detection and the magnitude of breach penalties.

Conversely, when international market supply is unstable, the discount rate $\rho$ and decay rate $\xi$ typically decrease. In extreme scenarios where ${\displaystyle \frac{\Lambda }{\left(1-\epsilon \right)\eta }}\ll {\displaystyle \frac{{\lambda }_1\alpha p\gamma }{\left(1-\epsilon \right)\eta \left(\rho +\xi \right)}}$, the profit-sharing ratio $\alpha$ becomes critical to decision-making. Under such conditions, domestic importers disregard potential gains from breach and instead focus on maintaining supply stability and securing steady revenues through long-term cooperation with foreign suppliers.

4.1. Regulatory Intensity

Corollary 1. 

When $P\left(\theta \right)>{\displaystyle \frac{\omega }{\tau +\omega }}$, enhancing regulatory intensity can significantly elevate the effort input level of domestic importers. A stringent regulatory environment effectively deters breach behaviour by domestic importers, while government subsidies exert a positive incentivising effect on their decision-making.

Proof of Corollary 1. 

From Equation (7), when $\Lambda <0$, equivalent to $P\left(\theta \right)>{\displaystyle \frac{\omega }{\tau +\omega }}$, $P\left(\theta \right),\epsilon$ and $I^{*}$ are directly proportional. The condition $\left(1-P\left(\theta \right)\right)\omega -\tau P\left(\theta \right)<0$, equivalent to $\left(1-P\left(\theta \right)\right)\omega \left(I_0-I^{*}\right)<\tau P\left(\theta \right)\left(I_0-I^{*}\right)$, indicates that the additional net gains from breach by domestic importers are lower than the income from keeping the contract, implying high breach costs. Consequently, enhancing regulatory intensity incentivises domestic importers to increase security effort input to sustain trade continuity and mitigate breach risks. Meanwhile, raising the government subsidy rate further amplifies their effort levels. □

Corollary 2. 

When ${\displaystyle \frac{\left(\omega -\left(1-\epsilon \right)\eta I_0\right)\left(\rho +\xi \right)-{\lambda }_1\alpha p\gamma }{\left(\tau +\omega \right)\left(\rho +\xi \right)}}<P\left(\theta \right)<{\displaystyle \frac{\omega \left(\rho +\xi \right)-{\lambda }_1\alpha p\gamma }{\left(\tau +\omega \right)\left(\rho +\xi \right)}}$, increasing regulatory intensity reduces domestic importers’ effort levels and lowers their total income. However, government subsidies exert a positive incentive effect on both decision-making and total income.

Proof of Corollary 2. 

From Equations (5) and (7),

$${{\pi }_I}^{*}=E\left\{{\int }_0^T{e}^{-\rho t}\left[A+{\displaystyle \frac{{\left(\Lambda \left(\rho +\xi \right)-{\lambda }_1\alpha p\gamma \right)}^2}{2\left(1-\epsilon \right){\eta }^2{\left(\rho +\xi \right)}^2}}+{\displaystyle \frac{\Lambda \left(B-\Lambda \left(\rho +\xi \right)+{\lambda }_1\alpha p\gamma \right)}{\left(1-\epsilon \right)\eta \left(\rho +\xi \right)}}\right]dt\right\}$$

(31)

where $A=\alpha p\left(q_0-\beta p+\gamma U\right)$, $B=\left(1-\epsilon \right)\eta \left(\rho +\xi \right)I_0$, ${\Lambda }_0={\displaystyle \frac{{\lambda }_1\alpha p\gamma }{\rho +\xi }}$, ${\Lambda }_1={\displaystyle \frac{\left(1-\epsilon \right)\eta \left(\rho +\xi \right)I_0+{\lambda }_1\alpha p\gamma }{\rho +\xi }}$, $P_1={\displaystyle \frac{\left(\omega -\left(1-\epsilon \right)\eta I_0\right)\left(\rho +\xi \right)-{\lambda }_1\alpha p\gamma }{\left(\rho +\xi \right)\left(\omega +\tau \right)}}$, $P_2={\displaystyle \frac{\omega \left(\rho +\xi \right)-{\lambda }_1\alpha p\gamma }{\left(\rho +\xi \right)\left(\omega +\tau \right)}}$.

The payoff function ${{\pi }_I}^{*}$ can be regarded as jointly determined by $y_0={\displaystyle \frac{{\left(\Lambda \left(\rho +\xi \right)-{\lambda }_1\alpha p\gamma \right)}^2}{2\left(1-\epsilon \right){\eta }^2{\left(\rho +\xi \right)}^2}}$ and $y_1={\displaystyle \frac{\Lambda \left(B-\Lambda \left(\rho +\xi \right)+{\lambda }_1\alpha p\gamma \right)}{\left(1-\epsilon \right)\eta \left(\rho +\xi \right)}}$, where both $y_0$ and $y_1$ are quadratic in $\Lambda$. By the properties of quadratic functions, $y_0$ attains its extremum at ${\Lambda }_0$ and $y_1$ at ${\Lambda }_1$, with ${\Lambda }_0<{\Lambda }_1$. Considering the opening directions of the curves for $y_0$ and $y_1$, when ${\Lambda }_0<\Lambda <{\Lambda }_1$ both $y_0$ and $y_1$ are increasing in $\Lambda$; therefore, $\Lambda$ is positively related to ${{\pi }_I}^{*}$. Since $\Lambda =\left(1-P\left(\theta \right)\right)\omega -\tau P\left(\theta \right)$, it follows that $P\left(\theta \right)$ is negatively correlated with ${{\pi }_I}^{*}$, while $\epsilon$ is positively correlated with ${{\pi }_I}^{*}$. At this point, $P_1<P\left(\theta \right)<P_2$, demonstrating that heightened regulatory intensity reduces total income for domestic importers. The potential reasons are threefold. First, stringent regulations typically entail higher compliance costs—such as environmental mandates, labour protections, and safety standards—which raise production costs and compress profit margins. Second, extended inspection and approval processes reduce production time and output volume, further suppressing revenue. Additionally, regulatory tightening may drive up product prices; if consumers are price-sensitive, demand could decline, intensifying market competition and eroding domestic importers’ market share. Overall, regulatory uncertainty and latent compliance risks amplify operational risks and costs for domestic importers, diminishing profit margins and adversely affecting expected returns. However, increasing the government subsidy rate can enhance domestic importers’ total revenue levels.

When $\Lambda >0$, equivalent to $P\left(\theta \right)<{\displaystyle \frac{\omega }{\tau +\omega }}$, $P\left(\theta \right)$ and $I^{*}$ are inversely proportional, $\epsilon$ and $I^{*}$ directly proportional, and $P_2<{\displaystyle \frac{\omega }{\left(\omega +\tau \right)}}$. Updating constraints to $P_1<P\left(\theta \right)<P_2$, with $\left(1-P\left(\theta \right)\right)\omega -\tau P\left(\theta \right)>0$, equivalent to $\left(1-P\left(\theta \right)\right)\omega \left(I_0-I^{*}\right)>\tau P\left(\theta \right)\left(I_0-I^{*}\right)$. This scenario indicates that the additional net gains domestic importers obtain from a breach in this regime exceed the net gains from compliance. Consequently, even when regulatory intensity is heightened, domestic importers prioritise short-term economic returns and exhibit a propensity toward breach. However, raising the government subsidy rate can elevate domestic importers’ effort input levels, effectively mitigating breach risks. □

4.2. Income Distribution Ratio

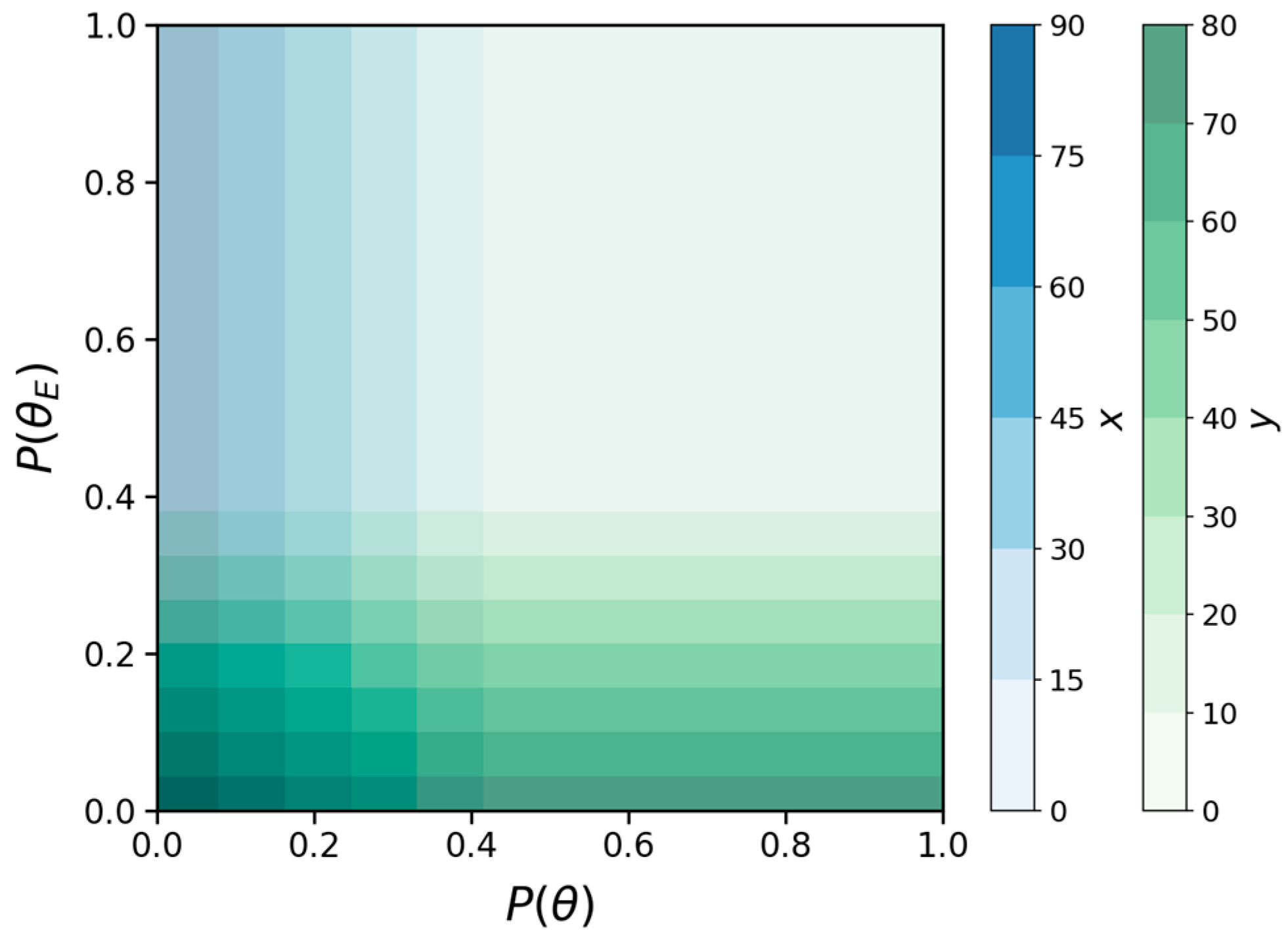
Corollary 3. 

When ${\displaystyle \frac{\left(\rho +\omega \right)\Lambda }{{\lambda }_{1}p\gamma }}<\alpha <1$ and ${\displaystyle \frac{\omega }{\omega +\tau }}-{\displaystyle \frac{{\lambda }_{1}p\gamma }{\left(\rho +\xi \right)\left(\omega +\tau \right)}}<P\left(\theta \right)<{\displaystyle \frac{\omega }{\omega +\tau }}$, the profit-sharing ratio exerts a positive incentivising effect on foreign suppliers’ security effort input levels, while also enhancing domestic importers’ total expected returns. However, under a lax regulatory environment, this mechanism fails to effectively promote domestic importers’ security effort levels.

Proof of Corollary 3. 

From Equations (7) and (8), $\alpha$ is negatively correlated with $I^{*}$ but positively correlated with $E^{*}$. Consequently, an increase in the profit-sharing ratio reduces the security effort input level of domestic importers, while conversely incentivising foreign suppliers to raise their security effort levels.

From Equation (31), when $\Lambda >0$, equivalent to $P\left(\theta \right)<{\displaystyle \frac{\omega }{\omega +\tau }}$, both $y_1=\left(q_0-\beta p+\gamma U\right)p{\alpha }_x$ and $y_2={\lambda }_{1}p\gamma \Lambda {\alpha }_x$ are increasing functions of ${\alpha }_x$. Additionally, the x-coordinate of the extremum point of $y_3={\left(\Lambda \left(\rho +\xi \right)-{\lambda }_{1}p\gamma {\alpha }_x\right)}^2$ can be calculated as ${\alpha }^{*}={\displaystyle \frac{\left(\rho +\omega \right)\Lambda }{{\lambda }_{1}p\gamma }}$, and it can be determined ${\alpha }^{*}>0$. Based on this analysis, if $0<{\alpha }^{*}<1$ and ${\alpha }^{*}<\alpha <1$, the functions $y_1$, $y_2$ and $y_3$ are increasing within their respective domains, with $\alpha$ being proportional to ${\pi }^{*}$, and at this point, $P\left(\theta \right)>{\displaystyle \frac{\omega }{\omega +\tau }}-{\displaystyle \frac{{\lambda }_{1}p\gamma }{\left(\rho +\xi \right)\left(\omega +\tau \right)}}$. □

Corollary 4. 

When $0<\alpha <1-{\displaystyle \frac{\left(\rho +{\omega }_E\right){\Lambda }_E}{{\lambda }_{2}p\gamma }}$ and ${\displaystyle \frac{{\omega }_E}{{\omega }_E+{\tau }_E}}-{\displaystyle \frac{{\lambda }_{2}p\gamma }{\left(\rho +\xi \right)\left({\omega }_E+{\tau }_E\right)}}<P\left({\theta }_E\right)<{\displaystyle \frac{{\omega }_E}{{\omega }_E+{\tau }_E}}$, the profit-sharing ratio exerts a positive incentivising effect on foreign suppliers’ security effort levels, but fails to effectively enhance their total expected returns.

Proof of Corollary 4. 

From Equations (7) and (8), $\alpha$ is negatively correlated with $I^{*}$ but positively correlated with $E^{*}$. Therefore, an increase in the profit-sharing ratio reduces the security effort input levels of domestic importers, while conversely incentivising foreign suppliers to raise their security effort input levels. From Equations (6) and (8),

$${{\pi }_E}^{*}=E\left\{{\int }_0^T{e}^{-\rho t}\left[A_1+{\displaystyle \frac{{\left({\Lambda }_E\left(\rho +\xi \right)-{\lambda }_2\left(1-\alpha \right)p\gamma \right)}^2}{2\left(1-{\epsilon }_E\right){{\eta }_E}^2{\left(\rho +\xi \right)}^2}}+{\displaystyle \frac{{\Lambda }_E\left(B_1-{\Lambda }_E\left(\rho +\xi \right)+{\lambda }_2\left(1-\alpha \right)p\gamma \right)}{\left(1-{\epsilon }_E\right){\eta }_E\left(\rho +\xi \right)}}\right]dt\right\}$$

(32)

where $A_1=p\left(q_0-\beta p+\gamma U\right)\left(1-\alpha \right)$, $B_1=\left(1-{\epsilon }_E\right){\eta }_E\left(\rho +\xi \right)E_0$.

From Equation (32), when ${\Lambda }_E>0$, equivalent to $P\left({\theta }_E\right)<{\displaystyle \frac{{\omega }_E}{{\omega }_E+{\tau }_E}}$, both $y_1=\left(q_0-\beta p+\gamma U\right)p\left(1-{\alpha }_x\right)$ and $y_2={\lambda }_{2}p\gamma {\Lambda }_E\left(1-{\alpha }_x\right)$ are decreasing functions of ${\alpha }_x$. Additionally, the x-coordinate of the extremum point of $y_3={\left({\Lambda }_E\left(\rho +\xi \right)-{\lambda }_{2}p\gamma \left(1-{\alpha }_x\right)\right)}^2$ can be calculated as ${{\alpha }_1}^{*}=1-{\displaystyle \frac{\left(\rho +{\omega }_E\right){\Lambda }_E}{{\lambda }_{2}p\gamma }}$, and it can be determined ${{\alpha }_1}^{*}<1$. Therefore, synthesising the above analysis, if $0<{{\alpha }_1}^{*}<1$, the functions $y_1$, $y_2$ and $y_3$ are decreasing functions within the interval $\left(0,{\alpha }_1^{*}\right)$, where $\alpha$ and ${{\pi }_E}^{*}$ are negatively correlated, and $P\left({\theta }_E\right)>{\displaystyle \frac{{\omega }_E}{{\omega }_E+{\tau }_E}}-{\displaystyle \frac{{\lambda }_{2}p\gamma }{\left(\rho +\xi \right)\left({\omega }_E+{\tau }_E\right)}}$ holds under these conditions. □

5. Numerical Analysis

To illustrate the dynamic behaviour of the model and derive managerial insights, we proceed with a numerical simulation. Based on the preceding analysis, when ${\displaystyle \frac{\left(\omega -\left(1-\epsilon \right)\eta I_0\right)\left(\rho +\xi \right)-{\lambda }_1\alpha p\gamma }{\left(\tau +\omega \right)\left(\rho +\xi \right)}}<P\left(\theta \right)<{\displaystyle \frac{\omega \left(\rho +\xi \right)-{\lambda }_1\alpha p\gamma }{\left(\tau +\omega \right)\left(\rho +\xi \right)}}$, there are fewer destabilising factors. Therefore, this paper selects this scenario as the optimal one and proceeds with subsequent numerical analysis. The parameter values are assigned based on a combination of empirical studies on the copper market, standard values used in the differential game literature, and reasonable assumptions that ensure the model’s equilibrium conditions are satisfied. The primary objective is to examine the relative effects and comparative statics rather than to achieve precise real-world calibration. The parameter assignments are shown in

Table 1. Variable assignments.

Parameters	Values	Parameters	Values	Parameters	Values
$\alpha$	0.4	$\epsilon$	0.1	$\omega$	10,000
$\sigma$	0.01	${\epsilon }_E$	0.1	${\omega }_E$	10,000
$\gamma$	1	$\eta$	100	${\lambda }_1$	10
$p$	100	${\eta }_E$	100	${\lambda }_2$	10
$P\left(\theta \right)$	0.48	$\tau$	6000	$\xi$	0.1
$P\left({\theta }_E\right)$	0.4	${\tau }_E$	6000	$\rho$	0.1

. The explanation of the parameter settings in Table 1 is provided in Appendix A.

5.1. Supply Security Utility and Optimal Decision-Making Outcomes Under the Optimal Scenario

Figure 1 and Figure 2 demonstrate the trajectory variations in supply security utility under the optimal scenario, along with trend dynamics between decision-making by domestic importers and foreign suppliers and their profit-sharing ratios. When domestic importers’ profit-sharing ratio remains inferior to that of foreign suppliers under the moderate regulatory intensity defined by our base-case parameters, the optimal supply security utility trajectory exhibits an ascending trend that ultimately converges within a bounded fluctuation range. This endogenously formed internal cooperation—driven by self-interest maximisation objectives—not only enhances collaborative efficiency but also substantially alleviates the Chinese government’s regulatory pressures and associated costs.

Figure 3 demonstrates the relationship between the optimal decisions of domestic importers and foreign suppliers under different regulatory intensities in the optimal scenario. It can be observed that when both domestic importers and foreign suppliers face extremely low regulatory intensity, they will maintain certain levels of security efforts. As regulatory intensity gradually strengthens, the optimal security investment levels for both domestic importers and foreign suppliers progressively increase. However, this outcome is contingent upon the premise of strong regulatory oversight over the counterparty, which corroborates the earlier analysis. Strict regulation of one entity can effectively prevent unnecessary interest losses for the other participating party from its perspective, thereby enabling them to engage in the collaboration process with greater assurance.

5.2. Impact of Influencing Factors on Supply Security Effectiveness

The following analysis examines the impacts of different influencing factors on supply security effectiveness, respectively. Figure 4 illustrates the effects of varying random disturbances on supply security utility, and Figure 5 presents the impacts of varying regulatory intensities on supply security utility.

5.2.1. Random Disturbances

Random disturbances refer to exogenous, high-frequency shocks captured by the Brownian term in the state equation for the supply-security utility. They summarize shipment and port delays, ore-quality variation and moisture risk, logistics and freight volatility, inspection or documentation rework, weather disruptions, and geopolitical interruptions. In the model, a higher diffusion scale reduces security effectiveness through two channels: (i) a direct volatility channel that raises short-run variance and the probability that the utility process drops below the cooperation-stability band; and (ii) an indirect effort channel, whereby under parameter regimes with regulatory intensity above the endogenous threshold, equilibrium safety efforts decrease, which lowers the drift of the utility process and depresses the expected level and recovery speed.

Figure 4 reveals that under varying random disturbances, the supply security utility exhibits an initial upward trend followed by stabilisation within a fluctuating range. During the ascending phase, the differential impacts of random disturbances on supply security utility are not pronounced. However, as fluctuations stabilise within a bounded range, larger random disturbances lead to a wider amplitude of utility fluctuations. This indicates that short-term instability factors in cross-border cooperation between domestic importers and foreign suppliers have negligible effects on the stability and realisation of copper supply security. In the long term, however, these destabilising factors gradually manifest, undermining the stability of trade processes and generating irreversible negative impacts on copper supply security. Consequently, both domestic importers and foreign suppliers must proactively mitigate instability factors to prevent disruptions in collaboration, thereby achieving systemic stability and maximising their respective interests.

5.2.2. Regulatory Intensity

In this study, regulatory intensity denotes the stringency of process oversight and enforcement attached to contract execution. In practice, it encompasses the frequency of inspection and sampling, the strictness of documentation and traceability requirements, the cadence and scope of audits, and the consistency of enforcement. Within the model, regulatory intensity shapes each party’s best-response effort schedule. Moderate strengthening can discipline opportunism and support cooperation; however, once oversight becomes overly stringent, the resulting compliance burden reduces the private return to sustained safety effort. The relationship is therefore non-monotonic and turns on whether oversight remains within a cooperation-stabilizing range or crosses the threshold beyond which additional tightening crowds out effort.

As shown in Figure 5, under varying regulatory intensities, the supply security effect exhibits a trend of initial growth followed by stabilisation within a fluctuating range. However, its influence on supply security utility differs significantly. Notably, when regulatory intensity exceeds the threshold, higher regulatory intensity corresponds to lower copper supply security utility. This pattern aligns with the corollary in Section 4.1, which shows that sufficiently stringent oversight leads to lower equilibrium safety efforts by both domestic importers and foreign suppliers. Reduced effort slows the improvement of the security utility and leaves the system more exposed to random disturbances, yielding a lower overall profile. This suggests that blindly enhancing regulatory stringency may not effectively improve copper supply security utility. Instead, practical considerations require maintaining regulatory intensity within an optimal range through continuous practical exploration—specifically, a level that stabilises copper trade processes while balancing oversight objectives.

6. Conclusions and Policy Recommendations

6.1. Conclusions

This study employs a stochastic differential game to characterise how China’s copper importers and foreign suppliers interact through incentives, constraints, and uncertainty in continuous time. Within a Hamilton-Jacobi-Bellman (HJB) framework, we derive closed-form feedback Nash equilibria and thereby link regulatory intensity, cooperative security effort, random disturbances, and a supply-security utility into an identifiable dynamic system. The approach not only relaxes the limitations of static analyses but also offers an operational route to conduct comparative statics and scenario simulations on policy parameters.

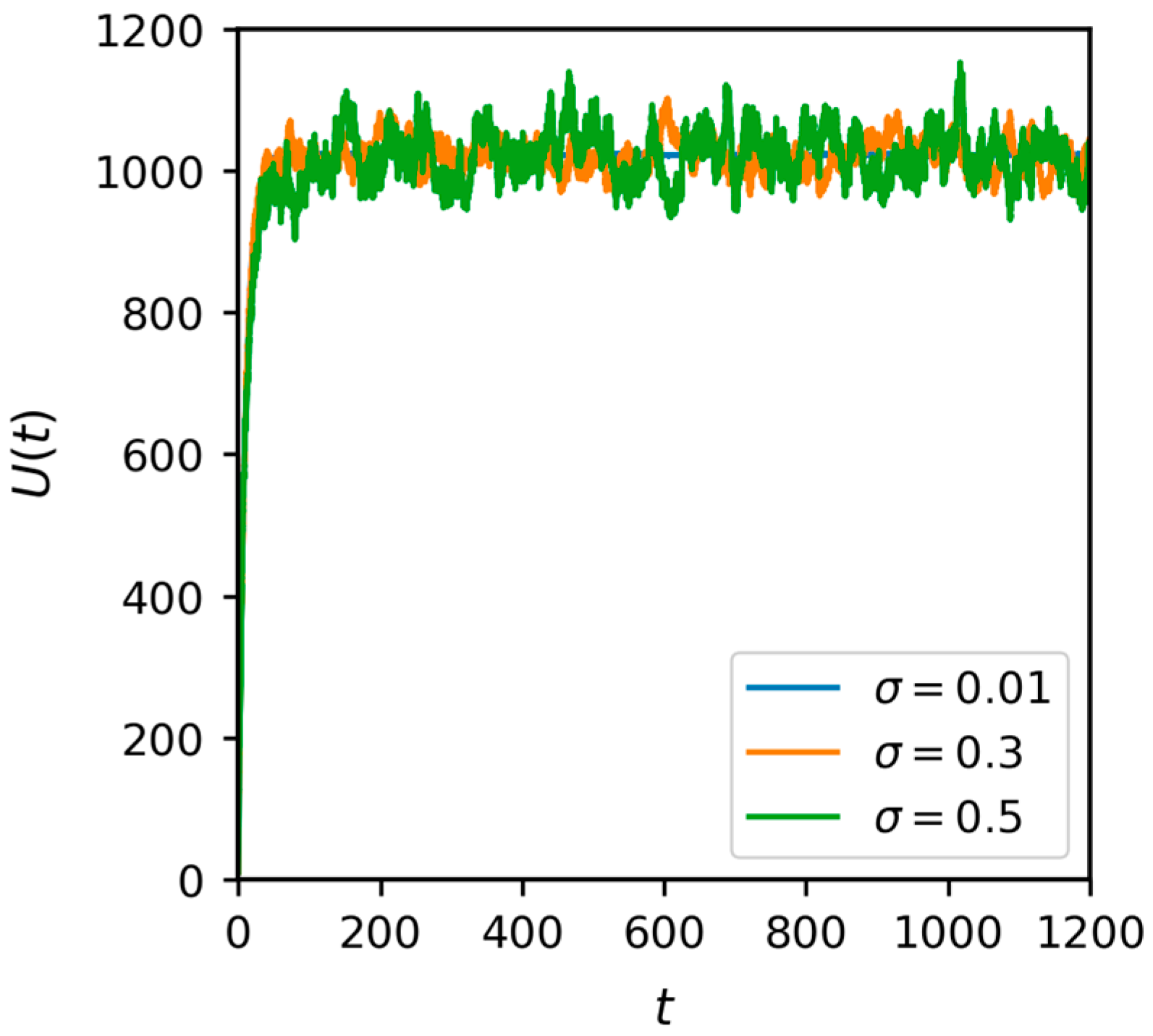
First, regarding the statistical properties of the utility measure, both the expected value and the variance of supply-security utility become increasingly sensitive to the parties’ security efforts over time. Although Brownian shocks cause realised trajectories to deviate around the expectation, these deviations remain bounded within the contract horizon, indicating forecastable and manageable volatility and providing a basis for designing safety bands [20].

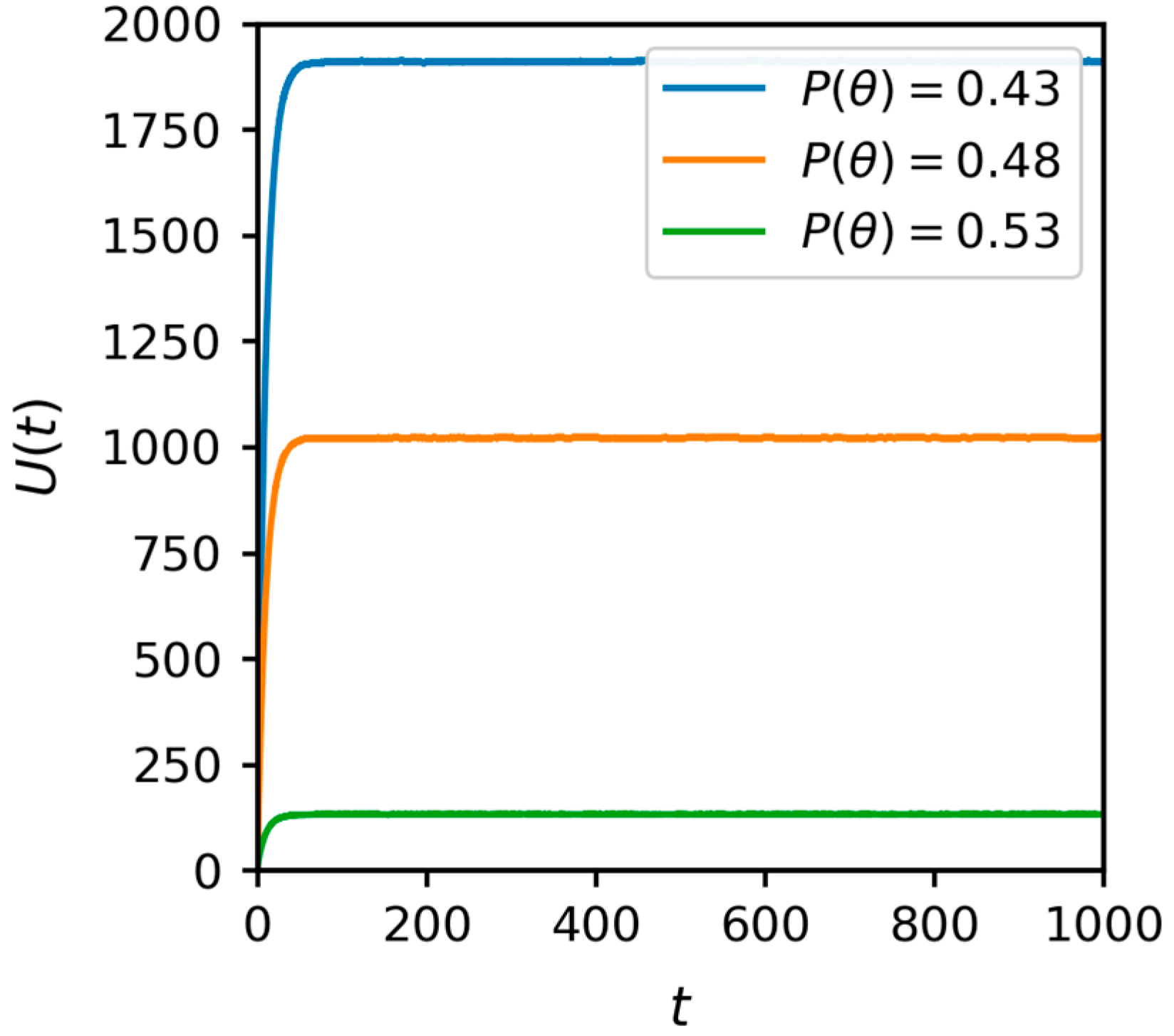
Second, at the institutional level, asymmetric regulation and profit-sharing jointly determine whether “self-enforcing cooperation” emerges. When domestic importers are subject to relatively stronger process-based regulation while foreign suppliers face lighter oversight, and the importer’s revenue share is set slightly below that of the supplier, cooperation becomes an endogenously stable equilibrium and regulatory costs decline. External shocks primarily manifest as short-term disturbances whose long-run effects are broadly controllable; however, if regulatory intensity exceeds a “moderate band,” rising compliance costs and an uncertainty premium depress the steady-state level of supply security [15,21], and revenue-sharing arrangements provide a canonical instrument for aligning incentives and sustaining participation under uncertainty [22].

Third, comparative statics reveal a context-switching mechanism in behavioural drivers. The importer’s optimal security effort is positively associated with the subsidy rate and the short-term gains from default, and negatively associated with the detection probability, the penalty coefficient, and the utility decay rate. When international supply is stable and discount/decay factors are high, firms are disciplined primarily by detection and penalties; when the external environment is unstable and discount/decay factors are low, the revenue-sharing rule exerts a stronger marginal influence on effort. This mechanism yields specific policy rebalancing rules rather than a general claim: (i) in high-volatility or persistent-shock environments, increasing regulatory intensity beyond the endogenous threshold reduces equilibrium efforts and depresses the supply-security utility; policy emphasis should shift from stricter enforcement to incentive-compatible instruments, namely higher effort subsidies and a modest supplier-favored profit distribution, to keep cooperation self-enforcing; (ii) when volatility is low and detection/penalty effectiveness is high relative to deviation gains, emphasis can shift toward process oversight of domestic importers with lighter oversight of foreign suppliers; (iii) under elevated upstream uncertainty or capacity risk, policy should prioritize longer-term contracting and participation incentives for suppliers; conversely, when downstream deviation risk dominates, emphasis should pivot to importer-side oversight.

6.2. Policy Recommendations

Based on the findings of this study, the following policy recommendations are proposed to foster self-enforcing cooperation and maintain supply chain security within manageable bounds: The first recommendation is to adopt a principle of moderate and asymmetric regulation. Since excessive regulatory stringency can be counterproductive by elevating compliance costs and undermining long-term security, regulatory intensity should be calibrated to deter opportunism without stifling cooperation. This entails implementing stronger, process-based oversight for domestic importers—such as through enhanced operational transparency and performance bonds—given their responsiveness to direct scrutiny. Meanwhile, a lighter, outcome-focused approach centered on delivery reliability and creditworthiness should be applied to foreign suppliers. This asymmetric yet moderate strategy establishes the institutional conditions conducive to self-enforcing cooperation, thereby reducing the overall burden and cost of supervision.

The second recommendation is to structure incentives to align interests and sustain cooperation. The model confirms that financial mechanisms, particularly profit-sharing arrangements and targeted subsidies, are potent tools for influencing the security efforts of both parties. Contracts should be designed with a profit distribution slightly favoring foreign suppliers, as this grants them a direct economic stake in the partnership’s continuity and lowers the need for external enforcement. In parallel, government subsidies for security efforts should be explicitly linked to performance metrics, transforming such support into a targeted instrument that rewards measurable contributions to supply chain security and reinforces long-term cooperative behavior.

Finally, we recommend implementing a dynamic monitoring and evaluation system to enhance governance responsiveness. Given that supply security utility fluctuates within statistically bounded and predictable ranges, a data-driven regime can be established to track key performance indicators—such as delivery timeliness, quantity stability, and price volatility—against pre-defined safety bands. Entities maintaining performance within these bands would qualify for streamlined oversight, rewarding compliance and stability. Conversely, those breaching the bands would trigger intensified inspections. Such a closed-loop system enables efficient allocation of regulatory resources and supports adaptive recalibration of policy parameters in a changing operational environment, thereby preserving long-term stability.

In summary, securing China’s copper supply chain requires a sophisticated policy mix that leverages the strategic incentives of market participants. By embracing moderate and asymmetric regulation, structuring financial incentives to align interests, and instituting dynamic data-informed governance, policymakers can cultivate a resilient and cooperative import environment robust to external shocks.

7. Limitations and Future Directions

Despite its contributions, this research has several limitations that warrant acknowledgement. First, the stochastic differential game framework necessarily simplifies the complex realities of copper supply chains. The model treats importers and suppliers as relatively homogeneous actors, abstracting from the heterogeneity of firm size, governance structures, and contract types. In practice, variations in ownership, market power, and strategic behaviour may produce more diverse outcomes than the stylised dynamics captured here. Second, although the model incorporates random disturbances to approximate exogenous shocks, the calibration relies largely on theoretical parameter assignments and stylised sensitivity analysis. The absence of high-frequency empirical data from customs records, shipping contracts, or firm-level performance indicators limits the capacity to fully validate the quantitative predictions. Third, regulatory and institutional contexts are modelled in a static form, whereas in reality, government policies, enforcement capabilities, and international trade rules evolve dynamically and may interact with firm strategies in more complex, path-dependent ways.

Furthermore, to bridge the gap between this theoretical model and practical policy, future work could focus on integrating data-driven methodologies for parameter calibration and model validation. The current framework relies on stylized parameter assignments, but its predictive power would be greatly enhanced by empirically estimating key variables such as cost coefficients ($\eta$, ${\eta }_e$), the impact of security efforts (${\lambda }_1$, ${\lambda }_2$), and the decay rate ($\xi$) from real-world trade and market data. This aligns with a broader trend of leveraging machine learning and explainable AI (XAI) to add physical or economic interpretability to complex models, as demonstrated in advanced manufacturing processes [23]. Such an approach could help validate the non-linear relationships and threshold effects predicted by the game-theoretic model.

By addressing these limitations, future research can enhance both the theoretical rigour and the practical policy relevance of copper supply security studies, thereby contributing to more effective governance of critical mineral resources under conditions of global uncertainty.