Group Efficiency Evaluation Under Fixed-Sum Output Constraints: A Cross-EEF Approach with Application to Industrial Carbon Emissions in China

Abstract

The existence of fixed-sum output constraints in real-world situations is widespread, such as market share and carbon dioxide emissions, etc. However, existing fixed-sum output data envelopment analysis (DEA) methods mostly focus on individual decision-making units (DMUs) and ignore the interactions between groups. Therefore, this study first establishes a systematic framework to quantify group performance by the average criterion, and constructs the equilibrium efficient frontier (EEF) to evaluate all groups on a common platform. To address the non-uniqueness issue of EEF, we further introduce the aggressive cross-efficiency mechanism, ultimately proposing a novel group cross-EEF methodology that explicitly accounts for competitive intergroup dynamics. The proposed method is applied in the assessment of carbon emission efficiency in the industrial sector for 30 provinces in China, and the validity of the method is verified. The result shows that (1) even though the average industrial carbon efficiency stands at 1.2015, half of the provinces exhibit values below 1; (2) significant regional heterogeneity is observed, with North China and East China exhibiting higher efficiency levels, while the Northeast and Northwest regions lag behind; (3) provinces such as Beijing, Guangdong, and Zhejiang demonstrate superior performance, in contrast to Ningxia, Hebei, and Qinghai, which remain at relatively low efficiency levels. This study provides theoretical and policy insights to support the advancement of low-carbon development in China’s industrial sector.

1. Introduction

Data envelopment analysis (DEA) [1], a data-driven tool, has become a widely used efficiency evaluation method for decision-making units (DMUs) [2]. These DMUs consume inputs and generate outputs [3], some of which an invariable total amount. But dependence among inputs and outputs is ignored in the conventional DEA models. A critical instance of such interdependence arises with fixed-sum outputs, where the total quantity of a specific output across all DMUs is constrained or fixed [4]. This constraint is prevalent in real-world scenarios. For example, the total amount of medals to be won in the Olympic Games is fixed when assessing the performance of participating countries [5]. A similar case is that of measuring firms’ performance, where the total market shares in the same industry is constant at 100% [6,7]. Therefore, focusing on the measurement performance of DMUs with fixed-sum outputs becomes significant.

As argued above, fixed-sum output situations have attracted the attention of many scholars [8]. That is why several DEA-based methods have been presented to address the situations. These methods have been divided into two main branches. As one of the branches, the zero-sum gains DEA (ZSGDEA) model was proposed by Lins et al. [9] to measure participant countries’ performance in the Olympic Games. Afterward, Gomes et al. [10] extended the ZSGDEA model by considering fixed-sum undesirable output cases. Then, Feng et al. [11] further extended the existing uniform frontier ZSGDEA method. In addition, the ZSGDEA approach has been broadly applied in different contexts, such as renewable energy quota [12], power sector [13], and science and technology resources [14].

Based on the research of [9], Yang et al. [15] found that the ZSGDEA model can only solve one-dimensional fixed output cases and other DMUs’ output losses greatly rely on their actual outputs. Therefore, the second branch of methods is based on the equilibrium efficient frontier (EEF), initially proposed by Yang et al. [16]. Since the EEFDEA approach presented by Yang et al. [15] is computationally cumbersome, Yang et al. [17] proposed a general EEF DEA (GEEFDEA) method, in which the EEF can be obtained in a single step regardless of the number of DMUs. Subsequently, several secondary goal methods were developed to obtain a unique EEF [18,19,20]. Zhu et al. [21] presented a new common EEFDEA (CEEFDEA) method, which can be used with fixed-sum inputs [22,23,24] or fixed-sum undesirable outputs [25,26]. Different fromthese studies, Li et al. [27] and Zhang et al. [28] extended the GEEFDEA method to the two-stage DEA approach.

In reviewing the studies concerning fixed-sum output DEA methodology, we find that there are direct competitive relationships among DMUs. In fact, groups consisting of several DMUs also compete to maintain their own interests [29]. Some individual DMUs are usually managed by different groups, and the decision maker cares more about the overall performance of the group rather than the performance of specific members in the group [30]. However, the previous fixed-sum output DEA approaches assess the performance of DMUs from individual perspective, with little consideration of group efficiency evaluation. Although Cook et al. [31] and Xia et al. [32] paid attention to groups, their ultimate goal was to assess the efficiency of individual DMUs. To our best knowledge, no clear research method has been presented in the existing literature to handle this evaluation scenario. Therefore, this study focuses on the performance evaluation of groups formed by multiple DMUs with fixed-sum outputs.

The motivation of the study is to extend the concept of a fixed-sum output DEA to the group level, which cannot be considered by any existing literature. In this study, the performance of a particular group is defined by the average criterion. This involves creating a composite DMU by aggregating the inputs and outputs of all DMUs in the group. Based on the definition of the average criterion, we first construct the EEF to evaluate all groups on a common platform. Afterward, the group performance evaluation model is proposed based on the EEF. For each DMU within the same group, its efficiency can be obtained using the same weights as the corresponding group. In addition, as was the case in the selection of EEF for individual DMUs, the common EEF for groups may not be unique. As a result, this study develops a group cross-EEF evaluation approach considering fixed-sum outputs in which each group can choose its most favorable EEF to assess itself and other groups. With this approach, the cross-EEF efficiency of a specific group under evaluation is regarded as the average of its self-evaluation efficiency and peer-evaluation efficiencies obtained with weight profiles given by all other groups.

Our study makes four major contributions to the methodology of fixed-sum output DEA which can be summarized as follows:

(1)

We provide a methodological framework to focus on the problem of competition among groups, and extend the methodology of fixed-sum output DEA to the group level, while the previous studies only assess the performance of DMUs from an individual perspective.

(2)

We extend the second model of the GEEFDEA methodology to take the concept of the group into account and combine the proposed method with the average criterion to develop a group performance evaluation approach. In addition, the efficiency of DMUs within the group may be greater than one, which can fully rank all DMUs based on efficiencies.

(3)

Compared with the group performance evaluation approach of Ang et al. [30], our proposed approach introduces the fixed-sum output constraint into group cases, in which we construct a common EEF for all groups, to guarantee the consistency of the evaluation criteria.

(4)

Compared to the previous fixed-sum output DEA approaches about the selection of EEF, the proposed group cross-EEF evaluation approach selects the same number of EEF as the groups for efficiency evaluation, providing rich decision information reflected in other EEFs.

The structure of the study is organized as follows. Section 2 mainly reviews the DEA-based theoretical basis. Section 3 proposes a group efficiency evaluation model based on the EEF and a group cross-EEF evaluation approach considering fixed-sum outputs. In Section 4, we apply the proposed methodology to empirical application. Section 5 concludes the study.

2. Preliminary

2.1. CCR Model and Cross-Efficiency

Assume that $n$ DMUs (${DMU}_j,j=1,\dots n)$ need to be assessed and each ${DMU}_j$ generates $s$ outputs $y_{rj}(r=1,\dots ,s)$ by using $m$ inputs $x_{ij}(i=1,\dots ,m)$. The classical CCR model [1] is given in model (1):

$$\begin{array}{cc}{E}_d=& max{\sum }_{r=1}^s{u}_{rd}{y}_{rd}\\ s.t.& \begin{array}{c}{\sum }_{i=1}^m{v}_{id}{x}_{id}=1\\ {\sum }_{i=1}^m{v}_{id}{x}_{ij}-{\sum }_{r=1}^s{u}_{rd}{y}_{rj}\ge 0,\forall j\\ v_{id}\ge 0,u_{rd}\ge 0,\forall i,r\end{array}\end{array}$$

(1)

The $v_{id}$ and $u_{rd}$ denote the weight of the $i^{th}$ input and the $r^{th}$ output, and $E_d$ is the optimal efficiency value of ${DMU}_d$ as well as self-evaluation efficiency. ${DMU}_d$ is relatively efficient when $E_d=1$, and otherwise inefficient. Assume that ${(v}_{id}^{\ast }{,u}_{rd}^{\ast })$ is the optimal solution of model (1), then the efficiency of peer-evaluation obtained by ${DMU}_k$ through the optimal weights of ${DMU}_d$ is:

$$E_{dk}={\displaystyle \frac{{\sum }_{r=1}^s{u}_{rd}^{\ast }{y}_{rk}}{{\sum }_{i=1}^m{v}_{id}^{\ast }{x}_{ik}}}$$

(2)

where $E_{dd}=E_d$. For ${DMU}_d$, the cross-efficiency is the average of the self-evaluation efficiency and all peer-evaluation efficiencies:

$${\overline{E}}_d={\displaystyle \frac{1}{n}}{\sum }_{j=1}^n{E}_{jd}$$

(3)

Note that multiple optimal solutions are usually generated by model (1) [33,34], which influences the accuracy of the cross-efficiency approach. To obtain the unique cross-efficiency value, Doyle and Green [35] proposed the secondary goal model, among which the benevolent and aggressive strategies are the most widely used. The benevolent strategy seeks to maximize the efficiencies of other DMUs, while the aggressive strategy aims to minimize them, both under the constraint that the DMU maintains its own optimal efficiency. The model is shown below, where ${\theta }_d^{\ast }$ repersents the optimal self-assessment efficiency obtained by ${DMU}_d$ through model (1).

$$\begin{array}{cc}Max/Min& {\sum }_{r=1}^s{u}_{rd}(\sum _{j=1,j\ne d}^n{y}_{rj})\\ s.t.& \begin{array}{c}{\sum }_{i=1}^m{v}_{id}\left(\sum _{j=1,j\ne d}^n{x}_{ij}\right)=1\\ \begin{array}{c}{\sum }_{r=1}^s{u}_{rd}{y}_{rd}-{\theta }_d^{\ast }\times {\sum }_{i=1}^m{v}_{id}{x}_{id}=0\\ \begin{array}{c}{\sum }_{r=1}^s{u}_{rd}{y}_{rj}-{\sum }_{i=1}^m{v}_{id}{x}_{ij}\le 0,\forall j\\ v_{id}\ge 0,u_{rd}\ge 0,\forall i,r\end{array}\end{array}\end{array}\end{array}$$

(4)

2.2. Construction of the EEF

Suppose that each DMU consumes $m$ inputs and produces $s$ outputs, while simultaneously generating $l$ fixed-sum outputs $f_{tj}(t=1,\dots ,l)$. As described in the introduction, the sum of the $t^{th}$ output across all DMUs is a fixed value, denoted by $F_t$. Therefore, Equation (5) is valid.

$${\sum }_{j=1}^n{f}_{tj}=F_t,\forall t$$

(5)

The GEEFDEA model constructs the EEF by adjusting the fixed-sum outputs of all DMUs, effectively addressing the presence of fixed-sum outputs. The formulation of the EEF is presented as follows:

$$\begin{array}{cc}min& {\sum }_{j=1}^n{\sum }_{t=1}^l{w}_t\left|{\delta }_{tj}\right|\\ s.t.& \begin{array}{c}{\displaystyle \frac{{\sum }_{r=1}^s{u}_r{y}_{rj}+{\sum }_{t=1}^l{w}_t(f_{tj}+{\delta }_{tj})}{{\sum }_{i=1}^m{v}_i{x}_{ij}}}=1,\forall j\\ \begin{array}{c}{\sum }_{j=1}^n{\delta }_{tj}=0,\forall t\\ f_{tj}+{\delta }_{tj}\ge 0,\forall t,j\end{array}\\ u_r,w_t,v_i\ge 0,{\forall r,t,i,\delta }_{tj}isfree\end{array}\end{array}$$

(6)

where $w_t$ and ${\delta }_{tj}$ represent the multiplier and amount of adjustment required for the $t^{th}$ fixed-sum output of ${DMU}_j$, respectively. ${\delta }_{tj}$ > 0 (or <0) represents the need for an increase (or decrease), while ${\delta }_{tj}$ = 0 remains unchanged. The objective of the model is to minimize the total adjustment across all DMUs, and the first constraint ensures that all DMUs become efficient after adjustment, thereby forming an EEF. Let ${\delta }_{tj}^{\prime }=w_t{\delta }_{tj}$, $a_{tj}=0.5\times (\left|{\delta }_{tj}^{\prime }\right|+{\delta }_{tj}^{\prime })$, and $b_{tj}=0.5\times (\left|{\delta }_{tj}^{\prime }\right|-{\delta }_{tj}^{\prime })$, model (6) can be transformed into the following linear model:

$$\begin{array}{cc}min& {\sum }_{j=1}^n{\sum }_{t=1}^l(a_{tj}+b_{tj})\\ s.t.& \begin{array}{c}{\sum }_{r=1}^s{u}_r{y}_{rj}-{\sum }_{i=1}^m{v}_i{x}_{ij}+{\sum }_{t=1}^l(w_t{f}_{tj}+a_{tj}-b_{tj})=0,\forall j\\ {\sum }_{j=1}^n(a_{tj}-b_{tj})=0,\forall t\\ \begin{array}{c}{\sum }_{i=1}^m{v}_i{x}_{ij}\ge M,\forall j\\ w_t{f}_{tj}+a_{tj}-b_{tj}\ge 0,\forall t,j\\ u_r,w_t,v_i,a_{tj},b_{tj}\ge 0,\forall r,t,i,j\end{array}\end{array}\end{array}$$

(7)

Here, $M$ is a given positive number. From model (7), we obtain the optimal solutions $u_r^{\ast }$, $w_t^{\ast }$, $v_i^{\ast }$, $a_{tj}^{\ast }$, $b_{tj}^{\ast }$, and ${\delta }_{tj}^{\ast }$. These can be expressed in vector form: $\mathit{u}={(u_1,\dots ,u_s)}^T$, $\mathit{w}={(w_1,\dots ,w_l)}^T$, $\mathit{v}={(v_1,\dots ,v_m)}^T$, and $\mathit{\delta }=\left({\delta }_{tj}\right),\forall t,j$. Accordingly, the feasible solution set for model (7) can be defined as

$$\mathit{S}=\left\{(\mathit{u},\mathit{v},\mathit{w},\mathit{\delta })|\mathit{u},\mathit{v},\mathit{w},\mathit{\delta }\mathrm{s}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{s}\mathrm{f}\mathrm{y}\mathrm{M}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}(7)\right\}$$

(8)

Since the set $\mathit{S}$ encompasses all EEFs, each evaluated group may select a frontier that is most advantageous to itself, thereby reducing the comparability of group efficiency scores. To address this issue, the concept of cross-efficiency is introduced into the group efficiency evaluation framework.

3. Proposed Models

As mentioned in the introduction, previous fixed-sum output DEA models have focused on the individual level, neglecting the interactions between groups in certain scenarios. Thus, this section innovatively extends the fixed-sum output DEA models to the group level and further proposes a new group cross-EEF model to obtain unique and robust assessment results.

3.1. Group Efficiency Assessment Model with Fixed-Sum Output

Assuming that the $n$ DMUs are divided into $K$ groups, each containing $D_k$ DMUs $(k=\mathrm{1,2},3,\dots ,K)$ and ${\sum }_{k=1}^K{D}_k=n.$ Each ${DMU}_{d_k}(d_k=1,\dots ,D_k)$ consumes $m$ inputs $x_{i{d}_k}(i=1,\dots ,m)$ to produce $s$ outputs $y_{r{d}_k}(r=1,\dots ,s)$ and $l$ fixed-sum outputs $f_{t{d}_k}(t=1,\dots ,l)$. According to the average criterion from Ang et al. [30], the integrated efficiency of a group is the average efficiency of all DMUs within the group as follows:

$$E_p={\displaystyle \frac{1}{D_p}}{\sum }_{d_p=1}^{D_p}{\displaystyle \frac{{\sum }_{r=1}^s{u}_{rp}{y}_{r{d}_p}+{\sum }_{t=1}^l{w}_{tp}{f}_{t{d}_p}}{{\sum }_{i=1}^m{v}_{ip}{x}_{i{d}_p}}}$$

(9)

where DMUs within the same group use the same set of weights to calculate the efficiency values. Considering the nonlinearity of Equation (9), with reference to Doyle and Green [35], this study replaces Equation (9) with aggregated virtual unit efficiency, whose inputs and outputs are the sum of inputs and outputs of the all DMUs in the group, respectively. The expression is as follows:

$$E_p={\displaystyle \frac{{\sum }_{r=1}^s{\sum }_{d_p=1}^{D_p}{u}_{rp}{y}_{r{d}_p}+{\sum }_{t=1}^l{\sum }_{d_p=1}^{D_p}{w}_{tp}{f}_{t{d}_p}}{{\sum }_{i=1}^m{\sum }_{d_p=1}^{D_p}{v}_{ip}{x}_{i{d}_p}}}$$

(10)

Equations (9) and (10) are mutually replaceable. As mentioned in the introduction, the EEF in model (7) is not unique, thus each group would choose an optimal EEF to maximize its own integrated efficiency. The model is constructed as follows:

$$\begin{array}{cc}{E}_p^{\ast }=& max{\displaystyle \frac{{\sum }_{r=1}^s{\sum }_{d_p=1}^{D_p}{u}_{rp}{y}_{r{d}_p}+{\sum }_{t=1}^l{\sum }_{d_p=1}^{D_p}{w}_{tp}{f}_{t{d}_p}}{{\sum }_{i=1}^m{\sum }_{d_p=1}^{D_p}{v}_{ip}{x}_{i{d}_p}}}\\ s.t.& \begin{array}{c}\begin{array}{c}{\sum }_{k=1}^K{\sum }_{d_k=1}^{D_k}{\sum }_{t=1}^l(a_{t{d}_k}+b_{t{d}_k})={opti}^{\ast }\\ {\displaystyle \frac{{\sum }_{r=1}^s{u}_{rp}{y}_{r{d}_k}+{\sum }_{t=1}^l(w_{tp}{f}_{t{d}_k}+a_{t{d}_k}-b_{t{d}_k})}{{\sum }_{i=1}^m{v}_{ip}{x}_{i{d}_k}}}=1,d_k=1,\dots ,D_k,k=1,\dots ,K\end{array}\\ {\sum }_{k=1}^K{\sum }_{d_k=1}^{D_k}(a_{t{d}_k}-b_{t{d}_k})=0,\forall t\\ \begin{array}{c}{w}_{tp}{f}_{t{d}_k}+a_{t{d}_k}-b_{t{d}_k}\ge 0,\forall t,d_k=1,\dots ,D_k,k=1,\dots ,K\\ u_{rp},w_{tp},v_{ip},a_{t{d}_k},b_{t{d}_k}\ge 0,\forall r,t,i,d_k=1,\dots ,D_k,k=1,\dots ,K\end{array}\end{array}\end{array}$$

(11)

where ${opti}^{\mathrm{*}}$ is the optimal value of model (7) to ensure the minimum adjustment strategy. It is noteworthy that, in most traditional decision analysis frameworks, the efficiency scores of DMUs are typically constrained within the interval (0, 1]. However, in model (11), if $a_{t{d}_k}-b_{t{d}_k}<0$ for all $t$, it may lead to ${\sum }_{r=1}^s{\sum }_{d_p=1}^{D_p}{u}_{rp}{y}_{r{d}_p}+{\sum }_{t=1}^l{\sum }_{d_p=1}^{D_p}{w}_{tp}{f}_{t{d}_p}>{\sum }_{i=1}^m{\sum }_{d_p=1}^{D_p}{v}_{ip}{x}_{i{d}_p}$, causing the efficiency $E_p^{\ast }$ to exceed 1. In other words, when $a_{t{d}_k}-b_{t{d}_k}<0$, the corresponding DMU lies outside the constructed EEF, and thus the efficiency $E_p^{\ast }$ is not confined to the interval (0, 1) [16]. When $a_{t{d}_k}-b_{t{d}_k}=0$, it signifies that, during the construction of the EEF, the DMU requires no adjustment to its fixed-sum outputs. In this case, the DMU is located precisely on the EEF, yielding an efficiency value of 1. Conversely, When $a_{t{d}_k}-b_{t{d}_k}>0$, the DMU must acquire or integrate additional input and output combinations from other DMUs to reach the EEF. Consequently, when the constructed EEF is adopted as the performance evaluation benchmark, the efficiency value of such a DMU will be less than 1.

With the Charnes–Cooper transformation [36], model (11) can be transformed into the following linear program:

$$\begin{array}{cc}{E}_p^{\ast }=& max{\sum }_{r=1}^s{\sum }_{d_p=1}^{D_p}{u}_{rp}{y}_{r{d}_p}+{\sum }_{t=1}^l{\sum }_{d_p=1}^{D_p}{w}_{tp}{f}_{t{d}_p}\\ s.t.& \begin{array}{c}\begin{array}{c}\begin{array}{c}{\sum }_{i=1}^m{\sum }_{d_p=1}^{D_p}{v}_{ip}{x}_{i{d}_p}=1\\ {\sum }_{k=1}^K{\sum }_{d_k=1}^{D_k}{\sum }_{t=1}^l(a_{t{d}_k}+b_{t{d}_k})={opti}^{\ast }\end{array}\\ {\sum }_{r=1}^s{u}_{rp}{y}_{r{d}_k}-{\sum }_{i=1}^m{v}_{ip}{x}_{i{d}_k}+{\sum }_{t=1}^l(w_{tp}{f}_{t{d}_k}+a_{t{d}_k}-b_{t{d}_k})=0,d_k=1,\dots ,D_k,k=1,\dots ,K\end{array}\\ {\sum }_{k=1}^K{\sum }_{d_k=1}^{D_k}(a_{t{d}_k}-b_{t{d}_k})=0,\forall t\\ \begin{array}{c}{w}_{tp}{f}_{t{d}_k}+a_{t{d}_k}-b_{t{d}_k}\ge 0,\forall t,d_k=1,\dots ,D_k,k=1,\dots ,K\\ u_{rp},w_{tp},v_{ip},a_{t{d}_k},b_{t{d}_k}\ge 0,\forall r,t,i,d_k=1,\dots ,D_k,k=1,\dots ,K\end{array}\end{array}\end{array}$$

(12)

Through model (12), the most favorable EEF for each group can be obtained, denoted as $\left(v_{rp}^{\mathrm{*}},u_{tp}^{\mathrm{*}},w_{tp}^{\mathrm{*}},a_{t{d}_k}^{\mathrm{*}},b_{t{d}_k}^{\mathrm{*}}\right)$. Note that all DMUs within the group use this common EEF to compute the efficiency, as shown below:

$$E_{d_p}^{\ast }={\displaystyle \frac{{\sum }_{r=1}^s{u}_{rp}^{\ast }{y}_{r{d}_p}+{\sum }_{t=1}^l{w}_{tp}^{\ast }{f}_{t{d}_p}}{{\sum }_{i=1}^m{v}_{ip}^{\ast }{x}_{i{d}_p}}},d_p=1,\dots ,D_p$$

(13)

3.2. Group Cross-EEF Evaluation Model

As expressed in Equation (8), the set $\mathit{S}$ formed by the optimal weights encompasses numerous EEFs, where each EEF represents a distinct evaluation criterion. Multiple evaluation criteria may bring about two drawbacks: first, under the self-evaluation mode, each group tends to select the EEF that is most favorable to itself, and the corresponding weights may be extreme, potentially leading to an inflated self-assessment; second, since different groups choose different EEFs, the evaluation standards are not uniform, resulting in the poor comparability of efficiency scores.

To overcome these limitations, we introduce the cross-efficiency evaluation framework, which integrates both self- and peer-assessments. In this setting, each group not only evaluates its own efficiency using its optimal EEF, but also assesses the performance of other groups based on the same weighting structure, thereby forming a cross-efficiency matrix. Cross-evaluation embodies a peer-benchmarking process: the optimal weighting scheme of one group represents its evaluation standard, and when this standard is applied to assess other groups, it serves as an external reference, revealing the potential efficiency of those groups under the first group’s evaluation criteria. After cross-evaluation, the efficiency of each group is closer to its true level. In addition, each group is assessed under the evaluation standards of all other groups, thereby achieving a unified set of evaluation criteria.

Nonetheless, the optimal solution in model (12) is generally not unique, causing cross-efficiency results to depend on arbitrary EEF selections. To ensure uniqueness and reflect competitive interactions under fixed-sum output constraints, we further introduce a secondary goal model that embodies an aggressive (competitive) strategy. In such contexts, the gain of one group necessarily implies the loss of another, leading groups to behave strategically rather than cooperatively. This design follows the logic of non-cooperative game theory [33,37], where each DMU seeks to maximize its own advantage by minimizing the relative efficiency of others while maintaining its own optimal performance. This aggressive orientation is consistent with competitive environments in fixed-sum systems [16,19]. This strategic optimization process is formally characterized by the following model:

$$\begin{array}{cc}{E}_{pq}=& Min{\displaystyle \frac{{\sum }_{r=1}^s{\sum }_{d_q=1}^{D_q}{u}_{rp}{y}_{r{d}_q}+{\sum }_{t=1}^l{\sum }_{d_q=1}^{D_q}{w}_{tp}{f}_{t{d}_q}}{{\sum }_{i=1}^m{\sum }_{d_q=1}^{D_q}{v}_{ip}{x}_{i{d}_q}}}\\ s.t.& \begin{array}{c}{\sum }_{k=1}^K{\sum }_{d_k=1}^{D_k}{\sum }_{t=1}^l(a_{t{d}_k}+b_{t{d}_k})={opti}^{\ast }\\ {\sum }_{r=1}^s{u}_{rp}{y}_{r{d}_k}-{\sum }_{i=1}^m{v}_{ip}{x}_{i{d}_k}+{\sum }_{t=1}^l(w_{tp}{f}_{t{d}_k}+a_{t{d}_k}-b_{t{d}_k})=0,d_k=1,\dots ,D_k,k=1,\dots ,K\\ \begin{array}{c}{\sum }_{k=1}^K{\sum }_{d_k=1}^{D_k}(a_{t{d}_k}-b_{t{d}_k})=0,\forall t\\ w_{tp}{f}_{t{d}_k}+a_{t{d}_k}-b_{t{d}_k}\ge 0,\forall t,d_k=1,\dots ,D_k,k=1,\dots ,K\\ \begin{array}{c}{\displaystyle \frac{{\sum }_{r=1}^s{\sum }_{d_p=1}^{D_p}{u}_{rp}{y}_{r{d}_p}+{\sum }_{t=1}^l{\sum }_{d_p=1}^{D_p}{w}_{tp}{f}_{t{d}_p}}{{\sum }_{i=1}^m{\sum }_{d_p=1}^{D_p}{v}_{ip}{x}_{i{d}_p}}}=E_p^{\ast }\\ u_{rp},w_{tp},v_{ip},a_{t{d}_k},b_{t{d}_k}\ge 0,\forall r,t,i,d_k=1,\dots ,D_k,k=1,\dots ,K\end{array}\end{array}\end{array}\end{array}$$

(14)

Model (14) enables group $p$ to minimize the efficiency score of group $q$ while maintaining its own efficiency at $E_p^{\ast }$. To facilitate computation, we reformulate this nonlinear program into an equivalent linear model, denoted as model (15):

$$\begin{array}{cc}{E}_{pq}=& Min{\sum }_{r=1}^s{\sum }_{d_q=1}^{D_q}{u}_{rp}{y}_{r{d}_q}+{\sum }_{t=1}^l{\sum }_{d_q=1}^{D_q}{w}_{tp}{f}_{t{d}_q}\\ s.t.& \begin{array}{c}\begin{array}{c}{\sum }_{i=1}^m{\sum }_{d_q=1}^{D_q}{v}_{ip}{x}_{i{d}_q}=1\\ {\sum }_{k=1}^K{\sum }_{d_k=1}^{D_k}{\sum }_{t=1}^l(a_{t{d}_k}+b_{t{d}_k})={opti}^{\ast }\end{array}\\ {\sum }_{r=1}^s{u}_{rp}{y}_{r{d}_k}-{\sum }_{i=1}^m{v}_{ip}{x}_{i{d}_k}+{\sum }_{t=1}^l(w_{tp}{f}_{t{d}_k}+a_{t{d}_k}-b_{t{d}_k})=0,d_k=1,\dots ,D_k,k=1,\dots ,K\\ \begin{array}{c}{\sum }_{k=1}^K{\sum }_{d_k=1}^{D_k}(a_{t{d}_k}-b_{t{d}_k})=0,\forall t\\ w_{tp}{f}_{t{d}_k}+a_{t{d}_k}-b_{t{d}_k}\ge 0,\forall t,d_k=1,\dots ,D_k,k=1,\dots ,K\\ \begin{array}{c}{\sum }_{r=1}^s{\sum }_{d_p=1}^{D_p}{u}_{rp}{y}_{r{d}_p}+{\sum }_{t=1}^l{\sum }_{d_p=1}^{D_p}{w}_{tp}{f}_{t{d}_p}-E_p^{\ast }\times {\sum }_{i=1}^m{\sum }_{d_p=1}^{D_p}{v}_{ip}{x}_{i{d}_p}=0\\ u_{rp},w_{tp},v_{ip},a_{t{d}_k},b_{t{d}_k}\ge 0,\forall r,t,i,d_k=1,\dots ,D_k,k=1,\dots ,K\end{array}\end{array}\end{array}\end{array}$$

(15)

where the optimal solution of model (15) is denoted as $\left(v_{rpq}^{\mathrm{*}},u_{tpq}^{\mathrm{*}},w_{tpq}^{\mathrm{*}},a_{t{d}_k}^{\mathrm{*}},b_{t{d}_k}^{\mathrm{*}}\right)$. Based on the EEF selected by group $p$, we evaluate the peer-evaluation efficiency of all DMUs within group $q$ through Equation (16) as follows:

$$E_{p{d}_q}^{\ast }={\displaystyle \frac{{\sum }_{r=1}^s{u}_{rpq}^{\ast }{y}_{r{d}_q}+{\sum }_{t=1}^l{w}_{tpq}^{\ast }{f}_{t{d}_q}}{{\sum }_{i=1}^m{v}_{ipq}^{\ast }{x}_{i{d}_q}}},d_q=1,\dots ,D_q$$

(16)

The final group cross-EEF efficiency for each DMU is the average of own group’s self-evaluation efficiency and the peer-evaluations from the other groups:

$$E_{d_q}^{cross-EEF}={\displaystyle \frac{1}{K}}{\sum }_{p=1}^K{E}_{p{d}_q}^{\ast }$$

(17)

4. Empirical Example

In recent years, rapid economic growth has posed significant challenges related to energy consumption and environmental pollution [38]. Since 2007, China has ranked among the highest in the world in terms of total energy consumption and carbon emissions, drawing increased attention to its worsening environmental issues [39,40]. China’s energy-intensive growth model no longer meets the requirements of high-quality economic transformation, and the resulting carbon emissions conflict with the goal of green development [41]. Without effective constraints and controls on CO₂ emissions, the dynamic balance of the carbon cycle may be disrupted, leading to climate change issues such as global warming [42,43]. Achieving the dual carbon goals—carbon peaking and carbon neutrality—requires controlling carbon emissions through the introduction of fixed-sum output constraints. The accurate assessment and analysis of carbon emission efficiency at the regional and industrial levels are crucial for effectively promoting energy conservation and low-carbon development. Consequently, numerous studies have examined carbon emission efficiency.

Research on carbon emission efficiency has historically occupied a prominent position in the literature on DEA. Based on the attribute of carbon emissions, existing research can be divided into two types. The first type treats carbon emissions as a variable-sum output without any constraints. For example, Liu et al. [44] assessed potential economic gains and emission cuts for the thermal power industry. Chen et al. [45] assessed the energy efficiency of the urban transportation sector in the Yangtze River Delta through the Window-DEA model. Wang et al. [46] evaluated regional energy efficiency based on the super-DEA model. Wang and Feng [47] applied a multi-tier meta-frontier DEA approach to decompose China’s carbon emission efficiency. Du et al. [48] employed the proposed hybrid Trigonometric Envelopment Analysis for Ideal Solutions (TEA-IS) model to assess the ecological efficiency of 248 Chinese cities. The second type takes into account the practical constraints on carbon emission, treating it as a fixed-sum output. Cui et al. [13] constructed a provincial dynamic carbon emission allocation model for China’s power sector. Li et al. [49] assessed provincial energy and environment efficiency for the transportation sector. Li et al. [50] employed the Malmquist–Luenberger index to conduct a dynamic analysis of carbon emission performance within the thermal power sector. Zhang et al. [37] evaluated the CO₂ emission efficiency of 30 provinces in China with a game cross-efficiency approach.

Prior studies have provided valuable insights by modeling carbon emissions as variable-sum or fixed-sum outputs across sectors and regions. However, the industrial sector, which is the largest contributor to China’s carbon emissions and accounts for nearly 80 percent due to its heavy reliance on fossil fuels, has not received sufficient attention. Furthermore, industrial carbon emissions are subject to total-sum constraints and exhibit pronounced fixed-sum output characteristics, making traditional assessment methods less suitable. The year 2021 marks the official launch of China’s national ‘Dual Carbon’ strategy, following the issuance of Opinions on Complete, Accurate and Comprehensive Implementation of the New Development Concept to Achieve Carbon Peak and Carbon Neutrality by the State Council (October 2021). It represents a critical turning point in China’s industrial low-carbon transition [51]. Against this backdrop, this section used the proposed group cross-EFF evaluation approach to assess the carbon dioxide emission efficiency of the industrial sector across 30 Chinese provinces in 2021.

4.1. Data Collection and Description

We reviewed existing literature on carbon emission efficiency and selected four input indicators and two output indicators that are frequently used in empirical research for application in this study, as shown in

Table 1. Indicator system for carbon emission efficiency.

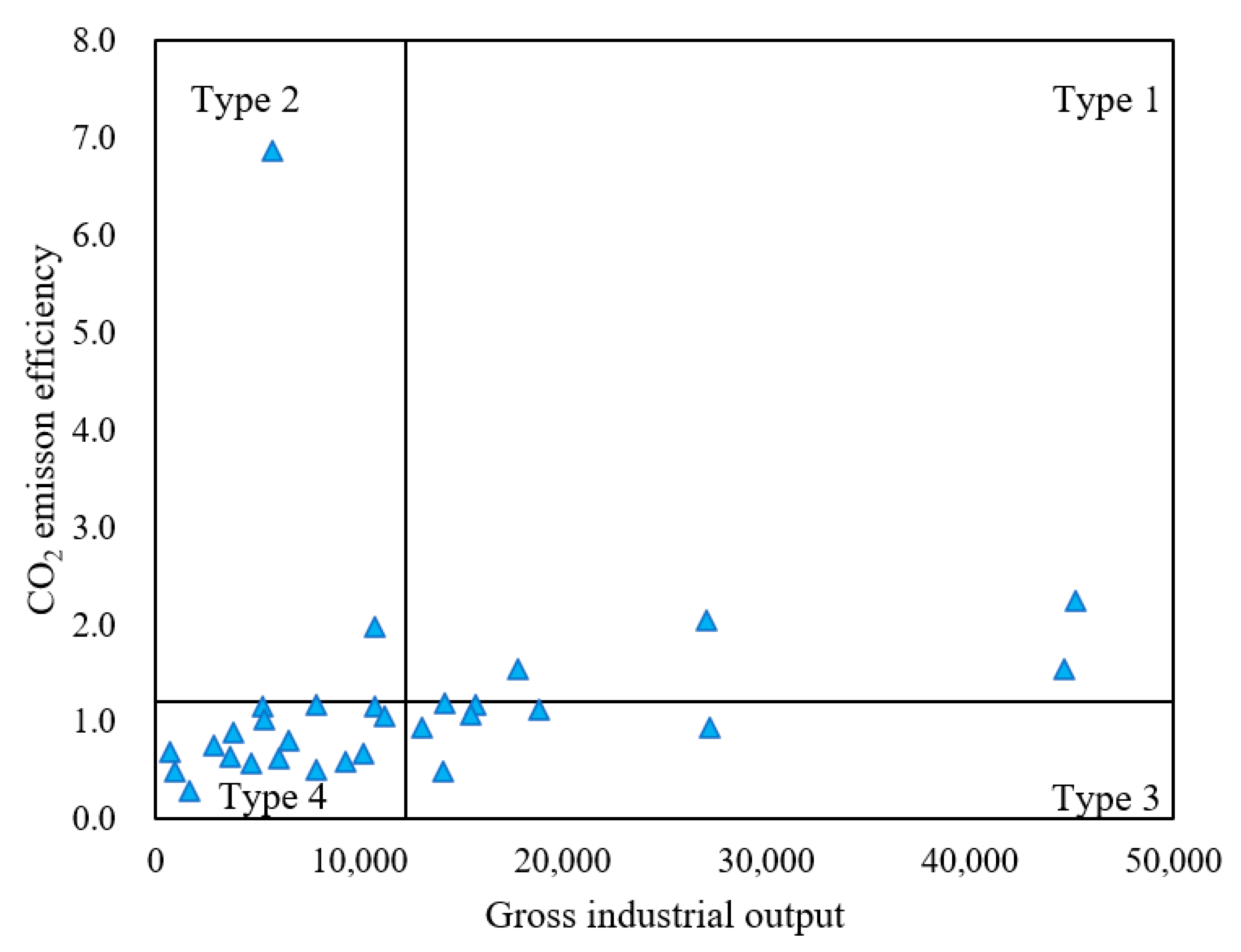
Indicators		Previously Used in
Inputs	Industrial energy consumption (IEC)	Gao et al. [52]; Han et al. [53]; Wu et al. [54];Wu et al. [55]; Zhang et al. [37]
	Industrial labor force (ILF)	Gao et al. [52]; Wu et al. [54]; Zhang et al. [37]; Xie et al. [56]
	Industrial capital (IC)	Gao et al. [52]; Wu et al. [54]; Wu et al. [55]; Zhang et al. [37]; Xie et al. [56]
	Investment in industrial pollution control (IIPT)	Wu et al. [55]; Wu et al. [57]
Outputs	Gross industrial output value (GIOV)	Han et al. [53]; Wu et al. [54]; Wu et al. [55]; Zhang et al. [37]
	Industrial CO2 emissions (ICE)	Han et al. [53]; Wu et al. [54]; Zhang et al. [37]; Xie et al. [56]

.

There are no official statistics on CO₂ emissions from the industrial sector at the provincial level in China. Therefore, this study estimates CO₂ emissions by a fuel-based carbon footprint model, which has been widely adopted in previous research [27]. According to the IPCC Guidelines for National Greenhouse Gas Inventories [58], CO₂ emissions from fossil fuels can be estimated using the following equation:

$${CO}_{2i}={\sum }_{i=1}^n(E_i\times {CCF}_i\times {NCV}_i\times {COF}_i\times {\displaystyle \frac{44}{12}})$$

(18)

In Equation (18), $E_i$ represents the actual consumption of energy type $i$ by the industrial sector in each province. Energy data for raw coal, coke, gasoline, kerosene, diesel fuel, fuel oil, liquefied petroleum gas (LPG), and natural gas were obtained from the China Energy Statistical Yearbook. ${CCF}_i$ is the carbon content factor, ${NCV}_i$ is the net calorific value, ${COF}_i$ is the carbon oxidation factor, and ${\displaystyle \frac{44}{12}}$ is the molecular weight ratio of CO₂ to carbon. According to the data of National Development and Reform Commission, the relevant parameters for calculating carbon dioxide emissions are shown in

Table 2. Parameters related to CO₂ emissions.

Energy	${\mathit{C}\mathit{C}\mathit{F}}_{\mathit{i}}$	${\mathit{N}\mathit{C}\mathit{V}}_{\mathit{i}}$	${\mathit{C}\mathit{O}\mathit{F}}_{\mathit{i}}$
Raw Coal	25.8 kgC/GJ	20,908 kJ/kg	1
Coke	29.2 kgC/GJ	28,435 kJ/kg	1
Gasoline	19.1 kgC/GJ	43,070 kJ/kg	1
Kerosene	19.6 kgC/GJ	43,070 kJ/kg	1
Diesel	20.2 kgC/GJ	42,552 kJ/kg	1
Fuel Oil	21.1 kgC/GJ	41,816 kJ/kg	1
Liquefied Petroleum Gas	17.2 kgC/GJ	50,179 kJ/kg	1
Natural Gas	15.3 kgC/GJ	38,931 kJ/kg	1

.

Data for ILF, IIPT, and GIOV were obtained from the China Statistical Yearbook for each province, while data for IEC and IC were collected from the official websites of provincial statistical bureaus. All indicators represent original data for the industrial sector in 30 Chinese provinces in 2021. Tibet was excluded due to the unavailability of relevant data.

Table 3. Statistical description of input and output data.

	Variables	Unit	Max	Min	Mean	Std. Dev
Inputs	ILF	104 persons	1354.20	11.50	255.95	284.24
	IC	CNY 108	70,715.10	2612.00	23,771.88	16,413.81
	IEC	104 ton	34,029.40	1106.30	11,463.92	7564.36
	IIPT	CNY 106	3806.07	63.50	1117.45	961.60
Outputs	GIOV	CNY 108	45,142.90	683.60	12,279.32	11,151.95
	ICE	104 ton	35,693.18	440.39	10,598.64	7760.21

provides the statistical description of input and output data.

4.2. Analysis of Assessment Results

To provide a more comprehensive analysis of the carbon emission efficiency of the industrial sector across Chinese provinces, this study further explores the relationship between regional groups and individual provinces, as well as the influence of groups on individual performance. Based on the references, the 30 provinces are classified into seven regions: North China, Northeast China, East China, Central China, South China, Southwest China, and Northwest China [59,60]. The provinces included in each region are listed in

Table 4. Seven groups and corresponding provinces.

Groups	Individuals (Provinces)
North China	Beijing, Tianjin, Hebei, Shanxi, Inner Mongolia
Northeast China	Liaoning, Jilin, Heilongjiang
East China	Shanghai, Jiangsu, Zhejiang, Anhui, Fujian, Jiangxi, Shandong
Central China	Henan, Hubei, Hunan
South China	Guangdong, Guangxi, Hainan
Southwest China	Chongqing, Sichuan, Guizhou, Yunnan
Northwest China	Shaanxi, Gansu, Qinghai, Ningxia, Xinjiang

.

Using MATLAB 2018b, we solved 49 linear programming problems to obtain the CO₂ emission efficiency values for the industrial sector across the 30 provinces, as presented in

Table 5. CO₂ emission efficiency of industrial sector cross 30 provinces in China.

Groups	Provinces	North China	Northeast China	East China	Central China	South China	Southwest China	Northwest China	Provinces		Groups
									Efficiency	Ranking	Efficiency
North China	Beijing	10.7564	1.9317	10.7564	9.9630	10.7564	1.9317	1.9317	6.8610	1	2.6138
	Tianjin	1.1176	1.1207	1.1176	1.3391	1.1176	1.1207	1.1207	1.1506	11
	Hebei	0.3412	0.6499	0.3412	0.4072	0.3412	0.6499	0.6499	0.4829	28
	Shanxi	0.5304	0.8144	0.5304	0.6043	0.5304	0.8144	0.8144	0.6627	22
	Inner Mongolia	0.3235	0.7508	0.3235	0.2927	0.3235	0.7508	0.7508	0.5022	27
Northeast China	Liaoning	0.4582	0.7429	0.4582	0.4958	0.4582	0.7429	0.7429	0.5856	25	0.8223
	Jilin	0.8084	0.9655	0.8084	0.8241	0.8084	0.9655	0.9655	0.8780	18
	Heilongjiang	0.5763	0.7599	0.5763	0.4520	0.5763	0.7599	0.7599	0.6372	23
East China	Shanghai	2.5639	1.4212	2.5639	1.8120	2.5639	1.4212	1.4212	1.9667	4	1.7112
	Jiangsu	1.7530	1.1765	1.7530	2.0031	1.7530	1.1765	1.1765	1.5416	6
	Zhejiang	2.5940	1.4162	2.5940	2.1885	2.5940	1.4162	1.4162	2.0313	3
	Anhui	0.9304	0.9620	0.9304	0.8751	0.9304	0.9620	0.9620	0.9361	16
	Fujian	1.9698	1.0344	1.9698	1.7891	1.9698	1.0344	1.0344	1.5431	5
	Jiangxi	1.2541	1.0405	1.2541	1.2232	1.2541	1.0405	1.0405	1.1581	10
	Shandong	0.9133	0.9774	0.9133	0.8423	0.9133	0.9774	0.9774	0.9306	17
Central China	Henan	1.1932	0.9635	1.1932	1.3307	1.1932	0.9635	0.9635	1.1144	12	1.2599
	Hubei	1.2026	1.1543	1.2026	1.1608	1.2026	1.1543	1.1543	1.1759	8
	Hunan	1.3081	1.0228	1.3081	1.2881	1.3081	1.0228	1.0228	1.1830	7
South China	Guangdong	3.5111	0.9213	3.5111	2.3577	3.5111	0.9213	0.9213	2.2364	2	1.5195
	Guangxi	0.5118	0.7580	0.5118	0.5002	0.5118	0.7580	0.7580	0.6157	24
	Hainan	0.5357	0.8809	0.5357	0.5409	0.5357	0.8809	0.8809	0.6844	21
Southwest China	Chongqing	1.1730	1.0811	1.1730	1.3699	1.1730	1.0811	1.0811	1.1617	9	1.0974
	Sichuan	1.0530	1.0408	1.0530	1.1509	1.0530	1.0408	1.0408	1.0618	13
	Guizhou	0.9311	1.1978	0.9311	0.7827	0.9311	1.1978	1.1978	1.0242	15
	Yunan	0.5830	1.0700	0.5830	0.6239	0.5830	1.0700	1.0700	0.7976	19
Northwest China	Shaanxi	0.8919	1.2204	0.8919	0.9859	0.8919	1.2204	1.2204	1.0461	14	0.8058
	Gansu	0.6116	0.9327	0.6116	0.5779	0.6116	0.9327	0.9327	0.7444	20
	Qinghai	0.3266	0.6721	0.3266	0.3713	0.3266	0.6721	0.6721	0.4811	29
	Ningxia	0.1766	0.4194	0.1766	0.1865	0.1766	0.4194	0.4194	0.2821	30
	Xinjiang	0.4073	0.7846	0.4073	0.4023	0.4073	0.7846	0.7846	0.5683	26
Average		1.3769	0.9961	1.3769	1.2914	1.3769	0.9961	0.9961	1.2015	-	1.4043

Note: The bolded entries in columns 3–9 denote the optimal self-assessment efficiency values, and the final row shows average efficiency of the 30 provinces.

. The bolded entries in columns 3–9 represent the optimal self-assessed efficiency values, while the remaining values reflect the peer-assessed efficiencies derived for each province from other groups. Columns 10 and 11, respectively, display the average CO₂ emission efficiency and ranking for each province, and the final column presents the CO₂ emission efficiency for the seven regions, calculated by averaging the optimal efficiency values of the provinces within each region.

According to Table 5, we present the following analysis on three levels:

At the national level, the average industrial carbon efficiency stands at 1.2015, indicating an overall “effective” or “relatively optimal” performance at the national level. This suggests that, under the current technological and input conditions, China’s industrial sector has achieved certain overall progress in controlling carbon emissions. However, although the average value exceeds 1, it is largely driven by a few provinces with exceptionally high efficiency values, such as Beijing (6.8610) and Guangdong (2.2364). Among the 30 provinces, 15 provinces exhibit efficiency values below 1, accounting for 50% of the total. This underscores the significant potential for achieving more balanced efficiency improvements nationwide and addressing the shortcomings in underperforming regions.

At the regional level, substantial spatial heterogeneity in industrial carbon emission efficiency is observed across China. North China exhibits the highest efficiency (2.6138), well above the national average, reflecting its leading position in energy utilization and low-carbon transition, with Beijing performing particularly strongly. East China (1.7112) and South China (1.5195) follow, both exceeding the national mean, benefiting from a solid technological foundation and advanced industrial restructuring. In contrast, Central China (1.2599) remains close to the national average, indicating moderate progress but room for improvement. Meanwhile, Northeast China (0.8223), Southwest China (1.0974), and Northwest China (0.8058) demonstrate relatively low efficiency. The results reveal a clear spatial pattern characterized by higher efficiency in the eastern and northern regions and lower efficiency in the western and northeastern regions.

At the provincial level, significant disparities are evident. High-performing provinces such as Beijing (6.8610), Guangdong (2.2364), and Zhejiang (2.0313) stand out with markedly superior efficiency, showcasing low-carbon, high-efficiency industrial development and providing strong demonstration effects. The majority of provinces record efficiency values within the 0.8–1.5 range, representing a medium level of performance. Although progress in energy saving and emission reduction has been achieved, a considerable gap remains compared with leading provinces. Conversely, provinces with relatively low efficiency, such as Ningxia (0.2821), Hebei (0.4829), and Qinghai (0.4811), remain heavily reliant on energy-intensive and high-emission industries. These regions urgently require industrial restructuring, the adoption of energy-saving technologies, and supportive policy measures to control carbon emission.

Table 5 highlights efficiency differences at both provincial and regional levels. At the individual level, efficiency values vary widely—Beijing and Shanghai exceed 2.0, while western provinces such as Ningxia and Qinghai fall below 0.5. Aggregating to the group level smooths these variations and reveals clearer regional patterns: East China (1.7112) and South China (1.5195) outperform Northwest China (0.8058) and Northeast China (0.8223). Compared with individual-level results, group-level analysis reduces sensitivity to outliers and provides a more integrated view of regional disparities and collaborative potential in industrial carbon efficiency.

4.3. Competitive Strategy Analysis

As previously discussed, the presence of multiple EEFs fosters competitive behavior among DMUs, as each selects the frontier that maximizes its own performance. Similar dynamics occur at the group level, where different regional groups adopt distinct competitive strategies in adjusting CO₂ emissions to construct their respective EEFs.

In practice, these strategies can be categorized into three representative types: (1) the approach adopted by North China, East China, and South China; (2) the approach used by Northeast China, Southwest China, and Northwest China; and (3) the distinct strategy followed by Central China. To ensure clarity and conciseness, we present three representative groups—North China, Northeast China, and Central China—as illustrative examples in

Table 6. The adjustment amount of CO₂ emission for three groups.

Provinces		North China		Northeast China		Central China
	Before Adjustment	Adjustment Amount	After Adjustment	Adjustment Amount	After Adjustment	Adjustment Amount	After Adjustment
Beijing	440.39	4463.63	4904.01	7880.32	8320.71	5656.35	6096.73
Tianjin	4033.66	475.24	4508.90	1615.28	5648.94	1461.16	5494.82
Hebei	35,693.18	−23,530.22	12,162.95	−21,799.54	13,893.64	−22,670.38	13,022.80
Shanxi	16,536.92	−7775.17	8761.74	−6646.77	9890.14	−7346.70	9190.21
Inner Mongolia	21,120.30	−14,303.03	6817.27	−7536.60	13,583.71	−21,120.30	0.00
Liaoning	17,603.81	−9548.42	8055.39	−9275.85	8327.96	−10,492.00	7111.81
Jilin	4098.92	−786.57	3312.34	−393.87	3705.05	−905.41	3193.51
Heilongjiang	5480.64	−2325.92	3154.72	−3318.48	2162.16	−4900.09	580.55
Shanghai	3607.81	5662.66	9270.47	9134.79	12,742.60	5315.38	8923.19
Jiangsu	21,972.39	16,574.11	38,546.50	19,218.63	41,191.02	24,687.32	46,659.71
Zhejiang	8973.00	14,351.20	23,324.20	22,785.56	31,758.57	16,204.09	25,177.09
Anhui	12,138.34	−845.36	11,292.97	−1481.72	10,656.62	−2061.46	10,076.88
Fujian	7790.53	7570.82	15,361.35	1695.54	9486.07	8665.52	16,456.05
Jiangxi	7416.15	1886.81	9302.96	1204.33	8620.49	2171.49	9587.65
Shandong	25,746.22	−2235.62	23,510.60	−1806.47	23,939.75	−5632.18	20,114.05
Henan	13,589.89	2629.52	16,219.41	−2045.20	11,544.69	5156.59	18,746.48
Hubei	11,264.53	2285.51	13,550.04	6021.69	17,286.22	2401.01	13,665.54
Hunan	9345.51	2883.83	12,229.34	906.60	10,252.11	3498.75	12,844.26
Guangdong	11,070.93	27,910.79	38,981.73	−11,070.93	0.00	28,712.73	39,783.66
Guangxi	10,250.81	−5009.74	5241.06	−5565.95	4684.86	−6703.35	3547.46
Hainan	1101.51	−512.30	589.21	−265.34	836.17	−640.79	460.72
Chongqing	5806.09	1005.87	6811.96	1698.36	7504.45	2352.76	8158.85
Sichuan	12,643.71	671.86	13,315.56	1737.82	14,381.52	2234.63	14,878.34
Guizhou	4947.88	−341.25	4606.63	2529.88	7477.76	−1637.01	3310.87
Yunan	9709.08	−4053.19	5655.89	1230.36	10,939.44	−4365.45	5343.63
Shaanxi	10,893.93	−1178.83	9715.10	5835.06	16,729.00	−178.37	10,715.57
Gansu	4021.17	−1564.45	2456.73	−590.21	3430.96	−2298.66	1722.51
Qinghai	2518.99	−1698.72	820.27	−1334.65	1184.34	−1782.60	736.39
Ningxia	8200.68	−6761.05	1439.63	−6665.52	1535.16	−8082.65	118.03
Xinjiang	9942.16	−5901.97	4040.19	−3697.15	6245.01	−7700.39	2241.78
Sum	317,959.13	0	317,959.13	0	317,959.13	0	317,959.13

Note: The bolded entries in columns 3–8 respectively represent the fixed-sum output before adjustment and adjustment amounts for provinces within each group, and the final row shows the total sum of adjustment amounts for each column.

. These examples effectively capture the diversity of strategic behaviors while avoiding redundancy, since other regions adopt equivalent strategic mechanisms. Furthermore, the adjusted CO₂ emissions of all provinces sum to zero, confirming the feasibility and internal consistency of the proposed model.

4.4. Suggestions

Based on the CO₂ emission efficiency and total industrial output value, the 30 provinces are classified into four types. As illustrated in Figure 1, the total industrial output value is plotted on the x axis and CO₂ emission efficiency on the y axis. Two reference lines are included: one represents the average total industrial output value (12,279.32) and the other represents the average CO₂ emission efficiency (1.2015). These lines divide the chart into four quadrants.

For Type 1, characterized by high gross industrial output and high CO₂ emission efficiency, four provinces are included (Guangdong, Jiangsu, Zhejiang, Fujian). These provinces demonstrate robust performance in both industrial output and energy utilization, and they should consolidate and maintain this positive trajectory. In addition, they are encouraged to intensify collaborative decarbonization initiatives with other provinces to advance green and low-carbon development.

For Type 2, which includes only Beijing and Shanghai, it is characterized by relatively low gross industrial output but high measured CO₂ emission efficiency. It should be noted that this “high efficiency” phenomenon may largely stem from industrial restructuring, as these regions have outsourced carbon-intensive manufacturing activities to other areas while maintaining high consumption levels and service-oriented economic structures. For example, a portion of the emissions generated from electricity production are attributed to energy-producing provinces rather than the actual areas of consumption, leading to an underestimation of their carbon responsibility. Therefore, rather than simply expanding industrial output, these provinces should focus on optimizing industrial structure, improving energy consumption patterns, and enhancing the transparency of inter-provincial carbon accounting.

For Type 3, characterized by high gross industrial output and low CO₂ emission efficiency, seven provinces are included (Shandong, Henan, Hubei, Sichuan, Hunan, Hebei, and Anhui). While these provinces make notable contributions to gross industrial output, their low CO₂ emission efficiency suggests that environmental protection has been neglected during past development. Consequently, it is advisable for these provinces to improve resource utilization efficiency and actively promote low-emission energy sources to realize more sustainable, green industrial practices.

For Type 4, characterized by low gross industrial output and low CO₂ emission efficiency, seventeen provinces are included (Guizhou, Yunan, Shaanxi, Gansu, Qinghai, Ningxia, Xinjiang, Tianjin, Shanxi, Inner Mongolia, Liaoning, Jilin, Heilongjiang, Jiangxi, Guangxi, Hainan, and Chongqing). These provinces face the dual challenges of promoting economic development and reducing emissions, reflecting a significant imbalance in China’s regional low-carbon transition process. It is recommended that they pursue a dual strategy of technological innovation and efficiency improvement. Specifically, they should support research and development of clean technologies, waste heat recovery, and other applicable solutions while establishing regional green technology sharing platforms. Simultaneously, they should implement energy management systems in high-energy-consuming industries such as iron, steel, and cement, and carry out energy-efficiency benchmarking to promote high-quality economic development.

5. Conclusions

In this study, we exploratively extend the fixed-sum output DEA models from the individual to the group level. Specifically, we define expression for group performance by applying an average criterion and construct an EEF to evaluate all groups. Furthermore, taking into account the non-uniqueness of the EEF and the competitive relationship between the groups, we propose the group cross-EEF approach, in which each group adopts an aggressive strategy to select an EEF to evaluate the other groups. This method fully considers the perspectives of all groups and effectively circumvents inconsistencies in evaluation criteria caused by the non-uniqueness of EEFs, ultimately producing evaluation results that are more broadly acceptable to all DMUs. To demonstrate the practical value of the proposed methodology, we applied it to assess the carbon emission efficiency of the industrial sector cross 30 Chinese provinces in 2021. The results indicate that the overall performance of China’s industrial sector is satisfactory, with an average carbon emission efficiency score of 1.2015. At the provincial level, Beijing and Guangdong exhibit the strongest performance, whereas Ningxia, Qinghai, and Henan lag behind. Regionally, North China performs best, while Northwest China registers the poorest performance. Finally, differentiated recommendations are provided for each province. This study establishes a solid theoretical framework and provides evidence-based policy recommendations to facilitate the low-carbon transition of China’s industrial sector, offering valuable insights for both academia and policymakers.

Three directions for future research are identified. First, the proposed method currently assumes purely competitive relationships between groups; however, in many real-world contexts, cooperation and competition often coexist. Future studies should therefore explore how to evaluate such hybrid interaction mechanisms. Secondly, this study relies on cross-sectional data, which limits the ability to capture temporal dynamics in group performance. Future research could extend the proposed framework to panel data to analyze the evolution of the efficiency and the long-term impact of policy interventions over time. Finally, this study does not account for the uncertainty associated with CO₂ emissions or the potential bias arising from inter-provincial carbon leakage, where carbon-intensive production may be outsourced to other regions. Addressing both emission uncertainty and consumption-based perspectives represents an important avenue for future research.