Simplified and Adjustable Graph Diffusion Neural Networks

Abstract

Graph Convolutional Networks (GCNs) have become a widely used framework for learning from graph-structured data due to their efficiency and performance in tasks such as node classification and link prediction. However, conventional GCNs are limited by a small receptive field, typically restricted to 1–2 hops, which prevents them from capturing long-range dependencies. Graph diffusion methods address this limitation by integrating multi-hop information, but they often introduce high computational costs and over-smoothing issues. To overcome these challenges, we propose a Simplified and Adjustable Graph Diffusion model. Our method employs a predefined diffusion stage and introduces two adaptive parameters: a distance parameter that specifies the diffusion depth and a diffusion control parameter that dynamically adjusts edge weights based on inter-node distances. This approach reduces computational overhead while enabling more effective information propagation. Extensive experiments on benchmark datasets demonstrate that our model achieved an average improvement of 1.9 percentage points in AUC for link prediction and 2.2 percentage points in accuracy for semi-supervised classification tasks. The improvements are particularly significant when leveraging structural information from distant nodes. The proposed framework strikes a balance between accuracy and efficiency, offering a practical alternative for scalable graph learning applications.

1. Introduction

A graph is a mathematical structure consisting of nodes connected by edges, serving as a fundamental representation for modeling relationships and interactions between entities [1]. Graphs provide a framework for capturing complex dependencies across diverse real-world domains, including social networks, e-commerce platforms, and biological systems [2].

Graph Neural Networks (GNNs) are a class of deep learning architectures designed to learn from graph-structured data by aggregating and transforming information from neighboring nodes [3,4].

Among various GNNs, Graph Convolutional Networks (GCNs) have gained widespread adoption due to their computational efficiency and superior performance. GCNs effectively integrate both node attributes and topological structure, enabling robust learning from non-Euclidean data such as social networks and molecular graphs [5].

A key limitation of standard Graph Convolutional Networks (GCNs) is their restricted receptive field, as they primarily aggregate information from only 1-hop or 2-hop neighbors, depending on the number of layers [6]. This constraint makes it challenging for GCNs to capture long-range dependencies within the graph, thereby limiting their effectiveness in scenarios where distant node interactions are crucial. Moreover, stacking too many layers to expand the receptive field often leads to over-smoothing, a phenomenon in which node representations become indistinguishably similar, thereby reducing model expressiveness.

To incorporate multi-hop neighborhood information, Graph Diffusion Convolution models have been developed [7,8]. These models aggregate information from extended neighborhoods through a weighted summation of transition matrix powers, thereby smoothing node representations and capturing long-range dependencies in graph topology. While this approach demonstrates performance improvements, it incurs computational overhead due to the matrix power computations required in the diffusion process. Moreover, the polynomial summation formulation may exacerbate the over-smoothing phenomenon.

In this study, we propose simplified graph diffusion, a novel framework that exploits richer node information than conventional GCNs while mitigating computational overhead. Additionally, we introduce adaptive parameters that modulate edge weights according to inter-node distances.

The proposed simplified graph diffusion framework offers practical advantages across diverse domains. In social networks, it efficiently captures multi-hop influence and community structures with reduced computational cost. For citation networks, it propagates information among distant yet topically related papers, improving link prediction and clustering. In molecular graphs, it models long-range interactions such as electron delocalization, enhancing molecular property prediction. These applications demonstrate that the framework achieves scalable and interpretable graph learning by balancing efficiency with long-range dependency modeling.

To reduce computational overhead, the proposed model predefines the diffusion stage and only utilizes the matrix used in the final diffusion stage as a graph convolution filter. Additionally, we introduce a diffusion control parameter during the normalization process to enable adjustment of edge weights based on the distance from the starting node. We then combine this simplified graph diffusion filter with a graph autoencoder model.

The paper is structured as follows: Section 2 provides a comprehensive review of related research; Section 3 outlines the methodology employed; Section 4 presents the experimental results and their analysis; and Section 5 offers conclusions and directions for future research.

2. Related Works

Graph Neural Networks (GNNs) constitute a class of deep learning architectures specifically designed to learn from graph-structured data by aggregating and transforming information from local neighborhoods via message passing, thereby revolutionizing representation learning on graphs. Traditional GNNs, such as Graph Convolutional Networks (GCNs), propagate only a few hops per layer, which limits the receptive field and can hinder performance on tasks requiring long-range dependencies [9]. To overcome this limitation, graph diffusion techniques incorporate diffusion processes—such as random walks, heat diffusion, or personalized PageRank (PPR)—into graph convolutions. By doing so, they allow information to flow beyond immediate neighbors systematically, aiming to bridge the global perspective of spectral methods with the local focus of spatial message passing [7].

Gasteiger et al. [9] proposed Personalized PageRank Propagation (PPNP), a method that integrates Personalized PageRank diffusion into Graph Neural Networks (GNNs). This approach enables GNNs to capture large receptive fields while effectively mitigating the problem of oversmoothing. By decoupling prediction from propagation, it achieves scalable and effective influence propagation. PPNP demonstrated improved classification performance compared to standard GCNs, and its propagation scheme can be combined with arbitrary neural network architectures during the prediction stage. However, PPNP requires storing the entire graph in memory, making it inefficient for large-scale graphs.

Traditional GNNs suffer from limited long-range dependency modeling and oversmoothing issues due to their reliance on local message passing. To address these limitations, Li et al. [8] proposed the Graph Diffusion Network (GDN), which incorporates diffusion processes into graph learning. The core idea of GDN is to utilize graph diffusion to model information propagation, enabling nodes to effectively leverage both local and global structural information. However, GDN has a significant computational limitation: the expensive preprocessing required to compute the diffusion matrix severely restricts its scalability to large-scale graphs.

Another foundational work is Graph Diffusion Convolution (GDC) [7], which replaces local message passing with a generalized diffusion operation. GDC constructs a sparsified adjacency matrix using diffusion processes such as the heat kernel or personalized PageRank, effectively rewiring the graph to capture higher-order connectivity. This diffusion-based adjacency enables each node to aggregate information from a broader neighborhood beyond immediate 1-hop neighbors, while maintaining spatial locality through sparsification.

Chamberlain et al. [10] introduced GRAND, which explicitly models GNN layers as a time-discretization of a diffusion partial differential equation (PDE) on graphs. The work demonstrated that viewing message passing as a diffusion process provides a principled way to design deeper GNNs, thereby motivating multi-scale diffusion designs that capture higher-order information more effectively.

Wang et al. [11] propose the Multi-Scale Graph Diffusion Convolutional Network (MSD-GCN), a framework for multi-view learning that captures high-order information without requiring multiple convolutional layers. By combining contractive mapping with multi-scale diffusion, it efficiently expands node receptive fields and fuses information across views.

Graph diffusion techniques have been leveraged in various application domains, including social networks, recommendation systems, and molecular chemistry. In recommendation systems, social diffusion GNNs have been introduced to leverage social influence for more accurate predictions. Wu et al. [12] proposed DiffNet, a deep model that treats social influence as a recursive diffusion process to refine user embeddings. DiffNet++ [13] further modeled interest diffusion along with influence and combined the two diffusion processes in a unified framework for social recommendation. These models demonstrated that graph diffusion is not only a tool for semi-supervised learning but also a powerful metaphor for social behavioral propagation, leading to improved collaborative filtering.

The recent success of transformer models has demonstrated the effectiveness of attention mechanisms in recommendation systems, which emphasize interaction features and capture user preferences. Building on this, attention mechanisms have been integrated with graph neural networks (GNNs) to model complex interaction features [14].

In molecular graphs, graph diffusion can model phenomena like electron delocalization or signal transduction across a molecule. Diffusion-based convolution addresses this by allowing information to travel through many bonds in a single operation. Elhag et al. [15] introduced Graph Anisotropic Diffusion (GAD) as a GNN that alternates between linear diffusion and anisotropic filtering.

In summary, although graph diffusion methods have made significant progress, they still face high computational overhead and challenges in controlling the diffusion process.

3. Methodology

This section introduces a simplified and adjustable graph diffusion (SimDiff) approach designed to improve the efficiency of existing graph diffusion neural network models.

Suppose $\mathcal{G}=(\mathcal{V},\mathcal{E})$ be a given graph with node set $\mathcal{V}$ and edge set $\mathcal{E}$. We denote the number of nodes with $N=\left|\mathcal{V}\right|$ and the number of nodes and the number of edges with E = $\left|\mathcal{E}\right|$. The adjacency matrix with $\mathrm{A}\in {\mathbb{R}}^{N\times N}$.

Whereas traditional diffusion methods add up the diffusion results of all n-hops and use them as a graph filter, simplified graph diffusion uses only the graph diffusion matrix at the nth hop to build the graph filter. Thus, the first parameter of the simplified graph diffusion is the distance parameter, n.

Let us define the second parameter, a diffusion control parameter, $\alpha \in \left(\mathrm{0,1}\right)$, in the renormalization trick of the GCN. The diffusion control parameter, α, denotes the probability that information is passed from a current node to its neighbors, and (1 − α) denotes the probability that information stays at a current node.

Then, it can be represented in a single matrix by multiplying the diagonal and off-diagonal components of the adjacency matrix, respectively. Then, let us define a modified adjacency matrix with self-connections, $\tilde{A}$, as follows:

$$\tilde{A}=\alpha A+\left(1-\alpha \right)I,$$

(1)

if α = 0.5, $\tilde{A}=A+\mathrm{I}$ represents the adjacency matrix with self-connections in [5]. Thus, Equation (1) can be seen as a normalized form of a diffusion control parameter(α) in [7], where $\tilde{A}=A+\lambda I$.

From a physical perspective, the diffusion control parameter α can be interpreted as a diffusion probability, analogous to transition probabilities in stochastic diffusion or random walk processes. In physical diffusion systems, a particle remains at its current position or moves to neighboring locations with probability determined by the diffusion coefficient. Similarly, α represents the probability that feature information propagates to adjacent nodes, while (1 − α) represents the probability of information remaining localized. This interpretation aligns with classical diffusion dynamics, where α governs the trade-off between self-preservation and spatial spreading. Therefore, tuning α controls the degree of information dispersion across the network, analogous to adjusting the diffusion coefficient in physical systems.

After normalizing GCN’s 1-hop graph convolution filter, a simplified polynomial filter can be obtained by squaring the distance parameter (n). Thus, a simplified polynomial filter for graph diffusion convolution, ${\widehat{A}}_{\mathrm{SimDiff}}$, is defined as

$${\widehat{A}}_{\mathrm{SimDiff}}=({\tilde{D}}^{-{\displaystyle \frac{1}{2}}}\tilde{A}{\tilde{D}}^{-{\displaystyle \frac{1}{2}}}{)}^n.$$

(2)

As the simplified filter contains all the edge information necessary for n-step graph diffusion, it can be used as an approximated filter of the traditional graph diffusion convolution filter. The propagation between the layers of the graph convolution is as follows. Note that σ represents the activation function, where the ReLU activation function is used.

$${\mathrm{H}}^{(l+1)}=\sigma \left({\widehat{A}}_{\mathrm{SimDiff}}{\mathrm{H}}^{\left(l+1\right)}{W}^{\left(l\right)}\right)$$

(3)

In general, an n-hop graph filter can be expressed as a polynomial expansion of the normalized adjacency matrix A:

$$H=\left(a_{0}I+a_{1}A+a_1{A}^2+\dots +a_1{A}^n\right)X,$$

(4)

where aₖ are constant coefficients and X ∊ ℝᴺˣᶠ denotes the node feature matrix with N nodes and F features per node. This formulation captures multi-hop propagation, where higher-order powers of A represent information diffusion from distant neighbors.

In the proposed model, the diffusion process is simplified by retaining only the first and last terms of the polynomial filter:

H′ = (I + Aⁿ)X

(5)

Although intermediate powers of A are omitted, the matrix Aⁿ inherently contains the relational information of all lower orders. Therefore, the simplified filter preserves the essential adjacency-based propagation pattern of the traditional polynomial diffusion filter while significantly reducing computational complexity and parameter dependencies.

Compared with state-of-the-art graph diffusion models such as GRAND [10], GDC [7], PPNP [9], and DiffNet++ [13], as well as physics-embedding approaches tailored for time-variant system reliability [16], SimDiff focuses on efficient and scalable topological propagation for abstract graphs. This distinguishes it from domain-informed models that prioritize interpretability or physical consistency at the cost of increased computational complexity.

In summary, SimDiff offers a lightweight and encoder-agnostic propagation framework that enhances structural information flow while maintaining scalability and simplicity. Unlike prior methods that rely on precomputed diffusion matrices or domain-specific priors, SimDiff operates directly on the raw graph topology without introducing additional architectural complexity.

4. Results

4.1. Benchmark Datasets

For both semi-supervised classification and link prediction experiments, we use the three benchmark datasets Cora, Citeseer, and Pubmed, which are commonly used to validate graph-deep neural network models [17], and the arXiv-condmat network data built from metadata provided by the article repository website arXiv [18].

In addition, the arXiv-condmat dataset is constructed from the arXiv metadata. The dataset is based on journal papers in the condensed matter category of Physics. Each paper has its own label, and the connectivity is determined by co-authorship. Node attributes are extracted from keywords in the paper titles. The details of each dataset are shown in

Table 1. Benchmark datasets.

Dataset	Connectivity	# of Nodes	# of Edges	# of Labels	# of Attributes
Cora	citation	2708	5278	7	1433
Citeseer	citation	3312	4536	6	3703
Pubmed	citation	19,717	44,324	3	500
arXiv-condmat	co-authorship	10,000	20,172	8	8200

.

Attribute data from the Cora, Citeseer, and arXiv-condmat datasets were embedded in binary or term-frequency format based on the occurrence of each keyword. In contrast, the Pubmed dataset was additionally weighted with term-frequency/inverse document frequency (TF/IDF) embedding to reflect the importance of the keyword in the document.

4.2. Link Prediction

4.2.1. Baseline Methods

Four baseline methods are used in the link prediction experiment.

• Graph AutoEncoder (GAE) [19] is an unsupervised neural network model that learns low-dimensional node embeddings by encoding graph structure and node features, and then reconstructs the graph from these embeddings [20].
• Variational Graph Autoencoder (VGAE) [21] combines the graph convolutional network with the variational autoencoder algorithm. While GAE learns deterministic node embeddings, VGAE learns probabilistic embeddings by modeling each node’s latent representation as a distribution, allowing for uncertainty estimation and graph generation.
• Spectral Clustering (SC) [22] is a graph-based clustering algorithm that partitions data by computing the eigenvectors of a graph Laplacian derived from a similarity matrix, thereby capturing the structure of the data manifold.
• DeepWalk (DW) [23] is an unsupervised graph representation learning algorithm. It obtains random walks on graphs and then trains the representation through neural networks.

4.2.2. Parameter Settings

For the GAE and VGAE models, a two-layer graph convolution was performed, with the input adjacency matrix encoded as a 32-dimensional representation in the first layer and a 16-dimensional representation in the second layer. We use the Adam optimizer for training and set the learning rate to 0.01. Training is performed for a total of 200 epochs.

As for the proposed graph diffusion model, experiments were conducted with the maximum node distance (n) in the range [1,5], and the diffusion control parameter (α) in the range [0.1, 0.3, 0.5, 0.7, 0.9]. Note that the simplified graph diffusion model with n = 1 and α = 0.5 corresponds to the baseline GAE and VGAE models.

The SC model used the default settings of Pedregosa et al. [24], encoding the input adjacency matrix in 128 dimensions. The DW model employed the negative sampling softmax, which was proposed in the node2vec model [25] as a more efficient alternative to the hierarchical softmax introduced by [22], during the encoding process based on the Skip-gram model.

For encoding with DW, we set the hidden representation dimension, step length, number of steps to be performed per node, window (or context) size, and number of epochs in the encoding process to 128, 80, 10, 10, and 1, respectively.

In the link prediction experiment, 10% of the total edges were used for evaluation, and 5% were used for validation. The adjacency matrix used for training was constructed by removing the edges in the evaluation and validation sets.

Link prediction experiments are conducted in two settings: with and without node attributes. In the setting with node attributes, the normalized adjacency matrix with graph regularization is multiplied by the node attributes. In the setting without node attributes, the identity matrix is multiplied after graph normalization and used as the input to the encoder. Model performance was evaluated using two complementary metrics. The area under the Receiver Operating Characteristic curve (AUC-ROC) quantifies the classifier’s overall ranking ability by plotting the true positive rate against the false positive rate across various thresholds. Average Precision (AP), defined as the area under the precision-recall curve, summarizes the trade-off between precision and recall across all thresholds.

The model was trained for 200 epochs without early stopping, using a fixed learning rate of 0.01, a weight decay coefficient of 0.0005, and a dropout rate of 0.5. The hidden layer dimension was set to 32. To improve the robustness of the evaluation, the experiments were conducted ten times with randomly sampled validation sets, effectively implementing a cross-validation scheme. Each experiment was performed 10 times.

4.2.3. Results

The results of the link prediction experiment without node attributes are presented in

Table 2. Link prediction results without node attributes. GAE-SimDiff and VGAE-SimDiff are extensions of GAE and VGAE with a simplified diffusion mechanism.

	Cora		Citeseer		Pubmed		arXiv-Condmat
	AUC	AP	AUC	AP	AUC	AP	AUC	AP
SC	84.85 ± 1.15	87.69 ± 1.23	77.59 ± 0.76	80.20 ± 1.01	80.27 ± 0.21	80.05 ± 0.37	90.61 ± 0.38	91.17 ± 0.39
DW	81.40 ± 0.86	82.91 ± 1.30	78.11 ± 1.26	81.82 ± 1.05	86.41 ± 0.50	86.02 ± 0.50	92.75 ± 0.24	92.81 ± 0.27
GAE	84.64 ± 0.71	88.39 ± 0.42	78.55 ± 1.52	84.03 ± 1.13	82.03 ± 0.57	87.35 ± 0.41	93.10 ± 0.29	95.27 ± 0.16
VGAE	84.63 ± 1.38	88.24 ± 1.00	78.89 ± 1.58	83.90 ± 1.43	82.73 ± 0.46	87.61 ± 0.33	92.75 ± 0.52	94.93 ± 0.35
GAE-SimDiff	86.66 ± 1.52	89.76 ± 1.30	79.91 ± 1.48	84.84 ± 1.20	84.31 ± 0.52	88.79 ± 0.29	93.28 ± 0.55	95.35 ± 0.35
(n, α)	(3, 0.3)		(5, 0.1)		(5, 0.3)		(5, 0.1)
VGAE-SimDiff	86.86 ± 1.13	89.66 ± 0.75	80.38 ± 1.14	84.95 ± 0.90	84.76 ± 0.39	89.05 ± 0.31	92.98 ± 0.28	95.19±0.17
(n, α)	(4, 0.7)		(5, 0.5)		(4, 0.7)		(4, 0.1)

. In this study, we propose two diffusion-based extensions of graph autoencoders. GAE-SimDiff incorporates a simplified diffusion mechanism into the standard Graph Autoencoder (GAE), enabling more effective propagation of structural information across the graph. Similarly, VGAE-SimDiff applies the same simplified diffusion process to the Variational Graph Autoencoder (VGAE), combining the advantages of variational inference with enhanced structural encoding. These models are designed to capture richer topological dependencies while maintaining computational efficiency.

As shown in Table 2, models incorporating simplified graph diffusion showed generally improved performance, with the best results obtained when information from nodes at distances of three or more was utilized.

As shown in

Table 3. Link prediction results with node attributes. GAE-SimDiff and VGAE-SimDiff are extensions of GAE and VGAE with a simplified diffusion mechanism.

	Cora		Citeseer		Pubmed		arXiv-Condmat
	AUC	AP	AUC	AP	AUC	AP	AUC	AP
GAE	91.05 ± 0.75	91.97 ± 0.75	89.44 ± 1.11	90.43 ± 1.43	96.25±0.27	96.41±0.26	94.53 ± 0.37	96.02 ± 0.25
VGAE	92.11 ± 0.57	93.08 ± 0.63	90.48 ± 0.97	91.65 ± 0.99	94.48 ± 0.40	94.65 ± 0.45	94.22 ± 0.29	95.73 ± 0.21
GAE-SimDiff	91.76 ± 1.00	92.95 ± 1.07	91.21 ± 0.50	92.08 ± 0.67	96.19 ± 0.27	96.29 ± 0.31	94.48 ± 0.38	96.06 ± 0.25
(n, α)	(1, 0.3)		(5, 0.1)		(1, 0.3)		(5, 0.1)
VGAE-SimDiff	92.00 ± 0.69	93.15 ± 0.62	90.88 ± 0.60	92.30 ± 0.40	94.39 ± 0.57	94.58 ± 0.43	94.50 ± 0.40	95.94 ± 0.22
(n, α)	(1, 0.3)		(1, 0.1)		(1, 0.3)		(4, 0.1)

, the results of the link prediction experiments with node attributes varied across datasets, with benchmark models performing better in some cases and the diffusion-based models achieving higher performance in others. Higher accuracy was generally obtained when information from nodes within two hops was utilized, and better results were observed with relatively low diffusion control parameters (α ≤ 0.3). Across both settings—with and without node attributes—the performance difference between GAE and VGAE remained insignificant.

In the link prediction experiments, we observed that simplified graph diffusion enhanced predictive performance by effectively leveraging connections from more distant nodes. However, when node attributes were incorporated, the performance did not differ significantly from the benchmark models. These findings suggest that, for the given datasets, structural connections from distant nodes provide useful information for link prediction, whereas node attributes from distant nodes contribute less to improving predictive accuracy.

4.3. Semi-Supervised Classification

4.3.1. Baseline Methods

• Logistic Regression (LR) is a statistical model used for binary classification tasks. It predicts the probability that a given input belongs to a particular class using the logistic function [23].
• A Multi-Layer Perceptron (MLP) is a type of feedforward artificial neural network composed of an input layer, one or more hidden layers, and an output layer. It can model complex nonlinear relationships between inputs and outputs.
• A GCN is a type of neural network designed to operate on graph-structured data. It extends convolutional operations to graphs by aggregating information from a node’s neighbors.

Note that the proposed simplified graph diffusion is applied in a graph convolutional process of a basic 2-layer GCN model [5].

4.3.2. Parameter Settings

We set the hidden layer dimension of the GCN model to 32, use the Adam optimizer, and set the learning rate to 0.01. The dropout rate is set to 50% and the weight decay is set to 0.0005. Two hundred epochs of training are performed.

The default settings of Pedregosa et al. [23] have been used in a logistic regression (LogReg) model and a basic multi-layer perceptron (MLP) model. Logistic regression employs a one-versus-rest algorithm, whereas MLP utilizes a single hidden layer and a learning rate of 0.05. Both models are trained for two hundred epochs.

For both the GCN and baseline models, we use 45% of the training set and 5% of the validation set, and compare their performance in terms of classification accuracy. Each experiment is repeated 10 times.

4.3.3. Results

Table 4. Semi-supervised Learning Classification Results in terms of accuracy.

	Cora	Citeseer	Pubmed	arXiv-Condmat
LogReg	74.73 ± 0.72	71.27 ± 0.95	85.15 ± 0.34	66.88 ± 0.58
MLP	72.94 ± 0.94	69.41 ± 0.77	85.16 ± 0.50	63.58 ± 0.40
GCN	86.25 ± 0.64	72.65 ± 0.93	87.27 ± 0.23	68.78 ± 0.50
GCN-SimDiff	87.20 ± 0.95	73.71 ± 0.95	88.77 ± 0.26	71.84 ± 0.35
(n, α)	(3, 0.3)	(1, 0.1)	(2, 0.1)	(1, 0.1)

presents the results of the semi-supervised classification experiments. Overall, the models incorporating simplified graph diffusion achieved higher performance, with the best results obtained when information from nodes within three hops and diffusion control parameters not exceeding 0.3 were used.

4.4. Computational Efficiency Analysis

To further evaluate the scalability of the proposed method, the computational efficiency of SimDiff was examined in comparison with the closed-form n-hop polynomial filter. The analysis focuses on runtime characteristics across multiple benchmark datasets to assess whether the diffusion efficiency of SimDiff is maintained as the propagation order increases.

The computational efficiency of the proposed SimDiff filter was evaluated against the closed-form n-hop polynomial filter using four benchmark datasets: Cora, Citeseer, Pubmed, and Arxiv-condmat.

The runtime of SimDiff increased almost linearly with the filter order $n,$ as expected from iterative sparse–dense matrix multiplications, whereas the closed-form polynomial filter exhibited approximately constant but substantially higher computation time due to the dense linear-system inversion.

At $n=5$, SimDiff was approximately 2.2× faster on Cora, 12.8× faster on Citeseer, 3.3× faster on Pubmed, and 9.4× faster on Arxiv-condmat. These results indicate that SimDiff provides a scalable and computationally efficient alternative to closed-form polynomial filtering for practical GNN applications with moderate diffusion orders. Although the closed-form approach offers theoretical compactness, its dense solver overhead limits efficiency and becomes advantageous only when the same operator is reused across multiple feature channels or diffusion steps.

4.5. Parameter Sensitivity Analysis

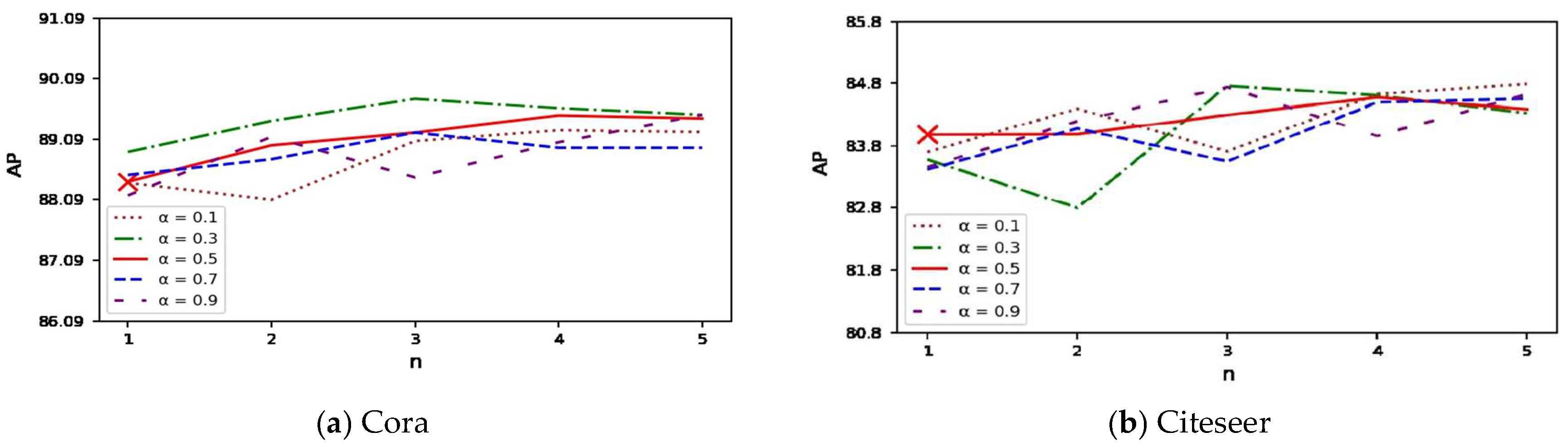
To evaluate the robustness and generality of the proposed simplified diffusion filter, we conducted an extensive parameter sensitivity analysis across four benchmark citation networks: Cora, Citeseer, Pubmed, and arXiv-condmat. For each dataset, we examined two tasks: (1) link prediction using GAE without node features, and (2) semi-supervised node classification using GCN. The diffusion step (n) and diffusion probability (α) were varied to analyze their joint impact on performance. The baseline configuration (n = 1, α = 0.5) is indicated with an “×” in all plots.

• GAE Link Prediction Results

As shown in Figure 1, the simplified diffusion filter exhibits consistent and stable behavior across all four datasets. For Cora and Citeseer, average precision (AP) increases as n grows from 1 to approximately 3, then saturates or slightly fluctuates. Moderate diffusion probabilities (α ∊ [0.3, 0.7]) yield the best performance, while very small values (α = 0.1) result in noticeably lower AP due to insufficient propagation strength.

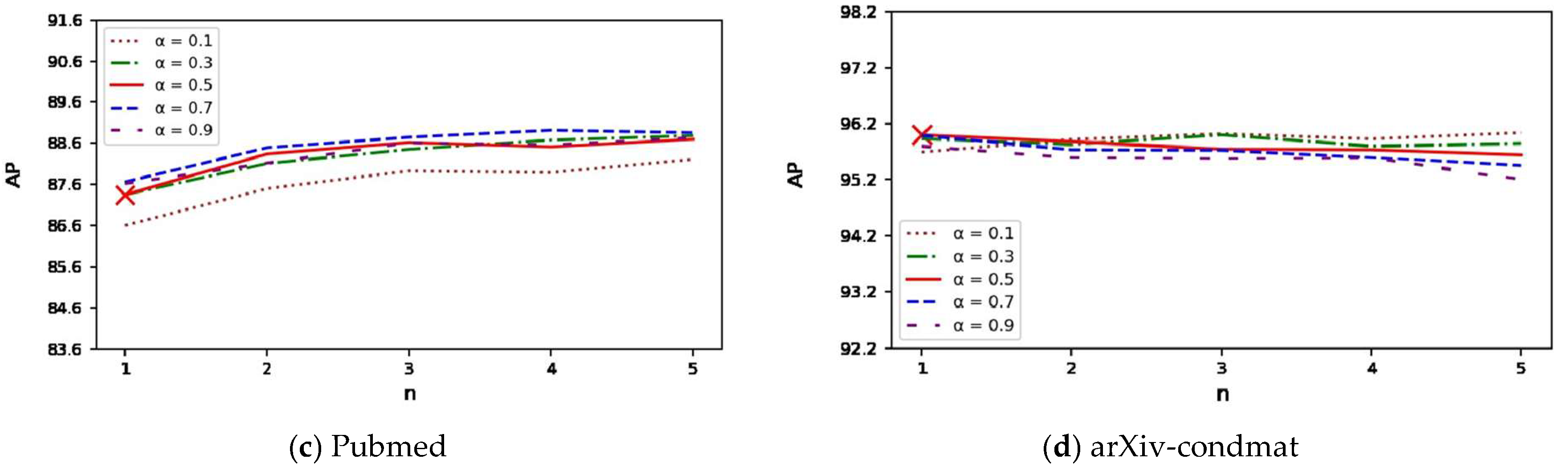
On Pubmed, which has a larger size and sparser connections, AP remains highly stable across all n and α values, demonstrating that the simplification maintains stability in large graphs. For the arXiv-condmat dataset, AP exhibits a mild upward trend as n increases to around 3–4, with moderate α values consistently outperforming extreme settings. Overall, the GAE experiments demonstrate that the simplified diffusion design preserves long-range information while avoiding hyperparameter sensitivity.

• GCN Node Classification Results

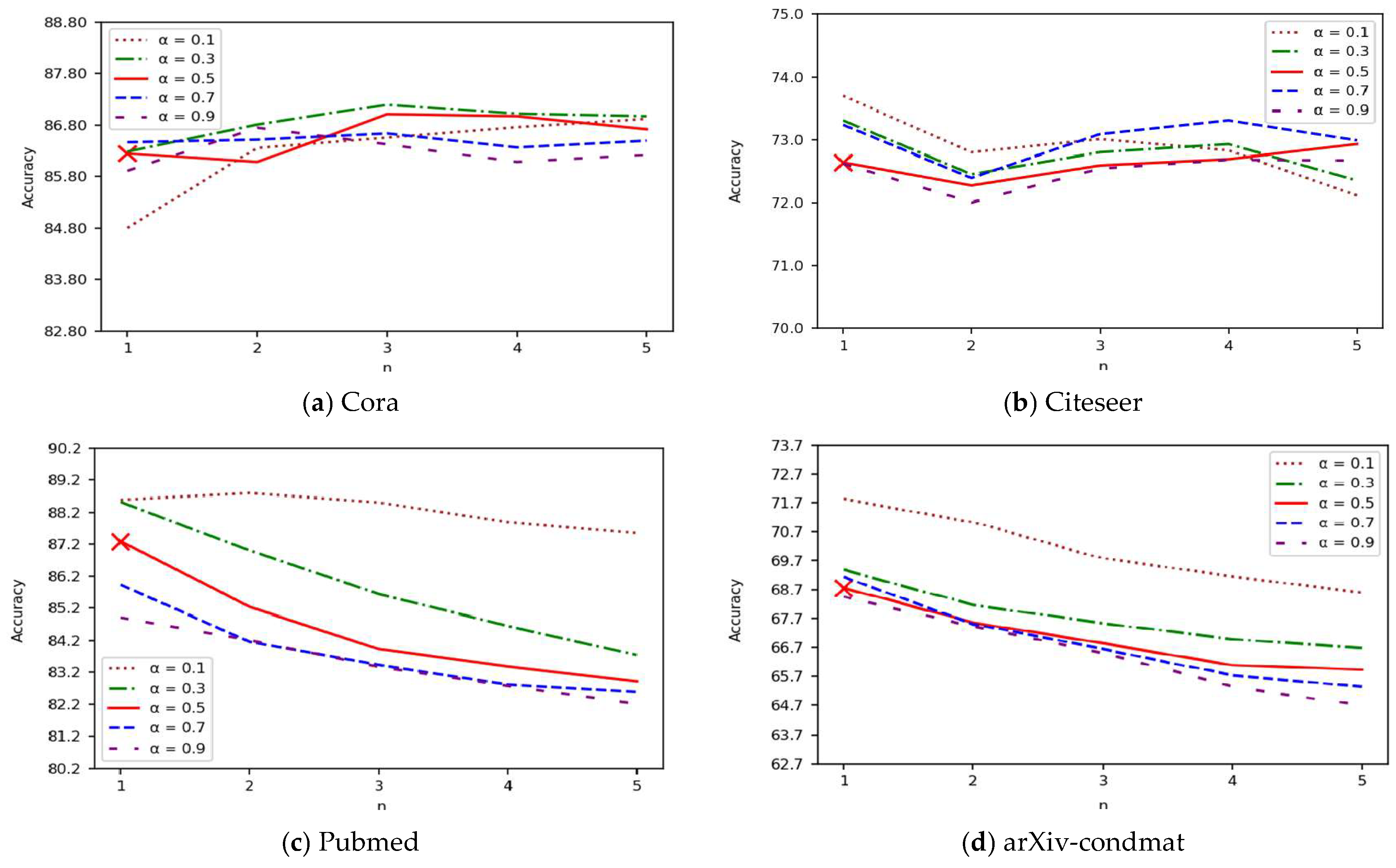
Figure 2 illustrates the parameter sensitivity analysis of the GCN-based node classification performance. On Cora and Citeseer, accuracy increases with diffusion depth, peaking around n = 3 before slightly declining due to over-smoothing. Moderate α values again yield the best accuracy, while high values (α = 0.9) occasionally degrade performance by excessively amplifying remote neighborhood information.

For Pubmed and arXiv-condmat, accuracy shows a decreasing pattern with larger diffusion steps, suggesting sensitivity to long-range propagation.

Overall, the proposed simplified diffusion filter exhibits stable behavior on small- and medium-scale datasets, with optimal performance typically occurring when n is within 2–3 and α lies between 0.3 and 0.7. For larger datasets such as Pubmed and arXiv-condmat, performance gradually decreases with deeper propagation, suggesting that excessive diffusion may introduce over-smoothing. Nonetheless, the model remains robust to parameter variations and requires minimal hyperparameter tuning.

5. Discussion and Conclusions

This study proposed a Simplified Graph Diffusion framework that integrates multi-hop neighborhood information into graph learning while reducing the computational overhead typically associated with graph diffusion methods. By introducing two key parameters—the distance parameter (n) and the diffusion control parameter (α)—the model enables efficient information propagation while mitigating oversmoothing. The approach strikes a balance between structural expressiveness and computational efficiency, addressing the shortcomings of conventional Graph Convolutional Networks (GCNs) and existing diffusion-based methods.

Extensive experiments on benchmark datasets validated the effectiveness of the proposed method across both link prediction and semi-supervised classification tasks. In link prediction, the simplified diffusion mechanism improved performance over baseline models, particularly when incorporating structural information from distant nodes (3–5 hops). Gains were more significant in settings without node attributes, suggesting that topological features play a critical role in predicting missing links.

In semi-supervised classification, the incorporation of simplified diffusion consistently enhanced accuracy, with optimal performance observed when n was small (≤3) and α was relatively low (≤0.3). These results highlight the importance of carefully balancing diffusion depth and control to capture useful long-range dependencies without excessive smoothing.

The sensitivity analysis further indicates that the simplified diffusion filter effectively balances local and long-range propagation, providing reliable performance across diverse graph structures. Notably, moderate parameter settings consistently achieve strong results, reinforcing the practical applicability of our approach when parameter tuning is limited or expensive.

This study demonstrates that a simplified diffusion mechanism can effectively balance model expressiveness and computational efficiency in graph learning. By relying on a final-stage diffusion matrix and adjustable parameters, the proposed framework reduces complexity while maintaining competitive accuracy. These results suggest that simplified graph diffusion offers a practical alternative to conventional diffusion methods, particularly for applications that require scalability and efficiency.

Despite the contributions, the study has several limitations. First, the performance gains were less substantial when node attributes were incorporated, suggesting that the model’s strengths lie primarily in leveraging structural rather than attribute-based information. Second, the experiments were conducted only on commonly used academic benchmarks, which may not fully reflect the diversity of real-world graphs, such as dynamic, heterogeneous, or extremely large-scale networks. Moreover, when the number of diffusion steps (n) becomes large, there is a potential risk of over-smoothing, which may blur discriminative node representations.

Future work may extend this framework in several directions. One potential direction is to explore the dynamic adjustment of diffusion parameters during training, enabling the model to adaptively balance the propagation of local and global information across different graph regions. Another direction is to integrate attention mechanisms or transformer-based modules with simplified diffusion to enhance the ability to weigh contributions from diverse neighborhoods. Additionally, extending the experiments to large-scale and heterogeneous graphs will help verify the scalability and generalization ability of the proposed approach, thereby broadening its practical applicability to complex real-world scenarios. Finally, investigating scenarios with rich node attributes will provide a deeper understanding of the interplay between structural and attribute-based information and further improve the adaptability of the proposed diffusion framework.