Capturing Dynamic User Preferences: A Recommendation System Model with Non-Linear Forgetting and Evolving Topics
Abstract
1. Introduction
- We proposed a novel multi-feature adaptive time weighting approach. It comprehensively considers the impact of user interest drift features on recommendation generation to enhance the accuracy of user preference prediction.
- We constructed a novel latent topic model for multi-interval individual topic reviews. The model can more accurately perceive hot topics in user reviews at different periods and capture the dynamic evolution of user preferences in time steps.
- We built a feature fusion model of multi-dimensional latent factors. It can learn user ratings’ synergistic temporal evolution features and multiple latent preference features of the topics to achieve high-accuracy user preference perception in data-sparse scenarios.
2. Related Work
2.1. Recommendation Based on Temporal Matrix Factorization
2.2. Recommendation Based on Deep Learning with Interest Drift
2.3. Recommendation Based on Review Mining
3. Preliminary
3.1. Problem Promotion
3.1.1. Adaptive Temporal Forgetting-Weight
3.1.2. User-Item Eigen Decomposition
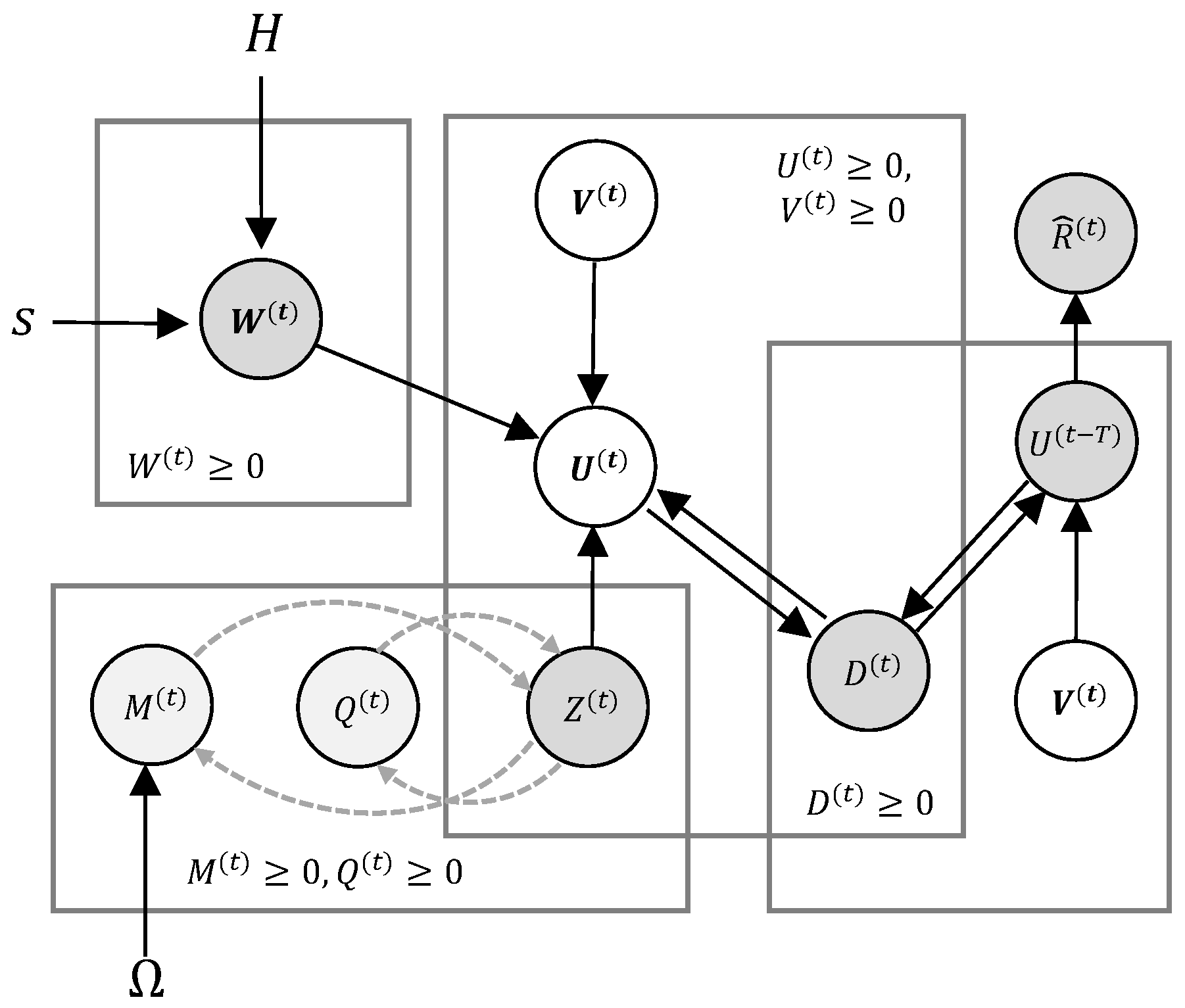
4. Methodology
4.1. Temporal Latent Rating Matrix Prediction Model
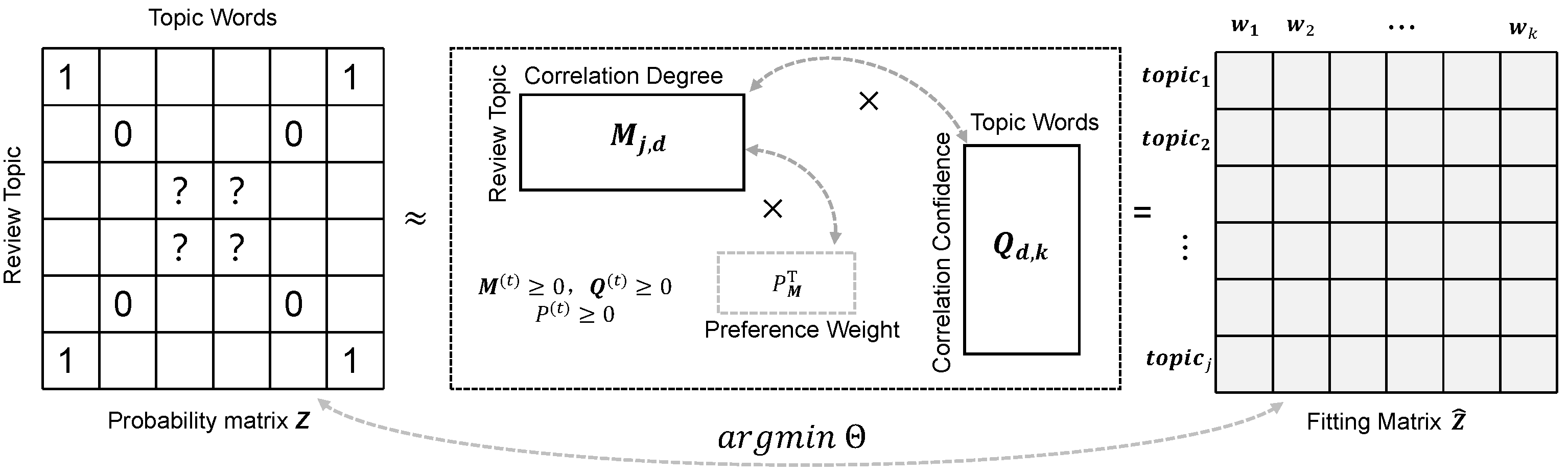
4.2. The Latent Topic Model
4.2.1. Topic Corpus Processing
4.2.2. Definition of the Basic Concept
4.2.3. The Objective Latent Topic Model
4.2.4. The Optimization of Topic Model
4.3. Joint Optimization Loss Function
| Algorithm 1: The proposed algorithm |
 |
4.4. Computational Complexity
5. Experiment and Analysis
5.1. Datasets
5.2. Evaluation Indicators
5.3. Experimental Parameter Setting
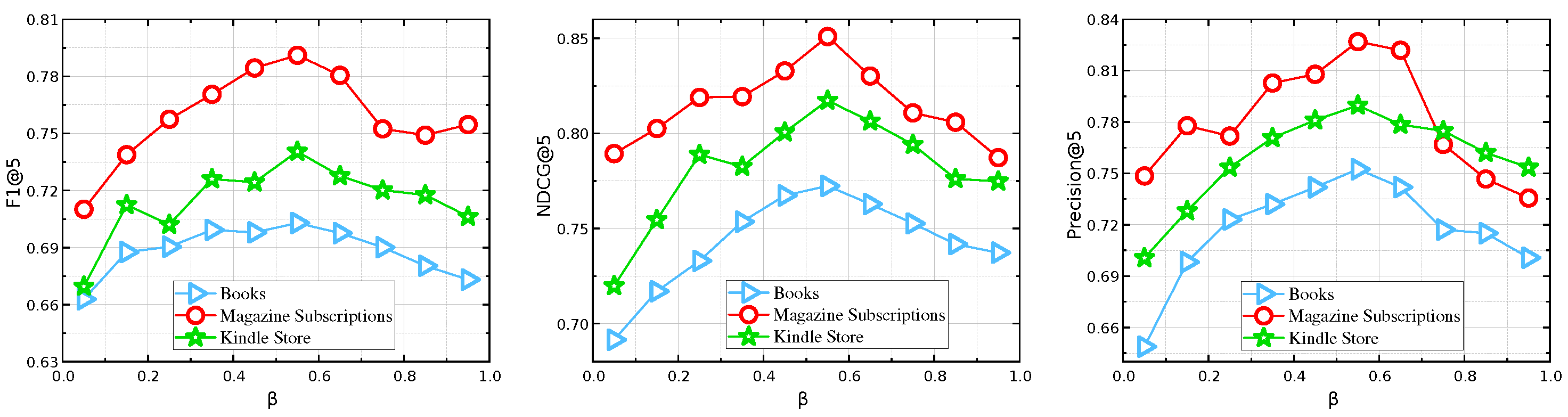
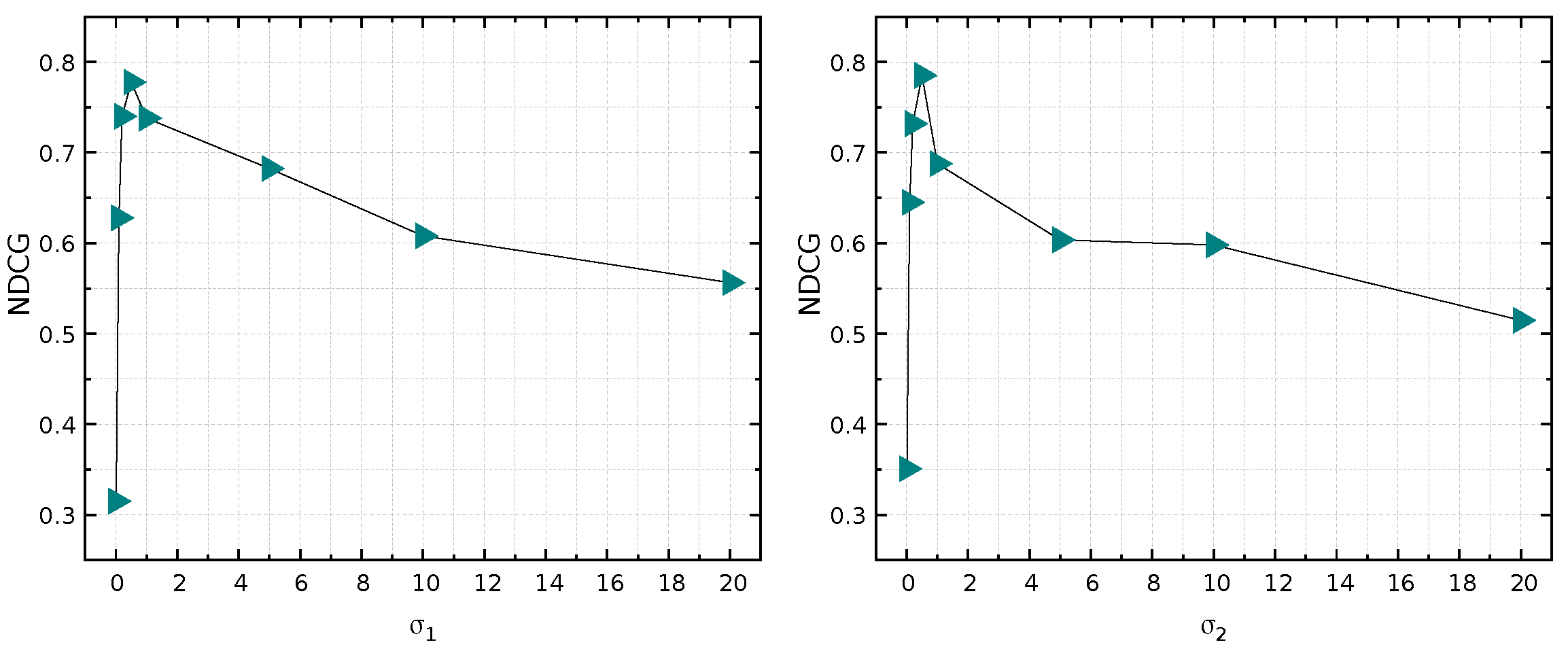
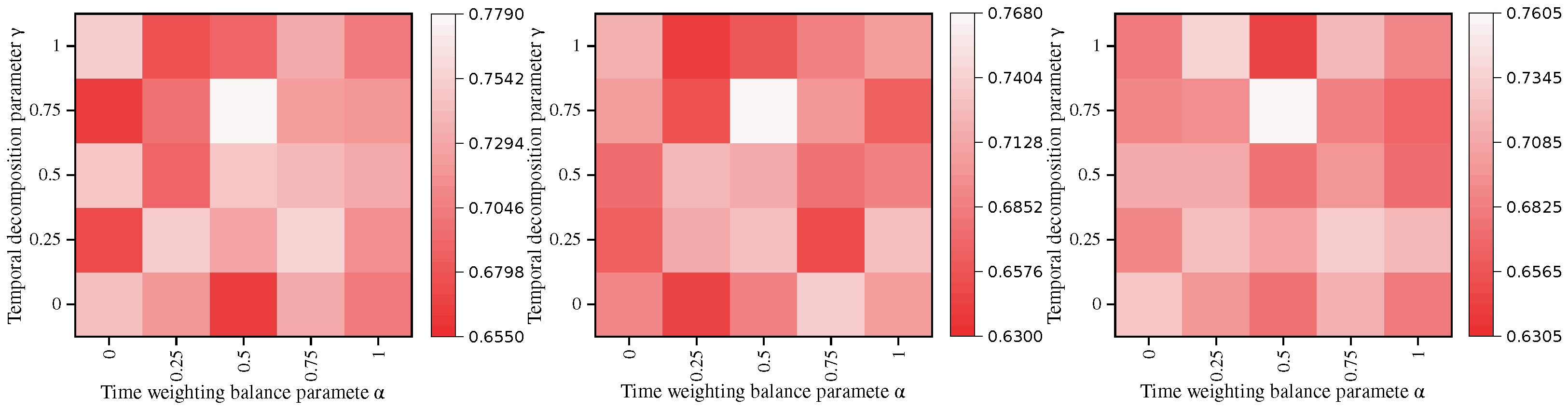
5.4. Parameter Analysis
5.5. Ablation Results
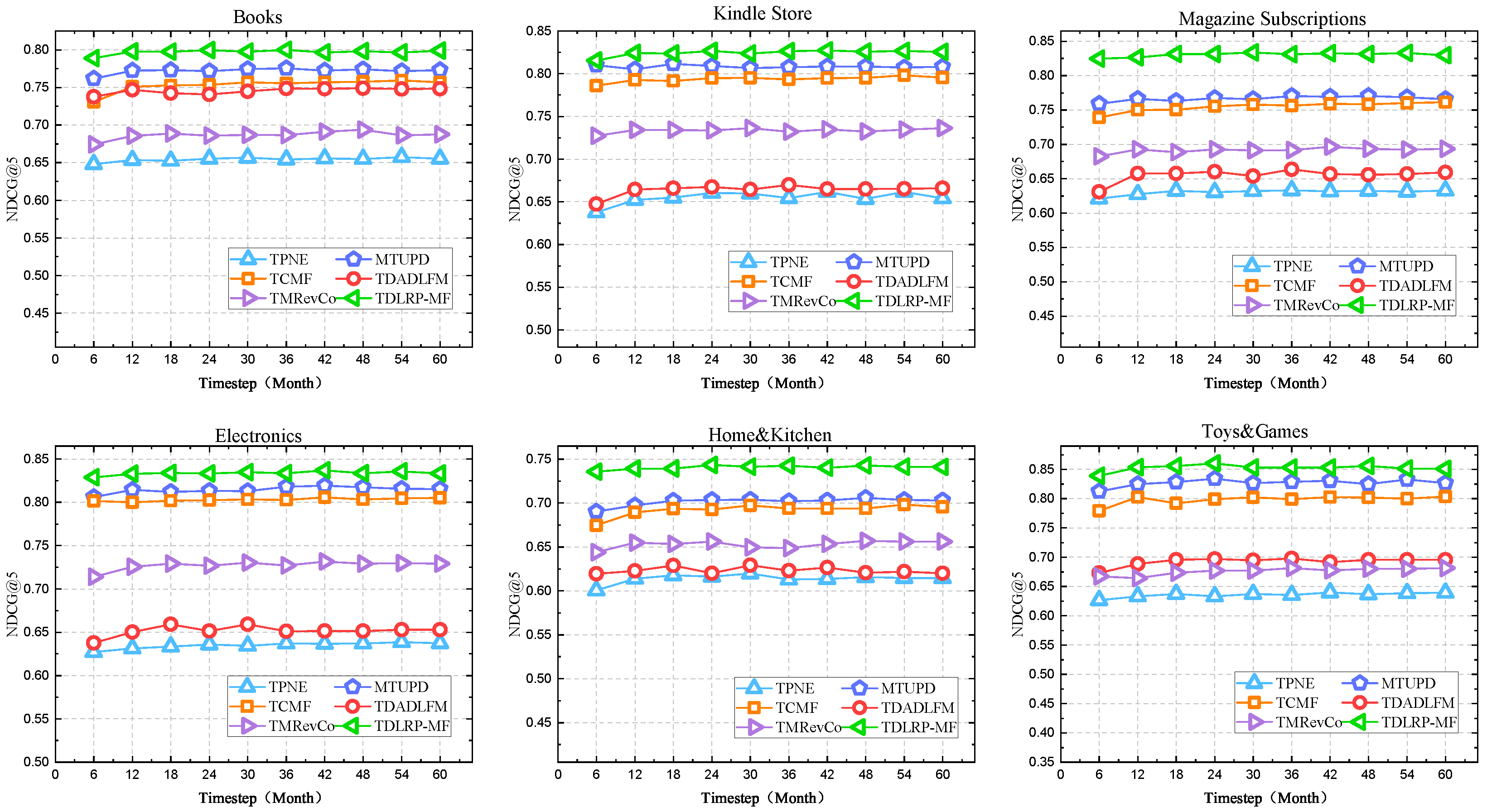
5.6. Performance Analysis and Case Study
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, X.; Liu, C. Design of Personalized News Recommendation System Based on an Improved User Collaborative Filtering Algorithm. Mob. Inf. Syst. 2023, 2023, 9898337. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, J.; Wu, Z.; Adomavicius, G. Efficient and flexible long-tail recommendation using cosine patterns. INFORMS J. Comput. 2025, 37, 446–464. [Google Scholar] [CrossRef]
- Jain, G.; Mahara, T.; Sharma, S.C. Effective time context based collaborative filtering recommender system inspired by Gower’s coefficient. Int. J. Syst. Assur. Eng. Manag. 2023, 14, 429–447. [Google Scholar] [CrossRef]
- Tanveer, J.; Lee, S.W.; Rahmani, A.M.; Aurangzeb, K.; Alam, M.; Zare, G.; Alamdari, P.M.; Hosseinzadeh, M. PGA-DRL: Progressive graph attention-based deep reinforcement learning for recommender systems. Inf. Fusion 2025, 121, 103167. [Google Scholar] [CrossRef]
- Parmezan, A.R.S.; Souza, V.M.; Batista, G.E. Evaluation of statistical and machine learning models for time series prediction: Identifying the state-of-the-art and the best conditions for the use of each model. Inf. Sci. 2019, 484, 302–337. [Google Scholar] [CrossRef]
- Pang, N. A Personalized Recommendation Algorithm for Semantic Classification of New Book Recommendation Services for University Libraries. Math. Probl. Eng. 2022, 2022, 8740207. [Google Scholar] [CrossRef]
- Wang, X.J.; Liu, T.; Fan, W. TGVx: Dynamic personalized POI deep recommendation model. INFORMS J. Comput. 2023, 35, 786–796. [Google Scholar] [CrossRef]
- Alabduljabbar, R.; Alshareef, M.; Alshareef, N. Time-Aware Recommender Systems: A Comprehensive Survey and Quantitative Assessment of Literature. IEEE Access 2023, 11, 45586–45604. [Google Scholar] [CrossRef]
- Koren, Y. Collaborative filtering with temporal dynamics. In Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Paris, France, 28 June–1 July 2009; pp. 447–456. [Google Scholar]
- Xiong, L.; Chen, X.; Huang, T.K.; Schneider, J.; Carbonell, J.G. Temporal collaborative filtering with bayesian probabilistic tensor factorization. In Proceedings of the 2010 SIAM International Conference on Data Mining, Columbus, OH, USA, 29 April–1 May 2010; pp. 211–222. [Google Scholar]
- Rafailidis, D.; Kefalas, P.; Manolopoulos, Y. Preference dynamics with multimodal user-item interactions in social media recommendation. Expert Syst. Appl. 2017, 74, 11–18. [Google Scholar] [CrossRef]
- Wu, T.; Feng, Y.; Sang, J.; Qiang, B.; Wang, Y. A novel recommendation algorithm incorporating temporal dynamics, reviews and item correlation. IEICE Trans. Inf. Syst. 2018, 101, 2027–2034. [Google Scholar] [CrossRef]
- Li, T.; Jin, L.; Wu, Z.; Chen, Y. Combined recommendation algorithm based on improved similarity and forgetting curve. Information 2019, 10, 130. [Google Scholar] [CrossRef]
- Pang, S.; Yu, S.; Li, G.; Qiao, S.; Wang, M. Time-Sensitive Collaborative Filtering Algorithm with Feature Stability. Comput. Inform. 2020, 39, 141–155. [Google Scholar] [CrossRef]
- Lv, Y.; Zhuang, L.; Luo, P.; Li, H.; Zha, Z. Time-sensitive collaborative interest aware model for session-based recommendation. In Proceedings of the 2020 IEEE International Conference on Multimedia and Expo (ICME), London, UK, 6–10 July 2020; pp. 1–6. [Google Scholar]
- José, E.F.; Enembreck, F.; Barddal, J.P. Adadrift: An adaptive learning technique for long-history stream-based recommender systems. In Proceedings of the 2020 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Toronto, ON, Canada, 11–14 October 2020; pp. 2593–2600. [Google Scholar]
- Rabiu, I.; Salim, N.; Da’u, A.; Nasser, M. Modeling sentimental bias and temporal dynamics for adaptive deep recommendation system. Expert Syst. Appl. 2022, 191, 116262. [Google Scholar] [CrossRef]
- Huang, C.; Wang, S.; Wang, X.; Yao, L. Modeling temporal positive and negative excitation for sequential recommendation. In Proceedings of the ACM Web Conference 2023, Austin, TX, USA, 30 April–4 May 2023; pp. 1252–1263. [Google Scholar]
- Wu, C.C.; Chen, Y.L.; Yeh, Y.H. A Deep Recommendation Model Considering the Impact of Time and Individual Diversity. IEEE Trans. Comput. Soc. Syst. 2023, 11, 2558–2569. [Google Scholar] [CrossRef]
- Sun, Y.T.; Guo, G.B.; Chen, X.; Zhang, P.H.; Wang, X.W. Exploiting review embedding and user attention for item recommendation. Knowl. Inf. Syst. 2020, 62, 3015–3038. [Google Scholar] [CrossRef]
- Wang, X.; Xiao, T.; Tan, J.; Ouyang, D.; Shao, J. MRMRP: Multi-source review-based model for rating prediction. In Proceedings of the Database Systems for Advanced Applications: 25th International Conference, DASFAA 2020, Jeju, Republic of Korea, 24–27 September 2020; Proceedings, Part II 25. Springer: Berlin/Heidelberg, Germany, 2020; pp. 20–35. [Google Scholar]
- Wu, S.; Zhang, Y.; Zhang, W.; Bian, K.; Cui, B. Enhanced review-based rating prediction by exploiting aside information and user influence. Knowl.-Based Syst. 2021, 222, 107015. [Google Scholar] [CrossRef]
- Hyun, D.; Park, C.; Cho, J.; Yu, H. Learning to utilize auxiliary reviews for recommendation. Inf. Sci. 2021, 545, 595–607. [Google Scholar] [CrossRef]
- Wang, P.P.; Li, L.; Wang, R.; Zheng, X.H.; He, J.X.; Xu, G.D. Learning persona-driven personalized sentimental representation for review-based recommendation. Expert Syst. Appl. 2022, 203, 117317. [Google Scholar] [CrossRef]
- Liu, Z.; Yuan, B.X.; Ma, Y. A multi-task dual attention deep recommendation model using ratings and review helpfulness. Appl. Intell. 2022, 52, 5595–5607. [Google Scholar] [CrossRef]
- Cai, Y.; Ke, W.M.; Cui, E.; Yu, F. A deep recommendation model of cross-grained sentiments of user reviews and ratings. Inf. Process. Manag. 2022, 59, 102842. [Google Scholar] [CrossRef]
- Liu, H.; Chen, Y.; Li, P.; Zhao, P.; Wu, X. Enhancing review-based user representation on learned social graph for recommendation. Knowl.-Based Syst. 2023, 266, 110438. [Google Scholar] [CrossRef]
- Wangwatcharakul, C.; Wongthanavasu, S. A novel temporal recommender system based on multiple transitions in user preference drift and topic review evolution. Expert Syst. Appl. 2021, 185, 115626. [Google Scholar] [CrossRef]
- Milovančević, N.S.; Gračanac, A. Time and ontology for resource recommendation system. Phys. A Stat. Mech. Its Appl. 2019, 525, 752–760. [Google Scholar] [CrossRef]
- Cheng, Y.; Qiu, G.; Bu, J.; Liu, K.; Han, Y.; Wang, C.; Chen, C. Model bloggers’ interests based on forgetting mechanism. In Proceedings of the 17th International Conference on World Wide Web, Beijing, China, 21–25 April 2008; pp. 1129–1130. [Google Scholar]
- Yu, Z.; Lian, J.; Mahmoody, A.; Liu, G.; Xie, X. Adaptive User Modeling with Long and Short-Term Preferences for Personalized Recommendation. IJCAI 2019, 7, 4213–4219. [Google Scholar]
- Lee, D.D.; Seung, H.S. Learning the parts of objects by non-negative matrix factorization. Nature 1999, 401, 788–791. [Google Scholar] [CrossRef]
- Zhao, Z.; Chen, J.; Zhou, S.; He, X.; Cao, X.; Zhang, F.; Wu, W. Popularity bias is not always evil: Disentangling benign and harmful bias for recommendation. IEEE Trans. Knowl. Data Eng. 2022, 35, 9920–9931. [Google Scholar] [CrossRef]
- Zhang, Y.; Feng, F.; He, X.; Wei, T.; Song, C.; Ling, G.; Zhang, Y. Causal intervention for leveraging popularity bias in recommendation. In Proceedings of the 44th International ACM SIGIR Conference on Research and Development in Information Retrieval, Virtual, 11–15 July 2021; pp. 11–20. [Google Scholar]
- Kuhn, H.W.; Tucker, A.W. Nonlinear programming. In Traces and Emergence of Nonlinear Programming; Springer: Basel, Switzerland, 2013; pp. 247–258. [Google Scholar]
- McAuley, J.; Leskovec, J. Hidden factors and hidden topics: Understanding rating dimensions with review text. In Proceedings of the 7th ACM Conference on Recommender Systems, Hong Kong, China, 12–16 October 2013; pp. 165–172. [Google Scholar]


| Notation | Description |
|---|---|
| T | Time periods. |
| Time decomposition dimension. | |
| The ratings matrix at time t. | |
| The ratings matrix at time . | |
| User latent factor matrix. | |
| Item latent factor matrix. | |
| Drift transition matrix. | |
| The enhanced time weighting. | |
| l | Number of review topics. |
| c | Number of review topic words. |
| Review topic words weight matrix. | |
| Review topic words probability matrix. | |
| Review topic words preference weight matrix. | |
| Standard deviation. | |
| The p-norm. | |
| The Frobenius norm. | |
| Time weighting balance parameter. | |
| Topic words feature weight adjustment coefficient. | |
| Temporal decomposition adjustment parameter. | |
| Regularization parameters. |
| Datasets | Users | Items | Ratings & Reviews | Sparsity | Time Range |
|---|---|---|---|---|---|
| Kindle Store | 346,457 | 29,357 | 1,767,612 | 99.9826% | April 1999–October 2018 |
| Books | 578,858 | 61,379 | 4,159,480 | 99.9883% | December 1997–October 2018 |
| Magazine Subscriptions | 438,645 | 37,250 | 2,638,219 | 99.9839% | March 1999–October 2019 |
| Electronics | 9,838,676 | 786,868 | 20,994,353 | 99.9997% | December 1997–October 2018 |
| Home&Kitchen | 9,767,606 | 1,301,225 | 21,928,568 | 99.9998% | November 1999–October 2018 |
| Toys&Games | 4,204,994 | 634,414 | 8,201,231 | 99.9997% | October 1999–October 2018 |
| Books | Kindle Store | Magazine Subscriptions | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Object | NDCG | F1 | NDCG | F1 | NDCG | F1 | ||||||
| @Top5 | @Top10 | @Top5 | @Top10 | @Top5 | @Top10 | @Top5 | @Top10 | @Top5 | @Top10 | @Top5 | @Top10 | |
| +NMF | 0.6878 | 0.6825 | 0.6392 | 0.6160 | 0.7353 | 0.7163 | 0.6936 | 0.6709 | 0.7168 | 0.7095 | 0.6508 | 0.6361 |
| +LSA | 0.6994 | 0.6873 | 0.6419 | 0.6313 | 0.7147 | 0.7237 | 0.6841 | 0.6450 | 0.7031 | 0.6931 | 0.6387 | 0.6345 |
| +pLSA | 0.7337 | 0.7190 | 0.6418 | 0.6255 | 0.7459 | 0.7179 | 0.6709 | 0.6598 | 0.7258 | 0.7163 | 0.6535 | 0.6435 |
| +LDA | 0.7158 | 0.7058 | 0.6461 | 0.6102 | 0.7327 | 0.7396 | 0.6794 | 0.6535 | 0.7237 | 0.7174 | 0.6567 | 0.6472 |
| 0.6979 | 0.6910 | 0.6609 | 0.6687 | 0.7549 † | 0.7543 | 0.6883 | 0.6856 | 0.7201 | 0.7273 | 0.6540 | 0.6544 | |
| 0.6931 | 0.6946 † | 0.6524 | 0.6571 | 0.7417 | 0.7427 | 0.6741 | 0.6750 | 0.7132 | 0.7179 | 0.6582 | 0.6598 | |
| 0.6678 | 0.6683 | 0.6123 | 0.6133 | 0.7380 | 0.7390 | 0.6841 | 0.6888 | 0.6989 | 0.7039 | 0.6371 | 0.6435 | |
| 0.6762 | 0.6762 | 0.6208 | 0.6212 | 0.7496 | 0.7464 | 0.6709 | 0.6793 | 0.7168 | 0.7126 | 0.6514 | 0.6592 | |
| 0.7026 | 0.7039 | 0.6340 | 0.6392 | 0.7649 ‡ | 0.7637 | 0.6829 | 0.6877 | 0.7307 | 0.7315 | 0.6614 | 0.6621 | |
| 0.6989 | 0.6968 | 0.6376 | 0.6355 | 0.7607 | 0.7664 | 0.6989 ‡ | 0.6909 | 0.7205 | 0.7248 | 0.6530 | 0.6613 | |
| 0.7807 | 0.7833 | 0.7047 | 0.7083 | 0.8515 | 0.8509 | 0.8029 | 0.8036 | 0.8193 | 0.8197 | 0.7913 | 0.7942 | |
| Comparison of Precision | ||||||||||||
| DataSets/Methods | TPNE | MTUPD | TCMF | TDADLFM | TMRevCo | TDLRP-MF | ||||||
| P@5 | P@10 | P@5 | P@10 | P@5 | P@10 | P@5 | P@10 | P@5 | P@10 | P@5 | P@10 | |
| Books | 0.5597 | 0.5397 | 0.7435 | 0.7218 | 0.7266 | 0.7098 | 0.6491 | 0.6167 | 0.7173 | 0.6946 | 0.7791 | 0.7652 |
| Kindle Store | 0.5471 | 0.5459 | 0.7371 | 0.7183 | 0.7627 | 0.7483 | 0.6373 | 0.6243 | 0.7134 | 0.6941 | 0.7986 | 0.7659 |
| Magazine Subscriptions | 0.5399 | 0.5334 | 0.7929 | 0.7834 | 0.7472 | 0.7574 | 0.6144 | 0.6038 | 0.7146 | 0.7374 | 0.8315 | 0.8191 |
| Electronics | 0.6126 | 0.5982 | 0.8172 | 0.7678 | 0.7824 | 0.7501 | 0.6385 | 0.6117 | 0.8081 | 0.7910 | 0.8437 | 0.8321 |
| Home&Kitchen | 0.5617 | 0.5636 | 0.7215 | 0.7156 | 0.7512 | 0.7390 | 0.6137 | 0.6105 | 0.7124 | 0.6917 | 0.7461 | 0.7435 |
| Toys&Games | 0.5631 | 0.5657 | 0.8261 | 0.8079 | 0.8021 | 0.7849 | 0.7631 | 0.7528 | 0.7224 | 0.6950 | 0.8594 | 0.8453 |
| Comparison of F1 | ||||||||||||
| DataSets/Methods | TPNE | MTUPD | TCMF | TDADLFM | TMRevCo | TDLRP-MF | ||||||
| F1@5 | F1@10 | F1@5 | F1@10 | F1@5 | F1@10 | F1@5 | F1@10 | F1@5 | F1@10 | F1@5 | F1@10 | |
| Books | 0.5811 | 0.5805 | 0.7058 | 0.6988 | 0.6960 | 0.6946 | 0.6581 | 0.6582 | 0.6698 | 0.6375 | 0.7232 | 0.7128 |
| Kindle Store | 0.5781 | 0.5766 | 0.7971 | 0.7754 | 0.7164 | 0.7052 | 0.7380 | 0.7553 | 0.6044 | 0.5972 | 0.8072 | 0.7984 |
| Magazine Subscriptions | 0.6744 | 0.6519 | 0.7175 | 0.7139 | 0.7113 | 0.7778 | 0.6537 | 0.6610 | 0.7024 | 0.6836 | 0.7361 | 0.7215 |
| Electronics | 0.6571 | 0.6581 | 0.7989 | 0.7992 | 0.7702 | 0.7667 | 0.7265 | 0.7341 | 0.7572 | 0.7336 | 0.8235 | 0.8196 |
| Home&Kitchen | 0.6309 | 0.6276 | 0.7057 | 0.6992 | 0.6987 | 0.6705 | 0.6726 | 0.6721 | 0.6421 | 0.6373 | 0.7238 | 0.7219 |
| Toys&Games | 0.6672 | 0.6513 | 0.7864 | 0.7727 | 0.7152 | 0.7079 | 0.7361 | 0.7174 | 0.5968 | 0.6008 | 0.8015 | 0.7952 |
| Comparison of NDCG (N) | ||||||||||||
| DataSets/Methods | TPNE | MTUPD | TCMF | TDADLFM | TMRevCo | TDLRP-MF | ||||||
| N@5 | N@10 | N@5 | N@10 | N@5 | N@10 | N@5 | N@10 | N@5 | N@10 | N@5 | N@10 | |
| Books | 0.6536 | 0.6524 | 0.7721 | 0.7504 | 0.7428 | 0.7310 | 0.7467 | 0.7457 | 0.6865 | 0.6624 | 0.7984 | 0.7769 |
| Kindle Store | 0.6659 | 0.6238 | 0.8020 | 0.7946 | 0.8067 | 0.8329 | 0.6598 | 0.6679 | 0.7309 | 0.7185 | 0.8269 | 0.8139 |
| Magazine Subscriptions | 0.6369 | 0.6291 | 0.7317 | 0.7233 | 0.7544 | 0.7318 | 0.6545 | 0.6472 | 0.6928 | 0.6620 | 0.8376 | 0.8273 |
| Electronics | 0.6478 | 0.6393 | 0.8102 | 0.7983 | 0.8032 | 0.8056 | 0.6577 | 0.6416 | 0.7215 | 0.7089 | 0.8347 | 0.8131 |
| Home&Kitchen | 0.6196 | 0.6157 | 0.7008 | 0.7104 | 0.6972 | 0.6916 | 0.6212 | 0.6190 | 0.6554 | 0.6490 | 0.7492 | 0.7413 |
| Toys&Games | 0.6338 | 0.6315 | 0.8322 | 0.8249 | 0.7993 | 0.7805 | 0.6957 | 0.6931 | 0.6679 | 0.6505 | 0.8613 | 0.8504 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, H.; Zhu, W.; Hu, G.; Bu, Z. Capturing Dynamic User Preferences: A Recommendation System Model with Non-Linear Forgetting and Evolving Topics. Systems 2025, 13, 1034. https://doi.org/10.3390/systems13111034
Ding H, Zhu W, Hu G, Bu Z. Capturing Dynamic User Preferences: A Recommendation System Model with Non-Linear Forgetting and Evolving Topics. Systems. 2025; 13(11):1034. https://doi.org/10.3390/systems13111034
Chicago/Turabian StyleDing, Hao, Weiwei Zhu, Guangwei Hu, and Zhan Bu. 2025. "Capturing Dynamic User Preferences: A Recommendation System Model with Non-Linear Forgetting and Evolving Topics" Systems 13, no. 11: 1034. https://doi.org/10.3390/systems13111034
APA StyleDing, H., Zhu, W., Hu, G., & Bu, Z. (2025). Capturing Dynamic User Preferences: A Recommendation System Model with Non-Linear Forgetting and Evolving Topics. Systems, 13(11), 1034. https://doi.org/10.3390/systems13111034






