Abstract
This research communication aims to present three mathematical methods for analyzing inventory management in dynamic supply chains, starting from the basic definition in differential equations for inventory levels, which relates with production and demand rates. Initially, the study adopts a systemic perspective to examine the role of energy within a production–inventory system. Subsequently, the analysis focuses on inventory dynamics under parameters expressed in complex variables, with the aim of quantifying fluctuations in a generic production system and demonstrating the influence of inventory variation rates on system behavior. Finally, the investigation addresses the impact of variable capacity on production system inventories, drawing on analogies with corresponding physical systems to support the analysis.
1. Introduction
Dynamic supply chains (DSCs) are a socioeconomic phenomenon that have generated special interest from the perspective of mathematical modeling in general systems theory. By definition, a dynamic supply chain is a dynamic system, described by inputs (raw materials) and outputs (finished products or services). In general, there are five flows around a DSC: raw materials, cash, information, energy, and labor force. From the perspective of decision-making, the stages typically presented are as follows: strategic, tactical, and operational. During and after the COVID-19 pandemic, decision-making at the geopolitical level has impacted supply chains due to issues of shortages in inventories.
Supply chain inventory management is a critical driver of operational efficiency, cost control, and competitive advantage in today’s global economy. The pursuit of optimal inventory policies has long been a central theme in operations research and management science [1,2,3,4,5,6,7]. Traditional approaches have largely relied on mathematical programming [8,9,10], and stochastic modeling [11]. Yet, the rise of Industry 4.0—marked by unprecedented data availability, increasing market volatility, and the need for real-time resilience—has highlighted the limitations of these classical methods in coping with modern supply chain dynamics [12,13,14,15,16].
Moreover, the impact of quantifying the level of inventories in the DSC presents three scenarios for supply and demand: overproduction, equilibrium, and shortages. Overproduction, in practical terms, occurs when the production–inventory system generates a higher rate of production than the level of demand. Balance in the system occurs when the production rate and demand are equal. Finally, scarcity is technically established when the production rate is lower than the demand rate.
In high-volume supply chains, inventory management critically shapes economic outcomes by reducing capital immobilization, storage costs, and obsolescence risks, while avoiding shortages that disrupt operations. Given the large production scale, small inefficiencies generate significant financial impacts. Applying advanced tools such as predictive analytics, dynamic safety stock, and real-time monitoring enables firms to optimize costs, improve service levels, and strengthen resilience, ensuring sustainable profitability in large-scale supply networks.
This research communication addresses the following assumptions:
- We assume a high-volume production context, where large and continuous flows resolve stochastic fluctuations. This makes deterministic models appropriate and highlights their economic importance in achieving scale efficiencies and service continuity.
- We present mathematical methods which quantify and analyze energy flows in high-volume supply chains, linking inventory dynamics, production, and variations in capacity.
- Complex-valued parameters in the inventory differential equation capture oscillations around equilibrium, allowing the model to represent cycles of overproduction and shortage.
- Modeling inventory levels, installed capacity, and production rates in high-volume supply chains are crucial to balance supply and demand, minimize costs, and ensure efficient continuous operations.
- Classical physics analogies make high-volume supply chain dynamics intuitive by linking inventories and flows to energy and oscillation concepts.
The remainder of this paper is organized as follows. Section 2 details the methodology employed for the literature review. Section 3 presents energy-based inventory management mathematical models. Section 4 provides a critical analysis of dynamic inventory management for parameters involving complex variables. In Section 5, mathematical modeling is performed for inventories subject to capacity analysis. In Section 6, a brief discussion of the results is provided. Finally, Section 7 concludes the paper by summarizing the key insights and outlining promising avenues for future research.
2. Literature Review
2.1. Mathematical Modeling for Inventory Modeling
This analysis is essential for tracing the trajectory from deterministic and stochastic operations research models to the contemporary era of algorithmic and AI-driven decision-support systems. The primary objectives of this review are to:
- Systematically classify the broad spectrum of modeling paradigms that have emerged and evolved.
- Map key technological trends and evaluate their impact on enhancing model capabilities and practical applicability.
- Critically examine persistent limitations, methodological trade-offs, and unresolved research questions within the current body of knowledge.
- Propose a forward-looking research agenda to address existing barriers and leverage future technological disruptions.
This represents a state-of-the-art evolution in mathematical modeling for inventory management and presents that a clear paradigm shift is underway, moving away from analytically tractable yet often restrictive mathematical models toward computationally intensive, data-driven frameworks [17,18,19,20]. This transformation is driven by advances in artificial intelligence (AI), metaheuristics, and simulation-based optimization, which collectively address the limitations of traditional models in terms of scalability, realism of assumptions, and adaptability under uncertainty [21,22,23,24,25]. Foundational contributions in areas such as Vendor-managed inventory (VMI) policy optimization [26] and multi-echelon systems [27] have been progressively expanded and, in some instances, replaced by techniques including deep reinforcement learning for risk-sensitive multi-echelon control, Bayesian optimization for unpredictable demand, and robust model predictive control for systems characterized by significant uncertain decay factors [28].
Despite the rapid proliferation of innovative methodologies, the academic literature still lacks a comprehensive and systematic synthesis that captures the full scope and trajectory of this evolution. Existing reviews tend to be narrowly focused, emphasizing specific methodologies such as simulation-optimization [29] or constrained to particular contexts, such as closed-loop [30] or cluster supply chains [31], or outdated, failing to reflect the transformative advancements of the past decade [32]. This has left a significant gap in understanding the convergence of traditional operations research with cutting-edge data science, the practical applicability of hybrid models, and the emerging research challenges that arise at this intersection. In addition, specialized frameworks have emerged to tackle niche challenges, such as integrating project management with material supply in project-driven environments [33].
2.2. Physics-Based Approaches for Dynamic Supply Chains
Nowadays, research on supply chains has addressed new theoretical approaches inspired by the physics of dynamic systems and advanced modeling methodologies. These approaches have emerged as robust alternatives for analyzing phenomena such as robustness, stability, resilience, and adaptability in high-uncertainty contexts [34,35,36,37,38]. Other authors have proposed hybrid approaches that combine simulation and optimization for the management of logistics networks. The studies in refs. [39,40,41,42,43] highlight that the use of models inspired by physical equations not only contributes to theoretical understanding but also allows for a more realistic representation of emergent phenomena and the impacts of external disruptions on system operations. In this regard, systems physics provides tools to quantify a system’s capacity to return to its equilibrium state after disturbances, which is essential in contexts of global uncertainty. Another widely discussed aspect is the structural stability of supply chains. In terms of stability analysis, ref. [44] has shown that being inspired by analogies with physical systems allows for predicting the behavior of supply chains under different configurations, assessing the robustness of implemented solutions, and designing preventive strategies against potential disruptions. Table 1 presents several research works in terms of resilience, robustness and energy (key performance indicators, KPI).

Table 1.
Physics-based approaches in supply chains with KPI.
In Section 3, an energy-based inventory management mathematical analysis is conducted from the use of the ordinary differential equation which describes the rate of change of inventory level with respect to production rate and demand rate, in a generic production inventory system.
3. Energy-Based Inventory Management
Estimating the energy of production–inventory systems offers a rigorous metric for capturing system dynamics, informing control policies, and enhancing both operational efficiency and sustainability within dynamic supply chains. Within production–inventory systems, the notion of energy can be conceptualized as a quantitative indicator of dynamic activity, capturing fluctuations in inventory levels, production rates, and material flows across the supply chain. This perspective provides a unifying framework to analyze system behavior and assess the efficiency of resource utilization, thereby offering valuable insights for both theoretical modeling and practical decision-making.
In general, the differential equation which describes the inventory dynamics, from [50], with respect to production rate S(t) and demand rate d(t) is presented as follows:
By squaring both terms of Equation (1), we have:
Arranging the terms of Equation (2):
which equals to:
Considering the equilibrium case where , Equation (4) becomes:
Equation (5) presents the form of:
By making GL the general Lagrangian:
In general, which represents the kinetic energy of the production–inventory system and , representing the potential energy of the production–inventory system.
In the case of overproduction where , Equation (3) holds. In the case of scarcity, , we have:
By adding Equations (3) and (8), for overproduction and scarcity we have:
In physical terms, Equation (9) represents the total energy of the production–inventory system.
In general, for the conservative system, the power and energy of the system are related by the following relation, which is a definition from classical physics:
In general, the power of the production–inventory system is:
In the next section, a proper mathematical model is presented considering complex variables in the parameters which leads to dissipation of energy in the inventory level of the system.
4. Mathematical Modeling of Inventories in Complex Variables
This section explores the mathematical modeling of production–inventory systems with complex variables in the parameters in order to consider the oscillations of the system.
Expressing Equation (1) in the form:
Equation (12) can be adapted with complex number , into the form:
In Equation (13), the part that integrates the dissipation in the inventory level corresponds to the variable that establishes the general inventory system oscillation, the corresponding mathematics is performed such that the value of the complex number i appears. Thereby, considering that does not produce oscillations in the system, only the dissipation term does.
By this means, after some algebra, a general expression for production–inventory systems under oscillations is:
Case 1. Under equilibrium (Refer to Appendix A)
Equation (14) becomes:
Solving Equation (15) by separable variables:
By integrating Equation (16), and after some algebra:
where C is an integration constant.
In order to add a damping approach to Equation (17), the following approach is addressed in Appendix A, where . When time evolution for inventory levels tends to zero, and when time , the inventory level is zero.
By taking the imaginary part of the inventory level in Equation (17), we have:
Therefore, the energy dissipation of the system is:
Case 2. Integrant factor (general form)
In the general form, Equation (12) can be solved by integrant factor approach as an ordinary differential equation, such as:
The integrant factor (IF) from Equation (20) is:
From which multiplying both sides of Equation (20) by IF:
By integrating with respect to time:
Assuming , where A is a constant, and solving for Equation (23):
where B is an integration constant. The imaginary part of Equation (24) is:
Therefore, the energy dissipation of the production–inventory system, for Equation (25), is:
5. Mathematical Modeling of Inventories for Dynamic Capacity
5.1. The Direct and Indirect Effects for Inventories
An indirect effect, in physics, occurs when a physical magnitude is calculated from other magnitudes that are measured directly, applying a known relationship. In production–inventory systems, it is possible to relate the variation in inventory, production, and capacity levels via the following inequalities (refer to Figure 1 and Table 2).
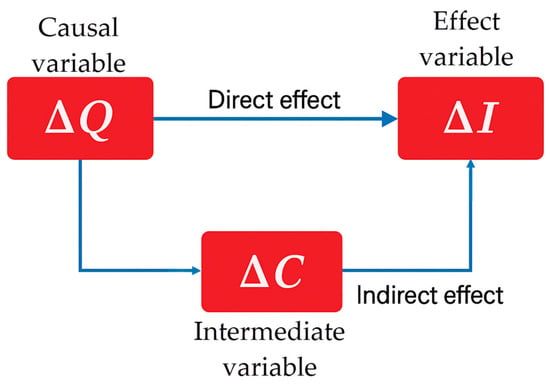
Figure 1.
Production–inventory systems’ direct and indirect effect.

Table 2.
Indirect and direct effects for inventories.
Inequality 1.
Inequality 2.
Inequality 3.
In general, EOQ corresponds to the economic order quantity and is used when products are bought for an external supplier. On the other hand, EPQ refers to economic production quantity and is used when the company manufactures its own products. (For an explanation on EOQ and EPQ, refer to Appendix B and Appendix C, respectively).
Inequality 4. (Direct effects)
Numerical approach,
To probe the inequalities in (27)–(29), lets follow the optimization problem via Lagrange multipliers of the form:
where
Applying the method of Lagrange multipliers for the optimization problem (31) with equalities constraints.
Constructing the Lagrangian:
By solving the system of equalities, for and , the optimal solution for the system is:
5.2. Dynamic Capacity ODE Approach
Mathematical modeling is essential for analyzing, designing, and optimizing production–inventory systems, especially in settings characterized by dynamic capacity and complex supply chain structures. In this context, dynamic capacity denotes the capability of production and storage resources to adapt output levels and inventory management over time in response to variations in demand, resource availability, or operational constraints.
A dynamic capacity ordinary differential equation is present as an analogy from variable mass systems in classical mechanics with the form:
Equation (33) represents the equation of motion for a variable mass system where
m = Mass of the system
Fext = External force for the system
Vrel = Relative velocity
= Rate of change of mass
= System acceleration
In order to present an approximation via proper analogies from Equation (33) with high-volume production systems, subject to dynamic capacity, we present:
Applying Little’s law, Equation (34) becomes , where, in a compact form:
Assuming the following ODE for capacity dynamics:
Considering the following approximation for Equation (36): , where represents the maximum capacity level in the system.
Then the following relation for capacity variation is: , which gives the following ordinary differential equation:
In the following, two cases for demand rate are considered to solve Equation (37):
Case 1.
By substituting demand rate into Equation (37), with and :
Completing the first integration with respect time:
By developing the second integration with respect time:
where and are constants.
Case 2. Cyclic demand rate with
By applying the trigonometric identity, , with and substituting:
By a similar procedure as in Case 1, the production level for cyclic demand rate is:
where and are constants.
6. Results
6.1. Numerical Example
By presenting a numerical example of the effectiveness of the proposal to minimize the energy of a production system as presented in Section 3, a two-link supply chain is presented below, for high-volume production, similar to [51].
For high-volume production, the dynamic optimization problem is given by:
Considering that the supply chain is high-volume, the optimization problem can be presented as a quadratic optimization problem as follows:
The quadratic optimization problem (44) is solved by Lagrange multipliers. The summarized results from four scenarios are presented in Table 3.

Table 3.
Results from the quadratic optimization problem for two echelon HVSC.
6.2. Discussion
This research addressed dynamic supply chains for high-volume systems which are socioeconomic systems that have attracted significant attention in mathematical modeling within general systems theory. They are dynamic in nature, characterized by inputs such as raw materials and outputs including finished products or services. This article presented classical physics concepts to offer solutions for various operational scenarios in high-volume supply chains, using overproduction, shortage, and equilibrium as reference points while recognizing that real-world fluctuations continually affect the balance between supply and demand.
In general, in supply chain theory, for high-volume systems the key performance indicators (KPIs) are stability, economies of scale, and throughput performance rather than flexibility. HVSC are designed to handle large quantities of goods flowing with throughput rates. This kind of supply chains is characterized by industries with predictable and steady demand, where products are standardized and efficiency is the mandatory approach. Otherwise, a low-volume supply chain is a supply network that encompasses the flow of goods produced in low quantities, where KPIs are flexibility, customization, and responsiveness. In comparison with HVSC, low-volume supply chains present responsiveness, adaptability, and reliability under uncertainty in demand.
Finally, we explicitly link these physical analogies with concrete KPIs commonly used in high-volume supply chains. Kinetic energy is explained as an analogy for throughput, capturing the combined effect of production rates. This connects directly with KPIs such as throughput rate and order fulfillment cycle time. High kinetic energy corresponds to rapid and consistent flows. Potential energy is described as the stored capacity in the system, directly tied to inventory levels, safety stock, and capacity utilization. In managerial terms, this reflects the “buffer” that allows the chain to absorb shocks. A high potential energy indicates excessive inventory (high carrying costs), whereas too low a level increases the risk of variability. Dissipation is reframed as inefficiencies and losses in the system, which map directly to KPIs such as scrap/rework rates, lead time variability, and logistics costs. Dissipation thus quantifies how much useful capacity and throughput are lost at operational level.
7. Conclusions
This research paper addresses the mathematical modeling of production–inventory systems, with particular emphasis on dynamic supply chains in high-volume. The analysis focuses on the formulation of a differential equation that characterizes inventory variations as a function of production and demand rates, thereby providing an analytical framework for the study of system energy. Moreover, the modeling approach incorporates parameters defined in the complex domain, which allows for the emergence of oscillatory behaviors within the system. In this context, the dissipated energy is derived from the imaginary component of the solution to the proposed differential equation, offering a novel perspective on inventory management dynamics. Considering that inventories are the actives in the company capital.
In addition, the study examines inventories through mathematical models that capture variations in installed capacity. Indeed, this article incorporates concepts from classical physics to provide diverse solutions to different situations in the operation of high-volume supply chains. It takes as a reference the situations of overproduction, shortage, and equilibrium, which in a real-life context will always present fluctuations in the attempt to balance supply with demand.
Finally, future research will focus on extending these models to empirical settings by calibrating them with real production–inventory data. Further work will also explore the control of the proposed differential equations through advanced methodologies in optimal and robust control theory.
Author Contributions
Conceptualization, Y.A.D., C.H.-S. and N.d.l.C.; methodology, C.H.-S., R.G.-A. and A.H.; valida-tion, Y.A.D., N.d.l.C., E.R. and C.H.-S.; formal analysis, F.F.T.-M., A.-M.R., A.H. and N.d.l.C.; in-vestigation, Y.A.D., C.H.-S. and R.G.-A.; resources, F.F.T.-M., C.H.-S., E.D.S. and A.-M.R.; data curation, A.F.R., A.H., F.F.T.-M. and C.H.-S.; writing—original draft preparation, Y.A.D., N.d.l.C., E.D.S. and C.H.-S.; writing—review and editing, Y.A.D., A.H. and A.F.R.; visualization, R.G.-A., A.F.R. and A.-M.R.; project administration, E.D.S., Y.A.D., C.H.-S., N.d.l.C., A.F.R., F.F.T.-M. and R.G.-A.; funding acquisition, E.D.S., A.-M.R., C.H.-S., R.G.-A., A.H., A.F.R. and F.F.T.-M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DSC | Dynamic Supply Chains |
| IM | Inventory Management |
| EOQ | Economic Order Quantity |
| EPQ | Economic Production Quantity |
| WIP | Work in Progress |
| CT | Cycle time |
| Th | Throughput |
Appendix A
This article applies classical physics concepts to address various operational scenarios in high-volume supply chains, focusing on overproduction, shortage, and equilibrium, while accounting for inevitable fluctuations as supply and demand seek balance.
For instance, the classical solution for Equation (1), in equilibrium is:
However, in general, the equilibrium condition is not a real case for high-volume supply chains, as in this case in Equation (17):
which, in general, has the complex form,
By taking the ,
For a more realistic approach, a damping coefficient is added to Equation (A2) which leads to the equation:
where , refers to throughput, which is the amount of material which is passing in the system.
Appendix B
The economic order quantity (EOQ) model serves as a straightforward yet highly effective approach to inventory optimization, enabling organizations to minimize waste, enhance cash flow, and ensure efficiency across production and supply chain processes. It is extensively applied in operations research, logistics, and production planning, where it functions as a foundational framework for the development of more advanced inventory models.
The canonical EOQ formula is:
where
D = annual demand (units per year),
S = cost per order (ordering/setup cost),
H = annual holding cost per unit.
Appendix C
The economic production quantity (EPQ) model is extensively applied in manufacturing systems, production planning, and inventory management as a means of determining optimal batch sizes that reduce costs while guaranteeing a continuous flow of supply. Its relevance is especially pronounced in industries characterized by high setup costs, including the automotive, electronics, and process manufacturing sectors.
The EPQ formula is:
where
D = annual demand (units per year),
S = cost per order (ordering/setup cost),
H = annual holding cost per unit,
P = production rate (units per year),
d = demand rate (units per year).
References
- Seliaman, M.E.; Cárdenas-Barrón, L.E.; Rushd, S. An Algebraic Decision Support Model for Inventory Coordination in the Generalized n-Stage Non-Serial Supply Chain with Fixed and Linear Backorders Costs. Symmetry 2020, 12, 1998. [Google Scholar] [CrossRef]
- Kovalchuk, M.; Bondarenko, S. Modeling of logistics processes using mathematical and computer approaches. Visn. Hmel’nyts’koho Nats. Univ. 2024, 339, 27–35. [Google Scholar] [CrossRef]
- Tan, Y.; Gu, L.; Xu, S.; Chen, Y. Supply chain inventory management from the perspective of “cloud supply chain”—A data driven approach. Mathematics 2024, 12, 573. [Google Scholar] [CrossRef]
- Khlie, K. Optimizing inventory control in supply chain management. In Proceedings of the 2024 IEEE Conference on Signal Processing and Its Applications (CSPA), Kuala Lumpur, Malaysia, 1–2 May 2024; pp. 210–214. [Google Scholar] [CrossRef]
- Aviv, Y. A time-series framework for supply-chain inventory management. Oper. Res. 2003, 51, 210–227. [Google Scholar] [CrossRef]
- Althaqafi, T. A study on inventory control system for a supply chain using Markov decision processes. Edelweiss Appl. Sci. Technol. 2024, 8, 1125–1142. [Google Scholar] [CrossRef]
- Gutiérrez, V.; Vidal, C.J. Inventory Management Models in Supply Chains: A Literature Review. Rev. Fac. Ing. Univ. Antioquia 2008, 44, 112–128. [Google Scholar] [CrossRef]
- Downs, B.; Metters, R.; Semple, J.H. Managing Inventory with Multiple Products, Lags in Delivery, Resource Constraints, and Lost Sales: A Mathematical Programming Approach. Manag. Sci. 2001, 47, 464–479. [Google Scholar] [CrossRef]
- Perez, H.D.; Hubbs, C.D.; Li, C.; Grossmann, I.E. Algorithmic Approaches to Inventory Management Optimization. Processes 2021, 9, 102. [Google Scholar] [CrossRef]
- Sanchis, R. Mathematical Programming Models for Sustainable Inventory Management in a Supply Chain. In Logistics 4.0 Digital Supply Chain Management; Springer: Cham, Switzerland, 2022; pp. 345–362. [Google Scholar] [CrossRef]
- Paeizi, A.; Makui, A.; Pishvaee, M.S. A Multi-Stage Stochastic Programming Approach for an Inventory–Routing Problem Considering Life Cycle. RAIRO-Oper. Res. 2023, 57, 2183–2205. [Google Scholar] [CrossRef]
- Bouazizi, E.; Khedr, A.E.; Elfaioumy, S.; Taha, Z. Inventory Optimization Using Data Science Technologies for Supply Chain 4.0. Int. Arab J. Inf. Technol. 2023, 21, 1093–1103. [Google Scholar] [CrossRef]
- Singh, B. Revolutionizing Supply Chains for Optimized Demand Planning, Inventory Management, and Logistics. In Advanced Business Strategy and Competitive Advantage; IGI Global: Hershey, PA, USA, 2025; pp. 298–322. [Google Scholar] [CrossRef]
- Winner, I.; Akwesie, B.; Sharma, V. A Data-Driven Research on Optimizing Supply Chain Logistics for Manufacturing Companies: A Predictive Modeling Approach; BSP Books: Hyderabad, India, 2023; pp. 1–12. [Google Scholar] [CrossRef]
- Palanki, V.C. Data-Driven Inventory Optimization: Leveraging Advanced Analytics for Supply Chain Efficiency. J. Mark. Supply Chain Manag. 2023, 2023, e111. [Google Scholar] [CrossRef]
- Rogulin, R. Systematic Review of the Supply Chain Management Problem: Future and Past Modeling Approaches. Nauchnye Tr. Vol’nogo Ekon. Obshch. Rossii 2022, 240, 228–256. [Google Scholar] [CrossRef]
- Duan, Q. A Metaheuristic-Based Simulation Optimization Framework for Supply Chain Inventory Management Under Uncertainty. Ph.D. Thesis, Louisiana State University, Baton Rouge, LA, USA, 2022. [Google Scholar]
- Maitra, S. A System-Dynamic Based Simulation and Bayesian Optimization for Inventory Management. arXiv 2024, arXiv:2402.10975. [Google Scholar] [CrossRef]
- Olaniyi, O.A.; Pugal, P.S. Optimising Inventory Management Strategies for Cost Reduction in Supply Chains: A Systematic Review. J. Akad. Baiturridha 2024, 10, 45–62. [Google Scholar] [CrossRef]
- Wu, G.; de Carvalho Servia, M.Á.; Mowbray, M. Distributional Reinforcement Learning for Inventory Management in Multi-Echelon Supply Chains. Digit. Chem. Eng. 2022, 5, 100073. [Google Scholar] [CrossRef]
- Chen, C.B.; Chang, K.S.; Lien, C.C. Converging Linear Particle Swarm Optimization and Intelligent Genetic Algorithm for a Simple Multi-Echelon Distribution and Multi-Product Inventory Control in a Supply Chain Model. J. Inf. Optim. Sci. 2009, 30, 1189–1205. [Google Scholar] [CrossRef]
- Sun, T.; Huang, Z.; Wu, D.; Li, Z.; Chen, Y. A Simulation-Optimization Approach for Inventory Management in a Multi-Echelon Supply Chain Network. In Proceedings of the 2024 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Bangkok, Thailand, 15–18 December 2024; pp. 1545–1549. [Google Scholar] [CrossRef]
- Mishra, P. Genetic Algorithm Approach for Inventory and Supply Chain Management: A Review. In Encyclopedia of Information Science and Technology, 4th ed.; IGI Global: Hershey, PA, USA, 2017; pp. 270–281. [Google Scholar] [CrossRef]
- Grygor, O.O.; Fedorov, E.; Nechyporenko, O.; Kolesnikova, O. Neural Network Forecasting Method for Inventory Management in the Supply Chain. Commun. Manag. Inf. Syst. 2021, 2021, 15–25. [Google Scholar] [CrossRef]
- Taboada, H.A.; Davizón, Y.A.; Espiritu, J.F.; Sanchez-Leal, J. Mathematical Modeling and Optimal Control for a Class of Dynamic Supply Chain: A Systems Theory Approach. Appl. Sci. 2022, 12, 5347. [Google Scholar] [CrossRef]
- Najafnejhad, E.; Tavassoli Roodsari, M.; Sepahrom, S.; Hosseini, S.M.H. A Mathematical Inventory Model for a Single-Vendor Multi-Retailer Supply Chain Based on the Vendor Management Inventory Policy. Int. J. Syst. Assur. Eng. Manag. 2021, 13 (Suppl. S1), 416–431. [Google Scholar] [CrossRef]
- Ghafour, K.M. An Enhanced Approximation Mathematical Model Inventorying Items in a Multi-Echelon System Under a Continuous Review Policy with Probabilistic Demand and Lead-Time. Ph.D. Thesis, University of Sulaimani, Sulaymaniyah, Iraq, 2015. [Google Scholar]
- Gumus, A.T.; Guneri, A.F. A Multi-Echelon Inventory Management Framework for Stochastic and Fuzzy Supply Chains. Expert Syst. Appl. 2009, 36, 5565–5575. [Google Scholar] [CrossRef]
- Ye, W.; You, F. A Simulation-Based Optimization Method for Solving the Integrated Supply Chain Network Design and Inventory Control Problem under Uncertainty. Chem. Eng. Trans. 2015, 45, 499–504. [Google Scholar] [CrossRef]
- Fleischmann, M.; Minner, S.; Dekker, R. Inventory Management in Closed Loop Supply Chains. In Reverse Logistics; Springer: Berlin/Heidelberg, Germany, 2003; pp. 115–138. [Google Scholar] [CrossRef]
- Yan, B.; Wu, J.-W.; Liu, L.; Gao, Y. Inventory management models in cluster supply chains based on system dynamics. RAIRO-Oper. Res. 2017, 51, 755–769. [Google Scholar] [CrossRef]
- Jian-qi, A. Review on Optimization Model in Supply Chain Inventory Management. Logist. Eng. Manag. 2009, 31, 88–90. [Google Scholar]
- Chen, C.-Y.; Zhao, Y. Project-Driven Supply Chains: Integrating Inventory Planning with Project Management. Nav. Res. Logist. 2009, 56, 350–366. [Google Scholar]
- Cerabona, T.; Benaben, F.; Montreuil, B.; Lauras, M.; Faugère, L.; Campos, M.R.; Jeany, J. The Physics of Decision Approach: A Physics-Based Vision to Manage Supply Chain Resilience. Int. J. Prod. Res. 2023, 61, 3201–3217. [Google Scholar] [CrossRef]
- Cerabona, T.; Lauras, M.; Faugère, L. A Physics-Based Approach for Managing Supply Chains. In Lecture Notes in Computer Science (LNCS, vol. 12438); Springer: Cham, Switzerland, 2020; pp. 450–465. [Google Scholar] [CrossRef]
- Cerabona, T.J.; Benaben, F.; Montreuil, B. Decision-Making Dynamics in Disrupted Supply Chains: A Physics-Inspired Perspective. Prod. Plan. Control. 2023, 34, 1234–1248. [Google Scholar] [CrossRef]
- Christopher, M.; Peck, H. Building the Resilient Supply Chain. Int. J. Logist. Manag. 2004, 14, 1–14. [Google Scholar] [CrossRef]
- Cerabona, T.; Lauras, M. Stability Analysis of Supply Chains under Uncertainty: A Physics-Oriented Framework. Syst. Res. Behav. Sci. 2022, 39, 415–428. [Google Scholar] [CrossRef]
- Gupta, A.; Singh, S. Resilience Metrics for Global Supply Chains: A Physics-Based System Dynamics Approach. J. Manuf. Syst. 2022, 64, 98–110. [Google Scholar] [CrossRef]
- Ivanov, P. Disruption Propagation in Supply Networks: Analogies with Complex Physical Systems. Ann. Oper. Res. 2022, 315, 567–584. [Google Scholar] [CrossRef]
- Dolgui, A.; Ivanov, D. Ripple effect and supply chain disruption management: New trends and research directions. Int. J. Prod. Res. 2021, 59, 102–109. [Google Scholar] [CrossRef]
- Lauras, M.; Faugère, L. Hybrid Simulation Models for Resilient Supply Chains: Physics-Informed Approaches. Simul. Model. Pract. Theory 2021, 117, 102470. [Google Scholar] [CrossRef]
- Chaudhary, I.; Kumar, A.; Borkakaty, B.; Ranjan N, R.; Ranakoti, O. Simulation-Driven Optimization for Supply Chain Agility. In Proceedings of the 2023 International Conference on Electrical, Computer and Energy Technologies (ICECET), Cape Town, South Africa, 16–17 November 2023. [Google Scholar] [CrossRef]
- Rahiel, N.; Addouche, S.; El Mhamedi, A.; Hachemi, K. Mathematical Modeling of Supply Chain Resilience: Structure, Dynamics, and Indicator-Based Evaluation. Available online: https://www.insticc.org/node/TechnicalProgram/IN4PL/2025/presentationDetails/137226 (accessed on 28 August 2025).
- Jillson, K.R.; Dozal-Mejorada, E.J.; Ydstie, P.B.E. The Supply Chain as a Dynamical System. In Process Systems Engineering: Volume 4: Supply Chain Optimization; Wiley-VCH: Weinheim, Germany, 2010. [Google Scholar] [CrossRef]
- Patel, K.; Desai, V. Resilient Supply Chain Design Using Dynamic System Modeling. Comput. Ind. Eng. 2019, 137, 106052. [Google Scholar] [CrossRef]
- Lauras, M. Resilience Engineering in Supply Chains: Physics of Stability. Int. J. Syst. Eng. 2019, 7, 455–468. [Google Scholar]
- Nguyen, A.; Lee, Y. Measuring Robustness of Networks: Applications in Supply Chain Physics. Physica A Stat. Mech. Appl. 2019, 521, 589–602. [Google Scholar]
- Babaei, A.; Tirkolaee, E.B.; Sorooshian, S.; Ali, S.S.; Wang, G. Efficiency enhancement of energy supply chains using a machine learning-driven network evaluation framework for blockchain adoption. Energy Strategy Rev. 2025, 61, 101816. [Google Scholar] [CrossRef]
- Ortega, M.; Lin, L. Control Theory Applications to the Production–Inventory Problem: A Review. Int. J. Prod. Res. 2004, 42, 2303–2322. [Google Scholar] [CrossRef]
- Chauhan, V.K.; Mak, S.; Parlikad, A.K.; Alomari, M.; Casassa, L.; Brintrup, A. Real-time large-scale supplier order assignments across two-tiers of a supply chain with penalty and dual-sourcing. Comput. Ind. Eng. 2023, 176, 108928. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).