A Multi-Objective Simulation–Optimization Framework for Emergency Department Efficiency Using RSM and Goal Programming

Abstract

This study presents a novel approach that integrates Discrete Event Simulation (DES) with Design of Experiments (DOE) techniques, framed within a stochastic optimization context and guided by a multi-objective goal programming methodology. The focus is on enhancing the operational efficiency of an emergency department (ED), illustrated through a real-world case study conducted in a Chilean hospital. The methodology employs Response Surface Methodology (RSM) to explore and optimize the impact of four critical resources: physicians, nurses, rooms, and radiologists. The response variable, formulated as a goal programming function, captures the aggregated patient flow time across four representative care tracks. The optimization process proceeded iteratively: early stages relied on linear approximations to identify promising improvement directions, while later phases applied a central composite design to model nonlinear interactions through a quadratic response surface. This progression revealed complex interdependencies among resources, ultimately leading to a local optimum. The proposed approach achieved a 50% reduction in the aggregated objective function and improved individual patient flow times by 7% to 26%. Compared to traditional metaheuristic methods, this simulation–optimization framework offers a computationally efficient alternative, particularly valuable when the simulation model is complex and resource-intensive. These findings underscore the value of combining simulation, RSM, and multi-objective optimization to support data-driven decision-making in complex healthcare settings. The methodology not only improves ED performance but also offers a flexible and scalable framework adaptable to other clinical environments seeking resource optimization and operational improvement.

1. Introduction

Simulation has become essential for understanding and managing complex systems, providing an effective approach to addressing challenges posed by unknown dynamics and highly uncertain scenarios [1]. In this context, hospitals and emergency care centers are especially important to examine because of the inherent complexities of these facilities [2]. Of particular interest are the emergency departments (EDs), which are essential components of hospital care, providing immediate attention to patients with acute or life-threatening conditions. However, their operation is often challenged by unpredictable demand, limited resources, and the inherent urgency of emergency care. Issues such as overcrowding, extended waiting times, and inefficient resource use have become increasingly common, affecting not only service quality but also patient safety.

Viewed through a systems lens, EDs function as complex adaptive systems, involving continuous interactions among diverse elements, including patients, medical staff, infrastructure, and clinical processes, whose interdependencies and nonlinear behaviors make prediction and control particularly difficult. In such settings, traditional management tools may fall short in capturing the full scope of operational complexity.

Discrete event simulation (DES) has emerged as a powerful method for analyzing healthcare operations. It enables decision-makers to model patient flows, experiment with resource configurations, and test performance under various scenarios without interfering with real-world activities. Nonetheless, while simulation provides valuable insights into system behavior, it typically lacks the ability to generate optimal solutions independently.

To bridge this gap, numerous studies have adopted hybrid simulation–optimization frameworks. These approaches enhance the decision-making potential of simulation by incorporating optimization techniques that can explore trade-offs and guide improvements. Among these, Response Surface Methodology (RSM) and goal programming offer promising capabilities, particularly in handling multiple, often conflicting, objectives. Despite their successful application in fields such as manufacturing and logistics, their use in emergency care remains relatively underexplored.

This study contributes to addressing that gap by developing and applying a simulation–optimization framework that integrates DES, RSM, and multi-objective goal programming. The aim is to support capacity planning and performance improvement in high-demand ED environments. The proposed methodology is implemented in a real-world setting, a private hospital in Santiago, Chile, which is currently facing rising demand and operational constraints.

By modeling the entire ED system and focusing on the interplay among key resources, physicians, nurses, treatment rooms, and radiology services, this work illustrates the potential of data-driven methods grounded in systems thinking. The findings demonstrate how integrating simulation and optimization techniques can support better resource allocation, reduce patient flow times, and enhance the system’s resilience in the face of growing healthcare needs.

2. Literature Review

2.1. Systems Simulation

For decades, simulation has played a crucial role in representing or imitating the behavior of real systems or processes, often using mathematical or computational models [3], where the advent of increasingly powerful computers has facilitated the expansion of simulation to various fields [4]. In particular, the application of Discrete Event Simulation (DES) has gained increasing relevance in emulating systems due to its ability to represent the stochastic nature, resource limitations, and process complexity inherent in diverse services and their operation [5]. By enabling virtual experimentation, DES provides decision-makers with a powerful tool to evaluate operational bottlenecks, test improvement strategies, and assess resource allocation without disrupting real operations. Its flexibility has led to its use across a broad spectrum of healthcare areas. In chronic disease modeling, Willis et al. [6] developed and validated a DES model to simulate the progression of diabetic kidney disease using clinical trial data from CREDENCE study (Canagliflozin and Renal Events in Diabetes with Established Nephropathy Clinical Evaluation). This model allowed the evaluation of long-term treatment strategies and healthcare resource usage, demonstrating how simulation can support decision-making in complex, long-term conditions. Similarly, in acute care access, Soorapanth & Young [7] applied DES to assess the impact of expanding access to thrombolytic therapy for stroke patients, quantifying the clinical and economic benefits of improvements in triage and coverage. Similarly, Ramis et al. [8] presented a simulator for a hospital’s medical imaging center. Their simulations resulted in reduced waiting times and increased utilization of imaging equipment. Pharmacy service delivery has also benefited from the use of simulation, where Furushima et al. [9] modeled the operations of a high-demand outpatient dispensing pharmacy in Japan, analyzing the effect of implementing one-dose packaging. Their results indicated that this operational change significantly reduced patient waiting times and improved resource utilization. In the context of specialized outpatient care, Lacinova et al. [10] presented the ENTIMOS model to enhance infusion suite efficiency for patients undergoing treatment for multiple sclerosis. The simulation examined the impact of changes in scheduling and staffing levels on patient flow and treatment delays, providing valuable insights into capacity management in chronic disease care settings. DES has also proven helpful in supporting blood center logistics. In this context, Baesler et al. [11] modeled the operational processes of a regional blood center, with a focus on internal operations. Their study demonstrated that with improved scheduling and resource coordination, the center could meet a doubling in demand without infrastructure expansion, highlighting DES as a powerful tool for strategic planning in support services.

2.2. Emergency Department Simulation

Building on its success across healthcare settings, DES has become particularly prominent in emergency department (ED) research, where managing variable patient arrivals, limited resources, and urgent care demands pose significant challenges. Numerous studies have demonstrated the capacity of DES to model the intricate dynamics of ED operations. Angler et al. [12], for instance, highlight the strong potential of DES for evaluating ED performance, while also emphasizing the growing importance and challenges of integrating artificial intelligence into process improvements. Abo-Hamad & Arisha [13] further extended this approach by integrating DES with a balanced scorecard and multi-criteria decision analysis to create a comprehensive decision support framework for ED management. Additionally, Wang et al. [14] investigated the influence of physician behavior on ED performance, revealing how provider decisions significantly affect patient outcomes and system efficiency. Additional recent contributions can be found in Castanheira-Pinto et al. [15] and Delos Reyes et al. [16], who offer updated perspectives on emergency department modeling. Additionally, a comprehensive review of simulation methods applied to emergency departments is available in Doudareva & Carter [17], who provide a thorough overview of validation techniques and methodological developments in the field.

2.3. Simulation Optimization in HealthCare

The integration of Discrete Event Simulation (DES) with optimization techniques has significantly broadened its applicability in healthcare decision-making, particularly in environments characterized by high uncertainty and resource constraints. Hybrid simulation–optimization models have emerged as powerful tools for addressing complex planning and operational challenges across a wide range of healthcare settings. For instance, Dehghanimohammadabadi et al. [18] combined DES with simulated annealing to solve intricate scheduling problems in a breast cancer treatment center, demonstrating how this approach can enhance oncology care planning. More recently, Yan et al. [19] employed DES in conjunction with a genetic algorithm to optimize rehabilitation service capacity for stroke patients in Alberta, Canada. Their model effectively identified optimal capacity expansions, achieved significant reductions in patient waiting times across multiple segments, and led to an estimated annual cost saving of $25.5 million, underscoring the economic and operational potential of such hybrid frameworks in post-acute care.

In the domain of primary care, Vázquez-Serrano et al. [20] developed a hybrid model that integrates DES with optimization to minimize patient wait times and ensure timely treatment for high-risk individuals. Their results demonstrated a dramatic reduction of up to 90% in average wait times, while ensuring that all priority patients were treated without delay. This finding reinforces the value of simulation–optimization approaches in improving access and service efficiency at the primary care level. In the context of healthcare crisis management, De Santis et al. [21] proposed a hybrid DES-optimization framework to assess ED performance under extreme demand scenarios. Their model was able to determine the maximum patient volume the system could sustain before collapsing and identify optimal resource configurations to maintain resilience, offering valuable insights for emergency preparedness and capacity planning.

Emergency care has also benefited from the application of metaheuristic algorithms within simulation models. For example, Ramirez-Nafarrate et al. [22] applied genetic algorithms to streamline ambulance diversion processes by minimizing non-value-added activities, thereby improving emergency medical logistics. Similarly, Yeh & Lin [23] integrated DES with genetic algorithms to optimize nurse scheduling, achieving improved service quality without the need to increase staffing levels. On the other hand, Ahmed & Alkhamis [24] implemented a DES-based optimization framework to reduce delays and enhance patient flow in a Kuwaiti ED. Weng et al. [25] combined DES with the OptQuest engine to optimize resource allocation, guided by performance indicators such as the National Emergency Department Overcrowding Scale (NEDOCS). A different approach, which includes machine learning, is presented by Hosseini-Shokouh et al. [26], who introduced an integrated framework that combines DES, artificial neural networks (ANN), and a fractional genetic algorithm to enhance emergency department operations in Iran. By simulating various staffing and equipment scenarios, they nearly eliminated triage wait times and reduced screening delays by approximately 159 min, while achieving 69% and 84% utilization in critical service units.

Together, these studies demonstrate the increasing maturity and versatility of simulation–optimization frameworks in healthcare. By combining the descriptive power of DES with the prescriptive capabilities of optimization techniques, particularly metaheuristics, these models provide robust, data-driven support for improving service delivery, reducing inefficiencies, and enhancing system resilience across various levels of healthcare provision.

2.4. Simulation Design of Experiments and Response Surface Methodology

Despite the proven effectiveness of simulation and optimization techniques in healthcare, incorporating Design of Experiments (DOE) and Response Surface Methodology (RSM) offers an additional and powerful avenue for addressing complex optimization problems. RSM has demonstrated considerable potential in capturing nonlinear relationships and identifying optimal conditions with relatively few experimental runs compared to metaheuristic approaches. While its application in healthcare remains limited, RSM has been widely adopted in other domains. For instance, Zhang & Brown [27] applied it to optimize police patrol districting strategies, while Dengiz & Belgin [28] used it to enhance efficiency in multi-stage manufacturing systems. In the context of inventory management, Dellino et al. [29] integrated RSM with simulation and Taguchi methods to improve system performance under uncertainty. Additionally, Yalcınkaya & Bayhan [30] employed RSM to optimize metro travel times while maintaining appropriate carriage occupancy, and Zhang et al. [31] leveraged it to evaluate the effectiveness of dispatching rules in semiconductor manufacturing. Some progress has been made in extending RSM to uncertain and nonlinear systems. Da Silva et al. [32] introduced a new RSM variant that incorporates uncertainty in parameter estimation, while Fu et al. [33] combined DES, sensitivity analysis, and fractional factorial design to optimize the deployment of automated guided vehicles (AGVs).

In the context of healthcare, relatively few studies were found that integrate simulation with DOE or RSM. Gjerloev et al. [34] present a review of the design of experiments with discrete event simulation where less than 8% of the articles belong to the healthcare industry. Some examples can be found in Sun & Li [35], where they optimized surgery start times using this hybrid method. On the other hand, Barnes et al. [36] used a factorial design to investigate the impact of hand hygiene compliance and staffing levels on Intensive Care Unit’s infection transmission. Recently, Al-Hawari et al. [37] applied DES and RSM to optimize patient throughput, staff utilization, and stay duration in an outpatient endocrine clinic.

However, when focusing specifically on emergency care, the integration of Discrete Event Simulation (DES) with Design of Experiments (DOE) and Response Surface Methodology (RSM) appears even less common. One contribution in this area was conducted by Baesler et al. [38], who combined DES and DOE to estimate the maximum patient demand that a private emergency department could accommodate, providing critical insights into capacity constraints under varying resource configurations. Zeinali et al. [39] also explored simulation-based metamodeling techniques to support resource planning in an Iranian ED; however, their work did not delve deeply into the application of RSM itself. A more recent example conducted by Atalan & Dönmez [40] highlights the practical benefits of this integration; by applying DOE in conjunction with DES, they managed to reduce the average patient waiting time in a small emergency department from 40.09 to 9.83 min, an impressive 75.5% improvement. These studies, although limited in number, underscore the significant potential of combining simulation and experimental design methods to address complex operational challenges in emergency healthcare settings.

This review reveals a clear opportunity to expand the use of RSM in emergency simulation. The present study contributes to bridging this gap by applying DES and RSM to optimize resource allocation in a Chilean emergency department, by adopting a multi-objective approach focused on minimizing patient flow time. The study highlights the practical relevance of combining simulation, DOE, and RSM in addressing real-world operational challenges in emergency care.

3. Materials and Methods

3.1. Case Study

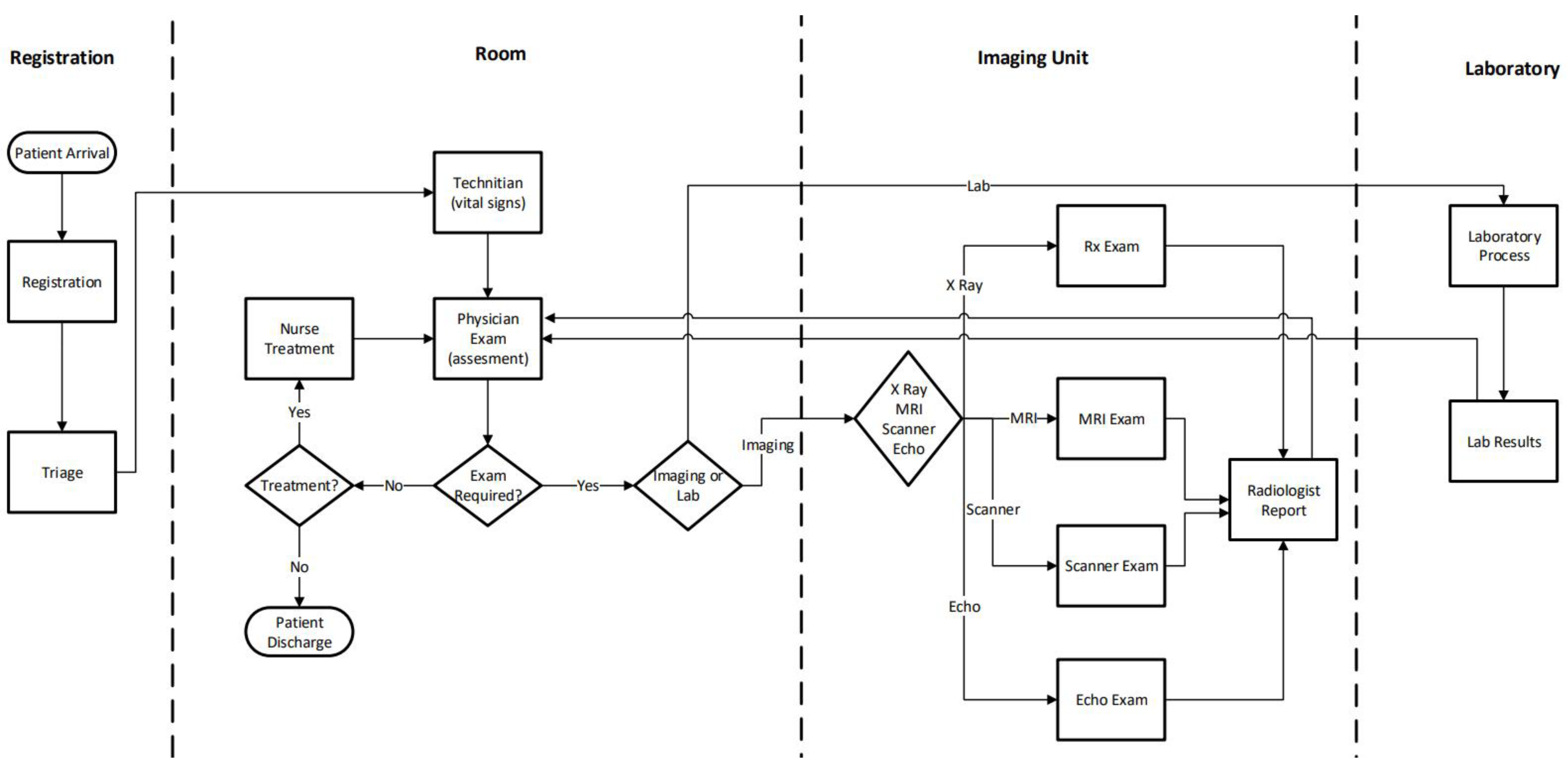
The emergency department analyzed in this study corresponds to the adult emergency unit of a private hospital located in Santiago, the capital of Chile. This unit plays a crucial role in the hospital’s healthcare delivery system, handling approximately 6000 adult patients per month. It is equipped with 30 examination rooms and supported by a multidisciplinary clinical team composed of 9 physicians, 8 nurses, and 10 nurse technicians, all working under varying schedules. Diagnostic imaging services, including five X-ray machines, three scanners, and three MRI machines, are shared across three patient categories: inpatients, scheduled imaging patients, and emergency cases, adding complexity to equipment scheduling and resource allocation. The general patient flow diagram is presented in Figure 1.

The diagram shown in Figure 1 illustrates the patient’s journey through the emergency department, encompassing clinical, diagnostic, and support processes. When patients arrive, they undergo registration and triage, during which their clinical urgency is assessed. Based on the triage results, they move to the physician examination stage, where medical evaluation and diagnostic orders are determined. Depending on the clinical case, patients may receive nursing care or be referred to diagnostic areas such as imaging or labs. The imaging process involves exams such as X-rays, CT scans, MRIs, and echocardiography, which are then interpreted and reported by a radiologist. Laboratory tests follow a similar flow, from sample collection to reporting results. Once all diagnostic results are available, the physician re-evaluates the patient and decides on the next step, either discharge with instructions or admission to a hospital bed. Throughout the process, patients may experience waiting times due to resource availability, reflecting typical operational constraints in emergency services.

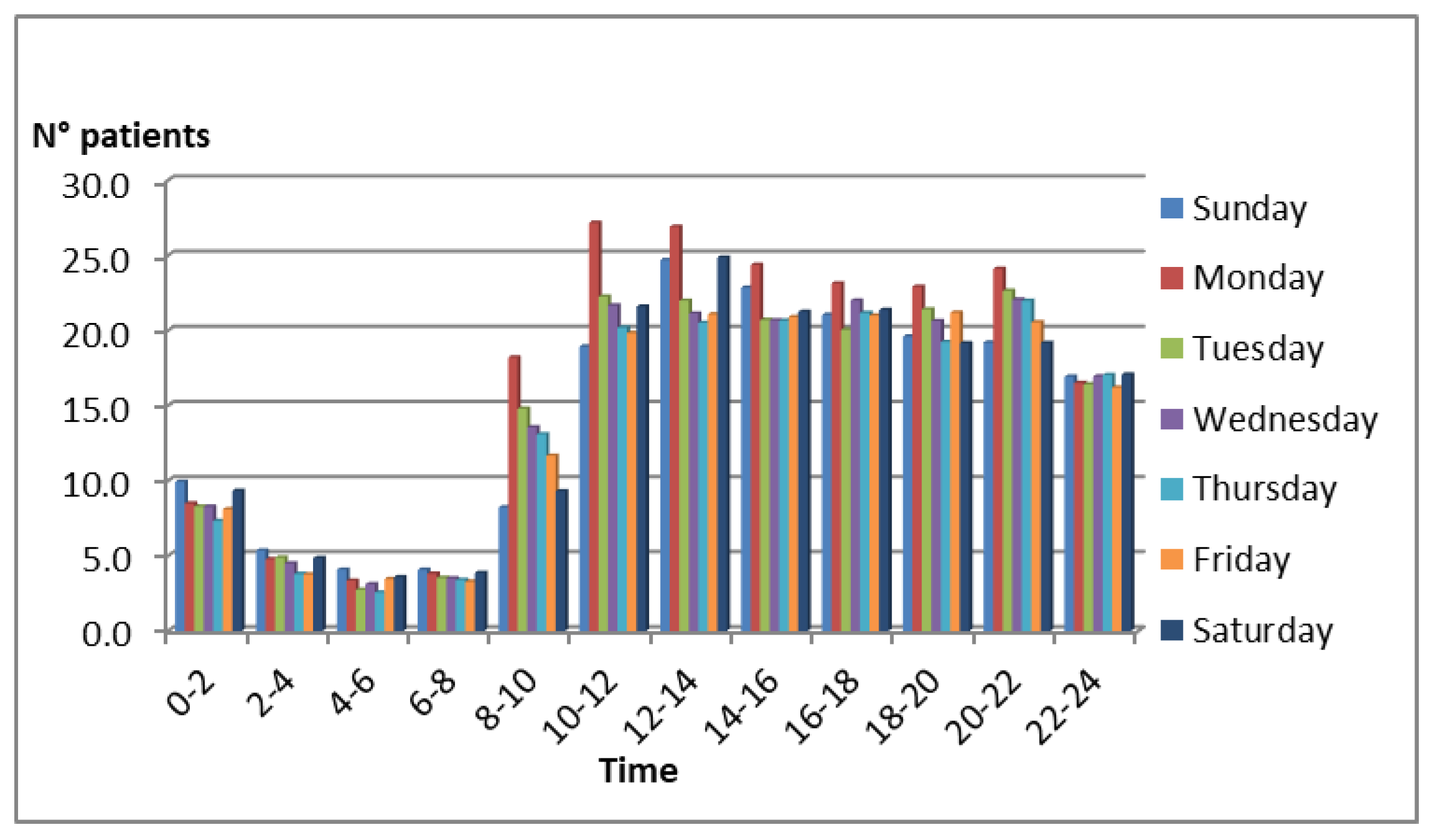
The arrival rate of emergency patients follows a non-stationary pattern, with peak inflows observed around 10:00 a.m., particularly on Mondays. This pattern was derived from historical data available in the hospital’s database and is depicted in Figure 2.

The arrival process was modeled as a non-stationary Poisson process (NHPP) with a piecewise constant rate function λ(t), estimated from the hospital’s historical arrival data. Specifically, patient arrivals were aggregated by hour for each day of the week, and the observed mean arrival rates were used to define the corresponding λ(t) segments. This approach captures the temporal variability of patient inflows—particularly the morning and early-week peaks—while maintaining analytical tractability in the simulation model. The choice of a Poisson process is consistent with previous studies in emergency department modeling.

To manage patient flow efficiently, the hospital identified 33 distinct patient tracks, each representing a predefined sequence of clinical activities required for diagnosis and treatment. These tracks may include physician consultations, nursing interventions, diagnostic imaging, laboratory testing, and specialist evaluations. A statistical analysis of historical records was conducted to determine the frequency of each track, allowing for a probabilistic representation of patient tracks in the simulation model. Upon arrival, each patient is assigned to a track based on these empirical probabilities, which guide their progression through the department and determine the resources involved at each stage. As an illustration, three representative tracks are provided below:

-

Physician consultation → treatment → laboratory exam → physician reevaluation → discharge

-

Physician consultation → specialist consultation → treatment → laboratory exam → CT scan → physician reevaluation → discharge

-

Physician consultation → X-ray → physician reevaluation → medical procedure → discharge

As part of the data collection process for simulation model development, a time study was conducted over a two-week period within the emergency department to measure the duration of key clinical activities. A total of 50 observations were recorded on-site, capturing the timing of physician and nursing procedures. Additionally, 70 records were extracted from the hospital’s imaging services database to quantify the time required for imaging-related activities among emergency patients. These two datasets, along with the estimated probabilities of track assignment, provided the empirical foundation for modeling patient flow and resource utilization in the discrete event simulation environment.

Table 1. ED Activity Distributions.

Activity	Distribution	Parameter Specification (Units = Minutes)
Physician exam	Lognormal (12.71, 0.46)	(scale, shape) form
Nurse treatment	Erlang (1.38, 10)	(mean per phase, shape k) form
Nurse technician treatment	Lognormal (4.89, 0.29)	(scale, shape) form
X-ray exam	Lognormal (5.61, 0.43)	(scale, shape) form
Scanner exam	Lognormal (11.36, 0.59)	(scale, shape) form
Echotomography exam	6.46 + Weibull (23.29, 1.94)	Offset of 6.46 plus Weibull (scale, shape)
MRI exam	Lognormal (30.88, 0.52)	(scale, shape) form
Waiting time for a specialist	2.94 + Weibull (56.6, 1.37)	Offset of 2.94 plus Weibull (scale, shape)
Radiologist exam interpretation	Triangular (15, 25, 50)	(min, mode, max) form
Laboratory exam	Uniform (45, 70)	(min, max) form

lists the set of activities incorporated into the model, along with their fitted statistical distributions expressed in minutes. The Kolmogorov–Smirnov goodness-of-fit test, applied at a 95% confidence level, confirmed that all selected distributions adequately represent the underlying data (p-values > 0.05). This combination of direct time measurements, historical records, and probabilistic track modeling ensured a realistic and data-driven simulation of emergency department operations.

The inherent complexity of this emergency unit, stemming from fluctuating demand, shared resources, and heterogeneous patient needs, motivated the development of a simulation-based optimization study. Based on the operational information and process data described above, a discrete-event simulation model was developed using FlexSim 19.1.0 Healthcare, representing the main patient flow, resource interactions, and service constraints. The aim was to determine optimal resource configurations that minimize patient flow time while maintaining service quality, particularly under a projected 40% increase in demand.

3.2. Methodology

In anticipation of a projected 40% increase in demand resulting from the planned expansion of services, the hospital initiated a strategic study aimed at identifying the optimal combination of resources to manage this growth effectively. The goal was to determine the most efficient resource configuration that could minimize patient flow times under these future operational conditions, thereby ensuring that quality of care and service levels are maintained despite the anticipated rise in patient volume. Although this is a single-objective problem, a multi-objective approach was taken because patient tracks may respond differently to changes in resources. For instance, adding an X-ray machine may affect the flow time of some patient tracks but not others. Among the 33 patient care tracks identified in the emergency department, a detailed frequency analysis revealed that 10 of these tracks account for approximately 80% of the total patient population. This distribution aligns with the Pareto principle, indicating that a relatively small subset of care pathways accounts for a significant portion of the demand for clinical resources. To ensure model tractability and focus the optimization on the most impactful scenarios, the simulation and optimization framework was therefore restricted to these 10 high-frequency tracks. To further streamline the optimization process and reduce computational complexity, a correlation analysis was conducted among the ten most frequent patient tracks, which together represent approximately 80% of the emergency department’s demand. The purpose of this analysis was to identify potential redundancies among the performance metrics, specifically patient flow times associated with each track. If certain tracks exhibited strong statistical correlations, it would be reasonable to assume that improvements in one could reflect improvements in others, thus allowing for aggregation or elimination of redundant objectives in the multi-objective optimization model.

The results of this analysis are summarized in

Table 2. Correlation Matrix.

Track	1	2	3	4	5	6	7	8	9	10
1	1.00
2	0.47	1.00
3	0.77	0.29	1.00
4	0.55	0.71	0.53	1.00
5	0.44	−0.06	0.43	0.28	1.00
6	0.57	0.12	0.68	0.45	0.62	1.00
7	0.72	0.07	0.71	0.56	0.77	0.70	1.00
8	0.50	−0.07	0.50	0.26	0.18	0.22	0.47	1.00
9	0.12	0.18	0.14	0.41	0.49	0.24	0.30	−0.07	1.00
10	0.07	0.00	0.17	0.20	0.32	0.18	0.24	0.05	0.81	1.00

, which presents the Pearson correlation matrix of flow times across the ten selected tracks. A threshold of 0.7 or higher was used to determine strong positive correlations, indicating a high degree of similarity in flow time behavior between tracks.

Based on the threshold considered (r > 0.7), the following groups of highly correlated tracks were identified:

• Track 7 showed strong correlations (r > 0.7) with Tracks 1, 3, 5, and 6, suggesting that these five tracks could be effectively represented by Track 7.
• Track 4 was highly correlated with Track 2.
• Track 9 and Track 10 are highly correlated and can therefore be represented by a single track.

Notably, Track 8 did not exhibit strong correlations with any other track, indicating that its flow time dynamics are unique and cannot be explained by the dynamics of other tracks. As a result, it must be included explicitly as an independent objective in the optimization.

Consequently, the number of objectives was reduced from ten to four representative tracks:

• Track 7 (representing Tracks 1, 3, 5, and 6)
• Track 4 (representing Tracks 2 and 4)
• Track 9 (representing Tracks 9 and 10)
• Track 8 (unique behavior, retained independently)

This dimensionality reduction approach helped preserve the diversity of patient tracks while making the multi-objective optimization problem more tractable, enabling more efficient exploration of the design space.

The process of narrowing down the ten most common patient tracks to four key ones was not just a statistical task. Although correlation analysis was used to spot redundancies, the grouping was later reviewed and approved by the hospital’s clinical team. Importantly, the tracks that were combined shared common resources and similar operational processes (such as physicians, diagnostic imaging, or treatment rooms), which helped keep the clinical logic of patient flows intact. This step ensured that the simplified model remained medically relevant and accurately depicted the decision-making environment of the emergency department.

3.2.1. Multi-Objective Approach

To address the performance of the emergency department under increased demand, this study adopted a goal programming (GP) approach to minimize patient flow times across the four representative patient tracks identified in the correlation analysis. Goal programming is particularly suitable in multi-objective healthcare environments, where multiple conflicting objectives such as reducing delays for different patient types must be managed simultaneously.

The structure of the GP model consists of an objective function that minimizes the weighted sum of deviations from predefined targets (goals) and a set of goal constraints for each track. The model can be mathematically expressed as shown in Equation (1):

$$\begin{array}{l}Min\hspace{0.33em}f=\hspace{0.33em}{\displaystyle \sum _{i=1}^N\left(\frac{w_i{n}_i+w_i{p}_i}{b_i}\right)}\\ s.t.\hspace{0.33em}\hspace{1em} E(x_i)+n_i-p_i=b_i;\hspace{0.33em}i=1,2,\dots ,N\end{array}$$

(1)

where f represents a global performance measure that combines multiple objectives related to patient flow time on different tracks, minimizing f is equivalent to minimizing the weighted deviations of flow times, which means improving the overall system performance, N = number of objectives, E(x_i) = expected flow time value for the patient track i, w_i = weight for objective i, n_i = negative deviation from goal i, p_i = positive deviation from goal i, and b_i = goal for objective i (desired flow time).

Since a negative deviation represents a value even smaller (shorter flow time) than the goal, b_i and n_i were eliminated. In this study, the goal programming model was based on current flow times observed in the emergency department rather than normative targets. This choice was made for two main reasons. First, the empirical flow times provided a realistic and consistent baseline that accurately reflected the hospital’s actual operating conditions, resource constraints, and patient mix complexity. Using these data ensured that the optimization model remained grounded in the system’s current capacity and variability. Second, normative goals such as those proposed by MINSAL are generally designed for public healthcare systems and may not directly apply to the operational dynamics of private emergency departments. However, the proposed framework can easily incorporate normative or policy-driven targets as goal parameters if available or needed in future applications. Therefore, selecting current flow times was intended to establish a data-driven baseline while maintaining flexibility for adaptation to different institutional or policy contexts.

Table 3. Patient Flow Time and Percentage.

Type of Patient	Flowtime Goal (Mins.)	Percentage (%)
Flowtime Track 1	130	112
Flowtime Track 2	185	63.7
Flowtime Track 3	210	6
Flowtime Track 4	78	19.1

presents the parameters for each of the four objectives, along with the new flow time goals under increased demand conditions. Some successful applications of goal programming in healthcare can be found in the literature. For instance, Kwak & Lee [41] employed a linear goal programming model for human resource planning in a healthcare organization, optimizing staffing levels while balancing cost-efficiency and patient service coverage. A successful application of goal programming in healthcare was presented by Rehman et al. [42], who integrated it with discrete-event simulation to optimize resource allocation in a public hospital’s emergency department, achieving a 61.7% reduction in patients leaving without being seen and significantly decreasing wait times.

The goal programming objective function is defined by the structure shown in Equation (2).

$$Min\hspace{0.33em}Z=0.112{\displaystyle \frac{(FT1-130)}{130}}+0.637{\displaystyle \frac{(FT2-185)}{185}}+0.06{\displaystyle \frac{(FT3-210)}{210}}+0.191{\displaystyle \frac{(FT4-78)}{78}}$$

(2)

where FT_i is the variable that represents the flow time for patient type i. The function is standardized by dividing each objective by the goal value. Each objective is multiplied by the percentage of patients for that particular track to represent the weight for each type of patient in the whole objective function.

3.2.2. Response Surface Methodology

To optimize the performance of the emergency department, we adopted the Response Surface Methodology (RSM), a technique introduced by Box & Wilson [43], which has proven effective in exploring complex systems influenced by multiple variables. RSM helps approximate the relationship between decision variables and system performance, allowing us to iteratively refining solutions based on simulation results.

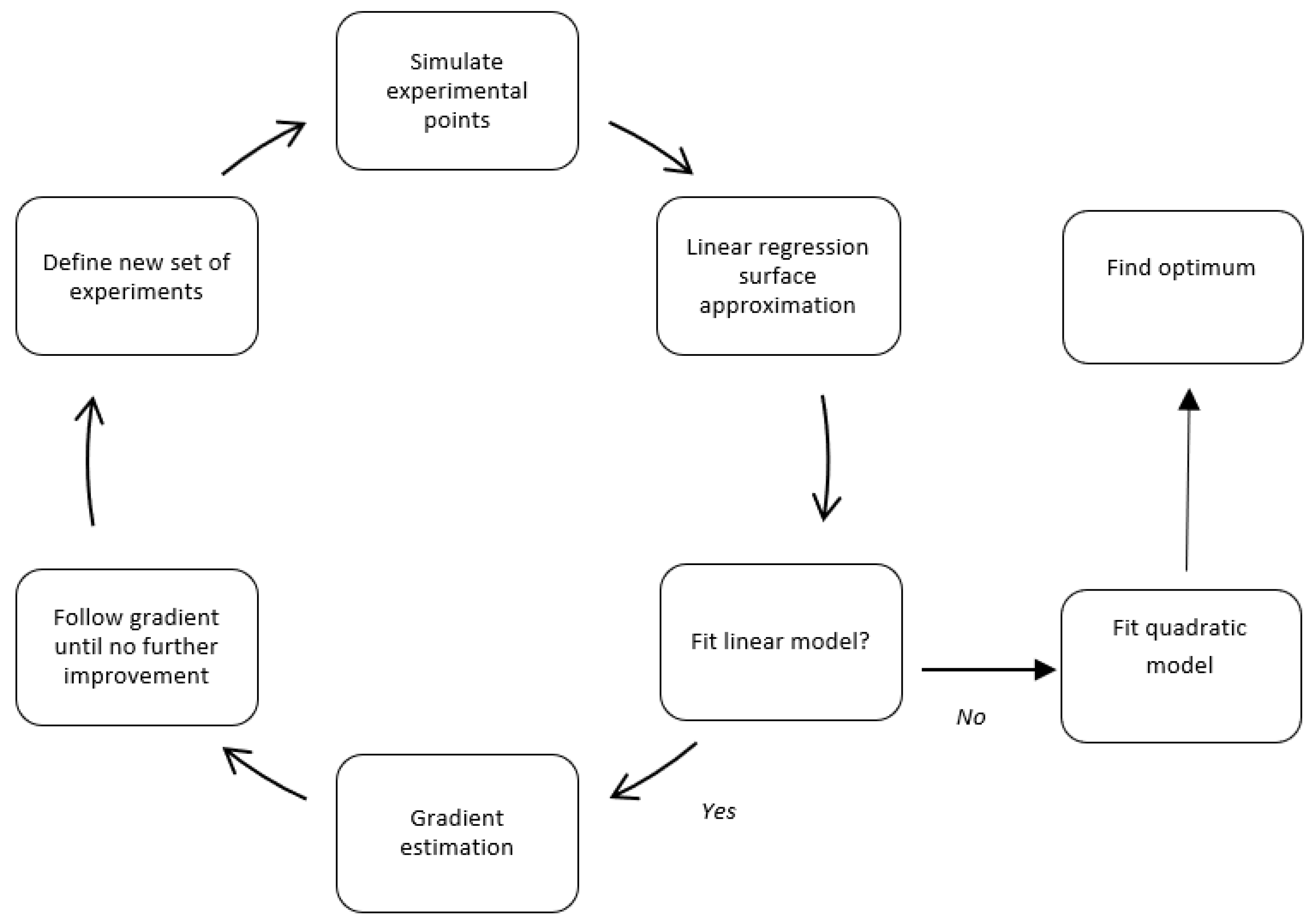
In our study, the discrete event simulation model serves as a virtual representation of the emergency department, capturing the dynamic behavior of patient flows and resource usage. Using a structured Design of Experiments (DoE), we selected specific configurations of resource levels, such as the number of physicians, nurses, or exam rooms, and evaluated their impact on patient flow time through simulation. These results were then used to fit a simplified mathematical model of the system’s response.

The process began with a linear approximation of the response surface, enabling the estimation of the direction in which improvements were likely to be found. Based on this gradient, we gradually adjusted the input variables and repeated the simulations. Once enough data points had been gathered, a second-order (quadratic) model was fitted to capture the curvature of the response surface better and identify a near-optimal region. Figure 3 illustrates this iterative optimization cycle.

For additional methodological background on simulation combined with RSM, see Law [44].

4. Results

In this study, a full factorial experimental design with two levels was employed to investigate the impact of key resources on emergency department performance. Specifically, four critical resources were selected as experimental factors: physicians (A), nurses (B), exam rooms (C), and radiologists (D). These factors were identified based on preliminary bottleneck analyses and consultations with hospital management, who highlighted them as the most impactful resources on patient flow. Other resource categories were excluded from the design due to their observed surplus capacity during peak demand scenarios.

Choosing only four factors was also a deliberate methodological decision to keep the design of experiments (DoE) computationally feasible. In the context of discrete event simulation, each experimental condition corresponds to a complete simulation scenario, requiring multiple replications to achieve statistical validity. Including more variables would exponentially increase the number of scenarios and simulation time, rendering the analysis impractical due to resource constraints.

To conduct the analysis, we used a full 2⁴ factorial design, which involved 16 core simulation runs to cover all possible combinations of the chosen resource levels. To better capture potential nonlinearities and enhance the reliability of the results, we included four center points, bringing the total number of scenarios to 20. Each scenario was run 15 times, with each run comprising a 1-day warm-up period followed by 5 full days of observable emergency department activity. The warm-up period was determined through preliminary testing, showing that the system reached steady-state operation within the first simulated day, preventing transient effects from skewing the results. The number of replications was arrived at via additional pilot tests to achieve a 5% precision level in the confidence interval of the response variable. This setup allowed for the estimation of the main response variable, the goal programming function, which integrates the flow times of the four key patient pathways with 95% confidence. This process ensured that the conclusions from the experiments were both reliable and statistically valid. An analysis of variance (ANOVA) was employed to assess the significance of main effects and interaction terms at each experimental stage. Residual diagnostics were carried out to verify compliance with statistical assumptions, including normality, independence, and homogeneity of variances. This approach confirmed that the relationships among factors were statistically valid and not due to random variation.

The decision to implement a full factorial design was guided by the need for a comprehensive and transparent exploration of the effects and interactions between the selected critical resources, physicians, nurses, rooms, and radiologists, on the performance of the emergency department. While alternative experimental designs, such as fractional factorials, Plackett-Burman, or Box–Behnken, could reduce the number of required simulation runs, they also risk overlooking higher-order interactions or confounding effects, especially in systems as complex and interdependent as hospital operations. In this study, the number of factors was deliberately limited to four, based on expert input from hospital management and prior bottleneck analyses, which identified these resources as the most impactful on patient flow. This constraint allowed the use of a full factorial design to remain computationally feasible, even with the inclusion of replications, while offering the advantage of capturing all main effects and interaction terms without ambiguity. This level of detail was essential for developing a reliable surface approximation in subsequent response surface modeling steps.

4.1. Initial Conditions

The first step in the optimization process is to define the experimental design’s starting point. The experimental design model for this study centers on the current hospital configuration shown in

Table 4. Current Configuration of Hospital Resources.

Factor	Resource	Initial Solution
A	Physicians	3 (24 h) 6 (12 h)
B	Nurses	3 (24 h) 5 (12 h)
C	Rooms	30
D	Radiologists	2850 min per day

.

To enable a standardized comparison across resources, physician and nurse staffing levels were converted into 12 h shift equivalents, assuming that one 24 h staff member equals two 12 h staff members. This transformation facilitates the design of experiments by aligning units of analysis.

Radiologists have non-standardized schedules. Some are hired for a few hours daily, while others work entire shifts. Therefore, this resource is represented in the radiologists’ available minutes daily.

The current configuration of physicians, nurses, rooms, and radiology time was defined as the center point (level 0) in the factorial design. Based on hospital managerial input and operational constraints, high (+1) and low (−1) levels were established to represent feasible variations in resource allocation. These values are presented in

Table 5. Factorial Design Levels.

Factor	Resource	Low Level (−1)	Initial Solution (Level 0)	High Level (+1)
A	Physicians	2 (24 h) + 4 (12 h) = 10 equiv.	3 (24 h) + 6 (12 h) = 12 equiv.	4 (24 h) + 8 (12 h) = 14 equiv.
B	Nurses	2 (24 h) + 4 (12 h) = 9 equiv.	3 (24 h) + 5 (12 h) = 11 equiv.	4 (24 h) + 6 (12 h) = 13 equiv.
C	Rooms	28 rooms	30 rooms	32 rooms
D	Radiologists’ time	2600 min/day	2850 min/day	3100 min/day

.

All the simulations were run with 40% additional patient demand.

Table 6. Current Hospital Scenario with Demand Expansion (level 0).

Type of Patient	Flowtime Base Scenario (Mins.)	Flowtime Goal (Mins.)
Flowtime Track 1	176	130
Flowtime Track 2	235	185
Flowtime Track 3	295	210
Flowtime Track 4	108	78

presents the mean results of this scenario for the four central points and the goal for each patient track.

4.2. Experimental Design and Linear Approximations

Using the current hospital configuration as the central point, the other 16 scenarios were simulated to perform the surface estimation.

Table 7. Full Factorial Design for Experiment 1.

Scenario	A (Doctors)	B (Nurses)	C (Rads)	D (Rooms)	FT1	FT2	FT3	FT4	Z
1	1	1	1	1	199	282	378	110	0.52
2	1	1	−1	−1	203	274	361	118	0.51
3	1	−1	1	1	195	259	322	113	0.43
4	1	−1	−1	−1	190	270	310	109	0.45
5	1	1	−1	1	192	247	310	105	0.36
6	1	1	−1	−1	178	233	301	104	0.3
7	1	−1	−1	1	178	231	286	106	0.29
8	1	−1	−1	−1	182	221	288	105	0.26
9	1	1	1	1	168	240	284	113	0.33
10	1	1	1	1	169	240	283	114	0.33
11	−1	−1	−1	1	173	231	298	110	0.3
12	1	−1	1	1	172	237	281	116	0.33
13	−1	1	−1	1	171	215	285	102	0.22
14	1	1	−1	1	169	233	292	102	0.28
15	−1	−1	−1	1	172	227	280	105	0.27
16	1	−1	−1	1	170	229	273	115	0.29
17	0	0	0	0	171	232	284	110	0.3
18	0	0	0	0	178	236	300	104	0.31
19	0	0	0	0	172	235	302	108	0.31
20	0	0	0	0	185	235	296	108	0.32

shows the results of the complete design. The Z value represents the response variable corresponding to the aggregated goal programming function obtained from the four patients’ flow times, and FT1 to FT4 represent the corresponding Flowtime Tracks 1 to 4.

Using the results of the 20 simulation scenarios generated through the 2⁴ full factorial design with added center points, a first-order linear regression model was fitted. This model, derived directly from the structured experimental design, regresses the response variable z on the main factors and their two-way interactions, enabling the estimation of both individual and joint effects of each resource on the system’s performance. Equation (3) presents the general form of the regression model. All statistical analyses and design of experiments were performed using the statistical software Statgraphics Centurion 17.0.

Z = β₀ + β_A A + β_B B + β_C C + β_D D + β_AB AB + β_AC AC + β_AD AD + β_BC BC + β_BD BD + β_CD CD

(3)

where

• Z is the response (goal programming value),
• A, B, C, and D are coded levels of the four factors,
• β₀ is the intercept,
• β_i are the coefficients associated with each factor and interactions.

The linear regression model that was obtained and presented in Equation (4),

$$\mathrm{y}=0.334+0.002\mathrm{A}-0.014\mathrm{B}-0.058\mathrm{C}-0.048\mathrm{D}+0.003\mathrm{A}\mathrm{B}-0.003\mathrm{A}\mathrm{C}+0.013\mathrm{A}\mathrm{D}+0.009\mathrm{B}\mathrm{C}+0.018\mathrm{B}\mathrm{D}+0.03\mathrm{C}\mathrm{D}$$

(4)

The ANOVA analysis yields an R-squared value of 0.95, indicating an excellent linear fit for the model. The resulting regression coefficients, along with their corresponding p-values, are presented in

Table 8. Regression Coefficients for Experiment 1.

Factors	Coefficients	p-Value
Intercept	0.334	9.4 × 10−13
A	0.002	0.763
B	−0.014	0.060
C	−0.058	1.1 × 10−5
D	−0.048	5.6 × 10−5
AB	0.003	0.633
AC	−0.003	0.628
AD	0.013	0.093
BC	0.009	0.222
BD	0.018	0.025
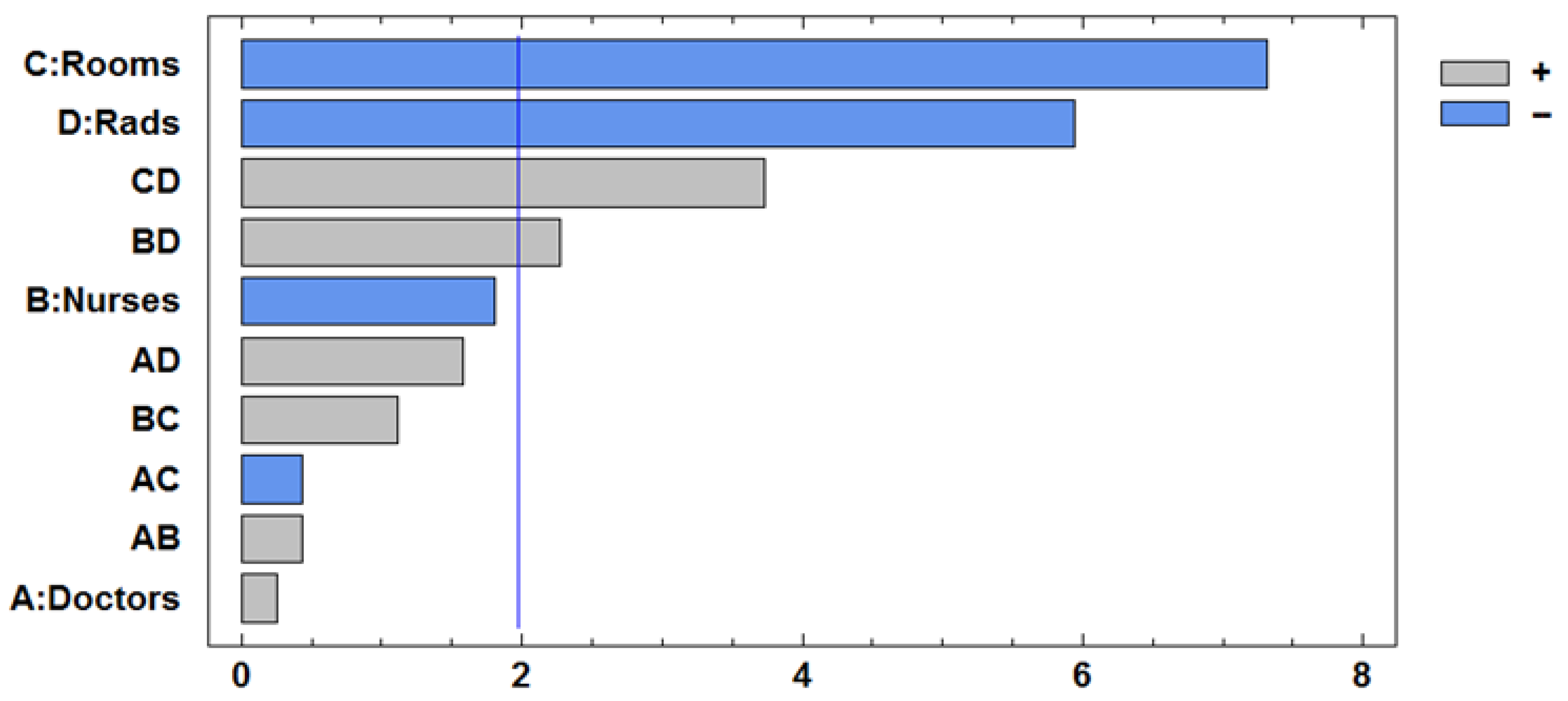
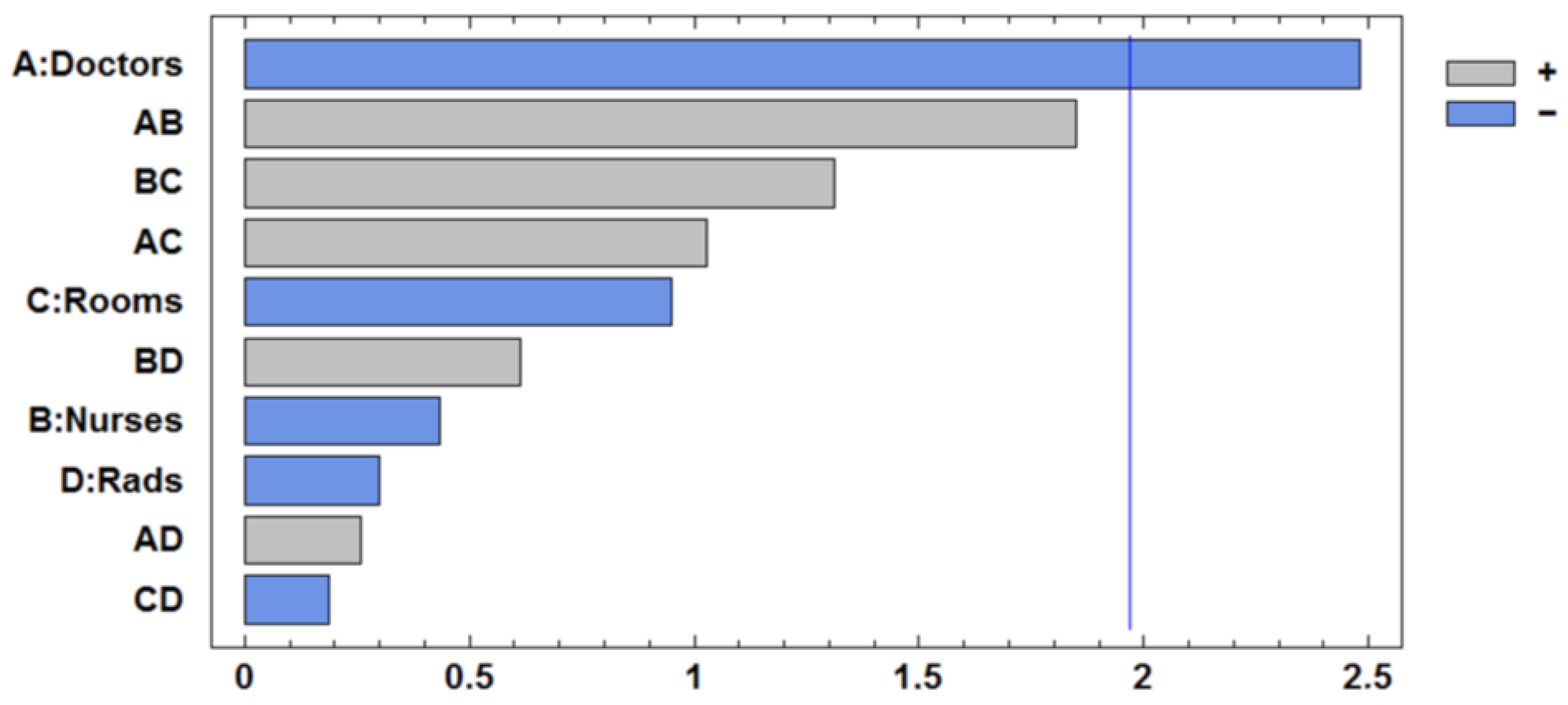
CD	0.030	0.002

. The number of rooms and radiologists is significant, as are factors C and D, as well as their interaction. The interaction BC is slightly substantial. The improvement direction is mainly a combination of the variables C and D. The Pareto Chart is presented in Figure 4.

The gradient of this linear surface is estimated, and experiments (simulation scenarios) in that direction (more rooms and more radiologists) were performed until no more improvement was achieved. To guide the optimization process, the step size for each resource was defined in practical, operationally meaningful units. These units represent realistic increments based on hospital capacity and scheduling constraints. The following increments were used for each factor:

• Physicians (A): One unit corresponds to the addition of a 12 h physician shift.
• Nurses (B): Similarly, one unit represents a 12 h nurse shift.
• Rooms (C): A step of 0.5 corresponds to the equivalent of adding a room for 12 h (i.e., partial-time room availability).
• Radiologists (D): Since radiologist availability is not standardized—some work partial shifts, others full days, this resource was quantified in available minutes per day. One step corresponds to an increment of 300 min of radiologist time.

The optimization proceeded in the direction indicated by the steepest descent of the fitted linear surface, which corresponded to the most statistically significant factors: rooms and radiologists. To follow the gradient, a proportional approach was used to guide resource adjustments based on the estimated regression coefficients.

For instance, the regression coefficients for rooms (C) and radiologists (D) are −0.058 and −0.048, respectively. This indicates that room availability has approximately a 21% greater impact on the objective function than radiologist availability. Therefore, by fixing the step for rooms at 0.5 units, the corresponding step for radiologist availability was adjusted proportionally using the ratio of coefficients 300 * (1 − 0.21) ≈ 249 min.

This adjustment ensured that each gradient step respected the relative contribution of each factor to the system’s performance while remaining feasible in practical terms. Because room increments are discrete (0.5 units), we opted to use this as the base step and scale radiologist availability accordingly. This gradient-based approach allowed for an efficient and interpretable search for improvements aligned with hospital constraints.

The iterative optimization process was terminated when a subsequent step in the gradient direction resulted in no further improvement, in fact, a slight deterioration in the value of the goal programming objective function. This finding suggests that the search had reached a local optimum within the evaluated experimental region, beyond which additional resource increments no longer contributed meaningfully to system performance.

Table 9. Search Process for Experiment 1.

Scenario	FT1	FT2	FT3	FT4	Z
1	175	233	295	108	0.30
2	182	226	317	89	0.244
3	175	218	299	98	0.227
4	194	240	323	99	0.328

shows these experiments (scenarios) with the resulting flow time (FT) for each patient track and the z value representing the aggregated goal programming objective function to be minimized. As shown in the table, improvements continued up to the third scenario, after which Z began to increase.

4.3. Iterative Optimization Process

As the next step in the process, a second full factorial experiment was designed and executed, this time centered around Scenario 3 from Table 9. The purpose of this new experiment was to refine the approximation of the response surface by fitting a more accurate model in the region of interest, where previous results indicated a promising local optimum. This design required running a new set of simulation scenarios to capture the system’s behavior with greater precision. Equation (5) presents the updated regression model derived from this second design.

$$y=0.33-0.035A-0.006B-0.013C-0.004D+0.026AB+0.015AC+0.004AD+0.019BC\hspace{0.33em}+ 0.008BD-0.002CD$$

(5)

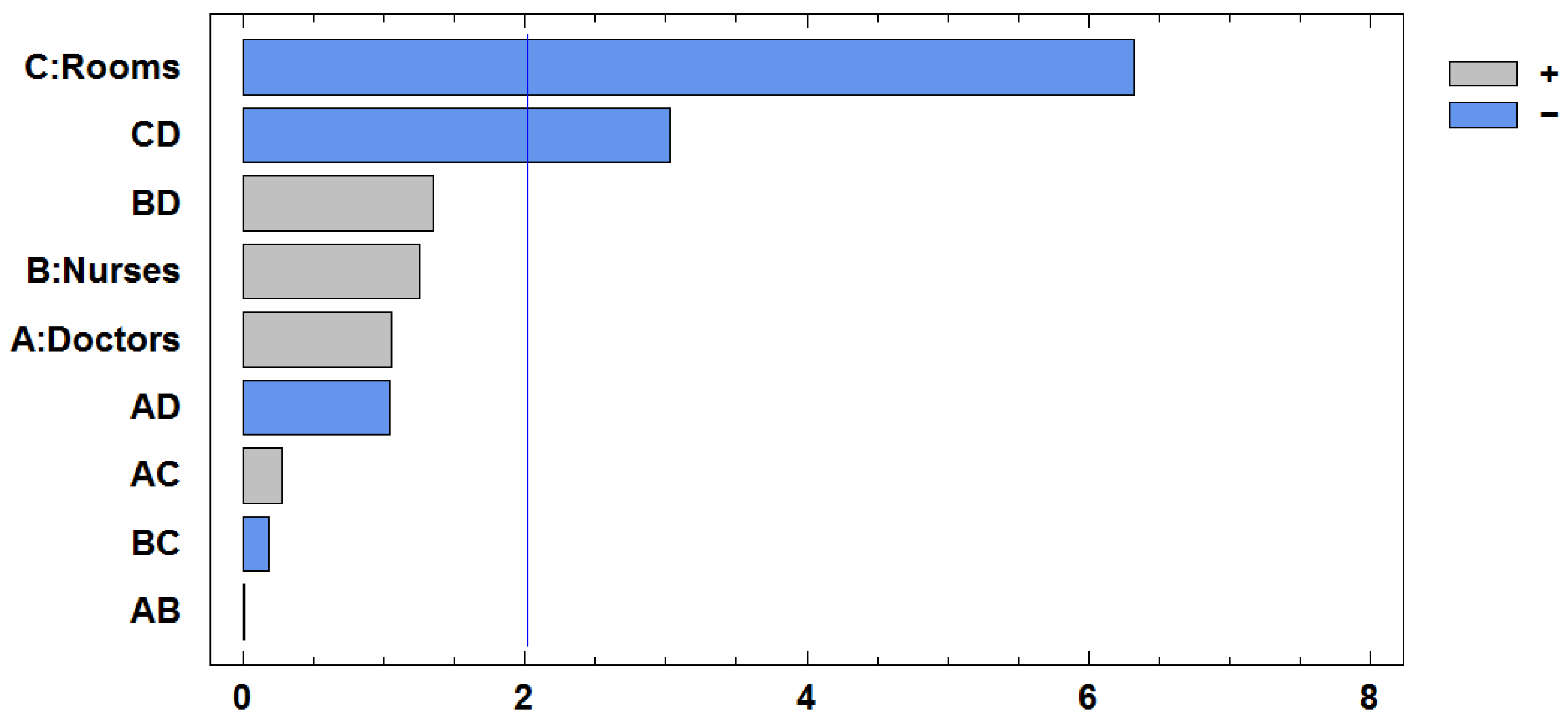
The ANOVA analysis shows a value of 0.6. From the regression coefficients table resumed in

Table 10. Regression Coefficients for Experiment 2.

Factors	Coefficients	$\mathit{p}$ Value
Intercept	0.331	9.7 × 10−10
A	−0.035	0.038
B	−0.006	0.674
C	−0.013	0.386
D	−0.004	0.774
AB	0.026	0.105
AC	0.015	0.336
AD	0.004	0.799
BC	0.019	0.227
BD	0.008	0.575
CD	−0.002	0.868

and the Pareto Chart presented in Figure 5, it is possible to see that the only significant factor is the number of physicians.

A search process followed the gradient direction (increased number of physicians). The results are shown in

Table 11. Search Process for Experiment 2.

Scenario	FT1	FT2	FT3	FT4	Z
1	168	220	287	97	0.222
2	176	222	311	88	0.220
3	175	221	303	89	0.216
4	175	234	307	90	0.265

. Improvement is possible until the third scenario; after that, Z increases.

A third design was conducted, with scenario 3 of experiment 2 as the central point. The resulting regression model is shown in Equation (6).

$$y=0.27+0.01A+0.01B-0.05C+0.03D-0.0001AB+0.0024AC-0.01AD-0.001BC+0.01BD-0.02CD$$

(6)

The ANOVA results shown in

Table 12. Regression Coefficients for Experiment 3.

Factors	Coefficients	p-Value
Intercept	0.27	3.30 × 10−12
A	0.01	0.234
B	0.01	0.156
C	−0.05	2.40 × 10−5
D	0.03	0.001
AB	−0.0001	0.983
AC	0.0024	0.714
AD	−0.01	0.231
BC	−0.001	0.843
BD	0.01	0.121
CD	−0.02	0.005

and Figure 6 indicate that rooms (C) and radiologists (D) are the most influential resources in reducing the value of the goal programming objective function. Both show statistically significant effects, and their interaction (CD) is also significant. This finding means that the impact of increasing one of these resources depends on the level of the other.

It is interesting to note that the individual effect of radiologists (D) is positive, which would typically suggest that adding more radiologist time worsens system performance. However, the interaction between rooms and radiologists (CD) is negative, indicating that when both resources are increased together, their combined effect improves performance. This result highlights the importance of considering interactions, not just individual effects, when optimizing resource configurations.

For this reason, the optimization process moved in a direction that combined increases in both rooms and radiologist availability. Rather than adjusting them independently, the changes were made in proportion to their relative impact, as captured by the regression coefficients. This approach allowed for a more effective and balanced exploration of improvement opportunities, aligned with the real dynamics observed in the system.

A new search process followed the gradient direction (increased number of rooms and radiologist time). The results are shown in

Table 13. Search Process Experiment 3.

Scenario	FT1	FT2	FT3	FT4	z
1	174	223	321	84	0.215
2	172	223	307	83	0.207
3	166	220	297	80	0.181
4	162	214	287	78	0.149
5	173	221	291	82	0.19

.

Table 13 shows that the response variable can be improved until the fourth simulated scenario in the gradient direction. The next step is to run a new experiment, with scenario 4 of experiment 3 as the central point of the new design. After performing this latest experiment, the ANOVA analysis yields a modest R-squared value of 0.14.

Table 14. Regression Coefficients for Experiment 4.

Factors	Coefficients	p-Value
Intercept	0.28	3.41 × 10−7
A	−0.02	0.492
B	−0.01	0.813
C	0.01	0.662
D	0.00	0.857
AB	0.0130	0.592
AC	−0.0089	0.712
AD	0.00	0.938
BC	0.004	0.862
BD	0.00	0.951
CD	−0.01	0.636

shows no significant variables in the model, indicating that the model does not fit the data well and that a curved surface is likely present.

4.4. Second-Order Model Estimation and Gradient-Based Optimization

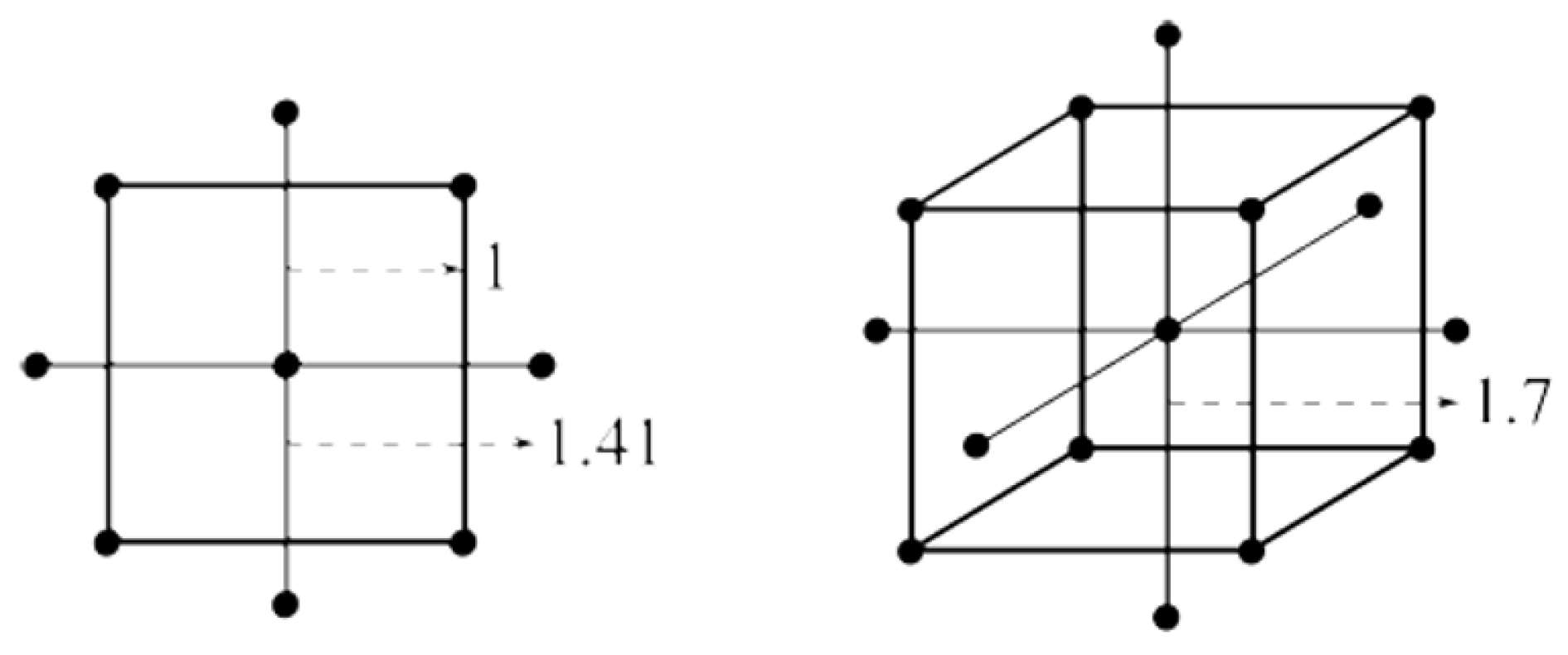
Since the linear model developed in the previous stage no longer adequately captured the behavior of the response surface, a more flexible modeling approach was required. To address this limitation, a second-order model was developed using a Central Composite Design (CCD). This type of design is specifically suited for capturing curvature in the response surface, enabling the modeling of nonlinear relationships and interaction effects more accurately. To achieve this, the CCD expands the original factorial design by adding 2k axial (or star) points located at a defined distance α from the center along each factor axis. These additional simulation scenarios allow for the estimation of quadratic effects, improving the precision of the optimization and helping to identify a local optimum in the experimental region. The α distance is (2k)0.25 = 2, for k = 4.

Figure 7 shows an example of the location of the axial points for 2 and 3 factors.

The composite design and the results of running all these experiments are presented in

Table 15. Central Composite Design.

Scenario	A	B	C	D	AB	AC	AD	BC	BD	CD	AA	BB	CC	DD	FT 1	FT 2	FT 3	FT 4	Z
1	−1	−1	−1	−1	1	1	1	1	1	1	1	1	1	1	189	231	326	88	0.267
2	1	−1	−1	−1	−1	−1	−1	1	1	1	1	1	1	1	168	236	326	87	0.264
3	−1	1	−1	−1	−1	1	1	−1	−1	1	1	1	1	1	194	248	350	91	0.343
4	1	1	−1	−1	1	−1	−1	−1	−1	1	1	1	1	1	185	232	297	89	0.261
5	−1	−1	1	−1	1	−1	1	−1	1	−1	1	1	1	1	181	264	306	92	0.378
6	1	−1	1	−1	−1	1	−1	−1	1	−1	1	1	1	1	176	257	263	95	0.343
7	−1	1	1	−1	−1	−1	1	1	−1	−1	1	1	1	1	183	240	335	88	0.294
8	1	1	1	−1	1	1	−1	1	−1	−1	1	1	1	1	185	238	313	93	0.295
9	−1	−1	−1	1	1	1	−1	1	−1	−1	1	1	1	1	173	258	294	97	0.360
10	1	−1	−1	1	−1	−1	1	1	−1	−1	1	1	1	1	193	236	307	100	0.312
11	−1	1	−1	1	−1	1	−1	−1	1	−1	1	1	1	1	174	223	278	92	0.224
12	1	1	−1	1	1	−1	1	−1	1	−1	1	1	1	1	187	238	309	92	0.295
13	−1	−1	1	1	1	−1	−1	−1	−1	1	1	1	1	1	204	242	281	102	0.342
14	1	−1	1	1	−1	1	1	−1	−1	1	1	1	1	1	167	209	293	99	0.191
15	−1	1	1	1	−1	−1	−1	1	1	1	1	1	1	1	194	252	312	86	0.336
16	1	1	1	1	1	1	1	1	1	1	1	1	1	1	183	236	309	105	0.316
17	−2	0	0	0	0	0	0	0	0	0	4	0	0	0	189	241	310	106	0.341
18	2	0	0	0	0	0	0	0	0	0	4	0	0	0	188	237	305	101	0.313
19	0	−2	0	0	0	0	0	0	0	0	0	4	0	0	191	241	294	96	0.313
20	0	2	0	0	0	0	0	0	0	0	0	4	0	0	187	244	299	93	0.315
21	0	0	−2	0	0	0	0	0	0	0	0	0	4	0	182	239	294	102	0.312
22	0	0	2	0	0	0	0	0	0	0	0	0	4	0	179	231	289	104	0.287
23	0	0	0	−2	0	0	0	0	0	0	0	0	0	4	188	236	293	99	0.301
24	0	0	0	2	0	0	0	0	0	0	0	0	0	4	189	241	310	101	0.329
25	0	0	0	0	0	0	0	0	0	0	0	0	0	0	162	214	287	78	0.149
26	0	0	0	0	0	0	0	0	0	0	0	0	0	0	163	215	275	80	0.155
27	0	0	0	0	0	0	0	0	0	0	0	0	0	0	161	216	271	81	0.158
28	0	0	0	0	0	0	0	0	0	0	0	0	0	0	167	215	272	79	0.155

.

After running this new design, the ANOVA analysis shows a value of 0.7. All the square factors are significant, as shown in

Table 16. Regression Coefficients for Experiment 5.

Factors	Coefficients	p Value
Intercept	0.155	1.8 × 10−5
A	−0.013	0.183
B	−0.004	0.705
C	0.005	0.617
D	−0.001	0.953
AB	0.013	0.289
AC	−0.009	0.462
AD	−0.002	0.875
BC	0.004	0.728
BD	0.001	0.903
CD	−0.011	0.353
AA	0.041	9.0 × 10−14
BB	0.038	0.002
CC	0.034	0.003
DD	0.038	0.002
	(1)

, concluding that a second-order model can be adjusted to obtain the quadratic function presented in Equation (7).

$$\begin{gathered} y=0.155-0.013A-0.004B+0.005C-0.001D+0.013AB-0.009AC-0.002AD+0.004BC+ \\ 0.0015BD-0.011CD+{0.041A}^2+{0.038B}^2+{0.034C}^2+{0.038D}^2 \end{gathered}$$

(7)

5. Discussion

Equation (7) represents an inflection point from the entire surface and a local optimal region. By using mathematical programming tools, it is possible to obtain one locally optimal solution, solving, in general, the nonlinear system of equations ∇f(x) = 0 where f is defined according to Equation (7) and x ∈ R⁴. The solution obtained from the optimization process is A = 0.1480, B = 0.029, C = −0.054, D = 0.0086, and Z = 0.1538. This result is close to zero and matches the average of the four central points of the quadratic surface, as shown in the last four scenarios of Table 16. In other words, the optimal solution for the surface is the central composite design’s central point.

Table 17. Search Process Summary.

FT1	FT2	FT3	FT4	Z
175	233	295	108	0.302
182	226	317	89	0.244
175	218	299	98	0.227
168	220	287	97	0.222
176	222	311	88	0.220
175	221	303	89	0.216
174	223	321	84	0.215
172	223	307	83	0.207
166	220	297	80	0.181
163	215	276	80	0.155

summarizes the complete search process from experiments 1 to 5.

The improvement obtained by comparing the initial and final solutions is presented in

Table 18. Final Comparison Table.

Solution	FT1	FT2	FT3	FT4	Z
Initial	176	235	295	108	0.310
Last	163	215	276	80	0.155
Improvement	7%	9%	6%	26%	50%

.

Table 18 shows that the Z function can be improved by 50% after optimization. In addition, all the individual objectives have improved, reducing the patient flow time from 7% to 26%. To obtain this solution, additional resources are required. The comparison between Z_initial and Z_last shows a statistically significant improvement. A Welch’s t-test based on 15 independent replications per configuration yielded p < 0.05, indicating that the improvement is statistically and practically meaningful.

Table 19. Resource Comparison.

Factor	Resource	Initial Solution	Final Solution
A	Physicians	3 (24 h) 6 (12 h)	3 (24 h) 9 (12 h)
B	Nurses	3 (24 h) 5 (12 h)	3 (24 h) 5 (12 h)
C	Rooms	30	34
D	Radiologists	2850 min per day	4350 min per day

shows the initial and final solutions in terms of hospital resources. The emergency department personnel work on different schedules. For example, some physicians and nurses work 24 h shifts, while others work 12 h shifts. Radiologists have non-standardized schedules. Some are hired for a few hours daily, while others work entire shifts. Therefore, this resource is represented in the radiologists’ available minutes daily.

Table 19 summarizes the additional resources needed to obtain the optimal solution. Three 12 h shift physicians must be added, nurses do not require extra staff, four more rooms are needed, and the radiologist availability has to be increased by approximately 53%.

This solution corresponds to an optimal point in a local context. Improved solutions could be obtained if other resources are included in the analysis, such as X-ray machines, MRI machines, Scanner machines, and nurse technicians. The initial study revealed that these resources had remaining capacity, making it unnecessary to include them in the optimization process. After reaching an optimal solution with the four main variables, the bottleneck may have shifted to those resources that initially had excess capacity. Further improvements could potentially be achieved through a new optimization process that includes these resources.

While our study focused on a private hospital in Santiago, Chile, the proposed framework is not limited to this context. Since it is based on discrete-event simulation and multi-objective optimization, the approach can be adapted to hospitals in Chile, Latin America, or other regions worldwide. However, generalization requires careful consideration of three aspects: resources (availability of physicians, nurses, diagnostic capacity, and physical infrastructure), operations (patient arrival patterns, care protocols, and scheduling practices), and management (budget constraints, staffing policies, and institutional priorities). These aspects determine how the model is calibrated for each setting. In this way, our methodology acts as a flexible metamodel: its structure remains constant, but its input data and constraints can be adjusted to reflect the real-world situation of different hospitals, ensuring both scalability and local relevance.

Although alternative simulation–optimization techniques such as R-SPLINE [45] and other metaheuristic methods (e.g., genetic algorithms, simulated annealing, or particle swarm optimization) have been successfully applied in discrete-event simulation contexts, their exploratory nature typically requires a substantially larger number of simulation evaluations to reach convergence. In contrast, the combination of Design of Experiments (DOE) and Response Surface Methodology (RSM) offers a structured and statistically grounded approach that balances computational feasibility with analytical interpretability. Beyond identifying optimal configurations, RSM allows decision-makers to understand how each resource influences system performance, to recognize emerging bottlenecks, and to visualize how trade-offs evolve across iterations. This interpretability is particularly valuable in healthcare operations, where decision support must combine analytical rigor with managerial insight.

6. Conclusions

This study presents a practical and efficient process for optimizing multiple objectives in emergency healthcare using Response Surface Methodology (RSM) in combination with Discrete Event Simulation (DES). The methodology enabled us to achieve a 50% improvement in the response variable, thereby significantly enhancing patient flow efficiency across different care tracks. Importantly, this was accomplished by addressing multiple objectives simultaneously, rather than relying on a single metric such as the average patient flow time. This distinction is crucial, as each patient’s track may respond differently to changes in resource allocation.

RSM proved to be a powerful and computationally efficient metamodeling approach. The entire optimization process required only 98 simulation scenarios, each replicated 15 times with a one-week run length, resulting in over two hours of computer time per scenario. In contrast, alternative simulation-based optimization techniques such as Genetic Algorithms or Simulated Annealing might demand a far greater number of simulations, making them less feasible for complex models like the one used in this study. In healthcare contexts, resource and staffing configurations are subject to strict physical and contractual constraints, meaning that feasible solutions typically lie close to the current operational configuration rather than in distant regions of the search space. Under these conditions, a global metaheuristic exploration is not necessarily more advantageous, as it may identify configurations that diverge substantially from practical feasibility and would also be computationally very demanding, requiring the evaluation of a large number of scenarios to converge toward feasible solutions.

Our results also suggest that further improvements could be achieved by incorporating additional variables that were initially held constant. As the optimization progressed, the system’s bottlenecks appeared to shift toward those resources with initial surplus capacity, highlighting the dynamic nature of system constraints and the value of iterative, adaptive planning.

The integration of RSM and goal programming provides a structured way to capture and balance competing goals, such as minimizing patient waiting time while maximizing resource efficiency. Moreover, the ability to model and understand nonlinear interactions between resources and patient outcomes contributes to more informed and robust decision-making.

We emphasize the importance of correlation analysis among different patient trajectories to help reduce dimensionality in multi-objective optimization problems without compromising solution quality. Additionally, any capacity planning effort must account for projected increases in demand to ensure that solutions remain effective and scalable in the long term.

The framework can be easily updated to accommodate higher or seasonal demand fluctuations. By recalibrating the response surface and goal programming components with new arrival data, the model can estimate the additional resources required to sustain service levels during peak periods, ensuring long-term operational sustainability.

In sum, this research highlights how hybrid approaches, combining simulation, RSM, and multi-objective optimization, can offer powerful tools for navigating the inherent complexity of emergency healthcare systems. These strategies support data-driven decisions that not only improve operational performance but also enhance the quality of patient care.

The proposed simulation–optimization framework proved effective in identifying feasible strategies to improve emergency department performance while maintaining operational realism. Operational costs were implicitly captured through the resource capacity constraints, which reflect real staffing availability and scheduling policies. Although the model did not include explicit cost functions, the optimization sought to enhance patient flow efficiency without increasing total resource utilization, maintaining consistency with the hospital’s operational and financial constraints. Future extensions could incorporate explicit cost parameters or budgetary limits to broaden the decision-making capabilities of the framework.

Despite its promising results, this study has some limitations. First, the model was applied to a single emergency department, and the results should be interpreted within that operational context. Second, the optimization relies on response surface approximations, which provide local but not necessarily global optima. Third, operational costs were implicitly captured through resource constraints rather than explicit cost functions. Finally, the model assumes a constant patient-mix distribution and staffing policy during the simulated horizon. Nevertheless, the proposed framework can be readily updated with new data or extended through metaheuristic or hybrid approaches to address these limitations in future research.