Abstract
This article, based on network science, aims to contribute to overcoming its geometric and technological phases. The novelty consists in considering links of networks as linked by superimposed networks, termed here multiple superimposed soft networks (MSSN), which is introduced as a research issue. Such links of links (termed here as passive links) concern, for instance, correspondences, incompatibilities, and temporal synchronizations between the occurrences of pairs of active links of effective networks, such as those based on electrical and telecommunication. A possible constitutive mechanism of such passive linkage consists of linkage representations for practices and histories of use expressed by their validating statistical reoccurrences. We consider the possible emergent nature of the passive linkage. The reason for introducing the design and usage of MSSN properties as a research issue involves making new approaches to profile and manage networks available. Correspondence between active linkage and MSSN properties should be a matter for an experiential, machine-learning approach. Research issues relate their possible usage on the active linkage such as for classification, comparations, detection of criticalities, diagnosis, performance evaluation, and regulatory as weak forces. Furthermore, the possible identification of standard corresponding configurations of passive and active linkage is finalized to avoid their establishment or, conversely, in facilitating their establishment and keeping their replication in different contexts (or partially and in combinations) and identifying related standardized approaches (also for classes of configurations having significant levels of equivalence). This research project has methodological generalizing aspects of trans-disciplinarity. We conclude by mentioning related research issues.
Keywords:
coherence; constitutive mechanism; domain; ergodic; incompleteness; linkage; profile; quasi; weakness 1. Introduction
This contribution is addressed to researchers in interdisciplinary areas of network science, and its background is given by the extensive literature related to it.
As the basic literature containing principles and approaches subsequently developed, we can cite texts such as [,].
Examples of subsequent developments and insights concern include the emergence of scaling in random networks [], the structure and dynamics of networks [], and the problem of network interventions [].
In Section 3, we mention examples of subsequent variations and implementations such as the study of networks of networks, multiple networks, multiplex networks, dual networks, and overlay networks.
This research project may act as a step forward for network science, for instance, in reference to the consideration that “… network science is not yet mature enough to be separated from its technological roots” ([], p. 9).
This article is part of the contributions aimed at overcoming the geometric and technological phases of network science, allowing the introduction of research approaches not only for the already consolidated network modeling of complex systems but also for their control, criticality diagnostics, and performance-evaluation-based on network representations of usage histories, phenomenological properties, and experience, which are quantified, for instance, in statistical values.
The purpose of this article is to introduce a research issue based on the consideration of the possibly multiple, hierarchical, and variable linkages among links of the networks under study. We explore the possible nature of these superimposed linkages, i.e., links between links, even at a level greater than one (i.e., links between links between links and so on), and the feedback on the network in which they are constituted. They may even possibly emerge in the same way as emergent properties that have effects on the systems from which they emerge.
The focus research question relates to the availability of network representations suitable to methodologically generalize approaches already considered for instance for autonomous adaptive networks (see Section 6.2).
The focus research question relates to the possibility of having representations of networks that are more flexible in nature than technological and geometric ones, having instead structural dynamic sensitiveness to actual and contextual use. Precisely because of their structural sensitivity to use, these representations are compatible and have applicability for diagnosis, operational criticalities detection, performance evaluation, and self-regulatory, self-profiling approaches (see Section 5.1)
We consider the phenomenological inevitability of the self-definition of such linkage, considered here as the profile of the network under study, and termed as multiple superimposed soft networks (MSSN) to distinguish it from other numerous terminologies already in use.
This is all the more important when considering that network science is considered essentially the science of systems. However, the science of networks may specify the science of systems in the sense that it can be a specification of the interaction mechanisms allowing for a system and its properties to emerge from a collection of interacting entities, avoiding, for instance, simple Brownian motion versions.
Such specification performed by using the network representation can help overcome the difficulty in intervening in the processes of emergence, whose explicit analytical description is inadequate or intractable for actions such as:
- Induce or deactivate the emergence of collective behaviors in populations of elements collectively interacting;
- Act on collective emergent phenomena with the purpose of changing, maintaining, and regulating acquired properties;
- Merge different collective emergent phenomena.
In Section 2, we consider the classic network nodes and links (termed here active) with the addition of nodes representing underlying links and links between them (termed passive, expressing existing or emerging relationships). In Section 3, we introduce the multiple superimposed soft networks as linked links.
In Section 4, we present two examples of MSSN on the active road and social networks.
In Section 5, we elaborate on the constitutive mechanisms of the MSSN linkage. In particular, on its self-definition as based on statistical properties (see Section 5.1) and its possible emergent nature (see Section 5.2). In Section 5.3, we consider aspects of the relationship between such linkage levels.
In Section 6, we introduce possible usages of the MSSN properties and profiles that allow for possible reverse effects on the active linkage, such as considering and applying MSSN-based classifications, driven modifying actions (see Section 6.1), and self-regulatory (see Section 6.2) based on machine learning in case of adaptive, autonomous networking.
In Section 7, we introduce the possibility of considering the passive linkage of the MSSN as weak forces, i.e., forces having low value, for instance, less than the minimum of all forces involved at the moment and local ranges of influence. In the case of collective behaviors, for instance, the weak forces relate to the breaking of the agents’ instantaneous equivalent conditions, the breaking of equilibria, and the setting of critical initial conditions in chaotic behaviors.
In Section 8, we list possible research issues on MSSN that are considered to have, among other issues, methodological and philosophical generalizing aspects of transdisciplinary (see Section Trans-Disciplinarity of the MSSN). In Section 9, we conclude by mentioning specific research directions and how the study of the MSSN, their properties, and their relationships with the network of active linkage may introduce new research approaches, also indicating currently undefined limits of network science.
2. Nodes and Links for a New Perspective
For the purposes of this article, with reference to graph theory and network theory, we will distinguish between the usual kinds of nodes and the ones consisting of the links themselves. We also distinguish between the usual kinds of links and the ones consisting of links between links.
2.1. Nodes
The term “node” is widely elaborated in the network science literature. In this article, we limit ourselves to consider the usual two kinds of nodes, and nodes as links of a network:
- (a)
- Nodes as input–output devices, whose activity ranges from performing connection activities; to summative of the input received through N input links, according to various possible ways, for example, non-linear, time-dependent, dependent on previous conditions, and weighs; until performing processing activities, for example, composing by using fixed or time-context-dependent rules, and selected input received. In the simplest case, it is a matter of passive, i.e., switching, conductive, connective nodes. In the latter case, such nodes may be intended just as extensions of the links, i.e., a networked configuration of the same material, for instance, networks made of the same electric conductive material. The nodes can be in an active or inactive state, in ways that vary over time in regular or random ways, where the role of the node is reduced, for instance, to an electric resistor or diode. Examples include electricity, road, telecommunications, and water networks.
- (b)
- Nodes as generic units, for instance, containers in a port warehouse, people in a community, vehicles in the traffic, and words of a text relationally connected. For instance, containers may relate to each other by weight and arrival time; people by their nationality or level of friendship in social networks; vehicles by their speed or by their registration period; and words by the fact that their meaning is semantically close or by the fact that they often both appear in single sentences (see Figure 1). Examples include air, bus, citation, naval, rail, and social networks. The difference with the situation considered in the previous point is not actually so precise, as the roles could even be partially or temporally interchangeable or even simultaneous.
- (c)
- Nodes consist of pairs of linked nodes of the network under study, as highlighted in Figure 2. Due to the undefined nature of the generic nodes, the case of nodes consisting of links, i.e., linked links (see Figure 3, Figure 4 and Figure 5 and Section 3), seems to be just a particular case of usual networks. However, the non-triviality of the case consists of the properties (in the case of self-definitory, see Section 5.1, and emergent, see Section 5.2) of such possibly multilayered linkages, i.e., the multiple superimposed soft networks (MSSN), considerable to profile and manage (see Section 6.1) networks. This term differentiates from others already in use for specific cases, such as dual networks, meta-networks, multiple networks, multiplex networks, networks of networks, and overlay networks (see Section 3.1).
2.2. Links
This term is also widely used and elaborated in the network science literature. In this article, we will distinguish between the usual kinds of links and the ones consisting of links between links:
- (a)
- Active links (for instance, pipes and cables conveying matter or energy) include road, naval, and air routes for passengers and cargo. The technological understanding of the active linkages presupposes additional characteristics, such as link coatings (where the coatings are to avoid electrical short circuits between links); sensitivity to environmental perturbations; formation and degeneration of the lining, such as the myelin-like coatings of neurological networks whose damage in certain neurological diseases, e.g., multiple sclerosis, generates the production of pathological scars. Moreover, we should consider the possible occurrence of properties and phenomena such as link acquisitions, capacity, combination, fluidity (level of internal friction), interconnectivity, loss, temporality, and virtuality when a phenomenon operates, moreover, also as a link as in social and citations networks; the occurrence of stable and variable links properties such as unidirectionality, bidirectionality, e.g., two-way, contextual sensitiveness, and weighing. Examples of active relational links include the linkage of social and citation networks. In this contribution, we consider the effective, parametrical, statistical, weighted usage of the network of active links, which is not only considered for its geometrical properties, i.e., networks as graphs. The geometrical network linkage is coupled, for instance, with effective uses characterizing the nodes and links of the networks, e.g., airlines, roads, social, and telecommunication. Users are represented by weights and statistical values related to the occurrence of properties. In the second case, networks as graphs, the focus is on geometrical properties, and effective usage is placed in the background (see Section 5.1).
- (b)
- Active interactional links represent the interactions, e.g., through the exchange of energy or information, between nodes, for instance, with the occurrence of multiple interactions and roles for component parts, as in ecosystems and collective behaviors.
- (c)
- Passive links express existing or emerging relationships between pairs of links of the active linkage under study and representing modes, practices of occurring, and interdependences between active links, for instance, being correspondingly in an active–inactive state, simultaneously in the same state, synchronized or not, and weights characterizing the intensities of the relationship. Passivity is considered given by their relational, representative rather than computational, connective, elaborative, and phenomenological nature. For instance, let us consider links of a road network that are characterized by their actual practicability or not, that are passable in two ways, in one-way only or in alternating directions. Passive links between pairs of such active links state their same or opposite levels of practicability; their being passable in two ways, in one-way only, and in alternating directions in combinations, e.g., when one is two-ways, the other is one-way, or when one is two-ways, the other is in alternating directions and have mutually direct or inverse proportional traffic values. The passive linkage is also applicable to links of the passive linkage themselves, i.e., links of links subject of this article as highlighted in Figure 5 (see Section 3.2 and Section 4, for examples).
In the case of point (a), i.e., active links, we have links as channels, connections to convey information, energy, and matter. Attention has been on phenomena such as node failures and weighted links, e.g., in neurological networks conveying electric signals and geometrical properties of such linkage, for instance, see earlier work [].
In the case of point (b), i.e., active interactional links, we consider the interaction as a link when the linkage is given by interactions. Two elements are said to interact when the behavior of one element influences the behavior of another, as in a system model consisting of ordinary differential equations where f represents the interaction between x1 and x2, i.e.,
The formal definition of Equation (1) may be applied to real cases, for instance, when f1 and f2 may be real interactions such as the exchange of kinetic energy and x1 and x2 may be energetic measures of the state of two colliding components.
Active interactional links play an essential role when considering systems as networks (see Section 6).
However, as we will see, the active interactional links have a character of intermediality between active and passive linkage, introduced below as a third case. This is given by the fact that the interaction may not be due to material interactions only—e.g., exchange of kinetic energy in collisions, economic transactions with the exchange of goods or financial transactions, and field influences (for example, gravitational or electromagnetic)—but due to immaterial interactions also, e.g., cognitive processing of reciprocal spatial positions over time as in animal collective behaviors and information relevant for economic decisions (for example, political and financial).
In the case of point c, i.e., passive links, we have links as edges in graph theory. However, they have an effective, parametrical, phenomenological, and statistical nature rather than a geometrical one, representing correspondences and relationships between links connecting nodes (see Figure 2, Figure 3, Figure 4 and Figure 5).
The subject links as nodes are considered, for instance, in []. Such links may be of any nature, each of which establishes a dedicated network related to properties, as in the examples above. The passive linkage may also be applicable to links of the passive linkage themselves, i.e., passive links between passive links. One passive link may correspond to another because they are related to similar phenomena, as they are generated within the same time range and have the same synchronizations. Examples include relationships stating the mutual states of two active links, such as those that are active–inactive, the same or opposite direction, the same or different levels of use, e.g., throughput, their weighing with corresponding variations, and equipped or not with covering.
Passive links between active links are established when the latter ones have one or more related properties, such as incompatible, matched, proportional, or synchronized. The same is true for subsequential passive links. Each property considered establishes a specific property related to MSSN, such as the red and green ones in Figure 4. However, we specify that the properties considered, and then the consequent related passive linkages, may occur in non-fixed and inhomogeneous ways, in irregular, random, recurring, but, nevertheless, statistically significant modalities (see Section 5.3).
3. Linked Links: The Multiple Superimposed Soft Networks
Research approaches have been introduced in the literature, such as:
- The study of “networks of networks”, i.e., interdependent networks or multilayer networks, such as in earlier papers [,].
- The study of “multiple networks”, is when a multiple system [] is considered as a set of systems whose components simultaneously belong to more systems, networks such as in [].
- The study of “multiplex networks”, when “… a multiplex complex system can indeed exhibit structural and dynamical properties that cannot be represented by its individual layer’s properties alone, establishing the network multiplexity as an essential ingredient in the new physics of network of networks” such as in previous work ([], p. 9; []).
- The usage of “dual networks” in electrical engineering is when, in two electrical networks, the mesh equations of one network are equal to the node equation of the other. In the smallest loop, which is a closed one and formed by using circuit components, the mesh must not have any other loop inside it. In short, the term “node equation” is used in electrical engineering to refer to a method (nodal analysis) of analyzing electrical circuits. Two electrical networks are dual networks if the mesh equations of one network are equal to the node equation of the other [].
- Examples of other variants include (a) meta-networks consisting of two learning components, a base learner, and a meta learner, also equipped with external memory [,,]; and (b) overlay networks, computer networks layered on top of each other. The overlay networking is distinct from the open systems interconnection (OSI) layered networks model, assuming that the underlay network is an internet protocol (IP) network [].
3.1. Multiple Superimposed Soft Networks
To differentiate from the previous terminologies, in the following, we use the less used name of “multiple superimposed soft networks”, or MSSN for short.
We specify that the term “soft” is related here to the concept of “soft computing”. Soft computing tools to deal with complex systems characterized by imprecision, stochasticity, and uncertainty intractable with analytical approaches. Soft computing tools include artificial life models, cellular automata, ensemble learning algorithms, fuzzy systems, genetic algorithms, multi-agent modeling, neural networks, and swarm intelligence models. Models based on soft computing allow easy tractability and a high tolerance for imprecision characterizing complex systems.
Furthermore, we refer to the concept of weak forces crucial in establishing initial conditions, breaking equivalences and equilibria (see Section 7.1).
The theoretical research perspective is to introduce this form of softness into network science.
The MSSN, on a network made of active linkage, is intended as a network of passive linkage, i.e., correspondences, matches, and relationships, between active links (and not between nodes), as in the cases considered above relating to modes, practices of usages, and occurring of links (see Section 2.2, point c).
In the simpler case, the MSSN is made of a single network of relationships (see Section 5 on their self-establishment as statistical properties) over the active linkage. In multiple-layered MSSN, the layer of passive links is (on their turn) superimposed on further passive linkage on the lower passive linkage.
The simplest definition of a graph G is given by considering it as defined by two sets N and L so that we can write G ≡ (N, L), where:
- The elements of N are the nodes;
- The elements of L are pairs of nodes, called links.
Some constraints usually considered for these two sets allow us to distinguish between different classes of networks. For instance, assuming that:
- The set N has an integer cardinality;
- The set can contain only ordered pairs of nodes (directed links);
- Each link is associated with a numerical weight.
Usually, graph theory is the mathematical term that identifies networks as being applied in different areas.
Considering the basic active network G ≡ (N, L) the MSSN related to it may be identified by
where:
MSSN1 ≡ (L, L1)
- L are links of the basic effective network G;
- L1 are links between pairs of links L, e.g., stating the simultaneous validity or non-validity of pair of links L, and by possible layered n-sequences of
MSSNn ≡ (Ln−1, Ln).
The MSSN is superimposed to the networks of active linkages (see Figure 1), connecting properties of their active links (see Figure 3 and Figure 4), and, in the example, their superimposed linkage (see Figure 5). The MSSN is then made of hierarchical sequences of superimposed networks of passive links (relation graphs) on the network of active linkages and, in this case, on underlying passive linkage (see Figure 5).
Simplified examples of the different phases (see Figure 3 and Figure 4) constituting the MSSN (see Figure 5) are presented, however repeatable in layers of any level and variations.
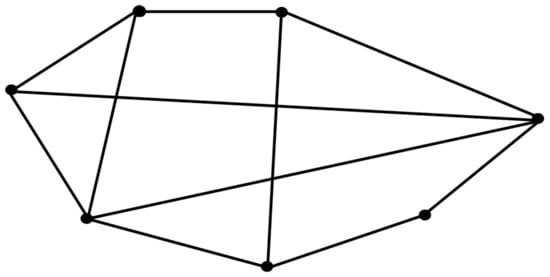
Figure 1.
A simplified example case of a network of black active links, for instance, conveying matter or energy for road networks (see Table 1 left column), where:  A black dot denotes a generic node, for instance, an airport, a neuron, or a traffic intersection in a road network, which are linked through active black links.
A black dot denotes a generic node, for instance, an airport, a neuron, or a traffic intersection in a road network, which are linked through active black links.  A thick black solid line is an active link, as in telecommunications and neural networks in the nervous system, where synapses are formed from axons to dendrites; it conveys, in this case, in terms of electrical signals (see Table 1 left column).
A thick black solid line is an active link, as in telecommunications and neural networks in the nervous system, where synapses are formed from axons to dendrites; it conveys, in this case, in terms of electrical signals (see Table 1 left column).

Table 1.
Examples of properties possessed by active links (see Figure 1).
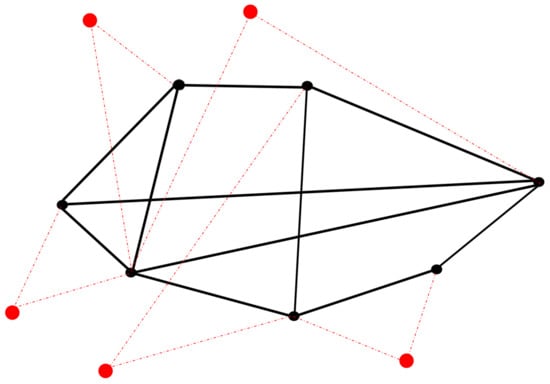
Figure 2.
A simplified example case of properties of active links (see Table 1 right column/Table 2 left column) represented by red nodes, where:  A red dot symbolizes a generic node indicator of the property of an active black link, e.g., temporary practicability or not; simultaneous two-ways availability; traffic values; being active–inactive (see Table 1 right column/Table 2 left column). This generic red node may, in turn, possibly link to another red node through the red passive linkage as in Figure 3.
A red dot symbolizes a generic node indicator of the property of an active black link, e.g., temporary practicability or not; simultaneous two-ways availability; traffic values; being active–inactive (see Table 1 right column/Table 2 left column). This generic red node may, in turn, possibly link to another red node through the red passive linkage as in Figure 3.  A fine solid red line indicates the correspondence of a generic red node with a black active link.
A fine solid red line indicates the correspondence of a generic red node with a black active link.

Table 2.
Examples of passive links as mutual intra-active links properties (see red and green links in Figure 4).
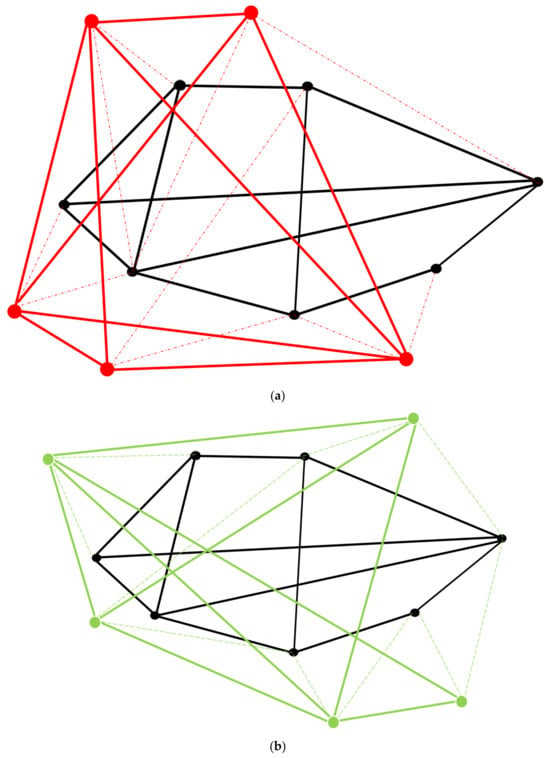
Figure 3.
(a) A simplified example case of a network of red passive links between red nodes representing properties of active links (see Table 2 right column), where:  A thick red solid line is a passive link between pairs of active links, represented by red nodes and stating, for instance, (see Table 2 right column) the occurrence of multiple temporal synchronizations and durations, admissibility or otherwise of simultaneity, compatibility–incompatibility, or temporal replicability and mutual temporal constraints between pairs of properties of black links (represented by red nodes). (b) A simplified example case of a network of green passive links between green nodes representing active links. It is one of the possible variations of the red case considered in Figure 3, (see Table 2 right column), where instead:
A thick red solid line is a passive link between pairs of active links, represented by red nodes and stating, for instance, (see Table 2 right column) the occurrence of multiple temporal synchronizations and durations, admissibility or otherwise of simultaneity, compatibility–incompatibility, or temporal replicability and mutual temporal constraints between pairs of properties of black links (represented by red nodes). (b) A simplified example case of a network of green passive links between green nodes representing active links. It is one of the possible variations of the red case considered in Figure 3, (see Table 2 right column), where instead:  A green dot signifies a generic node indicator of the property of an active black link (see Table 1 right column). This generic green node may, in turn, possibly link to another green node through the green passive linkage as in this figure.
A green dot signifies a generic node indicator of the property of an active black link (see Table 1 right column). This generic green node may, in turn, possibly link to another green node through the green passive linkage as in this figure.  A fine green solid line indicates the correspondence of a generic green node with a black active link.
A fine green solid line indicates the correspondence of a generic green node with a black active link.  A thick green solid line is a passive link between pairs of black active links, represented by green nodes and stating, for instance, instant incompatibility or synchronized occurrence between mutual active–inactive states of the pairs of black active links.
A thick green solid line is a passive link between pairs of black active links, represented by green nodes and stating, for instance, instant incompatibility or synchronized occurrence between mutual active–inactive states of the pairs of black active links.
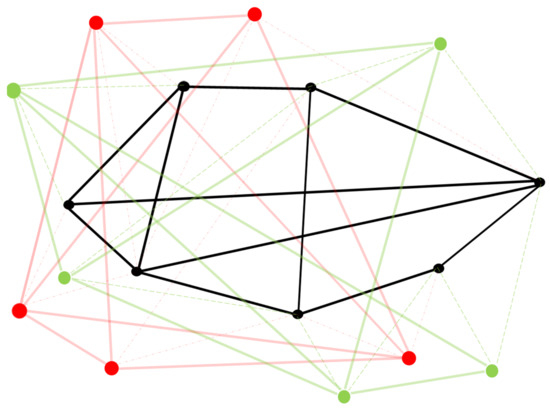
Figure 4.
A simplified example case of superimposed, transparent for reading convenience, red and green passive linkages representing a first level of the MSSN. The linkage can have an indefinite number of levels.
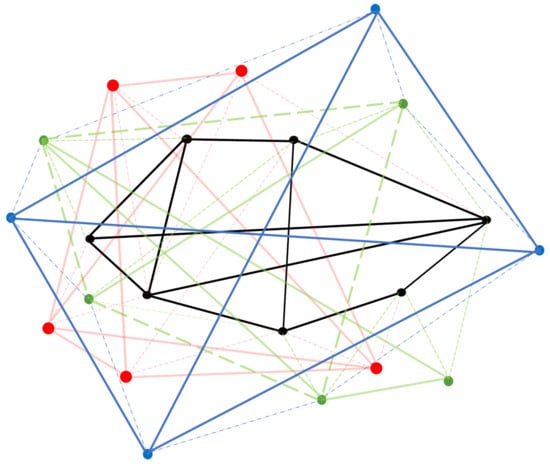
Figure 5.
A simplified example case of a network of red and green superimposed red and green passive linkages represented here with transparency effects. As stated above the red and green MSSN may be intended to represent, respectively, the linkage among properties as in Table 2 right columns. Furthermore, we consider a simplified example case of a second-level network of passive linkage in blue (see Table 3 right column), where:  A blue dot symbolizes a generic node indicator of the property of some specific passive, in this example green, links dotted in the figure to facilitate reading, see Table 2 right column/Table 3 left column. This generic blue node may, in turn, possibly link to another blue node through the blue passive linkage (see Table 3 right column).
A blue dot symbolizes a generic node indicator of the property of some specific passive, in this example green, links dotted in the figure to facilitate reading, see Table 2 right column/Table 3 left column. This generic blue node may, in turn, possibly link to another blue node through the blue passive linkage (see Table 3 right column).  A thick blue solid line is a passive link between pairs of passive links (dotted green in this example) represented by blue nodes, stating, for instance, related temporary shutdown, related parametrical variations, and the occasional validity or otherwise of contradictory states between states of passive links (dotted green in this example), see Table 3 right column. In addition, cases may arise in which nodes of one type are also part of a network of another type, e.g., a red node is linked to a green node through temporary equivalent red and green short linkage, where:
A thick blue solid line is a passive link between pairs of passive links (dotted green in this example) represented by blue nodes, stating, for instance, related temporary shutdown, related parametrical variations, and the occasional validity or otherwise of contradictory states between states of passive links (dotted green in this example), see Table 3 right column. In addition, cases may arise in which nodes of one type are also part of a network of another type, e.g., a red node is linked to a green node through temporary equivalent red and green short linkage, where:  A fine blue dotted line represents the correspondence of a generic blue node with the represented specific green passive dotted thick link.
A fine blue dotted line represents the correspondence of a generic blue node with the represented specific green passive dotted thick link.  A thick dotted green line represents a passive green link when represented by a blue node.
A thick dotted green line represents a passive green link when represented by a blue node.

Table 3.
Examples of passive links between passive links (see blue links in Figure 5).
3.2. Conceptual Examples
As introduced above, at the first level, the nodes of the MSSN are links expressing the intra-properties (see Table 2 right column/Table 3 right column) between properties (see Table 1 right column/Table 2 left column) of active links (see Table 1 left column), such as electrical and telecommunication lines and roads. Related cases consider, for instance, a network of correlations [] and a network of connections []. The focus is on the links themselves. Passive links consider, for instance, the state of activity or inactivity of pairs, as well as coupled active links.
Interdependences between active links can then be understood as represented by networks of passive links, e.g., relations. This generates a network superimposed on the active dynamic linkage.
The very first layer of the MSSN (see Table 2) consists of multiple red and green networks (one for each property of the active linkage) between links of the active linkage as in Figure 4.
At the second level, the MSSN consists of multiple bleu-networks of blue passive links (see Table 3 right column) between green-red passive links represented by blue dots (see Figure 5 and Table 3 right column). We notice how properties of the linkages may reoccur at possible subsequent levels of the MSSN.
Subsequent higher multiple, hierarchical, subsequent levels of hierarchy n are then possible. At first glance, passive links of subsequent levels should sequentially be all related to the same property repeatedly, or in different combinations even when applied to themselves, although some special cases are possible.
The MSSN may be considered as self-established, representative of a phenomenological status quo (see Section 5). Consequently, passive links can be detected as representing ways of operating the network of active links. This, however, is in a scenario of global, local homogeneous, or inhomogeneous dynamic acquisition and loss of passive links in structurally dynamic networks.
As a consequence, the MSSN is actually a collection of equivalent or non-equivalent active linkages’ phenomenological photographs (or video clips of possible structurally dynamic active linkages), which differ only in specificity in a cloud of possibilities. This cloud may be used as it is or forced to collapse into a specific MSSN, given sufficient parametric choices relating to interventions or the representation level considered.
4. Actual Examples of MSSN
We consider a couple of simple examples, having only low structural dynamics, high structural stability, and a low and stable number of nodes. As a first example, we consider road networks. It is possible to represent a road network as a weighted directed graph where the nodes are the traffic intersections, the links are the road segments, and the weights are some attributes of the road segments [,].
Road networks are subjects of different studies and approaches, for instance, with the purpose of identifying the emergency optimized road network structure in an earthquake and disastrous scenarios, i.e., finding emergency road networks (ERNs). This is an important part of local disaster prevention systems. The identification of the ERN structure is of great importance to promote disaster prevention and allow road safety in dangerous areas [,] and to identify the optimal distribution of areas and emergency services [].
We consider a road network, as in Figure 1, where the nodes are the traffic intersections. Moreover, the active links are the weighted links, i.e., roads, characterized, for instance, by their linearity or tortuosity, by climbs or slopes, by width, number of lanes, being active–inactive, and by being one-way, two-way, or alternating one-way.
Let us consider two nodes whose link has, for instance, the property to have simultaneous two-way availability.
Let us consider two different nodes whose link, for instance, has a specific carrying capacity.
Let us consider two other nodes whose link has, for instance, the property to have a specific level of fluidity.
Let us consider two different other nodes whose link, for instance, has the property of having high temporary practicability.
A dotted green passive link type of the MSSN between the first pair of active road links (simultaneous two ways availability and carrying capacity) above may establish, for instance, temporal synchronization (or compatibility, or mutual simultaneity, incompatibility, synchronization, similar temporal duration of their properties).
Another second dotted green passive link type of the MSSN between the second pairs of active road links (levels of generic fluidity and temporal practicability) above may establish, for instance, mutual compatibility.
Network properties, e.g., topological, of the first red level of the MSSN may state findings about the generic availability of the road network when considering hairpin bends, narrowings, unevenness, and windings.
The higher blue level of the passive links of the MSSN may state, for instance, the necessary temporary duration of the validity of the first type of green link (temporal synchronization) with that of the second (compatibility). Other examples include the impossible, unacceptable, or, on the contrary, the necessary simultaneity of the occurrence of pairs of such green links.
This example situation is depicted in Figure 6.
The blue link between two green links may state the inadmissibility of their contemporaneity because this would create an unacceptable lengthening of the route that the vehicles would have to travel, which would congest the network or part of it with consequent propagation effects.
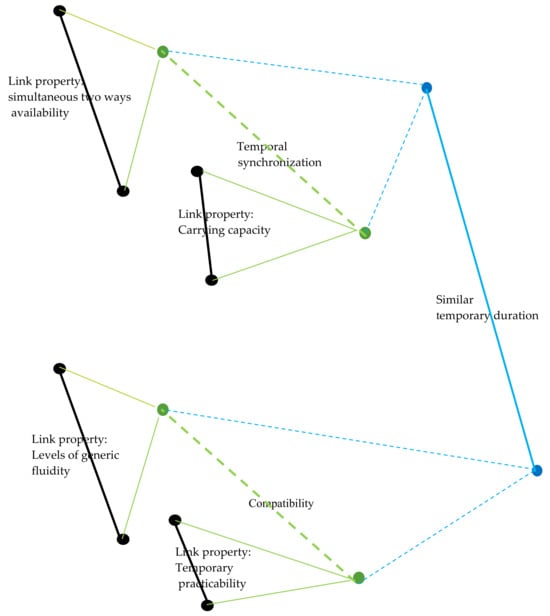
Figure 6.
Graphical representation of MSSN sections regarding the example concerning the road networks.
With regard to MSSN-driven actions, it is possible to consider the usage of the MSSN properties for the purposes of traffic diagnostics, profiling as a dangerous road network, performance verification, and regulatory as based on experiential learning (prospectively machine learning) processes. It is possible to identify standard configurations, to which we can always approximatively reduce with appropriate variational interventions, and on which to act in standardized ways whose effects have been learned. The use of the MSSN may be very effective for simulations and critical considerations, e.g., for emergency scenarios.
As a second example, we consider social networks, where social networking relates to using internet-based social media sites that allow for connection with colleagues, collaborators, customers, family members, and friends [,]. We consider a social network as in Figure 1. It is possible to represent a social network as a directed graph where the nodes are the users, the links are the internet or telephone connections. This geometrical network linkage is coupled, for instance, with its effective usage characterizing the nodes and links of the network established from time to time, with the link weights as statistical values of use and availability levels. In short, the purpose of a social network analysis (SNA) is to identify how people interact with one another within a specific communication network. The SNA is used to identify roles, such as levels of leadership, switching, and clustering within the network.
Let us consider two nodes whose link has, for instance, the property to have limited connection periods but high traffic capacity.
Let us consider two different nodes whose link, for instance, has the property of having limited traffic capacity, e.g., limited combinations of text, audio, image, and video.
Let us consider two other nodes whose link has, for instance, the property of having an irregular connection.
Let us consider two other different nodes whose link has, for instance, the property to be exposed to line disturbances.
A dotted green passive link type of the MSSN between the first pair of active links (limited connection periods but high traffic capacity and limited traffic capacity) above may establish, for instance, mutual incompatibility (or non-simultaneity, synchronization, and similar temporal durations).
Another second dotted green passive link type of the MSSN between the second pairs of active links (irregular connection and exposed to line disturbances) above may establish, for instance, mutual cases of probable simultaneity.
The higher blue level of the passive links of the MSSN between the two pairs of active links above may establish, for instance, mutual simultaneity, incompatibility, synchronization, and similar temporal duration of their properties.
This example situation is depicted in Figure 7.
More generally, the first green level of the passive links of the MSSN may state the temporal synchronization, local unavailability of the active links due, for instance, to the unavailability of communications links, local internet problems, lack of telephone coverage, software incompatibility, local malfunctions of computers or telephones, and failures of the electricity grid. It is about finding alternative optimal paths. Network properties, e.g., topological, of the first red level of the MSSN may state findings about criticalities of the network to avoid total blocks even of malicious origin.
The links of the higher blue level of the MSSN state about the same or different (clustered) instantaneous state for the MSSN links, such as being in a state of active–passive connection, involving particular (groups of) nodes and having a specific duration time. The emergence of the acquisition of properties, e.g., small-world and clustering, by the second blue level MSSN linkage on the first level linkage of the MSSN may state about types of relationships, of possible interest for crime and phishing prevention, marketing actions, police investigations, and about the most important ties that hold a network together, i.e., paradoxically, the “weak” ties as in social networks [,]. The tendency towards disintegration of these properties may indicate the emergence of situations of fragility of the network and the need for interventions or to establish new alternative support paths.
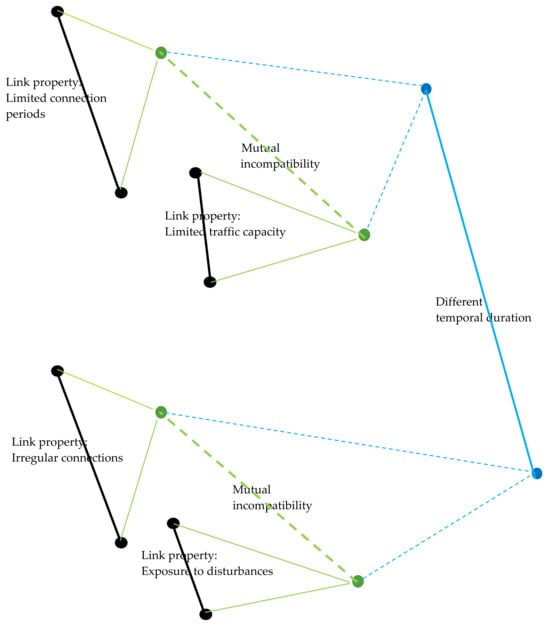
Figure 7.
Graphical representation of MSSN sections regarding the example concerning the social networks.
5. Constitutive Mechanisms of the MSSN Linkage
In the literature, emergence in networks is intended, for instance, as “… a process that results in a network topology that is not apparent by examination of the local algorithm, or microrule.” ([], p. 9) and “emergence means that a major change in global properties comes from many small changes at the local level.” ([], p. 15), such as the emergence of small worlds.
In systems science, we mention how self-organization is considered to consist of the recurrent acquisition of coherent sequences of variations of the same property. Examples of self-organization include the acquisition of properties of phenomena, such as the repetitive flying of swarms around light and whirlpools. We also mention the so-called Belousov–Zhabostinski reaction [,]. This is an oscillating chemical reaction that acquires emergent, periodic variation of striking color variations. Furthermore, we mention the formation of convective patterns of the so-called Rayleigh–Bénard cells in liquids evenly heated from below. The occurrence of convective patterns is predictable, however, only in incomplete ways, i.e., details of the patterns, such as their directions are not predictable [].
Furthermore, the usual understanding of emergence and emergent properties resides in their being acquired properties of the (emergent) system rather than of individual components; being the main property of a system, the property is to acquire properties and not only to possess properties as is usual for non-systems.
Emergence is considered to consist of the recurrent acquisition of coherent sequences of variations of structurally different properties. Examples include flocks, swarm collective behavioral properties, e.g., collective intelligence [], ecosystems, shapes acquisitions in collective behaviors, connectiveness, and robustness of social systems that are not reducible ([], pp. 8, 13) to properties of composing entities or to their linear combinations. In summary, we may consider emergence as constituted through coherent sequential communities of multiple, local, and temporary self-organization-like processes.
The problem is dealing with phenomena consisting of large quantities of irregularity, even if coherent interacting elements are present. Such phenomena are intractable with explicit analytical approaches and are, in fact, absolutely inadequate. In statistical physics, we consider systems established by a large number of entities, e.g., atoms and molecules. In this case, it is impossible to adopt analytical approaches and to study the full microscopic dynamics. An approach is to identify, for instance, atoms in a specific status (such as having a particular energy) and then consider the distribution function.
Another aspect to consider is suitable macroscopic indexes, such as temperature, to measure the global level of molecular agitation, which is describable only statistically. The temperature is just an index when it is understood as a result, the ongoing sum of the temperature of all the constituent elements. Temperature is, rather, an emergent property when it is considered established from the continuous interactions between all the constituent elements, i.e., exchanges of kinetic energy.
Among an enormity of approaches [], statistical physics-based approaches are used to model collective behaviors such as flocking, for instance, by the so-called “Vicsek Model” [,]. Such approaches relate to the multiplicity of complex systems where emergent, self-organizing, and chaotic phenomena occur, which are characterized by the fact that every model adopted is, in principle, partial and, via the incompleteness, allows for the continuous establishment of equivalences decided by fluctuations (see, for instance, previous works ([,,], pp. 98–102).
A representation of complex systems [,], in terms of complex networks [,,], is characterized by properties such as the occurrence of configurations of coherent values of parameters, such as the clustering coefficient (a measure of the network structure), degree distribution, fitness of nodes, idempotence, multiplicity and variability of the nodes and connectivity, power laws, randomness scale invariance, scale-freeness, self-similarity, and small-worlds, based on considering their components as nodes and interactions as edges.
In this regard, we only mention the so-called percolation theory, which deals with the behaviors of networked systems when some nodes or links are not available and allows for the study of issues such as network criticalities and topological transitions of networks beyond pairwise interactions. Percolation establishes the connectivity of complex networks that demonstrates, for instance, the robustness of scale-free networks under random damages [].
With this scenario in mind, we consider a possible constitutive mechanism of the MSSN linkage based on statistical properties (see Section 5.1) and its possible emergent nature (see Section 5.2). In Section 5.3, we consider aspects of the relationship between such linkage levels and possible reverse effects on the active linkage, such as considering and applying MSSN-based classifications and MSSN-driven modifying actions (see Section 6.2).
5.1. Self-Definition of the Passive Linkage
We specify, first of all, how the approach is different from considering networks with established interdependencies between links, constituting networks with fixed or adaptive constraints.
We consider the property story of active links, such as being active or inactive over time. In this regard, we consider passive links between the property story of pairs of active links and their possible properties, such as stating periodicity, regularities, randomness, interdependences, related time percentages of their occurrence, and even their possible ergodicity [], establishing the first levels of the passive linkage (see Table 2 and Figure 4).
Regarding ergodicity, we mention how physical entities of populations (the passive linkage in our case) assume ergodic relations, if they are related in such a way that when x% of the population (of links) is in a particular state at any moment in time, then each component (link) of the population spends x% of time in that state. Realistically, rather than each component (link), we consider levels of percentages that establish significant degrees of ergodicity. More generally, this introduces the possible consideration of ergodic networks intended as their evolutionary, behavioral property, in particular the quasi-ergodicity of the structural dynamics of the MSSN.
The ergodic hypothesis introduced by Ludwig Boltzmann (1844–1906) consists of assuming that, in the long run, a system of generic microscopic components, e.g., molecules (or, in general, of microscopic components), will assume all possible microstates compatible with the conservation of energy. More generally, the ergodic hypothesis states that, sooner or later, a system of microscopic components will go arbitrarily close to every conceivable microstate. In other words, the ergodic hypothesis states that, in an infinite time duration, the trajectory of the point representing the entire system in the phase space will pass through every point or as arbitrarily close to every point (as in the quasi-ergodic hypothesis) of the phase space.
In summary, the proportion of time spent by an ergodic system in a particular state is equivalent to the probability that it will be in that state at a random instant. Examples of applications of such hypothesis include:
- In geomorphology, when there is interest in using different approaches to consider and represent time, for instance, substitute space for time;
- In population studies, when reconstructing the past evolution of a population starting from actual data (the so-called inverse projection);
- In economics when, in the long run, or over a large scale, the distribution of income classes is independent of the transition probabilities ruling the evolution of the system from one state (classes of income) to another.
This evolutionary ergodic consistency is then attributable to networks ensuring the lack of acquisitions of unique, peak, unrepeatable configurations and sequences of interest to guarantee stability and homogeneity, even considering (in the long run) factors for particular long-lived networks, such as railway, submarine cable, and geo satellite communication networks.
Following what has been introduced above, the MSSN may be intended as virtual networks modeled by graphs of passive links. The softness of the MSSN lies in their statistical nature and virtuality as representative and relational. The question now is the establishment of the MSSN, which involves the specification of their possible self-definition as graphs on the active linkage between links of networks. We consider, in the following, a possible constitutional mechanism of self-definition.
The link’s constitutive mechanism can be considered as consisting of representations of phenomenological properties and practices of use, and in histories of use expressed, for example, by a couple of statistical relational values and their properties, which establish the passive links and their intensity as weight. Essentially, it is a matter of detecting and considering couplings owned by active linkage as links. Such statistically confirmed pairings are to be considered as MSSN links.
As stated above, such passive linkage represents periodicity and regularities, randomness, interdependences, related time percentages, and even the ergodicity between active links. However, it is more realistic to consider the quasi ([], pp. 151–166) versions of such properties as for quasi-systems, corresponding to the structural dynamics of complexity-, quasi-periodicity, quasicrystals [], and quasi-networks []. Considering suitable thresholds and duration time, a passive link (see Table 2 right column) is considered (quasi-)activated between two properties of the active links (see Table 1 right column/Table 2 left column) when statistically confirmed.
Consequently, the passive links have a related dynamic weight, dynamic since continuously established by their occurrence and quantified by statistical values. The activation of a passive link between a couple of properties of active links should require the occurrence of suitable duration time and thresholds of statistical values (such as frequency and modalities of their reoccurrence), allowing the quasi-case. The MSSN of passive links (see Table 2) is virtual, as given by the structural active dynamics since the passive links must be continuously confirmed by the acquired statistical values. We consider the phenomenological inevitability of such self-definition of passive links and the MSSN, as considered above when sufficient thresholds are reached and maintained for a significant time.
Furthermore, with appropriate sampling techniques [], it is possible to identify the network of dominant properties of active links, such as their prevailing temporal synchronizations and durations. Concretely, on the basis of the detection of statistical values regarding the occurrence of relational properties between couples of active links, such as those considered in Section 3.1 and Section 3.2, it is a question of carrying out the design of possible compatible MSSN operating on the basis of methodologies and approaches having suitable predefined standardizations (see Section 8).
However, the virtuality of the MSSN is also given by the validity of different approaches, such as admitting the persistence of passive links for established or context-sensitive time periods even in the face of the temporary lack of validity of the appropriate statistical values. A second and subsequent layer of the MSSN may be established by the same mechanism identifying, for instance, replicated networks of passive links on previous properties as in Table 3 right column.
The reason for making such representations lies in the fact that they are constituted by relationships between relational and phenomenological properties invisible from the network model of active links. Their usefulness, as we will see in Section 6, lies in being able to use them to profile, classify, diagnose, and decide on modifier approaches. We conclude this section by mentioning that, as stated at the end of Section 3.2, the MSSN is actually a collection of equivalent or non-equivalent active linkages’ representations of their actual dynamic phenomenology.
5.2. Emergence of the Passive Linkage
In the conceptual framework introduced above, the passive linkage constituting the MSSN is considered possibly emergent as constituted by continuously acquired interdependences represented by statistical data and properties. Since, in statistical physics, it is impractical to measure the exponential number parameters of complex systems, it is possible to choose random parameter values and study the emergent statistical properties at the system level, as for emergent statistical properties of a population of cells (see, for instance, previous research []) and emergent properties of ecosystems []. Properties of statistical values intended as passive linkage are not only virtual but may also be intended to have an emergent nature since they are continuously established by the interactive phenomenological dynamics in the population of the active linkage. This may be the reason why the properties of the MSSN cannot be reduced to properties of the active linkages. Furthermore, properties at level n of the MSSN cannot be reduced to properties at level n−1 of the MSSNn−1. However, the entire approach cannot be reduced to statistical evaluations and indexing since the (emerging) properties of the passive linkage network constituting the MSSN are considered.
The issue is to consider the acquisition of properties by the passive linkage(s) from lower linkage(s) as emergent (see Table 2 and Table 3) due to the underlying interactive phenomenological dynamics in the population of the active linkage whose proprieties interact, arrive and leave, also in varying combinations (see Table 1). If it is correct to consider this acquisition of such properties as emergent, then the various related models and properties could be applied to the MSSN. In particular, the incompleteness (see Section 7.1) of the processes of emergence is due to temporary loss and the recovery of local properties in such a way as to keep coherence, as in collective behaviors ([], pp. 87–90). Furthermore, it is possible to consider and apply approaches used for the so-called reverse emergence (see Section 6).
In our case, we refer to the emergence of the network’s profile continuously changing (see Section 6.1), but in a way that keeps its coherence. The emergence of the entire network MSSN is intended to be given not only by non-equivalent but also by having statistical regular -until there are forms of coherence- properties of the linkages.
This approach, based on considering the MSSN and their emergent properties, may be a way to profile [,,,] rather than model the process of emergence that considers network properties from the dynamics of networked constituents (see Section 6.1). We stress that by ‘profile’, we mean something different from the usual definition in telecommunications, which consists of the attributes for a connection to a basic service set (BSS) network. We now mention how it is possible to consider possibly hierarchical processes of emergence ([], pp. 255–258) of passive links from the network of active linkages (or, in any case, from multiple, multidimensional, networks of networks).
5.3. Relation between the Linkage Levels
We mention how temporary intra-levels are possible within the MSSN when nodes of one type are also part of a network of another type, e.g., a red node in Table 2 is linked to a green node through temporary equivalent red and short green linkage. This point is related to the concept of multiple systems, a set of systems whose components simultaneously belong to more coherent, i.e., correlated, systems ([], pp. 3–15). In the same way, we consider multiple networks where the same nodes belong to different simultaneous networks [].
The research subject we consider here is the intra-relations between the active linkage and the first MSSN level, as well as the subsequent levels of passive (possibly multiple linkages) of the MSSN. Due to the multiplicity of the first MSSN, deterministic correspondences with the active linkage are very improbable. Similar considerations relate to the relation between subsequent hierarchical levels and the initial passive linkage. The more hierarchical levels the MSSN has, the less likely it is that deterministic correspondences can be hypothesized. Different versions of MSSN are likely to be non-equivalent or even have aspects of partial equivalence.
Furthermore, the dynamic statistical nature of the passive linkage makes the identification of properties with stability non-trivial. However, once and if detected, they may characterize and classify the active linkage and profile in a specific period or recurring period. Visually, we can imagine the active linkage as superimposed by dynamically constituted successive levels of passive linkages, establishing a dynamic cloud of versions of MSSN.
Examples of possible relations are the occurrence of the same network properties, such as geometrical and topological, or their reoccurring possibly in dynamic combinations. Due to the statistical and possibly emergent nature of the passive linkages, their networks are given by links that arrive and leave with consequent processes of acquisition and disappearance of network geometrical properties, considering, for instance, the connectedness (given, for instance, by the mean of the degree distribution), density (ratio between the actual number of edges and the maximum possible number of edges in the network), scaling (for instance, scale-freeness, when the network has a high number of nodes with few links or a small number of nodes (hubs) with a high number of links). In scale-free networks, the probability that a node selected at random possesses a particular number of links follows a power law Y = kXα, where α is the power law exponent, and k is a constant.
Furthermore, another class of possible relations includes the occurrence and reoccurring of the same profiles or regular relationships between them. Examples of MSSN’s non-geometrical possible properties include the occurrence of properties of passive linkage paths, such as their length and composition, sequential variations with regularity, their quasi-stability, and quasi-repetition with negligible variations. Research and simulations should identify approaches suitable to detect correspondences not only between properties of the active linkage and the MSSN but also about levels of coherence, their possible multiplicity, reoccurrences, and quasi-regularities considerable, for instance, as signals and symptoms of processes in progress.
It is possible to consider approaches for the comparison [] between networks with the purpose of classifying the subsequent levels of the MSSN. Such a research issue relates to possible analytical representations of temporary, local, or global interlevel relationships. The situation conceptually recalls deep learning in machine learning models, which have the characteristic of being composed of different processing layers, each of which extracts a representation of the previous layer [,].
6. Usages of the MSSN Properties and Profiles
The concepts considered here are inspired by the role of acquired emergent properties reversely on the system from which they emerge in a process known as reverse emergence ([], pp. 258–272; [,]).
Examples of effects on active linkages of emergent acquired properties include the induction of individual behaviors in collective behaviors modeled as networks [,] such as flocking, effecting individual flying; behaviors induced by acquired cognitive properties, such as learning replacing linear stimulus–reaction processes as in collective intelligence; life establishing self-sustaining and autonomous processes, able to maintain a property such as to perform autopoietic reproduction; and cognitive properties deciding the usages of biological resources from which they emerge.
The research approaches considered below, i.e., profiling (see Section 6.1), self-regulatory mechanisms (see Section 6.2), and the passive linkage as weak forces (see Section 7), fall into the field of the contributions devoted to managing and controlling [] complex networks as complex systems [], when multiple levels of representation are required as well as the expansion of models from statistical physics integrating the notion of feedback, extension of control theory approaches [], and mesoscopic analysis and mesoscopic variables.
In this regard, we mention how the mesoscopic description level of complex processes may be intended as areas of continuous negotiations between micro and macro ([], pp. 110–113). This is approachable by statistical physics since it is impossible in principle, due to the intractability of the problem, to consider all the dynamic inter-relations between interacting elements, temporary systems, and the environment. As mentioned below, profiling rather than modeling also requires the integration of machine learning and data-driven approaches.
In a time when invisible passive links are established-detected, it is then possible to consider their possible reverse influence on the active network from which they emerge, when the active linkage is autonomous and adaptive (see Section 6.2). However, the self-acquired properties of the MSSN have no direct behavioral influence on the active linkage. Such properties (statistical and their network properties), together with their constitutive dynamic acquisition and loss of links (including emergence), correspondences, and regularities, are considerable for driving non-linear decisions based, e.g., on analogies, optimization, procedures, and protocols, actions on the active linkage network (see Section 6.2).
6.1. MSSN Properties and Profiles
We may consider the use of the MSSN properties, summarized in particular by their profiles, for the purposes of network performance evaluation, detection of critical configurational issues during the establishment phase, allowing prevention of unwanted properties and network disintegration, experience-based (machine-learned) diagnostics, and regulatory, MSSN-driven actions (see Section 6.2) on the active linkage as based on experiential learning (prospectively machine learning) processes.
Regarding profiling, we mention that while ideal modeling has the purpose of supporting understanding, profiling is intended as non-ideal, data-driven modeling, with their phenomenological, in case emergent, ongoing properties, such as the occurrence of coherences and correlations. A related differentiation is given by the difference between understanding and forecasting.
Ideal modeling supports understanding since it is aimed at conjecture, explanation, hypothesizing, replicating, simulating, and realizing fundamental properties of the phenomenon under study. For instance, the occurrence of attractors, bifurcation points, chaotic properties, network properties, non-equivalences, power laws, scale invariance and self-similarity, and symmetry breaking.
On the other hand, non-ideal modeling as profiling is data-driven, intended to represent ongoing properties that allow generic forecasting, comparison, and classifications based on the importance of the past, analogies, repetitiveness, coherences, and correlations, the identification of standardized configurations, and consider contextual conditions (see Table 4).

Table 4.
Examples of ideal and non-ideal modeling.
How data profiling [] relates to collecting data about data, i.e., metadata, see the last case of non-ideal modeling in Table 4 for information on big data, network profiling relates to collecting data, identifying their properties, and relates to ongoing usages and phenomenology of networks, in our case data related to the structurally dynamic networks of passive links establishing the MSSN. Therefore, MSSN profiling arises when considering the properties of specific passive linkages of the MSSN.
In the following, we will continue to use the term “profile” in the singular. However, it would be more accurate to use the term “profiles” in the plural as different profiles (equivalent, partially equivalent, or non-equivalent) are possible, differentiated depending on their use and purpose. With the use of the term “profile” in the singular, we will refer to the specific profile decided by the research needs, keeping in mind, however, that it is a choice for the levels of description. Furthermore, the term in the singular can be understood as referring to a generic profiling, suitable for considerations that are themselves generic (to be specified, if necessary).
The usage of MSSN properties for the purposes of network evaluations has two aspects:
- Use of formalized, e.g., geometrical, evaluations establishing correspondences and measurements between active linkage and MSSN properties;
- Use of experiential, i.e., related big data and machine-learned correspondences between active linkage and MSSN properties.
With reference to the first point, as is well-known, a network with N-labeled nodes is defined by the repertoire of N(N − 1)/2 possible links. It is possible to compute, as a first example of an MSSN profile, the level of the actual networking, e.g., in terms of percentages of the passive linkages per instant.
With reference to the second point, the subject of this article, in the following, we introduce simple examples of data on which to detect and calculate profile versions, i.e., network profiling. Profiles may be considered given by properties, e.g., distribution—linear, parabolic, and random—of points representing the values possessed over time by suitable vectors defined later, such as Vx(ti), Vy(ti), matrixes Mk(t), and properties of their temporal sequences, such as their interpolations and clustering.
We now mention how interpolation is a statistical method that uses known values to approximate and estimate related unknown values or a set of values []. Several approaches to community detection characterized by a specific property are available. Among them are techniques such as the so-called self-organizing map (SOM) and top-down and bottom-up clustering. SOM is a machine learning technique used to produce a low-dimensional, usually two-dimensional, representation of a higher-dimensional dataset while preserving the topological structure, e.g., structured (leaf) zones, agglomerations, and shapes of the data [,,].
Clustering deals with finding a structure in a collection of unlabeled data. A rough definition is a technique for organizing entities, e.g., numerical values, objects, patterns, and signals, into groups of members similar in some way. Several approaches and clustering techniques, often interpolation-based [], are available, such as algorithms so-called k-means, k-median, and k-medoids [,], multivariate data analysis (MDA) such as in previous research [], and cluster analysis [] to identify classes [].
As a first example of profiling data, we may consider some or all of the passive links in Table 2 and the number of occurrences in the instant under consideration, as in the vector Vx(ti) = [x1(t), …, x8(t)] in Table 5.

Table 5.
Example of the Vx(ti) in a nine-dimensional space.
The punctual properties of the trajectories are, e.g., continuity, topological (for example, knotting in knot theory)—the study of mathematical knots []—of the vector Vx(ti) in its eight-dimensional space, and intra-properties of the xn values (for example, ratios that represent a case of profiling of the first level of the MSSN).
For instance, the vector Vx(ti) = [0, 0, 0, 0, 7, 0, 0, 3, 0] represents the fact that the following are active at time tk:
- Seven passive links have “similar throughput”;
- Three passive links are “temporal synchronization between two linked active links”.
More appropriate evaluations may consider properties of the evolutionary trend over time of each or group of variables xn. Furthermore, it involves comparing the trend of the graphs representing the evolution of the xn variables over time, detecting, for example, correspondences and recurrences.
As a second example, we may consider that a subsequent level of profiling is obtained by considering some or all the passive links between passive links (as in Table 3 right column) and, also in this case, the number of occurrences in the instant under consideration, as in the vector Vy(ti) = [y1(t), …, y7(t)] in Table 6.

Table 6.
Example of Vy(ti) in a seven-dimensional space.
For instance, the vector Vy(ti) = [0, 4, 1, 0, 5] represents the fact that the following are active at time th:
- Four passive links “temporal duration properties between two linked passive links”;
- One passive link “temporal synchronization between two linked active links”;
- Five passive links “compatibility-incompatibility of the state on for the linked two passive links”.
In this second case, it is possible to apply also the approaches mentioned in the first example.
A third example of a network profile is given by considering time-dependent matrixes, which are generalizable and adaptable to specific research interests. For instance, in this case, an 8 × 3 matrix Mk(t) where (see Table 7) the lines represent the network passive links are considered and are active at time t (in this case, eight). The column parameters of interest are as follows (three in this example): (1) the number of passive links in a state among the eight considered occurring at time t; (2) the number of non-adjacent passive links among the eight considered occurring at time t; (3) the number of intermediate links among the eight considered, for instance, for routing problems [] occurring at time t, where:

Table 7.
Example of Mk (t).
The profiling considers the occurrence of temporal sequences of the matrix Mk(t) and their properties, such as interpolations, clustering, and their quasi-correspondences and recurrences. For instance, consider the matrix Mk at time th as follows:
This matrix state signifies that:
- Seven passive links “same-opposite practicability and directions of the connected active links” between active links occur at time th;
- Three passive links “same-opposite practicability and directions of the connected active links” out of seven active links are non-adjacent at time th;
- Six passive links with “similar throughput” occur at time th;
- Six passive links with “similar throughput” are separated by four intermediate links at time th;
- Three passive links “temporal synchronization between two linked active links” occur at time th;
- Two passive links with “temporal synchronization between two linked active links” are not adjacent at the time th;
- Three existing passive links “temporal synchronization between two linked active links” have one intermediate link at time th;
- Two passive links between active links “temporal duration properties between the two linked active links” occur at time th.
The profiling may consider values computed on temporal sequences of the Mk(t) detecting, for instance, regularities as stable reoccurrences and the occurrence of possible different versions considering groupages of interest, generic statistical, and ergodic-like properties.
In conclusion, beyond the occurrence of network geometric properties, network profiling should consider their specific temporal, relational, and behavioral properties, as well as the characteristics of the trajectories in the vectorial matrix space. The profile can highlight high synchronization or areas of high incompatibility as well as the opposite case. Moreover, the profile can highlight the state of activity or inactivity of the network and its occurrence in a localized or scattered manner. The profile can emphasize the occurrence of behavioral properties over time. The evolution of profiles (profiles of profiles) over time represents the dynamic phenomenology of a structurally static network having variable, multiple MSSN.
We may consider the use of the MSSN profiles as property for the purposes of network behavioral forecasting, comparison, and classification based on formalizations or experiential machine learning. We can mention how this network profiling differentiates from the usual profiling of digital communication and social networking, which deal with personal social network profiles [] and technologically considers a set of parameters that define network conditions.
Another purpose of the use of MSSN profiles is the identification of standard configurations (also specific to the type of application, e.g., telecommunication, airlines, and road networks) to be replicated or avoided as criticalities. It is also possible to identify classes of equivalent configurations on which to act in standardized ways, whose effects have been (machine) learned. This relates to approaches used to monitor and classify the collective behavior of cattle in order to evaluate the health and any problems or illnesses of the cows in the herd [,].
We can summarize by saying that MSSN properties are of interest for MSSN-driven actions, evaluations, and measurements, while MSSN profiles, as non-ideal models, are of interest for forecasting, comparison, and classification purposes and for self-regulatory processes for cases when the active linkage is autonomous and adaptive (see Section 6.2). Their joint use allows them to establish, for example, confirmatory redundancies, determine compatibility–incompatibility situations and configurations, and evolutionary tendencies to facilitate or avoid.
6.2. Self-Regulatory Mechanisms
The interest in possible self-regulatory mechanisms is based on suitable network models and simulations allowing for soft interventions on the active linkage having structural, diffused effects on the active linkage, such as solving or preventing the occurrence of inconsistencies, inefficiencies, deadlocks, unavailability, and unreliability. This may concretely occur when the active linkage consists, for instance, of autonomous networks such as adaptive networks.
Adaptive networks are a broad class of networks that can change over time their structural connectivity depending on their dynamical state. The fundamental property is that their function depends on their structure and vice versa. Adaptive networks may be defined as feedback loops between the local dynamics of the individual units and the dynamic changes in the network structure. Furthermore, adaptive networks fall into the category termed “autonomous networking”, a research field that has the purpose of transforming static networking into dynamic, programmable environment driven, for instance, by adaptation, analytics, and machine learning [,]. Examples are research and models related to neuronal synaptic plasticity, biological, chemical, epidemic, and technological systems, as in artificial intelligence, transport, and social systems, as presented in previous research [,,].
The relationship between the active linkage and its cloud of MSSN, in the case of machine learning, is a many-to-many relationship since an active linkage may correspond to different, multiple MSSNs, and a specific MSSN may represent different active linkage or, better yet, it cannot be denied in principle (for example, with a theorem). However, in the case of adaptive networks, it is possible to break the passive, only representative many-to-many relationship and consider suitably modified versions of the MSSN as regulatory prescriptive and adaptive factors for the active linkage.
In our case, we consider the adaptation process of an autonomous network as given by hypothetical feedback loops between the network of active adaptive linkage and its self-established (in the case emergent) properly modified and prescriptive MSSN passive linkage establishing an interactive structural dynamic between networks levels of active and passive linkages. In this case, the dynamic adaptation is activated by external MSSN-driven interventions on the MSSN, e.g., varying the linkage weights and the linkage itself by artificially suppressing or activating links.
The adaptation mechanism of autonomous networks is finalized to keep the coherence between the modified MSSN and the active linkage, re-establishing a correspondence of emergence. Furthermore, we stress how such perspective mechanisms of feedback loops are of great importance for simulations and network design.
7. Passive Linkage of Multiple Superimposed Soft Networks as Weak Forces
Forces may be characterized as “weak” when they have, for instance:
- Low value, for instance, less than the minimum of all forces involved at the moment;
- Local ranges of influence involve very few (in reference to the totality of elements considered) spatially adjacent composing elements.
Consequently, weak ([], pp. 11–12) forces have a range of influence and values insufficient to force changes in the properties of the elements or of the entire system, and in the properties of the ongoing interactions.
In the case of collective behaviors, the effectiveness of weakness relates to the breaking of agents’ instantaneous equivalent conditions, equilibria; roles of the high frequency, irregular, and unpredictable, weak actions replacing impossible and unsuitable strong, single actions. This has the advantage of flexibility, allowing for adaptation and implementation of collective properties such as a defensive collective strategy. This occurs in the case of flocks, swarms, e.g., invasions of locusts and wild herds, or ingestion of low but persistent dosages of drugs.
Furthermore, weak interactions may be considered at first as incomplete, tentative initial conditions of a self-establishing, quasi-convergent process, such as spontaneous synchronizations, e.g., applauses, fireflies, objects on vibrating surfaces, until a specific synchronization becomes predominant and quasi-identically iterated. We mention how weak forces also concern cases such as sub-symbolic processing, using tools such as artificial neural networks and cellular automata, where, respectively, networked small computations lead to an end (non-summative) result such as behavior, and regular grid of computed cells lead to emergent patterns in cellular automata.
In these cases, symbolic computation causes emergent properties to be acquired []. This point may allow for considerations on various types of emergencies, such as for a kind of artificial unconscious [], of interest since an (artificial) intelligence seems very limited without being exposed to decay, deficiencies, illnesses, and unconscious effects. Realistic, intelligent artificial devices should intrinsically and theoretically have the capacity to make mistakes, not always just be rational and right []. This point is important when requiring artificial creative reactions and behaviors, e.g., proposing strategies, commenting on scenarios, finding inconsistencies and contradictions reductionistically simulated by randomness, suitably varying probability of reactions, and admissible variations in what has been learned. Instead, the machine-like attitude of artificial intelligence is preferable for repetitive applications based on reliability and repetitiveness, albeit contextual, e.g., driverless driving and chatbots that professionally answer questions.
Properties of the MSSN and its profiles may be considered to have a role as weak forces: the higher the level in the passive linkage, the weaker the changes induced when consequently acting on the active linkage, but, counterintuitively, the higher their effectiveness when not replaceable by unsuitable, inadequate, incompatible strong forces as in ecosystems and social networks [].
7.1. Weakness and Theoretical Incompleteness
Furthermore, the concept of weakness may be considered compatible if not included in the one of “theoretical incompleteness”, considered necessary for the establishment of processes of emergence and quasi-systems ([], pp. 151–166):
- The emergence—in short, the acquisition of multiple, dynamic coherences as new properties irreducible to the previous ones—of complex systems requires theoretical incompleteness, i.e., theoretically incompletable distinguished from completable incompleteness. Classic cases of theoretical incompleteness are Heisenberg’s Uncertainty Principle, by which accuracy in measuring one variable is at the expense of another; the complementarity in theoretical physics, e.g., between wave and particle natures; and the incompleteness in Gödel’s theorems. Here, the theoretical incompleteness relates to the partial acquisitions, losses, and recovery of properties in processes of emergence in a dynamic of equivalences, for instance, of collective behaviors in which the different, but essentially microscopically equivalent, states that an agent can subsequently acquire have minimal differences. However, states that have minimal differences trigger crucial incomplete, irregular sequences of subsequent effects that then materialize in specific behaviors. Completeness can be thought of as the ‘worst enemy’ of emergence because it produces ruled contexts excluding equivalences, interchangeabilities, the role of weak forces -such as fluctuations- that decide equilibrium breakdowns and initiate linked sequences, and multiple roles on which the processes of self-organization, emergence, and their unicity are based. These are weakly regulated contexts and are, therefore, full of possibilities. Emergence is based on exploratory properties.
- Quasi-systems are not always systems, not only systems, and not always the same systems: their systemic nature, i.e., the ability to acquire properties, is present in a weaker mode, reoccurring but only variably predominant.
We conclude this section by considering the correspondence between:
- Systems science, complex systems science extended with the concepts of incompleteness and quasi-systems
- Network science is extended by combining networks and their clouded MSSN.
This helps to specify, in turn, the correspondence between systems science and network science.
7.2. Perspective Applications
We may consider MSSN-driven actions on the active linkage suitable to induce, for instance, local or global variations in increasing–reducing:
- Compatibilities;
- Incompatibilities;
- Simultaneities;
- Synchronizations;
- Temporal constraints.
with the purpose of keeping, for instance, forms of general or local, static, or dynamic homogeneity in the active network or their avoidance.
MSSN-driven actions may be considered as indirect, soft, weak actions on complex systems represented as networks, whereas direct, strong actions that are expected to have linear effects are, in reality, unfit. Such actions seem to be compatible, if not suitable, to induce or deactivate processes of emergence, act on processes of emergence with the purpose of regulating acquired properties, and allow phenomena of merging between different emergencies. Examples of perspective applications include actions on economic, infrastructural, logistic, and sociological properties of social systems, such as when considering workplace safety, which cannot be reduced to theoretically incomplete procedures, being actually emergent [].
Other examples of perspective applications include actions on biological and neurologic systems, as well as medicine, where actions relate to dosages of medicines of appropriate chemical strength. The suitability of the weakness of forces to act on complex systems is related to the fact that such forces are not non-binding, impositional, or invasive but have the nature of suggestions and, in the case of environmental options, aimed at activating appropriate processing by the complex system which then decides between equivalences (building its specific healing attempt). These are not repairs or replacements, but rather appropriate, non-invasive activation of processes to be preferred to invasiveness according to the circumstances.
We highlight how acting with strong forces is based on the conceptual assumption of knowing what is right to impose on the system, while in the case of weak forces, there is ethical respect for the system, for the so-called intelligence of matter ([], pp. 150–151), while respecting its autonomy. This applies to nature in general, even if the invasive approach is unfortunately dominant and generates non-strategic interventions and short-range actions.
However, the two approaches are not mutually exclusive: they should be applied depending on the opportunity, possibly even together. In conclusion, we notice how the more generic network reverses emergence and network properties transposition is possible by adaptivity interfaces and learning of autonomous networking.
8. Research Issues on MSSN and Trans-Disciplinarity
As mentioned above, the overall approach is based on the design of passive linkages, which have statistical origins in the effective phenomenological network composed of active links. It is necessary, first of all, to implement technological methodologies and tools to design (improved self-design) equivalent or non-equivalent MSSN on the active linkage under consideration.
Subsequently, it is a question of identifying the establishment and its modalities, e.g., correlated, ergodic, random, recurrent, and regular properties of the passive linkages. It is then a matter of identifying, for instance, through experiential, machine learning, statistically significant correspondences with properties and their dynamics of the active linkage. A research issue relates the possible replacement of experiential learning with machine learning approaches suitable to introduce perspective self-regulatory processes. Correspondences and profiles should be the subjects of research to identify their possible reverse usages on the active linkage such as for diagnosis, comparative, classification, performance evaluation, detection of criticalities, and regulatory purposes.
Another research issue relates to the possible identification of standard corresponding configurations of passive and active linkage. The possible interest is, for instance, in avoiding their establishment as corresponding to the creation of criticalities or, conversely, in facilitating their establishment and keeping, in their replication in different contexts (or partially and in combinations), and in identifying related standardized usages extended to classes of configurations having significant levels of equivalence, useful in case urgent interventions are required.
Having said this, specific research topics related to MSSN can be, for example, given below:
- (1)
- Implementation of methodologies and approaches to carry out software-based self-designed possible, equivalent, or non-equivalent MSSN on an active linkage under consideration, such as network design software and tools available on the market [].
- (2)
- Identify generic and possible formal properties of the MSSN layers.
- (3)
- Equivalence conditions between different levels or groups of levels of the MSSN.
- (4)
- Tools and approaches to detect properties of MSSN to be used as profiles.
- (5)
- Tools to identify emergence mechanisms from the network of active linkages (see Section 5.2).
- (6)
- Possible combinations, applications of the passive linkages to other networks of active linkages, introducing possible standardizations. Ability to store, generate, and transmit different MSSN.
- (7)
- Elaborate on profiling techniques, MSSN properties, their usages, and interdependence.
- (8)
- Research on cases of possible self-regulation through machine learning-based approaches on adaptive networks.
- (9)
- Given the soft nature of interdependences represented by the MSSN, they can be related to the weak forces considered in the literature (see Section 7). The properties of the MSSN and its profile may be considered to have a role as weak forces. Furthermore, the approach is conceptually considerable for processes without certain or certainly identifiable beginning events, such as for some economic transformations and illnesses. Moreover, the latter is the case for the generic inflammatory processes in biology at the beginning of (and not definitively causing) several pathologies and neurodegenerative diseases such as multiple sclerosis. In these cases, their profile can reveal pathological processes in the constitution (through compatibility considerations) or in progress.
- (10)
- In physics, fields are intended to prescribe a well-defined value to any entities at a point, such as electric and electromagnetic fields.Domains are intended as spatial regions of possible options available to entering entities, such as the permissible and compatible behaviors and states of an entity expected to respect the relevant constraints and degrees of freedom of the domain. This is the case of systemic domains, e.g., spaces within which collective behaviors occur, inducing (if not forcing) entering entities to behave systemically ([], pp. 170–175). The entering entities may face occasional scenarios of equivalent options in multiple superimposed domains that are then decided, for instance, by fluctuations. Domains may be considered non-continuous since zones with multiple options are possible.A network domain, identified by a domain name, is usually intended as the administrative grouping of multiple private computer networks or local hosts inside the same infrastructure. Here, in consideration of the virtuality of the MSSN, we generalize by considering networked domains where, taking it to the extreme, each point is the vertex of at least one network. More realistically, it will be a matter of considering the area of space at an appropriate level of granularity of vertexes constituting networked domains. In the case of multiple domains, these are multiple networks. We believe that networked domains constitute an interesting generic interdisciplinary field of study focused, for example, on the study of implicit and potential space of network properties possibly activated and collapsed by appropriate events.
Trans-Disciplinarity of the MSSN
We conclude this section by mentioning the interdisciplinary and transdisciplinary aspects of this research project. Interdisciplinarity arises when approaches, models, problems, solutions, and network models, such as the MSSN, of one discipline are applied to another.
This is the case of interdisciplinary properties, such as systemic properties, examples of which include allostasis (ability to maintain stability through continuous adaptive structural changes), anticipation (according to Rosen, a system is anticipatory when containing a predictive model of itself) [,], autopoiesis (ability to regenerate recursively), coherence (as the dynamic establishment and maintenance of a property), development (often reduced to generic growth, when in reality it is about coherent growths and, in this case, partial and temporary degrowth of interrelated systems), dissipation (when systems keep their coherence through a constant flux of matter from outside, e.g., vortex in a flux of running water, in atmospheric phenomena such as hurricanes and living systems), emergence (recurrent acquisition of coherent sequences of variations of different properties, e.g., flocks, ecosystems shapes acquisitions in collective behaviors as car traffic), homeostasis (ability to maintain characteristics in the face of changing environmental conditions through self-regulation mechanisms), properties of chaotic systems [] (for example, the double pendulum, such as the property to be very sensitivity to initial conditions, e.g., smoke diffusion and weather), (remote) synchronization [,], resilience (ability to adapt and self-repair in the face of disruptive events), and self-organization (recurrent acquisition of coherent sequences of variations of the same property, e.g., the Belousov–Zhabotinski reaction, the Rayleigh–Bénard cells, and swarm around a light and whirlpools).
We have a case of trans-disciplinarity, see, for instance [,], when dealing with problems and approaches aimed at the representation and management of knowledge. A specific case relates to approaches for knowledge representation and processing, such as in artificial intelligence (see, for instance, previous work []. A case is given by cognitive science when science studies itself. Trans-disciplinarity relates to knowledge about knowledge, for instance, meta-knowledge [], since meta-data relates to data about data.
More generally, trans-disciplinarity can be understood as the study of systemic properties per se and of intra-systemic properties having multiple, incomplete, fuzzy disciplinary applications. It is a matter of the trans-disciplinarity of properties of systemic properties, i.e., systemic properties without disciplinary contextualization. It is a matter to consider for relationships between systemic properties.
Examples of such trans-disciplinary properties include the modalities of occurring of systemic properties, e.g., with interdependence, regular or random reoccurrences, in temporal correspondences and durations, in correspondence, synchronized, in groupages, and according to compatibility and incompatibility. Trans-disciplinary research relates to properties of correspondence and analogies between approaches, models, and representations.
Trans-disciplinarity allows for the identification of scenarios emerging from collections of systemic properties, which are suitable for deciding tentative approaches and establishing similarities of contexts on which to learn repeatable approaches. Furthermore, in turn, a transdisciplinary attitude consists of comparing and considering different scenarios of systemic properties in which to identify, for example, analogies and correspondences. This is a particularly suitable approach for interacting with complex systems such as medicine, ecosystems, and social systems. It is a matter of scenarios constituted of symptoms scenarios and profiles.
We can consider such trans-disciplinarity representability through MSSN networks. For instance, we may account for disciplinary cases such as situations occurring in biology, chemistry, economics, electronics, engineering, informatics, medicine, physics, and psychology. Considering such disciplinary cases as nodes, the links between pairs of them may state that the approaches, models, problems, and solutions used in one disciplinary case also apply to the other one. That is an interdisciplinary linkage.
The further over-linkage of passive links among inter-disciplinary links may be considered to have a trans-disciplinary nature. Its links may state, for instance, that a couple of interdisciplinary links are, in turn, related, passively linked, stating, for instance, that when an interdisciplinary correspondence occurs between two disciplinary cases, then another occurs for another couple of disciplinary cases.
An example case is given by considering the following:
- Interdisciplinary “development” link between social systems and biological systems, for which development processes are described by similar models;
- Interdisciplinary link “resilience” between ecosystems, for which there is the ability to re-establish balance or coherence in the face of disturbances and materials, for which there is the ability to resist impacts and breakages by absorbing energy through their own deformation to then reorganize and return to the original shape as, for example, for rubber bands. The resilience processes are described by similar models.
A transdisciplinary link between these two links could represent not only compatibility but also the high probability of their occurrence in the same contexts. Such trans-disciplinarity can be considered adequate, for example, for linguistic contexts (text comprehension), image understanding, scenarios (economic, military, and social) understanding, and design.
The possible trans-disciplinarity lies in the fact that properties of the MSSN and network profiles may be considered for knowledge representations such as analogy, concordance, correlation, correspondence, image, and reasoning relationships. Finally, we mention how the MSSN may be considered for the controversial so-called theory-less knowledge when theory is considered replaced by suitable analogy, concordance, correlation, and correspondence [,], such as in the case of big data using data-driven approaches within very large databases [,].
9. Conclusions
This article proposes a new tentative field of research for the study, use, and management of networks that consider MSSN, their properties, and profiles as part of contributions aimed at overcoming the geometric and technological phase of network science, allowing for new generalizations. While the article considers and introduces topics in a general and abstract nature, the research could preferably focus on a few specific cases by designing appropriate specific versions of the MSSN, considering specific types of networks, and developing databases with their parametric values. To begin, cases of active linkage with low structural dynamics and stable network properties could probably be more easily tackled.
Such a database will be necessary to validate the outlined approach, possibly also specifying it for specific uses. Furthermore, computer-based methodologies and approaches should be developed to design the MSSN, starting from couplings owning to active linkage validated by the suitable occurrence of related statistical data.
We have listed various research subjects. However, these topics should be developed both disciplinarily, with reference to specific application areas, and interdisciplinary to identify methodologies and approaches of general use. Among the research topics, one is mentioned relating to networked domains that focused, for example, on the study of implicit and potential space of network properties.
This research project involved methodological and generalizing aspects of transdisciplinary value. It can be considered hypothetically for collections of networked systemic properties and approaches actually in use and having specific application histories.
Finally, we mention how the study of the MSSN, their properties, and their relationships with the network of active linkage may introduce new research approaches, also indicating currently undefined limits of network science.
In order to facilitate the conceptual understanding of the topics covered, we introduce a general summarizing conceptual scheme of the article in Figure 8.
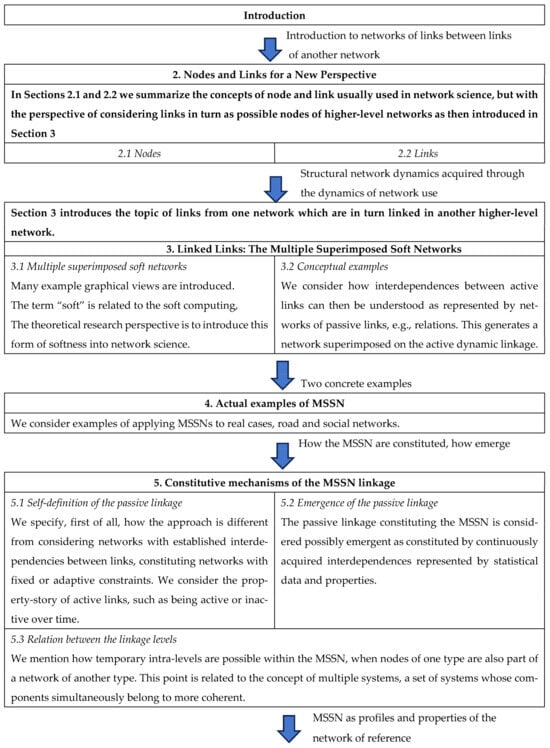
Figure 8.
The conceptual journey of the article.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Barabasi, A.L. Linked: The New Science of Networks; Perseus Publishing: Cambridge, MA, USA, 2002. [Google Scholar]
- Barabasi, A.-L. Network Science; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Barabasi, A.-L.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef] [PubMed]
- Newman, M.; Barabasi, A.-L.; Watts, D.J. (Eds.) The Structure and Dynamics of Networks; Princeton University Press: Princeton, NJ, USA, 2006. [Google Scholar]
- Valente, T.W. Network interventions. Science 2012, 337, 49–53. [Google Scholar] [CrossRef] [PubMed]
- Lewis, T.G. Network Science: Theory and Applications; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Boguñá, M.; Bonamassa, I.; De Domenico, M.; Havlin, S.; Krioukov, D.; Serrano, M.A. Network geometry. Nat. Rev. Phys. 2021, 3, 114–135. [Google Scholar] [CrossRef]
- Jing, F.; Liu, C.; Wu, J.L.; Zhang, Z.K. Toward Structural Controllability and Predictability in Directed Networks. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 7692–7701. [Google Scholar] [CrossRef]
- D’Agostino, G.; Scala, A. (Eds.) Networks of Networks: The Last Frontier of Complexity; Springer: New York, NY, USA, 2014. [Google Scholar]
- Kenett, D.Y.; Perc, M.; Boccaletti, S. Networks of networks—An introduction. Chaos Solitons Fractals 2015, 80, 1–6. [Google Scholar] [CrossRef]
- Minati, G.; Penna, M.P. (Eds.) Multiple Systems: Complexity and Coherence in Ecosystems, Collective Behavior, and Social Systems; Springer: New York, NY, USA, 2024. [Google Scholar]
- Magnani, M.; Rossi, L. Formation of Multiple Networks. In Social Computing, Behavioral-Cultural Modeling and Prediction, Proceedings of the 6th International Conference, SBP 2013, Washington, DC, USA, 2–5 April 2013; Lecture Notes in Computer Science; Greenberg, A.M., Kennedy, W.G., Bos, N.D., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 257–264. [Google Scholar] [CrossRef]
- Lee, K.M.; Kim, J.Y.; Lee, S.; Goh, K.I. Multiplex Networks. In Networks of Networks: The Last Frontier of Complexity. Understanding Complex Systems; D’Agostino, G., Scala, A., Eds.; Springer: Cham, Switzerland, 2014; pp. 53–72. [Google Scholar] [CrossRef]
- Nicosia, V.; Bianconi, G.; Latora, V.; Barthelemy, M. Growing multiplex networks. Phys. Rev. Lett. 2013, 111, 058701. [Google Scholar] [CrossRef] [PubMed]
- Urbano, M. Nodal Analysis: Circuit Analysis. In Introductory Electrical Engineering with Math Explained in Accessible Language; Urbano, M., Ed.; Wiley: New York, NY, USA, 2020; pp. 215–233. [Google Scholar] [CrossRef]
- Munkhdalai, T.; Yu, H. Meta Networks. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 2554–2563. [Google Scholar]
- Santoro, A.; Bartunov, S.; Botvinick, M.; Wierstra, D.; Lillicrap, T. Meta-learning with memory-augmented neural networks. In Proceedings of the 33rd International Conference on Machine Learning, New York, NY, USA, 20–22 June 2016; Balcan, M.F., Weinberger, K.Q., Eds.; PMLR: Breckenridge, CO, USA, 2016; Volume 48, pp. 1842–1850. Available online: https://proceedings.mlr.press/v48/ (accessed on 17 May 2024).
- Schmidhuber, J. A neural network that embeds its own meta-levels. In Proceedings of the IEEE International Conference on Neural Networks, San Francisco, CA, USA, 28 March–1 April 1993; Beygelzimer, A., Dauphin, Y., Liang, P., Wortman Vaughan, J., Eds.; IEEE: San Francisco, CA, USA, 1993; pp. 407–412. [Google Scholar] [CrossRef]
- Tarkoma, S. Overlay Networks: Toward Information Networking; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Uversky, V.N.; Giuliani, A. Networks of Networks: An Essay on Multi-Level Biological Organization. Front. Genet. 2021, 12, 706260. [Google Scholar] [CrossRef]
- Dornelas, V.; Ramos, M.; Anteneodo, C. Impact of network randomness on multiple opinion dynamics. Phys. A Stat. Mech. Its Appl. 2018, 506, 197–207. [Google Scholar] [CrossRef]
- Pung, J.; D’souza, R.M.; Ghosal, D.; Zhang, M. A road network simplification algorithm that preserves topological properties. Appl. Netw. Sci. 2022, 7, 79. [Google Scholar] [CrossRef]
- Reza, S.; Ferreira, M.C.; Machado, J.; Tavares, J.M.R. Road networks structure analysis: A preliminary network science-based approach. Ann. Math. Artif. Intell. 2022, 92, 215–234. [Google Scholar] [CrossRef]
- Huang, X.; Song, L. An emergency logistics distribution routing model for unexpected events. Ann. Oper. Res. 2018, 269, 223–239. [Google Scholar] [CrossRef]
- Wei, M.; Huang, Y.; Wan, D.; Deng, L. Emergency road network structure and planning optimization in mountainous regions in Southwest China under earthquake scenarios. J. Mt. Sci. 2022, 19, 771–780. [Google Scholar] [CrossRef]
- Rohr, A.; Priesmeier, P.; Tzavella, K.; Fekete, A. System Criticality of Road Network Areas for Emergency Management Services—Spatial Assessment Using a Tessellation Approach. Infrastructures 2020, 5, 99. [Google Scholar] [CrossRef]
- Marin, A.; Wellman, B. Social network analysis: An introduction. In The SAGE Handbook of Social Network Analysis; Scott, J., Carrington, P., Eds.; Sage Publications: London, UK, 2014; pp. 11–25. [Google Scholar] [CrossRef]
- Borgatti, S.P.; Everett, M.G.; Johnson, J.C.; Agneessens, F. Analyzing Social Networks; Sage Publications: London, UK, 2024. [Google Scholar]
- Granovetter, M. The Strength of Weak Ties. Am. J. Sociol. 1973, 78, 1360–1380. [Google Scholar] [CrossRef]
- Watts, D.; Strogatz, S. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef] [PubMed]
- Kinoshita, S. (Ed.) Pattern Formations and Oscillatory Phenomena & Belousov-Zhabotinsky Reaction; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Tyson, J.J. The Belousov-Zhabotinskii Reaction; Springer: Berlin/Heidelberg, Germany, 1976. [Google Scholar]
- Getling, A.V. Rayleigh-Bénard Convection: Structures and Dynamics; World Scientific: Singapore, 1998. [Google Scholar]
- Bostrom, N. Superintelligence: Paths, Dangers, Strategies; Oxford University Press: Oxford, UK, 2014. [Google Scholar]
- Huang, K. Introduction to Statistical Physics; Routledge: London, UK, 2010. [Google Scholar]
- Baglietto, G.; Albano, E.V. Finite-size scaling analysis and dynamic study of the critical behavior of a model for the collective displacement of selfdriven individuals. Phys. Rev. E 2008, 78, 021125. [Google Scholar] [CrossRef] [PubMed]
- Baglietto, G.; Albano, E.V. Nature of the order–disorder transition in the Vicsek model for the collective motion of self-propelled particles. Phys. Rev. E 2009, 80, 050103. [Google Scholar] [CrossRef]
- Bar-Yam, Y. Dynamics of Complex Systems; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Merelli, E.; Rucco, M. Topological characterization of complex systems: Using persistent entropy. Entropy 2015, 17, 6872–6892. [Google Scholar] [CrossRef]
- Minati, G.; Pessa, E. From Collective Beings to Quasi-Systems; Springer: New York, NY, USA, 2018. [Google Scholar]
- Lambiotte, R.; Rosvall, M.; Scholtes, I. From networks to optimal higher -order models of complex systems. Nat. Phys. 2019, 15, 313–320. [Google Scholar] [CrossRef]
- Lü, J.; Yu, X.; Chen, G.; Yu, W. Complex Systems and Networks—Dynamics, Controls and Applications; Springer: New York, NY, USA, 2016. [Google Scholar]
- Cohen, R.; Havlin, S. Complex Networks: Structure, Robustness and Function; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Estrada, E. The Structure of Complex Networks: Theory and Applications; Oxford University Press: Oxford, UK, 2016. [Google Scholar]
- Van der Hofstadt, R. Random Graphs and Complex Networks; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Li, M.; Liu, R.-R.; Lü, L.; Hu, M.-B.; Xu, S.; Zhang, Y.-C. Percolation on complex networks: Theory and application. Phys. Rep. 2021, 907, 1–68. [Google Scholar] [CrossRef]
- Halmos, P. Lectures on Ergodic Theory; Dover Books on Mathematics: Mineola, NY, USA, 2017. [Google Scholar]
- Janot, C. Quasicrystals: A Primer; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Gilles, R.; Ruys, P.H.M.; Jilin, S. Quasi-Networks in Social Relational Systems. Syst. Sci. Syst. Eng. 1992, 1, 25–33. [Google Scholar]
- Daniel, J. Sampling Essentials: Practical Guidelines for Making Sampling Choices; Sage Publications: London, UK, 2011. [Google Scholar]
- Banerji, C.R.S.; Miranda-Saavedra, D.; Severini, S.; Widschwendter, M.; Enver, T.; Zhou, J.X.; Teschendorff, A.E. Cellular network entropy as the energy potential in Waddington’s differentiation landscape. Sci. Rep. 2013, 3, 3039. [Google Scholar] [CrossRef] [PubMed]
- Diaz, R.M.; Ye, H.; Ernest, S.K.M. Empirical abundance distributions are more uneven than expected given their statistical baseline. Ecol. Lett. 2021, 24, 2025–2039. [Google Scholar] [CrossRef] [PubMed]
- Abedjan, Z. Data Profiling. In Encyclopedia of Big Data Technologies; Zomaya, A., Taheri, J., Sakr, S., Eds.; Springer: Cham, Switzerland, 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Abedjan, Z.; Golab, L.; Naumann, F. Data Profiling: A Tutorial. In Proceedings of the 2017 ACM International Conference on Management of Data (SIGMOD’17), Chicago, IL, USA, 14–19 May 2017; Meliou, A., Senellart, P., Eds.; Association for Computing Machinery: New York, NY, USA, 2017; pp. 1747–1751. [Google Scholar] [CrossRef]
- Davenport, T.H. Big Data at Work; Harvard Business Review Press: Boston, MA, USA, 2014. [Google Scholar]
- Franks, B. Taming the Big Data Tidal Wave: Finding Opportunities in Huge Data Streams with Advanced Analytics; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- Tantardini, M.; Ieva, F.; Tajoli, L.; Piccardi, C. Comparing methods for comparing networks. Sci. Rep. 2019, 9, 17557. [Google Scholar] [CrossRef] [PubMed]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Batouche, M.; Meshoul, S.; Al Hussaini, A. Image processing using quantum computing and reverse emergence. Int. J. Nano Biomater. 2009, 2, 136–142. [Google Scholar] [CrossRef]
- Djemame, S.; Batouche, M.; Oulhadj, H.; Siarry, P. Solving reverse emergence with quantum PSO application to image processing. Soft Comput. 2019, 23, 6921–6935. [Google Scholar] [CrossRef]
- di Bernardo, M. Controlling Collective Behavior in Complex Systems. In Encyclopedia of Systems and Control; Baillieul, J., Samad., T., Eds.; Springer: Cham, Switzerland, 2021; pp. 441–450. [Google Scholar] [CrossRef]
- Ciampaglia, G.L.; Ferrara, E.; Flammini, A. Collective behaviors and networks. EPJ Data Sci. 2014, 3, 37. [Google Scholar] [CrossRef][Green Version]
- Boccaletti, S.; Latora, V.; Moreno, Y.; Chavez, M.; Hwang, D.-U. Complex networks: Structure and dynamics. Phys. Rep. 2006, 424, 175–308. [Google Scholar] [CrossRef]
- D’Souza, R.M.; di Bernardo, M.; Liu, Y.Y. Controlling complex networks with complex nodes. Nat. Rev. Phys. 2023, 5, 250–262. [Google Scholar] [CrossRef]
- Lunardi, A. Interpolation Theory; Springer: New York, NY, USA, 2018. [Google Scholar]
- Kohonen, T. Self-Organizing Maps, 3rd ed.; Springer: New York, NY, USA, 2001. [Google Scholar] [CrossRef]
- Kohonen, T. Essentials of the self-organizing map. Neural Netw. 2013, 37, 52–65. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, J.T. Self-Organizing Neural Maps: The Retinotectal Map and Mechanisms of Neural Development: From Retina to Tectum; Academic Press: London, UK, 2019. [Google Scholar]
- Chen, W.; Tian, Z. Interpolation-based k-means Clustering Improvement for Sparse, High Dimensional Data. In Proceedings of the 2019 3rd International Conference on Cloud and Big Data Computing, Oxford, UK, 28–30 August 2019; pp. 11–15. [Google Scholar] [CrossRef]
- Aggarwal, C.C.; Reddy, C.K. Data Clustering: Algorithms and Applications; CRC Press: Boca Raton, FL, USA, 2013; Available online: https://people.cs.vt.edu/~reddy/papers/DCBOOK.pdf (accessed on 17 May 2024).
- Mirkin, B. Clustering: A Data Recovery Approach; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Hair, J.F., Jr.; Black, W.C. Multivariate Data Analysis; Pearson: Harlow, UK, 2013. [Google Scholar]
- Everitt, B.S.; Landau, S.; Leese, M.; Stahl, D. Cluster Analysis; Wiley: Chichester, UK, 2011. [Google Scholar]
- Christen, P. Data Matching: Concepts and Techniques for Record Linkage, Entity Resolution, and Duplicate Detection; Springer: New York, NY, USA, 2014. [Google Scholar]
- Banagl, M.; Vogel, D. (Eds.) The Mathematics of Knots, Theory and Application; Springer: New York, NY, USA, 2010. [Google Scholar]
- Fang, S.C. Routeing in a Network with Multi-Class Links. J. Oper. Res. Soc. 1984, 35, 637–640. [Google Scholar] [CrossRef]
- Mukherjee, S.; Mukhopadhyay, S.; Sarkar, S. Personal Social Network Profile Authentication through Image Steganography. Eng. Proc. 2023, 56, 129. [Google Scholar] [CrossRef]
- da Silva, S.A.; de Medeiros, V.W.C.; Gonçalves, G.E. Monitoring and classification of cattle behavior: A survey. Smart Agric. Technol. 2023, 3, 100091. [Google Scholar] [CrossRef]
- Gao, G.; Wang, C.; Wang, J.; Lv, Y.; Li, Q.; Ma, Y.; Zhang, X.; Li, Z.; Chen, G. CNN-Bi-LSTM: A Complex Environment-Oriented Cattle Behavior Classification Network Based on the Fusion of CNN and Bi-LSTM. Sensors 2023, 23, 7714. [Google Scholar] [CrossRef] [PubMed]
- Gilbert, M. (Ed.) Artificial Intelligence for Autonomous Networks; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Zschaler, G. Adaptive-network models of collective dynamics. Eur. Phys. J. Spec. Top. 2012, 211, 1–101. [Google Scholar] [CrossRef]
- Berner, R.; Gross, T.; Kuehn, C.; Kurths, J.; Yanchuk, S. Adaptive dynamical networks. Phys. Rep. 2023, 1031, 1–59. [Google Scholar] [CrossRef]
- Gross, T.; Sayama, H. Adaptive Networks. In Understanding Complex Systems; Gross, T., Sayama, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–8. [Google Scholar] [CrossRef]
- Sayama, H.; Pestov, I.; Schmidt, J.; Bush, B.J.; Wong, C.; Yamanoi, J.; Gross, T. Modeling complex systems with adaptive networks. Comput. Math. Appl. 2013, 65, 1645–1664. [Google Scholar] [CrossRef]
- Minati, G. Multiplicity, Logical Openness, Incompleteness, and Quasi-ness as Peculiar Non-reductionist Properties of Complexity. In From Electrons to Elephants and Elections: Saga of Content and Context; Wuppuluri, S., Stewart, I., Eds.; Springer: New York, NY, USA, 2022; pp. 151–173. Available online: https://link.springer.com/chapter/10.1007/978-3-030-92192-7_10 (accessed on 17 May 2024).
- Licata, I.; Minati, G. Emergence, Computation and the Freedom Degree Loss Information Principle in Complex Systems. Found. Sci. 2017, 22, 863–881. [Google Scholar] [CrossRef]
- Kellerman, H. The Unconscious Domain; Springer: New York, NY, USA, 2020. [Google Scholar]
- Minati, G.; Vitiello, G. Mistake Making Machines. In Systemics of Emergence: Applications and Development; Minati, G., Pessa, E., Abram, M., Eds.; Springer: New York, NY, USA, 2006; pp. 67–78. [Google Scholar]
- Bonometti, P. Improving safety, quality and efficiency through the management of emerging processes: The Tenaris Dalmine experience. Learn. Organ. 2012, 19, 299–310. [Google Scholar] [CrossRef]
- Wehrle, K.; Güneş, M.; Gross, J. (Eds.) Modeling and Tools for Network Simulation; Springer: Berlin, Heidelberg, Germany, 2010. [Google Scholar]
- Rosen, R. Anticipatory systems. In Anticipatory Systems: Philosophical, Mathematical, and Methodological Foundations; Rosen, R., Ed.; Springer: New York, NY, USA, 2011; pp. 313–370. [Google Scholar]
- Rosen, J. Robert Rosen’s Anticipatory Systems Theory: The Science of Life and Mind. Mathematics 2022, 10, 4172. [Google Scholar] [CrossRef]
- Ruelle, D. Chaotic Evolution and Attractors; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Boccaletti, S.; Kurths, J.; Osipov, G.; Valladares, D.L.; Zhouc, C.S. The synchronization of chaotic systems. Phys. Rep. 2002, 366, 1–98. [Google Scholar] [CrossRef]
- Nicosia, V.; Valencia, M.; Chavez, M.; Diaz-Guilera, A.; Latora, V. Remote synchronization reveals network symmetries and functional modules. Phys. Rev. Lett. 2013, 110, 174102–174106. [Google Scholar] [CrossRef] [PubMed]
- Le Hunte, B. Transdisciplinarity. In The Palgrave Encyclopedia of the Possible; Glăveanu, V.P., Ed.; Palgrave Macmillan: Cham, Switzerland, 2022; pp. 1669–1676. [Google Scholar] [CrossRef]
- Nicolescu, B. (Ed.) Transdisciplinarity—Theory and Practice; Hampton Press: Cresskill, NJ, USA, 2008. [Google Scholar]
- Yu, Y.X.; Gong, H.P.; Liu, H.C.; Mou, X. Knowledge representation and reasoning using fuzzy Petri nets: A literature review and bibliometric analysis. Artif. Intell. Rev. 2023, 56, 6241–6265. [Google Scholar] [CrossRef]
- Evans, J.A.; Foster, J.G. Metaknowledge. Science 2011, 331, 721–725. [Google Scholar] [CrossRef] [PubMed]
- Anderson, C. The End of Theory: The Data Deluge Makes the Scientific Method Obsolete. Wired Mag. 2008, 16. Available online: https://www.cs.hmc.edu/twiki/pub/CS5/Reading1Gold/end_of_theory.pdf (accessed on 17 May 2024).
- Pigliucci, M. The end of theory in science? EMBO Rep. 2009, 10, 534. [Google Scholar] [CrossRef]
- Calude, C.S.; Longo, G. The deluge of spurious correlations in big data. Found. Sci. 2016, 22, 595–612. [Google Scholar] [CrossRef]
- Coveney, P.V.; Dougherty, E.R.; Highfield, R.R. Big data need big theory too. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 280, 20160153. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).