Variable Neighborhood Search for Minimizing the Makespan in a Uniform Parallel Machine Scheduling
Abstract
1. Introduction
2. Literature Review
3. Research Methodology
3.1. Lower Bounds
3.2. Mathematical Formulation
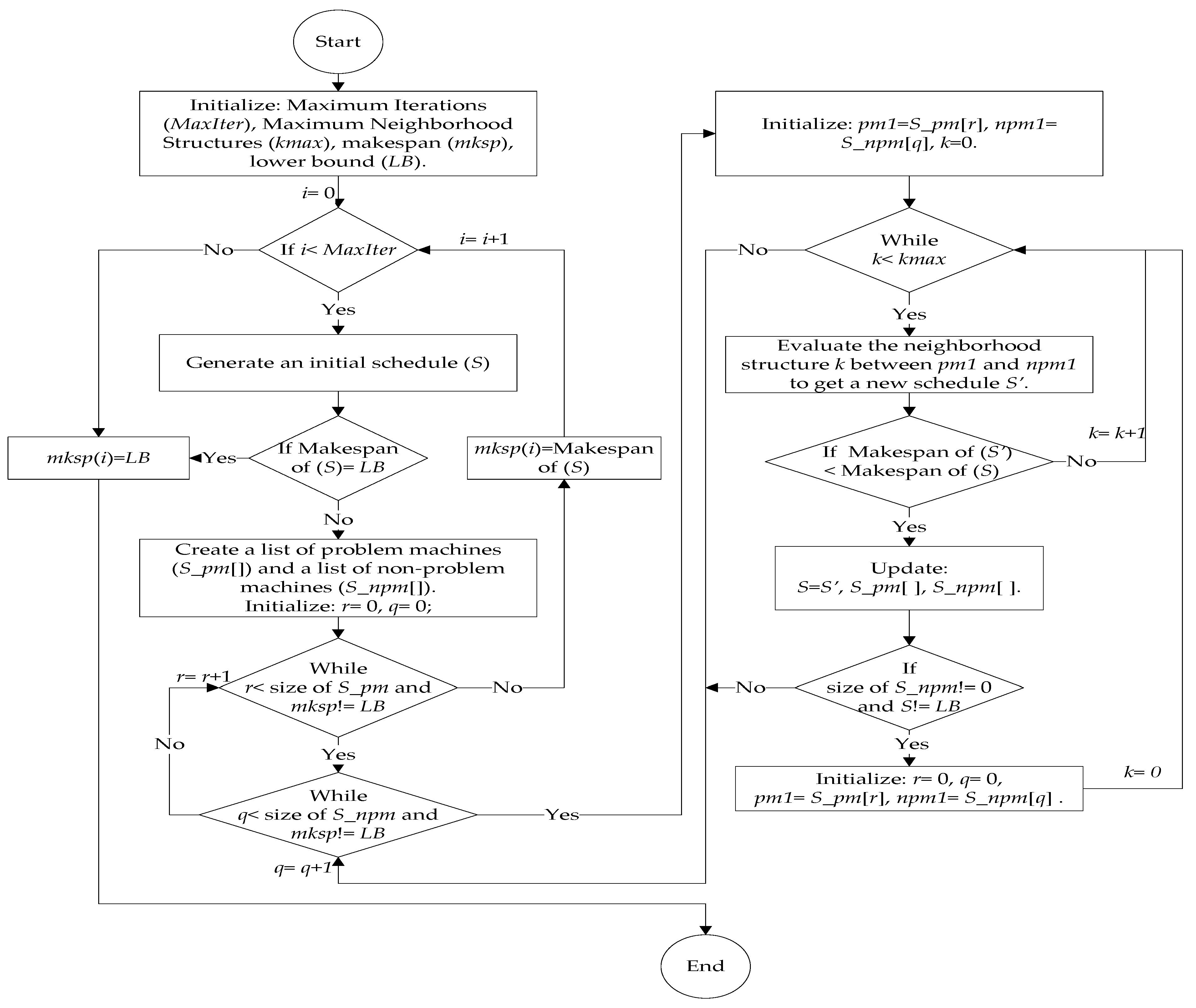
3.3. Variable Neighborhood Search Algorithms
3.3.1. Initial Solution
3.3.2. Neighborhood Structures
- Move (j): a job j is moved from pm to npm if the processing time of job j on the new non-problem machine, npm (pnpm,j), is less than the difference in completion times between (pm) and (npm), i.e., (Cpm − Cnpm).
- Exchange (j − k): a job j from pm is exchanged with a job k from npm if the resulting completion time for each machine does not exceed the makespan of pm “Cpm”. That is, (Cpm − ppm,j + ppm,k) < Cpm and (Cnpm − pnpm,k + pnpm,j) < Cpm.
- Exchange (j − k, l): two jobs, j and k, from pm are exchanged with one job, l, from npm if (Cpm − ppm,j − ppm,k + ppm,l) < Cpm and (Cnpm − pnpm,l+ pnpm,j + pnpm,k) < Cpm.
- Exchange (j, k − l): one job, j, from pm is exchanged with two jobs, k and l, from npm if (Cpm − ppm,j + ppm,k + ppm,l) < Cpm and (Cnpm − pnpm,k − pnpm,l + pnpm,j) < Cpm.
- Exchange (j − k, l − t): two jobs, j and k, from pm are exchanged with two jobs, l and t, from npm if (Cpm − ppm,j − ppm,k + ppm,l + ppm,t) < Cpm and (Cnpm − pnpm,l − pnpm,t + pnpm,j + pnpm,k) < Cpm.
3.3.3. Example
4. Computational Results and Discussion
- (i)
- The number of machines (m).
- (ii)
- The ratio of the number of jobs (n) to the number of machines (m), n/m.
- (iii)
- The processing times of each job, j, on the fastest machine, m, pm,j.
- (iv)
- The speed for each machine, i, to the fastest machine, Si.
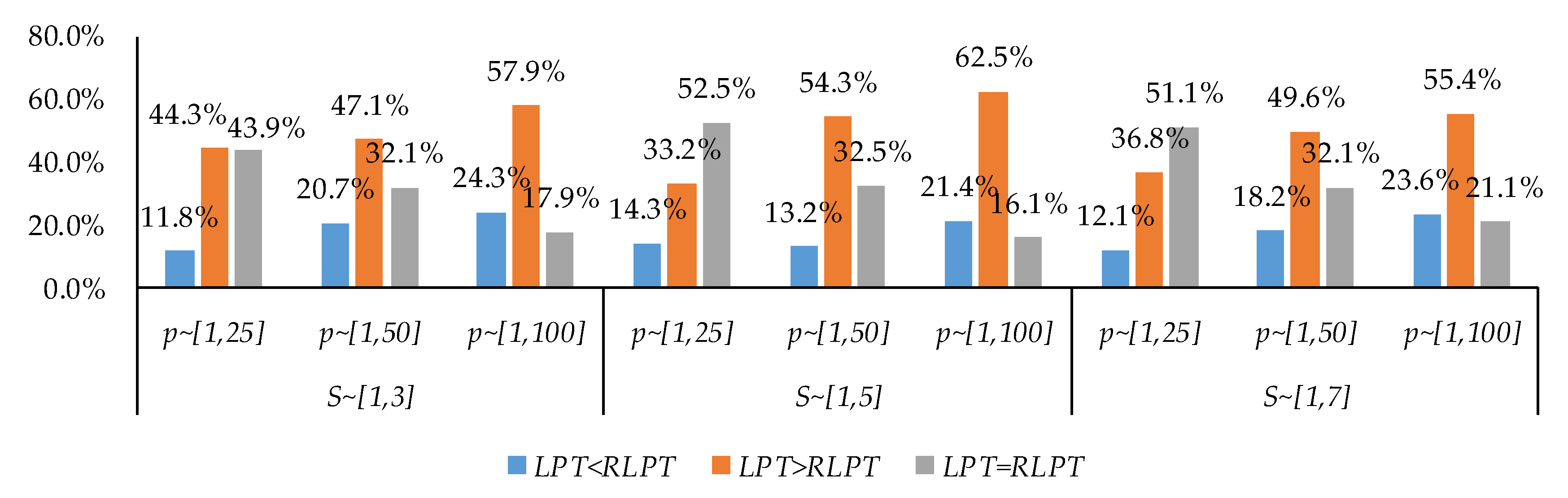
4.1. Comparison of the LPT Rule and RLPT Rule
4.2. Performance of the LVNS and RVNS Algorithms
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lee, J.-H.; Jang, H. Uniform parallel machine scheduling with dedicated machines, job splitting and setup resources. Sustainability 2019, 11, 7137. [Google Scholar] [CrossRef]
- Huang, J.; Wu, J.; Tang, Y.; Hao, Y. The influences of openness on China’s industrial CO2 intensity. Environ. Sci. Pollut. Res. 2020, 27, 15743–15757. [Google Scholar] [CrossRef] [PubMed]
- Graham, R.L.; Lawler, E.L.; Lenstra, J.K.; Kan, A.R. Optimization and approximation in deterministic sequencing and scheduling: A survey. In Annals of Discrete Mathematics; Elsevier: Amsterdam, The Netherlands, 1979; Volume 5, pp. 287–326. [Google Scholar]
- Garey, M.R.; Johnson, D.S. Computers and Intractability; Freeman: San Francisco, CA, USA, 1979; Volume 174. [Google Scholar]
- Li, K.; Leung, J.T.; Cheng, B.Y. An agent-based intelligent algorithm for uniform machine scheduling to minimize total completion time. Appl. Soft Comput. 2014, 25, 277–284. [Google Scholar] [CrossRef]
- Graham, R.L. Bounds on multiprocessing timing anomalies. SIAM J. Appl. Math. 1969, 17, 416–429. [Google Scholar] [CrossRef]
- Gonzalez, T.; Ibarra, O.H.; Sahni, S. Bounds for LPT schedules on uniform processors. SIAM J. Comput. 1977, 6, 155–166. [Google Scholar] [CrossRef]
- Della Croce, F.; Scatamacchia, R. The longest processing time rule for identical parallel machines revisited. J. Sched. 2020, 23, 163–176. [Google Scholar] [CrossRef]
- Friesen, D.K. Tighter bounds for LPT scheduling on uniform processors. SIAM J. Comput. 1987, 16, 554–560. [Google Scholar] [CrossRef]
- Mireault, P.; Orlin, J.B.; Vohra, R.V. A parametric worst case analysis of the LPT heuristic for two uniform machines. Oper. Res. 1997, 45, 116–125. [Google Scholar] [CrossRef][Green Version]
- Koulamas, C.; Kyparisis, G.J. A modified LPT algorithm for the two uniform parallel machine makespan minimization problem. Eur. J. Oper. Res. 2009, 196, 61–68. [Google Scholar] [CrossRef]
- Massabò, I.; Paletta, G.; Ruiz-Torres, A.J. A note on longest processing time algorithms for the two uniform parallel machine makespan minimization problem. J. Sched. 2016, 19, 207–211. [Google Scholar] [CrossRef]
- Mitsunobu, T.; Suda, R.; Suppakitpaisarn, V. Worst-case analysis of LPT scheduling on a small number of non-identical processors. Inf. Process. Lett. 2024, 183, 106424. [Google Scholar] [CrossRef]
- Friesen, D.K.; Langston, M.A. Bounds for multifit scheduling on uniform processors. SIAM J. Comput. 1983, 12, 60–70. [Google Scholar] [CrossRef]
- Chen, B. Tighter bound for MULTIFIT scheduling on uniform processors. Discret. Appl. Math. 1991, 31, 227–260. [Google Scholar] [CrossRef][Green Version]
- Li, K.; Zhang, S.-C. Heuristics for uniform parallel machine scheduling problem with minimizing makespan. In Proceedings of the 2008 IEEE International Conference on Automation and Logistics, Qingdao, China, 1–3 September 2008; IEEE: New York, NY, USA, 2018; pp. 273–278. [Google Scholar]
- Sivasankaran, P.; Kumar, M.R.; Senthilkumar, P.; Panneerselvam, R. Heuristic to minimize makespan in uniform parallel machines scheduling problem. Udyog Pragati 2009, 33, 1–15. [Google Scholar]
- Li, K.; Yang, S. Heuristic algorithms for scheduling on uniform parallel machines with heads and tails. J. Syst. Eng. Electron. 2011, 22, 462–467. [Google Scholar] [CrossRef]
- De Giovanni, D.; Ho, J.C.; Paletta, G.; Ruiz-Torres, A.J. Heuristics for Scheduling Uniform Machines. In Proceedings of the International MultiConference of Engineers and Computer Scientists, Hong Kong, China, 14–16 March 2018; Volume 2. [Google Scholar]
- Song, J.; Miao, C.; Kong, F. Uniform-machine scheduling problems in green manufacturing system. Math. Found. Comput. 2024. [Google Scholar] [CrossRef]
- Balin, S. Non-identical parallel machine scheduling using genetic algorithm. Expert Syst. Appl. 2011, 38, 6814–6821. [Google Scholar] [CrossRef]
- Noman, M.A.; Alatefi, M.; Al-Ahmari, A.M.; Ali, T. Tabu Search Algorithm Based on Lower Bound and Exact Algorithm Solutions for Minimizing the Makespan in Non-Identical Parallel Machines Scheduling. Math. Probl. Eng. 2021, 2021, 1856734. [Google Scholar] [CrossRef]
- Li, K.; Cheng, B.-Y. Variable neighborhood search for uniform parallel machine makespan scheduling problem with release dates. In Proceedings of the 2010 International Symposium on Computational Intelligence and Design, Hangzhou, China, 29–31 October 2010; IEEE: New York, NY, USA, 2010; Volume 2, pp. 43–46. [Google Scholar]
- Sevkli, M.; Uysal, H. A modified variable neighborhood search for minimizing the makespan on identical parallel machines. In Proceedings of the 2009 International Conference on Computers & Industrial Engineering, Troyes, France, 6–9 July 2009; IEEE: New York, NY, USA, 2009; pp. 108–111. [Google Scholar]
- Chen, J.; Li, J.-Q. Efficient variable neighborhood search for identical parallel machines scheduling. In Proceedings of the 31st Chinese Control Conference, Hefei, China, 25–27 July 2012; IEEE: New York, NY, USA, 2012; pp. 7228–7232. [Google Scholar]
- Alharkan, I.; Bamatraf, K.; Noman, M.A.; Kaid, H.; Nasr, E.S.A.; El-Tamimi, A.M. An order effect of neighborhood structures in variable neighborhood search algorithm for minimizing the makespan in an identical parallel machine scheduling. Math. Probl. Eng. 2018, 2018, 3586731. [Google Scholar] [CrossRef]
- Gharbi, A.; Bamatraf, K. An Improved Arc Flow Model with Enhanced Bounds for Minimizing the Makespan in Identical Parallel Machine Scheduling. Processes 2022, 10, 2293. [Google Scholar] [CrossRef]
- Cheng, W.; Guo, P.; Zhang, Z.; Zeng, M.; Liang, J. Variable neighborhood search for parallel machines scheduling problem with step deteriorating jobs. Math. Probl. Eng. 2012, 2012, 928312. [Google Scholar] [CrossRef]
- Senthilkumar, P.; Narayanan, S. GA Based Heuristic to Minimize Makespan in Single Machine Scheduling Problem with Uniform Parallel Machines. Intell. Inf. Manag. 2011, 3, 204–214. [Google Scholar] [CrossRef]
- Senthilkumar, P.; Narayanan, S. Simulated annealing algorithm to minimize makespanin single machine scheduling problem withuniform parallel machines. Intell. Inf. Manag. 2011, 3, 22. [Google Scholar] [CrossRef][Green Version]
- Kaabi, J. Modeling and solving scheduling problem with m uniform parallel machines subject to unavailability constraints. Algorithms 2019, 12, 247. [Google Scholar] [CrossRef]
- Kim, H.-J.; Lee, J.-H. Scheduling uniform parallel dedicated machines with job splitting, sequence-dependent setup times, and multiple servers. Comput. Oper. Res. 2021, 126, 105115. [Google Scholar] [CrossRef]
- Horowitz, E.; Sahni, S. Exact and approximate algorithms for scheduling nonidentical processors. J. ACM 1976, 23, 317–327. [Google Scholar] [CrossRef]
- De, P.; Morton, T.E. Scheduling to minimize makespan on unequal parallel processors. Decis. Sci. 1980, 11, 586–602. [Google Scholar] [CrossRef]
- Liao, C.-J.; Lin, C.-H. Makespan minimization for two uniform parallel machines. Int. J. Prod. Econ. 2003, 84, 205–213. [Google Scholar] [CrossRef]
- Lin, C.-H.; Liao, C.-J. Makespan minimization for multiple uniform machines. Comput. Ind. Eng. 2008, 54, 983–992. [Google Scholar] [CrossRef]
- Popenko, V.; Sperkach, M.; Zhdanova, O.; Kokosiński, Z. On Optimality Conditions for Job Scheduling on Uniform Parallel Machines. In Proceedings of the International Conference on Computer Science, Engineering and Education Applications, Kiev, Ukraine, 26–27 January 2019; Springer: New York, NY, USA, 2019; pp. 103–112. [Google Scholar]
- Berndt, S.; Brinkop, H.; Jansen, K.; Mnich, M.; Stamm, T. New support size bounds for integer programming, applied to makespan minimization on uniformly related machines. arXiv 2023, arXiv:2305.08432. [Google Scholar]
- Mallek, A.; Boudhar, M. Scheduling on uniform machines with a conflict graph: Complexity and resolution. Int. Trans. Oper. Res. 2024, 31, 863–888. [Google Scholar] [CrossRef]
- Soper, A.J.; Strusevich, V.A. Parametric analysis of the quality of single preemption schedules on three uniform parallel machines. Ann. Oper. Res. 2021, 298, 469–495. [Google Scholar] [CrossRef]
- Mokotoff, E. Parallel machine scheduling problems: A survey. Asia-Pac. J. Oper. Res. 2001, 18, 193. [Google Scholar]
- Senthilkumar, P.; Narayanan, S. Literature review of single machine scheduling problem with uniform parallel machines. Intell. Inf. Manag. 2010, 2, 457–474. [Google Scholar] [CrossRef][Green Version]
- Mladenović, N.; Hansen, P. Variable neighborhood search. Comput. Oper. Res. 1997, 24, 1097–1100. [Google Scholar] [CrossRef]


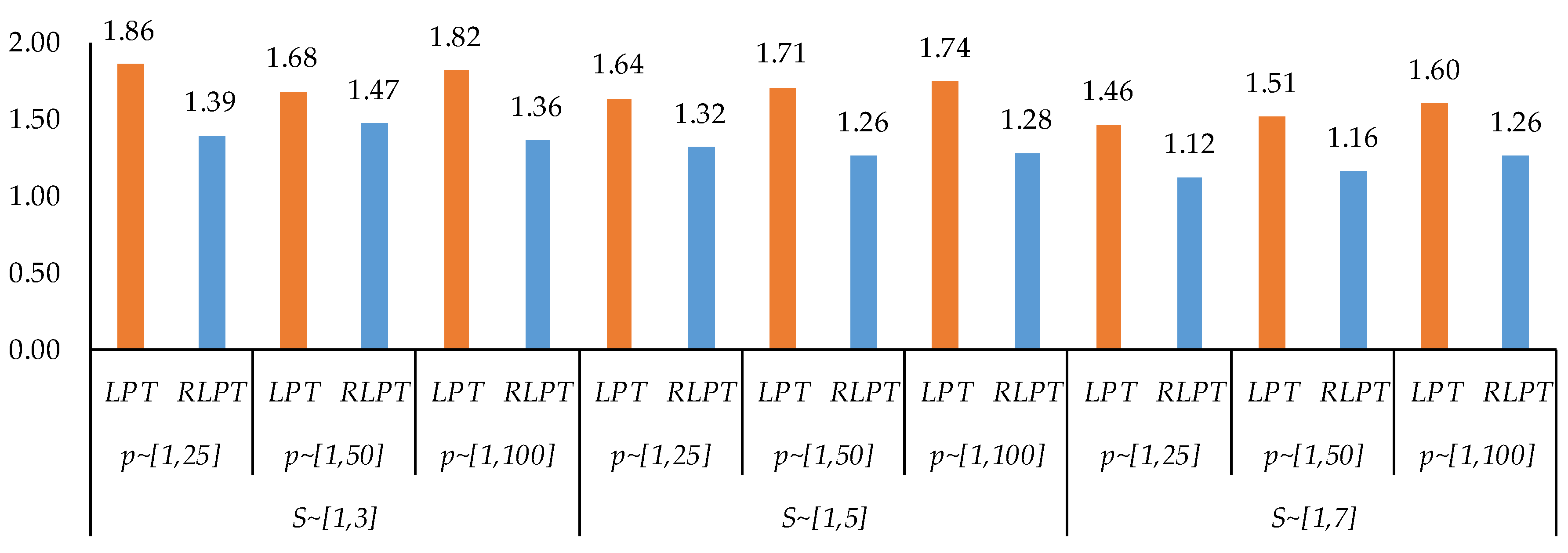


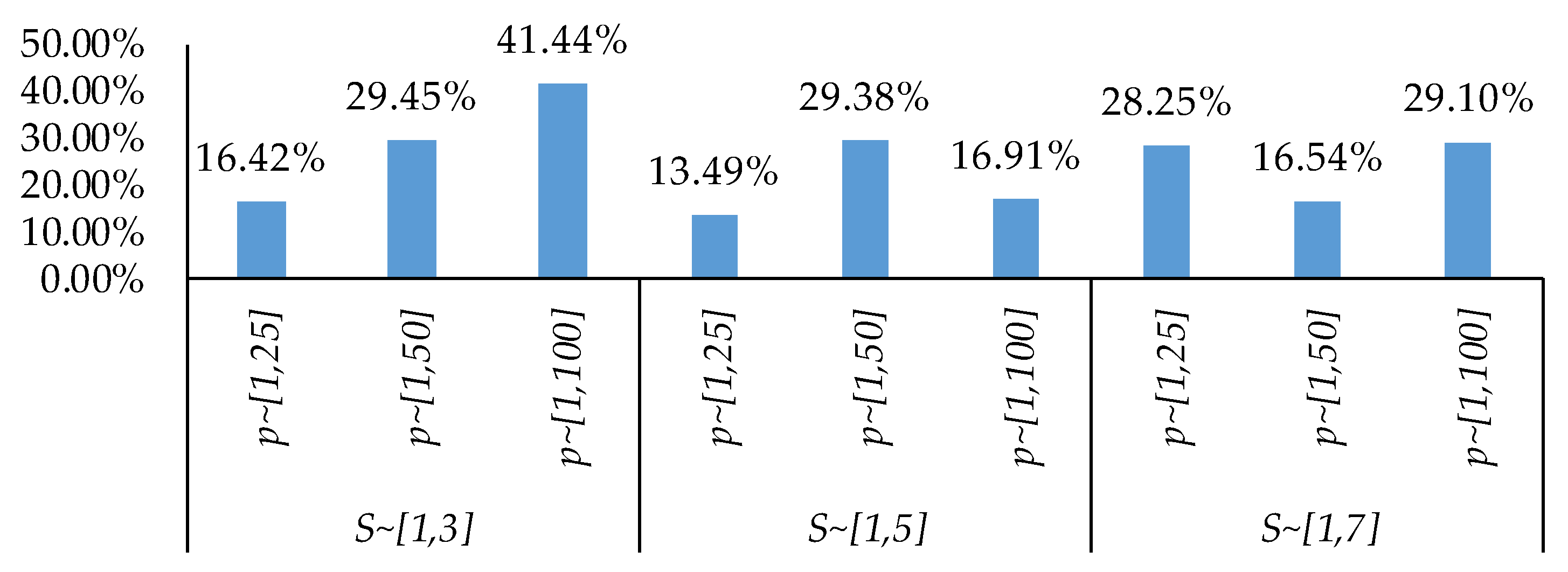
| Variable | Definition |
|---|---|
| Indices | |
| Index of a machine. | |
| Index of a job. | |
| Sets | |
| Set of machines | |
| Set of jobs | |
| Parameters | |
| Processing time of job j on machine i. . | |
| LB | Lower bound |
| UB | Upper bound |
| Decision Variables | |
| 1 if job j is processed on machine i, 0 otherwise. . | |
| Makespan of a schedule | |
| Machine | Speed | Job | |||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| 1 | 1.0000 | 3822 | 3458 | 2912 | 2730 | 2002 | 2002 |
| 2 | 1.3382 | 2856 | 2584 | 2176 | 2040 | 1496 | 1496 |
| 3 | 1.8200 | 2100 | 1900 | 1600 | 1500 | 1100 | 1100 |
| S~[1,3] | S~[1,5] | S~[1,7] | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n/m | m | n | p~[1,25] | p~[1,50] | p~[1,100] | p~[1,25] | p~[1,50] | p~[1,100] | p~[1,25] | p~[1,50] | p~[1,100] | |||||||||
| LPT | RLPT | LPT | RLPT | LPT | RLPT | LPT | RLPT | LPT | RLPT | LPT | RLPT | LPT | RLPT | LPT | RLPT | LPT | RLPT | |||
| 2 | 3 | 6 | 4.031 | 2.966 | 3.149 | 3.068 | 2.738 | 1.655 | 3.206 | 2.030 | 1.159 | 2.540 | 2.378 | 1.373 | 1.404 | 1.622 | 1.493 | 1.385 | 3.454 | 1.316 |
| 4 | 8 | 4.442 | 2.969 | 4.071 | 4.864 | 3.933 | 2.877 | 1.912 | 2.835 | 2.772 | 1.624 | 4.809 | 3.727 | 5.787 | 4.083 | 4.364 | 2.053 | 4.119 | 2.043 | |
| 5 | 10 | 5.291 | 5.315 | 3.538 | 3.707 | 4.839 | 3.306 | 6.543 | 4.975 | 3.200 | 2.814 | 3.863 | 3.518 | 2.608 | 1.137 | 3.529 | 3.433 | 3.309 | 3.919 | |
| 10 | 20 | 6.747 | 7.354 | 5.936 | 7.111 | 5.591 | 5.332 | 6.009 | 4.570 | 5.457 | 4.763 | 6.285 | 5.900 | 5.088 | 4.958 | 5.236 | 5.163 | 5.886 | 5.486 | |
| 3 | 3 | 9 | 2.351 | 1.646 | 3.942 | 1.117 | 2.374 | 1.000 | 3.156 | 2.491 | 2.834 | 1.768 | 4.790 | 1.859 | 2.262 | 1.336 | 3.675 | 1.833 | 2.276 | 0.675 |
| 4 | 12 | 4.277 | 2.329 | 3.398 | 2.787 | 5.576 | 3.898 | 2.837 | 1.989 | 3.064 | 2.368 | 2.759 | 1.926 | 2.442 | 1.759 | 2.577 | 1.570 | 2.693 | 2.441 | |
| 5 | 15 | 4.351 | 2.762 | 5.129 | 3.557 | 3.635 | 2.500 | 2.645 | 2.453 | 6.305 | 3.904 | 4.907 | 4.193 | 2.665 | 1.764 | 2.951 | 2.613 | 2.960 | 2.841 | |
| 10 | 30 | 4.628 | 3.266 | 2.997 | 2.735 | 3.873 | 3.844 | 5.035 | 4.699 | 4.429 | 4.007 | 3.227 | 2.513 | 4.154 | 3.634 | 3.230 | 2.735 | 4.030 | 4.113 | |
| 4 | 3 | 12 | 1.940 | 0.434 | 1.804 | 1.521 | 2.218 | 1.411 | 1.599 | 1.094 | 2.245 | 1.099 | 1.265 | 0.944 | 1.405 | 0.735 | 2.636 | 1.354 | 1.828 | 1.085 |
| 4 | 16 | 1.382 | 1.086 | 2.146 | 1.549 | 3.113 | 2.191 | 1.464 | 1.235 | 2.335 | 1.251 | 3.028 | 1.315 | 1.268 | 0.936 | 1.384 | 1.586 | 2.178 | 1.450 | |
| 5 | 20 | 1.939 | 1.412 | 2.266 | 1.756 | 2.898 | 1.844 | 1.310 | 1.143 | 2.156 | 1.585 | 1.572 | 1.201 | 1.527 | 1.514 | 1.654 | 1.432 | 2.339 | 1.877 | |
| 10 | 40 | 2.247 | 1.796 | 1.874 | 1.872 | 1.589 | 1.616 | 2.532 | 1.792 | 2.644 | 1.901 | 2.400 | 1.950 | 2.428 | 1.928 | 2.281 | 1.962 | 2.063 | 2.273 | |
| 5 | 3 | 15 | 1.159 | 0.441 | 1.167 | 0.704 | 1.471 | 0.974 | 1.387 | 0.592 | 1.664 | 1.027 | 1.478 | 0.661 | 0.985 | 0.512 | 0.647 | 0.501 | 1.443 | 0.972 |
| 4 | 20 | 0.599 | 0.381 | 0.941 | 0.669 | 1.334 | 0.997 | 0.557 | 0.241 | 1.320 | 0.582 | 1.362 | 0.945 | 1.010 | 0.668 | 1.232 | 0.636 | 1.466 | 0.876 | |
| 5 | 25 | 1.822 | 1.034 | 0.915 | 1.027 | 1.672 | 1.441 | 1.095 | 0.957 | 2.324 | 1.233 | 1.102 | 1.190 | 1.389 | 1.058 | 1.468 | 1.295 | 1.371 | 1.286 | |
| 10 | 50 | 1.390 | 1.275 | 1.349 | 1.246 | 1.614 | 1.451 | 1.702 | 1.316 | 1.451 | 1.163 | 1.400 | 1.074 | 1.634 | 1.360 | 1.487 | 1.242 | 1.342 | 1.142 | |
| 10 | 3 | 30 | 0.480 | 0.303 | 0.523 | 0.365 | 0.329 | 0.239 | 0.465 | 0.338 | 0.426 | 0.209 | 0.272 | 0.232 | 0.648 | 0.402 | 0.433 | 0.159 | 0.346 | 0.185 |
| 4 | 40 | 0.566 | 0.370 | 0.366 | 0.279 | 0.591 | 0.401 | 0.478 | 0.400 | 0.567 | 0.365 | 0.487 | 0.280 | 0.439 | 0.295 | 0.494 | 0.320 | 0.493 | 0.300 | |
| 5 | 50 | 0.630 | 0.382 | 0.396 | 0.259 | 0.472 | 0.318 | 0.407 | 0.314 | 0.427 | 0.281 | 0.397 | 0.337 | 0.428 | 0.351 | 0.462 | 0.378 | 0.294 | 0.243 | |
| 10 | 100 | 0.539 | 0.442 | 0.464 | 0.378 | 0.415 | 0.314 | 0.364 | 0.341 | 0.321 | 0.274 | 0.401 | 0.251 | 0.412 | 0.346 | 0.439 | 0.331 | 0.337 | 0.320 | |
| 20 | 3 | 60 | 0.154 | 0.106 | 0.116 | 0.084 | 0.089 | 0.058 | 0.157 | 0.112 | 0.135 | 0.058 | 0.143 | 0.052 | 0.150 | 0.135 | 0.140 | 0.067 | 0.101 | 0.048 |
| 4 | 80 | 0.213 | 0.131 | 0.089 | 0.069 | 0.114 | 0.079 | 0.179 | 0.179 | 0.079 | 0.061 | 0.100 | 0.059 | 0.132 | 0.126 | 0.086 | 0.079 | 0.085 | 0.069 | |
| 5 | 100 | 0.164 | 0.164 | 0.134 | 0.122 | 0.102 | 0.100 | 0.190 | 0.155 | 0.176 | 0.104 | 0.094 | 0.080 | 0.164 | 0.159 | 0.118 | 0.087 | 0.099 | 0.082 | |
| 10 | 200 | 0.215 | 0.171 | 0.099 | 0.093 | 0.095 | 0.070 | 0.172 | 0.172 | 0.141 | 0.098 | 0.110 | 0.095 | 0.168 | 0.168 | 0.109 | 0.098 | 0.114 | 0.085 | |
| 30 | 3 | 90 | 0.066 | 0.066 | 0.053 | 0.052 | 0.045 | 0.031 | 0.103 | 0.103 | 0.055 | 0.052 | 0.041 | 0.024 | 0.117 | 0.094 | 0.088 | 0.045 | 0.043 | 0.031 |
| 4 | 120 | 0.121 | 0.121 | 0.061 | 0.044 | 0.047 | 0.041 | 0.097 | 0.097 | 0.071 | 0.045 | 0.035 | 0.035 | 0.082 | 0.082 | 0.048 | 0.050 | 0.043 | 0.037 | |
| 5 | 150 | 0.097 | 0.097 | 0.070 | 0.055 | 0.036 | 0.045 | 0.116 | 0.109 | 0.058 | 0.053 | 0.043 | 0.037 | 0.089 | 0.089 | 0.065 | 0.051 | 0.048 | 0.036 | |
| 10 | 300 | 0.120 | 0.120 | 0.063 | 0.060 | 0.059 | 0.040 | 0.116 | 0.109 | 0.064 | 0.064 | 0.053 | 0.042 | 0.120 | 0.120 | 0.066 | 0.057 | 0.049 | 0.038 | |
| Average | 1.856 | 1.391 | 1.681 | 1.470 | 1.816 | 1.360 | 1.637 | 1.316 | 1.710 | 1.260 | 1.743 | 1.279 | 1.465 | 1.121 | 1.514 | 1.161 | 1.600 | 1.260 | ||
| p~[1,25] | p~[1,50] | p~[1,100] | |||||||
|---|---|---|---|---|---|---|---|---|---|
| LPT < RLPT | LPT > RLPT | LPT = RLPT | LPT < RLPT | LPT > RLPT | LPT = RLPT | LPT < RLPT | LPT > RLPT | LPT = RLPT | |
| S~[1,3] | 11.8% | 44.3% | 43.9% | 20.7% | 47.1% | 32.1% | 24.3% | 57.9% | 17.9% |
| S~[1,5] | 14.3% | 33.2% | 52.5% | 13.2% | 54.3% | 32.5% | 21.4% | 62.5% | 16.1% |
| S~[1,7] | 12.1% | 36.8% | 51.1% | 18.2% | 49.6% | 32.1% | 23.6% | 55.4% | 21.1% |
| Machine | Speed | Job | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 4 | 8 | 3 | 7 | 6 | 1 | 5 | 2 | 9 | ||
| 1 | 1 | 30 | 26 | 24 | 22 | 20 | 18 | 16 | 14 | 14 |
| 2 | 2 | 15 | 13 | 12 | 11 | 10 | 9 | 8 | 7 | 7 |
| 3 | 4 | 7.5 | 6.5 | 6 | 5.5 | 5 | 4.5 | 4 | 3.5 | 3.5 |
| 4 | 5 | 6 | 5.2 | 4.8 | 4.4 | 4 | 3.6 | 3.2 | 2.8 | 2.8 |
| Algorithm | Machine | Schedule of Jobs | Completion Time | Max. Iterations |
|---|---|---|---|---|
| GA | 1 | 5 | 14 | 12 |
| 2 | 1, 9 | 16 | ||
| 3 | 2, 6, 8 | 15.5 | ||
| 4 | 4, 7, 3 | 15.2 | ||
| TS | 1 | 2 | 14 | 5000 |
| 2 | 4 | 15 | ||
| 3 | 1, 3, 6 | 15.5 | ||
| 4 | 5, 7, 8, 9 | 15.6 | ||
| LVNS | 1 | 2 | 14 | 1 |
| 2 | 4 | 15 | ||
| 3 | 5, 6, 8 | 15.5 | ||
| 4 | 1, 3, 7, 9 | 15.6 | ||
| RVNS | 1 | 9 | 14 | 10 |
| 2 | 4 | 15 | ||
| 3 | 5, 6, 8 | 15.5 | ||
| 4 | 1, 2, 3, 7 | 15.6 |
| S~[1,3] | S~[1,5] | S~[1,7] | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n/m | m | n | p~[1,25] | p~[1,50] | p~[1,100] | p~[1,25] | p~[1,50] | p~[1,100] | p~[1,25] | p~[1,50] | p~[1,100] | |||||||||
| LVNS | RVNS | LVNS | RVNS | LVNS | RVNS | LVNS | RVNS | LVNS | RVNS | LVNS | RVNS | LVNS | RVNS | LVNS | RVNS | LVNS | RVNS | |||
| 2 | 3 | 6 | 9 | 10 | 10 | 10 | 9 | 10 | 8 | 10 | 10 | 10 | 9 | 10 | 10 | 9 | 10 | 10 | 9 | 10 |
| 4 | 8 | 8 | 10 | 9 | 10 | 7 | 10 | 8 | 10 | 8 | 9 | 9 | 10 | 9 | 10 | 9 | 10 | 6 | 10 | |
| 5 | 10 | 6 | 9 | 8 | 10 | 5 | 10 | 5 | 9 | 6 | 8 | 8 | 10 | 6 | 10 | 7 | 10 | 6 | 10 | |
| 10 | 20 | 0 | 2 | 0 | 3 | 1 | 2 | 1 | 4 | 0 | 3 | 1 | 1 | 1 | 2 | 1 | 5 | 1 | 2 | |
| 3 | 3 | 9 | 6 | 9 | 6 | 9 | 5 | 10 | 6 | 10 | 4 | 10 | 6 | 10 | 8 | 10 | 10 | 10 | 8 | 10 |
| 4 | 12 | 6 | 10 | 6 | 8 | 2 | 10 | 4 | 10 | 5 | 10 | 3 | 8 | 9 | 10 | 3 | 9 | 1 | 9 | |
| 5 | 15 | 6 | 10 | 6 | 9 | 1 | 8 | 4 | 10 | 4 | 8 | 2 | 7 | 7 | 9 | 6 | 10 | 2 | 7 | |
| 4 | 3 | 12 | 9 | 10 | 8 | 10 | 6 | 9 | 10 | 10 | 8 | 10 | 7 | 9 | 9 | 10 | 8 | 9 | 5 | 9 |
| 4 | 16 | 9 | 10 | 9 | 10 | 1 | 9 | 8 | 10 | 5 | 8 | 6 | 10 | 6 | 10 | 9 | 10 | 5 | 7 | |
| 5 | 20 | 10 | 10 | 7 | 10 | 5 | 9 | 9 | 10 | 6 | 10 | 5 | 8 | 8 | 10 | 7 | 10 | 3 | 9 | |
| 5 | 3 | 15 | 9 | 10 | 9 | 10 | 7 | 10 | 10 | 10 | 9 | 10 | 5 | 10 | 10 | 10 | 10 | 10 | 7 | 10 |
| 4 | 20 | 10 | 10 | 9 | 10 | 8 | 10 | 8 | 10 | 10 | 10 | 9 | 10 | 10 | 10 | 6 | 10 | 5 | 10 | |
| Average | 0.733 | 0.917 | 0.725 | 0.908 | 0.475 | 0.892 | 0.675 | 0.942 | 0.625 | 0.883 | 0.583 | 0.858 | 0.775 | 0.917 | 0.717 | 0.942 | 0.483 | 0.858 | ||
| S~[1,3] | S~[1,5] | S~[1,7] | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n/m | m | n | p~[1,25] | p~[1,50] | p~[1,100] | p~[1,25] | p~[1,50] | p~[1,100] | p~[1,25] | p~[1,50] | p~[1,100] | |||||||||
| LVNS | RVNS | LVNS | RVNS | LVNS | RVNS | LVNS | RVNS | LVNS | RVNS | LVNS | RVNS | LVNS | RVNS | LVNS | RVNS | LVNS | RVNS | |||
| 2 | 3 | 6 | 0.179 | 0.000 | 0.000 | 0.000 | 0.055 | 0.000 | 0.651 | 0.000 | 0.000 | 0.000 | 0.374 | 0.000 | 0.000 | 0.100 | 0.000 | 0.000 | 0.066 | 0.000 |
| 4 | 8 | 0.606 | 0.000 | 0.580 | 0.000 | 0.297 | 0.000 | 0.306 | 0.000 | 0.405 | 0.211 | 0.296 | 0.000 | 0.233 | 0.000 | 0.233 | 0.000 | 1.794 | 0.000 | |
| 5 | 10 | 0.623 | 0.023 | 0.807 | 0.000 | 1.373 | 0.000 | 2.866 | 0.267 | 0.318 | 0.154 | 0.102 | 0.000 | 0.430 | 0.000 | 0.581 | 0.000 | 0.573 | 0.000 | |
| 10 | 20 | 2.654 | 0.790 | 1.833 | 0.512 | 1.955 | 0.674 | 2.034 | 0.386 | 1.468 | 0.703 | 1.683 | 0.800 | 1.998 | 1.073 | 1.206 | 0.525 | 2.868 | 0.809 | |
| 3 | 3 | 9 | 0.496 | 0.149 | 0.409 | 0.060 | 0.524 | 0.000 | 0.438 | 0.000 | 0.704 | 0.000 | 0.688 | 0.000 | 0.586 | 0.000 | 0.000 | 0.000 | 0.100 | 0.000 |
| 4 | 12 | 0.408 | 0.000 | 0.286 | 0.096 | 0.779 | 0.000 | 0.873 | 0.000 | 0.337 | 0.000 | 1.018 | 0.234 | 0.071 | 0.000 | 0.633 | 0.033 | 0.955 | 0.027 | |
| 5 | 15 | 0.495 | 0.000 | 0.092 | 0.009 | 0.465 | 0.024 | 0.605 | 0.000 | 0.533 | 0.123 | 0.600 | 0.043 | 0.177 | 0.030 | 0.251 | 0.000 | 0.452 | 0.115 | |
| 10 | 30 | 1.247 | 1.065 | 1.059 | 0.665 | 0.740 | 0.386 | 1.154 | 1.021 | 0.777 | 0.697 | 0.693 | 0.386 | 1.367 | 1.178 | 1.110 | 0.545 | 0.847 | 0.534 | |
| 4 | 3 | 12 | 0.041 | 0.000 | 0.104 | 0.000 | 0.091 | 0.012 | 0.000 | 0.000 | 0.138 | 0.000 | 0.037 | 0.004 | 0.057 | 0.000 | 0.067 | 0.023 | 0.188 | 0.014 |
| 4 | 16 | 0.046 | 0.000 | 0.024 | 0.000 | 0.421 | 0.007 | 0.102 | 0.000 | 0.083 | 0.075 | 0.175 | 0.000 | 0.184 | 0.000 | 0.034 | 0.000 | 0.097 | 0.034 | |
| 5 | 20 | 0.000 | 0.000 | 0.040 | 0.000 | 0.094 | 0.017 | 0.042 | 0.000 | 0.153 | 0.000 | 0.104 | 0.028 | 0.053 | 0.000 | 0.157 | 0.000 | 0.342 | 0.018 | |
| 10 | 40 | 0.889 | 0.889 | 0.538 | 0.478 | 0.328 | 0.233 | 0.820 | 0.820 | 0.492 | 0.447 | 0.348 | 0.226 | 0.891 | 0.858 | 0.545 | 0.502 | 0.384 | 0.237 | |
| 5 | 3 | 15 | 0.058 | 0.000 | 0.053 | 0.000 | 0.022 | 0.000 | 0.000 | 0.000 | 0.062 | 0.000 | 0.135 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.072 | 0.000 |
| 4 | 20 | 0.000 | 0.000 | 0.010 | 0.000 | 0.011 | 0.000 | 0.076 | 0.000 | 0.000 | 0.000 | 0.018 | 0.000 | 0.000 | 0.000 | 0.082 | 0.000 | 0.071 | 0.000 | |
| 5 | 25 | 0.635 | 0.610 | 0.381 | 0.348 | 0.167 | 0.167 | 0.586 | 0.586 | 0.288 | 0.287 | 0.219 | 0.148 | 0.655 | 0.655 | 0.395 | 0.309 | 0.202 | 0.139 | |
| 10 | 50 | 0.663 | 0.663 | 0.418 | 0.395 | 0.187 | 0.172 | 0.654 | 0.654 | 0.342 | 0.340 | 0.200 | 0.176 | 0.704 | 0.704 | 0.351 | 0.326 | 0.191 | 0.172 | |
| 10 | 3 | 30 | 0.253 | 0.253 | 0.134 | 0.134 | 0.069 | 0.069 | 0.269 | 0.269 | 0.136 | 0.136 | 0.082 | 0.082 | 0.303 | 0.303 | 0.125 | 0.125 | 0.076 | 0.076 |
| 4 | 40 | 0.345 | 0.345 | 0.165 | 0.165 | 0.074 | 0.074 | 0.292 | 0.292 | 0.166 | 0.166 | 0.089 | 0.089 | 0.270 | 0.270 | 0.155 | 0.155 | 0.074 | 0.074 | |
| 5 | 50 | 0.328 | 0.328 | 0.158 | 0.158 | 0.075 | 0.075 | 0.297 | 0.297 | 0.159 | 0.159 | 0.080 | 0.080 | 0.332 | 0.332 | 0.157 | 0.157 | 0.087 | 0.087 | |
| 10 | 100 | 0.429 | 0.429 | 0.158 | 0.158 | 0.092 | 0.092 | 0.338 | 0.338 | 0.183 | 0.183 | 0.099 | 0.099 | 0.335 | 0.335 | 0.162 | 0.162 | 0.085 | 0.085 | |
| 20 | 3 | 60 | 0.106 | 0.106 | 0.067 | 0.067 | 0.032 | 0.032 | 0.112 | 0.112 | 0.058 | 0.058 | 0.031 | 0.031 | 0.135 | 0.135 | 0.067 | 0.067 | 0.028 | 0.028 |
| 4 | 80 | 0.131 | 0.131 | 0.068 | 0.068 | 0.031 | 0.031 | 0.173 | 0.173 | 0.061 | 0.061 | 0.032 | 0.032 | 0.126 | 0.126 | 0.058 | 0.058 | 0.035 | 0.035 | |
| 5 | 100 | 0.164 | 0.164 | 0.080 | 0.080 | 0.036 | 0.036 | 0.137 | 0.137 | 0.082 | 0.082 | 0.044 | 0.044 | 0.159 | 0.159 | 0.078 | 0.078 | 0.046 | 0.046 | |
| 10 | 200 | 0.165 | 0.165 | 0.084 | 0.084 | 0.044 | 0.044 | 0.172 | 0.172 | 0.079 | 0.079 | 0.045 | 0.045 | 0.168 | 0.168 | 0.089 | 0.089 | 0.042 | 0.042 | |
| 30 | 3 | 90 | 0.066 | 0.066 | 0.040 | 0.040 | 0.017 | 0.017 | 0.103 | 0.103 | 0.052 | 0.052 | 0.022 | 0.022 | 0.094 | 0.094 | 0.037 | 0.037 | 0.022 | 0.022 |
| 4 | 120 | 0.121 | 0.121 | 0.044 | 0.044 | 0.022 | 0.022 | 0.097 | 0.097 | 0.045 | 0.045 | 0.023 | 0.023 | 0.082 | 0.082 | 0.045 | 0.045 | 0.026 | 0.026 | |
| 5 | 150 | 0.097 | 0.097 | 0.053 | 0.053 | 0.024 | 0.024 | 0.109 | 0.109 | 0.051 | 0.051 | 0.027 | 0.027 | 0.089 | 0.089 | 0.051 | 0.051 | 0.025 | 0.025 | |
| 10 | 300 | 0.120 | 0.120 | 0.060 | 0.060 | 0.030 | 0.030 | 0.109 | 0.109 | 0.064 | 0.064 | 0.029 | 0.029 | 0.120 | 0.120 | 0.057 | 0.057 | 0.031 | 0.031 | |
| Average | 0.406 | 0.233 | 0.277 | 0.131 | 0.288 | 0.080 | 0.479 | 0.212 | 0.259 | 0.149 | 0.260 | 0.095 | 0.343 | 0.243 | 0.240 | 0.119 | 0.349 | 0.096 | ||
| p~[1,25] | p~[1,50] | p~[1,100] | |||||||
|---|---|---|---|---|---|---|---|---|---|
| LVNS < RVNS | LVNS > RVNS | LVNS = RVNS | LVNS < RVNS | LVNS > RVNS | LVNS = RVNS | LVNS < RVNS | LVNS > RVNS | LVNS = RVNS | |
| S~[1,3] | 0.0% | 11.4% | 88.6% | 0.4% | 17.1% | 82.5% | 1.1% | 28.6% | 70.4% |
| S~[1,5] | 0.4% | 13.9% | 85.7% | 0.7% | 17.9% | 81.4% | 1.1% | 26.1% | 72.9% |
| S~[1,7] | 0.4% | 11.1% | 88.6% | 0.0% | 16.4% | 83.6% | 1.1% | 27.9% | 71.1% |
| S~[1,3] | S~[1,5] | S~[1,7] | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n/m | m | n | p~[1,25] | p~[1,50] | p~[1,100] | p~[1,25] | p~[1,50] | p~[1,100] | p~[1,25] | p~[1,50] | p~[1,100] | |||||||||
| LVNS | RVNS | LVNS | RVNS | LVNS | RVNS | LVNS | RVNS | LVNS | RVNS | LVNS | RVNS | LVNS | RVNS | LVNS | RVNS | LVNS | RVNS | |||
| 2 | 3 | 6 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 4 | 8 | 0.000 | 0.001 | 0.000 | 0.001 | 0.000 | 0.001 | 0.000 | 0.001 | 0.000 | 0.001 | 0.000 | 0.001 | 0.000 | 0.001 | 0.000 | 0.001 | 0.000 | 0.001 | |
| 5 | 10 | 0.000 | 0.001 | 0.000 | 0.001 | 0.000 | 0.001 | 0.000 | 0.001 | 0.000 | 0.001 | 0.000 | 0.001 | 0.000 | 0.001 | 0.000 | 0.001 | 0.000 | 0.001 | |
| 10 | 20 | 0.000 | 0.004 | 0.000 | 0.005 | 0.000 | 0.005 | 0.000 | 0.004 | 0.000 | 0.005 | 0.000 | 0.006 | 0.000 | 0.005 | 0.000 | 0.005 | 0.000 | 0.005 | |
| 3 | 3 | 9 | 0.000 | 0.001 | 0.000 | 0.001 | 0.000 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 |
| 4 | 12 | 0.000 | 0.001 | 0.000 | 0.001 | 0.000 | 0.001 | 0.000 | 0.001 | 0.000 | 0.001 | 0.000 | 0.001 | 0.000 | 0.001 | 0.000 | 0.001 | 0.000 | 0.001 | |
| 5 | 15 | 0.000 | 0.001 | 0.000 | 0.002 | 0.000 | 0.002 | 0.000 | 0.001 | 0.000 | 0.002 | 0.000 | 0.002 | 0.000 | 0.001 | 0.000 | 0.002 | 0.000 | 0.002 | |
| 10 | 30 | 0.000 | 0.005 | 0.000 | 0.006 | 0.000 | 0.009 | 0.000 | 0.006 | 0.000 | 0.008 | 0.000 | 0.008 | 0.000 | 0.006 | 0.000 | 0.008 | 0.000 | 0.009 | |
| 4 | 3 | 12 | 0.000 | 0.001 | 0.000 | 0.001 | 0.000 | 0.001 | 0.000 | 0.001 | 0.000 | 0.001 | 0.000 | 0.001 | 0.000 | 0.001 | 0.000 | 0.001 | 0.000 | 0.001 |
| 4 | 16 | 0.000 | 0.001 | 0.000 | 0.001 | 0.000 | 0.002 | 0.000 | 0.001 | 0.000 | 0.001 | 0.000 | 0.002 | 0.000 | 0.001 | 0.000 | 0.001 | 0.000 | 0.002 | |
| 5 | 20 | 0.000 | 0.002 | 0.000 | 0.002 | 0.000 | 0.003 | 0.000 | 0.002 | 0.000 | 0.002 | 0.000 | 0.002 | 0.000 | 0.002 | 0.000 | 0.002 | 0.000 | 0.003 | |
| 10 | 40 | 0.000 | 0.006 | 0.000 | 0.008 | 0.000 | 0.011 | 0.000 | 0.006 | 0.000 | 0.009 | 0.000 | 0.012 | 0.000 | 0.007 | 0.000 | 0.010 | 0.000 | 0.013 | |
| 5 | 3 | 15 | 0.000 | 0.001 | 0.000 | 0.001 | 0.000 | 0.001 | 0.000 | 0.001 | 0.000 | 0.001 | 0.000 | 0.001 | 0.000 | 0.001 | 0.000 | 0.001 | 0.000 | 0.001 |
| 4 | 20 | 0.000 | 0.001 | 0.000 | 0.002 | 0.000 | 0.002 | 0.000 | 0.002 | 0.000 | 0.002 | 0.000 | 0.002 | 0.000 | 0.002 | 0.000 | 0.002 | 0.000 | 0.002 | |
| 5 | 25 | 0.000 | 0.002 | 0.000 | 0.003 | 0.000 | 0.004 | 0.000 | 0.002 | 0.000 | 0.003 | 0.000 | 0.004 | 0.000 | 0.003 | 0.000 | 0.003 | 0.000 | 0.004 | |
| 10 | 50 | 0.000 | 0.008 | 0.000 | 0.010 | 0.000 | 0.015 | 0.000 | 0.009 | 0.000 | 0.012 | 0.000 | 0.016 | 0.000 | 0.008 | 0.000 | 0.014 | 0.000 | 0.018 | |
| 10 | 3 | 30 | 0.000 | 0.005 | 0.000 | 0.006 | 0.000 | 0.007 | 0.000 | 0.005 | 0.000 | 0.006 | 0.000 | 0.007 | 0.000 | 0.006 | 0.000 | 0.006 | 0.000 | 0.007 |
| 4 | 40 | 0.000 | 0.011 | 0.000 | 0.011 | 0.000 | 0.014 | 0.000 | 0.012 | 0.000 | 0.013 | 0.000 | 0.014 | 0.000 | 0.011 | 0.000 | 0.014 | 0.000 | 0.016 | |
| 5 | 50 | 0.000 | 0.015 | 0.000 | 0.014 | 0.000 | 0.023 | 0.000 | 0.014 | 0.000 | 0.015 | 0.000 | 0.025 | 0.000 | 0.016 | 0.000 | 0.023 | 0.000 | 0.025 | |
| 10 | 100 | 0.000 | 0.035 | 0.001 | 0.058 | 0.001 | 0.079 | 0.000 | 0.044 | 0.000 | 0.062 | 0.001 | 0.084 | 0.000 | 0.061 | 0.001 | 0.080 | 0.001 | 0.120 | |
| 20 | 3 | 60 | 0.000 | 0.074 | 0.000 | 0.081 | 0.000 | 0.084 | 0.000 | 0.060 | 0.000 | 0.059 | 0.000 | 0.084 | 0.000 | 0.060 | 0.000 | 0.069 | 0.000 | 0.075 |
| 4 | 80 | 0.001 | 0.124 | 0.000 | 0.133 | 0.001 | 0.165 | 0.000 | 0.132 | 0.000 | 0.116 | 0.001 | 0.166 | 0.000 | 0.141 | 0.001 | 0.161 | 0.001 | 0.185 | |
| 5 | 100 | 0.001 | 0.178 | 0.001 | 0.212 | 0.001 | 0.264 | 0.001 | 0.257 | 0.001 | 0.220 | 0.001 | 0.234 | 0.001 | 0.215 | 0.001 | 0.247 | 0.001 | 0.275 | |
| 10 | 200 | 0.002 | 0.451 | 0.002 | 0.508 | 0.002 | 0.585 | 0.002 | 0.490 | 0.002 | 0.488 | 0.003 | 0.811 | 0.003 | 0.802 | 0.003 | 0.816 | 0.005 | 1.291 | |
| 30 | 3 | 90 | 0.001 | 0.349 | 0.001 | 0.396 | 0.001 | 0.389 | 0.001 | 0.312 | 0.001 | 0.361 | 0.001 | 0.348 | 0.001 | 0.329 | 0.001 | 0.328 | 0.001 | 0.386 |
| 4 | 120 | 0.003 | 0.640 | 0.002 | 0.522 | 0.002 | 0.788 | 0.002 | 0.630 | 0.002 | 0.708 | 0.003 | 0.833 | 0.003 | 0.819 | 0.002 | 0.732 | 0.003 | 0.952 | |
| 5 | 150 | 0.003 | 0.883 | 0.002 | 0.733 | 0.003 | 1.008 | 0.003 | 0.747 | 0.002 | 0.696 | 0.003 | 1.046 | 0.003 | 1.089 | 0.004 | 1.164 | 0.005 | 1.531 | |
| 10 | 300 | 0.007 | 1.536 | 0.008 | 2.540 | 0.011 | 3.200 | 0.008 | 2.329 | 0.012 | 3.528 | 0.012 | 4.005 | 0.013 | 4.093 | 0.017 | 5.027 | 0.011 | 3.793 | |
| Average | 0.001 | 0.155 | 0.001 | 0.188 | 0.001 | 0.238 | 0.001 | 0.181 | 0.001 | 0.226 | 0.001 | 0.276 | 0.001 | 0.274 | 0.001 | 0.311 | 0.001 | 0.311 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bamatraf, K.; Gharbi, A. Variable Neighborhood Search for Minimizing the Makespan in a Uniform Parallel Machine Scheduling. Systems 2024, 12, 221. https://doi.org/10.3390/systems12060221
Bamatraf K, Gharbi A. Variable Neighborhood Search for Minimizing the Makespan in a Uniform Parallel Machine Scheduling. Systems. 2024; 12(6):221. https://doi.org/10.3390/systems12060221
Chicago/Turabian StyleBamatraf, Khaled, and Anis Gharbi. 2024. "Variable Neighborhood Search for Minimizing the Makespan in a Uniform Parallel Machine Scheduling" Systems 12, no. 6: 221. https://doi.org/10.3390/systems12060221
APA StyleBamatraf, K., & Gharbi, A. (2024). Variable Neighborhood Search for Minimizing the Makespan in a Uniform Parallel Machine Scheduling. Systems, 12(6), 221. https://doi.org/10.3390/systems12060221







