Abstract
The product design process, fraught with uncertainties and ambiguities in its requirements and constraints, commonly traverses multiple stages, each emphasizing distinct design aspects. This engenders heterogeneity in decision-making criteria, rendering the effective integration of information from various stages of product design decision-making (PDDM) a pivotal task in identifying the optimal design solution. Surprisingly, limited research has attended to the challenge of consolidating such heterogeneous information across multiple PDDM stages. To bridge this gap, our study employs real numbers, interval numbers, and linguistic terms to capture the heterogeneous judgments of decision-makers. We fuse the Maximization Deviation Method with the analytic hierarchy process (AHP) for determining indicators’ weights, while decision-makers’ weights are derived through a dual consideration of uncertainty measure using fuzzy entropy and a distance-minimization model applied to the PDDM matrix for achieving consistency. Leveraging the advantage of axiomatic design, product design alternatives are evaluated based on their PDDM information content of PDDM matrices. Given the multistage nature of product design, stages’ weights are computed by assessing the information content and consistency degree of PDDM matrices at each stage. Ultimately, our approach achieves multistage heterogeneous decision-making fusion in product design through information axiom weighting. A case study involving the decision-making process for a specific numerical control machine design illustrates the efficacy of our method in integrating multistage heterogeneous PDDM data, yielding a comprehensive perspective on the viability of product design schemes. Results show that the ranking sequence of the product design schemes solidifies to x3 > x2 > x1 in stages 2 and 3 of PDDM, diverging from the initial order observed in stage 1 (x2 > x3 > x1), while the fused result from the multistage heterogeneous PDDM analysis aligns with the later stages’ rankings, indicating the credibility and persuasiveness are fortified. This methodology thus offers a robust framework for synthesizing and navigating the uncertainties and complexities inherent in multistage heterogeneous PDDM contexts.
1. Introduction
Product design is a crucial process in the development of any successful product and can help establish a competitive advantage for enterprises in a highly competitive market. It encompasses a range of activities from understanding user needs and market trends to conceptualizing, prototyping, and finalizing the design that will be manufactured. A pivotal stage within this sequence is ideation and concept generation. With research insights in hand, designers engage in brainstorming and generate multiple product ideas and concepts. Prior to transforming design concepts into physical prototypes, it is crucial to efficiently assess and choose the most viable design proposals based on a predefined set of criteria. This necessitates that decision-makers execute product design decision-making (PDDM) effectively. However, due to the ill-defined nature of design problems [1], iteration arises as an essential feature of the product design process. To accelerate the convergence in product design iterations, the integration of information processing and decision-making is paramount to facilitate the co-evolution of problems and solutions [2]. While achieving convergence usually necessitates going through multiple product design stages, rendering multistage PDDM and effective information fusion among multiple PDDM phases indispensable.
Generally, the PDDM process involves assessing and determining the optimal product on the basis of judgements and preferences of product design schemes provided by several decision-makers with respect to a set of attributes [3], which belongs to a typical multi-criteria group decision-making (GDM) problem. Product design schemes are evaluated against criteria such as feasibility, cost-effectiveness, user desirability, and alignment with business goals. Techniques like scoring models, weight obtaining, and group aggregating help in narrowing down the options to the most promising concepts. Decision-makers evaluate product design alternatives by assigning scores in accordance with a predefined criterion set. Weight identification is employed to ascertain the relative significance of both the criteria and the decision-makers themselves, guiding the integration of individual assessments through aggregation methodologies. Owing to the inherently interdisciplinary nature of product design, decision-makers with diverse professional backgrounds are enlisted to contribute to the PDDM process. Consequently, single type information is inadequate to express the decision-making information across various types of criteria. Real numbers, intervals, linguistic terms, and other types of fuzzy numbers [4,5,6] are employed to depict decision-makers’ evaluations and the aggregation of heterogeneous PDDM information emerges as a vital process in deriving the optimal design solution. To address the challenge of handling the heterogeneous PDDM information, numerous methodologies have been put forward, which involve heterogeneous information transformation [7], weight determination [8], consensus-reaching [9], and PDDM information aggregation [10]. These studies provide strong support for mitigating cognition bias, bridging knowledge disparities among decision-makers, and fortifying the reliability of obtained PDDM results. However, heterogeneity among multiple PDDM stages is the main barrier that impedes the attainment of a holistic and comprehensive understanding of product design schemes. Given that product design often spans several stages, the focus of PDDM evolves throughout the product development, and the derived heterogeneity among multiple PDDM stages is seldom scrutinized and is worthy of further study.
In addressing the heterogeneity challenge in product design, researchers tend to harmonize different information types-including triangular fuzzy numbers, interval numbers, and real numbers into a unified format. Subsequently, they employ distance algorithms to quantify the dissimilarities between two design alternatives as part of the information aggregation process. For instance, Wang et al. [11] transformed qualitative product evaluations from questionnaire into generalized trapezoidal fuzzy numbers and utilized cloud model for ranking product design schemes. Lai et al. [12] combined self-reporting, eye-tracking, and electroencephalogram data for the evaluation of product appearance design, and proposed to transfer the probabilistic linguistic term set with interval uncertainty from self-reporting data to a crisp number to facilitate the comparison of automobile appearance design schemes. Yang et al. [13] utilized three-parameter interval grey numbers to unify interval numbers and linguistic terms to depict decision-makers’ judgement about product design schemes. Nonetheless, in the context of multiple product design stages, each phase may prioritize distinct aspects and employ heterogeneous evaluation criteria. Simply unifying decision-makers’ diverse assessments and applying distance functions fails to adequately gauge the discrepancies between these stages, owing to the inconsistency among indicators. Furthermore, existing studies infrequently addresses the integration of multistage PDDM information to achieve a holistic perspective of product design schemes. These challenges constitute major impediments to the efficacious execution of PDDM. While the information axiom of axiomatic design is similar to that of multi-criteria GDM, it is conducive to gauging group information and has been applied to GDM in various fields of product design [6,14]. Following previous research, this study aims to tackle the challenge of heterogeneous information across multiple PDDM stages and to attain an integrated, comprehensive understanding of design solutions spanning these phases. To this end, we propose a novel multistage method for fusing heterogeneous information based on axiomatic design. This method incorporates real numbers, interval numbers, and linguistic terms to capture decision-makers’ appraisals, which serve to mitigate uncertainties stemming from individual variability and express the heterogeneity of PDDM criteria. Indicators’ weights are ascertained via a synergy of the maximizing deviation method and analytic hierarchy process (AHP), whereas decision-makers’ weights are derived by merging the uncertainty degree measured by fuzzy entropy and the consistency degree solved by a distance minimizing model of the PDDM matrix. Exploiting axiomatic design’s capacity to gauge information content, each product design scheme is assessed according to its information content. Stage-weight computations take into account both the information content and consistency of decision-making matrices at every stage. Finally, the multistage heterogeneous information fusion of PDDM is accomplished via the application of an information axiom-driven weighting methodology.
The remainder of this paper is organized as follows. A brief literature review of PDDM is given in Section 2. In Section 3, the description of heterogeneous PDDM information is discussed. Section 4 is devoted to weight calculation for decision-makers and PDDM indicators. The process of multistage heterogeneous information fusion of PDDM based on axiomatic design is studied in Section 5. Section 6 illustrates a case study of the proposed method and highlights the implications. The paper ends with conclusions in Section 7.
2. Literature Review
PDDM involves two critical steps, namely the determination of indicator weights and the ranking of design alternatives [11]. Inspired by the need to address cognitive bias among decision-makers, obtaining objective and reasonable weights forms the bedrock for producing a scientifically sound and dependable outcome of PDDM. A prominently and widely adopted technique is the AHP method proposed by Satty [15]. By integrating the fuzzy theory, Laarhoven and Pedrycz [16] proposed the use of the fuzzy AHP to replace precise pairwise comparisons with triangular fuzzy numbers. As interdependent relationships may exist within indicators, Satty [17] studied the Analytic Network Process (ANP) from the fundamental scale of AHP. Combined with the notion of a fuzzy set proposed by Zadeh [18], many GDM techniques are employed and applied for PDDM. For instance, Yang et al. [13] utilized an interval AHP to determine the weights of decision-making indicators and decision-makers. Ayag [19] proposed to calculate the weights of indicators and ranking alternatives based on technique for order preference by similarity to an ideal scheme (TOPSIS) and ANP. Sarwar and Bashir [20] integrated cloud rough numbers, AHP, and the VlseKriterijumska Optimizacija I Kompromisno Resenje (VIKOR) method to evaluate design concepts. However, PDDM encompasses a degree of subjectivity, as it relies, either fully or partially, on decision-makers’ subjective evaluations. In response, academics strive to explore alternative methodologies to mitigate this challenge. Mishre et al. [21] developed an objective weighting procedure by using the maximum deviation and general distance measure to compute attributes’ weights. Ullah et al. [22] used information entropy weighting method to calculate the criterion weights for a variety of attributes, where the lower the information entropy the more information it provides and the greater the criterion weights. Hayat et al. [23] integrated soft sets, TOPSIS, and the Shannon entropy weight method to capture and rank preferences based on customers’ subjective requirements. Sarwar [24] employed two types of hybrid weighting methods by using objective and subjective aspects of uncertainty to identify weights of assessment criteria. Touqeer et al. [25] established an optimization model based on maximizing deviation method to calculate the weight of indicators under unknown weight environment. Fei et al. [26] indicated that the reliability of decision-making data diminishes over time, and accordingly, they calculated period weight employing both the evidential best–worst method and entropy weight method to rank the alternatives.
In product design, decision-makers’ evaluations are notably diverse due to their varied knowledge backgrounds, experiences, and personal objectives [27]. To align these disparate perspectives and enhance decision-making efficacy, a consensus reaching process (CRP) is customarily implemented before ranking design alternatives, ensuring broad satisfaction and facilitating efficient product development implementation [28]. Several methodologies have been proposed to foster consensus effectively. Liang et al. [29] introduced a Dynamic Heterogeneous Social Network Consensus Reaching Model (DHSNCRM), utilizing a two-stage feedback mechanism and minimizing adjustment distances to guide experts towards consensus and establish a unified priority of failure modes, which is useful in scenarios where experts may have different initial preferences. Zhou et al. [30] developed the additive consistency index for Complete Interval Distributed Preference Relations (CIDPR) to quantify experts’ preference consistency, thereby aiding group consensus attainment. It focuses on the consistency of preferences expressed in interval form. Palomares et al. [31] employed fuzzy preference relations and clustering techniques to manage large decision-maker groups, enabling timely identification of non-cooperative individuals. This approach is aimed at identifying and managing dissent in large and diverse decision-making groups. Gupta [32] mapped the consensus evolution in GDM via analyzing members’ interrelationships, offering insights into the consensus-reaching dynamics. This allows for tracking and understanding how consensus is built or eroded over time. Lastly, Calache et al. [33] integrated intuitionistic and hesitant fuzzy sets to address the ambiguity in decision-makers’ evaluations, employing a genetic algorithm to determine decision-makers’ weights for achieving higher consensus levels without necessitating adjustments to initial assessments. This method allows for flexibility in handling uncertainty and diversity in evaluations. These approaches collectively contribute to advancing the field by enhancing consensus efficiency and accuracy in PDDM processes.
The aggregation of decision-making data into a cohesive framework is pivotal for pinpointing the most efficacious product design strategy. This crucial step has been approached through diverse methodologies by various researchers. Enyoghasi et al. [34] adopted the Bayesian Belief Network (BBN) to systematically evaluate design risks, pinpoint critical risk factors and their propagation pathways, leveraging an operational risk index for comprehensive risk assessment and optimal scheme identification. In a different vein, Ullah et al. [22] employed TOPSIS as their principal tool for selecting the superior design alternative. Li et al. [35] segmented the multi-objective analysis into two stages: optimizing solutions and subsequently selecting the ideal one, thereby adding a layer of meticulousness to the decision-making process. Zavadskas et al. [36] combined a quartet of methodologies—Minkowski distance, fuzzy TOPSIS, ARAS-F, and the fuzzy weighted product method—into a strategic model, enhancing the problem’s elucidation and facilitating the rationale behind the solution choice. Sarwar [24] ingeniously integrated interval rough numbers, cloud model theory, and the VIKOR method to consolidate decision-making data, specifically tailored for identifying the optimal refrigerator design. Lastly, Touqeer et al. [25] resorted to the fuzzy ordered weighted averaging technique to aggregate decision inputs, further enriching the array of strategies for consolidating and navigating complex decision-making landscapes in product design. Collectively, these methodologies underscore the multifaceted nature of aggregating and processing decision-making data, each contributing unique strengths to the pursuit of the most advantageous product design scheme.
While the aforementioned studies have marked notable progress in determining weights and aggregating PDDM information for ranking product design alternatives, the evolution of product design inherently necessitates the consideration of multistage PDDM processes. Owing to the heterogeneity of PDDM indicators and subjectivity among decision-makers, obtaining a significant level of uncertainty in the PDDM results is likely. The AHP-based method boasts the efficiency in promptly deriving a fixed weights of product indicators, yet it tends to overlook the variability in decision-makers’ judgements, particularly in multistage PDDM contexts where sequential assessments might amplify uncertainty effects. Conventionally, CRP entails iterative consensus measurement and feedback loops to ensure PDDM outcomes align with the majority viewpoint. However, the indicators are by and large not changed in this process, which does not accommodate the evolving design priorities across different stages encountered in our study. Given that design focuses shift, leading to varying indicators per stage, implementing CRP across multiple PDDM phases becomes impractical. Consequently, we forgo CRP and instead adopt consistency assessment as a preparatory step for integrating information from diverse PDDM stages, thereby facilitating a comprehensive decision-making framework. Furthermore, the outcomes from various product design stages in PDDM are interconnected and exert influence on the successive stages of product development. Effectively integrating PDDM insights across these stages is crucial for comprehensively embodying decision-makers’ viewpoints and understandings of design propositions. Failure to manage this integration adeptly can lead to unnecessary redundant iterations of product development. Nevertheless, research on heterogeneous information fusion of multistage PDDM is still rare. Prompted by preceding research, this study introduces a novel multistage heterogeneous information fusion method for PDDM, the overall framework illustrated in Figure 1. The approach employs concrete numbers, interval numbers, and linguistic variables to represent decision-makers’ assessments regarding the heterogeneous indicators of product design schemes. It harnesses the strengths of AHP and the maximizing deviation method to identify the indicators’ weights, combines fuzzy entropy and a distance minimizing model to ascertain decision-makers’ weights, and employs axiomatic design principles to calculate stage weights based on information content and consistency. This integrated strategy aggregates the multistage PDDM information across stages, thereby not only mitigating uncertainty in the product development process but also fostering a more cohesive and inclusive linkage among disparate PDDM phases.
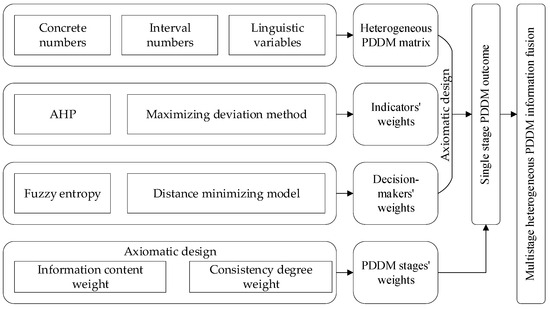
Figure 1.
The overall framework.
3. Description of Heterogeneous PDDM Information
Initiating with product designers proposing their respective design solutions in light of specified requirements and design constraints, a multidisciplinary panel of decision-makers, each bringing unique professional expertise, is assembled to embark on the PDDM procedure. Our research outlines a systematic approach comprising several sequential steps: (1) Decision-makers engage in discussions and share their expertise, culminating in a consensus on the key PDDM evaluation criteria; (2) Indicators are assessed in comparative pairs to establish their relative significance, generating a pairwise comparison matrix; (3) Each proposed design solution is meticulously evaluated against the established indicators; (4) Both indicator and decision-maker weights are computed, reflecting their relative importance and influence in the decision-making process; (5) Harnessing axiomatic design principles, the collective PDDM information from various decision-makers is synthesized into a cohesive analysis; (6) Based on the assessment outcomes, design alternatives are refined. The process then iterates, revisiting steps 1 to 5 as the PDDM enters subsequent stages, each time informed by the refinements and learnings of prior stages; (7) Finally, weights are assigned to each design stage, and the aggregated PDDM insights from all stages are consolidated, ensuring a comprehensive and iterative refinement of product designs over multiple phases.
Central to the effectiveness of this 7-step methodology is the portrayal of decision-makers’ assessments in an appropriate manner. Given the interdisciplinary nature of product design, a multitude of knowledge areas such as aesthetics, engineering, ergonomics, marketing, and psychology come into play. This blend of expertise from diverse fields, coupled with the inherent bounds of human experience, frequently engenders a heterogeneity in the PDDM information. To encapsulate this complexity, PDDM information is commonly described through concrete numbers, interval numbers, and linguistic variables [37]. For a PDDM problem, let E = (e1, e2, …, el) be the set of decision-makers, X = (x1, x2, …, xm) be the set of product design schemes, and C = (c1, c2, …, cn) be the set of indicators. Decision-makers employ concrete numbers, interval numbers, or linguistic variables to express their preferences towards product design schemes, and the heterogeneous PDDM matrix is formulated as , where denotes the judgement given by decision-maker ek regarding indicator cj of product design scheme xi.
Let be the judgement of n1 indicators represented by real numbers, be the judgement of n2 indicators represented by interval numbers, and be the judgement of n3 indicators represented by a symmetrical linguistic term set , where n1 + n2 + n3 = n. To eliminate the dimensional differences among heterogeneous PDDM indicators, P is standardized to by using Equation (1) as follows:
where C1 represents the subset of real numbers; C2 represents the subset of interval number; C3 represents the subset of linguistic variables; represents the subset of benefit indicators; and represents the subset of cost indicators.
4. Weight Determination of PDDM
4.1. Indicators’ Weights
A prevalent technique for ascertaining indicators’ weights of PDDM is the AHP [15], grounded in pairwise comparisons drawn from decision-makers’ experiential knowledge and subjective judgment [38], thereby inherently incorporating a degree of subjectivity [39]. To address this limitation, the maximizing deviation method [40] is introduced as a complementary tool for determining the indicators’ weights of PDDM. Fundamentally, the maximizing deviation method posits that an indicator receiving consistently similar judgement across different design alternatives should carry a lesser weight, whereas one provoking substantial variations in assessment is allotted a higher weight, emphasizing its discriminatory power. Therefore, the AHP and the maximizing deviation method are synergistically integrated in this context. The AHP serves to capture the structured pairwise comparisons of indicators reflecting decision-makers’ relative evaluations, which remain unchanged within a single PDDM phase. Conversely, the maximizing deviation method intervenes to navigate the ambiguity inherent in decision-makers’ fuzzy evaluations and to dynamically assign variable weights based on the observed disparities, enhancing the robustness and adaptability of the weighting process.
Let the indicators’ weights of PDDM be denoted as , which is composed of fixed weights calculated by the AHP and variable weights . Then, the weight of cj, indicated as wj, can be defined as:
For decision-maker ek, the deviation value d(cj) between product design scheme xi and xi’ (i′ ≠ i) regarding the indicator cj can be calculated as:
By aggregating the fixed weights, variable weights, and decision-makers’ weights, the total deviation D for all product design schemes is:
where represents the weight of decision-maker ek.
Based on the maximizing deviation method, a nonlinear programming model is constructed as follows to obtain :
To solve this model, the Lagrange function is constructed as:
where is a real number denoting the Lagrange multiplier. Differentiating Equation (6) with respect to and , and setting these partial derivatives equal to zero, the following set of equations is obtained:
Then, we can ascertain the variable weights:
where .
4.2. Decision-Makers’ Weights
In PDDM, the principle governing the assignment of decision-maker weights is inversely proportional to the fuzziness in their judgmental inputs. Essentially, this implies that when a decision-maker exhibits a higher level of ambiguity or uncertainty in their preference for a particular product design alternative, their judgment’s reliability is deemed lower, and consequently, they are allotted a reduced weight in the decision-making process. Consistency among decision-makers is another pivotal aspect considered. Greater alignment between an individual decision-maker’s assessments and the aggregate opinion of the group indicates a higher level of consensus, translating into enhanced reliability and therefore justifying a larger weight for that decision-maker’s input. Accordingly, decision-makers’ weights can be determined by a combination of the uncertain degree calculated with entropy and consistency degree computed with an optimization function to minimize the difference of the PDDM matrix.
4.2.1. Uncertainty Degree
Entropy can measure the uncertainty of decision-making information [41] and has been validated a good way to measure GDM factors impact on the uncertainty of decision-making results [42]. The higher the entropy, the greater the uncertainty of the PDDM matrix [43]. Following this principle, the entropy function can be constructed as [44]:
where x is a variable; monotonically increases in [0, 1/2] and decreases monotonically in the other half of the unit interval.
Then, the entropy function of , indicated as , can be defined as:
where is the membership function of x; is a triangular fuzzy number transformed from . If is a real number, then ; If is an interval number, then ; If is a linguistic term, , then , .
Then, the entropy of can be defined as:
where denotes the probability density function. Generally, if x conforms a uniform distribution in , we can set ( is a constant). Then, Equation (11) can be simplified as:
The total entropy of decision-maker ek can be calculated as follows:
Consequently, the judgement uncertainty degree of decision-maker ek can be determined as:
4.2.2. Consistency Degree
The decision-making result of product design scheme xi given by decision-maker ek can be ascertained with . By integrating the consistency degree , the collective result can be defined as . To obtain , we can construct an optimization function to minimize the difference between and :
where represents distance calculated with Equation (3). By integrating the uncertainty and consistency degree, the weight of decision-maker ek, indicated as , can be computed as follows:
Equation (16) indicates a normalization of decision-makers’ weights through the combination of uncertainty degree and consistency degree of the PDDM matrix.
5. Multistage Heterogeneous PDDM Information Fusion Based on Axiomatic Design
Axiomatic design, a framework conceptualized by Dr. Nam Suh, aims to introduce a rigorous and methodical standard for design endeavors. Its fundamental premise rests upon the axiom that the design possessing the least amount of information content is the best [45]. Notably, axiomatic design shares striking parallels with GDM [46], this study integrates axiomatic design within the realm of PDDM for product scheme selection. The process involves calculating the information content of the heterogeneous PDDM matrix, determining PDDM stages’ weights by integrating information content weight and consistency degree weight, and fusing the multistage decision-making information of each product design scheme.
5.1. Information Content Calculation
Axiomatic design contains three parts: design range, system range, and common range. Design range reflects decision-makers’ expectations and system range reflects the actual level of design schemes. The overlap between the design range and system range named common range is the region where acceptable solution appears. The relationship among the three parts is shown in Figure 2. In PDDM, the design range on benefit criterion is the maximal evaluation value of alternative on the corresponding criterion or the minimum value for cost-related criteria [47].
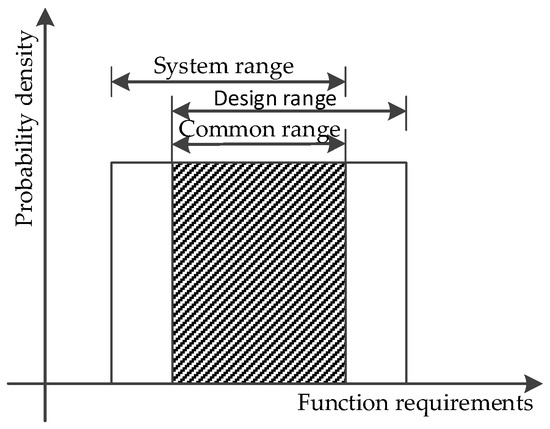
Figure 2.
The relationship among design range, system range, and common range.
According to axiomatic design theory, information content represents the probability of fulfilling the given function requirements. Therefore, information content I of the heterogeneous PDDM matrix can be defined as follows.
5.1.1. Information Content of Real Numbers
The information content of real numbers can be obtained as follows.
where and represents the system range and design range of indicators denoted by real numbers, respectively.
5.1.2. Information Content of Interval Numbers
The information content of interval numbers can be obtained as follows.
where and represents the system range and design range of indicators denoted by intervals, respectively.
5.1.3. Information Content of Linguistic Terms
The information content of linguistic terms can be obtained as follows.
where and represents the system range and design range of indicators denoted by linguistic terms, respectively.
Then, the total information of product design scheme xi can be calculated as follows:
According to axiomatic design, the smaller the information content, the better the product design scheme.
5.2. Multistage PDDM Fusion
The product design process unfolds sequentially through distinct stages, each with its unique focal points, necessitating the assignment of stage weights as a precursor to fusing multistage PDDM information. In evaluating the reliability of decision-making information, it is postulated that a higher information content in a given PDDM stage corresponds to increased uncertainty among decision-makers. Conversely, a lower consistency degree signifies a wider disparity in cognitive understanding among them. Guided by these dual premises, the determination of PDDM stage weights becomes a function of harmonizing both the information content weight and the consistency degree weight.
Let be a set of PDDM stages. According to the information content acquired with Equation (20), the information content weight of stage () can be calculated as follows:
where is the influence adjustment parameter of total information content; indicates the total information of product design scheme xi in stage .
The distance between decision-makers and regarding product design scheme xi can be calculated as follows:
The consistency degree of decision-makers regarding product design scheme xi in stage is:
Then, the consistency degree weight of stage is:
Combining and , we can ascertain the stage weight as:
where is the adjusting parameter.
By weighting the information content with its corresponding stage weights, the total information content of product design scheme xi can be calculated as:
The process of multistage heterogeneous PDDM information fusion is presented in Figure 3. Detailed implementation steps are described below.
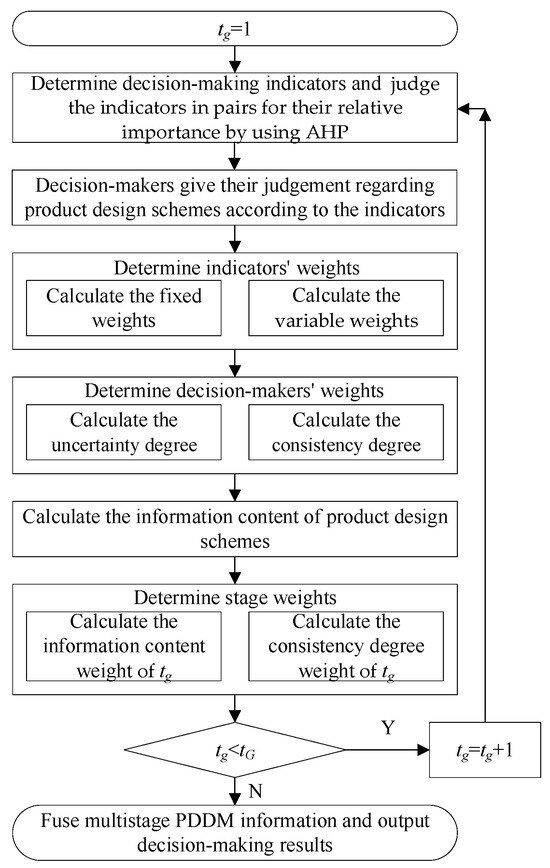
Figure 3.
The process of multistage heterogeneous PDDM information fusion.
Step 1: algorithms start and set ;
Step 2: Determine the heterogeneous PDDM indicators aligned with design requirements and constraints. Accordingly, decision-makers engage in a pairwise comparison of the indicators for their relative importance and generating a pairwise comparison matrix by using the AHP;
Step 3: employ concrete numbers, interval numbers, and linguistic variables to convey decision-makers’ judgments regarding product design schemes based on predefined indicators;
Step 4: calculate the fixed weights with the AHP and variable weights with the maximizing deviation method;
Step 5: calculate decision-makers’ weights with fuzzy entropy and consistency measurement;
Step 6: compute the information content of the PDDM matrix with axiomatic design methods regarding each product design scheme by incorporating both the indicators’ weights and decision-makers’ weights.
Step 7: determine the stage weights by combining the information content and consistency degree of PDDM about each product design scheme;
Step 8: Decide whether . If yes then let and go to Step 2, otherwise fuse multistage PDDM information and output the group decision-making results.
6. Case Study
The proposed method was adopted to develop a CNC machine design and three product design schemes were generated in all three design stages. As the product design process evolves through distinct phases, the priorities and focus of evaluation shift to accommodate the maturing design. Stage 1 focused on form beauty, color harmony and rationality of function layout, among which the former 2 indicators were described with linguistic terms and the last was depicted with intervals. Transitioning to stage 2, the PDDM indicators included aesthetic quality, rationality of function layout, ease of manufacturing, and rationality in processing. Except aesthetic quality, which was described with linguistic terms, the rest were depicted with intervals. In stage 3, ergonomic (described with linguistic terms) and cost (described with real numbers) factors were supplemented on the basis of indicators in stage 2. The linguistic term for criteria can be chosen from the following set: S = {s-3 = very low, s-2 = low, s-1 = slightly low, s0 = general, s1 = slightly high, s2 = high, s3 = very high}. Among these indicators, cost factor served as a cost indicator, while the rest were benefit indicators. To validate our proposed method, a comprehensive validation process was executed, the schematic overview of which is depicted in Figure 4 as a graphical flowchart. This visual representation outlines the sequential steps taken to test the efficacy and robustness of our approach, ensuring a clear understanding of the entire validation procedure.
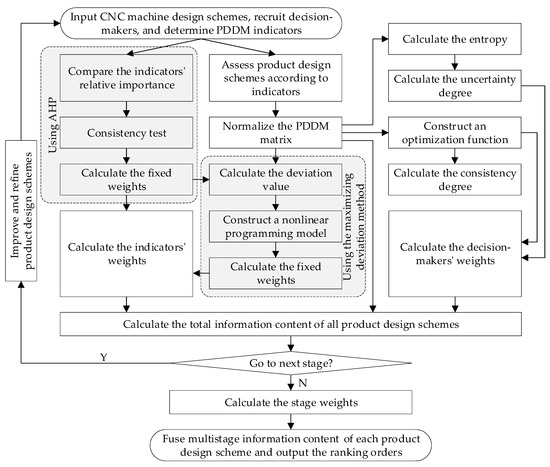
Figure 4.
Flow chart of the validation process.
6.1. PDDM in Stage 1
A diverse panel consisting of five decision-makers with distinct roles and perspectives was assembled. This multidisciplinary group comprised an experienced engineering designer, a product development manager, a senior executive, a customer, and a user. They engaged in a thorough discussion, scrutinizing and evaluating the three design schemes in stage 1 (shown in Figure 5). Their judgments and preferences were meticulously documented to compile the PDDM matrix, shown in Table 1, which serves as a pivotal dataset for subsequent analysis. Meanwhile, the same ensemble of decision-makers employed AHP to systematically compare and rank the significance of the indicators in stage 1. The fixed weights obtained for the indicators are W* = {0.528, 0.14, 0.333}. These weights signify the relative importance of each indicator within the context of stage 1. Notably, the consistency ratio calculated for these weights is 0.047, which falls well below the generally accepted threshold of 0.1. This indicates that the judgments made during the pairwise comparisons were consistent and reliable, thus validating the derived weights for informed decision-making.
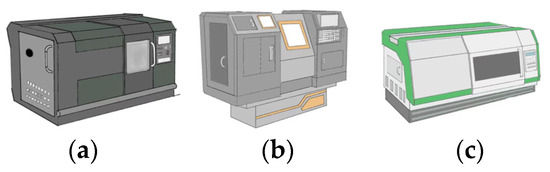
Figure 5.
Design schemes in product design stage 1: (a) x1; (b) x2; (c) x3.

Table 1.
The PDDM matrix in stage 1.
According to Equation (1), the heterogeneous PDDM matrix in stage 1 was normalized and decision-makers’ weights were obtained by using Equations (9)–(16), shown in Table 2.

Table 2.
Decision-makers’ weights in stage 1.
By using Equations (2)–(8), a nonlinear programming model was constructed for maximizing the total deviation of all product design schemes in stage 1. By weighting variable weights and fixed weights , the indicators’ weights were obtained, shown in Table 3. Then the total information content of all product design schemes in stage 1 were calculated with Equations (17)–(20). The results are I(xi) = {0.4639, 0.2666, 0.2694} and x2 has the smallest information content. Therefore, the ranking order of all product design schemes in stage 1 was x2 > x3 > x1 and decision-makers gave their recommendations for the refinement of product design schemes.

Table 3.
Indicators’ weights in PDDM stage 1.
6.2. PDDM in Stage 2
Following the integration of design optimization recommendations from stage 1, the design team implemented enhancements, yielding three more refined product design schemes. These updated designs are visually presented in Figure 6 for comprehensive evaluation. Subsequently, the decision-makers reassessed all the revised design schemes, with their detailed assessments shown in Table 4. Adhering to the established PDDM computation methodology utilized in stage 1, a new round of calculations was conducted to derive updated indicators’ weights and decision-makers’ weights. These calculated weights are documented in Table 4, Table 5 and Table 6, respectively, providing a refreshed basis for evaluation. Accordingly, the information content of all product design schemes in stage 2 were calculated, resulting in values of I(xi) = {0.8324, 0.1061, 0.0615}. It was clear that the ranking order of all product design schemes in stage 2 was x3 > x2 > x1 and also decision-makers gave their recommendations for further refinement.

Figure 6.
Design schemes in product design stage 2: (a) x1; (b) x2; (c) x3.

Table 4.
The PDDM matrix in stage 2.

Table 5.
Decision-makers’ weights in stage 2.

Table 6.
Indicators’ weights in stage 2.
6.3. PDDM in Stage 3
Continuing from stage 2, further refinements of the product design schemes were meticulously executed, which encompassed the finalization of overall dimension, ergonomic analysis, and 3D refinement design, shown in Figure 7. Meanwhile, two PDDM indicators, namely ergonomic and cost, were incorporated into the assessment framework in stage 3. These new dimensions broadened the scope of analysis, ensuring a holistic evaluation that accounts for both user-centric and financial aspects. The results are shown in Table 7, Table 8 and Table 9 and the information content set is I(xi) = {0.3443, 0.3442, 0.3114}. Notably, design scheme x3 maintained its position with the smallest information content, thereby confirming its optimal status within the refined design space. The ranking order of all product design schemes in stage 3 consequently stood as x3 > x2 > x1.
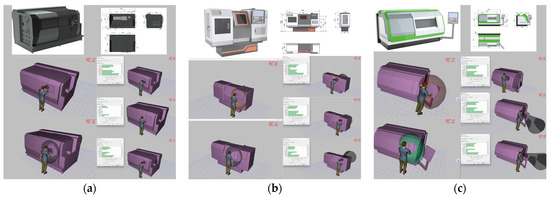
Figure 7.
Design schemes in product design stage 3: (a) x1; (b) x2; (c) x3.

Table 7.
The PDDM matrix in stage 3.

Table 8.
Decision-makers’ weights in stage 3.

Table 9.
Indicators’ weights in stage 3.
6.4. Multistage Heterogeneous PDDM Information Fusion
By using Equations (21)–(25), we calculated wI(tg) and wc(tg) regarding each product design scheme with different adjustment parameters. Then, the final information content Ii of each product design scheme was obtained with Equation (26). By adjusting the values of ψ and β, we analyzed the sensitivity of the overall fusion results, shown in Figure 8. Taking ψ = 0.7 and β = 0.3 as an example, the weights of information content, consistency degree, and PDDM stages are shown in Table 10, Table 11 and Table 12. The results indicated that the variations in ψ and β values do not affect the ranking results after multistage fusion. The final information content of each product design scheme was 0.5325, 0.2373 and 0.2153, respectively, and the ranking order was x3 > x2 > x1.

Figure 8.
Weight changes of PDDM stages varying with the value of ψ and β: (1) β = 0.1; (2) β = 0.3; (3) β = 0.5; (4) β = 0.7; (5) β = 0.9.

Table 10.
Information content weights of PDDM stages (ψ = 0.7).

Table 11.
Consistency weights of PDDM stages.

Table 12.
Weights of PDDM stages (ψ = 0.7, β = 0.3).
The detailed discussions are as follows:
- The multidisciplinary, progressive, and iterative nature of product development necessitates a dynamic approach to decision-making that adapts to the evolving priorities across multiple design stages. This evolution in focus leads to a diversification and heterogeneity of PDDM indicators. However, existing research has inadequately addressed the need for integrating the variability of indicators and harmoniously consolidating the heterogeneous information from successive stages of PDDM. Traditional methods fall short in distinguishing product design schemes effectively within a heterogeneous PDDM context. To bridge this gap, calculating information content grounded in axiomatic design principles emerges as a promising strategy. It offers a systematic and theoretically sound means to fuse and make sense of the heterogeneous data from multiple stages of the PDDM process. By quantifying the information content, this approach effectively manages complexity, reduces redundancy, and enhances the clarity of PDDM, even amidst a backdrop of evolving indicators and diverse data types;
- Through the meticulous examination of the outcomes across three successive PDDM stages, an intriguing pattern emerges: the ranking sequence of the product design schemes solidifies to x3 > x2 > x1 in stages 2 and 3, diverging from the initial order observed in stage 1 (x2 > x3 > x1). This progression suggests a reduction in individual cognitive biases among decision-makers as the design matures. Enhanced clarity and consensus in their assessments imply that as the design schemes undergo iterative refinements, the collective understanding and judgment converge, leading to a more unified perspective. Notably, while the fused result from the multistage, heterogeneous PDDM analysis aligns with the later stages’ rankings, its credibility and persuasiveness are fortified. This fused outcome is not merely a reflection of the latest stages; rather, it embodies a synthesis of insights garnered throughout the entire design phase. By integrating heterogeneous and evolving criteria across multiple stages, this comprehensive approach offers a richer, more nuanced understanding of design scheme evaluations, thereby fortifying the validity and robustness of the final decision. It highlights the value of a systematic approach that considers the entire design stages, ultimately yielding PDDM conclusions that are not only consistent but also deeply informed and highly persuasive;
- Figure 8 illustrates an intriguing pattern in the dynamics of stage weights across the design process, despite variations in the specific values of ψ and β. A common thread emerges in the trend of stage weight evolution: the stages 1 and 2, there is a noticeable shift where the stage weight attributed to design scheme x1 progressively decreases, paralleled by a steady rise in the weights of design schemes x2 and x3. This suggests a gradual recognition and appreciation of the merits in the latter product design schemes as the design evolves. Contrastingly, entering stage 3, the fluctuations in stage weights across all three design schemes become notably muted. The change curves flatten out, approximating horizontal lines, indicative of a stabilization or convergence in the perceived importance of each design scheme. This leveling off suggests that by the final stage, the relative worth assigned to each design alternative has reached an equilibrium, with minimal further differentiation observed. In summary, Figure 8 underscores a consistent narrative of evolving preferences and a convergent assessment among decision-makers across the different stages. It highlights a maturation in the decision-making process, moving from marked differentiation to a state of relative stability, where the value assigned to each design scheme stabilizes after iterative refinement and evaluation;
- Table 11 reveals a remarkable consistency in the decision-making process, with all stages exhibiting consistency weights exceeding 0.9. This high figure attests to the substantial agreement among decision-makers concerning the evaluation of product design schemes at every phase of the PDDM process. Achieving such a high consensus level is paramount for the successful integration of information from diverse stages and criteria in a multistage, heterogeneous PDDM context. Our study’s thorough debate and deliberation among decision-makers facilitated the attainment of this elevated consensus, underscoring the importance of open communication and critical evaluation in reaching informed and aligned decisions. Nonetheless, it is crucial to acknowledge that extensive discussion, while beneficial, does not inherently ensure a consensus degree that surpasses a pre-established threshold in every PDDM scenario. Should the consensus degree fall below 0.8—a benchmark often deemed acceptable for many decision-making contexts—alternative strategies must be considered. These could involve revisiting and potentially recalibrating the decision-makers’ judgments to better align individual perspectives, or refining the PDDM weighting scheme to reflect a more balanced and universally agreed-upon valuation of criteria. Such adjustments are pivotal to uphold the integrity and reliability of the PDDM process, especially in heterogeneous, multistage design environments where consensus is integral to effective PDDM fusion;
- Incorporating both the uncertainty inherent in the PDDM matrix and the varying consistency degrees among decision-makers, our approach assigns differential weights to each product design scheme with respect to the PDDM indicators, as well as to each decision-maker concerning the schemes themselves. This nuanced methodology contrasts with conventional practices that often rely on static, predetermined weights for indicators and decision-makers. Our study’s adaptive weighting strategy acknowledges the fluctuating nature of design evaluations across different stages and the subjective interpretations brought by diverse stakeholders. By dynamically reflecting these variations, it offers a more accurate and nuanced representation of decision-makers’ thought processes and the intricate evaluations they undertake when assessing product design schemes. The traditional approach, with its static weights, may oversimplify the complex dynamics of PDDM, potentially overlooking the subtleties of individual perspectives and the evolution of design priorities. Conversely, our model embraces the complexity, recognizing that as designs progress and more information is gathered, both the significance of individual indicators and the influence of decision-makers can shift. Ultimately, this tailored weighting system enriches the PDDM landscape, ensuring that the final PDDM results are deeply rooted in the collective, evolving wisdom of the decision-makers, thereby enhancing the authenticity and depth of the design appraisal process.
7. Conclusions
The interdisciplinary characteristic of product design brings into an iterative design process and heterogeneous indicators with varying emphasis across multiple stages, which impose challenges on selecting an optimal product design scheme in a holistic manner. Aiming at these issues, this study introduces axiomatic design to fuse multistage heterogeneous decision-making information in product design. The basis of our study is to describe decision-makers’ preferences about the heterogeneous PDDM indicators by employing real numbers, interval numbers, and linguistic terms. To integrate decision-makers’ judgement of the relative importance of indicators as well as embodying the assessment fuzziness and uncertainty in the PDDM matrix, the maximizing deviation method and AHP are integrated to determine indicators’ weights. By combining the uncertainty degree measured by fuzzy entropy and the consistency degree solved by a distance minimizing model of the PDDM matrix, decision-makers’ weights are obtained. Then, the concept of axiomatic design is introduced to compute the information content of product design schemes and determine the stage weights in terms of the information content and consistency degree of decision-making matrix in each PDDM stage. These sequential steps collectively contribute to the process of multistage heterogeneous PDDM information fusion.
In an empirical study, we examined the feasibility of the proposed method. The analysis of results indicate that the study can facilitate integrating decision-makers’ heterogeneous judgement in multiple stages and obtaining a holistic perspective regarding product design schemes. Results show that the ranking sequence of the product design schemes solidifies to x3 > x2 > x1 in stages 2 and 3 of PDDM, diverging from the initial order observed in stage 1 (x2 > x3 > x1), while the fused result from the multistage heterogeneous PDDM analysis aligns with the later stages’ rankings, indicating the credibility and persuasiveness are fortified.
Although the advantages of the proposed method have been verified, certain limitations remain. First, advanced methods for weight identification should be developed and employed for effective aggregation of subjective comparison and the PDDM matrix, and to reduce the influence from decision-makers’ vagueness. Second, CRP can be further integrated to guarantee the PDDM consistency among decision-makers.
Author Contributions
Conceptualization, Y.Y. and Q.Z.; methodology, Y.Y.; validation, Q.Z., K.Z., X.L., W.Y. and L.J.; investigation, Q.Z., K.Z., X.L., W.Y. and L.J.; data curation, Q.Z., K.Z., X.L., W.Y. and L.J.; writing—original draft preparation, Y.Y. and Q.Z.; writing—review and editing, Y.Y. and Q.Z.; visualization, Q.Z., K.Z., X.L., W.Y. and L.J.; supervision, Y.Y.; project administration, Y.Y.; funding acquisition, Y.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Humanities and Social Sciences Project of Ministry of Education of China (23YJC760141) and National Natural Science Foundation of China (51805043).
Data Availability Statement
Data are available upon request to the corresponding author.
Conflicts of Interest
Lijing Ji is the employee of the company Institute of Industrial Hygiene of Ordnance Industry, China North Industries Group Corporation Limited. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Kruger, C.; Cross, N. Solution driven versus problem driven design: Strategies and outcomes. Des. Stud. 2006, 27, 527–548. [Google Scholar] [CrossRef]
- Maher, M.L.; Poon, J. Modeling Design Exploration as Co-Evolution. Comput.-Aided Civ. Infrastruct. Eng. 1996, 11, 195–209. [Google Scholar] [CrossRef]
- Yu, Z.; Zhao, W.; Guo, X.; Hu, H.; Fu, C.; Liu, Y. Multi-Indicators Decision for Product Design Solutions: A TOPSIS-MOGA Integrated Model. Processes 2022, 10, 303. [Google Scholar] [CrossRef]
- Jiang, J.; Ren, M.; Wang, J. Interval number multi-attribute decision-making method based on TOPSIS. Alex. Eng. J. 2022, 61, 5059–5064. [Google Scholar] [CrossRef]
- Bueno, I.; Carrasco, R.A.; Porcel, C.; Kou, G.; Herrera-Viedma, E. A linguistic multi-criteria decision-making methodology for the evaluation of tourist services considering customer opinion value. Appl. Soft Comput. 2021, 101, 107045. [Google Scholar] [CrossRef]
- Fazeli, H.R.; Peng, Q.J. Generation and evaluation of product concepts by integrating extended axiomatic design, quality function deployment and design structure matrix. Adv. Eng. Inf. 2022, 54, 101716. [Google Scholar] [CrossRef]
- Jing, L.; Fan, X.; Feng, D.; Lu, C.; Jiang, S. A patent text-based product conceptual design decision-making approach considering the fusion of incomplete evaluation semantic and scheme beliefs. Appl. Soft Comput. 2024, 157, 111492. [Google Scholar] [CrossRef]
- Sahin, M. A comprehensive analysis of weighting and multicriteria methods in the context of sustainable energy. Int. J. Environ. Sci. Technol. 2021, 18, 1591–1616. [Google Scholar] [CrossRef]
- Pérez, I.J.; Cabrerizo, F.J.; Alonso, S.; Dong, Y.C.; Chiclana, F.; Herrera-Viedma, E. On dynamic consensus processes in group decision making problems. Inf. Sci. 2018, 459, 20–35. [Google Scholar] [CrossRef]
- Vaid, S.K.; Vaid, G.; Kaur, S.; Kumar, R.; Sidhu, M.S. Application of multi-criteria decision-making theory with VIKOR-WASPAS-Entropy methods: A case study of silent Genset. Mater. Today Proc. 2022, 50, 2416–2423. [Google Scholar] [CrossRef]
- Wang, Z.; Zhong, Y.; Chai, S.L.; Niu, S.F.; Yang, M.L. Product design evaluation based on improved CRITIC and Comprehensive Cloud-TOPSIS-Applied to automotive styling design evaluation. Adv. Eng. Inf. 2024, 60, 102361. [Google Scholar] [CrossRef]
- Lai, H.; Wu, Z.; Zhang, X.K.; Liao, H.C.; Zavadskas, E.K. A method for product appearance design evaluation based on heterogeneous data. Adv. Eng. Inf. 2023, 57, 102089. [Google Scholar] [CrossRef]
- Yang, Y.; Yang, Q.; An, W.; Gong, Z. Nonlinear fusion method for multistage product design decision-making using plant growth simulation algorithm. Adv. Eng. Inf. 2022, 53, 101712. [Google Scholar] [CrossRef]
- Li, J.F.; Wu, X.H.; Zhang, X.M.; Song, Z.H.; Li, W.J. Design of distributed hybrid electric tractor based on axiomatic design and Extenics. Adv. Eng. Inf. 2022, 54, 101765. [Google Scholar] [CrossRef]
- Saaty, T.L. The Analytical Hierarchy Process; McGraw Hill: New York, NY, USA, 1980. [Google Scholar]
- Van Laarhoven, P.J.M.; Pedrvycz, W. A Fuzzy extension of Saaty’s priority theory. Fuzzy Sets Syst. 1983, 11, 229–241. [Google Scholar] [CrossRef]
- Saaty, T.L. Fundamentals of the analytic network process-dependence and feedback in decision-making with a single network. J. Syst. Sci. Syst. Eng. 2004, 13, 129–157. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Ayağ, Z. An integrated approach to concept evaluation in a new product development. J. Intell. Manuf. 2014, 27, 991–1005. [Google Scholar] [CrossRef]
- Sarwar, M.; Bashir, F. Design concept evaluation based on cloud rough model and modified AHP-VIKOR: An application to lithography tool manufacturing process. Adv. Eng. Inf. 2024, 60, 102369. [Google Scholar] [CrossRef]
- Mishra, A.R.; Chen, S.-M.; Rani, P. Multiattribute decision making based on Fermatean hesitant fuzzy sets and modified VIKOR method. Inf. Sci. 2022, 607, 1532–1549. [Google Scholar] [CrossRef]
- Ullah, R.; Zhou, D.Q.; Zhou, P. Design Concept Evaluation and Selection: A Decision Making Approach. Appl. Mech. Mater. 2012, 155–156, 1122–1126. [Google Scholar] [CrossRef]
- Hayat, K.; Ali, M.I.; Karaaslan, F.; Cao, B.-Y.; Shah, M.H. Design concept evaluation using soft sets based on acceptable and satisfactory levels: An integrated TOPSIS and Shannon entropy. Soft Comput. 2019, 24, 2229–2263. [Google Scholar] [CrossRef]
- Sarwar, M. Decision making model for design concept evaluation based on interval rough integrated cloud VIKOR. J. Ambient Intell. Hum. Comput. 2022, 14, 3875–3897. [Google Scholar] [CrossRef]
- Touqeer, M.; Sulaie, S.A.; Lone, S.A.; Shaheen, K.; Gunaime, N.M.; Elkotb, M.A. A fuzzy parametric model for decision making involving F-OWA operator with unknown weights environment. Heliyon 2023, 9, e19969. [Google Scholar] [CrossRef]
- Fei, L.; Feng, Y. A dynamic framework of multi-attribute decision making under Pythagorean fuzzy environment by using Dempster–Shafer theory. Eng. Appl. Artif. Intell. 2021, 101, 104213. [Google Scholar] [CrossRef]
- Wu, T.; Liu, X.; Qin, J.; Francisco, H. Consensus evolution networks: A consensus reaching tool for managing consensus thresholds in group decision making. Inf. Fusion 2019, 52, 375–388. [Google Scholar] [CrossRef]
- Susskind, L.E.; Mckearnan, S.; Thomas-Larmer, J. The CONSENSUS Building Handbook: A Comprehensive Guide to Reaching Agreement; Sage Publications: London, UK, 1999. [Google Scholar]
- Liang, D.; Li, F.; Xu, Z. A group-based FMEA approach with dynamic heterogeneous social network consensus reaching model for uncertain reliability assessment. J. Oper. Res. Soc. 2023, 74, 33–47. [Google Scholar] [CrossRef]
- Zhou, M.; Guan, Z.-X.; Chen, Y.-W.; Zhou, Z.-P.; Wu, J.; Herrera-Viedma, E. Consistency and consensus reaching process for group decision making based on complete interval distributed preference relations under social network analysis. Inf. Fusion 2022, 88, 126–145. [Google Scholar] [CrossRef]
- Palomares, I.; Martinez, L.; Herrera, F. A Consensus Model to Detect and Manage Noncooperative Behaviors in Large-Scale Group Decision Making. IEEE Trans. Fuzzy Syst. 2014, 22, 516–530. [Google Scholar] [CrossRef]
- Gupta, M. Consensus Building Process in Group Decision Making-An Adaptive Procedure Based on Group Dynamics. IEEE Trans. Fuzzy Syst. 2018, 26, 1923–1933. [Google Scholar] [CrossRef]
- Calache, L.D.D.R.; Camargo, V.C.B.; Osiro, L.; Carpinetti, L.C.R. A genetic algorithm based on dual hesitant fuzzy preference relations for consensus group decision making. Appl. Soft Comput. 2022, 121, 108778. [Google Scholar] [CrossRef]
- Enyoghasi, C.; Badurdeen, F. Bayesian belief network-based risk likelihood assessment for sustainable product design decision making. J. Clean. Prod. 2023, 425, 138909. [Google Scholar] [CrossRef]
- Li, C.; Wu, R.; Yang, W. Optimization and selection of the multi-objective conceptual design scheme for considering product assembly, manufacturing and cost. SN Appl. Sci. 2022, 4, 91. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Turskis, Z.; Vilutienė, T.; Lepkova, N. Integrated group fuzzy multi-criteria model: Case of facilities management strategy selection. Expert Syst. Appl. 2017, 82, 317–331. [Google Scholar] [CrossRef]
- Yang, Y.P.; Lyu, L.W.; Yang, Q.X.; Liu, Y.K.; An, W.L. Trust-based consensus reaching process for product design decision-making with heterogeneous information. Adv. Eng. Inf. 2023, 56, 101934. [Google Scholar] [CrossRef]
- Zare, A.; Hoboubi, N.; Farahbakhsh, S.; Jahangiri, M. Applying analytic hierarchy process and failure likelihood index method (AHP-FLIM) to assess human reliability in critical and sensitive jobs of a petrochemical industry. Heliyon 2022, 8, e09509. [Google Scholar] [CrossRef]
- Zhu, J.; Ma, X.; Zhan, J.; Yao, Y. A three-way multi-attribute decision making method based on regret theory and its application to medical data in fuzzy environments. Appl. Soft Comput. 2022, 123, 108975. [Google Scholar] [CrossRef]
- Wang, Y. Using the method of maximizing deviations to make decision for multiindicies. J. Syst. Eng. Electron. 1997, 8, 21–26. [Google Scholar]
- Luca, A.D.; Termini, S. A definition of a nonprobabilistic entropy in the setting of fuzzy sets theory. Inf. Control 1972, 20, 301–312. [Google Scholar] [CrossRef]
- Yuan, J.; Luo, X. Approach for multi-attribute decision making based on novel intuitionistic fuzzy entropy and evidential reasoning. Comput. Ind. Eng. 2019, 135, 643–654. [Google Scholar] [CrossRef]
- Yan, S.L.; Zeng, Y.Y.; Gong, Z.W.; Wang, J.Y. Multi-attribute quantum group interference decision model considering minimum constraint and information entropy. Comput. Ind. Eng. 2024, 192, 110225. [Google Scholar] [CrossRef]
- Pedrycz, W. Why triangular membership functions. Fuzzy Sets Syst. 1994, 64, 21–30. [Google Scholar] [CrossRef]
- Suh, N.; Kim, S.; Bell, A.; Wilson, D.; Cook, N.; Lapidot, N.; Turkovich, B.V. Optimization of Manufacturing Systems through Axiomatics. Ann. ICRP 1978, 27, 383–388. [Google Scholar]
- Li, X.; Qiu, S.; Ming, H.X.G. An integrated module-based reasoning and axiomatic design approach for new product design under incomplete information environment. Comput. Ind. Eng. 2019, 127, 63–73. [Google Scholar] [CrossRef]
- Liu, A.H.; Wan, S.P.; Dong, J.Y. An axiomatic design-based mathematical programming method for heterogeneous multi-criteria group decision making with linguistic fuzzy truth degrees. Inf. Sci. 2021, 571, 649–675. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).