Sustainability under Active Inference

Abstract

In this paper, we explore the known connection among sustainability, resilience, and well-being within the framework of active inference. Initially, we revisit how the notions of well-being and resilience intersect within active inference before defining sustainability. We adopt a holistic concept of sustainability denoting the enduring capacity to meet needs over time without depleting crucial resources. It extends beyond material wealth to encompass community networks, labor, and knowledge. Using the free energy principle, we can emphasize the role of fostering resource renewal, harmonious system–entity exchanges, and practices that encourage self-organization and resilience as pathways to achieving sustainability both as an agent and as a part of a collective. We start by connecting active inference with well-being, building on existing work. We then attempt to link resilience with sustainability, asserting that resilience alone is insufficient for sustainable outcomes. While crucial for absorbing shocks and stresses, resilience must be intrinsically linked with sustainability to ensure that adaptive capacities do not merely perpetuate existing vulnerabilities. Rather, it should facilitate transformative processes that address the root causes of unsustainability. Sustainability, therefore, must manifest across extended timescales and all system strata, from individual components to the broader system, to uphold ecological integrity, economic stability, and social well-being. We explain how sustainability manifests at the level of an agent and then at the level of collectives and systems. To model and quantify the interdependencies between resources and their impact on overall system sustainability, we introduce the application of network theory and dynamical systems theory. We emphasize the optimization of precision or learning rates through the active inference framework, advocating for an approach that fosters the elastic and plastic resilience necessary for long-term sustainability and abundance.

1. Introduction

An understanding of the distinctive features and implications of sustainable and unsustainable practices gives us a good sense of its underlying patterns. Unsustainable practices exhaust system resources, precipitating the deterioration of its constituents [1,2]. The notion of sustainability is conceptualized through the environmental, economic, and social domains that are inherently linked to each other [3]. Ecologically unsustainable practices can lead to economic unsustainability [4,5]. Such practices span from the over-extraction of natural resources [6,7] to environmental contamination [2,4]. Notable examples include disproportionate water use in arid zones [8,9] and accelerated deforestation, e.g., of the Amazon basin [10,11]. This can lead to the decline of agents within the system, such as plants [12,13] and animals [13,14,15], as well as the decline of human populations that depend on those resources [16]. For example, the over-extraction of groundwater in California has led to a depletion of aquifers, impacting agriculture and local ecosystems [17]. We can also point to the degradation of coral reefs attributable to ocean acidification and contamination [18]. With the decline of these reefs, dependent marine species are compelled to seek alternative habitats or confront potential extinction, triggering a decline of entire ecosystems and a cascade of negative implications for the human population.

The significance of sustainability for humanity is directly connected to the phenomenon of climate change. Unsustainable practices have contributed to the current state of climate change through the excessive use of fossil fuels, which has led to increased greenhouse gas emissions and accelerated global warming [19,20]. This, in turn, has caused the loss of biodiversity [21], ecosystem degradation, and impacts on food security in many areas of the world, as it affects our capacity to grow crops or yield benefits from the sale of crops. Such low regulation also entails higher food prices, which further reinforces food insecurity.

Unsustainable practices also impact the economy by increasing unemployment. For instance, in the United States, industrial dependence on non-renewable resources, such as coal, has led to job losses and economic hardship for communities that once relied on coal mining [22]. The lack of foresight and investment in alternative industries, as well as low employment security, has exacerbated poverty and health issues in these areas [23,24,25].

Improper resource management adversely impacts individuals, both emotionally and socially, thereby diminishing their well-being. The Flint water crisis is a notable example, where the city’s water supply became contaminated with lead due to cost-cutting measures. This situation led to a higher level of depression, anxiety, and general social unrest in the affected community [26,27,28,29].

Unsustainable practices have critical negative effects on the environment, economy, and society. This is enough justification for us to look for ways to promote practices that are as sustainable as possible. But the issue seems thorny and hard to disentangle. Many factors seem at play, which are interconnected in ways that make the issue hard to grasp.

An interesting starting point is the relationship between sustainability, resilience, and well-being, which has been well established in the research field of ecological science. Resilience includes (i) inertia, the ability to resist change when subjected to a disturbing force; (ii) elasticity, the ability to flexibly return to good states following a perturbation; and (iii) plasticity, the ability to expand the repertoire of good states and courses of action in the face of a changing environment [30,31,32]. According to [30], these three dimensions of resilience can be mapped onto high-precision beliefs, the ability to find characteristic states, and the capacity for structural degeneracy and functional redundancy, respectively. Redundancy refers to the capacity of multiple components to perform the same function. Degeneracy, on the other hand, refers to the capacity of components to perform the same functionality under one set of conditions but different functionalities under other conditions. Refs. [30,33] quantify degeneracy by the entropy of posterior beliefs about the causes of sensations, while redundancy is the complexity cost incurred by forming those beliefs. (Ref. [33] provides a principled account of degeneracy and redundancy in terms of the free energy principle (FEP) and active inference. They demonstrate how degeneracy can be quantified by the entropy of posterior beliefs, while redundancy corresponds to the complexity cost incurred by those beliefs. This formalization allows for the measurement and comparison of degeneracy and redundancy in the same units, providing a solid foundation for the study of resilience within active inference. Ref. [30] builds upon the work of [33] and maps the three aspects of resilience (inertia, elasticity, and plasticity) onto specific elements of active inference. Inertia is mapped onto high-precision beliefs, elasticity is mapped onto the ability to seek out characteristic states, and plasticity is mapped onto functional redundancy and structural degeneracy. This mapping provides a formal interpretation of resilience within active inference, allowing for its quantitative study and simulation.) From this perspective, degeneracy and redundancy are complementary: active inference tries to minimize redundancy while maintaining degeneracy. Miller and colleagues presented a conceptual analysis of resilience using active inference and established a conceptual model that can be used to explore different forms of resilience. Building on this paper, we extend our paradigm from the resilience of an isolated system relative to a stressor to a system in a niche. Well-being comprises both eudaimonic well-being, the capacity to fulfill and develop one’s potential through the pursuit of goals that fit with one’s personal values—a long-term component, and hedonic well-being, which is closer to momentary positive affect and pleasures arising from social interactions and physical activities—a short-term component [34]. (Refs. [34,35] demonstrate how active inference can be used to understand and predict well-being. They relate well-being to a system’s ability to minimize prediction errors (free energy) and anticipate future well-being by estimating the divergence between its model and future observations (expected free energy).)

There are many definitions of sustainability. In a hallmark report, Brundtland defines sustainable development as “meet[ing] the needs of the present without compromising the ability of future generations to meet their own needs”. Similarly, the National Research Council describes it as “the reconciliation of society’s developmental goals with its environmental limits over the long term” [36]. Based on these definitions, we can consider that sustainable development is a process of change in which the consumption of resources, the direction of investments, the orientation of technological development, and institutional change all unfold harmoniously and enhance both the current and future potential to meet human needs and aspirations. This definition already highlights the importance of meeting the needs of the present without compromising the ability of future generations to meet their own needs. Twenty years later, to Crutzen, sustainability entails the maintenance of resources within a range of levels to ensure survival in an ever-changing environment. It is still arguably the greatest challenge of our time [37]. Evidently, in order to promote a sustainable system, we must understand the interdependencies between resources in the system, to promote resource renewal and harmony within the system, and to encourage self-organization and resilience, such that it is possible to satisfy necessities over time without exhausting the requisite resources [38]. These resources extend beyond merely Earth’s material wealth, including community network effects, care work, labor, and the accrued reservoir of knowledge inherited from preceding generations [38,39]. Numerous studies have examined how these concepts are interconnected and mutually reinforcing [40,41,42]. For example, sustainability practices that maintain ecosystem health and services can enhance the resilience of socioecological systems to disturbances, which in turn supports human well-being that depends on the benefits provided by well-functioning ecosystems [42,43]. Conversely, the erosion of ecosystem resilience through unsustainable practices undermines the ability of ecosystems to deliver services vital for human welfare over the long term [40,41]. This recognition of the linkages between sustainability, resilience and well-being has important implications for efforts to address major challenges like climate change through nature-based solutions [42,44]. There is a need to explicitly consider how nature-based solutions can simultaneously deliver across all three dimensions in an integrated manner [41,43]. Therefore, the search for effective and integrated instruments to promote sustainability remains an important task for scientists and practitioners. A systems-based approach seems most promising from this perspective. Prior attempts in the 1980s have linked sustainability to cybernetics. The Viable System Model proposed by Stafford Beer in the 1980s [45] provided a foundation for the discussion on system viability, leveraging the complexity and variety of systems applying principles of cybernetics to describe the necessary and sufficient conditions for a system to be sustainable. It proposes that a viable system must have five necessary interacting subsystems: implementation, coordination, control, intelligence, and policy. These work together to ensure that the system can respond effectively to various environmental disturbances, maintain its identity, and continue to fulfill its purpose. One key limitation of the Viable System Model is that it mostly is applicable to organizational structures and processes, but it says very little about the cognitive and perceptual aspects of how agents within the system interact with and make sense of their environment. This approach therefore does not directly address the role of beliefs, predictions, and active exploration in shaping the behavior and adaptation of agents within the system—key components which make the system more chaotic and harder to predict.

In this paper, we analyze the relationship that resilience and well-being hold in promoting sustainability under active inference applying a systems approach. We contend that sustainability, resilience, and well-being are emergent properties of complex systems that arise from the interactions between multiple components/agents and their environment over different spatial and temporal scales. This systems view highlights the hierarchical, nested nature of these systems, where higher levels (e.g., socioecological systems) are composed of interconnected lower-level systems (e.g., ecosystems, communities, individuals). The resilience of the lower levels contributes to the sustainability of the higher levels. In turn, sustainability also requires aligning the dynamics across levels to avoid the depletion of resources over extended time horizons. Well-being can be viewed as a critical functional output of these coupled human–natural systems. Active inference gives us a good way to model the perception–action cycles and belief updating of agents within these systems as they interact with their environment and other agents. Active inference is a unifying framework derived from the FEP that applies to cycles of perception and action and all the cognitive processes that depend on these cycles [30,34]. We will delve more deeply into these concepts in the following sections. If we pull from the Viable System Model, the notion of identity is particularly interesting as it brings us to consider how variational density plays a role in active inference, i.e., a probability distribution that represents the agent’s beliefs or expectations about the hidden states of the world, including its own internal states and the external states that it cannot directly observe, which effectively constitute its maintained identity—its ability to remain over time. Therefore, we value the combination of systems thinking with active inference, as it allows us to develop integrated models that capture both the macro-system dynamics and the micro-processes of sensing, learning, and behaving that ultimately shape sustainable outcomes.

The central research questions of this paper are how to understand sustainability, whether resilience alone is sufficient to lead to sustainable outcomes under active inference, and how this informs well-being. We argue that focusing solely on individual resilience may not adequately capture the complex interactions and dynamics that enable overall system resilience. Sustainability, therefore, requires a more comprehensive consideration of the interconnectedness between system components and the long-term viability of the system as a whole. To address this, we propose a mathematical formalism grounded in active inference that connects cognitive and social processes to more granular, physics-based models. This formalism aims to facilitate the development of computational models that can simulate the environment and our interactions with it, thereby informing the design and implementation of effective policies and approaches for sustainability. The results of this work can be utilized by modelers seeking to create sustainability simulations that incorporate a wide range of interconnected variables across multiple scales. Additionally, policymakers and decision-makers who wish to base their strategies on data-driven insights and modeled suggestions can benefit from this approach. Existing tools often struggle to properly map across scales, account for the intricate interdependencies within systems, and identify self-organized, sustainable outcomes. Our proposed framework aims to bridge these gaps and provide a more holistic understanding of sustainability.

2. Well-Being in Active Inference

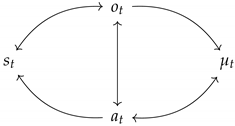
Before delving into how well-being and resilience should be formalized within active inference, it is necessary to outline some basic definitions. Specifically, we begin from stating what a system and an agent are. We denote a system that comprises an agent by four stochastic processes that interact as follows:

over some period of time $t\in [0,T]$, where T is known as the time horizon. In this diagram, $o_t$ represents the observations or sensory inputs of the agent at time t, $s_t$ represents the states of the external environment at time t, $a_t$ represents the actions taken by the agent at time t, and ${\mu }_t$ represents the internal states or beliefs of the agent at time t. The arrows indicate the interactions and dependencies between these processes: $o_t$ depends on $s_t$ (environment states influence observations), $a_t$ depends on ${\mu }_t$ (internal beliefs influence actions), ${\mu }_t$ depends on $o_t$ and $a_t$ (observations and actions update internal beliefs), and $s_t$ depends on $a_t$ (actions affect the environment states). Furthermore, an agent, over said period of time, is the whole of processes ${(o_t,a_t,{\mu }_t)}_{t\in [0,T]}$. In contrast, the external world or environment is the process ${\left(s_t\right)}_{t\in [0,T]}$. ${\left({\mu }_t\right)}_{t\in [0,T]}$ is the process that is internal to the agent. Under some simple conditions, an agent is cognitive in the sense that its internal trajectories are the parameters of beliefs about the external trajectories:

$$Q_{\mu \left[t\right]}\left(s\left[t\right]\right)\approx P(s\left[t\right]\mid o\left[t\right]),$$

(1)

where $·\left[t\right]$ denotes a trajectory over time.

(The equations for active inference are derived from first principles of stochastic processes, namely by postulating that the world and agent evolve together as a stochastic process and interact via a boundary called a Markov blanket comprising sensory and active states. Active inference just corresponds to implementing the equations of motion of internal and active states given sensory states. The derivations for continuous generative models are here [46,47] and those for discrete generative models are here [48]. A recent review by [49] attempted to look at the empirical validity of both predictive coding and active inference. For active inference, they found that most empirical studies so far have mostly focused on fitting models to behavior in order to identify and explain individual or group differences. So, active inference models tend to explain behavioral data. But it is true that there has not been a strong focus on testing the unique predictions of active inference against alternative models. It seems clear from this review that existing work demonstrates the promise of the active inference approach.) Consider an individual living in a forest. This individual may observe the world around it and infer how this forest works. Thus, the individual builds a representation of the world, which they can use to acquire what they need. On this basis, we can deal with the concept of well-being and how it can be described within active inference. According to [34], well-being inside an agent/system is about calibrating one’s internal model to the environment to minimize prediction error both presently and in the future. This concept is further explored by [50], who discuss resilience in the context of active inference. We can measure well-being using information theory, specifically through mutual information, which quantifies a system’s ability to predict and adapt to environmental shifts. The mutual information between two random variables, x and y, is given by

$$I(x,y)=H\left(x\right)-H\left(x\right|y)$$

(2)

Here, $I(x,y)$ represents the mutual information, $H\left(x\right)$ the entropy of x, and $H\left(x\right|y)$ the conditional entropy of x given y. These are defined as $H\left(x\right)=-{\sum }_{i}p\left(x_i\right)logp\left(x_i\right)$ and $H\left(x\right|y)=-{\sum }_{i}p\left(x_i\right|y_i)logp\left(x_i\right|y_i)$, and they measure the uncertainty or surprise associated with x, and the remaining uncertainty of x when y is known.

These equations are meant to represent the system’s ability to maintain an accurate model of the world, which is essential for resilience, as discussed by [50]. The FEP further quantifies well-being with an agent’s actions directed toward minimizing free energy. In other words, it shows that internal states and active states of an agent evolve to minimize free energy:

$$\begin{array}{cc}\hfill {\mu }_t,a_t\searrow F\left[Q_{\mu \left[t\right]}\left(s\left[t\right]\right)\right]& :={\mathbb{E}}_{Q_{\mu \left[t\right]}\left(s\left[t\right]\right)}[log{Q}_{\mu \left[t\right]}\left(s\left[t\right]\right)-logP(s\left[t\right],o\left[t\right])]\hfill \\ \hfill & =\underset{\mathrm{Complexity}}{\underbrace{D_{KL}[Q_{\mu \left[t\right]}\left(s\left[t\right]\right)\mid P\left(s\left[t\right]\right)]}}-\underset{\mathrm{Accuracy}}{\underbrace{{\mathbb{E}}_{Q_{\mu \left[t\right]}\left(s\left[t\right]\right)}[-logP\left(o\left[t\right]\right|s\left[t\right])]}}\hfill \end{array}$$

(3)

Here, the Kullback–Leibler divergence $D_{KL}[Q_{\mu \left[t\right]}\left(s\left[t\right]\right)\mid P\left(s\left[t\right]\right)]$ measures the discrepancy between the agent’s prior beliefs p and its approximate posterior beliefs q—the best guess the agent has about the world based upon observed data. This is the complexity term of F, which scores the complexity of the agent’s model of the world. In contrast, $E_{Q_{\mu \left[t\right]}\left(s\left[t\right]\right)}[-logP\left(o\left[t\right]\right|s\left[t\right])]$ is the accuracy term, which measures how well the agent’s model fits the observed data. Under the FEP, agents maximize the accuracy of their model of the world while minimizing its complexity. In the literature, a high free energy is associated with stress on the system [51], i.e., low well-being.

The Expected Free Energy (EFE) extends this concept to future states or trajectories of states, and it is conditioned upon a sequence of actions undertaken by the agent.

The (−log) distribution of active paths, given some past data observed by the agent (e.g., past observations; denoted as h) can be expressed by an expected free energy:

$$\begin{array}{cc}\hfill -logP\left(a\right[t]\mid h)& ={\mathbb{E}}_{P\left(s\right[t],o[t]\mid a[t],h)}[logP(s\left[t\right]\mid a\left[t\right],h)-logP(s\left[t\right],o\left[t\right]\mid h)]\hfill \\ & =\underset{\mathrm{Risk}}{\underbrace{D_{KL}\left[\stackrel{\mathrm{Predicted}\mathrm{paths}}{\overbrace{P\left(s\right[t]\mid a[t],h)}}\mid \stackrel{\mathrm{Preferred}\mathrm{paths}}{\overbrace{P\left(s\right[t]\mid h)}}\right]}}+\underset{\mathrm{Ambiguity}}{\underbrace{{\mathbb{E}}_{P\left(s\right[t]\mid a[t],h)}\left[H\left[P\right(o\left[t\right]\mid s\left[t\right],h\left)\right]\right]}}\hfill \end{array}$$

(4)

This means that the more likely an active trajectory, the more it minimizes expected free energy. The Risk term quantifies the divergence between the predicted paths (the distribution of states given an action sequence and past observations) and the preferred paths (the distribution of states given only past observations). In other words, it measures how much the predicted outcomes of an action sequence deviate from the agent’s preferred outcomes based on its prior beliefs. An agent that minimizes risk will favor actions that lead to states consistent with its preferences.

The Ambiguity term, on the other hand, measures the expected uncertainty in the mapping between states and observations given an action sequence and past observations. It quantifies the agent’s lack of confidence in its ability to predict the sensory consequences of being in a particular state. An agent that minimizes Ambiguity will prefer actions that lead to states with more predictable sensory outcomes, reducing its uncertainty about the world.

By minimizing EFE, an agent effectively balances the drive to fulfill its preferences (minimizing Risk) with the drive to reduce uncertainty about the world (minimizing Ambiguity). This allows the agent to adaptively navigate its environment, seeking out states that align with its goals while also gathering information to refine its internal models.

Any agent in the real world, in virtue of being cognitive, can be rewritten, expressed, and simulated through the free energy and EFE minimizing equations of motion. This is a correspondence between the prediction generative model and the preference generative model on the one hand and the agent’s behavior on the other hand. The prediction generative model $P\left(s\right[t],o[t\left]\right|a\left[t\right])$ encodes the agent’s representation of how its actions influence the external world and how the external world causes sensations. In turns, the preference generative model $P\left(s\right[t],o[t\left]\right)$ encodes the agent’s preferred external and sensory trajectories and the agent’s behavior as given by $a\left[t\right],\mu \left[t\right]$ in relation to observations $o\left[t\right]$.

In this way, as [34] suggest, the system tries to anticipate its future well-being by estimating the divergence between its model and future observations. Thus, we can assess the well-being of the system in terms of its ability to sustain actions that are self-evidencing, across different levels, ensuring the overall system’s sustainability. Well-being is not just about stability but also about maintaining a dynamic balance that allows for adaptation and evolution. Indeed, each individual or entity has a generative model of hidden causes of sensory data that is biased toward favorable outcomes. The free energy corresponds to the evidence of the data according to this generative model. If the free energy is low, the evidence is high and the data highly conform to the preferences—and vice versa. Well-being cannot be separated from resilience, which is a fundamental component of it. Indeed, the next section looks at resilience to show how it relates to well-being and how it can also be formalized through active inference.

Continuing with the example of an individual living in a forest, we can explore how well-being and resilience can be understood within the context of active inference:

The individual (agent) has an internal model of the forest (environment) that they use to navigate and survive. Their well-being can be measured by how well their internal model aligns with the actual state of the forest. If the individual can accurately predict and adapt to changes in the forest, such as seasonal shifts or the availability of resources, they will experience a higher level of well-being.

We can quantify this using mutual information. The mutual information between the individual’s internal model and the actual state of the forest represents their ability to predict and adapt to their environment. Higher mutual information indicates a better calibrated internal model and, consequently, higher well-being.

In this context, the individual will strive to maintain an accurate and parsimonious model of the forest (minimizing complexity) while ensuring that their model closely fits their observations (maximizing accuracy). A lower free energy corresponds to a higher level of well-being, as it indicates that the individual is successfully navigating their environment and minimizing stress.

EFE extends this concept to future states, allowing the individual to anticipate their future well-being by estimating the divergence between their model and expected future observations. By minimizing EFE, the individual balances the drive to fulfill their preferences (e.g., finding food and shelter) with the need to reduce uncertainty about the forest (e.g., exploring new areas).

Resilience in Active Inference

Broadly speaking, resilience is the ability to maintain well-being despite threats to that well-being [50]. When viewed through the lens of active inference, resilience can refer to one of three things: inertia, elasticity, and plasticity.

Inertia, which refers to the ability of a system to withstand change while maintaining itself in roughly the same state, is inherently linked to the precision of beliefs [52,53]. It corresponds to a generalization of inertia in physics, which describes the work required to move a system away from its current trajectory. Within the context of active inference, high-precision beliefs, akin to rigidity, predetermine the ability of agents to continue their current course of action regardless of external disturbances [30]. However, while it makes systems robust to possible insults to their integrity, rigidity in this sense is often accompanied by reduced adaptability. The stable occupation of a region of state space by a system with high-precision beliefs translates into selecting policies that do not lead to unexpected surprises: agents with high-precision beliefs are generally not receptive to new information that is inconsistent with their core assumptions [54]. As a result, agents with such beliefs are likely to minimize the expected free energy by selecting only those actions that reinforce or at least do not contradict their core assumptions.

Elasticity is the capacity of a system to return to a preferred state following a disturbance. Allostasis and homeostasis are the key examples of this dynamic [55]. Elasticity requires planning over long-term time horizons, highlighting the significance of deep temporal models [56,57]. An example of allostatic and homeostatic elasticity is the ability of a person to regulate body temperature when running [58]. At the same time, bad bootstraps can persist over time and eventually lead to the depletion of resources or paths to well-being. An individual or system stuck in a bad bootstrap will be more vulnerable to volatility. Thus, elasticity is also insufficient for capturing the essence of resilience. To account for long-term resilience, structures of generative models should be adjusted to enable a timely response to ever-changing environments.

Plasticity is the ability to adapt to a new situation, processing shocks and responses. This can be formalized through inference at several scales, and in particular, through structure learning, that is, changing the structure of the generative model and including new state factors to accommodate the change. In certain environments characterized by a high level of uncertainty, a simple avoidance of surprises is hardly sufficient for managing errors effectively owing to the introduction of a cascade of surprising events [34]. In this context, building resilience means ensuring that a model can function effectively in uncertain environments exhibiting high risks, “consume” errors (so to speak) and grow from them, and integrate information about these errors in its model of the world. Thus, a plastic system is likely to grow in the face of adversity and respond with plasticity to stressors that disrupt it [59].

All the above considered, we can claim that the conceptualization of resilience through the notions of plasticity, inertia, and elasticity builds an effective framework to examine the self-organization of complex structures, including social systems. But we are still missing the connection between the systems which is not given by the resilience framework.

The interconnectedness of resources within a system can promote the renewal of resources, ensuring the harmonious self-organization of the systems. Effectively, this entails that agents within a system can rely on each other, as the elasticity and plasticity of one system can feed into that of another system through their interconnectedness.

Resilience in isolation is insufficient to achieve sustainability. Resilience must be manifested across extended timescales and throughout all strata of the nested hierarchy within the system, encompassing the larger system as a whole. If resilience is only manifest at the level of individual system components, it can lead to resource depletion, due to a lack of diverse practices, practices based on non-renewable resources, and lack of consideration for the interdependencies between resources among the system components [60]. Quantifying the strength, nature, and direction of interdependencies requires tracking changes in interdependencies, which adds an extra layer of complexity.

One way to model this is through the use of network theory, where the interdependencies between resources in the system can be represented as a dynamic network of nodes and edges with the depletion of one resource represented as the removal of a node from the network. The impact of this on the system as a whole can be measured by connectivity and robustness. Interdependencies between resources can be represented mathematically through equations such as the following:

$$I(x_1,x_2)=\sum _{x_1,x_2}p(x_1,x_2)log\left(\frac{p(x_1,x_2)}{p_1\left(x_1\right)p_2\left(x_2\right)}\right),$$

(5)

where $I(x_1,x_2)$ represents the mutual information between two resources, indicating the interdependency between them. This simplification is specifically for the case of two variables, such as water $x_1$ and fertilizer $x_2$ if we choose an example from agriculture.

For scenarios involving more than two variables, the equation would be

$$I(x_1,\dots ,x_n)=I(x_1,\dots ,x_{n-1})-I(x_1,\dots ,x_{n-1}|x_n)$$

(6)

This recursive formulation handles multivariate interdependencies.

In the two-variable case, $I(x_1,x_2)$ directly quantifies the dependency between these variables. However, for multivariate cases, it is important to interpret interdependencies considering synergistic, redundant, or unique information contributions.

Continuing with the agricultural example, we assume the following probabilities:

• Joint probability: $p(x_1=1,x_2=1$ = 0.5, $p(x_1=1,x_2=0)=0.2$, $p(x_1=0,x_2=1)=0.1,$ and $p(x_1=0,x_2=0)=0.2$.
• Marginal probabilities: $p_1(x_1=1)=0.7$, $p_1(x_1=0)=0.3$, $p_2(x_2=1)=0.6$, and $p_2(x_2=0)=0.4$.

On these grounds, the impact of resource depletion can be represented as shown below:

$$D(x_1,x_2,\dots ,X_n)={\mathbb{E}}_{P(x_1,x_2,\dots ,x_n)}\left[\cos \mathrm{t}(x_1,x_2,\dots ,x_n)\right]$$

(7)

where $D(x_1,x_2$, $ldots,x_n)$ represents the expected impact of resource depletion, considering the joint probability distribution $P(x_1,x_2,\dots ,x_n)$ and a cost function cost $(x_1,x_2,\dots ,x_n)$. Expanding the expectation yields the equivalent expression:

$$D(X_1,X_2,\dots ,X_n)=\sum _{x_1}\sum _{x_2}\dots \sum _{x_n}P(x_1,x_2,\dots ,x_n)·\cos \mathrm{t}(x_1,x_2,\dots ,x_n)$$

(8)

where the sums run over all possible values of the variables $x_i$. This gives the overall expected cost due to resource depletion for the entire distribution of possible states of the system.

The dynamics of precision and optimization of learning rates explain how the system can actively seek out interesting slopes of error and maximize expected information gain [30], leading to a more elastic and plastic form of resilience.

Let us continue with the example of an individual living in a forest and explore how resilience can be understood. In the context of the forest, inertia could mean the individual having high-precision beliefs about their environment, such as the location of food sources and safe shelter. These beliefs make the individual more resistant to external disturbances, as they are less likely to deviate from their current course of action. However, this rigidity may also make the individual less adaptable to new situations.

If the individual’s usual food source becomes unavailable due to a seasonal change, elasticity would allow them to find alternative food sources and eventually return to their preferred state of having a stable food supply. This requires the individual to have a deep temporal model of the forest, allowing them to plan over long-term time horizons.

Now, if a new predator appears in the forest, the individual would need to update their generative model to include this new threat and adapt their behavior accordingly. A plastic individual is more likely to grow in the face of adversity and respond effectively to stressors.

We have now demonstrated how resilience is cast under active inference. We now dive concretely into how well-being and resilience help us understand and promote sustainability.

3. Sustainability

The relationships between entities in a system and the system’s capacity to support them over deep timescales must be intricately mapped to foster a resilient system. The notion of resilience captured by relationships among system components and the components themselves, therefore, is inherently linked to sustainability. To foster resilience and sustainability, the system must optimize the trade-off between complexity and efficiency, maximizing expected information gain and minimizing complexity. In this way, the system is able to adapt and learn in an efficient manner while also maintaining a degree of elasticity and plasticity necessary for long-term sustainability. Additionally, as an extension of plasticity, by maximizing degeneracy and therefore the space the system can explore while retaining some of its key functions, the system’s diversity and ability to adapt to changing environments increases. Achieving sustainability involves fostering the renewal of resources which are useful for the entities [61] and fostering a harmonious exchange between the entities in the system and the system itself [62]. The achievement of sustainability requires the establishment of a holistic system that addresses the main barriers to sustainability and customized economic, environmental, and social sustainability practices. It also involves practices that foster self-organization and resilience [63,64]. A system that promotes the adoption of sustainable practices must be capable of detecting unsustainable practices and responding to them in a swift manner by triggering their prevention. In other words, it must be able to detect and prevent any threats to sustainability through effective self-organization. Such a feature highlights the close link between sustainability and resilience [65,66]. The application of resilience within the context of sustainability involves not only the ability to withstand shocks but also the use of various instruments to facilitate the recovery of economic, social, and environmental systems from the harm brought about by unsustainable practices. A recent report by McKinsey outlines the integration of resilience into sustainable and inclusive growth [67]. It shows that resilience is key for meeting the challenges posed by crises to sustainable growth, ensuring that strategies across public and private sectors are coordinated to reduce the adverse impact of disruptions on sustainability, developing a holistic framework allowing each organization to use a common structure, language, and objectives for resilience, maintaining an effective framework to invest in, detect, prevent, and respond to disruptions, and promoting an agenda that explains the interconnectedness of crises [67]. The arguments laid out above illustrate that the significance of resilience for promoting sustainability has already been recognized by stakeholders, although the search for specific channels outlining the relationship between these two notions as well as the specific tools based on resilience that could contribute to the promotion of sustainability is ongoing. Furthermore, resilience is a homeostatic process, in the sense that there is no planning involved in the processes underlying resilience: just robustness (inertia), adaptiveness (plasticity), and reactivity (elasticity). Homeostasis refers to the maintenance of a stable equilibrium in a system through self-regulating mechanisms that counteract disturbances. In the context of resilience, this means that a system has inherent properties (robustness, adaptiveness, and reactivity) that allow it to absorb shocks and return to its original state without any conscious planning or intervention. While this is crucial for short-term survival, it may not be sufficient for long-term sustainability. In contrast, achieving sustainability might be considered an allostatic process. Allostasis involves the active adjustment of a system’s parameters to maintain stability in response to changing environmental demands. This concept can be applied to sustainability, as it requires the deliberate and proactive management of a system’s components to ensure their long-term viability and the harmonious exchange between entities and the system itself. Fundamentally, sustainability entails each component of the system enabling any given aspect of resilience as required such that the parts of the system feed off each other.

Promoting the regeneration of resources plays a great part in attaining sustainability. This may encompass activities such as implementing sustainable agricultural and forestry methods [68,69] as well as generating renewable energy [70,71]. Fostering sustainability also entails collaboration across many entities and the prudent utilization of resources such that we can ensure a harmonious interaction between the elements inside the system [72,73,74,75]. Finally, practices that promote self-organization and resilience are essential for attaining sustainability. These measures encompass activities like preserving biodiversity and mitigating the risks of disasters [65,66].

All the above considered, the next section goes toward mapping sustainability to active inference.

4. Tying It All Together: Sustainability to Active Inference

Sustainability under active inference is the capacity to find a cohesive steady state of the system across different spatial and temporal scales such that the resilience of things at each level of the hierarchy promotes the resilience of things across the hierarchy. This entails a systemic aptitude to align actions and adaptations over extended time horizons, fostering enduring harmonization with the environment, embodying a facet of resilience and long-term viability.

4.1. Abundance and Adaptive Capacity

The presence of abundance and the resulting redundancy enhances resilience [76]. Abundance serves as a guarantee of functional diversity, indicating that an ecosystem with a wide range of plant and animal species is likely to have all its necessary functional tasks or ’niches’ fully filled [77]. Every species, by fulfilling its unique ecological role, increases the overall resilience and flexibility of the system, hence improving its capacity to withstand environmental stressors and disturbances [78].

Deep ecology emphasizes the positive effects of abundance that flow through different levels of the food chain, strengthening the overall health and stability of the ecosystem [79]. In a wetland ecosystem, the presence of a large number of primary producers, such as aquatic plants and algae, guarantees a strong population of primary consumers, such as snails and insects [80]. Consequently, a well-functioning ecosystem is maintained, with a diverse population of secondary consumers such as frogs and tiny fish, which in turn provides sustenance for tertiary consumers such as birds and larger fish. The trophic balance is crucial for ecological processes including nutrient cycling, energy transfer, and habitat provision, which are essential for the overall health and resilience of the wetland ecosystem [81].

An abundance of biodiversity, resources, and ecological niches contributes to the adaptive capacity of ecosystems, since a diverse ecosystem with a variety of species and functional roles can display multiple responses to changing conditions [77,82]. In turn, ecosystems with limited diversity are more vulnerable to disruptions owing to the lack of flexibility. A similar logic can apply to the adaptive capacity of economic and social systems. The abundance of resources, knowledge, and opportunities within society generally contributes to adaptive capacity at both societal and individual levels [83]. Societies with significant natural, economic, and human resources are capable of swiftly responding to external shocks in an efficient manner, mitigating the negative effects of economic crises, natural disasters, and other external factors. Whereas the adaptive capacity of ecosystems is enabled by multiple functional roles and diverse flora and fauna, the adaptive capacity of social systems is based on their resources and the functional roles of different social groups and institutions [84]. The relationship between abundance and adaptive capacity manifests itself similarly for environmental and social systems.

Economic systems follow the same logic to ensure economic sustainability. Changes in the availability of financial resources, job opportunities, market demand, and other factors affecting economic activities shape agents’ behaviors—as well as agents’ expectations about particular resource availability [85]. The abundance of resources gives room to implement effective risk management strategies, engaging in learning, and dynamically adjusting to shocks [86]. At the level of economic systems, the abundance of the resources discussed above results in a higher flexibility of economic systems and their resilience in the face of economic crises, hostilities, shortages of resources, and other undesirable scenarios.

Thus, systems that promote abundance, but not overabundance (which could be cast as complexity, and leading to depletion of resources), are more likely to be sustainable. Those systems essentially have the right degree of redundancy. Maintaining abundance over time entails having the possibility to grow strategies such that no one strategy is overused or leaves the system open to vulnerabilities.

Continuing with the example of an individual living in a forest, we can explore how abundance and redundancy contribute to resilience and sustainability.

In a forest ecosystem, abundance refers to the presence of a wide range of plant and animal species, each fulfilling their unique ecological roles or niches. This functional diversity enhances the resilience of the forest, as it ensures that all necessary tasks are being performed, making the system more capable of withstanding environmental stressors and disturbances.

For the individual living in the forest, this abundance translates to a more stable and reliable environment. The presence of a diverse array of food sources, such as plants, insects, and small animals, increases the individual’s chances of finding sustenance even if one particular food source becomes scarce. Similarly, the abundance of materials for shelter, such as trees and vegetation, provides the individual with more options for constructing a safe haven.

The positive effects of abundance flow through different levels of the food chain, strengthening the overall health and stability of the forest ecosystem. A thriving population of primary producers, such as plants and algae, supports a diverse community of consumers, from insects to birds and mammals. This trophic balance is crucial for maintaining the ecological processes that keep the forest functioning, such as nutrient cycling and energy transfer.

The individual’s generative model of the forest would incorporate this abundance and redundancy. The model would include a rich array of states representing the various species, resources, and ecological interactions present in the forest. This diversity of states allows the individual to adapt more effectively to changing conditions, as they can switch between different strategies for finding food, shelter, and other necessities.

The abundance of resources in the forest also contributes to the individual’s adaptive capacity, which is their ability to respond to external shocks and changes. With a wide range of options available, the individual can more easily adjust their behavior and expectations when faced with challenges, such as a sudden shift in weather patterns or the disappearance of a particular food source.

4.2. The Mathematics of Sustainability

A system at steady state can exhibit dynamic behavior, as it constantly adapts and evolves to maintain stability and avoid collapsing into an equilibrium state, i.e., death. This means the system is able to maintain its own balance over time even as resources and entities within it change. We can calculate the equilibrium point of the system given a set of inputs and parameters. For example, a deep temporal steady state could be represented as

$$[x^{*}=g(u,p)]$$

(9)

where $x^{*}$ is the equilibrium point of the system, u is a set of inputs, and p represents a set of parameters.

We can include the impact of resource depletion represented by $D(x_1,x_2,\dots ,x_n)$ as a factor influencing the equilibrium point of the system in the equation $x^{*}=g(u,p)$ as

$$[x^{*}=g(u,p,D(x_1,x_2,\dots ,x_n))]$$

(10)

This equation suggests that the equilibrium point of the system, represented by $x^{*}$, is a function of a set of inputs u, a set of parameters p, and the impact of resource depletion $D(x_1,x_2,\dots ,x_n)$ on the system.

Additionally, it encompasses the system’s ability to uphold positive priors for the subordinate levels of the systems and to foster a large fitness landscape which enables the continued prediction over resources presence (plasticity). It also pertains to the system’s capacity to withstand volatility at every level.

A good indicator of the system being at steady state for its different components is well-being. Well-being in active inference is the capacity to tailor your model to the environment in such a way as to minimize error and expect low error in the future [50]. Well-being measurements, in this context, could indicate the sustainability of various components within the system. This refers to the system’s capacity for stability and adjustment to change. The calculation can be determined by analyzing the alteration in the system’s state over a period of time based on a particular set of inputs and parameters. For instance, the equation representing the resilience of systemic dynamics should be as follows:

$$\mathsf{\Delta }x\left(t\right)=f(x\left(t\right),u\left(t\right),I(x_1\left(t\right),x_2\left(t\right),\dots ,x_n\left(t\right)),\theta )$$

(11)

Here, the change in system state at time t, represented by $\mathsf{\Delta }x\left(t\right)$, is a function of the current state of the system $x\left(t\right)$, a set of inputs $u\left(t\right)$, the interdependency $I(x_1,x_2,\dots ,x_n)$ between resources $x_i\left(t\right)$, which are the various components of $x\left(t\right)$, and some parameters $\theta$.

In system dynamics resilience, the dynamical systems can thus be translated to

$$\dot{x}\left(t\right)=f(x\left(t\right),u\left(t\right),I(x_1\left(t\right),x_2\left(t\right),\dots ,x_n\left(t\right)),\theta )$$

(12)

where $x\left(t\right)$ is the state of the system at time t, $u\left(t\right)$ represents the input or external factors that affect the system at time t, and $\theta$ represents the system’s parameters. Here, we omitted the dependence on the mutual information since this is itself a function of $x\left(t\right)$.

The input, $u\left(t\right)$, may encompass exogenous factors such as external stressors, resource availability, or environmental fluctuations. The inputs can be either continuous or discrete and exhibit temporal variation, such as the quantity of rainfall, fluctuations in temperature, or human actions such as deforestation.

The parameter $\theta$ represents the stable or gradually changing characteristics of the system that dictate its behavior, such as the pace at which resources are used, the maximum capacity of the environment, or the intensity of interactions between different components of the system.

The system must predict future changes and resource needs. To model this, we calculate the likelihood of future states given a set of inputs and parameters. For example, the evolution of empirical priors could be represented in terms of a conditional distribution such as

$$p_{\theta }\left(x(t+1)\right|x\left(t\right),u\left(t\right))$$

scoring the likelihood of the system being in state $x(t+1)$ at time $t+1$, given the current state $x\left(t\right)$, inputs $u\left(t\right)$, and parameters $\theta$.

We can include the interdependency $I(x_1,x_2,\dots ,x_n)$ as a factor influencing the likelihood of future states in the equation $p_{\theta }(x(t+1)-x\left(t\right),u\left(t\right))$, which is

$$\left[p_{\theta }(x(t+1)-x\left(t\right),u\left(t\right),I(x_1,x_2,\dots ,x_n))\right]$$

(13)

This suggests that the likelihood of the system being in state $x(t+1)$ at time $t+1$, given the current state $x\left(t\right)$, inputs $u\left(t\right)$ and parameters $\theta$, also depends on the interdependency $I(x_1,x_2,\dots ,x_n)$ between resources $(x_1,x_2,\dots ,x_n)$.

In addition, to consistently predict the presence of resources, the system must sustain a diverse fitness landscape at various levels. The concept can be succintly expressed as the entropy of the probability distribution across different states, which quantifies the diversity of the fitness landscape. This is represented as

$$[H\left(p\right)=-\sum _{i}p\left(i\right)logp\left(i\right)]$$

(14)

where $p\left(i\right)$ denotes the chance of the system being in state i, and the summing is performed across all possible states. As the value of $H\left(p\right)$ increases, the diversity of the fitness landscape increases, providing the system with a greater range of alternatives for adaptation.

To incorporate the influence of resource depletion expressed by $D(x_1,x_2,\dots ,x_n)$, we can deduct it from the entropy equation to obtain the fitness landscape:

$$[\mathsf{\Phi }\left(x\right)=-\sum _{i}p\left(i\right)logp\left(i\right)-D(x_1,x_2,\dots ,x_n)]$$

(15)

The fitness landscape of the system $F\left(x\right)$ is determined by the entropy of the distribution of states $-{\sum }_{i}p\left(i\right)logp\left(i\right)$ and the effect of resource depletion $D(x_1,x_2,\dots ,x_n)$ on the system.

Well-being, resilience and sustainability are all related to how well a system can avoid succumbing to chaos, and they thrive from some degree of stability across space and time. Too much stability (i.e., low uncertainty, or entropy) is not necessarily the path toward these states. Systems that are highly insensitive or resistant may have low resilience due to limited capacity for adaptation and innovation. To achieve sustainability, a system should handle stressors of varying intensities without exhausting its resources in the long term.

Systems enhance their fitness landscape by inhabiting the boundary between order and unpredictability, which is commonly referred to as the edge of chaos. This location provides a multitude of options into the system. This subtle threshold, near the point of no return but never quite attaining it, signifies a domain of homeorhesis. Homeorhesis is the term used to describe the state of dynamic stability or “steady change” shown by a system that has achieved a non-equilibrium steady state. A system that remains within its “comfort zone” (marked by low uncertainty or entropy) without pushing toward its tipping point may become vulnerable to unforeseen issues, such as black swan events. These events can result in severe consequences, such as the extinction of the system or its significant destabilization and reduction [30]. Conversely, a system that approaches the edge of chaos and consistently avoids reaching its critical point is better equipped to deal with the unpredictability in its environment and minimize the difference between its predictions and the potential volatility. This leads to a reduced probability of unexpected and significant events occurring [87]. This system broadens the scope of its fitness landscape, reducing the significance of any particular condition for its survival and eliminating the necessity to completely exhaust resources associated with a single state. Implementing meticulous subgrouping based on interdependencies enhances resource utilization and reduces the points of failure within a system.

By adopting this approach, businesses can enhance their ability to produce precise forecasts and adapt efficiently to fluctuations in their surroundings. Promoting the well-being of individual entities within the system, over extended periods of time by using priors from the higher level entities of the system, allows each subgroup to adapt their behaviors to sustain the overall welfare of the system and reduce errors in predictions. Sustainability and resilience are necessary to the ongoing processes that prevent the agent from dissolving. By occupying a state of near chaos and enhancing the complexity of the environment, entities within the system are able to adjust and react to alterations in their surroundings, hence fostering resilience and sustainability [30]. Moreover, enhancing degeneracy and reducing the likelihood of rare and unpredictable events, the system becomes more adept at managing unforeseen disruptions, resulting in more sustainable results. Sustainability is upheld through relationships that may be understood as a series of interconnected cycles that adapt and are organized in a dynamic hierarchy across space and time. Resilience and sustainability involve keeping the relationships between the entities in a system rather than preserving the exact attributes of the system. This allows the entities to adapt and move within a range while retaining a similar probability distribution. In the next sections, we will look specifically at how this happens in both an agent and a system.

4.3. Processes Fostering Sustainability in an Agent

As stressed until now, resilience and all processes underlying it contribute to sustainability. However, resilience is not enough, as resilient behavior may not be sustainable. In short, sustainability implies resilience, but resilience does not necessarily ensure sustainability. When considering how to achieve sustainability in an agent, in addition to resilience, an important role is played by an allostatic process of preparedness over long periods of time. By this, we mean planning and prevention to avoid surprising sensory outcomes. Planning and prevention, or, in other words, optimal courses of action, are found by minimizing EFE. A careful look at the EFE demonstrates two complementary ways of ensuring sustainability, which comprise on the one hand risk minimizing behavior and on the other hand ambiguity minimizing behavior. The former ensures that preferences (i.e., needs) are continuously met over the timespan of planning. The latter, i.e., ambiguity, ensures that the model is continually improved so that risk can continuously be successfully minimized. In other words, it ensures an information gain for future generative model improvement. This improvement can take place in several ways: with an inference about the states of the environment, via learning the parameters of the dynamics of the environment, or, as a third way, through learning the structure of the environment (i.e., structure learning). This means that given a generative model of trajectories, taking actions that minimize EFE yields trajectories that are expected to be sustainable over the timespan of planning. In particular, these trajectories yield outcomes that conform to preferences and thus minimize free energy, and in addition, bring new information about the world so that the generative model is improved over time in order to better predict the future. Hence, subsequent EFE-minimizing actions have a higher chance of achieving free energy minimizing outcomes. One fundamental issue in planning is that optimal policies for a given time horizon might not be optimal for a longer time horizon (e.g., myopic policies). Thus, we say that a policy is sustainable if it is a subpolicy of a sustainable policy. In practice, sustainable policies are found by planning on the full time horizon. The right time horizon for planning is the timespan over which the agent has preferences, i.e., the time horizon that matters. However, this is not so straighforward. Indeed, it is often the case that an agent’s preferences are precise in the near future and imprecise in the far future, which leads to myopic behavior (e.g., smoking because it feels good in the moment but might lead to health issues in the long run). To mitigate this, it helps to teach the agent about the long-term consequences of its actions in relation to its fundamental preferences that are necessary for survival (e.g., cancer). It is only when the consequences of a behavior on long-term preferences and the certainty of that inference outweigh preference satisfaction in the short term that myopic behavior will cease. Myopic behaviors for the self can be attributed to a generative model where the inferences about the future consequences of actions do not align with reality. Fortunately, the generative models can be improved to stop these behaviors pre-emptively through the incorporation of new data acquired thanks to ambiguity minimizing behavior, improving future inferences. These maladaptive behaviors can also be stopped once the behavioral outcomes start to be in sharp contrast with short-term preferences (e.g., pain or disease). What affects the agent has implications for collectives, of course. In the next section, we will see how.

Continuing with our example, while resilience is crucial for the individual’s survival in the forest, it is not sufficient to ensure long-term sustainability. Resilient behavior, such as quickly adapting to a sudden food shortage, may help the individual survive in the short term but could lead to unsustainable practices if not accompanied by proper planning and prevention.

To achieve sustainability, the individual must engage in an allostatic process of preparedness over long periods of time. This involves minimizing the Expected Free Energy to find optimal courses of action that balance risk minimization and ambiguity minimization.

Risk minimization ensures that the individual’s preferences, or needs, are continuously met over the timespan of planning. For example, the individual may plan to store extra food during times of abundance to prepare for potential future scarcity. This helps minimize the risk of going hungry during lean times.

Ambiguity minimization, on the other hand, ensures that the individual’s generative model of the forest is continually improved, allowing for better prediction and minimization of risk in the future. This can occur through inference about the states of the environment (e.g., observing seasonal patterns), learning the parameters of the environment’s dynamics (e.g., understanding the growth cycles of edible plants), or structure learning (e.g., discovering new food sources or shelter options).

By taking actions that minimize EFE, the individual can follow trajectories that are expected to be sustainable over the timespan of planning. These trajectories yield outcomes that conform to the individual’s preferences, thus minimizing free energy, while also providing new information to improve their generative model for better future predictions.

However, the individual must be cautious of myopic policies, which may seem optimal for a given time horizon but fail to consider longer-term consequences. For example, overharvesting a particular plant species may provide ample food in the short term but lead to the depletion of that resource in the long run. To avoid such pitfalls, the individual must plan based on the full time horizon that matters, considering their long-term preferences and the consequences of their actions.

If the individual’s generative model does not accurately capture the long-term consequences of their actions, they may engage in myopic behaviors that satisfy short-term preferences but ultimately prove unsustainable. To mitigate this, the individual can incorporate new data acquired through ambiguity-minimizing behavior to improve their generative model and make better inferences about the future. Additionally, if the outcomes of their actions start to sharply contrast with their short-term preferences (e.g., experiencing hunger or illness due to resource depletion), the individual can adjust their behavior accordingly.

4.4. Fostering Sustainability of Collectives

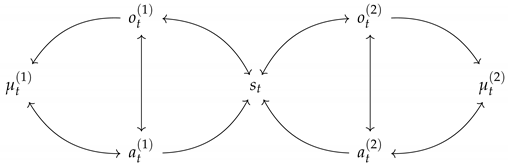
After having sketched how sustainability can be enhanced in an agent, we are going to address what happens when we deal with a system of collectives, i.e., when there are several agents interacting within one environment. To help clarify what we mean, here, we denote a system comprising two agents:

Then, the collective $(o_t^{\left(1\right)},o_t^{\left(2\right)},a_t^{\left(1\right)},a_t^{\left(2\right)},{\mu }_t^{\left(1\right)},{\mu }_t^{\left(2\right)})$ is an agent by the definition in Section 2, and the free energy principle and active inference apply. The same goes for any collective comprising finitely many agents.

According to the free energy principle, any collective of agents can be described by an (implicit) generative model such that the collective’s actions (i.e., the collection of individual actions) minimize the expected free energy for this generative model. Crucially, this generative model is generally not the product of the generative models embodied by the agents within, and it cannot currently be obtained straightforwardly.

To figure out why the implicit generative model describing the collective is not the product of the individual generative models, consider the following example: if it were, then the free energy of the collective would be the sum of the free energies of the individuals [88]. Then, consider two interacting agents, which are harmful to each other. Each agent is pursuing expected free energy-minimizing actions that increase the other’s free energy. This generally implies that out of all possible actions that the agents could take, the actual ones do not minimize the sum of free energies. However, these actions are certainly (tautologically so) free energy minimizing for the collective of agents by the free energy principle. This example illustrates a general point: although collectives take actions that minimize expected energy according to the collective generative model, the preferences encoded within the collective generative model may be misaligned with individual preferences in the group. This is analoguous to active inference accounts of computational psychiatry that describe maladaptive actions as free energy minimizing under a generative model with aberrant preferences [89]; the implicit preferences reflecting the collective’s actions may be aberrant from the perspective of the preferences of constituting individuals.

The policy problem at the level of the collective says that an optimal policy at the level of any individual (i.e., EFE minimizing for that individual) need not be beneficial for the collective, in the sense that it may increase the free energy of interacting agents, as in harmful behavior. From this, it follows that to achieve sustainability within a collective, we need the collective’s actions (that reflect the collective’s implicit preferences) to be aligned with individual preferences. Then, as the group works together to ensure these core preferences are satisfied over arbitrarily long timespans, it achieves a situation of sustainability. Hence, fostering sustainability at the level of the collective entails modifying the interactions between the agents within it so that each policy that is optimal at the level of the individual and also minimizes the free energy of interacting agents. At best, the EFE-minimizing policy of each individual together minimize the expected free energies of each individual agent [90]. We thence talk about full symbiosis between agents.

On this basis, it is also interesting to consider how these problems and observations translate at the level of public governance, for example when we consider the electoral setting. Indeed, the feedback loop of election and re-election motivates democratically elected leaders to align their actions to minimize each of their constituents’ free energies in order for their own preferences to be fulfilled (e.g., re-election). Leaders may do so by employing their own internal model of what the people desire and aim to fulfill those preferences. However, there is the definite problem that policies that minimize the people’s free energy within tenure are suboptimal to minimize their free energy in the long run (i.e., the timespan problem for policies). Therefore, free energy-minimizing decisions for the leader may not coincide with sustainable policies. To mitigate this, one might think of increasing the feedback loops from people to decision-maker so that the impact of policies beyond tenure have repercussions for the leader beyond tenure. This is but one way of increasing the alignment between expected free energy-minimizing actions for the decision-maker and minimizing the free energy of the people in the long run. Looking forward, one can define the best actions from a decision-maker toward a collective as follows: given a model of the collective’s preferences (e.g., the product of individual preferences), find the action that minimizes the EFE for that model. This corresponds to aiming to minimize the sum of free energies of each person within the collective. This is a selfless course of action in the sense that it is based solely on the inferred preferences of the people as opposed to the decision-maker’s own. It also says that an increase of free energy in an individual can only be justified by a larger decrease on the other’s free energies. In other words, the decision-maker should be an agent whose goal is to minimize an individual’s free energies over time. Finally, the timespan that should be considered during planning the course of action is the timespan over which the individual agents are inferred to have preferences.

If we recapitulate, to improve sustainability at the collective level in practice, we need to increase interconnectedness and plasticity, that is to augment the number and strength of two-sided interactions and feedback loops between agents (e.g., communication). This entails that any harmful policy for another might be reciprocated, creating accountability for each one’s actions, and a drive to select actions that benefit the collective so that the collective benefits ourselves. To increasing plasticity means to shift an agent’s preferences so that interactions result in a lower free energy for everyone. Depending on the context, this may translate into differentiation or alignment. The former, i.e., differentiation, is when agents must specialize to more effectively work together toward a common goal, e.g., preference biases toward doing the specialized activity that we do in society, such as habit formation. By the latter, i.e., alignment, we mean agreement on common values and fundamental goals, e.g., Declaration of Human rights. We can refer aligment to-risk minimizing behavior in an agent, as expressed in the previous section. Altogether, this might mean that low-level (i.e., closer to sensory input) preferences become differentiated, while high-level (i.e., fundamental) preferences become more aligned, so that agents naturally synchronize to achieve their common fundamental preferences and minimize their free energy.

5. Conclusions

The analysis presented in this paper serves the dual purpose of quantifying sustainability and promoting its development. We have reviewed the concepts of well-being, resilience and sustainability. We have suggested that they are interconnected with the ability of a system to prevent its dissipation and flourish with a certain level of stability. To achieve sustainability, we can implement strategies such as operating at the boundary between order and chaos, enhancing the complexity of the environment, optimizing redundancy, reducing the likelihood of unexpected and extreme events, establishing well-coordinated subgroups, and refining the agent’s prior knowledge to better understand the system. Sustainability and resilience are necessary to the ongoing processes that prevent the agent from dissolving. By occupying a state of near chaos and enhancing the complexity of the environment, entities within the system are able to adjust and react to alterations in their surroundings, hence fostering resilience and sustainability [30]. Moreover, enhancing degeneracy and reducing the likelihood of rare and unpredictable events, the system becomes more adept at managing unforeseen disruptions, resulting in more sustainable results. Agents can monitor their current state by monitoring and promoting their own well-being over time.

To clarify the use of our proposition, we will now lay out the potential blueprint for an application of our approach. Urban development is particularly interesting for the application of sustainability and resilience methods. As we saw, active inference allows policymakers to simulate and predict the outcomes of various urban development strategies. Through this method, we can model how actions affect urban systems and their ability to maintain equilibrium in the face of environmental, economic, and social stresses. These models can incorporate data from various sources, including demographic trends, economic data, environmental impacts, and infrastructure statistics. Consider a mid-sized city facing rapid population growth and limited natural resources. The city’s government could want to balance the need for expansion with the need to maintain a sustainable environment all the while ensuring the well-being of its residents. They would collect data about the current population and its expected growth, their consumption of water and energy, the available green spaces and their usage, the use of public transportation, infrastructure capacity, the housing development plans, the pollution levels and the health of the population with the assumption that pollution impacts it. Using these data, the government can model the relationships among these variables by laying out a state space. The model can represent the conditions of the infrastructure, population density, resource availability, and environmental quality. The city can model its possible actions like zoning changes, investment to improve public transport, the development of green spaces, and additional housing. The model would then predict outcomes like efficient resource usage, pollution levels, resident well-being and economic growth through the assumed relationships among these variables. The city’s government would define the system’s preferences and let scenarios play out to find a non-equilibrium steady state that allows for different scenarios to play out. The city’s government could then explore different scenarios. They could explore how a high-density urban development might impact urban sprawl, enhance public transportation and improve economic efficiency. Alternatively, they could consider investing in a lot of green spaces and different types of sustainable infrastructure (eco-friendly housing) to enhance environmental quality.

With this type of approach, we can thus implement meticulous subgrouping based on interdependencies to enhance resource utilization and reduce the points of failure within a system. Promoting the well-being of individual entities within the system, over extended periods of time by using priors from the higher level entities of the system, allows each subgroup to adapt their behaviors to sustain the overall welfare of the system and reduce errors in predictions.

To promote sustainability, we can consider the interconnectedness between the many components and the overall system and adopt a comprehensive approach toward the well-being of all of them. This encompasses the safeguarding of natural resources, the advancement of sustainable practices, and the cultivation of resilience and well-being across all levels of the system. It also involves consistently updating environmental projections and implementing actions to minimize errors. This perspective opens the opportunity for data-driven ethics in the sense that the most ethical course of action—defined as the one maximizing well-being, resilience and sustainability for the collective under consideration—is that which minimizes the expected free energy of the collective.