Analyzing Rear-End Crash Counts on Ohio Interstate Freeways Using Advanced Multilevel Modeling
Abstract
1. Introduction
1.1. Some Challenges Involved in Modeling Count Data
1.2. Study Contribution
2. Methodology
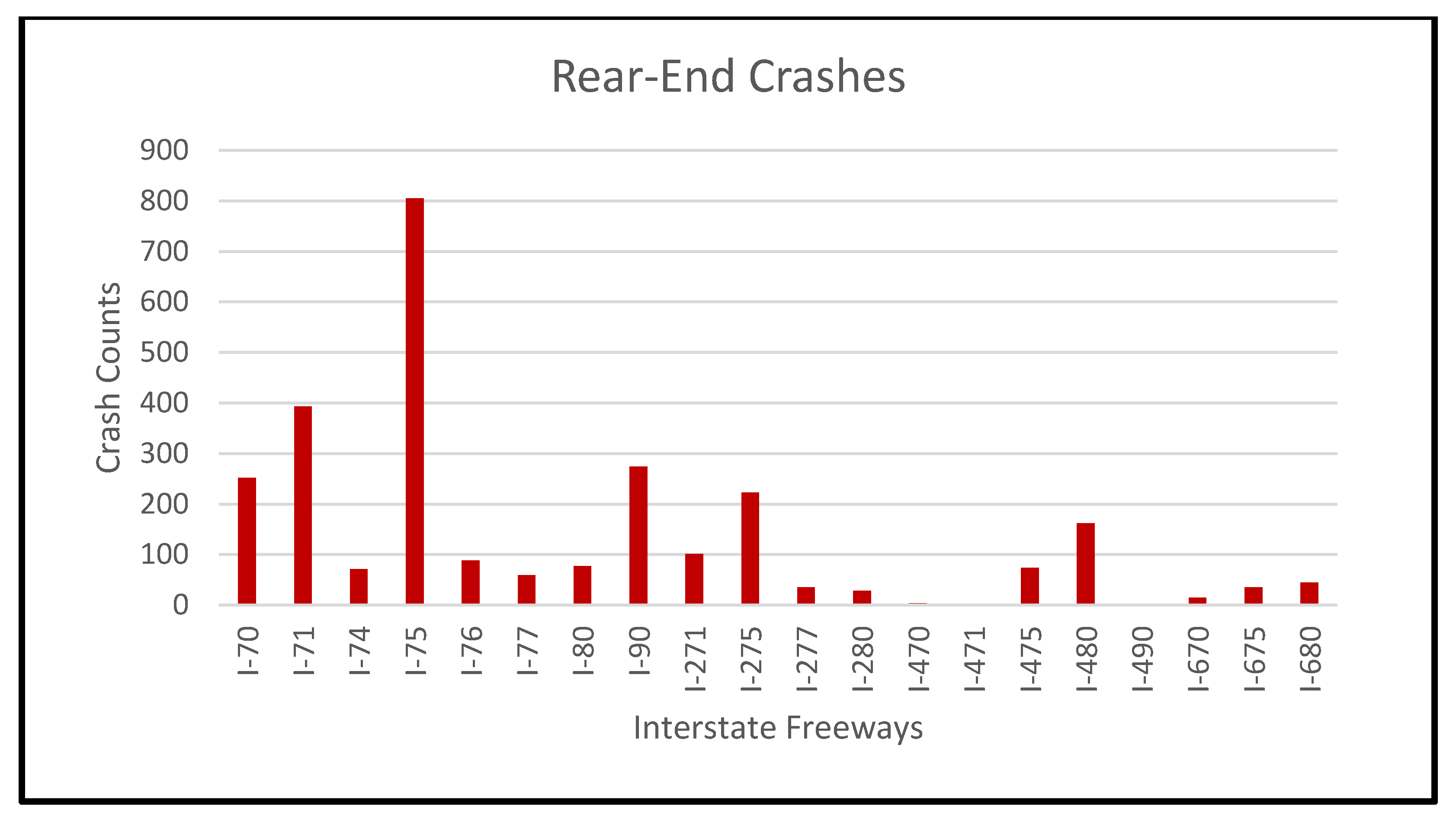
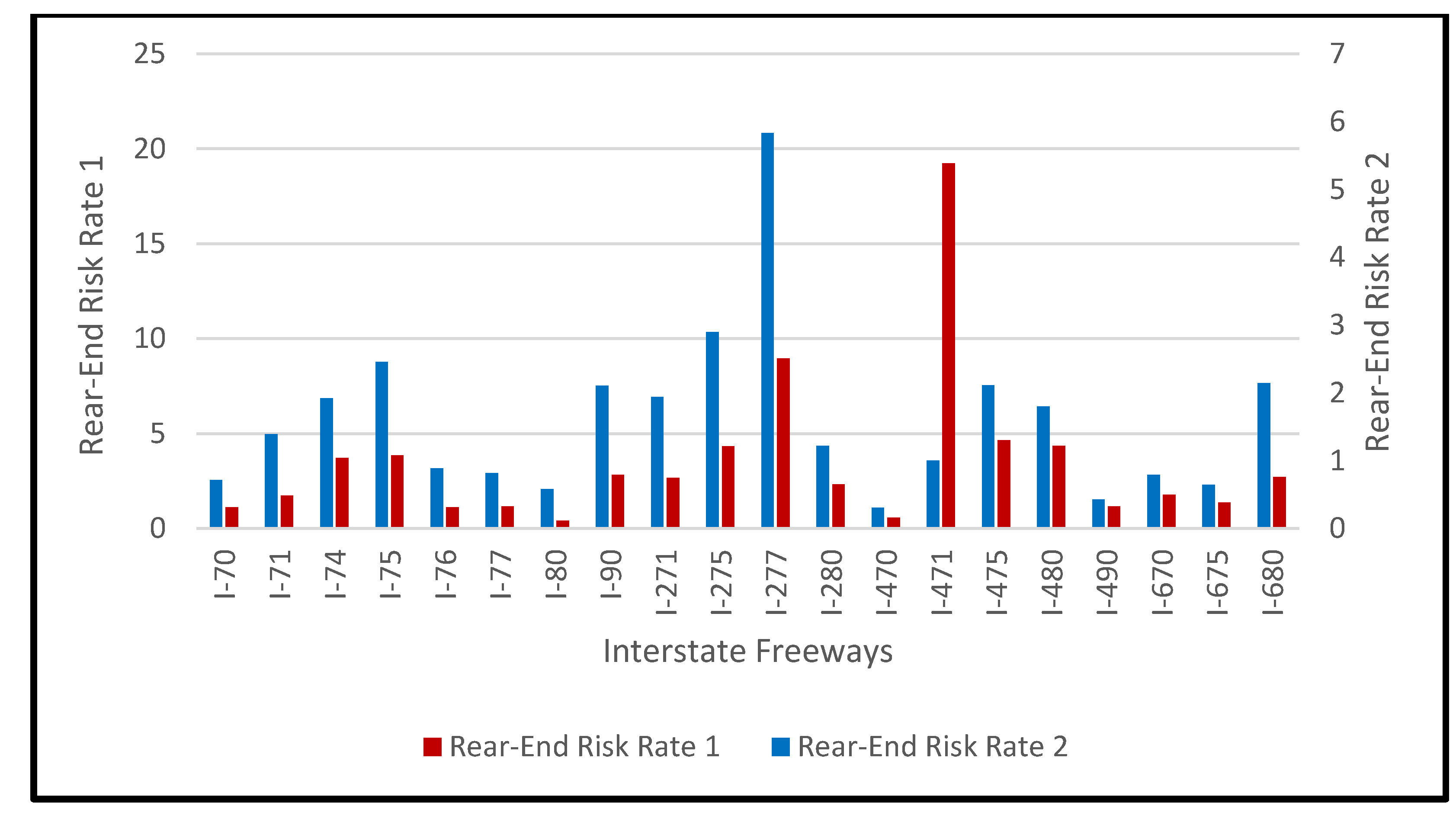
2.1. Study Data
2.2. Model Description
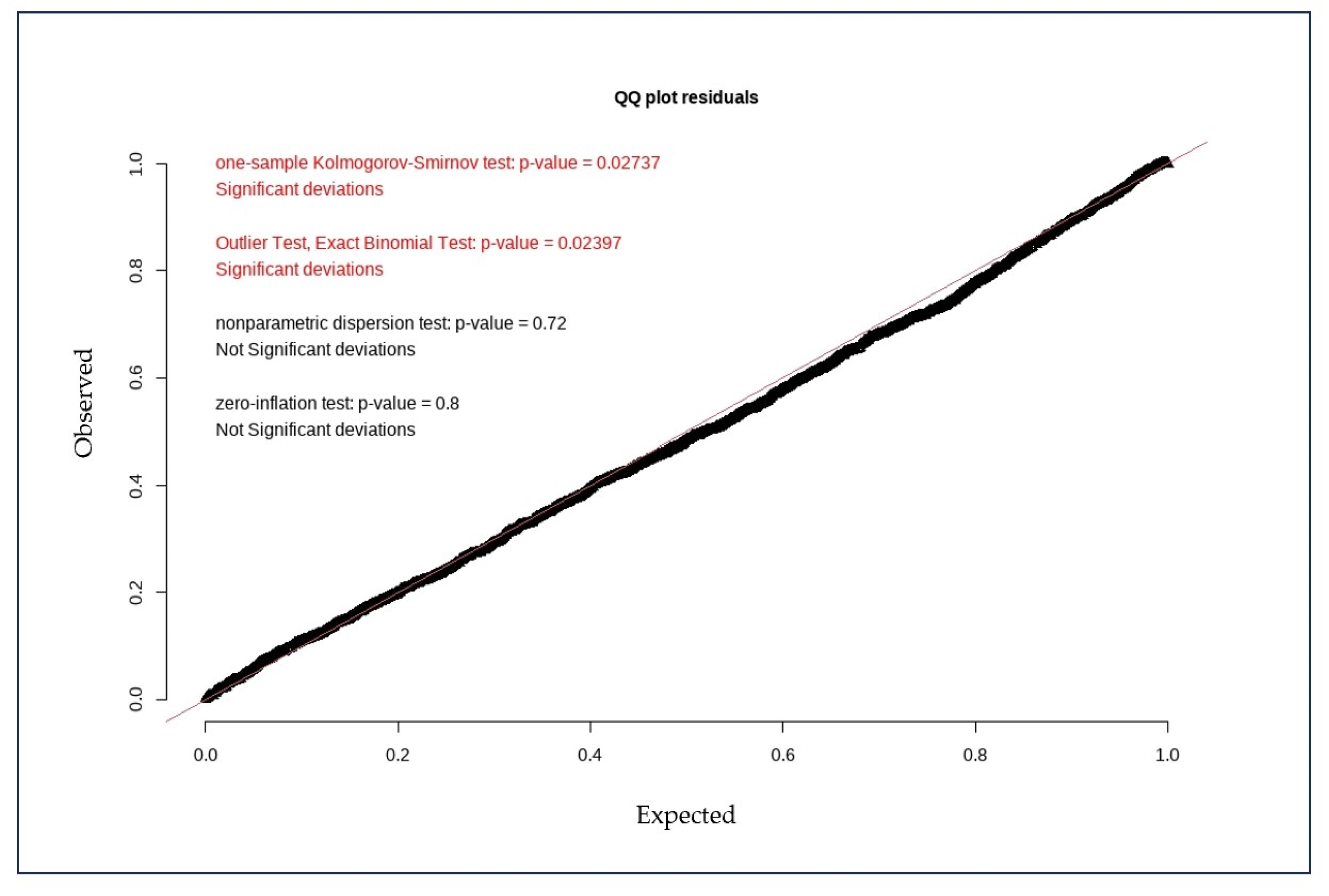
2.3. Evaluating Metrics
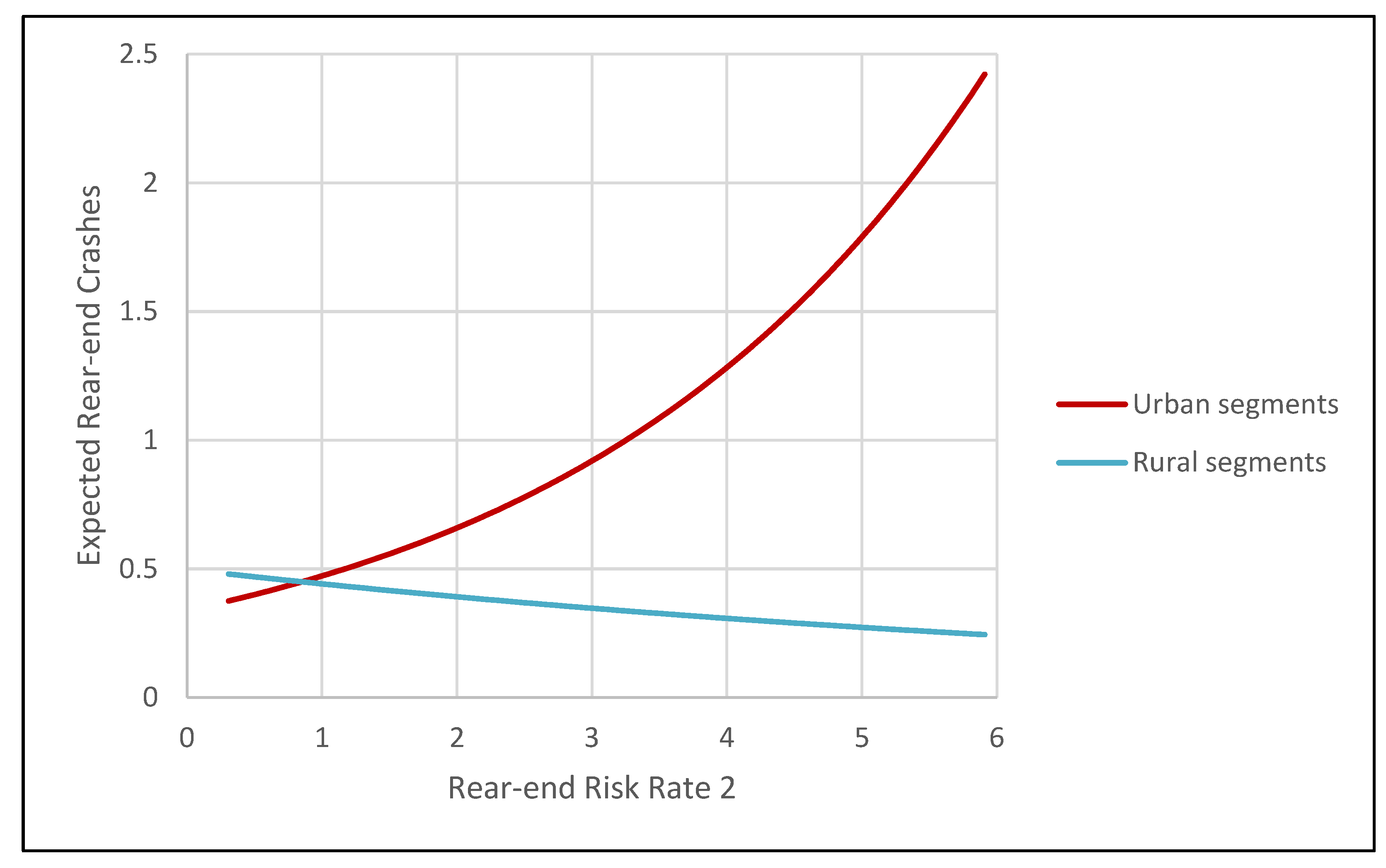
3. Study Results
4. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | Major interstate freeways: I-70, I-71, I-74, I-75, I-76, I-77, I-80, and I-90. Ring interstate freeways: I-271, I-275, I-277, I-280, I-470, I-471, I-475, I-480, I-490, I-670, I-675, and I-680. |
References
- Yuan, R.; Gu, X.; Peng, Z.; Xiang, Q. Exploring Differences in Injury Severity between Occupant Groups Involved in Fatal Rear-End Crashes: A Correlated Random Parameter Logit Model with Mean Heterogeneity. Transp. Lett. 2023. [Google Scholar] [CrossRef]
- Dimitriou, L.; Stylianou, K.; Abdel-Aty, M.A. Assessing Rear-End Crash Potential in Urban Locations Based on Vehicle-by-Vehicle Interactions, Geometric Characteristics and Operational Conditions. Accid. Anal. Prev. 2018, 118, 221–235. [Google Scholar] [CrossRef]
- Pešić, A.; Stephens, A.N.; Newnam, S.; Čičević, S.; Pešić, D.; Trifunović, A. Youth Perceptions and Attitudes towards Road Safety in Serbia. Systems 2022, 10, 191. [Google Scholar] [CrossRef]
- Swain, R.; Larue, G.S. Looking Back in the Rearview: Insights into Queensland’s Rear-End Crashes. Traffic Inj. Prev. 2024, 25, 138–146. [Google Scholar] [CrossRef]
- Chen, F.; Song, M.; Ma, X. Investigation on the Injury Severity of Drivers in Rear-End Collisions between Cars Using a Random Parameters Bivariate Ordered Probit Model. Int. J. Environ. Res. Public. Health 2019, 16, 2632. [Google Scholar] [CrossRef]
- Shao, X.; Ma, X.; Chen, F.; Song, M.; Pan, X.; You, K. A Random Parameters Ordered Probit Analysis of Injury Severity in Truck Involved Rear-End Collisions. Int. J. Environ. Res. Public. Health 2020, 17, 395. [Google Scholar] [CrossRef] [PubMed]
- Sharafeldin, M.; Farid, A.; Ksaibati, K. Injury Severity Analysis of Rear-End Crashes at Signalized Intersections. Sustainability 2022, 14, 13858. [Google Scholar] [CrossRef]
- Wang, C.; Xia, Y.; Chen, F.; Cheng, J.; Wang, Z. Assessment of Two-Vehicle and Multi-Vehicle Freeway Rear-End Crashes in China: Accommodating Spatiotemporal Shifts. Int. J. Environ. Res. Public. Health 2022, 19, 10282. [Google Scholar] [CrossRef]
- Wang, C.; Chen, F.; Zhang, Y.; Wang, S.; Yu, B.; Cheng, J. Temporal Stability of Factors Affecting Injury Severity in Rear-End and Non-Rear-End Crashes: A Random Parameter Approach with Heterogeneity in Means and Variances. Anal. Methods Accid. Res. 2022, 35, 100219. [Google Scholar] [CrossRef]
- Zou, R.; Yang, H.; Yu, W.; Yu, H.; Chen, C.; Zhang, G.; Ma, D.T. Analyzing Driver Injury Severity in Two-Vehicle Rear-End Crashes Considering Leading-Following Configurations Based on Passenger Car and Light Truck Involvement. Accid. Anal. Prev. 2023, 193, 107298. [Google Scholar] [CrossRef]
- Wang, C.; Chen, F.; Zhang, Y.; Cheng, J. Analysis of Injury Severity in Rear-End Crashes on an Expressway Involving Different Types of Vehicles Using Random-Parameters Logit Models with Heterogeneity in Means and Variances. Transp. Lett. 2023, 15, 742–753. [Google Scholar] [CrossRef]
- HSM Highway Safety Manual; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2010.
- Administration, F.H. Crash Prediction Module. Available online: https://highways.dot.gov/research/interactive-highway-safety-design-model/modules/crash-prediction-module (accessed on 11 September 2024).
- Al-Ahmadi, H.M.; Jamal, A.; Ahmed, T.; Rahman, M.T.; Reza, I.; Farooq, D. Calibrating the Highway Safety Manual Predictive Models for Multilane Rural Highway Segments in Saudi Arabia. Arab. J. Sci. Eng. 2021, 46, 11471–11485. [Google Scholar] [CrossRef]
- Erieba, O.; Pappalardo, G.; Hassan, A.; Said, D.; Cafiso, S. Assessment of the Transferability of European Road Safety Inspection Procedures and Risk Index Model to Egypt. Ain Shams Eng. J. 2024, 15, 102502. [Google Scholar] [CrossRef]
- Hasan, T.; Abdel-Aty, M. Short-Term Safety Performance Functions by Random Parameters Negative Binomial-Lindley Model for Part-Time Shoulder Use. Accid. Anal. Prev. 2024, 199, 107498. [Google Scholar] [CrossRef] [PubMed]
- National Academies of Sciences, Engineering and Medicine. Improved Prediction Models for Crash Types and Crash Severities; The National Academies Press: Washington, DC, USA, 2021. [CrossRef]
- Anastasopoulos, P.C.; Mannering, F.L. A Note on Modeling Vehicle Accident Frequencies with Random-Parameters Count Models. Accid. Anal. Prev. 2009, 41, 153–159. [Google Scholar] [CrossRef]
- Sawalha, Z.; Sayed, T. Traffic Accident Modeling: Some Statistical Issues. Can. J. Civ. Eng. 2006, 33, 1115–1124. [Google Scholar] [CrossRef]
- Choudhary, A.; Garg, R.D.; Jain, S.S. Safety Impact of Highway Geometrics and Pavement Parameters on Crashes along Mountainous Roads. Transp. Eng. 2024, 15, 100224. [Google Scholar] [CrossRef]
- Mannering, F.L.; Bhat, C.R. Analytic Methods in Accident Research: Methodological Frontier and Future Directions. Anal. Methods Accid. Res. 2014, 1, 1–22. [Google Scholar] [CrossRef]
- Champahom, T.; Se, C.; Jomnonkwao, S.; Kasemsri, R.; Ratanavaraha, V. Analysis of the Effects of Highway Geometric Design Features on the Frequency of Truck-Involved Rear-End Crashes Using the Random Effect Zero-Inflated Negative Binomial Regression Model. Safety 2023, 9, 76. [Google Scholar] [CrossRef]
- Bisht, L.S.; Tiwari, G. Assessment of Fatal Rear-End Crash Risk Factors of an Expressway in India: A Random Parameter NB Modeling Approach. J. Transp. Eng. A Syst. 2023, 149, 04022111. [Google Scholar] [CrossRef]
- Saeed, T.U.; Hall, T.; Baroud, H.; Volovski, M.J. Analyzing Road Crash Frequencies with Uncorrelated and Correlated Random-Parameters Count Models: An Empirical Assessment of Multilane Highways. Anal. Methods Accid. Res. 2019, 23, 100101. [Google Scholar] [CrossRef]
- Almutairi, O. A Nested Grouped Random Parameter Negative Binomial Model for Modeling Segment-Level Crash Counts. Heliyon 2024, 10, e28900. [Google Scholar] [CrossRef] [PubMed]
- Venkataraman, N.S.; Ulfarsson, G.F.; Shankar, V.; Oh, J.; Park, M. Model of Relationship between Interstate Crash Occurrence and Geometrics: Exploratory Insights from Random Parameter Negative Binomial Approach. Transp. Res. Rec. 2011, 2236, 41–48. [Google Scholar] [CrossRef]
- Yan, Y.; Zhang, Y.; Yang, X.; Hu, J.; Tang, J.; Guo, Z. Crash Prediction Based on Random Effect Negative Binomial Model Considering Data Heterogeneity. Phys. A Stat. Mech. Its Appl. 2020, 547, 123858. [Google Scholar] [CrossRef]
- Champahom, T.; Jomnonkwao, S.; Karoonsoontawong, A.; Ratanavaraha, V. Spatial Zero-Inflated Negative Binomial Regression Models: Application for Estimating Frequencies of Rear-End Crashes on Thai Highways. J. Transp. Saf. Secur. 2022, 14, 523–540. [Google Scholar] [CrossRef]
- Islam, A.S.M.M.; Shirazi, M.; Lord, D. Grouped Random Parameters Negative Binomial-Lindley for Accounting Unobserved Heterogeneity in Crash Data with Preponderant Zero Observations. Anal. Methods Accid. Res. 2023, 37, 100255. [Google Scholar] [CrossRef]
- Wang, W.; Yang, Y.; Yang, X.; Gayah, V.V.; Wang, Y.; Tang, J.; Yuan, Z. A Negative Binomial Lindley Approach Considering Spatiotemporal Effects for Modeling Traffic Crash Frequency with Excess Zeros. Accid. Anal. Prev. 2024, 207, 107741. [Google Scholar] [CrossRef]
- Hilbe, J.M. Negative Binomial Regression; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Zuur, A.F.; Ieno, E.N.; Walker, N.J.; Saveliev, A.A.; Smith, G.M. Mixed Effects Models and Extensions in Ecology with R; Springer: Berlin/Heidelberg, Germany, 2009; Volume 574. [Google Scholar]
- Mannering, F.L.; Shankar, V.; Bhat, C.R. Unobserved Heterogeneity and the Statistical Analysis of Highway Accident Data. Anal. Methods Accid. Res. 2016, 11, 1–16. [Google Scholar] [CrossRef]
- Brooks, M.E.; Kristensen, K.; van Benthem, K.J.; Magnusson, A.; Berg, C.W.; Nielsen, A.; Skaug, H.J.; Mächler, M.; Bolker, B.M. GlmmTMB Balances Speed and Flexibility among Packages for Zero-Inflated Generalized Linear Mixed Modeling. R J. 2017, 9, 378–400. [Google Scholar] [CrossRef]
- Zhang, H.; Yao, X.; Seong, J.T.; Alshanbari, H.M.; Albalawi, O. A New Weighted Probabilistic Model for Analyzing the Injury Rate in Public Transport Road Accidents. Alex. Eng. J. 2024, 101, 147–157. [Google Scholar] [CrossRef]
- Hartig, F. DHARMa: Residual Diagnostics for Hierarchical (Multi-Level/Mixed) Regression Models; R Packag Version 020 2018.
- Aljuaydi, F.; Wiwatanapataphee, B.; Wu, Y.H. Multivariate Machine Learning-Based Prediction Models of Freeway Traffic Flow under Non-Recurrent Events. Alex. Eng. J. 2023, 65, 151–162. [Google Scholar] [CrossRef]




| Model Type | Focus | Year Article |
|---|---|---|
| Random parameters bivariate ordered probit model | Investigated the factors contributing to driver injury severity in rear-end crashes. Modeled the drivers’ severity in the same crash together by allowing for the correlation between the drivers involved. Allowed the parameters to vary across observations. Highlighted the importance of considering both within-crash correlation and unobserved heterogeneity in injury severity analysis. | 2019 [5] |
| Random parameters ordered probit model | Studied the injury severity differences between car-strike-truck and truck-strike-car collisions. Found significant differences in contributing factors. Allowed parameters to vary across observations to account for unobserved heterogeneity. | 2020 [6] |
| Random parameters ordinal probit model | Investigated factors contributing to injury severity in rear-end crashes at signalized intersections. Allowed parameters to vary across observations to account for unobserved heterogeneity. | 2022 [7] |
| Random parameters logit model | Investigated factors contributing to injury severity in rear-end crashes on two freeways. Examined transferability and heterogeneity between two-vehicle and multi-vehicle crashes. Allowed parameters to vary across observations and accounted for heterogeneity in means and variances. | 2022 [8] |
| Random parameter multinomial logit model | Investigated factors contributing to injury severity in rear-end and non-rear-end crashes on two freeways. Examined the transferability and heterogeneity of injury severity over the years. | 2022 [9] |
| Multinomial logit model | Investigated factors contributing to injury severity in rear-end crashes involving passenger cars and light trucks. Employed a latent class model to account for heterogeneity in variable effects. | 2023 [10] |
| Random parameters logit model | Investigated factors contributing to injury severity in rear-end crashes on expressways involving different vehicle types. Allowed parameters to vary across observations and accounted for heterogeneity in means and variances. | 2023 [11] |
| Model Type | Focus | Year Article |
|---|---|---|
| Random parameter negative binomial model | Analyzed nine years of crash counts on interstate directional segments. Allowed parameters to vary across observations and employed a temporal correlation structure between consecutive years. | 2011 [26] |
| Random parameter negative binomial model | Modeled total crashes on interstate highways. Allowed parameters to vary across observations to account for unobserved heterogeneity. | 2020 [27] |
| Zero-inflated negative binomial regression | Modeled rear-end crashes on highways. Allowed random parameter to vary across jurisdictions of the department of highways. | 2022 [28] |
| Grouped random parameters negative binomial Lindley model | Modeled lane departure crashes on rural interstates. Allowed parameters to vary across counties to account for unobserved heterogeneity. | 2023 [29] |
| Negative binomial Lindley model | Modeled total crashes on rural two-way, two-lane highways. Employed various temporal and spatial correlation structures to account for data dependency. | 2024 [30] |
| Variables | Mean | Range | SD |
|---|---|---|---|
| Rear-end crash counts | 1.498 | 0–54 | 3.525 |
| Ln (AADT) of passenger car | 10.659 | 8.418–11.938 | 0.615 |
| Ln (segment length) (miles) | −1.267 | −6.908–2.520 | 1.539 |
| Inner shoulder width (feet) | 15.532 | 0–60 | 9.125 |
| Outer shoulder width (feet) | 20.679 | 0–40 | 3.366 |
| Area indicator(0 for urban and 1 for rural) | 0.267 | 0–1 | 0.443 |
| Rear-end crash risk rate 1 | 2.310 | 0.408–19.231 | 1.427 |
| Rear-end crash risk rate 2 | 1.498 | 0.308–5.833 | 0.788 |
| Number of lanes | 5.380 | 4–10 | 1.474 |
| Curved segment indicator (0 for straight segments, 1 for curved segments) | 0.014 | 0–1 | 0.116 |
| Ln (county population) | 12.467 | 10.273–14.091 | 1.141 |
| Model | Fixed Negative Binomial | Two-Level Negative Binomial | Correlated Two-Level Negative Binomial | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Fixed Parameters | Estimate | Std. Error | Z-stat | Estimate | Std. Error | Z-stat | Estimate | Std. Error | Z-stat |
| Intercept | −14.613 | 0.814 | −17.947 | −14.813 | 1.056 | −14.031 | −14.477 | 1.053 | −13.743 |
| Ln (AADT) | 1.410 | 0.078 | 18.182 | 1.420 | 0.101 | 14.075 | 1.387 | 0.101 | 13.740 |
| Ln (Segment length) (LSL) | 0.838 | 0.031 | 26.726 | 0.846 | 0.037 | 22.621 | 0.846 | 0.036 | 23.456 |
| Inner shoulder width (ISR) | −0.021 | 0.004 | −5.502 | −0.020 | 0.005 | −4.020 | −0.021 | 0.006 | −3.197 |
| Area indicator | 0.308 | 0.203 | 1.512 | 0.356 | 0.230 | 1.546 | 0.386 | 0.234 | 1.647 |
| Rear-end crash risk rate (RECRR) | 0.316 | 0.051 | 6.209 | 0.321 | 0.073 | 4.402 | 0.333 | 0.071 | 4.679 |
| RECRR-Area indicator interaction | −0.449 | 0.134 | −3.349 | −0.424 | 0.149 | −2.844 | −0.453 | 0.152 | −2.986 |
| Random parameters | |||||||||
| Standard deviation of intercept (Negative sign percentages) | - | - | - | 0.279 ≈100% | 0.053 | 5.290 | 0.555 ≈100% | 0.097 | 5.703 |
| Standard deviation of LSL (Negative sign percentages) | - | - | - | 0.126 ≈0% | 0.036 | 3.541 | 0.107 ≈0% | 0.036 | 2.970 |
| Standard deviation of ISR (Negative sign percentages) | - | - | - | 0.009 98.7% | 0.003 | 2.703 | 0.028 77.3% | 0.006 | 4.460 |
| Intercept-IRS Correlation | - | - | −0.88 | ||||||
| Model | Fixed Negative Binomial | Two-Level Negative Binomial | Correlated Two-Level Negative Binomial | |
|---|---|---|---|---|
| Goodness-of-fit measures | ||||
| Deviance | 4581.4 | 4556.1 | 4546.8 | |
| AIC | 4597.4 | 4578.1 | 4570.8 | |
| BIC | 4641.5 | 4638.8 | 4637 | |
| Degrees of freedom | 8 | 11 | 12 | |
| Likelihood ratio test | ||||
| Difference of degrees of freedom | 3 | 1 | ||
| Chi-square statistics | 25.313 | 9.272 | ||
| p-value | <0.0001 | 0.0023 | ||
| Forecasting accuracy | ||||
| RMSE | 2.597 | 2.453 | 2.452 | |
| Variables | Fixed Negative Binomial | Two-Level Negative Binomial | Correlated Two-Level Negative Binomial |
|---|---|---|---|
| Ln (AADT) | 2.120 | 2.099 | 2.0418 |
| Ln (segment length) | 1.259 | 1.252 | 1.2507 |
| Inner shoulder width | −0.0318 | −0.0288 | −0.0318 |
| Area indicator | −0.6049 | −0.4996 | −0.516 |
| Rear-end crash risk rate | 0.3885 | 0.395 | 0.406 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almutairi, O. Analyzing Rear-End Crash Counts on Ohio Interstate Freeways Using Advanced Multilevel Modeling. Systems 2024, 12, 438. https://doi.org/10.3390/systems12100438
Almutairi O. Analyzing Rear-End Crash Counts on Ohio Interstate Freeways Using Advanced Multilevel Modeling. Systems. 2024; 12(10):438. https://doi.org/10.3390/systems12100438
Chicago/Turabian StyleAlmutairi, Omar. 2024. "Analyzing Rear-End Crash Counts on Ohio Interstate Freeways Using Advanced Multilevel Modeling" Systems 12, no. 10: 438. https://doi.org/10.3390/systems12100438
APA StyleAlmutairi, O. (2024). Analyzing Rear-End Crash Counts on Ohio Interstate Freeways Using Advanced Multilevel Modeling. Systems, 12(10), 438. https://doi.org/10.3390/systems12100438









