1. Introduction
It is well-known that a public transportation system (PTS) can help cities to reach a sustainable status. A PTS represents the foundation of sustainable mobility in a large and densely populated city due to several factors like its efficiency, accessibility, potential for operational expansion by complementarity to micro-mobility vehicles or other traveling ways, etc. However, only a robust operation can increase a citizen’s trust in a PTS service and make them abandon the use of cars [
1,
2,
3,
4,
5]. The issue of PTS robustness has been the focus of many researchers [
6,
7,
8].
The concept of robustness is related to that of resilience together with the notion of vulnerability and reliability, and therefore the evaluation models are somewhat related to and derived from each other.
Service robustness is usually defined by the ability of the system to maintain a certain level of its service performance, and it is taken into account from the service design stage.
Early research focused on complex network aspects [
9,
10]. In these studies, the subway network is often built using graph theory, and different network topologies, such as index of betweenness, network diameter, and average degree, are typically employed for quantification of robustness. Further research evaluated the robustness of the subway network using additional metrics such as network demand and line capacity [
11,
12]. It is revealed that quantifying robustness (or vulnerability) needs both perspectives of transit operation and network properties. The paper’s objective is to evaluate the robustness of the existing Bucharest metro system. For this, we addressed the network topology/structure by employing the already-known metrics for network robustness; besides, we analyzed the metro system operation as the second part of the system analysis. We considered for the metro system operation assessment the statistics for dysfunctionalities, rather than good-operation statistics. This assessment aims to suggest potential improvements to enhance network robustness.
Although robustness assessments on PTS have been carried out in many cities around the world [
13,
14,
15], an assessment of the robustness of the metro system in Bucharest is missing at the moment, according to our best knowledge. The disruptions which occurred and their detailed analysis is also missing. Understanding the robustness of metro systems is important for stakeholders including urban planners, transportation authorities, emergency response teams, and daily commuters. Urban planners and transportation authorities can use these insights to design more resilient infrastructure, emergency response teams can better prepare for and manage disruptions, and commuters can enjoy more reliable transit services.
In the following section of the literature review, robustness, reliability, and vulnerability concepts are investigated. In the third section, the method and data collection are described and then the metro disruption causes and potential risks of the Bucharest metro network systems are determined. The computing of the robustness and discussions are in the fifth section and then several conclusions are synthesized.
2. Literature Review
Vulnerability research began in the field of disaster research in the 1970s and quickly extended to other areas of study, including transportation studies. “Transport system vulnerability” was the original term used to describe sensitivity indices to threats that could significantly affect the accessibility and usage of the network [
16]. While there is variation in the exact definition of the topic, studies on network vulnerability typically concentrate on two primary areas: (i)—identifying the essential components of the transport network’s vulnerability, and (ii)—assessing the probability that a disconnection/disturbance will negatively impact the transport network’s performance [
17]. According to the parameters outlined in the above analyses, any alterations that occur as a result of unexpected and disruptive incidents within network systems are classified as vulnerabilities. The disruption of a network’s regular operations by unforeseen events can reveal vulnerabilities within its infrastructure, thereby increasing the risk of security breaches or eventual system failures. It is essential to clarify that the focus here is on communication networks, distinct from traffic networks, to ensure an accurate interpretation of identified vulnerabilities and associated security concerns. The studies in question assess these interruptions and their resultant changes as potential points of risk that need to be addressed to ensure the integrity and reliability of the network. Studies on network vulnerability typically focus on identifying the essential components of a transport network’s vulnerability and assessing the probability of a disturbance negatively impacting network performance. These insights are invaluable to stakeholders such as municipal governments and transportation agencies, who must ensure the robustness and efficiency of public transit systems. Furthermore, emergency management professionals rely on such analyses to develop strategies for interventions mitigating the impact of network disruptions.
Studies on the vulnerability of transportation networks can be divided into three types: vulnerability of connections, vulnerability related to the capacity of transit when the connection is operational, and vulnerability concerning accessibility through the network. Each category is defined by the specific effects that the simulated disruptions have on the network’s functionality [
18]. While it is possible to consider accessibility gaps from the passenger perspective (at least as a perception), connectivity and connection capacity are two crucial elements for emergency preparedness and solutions included in response protocols. There are some distinctions among the different definitions of accessibility that have been proposed in the literature which were discussed in many different contexts. Ingram’s 1971 study on accessibility, which introduced the key concepts of “Relative Accessibility” and “Integral Accessibility”, still serves as a basis for assessing the accessibility of public transportation systems [
19]. Furthermore, a technique for utilizing accessibility and sub-accessibility numbers to assess the accessibility of public transportation was demonstrated.
Multi-criteria vulnerability assessment methodologies incorporate accessibility techniques as well. For example, the accessibility measures of transportation networks have been used to identify key links in the event of natural disasters and disruptions in transportation networks [
20]. Furthermore, certain/relevant locations can be found using vulnerability analysis, and these areas can subsequently be quantified using multiple accessibility criteria.
Berdica’s vulnerability concept, which is defined as the network’s susceptibility to events that cause a major impairment in its functionality [
16], lacked quantitative measurements. D’Este and Taylor used link choice probabilities obtained by applying Bell’s algorithm to solve a stochastic user equilibrium (SUE) problem to identify the weakest links and evaluate its effects on network dysfunctionality [
21]. Links with higher probabilities of being chosen into multiple routes in the network are regarded as potentially weak links. Once these connections are broken, the effects of network deterioration are evaluated.
System vulnerability is defined as the degree to which a system can be attacked or influenced. This means that it is vulnerable to damage and it cannot resist interference or recover from disturbances [
22,
23]. Since its inception in the 1950s by Robert Forrester, system dynamics (SD) has been widely recognized as a method to analyze the behavior of dynamic complex systems over time [
24]. The SD approach has several advantages, the most notable of which is its ability to model circular causalities among various factors. It overcomes the limitations of linear causal models (such as regression models) and enables the description of complex interactions and the modeling of non-linear systems [
25]. The SD approach supports the identification of time-delayed but also interlocking relationships among factors using feedback loops, stocks, and flows. This enables the modeling of the long-term dynamics of the entire system more accurately [
26].
The Knoop study determines also critical or weak connections in a network [
27] according to different analysis scenarios/methods. In the first scenario, a link may be closed whenever it deems appropriate due to various link-blocking causes (e.g., capacity degradations). Each link’s capacity is reduced independently from the others, and each traffic distribution problem in a degraded network environment is also fixed independently. In the second scenario, the potential weak links are determined using a particular selection criterion and their vulnerability levels are quickly evaluated before delving into a thorough analysis. The third method involves a game theory to find the critical connections.
3. Materials and Method
3.1. Study Area—Bucharest Metro Network
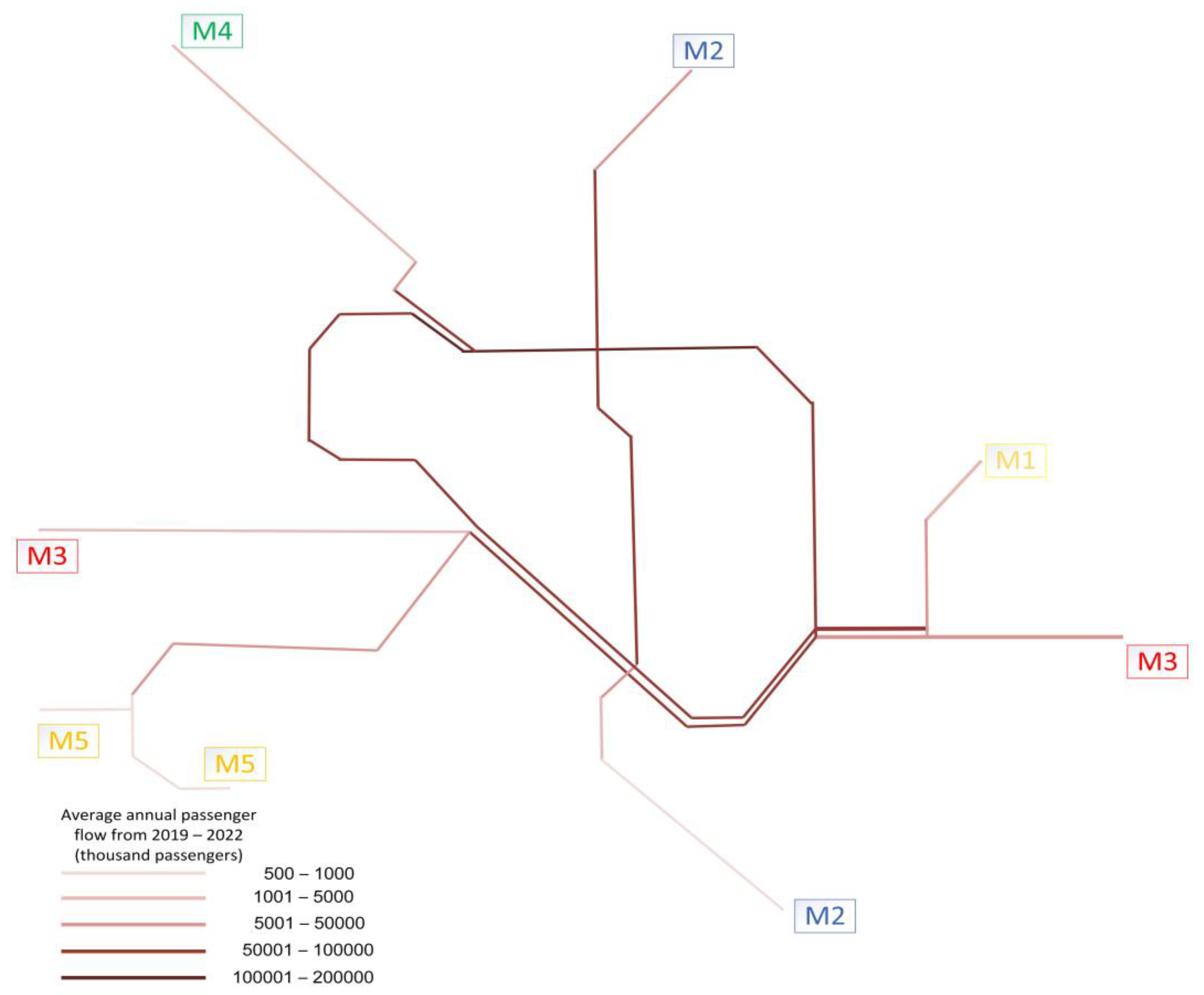
The Bucharest metro system started the operation of its first line, M1 (
Figure 1), in 1979, and since then it has gradually increased to the actual structures, containing five lines and 56 stations, and a total length of about 79 km. In 2020, the system carried 87,880,000 passengers according to Metrorex (metro services provider) [
28].
We may find the metro lines having ring, radial, loop, or branch topologies. For instance, line 1 (M1, in yellow) has a ring topology since it encircles the city center in a circular loop. Line 2 (M2, in blue), which stretches north and south under the city center, has a radial structure. Line 3 (M3, in red) uses a semi-circular route to connect two branches of line 1 and has a loop topology. Because line 4 (M4, in green) splits from line 1 and ends at the northern edge of the city, it features a branch topology. Line 5 (M5, in orange) links two branches of line M2 via a semi-circular path, resulting in a loop topology. There is also a planning line 6 (M6) that will have a radial topology.
The annual average train passenger flows on each edge on a typical workday are shown in
Figure 2. In normal circumstances, the Bucharest metro carries, on average, around 500.000 passengers/day, and over 15 million passengers/month. Line M1 and line M2 have larger flows than the other lines. An average of 70,000 thousand passengers are transported annually on line M1, which is the busiest line. For all lines, flow peaks occur during the morning congested hour (7:00–9:00) and evening congested hour (16:00–18:00).
3.2. Analysis of Disruptions at the Bucharest Metro
The metro system in Bucharest has experienced disruptions. Between January 2019 and December 2022, there were 352 disruption events in total. This paper provides an analysis of disruption data from the Bucharest metro system collected between January 2019 to December 2022, for each day. This includes the frequency, causes, and recovery times of disruptions, which are crucial for understanding the network’s current state. The five metro lines under investigation operate daily between 5 am and 11 pm [
28]. The Bucharest metro network has a higher frequency of disruptions due to train failures and technical failures. There is a need for enhanced maintenance protocols and real-time monitoring systems to predict and prevent such failures. This could involve the adoption of predictive maintenance technologies that utilize data analytics to foresee potential failures before they occur.
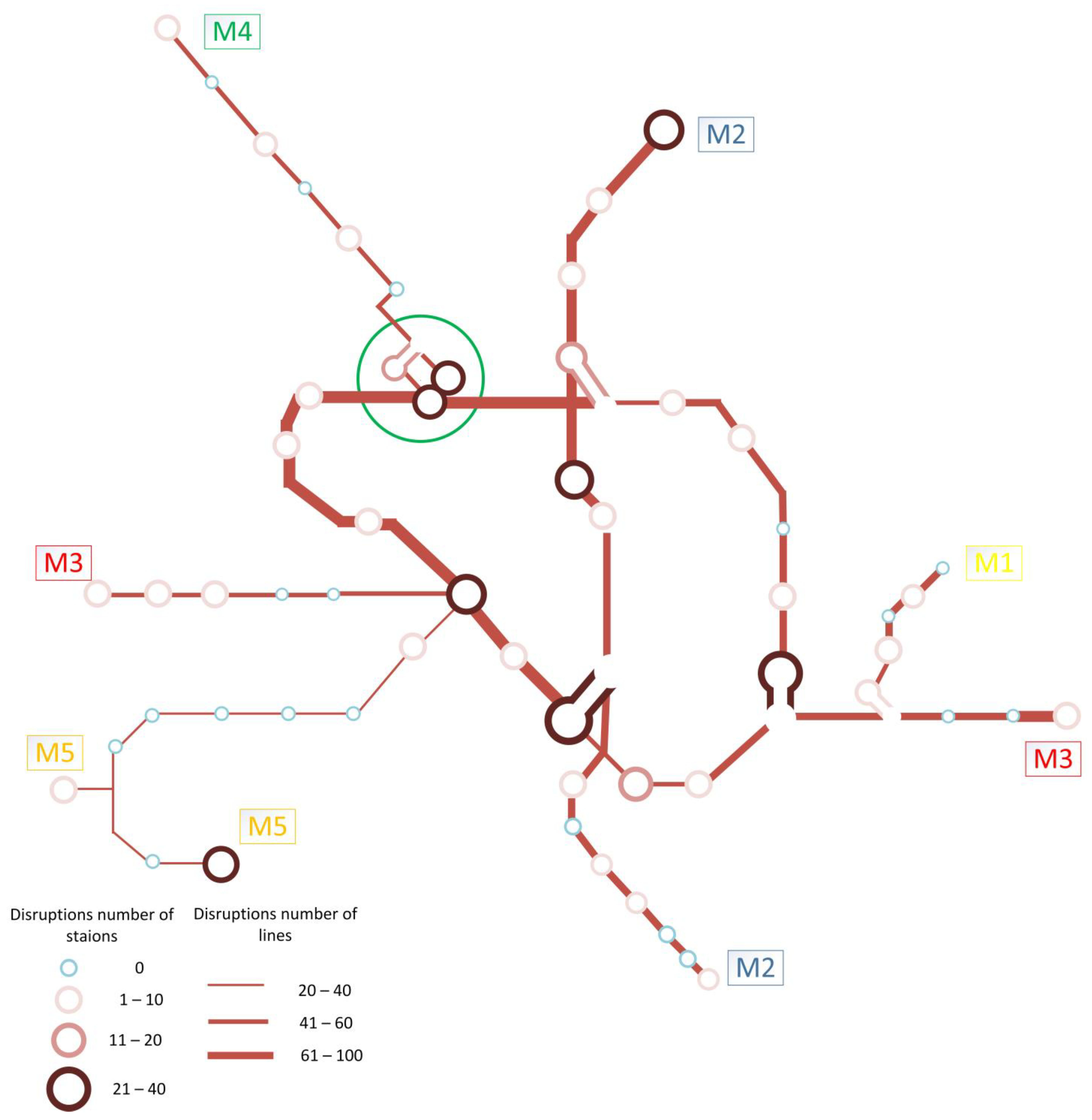
Each year’s disruption events are categorized by cause in
Table 1. With 105 disruptions, 2021 was the year with the highest count of incidents and 2019 with 61 disruptions is the lowest one. The most frequent causes of these incidents were technical failure (17.5%), train failure (16.95%), and passenger emergencies (14.65%). Train failures typically block a single line between two stations. This type of disruption should be analyzed for its impact on the line capacity and passenger rerouting options. For example, a train failure on line M1 could block the route between two major stations, necessitating the use of alternative routes or shuttle services to bypass the blockage. Passenger emergencies might cause temporary halts at specific stations without affecting the entire line. For instance, if a passenger emergency occurs at a major station like Gara de Nord, the impact would be significant during rush hours due to high passenger volume but might be less critical at off-peak times. However, this impact assessment of each type of failure is not covered in this paper. It will be addressed properly in the next research.
The causes of disruptions are grouped according to the place of occurrence and whether they are on a link or node. As can be seen (
Table 2), the total number of node- and link-based disruptions are close, and it can be deduced that investigating both groups is equally important.
The regional distribution of the disruptions (as numbers) is shown in
Figure 3. The majority of the incidents happened on routes with high passenger volumes, lines M2, M1, and M3, which means 27.6%, 16.9%, and 12.93%, respectively, of the total disruptions. More disruptions occurred at transfer stations with high passenger volumes than at other stations. With 11.21% occurrences between 2019 and 2022, Gara de Nord (with a green circle in
Figure 3) was the metro station with the most disruptions.
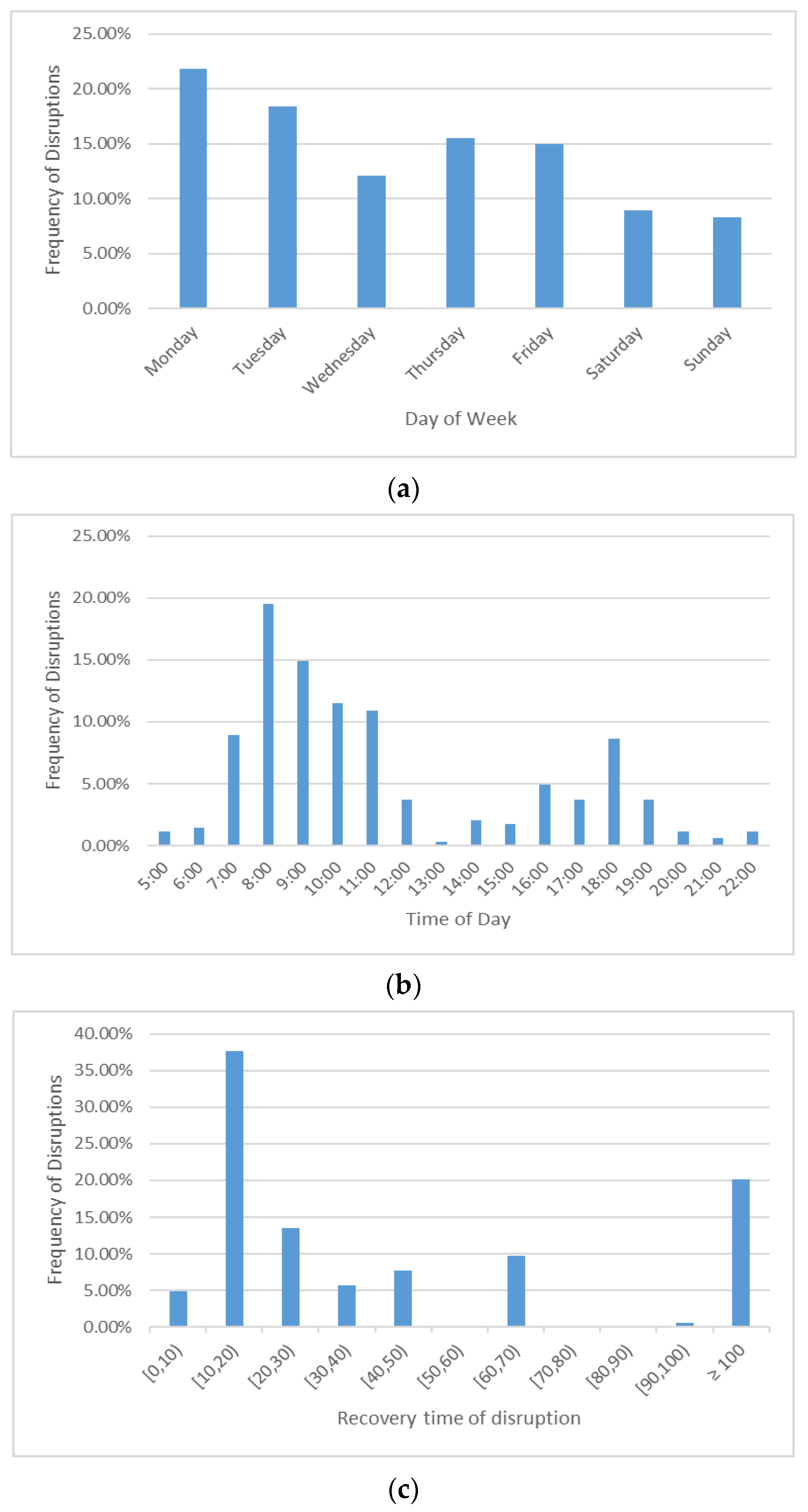
The distribution of the disruption frequency is represented in
Figure 4a,b. Almost 82.7% of the disruptions happened during the weekdays, and 60.63% of all disruptions happened during the morning and afternoon rush hours. It is obvious that this pattern is related to the high volume of passengers and the short train departure times during these times. For instance, the headway of services on line M1 is 6 min during rush hour and 9 min outside of rush hour. Based on the available statistics, the average disruption time was 21 min, and 79.31% of incidents had recovery times of less than one hour (
Figure 4c).
3.3. Method
The analysis in this paper revolves around the concept of node removal, which is important for assessing the robustness of the networks; at least, from the perspective of the passengers’ accessibility to service. We consider two types of station/nodes, transfer stations versus regular stations, and two removal strategies (as in real operation might appear).
Node Removal Strategies: The paper employs two strategies for node removal:
- ○
Random Node Removal: Nodes are removed randomly, simulating unforeseen failures.
- ○
Node Degree-Based Removal: Nodes with the highest degree (i.e., the most connected nodes) are removed first, simulating targeted intentions to make the network inactive.
These strategies are intended to test the network under different stress conditions.
Implications of Removing Different Nodes:
- ○
Removing Regular Stations: If a regular station is removed, the immediate impact is on the passengers using that station, who need to find alternative routes. However, trains can often skip that station and continue their running on track, minimizing the disruption impact on a broader network part.
- ○
Removing Transfer Stations: Removing a transfer station has more implications. Transfer stations are critical junctures where passengers switch lines. In case such a station is removed, it affects the passengers and disrupts the train flows of the important part of the network.
However, in the case of the transfer station having separate platforms, the train may continue moving on the track along the unaffected platform; here, more detailed analyses are needed.
The robustness curve (as shown in the paper) plots the size of the largest remaining connected paths in the network as certain nodes are removed. While this provides a high-level view, more granular metrics could be incorporated. For instance, measuring the increasing passenger travel time, or the number of isolated passengers, could offer a more nuanced impact assessment. These will be the tasks in future research.
The metro system is an urban transit system with an exclusive right-of-way, and an undirected graph can be used to model the metro network. In an undirected graph, the edges imply a two-way relationship.
Let us note the graph with G (N, L), L representing the network links and N the nodes. The rail tracks that physically connect the stations serve as the links and transfer stations serve as the nodes. An adjacency matrix A (which is an N × N symmetric matrix with the element if there is a line connecting nodes i and j, and otherwise), can fully represent the associated graph G of the metro network elements .
The Laplacian matrix , G is also a N × N matrix, and is the N × N diagonal degree matrix.
According to Van Mieghem [
29],
Q’s eigenvalues are non-negative and at least one is zero. The order of
Q’s eigenvalues
Q’s
. The number of connections of a node
i represents the node’s degree. The terminus stations have a degree equal to 1.
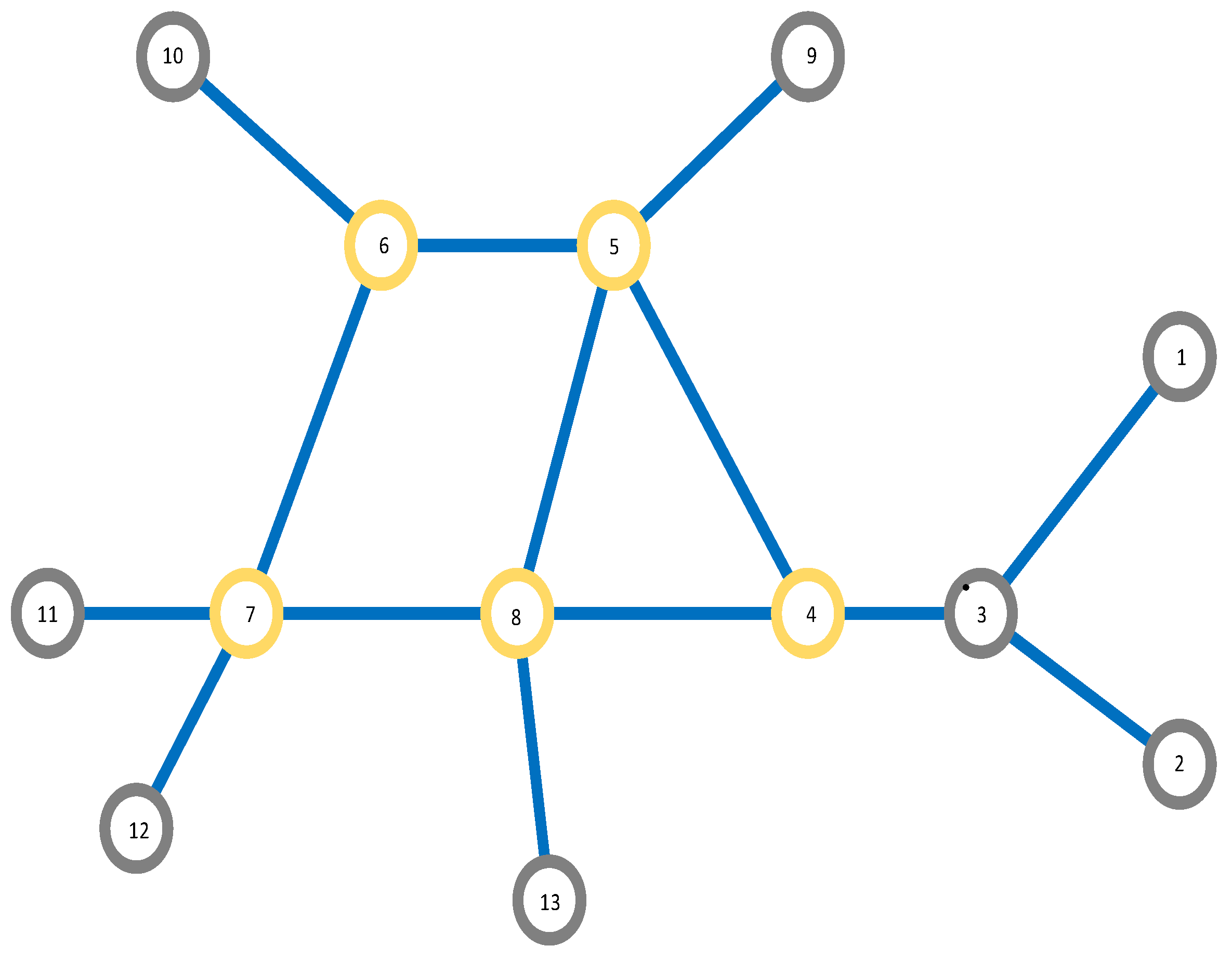
Figure 5 depicts the graph model
G with the nodes of transfer, the line’s split stations (in yellow), and the terminus stations (in grey), in total 13 nodes.
4. The Computing of Robustness and Discussions
As we already mentioned, two node removal methods were examined in this paper: (i)—random node removal, and (ii)—targeted (degree-base) node removal, which means that:
for the random removal method there is an equal chance of selecting randomly any node from the entire network to delete it.
for the targeted (degree-based) removal method, the network’s highest degree node is eliminated at a time. If more than one node has the highest degree, a single node is randomly selected with an equal chance from among all the highest-degree nodes. Nodes are eliminated one after the other. The eliminating nodes are in decreasing degree order.
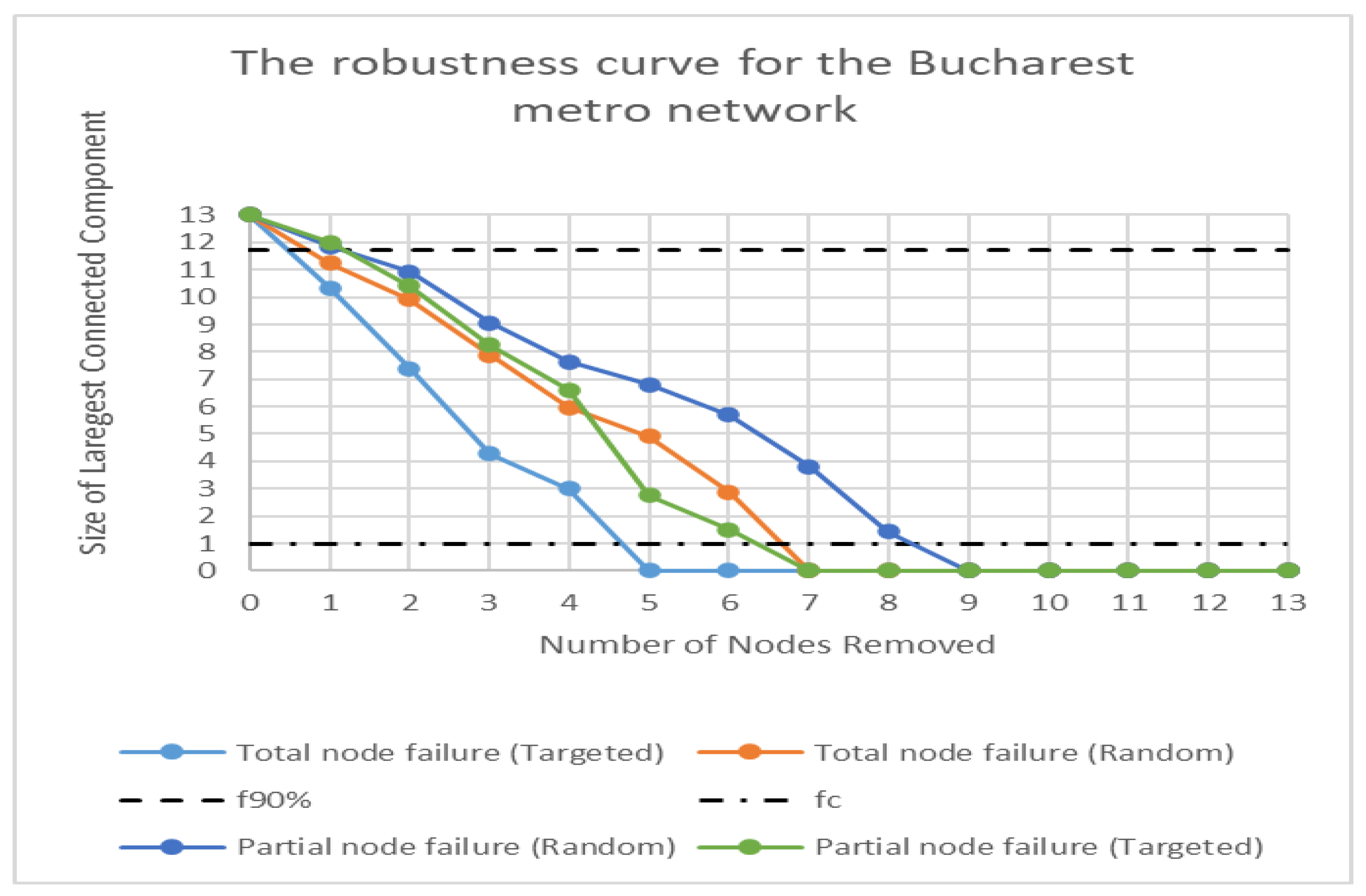
The number of connections for each node in the remaining network is ascertained after a node is eliminated. A robustness curve is produced by measuring the greatest linked component’s size for a range of removed nodes [1, N]. The crucial thresholds and are then ascertained based on the robustness curve.
The first point at which the greatest connected component’s size is less than 90% of the initial network size is defined as the critical threshold, denoted by .
Similarly, the greatest connected component’s size equals one at the critical threshold (
). The critical thresholds and the robustness curves for the Bucharest metro network are represented in
Figure 6.
A robustness curve is produced by calculating the greatest linked component size for nodes which are removed one-by-one (in total, 13 nodes). After eliminating the first node selected randomly, the greatest connected component’s size comes out to be 11.33, which is less than 90% × 13 = 11.7, or 90% of the network’s total size. Therefore, the critical threshold is determined as . Then, is determined similarly. The robustness level of metro networks is considered to be reached at critical thresholds.
Based on the topological features of the Bucharest metro network we can investigate other scenarios as well. In several stations (Piata Unirii, Eroilor, Piata Victoriei, Dristor, and Gara de Nord—respectively nodes 8, 7, 5, 4, 6 on the map in
Figure 5), passengers may change platform to use another metro line. For these stations, we use two assumptions: (1) in case of disruption occurring the whole platform is considered shut down, and (2) in case of disruption only one of the two platforms is considered shut down. We performed the method of node removal once again and computed the robustness curve (
Figure 7).
As is expected when we consider partial station disruption, , the critical threshold of the system shows better robustness. This is because the modeling of a transfer station with two nodes (each node for one of two separated platforms) contributes to robustness metrics enhancement, for both targeted and random failures. In other words, representing two platforms in a transferring station makes analyzing only a partial dysfunction of the transferring station possible. This improves the indicator of the system’s robustness.
In the following, we analyze the results for the measures discussed above by computing the robustness metrics
and
. Derrible and Kennedy propose the robustness indicator
, especially, for a metro network [
30]. According to this, the robustness of a metro network is measured considering the total number of nodes in the system and the number of alternate paths in the network topology, as follows:
where
represents the number of links between two nodes,
µ is the cyclomatic number that determines the total number of paths in a graph and
is the total number of stations.
As we already mentioned, only the transfer stations, split, and terminus nodes are considered. Thus, the modified Equation (1) becomes:
We introduced here the concept of the “potential difference between two nodes”,
i and
j when a unit flow is “injected” at node
i and “withdrawn” at node
j, which is known as the effective resistance
[
29]. The total of
for all pairs of nodes in the network is the effective graph resistance, or
. In this work, we employ the effective graph conductance, which is a normalized form of the effective graph resistance, defined as:
where
is satisfied by
. More robustness is shown by a greater
Table 3 synthesizes the values of the robustness metrics
and
computed by Equations (2) and (3) for the Bucharest metro network.
Our analysis reveals a robustness indicator rT of 0.1538 for the Bucharest metro network, indicating moderate robustness. For instance, enhancing transfer station platforms by creating separated layouts can significantly improve robustness. In practice, this means that urban planners should prioritize such designs to reduce the impact of disruptions.
The indicator of the robustness of larger networks with many different pathways (having larger connectivity of nodes) between any two nodes has a larger , and, on the contrary, networks with a large number of nodes but with few paths, have smaller .
Considering the spatial topography, the effective graph conductance of metro networks with loop shapes is contingent upon the quantity and length of loops, in addition to the network’s connection. Effective graph conductance is generally higher for larger and shorter loop counts. Because loop-shaped metro networks can offer more alternative paths and shorter detours, they are therefore more robust to random or targeted failures.
According to an analysis of the crucial threshold , Bucharest still has a robust metro network based on its critical threshold, , that means that 45% of the nodes must be eliminated before the network collapses.
However, this paper does not address the impact of each node failure, nor the link interruptions, and this is an aim of a future article.
5. Conclusions and Future Research
This study evaluates the robustness of the Bucharest metro network using established metrics, providing a detailed analysis of disruption data from 2019 to 2022. The main contributions include the calculation of robustness metrics (rT and CG) and the critical threshold (fc), which highlight the network’s resilience to disruptions. This evaluation serves as a benchmark for future studies and demonstrates the application of rigorous methodologies for robustness assessments. Future research should explore the impact of individual node failures and link interruptions to further enhance urban metro system robustness. Using the analysis of the available disruption data set of the Bucharest metro system, we have used a generic method for analyzing its robustness by computing three indices: robustness indicator , effective graph conductance , and critical thresholds. Furthermore, the critical thresholds were assessed for both the random and targeted failure of nodes. Our study advances the theoretical understanding of metro network robustness by demonstrating the significance of intersection platform designs in mitigating system disruptions. This aligns with and extends the work of prior research on network vulnerability, showing that targeted architectural modifications can enhance overall system resilience.
Overall, we find that effective graph conductance is relatively low, which implies that a lower level of coordination between stations (because of low communication) can lead to inefficient operations and reduced robustness, highlighting the importance of integrated stations’ management. Based on the topography of the Bucharest metro, the reason is that stations are not connected to many other nearby stations. Low effective graph conductance can be advantageous for increasing the resilience of the metro system due to the decreased likelihood of disruptions spreading throughout closely linked stations. Robustness indicator also shows that the Bucharest metro system is moderate. While the system’s ability to withstand disruptions is not extremely robust, it still provides a reasonable level of robustness. Based on our analysis, the Bucharest metro network demonstrates moderate robustness. The robustness indicator rT is 0.1538, and the effective graph conductance (CG) is 0.1. These values suggest that the network can handle disruptions but has room for improvement. Specifically, our findings indicate that the network can sustain functionality even with the removal of up to 45% of its nodes before experiencing total collapse.
Our findings indicate that designing intersection platforms with separated layouts improves robustness. When partial station disruption occurs, the system exhibits greater resilience in two nodes in both targeted and random failures. This underscores the importance of thoughtful network design in transportation systems. Understanding critical thresholds and optimizing the network layout can enhance the robustness of complex systems like metro networks. Our study contributes to transportation infrastructure planning, emphasizing the need for adaptable designs that minimize service disruptions. From a managerial perspective, our findings suggest that metro network administrators should prioritize the design of intersection platforms with separated layouts. This strategy could enhance resilience by ensuring that disruptions in one part of the network do not cascade throughout the system. Additionally, implementing regular maintenance checks and upgrading older nodes can prevent failures that could severely impact network operations.
Future research should explore the impact of real-time monitoring and adaptive response strategies on metro network robustness. Investigating the role of technological innovations, such as AI-based predictive maintenance, could also offer valuable directions for future research.
In synthesis, our future research focuses on the physical network and solutions to improve its robustness (solutions that are inevitably architectural in the stations and for connecting the lines between the stations), taking into account the different categories of potential interruptions/dysfunctions, each of them individually considered, but also in potential combinations (in several scenarios of the size of the affected network area). The second category of future research is related to operational robustness, which is built on the solutions for the improved robustness of the physical network (in different implementation scenarios and technological innovation), to ensure a certain accepted level of service quality, as perceived by users, but especially taking into account the maximum security of travelers.