An Approach for Multi-Item Product Sales Forecasting Based on Advancing the BCG Matrix with Matrix-Clustering and Time Modeling Techniques
Abstract
1. Introduction
2. Literature Review
2.1. Classic and Modern Time Series Forecasting Methodologies
2.2. BCG Matrix and Product Portfolio Analysis
2.3. k-Means Clustering and Market Segmentation
2.4. Multi-Item Sales Forecasting
3. Materials and Methods
3.1. Forecasting Method
3.1.1. Naïve Forecast
3.1.2. Autoregressive Integrated Moving Average (ARIMA)
3.1.3. Long Short-Term Memory (LSTM)
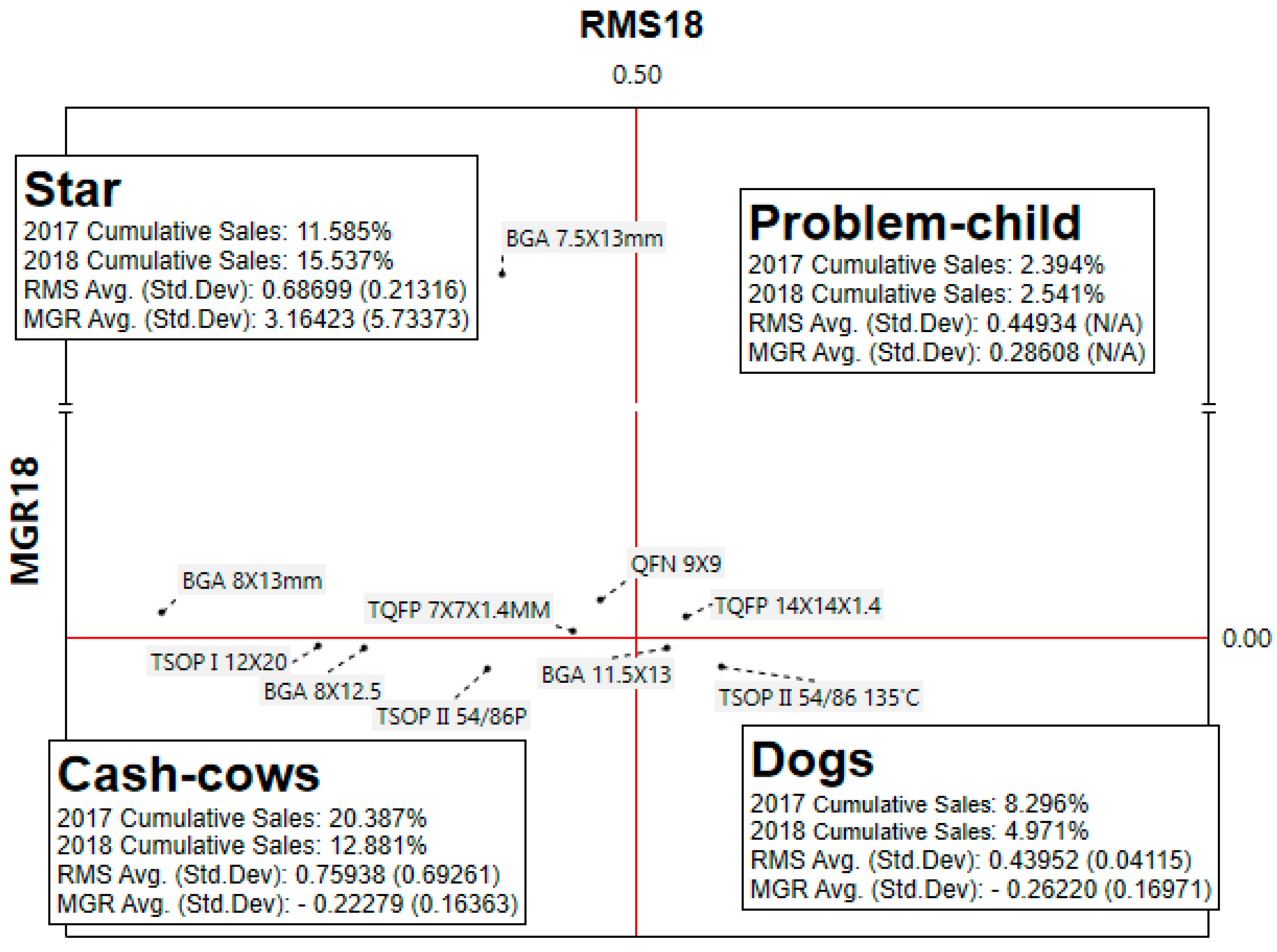
3.2. BCG Matrix and Product Portfolio
3.2.1. Portfolio Category and Market Strategy
- Stars: These products lead in high-growth markets, exhibiting both high growth rates and market share. While they theoretically generate cash, Stars require substantial investment to maintain their growth advantage. The primary goal for Stars is to maintain a balanced net cash flow, and their market strategy focuses on building and sustaining market share.
- Cash Cows: Cash Cows dominate in low or negative-growth markets and are characterized by high margins, resulting in strong positive cash flow and minimal investment requirements. These products can finance their own growth, and surplus cash can be redirected to support Stars or Problem Child products that could potentially evolve into future Cash Cows. The strategy here is to maintain market share.
- Dogs: These products have low market share in declining markets and neither generate significant cash nor justify further investment. In some cases, if Dogs show potential to evolve into Problem Child or Cash Cow products, the strategy might involve repositioning. However, if they fail to meet this criterion, the next step is typically to harvest or liquidate these products by discontinuing them and removing them from the product line.
- Problem Child: These products exhibit high growth rates but low market share. They require significant investment yet provide minimal short-term returns. Since Problem Child products have not yet achieved market dominance, they do not generate substantial cash. To gain market leadership, the company must invest heavily to build and sustain market share.
- Build: This strategy focuses on increasing market share by driving product sales. Since market share is a long-term objective, short-term profits are often sacrificed, with any generated cash reinvested into the market.
- Hold/Maintain: This strategy aims to preserve the current market share while continuing to generate significant cash flow, which is typically invested in other products.
- Harvest: This strategy is applied to weaker Cash Cows, Problem Child, and Dog products that lack future potential. The aim is to maximize short-term cash flow, even if this involves actions like raising prices or cutting costs, potentially at the expense of long-term benefits.
- Divest/Liquidation: This strategy applies to products with no future, such as Dogs with rapidly declining sales or Problem Child products with little chance of becoming Stars. The objective is to eliminate these products, negatively affecting the company’s financial performance. Resources allocated to these products can then be redirected to more promising opportunities.
3.2.2. Relative Market Share and Market Growth Rate
3.2.3. Mean Absolute Scaled Error (MASE)
3.2.4. Within-Mean Difference
3.3. Cluster-Based Forecasting for Multi-Item Products
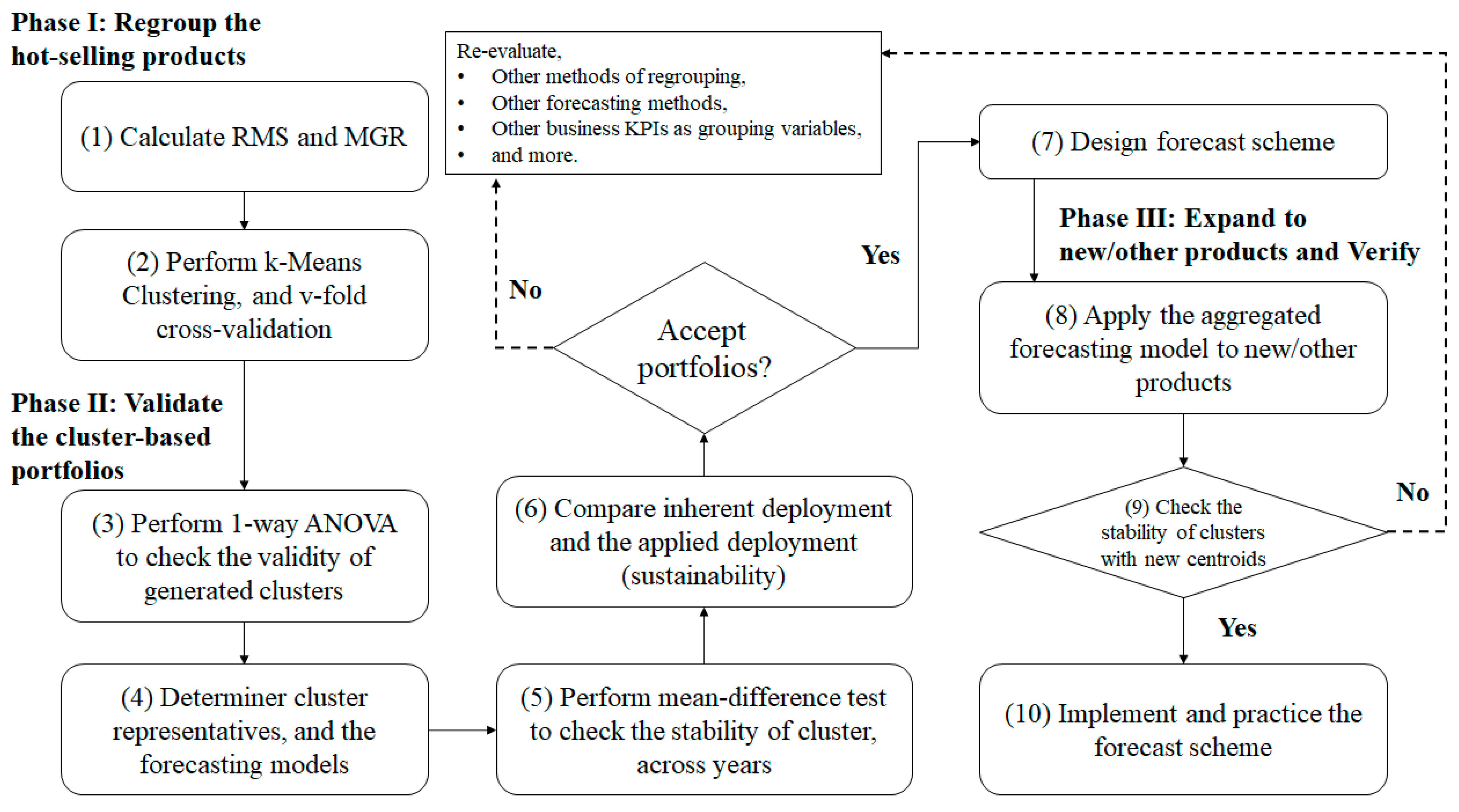
3.3.1. Phase I: Regroup the Products
- Task 1: Calculate the RMS and MGR of the products.
- Task 2: Perform k-means Clustering and use the v-fold cross-validation tool.
3.3.2. Phase II: Validate the Cluster-Based Portfolios
- Task 3: Perform a one-way Analysis of Variance to check the validity of clusters.
- Task 4: Determine cluster representatives and forecasting models.
- Task 5: Perform a Mean difference test to check the stability of clusters.
- Task 6: Compare inherent deployment and applied deployment.
- Task 7: Design a forecasting scheme.
3.3.3. Phase III: Expend to New/Other Products and Verify
- Task 8: Apply the aggregated forecasting model to new or other products.
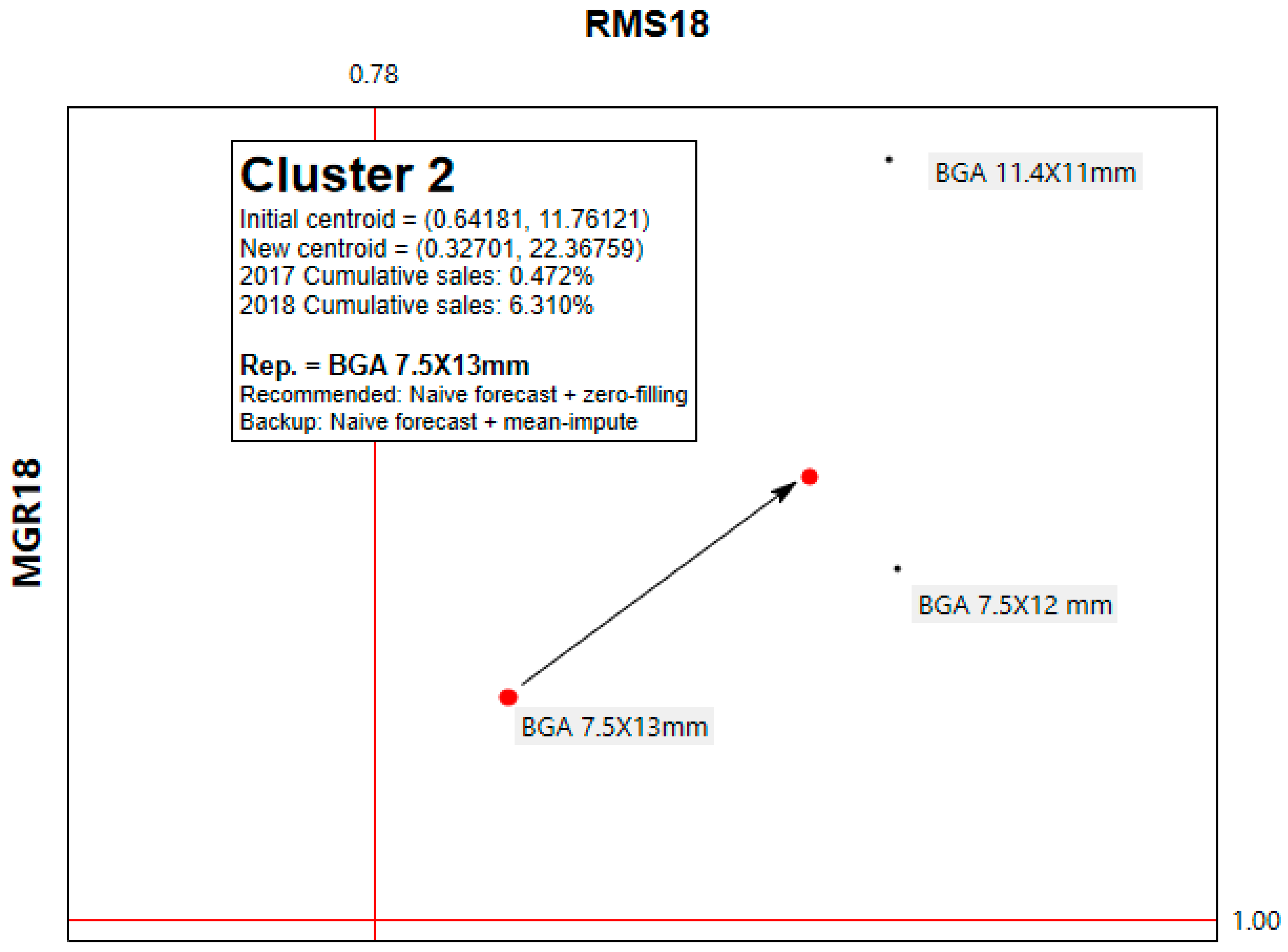
- Task 9: Check cluster stability with new centroids.
- Task 10: Implement the forecasting scheme and practice.
4. Analysis and Results
4.1. Background of the Used Data
4.2. Evaluating Time Series Forecasting Models for Hot-Sell Products
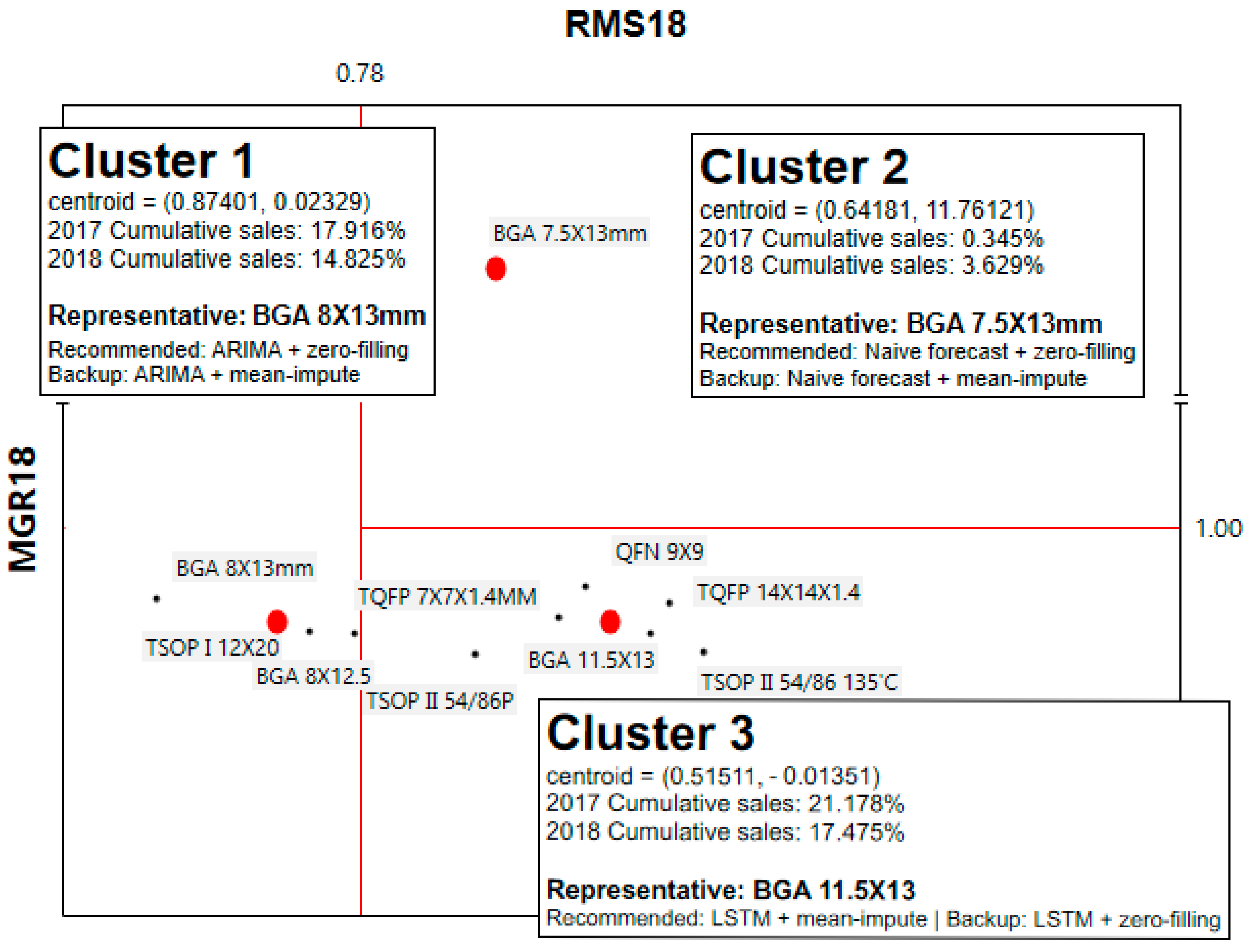
4.3. Establishing the Cluster-Based Portfolios
- This cluster, characterized by a high market share (0.87401) and a modest growth rate (0.023287), includes three products: BGA 8X13mm (classified as a ‘Star’) and TSOP I 12X20 and BGA 8X12.5 (both classified as ‘Cash Cows’) in the BCG Matrix.
- BGA 8X13mm, the product with the highest MGR in the cluster, should play a larger role in driving sales. The performance of the other two members should be closely monitored.
- The MGR for each product is critical for evaluation. If overall sales increase (or remain steady) due to the strong performance of the cluster representative while the other members underperform, gross margins may decline in the long run.
5. Discussion
5.1. The Matrix-Based Portfolios for the Top Ten Products
- A combined model of LSTM and zero-filling is suitable for “Dogs” products.
- The zero-filling method handles missing data for high market share products (Stars and Cash Cows).
- The mean imputation method is appropriate for addressing missing data in general market share products (Dogs and Problem Child).
- For Stars products like BGA 8X13mm, the recommended ARIMA + zero-filling model suggests increasing quarterly capacity by 16.817%. The alternative model, ARIMA + mean-imputation, offers a similar recommendation. For BGA 7.5X13mm, both the recommended and backup models indicate no need for significant capacity adjustments.
- For high-profitability products like BGA 8X12.5, the ARIMA + zero-filling model advises a 2.172% increase in capacity. Conversely, TSOP II 54/86P should see a 12.534% capacity reduction based on the naïve forecast + zero-filling model.
- For Dogs products, such as TSOP II 54/86 135 °C, the LSTM + mean-imputation model recommends a substantial 13.230% capacity increase, with a slightly lower recommendation from the backup model.
- For problematic products like TQFP 14X×14X1.4, both the recommended and backup models suggest a modest 3.049% capacity increase, or no adjustment if deemed unnecessary.
5.2. A Comparison of Matrix-Based and Cluster-Based Portfolios
6. Conclusions
6.1. Outline Product Portfolios by BCG Matrix
6.2. Revise BCG Matrix and Build Forecasting Schemes for Specific Portfolios
- Add more key performance indicators to enrich the forecast plan. The BCG Matrix’s static nature assumes that market growth is the sole indicator of attractiveness. This study validated that the cluster-based approach can more effectively forecast multi-item product portfolios. Incorporating other market factors will improve the generalizability of this approach.
- Introduce more time series forecasting and clustering techniques. Recent research has shown that deep-learning methods can outperform classical time series forecasters. Integrating deep-learning forecasters into the proposed framework could enhance the analysis process, yielding more accurate results.
- Gather more sales data to validate findings. Table 15 shows that 52.434% of data from the top twenty products were utilized, demonstrating that the cluster-based approach is more effective in improving data usage than the traditional matrix-based method. Increasing the data available for forecasting multi-item products through clustering could lead to more stable and reliable forecasting outcomes.
6.3. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Du, B.; Li, Z.; Yuan, J.; Zheng, J.; Shu, W.; Jin, Y. Customer’s Channel Selection Behavior on Purchasing Standardized and Customized Products: Optimized Prices and Channel Performances. Front. Psychol. 2022, 13, 1634. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.; Yao, J.; Lou, W.; Xie, S. On demand response management performance optimization for microgrids under imperfect communication constraints. IEEE Internet Things J. 2017, 4, 881–893. [Google Scholar] [CrossRef]
- Zsidisin, G.A.; Panelli, A.; Upton, R. Purchasing organization involvement in risk assessments, contingency plans, and risk management: An exploratory study. Supply Chain Manag. Int. J. 2000, 5, 187–198. [Google Scholar] [CrossRef]
- Cooper, D.R.; Gutowski, T.G. The environmental impacts of reuse: A review. J. Ind. Ecol. 2017, 21, 38–56. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice, 2nd ed.; OTexts: Melbourne, Australia, 2018. [Google Scholar]
- Wongoutong, C. Imputation methods in time series with a trend and a consecutive missing value pattern. Thail. Stat. 2021, 19, 866–879. [Google Scholar]
- Borges, C.E.; Kamara-Esteban, O.; Castillo-Calzadilla, T.; Andonegui, C.M.; Alonso-Vicario, A. Enhancing the missing data imputation of primary substation load demand records. Sustain. Energy Grids Netw. 2020, 23, 100369. [Google Scholar] [CrossRef]
- Box, G.E.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2015. [Google Scholar]
- Wang, C.C.; Chien, C.H.; Trappey, A.J. On the application of ARIMA and LSTM to predict order demand based on short lead time and on-time delivery requirements. Processes 2021, 9, 1157. [Google Scholar] [CrossRef]
- Yuan, X.; Zhang, X.; Zhang, D. Analysis of the impact of different forecasting techniques on the inventory bullwhip effect in two parallel supply chains with a competition effect. J. Eng. 2020, 2020, 2987218. [Google Scholar] [CrossRef]
- Abbasimehr, H.; Khodizadeh Nahari, M. Improving demand forecasting with LSTM by taking into account the seasonality of data. J. Appl. Res. Ind. Eng. 2020, 7, 177–189. [Google Scholar]
- Babu, C.N.; Reddy, B.E. A moving-average filter based hybrid ARIMA-ANN model for forecasting time series data. Appl. Soft Comput. 2014, 23, 27–38. [Google Scholar] [CrossRef]
- Kiefer, D.; Grimm, F.; Bauer, M.; van Dinther, C. Demand forecasting intermittent and lumpy time series: Comparing statistical, machine learning and deep learning methods. In Proceedings of the 54th Hawaii International Conference on System Sciences, Maui, HI, USA, 5–8 January 2021; HICSS. Grand Wailea: Maui, HI, USA, 2021; pp. 1425–1434. [Google Scholar]
- Hosseini, S.M.S.; Maleki, A.; Gholamian, M.R. Cluster analysis using data mining approach to develop CRM methodology to assess the customer loyalty. Expert Syst. Appl. 2010, 37, 5259–5264. [Google Scholar] [CrossRef]
- Siami-Namini, S.; Tavakoli, N.; Namin, A.S. A comparison of ARIMA and LSTM in forecasting time series. In Proceedings of the 17th IEEE International Conference on Machine Learning and Applications, Orlando, FL, USA, 17–20 December 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1394–1401. [Google Scholar]
- Smyl, S. A hybrid method of exponential smoothing and recurrent neural networks for time series forecasting. Int. J. Forecast. 2020, 36, 75–85. [Google Scholar] [CrossRef]
- Barksdale, H.C.; Harris, C.E., Jr. Portfolio analysis and the product life cycle. Long Range Plan. 1982, 15, 74–83. [Google Scholar] [CrossRef]
- Stummer, C.; Heidenberger, K. Interactive R&D portfolio analysis with project interdependencies and time profiles of multiple objectives. IEEE Trans. Eng. Manag. 2003, 50, 175–183. [Google Scholar]
- Udo-Imeh, P.T.; Edet, W.E.; Anani, R.B. Portfolio analysis models: A review. Eur. J. Bus. Manag. 2012, 4, 101–120. [Google Scholar]
- Mohajan, H.K. An Analysis on BCG Growth Sharing Matrix. Noble Int. J. Bus. Manag. Res. 2017, 2, 1–6. [Google Scholar]
- Nowak, M.; Mierzwiak, R.; Wojciechowski, H.; Delcea, C. Grey portfolio analysis method. Grey Syst. Theory Appl. 2020, 10, 439–454. [Google Scholar] [CrossRef]
- Chiu, C.C.; Lin, K.S. Rule-based BCG matrix for product portfolio analysis. In Software Engineering, Artificial Intelligence, Networking and Parallel/Distributed Computing; Springer: Berlin/Heidelberg, Germany, 2020; pp. 17–32. [Google Scholar]
- Hossain, H.; Kader, M.A. An analysis on BCG growth sharing matrix. Int. J. Contemp. Res. Rev. 2020, 11, 21899–21905. [Google Scholar] [CrossRef]
- Pradana, M.G.; Ha, H.T. Maximizing strategy improvement in mall customer segmentation using k-means clustering. J. Appl. Data Sci. 2021, 2, 19–25. [Google Scholar] [CrossRef]
- Syakur, M.A.; Khotimah, B.K.; Rochman, E.M.S.; Satoto, B.D. Integration k-means clustering method and elbow method for identification of the best customer profile cluster. IOP Conf. Ser. Mater. Sci. Eng. 2018, 336, 012017. [Google Scholar] [CrossRef]
- Wu, S.; Yau, W.C.; Ong, T.S.; Chong, S.C. Integrated churn prediction and customer segmentation framework for telco business. IEEE Access 2021, 9, 62118–62136. [Google Scholar] [CrossRef]
- Xiahou, X.; Harada, Y. B2C e-commerce customer churn prediction based on k-means, S.V.M. J. Theor. Appl. Electron. Commer. Res. 2022, 17, 458–475. [Google Scholar] [CrossRef]
- Abdulla, S.H.; Sagheer, A.M.; Veisi, H. Breast cancer segmentation using K-means clustering and optimized region-growing technique. Bull. Electr. Eng. Inform. 2022, 11, 158–167. [Google Scholar] [CrossRef]
- Altini, N.; De Giosa, G.; Fragasso, N.; Coscia, C.; Sibilano, E.; Prencipe, B.; Hussain, S.M.; Brunetti, A.; Buongiorno, D.; Guerriero, A.; et al. Segmentation and identification of vertebrae in CT scans using CNN, k-means Clustering and k-NN. Informatics 2021, 8, 40. [Google Scholar] [CrossRef]
- Jebarani, P.E.; Umadevi, N.; Dang, H.; Pomplun, M. A novel hybrid k-means and GMM machine learning model for breast cancer detection. IEEE Access 2021, 9, 146153–146162. [Google Scholar] [CrossRef]
- Khan, A.R.; Khan, S.; Harouni, M.; Abbasi, R.; Iqbal, S.; Mehmood, Z. Brain tumor segmentation using k-means Clustering and deep learning with synthetic data augmentation for classification. Microsc. Res. Tech. 2021, 84, 1389–1399. [Google Scholar] [CrossRef] [PubMed]
- Tian, K.; Li, J.; Zeng, J.; Evans, A.; Zhang, L. Segmentation of tomato leaf images based on adaptive clustering number of k-means algorithm. Comput. Electron. Agric. 2019, 165, 104962. [Google Scholar] [CrossRef]
- Zhang, H.; Peng, Q. PSO and K-means-based semantic segmentation toward agricultural products. Future Gener. Comput. Syst. 2022, 126, 82–87. [Google Scholar] [CrossRef]
- Guijo-Rubio, D.; Durán-Rosal, A.M.; Gutiérrez, P.A.; Troncoso, A.; Hervás-Martínez, C. Time-series clustering based on the characterization of segment typologies. IEEE Trans. Cybern. 2020, 51, 5409–5422. [Google Scholar] [CrossRef]
- Bandara, K.; Bergmeir, C.; Smyl, S. Forecasting across time series databases using recurrent neural networks on groups of similar series: A clustering approach. Expert Syst. Appl. 2020, 140, 112896. [Google Scholar] [CrossRef]
- Alqahtani, A.; Ali, M.; Xie, X.; Jones, M.W. Deep time-series clustering: A review. Electronics 2021, 10, 3001. [Google Scholar] [CrossRef]
- Hung, C.Y.; Wang, C.C.; Lin, S.W.; Jiang, B.C. An empirical comparison of the sales forecasting performance for plastic tray manufacturing using missing data. Sustainability 2022, 14, 2382. [Google Scholar] [CrossRef]
- Bunn, D.W.; Vassilopoulos, A.I. Comparison of seasonal estimation methods in multi-item short-term forecasting. Int. J. Forecast. 1999, 15, 431–443. [Google Scholar] [CrossRef]
- Xie, J.; Lee, T.S.; Zhao, X. Impact of forecasting error on the performance of capacitated multi-item production systems. Comput. Ind. Eng. 2004, 46, 205–219. [Google Scholar] [CrossRef]
- Taylor, J.W. Multi-item sales forecasting with total and split exponential smoothing. J. Oper. Res. Soc. 2011, 62, 555–563. [Google Scholar] [CrossRef]
- Spedding, T.A.; Chan, K.K. Forecasting demand and inventory management using Bayesian time series. Integr. Manuf. Syst. 2000, 11, 331–339. [Google Scholar] [CrossRef]
- Gopagoni, D.R.; Lakshmi, P.V.; Chaudhary, A. Evaluating machine learning algorithms for marketing data analysis: Predicting grocery store sales. Commun. Softw. Netw. 2021, 134, 155–163. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Koehler, A.B.; Ord, J.K.; Snyder, R.D. Prediction intervals for exponential smoothing using two new classes of state space models. J. Forecast. 2005, 24, 17–37. [Google Scholar] [CrossRef]

| Set | Period | # Of Weeks | The Use |
|---|---|---|---|
| Training | 1 January 2017–31 December 2018 | 104 (72.72%) | Train the models |
| Test | 1 January 2019–30 June 2019 | 26 (18.18%) | Test if the trained models are appropriate |
| Validation | 1 July 2019–30 September 2019 | 13 (9.09%) | Validate the performance of trained models deployed on unused data |
| 2017 | 2018 | 2019 January–September | |
|---|---|---|---|
| (1) Top ten products | 44.516% | 35.928% | 35.480% |
| (2) The recurring six | 26.619% | 20.658% | 22.011% |
| Difference = (1) − (2) | 17.897% | 15.2780% | 13.469% |
| Product | Model | Test (Model Evaluation) | Validation (Deployment) | |
|---|---|---|---|---|
| MASE | MASE | WD | ||
| BGA 8X13mm | A + Z (Recommended) | 0.82548 | 0.72481 | −16.817% |
| A + M (Backup) | 0.84080 | 0.74119 | −16.915% | |
| TSOP I 12X20 | N + Z (Recommended) | 0.60660 | 0.70566 | 9.248% |
| N + M (Backup) | 0.96284 | 0.69797 | 9.248% | |
| BGA 8X12.5 | A + Z (Recommended) | 0.41726 | 0.39119 | −2.172% |
| A + M (Backup) | 0.40284 | 0.39119 | −2.172% | |
| TSOP II 54/86P | N + Z (Recommended) | 0.38653 | 0.56681 | 12.534% |
| N + M (Backup) | 0.46659 | 0.56826 | 12.534% | |
| BGA 7.5X13mm | N + Z (Recommended) | 2.10839 | 2.16694 | −1.414% |
| N + M (Backup) | 1.67242 | 1.89118 | −1.414% | |
| TQFP 7X7X1.4MM | N + Z (Recommended) | 0.41522 | 0.64403 | 2.243% |
| N + M (Backup) | 0.41782 | 0.63529 | 2.243% | |
| QFN 9X9 | A + Z (Recommended) | 0.90446 | 0.93259 | 1.973% |
| A + M (Backup) | 0.92847 | 0.93259 | 1.973% | |
| BGA 11.5X13 | L + Z (Backup) | 0.78889 | 1.13025 | −23.588% |
| L + M (Recommended) | 0.73817 | 1.17246 | −25.090% | |
| TQFP 14X14X1.4 | N + Z (Backup) | 0.99793 | 1.84759 | −3.049% |
| N + M (Recommended) | 0.95987 | 1.83079 | −3.049% | |
| TSOP II 54/86 135′C | L + Z (Backup) | 0.62501 | 0.63586 | −12.818% |
| L + M (Recommended) | 0.56571 | 0.62717 | −13.230% | |
| Algorithm | k-Means |
|---|---|
| Used variable | RMS18, MGR18 |
| Distance method | Euclidean distances |
| Initial centers | Maximize initial distance |
| Cross-validation | 10-folds |
| Training error | 0.119240 |
| Number of clusters | 3 |
| Cluster-ID | RMS | MGR | Member |
|---|---|---|---|
| 1 | 0.87401 | 0.02329 | BGA 8X13mm, TSOP I 12X20, BGA 8X12.5 |
| 2 | 0.64181 | 11.76121 | BGA 7.5X13mm |
| 3 | 0.51511 | −0.01351 | TSOP II 54/86P, TQFP 7X7X1.4MM, QFN 9X9, BGA 11.5X13, TQFP 14X14X1.4, TSOP II 54/86 135′C |
| Cluster-ID | Member | RMS | MGR | Cluster Rep. and the criteria |
|---|---|---|---|---|
| 1 | BGA 8X13mm | 1.00000 | 0.32710 | BGA 8X13mm.
|
| TSOP I 12X20 | 0.83506 | −0.11552 | ||
| BGA 8X12.5 | 0.78697 | −0.14172 | ||
| Centroid 1 | 0.87401 | 0.02329 | ||
| 2 | BGA 7.5X13mm | 0.64181 | 11.76121 | BGA 7.5X13mm.
|
| Centroid 2 | 0.64181 | 11.76121 | ||
| 3 | TSOP II 54/86P | 0.65612 | −0.41113 | BGA 11.5X13.
|
| TQFP 7X7X1.4MM | 0.56781 | 0.08242 | ||
| QFN 9X9 | 0.53835 | 0.48619 | ||
| BGA 11.5X13 | 0.46862 | −0.14220 | ||
| TQFP 14X14X1.4 | 0.44934 | 0.28608 | ||
| TSOP II 54/86 135′C | 0.41042 | −0.38220 | ||
| Centroid 3 | 0.51511 | −0.01351 |
| Between SS | Degree of Freedom | Within SS | Degree of Freedom | F | p-Value | |
|---|---|---|---|---|---|---|
| RMS | 0.2577 | 2 | 0.065617 | 7 | 13.7436 | 0.003767 |
| MGR | 124.5226 | 2 | 0.797897 | 7 | 546.2219 | 0.000000 |
| Cluster-ID | Year | Mean (Std. Dev) | t-Test for Mean | Homogeneity of Variance | ||
|---|---|---|---|---|---|---|
| p-Value | 95% Confidence Interval | Levene p. | B-F p. | |||
| 1 | 2017 | 1,912,200 (226,192.2) | 0.919693 (NS) | (−540,147, 529,227) | 0.879153 (NS) | 0.920500 (NS) |
| 2018 | 1,917,660 (245,148.8) | |||||
| 2 | 2017 | 1051 (1627.8) | 0.000000 (S) | N/A | N/A | N/A |
| 2018 | 2250 (2734.0) | |||||
| 3 | 2017 | 1,302,233 (617,621.2) | 0.530495 (NS) | (−417,897, 761,956) | 0.130384 (NS) | 0.240139 (NS) |
| 2018 | 1,130,204 (197,831.8) | |||||
| Cluster-ID | Year | Mean (Std. Dev) | t-Test for Mean | Homogeneity of Variance | ||
|---|---|---|---|---|---|---|
| p-Value | 95% Confidence Interval | Levene p. | B-F p. | |||
| 1 | 2017 | 1,912,200 (226,192.2) | 0.919693 (NS) | (−540,147, 529,227) | 0.879153 (NS) | 0.920500 (NS) |
| 2018 | 1,917,660 (245,148.8) | |||||
| 2 | 2017 | 50,383 (52,350.4) | 0.061747 (NS) | (−1,592,078, 60,378) | 0.023436 (S) | 0.409057 (NS) |
| 2018 | 816,233 (512,766.7) | |||||
| 3 | 2017 | 867,056 (552,268.2) | 0.997595 (NS) | (−341,789, 340,778) | 0.119745 (NS) | 0.355106 (NS) |
| 2018 | 867,561 (284,487.7) | |||||
| Outline | |
| Portfolio code: | Stars Cash-cows |
| 2018 Actual Sale (unit): | 5,752,980 (14.825% of the year) |
| 2018 Avg. MGR: | 2.3287% |
| Cluster representative: | BGA 8X13mm |
| Other members: | TSOP I 12X20, BGA 8X12.5 |
| Forecasting Scheme | |
| Model of the cluster representative: | ARIMA + zero-filling |
| Forecast gap of the cluster representative (2018): | −16.817% (underestimated) |
| 2019 Baseline (unit): | 5,881,437 [=5,752,980 × (100 + 2.3287) %] |
| 2019 Optimism (unit): | 6,720,459 [=5,752,980 × (100 + |−16.817|) %] |
| 2019 Preserved (unit): | N/A |
Market Strategy
| |
| Outline | |
| Portfolio code: | Dream-chasing Child |
| 2018 Actual Sale (unit): | 4,095,800 (10.555% of the year) |
| 2018 Avg. MGR: | 6.197% |
| Cluster representative: | QFN 9X9 (Fewer missing data; same direction to centroid) |
| Other members: | BGA 11.5X13, TQFP 14X14X1.4, TSOP II 54/86 135′C |
| Forecasting Scheme | |
| Model of the cluster representative: | ARIMA + zero-filling |
| Forecast Gap of the cluster representative (2018): | 1.973% (overestimated) |
| 2019 Baseline (unit): | 4,349,617 [=4,095,800 × (100 + 6.197) %] |
| 2019 Optimism (unit): | N/A |
| 2019 Preserved (unit): | 4,014,990 [=4,095,800 × (100 − 1.973) %] |
Market Strategy
| |
| Outline | |
| Portfolio code: | Stable Office Workers |
| 2018 Actual Sale (unit): | 8,050,054 (20.744% of the year) |
| 2018 Avg. MGR: | −4.753% |
| Cluster representative: | TSOP II 54/86P (Fewer missing data; same direction to centroid) |
| Other members: | TQFP 7X7X1.4MM, LGA 14X17.2mm, BGA 27X27, MQFP 14X20, BGA 9X13, BGA 14X14mm, QFN 6X6, BGA 14X12mm, QFN 7X7 |
| Forecasting Scheme | |
| Model of the cluster representative: | Naïve forecast + zero-filling |
| Forecast Gap of the cluster representative (2018): | 12.534% (overestimated) |
| 2019 Baseline (unit): | 7,667,435 [=8,050,054 × (100 − 4.753) %] |
| 2019 Optimism (unit): | N/A |
| 2019 Preserved (unit): | 7,041,060 [=8,050,054 × (100 − 12.534) %] |
Market Strategy
| |
| Outline | |
| Portfolio code: | Grayed Loose Diamonds |
| 2018 Actual Sale (unit): | 2,448,700 (6.310% of the year) |
| 2018 Avg. MGR: | 2236.759% |
| Cluster representative: | BGA 7.5X13mm |
| Other members: | BGA 11.4X11mm, BGA 7.5X12mm |
| Forecasting Scheme | |
| Model of the cluster representative: | Naïve forecast + zero-filling |
| Forecast Gap of the cluster representative (2018): | −1.414% (underestimated) |
| 2019 Baseline (unit): | 57,220,218 [=2,448,700 × (100 + 2236.759) %] |
| 2019 Optimism (unit): | 2,483,325 [=2,448,700 × (100 + |−1.414|) %] |
| 2019 Preserved (unit): | N/A |
Market Strategy
| |
| Group | Product | Recommended Model | Managerial Recommendation for the Recommended Model | Backup Model | Managerial Recommendation for the Backup Model |
|---|---|---|---|---|---|
| Stars | BGA 8X13mm | ARIMA + zero-filling | Increase quarterly capacity by 16.817%. | ARIMA + mean-impute | Increase quarterly capacity by 16.915% |
| BGA 7.5X13mm | Naïve forecast + zero-filling | Increase quarterly capacity by 1.414%. Alternatively, do not do any capacity adjustment activities. | Naïve forecast + mean-impute | Increase quarterly capacity by 1.414%. Alternatively, do not do any capacity adjustment activities. | |
| TQFP 7X7X1.4MM | Naïve forecast + zero-filling | Decrease quarterly capacity by 2.243%. Alternatively, do not do any capacity adjustment activities. | Naïve forecast + mean-impute | Decrease quarterly capacity by 2.243%. Alternatively, do not do any capacity adjustment activities. | |
| QFN 9X9 | ARIMA + zero-filling | Decrease quarterly capacity by 1.973%. Alternatively, do not do any capacity adjustment activities. | ARIMA + mean-impute | Decrease quarterly capacity by 1.973%. Alternatively, do not do any capacity adjustment activities. | |
| Cash-cows | BGA 8X12.5 | ARIMA + zero-filling | Increase quarterly capacity by 2.172%. Alternatively, do not do any capacity adjustment activities. | ARIMA + mean-impute | Increase quarterly capacity by 2.172%. Alternatively, do not do any capacity adjustment activities. |
| TSOP II 54/86P | Naïve forecast + zero-filling | Decrease quarterly capacity by 12.534%. | Naïve forecast + mean-impute | Decrease quarterly capacity by 12.534%. | |
| TSOP I 12X20 | Naïve forecast + mean-impute | Decrease quarterly capacity by 9.248%. | Naïve forecast + zero-filling | Decrease quarterly capacity by 9.248%. | |
| Dogs | TSOP II 54/86 135′C | LSTM + mean-impute | Increase quarterly capacity by 13.230%. | LSTM + Zean-filling | Increase quarterly capacity by 12.818%. |
| BGA 11.5X13 | LSTM + mean-impute | Increase quarterly capacity by 25.090%. | LSTM + zero-filling | Increase quarterly capacity by 23.588%. | |
| Problem-Child | TQFP 14X14X1.4 | Naïve forecast + mean-impute | Increase quarterly capacity by 3.049%. Alternatively, do not do any capacity adjustment activities. | Naïve forecast + zero-filling | Increase quarterly capacity by 3.049%. Alternatively, do not do any capacity adjustment activities. |
| Type | Matrix-Based, Top Ten Only | Cluster-Based, Top Twenty |
|---|---|---|
| Method | BCG Matrix | k-Means Clustering |
| Used variable | RMS, MGR | RMS, MGR. |
| Pros | Easy to build, fast to read | Science-based and data-driven |
| Cons | Lack of technical indicators | Complicated computation |
| Management | Top-down | Cross and interactive |
| Reference Line | RMS = 0.500, and MGR = 0.000 | RMS = 0.780, and MGR = 1.000 |
| Code | Stars | Stars Cash-cows |
| Criteria | RMS ≧ 0.500, and MGR < 0.000 | RMS ≧ 0.780 |
| 2018 Sales (%) | 15.537% | 14.825% |
| Market Strategy | Build and then maintain | Build for the representative and maintain the current market for the Others. |
| Code | Cash-cows | Stable Office Workers |
| Criteria | RMS ≧ 0.500, and MGR ≦ 0.000 | 0.780 > RMS ≧ 0.000, and M.G.R. < 0.000 |
| 2018 Sales (%) | 12.881% | 20.744% |
| Market Strategy | Maintain as prior | Take a wait-and-see strategy. If the decline becomes apparent, postpone or even terminate production. |
| Code | Dogs | Dream-chasing Child |
| Criteria | 0.500 > RMS ≧ 0.000, and M.G.R. < 0.000 | 0.780 > RMS ≧ 0.000, and MGR ≧ 0.000 |
| 2018 Sales (%) | 4.970% | 10.555% |
| Market Strategy | Harvest, even Liquid/Terminate | Build and expand market share as much as possible without worrying about being unprofitable in the short term. |
| Code | Problem-child | Grayed Loose Diamonds |
| Criteria | 0.500 > RMS ≧ 0.000, and MGR ≧ 0.000 | 0.780 > RMS ≧ 0.000, and MGR ≧ 1.000 |
| 2018 Sales (%) | 2.541% | 6.310% |
| Market Strategy | Build and maintain | Build and expand market share as much as possible without worrying about being unprofitable in the short term. |
| Used Data Amount | Top ten products (35.928%) only | Top twenty products (52.434%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hung, C.-Y.; Wang, C.-C. An Approach for Multi-Item Product Sales Forecasting Based on Advancing the BCG Matrix with Matrix-Clustering and Time Modeling Techniques. Systems 2024, 12, 388. https://doi.org/10.3390/systems12100388
Hung C-Y, Wang C-C. An Approach for Multi-Item Product Sales Forecasting Based on Advancing the BCG Matrix with Matrix-Clustering and Time Modeling Techniques. Systems. 2024; 12(10):388. https://doi.org/10.3390/systems12100388
Chicago/Turabian StyleHung, Che-Yu, and Chien-Chih Wang. 2024. "An Approach for Multi-Item Product Sales Forecasting Based on Advancing the BCG Matrix with Matrix-Clustering and Time Modeling Techniques" Systems 12, no. 10: 388. https://doi.org/10.3390/systems12100388
APA StyleHung, C.-Y., & Wang, C.-C. (2024). An Approach for Multi-Item Product Sales Forecasting Based on Advancing the BCG Matrix with Matrix-Clustering and Time Modeling Techniques. Systems, 12(10), 388. https://doi.org/10.3390/systems12100388







