Technology-Driven Financial Risk Management: Exploring the Benefits of Machine Learning for Non-Profit Organizations

Abstract

This study explores how machine learning can optimize financial risk management for non-profit organizations by evaluating various algorithms aimed at mitigating loan default risks. The findings indicate that ensemble learning models, such as random forest and LightGBM, significantly improve prediction accuracy, thereby enabling non-profits to better manage financial risk. In the context of the 2008 subprime mortgage crisis, which underscored the volatility of financial markets, this research assesses a range of risks—credit, operational, liquidity, and market risks—while exploring both traditional machine learning and advanced ensemble techniques, with a particular focus on stacking fusion to enhance model performance. Emphasizing the importance of privacy and adaptive methods, this study advocates for interdisciplinary approaches to overcome limitations such as stress testing, data analysis rule formulation, and regulatory collaboration. The research underscores machine learning’s crucial role in financial risk control and calls on regulatory authorities to reassess existing frameworks to accommodate evolving risks. Additionally, it highlights the need for accurate data type identification and the potential for machine learning to strengthen financial risk management amid uncertainty, promoting interdisciplinary efforts that address broader issues like environmental sustainability and economic development.

1. Introduction

Managing risk effectively is a perpetual challenge in the financial markets, where uncertainty reigns. The economic landscape is fraught with various risks, including credit, operational, liquidity, and market risks, each presenting unique hurdles [1,2]. The 2008 subprime mortgage crisis, triggered by the U.S. real estate market collapse, serves as a stark reminder of the dire consequences of inadequate risk management, underscoring the need for accurate risk prediction and control [3,4]. According to a report by the International Monetary Fund (IMF), the global financial system remains vulnerable to systemic risks, with potential for significant crises if risk management practices are not enhanced [5,6]. Moreover, a study by Allen et al. highlights that financial institutions that effectively manage risk are more likely to achieve long-term success and stability [4]. These findings emphasize the urgency for improved methodologies in financial risk management, particularly those leveraging advanced technologies such as machine learning [7,8].

The financial sector is constantly evolving, and the need for innovative approaches to risk management has become increasingly pressing. Machine learning (ML) offers a powerful toolset for modeling and predicting risks, especially pertinent for non-profit organizations engaged in large-scale public welfare projects. These organizations face significant lending risks and require effective risk control strategies to ensure the integrity of their operations [9,10,11]. Research indicates that machine learning can enhance the capacity for financial oversight and risk management [12], and various classical algorithms such as logistic regression, support vector machines, decision trees, and advanced ensemble learning algorithms like random forest and LightGBM are being explored [13,14]. However, applying these models poses significant challenges, particularly regarding privacy and operational risks [15,16]. Studies have pointed out that financial institutions must address these concerns to maintain compliance and efficiency in risk management practices [17].

Despite the growing interest in machine learning for financial risk control, significant research gaps exist in the literature. Existing studies often focus on specific aspects of risk management, such as credit or market risk, without providing a comprehensive overview of the field [7,18]. Moreover, most of these studies rely on traditional machine learning algorithms, neglecting the potential of advanced ensemble learning methods [8,19]. The need for innovative machine learning models that can better adapt to the complexities of financial data is increasingly evident [20,21]. Non-profit organizations operate under unique financial constraints, as their primary funding often comes from donations, grants, or government funding, which are more volatile than revenues from commercial activities [22]. Furthermore, non-profits face significant pressure to maintain public trust and transparency in their financial dealings, making them particularly vulnerable to reputational damage caused by financial mismanagement [23]. Recent studies have shown that machine learning offers non-profits a powerful tool for optimizing resource allocation and mitigating risks related to financial instability [24]. For instance, advanced predictive analytics can enhance decision-making by identifying potential pitfalls in financial transactions [25,26].

This study aims to fill these research gaps by developing an effective machine learning-based financial risk control model that addresses the unique challenges faced by non-profit organizations. This research will examine the efficacy of various machine learning algorithms in risk control model construction, emphasizing the importance of privacy and operational risks in applying these models [27]. The primary objective of this study is to develop a comprehensive machine learning-based financial risk control model that can effectively mitigate lending risks for non-profit organizations engaged in large-scale public welfare projects. These organizations often operate with limited resources and need help managing lending risks, which can jeopardize their ability to achieve their social impact goals [28]. By developing an effective risk control model, this study aims to provide non-profit organizations with a powerful tool to optimize their lending practices, ensuring that funds are allocated to projects with the highest potential for success while minimizing the risk of default or misuse [28].

Specifically, this research aims to investigate the performance of various machine learning algorithms, including classical methods such as logistic regression and support vector machines, and advanced ensemble learning algorithms like random forest and LightGBM in constructing robust risk control models [29,30]. Additionally, the study will assess the impact of privacy and operational risks on the application of these models, recognizing the sensitive nature of financial data and the potential for machine learning to introduce new risks [31,32]. This section provides a detailed analysis of specific financial risks faced by non-profit organizations, particularly focusing on credit risk and loan default risk. For instance, in the case of mortgage evaluations, machine learning algorithms can be applied to predict borrower default probabilities based on historical data such as credit scores, income, and employment history. These models not only identify high-risk borrowers but also predict potential loan defaults, offering non-profits more reliable decision-making tools for fund allocation.

Moreover, credit risk assessments using ensemble learning methods such as random forest and LightGBM have demonstrated superior performance in accurately predicting loan defaults [33]. These models improve risk prediction by analyzing a wide range of variables, including macroeconomic indicators and borrower-specific data, thus allowing non-profit organizations to minimize financial risks while optimizing resource allocation. The intersection of data science and risk management demonstrates how innovation can improve productivity and mitigate financial risks [20]. By incorporating insights from economics, management, law, and data science, this study highlights the role of knowledge and technology in solving real-world problems. This integration underscores the potential of innovation to address systemic issues in the financial sector, supporting economic development and sustainability [34,35].

In financial risk management, four primary types of risks are widely recognized: credit risk, operational risk, liquidity risk, and market risk. Credit risk refers to the possibility that a borrower will fail to meet their debt obligations, often measured using credit scoring models such as those proposed by Altman [36]. Machine learning has been increasingly used to enhance credit risk predictions, improving accuracy in identifying potential defaults [37]. Operational risk involves risks resulting from failed internal processes, systems, or human errors [38]. This risk has been standardized in regulations such as Basel II [39], which has influenced how banks address operational vulnerabilities. Liquidity risk concerns the ability of an organization to convert assets into cash quickly without significant loss, as described in the seminal work by Diamond and Dybvig [40]. Finally, market risk arises from fluctuations in market prices, such as interest rates or stock prices, as examined by Jorion [41] in his comprehensive study of Value at Risk (VaR) models.

The structure of this paper is designed to provide a clear and comprehensive understanding of the research. The introduction sets the stage by emphasizing the importance of effective risk management in the financial sector while identifying gaps in the existing literature. The literature review evaluates prior research on the use of machine learning in financial risk control, highlighting key findings as well as limitations [42]. The methodology section details the machine learning algorithms employed in the study, along with the data analysis procedures. The results section presents the study’s findings, including the performance of the models and their implications for risk management practices. The discussion section offers recommendations based on the findings and acknowledges the research’s limitations. Finally, the conclusion summarizes the key results, discusses their impact, and provides suggestions for future research, aiming to offer non-profit organizations a powerful tool to optimize lending practices and minimize the risks of default or misuse. The term ‘default and/or misuse risk’ refers to two distinct financial risks: default risk, which occurs when a borrower fails to meet repayment obligations, potentially causing financial loss to the lender, and misuse risk, which arises when loaned funds are not used for their intended purpose, leading to ineffective outcomes, particularly in non-profit projects. By leveraging machine learning models, it becomes possible to monitor both types of risks concurrently, offering non-profits a more comprehensive approach to financial risk management.

2. Theoretical Research on Financial Risk Control Technology

Drawing upon the foundational theories of machine learning and risk control models, this study explores the pertinent literature to assimilate the intricate machine learning theories, and the theoretical frameworks of risk control models established by scholars both domestically and internationally. This theoretical exploration serves as the bedrock for developing sophisticated risk control models tailored to the dynamic landscape of Internet finance.

The empirical portion of this study utilizes loan data from an online financial platform, conducting a comprehensive analysis that includes data preprocessing, model construction, and a comparative evaluation of various machine learning algorithms in financial risk control. The goal is to examine the performance differences of these algorithms within the context of risk control models and explore the potential of model fusion techniques to enhance their effectiveness. A key reference underpinning this study is the work by Guo et al. (2021) [43], which investigated the application of selective ensemble-based online adaptive deep neural networks to handle streaming data with concept drift, providing a modern perspective on advanced machine learning architectures for financial risk mitigation.

This study employs several machine learning models to manage different types of financial risks. For example, Esteva et al. (2019) [37] explored the potential of deep learning in various high-risk domains, demonstrating its usefulness in healthcare, a field that shares similar data complexity and risk profiles with financial sectors. Meanwhile, LightGBM, as demonstrated by Ke et al. (2017) [17], is highly efficient in managing large datasets and capturing non-linear relationships in financial markets, making it a valuable tool for managing market risk. Moreover, Mishchenko et al. (2021) [44] highlight the importance of innovation risk management in financial institutions, emphasizing the role of advanced machine learning models in detecting and mitigating potential financial threats. Additionally, Moscatelli et al. (2020) [45] demonstrated that machine learning algorithms, such as those used for corporate default forecasting, can greatly enhance the predictive accuracy of financial models, further underscoring the value of these methods in risk management.

Random forest and LightGBM were selected for this study due to their effectiveness in handling imbalanced datasets and their high predictive accuracy. Random forest, with its ensemble of decision trees, is particularly suited for datasets that are common in non-profits with limited financial records, offering higher model interpretability—crucial for organizations that require transparent decision-making processes, as shown in Breiman (2001) [16]. LightGBM, on the other hand, is particularly efficient in processing large-scale datasets with faster training times and lower memory consumption, making it ideal for real-time credit risk prediction, as demonstrated by Ke et al. (2017) [46]. Furthermore, Bisias et al. (2012) [46] highlighted the growing importance of systemic risk analytics, underscoring the role of machine learning models such as LightGBM in developing a more comprehensive understanding of risk in financial institutions.

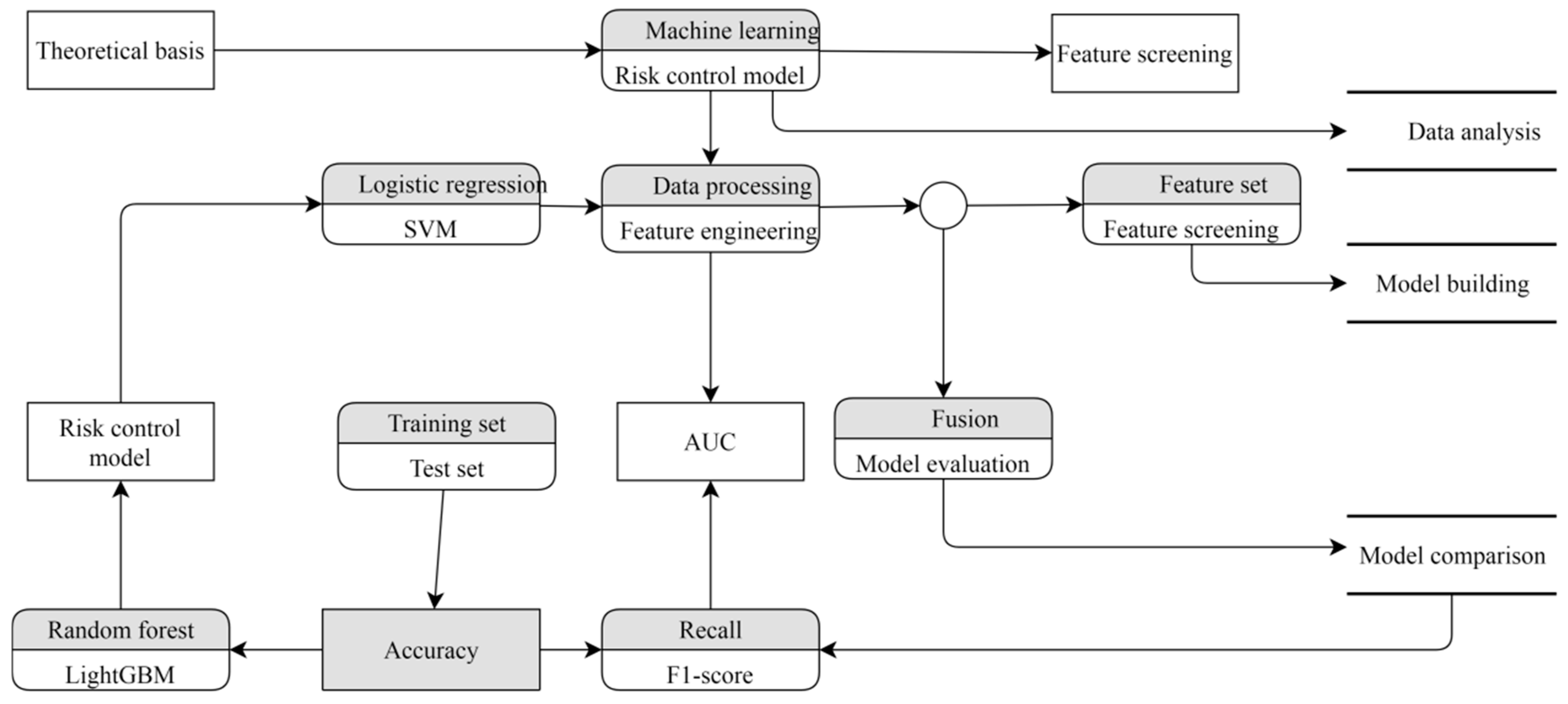
Figure 1 is a flowchart that outlines a typical machine-learning process. It begins with the theoretical basis, which provides the statistical and risk control models and feature engineering techniques that underpin the machine learning model. Data analysis follows, involving the collection, cleaning, transformation, and feature selection necessary to prepare the data. Model building includes splitting the data into training and test sets, training the model, and evaluating its performance. Model evaluation assesses the model’s performance on unseen data using accuracy, precision, recall, and F1 score metrics. Model comparison then identifies the best-performing model by comparing different options. The flowchart also highlights the importance of feature engineering, which involves creating new features from raw data to improve model performance, and feature screening, which selects a subset of features to reduce dimensionality and enhance performance. The risk control model is also crucial for assessing the risk of events such as fraud detection and credit scoring.

The creation of a comprehensive financial risk control system, leveraging the capabilities of mainstream big data open-source technologies, marks a significant milestone in the evolution of risk management. By integrating sophisticated machine learning algorithms, this system can construct highly accurate, personalized behavior models that can identify even the most subtle anomalies, thereby providing a robust framework for risk management. Deployed within a distributed environment, this platform ensures high availability and concurrency, effectively catering to the extensive demands of banking operations (Brandt et al., 2017) [47], (Liu et al., 2019) [48]. This distributed architecture enables the system to handle massive volumes of data in real-time, ensuring that risk assessments are made promptly and accurately (Huo et al., 2020) [49], (Voinea & Anton, 2009) [50]. The system’s scope is further enhanced by its ability to incorporate many data sources, including operation and maintenance logs, processes, permissions, and configurations. This holistic view of the bank’s operational landscape provides a comprehensive understanding of the organization’s risk profile, enabling data-driven decision-making and proactive risk mitigation strategies (Gadomer & Sosnowski, 2020) [38]. Moreover, adaptive learning methods like those described by Ibrahim et al. (2019) [51] further optimize the system’s ability to evolve and address multi-objective risk scenarios through genetic evolutionary algorithms for backpropagation neural networks.

This platform employs a dual approach to compliance inspection, combining a ‘data + rules’ model with machine learning algorithms to create a robust and adaptive system. The ‘data + rules’ model, supported by big data technology, analyzes vast amounts of data to detect patterns and anomalies indicative of non-compliance (Jie et al., 2023) [52], (Johnson & Khoshgoftaar, 2019) [53]. This universal framework ensures that all transactions are evaluated against predefined rules and regulations. In contrast, machine learning algorithms offer a more personalized inspection, adapting to the unique behaviors of individual users to identify potential risks and instances of non-compliance in a more targeted manner (Jolly, 2018) [54], (Khan et al., 2020) [55]. Integrated with real-time monitoring systems, the platform issues immediate alerts for high-risk violations, allowing for swift and effective remediation (Kim et al., 2020) [56]. Additionally, the system connects with operation and maintenance platforms, streamlining the resolution process and ensuring that issues are addressed efficiently (Giudici, 2018) [10]. This comprehensive approach not only identifies risks but also includes ‘self-immunity’ capabilities such as preventing unauthorized access and automatically rectifying security baselines, ensuring the system remains resilient against potential threats (Kou et al., 2019) [57]. By integrating with other systems, the platform provides a seamless, coordinated response to compliance issues, helping financial institutions maintain the highest standards of risk management and regulatory adherence (Aziz & Dowling, 2019) [36].

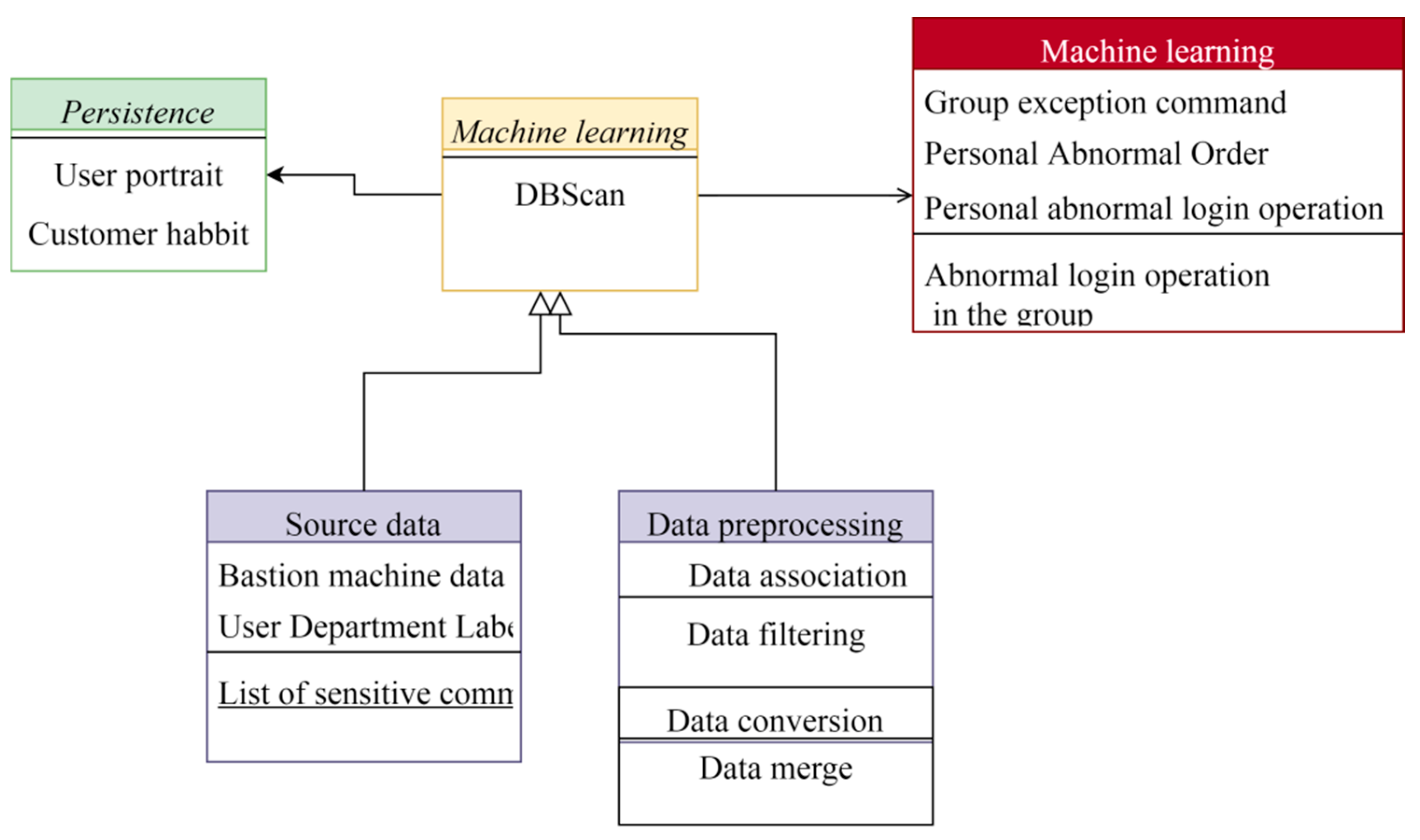
Figure 2 is a flowchart depicting a machine-learning process. It begins with persistence, which involves the ongoing capture and analysis of data related to user behavior. User portrait generates profiles of users based on their department, typical commands, and login history. Customer habit identifies typical customer behavior patterns. Source data, including bastion machine data, user department labels, and lists of sensitive commands, is the raw input for the model. Data preprocessing cleans and prepares this data through filtering, conversion, integration, and reduction. Data association then merges the preprocessed data into a cohesive dataset. The core machine learning stage involves training the model to identify patterns for predictions or classifications. DBSCAN, a clustering algorithm, identifies groups of users with similar behavior. Group exception command flags unusual or suspicious commands within a user group, while personal abnormal order and personal abnormal login operation detect unusual activities for individual users. Abnormal login operations in the group highlight suspicious login attempts that deviate from typical group behavior. This comprehensive process enhances security and risk management through detailed analysis and anomaly detection.

In machine learning-based data systems, the hierarchical organization of data into distinct layers is crucial for effective data processing and analysis. These systems typically consist of three primary layers: data collection and organization, data modeling, and data application.

The study explores the data architecture within the risk control system, which plays a critical role in managing financial risks across various lending stages. The system integrates data related to pre-lending, during-lending, and post-lending phases, all within the described framework. Pre-lending data are essential for identifying and mitigating potential risks or aberrant behaviors before loan issuance, ensuring that lending decisions are well-informed and responsible [58,59]. During-lending data facilitate the application of various process models, particularly for risk evaluation, allowing continuous monitoring and assessment of lending activities [60,61]. Post-lending data are critical for validating model effectiveness and refining model accuracy, ensuring that the risk control system remains adaptive and efficient [62,63].

A key aspect of this architecture is the pervasive nature of functionalities like offline batch processing and real-time computing, which are not confined to any single layer but span across all layers to ensure a seamless operation. This integrated approach enables the system to efficiently handle large volumes of data, allowing for lending decisions based on accurate and timely information [64,65]. The architecture is designed to support the entire lending process, from the initial assessment to post-lending evaluation, offering a comprehensive framework for managing financial risks effectively [66,67].

The data collection and organization layer serves as the foundation, functioning as a repository for various raw and pre-processed data types, including traditional databases, NoSQL data, semi-structured data, and diverse logs [68,69]. Data are autonomously retrieved daily from target systems, encompassing multiple business operations, logging frameworks, and transaction ledgers [70]. A sophisticated scheduling mechanism ensures the consistent and reliable extraction of data from various sources [71]. Once retrieved, the data undergoes transformation through selected ETL (Extract, Transform, Load) scripts, which prepare raw data into structured product data, ensuring it is ready for analysis [72,73].

Leveraging the Hadoop ecosystem for distributed storage and computing, this layer supports large-scale data analytics, addressing the limitations of single-node systems [74]. Hadoop’s distributed architecture allows for the parallel processing of massive datasets, speeding up data analysis [75,76]. This capability is especially crucial in financial risk management, where real-time analysis of large data sets is necessary to identify potential risks and opportunities [77]. Additionally, the system’s flexibility to handle both structured and unstructured data, along with its ability to integrate with various data processing tools and frameworks, makes it highly scalable and ideal for managing complex financial data [78,79].

The data modeling layer operates with production-ready, cleansed data that are categorized under specific business tags and detailed profiles of members and devices [80,81]. This layer serves as the central hub for all business-critical data, ensuring accuracy, completeness, and accessibility [82]. The system segments data into specific data marts tailored to meet different business requirements, enabling it to provide actionable insights that support precise business decisions [83]. For example, data marts focusing on customer segmentation can help identify high-value customers, while product analysis marts can optimize product offerings [84,85].

The data application layer is where data-driven insights are applied to business processes. This layer is deeply integrated with business operations, enhancing decision support systems and providing precise recommendations for financial risk management [86]. Moreover, the system’s distributed computing architecture allows for faster data processing while maintaining high accuracy and timeliness [87]. This gives financial institutions the agility to adapt to rapidly changing market conditions, helping them mitigate risks through data-driven decision-making [88]. The integration of machine learning models into this layer is particularly effective in handling complex data integration and analysis processes, playing a vital role in risk evaluation and prediction [89].

3. Adaptive Algorithms Based on Cognitive Simulation

In the middle layer, the adaptive learning process of the neural network is a dynamic and iterative process that enables the network to refine its learning strategy and optimize its performance continuously [90]. This adaptive learning process is manifested in the selection and replacement of the neural network learning function, which allows the network to adapt to changing data distributions, handle noisy or missing data, and improve its learning speed. Optimizing the multi-objective neural network structure enables the network to balance competing objectives and achieve optimal performance [91,92]. During the learning process, the neural network selects an appropriate learning function according to the learning samples and different stages of learning, ensuring that it can effectively learn and generalize from the data. This adaptive learning process enables the neural network to learn and improve over time, making it an essential component of its ability to achieve high-performance results in complex and dynamic environments [43,93].

$$W_{ik}=g\left(y_{ik}\right)\times \left(t_{ik}-y_{ik}\right)$$

(1)

Among them, $g(y_{ik})$ is in different stages of neural network learning and cos(y) can be taken as needed, where $y=1/(1+e^{-x})$ is to improve the learning speed of the neural network and $t_{ik}$ is the expected output value of neuron $i$ when inputting mode $k$.

Through research, it is found that when the expected output value of neuron $i$ is 1 when inputting mode $k$, and the actual output value is 0, selecting $\cos (y)$ as the learning function can obtain a high convergence speed. Multi-objective neural network structure optimization involves a sophisticated process that begins with defining multiple objective functions, which may be mutually restricted. The goal is to optimize the structure of the neural network by learning multiple specific functional areas, or functional cores, that collectively enable the network to achieve optimal performance across various objectives [94]. This process involves the neural network adapting its architecture to accommodate the complex interplay between the different objectives, resulting in a highly optimized and specialized structure tailored to the specific problem [25]. Specifically, it is to minimize the multi-objective error energy function:

$$E=W_1\times E_f+W_2\times W_b+W_3\times E_d$$

(2)

where $E_f$ is the derivative with respect to the $j$th node of the input layer. In Equation (2), $E$ represents the expected output value used to calculate the response functions for different neurons. Specifically, $E$ serves as the response variable that is iteratively optimized during the model training process. The presence of $E$ on both sides reflects its role in adjusting the model’s performance through multiple iterations, ensuring that predicted outputs align with expected outcomes.

From a holistic perspective, the adaptive capabilities of neural networks are genuinely remarkable. These powerful algorithms can automatically select the most appropriate learning methods based on the specific problem, enabling them to achieve optimal learning outcomes. It is essential to recognize that the knowledge gained through theoretical study is not merely abstract concepts but rather a foundation for solving real-world problems encountered in the future. This knowledge can also serve as a guiding light for future learning endeavors [73,95].

The adaptive ability of neural networks lies in their capacity to extract symbolic knowledge from the distribution of knowledge that is inherently embedded within their intricate structure. This symbolic knowledge represents a higher-level understanding of the problem domain, which can then be leveraged to guide and enhance the learning process [96]. By tapping into this symbolic knowledge, neural networks can adapt their learning strategies, optimize their performance, and tackle increasingly complex problems more efficiently and accurately [81].

For the convenience of description, this section only discusses the structure of single-layer and multi-layer neural networks. For a single-layer neural network, Hebb’s rule can be used as the learning rule of the network, namely:

$$\Delta W_{ij}=X\times a_i\times a_j$$

(3)

where $X$ is the learning rate, $a_i$ is the activation value of neuron $i$, $a_j$ is the activation value of neuron $j$, and $\Delta W_{ij}$ is the amount of change in the connection weight between neuron $i$ and neuron $j$.

Through iterative learning processes, neural networks accumulate insights from diverse instances, integrating this knowledge into the intricate fabric of their architecture [97]. This distributed knowledge framework enables neural networks to generalize patterns, adapt to new data, and make informed decisions across various tasks and scenarios. For a multi-layer neural network, the backpropagation (BP) algorithm is used to train the neural network, namely:

$$\Delta W_{ij}=T\times W_{pi}\times P_{pj}$$

(4)

when neuron $j$ is the output neuron,

$$W_{pj}=(t_{pj}-a_{pj})\times f_j(ne{t}_{pj})$$

(5)

when neuron $j$ is a hidden neuron,

$$W_{pj}=f_j(ne{t}_{pj})\times W_{pk}\times W_{kj}$$

(6)

where $\Delta W_{ij}$ is the amount of change in the connection weight between neuron $i$ and neuron $j$, $X$ is the learning rate, $a_{pj}$ is the activation value of neuron $j$ with respect to input pattern $p$, and $W_{pj}$ is the connection weight connected to neuron $i$ with respect to input pattern $p$ The amount of change in, $t_{pj}$ is the expected activation value of neuron $j$ with respect to the input pattern $p$.

The neural network extracts the knowledge points obscured in the sample data through a process of study, and this knowledge is distributed and stored within the network’s fabric [98]. This knowledge is not merely a collection of isolated facts but a complex web of interconnected concepts and relationships woven to form a rich tapestry of understanding. The neural network’s ability to extract knowledge from sample data is a testament to its power and versatility, as it can learn from a wide range of data sources and adapt to new information [99].

The adaptive machine learning method based on cognitive simulation discussed in this section first employs the connectionist learning method (including the state and transition of neurons, multi-objective optimization neural network, etc.) to obtain the knowledge embedded in the sample data [100]. This method allows the neural network to learn from the data and identify patterns, relationships, and correlations that are not immediately apparent. Once the neural network has obtained the knowledge from the sample data, it uses various methods to extract symbolic knowledge from the neural network structure. This symbolic knowledge represents a higher-level understanding of the problem domain and is used to guide and enhance the learning process [101]. The methods used to extract symbolic knowledge include rule extraction, decision tree induction, and clustering analysis [102].

For the learning of a single-layer neural network, first, find out $W_{ik}$ after learning to make it meet the following requirements:

$$W_{ik}=\max \left(W_{1k},W_{2k},\dots ,W_{mk}\right)$$

(7)

where $W_{ik}$ is the link weight between neuron $i$ and neuron $k$. At this point, select:

$$W_{jk}\ge X\times W_{ik}$$

(8)

where $X$ is the scaling factor. According to the above formula, the following rules are constructed:

$$IF{a}_j\left[and{a}_j\right]\to b_k$$

(9)

where $a_j$ is the activation value of input neuron $a_j$, and $b_k$ is the output of output neuron $k$.

Through iterative refinement, the neural network continuously uncovers deeper insights concealed within the sample data, refining its understanding of complex patterns and relationships.

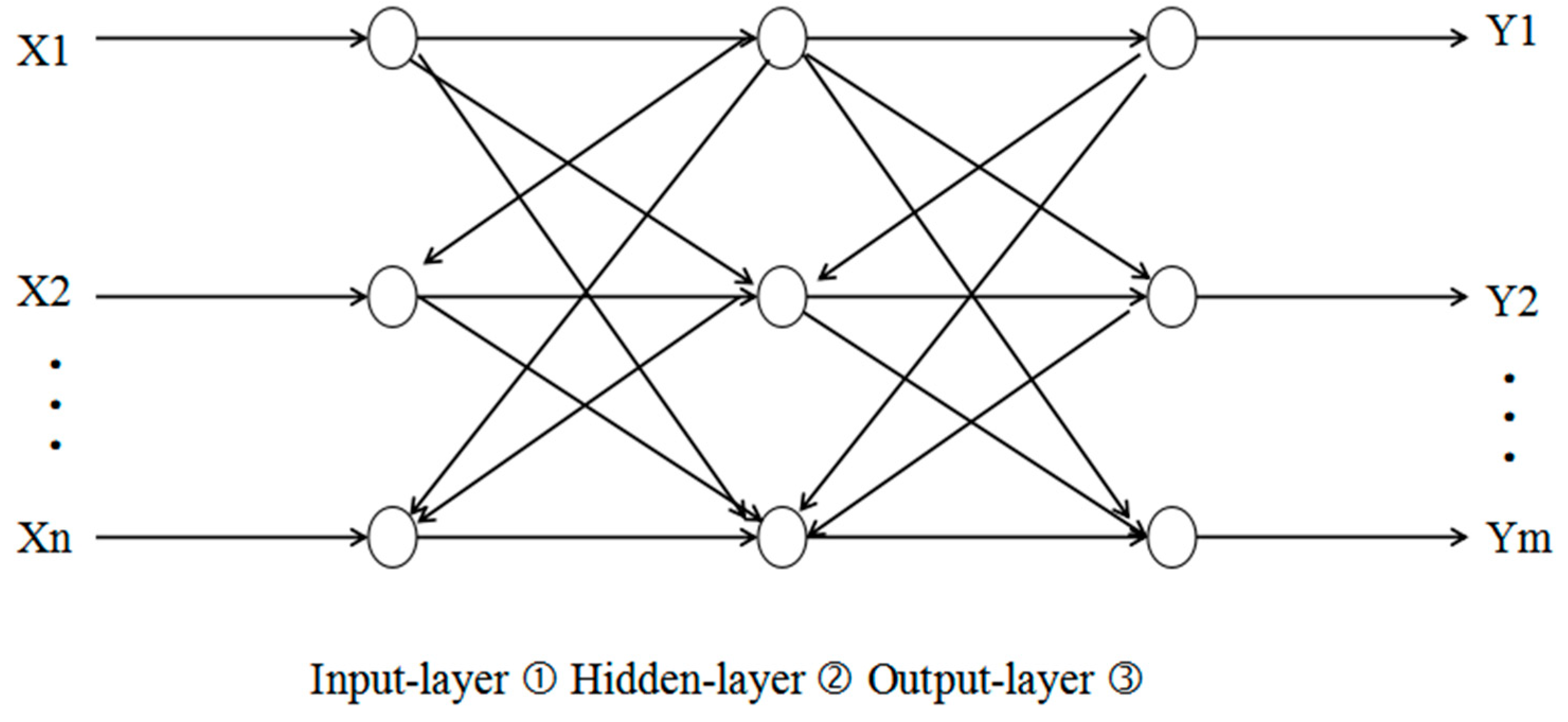
Figure 3 depicts a multi-layer neural network comprising an input, hidden, and output layer. The input layer, represented by nodes X1 through Xn, receives initial data, with each node signifying a distinct feature or value from the input dataset. The hidden layer, where most computations occur, consists of interconnected nodes, although unlabeled in the figure, indicated by vertical lines connecting input nodes to hidden nodes and then to the output layer. The output layer, denoted by nodes Y1 through Ym, generates the network’s final output. Neural networks learn through weight adjustments of connections between nodes, determining each node’s influence on the network’s output. The network refines these weights through training on a dataset, enabling it to effectively map inputs to desired outputs.

When selecting features for a decision tree, we typically follow a two-step approach. First, we identify the feature with the most significant classification ability from the training sample, using it as the head node for splitting the tree. Next, we select the appropriate splitting points for the subsequent features. This process is essential to optimizing the decision tree for accurate classification and prediction of the target variable. The choice of the head node is particularly critical as it forms the foundation of the tree, ensuring that the model is built on the feature that provides the highest classification ability [103,104].

The key question in this process is how to assess the classification ability of a feature, which hinges on two core concepts: entropy and information gain. Entropy quantifies the uncertainty of a random variable and measures the degree of randomness in the data, helping to evaluate how effectively a feature reduces this uncertainty when splitting the data [105,106]. Information gain, in turn, reflects the reduction in entropy that occurs when a feature is used for data splitting, calculated as the difference between the entropy of the parent node and that of the child nodes. By combining entropy and information gain, we can accurately evaluate the classification power of features and select the most informative ones to construct an optimized decision tree [34,107].

Suppose $X$ is a discrete random variable with a finite number of values, subject to the following probability distribution:

$$P(X=x_i)=p_i,i=1,2,\dots ,n$$

(10)

Because of the concept of entropy, we introduce the notion of information gain, which represents the degree to which information uncertainty is reduced under the given conditions of a specific feature $X$. The decision tree model employs information gain as a pivotal criterion for feature selection, with a preference for features exhibiting higher information gains due to their enhanced classification capability. This selection process forms the basis of various decision tree algorithms, including ID3, C4.5, and CART, each characterized by its unique tree generation method.

However, the construction process, mainly when dealing with numerous features, often leads to overfitting, where the model performs exceptionally on the training set but poorly on the test set, indicative of a lack of generalization. This overfitting is attributed to the excessive complexity of the decision tree, which overlearns from the training samples, capturing noise and quirks specific to the training data [3]. As a result, the model needs to generalize better to new, unseen data, limiting its practical application. Pruning emerges as a crucial step in mitigating this issue by simplifying the decision tree to bolster its generalization ability. Pruning techniques, such as pre- and post-pruning, aim to strike a balance between the decision tree’s complexity and its ability to accurately classify new instances [108]. By removing unnecessary branches and nodes, pruning reduces the risk of overfitting. It enhances the model’s performance on unseen data, making it a vital component in developing robust and reliable decision tree models [109].

In a different domain, neural networks are adept at classifying familiar electrocardiogram waveforms and those bearing resemblances, directly providing accurate classification criteria. This capability is particularly noteworthy in electrocardiogram analysis, where accurately classifying waveforms is crucial for diagnosing and managing cardiovascular conditions [110]. By leveraging their inherent pattern recognition capabilities, neural networks can quickly and accurately identify familiar waveforms, providing valuable insights for clinicians. However, when faced with unfamiliar or significantly different waveforms, the system resorts to a cognitive simulation-based approach, leveraging machine learning algorithms to extract symbols and derive insights. This method enables the system to analyze and deduce the classification of electrocardiogram waveforms through a reasoned process, effectively bridging the gap between familiar and unfamiliar patterns [111].

Table 1. Experimental Results of Adaptive Learning Algorithms.

Learning Sample Data	Knowledge Representation	Correct Recognition Rate (%)		Classification Time (s)
		Learning Time	Learned Pattern	Non-Learned Pattern	Learned Pattern	Non-Learned Pattern
Electrocardiogram T100–T221	Topology of Neural Networks	15 min	100	98.3	5	20

presents the experimental results of adaptive learning algorithms applied to electrocardiogram (ECG) waveforms, showcasing the effectiveness of a cognitive simulation-based machine learning algorithm. The learning sample data consists of electrocardiogram signals labeled as T100–T221. The knowledge representation method employed is the topology of neural networks. The algorithm achieved a correct recognition rate of 100% for learned patterns and 98.3% for non-learned patterns. The classification time for learned patterns was 5 s, while for non-learned patterns it was 20 s. These findings indicate the algorithm’s proficiency in accurately discerning and categorizing ECG patterns with a notable efficiency in classification time, particularly for learned patterns.

Adaptive machine learning algorithms that employ cognitive simulation stand out due to their flexible learning approaches and sophisticated knowledge representation methods, providing a significant edge over traditional BP neural network-based algorithms [25]. This advantage concerns algorithmic efficiency and the potential to uncover more profound insights into human cognitive and learning mechanisms. Such algorithms are designed to mimic the complexity and adaptability of human thought processes, offering a more nuanced and practical approach to machine learning tasks. By leveraging cognitive simulation, these algorithms can learn from experience, adapt to changing environments, and represent knowledge more abstractly and symbolically, allowing for more effective reasoning and problem solving [26,91,112].

These algorithms are particularly well-suited for complex and dynamic domains, where traditional machine learning algorithms may need help to provide accurate results. Cognitive simulation-based algorithms can better handle uncertainty, ambiguity, and context-dependent information by mimicking the human thought process, leading to more precise and reliable predictions [110]. Additionally, these algorithms can be designed to incorporate domain-specific knowledge and expertise, allowing for more effective transfer learning and adaptation to new tasks [95].

However, traditional algorithms like the perceptron face significant challenges due to their design, which allows for arbitrary initial values, leading to a vast array of possible separating hyperplanes. This can cause a bias towards specific categories and affect the model’s generalization performance, resulting in suboptimal performance and limited scalability. Furthermore, these algorithms must effectively capitalize on key training elements, necessitating complete re-learning and adding new data, which is time-consuming and inefficient [105,113]. This reveals a fundamental limitation in their learning process, underscoring the need for advanced machine-learning models capable of incremental learning and knowledge retention.

3.1. Comparison of Improved Algorithms

In this comprehensive comparative study, three distinct clustering algorithms were rigorously evaluated to determine their efficacy in clustering tasks. The first algorithm under scrutiny is the NJW algorithm, conveniently available in Python 3.6. The approach to assess the NJW algorithm’s performance involved partitioning the range from 0 to 10 into 20 equal segments, utilizing these as scale parameters for the Gaussian function. This allowed for a nuanced exploration of the algorithm’s sensitivity to different scale parameters. By leveraging the Python 3.6 built-in function, the NJW algorithm was executed 20 times, each with a unique scale parameter. The iteration yielding the highest accuracy was selected as the optimal scale parameter for subsequent runs. To further validate the results, the NJW algorithm was run ten additional times using this optimal scale parameter, and the average accuracy and average normalized mutual information (NMI) were recorded as the final benchmarks. All other parameters were set to their default values except the scale parameter, which was carefully tuned to optimize the algorithm’s performance. This rigorous testing process enabled a thorough assessment of the NJW algorithm’s capabilities and its robustness to varying scale parameters.

The second algorithm examined was the MVFS algorithm, which leverages the scale parameter derived from the NJW algorithm’s optimal performance as its Laplacian matrix L. This innovative approach allows the MVFS algorithm to build upon the strengths of the NJW algorithm, utilizing the scale parameter that yielded the highest accuracy in the NJW algorithm’s testing. By adopting this scale parameter as the basis for its Laplacian matrix, the MVFS algorithm aims to achieve comparable or even superior clustering performance. Like the NJW algorithm, the MVFS algorithm was executed ten times, and the results—average accuracy and average NMI—served as the final evaluation metrics. This testing methodology provides a direct comparison between the two algorithms, enabling researchers to assess the effectiveness of the MVFS algorithm’s approach in leveraging the NJW algorithm’s optimal scale parameter. The results of this comparative analysis will shed light on the MVFS algorithm’s ability to enhance clustering performance by building upon the foundations established by the NJW algorithm.

The third algorithm, AEMVFS, was subjected to a comprehensive testing regimen, executed ten times independently to assess its performance. The algorithm’s efficacy was evaluated based on two key metrics: average accuracy and average normalized mutual information (NMI). These metrics served as the ultimate reference standards for comparison, providing a comprehensive understanding of the algorithm’s performance. The experimental outcomes revealed that the NJW algorithm achieved the most favorable clustering effect within the 0 to 10 range, setting a benchmark for subsequent algorithms. The MVFS algorithm’s performance was assessed based on the optimal clustering effect attained by the NJW algorithm, operating under the same accuracy scale parameter. This allowed for a direct comparison between the two algorithms, highlighting their strengths and limitations. The AEMVFS algorithm introduced a novel approach, leveraging its unique features to evaluate its efficacy against the established metrics of average accuracy and NMI. The results from these experiments provided insightful benchmarks for comparing the three clustering algorithms, highlighting their respective strengths and limitations in clustering tasks.

Table 2. The clustering accuracy corresponding to each algorithm.

Data Set	NJW	MVFS	AEWVFS
Iris	0.8265	0.9365	0.9652
Glass	0.2658	0.2365	0.2596
Wine	0.3652	0.6852	0.7852
4k2-far	1	1	1
Leuk72-3k	0.9523	0.9412	0.9523
Seeds	0.7854	0.9522	0.9214
Seybean	1	1	1

offers insights into the clustering performance of three algorithms, where accuracy rates serve as the primary measure. Across various datasets, except for Glass, where differences are minimal, the AEMVFS algorithm demonstrates superior performance compared to NJW and MVFS. This exceptional performance stems from AEMVFS’s adaptive scale parameter selection under the normalized cut criterion, effectively navigating the intricate balance between dataset characteristics and clustering outcomes. AEMVFS also tackles feature redundancy within datasets, thus significantly enhancing spectral clustering efficacy. Both AEMVFS and MVFS boast adjustable parameters, augmenting their adaptability in diverse clustering scenarios, as highlighted by detailed parameter values in experimentation. This adaptability, coupled with a nuanced understanding of dataset nuances and clustering quality, underscores AEMVFS’s robustness and potential for broader applications in clustering tasks, marking a significant advancement in machine learning algorithms.

Table 3. Parameter values corresponding to AEMVFS.

	Accuracy			Standard Mutual Information
Data Set	α	β	γ	A	Β	Γ
Iris	0.2	0.7	0.47	0.1	0.6	0.7
Glass	0.6	0.2	0.5	0.2	0.2	0.2
Wine	0.1	1	0.1	0.3	0.8	0.8
4k2-far	0.1	0.2	0.8	0.9	0.1	0.1
Leuk72-3k	0.1	0.6	0.1	0.1	0.9	0.2
Seeds	1	0.1	0.3	0.1	0.1	0.1
Seybean	0.2	0.4	0.1	0.9	0.4	0.9

presents the parameter values corresponding to the AEMVFS algorithm across various datasets, with α, β, and γ denoting specific parameters. The accuracy and standard mutual information metrics evaluate the algorithm’s performance. Observing the parameter values, notable variations exist across different datasets, indicating the algorithm’s adaptability to dataset characteristics. For instance, in the Iris dataset, α and β values are relatively low, while γ is moderately high, suggesting a balanced weighting of different factors. Conversely, in the Glass dataset, α and β values are higher, indicating a greater emphasis on certain features.

Interestingly, the 4k2-far dataset exhibits high α and γ values, reflecting a stronger focus on specific attributes. Furthermore, the Leuk72-3k dataset displays diverse parameter values, indicating the algorithm’s ability to adjust to varying dataset complexities. The tailored parameter values highlight AEMVFS’s flexibility and effectiveness in accommodating different dataset structures, contributing to its robust performance across diverse clustering tasks.

3.2. Evaluation of Risk Control Models

In assessing model quality, particularly in financial risk management, more than reliance on accuracy is needed to gauge effectiveness. This holds particularly true when the goal is to discern a small subset of high-risk individuals from a vast pool of borrowers [114]. Consider a scenario where a dataset consists of 1000 borrowers, with 990 deemed regular users and only ten flagged as at risk of default. In such cases, a model that correctly identifies the regular users but overlooks the at-risk individuals would still yield an impressive 99% accuracy (990 out of 1000). However, despite this seemingly high accuracy rate, the model’s efficacy for risk control remains compromised as it fails to pinpoint the crucial at-risk cases, underscoring the importance of employing additional metrics beyond accuracy to evaluate model performance comprehensively.

This underscores the importance of choosing evaluation metrics that accurately reflect the problem’s nature and the model’s intended application. Particularly in scenarios where identifying the minority class, such as default-prone individuals, is paramount, metrics like recall and precision assume heightened significance. Recall assesses the model’s ability to capture actual positives, representing its sensitivity in detecting these pivotal cases. Conversely, precision gauges the model’s accuracy in correctly identifying positive instances, thus emphasizing specificity. By incorporating these nuanced metrics alongside accuracy, a more comprehensive understanding of the model’s performance emerges, enabling better-informed decisions in risk management and other critical domains [88].

A confusion matrix is a valuable tool that provides a visual and quantitative representation of the model’s predictions to assess credit risk models’ performance comprehensively. This matrix categorizes predictions into true positives, false positives, and false negatives, allowing for a detailed analysis of the model’s ability to identify at-risk individuals while minimizing false alarms accurately [73]. By examining the confusion matrix, lenders can gain a nuanced understanding of the model’s performance, including its sensitivity to detecting default-prone borrowers and specificity in avoiding false positives. This information is crucial for risk management, as it enables lenders to make informed decisions about credit risk assessment and forecasting, ultimately reducing the likelihood of financial losses and improving overall portfolio performance [115].

Figure 4 illustrates a confusion matrix under downsampling, which is a visual tool commonly employed to assess the performance of classification algorithms, particularly in supervised learning tasks. The rows represent the actual classes of the data samples, while the columns indicate the predicted classes. This matrix corresponds to a binary classification problem, with class labels 0 and 1. The matrix shows that 129 instances were correctly classified as class 0 (true negatives), and 139 instances were correctly classified as class 1 (true positives). However, there were 20 occurrences where data points from class 0 were incorrectly classified as class 1 (false positives), and 10 instances where data points from class 1 were incorrectly classified as class 0 (false negatives). These results provide critical insights into the model’s performance, highlighting areas where misclassifications occurred and offering opportunities for further refinement to improve predictive accuracy.

The initial validation of the model was conducted using a downsampling strategy aimed at addressing the significant imbalance in the dataset by reducing the size of the dominant class to match the minority class. This approach ensures that the model is not biased towards the more prevalent class, which, in the context of financial risk assessment, would typically be the regular users instead of the default-prone individuals. By downsampling the dominant class, the model must focus on the minority class, thereby improving its ability to detect and accurately classify default-prone individuals [116]. This is particularly important in financial risk assessment, where the consequences of inaccurate predictions can be severe.

Moving forward, the focus shifts to an oversampling strategy, which contrasts with downsampling by increasing the minority class’s size to equal that of the majority class rather than reducing the majority class [114]. This involves generating new data points for the minority class to achieve a balance between the two classes. Oversampling can help overcome the information loss issue with downsampling by preserving all the original data from the majority class while augmenting the minority class to ensure equal representation [117]. This approach can be efficient in financial risk assessment, where the minority class of default-prone individuals is often small and may not provide sufficient data for accurate modeling. By oversampling the minority class, the model can be trained on a more balanced dataset, reducing the risk of bias and improving its ability to detect and accurately classify default-prone individuals [115].

The procedural steps for oversampling closely mirror those of downsampling, involving data preparation, model training, and validation. However, the critical difference arises during the data augmentation phase, where advanced techniques like SMOTE (synthetic minority over-sampling technique) and ADASYN (adaptive synthetic sampling) are utilized [118]. These methods strategically generate synthetic instances of the minority class based on existing data points, rebalancing the class distribution. By augmenting the minority class, oversampling aims to extend the model’s learning capability, ensuring a more balanced representation of both classes in the training dataset [110]. This enhances the model’s ability to detect patterns and make accurate predictions across diverse data distributions, improving its overall performance in classification tasks. During the data preprocessing phase, we employed SMOTE to address the imbalance in non-profit financial data by oversampling the minority class [119]. For model training, a 5-fold cross-validation method was implemented to mitigate the risk of overfitting. Additionally, hyperparameters, such as the number of trees in the random forest and the learning rate in LightGBM, were fine-tuned using grid search to optimize performance. Regularization techniques like L2 regularization were applied to further prevent overfitting and improve model robustness.

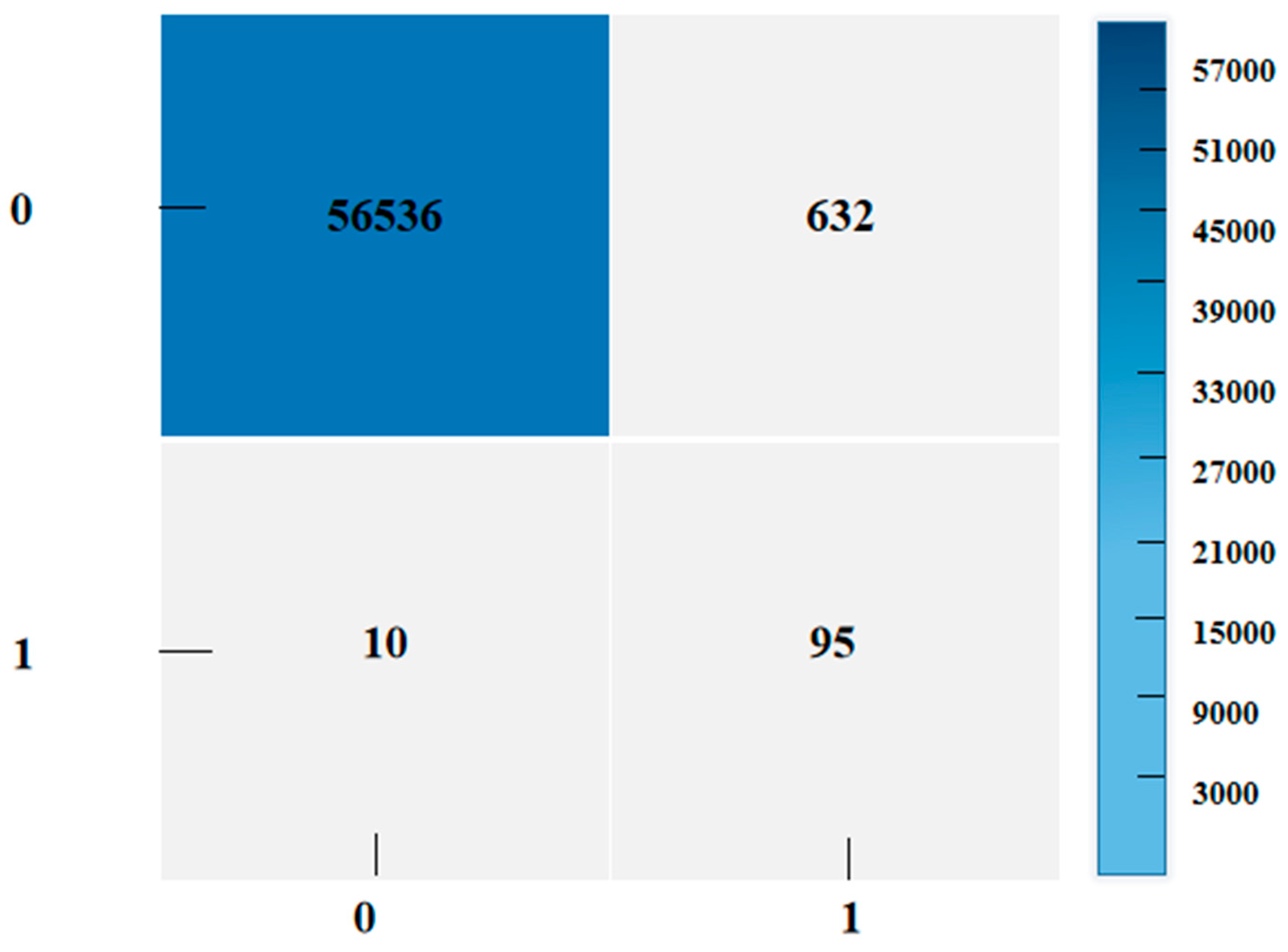
Figure 5 illustrates the performance of a classification model implemented with oversampling, a technique used to balance class distribution in the dataset. The rows represent the actual classes, while the columns indicate the predicted classes. Each cell in the matrix contains the count of data points in each category. The model attempts to classify data points into two classes, labeled 0 and 1. For class 0, the model correctly identifies 56,536 data points as true negatives, while 632 instances are incorrectly classified as class 1 (false positives). For class 1, 95 data points are correctly identified as true positives, and 10 instances are incorrectly classified as class 0 (false negatives). The application of oversampling suggests that class 1 was likely the minority class in the original dataset, and its representation was increased to achieve a balanced dataset. Although the model shows strong performance in identifying class 0 data points, it exhibits lower precision in classifying class 1 due to the smaller number of true positives. Despite these misclassifications, the overall classification performance of the model remains robust, as reflected by the high number of true negatives and true positives.

The application of logistic regression on oversampled datasets, as visualized by the confusion matrix, highlights the efficacy of data augmentation techniques like oversampling in machine learning operations, particularly within financial risk control [3]. Oversampling addresses the issue of class imbalance by artificially increasing the representation of minority classes, thereby allowing algorithms to learn from a more balanced dataset [120,121]. This approach enhances the model’s capacity to identify crucial risk factors among less represented classes. It expands the applicability of machine learning models to a broader range of tasks where class imbalance is a significant concern. By leveraging oversampling, machine learning models can better capture the nuances of financial risk and make more accurate predictions, ultimately contributing to more effective risk management strategies [116]. Turning attention to the XGBoost algorithm represents a significant advancement in the evolution of financial risk control models. This sophisticated iteration of gradient boosting stands out for its remarkable adaptability and efficiency, especially in navigating the intricacies of complex and imbalanced datasets inherent in financial contexts. XGBoost’s robust capabilities empower it to handle the nuances of economic data and position it as a formidable tool for enhancing predictive accuracy and reliability in risk management applications. By harnessing the strengths of XGBoost, financial institutions can unlock new possibilities for refining risk control strategies and bolstering their resilience in an ever-evolving landscape.

Figure 6 explores the nuanced intricacies of XGBoost parameters, offering a strategic opportunity to finely calibrate the model for optimal performance in navigating financial risk data landscapes. The model can achieve a delicate equilibrium between sensitivity to critical risk indicators and resilience against overfitting tendencies through meticulous analysis and iterative adjustment of these parameters. This meticulous calibration process elevates the precision and reliability of financial risk predictions. It instills confidence in the model’s capacity to discern subtle patterns within the complexities of financial data environments. Such meticulous optimization positions XGBoost as a formidable ally in the arsenal of financial risk management, primed to furnish actionable insights and fortified defenses against potential risks, reinforcing financial institutions’ stability and resilience in dynamic market conditions.

In addressing the challenge of insufficient default events within the dataset, two primary strategies emerge: downsampling and oversampling. The essence of oversampling lies in equalizing the representation of both classes within the dataset, thereby creating a balanced environment for model training [114]. This approach is efficient when dealing with imbalanced datasets where the majority class dominates the minority class. By oversampling the minority class, the model is exposed to a more representative data distribution, allowing it to learn more effectively from both classes. In contrast, downsampling achieves balance through a reductionist approach, selecting a subset from the majority class to match the size of the minority class [3]. This method ensures that the data remains representative without the complication of generating synthetic data, which can be prone to errors and may not accurately reflect the underlying distribution of the data [122].

Post-data preparation, the subsequent step involves partitioning the dataset into two segments: 70% allocated for the training set and 30% designated as the test set. This division is pivotal, especially in maintaining a balanced distribution of classes within both subsets to mitigate the risk of overfitting and ensure the model’s generalization capability. By allocating a significant portion of the data to the training set, the model can learn from a robust and diverse set of examples, thereby improving its ability to generalize to unseen data. Conversely, the test set serves as a validation mechanism, providing an unbiased assessment of the model’s performance on unseen data. This division allows for a comprehensive evaluation of the model’s capabilities, including its ability to classify new instances accurately and its robustness to overfitting.

Utilizing the logistic regression library from sklearn in a Jupyter Notebook environment, the model is constructed with the logistic regression algorithm’s default parameters for the training phase [123]. This approach enables the model to leverage the strengths of logistic regression, including its ability to handle binary classification problems and its interpretability through using coefficients and odds ratios. The model can be trained without extensive hyperparameter tuning using the default parameters, allowing for a more streamlined and efficient development process [118].

Figure 7 unveils the evaluation of the model’s efficacy through scrutiny using the test set, encapsulating performance metrics and outcomes to shed light on the predictive accuracy and practical applicability in financial risk assessment scenarios. A recurring theme in machine learning model evaluation emerges: the performance metrics on the test set consistently lag behind those on the training set. This common phenomenon often stems from the model’s inclination to overfit the training data during the logistic regression algorithm’s training phase. Overfitting manifests when the model excessively tailors itself to the nuances of the training data, capturing noise and intricacies that fail to generalize effectively to unseen data, thus resulting in diminished performance on the test set. This disparity underscores the critical need for techniques like regularization and cross-validation to mitigate overfitting and bolster the model’s robustness and generalizability across diverse datasets.

To effectively address the limitations of the financial risk control model constructed via the logistic regression algorithm and enhance its predictive accuracy and reliability, this process commences with a thorough understanding of the model and its parameters, including their respective roles, potential impacts, and reasonable value ranges [124]. This clarity ensures that parameter adjustments are meaningful and directed towards enhancing model generalization, thereby minimizing the risk of overfitting and improving the model’s ability to generalize to new, unseen data.

Subsequently, cross-validation techniques are systematically applied to identify the optimal parameter settings. This process involves iteratively training and evaluating the model across various parameter combinations and data subsets [125]. By using this approach, the model’s robustness is enhanced, allowing it to effectively manage diverse scenarios and data distributions, thereby increasing its predictive power and reliability. By methodically exploring the parameter space and assessing the model’s performance under different conditions, the risk of overfitting is minimized, and the model’s generalizability is improved [126].

Although parameter optimization can be a time-intensive process, it is a crucial step in refining the model’s predictive accuracy and reliability. It requires a high level of precision and patience to achieve the desired enhancements in model efficacy [127]. Through careful parameter tuning, the likelihood of poor performance or inaccurate predictions is significantly reduced, ultimately resulting in more informed decision-making and improved financial risk management.

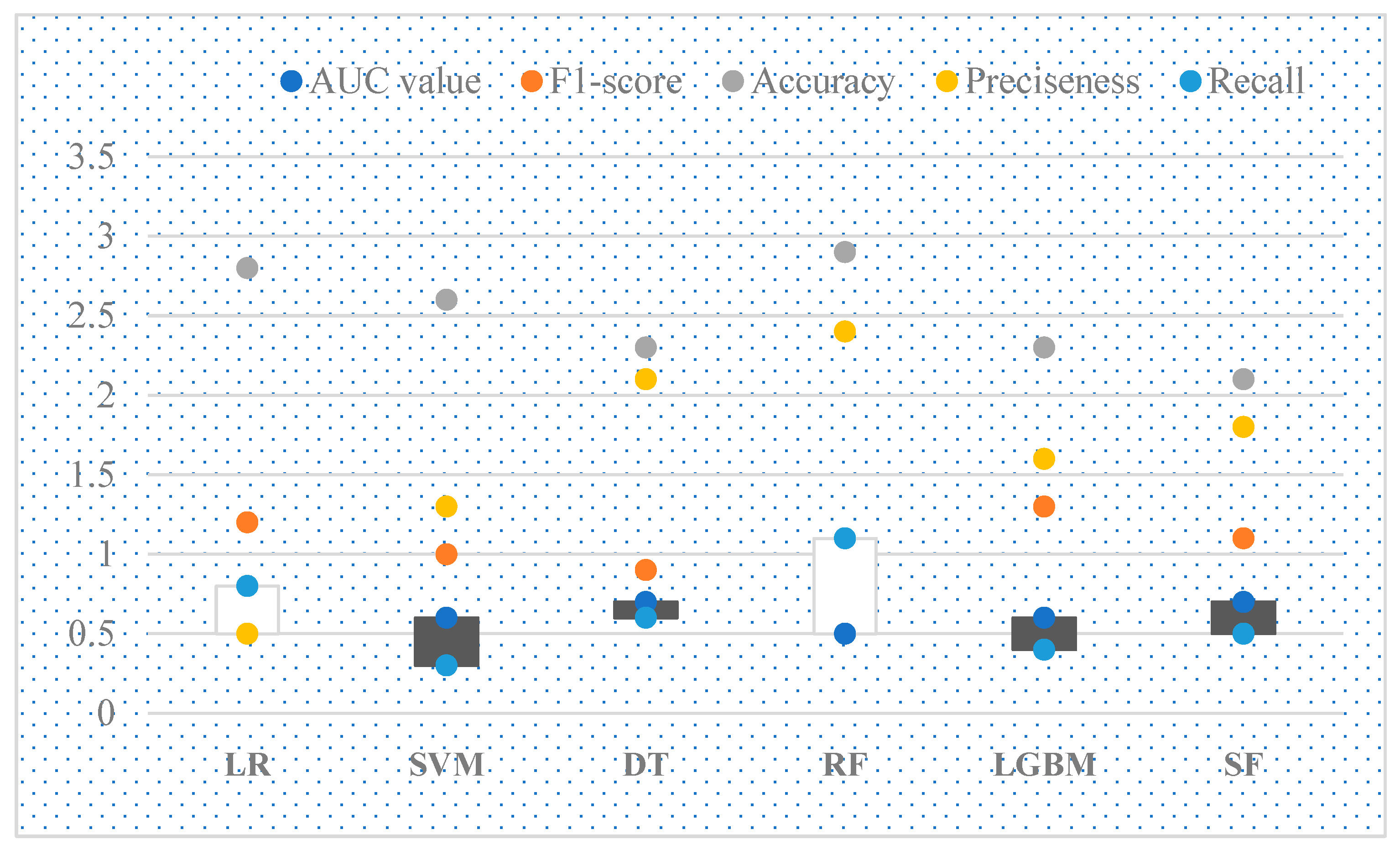
Figure 8 provides a comprehensive comparison of the performance of different models, revealing a clear superiority of the ensemble or fusion model over its counterparts in terms of overall efficacy. This observation underscores the potency of leveraging ensemble techniques to harness the collective strengths of multiple predictive models, thereby achieving heightened predictive accuracy and robustness. Notably, the logistic regression and LightGBM models emerge as strong contenders, performing comparably and securing the second position in the performance ranking. In contrast, the decision tree model trails behind, highlighting potential limitations in its predictive capabilities compared to the other models. This comparative analysis informs the selection of the most effective modeling approach. Further analysis demonstrates that random forest and LightGBM algorithms are particularly effective in predicting credit risk. These algorithms identify patterns in historical loan data to predict the probability of borrower default. The models leverage various input variables, including credit scores, loan terms, and interest rates, to enhance prediction accuracy through ensemble learning techniques. By iterating over multiple decision trees in random forest and employing gradient boosting in LightGBM, the models achieve higher sensitivity and specificity, providing more reliable risk assessments. This approach helps financial institutions and non-profit organizations better anticipate and mitigate the risks of default, ultimately improving decision making in loan approvals and fund allocation. Figure 8: Performance comparison of different models. The different colors represent various performance metrics: blue (AUC value), orange (F1-score), gray (Accuracy), yellow (Preciseness), and light blue (Recall). The ensemble models demonstrate superior overall performance.

Table 4. Model Performance Comparison.

Metric	Random Forest	LightGBM
Accuracy (%)	85.6	89.2
AUC	0.85	0.89
Precision	0.81	0.87
Recall	0.78	0.85
F1 Score	0.79	0.86
Training Time (s)	120	45
Interpretability	High	Medium

compares the performance of random forest and LightGBM based on key evaluation metrics such as accuracy, AUC, precision, and recall. As shown, LightGBM outperforms random forest in most metrics, including accuracy and AUC, primarily due to its ability to handle large and imbalanced datasets efficiently [128]. While random forest exhibits slightly lower accuracy, its interpretability makes it a valuable option for non-profits requiring transparency in decision-making [129].

This hierarchical performance layout reinforces that ensemble methods, such as random forest and LightGBM, can substantially elevate model performance. These ensemble methods leverage the diversity of multiple learning algorithms or iterations of the same algorithm to reduce variance (in the case of bagging methods like random forest) or bias (in boosting methods like LightGBM), leading to more accurate and generalized models [87]. The underperformance of the singular decision tree model relative to its ensemble counterparts further corroborates the efficacy of model fusion, highlighting its capacity to mitigate the limitations inherent in individual models and harness their collective strengths for enhanced predictive performance [130].

Random forest, for instance, is a popular ensemble method that combines multiple decision trees to improve predictive performance. By aggregating the predictions of various trees, random forest can reduce the variance of individual trees and enhance the model’s overall accuracy [131]. This is particularly useful in credit risk prediction, where noise and outliers in the data can lead to inaccurate predictions. LightGBM, on the other hand, is a gradient-boosting algorithm that combines multiple weak models to create a robust predictive model. By iteratively training various models and combining their predictions, LightGBM can reduce individual models’ bias and improve the model’s overall accuracy [132]. This is particularly useful in credit risk prediction, where accurate and reliable predictions are critical.

4. Discussions

This study provides valuable insights into the effectiveness of machine learning models in financial risk control, particularly in addressing class imbalance and enhancing model performance through ensemble methods. The results align with the research questions and hypotheses outlined in the introduction, which aimed to investigate the potential of machine learning models in managing financial risk [118,133].

The exploration of data augmentation techniques, notably downsampling and oversampling, reveals their pivotal role in addressing class imbalance within datasets. Oversampling by equalizing class representation and downsampling through selective data reduction aim to create a more balanced learning environment for the models [8]. This study’s findings underscore the necessity of maintaining class balance to prevent model overfitting and enhance the generalizability of the models across unseen data [134].

The performance of the logistic regression model, as shown in the confusion matrices and performance metrics, highlights the potential risks of overfitting, where models excel on training data but fail to generalize to test datasets [3]. In comparison to individual models such as logistic regression, LightGBM, and decision tree models, the ensemble or fusion models stand out by demonstrating the advantages of model fusion in financial risk control. By combining the strengths of multiple models, the ensemble approach effectively reduces both variance and bias, thereby enhancing model accuracy and robustness [97,135]. The relatively lower performance of the decision tree model further validates the benefits of ensemble methods, reinforcing the value of diversity in model selection and the strategic integration of multiple algorithms to address the limitations of singular models [43,136]. Additionally, the study emphasizes the importance of parameter optimization in logistic regression, where iterative cross-validation for optimal parameter selection mitigates overfitting and ensures the models are fine-tuned to the specific intricacies of financial risk data [131,137]. These findings align with existing literature, which highlights the effectiveness of ensemble methods in improving predictive performance and reducing overfitting risks. For instance, Munkhdalai et al. [138] found that ensemble methods like random forest and gradient boosting consistently outperformed individual models in credit scoring, while Esenogho et al. [25] demonstrated their efficacy in detecting credit card fraud. This study confirms the role of machine learning in financial risk control by addressing class imbalance and enhancing performance through ensemble methods. The superior performance of ensemble models, compared to individual algorithms, underscores the importance of parameter optimization and cross-validation in producing finely-tuned models [118]. Overall, these insights illustrate how machine learning can be a transformative tool in addressing global challenges through financial risk management.

Several recommendations can be made to enhance the effectiveness of machine learning models in financial risk control. First, financial institutions should prioritize the use of ensemble methods, such as random forest and LightGBM, as they have demonstrated superior performance compared to individual models. By leveraging the collective strengths of multiple models, ensemble methods can effectively reduce variance and bias, leading to improved model accuracy and robustness [88,139]. Second, financial institutions should invest in data augmentation techniques, particularly oversampling, to address class imbalances within datasets. Oversampling can help create a more balanced learning environment for the models, preventing overfitting and enhancing the generalizability of the models across unseen data [140]. Third, financial institutions should emphasize parameter optimization for their machine learning models, using techniques such as cross-validation to identify the optimal parameter settings. This process mitigates the risk of overfitting and ensures that the models are finely tuned to the intricacies of financial risk data. Fourth, financial institutions should prioritize the interpretability of their machine learning models, ensuring that the model’s predictions are transparent and accountable. This can be achieved using interpretable machine learning techniques, such as SHAP (Shapley Additive Explanations) or LIME (Local Interpretable Model-agnostic Explanations). Fifth, financial institutions should consider their machine learning models’ computational complexity and resource requirements, ensuring they are efficient and scalable to handle large datasets and real-time data streams. Finally, regulatory bodies should reevaluate existing regulatory frameworks to ensure that they are aligned with the advancements in machine learning technology. Regulatory bodies can help foster a more efficient and responsive regulatory environment by harmonizing and refining regulatory measures with technological progressions [141].

While this study offers important insights into the use of machine learning for financial risk control, it has several limitations. The findings are based on a specific dataset, limiting their generalizability to other financial contexts. Additionally, the study focuses on a narrow set of algorithms, and future research should explore a broader range of machine learning models. The impact of feature engineering and model interpretability, both crucial in financial risk management, were not fully addressed, and further exploration in these areas is needed. Lastly, computational complexity was not deeply considered, which is critical for real-world applications dealing with large-scale data.

5. Conclusions

The integration of machine learning into the financial sector has significantly expanded the capabilities of financial oversight, risk management, compliance, and systemic risk monitoring. This technological advancement not only streamlines regulatory processes for both supervisory bodies and financial institutions but also reduces regulatory burdens, creating a more efficient and responsive regulatory framework. The application of machine learning in developing risk control models emphasizes the critical need for a thorough understanding of financial data types. Such knowledge enables the creation of models that are specifically tailored to the characteristics of the data while optimizing their overall performance. One of the key challenges lies in accurately identifying the nature of financial data and aligning it with the most suitable machine learning algorithms. Addressing this challenge presents a promising direction for future research, as it could lead to methodologies that enhance the precision, adaptability, and effectiveness of machine learning models in financial risk control, thereby strengthening the resilience and stability of the financial sector in response to evolving risks. Our results demonstrate that LightGBM and random forest are effective tools for financial risk management in non-profits. These models can be integrated into non-profits’ existing financial systems to provide real-time risk assessments and improve resource allocation. However, the study is limited by the relatively small dataset, which may limit the generalizability of the findings. Future research should explore larger, more diverse datasets and investigate the use of explainable AI techniques to enhance the interpretability of the models for non-profit organizations [142].

Moreover, this study highlights how the integration of machine learning into financial processes can improve oversight, risk management, and regulatory efficiency. It reinforces the importance of understanding financial data to optimize model performance, especially in terms of matching data types with appropriate algorithms. By optimizing these processes, machine learning can significantly enhance the efficacy of financial risk control and bolster the industry’s resilience. Furthermore, this research advocates for innovation—particularly through the use of machine learning—as a vital tool for addressing global challenges, extending its impact beyond the financial sector alone.

5.1. Theoretical Implications

Integrating machine learning into the financial sector has significant theoretical implications for financial risk management. The study highlights the importance of understanding the nature of financial data and matching it with the most suitable machine learning algorithm, which is crucial for developing models tailored to the specific characteristics of the data and optimized for performance [143]. The study’s findings suggest that machine learning can enhance the capabilities of financial oversight, risk management, compliance, and systemic risk monitoring by streamlining regulatory processes and alleviating the regulatory burden, fostering a more efficient and responsive regulatory environment. The study’s emphasis on data understanding and algorithm selection has significant theoretical implications for developing machine learning models in financial risk control, representing a promising avenue for future research. Exploring this challenge could unveil methodologies that further refine the precision, adaptability, and efficacy of machine learning models in financial risk control, contributing to the resilience and stability of the financial industry in the face of evolving risks and challenges [135]. Additionally, the study’s findings have implications for the development of regulatory frameworks, necessitating authorities to reevaluate existing regulatory frameworks to ensure they effectively address the challenges posed by machine learning in financial risk management.

5.2. Policy Implications

The policy implications drawn from this research are multifaceted and impactful. Firstly, policymakers should recognize the critical role of machine learning models in financial risk control and prioritize initiatives to foster the adoption of these advanced techniques within regulatory frameworks [3]. Given the effectiveness of ensemble methods in improving predictive performance and mitigating model limitations, policymakers should encourage financial institutions to incorporate ensemble modeling approaches into their risk management strategies. Additionally, policymakers must support ongoing research and development efforts focused on refining machine learning algorithms and techniques, particularly in addressing class imbalance and enhancing model robustness [118,133]. Moreover, policymakers should promote transparency and standardization in model evaluation and validation processes to ensure accountability and reliability in financial risk assessment practices. Furthermore, collaboration between policymakers, researchers, and industry stakeholders is essential to facilitate knowledge exchange and foster innovation in financial risk management practices. Ultimately, the policy implications of this research underscore the importance of embracing technological advancements in machine learning to strengthen financial risk control frameworks and enhance the stability and resilience of financial systems.

5.3. Ideas for the Future

Future research aimed at enhancing the effectiveness of machine learning models in financial risk control could explore several promising avenues. Refining ensemble techniques by investigating novel methods or hybrid approaches that combine multiple ensemble algorithms may lead to higher predictive accuracy and improved model robustness, particularly in dynamic and evolving financial risk environments. Integrating explainable AI techniques into machine learning models could significantly enhance model interpretability and transparency, empowering stakeholders to make more informed and accountable risk management decisions. The development of adaptive learning systems capable of autonomously adjusting model parameters in response to changing market dynamics and emerging risk factors could further improve proactive risk identification and mitigation. Additionally, the integration of multi-modal data sources, including both structured and unstructured data, could broaden the feature space, boosting the predictive power of machine learning models. Addressing ethical and regulatory challenges, such as ensuring fairness, accountability, and transparency, will be critical for the responsible and ethical deployment of AI in financial risk management. By advancing these areas, future research can contribute to building more resilient, adaptive, and sustainable financial systems.