Dynamic Scheduling Optimization Method for Multi-AGV-Based Intelligent Warehouse Considering Bidirectional Channel

Abstract

With the implementation of AGV technology and automated scheduling, storage and retrieval systems have become widely utilized in warehouse management. However, due to the use of unidirectional channels, AGV movement is restricted, and detours may occur frequently. Additionally, as the number of AGVs increases, deadlocks can arise, which lead to delays in order packaging and a decrease in overall warehouse performance. Hence, this paper proposes a dynamic scheduling method for task assignment and route optimization of AGVs to prevent collisions. The routing optimization method is based on an improved A* algorithm, which takes into account the dynamic map as input. Moreover, this paper investigates highly complex collision scenarios in bidirectional channels. Through simulation experiments, it is evident that scheduling methods based on bidirectional channels offer a clear advantage in terms of efficiency compared to those based on unidirectional channels.

1. Introduction

With the rapid development of e-commerce, the traditional labor-intensive logistics system can no longer meet industry requirements. In order to enhance logistics efficiency, intelligent warehouses have been introduced and become one of the hottest topics in intelligent systems [1]. As the cornerstone of intelligent warehouse, the automatic guided vehicle (AGV) has been extensively adopted by numerous companies (e.g., Cainiao and Amazon). AGV is a type of autonomous transport vehicle used in industrial settings for tasks such as material handling, navigating along predefined paths without human intervention.

The research of AGV-based intelligent warehouse systems focuses on six key aspects:

• route planning method,
• AGV scheduling,
• task allocation and coordination,
• avoiding collisions and jams,
• the layout of intelligent warehouses,
• location.

In terms of route planning methodology, Adel et al. (2016) [2] utilized a network mapping structure to approximate the optimal route and proposed both a time linear relaxation Dijkstra algorithm and an A* algorithm. Fu et al. (2018) [3] introduced an improved A* algorithm for AGV routing, incorporating post-processing optimization techniques to refine local routes obtained from the initial plan. Quang et al. (2021) [4] developed a hybrid adaptive large neighborhood search with integrated local research methods aimed at minimizing tardiness costs. Based on the distance between AGVs, targets and obstacles, Zhang et al. (2018) [5] prioritized allocation according to the remaining power of AGVs and planned a route for a multi-AGV system based on priority and ant colony algorithm. Muthukumaran and Sivaramakrishnan (2019) [6] established two objective functions of optimization and obstacle avoidance, respectively, utilizing the dragonfly algorithm to obtain an optimal route. By incorporating the total distance of multiple AGVs and individual distances as constraints, Contreras et al. (2015) [7] proposed a method, which combined artificial bee colony algorithm with evolutionary planning algorithm to refine feasible routes through local processes for solving multi-AGV route planning problems. Chen et al. (2016) [8] investigated an online routing approach based on ant colony algorithm to determine multi-AGV routes under uncertain time. Han et al. (2017) [9] used a genetic algorithm to plan routes for multiple automated guided vehicles. Zhang et al. (2018) [5] proposed an improved A* algorithm based on traffic regulations and appointment tables to tackle a collaborative multi-AGV routing problem. Zhang et al. (2023) [10] presented a novel method, which combines reinforcement learning (RL) and Dijkstra’s algorithm to accelerate route planning, alongside proposing a novel multi-AGV route-planning method integrating dynamic programming and Monte-Carlo tree search to effectively reduce system energy costs.

In terms of AGV scheduling, Miyamoto and Inoue (2016) [11] discussed collision avoidance, system components’ capabilities and convenience of route modification, and they proposed a local search method to solve the conflict-free scheduling problem in AGV systems. Samaneh and Hamed (2017) [12] provided a simultaneous AGVs scheduling approach. Li et al. (2020) [13] investigated multi-AGV scheduling mechanism based on a particle swarm algorithm for dynamic customer demand. Mousavi et al. (2017) [14] developed a multi-objective scheduling model and proposed a hybrid approach, which integrated the genetic algorithm and particle swarm algorithm. Ye et al. (2017) [15] investigated the application of the pyrotechnic algorithm to address a multi-AGV scheduling problem. Barenji et al. (2017) [16] explored a multi-agent-based production line for rescheduling and reconfiguration in modern manufacturing systems. Cheng et al. (2023) [17] proposed a novel genetic algorithm to solve the scheduling problem of multiple AGVs and minimize the maximum completion time of AGV scheduling in intelligent warehouses.

In terms of task allocation and coordination, Zhou et al. (2014) [18] proposed a multi-AGV task allocation mechanism in intelligent warehouses, which evenly distributes the workload and minimizes travel costs. Dou et al. (2015) [19] presented a hybrid solution, which combined a genetic-algorithm-based task scheduling method with a reinforcement-learning-based route planning method to enhance the efficiency of intelligent warehouses. Xue et al. (2019) [20] proposed a collision-free task allocation scheme, which transformed the multi-AGV task allocation problem into a transportation problem, thereby enhancing the AGVs’ task processing capabilities. In terms of AGV control methods, Simeon et al. [21] initially adopted a centralized control method to enable uniform handling of collision coordination problems by a central control system for AGVs. Maria et al. (2018) [22] employed a distributed control method to coordinate and manage the AGVs. Nguyen et al. (2023) [23] introduces a model of automated guided vehicle (AGV) manipulation based on EtherCAT within the Unity platform for intelligent warehouse management, which achieved high-performance outcomes, characterized by flexibility and seamless motion.

In terms of collision and congestion avoidance, Digani et al. (2016) [24] proposed a probabilistic model for intelligent warehouse traffic to predict congested areas and optimize AGV route planning accordingly. Zhang et al. (2018) [25] categorized collisions between AGVs into four scenarios and proposed corresponding solutions for each, with the goal of achieving collision-free operations among AGVs.

In terms of intelligent warehouse layout, Zhang et al. (2019) [26] provided a two-layer evolutionary algorithm to optimize the design.

In terms of location, Monica and Ferrari (2015) [27] utilized an analytical approach to optimize anchor node placement for ultrawide band-based localization of a target node moving along a corridor in large indoor scenarios. Cho et al. (2018) [28] proposed an autonomous AGV equipped with simultaneous localization and map building based on the matching method, which was further enhanced by extending the Kalman filter to address the localization problem. Yang et al. (2020) [29] employed an extended Kalman filter algorithm to match sensor observations with existing features in the map for precise positioning of AGVs. Yang et al. (2022) [30] proposed a multi-AGV tracking system with reduced time complexity, efficiently tracking a fleet of AGVs with higher positioning accuracy compared to traditional navigation methods and other tracking algorithms based on various location patterns.

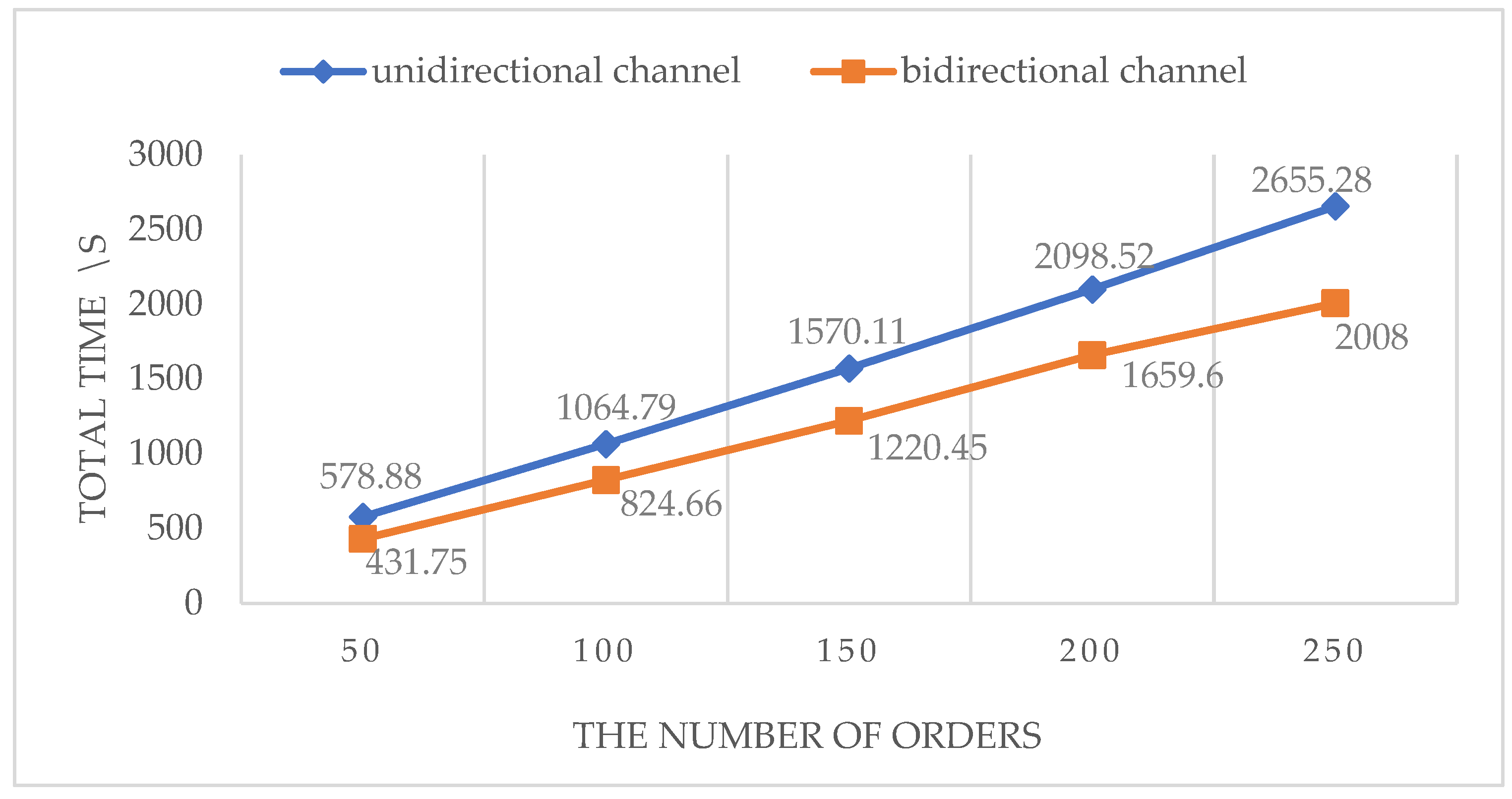
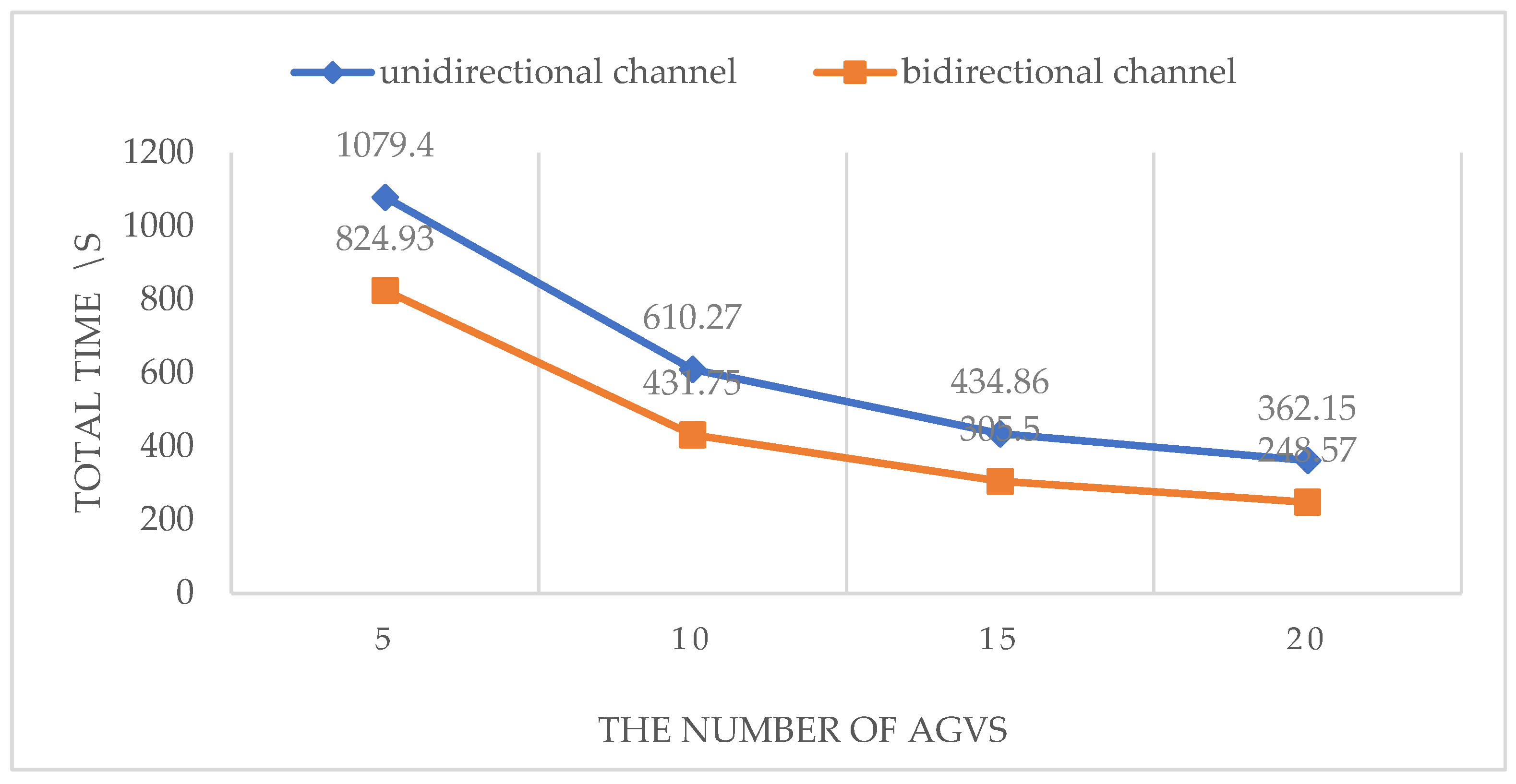
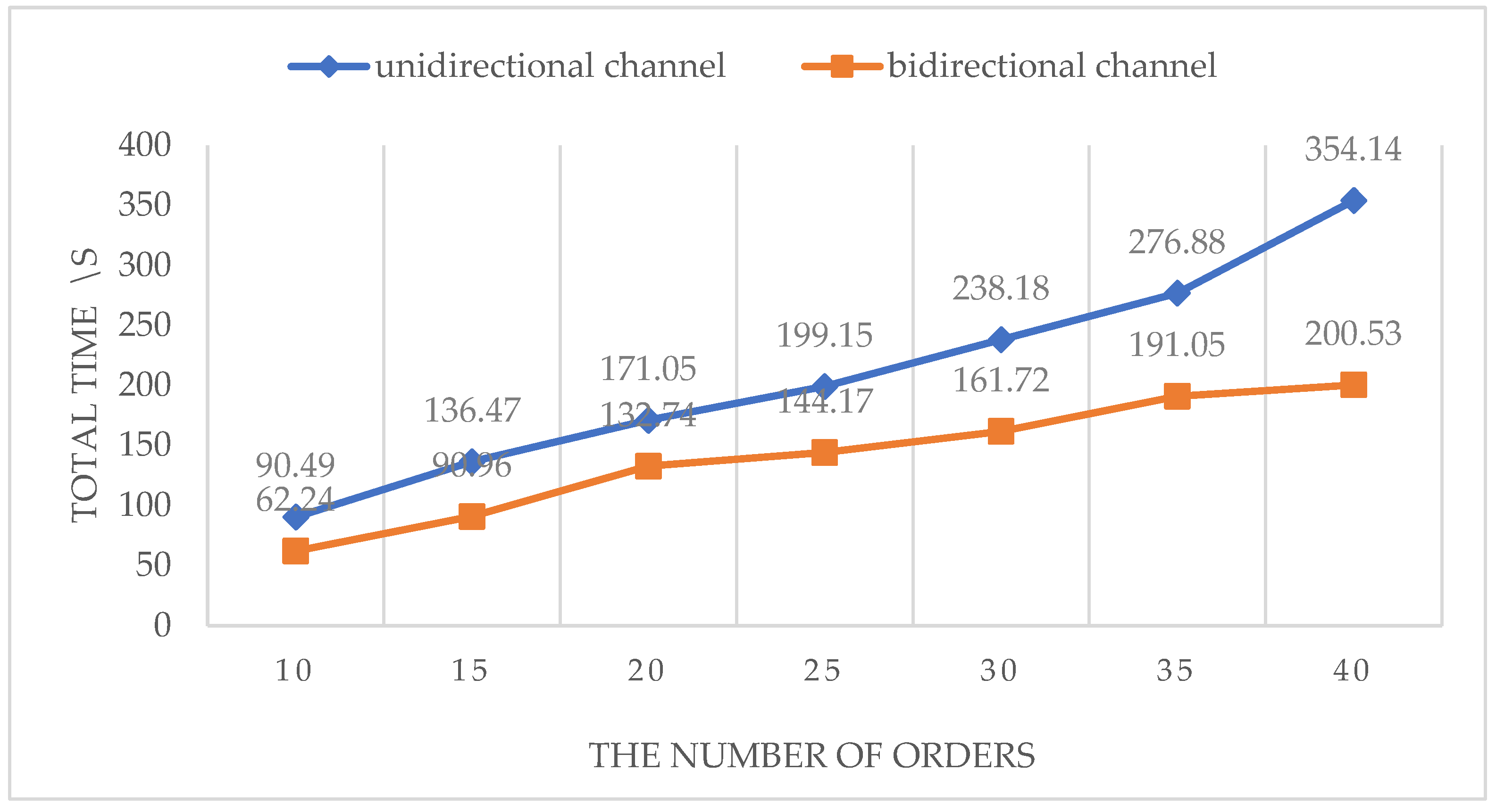
As previously mentioned, while there have been studies conducted on intelligent warehouse systems, few have utilized bidirectional channels in grid map-based multi-AGV routing methods. It is evident that unidirectional channels pose a significant disadvantage compared to their bidirectional counterparts, as they increase the likelihood of collisions and deadlocks between AGVs and significantly lengthen travel distances. Currently, while indoor positioning technology is a key enabler for bidirectional channels, it is not the sole determining factor due to the maturity of SLAM technology and the mass production of corresponding sensors, such as lidar. Therefore, this paper aims to present a dynamic scheduling optimization method for intelligent warehouses based on multi-AGV systems, taking bidirectional channels into consideration. It proposes an enhanced A* algorithm to ensure AGVs adhere to the traffic rule of ‘move on the right’ within a dynamic map, thereby closely aligning with real-life traffic situations. Furthermore, it discusses and categorizes various collision scenarios among AGVs, providing corresponding strategies to achieve advanced levels of intelligent driving. Through experimental validation, it is demonstrated that the method and the strategies significantly enhance the overall efficiency and traffic management capabilities of AGVs in intelligent warehouses.

2. Intelligent Warehouse Model

The notations and parameters of the intelligent warehouse model is given in

Table 1. The notations and parameters of the model.

Parameters	Descriptions
$P=\{p_1,p_2,...,p_{30}\}$	The packing area.
$G=\{g_1,g_2,...,g_m\}$	The shelf area; $m$ represents the number of shelves.
$C=\{c_1,c_2,...,c_{33}\}$	The charging area.
$R=\{r_1,r_2,...,r_n\}$	A fleet of AGVs; $n$ represents the number of AGVs.
v and vr	The constant velocity of AGV.
L	The length of shelf stations.
(m, n)	The sequence number of sub-area; $m$ represents the row number; and $n$ represents the column number.
$f\left(n\right)$	The route cost of traversing from the starting point to grid $n$.
$g\left(n\right)$	The actual cost of traversing from the starting point to grid $n$.
$d$	The actual distance from the current grid to the target grid.
$d_n$	The Manhattan distance from the current grid to the target grid.
$h\left(n\right)$	A heuristic function representing the estimated cost of traveling from the current grid to the target grid.
$C_m^n$	The coordinate of a node with sequence number $m$ in the route of the AGVn.
${\tau }_m^n$	The arrival time of AGVn at the node with sequence number $m$ in its route.
$t_m^n$	The processing time required for AGVn on the node with se-quence number $m$ in its route.
$\delta$	The time window for collision.
R	The coordinate collection of the crossroads.
T	The coordinate set of the T-crossroads.
N	The coordinate set of the non-channel areas, including the shelf area, the packing area and the charging area.
H	The horizontal channels, excluding the area of crossroads and T-crossroads.
L	The longitudinal channels, excluding the area of crossroads and T-crossroads.

.

This paper provides an efficient and adaptable intelligent warehouse model, which incorporates the appearance and operational characteristics of AGVs, as well as defining the key terms used in intelligent warehousing. Additionally, this paper introduces the working principle of the warehouse based on two distinct control methods.

• Centralized control system allocates orders to the most suitable AGV for optimizing overall benefits.
• Each AGV utilizes a distributed control method to strategize routes and circumvent congestion.

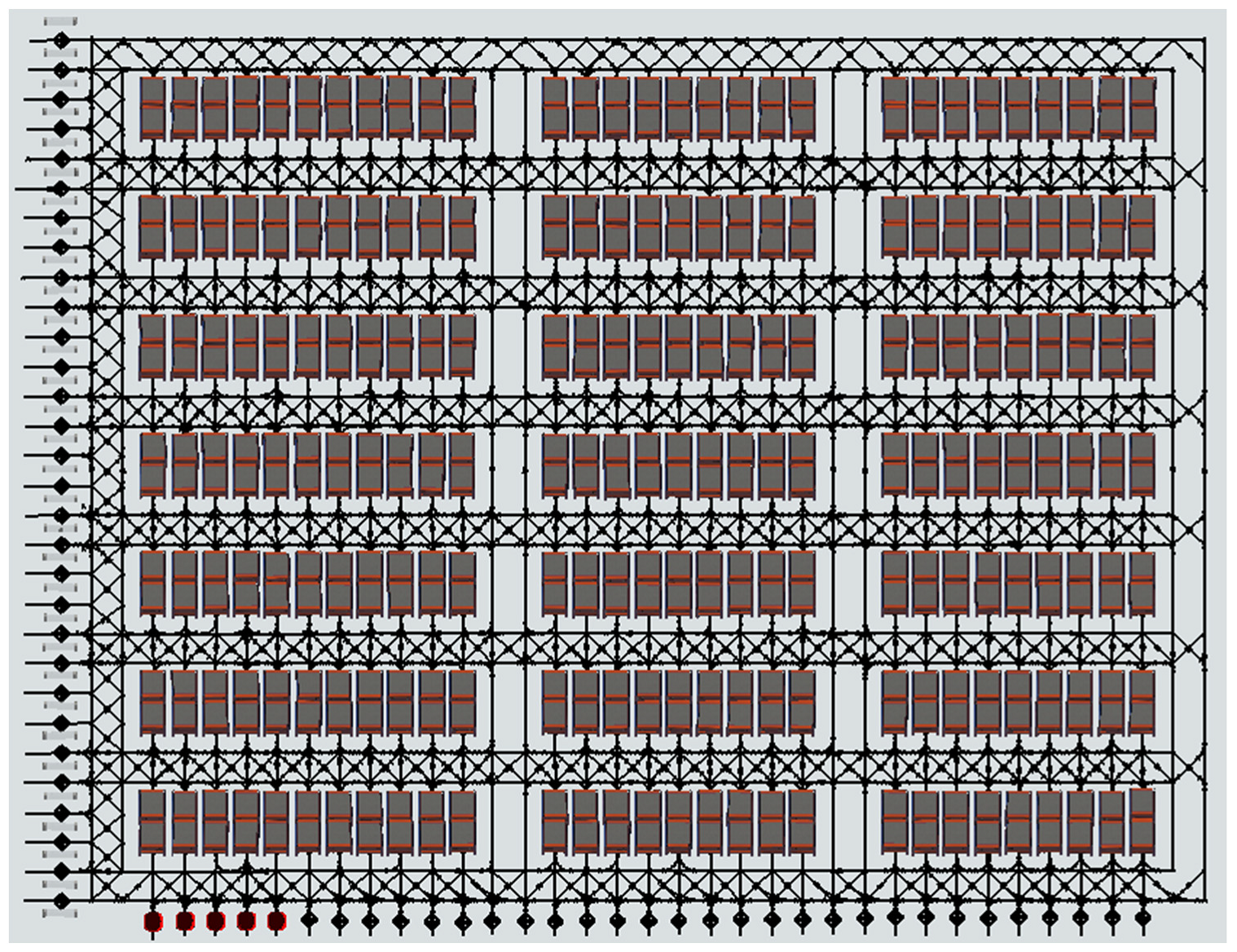
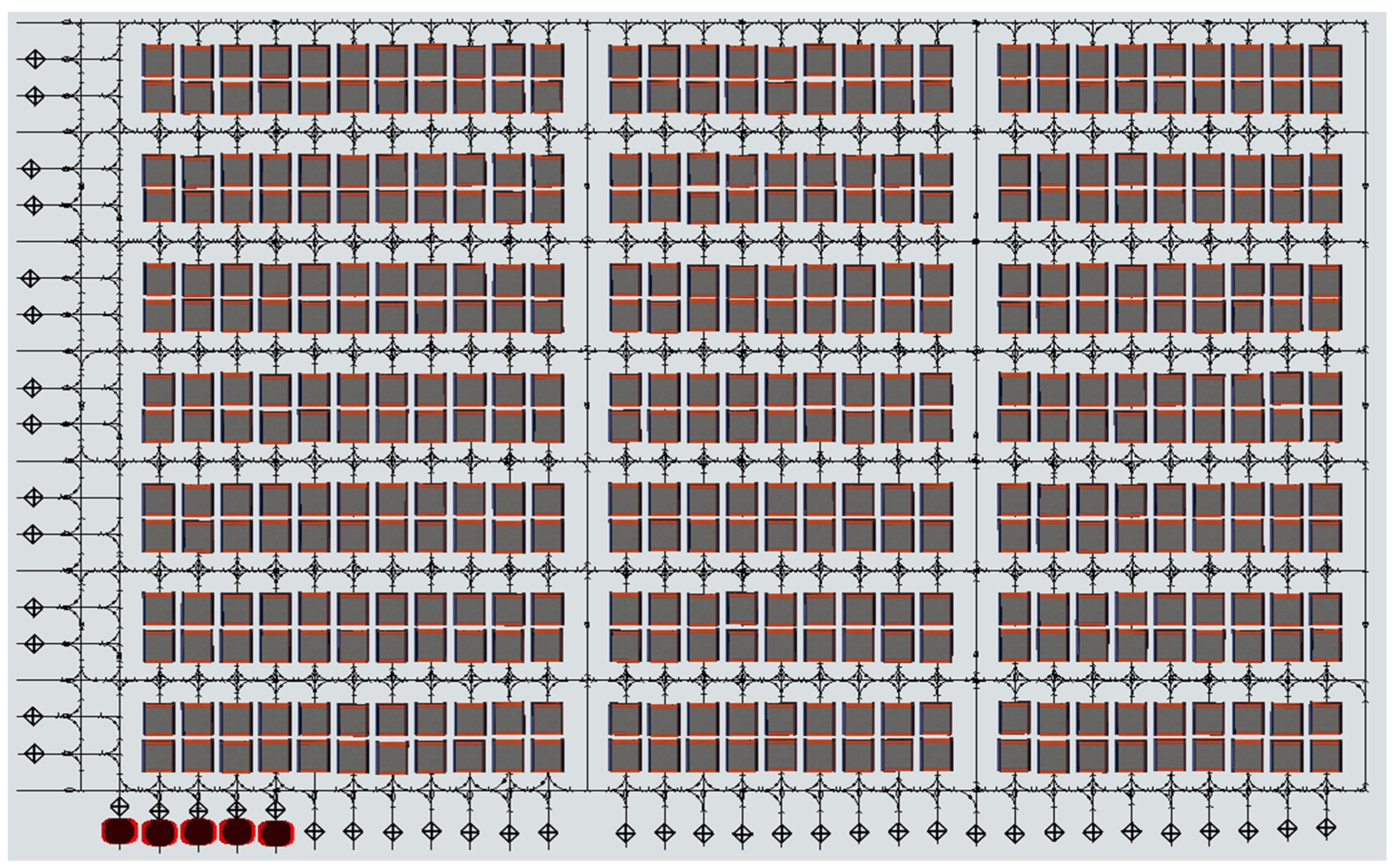
The intelligent warehouse model represented by a grid is adopted. The model’s environment is flexible and reconfigurable, as depicted in Figure 1. The grid map is divided into four sections:

(1)

The packing area, denoted as (i.e., $P=\{p_1,p_2,\dots \dots ,p_{30}\}$), is situated on the left-hand side of the map. Each packing station is staffed with a dedicated worker for efficient packaging operations.

(2)

The bidirectional channel consists of two adjacent rows or columns, while the single row or column channel only permits unidirectional traffic. Each AGV is required to adhere to the traffic rule of ’move on the right’.

(3)

The shelf area comprises individual shelves (i.e., $G=\{g_1,g_2,...,g_m\}$, where $m$ is the number of shelves), which can be moved independently and are transported to the packing station by AGVs. Once the packing task is completed, the AGV delivers the shelf to its nearest available location within a vacant shelf area. In absence of new orders, the AGV remains stationary directly beneath its assigned shelf.

(4)

The charging area, denoted as (i.e., $C\hspace{0.17em}=\{c_1,c_2,...,c_{33}\}$), is situated at the topmost part of the map. The AGV is obligated to return to the designated charging area once its battery level falls below 20%.

2.1. Working Characteristics of AGVs

As illustrated in Figure 2, a fleet of AGVs denoted by $R=\{r_1,r_2,...,r_n\}$, where $n$ represents the number of AGVs, are efficiently transporting shelves within the warehouse at a constant velocity v. Upon receiving task instructions, each AGV is capable of autonomously devising its own optimal route based on an individualized map, which is tailored to its unique starting and ending locations.

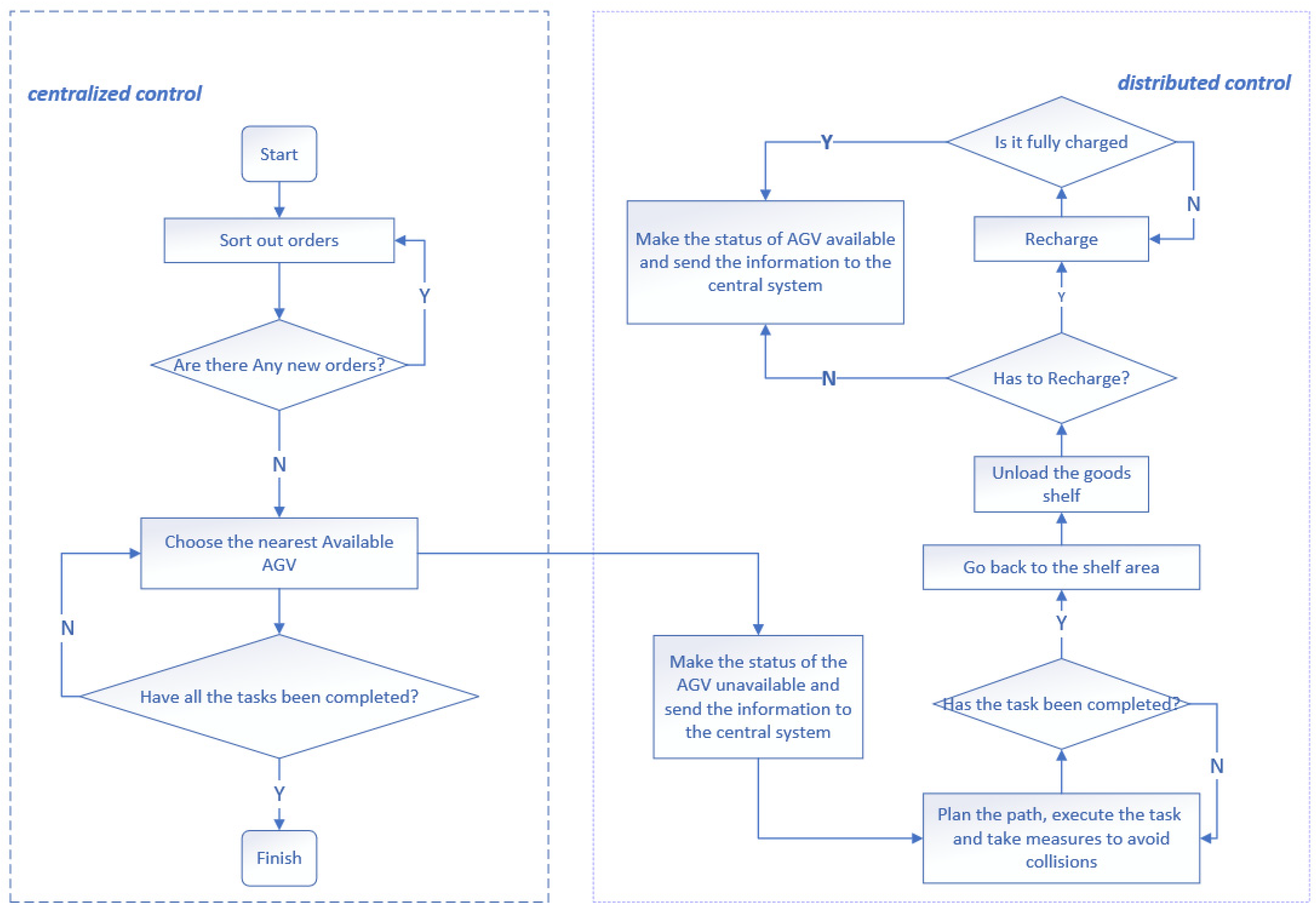
2.2. Centralized and Distributed Control Process

The proposed centralized and distributed control process for intelligent warehouse is illustrated in Figure 3.

Initially, the central processing system categorizes orders based on their time, location, type and other relevant information. Since this paper focuses primarily on bidirectional channel-based multi-AGV route planning methods, the orders are sorted according to the distance between the multi-AGV and target shelf. The central control system maintains and updates all location and status information. The order information will be transmitted to the central system in real time, containing details of the goods and their corresponding shelves. The central control system will calculate the distance between these shelves and all available AGVs before dispatching orders to the nearest idle AGV. Subsequently, the status of the assigned AGV becomes unavailable.

Then, the AGV plans its path and directly reaches the designated shelf location. At this point, the central control system transmits information regarding the nearest available picking station to the AGV while simultaneously updating the status of the packing station to ‘unavailable’. Once the AGV departs, the shelf station’s status returns to ‘available’. Once the AGV plans the path and completes the unloading, the status of the picking station becomes ‘available’. The central control system will transmit the location information of the nearest available shelf station to the AGV.

Once the AGV delivers the shelf to its destination, the corresponding shelf station will become ‘unavailable’. However, if an AGV has to meet certain conditions before charging, this may cause stagnation in warehouse logistics. If all AGVs operate simultaneously after being fully charged, they will reach the charging condition at roughly the same time due to their similar working time and power consumption speed. The aforementioned issue may arise when simultaneous charging occurs; hence, it is imperative to have multiple AGVs with the highest power capacity continue operations to prevent order backlog. Meanwhile, the remaining AGVs should return to the charging station upon task completion. The number of operational AGVs can be adjusted based on order generation speed.

The central control system discussed in this paper fulfills several key functions. First, it is responsible for storing and updating the location and status information of all devices. For instance, order information containing details about the goods and their corresponding shelves will be transmitted to the central control system. Second, the central control system will compute the distance between corresponding shelves and all available AGVs, subsequently dispatching orders to the nearest idle AGV in proximity to the said shelf. Third, the AGV plans its path and directly reaches the designated shelf location. At this point, the central control system transmits information regarding the nearest available picking station to the AGV. Upon departure of the AGV, the status of the shelf station will become ‘available’. Finally, once the AGV plans its path and completes the unloading process, the central control system will transmit the location information of the nearest available shelf station to the AGV.

3. Dynamic Map Design

The current research on multi-AGV route planning within warehouses predominantly employs unidirectional channels. While these channels may seem advantageous for space conservation purposes, their drawbacks are equally evident. For instance, as shown in Figure 4, when facing Situation A, AGV_1 will not remain stationary but instead execute a right turn directly based on the mathematical model of collision avoidance due to its prior arrival at the intersection. Consequently, deadlock inevitably occurs. In Situation B, congestion arises because AGV_1 has to wait for AGV_2 to enter the shelf area before proceeding, resulting in the immobilization of AGV_3–6 and significantly compromising transport efficiency.

Zhang (2018) [31] proposed a dynamic weighted map to indicate the level of congestion on each road, which enabled the route planner to avoid congested channels. However, this may result in suboptimal routes. When AGVs encounter highly congested destination areas, blockages and deadlocks are still likely to occur. To address this issue, this paper draws inspiration from real-world traffic and employs bidirectional channels for planning routes for multiple AGVs. However, previous research has shown that the implementation of the ‘move on the right’ rule presents a challenge for the A* algorithm, as it cannot automatically select the appropriate channel for AGVs. To address this issue, this paper proposes a solution based on dynamic maps. With this approach, each AGV will have its own independent map, which is dynamically updated to ensure compliance with traffic rules. According to the starting and ending points of AGVs, the algorithm dynamically sets up obstacles in the left channel of potential routes and utilizes the updated map as an input for route-planning algorithms to obtain optimal routes. The specific methodology is presented as follows:

(1)

Divide the map into different regions

According to the allocation of the shelf and packing areas, the entire warehouse is divided into multiple regular sub-areas, as shown in Figure 5. Each shelf area comprises several shelving stations with a size of 2*L. The sub-area is identified by its sequence number (m, n), where m represents the row number, and n represents the column number. The location of the packing area is designated as (0,0). It is noted that generalizations facilitate the modeling of a real warehouse, while Figure 5 serves to illustrate its operations and is exemplified by the inclusion of two numbers (29,38) to delineate the scope of the warehouse.

(2)

The basic rules of changing the map

The modification of the map should take into account three factors: the starting point, ending point and middle area. As AGVs strictly adhere to the traffic rule of ‘move on the right’, the left channels must be designated as obstacles. Assuming that the coordinate of the starting point is (x₁, y₁), then the sub-area sequence number for the starting point is (m₁, n₁). The set of new obstacle coordinates in the starting area can be obtained by Algorithm 1.

Algorithm 1. The set of new obstacle coordinates in the starting area
Input:    (x1, y1),(m1, n1)
Output:    map[a: b, c: d] = x
1:	if n1 = 0 then
2:	map[(y1 + 1):29,1] = 0
3:	map[0:(y1 − 1),2] = 0
4:	map[4k: (4k + 1), 2] = 1, k = 0, 1, 2, 3, 4, 5, 6, 7
5:	end if
6:	if m1 = 1 and n1 ≠ 0 then
7:	map[2:3, k(L + 1) + 1] = 0, k = 1, 2, 3
8:	map[0,3: (x1 − 1)] = 0
9:	map[1,(x1 + 1):35] = 0
10:	map[1,k(L + 1) + 1 : k(L + 1) + 2] = 1, k = 1, 2
11:	end if
12:	if 2 ≤ m1 ≤ 7 and n1 ≠ 0 then
13:	row = 2 + (m1 − 2)*4
14:	map[row: (row + 1),2 + k(L + 1)] = 0, k = 0, 1, 2, 3
15:	map[(row + 4): (row + 5), k(L + 1) + 1] = 0, k = 1, 2, 3
16:	map[(row + 2),3: (x1 − 1)]] = 0
17:	map[(row + 3), (x1 + 1):35]] = 0
18:	map[(row + q), k(L + 1) + 1: k(L + 1) +2] = 1, k = 1, 2; q = 2, 3
19:	end if
20:	if m1 = 8 and n1 ≠ 0 then
21:	map[26:27, k(L + 1) + 2] = 0, k = 0, 1, 2, 3
22:	map[28,3: (x1 − 1)] = 0
23:	map[29, (x1 + 1): 35] = 0
24:	map[28, k(L + 1) + 1: k(L + 1) + 2] = 1, k = 1, 2
25:	end if
26:	return map[a: b, c: d] = x

Note: map[a: b, c: d] = x indicates the assignment of rows from a to b and columns from c to d in the map to x. Obstacles are represented by 0, while channels are represented by 1.

Assuming that the coordinate of the ending point is (x₂, y₂), the sub-area sequence number for the ending point can be represented as (m₂, n₂). The set of new obstacle coordinates in the ending area can be obtained by Algorithm 2.

Algorithm 2. The set of new obstacle coordinates in the ending area
Input:    (x1, y1),(m1, n1)
Output:    map[a: b, c: d] = x
1:	if n2 = 0 then
2:	map[(y2 + 1):29,2] = 0
3:	map[0: (y2 − 1),1] = 0
4:	map[4k: (4k + 1), 2] = 1, k = 0, 1, 2, 3, 4, 5, 6, 7
5:	end if
6:	if m2 = 1 and n2 ≠ 0 then
7:	map[2: 3, k(L + 1) + 2] = 0, k = 0, 1, 2, 3,
8:	map[1,3: (x2 − 1)] = 0
9:	map[0,(x2 + 1):35] = 0
10:	map[1, k(L + 1) + 1 : k(L + 1) + 2] = 1, k = 1, 2
11:	end if
12:	if 2 ≤ m2 ≤ 7 and n2 ≠ 0 then
13:	row = 2 + (m2 − 2)*4
14:	map[row: (row + 1), k(L + 1) + 1] = 0, k = 1, 2, 3
15:	map[(row + 4): (row + 5),k(L + 1) + 2] = 0, k = 0, 1, 2, 3
16:	map[(row + 3),3: (x2 − 1)]] = 0
17:	map[(row + 2), (x2 + 1):35]] = 0
18:	map[(row + q), k(L + 1) + 1: k(L + 1) + 2] = 1, k = 1, 2; q = 2, 3
19:	end if
20:	if m2 = 8 and n2 ≠ 0 then
21:	map[26: 27, k(L + 1) + 1] = 0, k = 1, 2, 3
22:	map[29,3: (x2 − 1)] = 0
23:	map[28,(x2 + 1):35] = 0
24:	map[28, k(L + 1) + 1: k(L + 1) + 2] = 1, k = 1, 2
25:	end if
26:	return map[a: b, c: d] = x

The obstacles within the middle area can be strategically positioned in relation to the established starting and ending points as Algorithms 3-1–3-4.

Algorithm 3-1. The set of new obstacle coordinates the middle area
Input:    (m1, n1)
Output:    map[a: b, c: d] = x
1:	if n2 < n1 and m2 > m1 (The end point is at the top left of the start point, as seen in Figure 6) then
2:	if n2 ≠ 0 then
3:	for each i ∈ [m1 + 1 , m2 − 1] do
4:	a = 4*(i − 1)
5:	map[a,3 + k(L + 2): 3 + k(L + 2) + (L − 1)] = 0, k = 0, 1, 2
6:	map[(a − 2): (a − 1), k(L + 1) + 1] = 0, k = 1, 2, 3
7:	end for
8:	else if n2 = 0 then
9:	for each i ∈ [m1 + 1 , m2] do
10:	a = 4*(i − 1)
11:	map[a, 3 + k(L + 2): 3 + k(L + 2) + (L − 1)] = 0, k = 0, 1, 2
12:	map[(a − 2): (a − 1), k(L + 1) + 1] = 0, k = 1, 2, 3
13:	end for
14:	end if
15:	end if
16:	return map[a: b, c: d] = x

Algorithm 3-2. The set of new obstacle coordinates the middle area
Input:    (m1, n1)
Output:    map[a: b, c: d] = x
1:	if n2 < n1 and m2 < m1 (The end point is at the bottom left of the start point, as seen in Figure 7) then
2:	if n2 ≠ 0 then
3:	for each i ∈ [m2 + 1, m1 − 1] do
4:	a = 4*(i − 1)
5:	map[a,3 + k(L + 2): 3 + k(L + 2) + (L − 1)] = 0, k = 0, 1, 2
6:	map[(a + 2): (a + 3), k(L + 1) + 2] = 0, k = 1, 2, 3
7:	end for
8:	else if n2 = 0 then
9:	for each i ∈ [m2, m1 − 1] do
10:	a = 4*(i − 1)
11:	map[a, 3 + k(L + 2): 3 + k(L + 2) + (L − 1)] = 0, k = 0, 1, 2
12:	map[(a + 2): (a + 3), k(L + 1) + 2] = 0, k = 0, 1, 2, 3
13:	end for
14:	end if
15:	end if
16:	return map[a: b, c: d] = x

Algorithm 3-3. The set of new obstacle coordinates the middle area
Input:    (m1, n1)
Output:    map[a: b, c: d] = x
1:	if n2 > n1 and m2 > m1 (The end point is at the top right of the start point, as seen in Figure 8) then
2:	if n1 ≠ 0 then
3:	for each i ∈ [m1 + 1, m2 − 1] do
4:	a = 4*(i − 1) + 1
5:	map[a, 3 + k(L + 2): 3 + k(L + 2) + (L − 1)] = 0, k = 0, 1, 2
6:	map[(a + 1): (a + 2), k(L + 1) + 1] = 0, k = 1, 2, 3
7:	end for
8:	else if n1 = 0 then
9:	for each i ∈ [m1, m2 − 1] do
10:	a = 4*(i − 1) + 1
11:	map[a, 3 + k(L + 2): 3 + k(L + 2) + (L − 1)] = 0, k = 0, 1, 2
12:	map[(a + 1): (a + 2), k(L + 1) + 1] = 0, k = 1, 2, 3
13:	end for
14:	end if
15:	end if
16:	return map[a: b, c: d] = x

Algorithm 3-4. The set of new obstacle coordinates the middle area
Input:    (m1, n1)
Output:    map[a: b, c: d] = x
1:	if n2 > n1 and m2 < m1 (The end point is at the bottom right of the start point, as seen in Figure 9) then
2:	if n1 ≠ 0 then
3:	for each i ∈ [m2 + 1, m1 − 1] do
4:	a = 4*(i − 1) + 1
5:	map[a, 3 + k(L + 2): 3 + k(L + 2) + (L − 1)] = 0, k = 0, 1, 2
6:	map[(a − 3): (a − 2), k(L + 1) + 2] = 0, k = 1, 2, 3
7:	end for
8:	else if n1 = 0 then
9:	for each i ∈ [m2 + 1, m1] do
10:	a = 4*(i − 1) + 1
11:	map[a, 3 + k(L + 2): 3 + k(L + 2) + (L − 1)] = 0, k = 0, 1, 2
12:	map[(a − 3): (a − 2), k(L + 1) + 2] = 0, k = 1, 2, 3
13:	end for
14:	end if
15:	end if
16:	return map[a: b, c: d] = x

4. Route Planning

The A* algorithm is widely recognized as a best first heuristic algorithm, specifically designed for identifying optimal routes in grid environments. However, the conventional A* algorithm relies on static maps and primarily focuses on planning relatively short routes based solely on this information. As a result, it is only applicable to intelligent warehouses with unidirectional channels, where AGVs are mandated to exclusively move along the right-hand side (i.e., AGVs cannot meet the rule of ‘move on the right’). Additionally, the conventional A* algorithm solely accounts for route cost and disregards AGV travel time. Therefore, this paper proposes a dynamic map alteration algorithm based on the A* algorithm to enable the alteration of bidirectional channels in intelligent warehouses.

The proposed algorithm involves the following main steps:

(1)

Create two point sets: open list and close list. The open list is utilized to store potential route points, while the close list is used for those, which cannot be considered as such.

(2)

Search for eight adjacent grids surrounding the current grid.

(3)

Evaluate each grid. If the grid lies within the channel area and has not been added to either list, then its route cost $f\left(n\right)$ would be estimated.

(4)

Choose the grid with the lowest $f\left(n\right)$ value in the open list as the current point, and designate it as the parent node of the previous point before moving it to the close list.

(5)

Repeat steps (2)–(4) until the current point becomes the end point.

(6)

Starting from the end point, trace back each point’s parent node until arriving at the start point to obtain a satisfactory route.

The process for calculating the route cost $f\left(n\right)$ is presented as

$$f\left(n\right)\hspace{0.17em}=\hspace{0.17em}g\left(n\right)+h\left(n\right)$$

(1)

In Equation (1), $g\left(n\right)$ represents the actual cost of traversing from the starting point to grid $n$, given as

$$g\left(n\right)\hspace{0.17em}=g\left(n-1\right)+d/v_r$$

(2)

where $v_r$ denotes the velocity of AGV, and $d$ denotes the actual distance from the (n − 1)th grid to the nth grid. In general, $d$ equals 1 when the nth grid is located horizontally or vertically to the (n − 1)th grid, and $d$ equals 1.4 when the nth grid is positioned diagonally to the (n − 1)th grid.

In Equation (1), $h\left(n\right)$ is a heuristic function, representing the estimated cost of traveling from the current grid to the target grid, given as

$$h\left(n\right)\hspace{0.17em}=\hspace{0.17em}{d}_n/v_r$$

(3)

where $d_n$ is the Manhattan distance from the current grid to the target grid, presented as

$$d_n\hspace{0.17em}=\hspace{0.17em}abs\left(n\_x\hspace{0.17em}-\hspace{0.17em}goal\_x\right)\hspace{0.17em}+\hspace{0.17em}abs\left(n\_y\hspace{0.17em}-\hspace{0.17em}goal\_y\right)$$

(4)

As an illustration, three AGVs are concurrently in motion, and their respective travel paths are depicted in Figure 10.

5. Collision Avoidance

As the proposed method only allows for individual route planning of each AGV, collisions and deadlocks remain significant challenges in multi-AGV scheduling problems. Compared to unidirectional channel-based intelligent warehouses, bidirectional channel-based ones present a wider range of collision scenarios. This paper classifies collisions based on different road conditions and provides corresponding avoidance strategies accordingly.

To ensure collision avoidance, AGVs must establish communication and share their operational status with other AGVs, which may pose a conflict. By doing so, each AGV can integrate its own state with those of the surrounding AGVs and apply appropriate avoidance rules to take reasonable actions.

5.1. Collision Classification

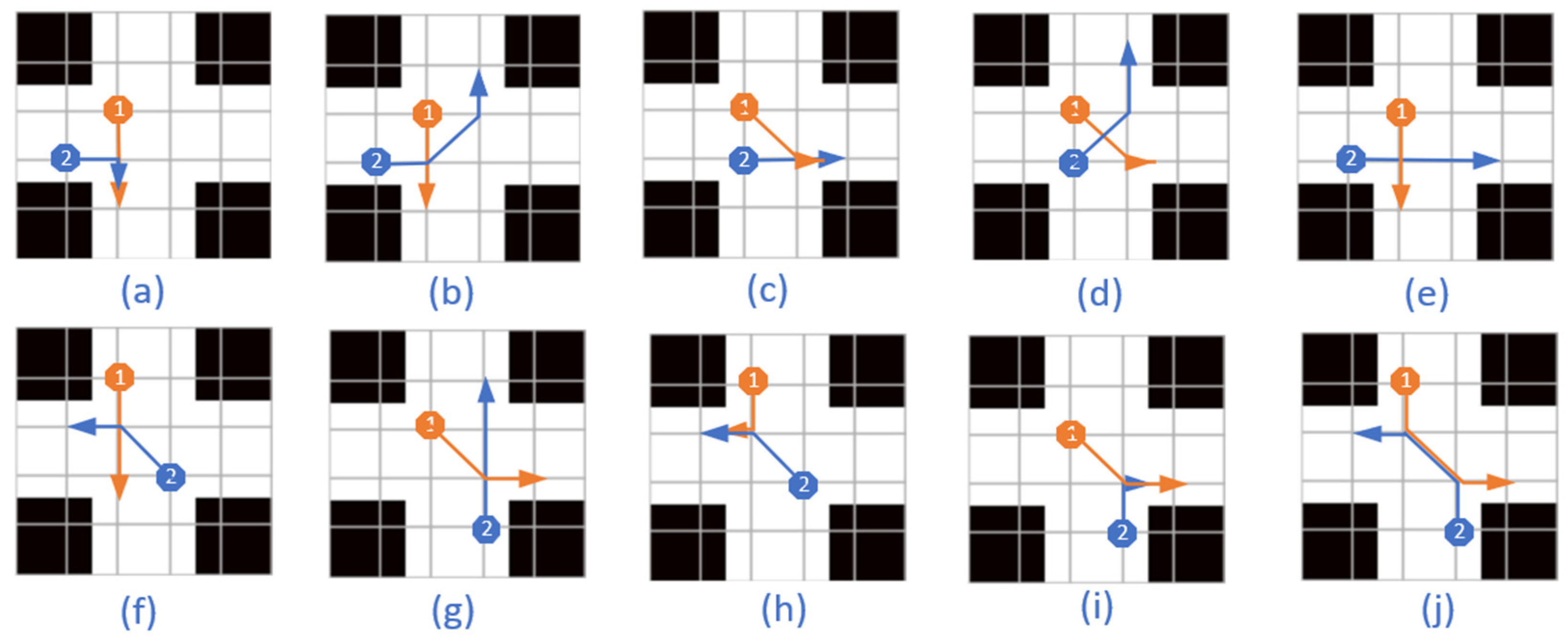
(1)

Collisions in crossroad

When two vehicles cross a junction simultaneously, they are susceptible to collisions. As illustrated in Figure 11, there exist 10 distinct collision scenarios. In cases (a)–(e), two AGVs approach from mutually perpendicular channels, while in cases (f)–(j), two AGVs approach from parallel but opposing channels. In case (j), collisions occur on the route between two nodes rather than at the nodes themselves. In all other scenarios, collisions occur directly at the nodes. When two AGVs approach a crossroad from opposite directions, their relative positions and collision scenarios remain consistent. Therefore, this paper only presents one representative case for each collision scenario in the analysis.

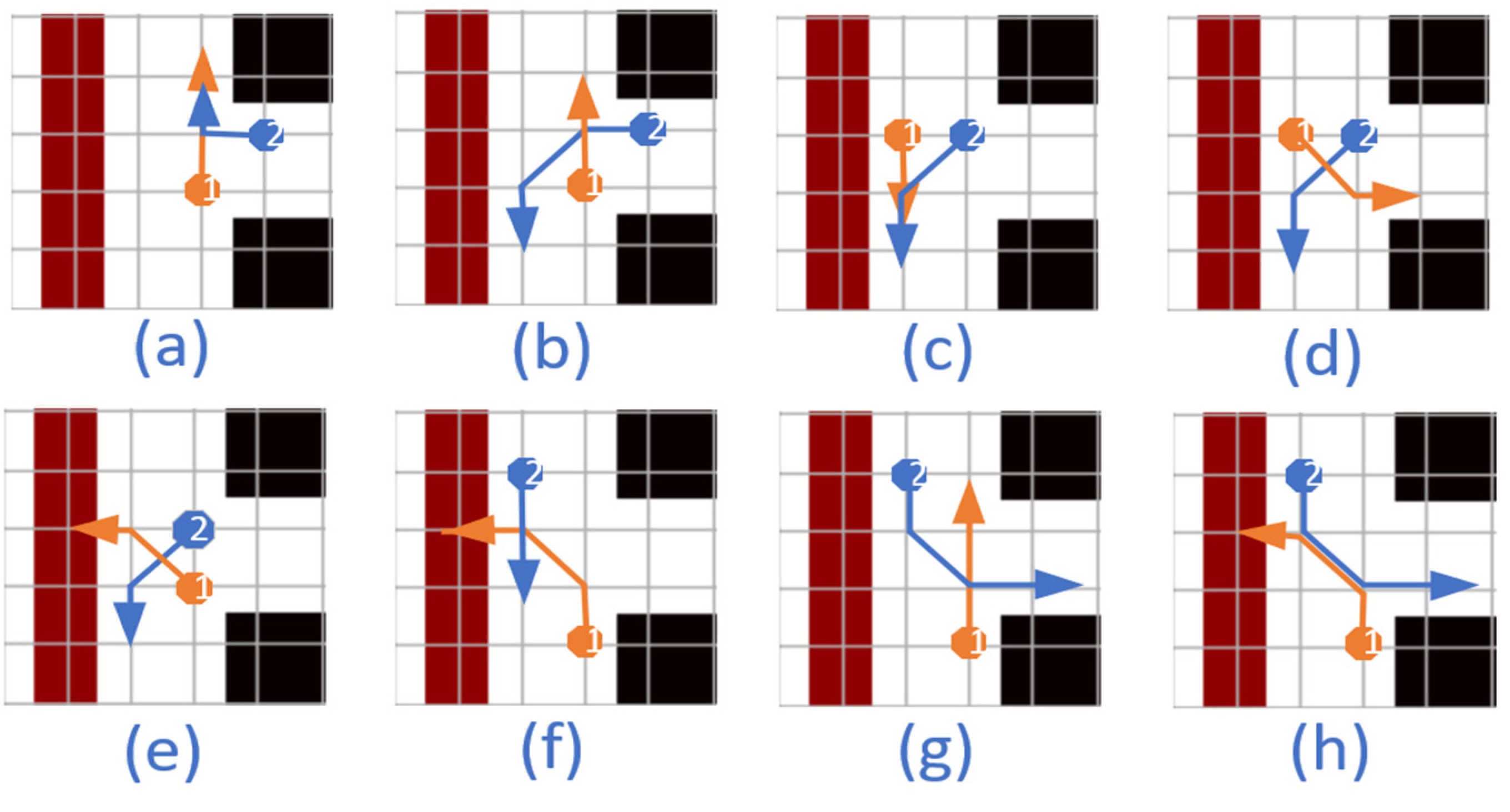
(2)

Collisions in T-crossroad

The T-crossroad is situated at the periphery of the warehouse, which also happens to be a high-risk zone for collisions. As depicted in Figure 12, there exist eight distinct collision scenarios. In cases (a)–(e), two AGVs approach from the transverse and longitudinal channel, respectively, while in cases (f)–(h), both AGVs approach from the longitudinal channel. In cases (a)–(c) and (f)–(g), one AGV proceeds straight while the other turns; in cases (d)–(e) and (h), both AGVs turn. The T-crossroad depicted in Figure 12 is situated on the leftmost edge of the warehouse. As the collision patterns at T-crossroads located on different edges are identical, this paper only presents one case for collision analysis.

(3)

Collisions in bidirectional channel

Under normal circumstances, bidirectional channels do not result in collisions. However, when an AGV returns to the channels from a non-channel area (such as charging, packing or shelf areas) or needs to traverse reverse channels into non-channel areas on the opposite side, conflicts may arise with AGVs moving along the corresponding channels. As illustrated in Figure 13, there exist eight distinct collision scenarios. In cases (a)–(d), one AGV proceeds straight while the other turns; in cases (e)–(h), both AGVs turn. In cases (a)–(c) and (e)–(g), one AGV enters the channel from a non-channel area; in cases (d) and (h), at least one AGV enters a non-channel area from the channel. Given that the collision scenarios are identical across different non-channel areas, this paper solely analyzes bidirectional channels within shelf areas.

5.2. Collision Detection

The following symbols are quoted for the purpose of providing a clear explanation.

(1)

$C_m^n$ denotes the coordinate of a node with sequence number m in the route of the AGV_n. It should be noted that the same node may have different serial numbers for different AGVs. For example, if node x exists both in the route of AGV₁ and AGV₂, its sequence number in the route of AGV₁ is $\alpha$, while its sequence number in the route of AGV₂ is $\beta$. Hence, for AGV₁, the coordinate of node x is $C_{\alpha }^1$; for AGV₂, the coordinate of node x is $C_{\beta }^2$. Notably, $C_{\alpha }^1$ equals to $C_{\beta }^2$ in this scenario. Moreover, $C_{\alpha +1}^1$ denotes the next node after the target node with sequence number α on the route of AGV₁, while $C_{\alpha -1}^1$ represents its preceding node.

(2)

${\tau }_m^n$ represents the arrival time of AGV_n at the node with sequence number $m$ in its route.

(3)

$t_m^n$ represents the processing time required for AGV_n on the node with sequence number $m$ in its route.

In this paper, collisions are detected across three distinct road conditions, presented as follows.

(a)

In Figure 11, the collisions in cases (a)–(c) and (e)–(i) occur on the nodes. These collisions will occur if conditions (5)–(6) are met.

$$|{\tau }_{\alpha }^1-{\tau }_{\beta }^2|\le \delta$$

(5)

$$C_{\alpha }^1=C_{\beta }^2$$

(6)

where $\delta$ represents the time window for collision. The value of $\delta$ is dependent on the velocity and size of the AGV, as well as the angle between their respective velocity directions.

The collision in case (j) occurs between two nodes. The route points with sequence numbers $\alpha$ and $\alpha$ + 1 of the AGV₁ correspond to those with sequence numbers $\beta +1$ and $\beta$ of the AGV₂. If conditions (7)–(9) are satisfied, the collision in case (j) will occur.

$$|{\tau }_{\alpha }^1-{\tau }_{\beta }^2|\le \delta$$

(7)

$$C_{\alpha +1}^1=C_{\beta }^2$$

(8)

$$C_{\alpha }^1=C_{\beta +1}^2$$

(9)

The collision in case (d) occurs between two nodes. The route points with sequence numbers $\alpha$ and $\alpha$ + 1 of the AGV₁ do not correspond to the route points with sequence numbers $\beta +1$ and $\beta$ of the AGV₂. If conditions (10)–(11) are satisfied, the collision in case (d) will occur.

$$|{\tau }_{\alpha }^1-{\tau }_{\beta }^2|\le \delta$$

(10)

$$(C_{\alpha +1}^1\hspace{0.17em}+\hspace{0.17em}{C}_{\alpha }^1)/ 2=(C_{\beta +1}^2\hspace{0.17em}+\hspace{0.17em}{C}_{\beta }^2)\hspace{0.17em}/2$$

(11)

(b)

In Figure 12, the collisions in cases (a)–(c) and (f)–(g) occur at the nodes. If the above Equations (5) and (6) are satisfied, the collisions in cases (a)–(c) and (f)–(g) will occur. The collisions in cases (d)–(e) occur between two nodes. The route points with sequence numbers $\alpha$ and $\alpha$ + 1 of the AGV1 do not correspond to the route points with sequence numbers $\beta +1$ and $\beta$ of the AGV2. If the above Equations (10) and (11) are satisfied, the collisions in cases (d)–(e) will occur. The collision in case (h) occurs between two nodes. The route points with sequence numbers $\alpha$ and $\alpha$ + 1 of the AGV1 correspond to the route points with sequence numbers $\beta +1$ and $\beta$ of the AGV2. If conditions (7)–(9) are satisfied, the collision in case (h) will occur.

(c)

In Figure 13, the collisions in cases (a)–(d) and (g) occur at the nodes. If the above Equations (5) and (6) are satisfied, the collisions in cases (a)–(c) and (g) will occur. The collisions in cases (e)–(f) occur between two nodes. The route points with sequence numbers $\alpha$ and $\alpha$ + 1 of the AGV1 do not correspond to the route points with sequence numbers $\beta +1$ and $\beta$ of the AGV2. If the above Equations (10) and (11) are satisfied, the collisions in cases (e)–(f) will occur. The collision in case (h) occurs between two nodes. The route points with sequence numbers $\alpha$ and $\alpha$ + 1 of the AGV1 correspond to the route points with sequence numbers $\beta +1$ and $\beta$ of the AGV2. If conditions (7)–(9) are satisfied, the collision in case (h) will occur.

5.3. Collision Solution Strategies

When a collision is detected, different collision avoidance strategies are adopted according to different road conditions. Thus, it is vital to determine the road conditions where the collisions occur.

There are several coordinate sets introduced, as seen in Figure 14, given as follows:

(1)

R represents the coordinate collection of the crossroads;

(2)

T represents the coordinate set of the T-crossroads;

(3)

N represents the coordinate set of the non-channel areas, including the shelf area, the packing area and the charging area;

(4)

H represents horizontal channels, excluding the area of crossroads and T-crossroads;

(5)

L represents the longitudinal channels, excluding the area of crossroads and T-crossroads.

For the collision avoidance strategy under three road conditions, due to the poor continuity of the longitudinal channel, if three AGVs are waiting for the longitudinal channel in a row, the AGVs on the horizontal channel should go first; then, the AGVs on the next longitudinal channel have to wait, which means that this condition will conflict with the strategy itself. The contradiction between two strategies will inevitably lead to deadlock. Thus, when two AGVs come from the horizontal and longitudinal channels, respectively, the AGV priority strategy in the longitudinal channel is usually adopted.

(1)

When a collision is detected and Equation (12) is satisfied, the collision in Figure 11 occurs.

$$C_{\alpha }^1\hspace{0.17em},C_{\beta }^2\hspace{0.17em}\hspace{0.17em}\subseteq \hspace{0.17em}R$$

(12)

$$C_{\alpha -2}^1\hspace{0.17em}\subseteq \hspace{0.17em}H\cap C_{\beta -2}^2\hspace{0.17em}\subseteq \hspace{0.17em}L\hspace{0.17em}or\hspace{0.17em}{C}_{\alpha -2}^1\hspace{0.17em}\subseteq \hspace{0.17em}L\cap C_{\beta -2}^2\hspace{0.17em}\subseteq \hspace{0.17em}H$$

(13)

$$C_{\alpha -2}^1\hspace{0.17em}\subseteq \hspace{0.17em}H\cap \hspace{0.17em}{C}_{\beta -2}^2\hspace{0.17em}\subseteq \hspace{0.17em}H\hspace{0.17em}or\hspace{0.17em}{C}_{\alpha -2}^1\hspace{0.17em}\subseteq \hspace{0.17em}L\cap \hspace{0.17em}{C}_{\beta -2}^2\hspace{0.17em}\subseteq \hspace{0.17em}L$$

(14)

When Equation (13) is satisfied, this means that the two AGVs come from the horizontal and longitudinal channels, respectively. If AGV₁ travels horizontally and AGV₂ travels longitudinally, the strategy adopted in this case is as follows: If $C_{\alpha -1}^1\hspace{0.17em}\subseteq \hspace{0.17em}H$, then AGV₁ waits at waypoint $\alpha -1$ until AGV₂ passes through the collision point; if $C_{\alpha -1}^1\hspace{0.17em}\not\subset \hspace{0.17em}H$, then AGV₁ waits at waypoint $\alpha -2$ until AGV₂ passes through the collision point.

When Equation (14) is satisfied, this means that both AGVs are on the horizontal or longitudinal channel. The strategy adopted in this case is to compare the values of ${\tau }_{\alpha +1}^1$, ${\tau }_{\beta +1}^2$. If ${\tau }_{\alpha +1}^1$ > ${\tau }_{\beta +1}^2$, the time for AGV₂ to pass through the collision point is relatively short. Then, AGV₁ waits at waypoint $\alpha -1$ until AGV₂ passes through the collision point.

(2)

When a collision is detected and Equation (15) is satisfied, the collision in Figure 12 occurs.

$$C_{\alpha }^1\hspace{0.17em},C_{\beta }^2\hspace{0.17em}\hspace{0.17em}\subseteq T$$

(15)

$$C_{\alpha -2}^1\hspace{0.17em}\subseteq \hspace{0.17em}L\cap \hspace{0.17em}{C}_{\beta -2}^2\hspace{0.17em}\subseteq \hspace{0.17em}L$$

(16)

When Equation (16) is satisfied, this means that both AGVs are on the longitudinal channel. The strategy adopted in this case is to compare the value of ${\tau }_{\alpha +1}^1$, ${\tau }_{\beta +1}^2$. If ${\tau }_{\alpha +1}^1$ > ${\tau }_{\beta +1}^2$, the time for AGV₂ to pass through the collision point is relatively short. Then, AGV₁ waits at waypoint $\alpha -1$ until AGV₂ passes through the collision point.

(3)

When a collision is detected and Equation (17) is satisfied, the collision in Figure 13 occurs.

$$C_{\alpha }^1\hspace{0.17em},C_{\beta }^2\hspace{0.17em}\hspace{0.17em}\subseteq H\hspace{0.17em}or\hspace{0.17em}L$$

(17)

$$C_{\alpha }^1\subseteq N or C_{\beta }^2\subseteq N$$

(18)

When Equation (18) is satisfied, this means that one AGV is in the non-channel area, and the other is moving on the channel. If AGV₁ is in the non-channel area, the strategy adopted in this case is as follows: AGV₁ waits where it is until AGV₂ passes through the collision point.

When Equation (14) is satisfied, this means that both AGVs are on the horizontal or longitudinal channel. The strategy adopted in this case is to compare the value of ${\tau }_{\alpha +1}^1$, ${\tau }_{\beta +1}^2$. If ${\tau }_{\alpha +1}^1$ > ${\tau }_{\beta +1}^2$, the time for AGV₂ to pass through the collision point is relatively short. Then, AGV₁ waits at waypoint $\alpha -1$ until AGV₂ passes through the collision point.

6. Simulation Experiments

The advanced discrete event simulation software FlexSim, developed by FlexSim Software Products, Inc., is renowned for its expertise in simulating and optimizing complex systems within the manufacturing, logistics and supply chain management domains. With its intuitive user interface, robust modeling capabilities and extensive customization options, FlexSim empowers users to effectively analyze and enhance the performance of intricate systems. In this paper, Flexsim2019 is used for simulation experiments, and the proposed route-planning method is compared with the scheduling method based on the unidirectional channel. The simulation experiments are designed as follows:

(1)

The total number of shelves is 406, with each shelf handling one order at a time.

(2)

The system simultaneously dispatches 50, 100, 150, 200, 250 orders, which are randomly distributed across the shelves. There are a total of 10 AGVs in the warehouse.

(3)

Both models have identical AGV velocities.

(4)

The residence time of AGVs in the packing area remains consistent at 10 s.

(5)

The system releases batches of 50 orders simultaneously while varying the number of AGVs between models to include options such as 5, 10, 15 and 20.

The simulation results for different intelligent warehouse models are illustrated as below, which proves that the bidirectional channel can effectively improve the operating efficiency of AGVs in the intelligent warehouse.

(1)

Figure 15 shows the intelligent warehouse based on bidirectional channels. The control system sends out the order information and selects the available AGV nearest to the target shelf. The AGV becomes unavailable after taking the order and goes to the target shelf from the bottom control point. Meanwhile, the status of the target shelf becomes unavailable. The AGV selects the packing station nearest to itself, changes the status of the station to unavailable and plans the route. After arriving at the packing station, the AGV stays for 10 s and then leaves back to the nearest available shelf area. The status of the packing station becomes available. After the AGV is unloaded from the shelf, the status of the shelf and the AGV itself become available. The AGV waits under the shelf until it receives a new task again.

(2)

Figure 16 shows the intelligent warehouse based on the unidirectional channel, and its scheduling principle is the same as that of the intelligent warehouse based on the bidirectional channel.

(3)

Figure 17 shows the total time consumed by the AGVs to complete all the orders in two different types of warehouses. The number of AGVs in both types of warehouses is 10, and the number of orders is 50, 100, 150, 200 and 250. In general, the total working time for the AGVs in two types of warehouses increases with the increase in the order number, but the warehouse based on the bidirectional channel can save nearly a quarter of the time. It is obvious that the bidirectional channel can greatly improve the operating efficiency of the intelligent warehouse.

(4)

Figure 18 shows the total time taken by the AGVs to complete 50 orders in two different types of warehouses. The number of AGVs is 5, 10, 15 and 20. Generally, the time required for the AGVs to complete the task decreases with the increase in the number of AGVs. Compared with the unidirectional channel, the bidirectional channel can effectively reduce the processing time of the AGVs. However, when the number of AGVs reaches a certain value, the decrease in the time required for the AGVs to complete the orders will slow down. Because the number of AGVs increases, the blocking degree and waiting time for AGVs also increase. Therefore, it is necessary to adjust the number of AGVs according to the size of the warehouse in order to make a more rational use of the resources.

(5)

To demonstrate the efficiency of AGVs when orders are concentrated in a small area, all the orders are generated in the shelf area in the lower left corner. Figure 19 shows the total time required by AGVs to complete different orders in two different types of warehouses. The numbers of orders are 10, 15, 20, 25, 30, 35 and 40, and the number of AGVs is 10. Generally, the time required for the AGVs to complete the task increases with the increased orders. Compared with the unidirectional channel, the bidirectional channel can effectively reduce the processing time of the AGVs. When all AGVs work in a small area at the same time, congestion in the unidirectional channel increases significantly with the increase in orders, which is demonstrated by the derivative of the upper line in Figure 19. In this case, the advantage of the bidirectional channel can be well displayed.

7. Conclusions and Future Work

The primary contribution of this paper lies in dynamically constraining the grid map and utilizing the updated map as an input to the A * algorithm, thereby obtaining an optimized route, which enhances efficiency, reduces costs and conserves resources. The dynamic scheduling optimization method proposed in this paper enables the implementation of the ‘move on the right’ traffic rule in AGVs, which is not achievable using traditional algorithms. The utilization of the bidirectional channel can effectively address both deadlock and congestion issues, thereby significantly enhancing the overall efficiency of AGVs. In order to address the challenges posed by bidirectional channels in collision avoidance problems, this paper thoroughly examines all collision scenarios and proposes corresponding strategies for each scenario. This approach enhances the alignment of this scheduling optimization method with real-world traffic situations. Through simulation experiments, the results demonstrate the high feasibility and efficiency of achieving a sophisticated level of intelligent driving.

Future research will focus on investigating the potential unnecessary pauses of AGVs during turning in order to optimize the path planning. Additionally, there will be an expansion of the warehouse model from 2D to 3D to enhance its storage space utilization.