NativeVRF: A Simplified Decentralized Random Number Generator on EVM Blockchains

Abstract

Smart contracts refer to small programs that run in a decentralized blockchain infrastructure. The blockchain system is trustless, and the determination of common variables is done by consensus between peers. Developing applications that require generating random variables becomes significantly challenging—for instance, lotteries, games, and random assignments. Many random number generators (RNGs) for smart contracts have been developed for the decentralized environment. The methods can be classified into three categories: on-chain RNG, Verifiable Random Function (VRF), and the Commit–reveal scheme. Although the existing methods offer different strengths and weaknesses, none achieves the three important requirements for an ideal RNG solution: security, applicability, and cost efficiency. This paper proposes a novel RNG approach called Native VRF, which offers application development simplicity and cost efficiency while maintaining strong RNG security properties. Experimental results show that Native VRF has the same security properties as the widely used RNG methods, i.e., Randao and Chainlink VRF. On top of that, our work offers a much simpler setup process and lower hardware resources and developer expertise requirements. Most importantly, the proposed Native VRF is compatible with all Ethereum virtual machine (EVM) blockchains, contributing to the overall growth of the blockchain ecosystem.

1. Introduction

A random number generator (RNG) is essential in developing applications, such as gaming [1], and gambling [2] applications, that ensure fair distribution of resources and rewards [3]. These activities accumulate a huge amount of value. The non-fungible token (NFT) market and blockchain gaming market value surpassed $44 million, according to Chainalysis report [4]. NFTs are randomly generated and transferred to people who pay to create them. People obtain NFTs with different rarities affecting their prices on the market. Pooltogether, a blockchain-based lottery system, earns over $10 million per week from users worldwide1. It randomly distributes over $8000 weekly rewards for participants. More importantly, the Ethereum Proof-of-Stake (POS) consensus algorithm randomly selects a miner to record data on-chain. The blockchain relies on a decentralized RNG to maintain network security. The Ethereum market cap accumulates $585 billion over the network. Regarding the huge amount of value on the distributed network, a strong RNG is necessary to maintain its security. The loss is tremendous if the network cannot generate truly random numbers.

A smart contract refers to a collection of distributed software programs that is independently responsible for its own verification and execution while being resistant to tampering. Using the smart contract, developers can offer fewer intermediaries, lower costs, and new business or operational models [5]. Generating truly random numbers in the smart contract needs to ensure the fairness and security of the applications [5,6,7]. However, generating true random numbers in a blockchain is challenging. This is because a blockchain is a decentralized and trustless environment where the random number generation can easily be manipulated or biased by any party in the network. To address the aforementioned issues, various approaches have been proposed for generating pseudo-random numbers in smart contracts, for example, public randomness source [8], random zoo [9], and randomness beacons [10].

This paper classifies existing RNG approaches into three categories. In the first category are on-chain RNGs, utilizing the naïve approach, and relying on sources of randomness available on the blockchain. This method does not require any external sources of randomness and can be implemented in a decentralized manner. The widely used method in this category is ERC721R [11], used in an NFT collection called Mphers. However, it has been exploited using a smart contract brute force technique, where the attacker generates multiple smart contracts to inject random inputs and guarantees minting a rare Mphers [12].

The second category consists of RNGs employing a cryptographic technique, called a verifiable random function (VRF). Chainlink VRF [13] is the most used implementation in this category. The verifiable off-chain random source makes Chainlink VRF more secure than the on-chain RNG. It allows a prover to demonstrate to a verifier that a given output was generated randomly without revealing the output itself. This solution is widely used in many applications as a trusted, decentralized RNG, such as in [3,14,15,16,17]. However, developing applications using Chainlink VRF requires high technical expertise because of the complexity and system requirements. Most importantly, no guideline for adding new networks on Chainlink VRF is provided. This makes it challenging to scale to other new blockchains. Hence, an alternative developer-friendly, yet secure, RNG technique is required.

The third category is that of the Commit–reveal scheme, which is one of the most used RNG methods, and can be implemented natively on-chain. This method does not require external data to be fed into the networks. Randao [18] is an instance of the Commit–reveal scheme RNG, where participants “commit” a hash value to the Randao smart contract and then reveal an actual value later. In other words, people can directly and easily feed seed numbers to the Randao smart contract. This allows random numbers to be generated in a decentralized manner. Randao offers certain benefits. Firstly, it does not rely on any organization or development team. Secondly, there is no system requirement or complicated setup to be prepared before joining it. Hence, it is easy to adopt and scale to new blockchains. However, Randao’s significant limitation is the cost-efficiency issue. Computing a random number using the Randao method invokes many transactions. Thus, it is considered an expensive method compared to the others.

This paper proposes a novel approach to address the limitations of the three most widely used RNG techniques, namely ERC721R, Chainlink VRF, and Randao. Specifically, the proposed approach is a decentralized Native VRF RNG that employs a verifiable random function to ensure security and simplifies the participation process to reduce complexity. The native in this context means the system does not rely on external infrastructure to generate random numbers. An example of a non-native RNG is Chainlink VRF, which requires the Chainlink network as the external trusted source of information. The primary objectives of the study are the following: (i) to mitigate the security issue associated with ERC721R, (ii) to alleviate the complexity issue of Chainlink VRF, and (iii) to reduce the overhead cost issue of Randao. The efficacy of the proposed method is evaluated based on three criteria: security, applicability, and cost efficiency. The contributions of this work are as follows:

(i)

Classify the decentralized random methods most commonly used by famous platforms (Section 2.4).

(ii)

Propose the novel Native VRF method that achieves a high-security property, is practical for developers, and is cost-effective (see Section 3).

(iii)

Give insight analysis of random functions in a smart contract in Section 5.

(iv)

Provide an implementation framework from our proposed solution on Github2. Our Native VRF framework can be implemented on any Ethereum virtual machine (EVM) compatible chain. It does not need any technical support to be adopted. Developers can use the example source code provided in this paper to apply this framework.

The rest of this paper is organized as follows. Section 2 discusses the state-of-the-art and related issues. We explain Native VRF in Section 3. Section 4 describes our testing methodology and how we measured the results. The testing results are then analyzed in Section 5. Finally, we conclude the work in Section 6.

2. Literature Review

This section discusses related works from industry and academia. Firstly, our research methodology for selecting benchmark RNGs is presented in Section 2.1. Then, we compare centralized against decentralized RNGs in Section 2.2. In Section 2.3, we investigate many RNG incidents and analyze the severity of RNG attacks. To understand the state-of-the-art decentralized RNGs, we study existing RNGs widely used to date and examine their strengths and weaknesses in Section 2.4.

2.1. RNG Benchmark Selection

Various sources from educational and industrial domains were studied to identify the most used RNG methods in different categories. Since decentralized RNG was in an early stage, we found a limited number of published research articles. Chatterjee et al. [19] categorize the state-of-the-art into three groups: (1) using on-chain block hash and time stamp (on-chain RNG), (2) using an oracle source, and (3) using the Commit–reveal scheme. In regard to the first category, Wang et al. [20] stated that ERC721R is the main implementation of the on-chain RNG. It has also been deployed in production, such as in [12,21]. Meanwhile, Chainlink VRF is mentioned by researchers [22,23] as a trusted oracle RNG source. Many decentralized applications [3,13,14,15] utilize Chainlink VRF as a core RNG. On the other hand, Randao is an implementation classified as a Commit–reveal scheme RNG by several research works [9,10,19]. Randao is also used as a base implementation for the Ethereum proof of stake miner selection process, as mentioned in [18]. Hence, we chose these RNG methods (i.e., ERC721R, Chainlink VRF, and Randao) to benchmark our proposed work in this paper.

2.2. Centralized versus Decentralized Random Number Generators

General RNGs have been used in a centralized environment for decades and, hence, various random number algorithms are proposed for multiple domains, including network security, electronics and mechanics [24,25,26,27]. Several RNG methods aim to provide high data throughput [28,29,30], while ensuring at least similar security and simplicity. These algorithms work fine in the off-chain environment, where private data (i.e., seed) can be easily protected.

On the other hand, generating random numbers in a decentralized environment can be challenging as developers need to ensure that the input values used for the RNG are truly random and not predictable or biased by peers in the distributed network. Many RNG approaches for the distributed context have been proposed and implemented in real-world applications, such as [1,2,3]. Unfortunately, the general RNG approach cannot guarantee the trust, integrity, verifiability, and availability required in the distributed applications, particularly EVM blockchains, emphasized in this paper.

2.3. Attacks on the Decentralized Random Number Generator

RNG vulnerabilities can cause severe damage to the Ethereum ecosystem [31], especially when the system accumulates high values. NFT random distribution is a typical case that holds a high value. According to Chainalysis research [4], the sales volume of the NFT market reached $44 billion in 2022. An important incident on NFT random mining occurred in a project called Meebits, developed by a famous team, LavarLab. During the incident, $765,000 worth of NFT was accidentally exploited using the random brute force attack3. Meebits was launched on 3 May 2021. It contains 20,000 unique 3D characters, which can be created (i.e., minting) in two ways: (i) community minting with CryptoPunks NFT, and (ii) normal minting with Ethereum coins (ETH). Meebits minting involves an on-chain random function, which obtains on-chain data to generate a random number, as depicted in Figure 1.

Unfortunately, the Meebits platform was exploited ove4r thye period 3–9 May 2021. The exploit occurred in the community minting. The cause of the incident was that Meebits rarities are publicly visible, and random function relies on on-chain data. These facts allowed an attacker to pre-compute the result using a smart contract. The attacker deployed the contract containing brute-force minting and reverted if they could not get the desired Meebits. In this incident, the attacker used the #4466 CryptoPunks to mint the rare #16647 Meebits, sold for 200 ETH ($765,000 worth over the attacking period).

A similar case also happened to the Mphers NFT collection [12] and Cryptogs [32]. Mphers NFT collection contains 6969 unique characters. There are eight rare characters among them. People pay Ethereum coins to pick an NFT character from the pool randomly. The process is on-chain and treated as true randomness. Unfortunately, an attacker exploited Mphers by means of brute-force random inputs to obtain the rare Mphers. After the incident, developers improved ERC721R implementation by preventing function invocation from a smart contract. Only an externally owned address (EOA), i.e., an account controlled by a private key, most used in a crypto-wallet, can call the ERC721R smart contracts. This workaround makes ERC721R more difficult to attack. However, it is still breakable by dishonest miners if the reward is high enough for them. These incidents demonstrate that an on-chain random function is vulnerable. Although many on-chain RNG solutions have been invented since the early stages of blockchain development, only a few are adapted and considered secure methods.

2.4. A Comparison of Blockchain-Based Random Number Generation Methods

Figure 2 compares the strengths and weaknesses of the three existing methods that are widely used, as well as those of our proposed solution in this paper. The up (↑) and down (↓) arrows demonstrate strengths and weaknesses, whereas the dash (–) refers to common attributes. The methods ERC721R, Chainlink VRF, and Randao are commonly used in real-world applications. However, they differ in the ways they generate random numbers. Firstly, ERC721R is the simplest and cheapest method [11]. It is suitable for small and low-value transactions. Using ERC721R with high-value applications is not recommended as it could lead to severe damage, such as the damage that ensued form the incidents mentioned earlier in Section 2.3. Second, Chainlink VRF is the most popular RNG method, used by many applications in the production stage. It is usually the first option developers choose when RNG is necessary in a smart contract. While producing random numbers from Chainlink VRF is very simple, participating in the Chainlink network requires advanced technical skills, hardware requirements, and costly collateral [13]. This makes Chainlink VRF hard to scale in new blockchains due to the barrier for entry-level participants. Another high-security RNG, which is considered a native solution, is Randao [18]. It allows interested participants to join random number generation without hardware requirements. This method can be deployed in any blockchain without a complex setup. However, Randao incorporates many transactions to generate a random number. This makes Randao an expensive method compared to Chainlink VRF. Lastly, our proposed Native VRF method preserves high security and simplicity, while maintaining moderate cost efficiency.

2.4.1. On-Chain Based Methods

The simplest way to generate a random number on-chain is to compute a hash of blockchain data, such as smart contract states, timestamps, block numbers, and block hashes. The ERC721R standard [11] extends the NFT random minting standard and utilizes on-chain metadata to produce random numbers. This process involves processing hash data using the keccak256 function, which obtains byte data parameters (see Figure 3).

Although this function produces a seemingly random number, it is not truly random because the block hash is deterministic depending on the contents of the block. The incident referred to in Section 2.3 highlights a vulnerability in ERC721R, exploited by the attacker using brute force to revert transactions until the desired random result was obtained. To mitigate this vulnerability, the ERC721R standard was upgraded to disallow smart contracts requesting random numbers [12]. This modification makes it more challenging for defrauders to perform brute-force attacks. However, corrupted miners can still bypass this modification by pre-calculating the random result and exploiting the system.

2.4.2. Verifiable Random Function-Based Methods

A more secure method for generating random numbers on the Ethereum blockchain involves using a randomness beacon and verifiable random function (VRF). Chainlink VRF [13] is a service allowing users to obtain a truly random number from a decentralized source. When a random number is requested, the smart contract sends a request to Chainlink VRF. The random result is fulfilled in later blocks by a Chainlink node. Therefore, Chainlink VRF relies on the Chainlink network to maintain its security and decentralization. The Chainlink network is available for public participation. People can join it by following the requirements and instructions on Chainlink’s official website. However, joining the Chainlink network requires high technical expertise because of the complexity and system requirements. Although several documents are well prepared, our research has yet to find information for adding new networks on Chainlink VRF.

Figure 4 demonstrates the procedure of generating a random number on Chainlink VRF. The process incorporates two (2) blockchain transactions. First, in step (1.1), a user specifies “keyHash”, which associates with an off-chain random number generator. In step (1.2), the user smart contract requests a random number from the Chainlink VRF coordinator. A corresponding Chainlink node acknowledges the random number request, i.e., step (2.1). It then iterates the computation of random proof using the “secp256k1” algorithm. To make the random proof valid, the Chainlink node must follow the elliptic curve requirements [33]. In step (2.2), the Chainlink node submits the random proof to fulfill the pending random request on the VRF coordinator contract. The coordinator contract verifies the random proof in step (2.3). Referring to step (2.4), if the proof is valid, it returns the random result to the client’s smart contract. Otherwise, it rejects fulfillment. This procedure guarantees that the provided data is truly random.

Furthermore, this method separates request and fulfillment transactions to prevent brute-force attacks. Although Chainlink VRF provides secured and decentralized RNG, joining the network requires a certain level of technical expertise. The system has complex processes and system requirements. Additionally, this method does not natively support all networks. It may require technical support to add a new chain. Hence, this approach may not be suitable for scaling to new blockchains.

2.4.3. Commit–Reveal Scheme-based Methods

The Commit–reveal scheme is a decentralized alternative for generating random numbers, which can be natively implemented on the Ethereum blockchain. Randao, the main Commit–reveal RNG implementation, utilizes data feeds from the public and incentivizes participation in random number generation. The Randao procedure comprises four (4) steps, illustrated in Figure 5. First, the application requests a random number and deposits a reward for generators, i.e., step (1). Second, EOAs participate in the random request by uploading a hash value of the prepared data feed to ensure unpredictability, step (2). Third, hash committers reveal their actual numbers to be used as random feed and can withdraw their deposit and a portion of the reward upon successful reveal. Fourth, after the reveal phase, EOAs fulfill the random result by aggregating the numbers revealed in step (3). Finally, every revealer claims deposits and rewards after completing the random number generation in step (4).

The Randao approach effectively prevents brute-force attacks by separating transactions and keeping the actual input numbers hidden during the generation process. The Randao approach operates on a decentralized network, where all participants have incentives to generate random numbers and do not rely on any external infrastructure. This makes Randao suitable for native blockchain implementation. However, due to the high number of transactions required to generate a random number, Randao suffers from cost inefficiency, which limits its adoption in several use cases.

Overall, we describe each widely used RNG method and highlight significant limitations in detail. ERC721R is vulnerable for miners to extract values. Participating in the secured Chainlink VRF network is difficult for typical users or entry-level developers. On the other hand, using the native Randao method to generate numbers is expensive. Hence, developers need to analyze the requirements and constraints of their applications when adopting an RNG method. Unfortunately, selecting an optimized method for each use case is not a simple task for most people. To fulfill the shortcomings mentioned above, we propose a novel RNG method, named “Native VRF”. It is a decentralized RNG that addresses the security issue of ERC721R, and the complexity issue of Chainlink VRF, as well as Randao’s high-cost issue.

3. The Proposed Native VRF

Native VRF applies a verifiable random function and simplifies the process of participation. It combines on-chain data and random feed from the public to generate a random number. In order to secure data feed, Native VRF requires data feeders to generate a valid signature with a corresponding random input before publishing it to a blockchain. The Native VRF system is easy to set up because it only needs one-time deployment. Furthermore, it is open for anyone to feed random seeds to incentivize the generating of random numbers. Native VRF is a native approach, so it can be implemented on any EVM blockchain. Therefore, Native VRF provides secure random number generation, while being simple for participants. Details of the Native VRF approach are discussed in the following sections.

3.1. Random Number Generation Process

The random number generation process of Native VRF is more simple than that of Randao. It involves only two main steps to process a random number compared to Randao, which requires four steps (refer to Section 2.4.3). Figure 6 demonstrates the Native VRF random number generation process, which has the following details:

(1)

Request randomness: a user requests random number generation, Figure 6 (1.1). The request is stamped into the smart contract and attached with an identifier number ($request\_id$). The smart contract then broadcasts the request to the public in step (1.2).

(2)

Fulfill result: once a request is recorded in a smart contract, anyone can feed random data to that request by specifying $request\_id$. Data feeders compute the $signature$ using their private key and a message, which takes $random\_input$ and the previous random result as parameters, as shown in Figure 6 (2.1). The published information must meet the following requirements in order to fulfill the request:

(i)

The $request\_id$ must be valid (i.e., already have a requester).

(ii)

The $request\_id$ must not have been fulfilled.

(iii)

The prior $request\_id$ must have been fulfilled.

(iv)

The data must be published by EOAs, see step (2.2). Data fed via a smart contract is rejected to protect against brute-force attack.

(v)

In step (2.3), the $signature$ must be validated. Then, the random numbers are generated using $random\_input$, prior random result, and data from the blockchain. Details of the data forming and signature verification processes are discussed in Section 3.2 and Section 3.3.

(vi)

Finally, in step (2.4), data feeders publish the output random numbers to the requester.

The proposed Native VRF is secure from pre-determination attack. Specifically, attackers cannot try to execute the contract to simulate the results until the desired number is achieved because the random number result is created in different transactions from feeders.

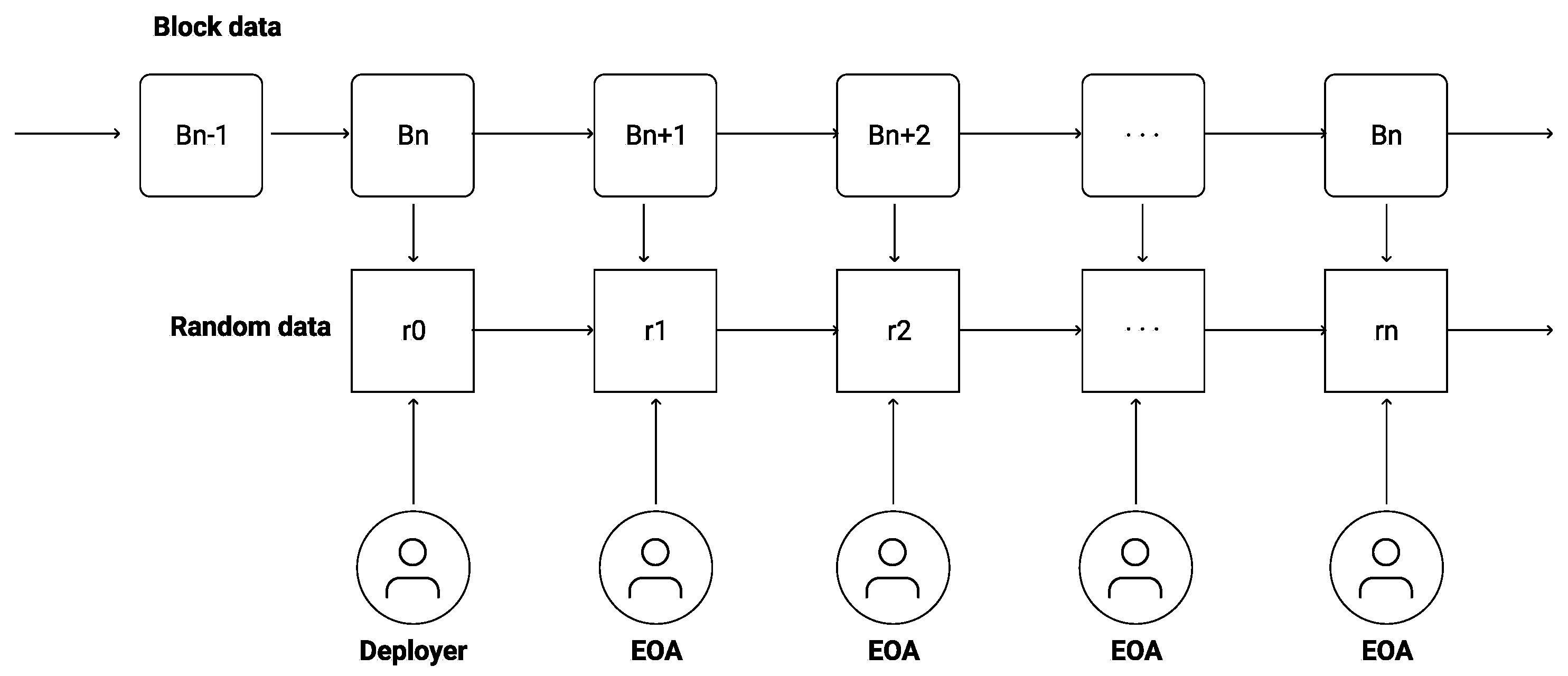
3.2. Data Forming

Figure 7 demonstrates a block diagram of Native VRF data forming. Each random number takes a prior random result as a component. The prior random result is an input of signatures generated by data feeders.

The Native VRF utilizes any EVM-compatible chains to deploy the smart contract at a block number (Bn). The initial random seed is defined as the Deployer. The first random data (r0) is computed using the initial random seed combined with blockchain data at the deployment time. When there is any RNG request, anyone that owns EOA can generate a verifiable random feed to the smart contract. The random results (i.e., r1 to rn) are computed using the feed data, previous random number, and blockchain data during the generating time. The Native VRF smart contract continuously generates random numbers after that.

3.3. Signature Verification Process

The Native VRF requires a data feeder to prove that the submitted $random\_input$ is truly random. Hence, the signature requirement is established herein. The schema of the Native VRF message is defined in Figure 8. Basically, a signature is created by using a private key and a message. When a data feeder publishes $random\_input$ and $signature$ to the smart contract, the data validation process is as follows.

(i)

The Native VRF smart contract computes a $message\_hash$ using a prior random result and $random\_input$.

(ii)

The computed $message\_hash$ and the published $signature$ are parameters in the $ecrecover$ function to obtain the signer $public\_key$.

(iii)

The recovered $public\_key$ and the transaction sender public key are compared. If they are mismatched, the signature is invalid.

(iv)

The smart contract requires the $signature$ to be divided by the $difficulty$. The signature is invalid if this condition is not satisfied. This process ensures that the submitted signature is truly random.

The signature requirement ensures data feeders pay to generate a random number, i.e., computation cost. Specifically, they need to attempt to put $random\_input$ into the message signing process to find a valid signature. The difficulty in generating a valid signature is relative to the value of $difficulty$. The smart contract adjusts the $difficulty$ to allow legitimate data feeders to publish authentic signatures. Conversely, fraudulent data feeders must pay a high price to manipulate the random number generation. In the following section, we delve into the appropriate adjustment of the $difficulty$ value.

3.4. Difficulty Adjustment

By definition, the $difficulty$ is the number of attempts to generate a valid signature within a specific period. Usually, the period is 15–30 s per 1–2 blocks. This value is determined based on the regular fulfillment period in other RNG frameworks (e.g., Chainlink VRF and Randao). Therefore, the higher the value of $difficulty$, the more attempts to generate a valid signature (i.e., the harder to attack) and the longer the time to generate the valid signature. The probability of generating a valid signature can be determined as in Equation (1), wherein $P\left(success\right)$ is the probability of generating a valid signature. The larger the value of $difficulty$, the harder it is to generate a valid signature.

$$P\left(success\right)=\frac{1}{difficulty}$$

(1)

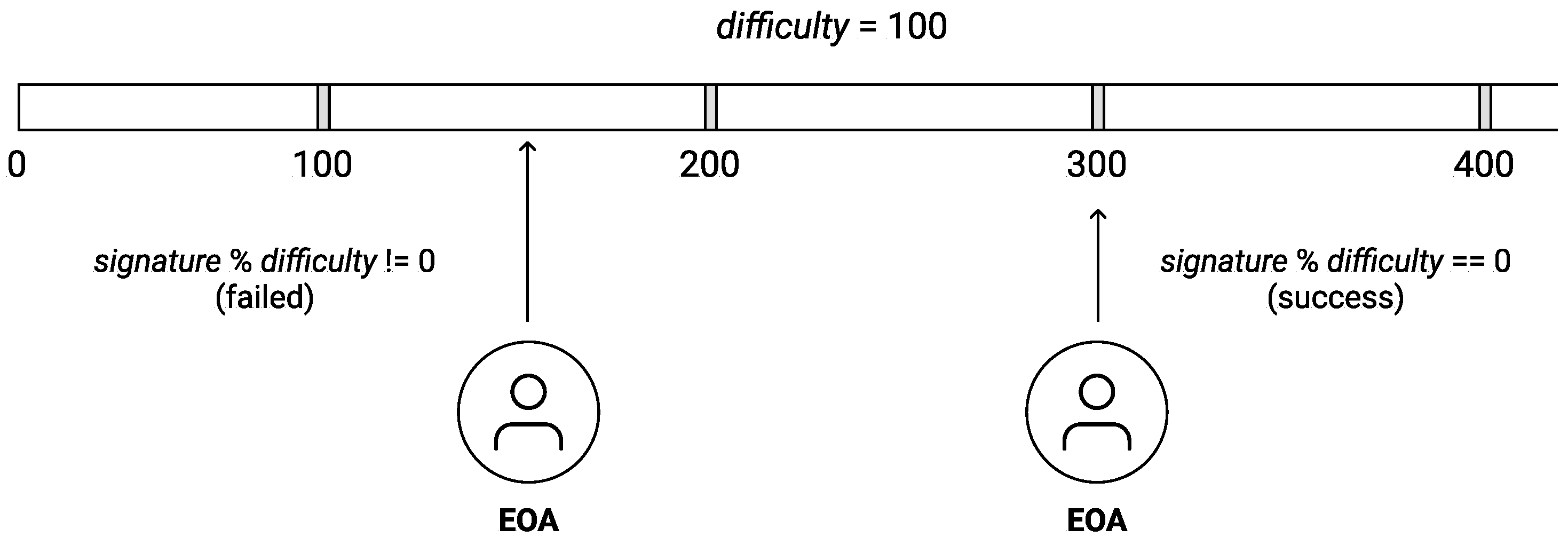
The relationship between the signature verification process and the $difficulty$ is shown in Figure 9. A Native VRF smart contract validates signatures submitted by EOAs. Initially, signatures are represented in a 130-bytes hex string. They are then converted into an unsigned integer format and validated. Transactions are successful when the submitted $signature$ is evenly divided by $difficulty$ (i.e., $signaturemoddifficulty$ equals zero). Otherwise, transactions fail.

The Native VRF automatically optimizes the value of $difficulty$ using a smart contract by adjusting the amount of effort to generate a valid random input. The ideal random fulfillment should not be too simple to guess or take too long to calculate. Hence, the likelihood of guessing the correct value and the calculation time must be adjusted to yield the optimal $difficulty$ value. We designed an adjustment model in Equation (2),

$$difficulty=t_{fulfill}\times r_{hash}\times (n_{fulfills}/n_{blocks}),$$

(2)

where $t_{fulfill}$ denotes the expected duration for random fulfillment, and $r_{hash}$ is the estimated average hash rate of data feeders. The configurations $t_{fulfill}$ and $r_{hash}$ are defined by the smart contract owner (e.g., maintainers or decentralized autonomous organizations (DAOs)). Then, $n_{fulfills}$ stores the amount of random fulfillment in the last block. Lastly, $n_{blocks}$ accumulates the number of blocks until the random request is fulfilled. The smart contract automatically adjusts the $difficulty$ to align it with the expected fulfillment time ($t_{fulfill}$) and the average hash rate of data feeders ($r_{hash}$). The value of $difficulty$ is recomputed according to Equation (2) every time a new random number is generated.

Figure 10 illustrates an example of $difficulty$ adjustment. The value is initially 1500, which is the expected value. Then, a random data feeder successfully generates five random outputs within one block. This rate is considered too fast for the current configuration (i.e., $t_{fulfill}=15$ and $r_{hash}=100$). Thus, the smart contract increases the $difficulty$ to 7500. Random feeders need more attempts to generate a valid signature with this $difficulty$ value. It is assumed there are no random outputs generated in Block 2. After this, some people can submit valid signatures to the smart contract. The $difficulty$ decreases because the generation rate is closer to the expectation (3 outputs within two blocks or 1.5 outputs per block). This mechanism stabilizes the system’s security and applicability. When more participants interact in the network, Native VRF is more secure.

4. Evaluation Model, Observation Scope, and Experimental Procedure

This section benchmarks several aspects of the proposed Native VRF system, namely, the security, simplicity, and cost efficiency of various random number generation (RNG) methods. Details of security model formulations and experimental settings are discussed.

4.1. Definition of Security Models

The term “security level”, in the context of the security level of an RNG, is the ability to protect random output determination. This means the RNG method that produces hard-to-predict outputs has a high-security level. Therefore, the output determination attack was used to simulate attacks against RNG methods so as to analyze the security level. Specifically, we defined probability models that reflected the probability of successful attacks against each RNG method. The lower the successful attack probability, the higher the security level of the approach.

4.1.1. ERC721R

The ERC721R algorithm utilizes the hash output of on-chain data to generate random numbers. It mitigates brute-force attacks using smart contracts by preventing attackers from iterating the RNG on-chain until a predictable outcome is achieved in a single transaction. However, off-chain pre-computation of random results remains possible. In the case of the variables depicted in Figure 1, certain variables fluctuate during transaction submission, such as the $block.timestamp$, which may vary slightly for each block of data.

Figure 11 illustrates an ERC721R attack technique where an attacker employs brute force to generate a desired random number. In step ➊, an attacker generates new wallets and computes a random output using a hash function and inputs. Upon obtaining the desired random output, in step ➋, the attacker calls the ERC721R smart contract through the generated wallets to trigger an action using the desired random number.

The ERC721R security model can be expressed as Equation (3), where $R_r$ represents the range of random numbers and $R_b$ denotes the number of block time ranges. The probability of a successful ERC721R attack depends on the block time range, and the likelihood of an attack exponentially increases with a broader random output range.

$$P_{ERC721R}={\left(\frac{1}{R_b}\right)}^{R_r}$$

(3)

The probability of a successful ERC721R attack depends on the range of the random output. The broader the random output range, the more computational power is required. Another variable affecting an attack’s completion rate is the block time value, which fluctuates, based on network congestion, over a given period.

Table 1. Block time range on 22 January 2023.

Blockchain Network	Possible Block Time (s)	Range
ETH	12	1
BSC	3	1
Arbitrum	0, 1	2
Optimism	0, 15	2

presents each blockchain network’s block time range values at the time of the investigation. This variable influences the completion rate of an attack because the attacker must select a block time value as an input for random number computation, and the attack fails if the wrong block time value is selected.

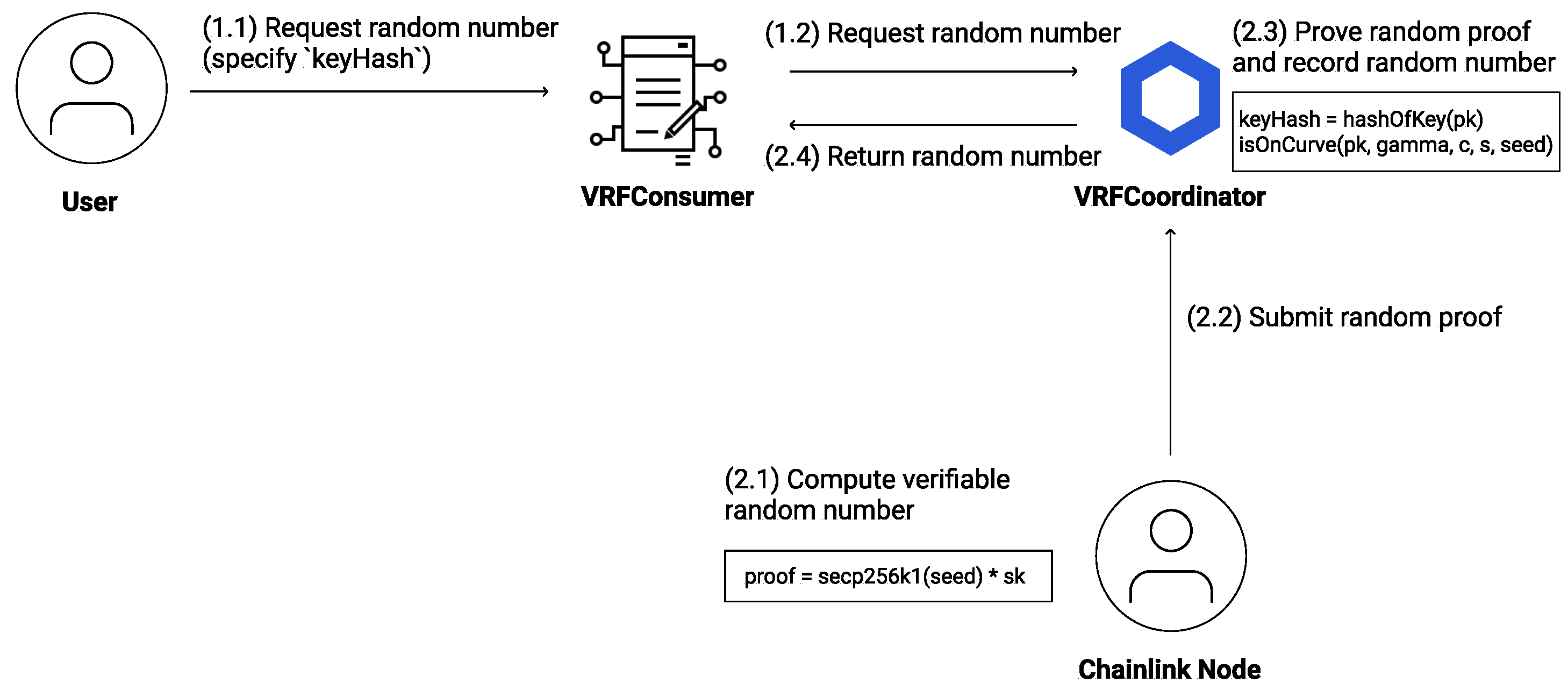
4.1.2. Chainlink VRF

The VRF is an effective technique for generating truly random numbers in the Chainlink protocol. Since the VRF accepts off-chain pseudo-random generation and relies on the strong cryptography function secp256k1 and elliptic curve requirements [33], the strength of the secp256k1 algorithm is used to determine the security level of the Chainlink VRF model.

However, the data feeder for the Chainlink VRF is chosen by the consumer. This poses a potential vulnerability as the requesters may select their nodes as data feeders. This allows them to attempt to pre-compute and feed the desired random output. Figure 12 illustrates the technique used in attacking the Chainlink VRF RNG. An attacker may follow the steps below to pre-compute random numbers via Chainklink VRF. In step ➊, the attacker requests random generation from the smart contract and selects their data feeder nodes. Then, in step ➋, the feeder attacker attempts to compute the desired random number that satisfies the elliptic curve requirements within a defined time limit (e.g., normally 15–30 s or 2 block time). Once the desired random input is found, the attacker can submit the transaction to the smart contract in step ➌.

The success of this attack relies on the attacker’s ability to find the desired random number within the defined time limit. However, if the attacker has enough computing power and time, they may be able to successfully pre-compute the desired output. The probability of successfully generating the predicted random output can be determined from Equation (4),

$$P_{CH\_VRF}={P_{ec}}^{R_r},$$

(4)

where $P_{ec}$ denotes the probability of successfully generating a random proof that complies with the elliptic curve requirements. The probability value is referred to in [34].

4.1.3. Randao

Randao employs a transparent and open approach to prevent fraudulent random number generation. This technique uses the so-called “interruption layer,” and requires attackers to recompute their attack inputs each time new participants enter the system, effectively disrupting their attempts to generate pre-computed random outputs.

Figure 13 demonstrates the method attackers use to generate a desired random output via the Randao RNG. To successfully generate a desired random output, the attacker first initiates a request for a random generation to the Randao smart contract (step ➊). In step ➋, the attacker observes the hash commitment values submitted by other nodes (i.e., EOAs) and extracts the actual value of the committed hashes. The attacker calculates an input value that yields the expected output when aggregated with the current inputs submitted by other nodes in step ➌. Finally, in step ➍, the attacker submits the hash of the calculated value to the smart contract, ensuring no further commitment from other nodes occurs after the transaction is submitted. Otherwise, the expected output is not obtained.

Before calculating the probability of a successful attack on Randao, it is necessary to determine the current interruption rate, which can be calculated by considering the likelihood of a new participant joining the random number generation process. The rate is computed based on the remaining commit time ($tr$), the total incentive amount ($rw$), the total commit time ($tc$), the total transaction cost for generating an input ($c{h}_{randao}$), and the number of current commitments ($nc$), as shown in Equation (5).

$$P_{interruption1}=\frac{tr\times rw}{tc\times c{h}_{randao}\times (nc+1)}$$

(5)

When computing the interruption layer, the number of commitments must be adjusted by adding one to the total number of commitments, as the reward is distributed among all pledges. The probability of successfully generating a desired random number on Randao can be expressed by Equation (6).

$$P_{Randao}={\left(\frac{1}{R_r}\right)}^{R_r+nc+1}\times (1-P_{interruption1})$$

(6)

The attack steps are as follows. First, the attacker must extract all committed hashes, where $nc$ represents the current number of commitments, and $R_r$ denotes the input data range. Next, the attacker must compute another input number with the desired random output. In the last step, the attacker must commit the data to bypass the interruption layer.

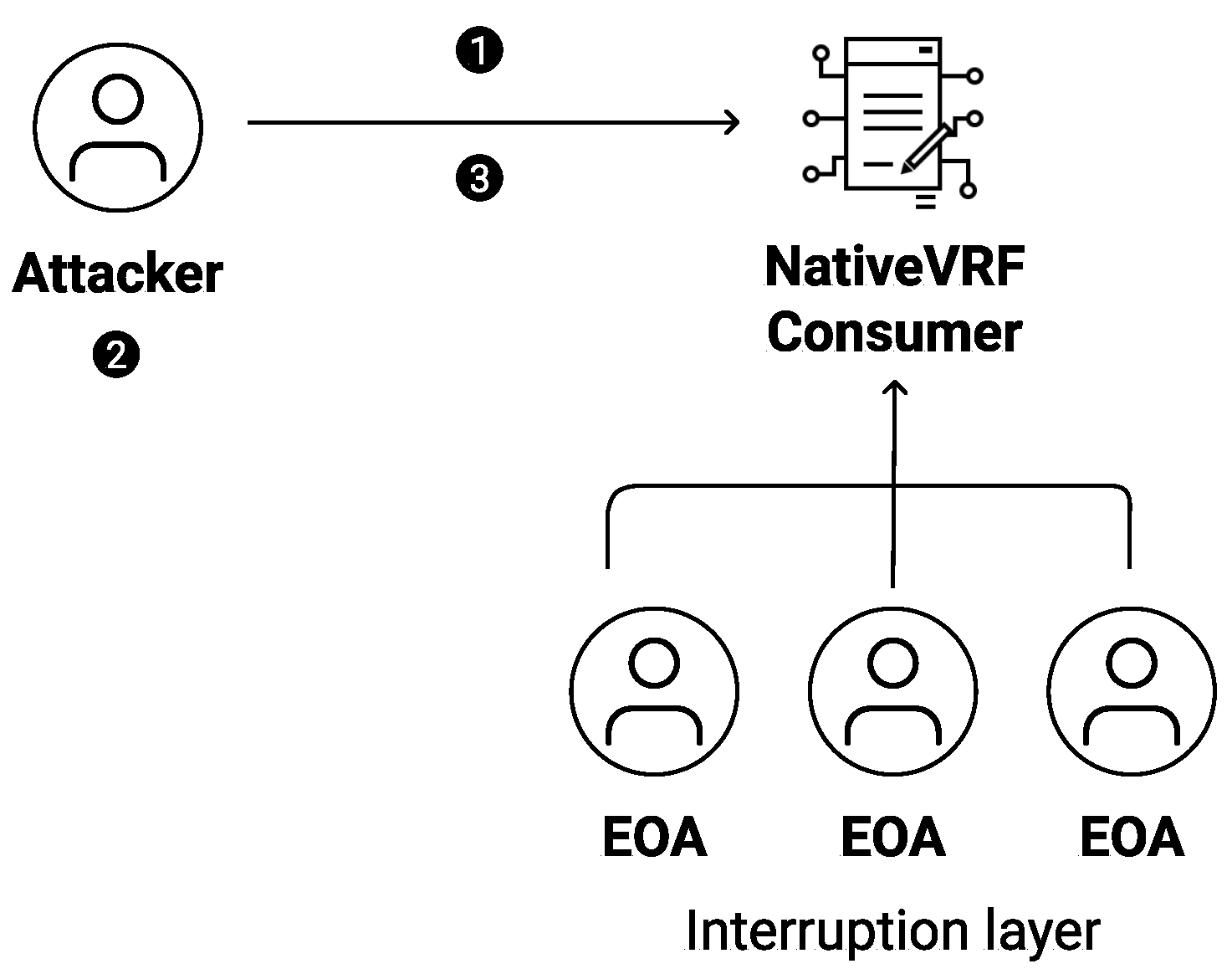
4.1.4. Native VRF

The Native VRF presents a simplified process for generating random numbers while preserving system security. Like the Randao, our approach uses an interruption layer, which hinders attacks from malicious feeders. Since users must submit a request to obtain a random number before the public can feed a random number into the system, an attacker seeking to generate a desired random number must quickly compute an input and be the first to provide data in a specific row. Therefore, the attacker must win all legitimate data feeders in the network. Particularly, the Native VRF relies on the network’s decentralized hashing power derived from economic incentives. When the cost and reward ratio is acceptable, more legitimate participants contribute to the random network, which enhances security.

Additionally, our approach enables the creation of pre-computed random numbers at a high cost while keeping the process of generating honest random input inexpensive. The system is designed to prevent fraudulent data feeders from generating a signature that provides the desired random output. In the meantime, the smart contract only allows honest random data feeders who generate a valid signature with minimum computation power. Although we cannot 100% guarantee honest feeders, to successfully attack the system, the adversary needs to compromise more than 50% of the network’s computation power.

Figure 14 illustrates the steps involved in an attack on the Native VRF RNG. An attacker must undertake the following steps to generate the expected random output. First, the attacker requests random generation to the Native VRF smart contract (step ➊). After that, they compute an input value aggregated with the message hash, signature, previous random output, and on-chain data. The attacker obtains the desired output in step ➋. They submit the transaction using the computed input value in ➌ at the final step. The attacker must complete all steps before other nodes fulfill the random request. In this scenario, the attacker obviously needs to control the network’s computational power to successfully attack the Native VRF RNG.

Equation (7) demonstrates the calculation of the Native VRF interruption layer, which is essentially the network’s computational power. The interruption layer reduces the opportunity to attack random number generation. Anyone who attempts to attack the system must dominate computational power over the network (i.e., EOAs in Figure 14). Here, $P_{interruption2}$ is the probability when some nodes successfully fulfill a random request before attackers, $rw$ represents the total reward for a data feeder, $ch$ denotes the cost per hash, and the attacker’s hash rate is denoted as $rh$.

$$P_{interruption2}=\left\{\begin{array}{cc}\frac{rw}{ch\times rh},\hfill & \mathrm{if}rw<\left(ch\times rh\right)\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(7)

The data feeders must comply with the signature requirements (See Section 3.3) to validate the random input. The Native VRF adjusts the optimal $difficulty$ value to ensure system security, as stated in Equation (1). The probability of a successful attack on the Native VRF is determined by Equation (8),

$$P_{NativeVRF}={\left(\frac{1}{difficulty}\right)}^{R_r}\times (1-P_{interruption2}).$$

(8)

Here, the attacker must repeatedly inject an input that delivers the desired random output. The current value is denoted as $difficulty$, and $R_r$ represents the range of random input values. This means attackers must attempt to generate a valid signature regarding the $difficulty$. Moreover, they need to keep trying multiple rows regarding the $R_r$ value. The attack is deemed successful only if the attacker can feed the computed input faster than other feeders in the network.

4.2. Simplicity

The simplicity of RNG methods is crucial in determining their practicality and applicability. An ideal RNG method should be easy to use, so as to encourage more people to adopt it. Intuitively, in the distributed system, the larger the group of participants, the stronger the RNG network. Two criteria determine the simplicity of RNG methods.

• Resource requirements: assets, tooling, and infrastructure.
• Technical requirements: the basic knowledge for setting up the system, the specific understanding of each method, and code complexity.

We observed all the requirements from the list of references provided on Chainlink official website4 and GitHub repositories (ERC721R5, Chainlink6, Randao7 and Native VRF8).

4.3. Cost Efficiency

To assess the cost efficiency of the RNG methods, token cost and processing time were used. The experiment was conducted as follows.

• Implementation of a Test Script: the test script was implemented using Node.js. The test script was used to submit multiple transactions for the four methods (i.e., ERC721R, Chainlink VRF, Randao, and Native VRF).
• Results collection: multiple transactions were submitted to the network, and the test script recorded each method’s token cost and speed.
• Ethereum network was used to perform the simulations: smart contracts were deployed on the Ethereum Goerli Test Network. For experimental purposes, the Alchemy free-tier RPC endpoint was selected. A public Chainlink node on the Ethereum Goerli Network was also used to generate random numbers.

5. Results

The security aspect, implementation simplicity, and cost efficiency are discussed in this section, based on the experimental results and analyses, and detailed below.

5.1. Security Comparison

Since each method had different parameters, affecting the security aspect, several parameters were adjusted to normalize the differences for this comparison. The values of the various parameters are listed in

Table 2. Configuration for RNG methods.

Parameter	Method	Value	Description
$R_r$	Every method	100	Range of random input values.
$R_b$	ERC721R	2	Possible block time difference in a period
$P_{ec}$	Chainlink VRF	0.05	Probability of successfully generating a set of inputsthat satisfies the elliptic curve requirement
$tc$	Randao	24	Total commitment time
$tr$	Randao	12	Remaining time before ending of commitment period
$nc$	Randao	1	Current number of participants
$ch$ (Randao)	Randao	15	Cost
$rw$	Randao, Native VRF	30	Reward
D	Native VRF	200	Difficulty
$ch$ (Native VRF)	Native VRF	6	Cost per hash
$rh$	Native VRF	1000	Attacker hash power

.

First, the random output range $R_r$ was set to 100 for all methods to highlight the differences when comparing the methods. Too large or too small $R_r$ differences would result in too huge or too small gaps. The $R_b$ value was suggested by Ethereum.9 This parameter only affected the ERC721 method. The $P_{ec}$ probability value was suggested by [34]. This parameter affected the result of the Chainlink VRF method.

Concerning the Randao method, $tc$ was set to two block times (i.e., 24 s), because the Chainlink VRF usually spends the duration of two block times to generate a random output.10 Meanwhile, $tr$ was set to 12 s, the middle of the maximum and the minimum. The number of participants ($nc$) was set to 1 person to simulate the opportunity of having more participants in the commitment period. Note that this value must be considered along with cost ($ch$) and reward ($rw$) values. From our experiment, the cost per hash of Randao was $15, and the reward was then set to $30 to incentivize participants (explained in the next section).

Native VRF parameters were set as follows. The reward ($rw$) was equal to Randao’s. The $difficulty$ (i.e., D) was 200 hashes, since our machine could produce this in around 12 s of block time. The cost per hash ($ch$) was about $6, whereas the attacker hash power ($rh$) was five (5) times that of the generic computer (i.e., 1000 hash per second).

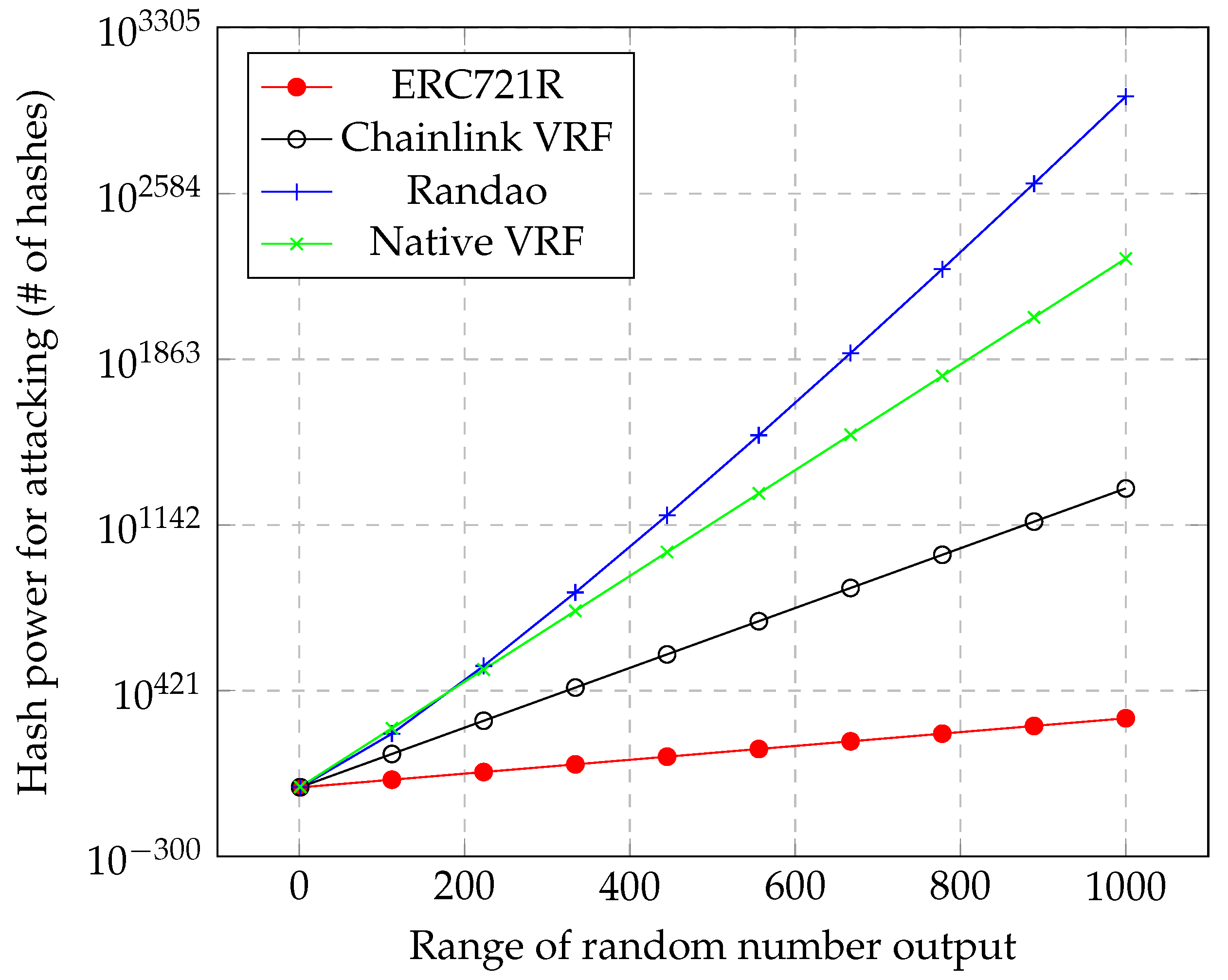
Based on security models (i.e., Equations (3)–(8) and parameters in Table 2), the security levels of each RNG were compared, and are provided in Figure 15. The chart uses a random output range as an input and provides the hash power required for attacking each method. Note that the Y axis is in the log scale. The experimental results demonstrated that Randao required the most hash power to be attacked. Native VRF, Chainlink VRF, and ERC721R offered lower security levels. When the highest hash rate of the Ethereum network was 1126 TH/s ($11.26\times {10}^{14}$),11 the security level of each method was high compared to the network hash rate. This meant that these RNG methods were protected against brute-force attack. Specifically, the proposed method, Native VRF, was at a similar security level to the currently popular methods. Similar to Randao, the Native VRF also relies on the number of random data feeders. Hence, the security level of both methods could be low when the number of participants is small. Conversely, they are both secure when many feeders join a network.

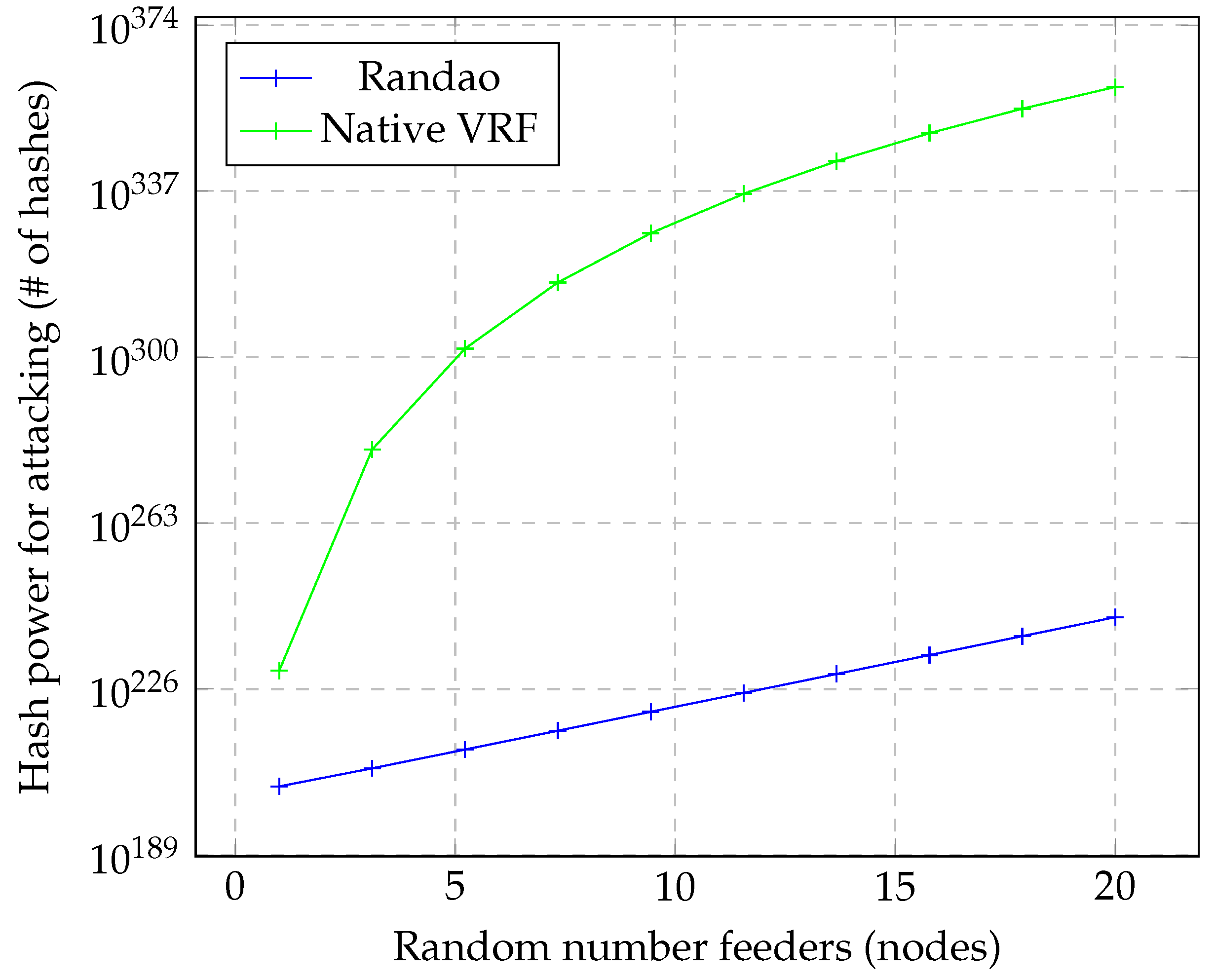
Figure 16 depicts the security sensitivity of both systems using the number of participants as inputs to calculate the hash power required to attack both RNGs. The Y axis is a log scale. While Randao and Native VRF had different variables related to the number of participants, they could be compared based on the following parameters. For Randao, the number of participants represented the number of commitments (i.e., $tc=participants$). For Native VRF, each participant contributed approximately 200 hashes per second (i.e., $D=200\times participants$). Except for some variables, most parameters used in this chart were equal (see Table 2). The inputs for Randao and Native VRF were $tc$ and D, respectively. The random output range was fixed at 100. Here, we observed that the number of random feeders directly affected the security level of both RNG methods. Native VRF provided a higher security level when there were more data feeders. Compared to the Ethereum hash power benchmark (i.e., $11.26\times {10}^{14}$), both RNGs offered high security, even with only one random data feeder. This meant that only a few participants were sufficient to protect both RNGs from brute-force attacks.

5.2. Simplicity of Implementation

The ease of participating in an RNG network is crucial and relates to the security level of each method. As demonstrated previously, methods with more feeders are considered more secure. To compare the simplicity of implementation, we considered two aspects, resource and technical requirements. Therefore, our chosen criteria were hardware requirements, the employees’ technical expertise, and the source code’s complexity.

5.2.1. Hardware Resource Requirements

Table 3. RNGs resource requirements comparison.

Topic	Chainlink VRF	Randao	Native VRF	ERC721R
Server	2 cores; 4 GB RAM ($1552.71)	1 core; 512 MB RAM ($6)	1 core; 512 MB RAM ($6)	None
Database	2 cores; 4 GB RAM and 100 GB storage ($1567.71)	None	None	None
Blockchain node	External service	External service	External service	None
Gas	ETH coin	ETH coin	ETH coin	None
Collateral	Link token	ETH coin	None	None

compares each RNG method’s resource requirements (i.e., minimum requirements). Chainlink VRF required participants to prepare a server and database capable of handling Chainlink network node operation. Operating a Chainlink node with minimum specifications costs around $3120.42 per month. On the other hand, other methods can run on a minimal server, which costs only $6 per month. ERC721R did not require a node operator. Thus, there was no cost for operating the ERC721R system. Node operators required ETH coins to pay transaction fees (gas) when fulfilling random results. Chainlink VRF and Randao required some collateral to maintain the good behavior of RNG nodes. Native VRF did not need any collateral because it opens for data feed publicly in one transaction. Regarding resource requirements, Chainlink VRF was the most expensive compared to the others.

5.2.2. Employee Technical Knowledge Requirements

Technical skill requirements to set up random feeder nodes are listed in

Table 4. Technical knowledge required for feeder node setup.

Topic	Chainlink VRF	Randao	Native VRF	ERC721R
Solidity	✓	✓	✓	✓
TypeScript	✓	✓	✓	✓
Rust	✓	✗	✗	✗
Job Scheduler	✓	✗	✗	✗
Docker	✓	✗ a	✗ a	✗
AWS	✓	✗ a	✗ a	✗
Proprietary spec.	✓	✗	✗	✗

^a Beneficial, but not mandatory.

. All methods require Solidity and TypeScript skills, i.e., the fundamental decentralized application development knowledge. Chainlink VRF requires more technical skills to maintain its nodes. Node operators must understand Rust language to set some configurations in TOML files. Chainlink VRF requires an understanding of the Job Scheduler to determine node functionality. The operator must correctly configure jobs for nodes to keep its performance. DevOps best practices are required for Chainlink VRF node operators. They must understand how to use Docker and maintain an AWS server properly. Randao and Native VRF can be operated using Vanilla Node.js. Docker and AWS knowledge are used to reduce deployment errors in many environments. Chainlink introduces many proprietary specifications, such as Operator contracts, Forwarder contracts, jobs, address white listings, and payment subscriptions. Conversely, other RNG methods do not require that technical knowledge but can still provide similar levels of security. According to the necessary technical skills, Chainlink VRF can be treated as a complex system compared to the others.

5.2.3. Source Code Complexity

Aside from staff technical skills, code complexity is usually an essential consideration for the development team.

Table 5. Line counts of RNG methods.

Method	Component	Languages	LOC	Total LOC
ERC721R	Generator	Solidity	257	257
Chainlink VRF	Generator	Solidity	2372	304,744
	Feeder	Go	302,372
Randao	Generator	Solidity	229	504
	Feeder	TypeScript	275
Native VRF	Generator	Solidity	139	293
	Feeder	TypeScript	154

compares each method’s line of codes (LOC) in each component (i.e., Generator and Feeder). The implementation of the Feeder varies among the different RNG methods. Specifically, the Chainlink VRF utilizes Go lang for Feeder development, while Randao, Native VRF, and ERC721R rely on TypeScript. Our observations revealed that Chainlink VRF was the most complex method, exhibiting the highest LOC, having a more significant number of components, and a deeper depth of inheritance. At the same time, Randao, Native VRF, and ERC721R were relatively simple methods with a much smaller number of LOC.

5.3. Cost Efficiency

Figure 17 illustrates the transaction cost of producing random numbers for each RNG method based on the number of random numbers and the accumulated token cost used in generating them. Note that the gas price used in the experiment was 20 GWEI, and the Ethereum coin price was $1570 at the time of writing. Randao was found to be the most expensive method, due to the requirement for multiple transactions and the number of participants. In contrast, Chainlink VRF was less expensive than Randao but incurred additional costs due to the enforcement by Chainlink nodes and the need to maintain incentives for the Chainlink network. The Native VRF method was cheaper than Chainlink VRF as it is a pure solution that does not require additional costs. Lastly, ERC721R was the cheapest method as it is the smallest solution requiring only one transaction.

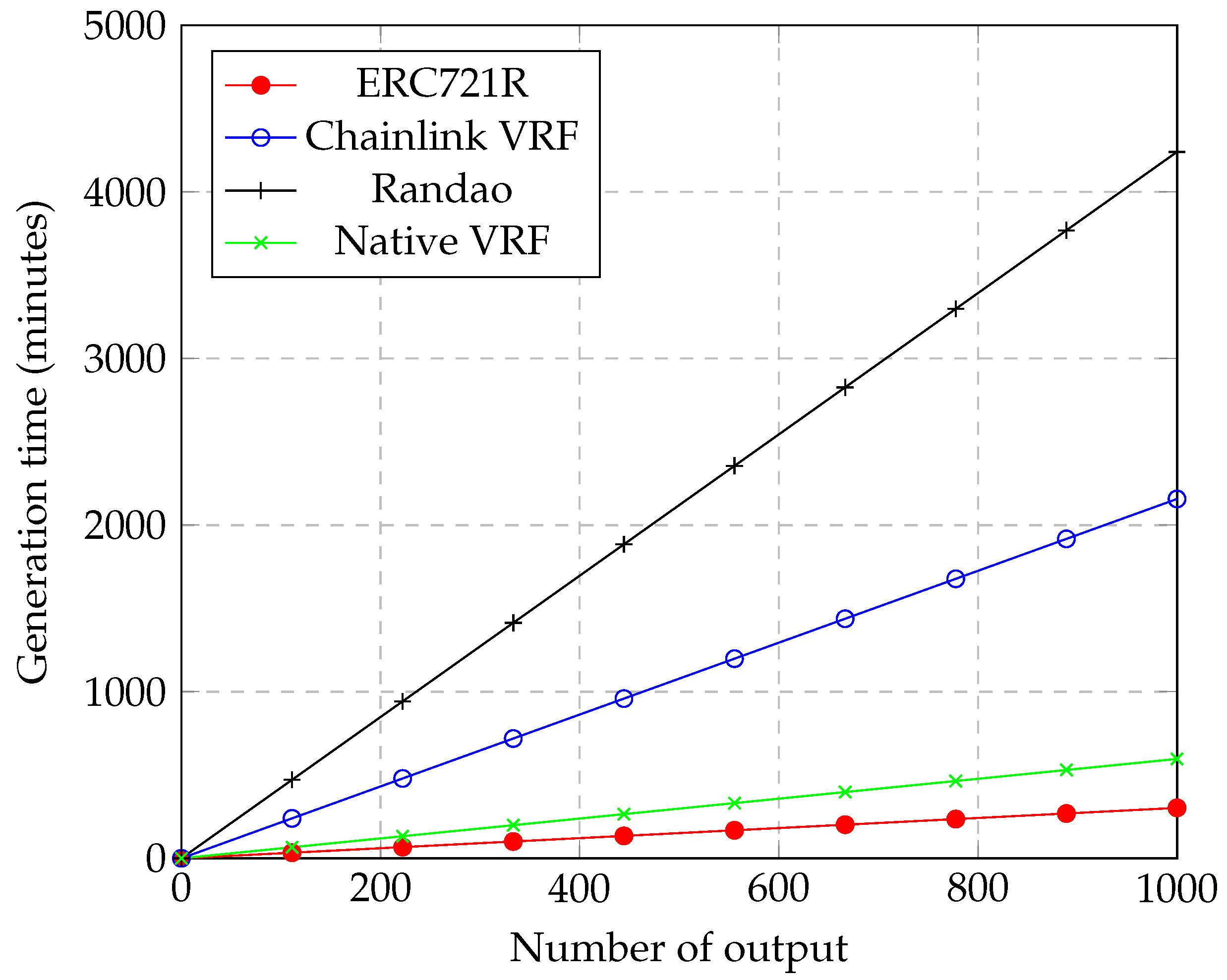
On the other hand, the speed of producing the random number was also compared. Figure 18 shows the throughput of each RNG. The x-axis represents the time elapsed in minutes. The y-axis indicates the number of random outputs generated in a period. ERC721R offered the highest throughput because it was the most straightforward method that only incurred one transaction per random generation. ERC721R could produce 3.3 outputs per minute. Native VRF provided higher speed than Chainlink VRF and Randao. This was because it only required two main transactions, request and fulfill. As a simplified process, Native VRF maintained a high speed with 1.67 random outputs per minute. Chainlink VRF was much slower than Native VRF because it incorporated Chainlink network operation, which was a complex process. It could generate 0.5 output per minute. Lastly, Randao was the slowest method since it contained five transactions for each random generation. It produced 0.25 output per minute. Overall, Native VRF was fast compared to other popular methods.

5.4. Our Insights

Table 6. RNG key aspects summary.

	RNG Method	Chainlink VRF	Randao	Native VRF	ERC721R
Key Aspect
Simplicity		−	0	+	+
Security		+	+	+	−
Cost efficiency		0	−	0	+

summarizes three main aspects of the existing decentralized RNG methods compared to our proposed Native VRF approach. Overall, the Native VRF is excellent in simplicity and security while maintaining acceptable cost efficiency. Although our approach is not the best in all aspects, it is the best overall RNG approach with high security and simplicity. As discussed in Section 5.1, when considering security the Native VRF and Randao are the most secure decentralized RNGs, which are resilient against brute-force attacks given a limited number of network participants. However, the critical limitation of Randao is the high transaction cost. This is why Randao has not been very popular compared to less secure methods, i.e., Chainlink VRF. Our experiment showed that Native VRF offered cheaper transaction costs and was faster than Chainlink VRF. Hence, our approach is the best choice for security and cost efficiency.

When considering the simplicity property, we can rank RNG methods from easiest to hardest applicability as follows: ERC721R, Native VRF, Randao, and Chainlink VRF. We observed that Chainlink VRF was particularly hard to scale in existing and new networks. At the time of writing, there were 300 active Chainlink nodes.12 The nodes produced approximately 30,000 random requests per day.13 The number of nodes was relatively low compared to the number of requests. This was caused by the resource and technical requirements, which introduced barriers to entry for participants. Chainlink VRF was hard to scale in the existing and new networks. Setting up Chainlink VRF in a new network cannot be done publicly. It required the Chainlink team to handle this.

In contrast, the other methods were easy to set up. Most importantly, they could be deployed and maintained by anyone. With the simplicity of Randao, ERC721R, and Native VRF, these methods can be scaled easily in any network. Moreover, the simplicity encourages overall security of the RNGs as they have more participants in the network (hence more secure).

A limitation of this work was that it solely focused on discussing RNGs within EVM-compatible blockchain chains. This narrow scope was justified by the prevalence of such chains in the current landscape of blockchain applications. However, it is important to acknowledge that other blockchain networks, such as Solana, Near protocol, Cosmos, and numerous others, possess distinct infrastructures that may introduce unique challenges and approaches to RNG implementation. While these aspects were not covered in this work, they present intriguing topics that warrant further exploration.

6. Conclusions

This work investigated random number generators in decentralized systems. Since blockchain is a trustless system, producing truly random numbers is challenging. To date, three popular RNG methods are used in real projects, namely ERC721R, Chainlink VRF, and Randao. These methods have their strengths and weaknesses. We analyzed the pros and cons and proposed a novel RNG method, named Native VRF. This method overcomes the inadequacies of the previous techniques while maintaining their strengths. We conducted experiments to measure each RNG’s security, simplicity, and scalability. The results of the experiments indicated that Native VRF carries the same level of protection as Randao and Chainlink VRF against brute-force attacks. It offers a high level of simplicity, compared to the complex Chainlink VRF. Native VRF does not require many resources and technical skills. The code base of Native VRF is much simpler than that of Chainlink VRF. Finally, it maintains a cheap transaction cost and high speed in producing random numbers. Native VRF is portable to any EVM-compatible blockchain network. Therefore, the proposed Native VRF is a good alternative for many applications that need decentralized RNG.

In future work, we have two primary objectives for enhancing our proposed approach. Firstly, we aim to address the issue of throughput in generating random numbers. It is well-known that throughput is an inherited limitation for all blockchain-based applications, and Native VRF RNG is no exception. We will explore strategies to optimize our RNG’s efficiency and speed to increase throughput. Additionally, we plan to investigate methods to reduce the cost of generating random numbers. One potential approach for achieving this is integrating zero-knowledge proofs into the signature verification process. Hence, we could streamline the verification process and potentially lower the cost of generating random numbers. This strategy will be explored further to enhance the cost-effectiveness of our proposed RNG solution.