Research on Risk Evaluation of Hydropower Engineering EPC Project Based on Improved Fuzzy Evidence Reasoning Model
Abstract
1. Introduction
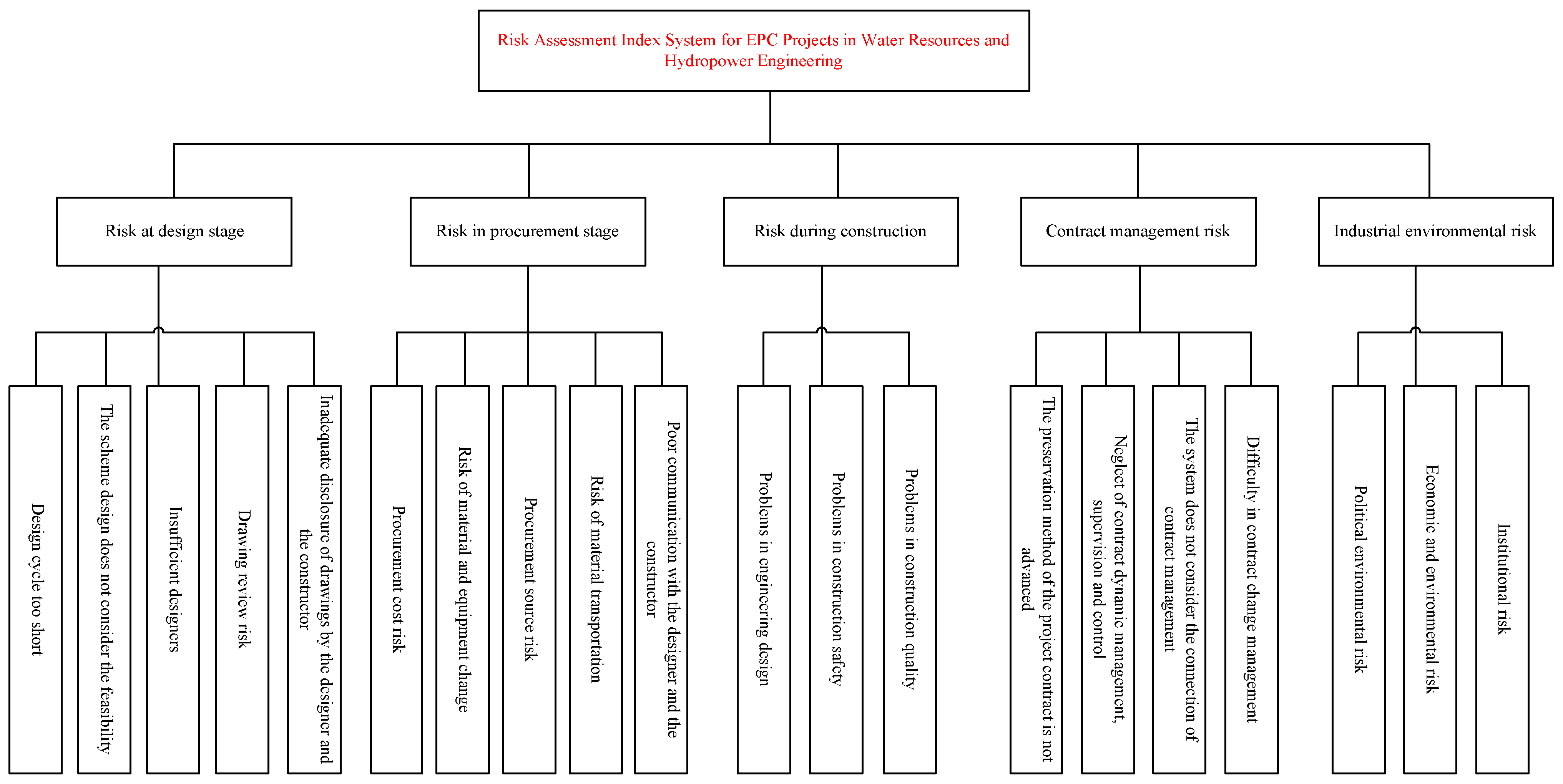
2. Risk Evaluation Index System for Hydropower Engineering EPC Project
2.1. Design Stage Risk
2.2. Procurement Stage Risk
2.3. Construction Stage Risk
2.4. Contract Management Risk
2.5. Industrial Environmental Risk
3. Risk Evaluation Model for Hydropower Engineering EPC Project
3.1. Calculation of Weight by Combination Weighting Approach
3.1.1. Subjective Weight Determination Based on Order Relation Method
3.1.2. Objective Weight Determination Based on Entropy Weight Method [33]
3.1.3. Combination Weight Determination Based on Linear Weighted Combination Method
3.2. Risk Evaluation Model Based on Fuzzy Evidential Reasoning [39]
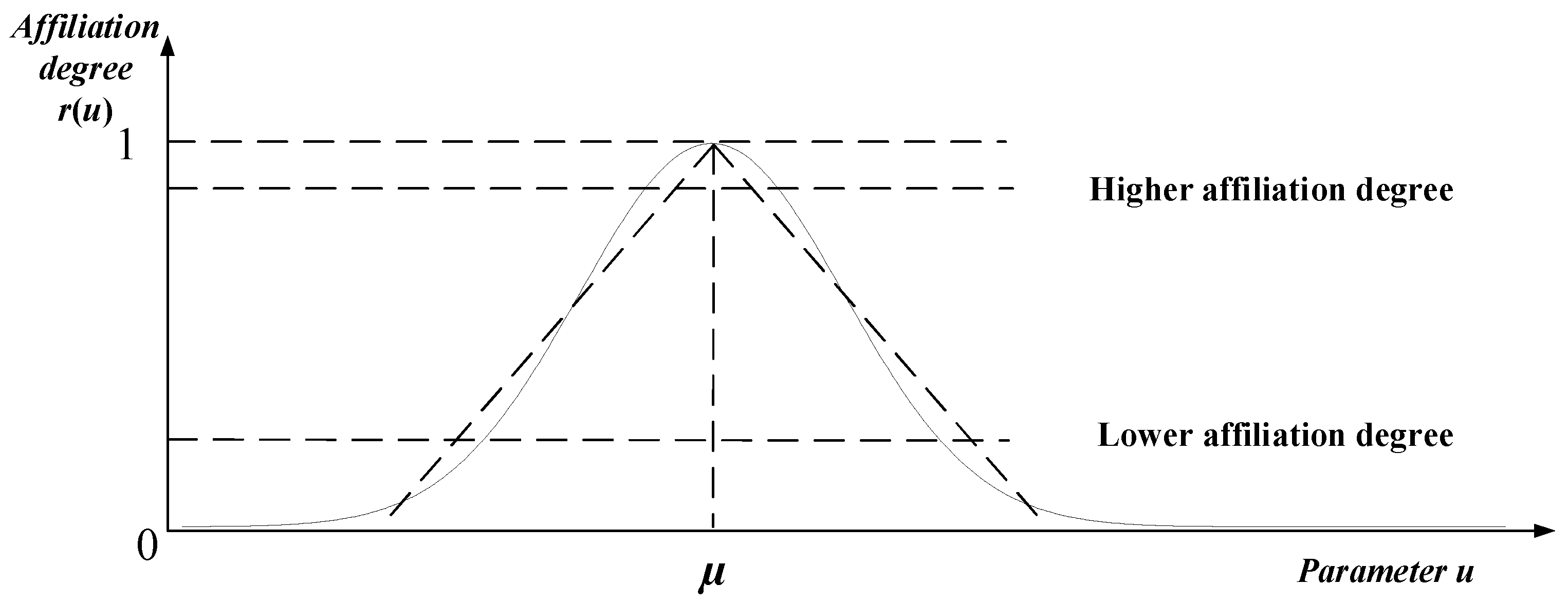
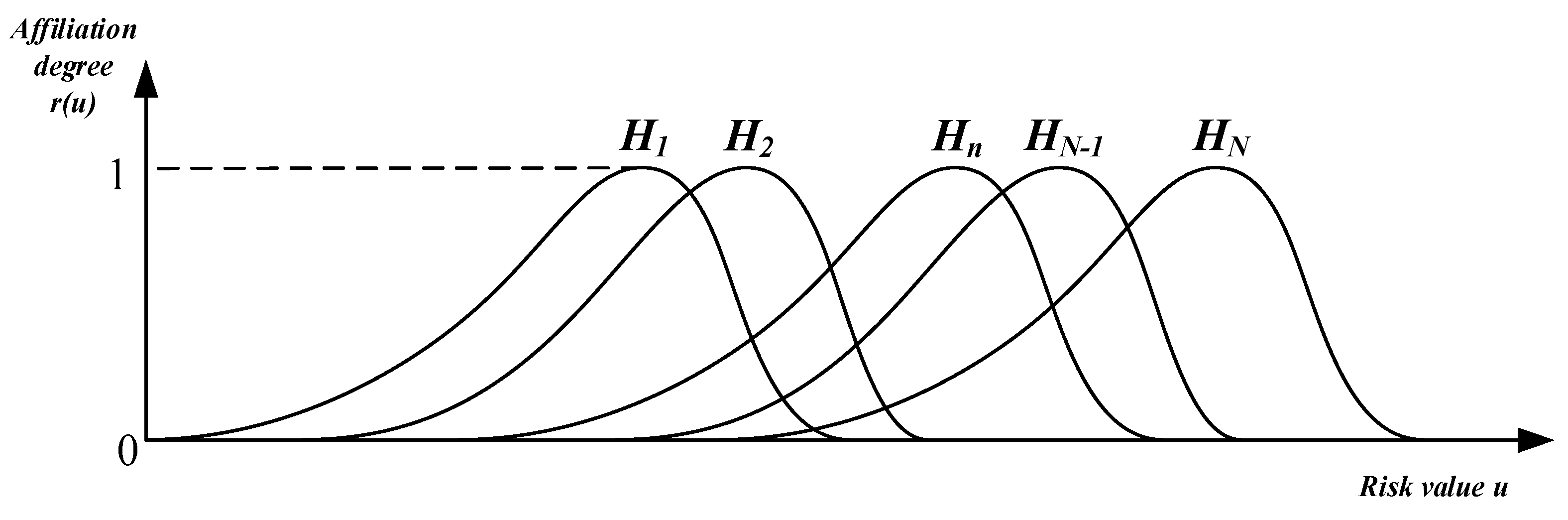
3.2.1. Improved Fuzzy Reliability Structure Model
3.2.2. Fuzzy Evidential Reasoning Algorithm
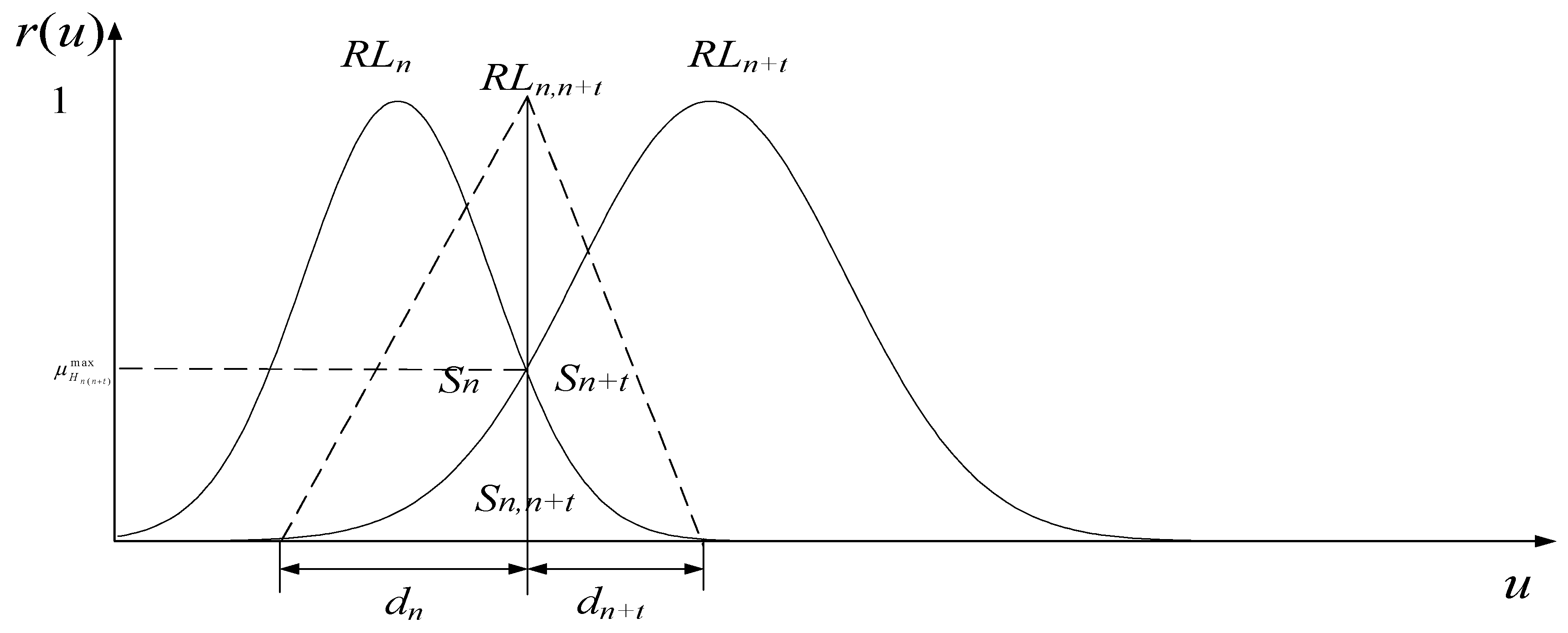
3.2.3. Fuzzy Intersection Reliability Allocation [41]
4. Case Analysis
4.1. Project Overview
4.2. Determination of Comprehensive Weight of Risk Indexes
4.2.1. Subjective Weights Based on the Order Relation Method
4.2.2. Objective Weights Based on the Entropy Weight Method
4.2.3. Determination of Comprehensive Weight
4.3. Comprehensive Risk Evaluation
5. Discussion
- (I).
- Design phase risk is a type of risk that needs to be highly valued in hydropower EPC projects. Due to the early involvement of the design unit and the advantage of providing feasibility study and design consulting services for the owner, the design unit can deeply participate in the owner’s early project planning and strengthen the review and supervision of the design stage. During the owner’s bidding process, the design unit will also undertake project management work, so it is necessary for the general contracting unit to have more strength and bear greater risks. When bidding, it is necessary to objectively analyze and accurately evaluate the bidding conditions of the owner, and sign as comprehensive an agreement as possible in case of disputes. In the process of project implementation, a perfect EPC contract should be signed as far as possible, a perfect design Change control process should be formulated, and a corresponding EPC design management system and project management organization should be established.
- (II).
- The procurement process plays a connecting role in EPC general contracting projects, so the risks in the procurement stage must also be taken seriously. There are various risk factors in the procurement process of planning, implementation, and execution. The procurement process, procurement sources, procurement coordination, etc. will all be risk points, especially with the high and low prices of equipment and materials procurement directly affecting the comprehensive benefits of hydropower projects. Therefore, in the EPC project of hydropower engineering, it is necessary to strengthen procurement management, do a good job in procurement layout and planning, strictly control and manage the procurement process, fully investigate and evaluate the supply channels, and timely follow up on market changes.
- (III).
- Due to the long construction period of hydropower projects, they are affected by many factors during the construction process, so construction risks are also relatively high. Preventing construction risks is crucial. In the preparation stage, it is necessary to strictly review the construction drawings, repeatedly test the corresponding technologies, and select the most suitable technology for hydropower engineering construction, in order to more accurately determine the construction technology. Before the construction of the project, the contractor should invite professional technical personnel and consulting experts to comprehensively investigate the surrounding environment of the project, and then write a detailed investigation and analysis report. During the construction process, a sound quality management system should be established, strict management methods and norms should be established, process monitoring and stable control should be strengthened, and problems discovered during construction should be corrected in a timely manner. At the same time, it is necessary to enhance the safety awareness of all personnel, establish a systematic safety management system, and take necessary measures in a timely manner to eliminate or reduce safety hazards.
- (IV).
- Contract management risk and industry environmental risk are different from the first three types of risks. They run through various stages of hydropower EPC projects and are also two very important types of risks. The EPC project of hydropower engineering involves multiple participants, and the task of contract management is heavy. Contract risks are directly related to factors such as the total contract amount, technical difficulty, construction period, and management quality. In contract management risks, a precise grasp of contract terms, dynamic supervision of contract performance, and strict control of contract changes are all important risk points. It is necessary to ensure that all contract terms are clear and operable and to develop unified change management rules and processes to ensure contract performance. For all parties involved, we should attach importance to win-win cooperation, establish a correct overall view of the project, have a strong sense of performance, ensure the quality of performance, and strive to minimize the risks caused by execution. In industry environmental risks, policy environment, economic environment, market environment, construction environment, etc. are all important risk points. It is necessary to closely monitor policy dynamics, make timely adjustments and improvements, maintain competitiveness and sustainability, and create a good construction environment.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, Y.; Li, H. Study on the Selection of Equipment Suppliers for Wind Power Generation EPC Project. In Proceedings of the 1st International Global on Renewable Energy and Development, IGRED 2017, Singapore, 22–25 December 2017. [Google Scholar]
- Jixiang, Z.; Huifang, G. Research on Contract Risk of EPC Water Conservancy Project Led by Design Enterprise: Based on Set Pair Analysis Method. Constr. Econ. 2020, 41, 136–139. [Google Scholar] [CrossRef]
- Wang, T.; Gao, S.; Li, X.; Ning, X. A meta-network-based risk evaluation and control method for industrialized building construction projects. J. Clean. Prod. 2018, 205, 552–564. [Google Scholar] [CrossRef]
- Bhattarai, S.S.; Kisi, K.P.; Kayastha, R. Contractors’ Claims in an EPC and Turnkey Contract: Lessons Learned from a Hydropower Project. J. Leg. Aff. Disput. Resolut. Eng. Constr. 2023, 15, 1–8. [Google Scholar] [CrossRef]
- Tao, Y.; Yong, X.; Yang, J.; Jia, X.; Chen, W.; Zhou, J.; Wu, Y. Risk Early-Warning Framework for Government-Invested Construction Project Based on Fuzzy Theory, Improved BPNN, and K-Means. Math. Probl. Eng. 2022, 2022, 5958472. [Google Scholar] [CrossRef]
- Zhiguo, W.; Zhihai, T.; Ji, Y. On the deep integration of design and construction under the EPC mode. Water Resour. Hydropower Eng. 2022, 53, 330–332. [Google Scholar] [CrossRef]
- Hongyu, L.; Hao, Z.; Yuxin, W.; Sujuan, C. Risk Analysis and Countermeasures of EPC Project Contract Based on the Principle of Responsibility, Right and Interest. Constr. Econ. 2021, 42, 128–131. [Google Scholar] [CrossRef]
- Chaojuan, L.; Fuzhou, L. Risk Management Research of EPC Contracting Model in Hydropower Project. Yellow River 2013, 35, 115–117. [Google Scholar]
- Hung, M.S.; Wang, J.Q.; Thanh, M.S. Research on delay risks identification and control in the construction progress of epc hydropower projects in Vietnam. Bol. Tec./Tech. Bull. 2017, 55, 610–623. [Google Scholar]
- Ding, Y.; Zhang, X.; Zhou, L.; Xu, C. Investment Risk Assessment of EPC Power Transmission and Transformation Projects under New Energy Grid Connection Based on the Owner’s Perspective. Math. Probl. Eng. 2022, 2022, 2258938. [Google Scholar] [CrossRef]
- Xu, G. Quality control of mechanical and electrical engineering of large pumped storage power plants under EPC mode. Water Resour. Hydropower Eng. 2022, 53, 333–337. [Google Scholar] [CrossRef]
- Yanping, L.; Zuowen, W.; Wanli, P. Cost risk evaluation of prefabricated building project under EPC mode based on combination weighting-evidence theory-fuzzy comprehensive evaluation method. Sci. Technol. Eng. 2022, 22, 4562–4571. [Google Scholar]
- Hui, L. Triangular fuzzy number-based study on bidding risk evaluation model for water conservancy and hydropower EPC project. Water Resour. Hydropower Eng. 2016, 47, 55–60. [Google Scholar] [CrossRef]
- Dong, S.; Li, S.; Yu, F.; Wang, K. Risk Assessment of Immersed Tube Tunnel Construction. Processes 2023, 11, 980. [Google Scholar] [CrossRef]
- Zhiding, C.; Hao, L.; Fang, X. Risk assessment for EPC procurement of hydropower projects. Yangtze River 2015, 46, 109–112. [Google Scholar] [CrossRef]
- Kaichang, S.; Quan, L.; Zhiwei, Y. Study on G1—Grey evaluation method for emergency capability in hydraulic engineering construction. Water Resour. Hydropower Eng. 2017, 48, 43–47. [Google Scholar] [CrossRef]
- Kun, L.; Minhao, X.; Jiaye, Q. Value Evaluation System Construction and Empirical Study of Disruptive Technology—Based on AHP and Information Entropy. Forum Sci. Technol. China 2023, 322, 30–38. [Google Scholar] [CrossRef]
- Bognár, F.; Hegedűs, C. Analysis and Consequences on Some Aggregation Functions of PRISM (Partial Risk Map) Risk Assessment Method. Mathematics 2022, 10, 676. [Google Scholar] [CrossRef]
- Li, H.; Liang, M.; Zhang, C.; Cao, Y. Risk Evaluation of Water Environmental Treatment PPP Projects Based on the Intuitionistic Fuzzy MULTIMOORA Improved FMEA Method. Systems 2022, 10, 163. [Google Scholar] [CrossRef]
- Rihong, L.; Jinlin, H.; Jianwei, Z. Dike safety evaluation based on combined weighting and cloud model. South-North Water Transf. Water Sci. Technol. 2021, 19, 1217–1226. [Google Scholar] [CrossRef]
- Wei, D.; Xu, D.; Zhang, Y. A fuzzy evidential reasoning-based approach for risk assessment of deep foundation pit. Tunn. Undergr. Space Technol. 2020, 97, 103232. [Google Scholar] [CrossRef]
- Tian, F.; Jing, Z.; Zhao, H.; Zhang, E.; Liu, J. A synthetic condition assessment model for power transformers using the fuzzy evidence fusion method. Energies 2019, 12, 857. [Google Scholar] [CrossRef]
- Qiao, X.; Shi, D.; Aguirre-Hernandez, B. Risk Analysis of Emergency Based on Fuzzy Evidential Reasoning. Complexity 2019, 2019, 5453184. [Google Scholar] [CrossRef]
- Zhou, H.; Cao, P. A fuzzy AHP approach to select supporting schemes for city foundation pit in soft soil. Zhongnan Daxue Xuebao (Ziran Kexue Ban)/J. Cent. South Univ. (Sci. Technol.) 2012, 43, 3582–3588. [Google Scholar]
- Di, Z.; Jinfen, Z.; Xinping, Y. Navigation Risk Assessment for Inland Waterway Transportation System Based on Fuzzy Rule Base and Evidential Reasoning. Navig. China 2014, 37, 71–75+98. [Google Scholar]
- Bao, X.-H.; Fu, Y.-B.; Huang, H.-W. Case study of risk assessment for safe grade of deep excavations. Yantu Gongcheng Xuebao/Chin. J. Geotech. Eng. 2014, 36, 192–197. [Google Scholar] [CrossRef]
- Xu, C.; Ren, Q. Fuzzy-synthetical evaluation on stability of surrounding rockmasses of underground engineering. Yanshilixue Yu Gongcheng Xuebao/Chin. J. Rock Mech. Eng. 2004, 23, 1852–1855. [Google Scholar]
- Daojiang, W.; Yong, Z.; Min, A. Fuzzy witness reasoning-based approach to the risk assessment of the deep foundation pit construction. J. Saf. Environ. 2021, 21, 512–520. [Google Scholar] [CrossRef]
- Jiang, J.; Xuan, L.; Li-ning, X.; Yingwu, C. System risk analysis and evaluation approach based on fuzzy evidential reasoning. Syst. Eng.—Theory Pract. 2013, 33, 529–537. [Google Scholar]
- Fenghua, J.; Baimei, Y.; Hongwei, M. The Yangtze River Delta city cluster logistics resilience measurement. Stat. Decis. 2022, 38, 102–105. [Google Scholar] [CrossRef]
- Zhengyang, L.; Yong, Z.; Zhimei, W.; Jiying, L. Effectiveness Evaluation of Carrier Aircraft Support Mission Scheme Based on Improved Order Relation Method and Grey Relation Analysis. J. Ordnance Equip. Eng. 2020, 41, 234–240. [Google Scholar]
- Chen, L.; Yan-zhang, W. Research on TOPSIS integrated evaluation and decision method based on entropy coefficient. Control Decis. 2003, 456–459. [Google Scholar] [CrossRef]
- Chi, Y.; Lv, C.; Wang, D.; Geng, J.; Jin, Y. An Objective Weight Determination Method Based on Model Healthy status Recognition Rate. In Proceedings of the 31st European Safety and Reliability Conference, ESREL 2021, Angers, France, 19–23 September 2021; pp. 1040–1046. [Google Scholar]
- Wei, Z.; Li, J.; Zhang, N. Performance Evaluation Model of Urban Road Asphalt Pavement Based on Attribute Hierarchical Model and Entropy Weight Method. In Proceedings of the 22nd COTA International Conference of Transportation Professionals, CICTP 2022, Changsha, China, 8–11 July 2022; pp. 2221–2231. [Google Scholar]
- Zhao, J.; Tian, J.; Meng, F.; Zhang, M.; Wu, Q. Safety assessment method for storage tank farm based on the combination of structure entropy weight method and cloud model. J. Loss Prev. Process Ind. 2022, 75, 104709. [Google Scholar] [CrossRef]
- Li, F.; Su, M.; Li, D. Combination Evaluation Model Based on Entropy Weight Method. In Proceedings of the 2021 2nd International Conference on Machine Learning and Computer Application, ICMLCA 2021, Shenyang, China, 17–19 December 2021; pp. 252–256. [Google Scholar]
- Zhang, Z.; Geng, Y.; Wu, X.; Zhou, H.; Lin, B. A method for determining the weight of objective indoor environment and subjective response based on information theory. Build. Environ. 2022, 207, 108426. [Google Scholar] [CrossRef]
- Xie, Y.; Wang, L.; Sun, D.a.; Zhang, L.; Liu, C.; Xu, Y. Health diagnosis model with combination weight and clustering method for protection works of expansive soil slope and its application. Zhongnan Daxue Xuebao (Ziran Kexue Ban)/J. Cent. South Univ. (Sci. Technol.) 2022, 53, 258–268. [Google Scholar] [CrossRef]
- Du, X.-L.; Zhang, X.-F.; Zhang, M.-J.; Hou, B.-W. Risk synthetic assessment for deep pit construction based on evidence theory. Yantu Gongcheng Xuebao/Chin. J. Geotech. Eng. 2014, 36, 155–161. [Google Scholar] [CrossRef]
- Jiang, J.; Liu, G.; Huang, X.; Ou, X. Risk Assessment of Constructing Deep Foundation Pits for Metro Stations Based on Fuzzy Evidence Reasoning and Two-tuple Linguistic Analytic Network Process. Shock Vib. 2022, 2022, 2650627. [Google Scholar] [CrossRef]
- Yao, T.; Miao, R.; Wang, W.; Li, Z.; Dong, J.; Gu, Y.; Yan, X. Synthetic damage effect assessment through evidential reasoning approach and neural fuzzy inference: Application in ship target. Chin. J. Aeronaut. 2022, 35, 143–157. [Google Scholar] [CrossRef]
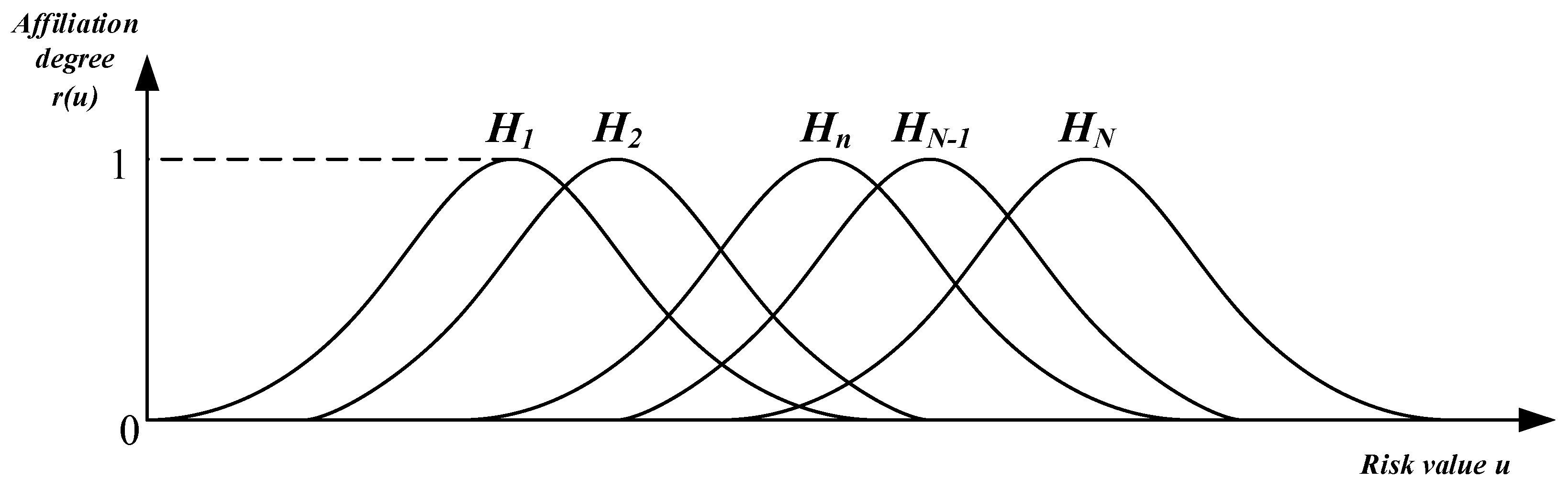


| Meaning | |
|---|---|
| 1.0 | Index and index are equally important |
| 1.2 | Index and index are slightly important |
| 1.4 | Index and index are obviously important |
| 1.6 | Index and index are strongly important |
| 1.8 | Index and index are extremely important |
| Intermediate value | The above neighbors determine the intermediate value |
| Sort | |||||
|---|---|---|---|---|---|
| 1 | , 0 | , 0 | , 0 | , 0 | , 0 |
| 2 | , 1.1 | , 1.2 | , 1.1 | , 1.1 | , 1.2 |
| 3 | , 1.2 | , 1.1 | , 1.2 | , 1.2 | , 1.2 |
| 4 | , 1.2 | , 1.2 | , 1.2 | , 1.2 | , 1.2 |
| 5 | , 1.3 | , 1.3 | , 1.2 | , 1.3 | , 1.3 |
| Index | J1 | J2 | J3 | J4 | J5 |
|---|---|---|---|---|---|
| C1 | 0.163 | 0.179 | 0.175 | 0.175 | 0.171 |
| C2 | 0.148 | 0.148 | 0.146 | 0.146 | 0.143 |
| C3 | 0.235 | 0.216 | 0.231 | 0.231 | 0.226 |
| C4 | 0.258 | 0.260 | 0.254 | 0.255 | 0.272 |
| C5 | 0.196 | 0.197 | 0.194 | 0.193 | 0.188 |
| First Level Index | Weight | Second Level Index | Weight |
|---|---|---|---|
| C1 | 0.173 | C11 | 0.167 |
| C12 | 0.136 | ||
| C13 | 0.239 | ||
| C14 | 0.248 | ||
| C15 | 0.210 |
| Index | C1 | C2 | C3 | C4 | C5 |
|---|---|---|---|---|---|
| Weight | 0.173 | 0.146 | 0.228 | 0.260 | 0.193 |
| Index | C1 | C2 | C3 | C4 | C5 |
|---|---|---|---|---|---|
| Entropy | 1.6090 | 1.6088 | 1.6089 | 1.6088 | 1.6086 |
| Index | C1 | C2 | C3 | C4 | C5 |
|---|---|---|---|---|---|
| Weight | 0.156 | 0.191 | 0.186 | 0.192 | 0.275 |
| Index | C1 | C2 | C3 | C4 | C5 |
|---|---|---|---|---|---|
| Weight | 0.163 | 0.172 | 0.203 | 0.221 | 0.241 |
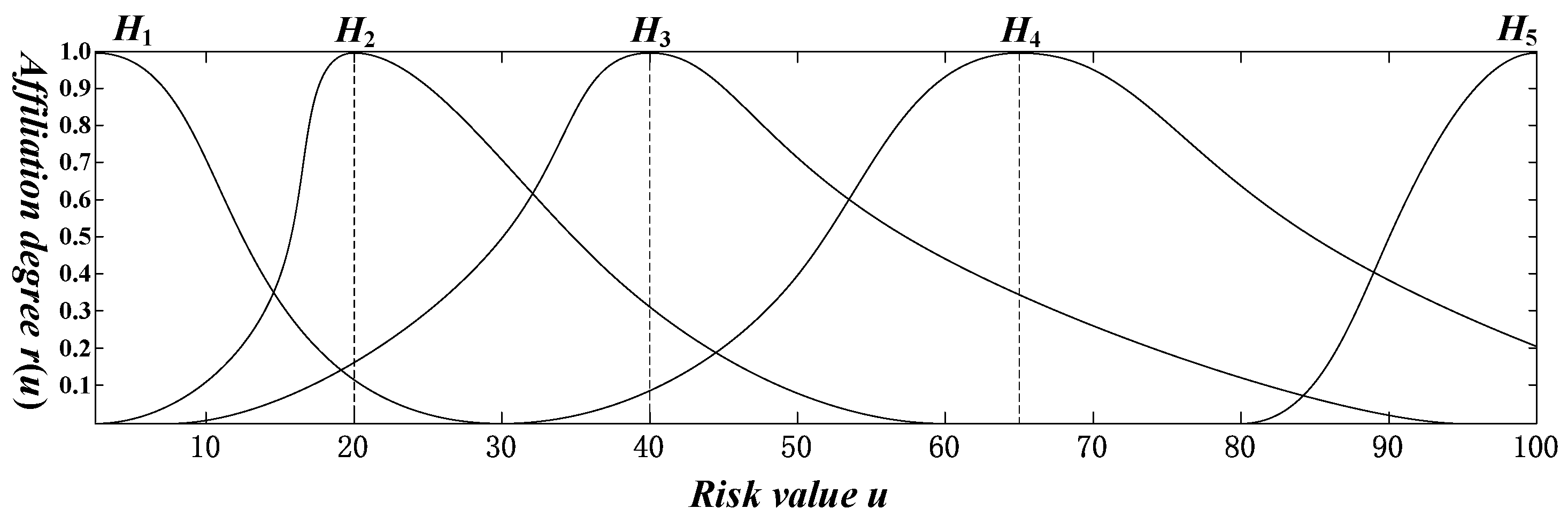
| Risk Level | Severity | Risk Value Range | Affiliation Function μ σ |
|---|---|---|---|
| Level 1 | low | 0 < u ≤ 45 | μ = 0, σ = 15 |
| Level 2 | lower | 0 < u ≤ 60 | μ = 30, σ = 10 |
| Level 3 | medium | 5 < u ≤ 95 | μ = 50, σ = 15 |
| Level 4 | higher | 30 < u ≤ 100 | μ = 75, σ = 15 |
| Level 5 | high | 70 < u ≤ 100 | μ = 100, σ = 10 |
| Risk Level | Severity | Risk Value Range | Affiliation Function μ σ |
|---|---|---|---|
| Level 1 | Low | 0 < u ≤ 30 | μ = 0, σ = 10 |
| Level 2 | Lower | 0 < u ≤ 20 | μ = 20, σ = 20/3 |
| 20 < u ≤ 60 | μ = 20, σ = 40/3 | ||
| Level 3 | Medium | 5 < u ≤ 40 | μ = 40, σ = 35/3 |
| 40 < u ≤ 95 | μ = 40, σ = 55/3 | ||
| Level 4 | Higher | 30 < u ≤ 65 | μ = 65, σ = 35/3 |
| 65 < u ≤ 100 | μ = 65, σ = 55/3 | ||
| Level 5 | High | 80 < u ≤ 100 | μ = 100, σ = 20/3 |
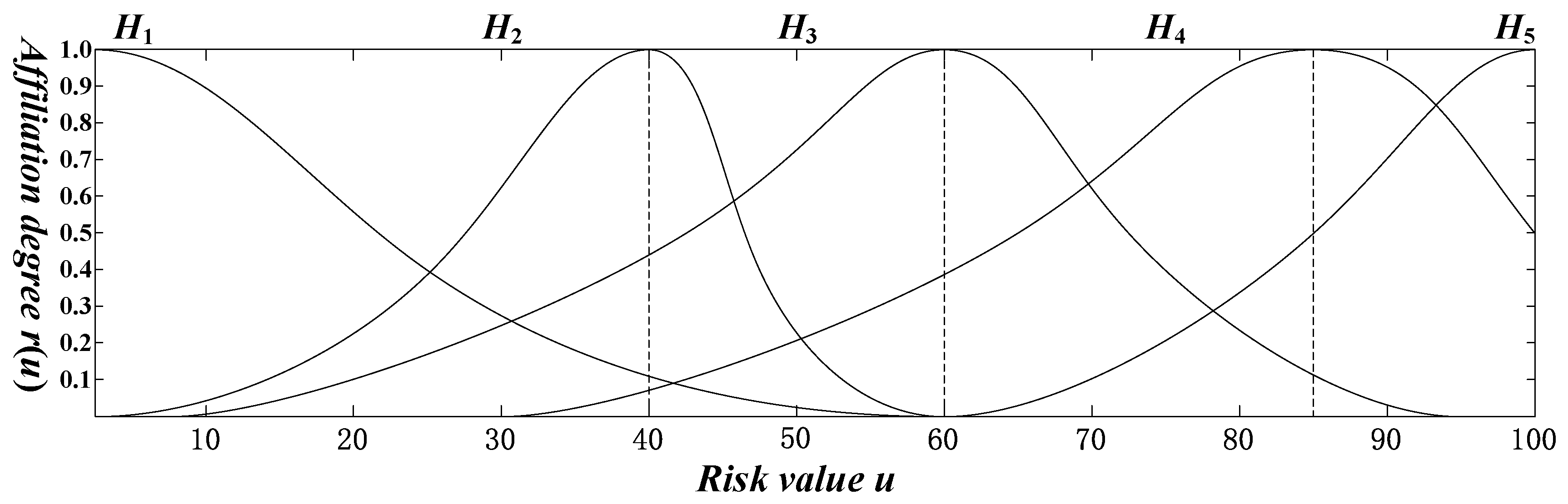
| Risk Level | Severity | Risk Value Range | Affiliation Function μ σ |
|---|---|---|---|
| Level 1 | Low | 0 < u ≤ 60 | μ = 0, σ = 20 |
| Level 2 | Lower | 0 < u ≤ 40 | μ = 40, σ = 40/3 |
| 40 < u ≤ 60 | μ = 40, σ = 20/3 | ||
| Level 3 | Medium | 5 < u ≤ 60 | μ = 60, σ = 55/3 |
| 60 < u ≤ 95 | μ = 60, σ = 35/3 | ||
| Level 4 | Higher | 30 < u ≤ 85 | μ = 85, σ = 55/3 |
| 85 < u ≤ 100 | μ = 85, σ = 35/3 | ||
| Level 5 | High | 60 < u ≤ 100 | μ = 100, σ = 40/3 |
| 1 | 0.4868 | 0.2494 | 0.0439 | 0 | |
| 1 | 0.726 | 0.198 | 0 | ||
| 1 | 0.707 | 0.135 | |||
| 1 | 0.6065 | ||||
| 1 |
| 1 | 0.4868 | 0.1819 | 0 | 0 | |
| 1 | 0.7261 | 0.1979 | 0 | ||
| 1 | 0.7066 | 0.0561 | |||
| 1 | 0.1617 | ||||
| 1 |
| 1 | 0.487 | 0.294 | 0.0439 | 0 | |
| 1 | 0.726 | 0.086 | 0 | ||
| 1 | 0.707 | 0.278 | |||
| 1 | 0.835 | ||||
| 1 |
| n | |||||
|---|---|---|---|---|---|
| 1 | 0.0611 | ||||
| 2 | 0.1291 | 0.0075 | |||
| 3 | 0.1629 | 0.0058 | 0.029 | ||
| 4 | 0.1354 | 0.0014 | 0.0065 | 0.0275 | |
| 5 | 0.0575 | 0.0000 | 0.0000 | 0.0046 | 0.0114 |
| k = 1.151; = 0.3773; = 0.3773 | |||||
| 0.107 | 0.24 | 0.298 | 0.242 | 0.097 | |
| 0.114 | 0.299 | 0.348 | 0.162 | 0.058 | |
| 0.117 | 0.302 | 0.365 | 0.149 | 0.048 | |
| 0.083 | 0.143 | 0.273 | 0.319 | 0.167 | |
| 0.116 | 0.237 | 0.315 | 0.223 | 0.095 | |
| 0.093 | 0.235 | 0.324 | 0.227 | 0.091 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Guo, Y.; Wang, B.; Chen, Y.; Xie, J.; Wen, C. Research on Risk Evaluation of Hydropower Engineering EPC Project Based on Improved Fuzzy Evidence Reasoning Model. Systems 2023, 11, 327. https://doi.org/10.3390/systems11070327
Li Q, Guo Y, Wang B, Chen Y, Xie J, Wen C. Research on Risk Evaluation of Hydropower Engineering EPC Project Based on Improved Fuzzy Evidence Reasoning Model. Systems. 2023; 11(7):327. https://doi.org/10.3390/systems11070327
Chicago/Turabian StyleLi, Qian, Ying Guo, Bo Wang, Yingqi Chen, Jiaxiao Xie, and Chuanhao Wen. 2023. "Research on Risk Evaluation of Hydropower Engineering EPC Project Based on Improved Fuzzy Evidence Reasoning Model" Systems 11, no. 7: 327. https://doi.org/10.3390/systems11070327
APA StyleLi, Q., Guo, Y., Wang, B., Chen, Y., Xie, J., & Wen, C. (2023). Research on Risk Evaluation of Hydropower Engineering EPC Project Based on Improved Fuzzy Evidence Reasoning Model. Systems, 11(7), 327. https://doi.org/10.3390/systems11070327





