This section dissects the performance of the proposed method in more detail. It begins with the computational complexity of the technique and then provides empirical results on both machine learning and general function optimization tasks.
3.1. Computational Complexity
Forming the hierarchical structure and conducting the collaborative searching process are the two major stages of the proposed method and these stages need to be conducted in sequence. The rest of this section investigates the complexity of each step separately and in relation to one another.
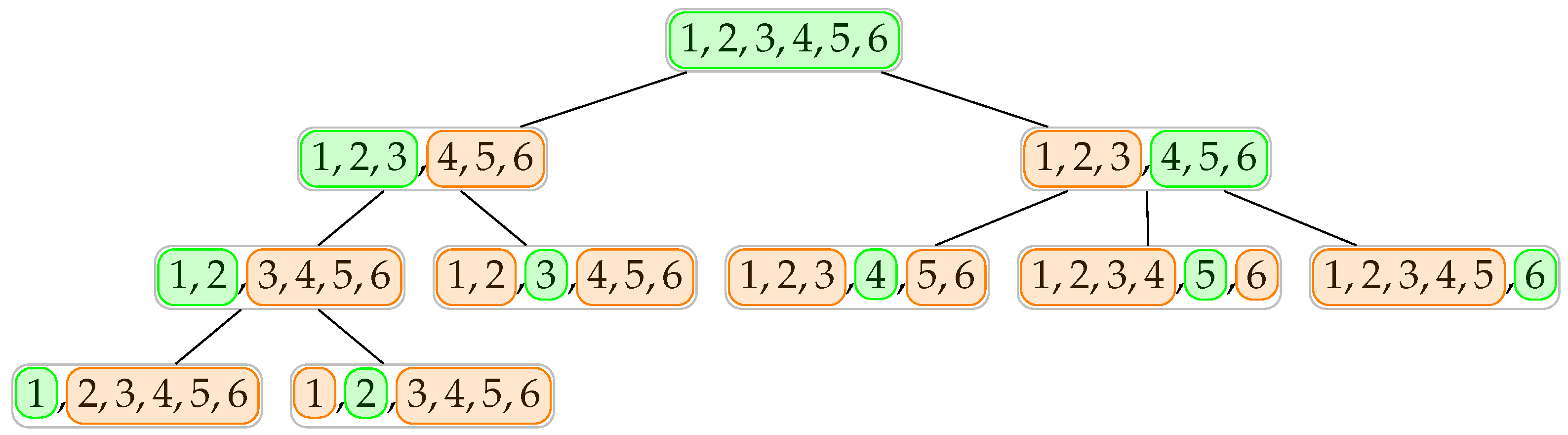
Regarding the structural formation phase of the suggested method, the shape of the hierarchy depends on the maximum number of connections that each agent can handle; the fewer the number of manageable concurrent connections, the deeper the resulting hierarchy. Using the same notations presented in
Section 2.1 and assuming the same
for all agents, the depth of the formed hierarchy is
. Thanks to the distributed nature of the formation algorithm and the concurrent execution of the agents, the worst-case time complexity of the first stage will be
. With the same assumption, it can be easily shown that the resulting hierarchical structure is a complete tree. Hence, denoting the total number of agents in the system by
, this quantity would be:
With that said, the space complexity for the first phase of the proposed technique would be . It is worth noting that among all created agents, only terminal agents would require dedicated computational resources as they are completing the actual searching and optimization process, and the remaining can all be hosted and managed together.
The procedures in each round of the second phase of the suggested method can be broken down into two main components: (i) transmitting the start coordinates from the root of the hierarchy to the terminal agents, transmitting the results back to the root, and preparing the feedback; and (ii) conducting the actual searching process by the terminal agents to locate a local optimum. The worst-case time complexity of preparing the feedback based on the algorithms that were discussed in
Section 2 would be
, which is because it finds the best candidate among all returned results. In addition, due to the concurrency of the agents, the first component is only processed at the height of the built structure. Therefore, the time complexity of component (i) would be
. The complexity of the second component, moreover, depends on both the budget of the agent, i.e.,
b, and the complexity of building and evaluating response function
. Let
denote the time complexity of a single evaluation. As a terminal agent makes a
b number of such evaluations to choose its candidate optima, the time complexity for the agent would be
. As all agents work in parallel, the complexity of a single iteration at the terminal agents would be
, leading to the overall time complexity of
. In machine learning problems, we often have
. Therefore, if
denotes the number of iterations until the second phase of the tuning method stops, the complexity of the second stage would be
. The space complexity of the second phase of the tuning method depends on the way that each agent is implementing the main functionalities, such as the learning algorithms they represent, transmitting the coordinates, and providing feedback. Except for the ML algorithms, all internal functionalities of each agent can be implemented using
space. Moreover, we have
agents in the system, which leads to a total space complexity of
for non-ML tasks. Let
denote the worst-case space complexity of a machine learning algorithm that we are tuning. The total space complexity of the second phase of the proposed tuning method would be
. Similar to the time complexity, in machine learning, we often have
, which makes the total space complexity of the second phase
. Please note that we have factored out the budgets of the agents and the number of iterations because we did not store the history between different evaluations and iterations.
Considering both stages of the proposed technique and due to the fact that they are conducted in sequence, the time complexity of the entire steps in an ML hyperparameter tuning problem, from structure formation to completing the searching operations, would be . Similarly, the space complexity would be .
3.2. Empirical Results
This section presents the empirical results of employing the proposed agent-based randomized searching algorithm and discusses the improvements resulting from the suggested inter-agent collaborations. Hyperparameter tuning in machine learning is basically a back-box optimization problem, and hence, to enrich our empirical discussions, this section also includes results from multiple multi-dimensional optimization problems.
The performance metrics used for the experiments are based on those that are commonly used by the ML and optimization communities. Additionally, we analyze the behavior of the suggested methodology based on its own design parameter values, such as budget, width, etc. The methods that have been chosen for the sake of comparison are the standard random search and the Latin hypercube search methods [
1] that are commonly used in practice. Our choices are based on the fact that not only are these methods embarrassingly parallel and among the top choices to be considered in distributed scenarios, but they are also used as the core optimization mechanisms of the terminal agents in the suggested method, and hence can better present the impact of the inter-agent collaborations. In its generic format, as emphasized in [
20], one can easily employ alternative searching methods or diversify them at the terminal level, as needed.
Throughout the experiments, each terminal agent runs on a separate process, and to make the comparisons fair, we keep the number of model/function evaluations fixed among all of the experimented methods. To put it in more detail, for a budget value of b for each of terminal agents and number of iterations, the proposed method will evaluate the search space in coordinates. We use the same number of independent agents for the compared random-based methodologies and, keeping the evaluation budgets of the agents fixed—the budgets are assumed to be enforced by the computational limitations of devices or processes running the agents—we repeat those methods times and report the best performance among all agents’ repetition histories as their final result.
The experiments assess the performance of the proposed method in comparison to the other random-based techniques in four categories: (1) iteration-based assessment, which checks the performance of the methods for a particular iteration threshold. In this category, all other parameters, such as budget, connection number, etc., are kept fixed; (2) budget-based assessment, which examines the performance under various evaluation budgets for the terminal agents. It is assumed that all agents have the same budget; (3) width-based assessment, which checks how the proposed method performs for various exploration criteria specified by the slot width parameter; and finally, (4) connection-based evaluation, which inspects the effect of the parallel connection numbers that the internal agents can handle. In other words, this evaluation checks if the proposed method is sensitive to the way that the hyperparameter or decision variables are split during the hierarchy formation phase. All implementations use Python 3.9 and the scikit-learn library [
26], and the results reported in all experiments are based on 50 different trials.
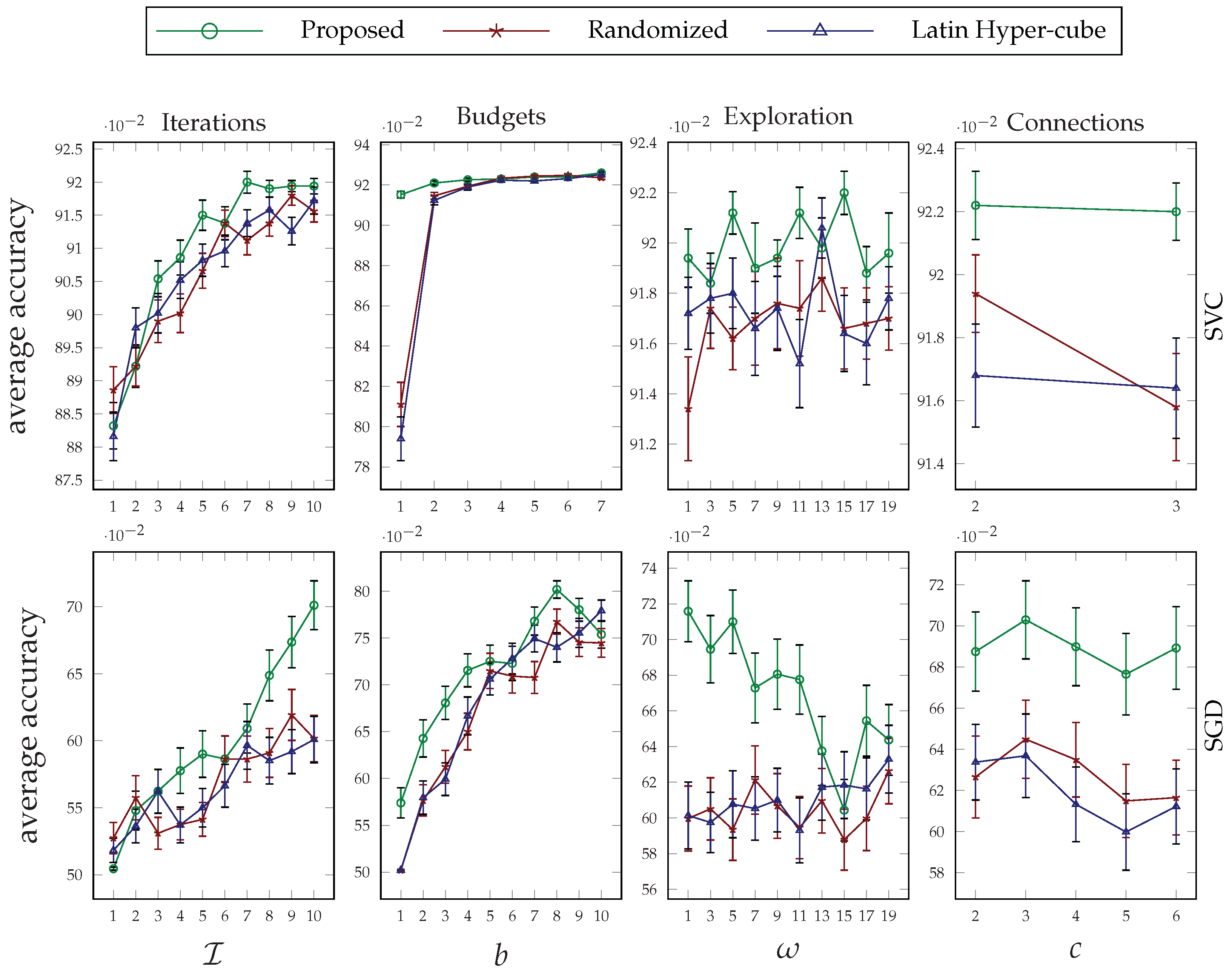
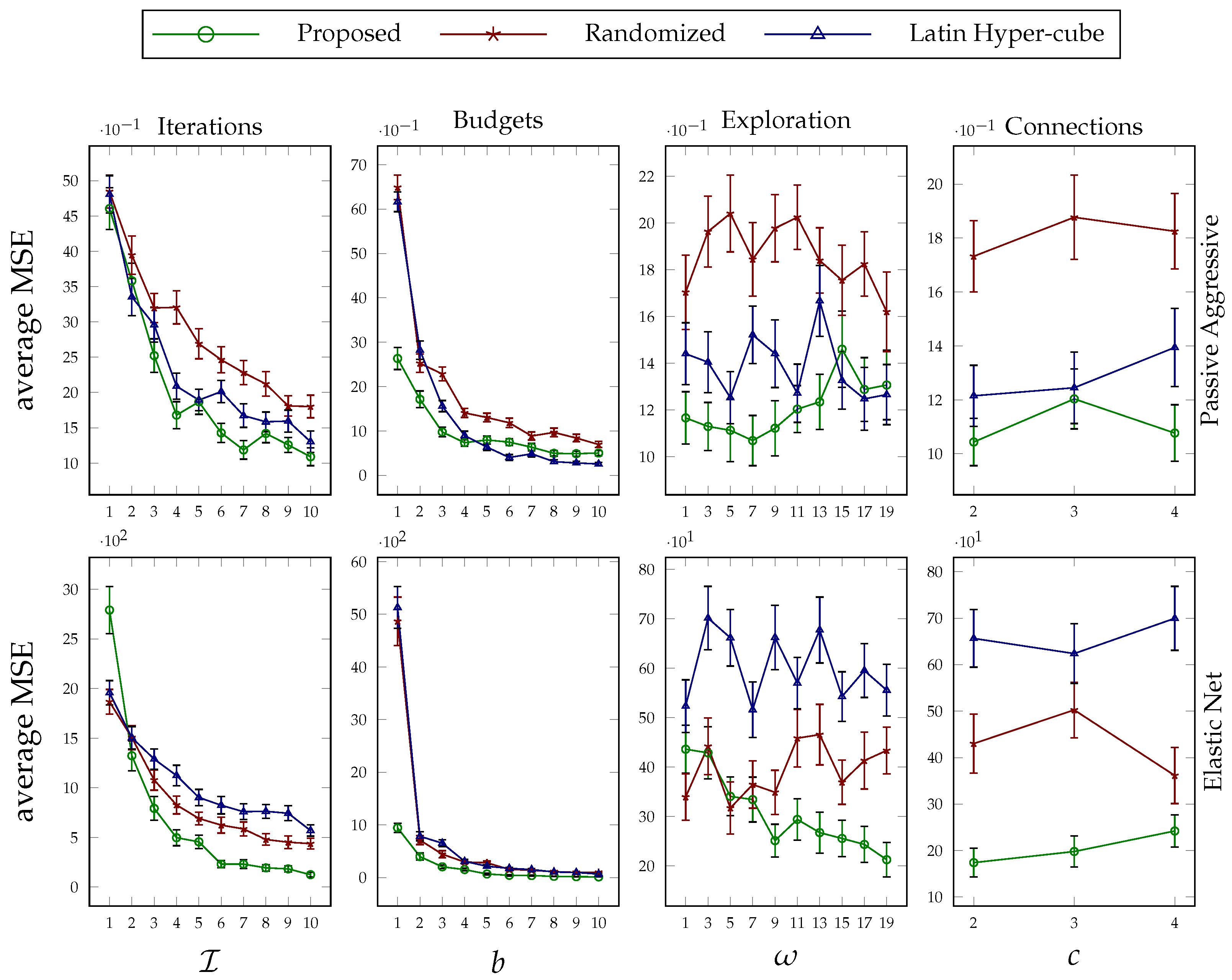
For the ML hyperparameter tuning experiments, we have dissected the behavior of the proposed algorithm in two classifications and two regression problems. The details of such problems, including the hyperparameters that are tuned and the used datasets are presented in
Table 1. In all of the ML experiments, we have used five-fold cross-validation as the model evaluation method. The results obtained for the classification and regression problems are plotted in
Figure 3 and
Figure 4, respectively. Please note that there are numerous ML algorithms that can be used to evaluate our approach. Our selected algorithms are representative of different types of classifiers/regressors, including linear and non-linear models with different regularization methods, and we found them widely used in hyperparameter tuning literature based on their performance sensitivity to the choice of hyperparameter values. We also experienced this empirically during our evaluations of some other ML algorithms. We found that all of the compared models converged to a local optimum point quickly, potentially due to the geometry of their response functions, which would not demonstrate the improvements of our model. By comparing the performance of the presented methods on these models, we hope to draw more general conclusions about the effectiveness of the methods in various settings.
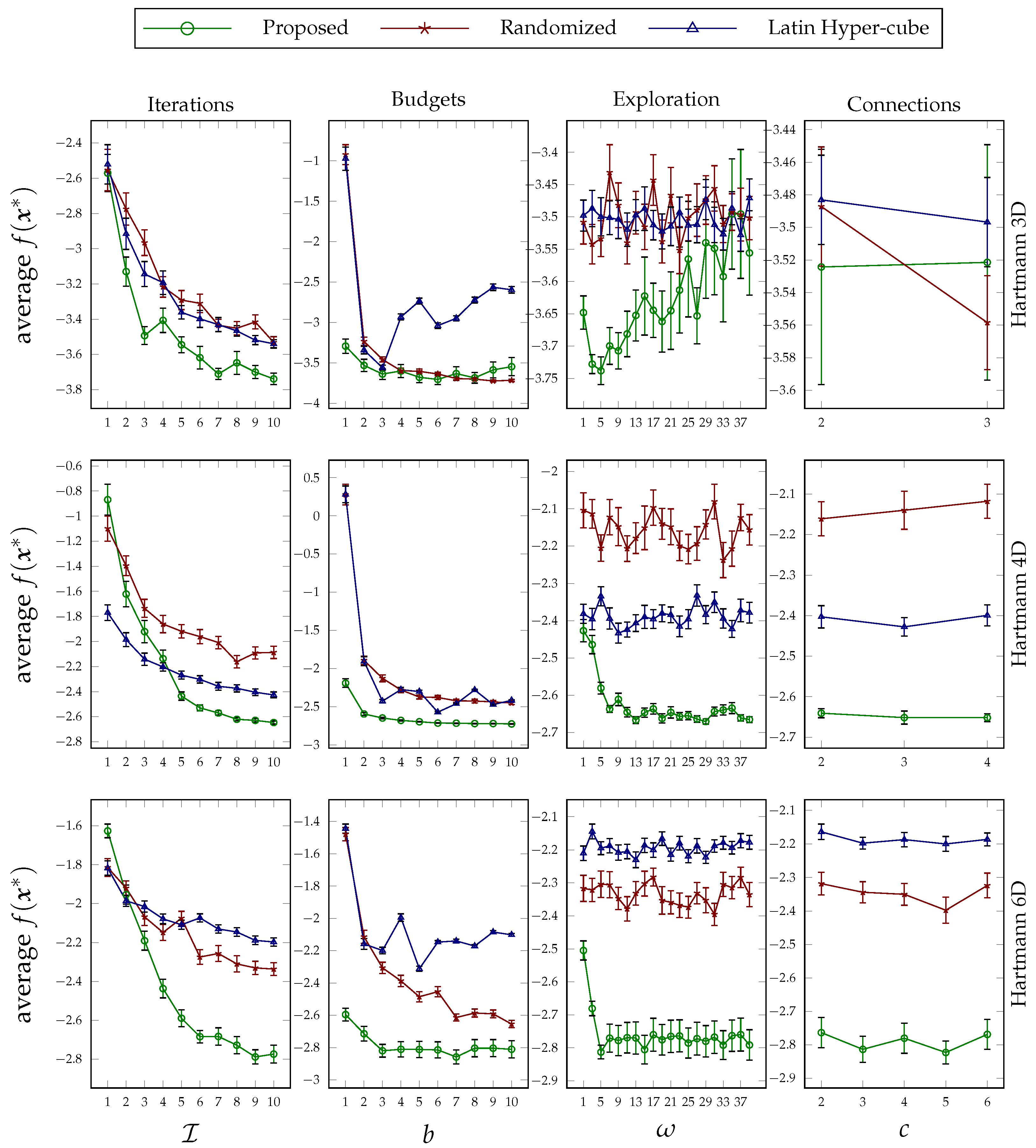
For the
iterations plot in the first column plots of
Figure 3 and
Figure 4, we fixed the parameters of the proposed method for all agents as follows:
. As can be seen, when the proposed method is allowed to run for more iterations, it yields better performance, and its superiority against the other two random-based methods is evident. Comparing the relative performance improvements resulting from the proposed method in the presented ML tasks, it can be seen that as the search space of the agents and the number of hyperparameters needed to be tuned increased, the proposed collaborative method achieved a higher improvement. For the Stochastic Gradient Descent (SGD) classifier, for instance, the objective hyperparameter set comprises six members with continuous domain spaces, and the number of improvements that have been made after 10 iterations is much higher, about 17%, than in the other experiments with three to four hyperparameters and mixed continuous and discrete domain spaces.
Table 1.
The details of the machine learning algorithms and the datasets used for hyperparameter tuning experiments.
Table 1.
The details of the machine learning algorithms and the datasets used for hyperparameter tuning experiments.
| ML Algorithm | | Dataset | Performance Metric |
|---|
| C-Support Vector Classification (SVC) [26,27] | 1 | artificial (100,20) † | accuracy |
| Stochastic Gradient Descent (SGD) Classifier [26] | 2 | artificial (500,20) † | accuracy |
| Passive Aggressive Regressor [26,28] | 3 | artificial (300,100) ‡ | mean squared error |
| Elastic Net Regressor [26,29] | 4 | artificial (300,100) ‡ | mean squared error |
The second column of
Figure 3 and
Figure 4 illustrate how the performance of the proposed technique changes when we increase the evaluation budgets of the terminal agents. For this set of experiments, we set the parameter values of our method as follows:
. By increasing the budget value, the performance of the suggested approach per se improves. However, the rate of improvement slows down for higher budget values, and comparing it against the performance of the other two random-based searching methods, the improvement is significant for lower budget values. In other words, the proposed tuning method surpasses the other two methods when the agents have limited searching resources. This makes our method a good candidate for tuning the hyperparameters of deep learning approaches with expensive model evaluations.
The behavior of the suggested method under various exploration parameter values can be seen in column 3 of
Figure 3 and
Figure 4. The
values on the x-axis of the plots are used to set the initial value for the slot width parameter of all agents using
. Based on this configuration, higher values of
yield lower values of
, and as a result, there is more exploitation around the starting coordinates. The other parameters of the method are configured as follows:
. Recall from
Section 2 that the exploration parameter is used by an agent for the dimensions that it does not represent. Based on the results obtained from various tasks, choosing a proper value for this parameter depends on the characteristics of the response function. Having said that, the behavior for a particular task remains almost consistent. Hence, trying one small and one large value for this parameter in a specific problem will reveal its sensitivity and help choose an appropriate value for it.
Finally, the last set of experiments investigates the impact of the number of parallel connections that the internal agents can manage, i.e.,
c, on the performance of the suggested method. The results of this study are plotted in the last column of
Figure 3 and
Figure 4. The difference in the number of data points in each plot is because of the difference in the size of the hyperparameters that we tune for each task. The values of the parameters that we kept fixed for this set of experiments are as follows:
. As can be seen from the illustrated results, the proposed method is not very sensitive to the value that we choose or that is enforced by the system for parameter
c. This parameter plays a critical role in the shape of the hierarchy that is distributedly formed in phase 1 of the suggested approach; therefore, one can opt to choose a value that fits with the connection or computational resources that are available without sacrificing performance very much.
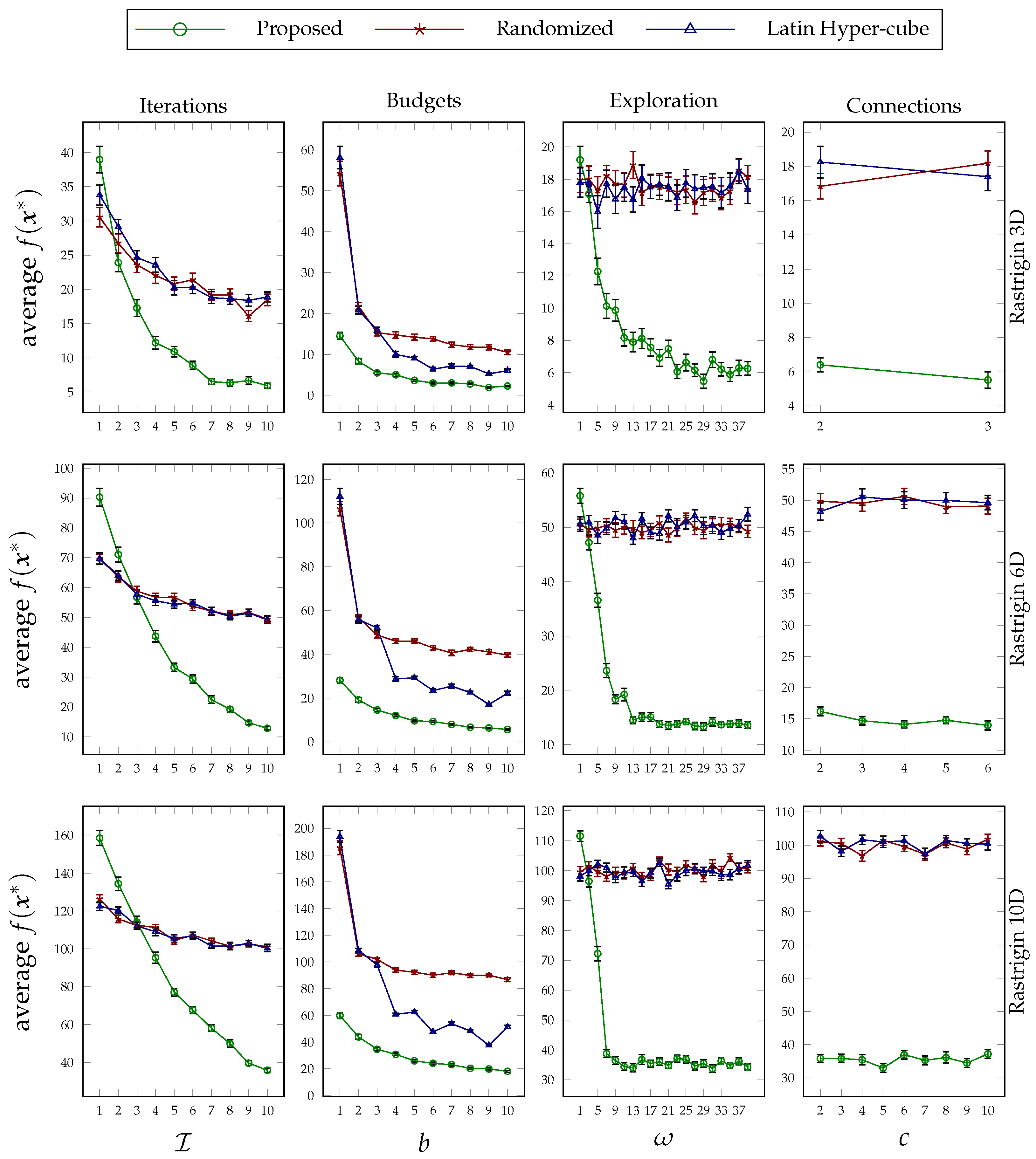
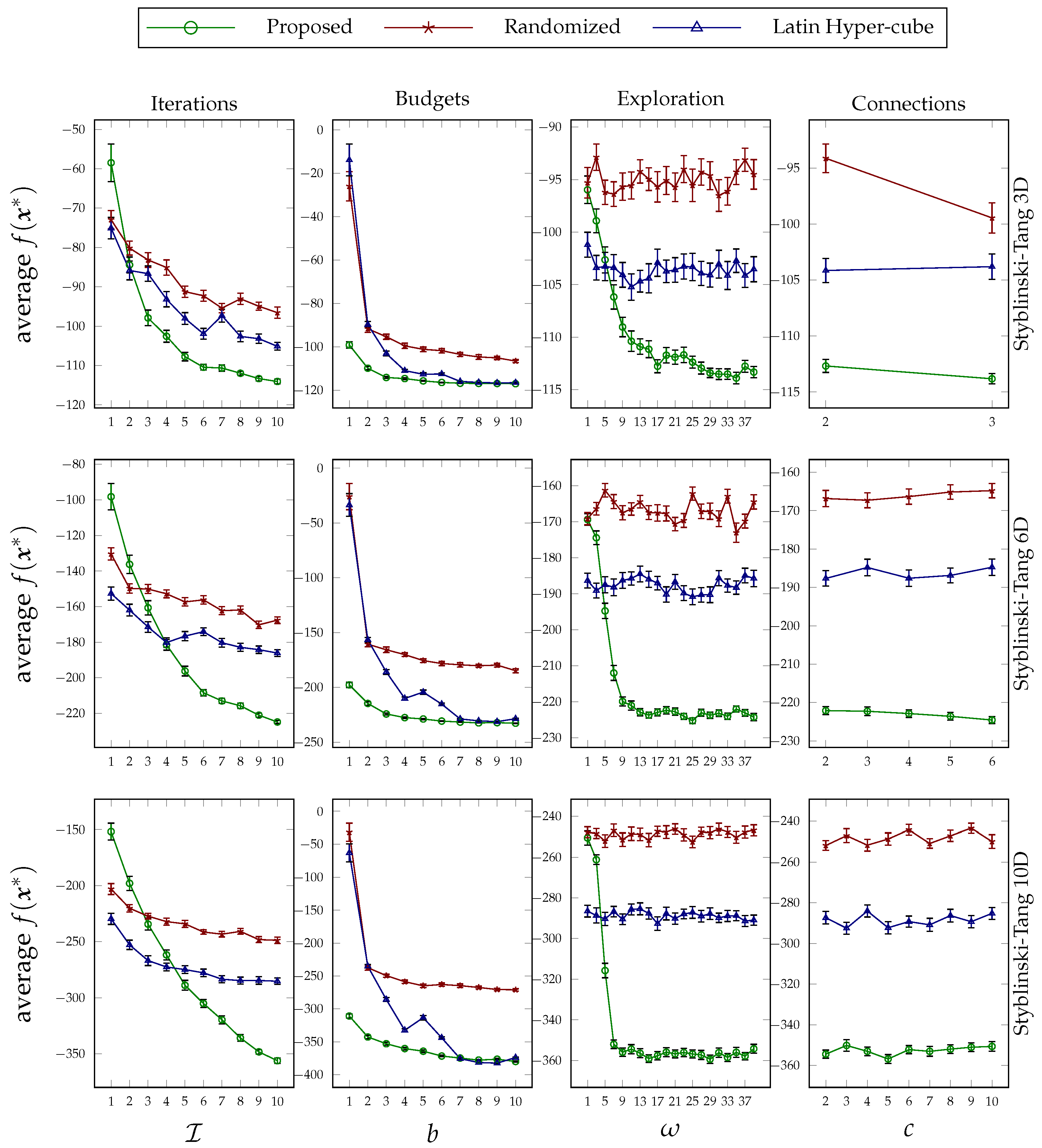
As stated before, we have also studied the suggested technique for the black-box optimization problem to see how it performs in finding the optima of various convex and non-convex functions. These experiments also help us to closely check the relative performance improvements in higher dimensions. We have chosen three non-convex benchmark optimization functions and a convex toy function, the details of which are presented in
Table 2. For each function, we run the experiments in three different dimension sizes, and the goal of the optimization is to find the global minimum. Very similar to the settings that we discussed for ML hyperparameter tuning, whenever we mean to fix the value of each parameter value in different experiment sets, we use the following parameter values:
.
Table 2.
The details of the multi-dimensional functions used for black-box optimization experiments.
Table 2.
The details of the multi-dimensional functions used for black-box optimization experiments.
| Function | | Domain | |
|---|
| Hartmann, 3D, 4D, 6D [31] | | | 3D:−3.86278, 4D:−3.135474, 6D:−3.32237 |
| Rastrigin, 3D, 6D, 10D [32] | | | 3D:0, 6D:0, 10D:0 |
| Styblinski–Tang, 3D, 6D, 10D [33] | | | 3D:−117.4979, 6D:−234.9959, 10D:391.6599 |
| Mean Average Error, 3D, 6D, 10D † | | | 3D:0,6D:0, 10D:0 ‡ |
The plots are grouped by functions and can be found in
Figure 5,
Figure 6,
Figure 7 and
Figure 8. The conclusion that was drawn concerning the behavior of the proposed approach under different values of its design parameters applies to these optimization experiments as well. That is, the more the proposed method runs, the better performance it achieves; its superiority on low budget values is clear; its sensitivity to exploration parameter values is consistent; and the way that the decision variables are broken down during the formation of the hierarchy does not affect the performance very much. Furthermore, as can be seen in each group figure, the proposed algorithm yields a better minimum point in comparison to the other two random-based methods when the dimensionality of a function increases.
Disregarding its multi-agent formulation, autonomy, and inter-agent collaborations, the proposed method shares similarities with heuristic and population-based black-box optimization approaches. We believe that even with such a viewpoint, our method can be more applicable due to its simple architecture, low number of hyperparameters, its innate distribution, and because it requires less domain knowledge.
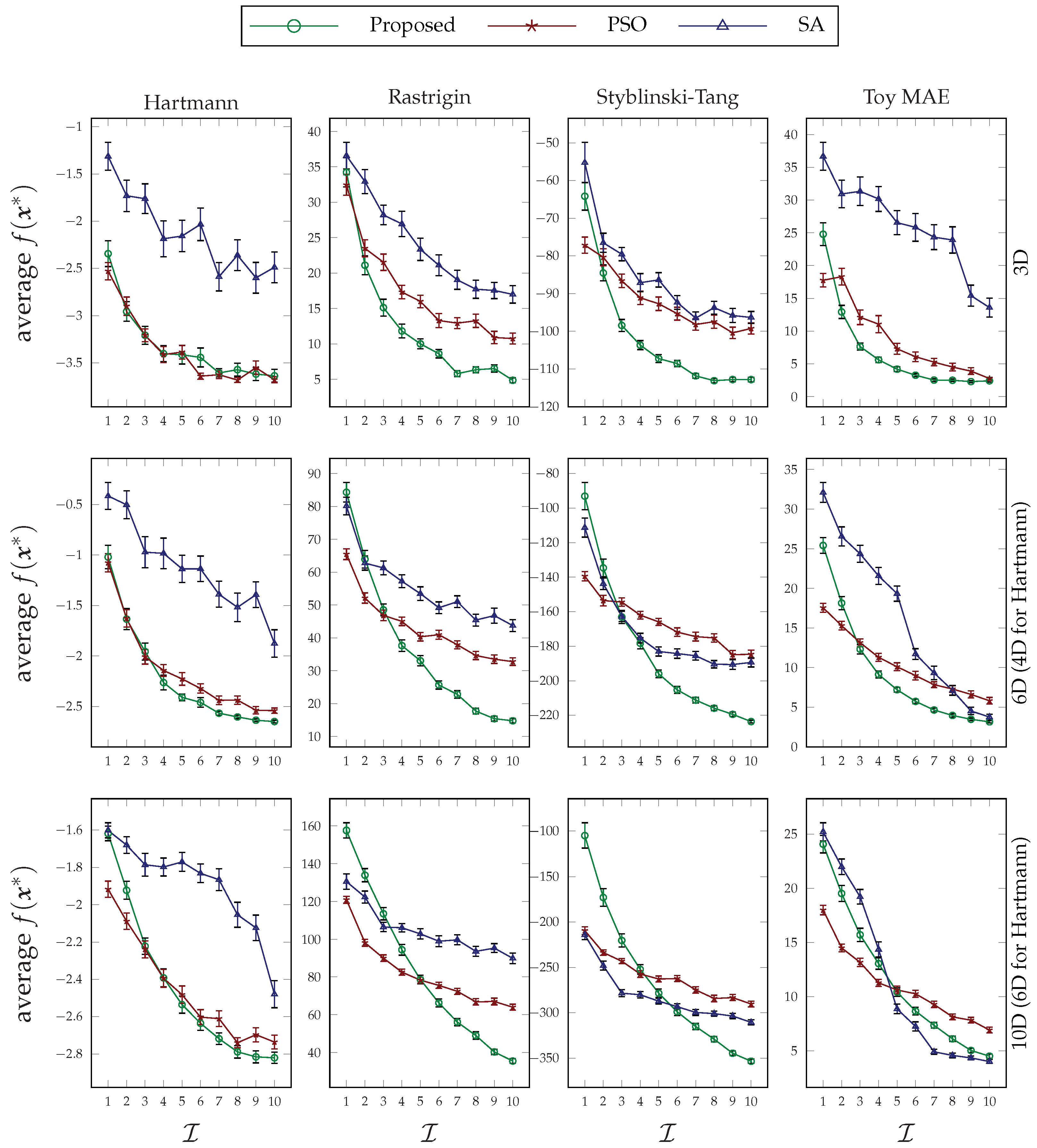
Figure 9 and
Figure 10 provide a comparison between the performance of our agent-based method and the ones of particle swarm optimization (PSO) [
34] and simulated annealing (SA) [
35]. Please note that these comparisons are not to prove our method’s superiority over population-based and/or heuristic methods, but to give a glimpse into some additional behaviors and the potentiality of the agent-based solution. In its current immature condition, we do not doubt that our immature approach will most probably be outperformed by the many mature heuristic methods available.
For the PSO algorithm, we have employed the standard version and set its hyperparameter values as
and
. As for the SA algorithm, we have used Kirkpatrick’s method [
35] to define the accepting probabilities with
and the geometric process for the annealing schedule, i.e.,
with
. Please note that our choices for the aforementioned values are based on multiple trials and errors and the general practical suggestions found in the literature. Finally, the values that we have utilized for our agent-based solution are as follows:
and
, whenever they are assumed fixed. Please note that these values are the same as the ones we applied in the previous set of analyses, and we have not conducted any optimization to choose the best possible values.
Due to the different underlying principles used in each of these algorithms, providing an absolutely fair comparison would not be possible. For instance, in our method, the number of agents is fixed, and each agent has an evaluation budget. In the PSO algorithm, however, the population size is a hyperparameter, and each particle makes a single evaluation. The SA, moreover, is a single-agent, centralized approach with one evaluation in each of its iterations. To the best of our ability, in this empirical comparison, we have tried to keep the total number of evaluations fixed among all experiments. Strictly speaking, we set the same number of iterations, i.e., , in the PSO but set its population size to . Similarly, in the SA, we set the number of iterations to .
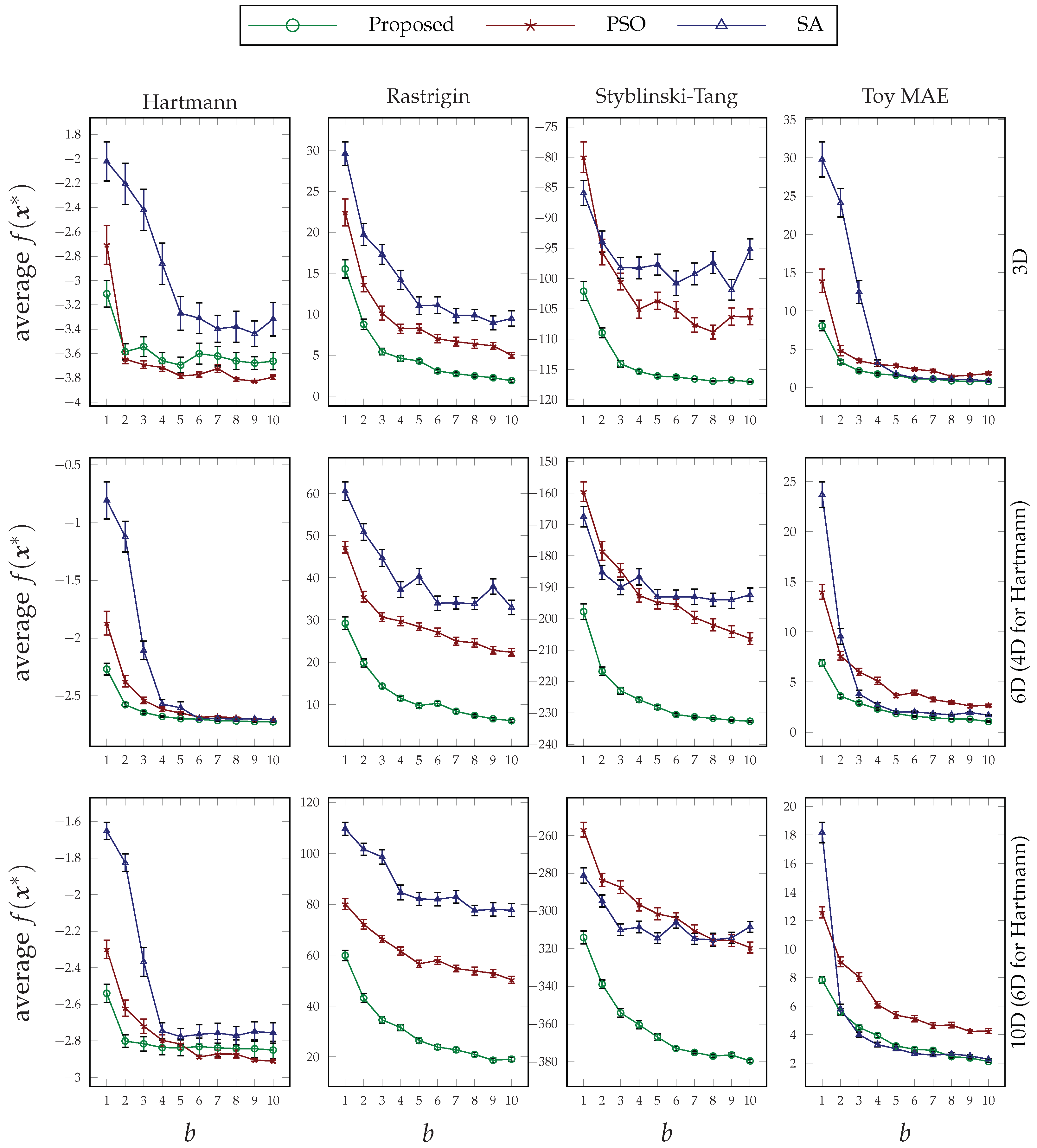
The results presented in
Figure 9 show how each different method behaves under different numbers of iterations in each of the benchmark problems. As can be seen, in most benchmarks, the proposed method has outperformed both PSO and SA in higher iteration numbers. Recalling the true optimal function values from
Table 2, the tied or close conditions among all methods happen near the global optima, which we believe can be improved through an adaptive exploitation method. Furthermore, due to the relatively higher improvements in the Rastrigin and Styblinski–Tang functions and the fact that these two functions are composed of several local optima, we can conclude that our proposed method has better capability to escape those local positions.
The results exhibited in
Figure 10 show the behavior of the tested optimization algorithms under various budget restrictions. In this set of experiments, we have fixed the number of iterations to
, and the results show a promising success of our method in outperforming the other two in most problems. Similar to the rationale provided above, the amount of improvement in Rastrigin and Styblinski–Tang functions is evident. Moreover, our method also shines when we have a low budget for the number of evaluations in each iteration. In other words, it can be a good candidate for optimizing expensive-to-evaluate problems or its use in computationally limited devices.
Regarding the computational time, we extend our analysis of the time complexity of the proposed methods in the previous section to the compared random-based methods. Let , and denote the evaluation budget of each agent, the number of iterations, and the total number of hyperparameter/decision variables to be optimized, respectively. As we have compared the methods under fair conditions, i.e., giving each agent the opportunity to run its randomized algorithm for times, and since we have assumed that all agents run independently in parallel, the time complexity of both “randomized” and “Latin hypercube” methods would be , where denotes the complexity of the underlying ML model or function evaluation. Recall from the previous section that the time complexity of the proposed method is due to its initial structure formation phase and the vertical communication of non-terminal agents. In other words, our proposed approach requires additional computational time in the worst case. The worst case occurs when the computational time complexity of the evaluation of the objective function or the ML model, i.e., , is low. In almost all ML tasks however, we have , hence the time difference is negligible. It is worth emphasizing that this comparison is based on the assumption of a fair comparison and parallel execution of the budgeted agents. It is clear that any changes applied to the benefit of a particular method will definitely change the requirements. For instance, if we limit the number of evaluations in randomized methods, they will require less time to find a local minimum; however, the result will be of lower quality. Regarding the tested heuristic methods, as we have kept the number of evaluations fixed and due to using a similar amount of work internally, we expect a computational complexity similar to our approach for them.
It is worth reiterating that the contribution of this paper is not to compete with the state-of-the-art algorithms in function optimization, but to propose a distributed tuning/optimization approach that can be deployed on a set of distributed and networked devices. The discussed analytical and empirical results not only demonstrated the behavior and impact of the design parameters that we have used in our approach, but also suggested the way that they can be adjusted for different needs. We believe the contribution of this paper can be significantly improved with more sophisticated and carefully chosen tuning strategies and corresponding configurations.