Agent-Based Modeling of Consensus Group Formation with Complex Webs of Beliefs

Abstract

Formation of consensus groups with shared opinions or views is a common feature of human social life and also a well-known phenomenon in cases when views are complex, as in the case of the formation of scholarly disciplines. In such cases, shared views are not simple sets of opinions but rather complex webs of beliefs (WoBs). Here, we approach such consensus group formation through the agent-based model (ABM). Agents’ views are described as complex, extensive web-like structures resembling semantic networks, i.e., webs of beliefs. In the ABM introduced here, the agents’ interactions and participation in sharing their views are dependent on the similarity of the agents’ webs of beliefs; the greater the similarity, the more likely the interaction and sharing of elements of WoBs. In interactions, the WoBs are altered when agents seek consensus and consensus groups are formed. The consensus group formation depends on the agents’ sensitivity to the similarity of their WoBs. If their sensitivity is low, only one large and diffuse group is formed, while with high sensitivity, many separated and segregated consensus groups emerge. To conclude, we discuss how such results resemble the formation of disciplinary, scholarly consensus groups.

1. Introduction

The formation of groups with shared beliefs, opinions, and views has been and continues to be a topic of great interest, discussed in sociology, political science, communication, and organizational science, as well as studies focusing on structure of science (see, e.g., [1,2,3,4,5] for the diversity of topics and areas of studies). In all these cases, one key issue is to understand the dynamics which drive the segregation and consolidation of groups, even in conditions where communication and sharing of beliefs is common and frequent (for reviews, see [3,4,5]).

The computational modeling of opinion group formation [5,6,7], the formation of collaborative groups and collective decision making [2,8,9], as well as disciplinary fragmentation and progress in science [10], has shed light on the social dynamics behind group formation, segregation, and consolidation, often revealing the unexpectedly simple but self-reinforcing interactions behind such complex phenomena. Consequently, consensus group formation and opinion adoption, and their change and evolution, have been modeled using a variety of idealized models, many of them founded on one or another theoretical view about social influence and interaction or social learning, some of them being computational renderings of empirical findings. The models of opinion dynamics are as diverse as are the their theoretical underpinnings and intended scopes of applications. However, many of the models of opinion dynamics, where formation of consensus groups is of interest, can be classified in three groups [3]: (1) models of assimilative social influence; (2) models with similarity biased influence, and; (3) models with repulsive influence. In addition, it is possible to recognize models that are hybrids of these three classes [3]. Different well-known models in each class, their theoretical background and motivation, and most well-known computational implementations and empirical applications and justification (when it exists) are reviewed in detail elsewhere [3,4,5], and therefore we provide here only a brief summary of the most important aspects of models with similarity bias to the extent needed to put in perspective the model introduced here.

Models with similarity bias do not assume a structurally fixed connection between agents, but instead, agents can interact if they have sufficiently similar opinions (or beliefs) or if they are sufficiently similar regarding some other pertinent feature. If the similarity (opinions or other preferred feature) is too distant, interactions are no longer possible. Such a threshold of interaction can be interpreted as a confidence to interact and modify one’s opinion and can be assumed to arise from a variety of psychological or sociological reasons [3,4,5]. Therefore, many similarity bias models are referred to as bounded confidence models [11,12] owing to the existence of a kind of a confidence threshold to interact. These models typically give rise to persistent opinion clusters, where agents are similar and dissimilar to agents in other clusters. In these models, the cluster formation is an outcome of similarity bias homophily; the more stringent the threshold for required similarity, the more numerous are the segregated non-interacting clusters. In most bounded confidence models, the threshold is sharp and deterministic, and stochastic variation is included by adding a stochastic noise  [11,12]. Interestingly, the addition of noise may fundamentally affect the consensus cluster formation [3,4,5]. The role of noise and its non-trivial effects in deterministically thresholded bounded confidence models suggests that to model the bounded regions of interactions due to similarity bias, genuinely stochastic and probabilistic rules to decide whether or not the interactions happen are sometimes preferable [13,14]. Finally, important and interesting recent generalizations of bounded confidence models are models where opinions or beliefs are multidimensional [15,16,17], or in one way or another, more complex structures of beliefs and related opinion elements [2,7,9,18]. Such models allow more realistic modeling of complex opinions, give rise to richer dynamics than one-dimensional bounded confidence models, and, moreover, the emerging clusters of opinions are in these cases more diverse than those found in one-dimensional models.

Paralleling the above briefly summarized recent generalizations of similarity-biased models of consensus formation, the agent-based model (ABM) proposed here is meant to be another step towards generalizations applicable to model complex sets of beliefs, where interactions between agents and dynamics of the change in beliefs are modeled as a genuine stochastic process. The model, however, adopts the simple view where agents modify their views by acquiring and accommodating their sets of views present in to a collection of all agents; no new elements emerge.

The ABM proposed here, given its restriction to describe the creation of new elements of opinion beliefs, and instead describing the evolution of consensus groups with complex sets of beliefs, has two possible areas of applications. One area of interest is the formation of disciplinary scholarly groups and schools, along with their characteristic ways of using scientific terms and forming various research programs [19,20,21,22]. Research fields always contain disciplinary groups where key scientific terms differ, and the same terms may be used differently in discussing and framing the key problems within the field [21,22]. In this case, within the established paradigms of research, new disciplinary groups are often formed within the existing fields. Such strong disciplinary fragmentation seems to be particularly apparent and typical in the human and behavioral sciences [23,24,25]. Another situation of interest, where the creation and generation of new knowledge is not necessarily of primary interest, but where differing disciplinary views about thematic topics can be recognized, is related to the disciplinary views of science education scholars [26,27] as well as science students, where student groups may have consensus views that differ from those of other student groups views, even when they have used the same study materials [28,29]. To address situations in which the knowledge or meaning structures of interest are complex systems of terms, concepts, or conceptions characteristic of the disciplinary group, it seems appropriate to use the expression “webs of beliefs” (compare e.g., ref. [30]), to be referred to briefly as WoBs in what follows. In this study, we approach such a disciplinary group formation through convergence and consolidation of WoBs, where the dynamics are driven by similarity and consensus seeking, without posing explicit bounds of confidence to constrain interactions (as in so-called bounded confidence models, [1,2,3]). In the ABM presented here, agents possess generic WoBs in the form of a complex network. Agents compare their WoBs and exchange bits and pieces of them, guided by similarity-seeking dynamics (i.e., homophily). The comparison-triggered adjustment of WoBs leads to their convergence but also divergence, and thus to the formation of segregated disciplinary consensus groups. The model is highly idealized, generic, and simple, but as discussed in the final section, it has features that resemble the real situations of disciplinary group formation. Thus, the model presented here is a first attempt towards agent-based modeling of consensus group formation where views and opinions are complex webs of beliefs.

2. Materials and Methods

The computational model presented here is an agent-based multi-optional model for the formation, consolidation, and segregation of consensus groups based on agents’ webs of beliefs (WoBs). The dynamics of the model are driven by agents’ repeated comparison of their WoBs, guided by the utility of adjusting the WoB for better mutual similarity. We describe first the constructions of agents’ WoBs, second the multi-state probabilistic model of selection of partners for comparison, and third, update dynamics for the change in WoBs. Simulations are carried out using an event-based roulette-wheel method [31,32]. Symbols and their meaning in the study are summarized in

Table 1. Summary of symbols and abbreviations used recurrently in the text and figures. In the sub-indexes, $\xi$ and $\gamma$ refer to a pair of agents, Ens. avrg. denotes ensemble averages, and Dim[{ · }] refers to a dimension of set.

Symbol/Abbreviation		Symbol/Abbreviation
$\left\{\mathrm{e}\right\}$	Set of edges (E = Dim[{$\mathrm{e}$}])	$P_{\pm }$	Prob. to add/delete elements
$\left\{\mathrm{v}\right\}$	Set of vertexes (V = Dim[{$\mathrm{v}$}])	$\beta$	Sensitivity to similarity
$P_{\xi \gamma }$	Probability of interaction	${\beta }^{*}$	Confidence to add/delete
$S_{\xi \gamma }$	Similarity function	N	Ens. avrg. of cluster number
$S_E$	Similarity, edges	R	Ens. avrg. of relat. occupancy
$S_V$	Weighted adjac. matrix	S	Ens. avrg. of similarity
${\Delta }_{\pm }$	Utility to add/delete elements	H	Entropy of cluster distribution

.

2.1. Model of Webs of Beliefs (WoBs)

The WoBs of interest, which mimic real scholarly conceptual or semantic structures, can be characterized as complex in the sense that they consist of several elements (vertexes or nodes) connected (by edges or links) in complex ways to their other elements. Such WoBs have a distribution of vertexes with broad difference in their connectivity; some vertexes have a high connectivity, while many are loosely connected (see e.g., [28,29,33,34]). Consequently, appropriate WoBs can be characterized as sparse complex networks with about 100 vertexes, with low average degrees of about 3 or 4 but with very few nodes having larger degrees up to 10.

Generic initial WoBs of agents are obtained by sampling a larger template network with desired properties, generated by a generative model previously introduced to produce networks with broad distributions of connectivities of vertexes [35]. In constructing the generic networks, they are pruned by removing auxiliary vertexes possessing only one edge, so that to only two cores (nodes with at least two edges) are taken into account. The template network has approximately 200 vertexes (i.e., nodes) and 400 edges (i.e., links), with the degrees (i.e., number of attached links) of the vertexes distributed according to inverse power law, with an inverse power close to 3.0 (see Appendix A for details of rationalization of this choice). With these parameters, the average degree of vertexes is about 3 to 4, with very few vertexes having a degree of about 8 to 12. From the template networks, a set of initial edges $E_0=120\pm 20$ are drawn at random, and connected networks (discarding unconnected parts) are formed to serve as individual WoBs for each agent. With these choices, WoBs contain about 40–100 vertexes (in some rare cases only about 20) and are always sub-networks of the template. The WoBs thus obtained from the template are stochastically generated and have in each case a slightly different detailed structure. The details of the generative model, briefly summarized in Appendix A, are reported elsewhere [35] and are of no further interest here.

2.2. Interaction Dynamics of Agents

The interaction between agents in the agent-based model (ABM) introduced here comprises N agents, where one agent $\xi$ selects an agent $\gamma$ to interact among $N-1$ other agents. The selection is based on the similarity $S_{\xi \gamma }$ of lexicons between the agents. The probability $P_{\xi \gamma }$ that agent $\xi$ selects agent $\gamma$ is assumed to follow the (Gibbs-like) probability distribution (compare with refs. [36,37,38])

$$P_{\xi \gamma }=\frac{S_{\xi \gamma }exp\left[\beta S_{\xi \gamma }\right]}{{\sum }_{i\ne \xi }{S}_{\xi i}exp\left[\beta S_{\xi i}\right]},\xi \ne \gamma$$

(1)

where $\beta$ is a parameter related to the sensitivity to similarity, with $\beta <1$ (here, in practice $\beta \approx 1$) indicating low sensitivity (i.e., high noise or randomness) and $\beta \gg 1$ high sensitivity (i.e., low noise or randomness). The prefactors in Equation (1) ensure that at the limit $\beta \to 0$, the decision probabilities attain values corresponding to the ordinary rational, non-probabilistic choice (for details, see [37,38]).

The similarity of the agents is defined simply as the ratio of the number of shared elements (vertexes and edges) to all elements. Denoting the set of elements as $\left\{\mathrm{X}\right\}=\left\{\mathrm{v}\right\}$ for vertexes and $\left\{\mathrm{X}\right\}=\left\{\mathrm{e}\right\}$, the similarity of agents $\xi$ and $\gamma$ based on either edges or vertexes is given simply as a ratio of non-shared to shared elements,

$$S_{\xi \gamma }\left[\mathrm{X}\right]=\frac{\mathrm{Dim}[{\left\{\mathrm{X}\right\}}_{\xi }\cap {\left\{\mathrm{X}\right\}}_{\gamma }]}{\mathrm{Dim}[{\left\{\mathrm{X}\right\}}_{\xi }\cup {\left\{\mathrm{X}\right\}}_{\gamma }]},$$

(2)

where $\mathrm{X}$ denotes either edges (e) or vertexes (v) and Dim[ ·] means dimension (number of elements) in a given set. In defining the similarity, we chose to keep it symmetric and as simple as possible, although more elaborate definitions are possible, for example, taking into account the role of asymmetry and different number of non-shared elements. However, the definition of similarity is always a matter of choice, and no unambiguous definition seems to be possible because choices need to be made about what features are taken into account in similarity, as discussed in detail in, e.g., ref. [39].

We assume that both vertex and edge similarities need to have high values for a high similarity, and thus, in the effective similarity used in simulations, the effective similarity is taken as a geometric mean of vertex and edge similarities.

$$S_{\xi \gamma }=\sqrt{S_{\xi \gamma }\left[\mathrm{e}\right]S_{\xi \gamma }\left[\mathrm{v}\right]}$$

(3)

This choice of defining the similarity is a trade-off between simplicity and taking enough detail into account to characterize the WoBs. Here, given the generic nature of the WoBs, a simple symmetric similarity $S_{\xi \gamma }=S_{\gamma \xi }$ based on the counting of elements and constrained in the range of values from zero to one is satisfactory for the present purposes. In fact, we tried out more elaborated similarity definitions, but in the present ABM, they had little effect on the final results.

The selection criterion in Equation (1) with similarity defined as in Equation (2) prefers similar agents (i.e., homophilic preference) and, in that sense, it closely resembles the selection criteria in bounded confidence models and their variants [1,3], where homophilic cut-off criterion constrains the possibility of interactions. The present model, however, belongs to a class of probabilistic similarity-biased models [3,13], where no interaction possibilities are ruled out a priori, but partners with high similarity are prioritized.

2.3. Updating the WoBs

In the interaction events, agents update their WoBs, seeking to improve their consensus. When agent $\xi$ has decided on the partner $\gamma$ it will interact with, the update of WoBs for optimized communication takes place in two steps. First, agents $\xi$ and $\gamma$ pick out a common vertex, which is a center element in their interaction (i.e., shared term or concept for their belief). Second, they check the neighborhood of that selected vertex and check the number of available new edges to neighborhood vertexes their partner possesses but the agent itself does not yet possess (i.e., possible new elements and connections the agent can acquire to adopt a new edge and possibly a new vertex connected to it). Both agents have then two choices of how to increase mutual similarity: either to add a new edge, or to delete an edge not possessed by the interaction partner. The decision to add or delete an edge is made on the basis of the utilities, based on the changes in the similarity, which are taken to be changes in similarity by addition or deletion of an edge or a vertex (contained in the neighborhood of the common vertex). The advantage of such a simplified procedure is that utilities of addition can be estimated through changes in similarities, when number of elements for one agent changes while remaining intact for the other agent. Now, four possibilities are available, either agent $\gamma$ changes its WoB or agent $\xi$ does, but only one event happens at a time. In both cases, however, the changes are computable as a difference ${\Delta }_{\pm }\left[X\right]=S\left[\mathrm{X}\pm 1\right]-S\left[\mathrm{X}\right]$ for addition (+) and deletion (−), respectively, where indexes referring to agents are dropped because of symmetry in regard to the agents. For faster computation, the differences are approximated by the first linear terms, which are obtained through direct calculation, in the form

$$\begin{array}{ccc}\hfill {\Delta }_{+}\left[\mathrm{X}\right]& =& (1-S\left[X\right])\mathrm{Dim}{[{\left\{\mathrm{X}\right\}}_{\xi }\cup {\left\{\mathrm{X}\right\}}_{\gamma }]}^{-1}\hfill \end{array}$$

(4)

$$\begin{array}{ccc}\hfill {\Delta }_{-}\left[\mathrm{X}\right]& =& S\left[X\right]\mathrm{Max}{[1,\mathrm{Dim}\left[{\left\{\mathrm{X}\right\}}_{\xi }^C\right]+\mathrm{Dim}\left[{\left\{\mathrm{X}\right\}}_{\gamma }^C\right]]}^{-1}\hfill \end{array}$$

(5)

where $\mathrm{X}$ denotes either vertexes or edges and notation ${\{·\}}^C$ complements of sets. Note that in all expressions containing S and ${\Delta }_{\pm }$ or related to them, indexes referring to agents are dropped in what follows. In Equation (5), the minimum value allowed in the denominator is 1, in order to prevent division by zero (this occurs rarely and has no consequences on results). In case only an edge is added/deleted but no new vertex becomes added/deleted, utilities are simply for edges ($\mathrm{X}=\mathrm{e}$). In the case that the added/deleted edge contains a new vertex, the effective utility ${\Delta }_{\pm }$ corresponding to addition (+) or deletion (−) of a vertex and its neighborhood is taken to be the geometric average of utilities for $\mathrm{X}=\mathrm{e}$ and $\mathrm{X}=\mathrm{v}$.

$${\Delta }_{\pm }=\sqrt{{\Delta }_{\pm }\left[\mathrm{e}\right]{\Delta }_{\pm }\left[\mathrm{v}\right]}$$

(6)

Probabilities of addition and deletion are then given as

$$P_{\pm }=Z^{-1}{\Delta }_{\pm }exp\left[{\beta }^{*}{\Delta }_{\pm }\right]$$

(7)

where parameter ${\beta }^{*}$ has the role of confidence of the decision to add or delete on the basis of utility. The factor $Z={\Delta }_{-}exp\left[{\beta }^{*}{\Delta }_{-}\right]+{\Delta }_{+}exp\left[{\beta }^{*}{\Delta }_{+}\right]$ is the normalization factor. The rationalization to include prefactors is similar to the case of probability in Equation (1) selecting the partner for interactions. The choice is always between addition and deletion; staying intact (which is not counted as an event) is not included. This is related to the choice that simulations are event-driven; only events that make a difference (i.e., change the state of the agent) are taken into account. Note that in each interaction event, only one outcome of the four possibilities is allowed.

2.4. Simulations

Simulations of the ABM are based on the probabilities of selection $P_{\xi \gamma }$ in Equation (1) an $P_{\pm }$ in Equation (7), with each event of an agents’ interaction consisting of both updates. Simulations are event-based, consisting of sequences of events $\tau =1,2,\dots {\tau }_{\mathrm{MAX}}$ events. At each instant, when the value of $\tau$ increases by 1, it is decided: (1) which agents are going to interact and (2) whether an edge (and possibly, a vertex) is added or deleted. Each of the event selections is carried out by the roulette-wheel method [31,32]. In the roulette-wheel method, a discrete set of N possible events k with probabilities $p_k$ is arranged with cumulative probability

$${\Phi }_k=\sum _{i=1}^k{p}_i/\sum _{i=1}^N{p}_i.$$

(8)

The event k is selected if a random number $0<r<1$ falls in the slot ${\Phi }_{k-1}<r<{\Phi }_k$. In case (1), the probabilities $p_k$ are given by $P_{\xi \gamma }$ in Equation (1), while in case (2), one has only two probabilities $p_k=P_{\pm }$ defined by Equation (7). The roulette-wheel method is thus entirely event-based, where the occurrence of events is predicted on the basis of cumulative distribution. Consequently, there are no constant time-like intervals between events. All simulations are carried out for N = 25 agents, with ${\tau }_{\mathrm{MAX}}=50·{10}^3$ events, corresponding to about 30 updates for each edge in a set of WoBs of 25 agents. However, only a fraction, usually about 2–3%, eventually leads to addition or deletion of and edge, since after the onset of formation of consensus groups, many neighborhoods are already identical. In practice, this means from 40 to 60 changes per agent in the course of simulations, and as is seen, a stabilized situation is reached well before ${\tau }_{\mathrm{MAX}}$ is reached. In the simulations, only one affinity distribution is used, corresponding to an inverse power of 2.9, close to the marginal value of 3 (see Appendix A for details). The simulations are repeated for the ensemble of 36 = 6 × 6 different initial states, sampled for six different initial templates and each six times for different initial WoBs. Simulations and numerical computations are realized using Mathematica [40].

2.5. Representation of Data

The simulations track the evolution of agents’ WoBs, and on that basis, agents’ similarities based on shared edges and vertexes are the outcome of the simulations. The agents are classified in clusters according to the effective similarity $S=\sqrt{S_{\mathrm{E}}{S}_{\mathrm{V}}}$ and geometric average of size $\sqrt{\mathrm{E}\mathrm{V}}$, where $\mathrm{E}=\mathrm{Dim}\left[\right\{\mathrm{e}\left\}\right]$ and $\mathrm{V}=\mathrm{Dim}\left[\right\{\mathrm{v}\left\}\right]$. In finding the clusters, we use Mathematica’s [40] DBSCAN algorithm, which partitions the datasets into clusters using density-based classification with noise [41]. DBSCAN proved to be a reliable and fast method for finding clusters not constrained by a prefixed number of clusters for the data generated by simulations. When clusters are detected, the number of clusters N and agents in a given cluster are counted to obtain the relative occupancy R as the average value of the fraction of agents that belongs to a given cluster.

In addition to cluster statistics condensed in average values N and r and their standard deviations, the Shannon entropy H of cluster distribution is calculated, given by

$$H=-\sum _{i,j}{p}_{ij}log\left[p_{ij}\right]$$

(9)

where $p_{ij}\ne 0$ is the probability density of agents with discretized values of similarity and size, $(S,\sqrt{\mathrm{E}\mathrm{V}})$. The entropy H is useful to monitor the consolidation of the cluster distribution.

In what follows, cluster formation, consolidation, and segregation are monitored by using the quantites N, R, S, and H. Of these, N, R, and H are of the greatest interest, because owing to the choice of simulation parameters to maintain average similarity close to a constant, similarity S is always nearly the same in the stabilized states, and thus, contains little information about the differences of cluster distributions in the stabilized state.

3. Results

The simulations are carried out for 25 agents, which possess different but partially overlapping WoBs about $E_0\pm \Delta E_0$ (here $E_0$ = 120 and $\Delta E_0$ = 20) edges, which are randomly selected parts of the same template network consisting of 200 vertexes (i.e., nodes) and 400 edges (i.e., links). However, only 2-core (i.e., each vertex has at least two edges attached) and fully connected WoBs are included as initial states, and thus the initial number of vertexes $V_0$ in the WoBs, when pruned to connected networks, varies roughly from 40 to 100 (with a few exceptional cases of 20 to fewer than 40 vertexes). The parameter affecting mostly the evolution of WoBs during the simulations is the sensitivity $\beta$ to similarity of partners (i.e., sensitivity to homophily). Note that simulations are carried out for this parameter in the range from 10 to 300, but results are reported for scaled values $\beta \to \beta /10$ to allow easy presentation in logarithmic scale. The parameters $E_0$ and $\Delta E_0$ are the next most important in affecting the outcome of simulations. The effect of these parameters is tested by keeping ratio $E_0/\Delta E_0$ fixed and changing the absolute values by $\pm \%20$ by scaling them with a factor of $\eta$ = 0.8 and 1.2.

In simulations with unfolding interaction events $\tau$, the agent selects another agent to compare and adjust its WoB to better match the other agent’s WoB. The selection probability of the agent to interact depends on the similarity between the agents and the agent’s sensitivity $\beta$ to similarity in that selection. In comparison events of WoBs, interacting agents either adopt or delete an edge to increase their mutual similarity.

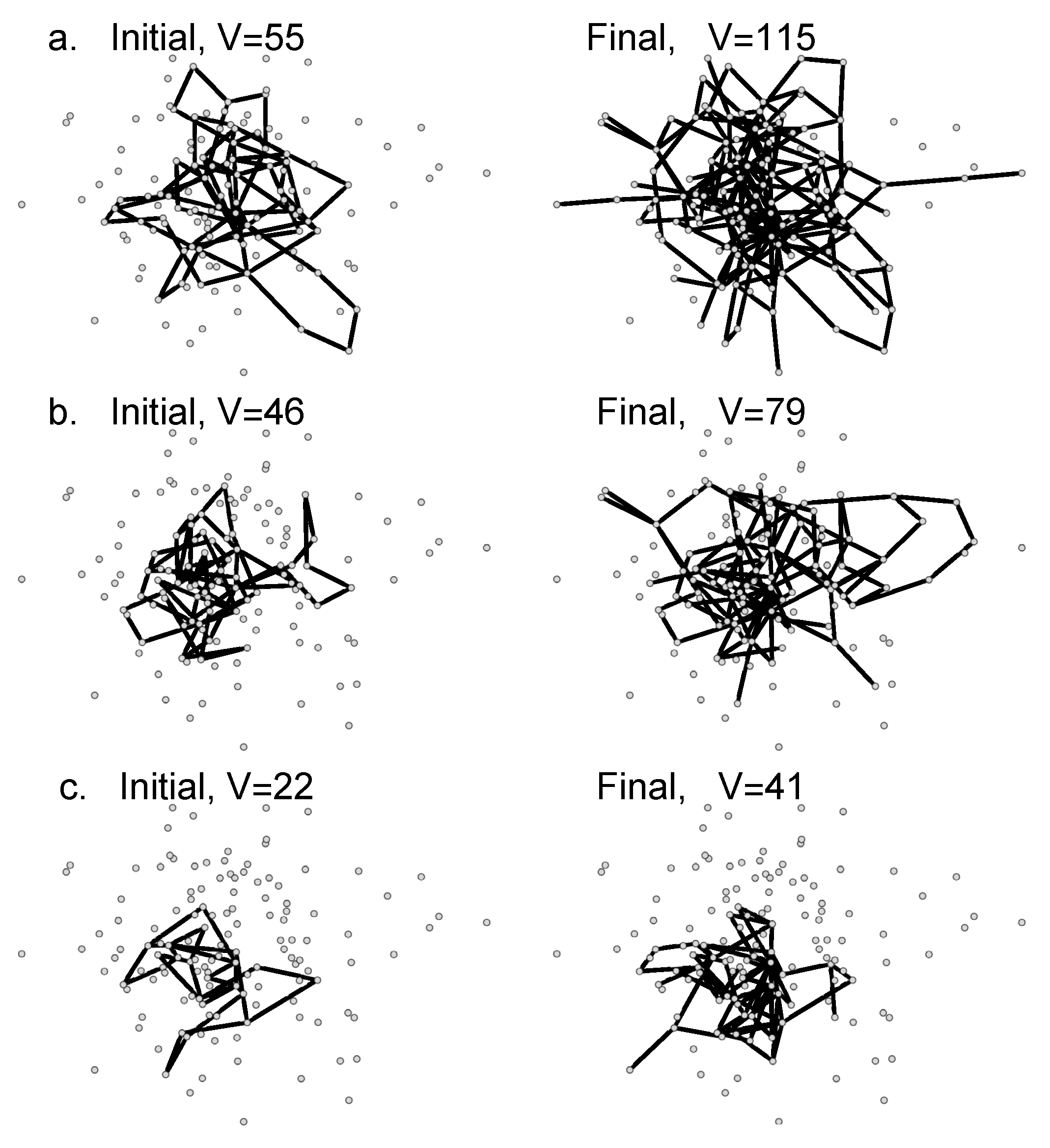
In Figure 1, examples of initial and final WoBs are shown. In all cases, the number of vertexes V (and edges) increase because the utility function favors the addition of edges and vertexes, thus favoring the growth of WoBs. However, initial and resulting final WoBs may have quite different sizes. Note that the initial WoBs are always 2-core networks, but during their evolution, singly connected vertexes may appear. In the final state ensemble, averaged values characterizing WoBs are not changing anymore, although slight changes in details of the structure may take place.

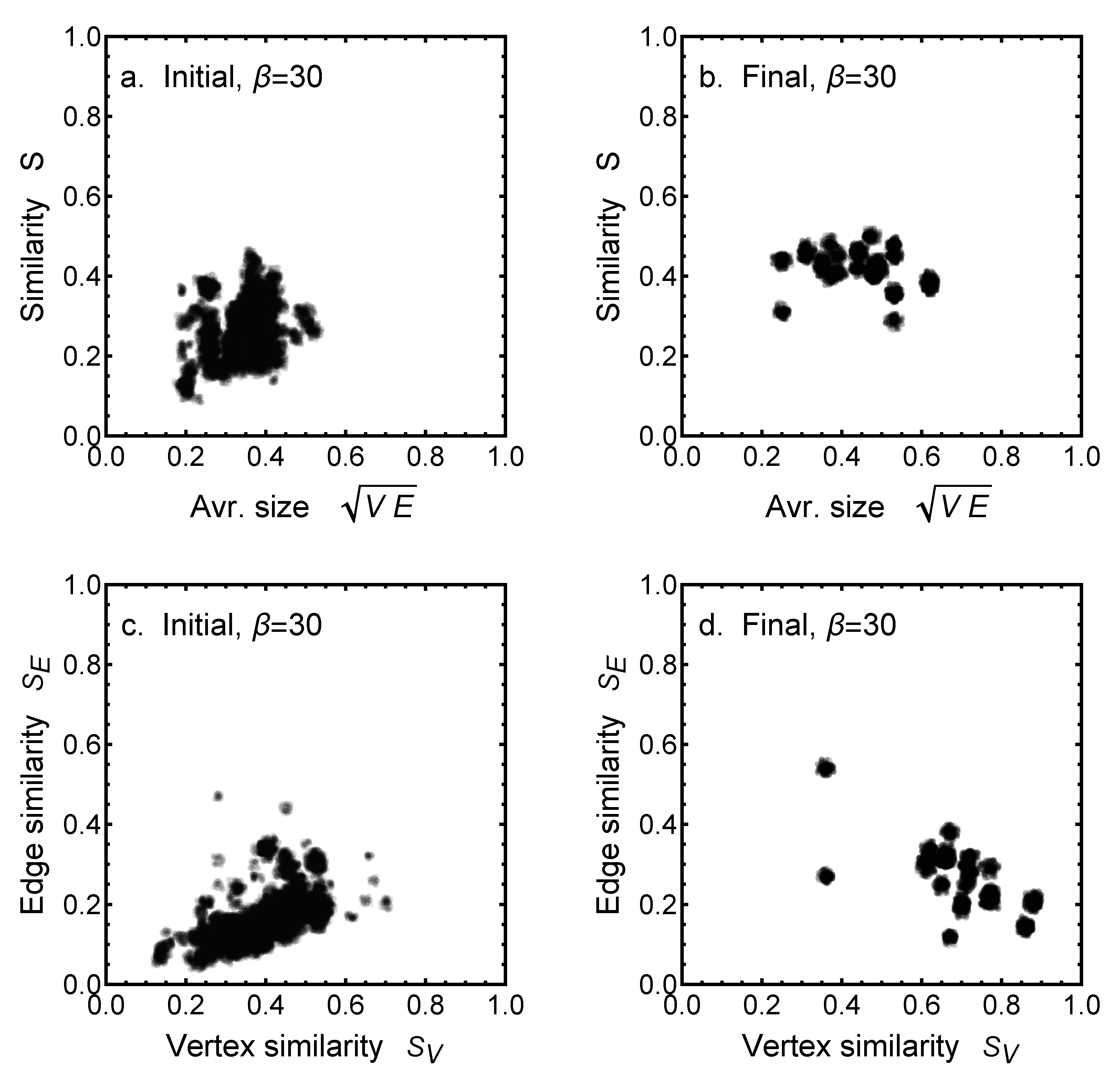
The dynamic changes in WoBs, driven by the similarity bias of interactions, eventually leads to a formation of consensus clusters. In Figure 2, an example of a similarity cluster in the initial stage is shown, and then in the stabilized final stage for agents making confident choices of interaction partners with $\beta =30$ (recall that this is a scaled value $\beta /10$). The stabilization of the cluster distributions with $\beta =30$, as shown in Figure 2b, is obtained with about 30,000 interaction events in a group of 25 agents, each of them possessing about 100 edges on average (originating from a sampled set 120 edges on average). Roughly, this means that agents need about 10 interaction events for each edge if they are to reach consensus states. Note that in what follows, we report interaction events $\tau$ scaled by a factor of 1000.

In Figure 2a,b, clusters are shown as a density plot of effective similarity S versus the (geometric) average size $\sqrt{\mathrm{E}\mathrm{V}}$ of the WoB, normalized to a maximum $\sqrt{{\mathrm{E}}_0{\mathrm{V}}_0}$, with both values discretized into bins of 0.01 ranging from 0 to 1. It is seen how the initial diffuse cluster (Figure 2a) segregates and consolidates to several smaller ones; in practice, six separate clusters (Figure 3a), as resolved by DBSCAN. In the case shown in Figure 2b, the DBSCAN routine finds seven or eight clusters (depending on parameters), but due to thresholding, which ignores very low-populated clusters, six remain to be counted as significant clusters. In Figure 2a, DBSCAN detects two clusters. In Figure 2c,d, the same case is shown, but now as a density plot of edge similarity $S_{\mathrm{E}}$ and vertex similarity $S_{\mathrm{V}}$ of the WoB. The similarities and sizes shown in Figure 2 are aggregated over the last few stable ensembles corresponding to the range $45<\tau <50$.

In reading the relevant information from Figure 2, it should be noted that while the high-similarity groups are clearly seen, so are the groups where agents are dissimilar (one agent can well belong to both groups, since similarity is a pairwise property). Therefore, we see not only groups where similarity has increased but also groups where it has decreased. Such behavior is a natural hallmark of the segregation of consensus groups.

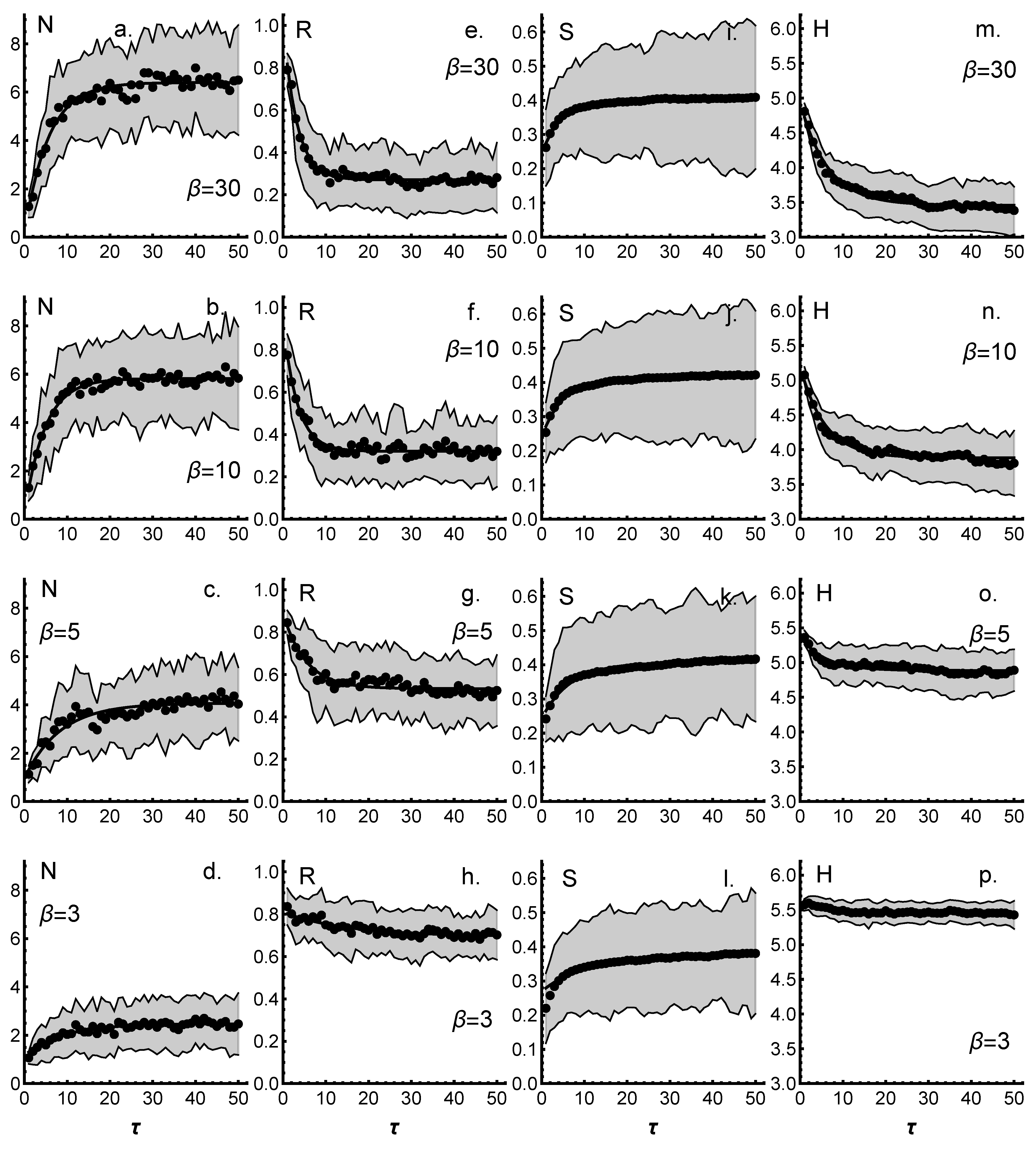
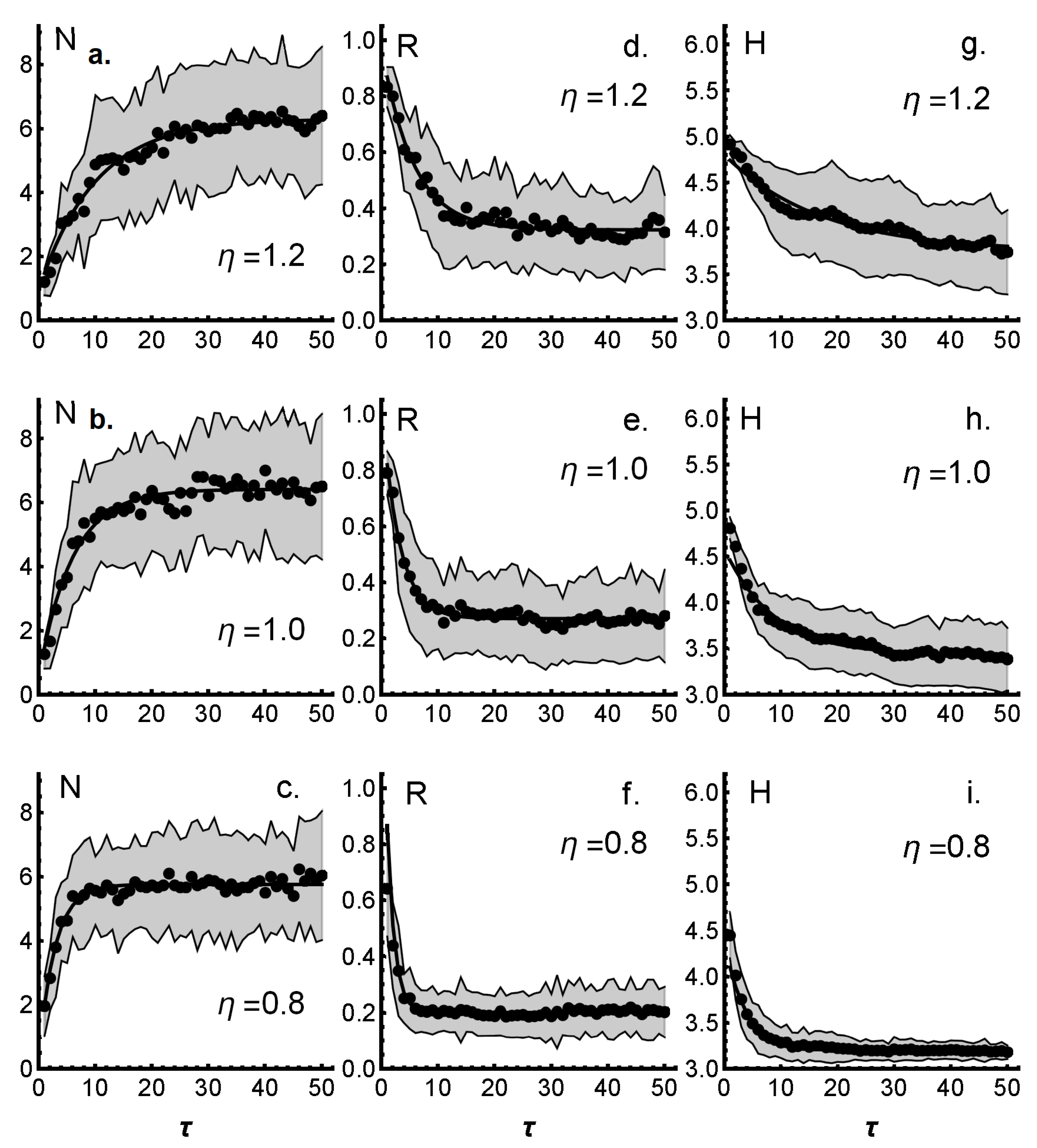
Consensus cluster formation proceeds gradually from the diffuse initial state to a stabilized final state, depending on the number of interaction events. Figure 3 shows the dynamics of cluster formation as it is monitored through number of clusters N (Figure 3a–d), relative occupancy (average fraction of agents in a cluster) R (Figure 3e–h), and average similarity S (Figure 3i–l) of clusters, as well as through entropy H of cluster distribution (Figure 3m–p). Results are shown for different strengths of sensitivity to similarity $\beta$ (scaled by a factor of 10) from high ($\beta =30$) and to low sensitivity ($\beta =3$) as a function of update events $\tau$ (scaled by a factor of 1000). For $\beta \le 3$ and $\beta \ge 30$, results remain essentially the same as for the corresponding limiting values shown in Figure 3. In all cases, dynamic behavior can be fitted to an exponentially decaying function (exponential fits are shown in Figure 3 but are barely visible).

The average number N of consensus clusters in the final, stabilized state (Figure 3a–d) depends on the sensitivity $\beta$ of agents to similarity in making choices to interact with other agents. For high-sensitivity $\beta =30$ (scaled), the number of clusters in stabilized state is on average about six (see Figure 3a), but fluctuations as measured by the standard deviation of the ensemble averages are large. The relative occupation R of clusters shown in Figure 3e is on average about 0.30, corresponding to six or seven agents in a cluster. Increasing the level of sensitivity by increasing values of $\beta$ does not change the situation, and thus results for $\beta =30$ appear to represent the most extreme segregation found in the group of 25 agents. As seen later, changing the number of edges and vertexes in initial WoBs about by $\pm 20\%$ also leaves the number of clusters in this case nearly intact. When the sensitivity to similarity in making choices becomes smaller, and values of $\beta$ are reduced (Figure 3b–d), the number of clusters decreases steadily, reaching the lowest attainable values of about two clusters on average for $\beta =3$. Additional reduction in $\beta$ appears not to lead to a definite monocluster situation, although single clusters become more abundant. As is seen from Figure 3f–h, the relative occupancy R of clusters follows roughly inversely the behavior of the average number of clusters, so that the product $N\times R$ remains roughly a constant, indicating relatively uniform distribution of agents in different clusters. In all cases, the similarity S (Figure 3i–l) has nearly the same average value, owing to the choice of parameter ${\beta }^{*}=10.0$ controlling the ratio of utility of addition to deletion. The larger the value of ${\beta }^{*}$, the larger the bias towards addition, and thus growth of clusters. The choice to keep the bias from growth moderate, and average similarity close to a constant value, makes the interpretation of consensus cluster formation easier and rules out the possibility that the formation of high-similarity clusters is mainly due to bias towards systematically higher average similarities.

The entropy H of the cluster distribution (Figure 3m–p) relaxes considerably more slowly to a stable value in comparison with cluster number N and relative occupancy R. This indicates that consolidation of clusters and segregation of clusters occurs only partly simultaneously, and within the clusters, WoBs continue to evolve more similarly, as also indicated by the slow convergence of similarity S; clusters consolidate without further segregation.

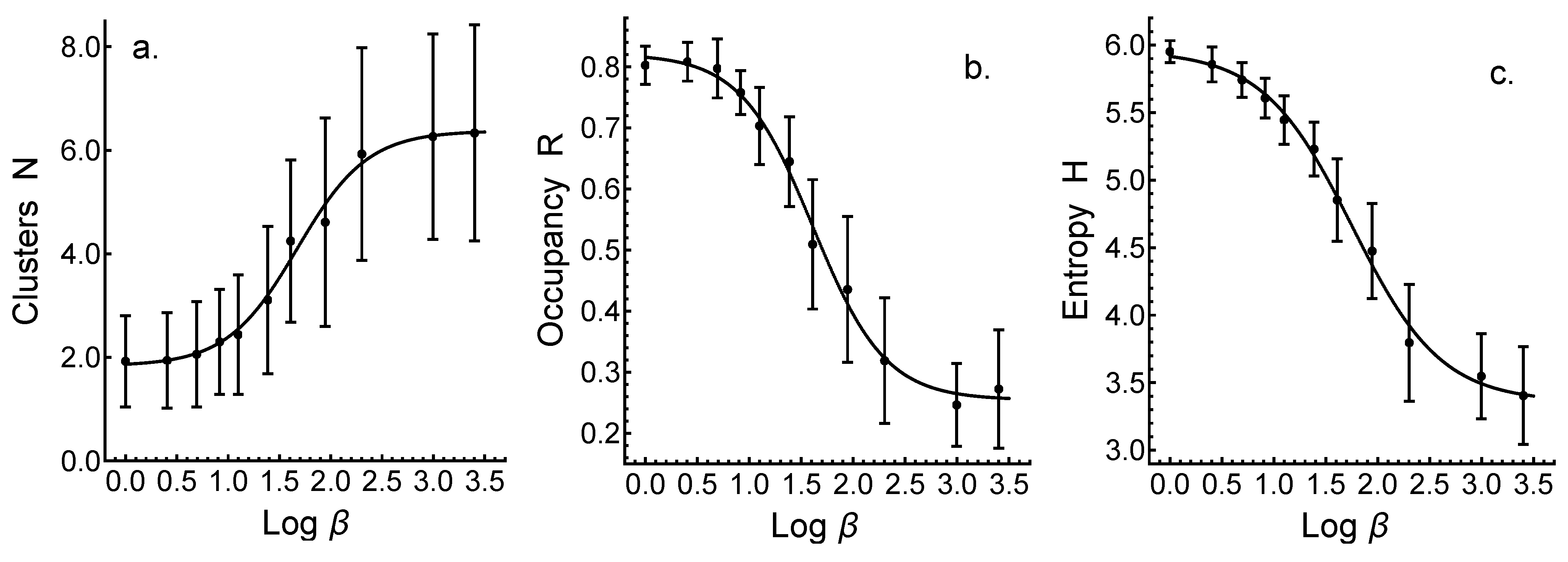
The stabilized, final values of cluster number N, entropy H, and the average occupancy R as a function of the sensitivity $\beta$ is shown in Figure 4 for a range of values from $\beta =1$ to $\beta =30$, on a (natural) log-scale. It is now seen (Figure 4a) that if the sensitivity to similarity is high enough ($\beta >10$), cluster formation takes place, and in the group of 25 agents about 6–7 are formed, with roughly equal numbers of 5–6 agents ($R\approx 0.3$) in a cluster (Figure 3c), with entropy $H\approx 3.5$, which roughly corresponds to cases such as the one shown in Figure 2b. However, in all cases, variations around mean values are large, as indicated by the error bars showing the standard deviation of values. In all cases, a transition to single cluster takes place around the value $\beta \approx 5$. After the transition, only two clusters are obtained on average, with high entropy ($H\approx 5.5$), roughly corresponding to two large and diffuse clusters of similar type as an initial cluster, shown in Figure 2a.

The results in Figure 4 show that the high sensitivity of agents to similarity in selecting similar partners (i.e., strong homophily) for interaction and for updating their WoBs invariably leads to the formation of segregated consensus groups. In addition to parameter $\beta$ regulating the sensitivity to similarity, the parameter ${\beta }^{*}$ for regulating agents’ confidence in decisions to add or delete edges affects the dynamics. Here, the value ${\beta }^{*}=10.0$ is chosen to maintain the average similarity in stabilized stage nearly a constant. Parameter ${\beta }^{*}$ regulates mainly the number of events needed for the relaxation and progress in harvesting new vertexes and edges. At low values of ${\beta }^{*}/E_0<1$, there is no average growth in similarity, at high values of beta ${\beta }^{*}/E_0>>1$ in the region of a confident decision to add or delete, the growth is maximal, constrained only by the new options allowed for the addition of edges within the consensus clusters. In particular, ${\beta }^{*}$ has no effect on the transition from single to multiple clusters.

Finally, the effect of the initial number of edges $E_0$ in WoBs and their variation $\Delta E_0$ is checked by changing their absolute values by $\pm \%20$, scaling both values by a factor of $\eta$ = 0.8 and 1.2 but keeping the ratio $E_0/\Delta E_0$ fixed. Figure 5 shows the evolution of cluster number N (Figure 5a–c), occupancy R (Figure 5d–f), and entropy H (Figure 5g–i) for the altered configurations with high sensitivity $\beta$ (the most interesting case with a high number of clusters) for values $\eta =1.2$ (the upper row) and $\eta =0.8$ to be compared with the results shown in Figure 3, corresponding to $\eta =1.0$ (reproduced in the middle row). The evolution of similarity is essentially similar to the results shown in Figure 4 and is thus omitted in Figure 5. As can be seen from the results, the increase in size of the WoB corresponding to factor $\eta =1.2$ slightly increases the number of clusters, but relaxation to steady state then requires more interaction events. This is as expected, because agents now have more choices available (i.e., more edges and vertexes) to change their WoBs, and thus more comparison events are needed to reach consensus. When the initial WoBs are smaller, corresponding to the choice $\eta =0.8$, the number of consensus clusters is slightly smaller than for $\eta =1.0$, and the events needed for relaxation are fewer. Qualitatively, for other values of $\beta$, the results remain essentially similar to the cases shown in Figure 3.

4. Discussion

In many respects, the ABM presented here describing the formation of consensus clusters resembles the so-called bounded confidence models (see e.g., [1,2,3,5] but differs from those models in two important ways. First, the ABM model describes the space of states of the agents (i.e., opinion-like states) as complex networks (WoBs) of elements related to each other, mimicking conceptual or semantic networks, not as discrete sets of choices or fixed to a few choices as in most bounded confidence models. To extend the applicability of consensus formation models provides understanding of not only choices of existing opinions (e.g., as in political or consumer choices) but allow the evolution of opinions. It is important to find ways to use flexible, dynamic, and changing states of agents, and furthermore, allow these states to be affected by choices that the agents make during the course of the unfolding interaction events. Such features provide a more realistic basis to model the formation of consensus groups in comparison with traditional models of predetermined fixed choices between different opinion states. Second, the ABM model introduced here does not assume a fixed bounded confidence criterion for the realization of the interactions. Instead, decisions to interact are made stochastically on the basis of utility-type evaluations of the prospect of increasing similarity. Therefore, there is no sharp exclusion of interactions, but instead, bias for similarity (homophily). In this respect, the WoBs introduced here parallel some other recent attempts to extend the consensus and opinion formation models [7,13].

Another set of models that resemble the ABM presented here are the so-called epistemic landscape models, which have found several potential applications in describing the formation and segregation of collaborative or consensus groups. The epistemic landscape models assume a fixed landscape of “knowledge” that agents explore [42,43] or closely related structures of fixed ground truths [10] or epistemic landscapes with agents sensing the distance from the ground truths or the gradients toward them. Such models assume a fixed, pre-existing landscapes of “knowledge” to be explored by agents, and thus the outcomes of the exploration are more or less predetermined by the structure of the landscape and its gradients [10,42,43]. The epistemic landscape models have turned out to be relevant to discussions of division of labor and how the ability of agents affects their collaboration, but such models do not easily yield to situations where dynamic changes in the landscape or the problem space are of interest.

The present ABM has two major limitations. First, the WoBs utilized in it are always substructures of more extensive templates. Although individual agents’ WoBs evolve, no new elements or connections are created, and WoBs will always remain as partial structures of the initial template. This, however, may not be a severe restriction in cases of intended applications where the targeted area of knowledge is opinions, views or belief of existing knowledge (i.e., discovery and creation of new knowledge is not in focus). Second, the WoBs and their update rules do not take into account the coherence of elements in the WoBs, nor requirements of coherence when elements are added or deleted. In some recent ABM approaches, the structure and coherence of agents’ opinions (or beliefs) are taken into account, allowing more realistic description of complex opinion and belief systems [7,44,45]. The inclusion of coherence of belief elements as part of ABM is, however, not unproblematic; diverse opinions exist regarding how to implement that notion as part of the idea of network-like knowledge. In some views, cognitive dissonance is important [46], and such aspects have been successfully implemented in ABM, where a model of cognitive (or conceptual) structures co-evolves with structural agents’ interactions [44]. In the present model, the coherence of belief systems arises from its dovetailed network structure, which is also a form of coherence of knowledge (see e.g., [47]). In that picture, adoption or deletion of nodes depends on their neighborhoods, where changes take place, always requiring the network to remain connected, but dissonant aspects of coherence are not taken into account. A lack of attention on dissonant connection is a clear restriction of the ABM introduced here.

Recent extensions of ABM have also included many other complex relevant features, for example: opinion dynamics making a separation between private and public opinions and the role of social hierarchies in interactions [48]; prior beliefs and knowledge-making decisions to adopt new beliefs [14,49]; and collective cognitive alignment, when group members perceive and recall the information they receive in aligned ways [50]. In addition to such features, it is possible to imagine many other socially important aspects the future ABM should take into account, for example, trust and its effects on social interactions [51]. While it is unreasonable to assume that at present any ABM can meet such diverse requirements, it is useful to keep in mind that omitting such features unavoidably limits the applicability of any suggested model, but in different ways.

In the current simple and idealized model presented here, many advanced and complex features are omitted. The goal of the model is to take a moderate further step to use more complex belief systems in similarity-biased models to show that even in the case of WoB-like structures, robust consensus clusters are formed; segregation and formation of consensus groups may well arise from the distribution of continuously evolving systems describing complex WoBs. Moreover, the dynamics of the formation of disciplinary consensus groups based on WoBs need not be overly complex; simple reinforcing similarity-seeking dynamics may clarify many empirically found features of how disciplinary groups and their boundaries are formed.

The most obvious areas of applications of the present model are found at least in three special cases. First, in disputes regarding how to frame and understand the meaning of abstract words or terms central to given scientific paradigms, where paradigms have their own specialized lexicons. Different ways of using scientific terms and framing problems are an interesting area of applications related to the social nature of science, the role of scientific discourse, and the argumentation and agreement of truth of scientific claims, as discussed extensively in the philosophy of science [19,20,21,22], as well as finding a tenable grounding on empirical research about scientific activity and formation of disciplinary groups [23,24,52,53]. Second, the ABM presented here may find applications in making sense of the formation of disciplinary groups in scholarly disputes about a given pre-existing corpus of study, for example, in disputes in the humanistic sciences about how to interpret the work of some renowned but difficult to follow scholar (e.g., Hegel, Kant or Wittgenstein), where the amount of interpretative literature with differing and even opposing views may be extensive and exceed the amount of original work. Third, and perhaps with the most foreseeable practical utility, to describe group formation in learning situations, where a group of students tries to make sense of a limited amount of sources about a given topic; in the simplest case, using a single textbook (see e.g., [28,29,35]. In such cases, due to sharing of views and opinions about same sources, one can nevertheless assume formation of different groups of consolidated views.

The possibility to connect the results of the current ABM more securely to existing empirical findings is not, however, straightforward. The ABM provides some insight structure and formation of discourse groups in learning and teaching, where groups of the size from three to about five to six students appear to perform the best [54,55,56,57], but in larger groups the phenomenon of isolation emerges [58,59]. While many unrelated factors (e.g., teaching arrangements and designs) affect group sizes, it is a plausible assumption that at least in the case of discourse groups, shared meanings of key terms and concepts is also a factor affecting group stability and how the number of students in a group evolves. For example, the isolation and break-up of small isolated groups from larger ones may well be a phenomenon related to similarity bias. In the case of scholarly disciplinary groups, empirical evidence of group sizes is more elusive and unclear. Scientometric analyses of the number of co-authors in publications provide some information, showing that small co-author groups are the most common, signaled as a fat-tailed distribution of number of authors [60,61]. This notion is supported also by results based on the size of scholarly groups that introduce (and thus use) new concepts, in which case small groups are also the most active [62,63]. Interestingly, reminiscent formation of disciplinary groups are found within focused research areas [64], as well as in case of non-scientific but organized beliefs groups (i.e., religion), [65]. In all these cases, however, the assumption that similarity bias guiding the formation of groups is a factor affecting the formation, segregation, and consolidation of groups is only tentative, although plausible. Without better knowledge of how, for example, that the changes in shared vocabulary or lexicons used by groups are correlated with group formation it is difficult to make more conclusive inferences on, or to propose more specific empirically testable hypotheses.

Nevertheless, due to the obvious tentativeness and generic nature of the results presented in this study, the present ABM model, where similarity is monitored through WoBs and where changes in WoBs are the basis of group formation dynamics, suggests that in future, more detailed studies, paying attention to correlations between consensus group formation and changes in WoBs or related structures may provide essentially new important insights on group dynamics. In that, ABM may also significantly guide designs of empirical research.

5. Conclusions

We presented an agent-based model (ABM) of the formation of consensus clusters when the agents possess a complex network of knowledge or belief elements, which form a web of beliefs (WoBs). The WoBs affect the ways they can communicate with each other, and they are dynamically changed as an outcome of the interactions. The ABM takes into account dynamic changes in WoBs due to the sharing of their elements in events of interactions (i.e., communication). The dynamics are driven and constrained by similarity evaluations between agents (i.e., homophilic dynamics), evaluated on the basis of the similarity of WoBs.

The results of the model show that a group of agents, if their sensitivity to similarity is sufficiently high, will eventually form consensus groups, where agents have more or less similar WoBs. If the sensitivity to similarity is low, no segregation takes place, and agents remain in one or two large and diffuse groups. The main message of the ABM and its results is that even in the case of complex webs of beliefs, which are allowed to change dynamically in interactions between agents, a very simple dynamic is enough to produce segregation and consolidation of consensus groups in the presence of sensitivity to similarity (as described by webs of beliefs).

The simple and idealized agent-based model presented here is one step towards a better understanding of such complex situations and may also help to construct empirical settings of investigations to resolve the auxiliary features from the core features in driving consensus formation.