Practical Formalism-Based Approaches for Multi-Resolution Modeling and Simulation

Abstract

Multi-resolution modeling (MRM) has been considered as an ideal form of simulation to acquire low-resolution scalability as well as high-resolution modeled details. Although both practical and theoretical interests exist in MRM, actual implementations were quite different in terms of cases and methods. Specifically, MRM implementations range from parameter-based interoperation to model exchanges with different resolutions, yet it is difficult to observe a method that focuses on both of these aspects. To this end, this paper introduces a formalism or multi-resolution translational Discrete Event System Specification (MRT-DEVS). Focusing on the practical perspective, MRT-DEVS intends to ease the implementation’s difficulty and reduce the simulation’s execution costs. Specifically, MRT-DEVS embeds state and event translation functions into the model’s specifications so that it enables MRM with less complex mechanisms in terms of operations. Using the provided case study and a reduction to other MRM methods, the theoretical soundness of the proposed method is supported. Moreover, we discussed the pros and the cons of the proposed method from various MRM perspectives. We expect that with all the provided information, MRMS users would consider the proposed method as a practical option to implement their models.

1. Introduction

This paper introduces a formalism for multi-resolution translational discrete event system specification (MRT-DEVS) to enable MRMs with less complex mechanisms with respect to operations. The proposed method is based on discrete event system specification (DEVS) formalism [1]. The previous DEVS-based formalisms are solid and sound, with complete expressions in MRM scenarios. However, we note that their hidden challenge is the difficulty that field engineers face when implementing multi-resolution (MR) models by following such formalisms. For example, MR modeling with previous formalisms requires components for different resolution models and resolution conversions, which eventually increases the total implementation’s complexity. The proposed MRT-DEVS intends to ease the implementation difficulty by relaxing an assumption of the DEVS. Specifically, MRT-DEVS absorbs the resolution conversion into the models for each resolution, and the state information is converted within the model, which does not require additional models for the conversion’s purpose. This reduces the practical implementation burden, but relaxing the assumption can cause a trade-off relationship, which is investigated from various perspectives.

The utility of simulation often originates from the emergence of target systems that is difficult to anticipate before the execution of actual system operations as well as the comprehensive description of systems. To embody these two aspects, simulation practices need to be comprehensive for the expression and scalable for the emergence [2,3]. For example, if only a handful of objects are involved in a simulation, the complexity that lies in the system would be difficult to observe in emergent phenomena. On the other hand, to simulate many objects, the descriptions of the objects may be over-abstracted and even simplified, which would fail to deliver a comprehensive description. Therefore, the objectives of comprehensive expression and scaled emergence result in a dilemma [4,5] when we assume limited resource in modelers, computing resources, available data, etc.

To confront this dilemma, researchers proposed a form of multi-resolution modeling (MRM) that describes a target system with different resolution components; thus, the model’s details can change according to their compositions [6,7,8]. This approach can resolve the dilemma by implementing a high-resolution model for completeness and a low-resolution model for scalability [9]. Moreover, the resolution levels of model components change during simulation executions using internal or external triggers (e.g., events coming from external or inner states) through an arbiter that is implemented by users [10,11]. Ideally, MRM simulations may execute the modeled details with accelerated or simplified behaviors that intervene in periods. This ideal framework has drawn interest from practitioners and researchers; thus, works related to the MRM approach have been published.

Although both practical and theoretical interests exist in MRM, actual implementations were quite different in terms of cases and methods. The implementation of MRM ranges from a parameter-based interoperation to model exchanges among different resolutions. In particular, model exchange has been conducted in rather complex ways because the objects and the associated information, such as model states, should be properly converted with respect to a new resolution. In this conversion process, an ad hoc approach is often applied due to its lower development costs [12,13,14,15]. However, we argue that the conversion should be rather disciplined so that the developed models can be maintainable, flexible, and transparent. A number of proposals have followed such a suggestion, especially the formalism-based method: MRM formalisms [10,11] generally specify models for different resolutions and require an additional model to deal with the conversion process.

After introducing the MRT-DEVS formalism, we argues its expression in two ways: First, we show an illustrative example with a dynamic resolution-change sequence to demonstrate how MRT-DEVS models MR scenarios; second, we reduce MRT-DEVS formalism to previous MRM formalisms so that MRT-DEVS can convey the same amount of information that was expressed in previous formalisms. Lastly, we discuss trade-off relationships in MRT-DEVS.

2. Previous Research

This section provides a survey of the previous research studies on MRM. Specifically, we examine how MRM works, particularly in MRM applications and methods.

2.1. Multi-Resolution Modeling Applications

Before diving into the survey, we intend to begin with a formal definition of MRM. In modeling and simulation (M&S), the resolution of a model refers to the level of an abstraction of a target system, which could differ according to the objective of simulations performed with the model. For example, when we simulate a squad-level engagement, its objectives could vary with respect to the modeler’s interests: For instance, one may have an interest in either squad maneuver tactics or individual engagement tactics in the squad. In this sense, the model’s resolution has become a frequent topic in discussions among M&S experts [16,17,18].

MRM, as a concept extended from model resolution, describes a target system as a set of models with different resolution levels. More formally, MRM was defined as “building a single model with alternative user models that have different levels of resolution for the same phenomena” [19,20]. To meet the potential capability expected from the definition, many MRM research studies have been conducted and developed in various domains.

Rauscher et al. conducted a large number of aqua planet experiments using the multi-resolution model for predication across diffirent scales of hydrostatic dynamical cores [21]. Jeschke and Uhrmacher applied MRM methods to develop a molecular crowding simulation model in which a combination of individual and lattice-population-based algorithms were used to manage macromolecular crowding phenomena [22]. Tan et al. dealt with MRM problems, such as aggregation and disaggregation among federates of different resolution levels, in a high level architecture (HLA) environment [23]. Zeigler and Kim proposed an efficient approach for MRM, particularly for UAV-based service systems using DEVS-based system entity structures (SESs) [24].

Although MRM is used to capture various aspects of a target system, there is another method used for applying MRM, such as securing simulation efficiency. Yoon et al. [25] developed grid models of focused ultrasound propagation, and they assessed their computational efficiency by various combinations of resolution grid settings. Ringler et al. [26] proposed an MRM method for the global ocean system, and the simulation based on the proposed method was efficiently evaluated by using MRM concepts. Choi et al. [27] applied an MRM method to improve simulation execution speeds while reducing errors and increasing future model reuses.

2.2. Multi-Resolution Modeling Methods

Although MRM applications are widespread, many researchers have shown an interest in using different methods to develop MR models efficiently. In MRM contexts, maintaining the consistency between different levels of resolution models is important, because models of various resolution levels have to be exchanged during the simulation’s execution [28,29,30]. Consistency maintenance is mainly about current model information, such as the model’s states and external inputs to the model, and the conversion process on this information is referred to as state and event translation in this paper.

Although a number of ways to realize MRM exist, we focus on the formalism-based methods. Considering the importance of consistency maintenance in MRM, we also argue that a method for MRM should provide a clear view of the conversion process so that users can understand how it works and eventually manipulate it for what they want to develop. Among M&S formalisms, DEVS is often considered as one of the remarkable candidates because of its systematic modeling capability. Hence, a number of MRM methods have been based on DEVS [11,31,32,33], and the proposed method is another variant of DEVS.

Among past DEVS variants, we focused on Baohong’s [11] and Hong’s [33] studies because their approaches are similar to ours. Baohong proposed a formal specification for MRM based on DEVS. To this end, he proposed a concept of an MR model family (MF) where different resolution models and their relations are involved. Technically, he made two efforts for his proposed MRM formalism: (1) he introduced a set of model resolutions ($\gamma$) and the associated functions ($\psi$, $\pi$, and $\chi$) for embedding model resolutions into his work; (2) he adapted the specifications from dynamic structure DEVS [34] for describing more resolution changes via a change in model structure.

Hong also proposed a formalism for MR modeling and simulation, and it focused on the method of implementing MR simulations with existing models (e.g., federates in HLA) and not methods for specifying the actual MR model. In any case, the main body of her formalism was formed using a structure similar to Baohong’s, yet Hong introduced a concept of resolution-conversion protocols (using $C_R$ and $Y_R$) that enables triggering a model’s resolution changes from its inner components.

Although it is obvious that the above-mentioned MRM methods provide sound theoretical frameworks for MRM, two drawbacks cause hesitency in their applications in actual model development. The first is that their formalisms possess structure that is too and have too many elements that should be specified by users. This trait may oppose the direction of DEVS because DEVS has become one of the most popular formalisms in M&S due to its simple and explicit expression. The second drawback is that according to their complex structure, its simulation would be inefficiently executed. Moreover, in handling resolution changes, they introduced additional components, such as a converter ($\chi$) or additional event exchange protocols ($C_R$ and $Y_R$), and these efforts require more costs, including incresaed simulation time and resource usage.

To tackle these problems, this paper proposes an MRM formalism. The proposed method is an extension of DEVS formalism, but the modification is minimized to convey the easy modeling resulting from DEVS. Moreover, the proposed method hides most of the converter and event-exchange protocols for model resolution changes, which were enabled by releasing modular characteristics in DEVS. Through this improvement, the cost of MRM development and its simulation in practice would be reduced. The details on the pros and the cons of the proposed method are discussed in a later section.

3. Multi-Resolution Translational DEVS Formalism

This section introduces the proposed formalism, MR translational discrete event system specification formalism (MRT-DEVS), with resepct to two aspects: the first is the definition and semantics of the formalism; the second is the operation of the specified MR system following the MRT-DEVS formalism.

3.1. Specification of MRT-DEVS Formalism

In this section, we introduce the specifications of the MRT-DEVS formalism, which extends the DEVS formalism with a minimal variation in order to enable MR modeling. MRT-DEVS consists of two definitions: the atomic model and the coupled model. Equations (1) and (2) define the atomic model and the coupled model, respectively.

$$\begin{array}{cc}\hfill AM& = <X,Y,S_M,S_R,{\delta }_{ext},{\delta }_{int},{\delta }_{res},\lambda ,ta>\hfill \\ \hfill & X\mathrm{and}Y\mathrm{are}\mathrm{sets}\mathrm{of}\mathrm{input}\mathrm{and}\mathrm{output}\mathrm{events}\hfill \\ \hfill & S_M\mathrm{and}{S}_R\mathrm{are}\mathrm{sets}\mathrm{of}\mathrm{model}\mathrm{and}\mathrm{resolution}\mathrm{states}\hfill \\ \hfill & {\delta }_{ext}:Q\times X\to S_M,\mathrm{external}\mathrm{transition}\mathrm{function}\hfill \\ \hfill & \mathrm{where}Q=\left\{(s,e)\right|s\in S_M,0\le e\le ta\left(s\right)\}\hfill \\ \hfill & {\delta }_{int}:S_M\to S_M,\mathrm{internal}\mathrm{transition}\mathrm{function}\hfill \\ \hfill & {\delta }_{res}:S_M\times S_R\to S_R,\mathrm{resolution}\mathrm{transition}\mathrm{function}\hfill \\ \hfill & \lambda :S_M\to Y,\mathrm{output}\mathrm{function}\hfill \\ \hfill & ta:S_M\to R^{+},\mathrm{time}\mathrm{advance}\mathrm{function}\hfill \end{array}$$

(1)

Equation (1) enumerates the atomic model tuple. In detail, X is a set of input events, Y is a set of output event, and $S_M$ and $S_R$ are sets of state variables representing the model and the resolution states, respectively. ${\delta }_{ext}$ is the external transition function that determines the next $S_M$ with the current $S_M$ and the input event instance; ${\delta }_{int}$ is the internal transition function that determines the next $S_M$ with the current $S_M$; ${\delta }_{res}$ is the resolution transition function that determines the next $S_R$ with the current $S_R$ and the current $S_M$; $\lambda$ is the output function to generate an output event instance based on the model state $S_M$; $ta$ specifies the lifespan of a model state (i.e., next time advance time), $t_{adv}\in [0.\infty )$, by depending on $S_M$.

Compared to the original DEVS formalism, the atomic model of MRT-DEVS adds $S_R$ and ${\delta }_{res}$, which are the resolution state and resolution transition function. This formalism design intends to minimize the modifications of potentially existing atomic models, and particularly, the formalism limits alterations on existing transition functions of ${\delta }_{ext}$ and ${\delta }_{int}$ because these are often considered as key features for modeling discrete-event systems. For example, the proposed formalism minimizes the modification on DEVS by adding two tuple elements regarding the model’s resolution to the DEVS atomic model.

$$\begin{array}{cc}\hfill CM& = <X,Y,M,S_R,RMS,{\delta }_{res},{\delta }_{strans},{\delta }_{etrans}>\hfill \\ \hfill & X\mathrm{and}Y\mathrm{are}\mathrm{sets}\mathrm{of}\mathrm{input}\mathrm{and}\mathrm{output}\mathrm{events}\hfill \\ \hfill & M\mathrm{is}\mathrm{a}\mathrm{set}\mathrm{of}\mathrm{model}\mathrm{components}\hfill \\ \hfill & S_R\mathrm{is}\mathrm{a}\mathrm{set}\mathrm{of}\mathrm{resolution}\mathrm{states}\hfill \\ \hfill & RMS\subseteq S_R\times {\Sigma }_r(r\in S_R),\mathrm{resolution}\mathrm{model}\mathrm{structure}\hfill \\ \hfill & \mathrm{where}{\Sigma }_r=\{M_r,EI{C}_r,EO{C}_r,I{C}_r,Selec{t}_r\},\hfill \\ \hfill & \mathrm{coupling}\mathrm{relations}\mathrm{at}\mathrm{model}\mathrm{resolution}\mathrm{state}\left(r\right)\hfill \\ \hfill & {\delta }_{res}:S_R\times {\cup }_{m\in {\Sigma }_r.M_r}m.S\to S_R,\hfill \\ \hfill & \mathrm{resolution}\mathrm{transition}\mathrm{function}\hfill \\ \hfill & {\delta }_{strans}:S_R\times {\cup }_{m\in {\Sigma }_r.M_r}m.S\to {\cup }_{m\in {\Sigma }_r.M_r}m.S,\hfill \\ \hfill & \mathrm{state}\mathrm{translation}\mathrm{function}\hfill \\ \hfill & {\delta }_{etrans}:S_R\times X\to m.X,\mathrm{where}m\in {\Sigma }_r.M_r\hfill \\ \hfill & \mathrm{event}\mathrm{translation}\mathrm{function}\hfill \end{array}$$

(2)

Equation (2) enumerates the coupled model tuple: X is the input events, Y is the output events, and M is a set of model components, which are identical to the DEVS coupled model. To embed the model resolution concept in the coupled model, MRT-DEVS introduces a resolution state ($S_R$) and the associated transition functions (i.e., ${\delta }_{res}$, ${\delta }_{strans}$, and ${\delta }_{etrans}$), which are not allowed in the classic DEVS coupled model. Moreover, MRT-DEVS holds a resolution model set ($RMS$), which is defined as a set of activated models and their coupling relations for a certain resolution state. Specifically, at a certain resolution state denoted by $S_R$, $RMS$ becomes a tuple of the coupling information according to the resolution state, ${\Sigma }_r$. In this paper, ${\Sigma }_r$ consists of activated models ($M_r$) and a union set of external input couplings, $EI{C}_r$; external output couplings, $EO{C}_r$; internal couplings, $I{C}_r$; and a tie-breaking function, $Selec{t}_r$, in the classic DEVS coupled model. We denote this union of coupling information as $\Sigma$ by following the notation of the DS-DEVS [34].

MRT-DEVS proposes a transition function, ${\delta }_{res}$, for $S_R$. By definition, ${\delta }_{res}$ accesses information from two separate sources: the specifying model’s resolution state, $S_R$, and the union of the currently activated model’s state, ${\cup }_{m\in {\Sigma }_r.M_r}m.S$. Here, it should be noted that we are suggesting that a coupled model accesses the states of its components. This has been regarded as a violation of the black-box assumption, or modular modeling, which has been prohibited in DEVS. We will return to this discussion in later sections in this paper. If we accept the definition of $RMS$, the definition of ${\delta }_{res}$ becomes trivial because it changes the resolution state’s information, $S_R$, by the state of the child models that is affected by input events or the expiration time.

While accepting the definition of ${\delta }_{res}$ requires the read privilege of the child models, or components, the state translation function of ${\delta }_{strans}$ requires writing privileges. ${\delta }_{strans}$ is the function to change the state information in the activated models at a certain resolution state r (${\Sigma }_r.M_r$). Previous approaches used event messages to change the state information of the activated models, but we note that this increases modeling and simulation costs, such as increased message passing counts and the modeling concerns for handling them. Specifically, Lee and Kim [35] identified that message passing is the most influent factor for simulation overheads. Hence, we relaxed the black-box model assumption to alter the state information of the child models directly. The justification for this assumption violation will follow in the Discussion section. The main role of this state translation is data aggregation and disaggregation because of resolution changes. For instance, a low-resolution model will generate a set of state information for a high-resolution model through data disaggregation, and data aggregation denotes the scenario from a high resolution to a low resolution. Eventually, every piece of information is stored as state information; thus, data aggregation/disaggregation can be realized by manipulating state information.

Finally, MRT-DEVS requires a function for event translation, ${\delta }_{etrans}$, between resolution changes. An event from the outside model assumes a certain resolution of a receiver model, but the receiver model might change its resolution by alternatively using a different set of $RMS$. Therefore, the outside event needs to be adjusted by the activated model resolution that is determined by $S_R$. As a notation, ${\delta }_{etrans}$ accepts $S_R$ and the input event from the outside X, which is indifferent to the resolution state of the receiver model, and ${\delta }_{etrans}$ turns the input event into inputs of the activated components, which is called an event translation adjusted to fit the model of a certain resolution, $S_R$. In previous MR methods, this was implemented as another converter model, and this method requires exchanges of event messages as well as the resolution setting message. Therefore, we removed the converter model by violating the black-box model assumption; more specifically, we replaced the converter model with a function of the coupled model.

3.2. Operation of MRT-DEVS Formalisms

Once we define the MRT-DEVS formalism, it is important to understand how the specified models work (i.e., their operational procedures). The proposed MRT-DEVS defines the resolution’s state transition in both atomic and coupled models; thus, this paper introduces the operation of both models in turn.

Algorithm 1 illustrates the operation flow of the atomic model in MRT-DEVS in contrast to the classic DEVS (additional parts for MRT-DEVS are presented in bold in Algorithm 1). In the classic DEVS, the atomic model is introduced for modeling behaviors in discrete event systems. Once users design atomic models, the DEVS simulation algorithm supports the simulation of system behaviors with resepct to a discrete event system. For example, setting up the last event time (tl) and next event time (tn) is essential in discrete event simulation.

Algorithm 1 Simulation Algorithm for MRT-DEVS Atomic Models

Require:  $parent$ {parent model},     $tl$ {last event time},     $tn$ {next event time} 1: while not at the end of simulation do 2:         if receiving an initialization message at time t then 3:                 $tl$ = t − e {e: elapsed time} 4:                 $tn=tl+ta\left(S_M\right)$ {$S_M$: model state} 5:         else if receiving a state transition event at time t then 6:                 y = $\lambda$($S_M$) 7:                 send an output event to $parent$ (y, t) 8:                 $S_M={\delta }_{int}\left(S_M\right)$ 9:                 ${\mathit{S}}_{\mathit{R}}\mathbf{=}{\mathsf{\delta }}_{\mathit{res}}\mathbf{(}{\mathit{S}}_{\mathit{M}}\mathbf{,}{\mathit{S}}_{\mathit{R}}\mathbf{)}$ {$S_R$: resolution state} 10:                $tl=t$ 11:                $tn=tl+ta\left(S_M\right)$ 12:         else if receiving an input event x at time t then 13:                 $e=t-tl$ 14:                 $S_M={\delta }_{int}(S_M,e,x)$ 15:                 ${\mathit{S}}_{\mathit{R}}$ = ${\mathsf{\delta }}_{\mathit{r}\mathit{e}\mathit{s}}\mathbf{(}{\mathit{S}}_{\mathit{M}}\mathbf{,}{\mathit{S}}_{\mathit{R}}\mathbf{)}$ 16                  $tl=t$ 17:                 $tn=tl+ta\left(S_M\right)$ 18:         end if 19: end while

As Algorithm 1 shows, the simulation algorithm for the DEVS atomic model handles events, or messages, from two perspectives. In one case, it involves receiving a state transition message from the parent model where the atomic model is involved. In this case, the atomic model generates an output event based on its current state ($\lambda$), changes its model state (${\delta }_{int}$), and sets up a time duration for staying in the changed state (time advance, $ta$). In the other case, it receives an input event from the outside. In this case, the atomic model changes its state depending on the current state and the input event (${\delta }_{ext}$), and similarly to the previous case, it updates the time duration for the new state with its time advance function.

As mentioned above, the proposed MRT-DEVS atomic model does not alter the classic one much and introduces resolution states ($S_R$) and the associated transition function (${\delta }_{res}$). Similarly, the simulation algorithm for the MRT-DEVS adds calling the resolution state-transition function after the model’s state transitions (${\delta }_{int}$ (line 9) and ${\delta }_{ext}$ (line 15), which are marked in bold in Algorithm 1) into the classic state.

Algorithm 2 illustrates the simulation algorithm of the coupled model in MRT-DEVS, which is also based on DEVS (additional parts are marked in bold). In DEVS, the coupled model is for reflecting the structure of a target system. However, the simulation algorithm for the coupled model coordinates the simulation’s execution within it and its components; specifically, it helps synchronize simulation times and manage event exchanges among the coupled model and its components.

Setting aside the initialization, the simulation algorithm of the DEVS-coupled model considers three event cases (refer to Algorithm 2). The first case is when the coupled model receives a state transition event, which means any component of the coupled model is ready to change its state (either or both of its model and resolution states). In this case, the simulation algorithm sends a state transition event to an imminent child, $m\ast$, and its time advance is identical to its next event time, $tn$, and the imminent child, if it is an atomic model, changes its state following a case in which it receives a state transition message in Algorithm 1. Then, the time information, such as $tl$ and $tn$, is updated by considering the results of the state transition.

Second, when the associated coupled model obtains an input event, x, the simulation algorithm finds a set of models, $M_{receiving}$, that is related with the input event. To this discovery, the coupling information takes the role of condition (${\Sigma }_r$). Then, the simulation algorithm requests every model in $M_{receiving}$ to handle the input event (refer to when receiving an input event case in Algorithm 1). Considering the result of the followed state transitions, the simulation algorithm update its time information.

Lastly, when the coupled model receives an output event, y, generated from its components, the simulation algorithm defines $M_{receiving}$ of the output event using coupling relations. Similarly, output event y is forwarded to every model in $M_{receiving}$. Specifically, in a case in which the parent model is identified as a receiving model (i.e., the parent model is included in $M_{receiving}$), the simulation algorithm sends y as an output event of the parent model; otherwise, it sends y as an input event of the component models. Then, an update of the time information follows.

Based on the above explanation, the modifications for the simulation algorithm for the MRT-DEVS-coupled model are conducted in three parts: resolution transition function (${\delta }_{res}$), state translation function (${\delta }_{strans}$), and event translation function (${\delta }_{event}$). Similarly to the MRT-DEVS atomic model case, the resolution transition function calls after resolution state transitions of the components. Specifically, such transitions can occur in the above three cases (i.e., when the cases of receiving a state transition (lines 11–14), an input event (lines 23–26), and an output event (lines 38–41) cases in Algorithm 2). After the resolution state function, the state translation function always follows to update it and the component’s states (including model and resolution states). However, the event translation function is called only when an input event is forwarded to components (line 19 in Algorithm 2). Through the event translation function, the input event is transformed into a new form of an input event that is more proper to the resolution state of the receiving component.

The operation flows of MRT-DEVS modify the simulation algorithms of the classic DEVS by adding several function calls for handling state and event conversions due to resolution changes. With such a small modification, MRT-DEVS can not only help enable MR modeling for discrete event simulations but can also aid many users by facilitating easy modeling with DEVS semantics.

Algorithm 2 Simulation Algorithm for the MRT-DEVS-Coupled Model

Require:  $parent$, $tl$ ,$tn$ 1: while not at the end of simulation do 2:         if receiving an initialization message at time t then 3:                  for m in MM: children components do 4:                          send initialization message to m 5:                  end for 6:                  tl = $max\left\{t{l}_m\right|m\in M\}$ 7:                  tn = $min\left\{t{n}_m\right|m\in M\}$ 8:                  $m\ast =argmi{n}_{m\in M}\left\{t{l}_m\right\}$ {$m\ast$: imminent child} 9:         else if receiving a state transition event at time t then 10:                send state transition event to $m\ast$ 11:                if m∗ changed its resolution state then 12:                        ${\mathit{S}}_{\mathit{R}}\mathbf{=}{\mathsf{\delta }}_{\mathit{res}}\mathbf{(}{\mathit{S}}_{\mathit{R}}\mathbf{,}{\mathbf{\cup }}_{\mathit{m}\mathbf{\in }{\mathbf{\Sigma }}_{\mathit{r}}\mathbf{.}{\mathit{M}}_{\mathit{r}}}\mathit{m}\mathrm{.}\mathit{S}\mathbf{)}$ 13:                        ${\mathbf{\cup }}_{\mathit{m}\mathbf{\in }{\mathbf{\Sigma }}_{\mathit{r}}\mathbf{.}{\mathit{M}}_{\mathit{r}}}\mathit{m}\mathbf{.}\mathit{S}\mathbf{=}$                              ${\mathsf{\delta }}_{\mathit{strans}}\mathbf{(}{\mathit{S}}_{\mathit{R}}\mathbf{,}{\mathbf{\cup }}_{\mathit{m}\mathbf{\in }{\mathbf{\Sigma }}_{\mathit{r}}\mathbf{.}{\mathit{M}}_{\mathit{r}}}\mathit{m}\mathbf{.}\mathit{S}\mathbf{)}$ 14:                end if 15:                $tl=t$ , $tn=min\left\{t{n}_m\right|m\in M\}$ 16:                $m\ast =argmi{n}_{m\in M}\left\{t{l}_m\right\}$ 17:         else if receiving an input event x at time t then 18:                define $m_{receiving}$ {$m_{receiving}$: models receiving x} according to coupling relations (${\Sigma }_r$) 19:                $\mathit{m}\mathbf{.}\mathit{x}\mathbf{=}{\mathsf{\delta }}_{\mathit{etrans}}\mathbf{(}{\mathit{S}}_{\mathit{R}}\mathbf{,}\mathit{x}\mathbf{)}$ 20:                for m in $m_{receiving}$ do 21:                          send an input event to m ($m.x$,t) 22:                end for 23:                if m∗ changed its resolution state then 24:                        ${\mathit{S}}_{\mathit{R}}\mathbf{=}{\mathsf{\delta }}_{\mathit{res}}\mathbf{(}{\mathit{S}}_{\mathit{R}}\mathbf{,}{\mathbf{\cup }}_{\mathit{m}\mathbf{\in }{\mathbf{\Sigma }}_{\mathit{r}}\mathbf{.}{\mathit{M}}_{\mathit{r}}}\mathit{m}\mathrm{.}\mathit{S}\mathbf{)}$ 25:                        ${\mathbf{\cup }}_{\mathit{m}\mathbf{\in }{\mathbf{\Sigma }}_{\mathit{r}}\mathbf{.}{\mathit{M}}_{\mathit{r}}}\mathit{m}\mathbf{.}\mathit{S}\mathbf{=}$                              ${\mathsf{\delta }}_{\mathit{strans}}\mathbf{(}{\mathit{S}}_{\mathit{R}}\mathbf{,}{\mathbf{\cup }}_{\mathit{m}\mathbf{\in }{\mathbf{\Sigma }}_{\mathit{r}}\mathbf{.}{\mathit{M}}_{\mathit{r}}}\mathit{m}\mathbf{.}\mathit{S}\mathbf{)}$ 26:                end if 27:                $tl=t$ , $tn=min\left\{t{n}_m\right|m\in M\}$ 28:                $m\ast =argmi{n}_{m\in M}\left\{t{l}_m\right\}$ 29:         else if receiving an output event y from $m\in M$ at time t then 30:                define $m_{receiving}$ according to coupling relations (${\Sigma }_r$) 31:                for m in $m_{receiving}$ do 32:                          if m is $parent$ then 33:                                  send an output event to $parent$ (y,t) 34:                          else 35:                                  send an input event to m (y,t) 36:                          end if 37:                end for 38:                if m∗ changed its resolution state then 39:                        ${\mathit{S}}_{\mathit{R}}\mathbf{=}{\mathsf{\delta }}_{\mathit{res}}\mathbf{(}{\mathit{S}}_{\mathit{R}}\mathbf{,}{\mathbf{\cup }}_{\mathit{m}\mathbf{\in }{\mathbf{\Sigma }}_{\mathit{r}}\mathbf{.}{\mathit{M}}_{\mathit{r}}}\mathit{m}\mathrm{.}\mathit{S}\mathbf{)}$ 40:                        ${\mathbf{\cup }}_{\mathit{m}\mathbf{\in }{\mathbf{\Sigma }}_{\mathit{r}}\mathbf{.}{\mathit{M}}_{\mathit{r}}}\mathit{m}\mathbf{.}\mathit{S}\mathbf{=}$                              ${\mathsf{\delta }}_{\mathit{strans}}\mathbf{(}{\mathit{S}}_{\mathit{R}}\mathbf{,}{\mathbf{\cup }}_{\mathit{m}\mathbf{\in }{\mathbf{\Sigma }}_{\mathit{r}}\mathbf{.}{\mathit{M}}_{\mathit{r}}}\mathit{m}\mathbf{.}\mathit{S}\mathbf{)}$ 41:                end if 42:                $tl=t$ , $tn=min\left\{t{n}_m\right|m\in M\}$ 43:                $m\ast =argmi{n}_{m\in M}\left\{t{l}_m\right\}$ 44:         end if 45: end while

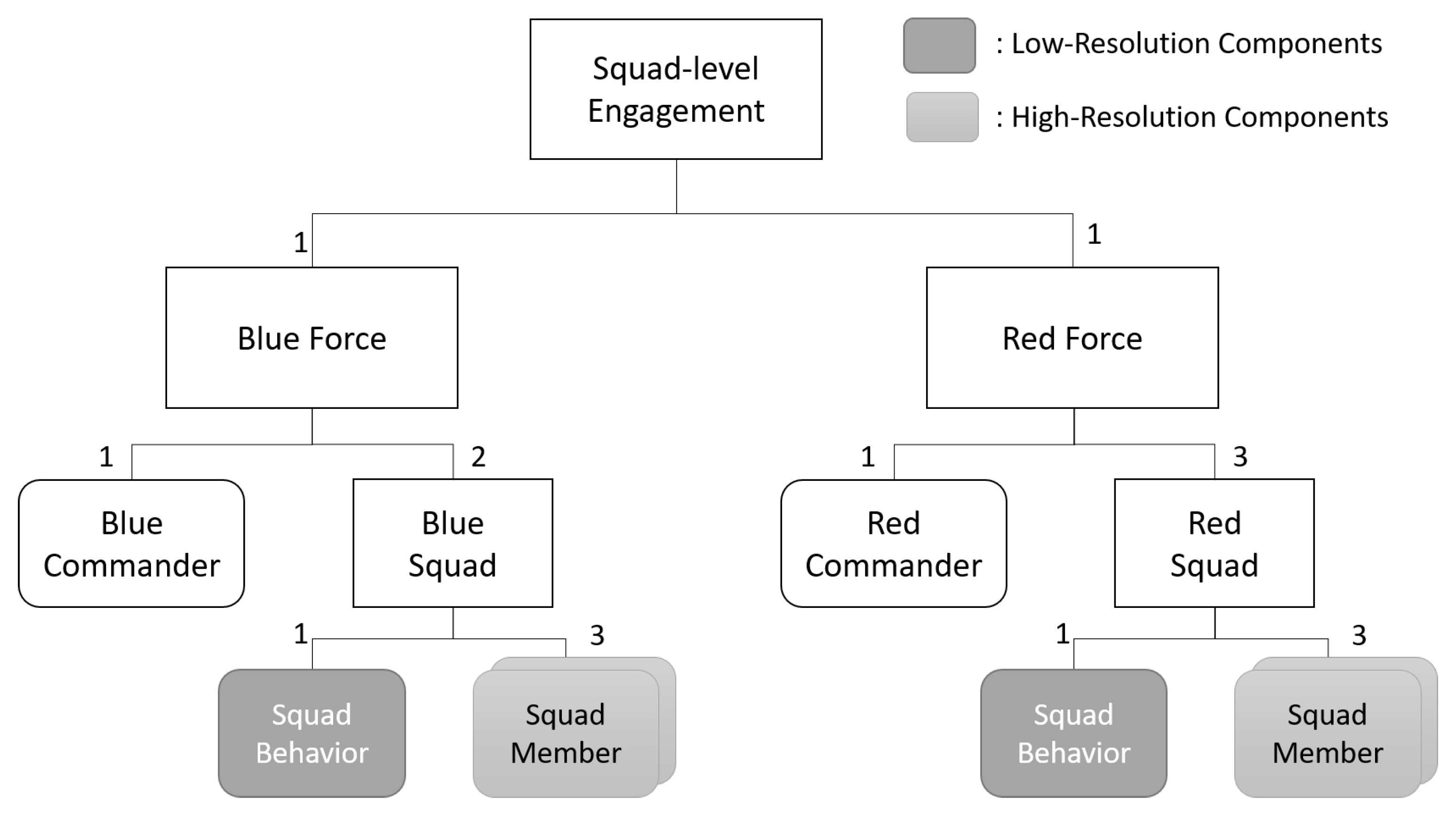
4. Case Study

This section presents a case study utilizing a model developed by the proposed MRT-DEVS. By examining this case study, we provide an example of the MRT-DEVS and address the way MRM is properly realized with its semantics.

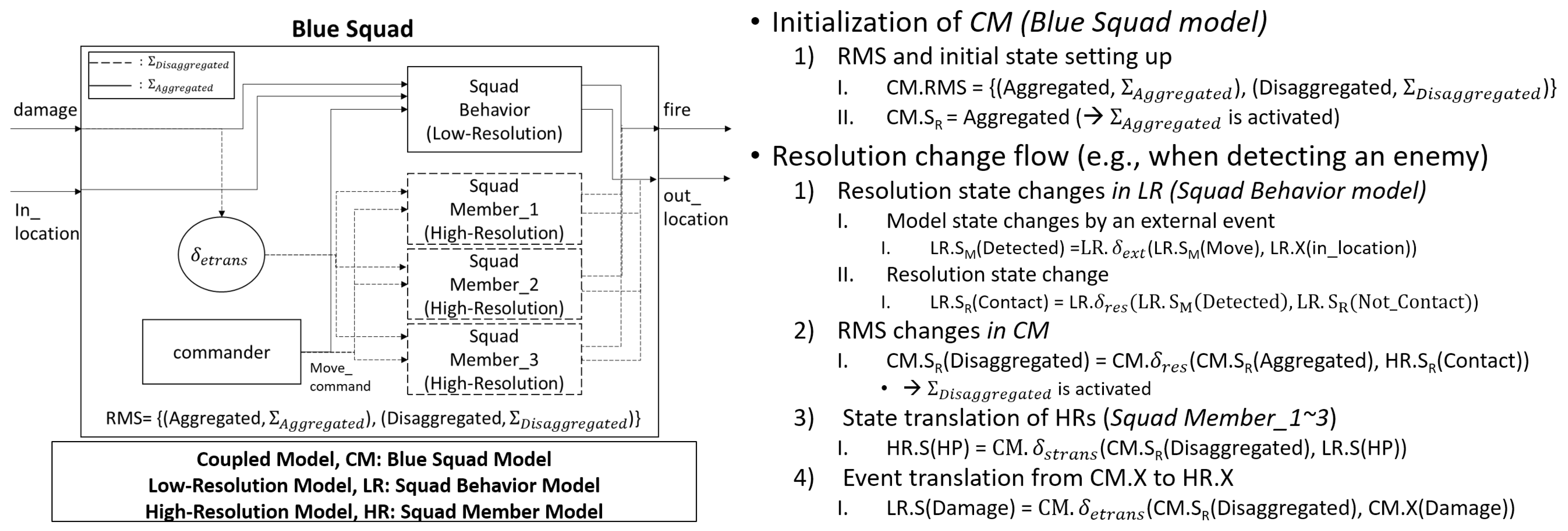
4.1. Illustrative Example in MRT-DEVS

The example model used in the case study describes a squad-level engagement. Figure 1 shows the structure of the squad-level engagement model. The proposed MRT-DEVS primarily follows DEVS semantics, so the example model has a hierarchical structure: The highest level model consists of blue and red force models. Each force involves a commander and multiple squad models. The command model controls its subordinate squad models, such as in terms of squad maneuver, detection, and engagement. While the number of the subordinate squad models can be determined by users, the case study has two and three squad models in blue and red forces, respectively (see the numbers on the edges in Figure 1). By their combat circumstances, squad models are described at two resolution levels: one is at low-resolution level modeling with respect to squad maneuver and detection. At the row-resolution level, the squad behavior model (dark gray in Figure 1) is the only active component in the squad model; the other resolution level is the high-resolution modeling of squad engagement. At the high-resolution level, three squad member models (light gray Figure 1) are activated in the squad model. The resolution changes in the squad model are triggered by the detection of enemy forces. Squad behavior and squad member models are developed by the MRT-DEVS atomic model; others are developed by the coupled model.

Using the above example model, we designed a simulation scenario about an engagement between blue and red forces. The following is a brief illustration of the simulation scenario: (a) Three squads of red force and two squads of blue force are deployed to the north and south of a battlefield, respectively; (b) the squad models of the two forces approach each other, and they are at the squad level (i.e., low-resolution level, LR); (c) when they detect each other, each squad model turns into three squad member models, which are at the high-resolution level, HR, and they enter a firefight; (d) when the firefight ends, the remaining squad member models assemble into their squad models, and they continue to march as a low-resolution model. Figure 2 presents snapshots of the simulation’s execution following the scenario, and they highlight two resolution changes in the squad models, which occur when each force recognizes its enemy (from low-resolution to high-resolution) and when they no longer detect an enemy after a gunfight (from HR to LR).

4.2. Progress of Model Resolution Changes

Although we illustrated an example of MRM and the way MRM is specified via the proposed method, this subsection focuses on how resolution changes in MRM are realized through MRT-DEVS’s semantics. In the above simulation scenario, the squad model changes its resolution level due to the detection of the enemy. For an improved understanding of this changing process, Figure 3 presents the structure of the blue squad model as an example. The blue squad model was developed based on the coupled model, and it has two resolution states ($S_R$): “Aggregated (as a low-resolution level)” and “Disaggregated (as a high-resolution level)”. According to the resolution states, the $RMS$ of the squad model was also specified (refer to the model diagram in Figure 3): (a) For the “Aggregated” state, the squad behavior model is set for activation, and its input and output events are connected with those of the squad models, which are specified in ${\Sigma }_{Aggregated}$. (b) For the “Disaggregated” state, three squad member models are set for activation, and their input and output events are connected with those of the squad models as well (${\Sigma }_{Disaggregated}$). In particular, before being forwarded to squad members, an input event named “damage” with resepct to the squad model is transformed by the event translation function (${\delta }_{etrans}$). Specifically, in the case study, the “damage” event of the squad model would be distributed into “damage” events of the three squad member models. We note that such event translations have relatively lower costs in the model development than previous methods that use a converter model (e.g., when taking an event, the converter model requires another simulation loop in the DEVS simulation algorithm [1].

Based on the above specifications of the squad model, we examine detailed procedures of its resolution changes in the case study. The right side of Figure 3 illustrates setting the initial resolution state and changing the resolution state of the squad model (coupled model, CM). Following the simulation scenario, the squad model conducts maneuver and scouting operations, so its initial resolution state is at a low-level resolution according to the model’s specifications. More specifically, the resolution state of the squad model ($S_R$) is set as “Aggregated”, and the associated RMS (${\Sigma }_{Aggregated}$), which includes a squad behavior model (low-resolution component, LR), is also activated. While conducting operations, the squad model changes its resolution state when it detects an enemy squad. When the enemy is detected, the squad model is still at the low-resolution level: The detection of the enemy is determined by the external transition function (${\delta }_{ext}$) of the squad behavior model. After detecting an enemy, the squad behavior model changes its resolution state to “Contact”. When the component model changes its resolution state, the resolution transition function (${\delta }_{res}$) of its coupled model is also conducted (refer to line 26 of Algorithm 2). Hence, the squad model also changes its resolution state from “Aggregated” to “Disaggregated” for a gunfight against the detected enemy. After its resolution state changes, the associated RMS (${\Sigma }_{Disaggregated}$), which includes three squad member models (high-resolution component, HR), is activated; otherwise, the RMS of “Aggregate” state (${\Sigma }_{Aggregated}$) is deactivated. During resolution level changes, some states of the low resolution model need to be transferred to those of high-resolution models. For example, in the case study, the HP state of the squad’s behavior (LR) should be translated into the HP state of squad members (HR), and this translation is conducted by the state transition function (${\delta }_{strans}$) of the squad model (CM). After exisitng at high-resolution states, the two forces fall into an engagement. During the engagement, damage from the enemy would come to the squad model as its input event. This damage input is translated by the event translation function (${\delta }_{etrans}$) of the squad model before it reaches the squad members. The translation result represents, for example, the damage of each squad members, so a squad member that receives too much damage would die. After all squad members of one force have died, the remaining squad changes its resolution state from “Disaggregated” to “Aggregated” to carry on the maneuver and scout operations, and similar operations would follow.

5. Discussion

MRT-DEVS shares a theoretical background with the classic DEVS formalism, yet as we mentioned before, it relaxes a black box assumption of DEVS to achieve lower costs in MRMS. From various perspectives, including the relaxation, this section investigates strong and weak points of the MRT-DEVS. Before diving into details, we analyze the functional analogy of MRT-DEVS, which was conducted by comparing the expressiveness power of MRT-DEVS with previous studies, such as Baohong’s [11] and Hong’s [33] studies.

Table 1. Relations between the features of multi-resolution modeling (MRM) and the elements from the associated formalisms (previous (Baohong’s and Hong’s) and proposed ones (MRT-DVEVS)).

MRM Features	Baohong’s	Hong’s	MRT-DEVS
Resolution State	$\gamma$	r	$S_R$
Resolution Model Family	$M_k$	$R{M}_i$	$RMS$
Model Structure Function/Info	$M_{\psi }$	$\psi ,\rho$	${\delta }_{res}$
Model State Translation Function	$\pi$	-	${\delta }_{strans}$
Event Conversion Function	$\pi$	$MREI$	${\delta }_{etrans}$
Resolution Change Event Structure	-	$C_R,Y_R$	(Embedded in simulation algorithm)
Resolution Change Controller	$\chi$	$MRCI$	(Embedded in simulation algorithm)

presents the relationships between the features of multi-resolution modeling (MRM) and the elements of the associated formalisms, including previous (Baohong’s and Hong’s) and the proposed one (MRT-DVEVS). Table 1 shows that the elements of MRT-DEVS have more matched elements compared to past MRM methods, which demonstrates two benefits of the proposed method: The first benefit, conservatively, is that the proposed MRT-DEVS is reducible to past MRM methods, which means that the proposed method is theoretically sufficient for MRM as previous ones provide; the second benefit is that both previous methods fail to match some parts of the MRM’s features (e.g., the model state translation function in Hong’s and the resolution change event structure in Baohong’s), and the proposed method, however, covers it. As such, the proposed method has a larger coverage on MRM features, so we argue that from this point of view, the proposed method provides more applicabilities in MRMS.

Let us address the details of the efficiency of the MRT-DEVS using the case study. We argue that the contribution of this research is in providing an option for MRM from a practical perspective, and this practicality comes from the ease in MRM development and lower costs for simulation executions. Having said that, we note that it is difficult, or even infeasible, to quantitatively compare the efficiency of the proposed method due to the following reasons: (1) The ease of the model’s development is difficult to measure and even strongly dependent on modelers, which means that it cannot be appropriately used as a performance measure for the comparison; (2) to quantitatively compare the efficiency of the proposed method, comparison targets are required (i.e., the implementations of Baohong’s and Hong’s idea). However, to the best of our knowledge, their implementations are not available to the public.

As such, we rather provide another method to prove our outperformance by using an abstract comparison. Specifically, for the ease of model developments, we consider a practical problem in MRM development practices: In recent practices, MRM users should consider not only MRM for their target systems but also for handling resolution changes (e.g., as the resolution converter). This means that there is a high hurdle in MR’s model development. However, at this point, the proposed method helps the modelers to focus only on modeling itself, setting aside additional MR considerations.

For the simulation’s efficiency, we can analyze their simulation efficiencies at an abstract level and eventually compare their expected performance. the main feature of the proposed method is embedding state and event translation functions into the coupled model, so the resolution conversion process is performed within the simulation algorithm (Algorithm 2). Due to embedded MR functions, modelers eventually use less efforts in MR modeling. Specifically, compared to past methods that adapt these translation functions at another component (e.g., implementing a converter model), the proposed method permit disregarding the details of the resolution’s change. Developing the converter model may not require a heavy cost, but establishing and maintaining connections between the converter model with other models (e.g., responding to the resolution changes) definitely require heavy costs; the converter model should take a role for transferring all input/output events associated with the entire model’s components during the simulation, so its connection structure becomes complex and requires expensive costs. More specifically, considering the method of DEVS simulation execution [1], such translations through a converter model are implemented by additional event handling and state transitions of a DEVS atomic model, which was identified as a critical factor for delaying DEVS simulation execution times in various studies [35,36,37,38,39]. In contrast, the proposed MRT-DEVSs permit event and state translations by functions in the coupled model. Such treatments require no extra event exchanges and, thus, generate no negative effects with respect to the simulation algorithm, which eventually lessens costs in both model development and simulation execution.

Having said that, we also admitted that the proposed method involves a potential shortcoming induced by removing the black-box assumption. The black box assumption, or modularity, enables the construction of a structured model by an integration of a number of small blocks (which are DEVS atomic and coupled models). Such a trait makes it easier to not only develop a complex model but also maintains the developed model, such as reuses in another model development [5]. Due to the loss of the modular property, the proposed method holds a limitation on the development of simulation models across various domain systems in which a number of model reuses can happen. Nonetheless, we still hold that it cannot induce much damage on MRMS. As we have argued thoruhgout this paper, increasing the practicality of MRMS is the important motivation of this study. The importance of the model’s reusability in modeling and simulation has been discussed in M&S communities [5,40], yet its practical examples over various domains are rarely observed. Still, we observe that there is a trade-off relationship between efficiency and model reuses in MRMS, and we note that the proposed method offers a practical option that is worthy of consideration for MRMS users.

6. Conclusions

Multi-resolution modeling and simulation (MRMS) is a useful option for gleaning insights with respect to target systems from various resolution levels. Many methods have been developed to support MRMS, but contrary to their theoretical completeness, their practical usages are rarely observed. We see that this distance is derived from inefficiencies, such as such indigestible model specifications and expensive simulation costs. The proposed MRT-DEVS tackles such inefficiencies by embedding state and event translation functions into the model’s specification. The provided case study illustrates how the proposed method is applied to MRM and the detailed procedures of resolution changes via the suggested model specifications. Moreover, by engaging in discussions on the proposed method, we offered more considerations about MRMS to users. With all the provided information, we expect that MRMS users would consider the proposed method as a practical option to implement their models.