Early Warning of Systemic Financial Risk of Local Government Implicit Debt Based on BP Neural Network Model
Abstract
1. Introduction
2. Literature Review
2.1. Hidden Debt Risks of Local Government
2.2. Systemic Financial Risks
3. Theoretical Analysis
3.1. The Contagion Effect of Local Government Debt Risk on Financial Risk Based on Global Sovereign Debt
3.2. The Contagion Effect of Hidden Debt of Chinese Local Governments on Systemic Financial Risks
4. Local Government Hidden Debt Risks and Systemic Financial Risks Estimation
4.1. Local Government Hidden Debt Risks Measurement
4.1.1. Measurement of the Scale of Local Government Implicit Debt
4.1.2. Model Selection and Index System Construction
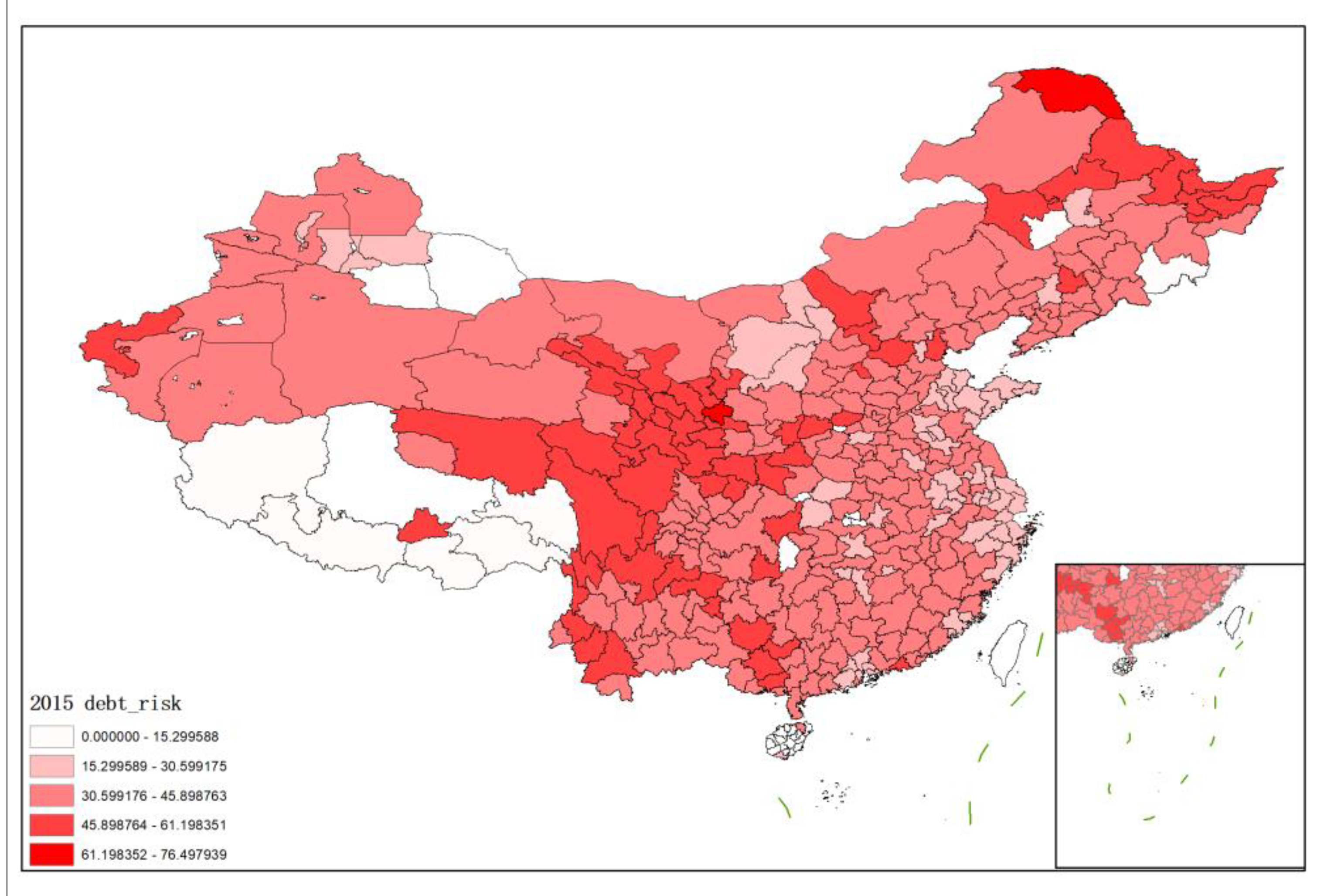
4.1.3. Risk Measurement Results
4.2. Systemic Financial Risks Measurement
4.2.1. Model Selection and Indicator System Construction
4.2.2. Analysis of Measurement Results
5. Research Design
5.1. Introduction to BP Neural Network Model
5.2. Index System Construction and Data Processing
5.2.1. Determination of Explanatory Variables and Explained Variables
5.2.2. Data Sources and Data Processing
5.3. BP Neural Network Model Optimization
5.3.1. Input and Output Data Preprocessing
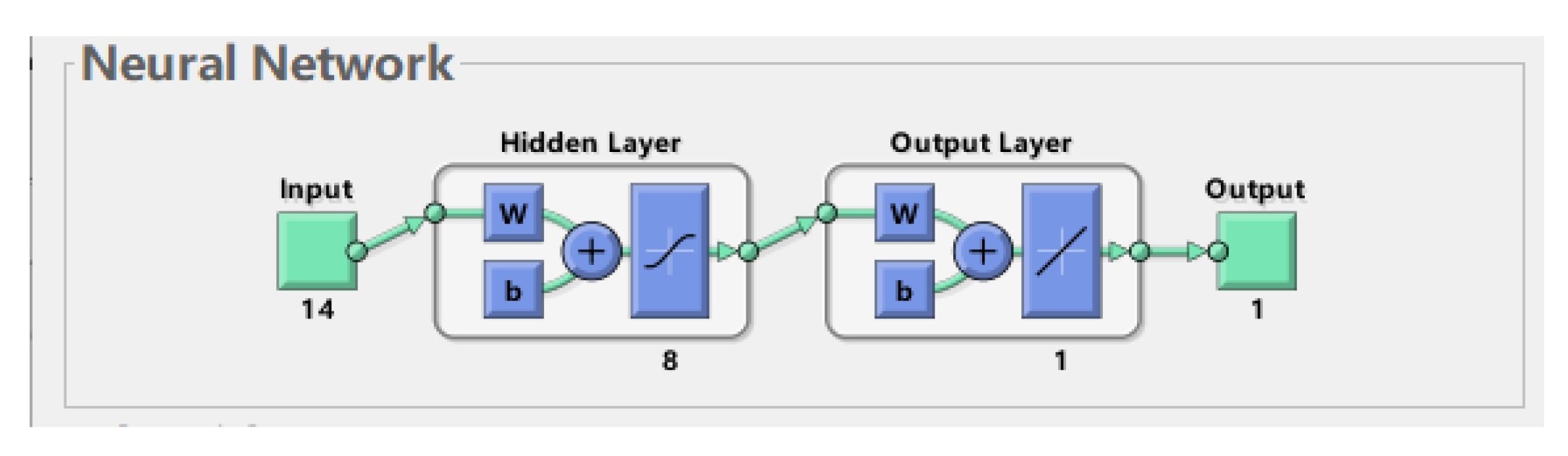
5.3.2. BP Neural Network Structure Design
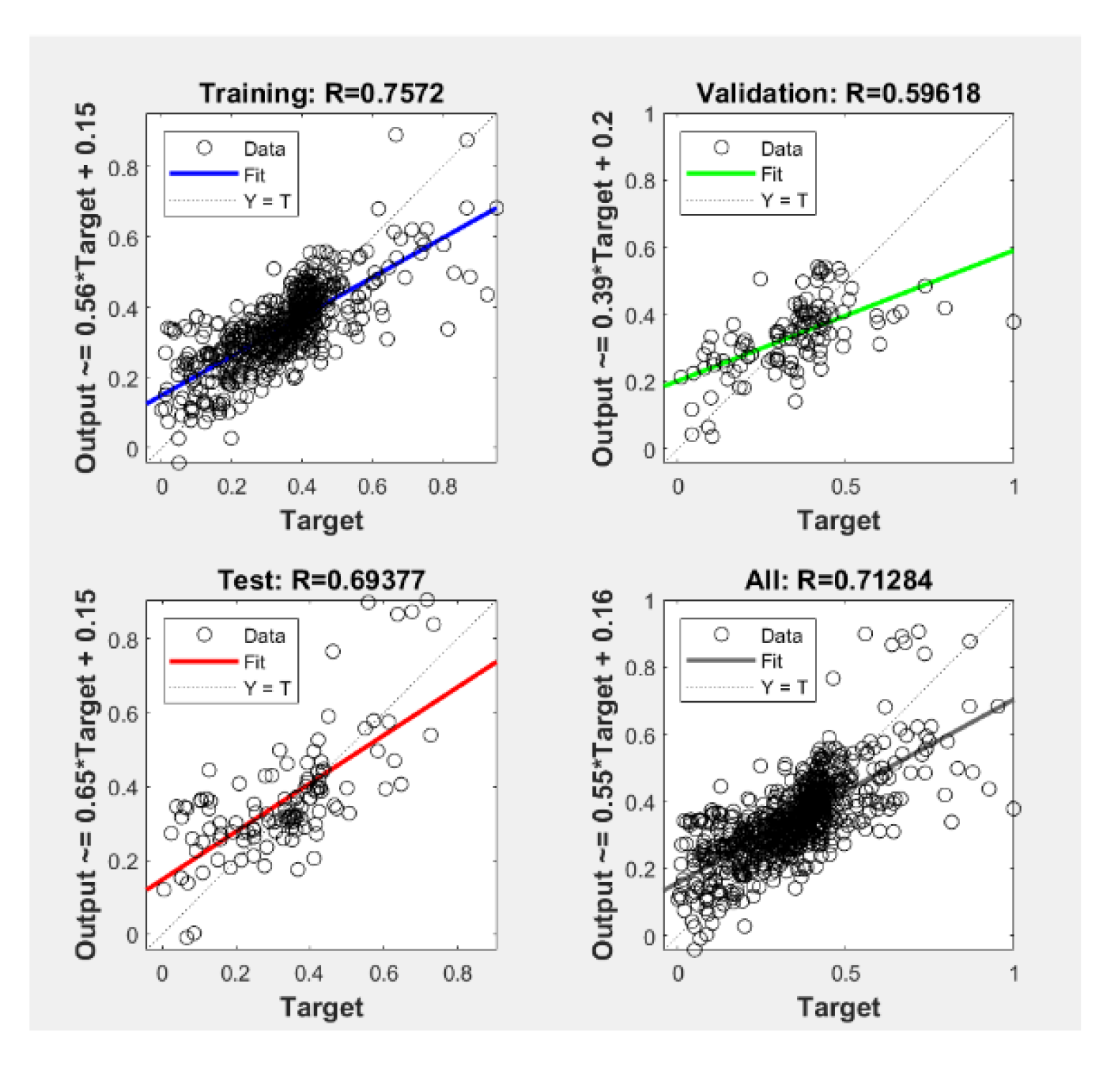
5.3.3. Comparative Analysis of the Results of Different BP Neural Network Models
5.4. Analysis of Training Results of BP Neural Network Model
6. Analysis of Early Warning of Systemic Financial Risks
6.1. Risk Contagion Effect Analysis
6.1.1. The Weight Contribution Rate of the Input Node
6.1.2. Analysis of Explanatory Variable Importance
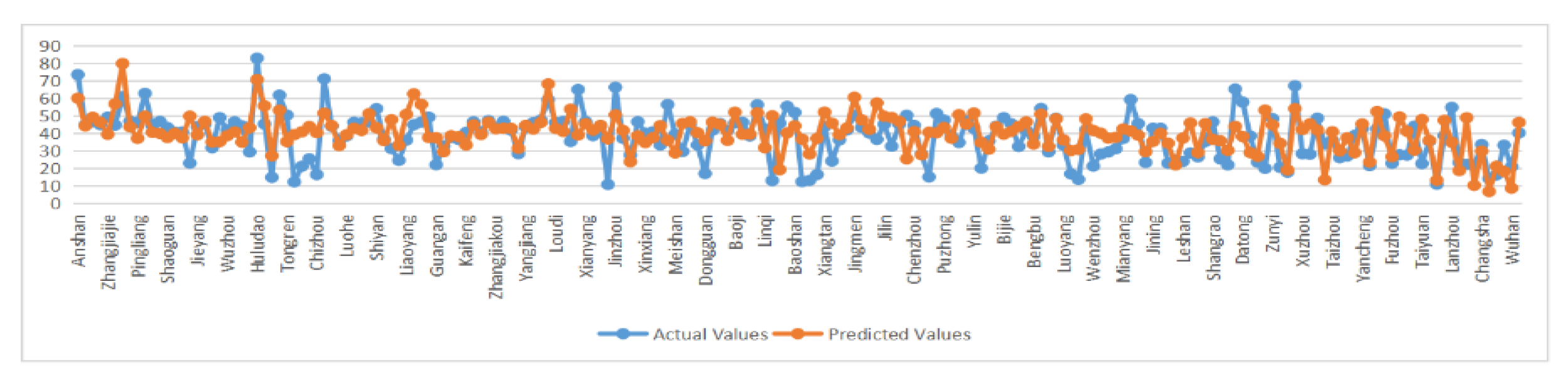
6.2. Risk Early Warning Analysis
6.3. Early Warning Stress Test
7. Conclusions and Recommendations
7.1. Conclusions
- (1)
- Local government hidden debt has a significant contagion effect on systemic financial risk. Among the many factors affecting systemic financial risk, macro indicators of local government hidden debt risk explain the systemic financial risk to a higher extent. The scale of financing platform bank debt at the micro level has a greater impact on systemic financial risk, and the scale of PPP and urban investment debt also have a certain degree of impact on systemic financial risk;
- (2)
- All categories of local government implicit debt indicators, including macro and micro levels, are the best early warnings of systemic financial risks. Through the training and testing of the BP neural network, the systemic financial risk at the prefecture-level city level can provide an early warning with a certain degree of reliability. That is, the signals from the data of relevant indicators of local government hidden debts can be used to provide an early warning of systemic financial risks in China through neural network models with high applicability;
- (3)
- When the implicit debt of local governments changes under different stress, the constructed neural network model can sensitively predict changes in systemic financial risks, which has a good early warning effect. When the level of hidden debt risk, the scale of financing platform bank debt, the scale of urban investment bonds, and the scale of PPP pressure changes simultaneously, or when the level of hidden debt risk and different types of micro-variables undergo stress changes independently, they will all significantly transmit to systemic financial risks. It has a large negative impact on the stability of the financial system.
7.2. Suggestions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, T.; Jin, H.; Zhu, J. Research on regional financial risks arising from local government debts and countermeasures. Inn. Mong. Financ. Res. 2012, 4, 38–40. [Google Scholar]
- Harvey, S.R. Fiscal Science; People’s University of China Press: Beijing, China, 2002. [Google Scholar]
- Brixi, H.P. Contingent Government Liabilities: Fiscal Threat to the Czech Republic? Post-Sov. Geogr. Econ. 2000, 41, 63–76. [Google Scholar] [CrossRef]
- Ponds, E.; Severinson, C.; Yermo, J. Implicit Debt in Public-sector Pension Plans: An International Comparison. Int. Soc. Secur. Rev. 2012, 65, 75–101. [Google Scholar] [CrossRef]
- Wenxiu, H.; Cheng, L. Potential and Sustainability of Active Fiscal Policy; Economic Science Press: Beijing, China, 2000; Chapter 4; pp. 62–81. [Google Scholar]
- Shaobo, L.; Wenqing, H. Study on the status of local government hidden debt in China. Fisc. Res. 2008, 9, 64–68. [Google Scholar]
- Moody. Public Finance-General Obligation Bonds Issued by U.S. Local Governments. Rat. Methodol. 2009, 7, 11–19. [Google Scholar]
- Ming, Y. An analysis of local government hidden debt risk prevention—Based on information disclosure and full-caliber budget supervision. Financ. Account. Newsl. 2019, 35, 106–109. [Google Scholar]
- Pabuçcu, H.; Ayan, T.Y. The development of an alternative method for the sovereign credit rating system based on adaptive neuro-fuzzy inference system. Am. J. Oper. Res. 2016, 7, 41–55. [Google Scholar] [CrossRef][Green Version]
- Sarlin, P. Sovereign debt monitor: A visual self-organizing maps approach. In Proceedings of the 2011 IEEE Symposium on Computational Intelligence for Financial Engineering and Economics (CIFEr), Paris, France, 11–15 April 2011; pp. 1–8. [Google Scholar]
- Lehar, A. Measuring Systemic Risk: A Risk Management Approach. J. Bank. Financ. 2005, 29, 2577–2603. [Google Scholar] [CrossRef]
- Matheson, T.D. Financial conditions indexes for the United States and euro area. Econ. Lett. 2012, 115, 441–446. [Google Scholar] [CrossRef]
- Celik, S. The More Contagion Effect on Emerging Markets: The Evidence of DCC-GARCH Model. Econ. Model. 2012, 24, 1946–1959. [Google Scholar] [CrossRef]
- Shoudong, C.; Dakun, Z.; Xianliang, C. Using binary choice model to establish a financial early warning model in China. Learn. Explor. 2006, 1, 237–239. [Google Scholar]
- Shoudong, C.; Hui, M.; Chunzhou, M. MS-VAR model for financial risk early warning in China and the study of zone system state. J. Soc. Sci. Jilin Univ. 2009, 49, 110–119+160. [Google Scholar]
- Mengyu, L. Research on the construction of financial risk early warning system in China based on K-mean clustering algorithm and BP neural network. J. Cent. Univ. Financ. Econ. 2012, 10, 25–30. [Google Scholar]
- Yin, D.; Ziqing, M.; Tao, Z.; Dongfa, F. Progress in the application of big data methods in systemic financial risk monitoring and early warning. Financ. Dev. Res. 2022, 2, 3–12. [Google Scholar]
- Sosa-Padilla, C. Sovereign defaults and banking crises. J. Monet. Econ. 2012, 99, 88–105. [Google Scholar] [CrossRef]
- Gennaioli, N.; Martin, A.; Rossi, S. Sovereign default, domestic banks, and financial institutions. J. Financ. 2014, 69, 819–866. [Google Scholar] [CrossRef]
- Magkonis, G.; Tsopanakis, A. The financial and fiscal stress interconnectedness: The case of G5 economies. Int. Rev. Financ. Anal. 2016, 46, 62–69. [Google Scholar] [CrossRef]
- Silva, T.C.; Guerra, S.M.; Tabak, B.M. Fiscal risk and financial fragility. Emerg. Mark. Rev. 2020, 45, 100711. [Google Scholar] [CrossRef]
- Zhengyao, W. Research on the Linkage between Fiscal Risk and Financial Risk in China during the Transition Period; Southwest University of Finance and Economics: Chengdu, China, 2006; p. 212. [Google Scholar]
- Shucai, M.; Xia, H.; Yunhong, H. The transmission mechanism of local government debt affecting financial risk--a study based on the perspective of real estate market and commercial banks. Financ. Forum 2020, 25, 70–80. [Google Scholar]
- Xudong, Z. Local Government Debt and Regional Financial Risks; Lanzhou University: Lanzhou, China, 2021; p. 51. [Google Scholar]
- Kotlikoff, L. Is the United States Bankrupt? Fed. Reserve Bank St. Louis Rev. 2006, 88, 235–249. [Google Scholar] [CrossRef][Green Version]
- Moro, B. Lessons from the European economic and financial great crisis: A survey. Eur. J. Political Econ. 2014, 34, S9–S24. [Google Scholar] [CrossRef]
- Sibbertsen, P.; Wegener, C.; Basse, T. Testing for a break in the persistence in yield spreads of EMU government bonds. J. Bank. Financ. 2014, 41, 109–118. [Google Scholar] [CrossRef]
- Ludwig, A. Credit risk-free sovereign bonds under Solvency II: A cointegration analysis with consistently estimated structural breaks. Appl. Financ. Econ. 2014, 24, 811–823. [Google Scholar] [CrossRef]
- Gruppe, M.; Lange, C. Spain and the European sovereign debt crisis. Eur. J. Political Econ. 2014, 34, S3–S8. [Google Scholar] [CrossRef]
- Basse, T.; Wegener, C.; Kunze, F. Government bond yields in Germany and Spain—Empirical evidence from better days. Quant. Financ. 2018, 18, 827–835. [Google Scholar] [CrossRef]
- Hsing, Y. Determinants of the government bond yield in Spain: A loanable funds model. Int. J. Financ. Stud. 2015, 3, 342–350. [Google Scholar] [CrossRef]
- Aizenman, J. The eurozone crisis: Muddling through on the way to a more perfect euro union? Soc. Sci. 2013, 2, 221–233. [Google Scholar] [CrossRef]
- Merrick, J.J., Jr. Crisis dynamics of implied default recovery ratios: Evidence from Russia and Argentina. J. Bank. Financ. 2001, 25, 1921–1939. [Google Scholar] [CrossRef]
- Hébert, B.; Schreger, J. The costs of sovereign default: Evidence from Argentina. Am. Econ. Rev. 2017, 107, 3119–3145. [Google Scholar] [CrossRef]
- Feng, X. Local government debt and municipal bonds in China: Problems and a framework of rules. Cph. J. Asian Stud. 2013, 31, 23–53. [Google Scholar] [CrossRef]
- Zhenhua, M.; Haixia, Y.; Xinhe, L.; Qiufeng, W.; Yuanhui, W. Analysis of current local government debt risk and transformation of financing platform in China. Fisc. Sci. 2018, 5, 24–43. [Google Scholar]
- Ben, Y.; Yanjin, L.; Shengyin, O.; Shourong, M. Statistical Accounting and Causal Analysis of Local Hidden Debt Scale. Financ. Theory Pract. 2022, 43, 95–103. [Google Scholar]
- Diakoulaki, D.; Mavrotas, G.; Papayannakis, L. Determining objective weights in multiple criteria problems: The critic method. Comput. Oper. Res. 1995, 22, 763–770. [Google Scholar] [CrossRef]
- Hwang, C.L.; Yoon, K. Methods for multiple attribute decision making. In Multiple Attribute Decision Making; Springer: Berlin/Heidelberg, Germany, 1981; pp. 58–191. [Google Scholar]
- Huaidong, Y.; Shuyue, C. Term mismatch, shadow banking interest rates and local government implicit debt risk. Wuhan Financ. 2021, 10, 35–42+77. [Google Scholar]
- Zhenyi, X. Local Government Hidden Debt Risk Measurement and the Contagion Effect on Systemic Financial Risk; Sichuan University: Chengdu, China, 2021; p. 77. [Google Scholar]
- Jinming, W. The measurement and influencing factors of systemic financial risk. Bus. Res. 2016, 2, 73–80. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning Representations by Back-propagating Errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Shoudong, C.; Zhuo, L.; Sihan, L. The spatial spillover effect of local government debt risk on regional financial risk. J. Xi’an Jiaotong Univ. Soc. Sci. Ed. 2020, 40, 33–44. [Google Scholar]
- Lizhen, L. Research on the construction and application of local government contingent hidden debt risk early warning system--based on BP neural network analysis method. Financ. Econ. Ser. 2021, 3, 14–25. [Google Scholar]
- Peiyu, Y. Research on the Impact of Two-Child Policy on China’s Population Structure Based on BP Neural Network; Qingdao University: Quingdao, China, 2018; p. 44. [Google Scholar]
- Wenqian, W. Research on Factors Influencing Credit Spreads of Real Estate Enterprises’ Bonds Based on BP Neural Network Model; Shanghai University of Finance and Economics: Shanghai, China, 2020; p. 50. [Google Scholar]
- Zuoyong, L.; Hengkang, D.; Jing, D. BP network weighting analysis model for atmospheric particulate matter source analysis. J. Sichuan Univ. Nat. Sci. Ed. 2004, 5, 1026–1029. [Google Scholar]



| Index Name | Calculation Method | Indicators Category |
|---|---|---|
| Implicit Debt Ratio | Scale of hidden debt of local government/comprehensive financial resources of government | Positive |
| Implicit Debt Per Capita | Scale of hidden debt of local government/the urban population | Positive |
| Household Debt-to-Deposit Ratio | Scale of hidden debt of local government/deposit of residents | Positive |
| Implicit Debt Burden Ratio | Scale of hidden debt of local government/the local GDP | Positive |
| Fiscal Self-sufficiency Rate | Local fiscal revenue/local government expenditure | Negative |
| Growth Rate of Government Budget Revenue | Increase in government budget revenue/government budget revenue for the previous year | Negative |
| Implicit Debt Ratio of Local State-owned Enterprises | Debt of local State-owned Enterprises/assets of local state-owned enterprises | Positive |
| The Economy’s Implicit Debt Elasticity | Growth rate of local government hidden debt/the GDP growth rate | Positive |
| Elasticity of Implicit Debt of Resident Deposits | Growth rate of local government hidden debt/growth rate of household deposits | Positive |
| Hidden Debt Risk Score of Local Governments from 2015 to 2019 | |||||
|---|---|---|---|---|---|
| City | 2015 | 2016 | 2017 | 2018 | 2019 |
| DaLian | 28.91195865 | 27.01909757 | 27.01909757 | 26.82933379 | 27.13279683 |
| FoShan | 24.88427547 | 20.69429354 | 21.00837985 | 20.68418926 | 22.80717264 |
| GuiYang | 35.82599862 | 41.29675679 | 42.89506015 | 43.58357522 | 46.21221067 |
| HangZhou | 22.31973813 | 22.68887937 | 23.97975023 | 24.96269211 | 25.67033526 |
| HeFei | 26.44453195 | 27.38022434 | 28.66337798 | 27.63176307 | 28.6051096 |
| ChengDu | 29.09142402 | 31.38266027 | 32.27327735 | 32.299866 | 33.69958921 |
| NanJing | 31.58680464 | 35.4738262 | 37.70630978 | 37.75690817 | 38.34087508 |
| QingDao | 22.63640076 | 23.48652464 | 23.96435764 | 24.89896249 | 25.40073198 |
| XiaMen | 20.56937056 | 21.98883352 | 21.86581334 | 22.43105817 | 22.51233708 |
| WuHan | 26.24344645 | 29.10143112 | 32.36544172 | 32.88963164 | 35.74540001 |
| ChangSha | 29.77736434 | 31.85709377 | 33.90888629 | 33.77429626 | 33.64897213 |
| TaiYuan | 36.81320446 | 36.99256896 | 37.21894672 | 35.06612106 | 36.15748302 |
| YinChuan | 30.97243077 | 31.59271035 | 31.80064509 | 32.68492259 | 34.39953412 |
| ZhengZhou | 24.82557524 | 27.16760343 | 30.26104457 | 31.36780589 | 31.92575389 |
| ZunYi | 36.95828029 | 39.5503283 | 41.18212671 | 43.50457706 | 44.21434143 |
| Index Name | Calculation Method | Indicators Category |
|---|---|---|
| A bank’s equity to debt ratio | Owner’s equity/the total amount of liabilities | Negative |
| Income ratio on bank assets | Earnings before interest and tax/the total assets | Negative |
| Bank loan provision ratio | Loss reserve balance/loan balance | Negative |
| Foreign exchange deposit growth ratio of local banks | Increase in foreign exchange deposits/balance of previous period | Negative |
| Local GDP growth rate | Local GDP value added/GDP of the previous period | Negative |
| Local government expenditure growth ratio | Increase in government expenditure/expenditure of the previous period | Positive |
| Local government revenue growth ratio | Increase in government revenue/revenue in the previous period | Negative |
| The depth of the insurance | The premium income/the local GDP | Negative |
| The density of insurance | The premium income/population of prefecture-level cities | Negative |
| Premium income growth ratio | Premium Income appreciation/stock of premium income for the previous period | Negative |
| House price growth ratio | Increase in house price/house price for the previous period | Positive |
| Registered urban unemployment rate | Number of registered unemployed in urban areas/(number of urban employees + the number of registered unemployed in urban areas which was actually recorded) | Positive |
| Growth rate of foreign investment | Increase in actual foreign investment/investment in previous period | Negative |
| Debt to assets ratio | Total liabilities of enterprises above designated size/total assets | Positive |
| Rate of profit growth | The increase in profits of enterprises above designated size/profit of previous period | Negative |
| Local Systemic Financial Risks Score from 2015 to 2019 | |||||
|---|---|---|---|---|---|
| City | 2015 | 2016 | 2017 | 2018 | 2019 |
| ChangZhou | 38.20756056 | 42.30275228 | 28.98779277 | 24.45106123 | 27.48464988 |
| ChaoYang | 89.56932006 | 69.98286175 | 65.83319308 | 41.31064849 | 60.90540575 |
| ChengDu | 33.55807298 | 53.64490021 | 22.94075988 | 29.17260199 | 9.368536512 |
| DaLian | 78.09844909 | 26.22328099 | 11.48458561 | 26.1926513 | 31.14410454 |
| DeYang | 45.42555018 | 42.33301124 | 44.59671256 | 22.16285414 | 43.36796506 |
| GuangZhou | 25.74234059 | 41.50747432 | 19.74169279 | 25.19470724 | 33.14337413 |
| QingDao | 25.19847995 | 31.98539797 | 32.47204164 | 39.23882547 | 26.02047333 |
| WeiHai | 29.9857466 | 33.16174856 | 25.84446234 | 56.07923056 | 28.32955548 |
| WuHan | 25.76591622 | 31.63427358 | 20.49237223 | 18.02283144 | 20.90894899 |
| XiAn | 12.12126201 | 17.45043196 | 4.782075525 | 14.65546229 | 14.15206846 |
| ChangChun | 42.45182789 | 34.73496561 | 40.09737321 | 35.33977111 | 27.02704911 |
| ZhuHai | 24.17845354 | 24.22689292 | 34.67281304 | 17.42236564 | 20.52817343 |
| HangZhou | 15.37049824 | 25.03725261 | 14.01116599 | 8.260911013 | 21.37019523 |
| NanJing | 20.11287882 | 19.11042375 | 36.56750808 | 18.34679802 | 37.53503965 |
| FuXin | 100 | 70.26313263 | 56.41968825 | 52.7655466 | 66.54459868 |
| Variable Symbol | Variable Name | ||
|---|---|---|---|
| Explained Variable | fr_topsis | The level of systemic financial risk | |
| Core explanatory variables | Macro core explanatory variables | dr_topsis | The level of hidden debt risks of local governments |
| Micro core explanatory variables | platform | Scale of financing platform bank debt | |
| bond | Scale of urban investment bonds | ||
| PPP | Scale of PPP | ||
| Variable Symbol | Variable Name | Variable Definitions |
|---|---|---|
| X1 | GDP per capita | GDP/total population of the region |
| X2 | Loan-to-deposit ratio | RMB loans/RMB deposits |
| X3 | Economic openness | total import and export/GDP |
| X4 | Proportion of real estate development investment | real estate development investment/GDP |
| X5 | Urbanization level | urban population/total population |
| X6 | Proportion of retail sales of social consumer goods | retail sales of social consumer goods/GDP |
| X7 | Proportion of fixed asset investment | total fixed asset investment/GDP |
| X8 | Urban basic education level | — |
| X9 | The proportion of value-added in secondary production | secondary industry added value/GDP |
| X10 | Population density | population/land area |
| Core Explanatory Variables | MSE | Training:R | Validation:R | Test:R | ALL:R |
|---|---|---|---|---|---|
| dr_topsis | 0.0115 | 0.63208 | 0.54175 | 0.51753 | 0.59908 |
| dr_topsis, PPP | 0.0108 | 0.67956 | 0.58974 | 0.55209 | 0.64012 |
| dr_topsis, PPP, platform | 0.00994 | 0.74429 | 0.61186 | 0.49528 | 0.68938 |
| dr_topsis, PPP, platform, bond | 0.00976 | 0.7572 | 0.59618 | 0.69377 | 0.71284 |
| Explanatory Variable Symbols | Weight Contribution Rate (%) | Explanatory Variable Name |
|---|---|---|
| platform | 7.06017419973742 | Scale of financing platform bank debt |
| bond | 5.5089920219434 | Scale of urban investment bonds |
| ppp | 5.7141804836627 | Scale of PPP |
| dr_topsis | 9.63355766336391 | The level of hidden debt risks of local governments |
| x1 | 6.67543190738213 | GDP per capita |
| x2 | 6.53953061839073 | Loan-to-deposit ratio |
| x3 | 7.17573766322704 | Economic openness |
| x4 | 7.41645669864381 | Proportion of real estate development investment |
| x5 | 8.40474594921744 | Urbanization level |
| x6 | 5.14368458380196 | Proportion of retail sales of social consumer goods |
| x7 | 5.48470869969032 | Proportion of fixed asset investment |
| x8 | 10.4681165059406 | Urban basic education level |
| x9 | 6.75215545564988 | The proportion of value added in secondary production |
| x10 | 8.0225275493487 | Population density |
| City | Heihe | Wuzhong | Tonghua | Huludao | Yueyang | Weihai | Huzhou | Fuzhou | Yibin |
|---|---|---|---|---|---|---|---|---|---|
| Actual Values | 44.81 | 44.91 | 44.69 | 82.90 | 44.87 | 28.33 | 17.77 | 22.85 | 40.52 |
| Predicted Values | 44.22 | 46.32 | 56.81 | 70.69 | 46.53 | 31.38 | 18.98 | 26.59 | 40.03 |
| Relative Error | −1% | 3% | 27% | −15% | 4% | 11% | 7% | 16% | −1% |
| Risk State | Middle Warning | Middle Warning | Middle Warning | High Warning | Middle Warning | Low Warning | Low Warning | Low Warning | Middle Warning |
| Platform (Change Value) | Bond (Change Value) | Ppp (Change Value) | Dr_Topsis (Change Value) | Fr_Topsis (Change Value) | ||
|---|---|---|---|---|---|---|
| Stress range | Mild stress | 10% | 10% | 10% | 10% | 13.36% |
| 10% | 1.06% | |||||
| 10% | 6.66% | |||||
| 10% | 1.97% | |||||
| 10% | 11.43% | |||||
| Moderate stress | 20% | 20% | 20% | 20% | 18.41% | |
| 20% | 2.02% | |||||
| 20% | 4.16% | |||||
| 20% | 3.67% | |||||
| 20% | 20.23% | |||||
| Severe stress | 30% | 30% | 30% | 30% | 22.87% | |
| 30% | 1.26% | |||||
| 30% | 4.44% | |||||
| 30% | 1.57% | |||||
| 30% | 19.14% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Li, Y.; Feng, C.; Gong, C.; Tan, H. Early Warning of Systemic Financial Risk of Local Government Implicit Debt Based on BP Neural Network Model. Systems 2022, 10, 207. https://doi.org/10.3390/systems10060207
Zhao Y, Li Y, Feng C, Gong C, Tan H. Early Warning of Systemic Financial Risk of Local Government Implicit Debt Based on BP Neural Network Model. Systems. 2022; 10(6):207. https://doi.org/10.3390/systems10060207
Chicago/Turabian StyleZhao, Yinglan, Yi Li, Chen Feng, Chi Gong, and Hongru Tan. 2022. "Early Warning of Systemic Financial Risk of Local Government Implicit Debt Based on BP Neural Network Model" Systems 10, no. 6: 207. https://doi.org/10.3390/systems10060207
APA StyleZhao, Y., Li, Y., Feng, C., Gong, C., & Tan, H. (2022). Early Warning of Systemic Financial Risk of Local Government Implicit Debt Based on BP Neural Network Model. Systems, 10(6), 207. https://doi.org/10.3390/systems10060207





