Abstract
In recent years, financial fraud of listed internet companies has emerged one after another. Under the strategic goal of full audit coverage, the problems caused by audit failure have attracted more and more attention in China. We use the bounded rationality theory to analyze the strategy selections of listed internet companies, accounting firms, and audit regulators, and put forward three hypotheses: the hypothesis of participants, the hypothesis of strategy selections, and the hypothesis of model parameters. Next, the three-party evolutionary game model is constructed, and only one stable equilibrium point is found. In numerical simulation analyses, we discuss the strategy selections of the three parties under the impact of different model parameters. The research framework of this paper enriches the existing research on financial fraud and audit supervision and deepens the evolutionary mechanism of three-party strategy selections.
1. Introduction
Financial fraud emphasizes that enterprises do not comply with the financial and accounting reporting standards, and consciously distort the financial situation of enterprises on a specific date by utilizing artificial fabrication or adjusting relevant financial data, to mislead the economic decisions of market participants. The root causes of financial fraud lie in the imperfect corporate governance structure and the defect of the accounting and auditing system. With the continuous improvement of science and technology, some listed internet companies implement financial fraud through some hidden and imperceptible means to maximize their interests. These behaviors of enterprises not only damage the interests of investors, but also harm the development of China’s capital market and the stable operation of the economy.
According to data released by the China Securities Regulatory Commission in 2019, listed internet companies were fined up to 6.8 million yuan for fictitious profits, and 13 cases were handled with an average penalty of 0.52 million yuan per case. From January to October 2020, listed internet companies were fined 6.4 million yuan for fictitious profits and dealt with 11 cases. The average penalty per case was over 0.58 million yuan, an increase of 0.06 million yuan per case over the previous year. It reflected that the government supervision over the financial fraud of listed internet companies was constantly strengthening. Effective identification of accounting fraud behavior and effective governance of the accounting fraud phenomenon could positively impact the healthy and stable development of China’s capital market in the long term. The Development Plan of National Audit issued by the China National Audit Office in 2021 proposed to pay close attention to the operation of capital markets and conducted overall and multi-level audit supervision over the financial markets following the law. At present, it is essential to prevent audit collusion and safeguard the fairness of the market environment to promote the healthy development of the capital market.
The cases of financial fraud and audit failures often occur in reality. Taking Ruihua accounting firm (China’s largest accounting firm) as an example, Ruihua’s continuous audits of two listed companies (Huaze Cobalt and Nickel and Yatai Holding Group) failed. The certified public accountants in the Ruihua accounting firm failed to fulfill their responsibilities in performing audit services and issued audit reports with false records. This was subject to administrative punishment in December 2016 and January 2017, respectively. In February 2018, the Ruihua accounting firm was suspended from undertaking new business by the China Securities Regulatory Commission (CSRC).
The barbaric growth of internet financial platforms brought significant impacts on the traditional financial industry. To purify the market environment of internet finance and optimize the operation and competition order of the financial market, internet finance was written into the government work report for five consecutive years from 2015, and the expression of the government work report was changed from the healthy development to sound supervision of internet finance. However, in June 2018, the collapse of internet financial platforms swept the country. Within 50 days, 212 internet credit platforms encountered various problems, such as executives running away, corporate representatives losing contact, overdue payments on the network platform, and so on.
All types of financial fraud cannot be separated from the primary attributes of fraud which includes intent, objective, and motive [1]. The intent indicates that financial fraud is intentional. The objective includes deception, trickery, concealment, and evasion [2]. The motive is significant in fraudulent activities, including the financial motive and the non-financial motive [2]. Based on the fraud classification framework of the Association of Certified Fraud Examiners (ACFE), we design a fraud tree to analyze the fraud classification of listed internet companies in China [3]. First, the implementation channels of financial fraud can be divided into online channels and offline channels. Second, the fraud categories mainly include asset misappropriation, fraudulent statements, tax evasion, and corruption. It should be noted that no matter what type of financial fraud it is, it can happen through online or offline channels. For each fraud category, many sub-branches can be seen in Figure 1. Asset misappropriation mainly includes holding illegal cash assets, holding illegal tangible and intangible property, and manipulating securities. Fraudulent statements are a relatively common form of financial fraud, including falsification of documents and accounting records, omission of accounting records that occurred, and illegal overstatement or understatement of assets and liabilities. For tax evasion, the main types are concealment of actual income, falsification of accounting vouchers, and falsification of tax declaration. The last is corruption, which includes bribery in transactions, bribery through financial assets, and illegal gratuities.
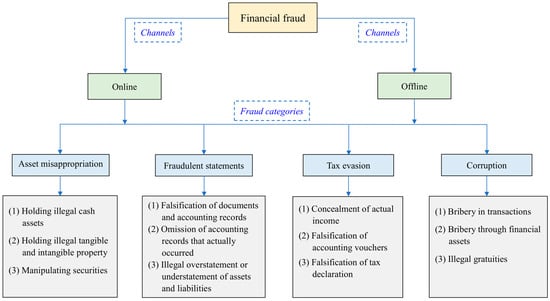
Figure 1.
The fraud tree of listed internet companies.
Under the current management system of listed companies in China, the external audit plays a vital role in supervising the financial behavior of listed internet companies. The fierce competition in the audit industry leads to the embarrassing situation that the audit fees continue to decline, and the auditor’s independent status is threatened. The auditor can only point out the financial fraud of listed internet companies in a discreet way and is even forced to participate in financial fraud. Thus, an important question needs further consideration. Why does the external audit fail? We can further explore this problem from the perspective of a three-party evolutionary game, including listed internet companies, accounting firms, and audit regulators. Specifically, a game relationship between accounting firms and audit regulators always exists between external independent audit and audit supervision. Accounting firms have the motivation to conduct a loose audit strategy for individual or collective interests, and the experience and supervision level of audit regulators are likely to affect the strategy selection of listed internet companies. Therefore, studying the relationship among them through evolutionary game analysis is of great significance to prevent financial fraud and improve the level of audit supervision. This paper has two research objectives. The first is to build a research framework based on the strategy selections of listed internet companies, accounting firms, and audit regulators. In this research framework, we can better analyze the factors affecting the strategy selections of the three parties. The second is to propose the optimal path of the three-party strategy selection. Through analyzing the stable equilibrium point in a three-party evolutionary game, this paper discusses the changes in three-party strategy selections under different parameters.
The contributions of this paper are mainly in the following aspects. First, we construct a three-party evolutionary game, expanding the two-party game model of listed internet companies and auditors in the existing literature, and replacing the auditors with accounting firms. The three-party evolutionary game model constructed in this paper can help audit regulators establish a dynamic supervision mechanism more accurately. Second, we fully consider the revenues and costs of the three parties, and further discuss the dynamic evolution process of three-party strategy selections with the changes in the revenues and costs. This study introduces the different combinations of rewards and penalties into the three-party evolutionary game model, overcoming the shortcoming of the existing literature that only focuses on the stable equilibrium state of financial fraud. Third, we abandon the assumption in the current literature that the revenues and costs of audit regulators are unchanged, and analyze the impact of the revenues and costs on the strategy selection of audit regulators. In the actual cases of listed internet companies, the revenues and costs of regulators are not fixed. However, most scholars often assume that they are stable in the evolutionary game model. Therefore, it is difficult for the existing research to reflect the dynamic characteristics of the reward-and-punishment mechanism. In a word, this paper constructs a three-party evolutionary game model to explore the stable equilibrium states of three parties, and further analyzes the impacts of the changing revenues and costs on the strategy selection. This paper enriches the existing research on strategy selections in financial fraud and audit supervision.
2. Related Works
2.1. Financial Fraud
When a listed company is in poor financial condition and faces difficulties in capital turnover and falling stock price, the management of the company is likely to conduct financial fraud through the concealment of financial statements [4]. Fich and Shivdasani (2007) randomly selected 216 companies as the research sample, to analyze the influence of financial fraud on the reputation of external directors [5]. In the fraud classification framework of ACFT, there are three categories of fraud, which are asset misappropriation, financial statement fraud, and corruption [3]. On this basis, the fraud tree is usually used for analyzing financial fraud and audit supervision. For example, Blackwell (2014) studied internet credit card fraud by a fraud tree and discussed the responsibilities of enterprises in the audit [6]. Onwubiko (2020) proposed a comprehensive taxonomy of fraud based on the analysis of a fraud tree and fraud matrix, and paid attention to triangular attributes of fraud, fraud channels, taxonomy of fraud, and classification of fraud [2]. Todorović et al. (2020) designed a structured questionnaire to study anti-fraud strategies after analyzing the fraud classification by the theory of the fraud tree [7].
Some scholars also studied financial fraud cases of listed internet companies through game theory. For example, we explored the strategies of listed companies from the perspective of audit supervision. It is found that controlling costs and obtaining revenues were the primary motivations for listed internet companies to commit financial fraud [8]. With the deepening of research, the construction of the audit game model was also changed from a simple static strategy game to a complex dynamic game. Based on a dynamic game model between listed internet companies and certified public accountants, it was found that the increase in audit fees reduced the possibility of financial fraud [9]. Based on the dynamic game system established by internal managers and external auditors, Zhang and Qi (2020) found that the significant increase in audit fees encouraged the auditors to use more financial statements for audit activities, and effectively reduce the financial fraud of listed internet companies [10]. After analyzing financial fraud reports of enterprises, Srebro et al. (2021) predicted the probability of enterprise bankruptcy using Z-score models, and emphasized the importance of financial statements [11].
Based on studying financial fraud incentives, many scholars began to pay attention to financial fraud supervision. For example, Matsumura and Tucker (1992) further expanded Fellingham and Newman’s research on financial fraud, and designed a dynamic game model including managers and auditors as the leading players to supervise financial fraud [8,12]. It was found that the regulators designed the regulatory plan based on the parameter setting of the evolutionary game system to reach a stable state [12]. Bo and Yao (2013) analyzed financial fraud of companies and accounting supervision using the incomplete information static game model, and put forward some suggestions for accounting supervision of companies in China [13]. Taking the financial fraud of companies as an example, Li et al. (2015) analyzed the evolutionary path of financial fraud from the perspective of a static game, and suggested that the regulators should pay more attention to the companies with possible financial fraud to achieve prior monitoring [14]. In addition, the relationship between the merger of accounting firms and audit quality was analyzed from the perspective of accounting firms. Using game theory, Zhang (2018) found that the merger of accounting firms increased their management difficulty [15]. In this case, accounting fraud was prevented by reducing audit costs and improving the efficiency of external audits [16]. The game analysis was further discussed in combination with experimental economics. Bloomfield (1997) found that the accuracy of auditors’ risk assessment was negatively related to the strategic dependence between auditors and managers, and the erroneous estimation of fraud risk led to the payment level of auditors and business managers being lower than the equilibrium level in the game [17]. Baiman et al. (2019) established an evolutionary game model based on the traditional audit relationship among owners, operators, and auditors, and found that the contract among the three parties significantly reduced the possibility of financial fraud of operators, and the rationality of signing the contract among the three parties directly determined the possibility of financial fraud of operators [18].
2.2. Auditing Supervision
The early studies on risk supervision of internet finance mainly focused on policy suggestions based on the analytical framework of financial theory. As a result of a large number of listed internet companies and the poor self-discipline of financial platforms, audit regulators were faced with obvious information asymmetry. Especially with the development of internet finance, audit works were faced with more complicated inherent and inspection risks [19]. Under the bottom-line thinking and the regulatory red line, audit regulators need to clarify the principles of internet financial supervision based on appropriate supervision and coordinated supervision, and encourage listed internet companies to carry out financial innovation to promote the healthy development of companies [20]. Based on the research framework of financial stability, Yang (2016) fully explained the theoretical advantages of government financial audits in maintaining financial stability under the macro-prudential supervision mode [21]. When accounting firms audited the annual financial statements of listed internet companies, they often faced a more severe audit environment. The prudent supervision mode helps accounting firms to better identify and guard against internet financial risks in practice. With the continuous development of big data and financial intelligence systems, accounting firms have paid more and more attention to the audit risk supervision of listed internet companies, and they have established a long-term supervision mechanism for internet financial risks from the following aspects: the construction of cloud audit system, the announcement of audit results and the unified supervision platform [22].
In recent years, many scholars tend to use game theory to analyze the risk governance of listed internet companies. For example, Wang et al. (2016) applied principal-agent theory to study the investment income sharing contracts among traditional financial institutions, e-commerce platforms, and small and medium-sized enterprises in internet finance [23]. Liu et al. (2017) used evolutionary game theory to study the dynamic evolution characteristics of internet financial platforms and regulators, and discussed the equilibrium state in the gaming process between internet financial platforms and financial regulators under the fixed punishment mechanism and the dynamic punishment mechanism [24]. In addition, internet financial regulation and financial innovation show a process of mutual promotion. Both sides repeat a game on the balanced path of regulation and violation, innovation and supervision. Thus, a win-win situation probably exists [25]. Due to the complexity of internet financial risks, the supervision of different participants faces some difficulties. They are mainly reflected in the game between institutions and investors, the game between institutions and fundraisers, and the game between investors and fundraisers [26]. In the evolutionary path of internet financial regulation and innovation, supervision efficiency should be improved from the perspective of risk assessment and risk control.
Currently, most studies focus on the evolutionary game between listed internet companies and auditors, listed internet companies and audit regulators, auditors and audit regulators [27]. Few studies involve the above three parties at the same time in an evolutionary game model, and study their dynamic evolution characteristics through simulation analysis. Compared with auditors, accounting firms are more representative in the financial fraud analysis of listed internet companies [28]. Based on the existing research, this paper simulates the strategy selections of listed internet companies, accounting firms, and audit regulators using a three-party evolutionary game model, and explores the effects of the revenues and costs on the strategy selections of three parties.
3. Evolutionary Game Model
In evolutionary game theory, the subjects having bounded can adjust their strategies continuously by obtaining information from other participants and the outside world, and finally reach an equilibrium state. Evolutionary game theory applies to China’s current internet financial ecology, considering that listed internet companies are the operating subjects of the internet financial industry and the trading media of internet financial users. However, under the influence of profit-seeking capital, listed internet companies are likely to disobey the market rules and implement financial fraud. Therefore, this paper holds that the leading players are listed internet companies, accounting firms, and audit regulators. In an audit process, audit regulators should encourage the self-discipline management of the listed internet companies to reduce the cost of audit supervision, and strictly supervise listed internet companies to prevent financial risks. The equilibrium strategies are finally formed after many games among the three parties.
3.1. Hypothesis of the Evolutionary Game Model
Information asymmetry exists among listed internet companies, accounting firms, and audit regulators, and the behavior of the three parties constitutes a dynamic game process. Establishing an internet audit framework needs a comprehensive audit defense system with government financial audits as the leading force, private financial audits as the main force, and internal financial audits as the core force [29]. To facilitate the analysis using the evolutionary game model, we present the following hypotheses, combined with the current situation of audit supervision of listed internet companies.
H1 is the hypothesis of participants in the model. The participants are bounded rational players, including listed internet companies, accounting firms, and audit regulators.
H2 is the hypothesis of strategy selections for participants. First, listed internet companies have two strategies: financial fraud and non-fraud. Second, accounting firms choose two strategies: loose audit and strict audit. Third, the two strategic selections of audit regulators are active supervision and negative supervision.
H3 is the hypothesis of model parameters (revenues and costs of three parties).
The revenue of listed internet companies under normal operation is expressed as e1, the extra revenue obtained through financial fraud of listed internet companies is represented by k, and the rent-seeking cost of listed internet companies bribing accounting firms is written as c1.
In the strict audit, the normal revenue and audit cost of accounting firms are denoted as r1 and c2, respectively. In the loose audit, the extra revenue and audit cost of accounting firms are represented as c1 and c3 in turn.
When audit regulators discover the financial fraud of listed internet companies, the fine imposed on listed internet companies is p1. The fine imposed on accounting firms is p2. If accounting firms receive bribes from listed internet companies, audit regulators will confiscate these bribes and impose a fine on listed internet companies. So, the active supervision revenue of audit regulators equals c1 + p1 + p2. At this point, the active supervision cost is c4. Otherwise, it is 0. Let us assume that the following relation holds: p2 > c4; c1 + p1 > c4; c1 + p1 + p2 > c4.
Additionally, it should be noted that whether audit regulators conduct active supervision or not, accounting firms can obtain audit revenue (r1) paid by listed internet companies. An important reason for accounting firms to choose a loose audit strategy is to obtain additional benefit (c1), which is assumed to be much larger than r1. The parameters of the evolutionary game model are shown in Table 1.

Table 1.
The parameters of the evolutionary game model.
3.2. Payoff Matrix
Based on the above hypotheses, the strategy matrix of the three parties is shown in Table 2. The probability of financial fraud of listed internet companies is x. Otherwise, it is 1 − x. For accounting firms, the probability of strict audits is y, and the probability of loose audits is 1 − y. In addition, the probability of active supervision is z for audit regulators, and the probability of negative supervision is 1 − z. It should be noted that when audit regulators adopt a negative supervision strategy, the supervision revenue and supervision cost are equal to 0. In the three-party evolutionary game model, each party has two strategic selections. Therefore, the payoff matrix of the three parties is shown in the last two columns of Table 2.

Table 2.
The payoff matrix of the three parties.
3.3. Replicator Dynamics Equation
3.3.1. Replicator Dynamics Equation of Listed Internet Companies
When listed internet companies choose a financial fraud strategy, the expected revenue function () is represented as Equation (1). Otherwise, the expected revenue function () is indicated as Equation (2). The average expected return function () is shown in Equation (3).
The replicator dynamics equation of listed internet companies is shown in Equation (4).
When F(x) equals 0, the stable points of the replicator dynamics equation can be obtained, as seen in Equation (5).
According to the stability principle of differential equations, the first derivative of the replicator dynamics equation must be less than 0 at the stable point, i.e., .
The first derivative of the replicator dynamics equation of the listed internet companies is shown in Equation (6).
3.3.2. Replicator Dynamics Equation of Accounting Firms
When accounting firms choose a strict audit strategy, the expected revenue function () is shown in Equation (7). Under a loose audit strategy, the expected revenue function () is written as Equation (8).
The average expected return function () can be written as Equation (9).
The replicator dynamics equation of accounting firms is shown in Equation (10), and the stable points are represented in Equation (11).
The first derivative of the replicator dynamics equation of accounting firms is shown in Equation (12).
3.3.3. Replicator Dynamics Equation of Audit Regulators
The expected revenue function of audit regulators adopting the active supervision strategy is expressed as in Equation (13).
Furthermore, the expected revenue function is written as () in Equation (14), when audit regulators choose a negative supervision strategy.
The average expected revenue function of audit regulators () is represented in Equation (15).
The replicator dynamics equation and the stable points are shown in Equation (16) and Equation (17), respectively.
The first derivative of the replicator dynamics equation of audit regulators is shown in Equation (18).
3.4. Stability Analysis of Evolutionary Game Model
Let the above replicator dynamics equations be equal to 0 in expressions (4), (10), and (16), then, we can obtain nine probable stable equilibrium points: A(0, 0, 0), B (0, 1, 0), C (0, 0, 1), D(0, 1, 1), E(1, 0, 0), F(1, 0, 1), G(1, 1, 1), H(1, 1, 0), and I(x*, y*, z*). Particularly, I(x*, y*, z*) is the solution of Equation (19).
The premise of Nash equilibrium is that, in the presence of the optimal strategy of game players, each player must make an optimal response to other players at the same time [30]. However, the values of x, y, and z in I(x;, y;, z;) are not uniquely determined. In this situation, the stability criteria of the evolutionary game model for multi-players cannot be met [31,32,33]. Briefly, I(x*, y;, z;) is the non-strict Nash equilibrium, which leaves the three parties with no optimal solution in the evolutionary game model. In addition, audit regulators hardly adopt a negative supervision strategy in reality, for performing the government supervision function. Thus, only four probable stable equilibrium points, C(0, 0, 1), D(0, 1, 1), F(1, 0, 1), and G(1, 1, 1), are further analyzed below.
Based on the replicator dynamics equations of listed internet companies, accounting firms, and audit regulators, i.e., expressions (4), (10), and (16), this paper uses the analytical method of the evolutionarily stable strategy (ESS) proposed by Friedman [34]. The Jacobian matrix is shown as Equation (20).
According to the Lyapunov stability theory, when all eigenvalues of the Jacobian matrix are negative, this equilibrium point is in a stable equilibrium state [34,35]. Otherwise, the strategy combination is unstable. The results of stability analysis for each equilibrium point are shown in Table 3.

Table 3.
Stability analysis of equilibrium points in the three-party evolutionary game model.
Table 3 shows that an ESS exists. The only stable equilibrium point is F(1, 0, 1). Other equilibrium points, C(0, 0, 1), D(0, 1, 1), and G(1, 1, 1), cannot reach stable equilibrium states.
4. Numerical Simulation Analysis
Following the above analysis, we use numerical simulations further to analyze the equilibrium point F(1, 0, 1). Before the numerical simulations are performed, the model parameters are assigned with initial values in Table 4. They satisfy the following relationship: c1 + p1 − k < 0, −c1 − c2 + c3 + p2 < 0, and c4 − c1 − p1 − p2 < 0.

Table 4.
The initial values of model parameters.
4.1. The Evolutionary Game Analysis of Three-Party Strategy Selections
First, the initial probabilities of the three parties are set to 0.5, i.e., x = y = z = 0.5. The evolutionary process of three-party strategy selections is shown in Figure 2. The horizontal axis represents the evolution time (t) and the vertical axis shows the decision probability of different parties (p). As time passes, the evolution time (t) presents different characteristics. When a decision probability is less than 0.005 or larger than 0.995, it is assumed to be equal to 0 or 1.
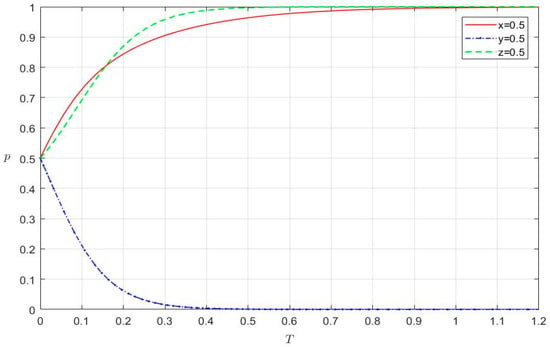
Figure 2.
The evolutionary process of three-party strategy selections.
- For the red line (x = 0.5), when t equals 0.9153, the probability of financial fraud of listed internet companies equals 1.
- For the blue line (y = 0.5), when t equals 0.3911, the probability of strict audits of accounting firms equals 0.
- For the green line (z = 0.5), when t equals 0.4732, the probability of active supervision of audit regulators equals 1.
As shown in Figure 2, the three parties reach a stable equilibrium state. Listed internet companies, accounting firms, and audit regulators, respectively, choose a financial fraud strategy, a loose audit strategy, and an active supervision strategy. In other words, the three parties choose the strategy (1, 0, 1). This result again indicates that the equilibrium point F(1, 0, 1) is stable. To better analyze the evolution process of the three-party strategy selection, we change initial parameters to continue simulation analyses.
4.2. The Evolutionary Game Analysis of Listed Internet Companies
Assuming that the initial probability of the financial fraud of listed internet companies (x) is 0.5, y and z are, respectively, taken as different values of four groups, (0.1, 0.1); (0.5, 0.1); (0.1, 0.5); and (0.8, 0.8). The simulation analyses are performed for different values of (x, y, z). Additionally, we discuss whether the strategy selection of listed internet companies is affected by the strict audit of accounting firms and the active supervision of audit regulators. The evolution time (t) is short and no more than 0.9920 in the four situations in Figure 3.
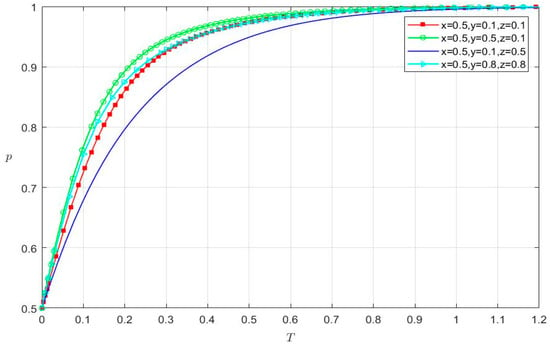
Figure 3.
The strategy selection of listed internet companies.
- For the red line (x = 0.5; y = 0.1; z = 0.1), when t is 0.8545, the probability of financial fraud of listed internet companies equals 1.
- For the green line (x = 0.5; y = 0.5; z = 0.1), when t is 0.7912, the probability of financial fraud of listed internet companies equals 1.
- For the blue line (x = 0.5; y = 0.1; z = 0.5), when t is 0.9916, the probability of financial fraud of listed internet companies equals 1.
- For the cyan line (x = 0.5; y = 0.8; z = 0.8), when t is 0.8541, the probability of financial fraud of listed internet companies equals 1.
With the increase in y or z, the probability of financial fraud of listed internet companies converges to 1. When y and z increase at the same time, the increase in probability becomes faster in the initial phase, but less obvious in the later stage. Additionally, with the increase in y (or z), the probability of financial fraud of listed internet companies presents an increasing trend of accelerating (or decelerating). In brief, no matter how accounting firms and audit regulators choose their strategies, listed internet companies still choose a financial fraud strategy. Relative to the active supervision of audit regulators, the strict audit of accounting firms causes listed internet companies to spend less time making a financial fraud strategy.
Keeping other conditions unchanged, we study the strategy selection of listed internet companies under the impact of the extra revenue from financial fraud (k) and the fine for financial fraud found by audit regulators (p1). When k is 2, 5, 25, and 30, respectively, the strategy selection of listed internet companies is shown in Figure 4.
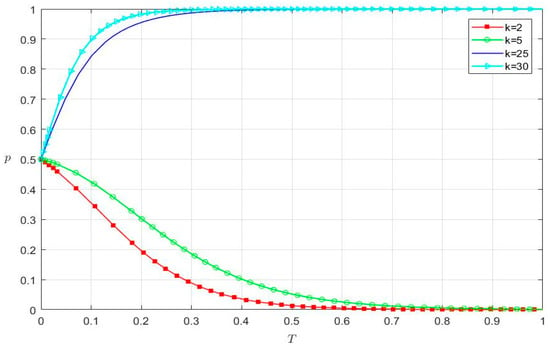
Figure 4.
The impact of k on the strategy selection of listed internet companies.
- For the red line (k = 2), when t is 0.6034, the probability of financial fraud of listed internet companies equals 0.
- For the green line (k = 5), when t is 0.8429, the probability of financial fraud of listed internet companies equals 0.
- For the blue line (k = 25), when t is 0.3886, the probability of financial fraud of listed internet companies equals 1.
- For the cyan line (k = 30), when t is 0.2731, the probability of financial fraud of listed internet companies equals 1.
In Figure 4, the probability of financial fraud of listed internet companies converges to 0 or 1 under different values of k. When k = 2 and k = 5, the probability of financial fraud converges to 0. In this case, listed internet companies do not choose a financial fraud strategy for the smaller extra revenue. In addition, when k = 25 and k = 30, the probability of financial fraud converges to 1. Listed internet companies probably commit financial fraud to obtain the larger extra revenue. Thus, the extra revenue from financial fraud (k) is an important factor influencing the strategy selection of listed internet companies.
When the fine for financial fraud found by audit regulators (p1) is 1, 5, 15, and 20, respectively, the strategy selection of listed internet companies is shown in Figure 5.
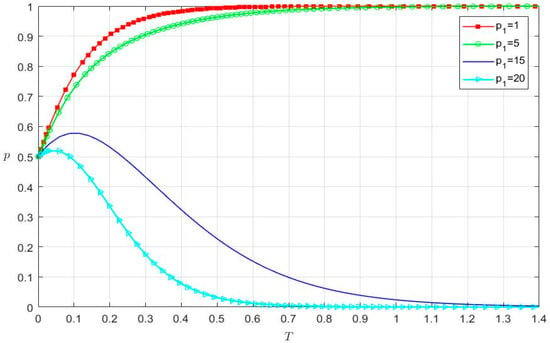
Figure 5.
The impact of p1 on the strategy selection of listed internet companies.
- For the red line (p1 = 1), when t is 0.5360, the probability of financial fraud of listed internet companies equals 1.
- For the green line (p1 = 5), when t is 0.9153, the probability of financial fraud of listed internet companies equals 1.
- For the blue line (p1 = 15), when t is 1.3445, the probability of financial fraud of listed internet companies equals 0.
- For the cyan line (p1 = 20), when t is 0.6917, the probability of financial fraud of listed internet companies equals 0.
In Figure 5, the probability of financial fraud of listed internet companies converges to 0 under a larger value of p1. Otherwise, it converges to 1. Specifically, when p1 decreases from 5 to 1, the convergence speed of the probability gradually accelerates to 1. However, the probability of financial fraud of listed internet companies approaches 0 at a fast convergence rate, when p1 increases from 15 to 20. Therefore, the smaller fine for financial fraud found by audit regulators promotes listed internet companies to choose a financial fraud strategy. Comparing Figure 4 and Figure 5, we can see that listed internet companies choose a financial fraud strategy under the higher extra revenue (k) and the smaller fine (p1).
4.3. The Evolutionary Game Analysis of Accounting Firms
Assuming that the initial probability of strict audits of accounting firms (y) is 0.5, x and z are, respectively, taken as different values of four groups, (0.1, 0.1); (0.5, 0.1); (0.1, 0.5); and (0.8, 0.8). The simulation analyses are carried out for different values of (x, y, z). We also analyze whether the strategy selection of accounting firms is influenced by the financial fraud of listed internet companies and the active supervision strategy of audit regulators. Figure 6 shows that the probability of strict audits of accounting firms converges to 0 in the four situations.
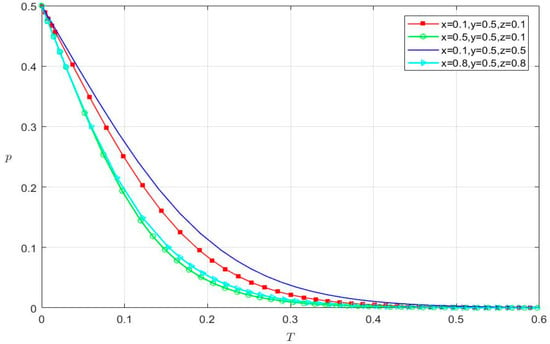
Figure 6.
The strategy selection of accounting firms.
- For the red line (x = 0.1; y = 0.5; z = 0.1), when t is 0.4011, the probability of strict audits of accounting firms equals 0.
- For the green line (x = 0.5; y = 0.5; z = 0.1), when t is 0.3553, the probability of strict audits of accounting firms equals 0.
- For the blue line (x = 0.1; y = 0.5; z = 0.5), when t is 0.4605, the probability of strict audits of accounting firms equals 0.
- For the cyan line (x = 0.8; y = 0.5; z = 0.8), when t is 0.3756, the probability of strict audits of accounting firms equals 0.
With different values of x and z, the evolution time (t) is quite different in Figure 6. When z remains constant, the evolution time (t) becomes shorter by increasing x. Similarly, when x remains constant, the evolution time (t) is prolonged by increasing z. If x and z increase simultaneously, the evolution time (t) is still shortened. Finally, it should be noted that no matter how x and z change, they do not affect accounting firms choosing a loose audit strategy. Relative to the active supervision of audit regulators, the financial fraud of listed internet companies promotes accounting firms to spend less time creating a loose audit strategy.
Keeping other parameters unchanged, we study the strategy selection of accounting firms under the impact of the audit cost in strict audits (c2) and the fine after loose audits found by audit regulators (p2). When c2 is 2, 4, 8, and 12, respectively, the strategy selection of accounting firms is shown in Figure 7.
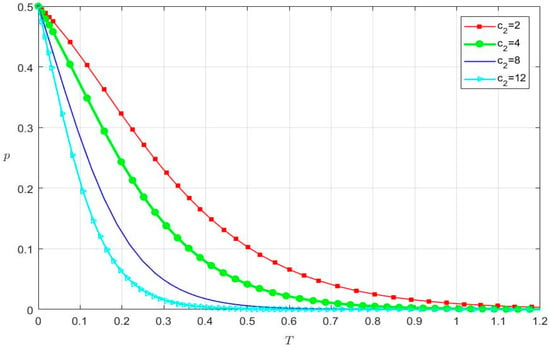
Figure 7.
The impact of c2 on the strategy selection of accounting firms.
- For the red line (c2 = 2), when t is 1.1391, the probability of strict audits of accounting firms equals 0.
- For the green line (c2 = 4), when t is 0.8338, the probability of strict audits of accounting firms equals 0.
- For the blue line (c2 = 8), when t is 0.5336, the probability of strict audits of accounting firms equals 0.
- For the cyan line (c2 = 12), when t is 0.3911, the probability of strict audits of accounting firms equals 0.
Figure 7 shows that accounting firms choose a loose audit strategy regardless of the value of c2. However, it should be noted that the change in c2 changes the evolution time of the model. When the strict audit cost (c2) is larger, the convergence speed is faster and the simulation time is shorter. For example, when c2 increases from 2 to 12, accounting firms spend less time choosing a loose audit strategy.
When the fine after loose audits found by audit regulators (p2) is 4, 9, 25, and 35, respectively, the strategy selection of accounting firms is shown in Figure 8.
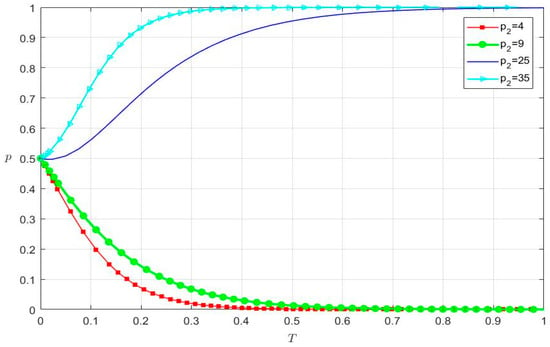
Figure 8.
The impact of p2 on the strategy selection of accounting firms.
- For the red line (p2 = 4), when t is 0.4144, the probability of strict audits of accounting firms equals 0.
- For the green line (p2 = 9), when t is 0.6196, the probability of strict audits of accounting firms equals 0.
- For the blue line (p2 = 25), when t is 0.8527, the probability of strict audits of accounting firms equals 1.
- For the cyan line (p2 = 35), when t is 0.3627, the probability of strict audits of accounting firms equals 1.
Figure 8 shows that accounting firms choose a loose audit strategy because of a small fine after loose audits found by audit regulators (such as p2 = 4 and p2 = 9), and the probability of accounting firms choosing a strict audit strategy approaches 0. However, accounting firms are inclined to choose a strict audit strategy with the increase in p2. When p2 increases from 25 to 35, the evolution time (t) is shortened from 0.8527 to 0.3627. Thus, a larger fine after loose audits found by audit regulators (p2) prompts accounting firms to choose a strict audit strategy. Otherwise, they make a loose audit strategy with a small p2. Comparing Figure 7 and Figure 8, it can be seen that the change in the strict audit cost (c2) does not change the strategy selection of accounting firms, but a larger fine after loose audits found by audit regulators (p2) prompts accounting firms to create a strict audit strategy.
4.4. The Evolutionary Game Analysis of Audit Regulators
Assuming that the initial probability of active supervision of audit regulators (z) is 0.5, x and y are respectively taken as different values of four groups, (0.1, 0.1); (0.5, 0.1); (0.1, 0.5); and (0.8, 0.8). The numerical simulation is used for analyzing the strategy selection of audit regulators under the influence of the financial fraud of listed internet companies and the strict audit of accounting firms. The evolution time (t) differs in the four situations in Figure 9.
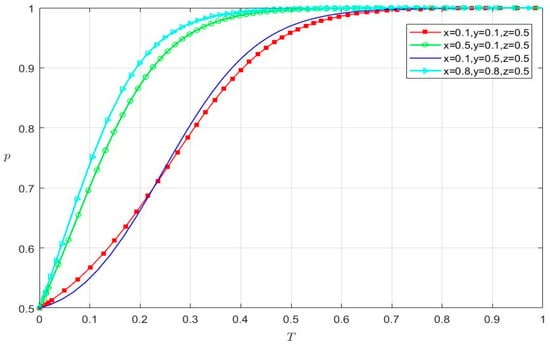
Figure 9.
The strategy selection of audit regulators.
- For the red line (x = 0.1, y = 0.1, z = 0.5), when t is 0.6902, the probability of active supervision of audit regulators equals 1.
- For the green line (x = 0.5, y = 0.1, z = 0.5), when t is 0.4835, the probability of active supervision of audit regulators equals 1.
- For the blue line (x = 0.1, y = 0.5, z = 0.5), when t is 0.6508, the probability of active supervision of audit regulators equals 1.
- For the cyan line (x = 0.8, y = 0.8, z = 0.5), when t is 0.4272, the probability of active supervision of audit regulators equals 1.
As shown in Figure 9, audit regulators choose an active supervision strategy, when the initial probability of active supervision of audit regulators (z) is 0.5. The different values of x and y only affect the evolution time (t). When x and y are larger simultaneously (such as x = y = 0.8), the evolution time is shorter (t = 0.4272). Additionally, when x and y are smaller, the evolution time (t) is prolonged (t = 0.6902). Compared with the red line and the green line in Figure 9, we see that the increase in x shortens the evolution time (t). After comparing the red line with the blue line, we come to the same conclusion with the increase in y. Therefore, no matter how listed internet companies and accounting firms choose their strategies at the initial time, audit regulators still choose an active supervision strategy. The financial fraud of listed internet companies and the strict audit of accounting firms make audit regulators spend less time implementing a positive supervision strategy.
Keeping other parameters unchanged, we study the strategy selection of audit regulators under the impact of the active supervision cost (c4). When c4 is 1, 3, 20, and 25, respectively, the simulation results of the strategy selection of audit regulators are shown in Figure 10.
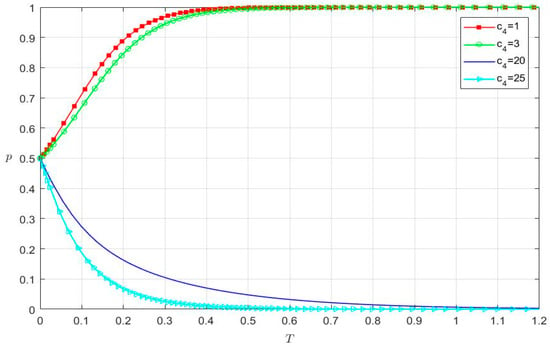
Figure 10.
The impact of c4 on the strategy selection of audit regulators.
- For the red line (c4 = 1), when t is 0.4341, the probability of active supervision of audit regulators equals 1.
- For the green line (c4 = 3), when t is 0.5119, the probability of active supervision of audit regulators equals 1.
- For the blue line (c4 = 20), when t is 1.0748, the probability of active supervision of audit regulators equals 0.
- For the cyan line (c4 = 25), when t is 0.4856, the probability of active supervision of audit regulators equals 0.
Figure 10 shows two different evolutionary paths of the strategy selection of audit regulators. With varying values of c4, the probability of active supervision of audit regulators converges to 0 or 1. Specifically, when the active supervision cost is larger (such as c4 = 20 and c4 = 25), audit regulators will choose a negative supervision strategy, and the probability of active supervision converges to 0. When the active supervision cost (c4) increases from 20 to 25, the evolution time (t) is shortened from 1.0748 to 0.4856. When the active supervision cost (c4) gradually decreases, the probability of active supervision of audit regulators gradually increases. For example, when the active supervision cost takes a smaller value (such as c4 = 1 and c4 = 3), audit regulators choose an active supervision strategy, and the probability of active supervision converges to 1. If c4 is reduced from 3 to 1, the evolution time (t) will be shortened from 0.5119 to 0.4341.
In short, the active supervision cost (c4) directly affects the strategy selection of audit regulators. When the cost of active supervision is higher, audit regulators conduct negative supervision. Conversely, the lower supervision cost promotes them to conduct active supervision.
5. Discussion
The sound development of listed internet companies is an important foundation for economic operation. With the rapid growth of China’s internet economy, the financial fraud of listed internet companies has occurred from time to time. In the meantime, cases of financial fraud of listed internet companies are easy to be found in many countries. How to prevent financial fraud of listed internet companies has become a hot spot in academia. When the financial fraud of listed internet companies appears, the audit works of accounting firms become particularly important. However, due to audit fraud and audit negligence, the phenomenon of audit failure of accounting firms often happens. In the face of financial fraud and audit failures, audit regulators also feel tremendous regulatory pressure. In the current research on financial fraud and audit supervision, the research framework of the three-party evolutionary game is rare. Most studies focus on listed internet companies and auditors, and less on audit regulators. The dynamic evolution mechanism of three-party strategy selections is still unclear after introducing audit regulators. Therefore, it is of great theoretical and practical significance to study the strategic selection of the three parties for preventing the occurrence of financial fraud and improving the level of audit supervision.
In this study, we construct a three-party evolutionary game model by analyzing their payoff matrix and exploring the dynamic evolution mechanism of three-party strategy selections under the influence of different parameters. With the change in the initial probability of any party, the stable equilibrium strategy of the three parties does not change. However, the changes in revenues and costs in the three-party evolutionary game probably influence the stable equilibrium strategy of the three parties. Particularly, we should pay attention to the following model parameters: the extra revenue from financial fraud of listed internet companies (k), the fine for financial fraud found by audit regulators (p1), the audit cost in strict audits of accounting firms (c2), the fine after loose audits found by audit regulators (p2), and the active supervision cost of audit regulators (c4). The previous studies demonstrated that the primary motivation for listed internet companies to commit financial fraud was to obtain higher revenues [8], and the strict audit was conducive to preventing financial fraud [9,16]. These conclusions are consistent with our findings. The larger extra revenue from financial fraud (k) prompts listed internet companies to choose a financial fraud strategy in less time. Moreover, the larger fine after loose audits found by audit regulators (p2) enables accounting firms to apply a strict audit strategy to prevent the financial fraud of listed internet companies. Through numerical simulation analyses, we discuss the dynamic evolution mechanism of three-party strategy selections. This paper expands the existing research framework of financial fraud and audit supervision, and builds an evolutionary game model based on listed internet companies, accounting firms, and audit regulators. The research methods and conclusions complement and enrich the existing literature.
As for the setting of model parameters, we put forward hypothesis H3, which involves the revenues and costs of the three parties. Although the expected revenue function and the replicator dynamics equation are the critical factors in finding the stable equilibrium point, we only consider the model parameters that affect three-party strategy selections. Some factors that affect the revenues or costs of one party and do not affect the strategic selections of other parties are not considered in the evolutionary game model. Therefore, our research framework depends on model assumptions and parameter settings. Under different market environments and regulatory systems, the stable equilibrium strategies of the three parties are probably different. The future research direction can be summarized as follows. First, the model parameters should be optimized based on the analysis of financial fraud cases. Many cases of financial fraud are affected by the revenues and costs of all parties. With the changes in revenues and costs, the strategic selections of listed internet companies, accounting firms, and audit regulators change accordingly. Through a practical case, the model parameters can be further revised and the three-party evolutionary game model can be further optimized. Second, an early warning mechanism for financial fraud of listed internet companies should be established. We find that the initial probability of the strategy selection does not affect the final strategy of the three parties. However, other model parameters related to the revenues and costs can directly affect the final strategies of the three parties. Thus, we should further analyze the influence of different model parameters on the probabilities of three-party strategy selections through many numerical simulations and create warning plans for the financial fraud of listed internet companies in advance.
6. Conclusions
Based on the constructed three-parties evolutionary game model, this paper simulates the strategy selections of listed internet companies, accounting firms, and audit regulators, and studies the influence of the change in model parameters on the strategy selections of the three parties. First of all, we discuss the strategy selection of listed internet companies under the impact of the extra revenue from financial fraud (k) and the fine for financial fraud found by audit regulators (p1). Afterward, we analyze the strategy selection of accounting firms under the impact of the audit cost in strict audits (c2) and the fine after loose audits found by audit regulators (p2). In the end, we study the strategy selection of audit regulators under the impact of the active supervision cost (c4). The conclusions are summarized as follows.
First, the three-party evolutionary game model shows the strategy selection of either party is not influenced by the other two parties’ strategies. Regardless of which initial strategy the three parties choose, their final strategy selections remain unchanged. However, changes in the three-party strategy influence the evolution time of the model. For listed internet companies, the strict audit of accounting firms lets them spend less time creating a financial fraud strategy, relative to the active supervision of audit regulators. For accounting firms, the financial fraud of listed internet companies causes them to spend less time creating a loose audit strategy, relative to the active supervision of audit regulators. For audit regulators, the financial fraud of listed internet companies and the strict audit of accounting firms allow them to spend less time making a positive supervision strategy.
Second, changes in model parameters can directly affect the strategy selections of the three parties in the evolutionary game model. For listed internet companies, the larger extra revenue from financial fraud promotes them to choose a financial fraud strategy. On the contrary, listed internet companies make a non-fraud strategy. Moreover, the smaller fine for financial fraud found by audit regulators prompts listed internet companies to create a financial fraud strategy. For accounting firms, the larger audit cost of strict audits only shortens the simulation time and does not change their strategy selections. Additionally, the smaller fine after loose audits found by audit regulators motivates accounting firms to choose a loose audit strategy. For audit regulators, the larger supervision cost prompts them to choose a negative supervision strategy. Otherwise, they choose an active supervision strategy.
Author Contributions
Conceptualization, J.Y. and M.Z.; methodology, J.Y.; software, J.Y. and G.F.; validation, B.W.; formal analysis, B.W. and J.Y.; data curation, G.F.; writing—original draft preparation, B.W. and J.Y.; writing—review and editing, B.W.; visualization, B.W.; funding acquisition, B.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Social Science Fund of China (Grant No. 21XJY014).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We express our most sincere gratitude to the editors and reviewers for their careful review of this study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mackevičius, J.; Kazlauskienė, L. The fraud tree and its investigation in audit. Ekonomika 2009, 85, 90–101. [Google Scholar] [CrossRef]
- Onwubiko, C. Fraud matrix: A morphological and analysis-based classification and taxonomy of fraud. Comput. Secur. 2020, 96, 101900. [Google Scholar] [CrossRef]
- ACFE. The Fraud Tree. Occupational Fraud and Abuse Classification System by the Association of Certified Fraud Examiners (ACFE), 2016. Available online: https://www.acfe.com/fraud-tree.aspx (accessed on 18 September 2022).
- Steven, P. On financial frauds and their causes: Investor overconfidence. Am. J. Econ. Sociol. 1998, 57, 405–421. [Google Scholar]
- Fich, E.M.; Shivdasani, A.M. Financial fraud, director reputation, and shareholder wealth. J. Financ. Econ. 2007, 86, 306–336. [Google Scholar] [CrossRef]
- Blackwell, C. Using fraud trees to analyze internet credit card fraud. In Proceedings of the IFIP International Conference on Digital Forensics, Vienna, Austria, 8–10 January 2014; Springer: Berlin/Heidelberg, Germany, 2014; pp. 17–29. [Google Scholar]
- Todorović, Z.; Tomaš, D.; Todorović, B. Anti-Fraud Strategy. Ekonomika 2020, 8, 69–78. [Google Scholar] [CrossRef]
- Fellingham, J.C.; Newman, D.P. Strategic considerations in auditing. Account. Rev. 1985, 60, 634–650. [Google Scholar]
- Zhang, J.S.; Chen, G.H. Certified public accountants and audit charges for financial fraud game of listed companies—Empirical evidence from listed companies in China. Res. Financ. Econ. Issues 2011, 2011, 114–123. [Google Scholar]
- Zhang, Z.Y.; Qi, T.H. Research on national audit risk from the perspective of tripartite evolutionary game. Jilin Univ. J. Soc. Sci. Ed. 2020, 60, 128–139. [Google Scholar]
- Srebro, B.; Mavrenski, B.; Bogojević Arsić, V.; Knežević, S.; Milašinović, M.; Travica, J. Bankruptcy Risk Prediction in Ensuring the Sustainable Operation of Agriculture Companies. Sustainability 2021, 13, 7712. [Google Scholar] [CrossRef]
- Matsumura, E.M.; Tucker, R.R. Fraud detection: A theoretical foundation. Account. Rev. 1992, 67, 753–782. [Google Scholar]
- Bo, L.; Yao, H.X. A game analysis on financial fraud of listed companies and external auditing: A dynamic game model with incomplete information. J. Audit Econ. 2013, 28, 43–49. [Google Scholar]
- Li, J.B.; Yin, X.L.; Ren, X. Audit game and audit quality in an experimental market: A comparative institutional experiment on auditor reputation and internal supervision. J. Financ. Econ. 2015, 41, 132–144. [Google Scholar]
- Zhang, J.H. Analysis of relationship between mergers and audit quality of accounting firms with game theory. Chin. Certif. Public Account. 2018, 2018, 64–67. [Google Scholar]
- Hao, S.L.; Li, M.Q. Evolutionary game analysis for national auditing supervision to suppress earning management of state-owned enterprises behavior. J. Audit Econ. 2019, 34, 10–18. [Google Scholar]
- Bloomfield, R.J. Strategic dependence and the assessment of fraud risk: A laboratory study. Account. Rev. 1997, 72, 517–538. [Google Scholar]
- Baiman, S.; Evans, J.; Nagarajan, N.J. Collusion in auditing. J. Account. Res. 2019, 29, 1–18. [Google Scholar] [CrossRef]
- Wang, C.Y. Discussion on audit risk of internet financial enterprises. Commun. Financ. Account. 2016, 2016, 120–121. [Google Scholar]
- Wei, P. A study of the risks and regulation of Chinese internet finance. Financ. Forum 2014, 19, 3–9. [Google Scholar]
- Yang, S.H. Financial system audit and financial stability under the macro-prudential supervision mode. Audit. Res. 2016, 2016, 56–62. [Google Scholar]
- Cao, Y.F.; Xiong, Y. Study on long-term governance mechanism of internet financial risk from the perspective of government audit embedment. Econ. Prob. 2018, 2018, 91–96. [Google Scholar]
- Wang, Z.R.; Yang, M.; Zhou, Y.J. Logic of the emergence of internet finance: Investor’s perspective. Syst. Eng. Theory Pract. 2016, 2016, 2791–2801. [Google Scholar]
- Liu, W.; Xia, L.Q.; Wang, Y.L. Analysis on the behavior of internet finance platform and regulation strategy under dynamic punishment mechanism based on evolutionary game theory. Syst. Eng. Theory Pract. 2017, 2017, 1113–1122. [Google Scholar]
- Song, Y.; Xu, Y.D.; Zhang, Z.Y. Internet financial innovation and regulation win-win: Game analysis of avoidance and regulation. Soc. Sci. Res. 2018, 2018, 25–31. [Google Scholar]
- Tian, M.; Yan, S. Study on the assessment of internet-financial risk based on fuzzy analytic hierarchy process. J. Simul. 2021, 9, 121–126. [Google Scholar]
- He, B.C.; Ruan, X.Q.; Zhao, D. Legal environment and audit collusion: An analysis based on evolutionary game and PSM-Logit model. Commun. Financ. Account. 2020, 2020, 15–20. [Google Scholar]
- Jia, X.; Feng, J.K.; Wang, L. Strengthen the internal audit and external audit supervision joint force: Media supervision moderating effect. J. Xi’an Univ. Financ. Econ. 2020, 33, 71–80. [Google Scholar]
- Zhao, D.; Zhang, H.Y. Construction of internet financial audit framework. Commun. Financ. Account. 2015, 2015, 103–105. [Google Scholar]
- Szabó, G.; Bunth, G. Social dilemmas in multistrategy evolutionary potential games. Phys. Rev. E 2018, 97, 012305. [Google Scholar] [CrossRef]
- Skousen, C.J.; Smith, K.R.; Wright, C.J. Detecting and Predicting Financial Statement Fraud: The Effectiveness of the Fraud Triangle and SAS No. 99; Emerald Group Publishing Limited: Bingley, UK, 2009. [Google Scholar]
- Noble, M.R. Fraud diamond analysis in detecting financial statement fraud. Indones. Account. Rev. 2019, 9, 121–132. [Google Scholar] [CrossRef]
- Maria, E.; Halim, A.; Suwardi, E. Financial distress, regional independence and corruption: An empirical study in Indonesian local governments. J. Account. Strateg. Financ. 2021, 4, 54–70. [Google Scholar] [CrossRef]
- Friedman, J.W. Low information nash equilibria for oligopolistic markets. Inf. Econ. Policy 1983, 1, 3–10. [Google Scholar] [CrossRef]
- Yang, W.; Yang, Y.; Chen, H. How to stimulate Chinese energy companies to comply with emission regulations? Evidence from four-party evolutionary game analysis. Energy 2022, 258, 124867. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).