On a Coupled Time-Dependent SIR Models Fitting with New York and New-Jersey States COVID-19 Data
Abstract
1. Introduction and Model
2. Numerical Simulations, Data and Dynamics
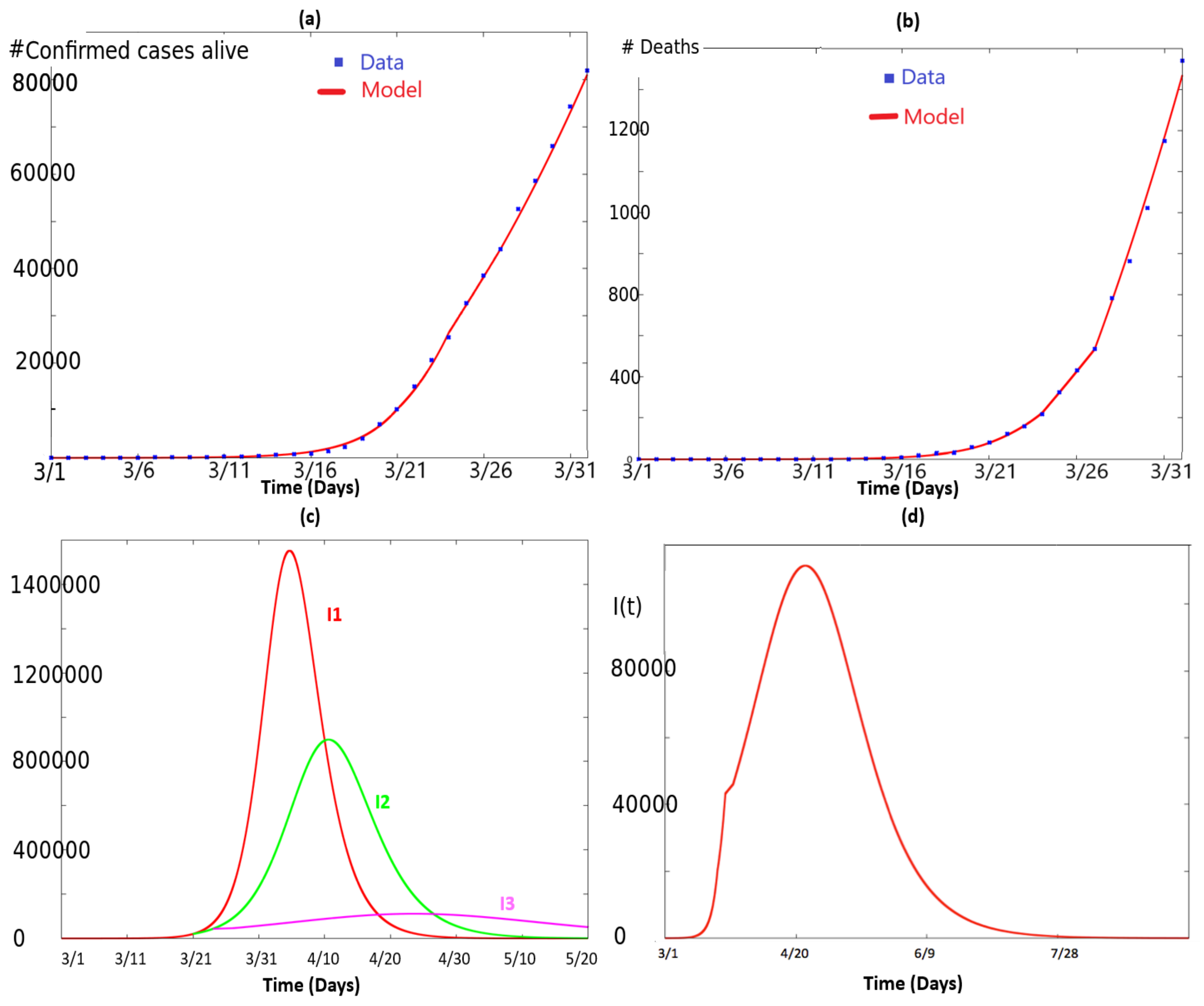
2.1. Fitting the Total Number of Infected People and the Number of Deaths
- The curve in red corresponds to the simulation of (2) with and for all time.
- The curve in green corresponds to the simulation of (2) with and for , and and for .
- The curve in pink corresponds to the simulation of (2) with as given in (3), i.e., and , , with .
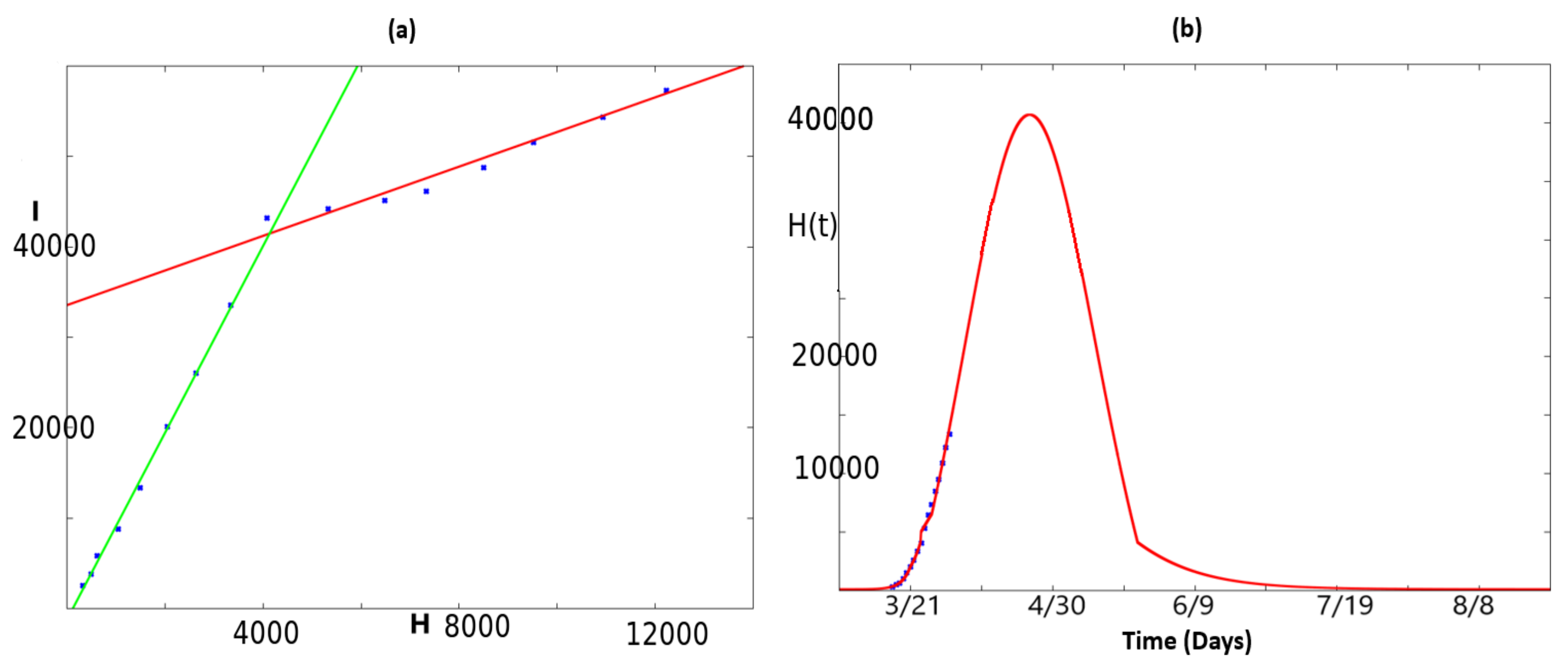
2.2. Fitting the Total Number of People at Hospital
2.3. Dynamics
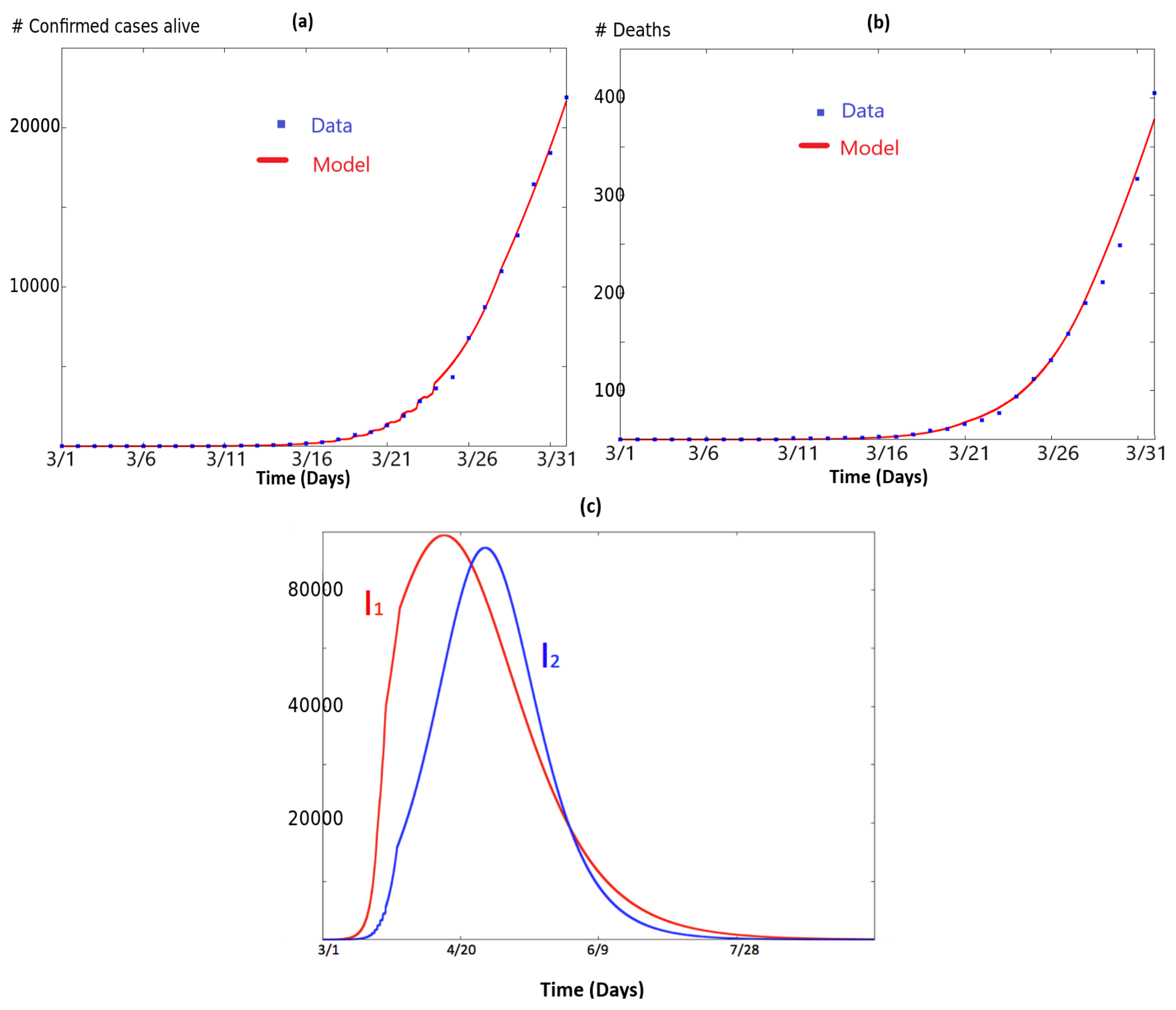
3. Two Coupled SIR Systems Fitting COVID-19 for NY and NJ States
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kermack, W.O.; McKendrick, A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Character 1927, 115, 700–721. [Google Scholar] [CrossRef]
- Murray, J. Mathematical Biology; Springer-Verlag: New York, NY, USA, 2010. [Google Scholar]
- Hui, D.S.; Zumla, A. Severe Acute Respiratory Syndrome. Infect. Dis. Clin. N. Am. 2019, 33, 869–889. [Google Scholar] [CrossRef] [PubMed]
- Lin, Q.; Zhao, S.; Gao, D.; Lou, Y.; Yang, S.; Musa, S.S.; Wang, M.H.; Cai, Y.; Wang, W.; Yang, L.; et al. A conceptual model for the coronavirus disease 2019 (COVID-19) outbreak in Wuhan, China with individual reaction and governmental action. Int. J. Infect. Dis. 2020, 93, 211–216. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.M.; Rui, J.; Wang, Q.P.; Zhao, Z.Y.; Cui, J.A.; Yin, L. A mathematical model for simulating the phase-based transmissibility of a novel coronavirus. Infect. Dis. Poverty 2020, 9, 24. [Google Scholar] [CrossRef] [PubMed]
- Kuniya, T. Prediction of the Epidemic Peak of Coronavirus Disease in Japan, 2020. J. Clin. Med. 2020, 9, 789. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Magal, P.; Seydi, O.; Webb, G. Understanding Unreported Cases in the COVID-19 Epidemic Outbreak in Wuhan, China, and the Importance of Major Public Health Interventions. Biology 2020, 9, 50. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Magal, P.; Seydi, O.; Webb, G. Predicting the cumulative number of cases for the COVID-19 epidemic in China from early data. arXiv, 2002; arXiv:2002.12298. [Google Scholar] [CrossRef]
- Tang, B.; Wang, X.; Li, Q.; Bragazzi, N.L.; Tang, S.; Xiao, Y.; Wu, J. Estimation of the Transmission Risk of the 2019-nCoV and Its Implication for Public Health Interventions. J. Clin. Med. 2020, 9, 462. [Google Scholar] [CrossRef] [PubMed]
- Aziz-Alaoui, M.A.; Gakkhar, S.; Ambrosio, B.; Mishra, A. A network model for control of dengue epidemic using sterile insect technique. Math. Biosci. Eng. 2017, 15, 441–460. [Google Scholar] [CrossRef] [PubMed]
- Moulay, D.; Aziz-Alaoui, M.; Cadivel, M. The chikungunya disease: Modeling, vector and transmission global dynamics. Math. Biosci. 2011, 229, 50–63. [Google Scholar] [CrossRef] [PubMed]
- Moulay, D.; Aziz-Alaoui, M.; Kwon, H. Optimal control of chikungunya disease: Larvae reduction, treatment and prevention. Math. Biosci. Eng. 2012, 9, 369–392. [Google Scholar] [CrossRef] [PubMed]
- Thompson, R.N.; Morgan, O.W.; Jalava, K. Rigorous surveillance is necessary for high confidence in end-of-outbreak declarations for Ebola and other infectious diseases. Philos. Trans. R. Soc. B Biol. Sci. 2019, 374, 20180431. [Google Scholar] [CrossRef] [PubMed]
- Gao, L.; Hethcote, H. Disease transmission models with density-dependent demographics. J. Math. Biol. 1992, 30, 717–731. [Google Scholar] [CrossRef] [PubMed]
- Yoshida, N.; Hara, T. Global stability of a delayed SIR epidemic model with density dependent birth and death rates. J. Comput. Appl. Math. 2007, 201, 339–347. [Google Scholar] [CrossRef]
- Lachmann, A.; Jagodnik, K.M.; Giorgi, F.M.; Ray, F. Correcting under-reported COVID-19 case numbers: Estimating the true scale of the pandemic. medRvix 2020. [Google Scholar] [CrossRef]
- WHO. Report of the World Health Organization-China Joint Mission on Coronavirus Disease 2019 (COVID-19); Report; WHO: Geneva, Switzerland, 16–24 February 2020. [Google Scholar]
- Baud, D.; Qi, X.; Nielsen-Saines, K.; Musso, D.; Pomar, L.; Favre, G. Real estimates of mortality following COVID-19 infection. Lancet Infect. Dis. 2020. [Google Scholar] [CrossRef]
- Roques, L.; Klein, E.K.; Papaïx, J.; Sar, A.; Soubeyrand, S. Using Early Data to Estimate the Actual Infection Fatality Ratio from COVID-19 in France. Biology 2020, 9, 97. [Google Scholar] [CrossRef] [PubMed]
- We’re Sharing Coronavirus Case Data for Every U.S. County. The New York Times. 28 March 2020. Available online: https://www.nytimes.com/article/coronavirus-county-data-us.html?action=click&module=Spotlight&pgtype=Homepage (accessed on 15 April 2020).
- Official Oral Report of New York Governor on COVID19. PBS News, 23 April 2020.
- 21 Percent Of NYC Residents Tested In State Study Have Antibodies From COVID-19. Gothamist. 23 April 2020. Available online: https://gothamist.com/news/new-york-antibody-test-results-coronavirus (accessed on 23 April 2020).
- The Institute for Health Metrics and Evaluation, University of Washington. COVID-19 Projections. 2020. Available online: https://covid19.healthdata.org/united-states-of-america/new-york (accessed on 1 May 2020).
- Official Oral Report of New York Governor on COVID19. PBS News, 2 April 2020.
| Day | 3/1 | 3/2 | 3/3 | 3/4 | 3/5 | 3/6 | 3/7 | 3/8 | 3/9 | 3/10 | 3/11 |
| Number of Cases | 1 | 1 | 2 | 11 | 22 | 44 | 89 | 106 | 142 | 173 | 217 |
| Day | 3/12 | 3/13 | 3/14 | 3/15 | 3/16 | 3/17 | 3/18 | 3/19 | 3/20 | 3/21 | 3/22 |
| Number of Cases | 326 | 421 | 610 | 732 | 950 | 1374 | 2382 | 4152 | 7102 | 10356 | 15168 |
| Day | 3/23 | 3/24 | 3/25 | 3/26 | 3/27 | 3/28 | 3/29 | 3/30 | 3/31 | 4/1 | |
| Number of Cases | 20875 | 25665 | 33066 | 38987 | 44635 | 53363 | 59568 | 67174 | 75832 | 83804 |
| Day | 3/1 | 3/2 | 3/3 | 3/4 | 3/5 | 3/6 | 3/7 | 3/8 | 3/9 | 3/10 | 3/11 |
| Number of Deaths | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Day | 3/12 | 3/13 | 3/14 | 3/15 | 3/16 | 3/17 | 3/18 | 3/19 | 3/20 | 3/21 | 3/22 |
| Number of Deaths | 0 | 0 | 2 | 6 | 10 | 17 | 27 | 30 | 57 | 80 | 122 |
| Day | 3/23 | 3/24 | 3/25 | 3/26 | 3/27 | 3/28 | 3/29 | 3/30 | 3/31 | 4/1 | |
| Number of Deaths | 159 | 218 | 325 | 432 | 535 | 782 | 965 | 1224 | 1550 | 1941 |
| if ; otherwise | if ; otherwise | |
| if | if |
| Day | 3/16 | 3/17 | 3/18 | 3/19 | 3/20 | 3/21 | 3/22 | 3/23 | 3/24 | 3/25 |
| Total Number of Hospitalized | 326 | 496 | 617 | 1042 | 1496 | 2043 | 2629 | 3343 | 4079 | 5327 |
| Day | 3/26 | 3/27 | 3/28 | 3/29 | 3/30 | 3/31 | 4/1 | |||
| Total Number of Hospitalized | 6481 | 7328 | 8503 | 9517 | 10929 | 12226 | 13383 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ambrosio, B.; Aziz-Alaoui, M.A. On a Coupled Time-Dependent SIR Models Fitting with New York and New-Jersey States COVID-19 Data. Biology 2020, 9, 135. https://doi.org/10.3390/biology9060135
Ambrosio B, Aziz-Alaoui MA. On a Coupled Time-Dependent SIR Models Fitting with New York and New-Jersey States COVID-19 Data. Biology. 2020; 9(6):135. https://doi.org/10.3390/biology9060135
Chicago/Turabian StyleAmbrosio, Benjamin, and M. A. Aziz-Alaoui. 2020. "On a Coupled Time-Dependent SIR Models Fitting with New York and New-Jersey States COVID-19 Data" Biology 9, no. 6: 135. https://doi.org/10.3390/biology9060135
APA StyleAmbrosio, B., & Aziz-Alaoui, M. A. (2020). On a Coupled Time-Dependent SIR Models Fitting with New York and New-Jersey States COVID-19 Data. Biology, 9(6), 135. https://doi.org/10.3390/biology9060135






