Novel Dynamic Structures of 2019-nCoV with Nonlocal Operator via Powerful Computational Technique
Abstract
1. Introduction
2. Preliminaries
- (i)
- (ii)
- (iii)
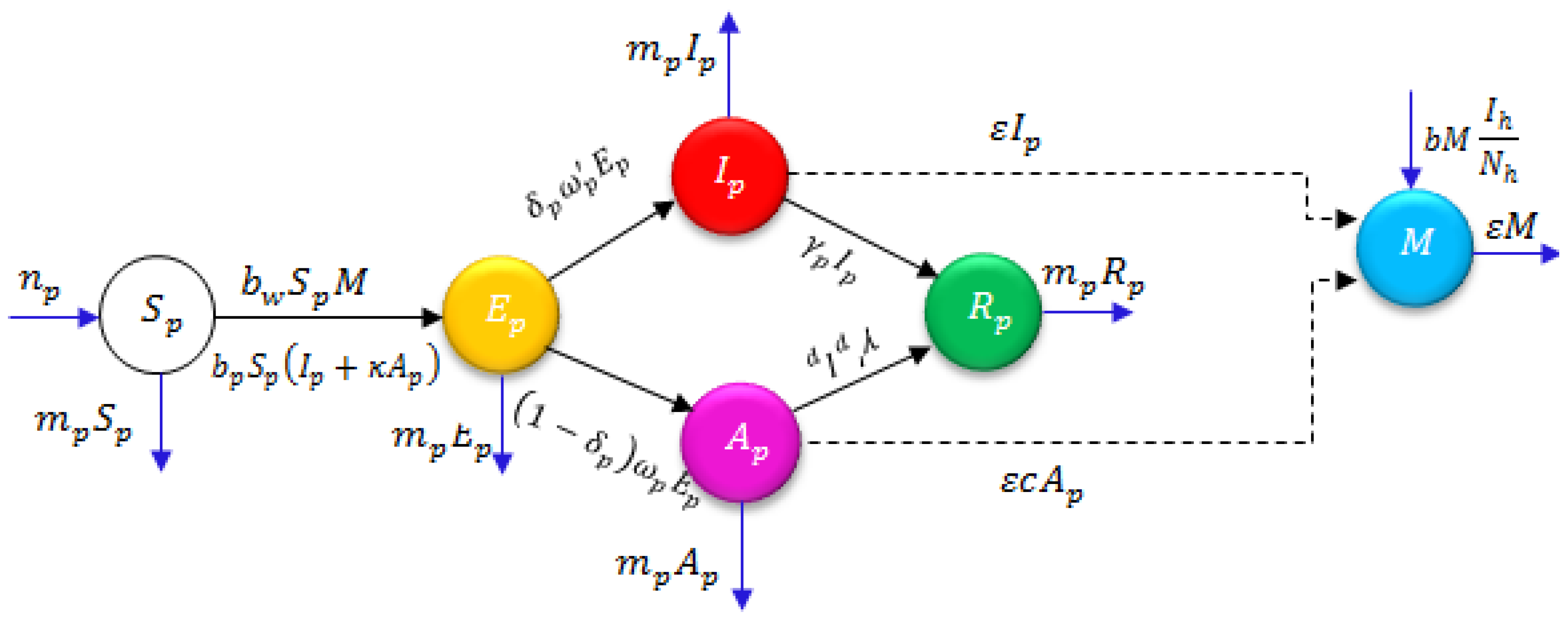
3. Method of Solution for the Projected System
4. FNDM Solution for the Projected System
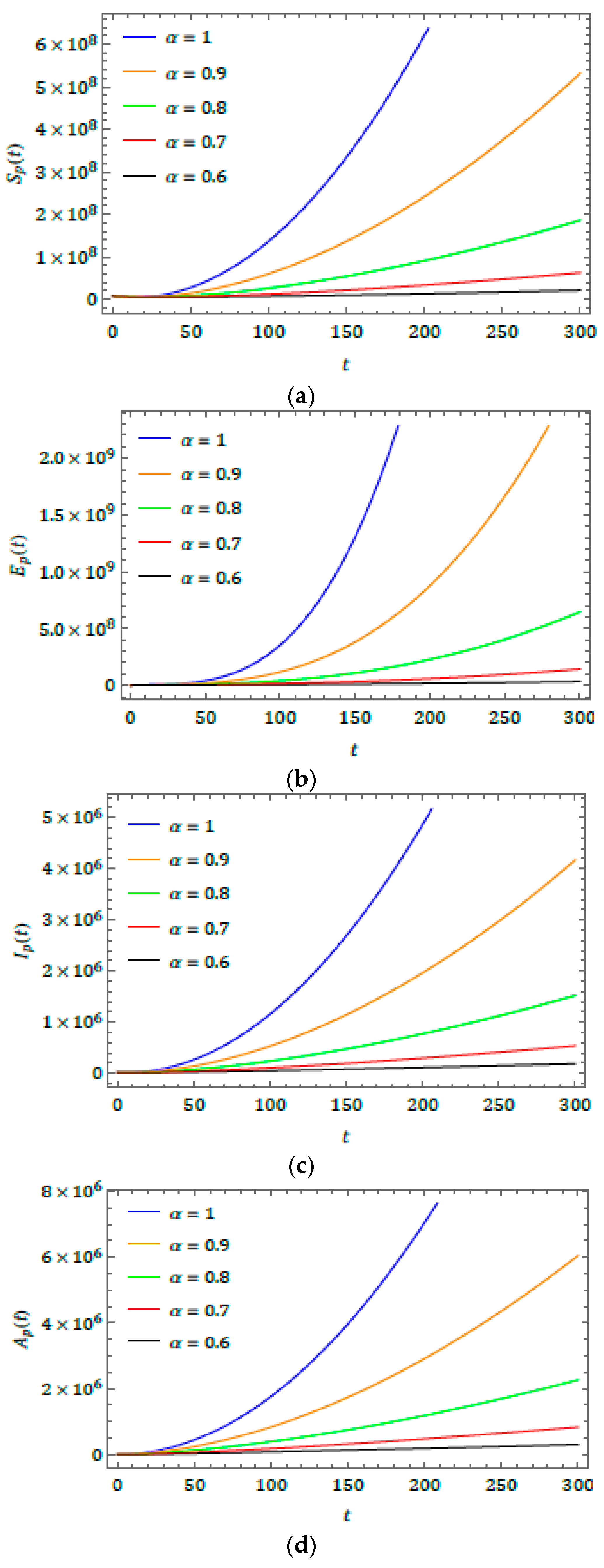
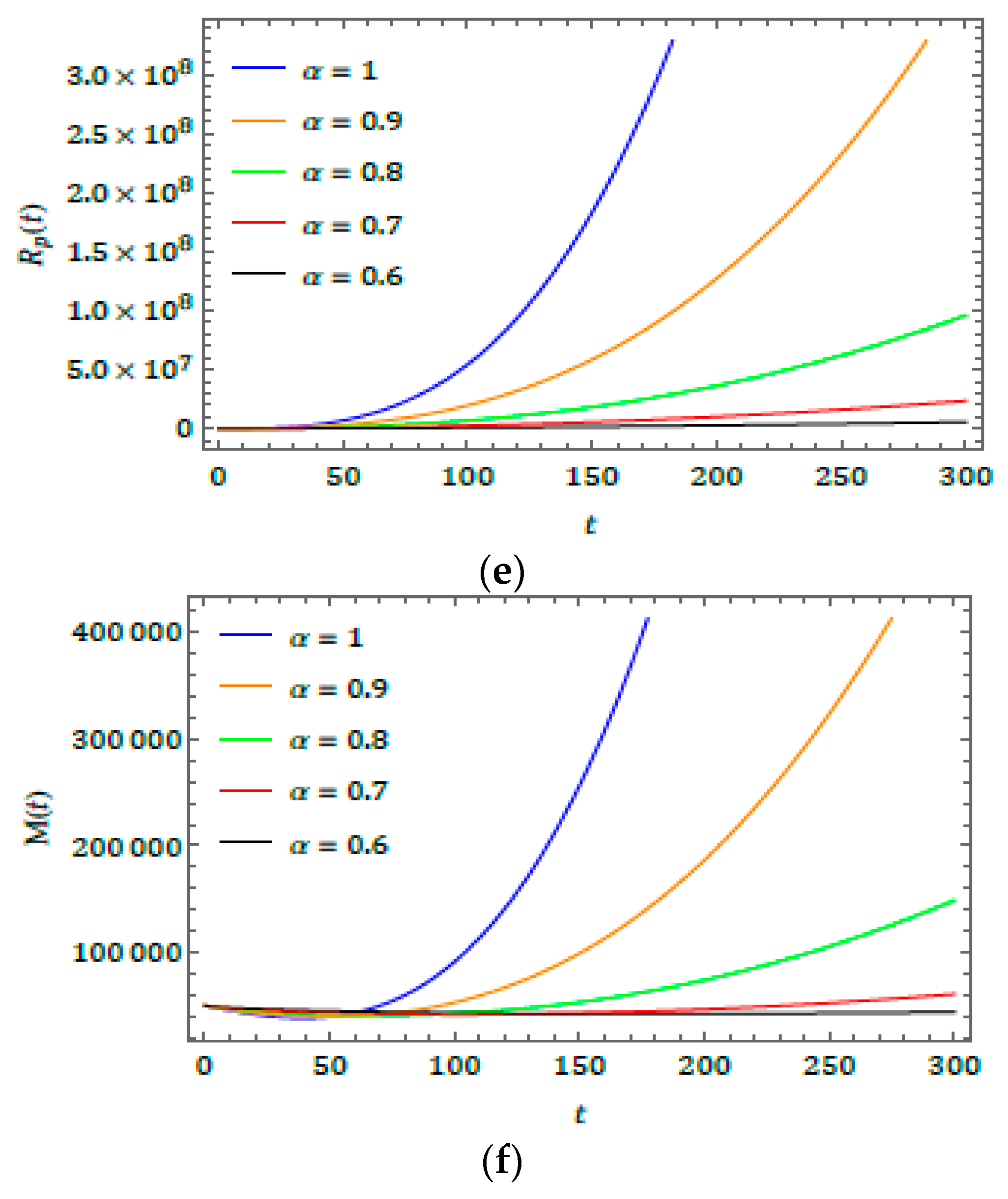
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chan, J.F.; Kok, K.H.; Zhu, Z.; Chu, H.; To, K.K.; Yuan, S.; Yuen, K.Y. Genomic characterization of the 2019 novel human-pathogenic coronavirus isolated from patients with acute respiratory disease in Wuhan, Hubei, China. Emerg. Microbes Infect. 2020, 9, 221–236. [Google Scholar] [CrossRef]
- Lu, H.; Stratton, C.W.; Tang, Y.W. Outbreak of Pneumonia of Unknown Etiology in Wuhan China: The Mystery and the Miracle. J. Med. Virol. 2020. [Google Scholar] [CrossRef] [PubMed]
- Ji, W.; Wang, W.; Zhao, X.; Zai, J.; Li, X. Homologous recombination within the spike glycoprotein of the newly identified coronavirus may boost cross-species transmission from snake to human. J. Med. Virol. 2020. [Google Scholar] [CrossRef]
- World Health Organization. Coronavirus Disease 2019 (COVID-19) Situation Report-62. 2020. Available online: https://www.who.int/emergencies/diseases/novel-coronavirus-2019/situation-reports (accessed on 4 May 2020).
- Chen, Y.; Guo, D. Molecular mechanisms of coronavirus RNA capping and methylation. Virol. Sin. 2016, 31, 3–11. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.F.; Shi, Z.; Zhang, S.; Field, H.; Daszak, P.; Eaton, B.T. Review of bats and SARS. Emerg. Infect. Dis. 2006, 12, 1834–1840. [Google Scholar] [CrossRef]
- Ge, X.Y.; Li, J.L.; Yang, X.L.; Chmura, A.A.; Zhu, G.; Epstein, J.H.; Mazet, J.K.; Hu, B.; Zhang, W.; Peng, C.; et al. Isolation and characterization of a bat SARS-like coronavirus that uses the ACE2 receptor. Nature 2013, 503, 535–538. [Google Scholar] [CrossRef]
- Lu, R.; Zhao, X.; Li, J.; Niu, P.; Yang, B.; Wu, H.; Wang, W.; Song, H.; Huang, B.; Zhu, N.; et al. Genomic characterisation and epidemiology of 2019 novel coronavirus: Implications for virus origins and receptor binding. Lancet 2020, 395, 565–574. [Google Scholar] [CrossRef]
- Zhou, P.; Yang, X.-L.; Wang, X.G.; Hu, B.; Zhang, L.; Zhang, W.; Si, H.-R.; Zhu, Y.; Li, B.; Huang, C.-L.; et al. A pneumonia outbreak associated with a new coronavirus of probable bat origin. Nature 2020. [Google Scholar] [CrossRef]
- Tian, X.; Li, C.; Huang, A.; Xia, S.; Lu, S.; Shi, Z.; Lu, L.; Jiang, S.; Yang, Z.; Wu, Y.; et al. Potent binding of 2019 novel coronavirus spike protein by a SARS coronavirus-specific human monoclonal antibody. Emerg. Microbes Infect. 2020. [Google Scholar] [CrossRef]
- Ahmed, S.F.; Quadeer, A.A.; McKay, M.R. Preliminary identification of potential vaccine targets for 2019-nCoV based on SARS-CoV immunological studies. Viruses 2020, 12, 254. [Google Scholar] [CrossRef]
- Rambaut, A. Phylogenetic Analysis of 23 nCoV-2019 Genomes. 2020. Available online: http://virological.org/t/phylogenetic-analysis-of-23-ncov-2019-genomes-2020-01-23/335 (accessed on 23 January 2020).
- Poon, L.L.M.; Chu, D.K.W.; Chan, K.H.; Wong, O.K.; Ellis, T.M.; Leung, Y.H.C.; Lau, S.K.P.; Woo, P.C.Y.; Suen, K.Y.; Yuen, K.-Y.; et al. Identification of a novel coronavirus in bats. J. Virol. 2005, 79, 2001–2009. [Google Scholar] [CrossRef] [PubMed]
- Chaudhury, S.; Berrondo, M.; Weitzner, B.D.; Muthu, P.; Bergman, H.; Gray, J.J. Benchmarking and analysis of protein docking performance in Rosetta. PLoS ONE 2011, 6, e22477. [Google Scholar] [CrossRef]
- Althaus, C.L. Ebola super spreading. Lancet Infect. Dis. 2015, 15, 507–508. [Google Scholar] [CrossRef]
- Huang, C.; Wang, Y.; Li, X.; Ren, L.; Zhao, J.; Hu, Y.; Zhang, L.; Fan, G.; Xu, J.; Gu, X.; et al. Clinical features of patients infected with 2019 novel coronavirus in Wuhan, China. Lancet 2020. [Google Scholar] [CrossRef]
- Benvenuto, D.; Giovannetti, M.; Ciccozzi, A.; Spoto, S.; Angeletti, S.; Ciccozzi, M. The 2019-new coronavirus epidemic: Evidence for virus evolution. J. Med. Virol. 2020. [Google Scholar] [CrossRef]
- Ferguson, N.M.; Cummings, D.A.; Fraser, C.; Cajka, J.C.; Cooley, P.C.; Burke, D.S. Strategies for mitigating an influenza pandemic. Nature 2006, 442, 448–452. [Google Scholar] [CrossRef]
- Koonin, L.M.; Cetron, M.S. School closure to reduce influenza transmission. Emerg. Infect. Dis. 2009, 15, 137–138. [Google Scholar] [CrossRef]
- Chen, T.M.; Rui, J.; Wang, Q.P.; Zhao, Z.Y.; Cui, J.A.; Yin, L. A mathematical model for simulating the phase-based transmissibility of a novel coronavirus. Infect. Dis. Poverty 2020, 9. [Google Scholar] [CrossRef]
- Mittag-Leffler, G.M. Sur la nouvelle function Eα(x). C. R. Acad. Sci. Paris 1903, 137, 554–558. [Google Scholar]
- Khan, Z.H.; Khan, W.A. N-Transform-Properties and Applications. NUST J. Eng. Sci. 2008, 1, 127–133. [Google Scholar]
- Loonker, D.; Banerji, P.K. Solution of fractional ordinary differential equations by natural transform. Int. J. Math. Eng. Sci. 2013, 12, 1–7. [Google Scholar]
- Adomian, G. A new approach to nonlinear partial differential equations. J. Math. Anal. Appl. 1984, 102, 420–434. [Google Scholar] [CrossRef]
- Brzeziński, D.W. Review of numerical methods for NumILPT with computational accuracy assessment for fractional calculus. Appl. Math. Nonlinear Sci. 2018, 3, 487–502. [Google Scholar] [CrossRef]
- Rawashdeh, M.S. The fractional natural decomposition method: Theories and applications. Math. Meth. Appl. Sci. 2017, 40, 2362–2376. [Google Scholar] [CrossRef]
- Rawashdeh, M.S.; Maitama, S. Finding exact solutions of nonlinear PDEs using the natural decomposition method. Math. Meth. Appl. Sci. 2017, 40, 223–236. [Google Scholar] [CrossRef]
- Prakasha, D.G.; Veeresha, P.; Rawashdeh, M.S. Numerical solution for (2 + 1)-dimensional time-fractional coupled Burger equations using fractional natural decomposition method. Math. Meth. Appl. Sci. 2019, 42, 3409–3427. [Google Scholar] [CrossRef]
- Veeresha, P.; Prakasha, D.G.; Singh, J. Solution for fractional forced KdV equation using fractional natural decomposition method. AIMS Math. 2019, 5, 798–810. [Google Scholar] [CrossRef]
- Rawashdeh, M.S. Solving fractional ordinary differential equations using FNDM. Thai J. Math. 2019, 17, 239–251. [Google Scholar]
- Prakasha, D.G.; Veeresha, P.; Baskonus, H.M. Two novel computational techniques for fractional Gardner and Cahn-Hilliard equations. Comput. Math. Methods 2019, 1, 1–19. [Google Scholar] [CrossRef]
- Veeresha, P.; Prakasha, D.G. An efficient technique for two-dimensional fractional order biological population model. Int. J. Model. Simul. Sci. Comput. 2020, 11, 2050005. [Google Scholar] [CrossRef]
- Gao, W.; Veeresha, P.; Prakasha, D.G.; Baskonus, H.M.; Yel, G. New numerical results for the time-fractional Phi-four equation using a novel analytical approach. Symmetry 2020, 12, 478. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, J.; Baleanu, D. Analysis of regularized long-wave equation associated with a new fractional operator with Mittag-Leffler type kernel. Physica A 2018, 492, 155–167. [Google Scholar] [CrossRef]
- Veeresha, P.; Baskonus, H.M.; Prakasha, D.G.; Gao, W.; Yel, G. Regarding new numerical solution of fractional Schistosomiasis disease arising in biological phenomena. Chaos Solitons Fractals 2020, 133, 109661. [Google Scholar] [CrossRef]
- Yokus, A. Numerical solution for space and time fractional order Burger type equation. Alexandria Eng. J. 2018, 57, 2085–2091. [Google Scholar] [CrossRef]
- Yang, X.J.; Gao, F. A new technology for solving diffusion and heat equations. Therm. Sci. 2017, 21, 133–140. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D. New fractional derivatives with nonlocal and non-singular kernel theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef]
- Esen, A.; Tasbozan, O. Cubic B-spline collocation method for solving time fractional gas dynamics equation. Tbilisi Math. J. 2015, 8, 221–231. [Google Scholar] [CrossRef]
- Singh, J.; Kumar, D.; Baleanu, D.; Rathore, S. On the local fractional wave equation in fractal strings. Math. Meth. Appl. Sci. 2019, 42, 1588–1595. [Google Scholar] [CrossRef]
- Kaya, D.; Gulbahar, S.; Yokus, A. Numerical solutions of the fractional KdV-Burgers-Kuramoto Equation. Therm. Sci. 2018, 22, S153–S158. [Google Scholar] [CrossRef]
- Atangana, A.; Alkahtani, B.T. Analysis of the Keller-Segel model with a fractional derivative without singular kernel. Entropy 2015, 17, 4439–4453. [Google Scholar] [CrossRef]
- Goyal, M.; Baskonus, H.M.; Prakash, A. An efficient technique for a time fractional model of lassa hemorrhagic fever spreading in pregnant women. Eur. Phys. J. Plus 2019, 134, 482. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, J.; Baleanu, D. A new numerical algorithm for fractional Fitzhugh-Nagumo equation arising in transmission of nerve impulses. Nonlinear Dyn. 2018, 91, 307–317. [Google Scholar] [CrossRef]
- Yang, X.J.; Baleanu, D.; Lazarević, M.P.; Cajić, M.S. Fractal boundary value problems for integral and differential equations with local fractional operators. Therm. Sci. 2015, 19, 959–966. [Google Scholar] [CrossRef]
- Atangana, A.; Alkahtani, B.T. Analysis of non- homogenous heat model with new trend of derivative with fractional order. Chaos Solitons Fractals 2016, 89, 566–571. [Google Scholar]
- Yang, X.J. New rheological problems involving general fractional derivatives with nonsingular power-law kernels. Proc. Rom. Acad. Ser. A Math. Phys. Tech. Sci. Inf. Sci. 2018, 19, 45–52. [Google Scholar]
- Yang, X.J.; Gao, F.; Ju, Y.; Zhou, H.W. Fundamental solutions of the general fractional-order diffusion equations. Math. Meth. Appl. Sci. 2018, 41, 9312–9320. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, J.; Al-Qurashi, M.; Baleanu, D. A new fractional SIRS-SI malaria disease model with application of vaccines, anti-malarial drugs, and spraying. Adv. Diff. Equ. 2019, 2019, 278. [Google Scholar] [CrossRef]
- Atangana, A. Fractional discretization: The African’s tortoise walk. Chaos Solitons Fractals 2020, 130, 109399. [Google Scholar] [CrossRef]
- Shah, K.; Khalil, H.; Khan, R.A. Analytical solutions of fractional order diffusion equations by natural transform method. Iran. J. Sci. Technol. Trans. A Sci. 2018, 42, 1479–1490. [Google Scholar] [CrossRef]
- Shah, K.; Junaid, M.; Ali, N. Extraction of Laplace, Sumudu, Fourier and Mellin Transform from the Natural Transform. J. Appl. Environ. Biol. Sci. 2015, 5, 108–115. [Google Scholar]
- Shah, K.; Khan, R.A. The applications of natural transform to the analytical solutions of some fractional order ordinary differential equations. Sindh Univ. Res. J. (Sci. Ser.) 2015, 47, 683–686. [Google Scholar]
- Shah, K.; Jarad, F.; Abdeljawad, T. On a nonlinear fractional order model of dengue fever disease under Caputo-Fabrizio derivative. Alexandria Eng. J. 2020, 1–20. [Google Scholar] [CrossRef]
- Al-Ghafri, K.S.; Rezazadeh, H. Solitons and other solutions of (3+1)-dimensional space–time fractional modified KdV–Zakharov–Kuznetsov equation. Appl. Math. Nonlinear Sci. 2019, 4, 289–304. [Google Scholar] [CrossRef]
- Shah, K.; Alqudah, M.A.; Jarad, F.; Abdeljawad, T. Semi-analytical study of Pine Wilt Disease model with convex rate under Caputo–Fabrizio fractional order derivative. Chaos Solitons Fractals 2020, 135, 109754. [Google Scholar] [CrossRef]
- Khan, A.; Abdeljawad, T.; Gómez-Aguilar, J.F.; Khan, H. Dynamical study of fractional order mutualism parasitism food web module. Chaos SolitonsFractals 2020, 134, 109685. [Google Scholar] [CrossRef]
- Sene, N. Stability analysis of electrical RLC circuit described by the Caputo-Liouville generalized fractional derivative. Alexandria Eng. J. 2020, 1–8. [Google Scholar] [CrossRef]
- Yokus, A.; Gulbahar, S. Numerical solutions with linearization techniques of the fractional Harry Dym equation. Appl. Math. Nonlinear Sci. 2019, 4, 35–42. [Google Scholar]
- Sene, N. Second-grade fluid model with Caputo–Liouville generalized fractional derivative. Chaos Solitons Fractals 2020, 133, 109631. [Google Scholar] [CrossRef]
- Thiao, A.; Sene, N. Fractional optimal economic control problem described by the generalized fractional order derivative. In Proceedings of the International Conference on Computational Mathematics and Engineering Sciences (CMES 2019), Antalya, Turkey, 20–22 April 2019; pp. 36–48. [Google Scholar] [CrossRef]
- Ionescu, C.; Lopes, A.; Copot, D.; Machado, J.A.T.; Bates, J.H.T. The role of fractional calculus in modeling biological phenomena: A review. Commun. Nonlinear Sci. Numer. Simul. 2017, 51, 141–159. [Google Scholar] [CrossRef]
- Qureshi, S. Real life application of Caputo fractional derivative for measles epidemiological autonomous dynamical system. Chaos Solitons Fractals 2020, 134, 109744. [Google Scholar] [CrossRef]
- Khan, M.A.; Atangana, A. Modeling the dynamics of novel coronavirus (2019-nCov) with fractional derivative. Alexandria Eng. J. 2020. [Google Scholar] [CrossRef]
- Bulut, H.; Baskonus, H.M. Regarding on the prototype solutions for the nonlinear fractional-order biological population model. AIP Conf. Proc. 2016, 1738, 290004. [Google Scholar]
- Gao, W.; Veeresha, P.; Prakasha, D.G.; Baskonus, H.M.; Yel, G. New approach for the model describing the deathly disease in pregnant women using Mittag-Leffler function. Chaos Solitons Fractals 2020, 134, 109696. [Google Scholar] [CrossRef]
- Bulut, H.; Kumar, D.; Singh, J.; Swroop, R.; Baskonus, H.M. Analytic study for a fractional model of HIV infection of CD4+TCD4+T lymphocyte cells. Math. Nat. Sci. 2018, 2, 33–43. [Google Scholar] [CrossRef]
- Ilhan, O.A.; Esen, A.; Bulut, H.; Baskonus, H.M. Singular Solitons in the Pseudo-parabolic Model Arising in Nonlinear Surface Waves. Results Phys. 2019, 12, 1712–1715. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, W.; Veeresha, P.; Prakasha, D.G.; Baskonus, H.M. Novel Dynamic Structures of 2019-nCoV with Nonlocal Operator via Powerful Computational Technique. Biology 2020, 9, 107. https://doi.org/10.3390/biology9050107
Gao W, Veeresha P, Prakasha DG, Baskonus HM. Novel Dynamic Structures of 2019-nCoV with Nonlocal Operator via Powerful Computational Technique. Biology. 2020; 9(5):107. https://doi.org/10.3390/biology9050107
Chicago/Turabian StyleGao, Wei, P. Veeresha, D. G. Prakasha, and Haci Mehmet Baskonus. 2020. "Novel Dynamic Structures of 2019-nCoV with Nonlocal Operator via Powerful Computational Technique" Biology 9, no. 5: 107. https://doi.org/10.3390/biology9050107
APA StyleGao, W., Veeresha, P., Prakasha, D. G., & Baskonus, H. M. (2020). Novel Dynamic Structures of 2019-nCoV with Nonlocal Operator via Powerful Computational Technique. Biology, 9(5), 107. https://doi.org/10.3390/biology9050107






