X-ray Diffraction Evidence for Low Force Actin-Attached and Rigor-Like Cross-Bridges in the Contractile Cycle
Abstract
:1. Introduction
2. Material and Methods
2.1. Specimen Preparation and Optimisation
2.1.1. Plaice Fin Muscle Anatomy and Dissection
2.1.2. Optimising the Contractile Response
2.2. Design of a Length Control System for Whole Plaice Fin Muscle
2.2.1. Mounting Muscle Preparations
2.2.2. SL Control System
2.2.3. Use of Two Reflections versus One
2.3. Recording X-ray Diffraction Data
2.4. Analysis of the X-Ray Data
2.4.1. Centring and Alignment
2.4.2. Background Subtraction
2.4.3. Conversion to Reciprocal Space and Peak Fitting
2.5. Equatorial Time-Course Modelling
3. Results
3.1. Recording and Control of Sarcomere Length Changes
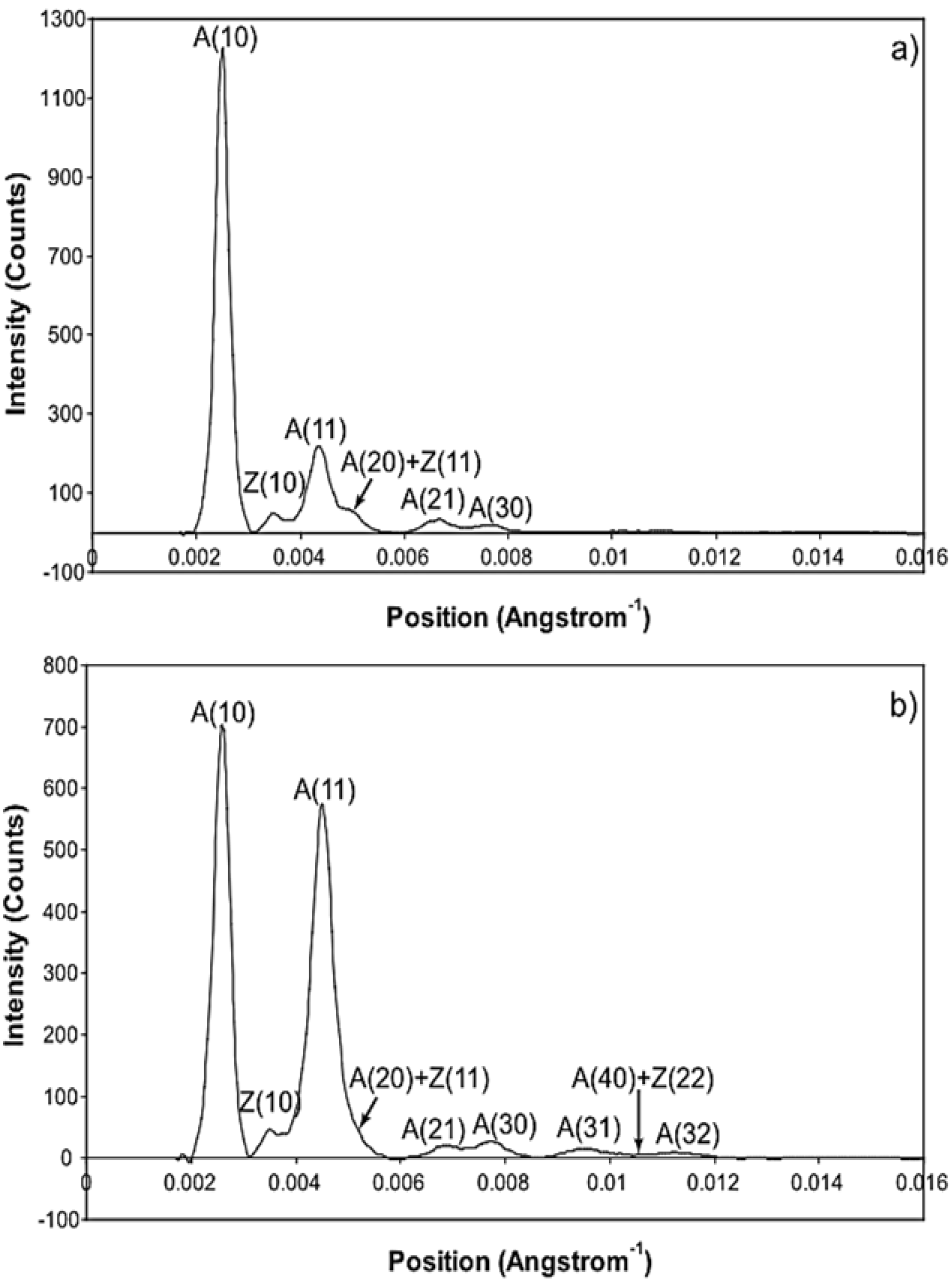
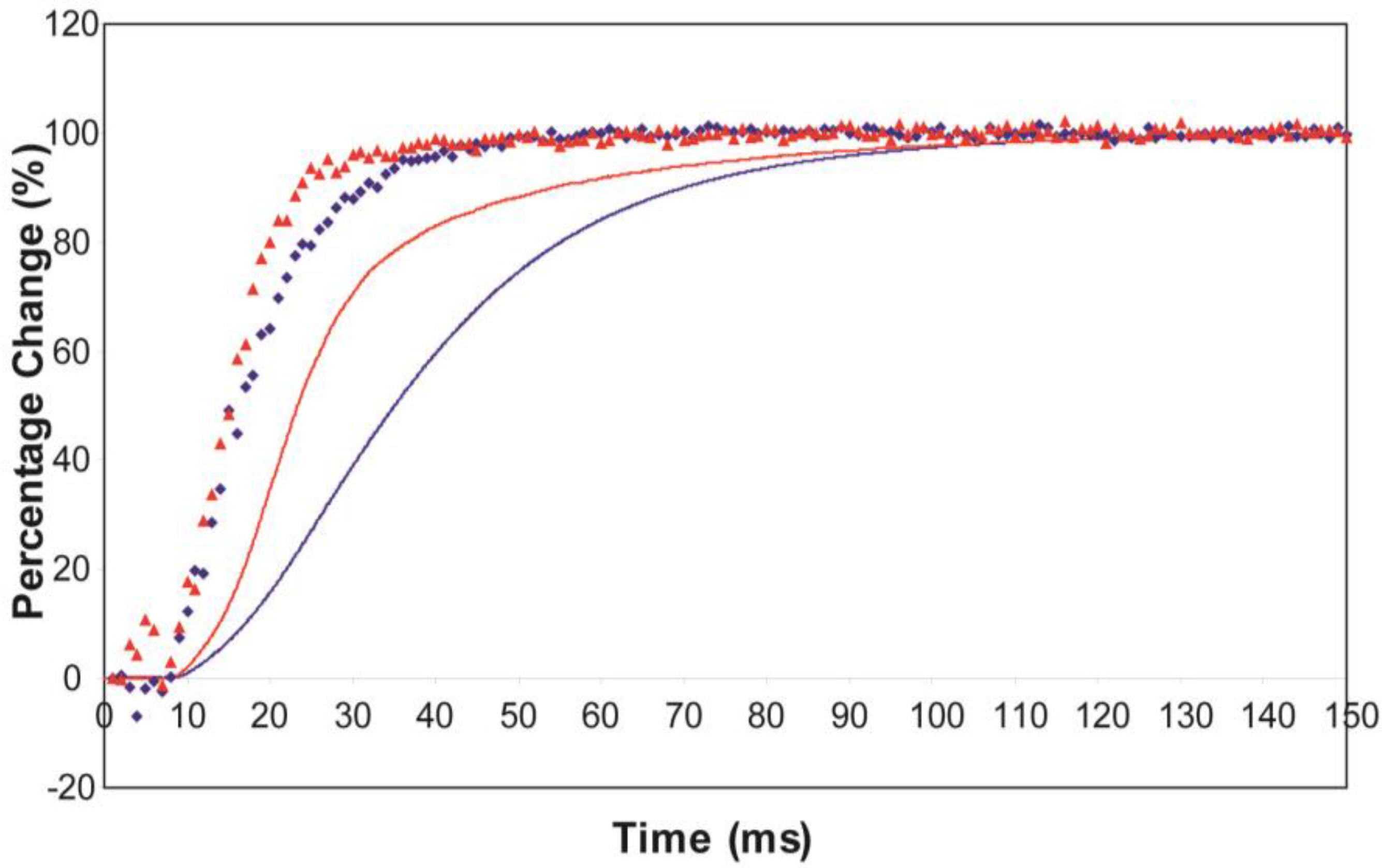
3.2. Equatorial X-Ray Diffraction from Resting and Active Muscle
4. Discussion
4.1. Plaice Fin Muscle Handling and Properties
4.2. Deductions about the Cross-Bridge Mechanism
4.3. Modelling the Equatorial Time-Courses
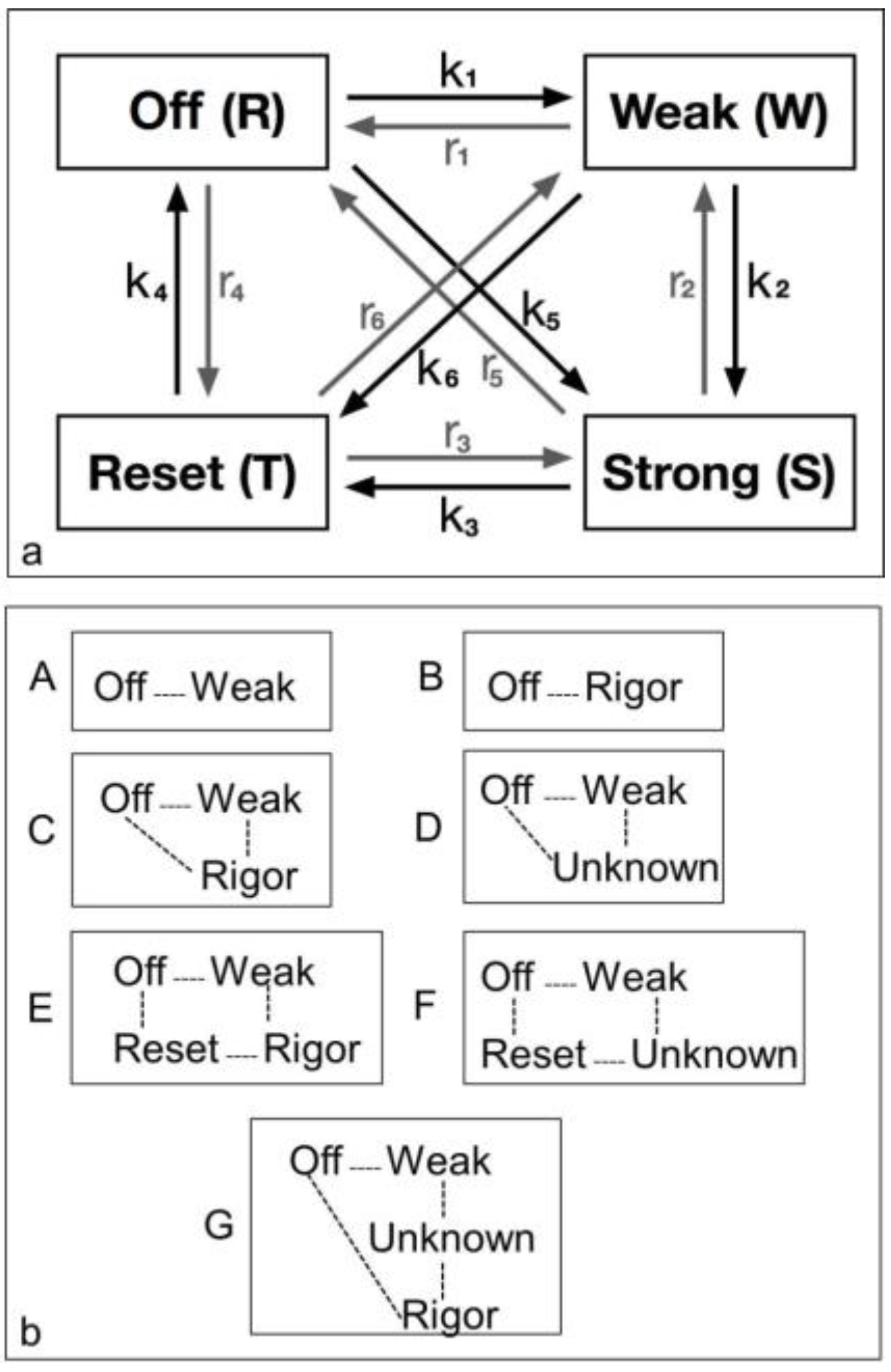
4.3.1. Two-State Models
4.3.2. Three-State Models
4.3.3. Four-State Models
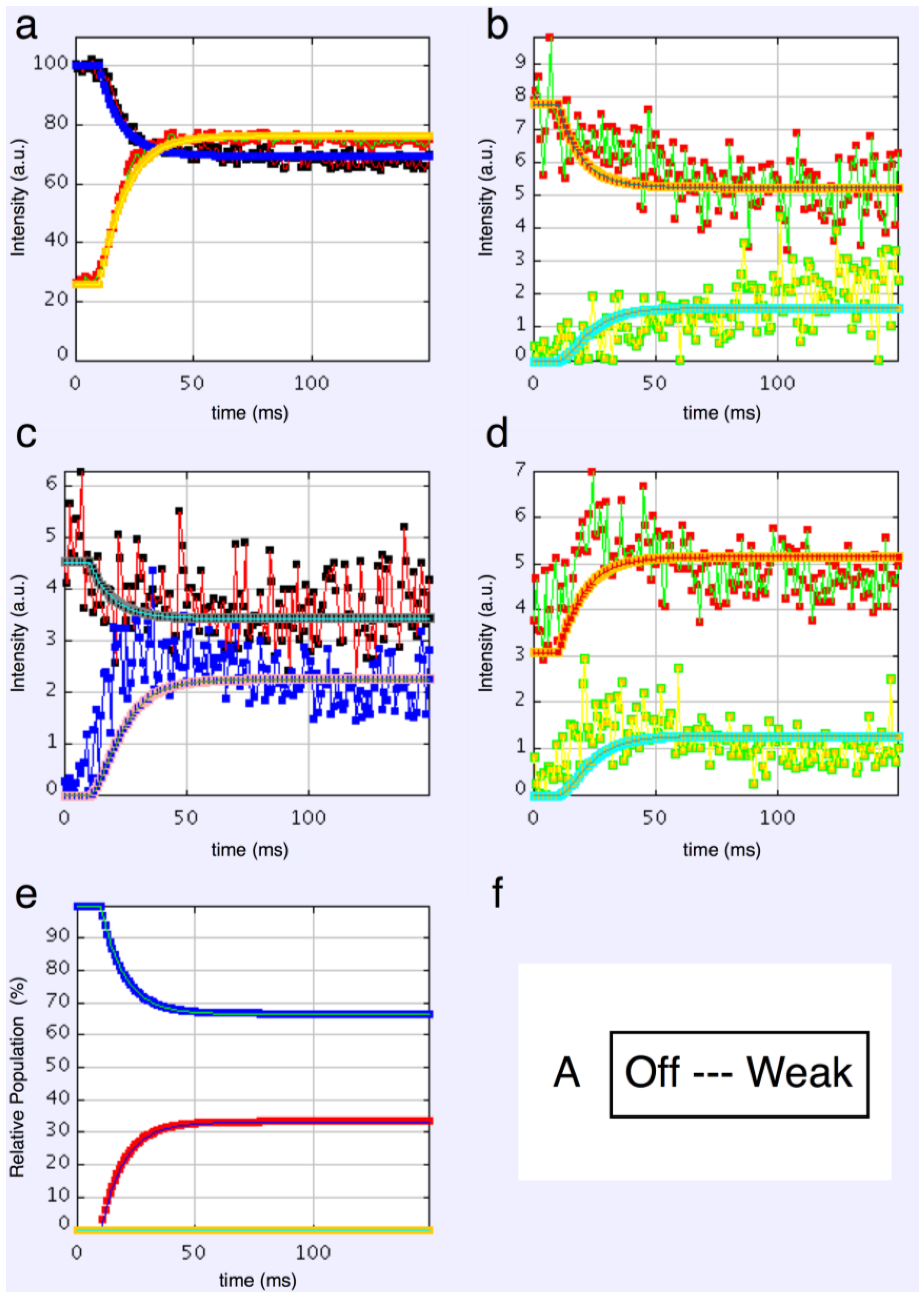
4.3.4. Modelling Summary
- (1)
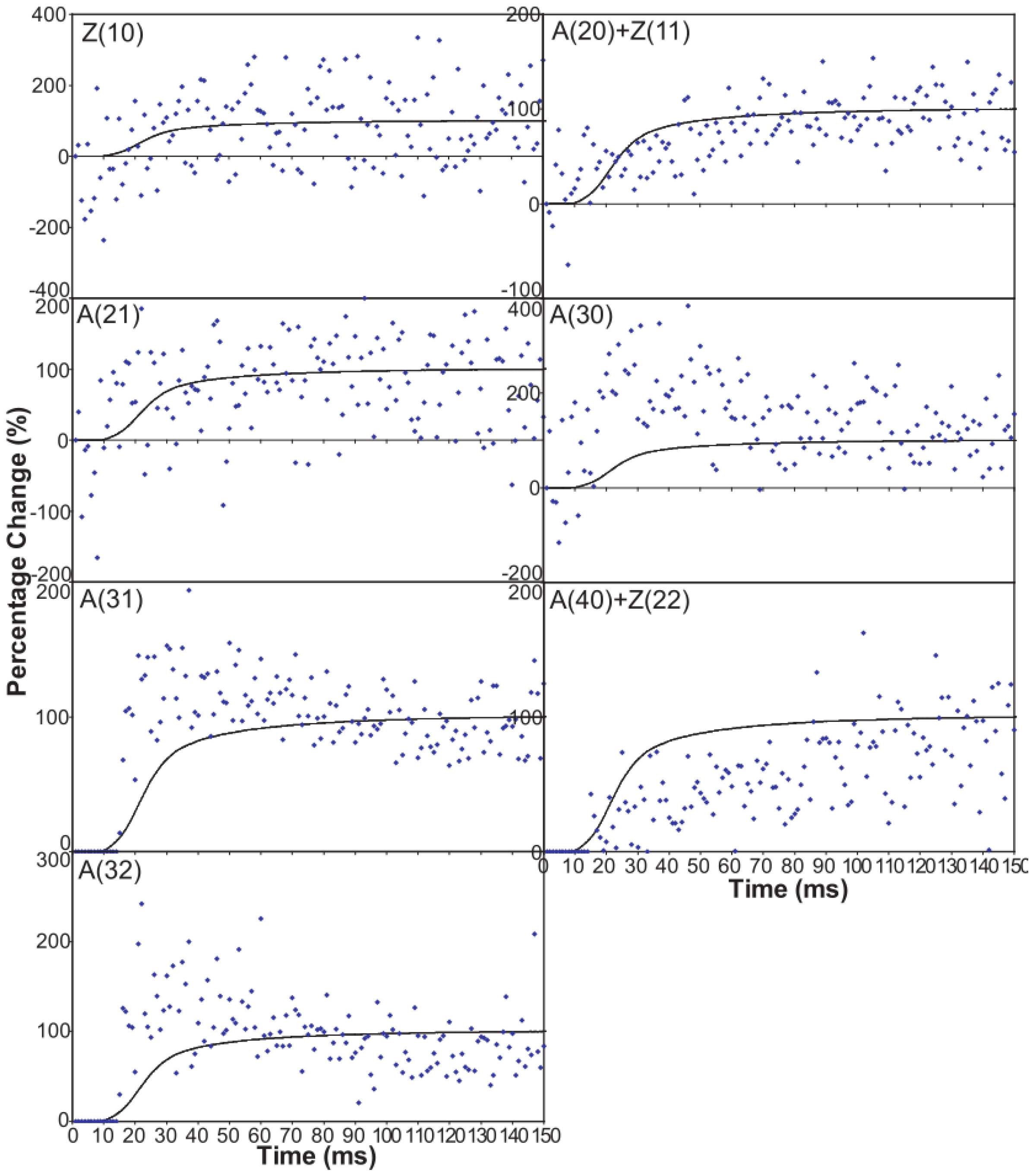
- The observed higher order reflection time-courses can be modelled quite well.
- (2)
- There must be more than two states to explain the observed overshoot of the A(11) and particularly the higher order A(30) and A(31) peaks.
- (3)
- Despite the rapidly increasing number of parameters to fit, there is no compelling reason to go from three to four states. The fit only changes marginally on going from 19 to 28 parameters or 23 to 33 parameters (Table 4), where one might expect a substantially better fit if the extra step is important.
- (4)
- Including rigor as one of the attached states gives as good results as anything else.
- (5)
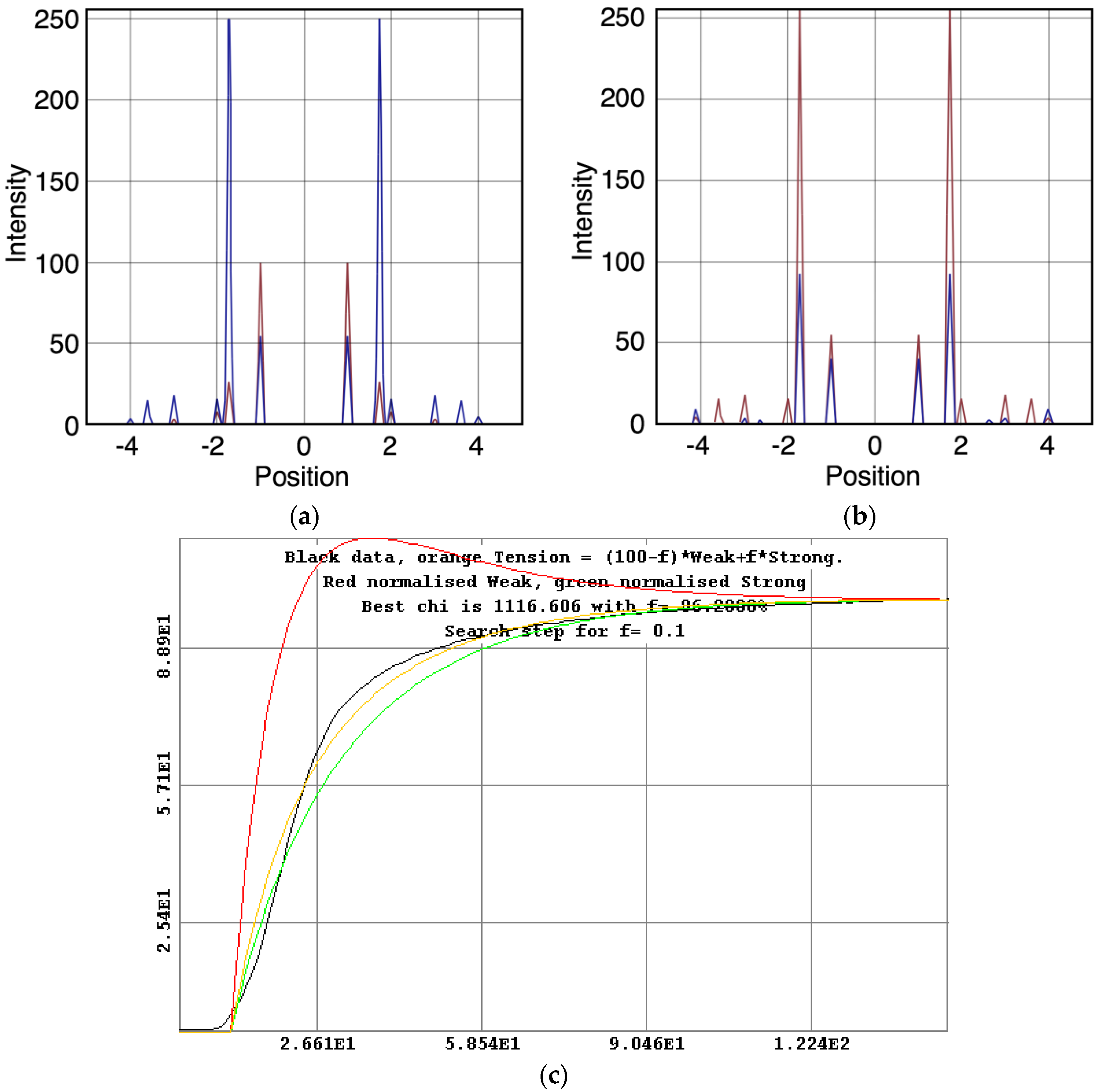
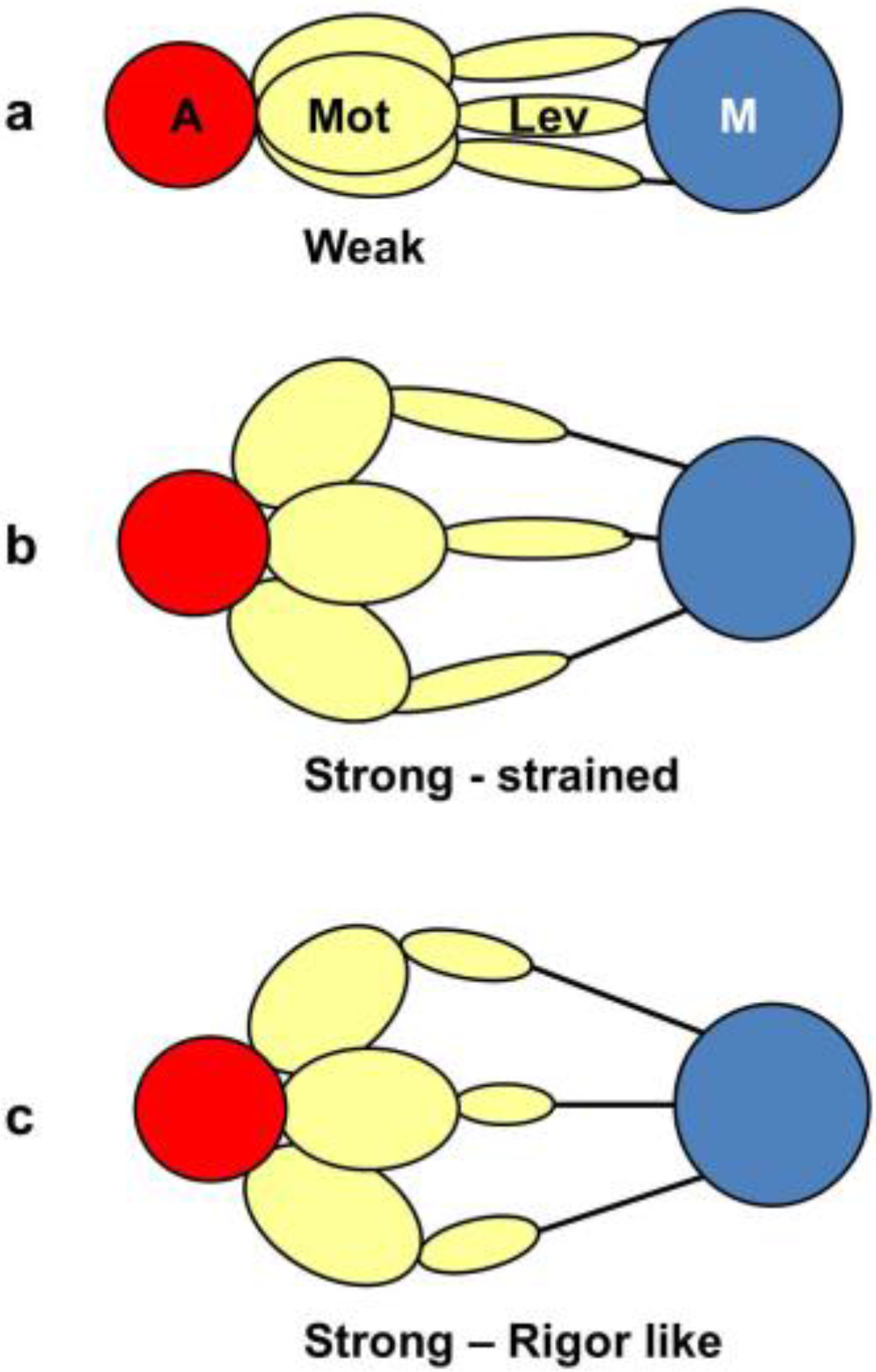
- The “weak” state that needs to be added, whether with 2-, 3- or 4-state models, always has the same sort of transform. The A(11) and other intensities in the rigor pattern are not enough to give the observed overshoots. The weak state (Table 5; Figure 10a,b) has an exceptionally strong A(11) reflection.
4.4. The Weak State
4.5. The Rate Constants
4.6. The Population of States
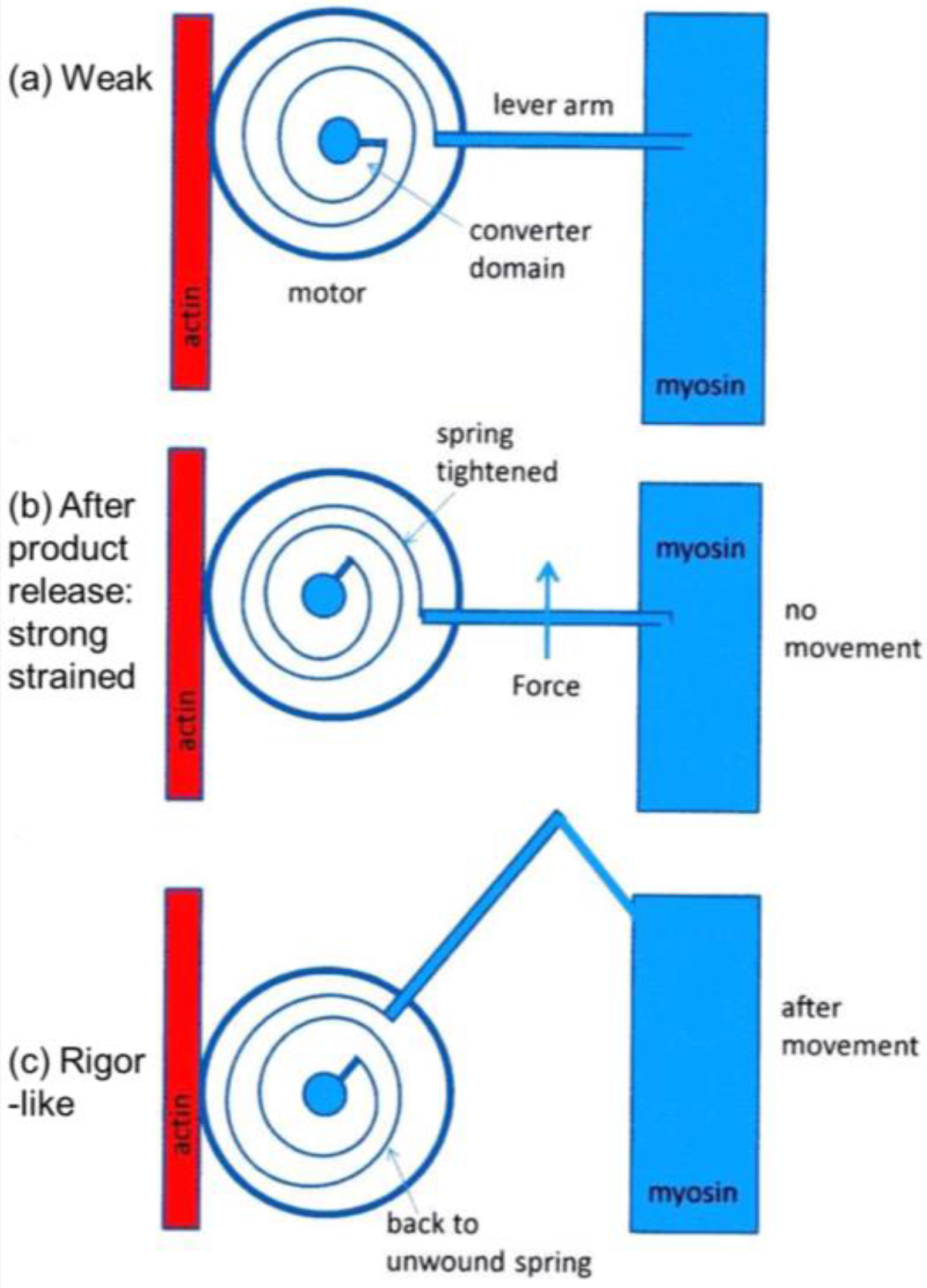
4.7. The Tension Distribution and the Crossbridge Mechanism
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| ADP | Adenosine DiPhosphate |
| ATP | Adenosine TriPhosphate |
| Pi | Inorganic Phosphate |
| 2D | Two-Dimensional |
| SL | Sarcomere Length |
References
- Wulf, S.F.; Ropars, V.; Fujita-Becker, S.; Oster, M.; Hofhaus, G.; Trabuco, L.G.; Pylypenko, O.; Sweeney, H.L.; Houdusse, A.M.; Schröder, R.R. Force-producing ADP state of myosin bound to actin. Proc. Natl. Acad. Sci. USA 2016, 113, E1844–E1852. [Google Scholar] [CrossRef] [PubMed]
- Squire, J.M.; Al-Khayat, H.A.; Knupp, C.; Luther, P.K. Molecular architecture in muscle contractile assemblies. Adv. Protein Chem. 2005, 71, 17–87. [Google Scholar] [PubMed]
- Lymn, R.W.; Taylor, E.W. Mechanism of adenosine triphosphate hydrolysis by actomyosin. Biochemistry 1971, 10, 4617–4624. [Google Scholar] [CrossRef] [PubMed]
- Rayment, I.; Holden, H.M.; Whittaker, M.; Yohn, C.B.; Lorenz, M.; Holmes, K.C.; Milligan, R.A. Structure of the actin-myosin complex and its implications for muscle contraction. Science 1993, 261, 58–65. [Google Scholar] [CrossRef] [PubMed]
- Rayment, I.; Rypniewski, W.R.; Schmidt-Base, K.; Smith, R.; Tomchick, D.R.; Benning, M.M.; Winkelmann, D.A.; Wesenberg, G.; Holden, H.M. Three-dimensional structure of myosin subfragment-1: A molecular motor. Science 1993, 261, 50–58. [Google Scholar] [CrossRef] [PubMed]
- Dominguez, R.; Freyzon, Y.; Trybus, K.M.; Cohen, C. Crystal structure of a vertebrate smooth muscle myosin motor domain and its complex with the essential light chain: Visualization of the pre-powerstroke state. Cell 1998, 94, 559–571. [Google Scholar] [CrossRef]
- Holmes, K.C.; Schröder, R.R.; Sweeney, H.L.; Houdusse, A. The structure of the rigor complex and its implications for the power stroke. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2004, 359, 1819–1828. [Google Scholar] [PubMed]
- Conibear, P.B.; Bagshaw, C.R.; Fajer, P.G.; Kovacs, M.; Malnasi-Csizmadia, A. Myosin cleft movement and its coupling to actomyosin dissociation. Nat. Struct. Biol. 2003, 10, 831–835. [Google Scholar] [CrossRef] [PubMed]
- Goody, R.S. The missing link in the muscle cross-bridge cycle. Nat. Struct. Biol. 2003, 10, 773–775. [Google Scholar] [CrossRef] [PubMed]
- Huxley, H.E.; Brown, W. The low angle X-ray diagram of vertebrate striated muscle and its behaviour during contraction and rigor. J. Mol. Biol. 1967, 30, 383–434. [Google Scholar] [CrossRef]
- Elliott, G.F.; Lowy, J.; Millman, B.M. Low-angle X-ray diffraction studies of living striated muscle during contraction. J. Mol. Biol. 1967, 25, 31–45. [Google Scholar] [CrossRef]
- Haselgrove, J.C.; Stewart, M.; Huxley, H.E. Cross-bridge movement during muscle contraction. Nature 1976, 261, 606–608. [Google Scholar] [CrossRef] [PubMed]
- Huxley, H.E.; Kress, M. Cross-bridge behaviour during muscle contraction. J. Muscle Res. Cell Motil. 1985, 6, 153–161. [Google Scholar] [CrossRef] [PubMed]
- Cecchi, G.; Colomo, F.; Lombardi, V.; Piazzesi, G. Stiffness of frog muscle fibres during rise of tension and relaxation in fixed-end or length-clamped tetani. Pflug. Arch. 1987, 409, 39–46. [Google Scholar] [CrossRef]
- Harford, J.J.; Squire, J.M. Evidence for structurally different attached states of myosin cross-bridges on actin during contraction of fish muscle. Biophys. J. 1992, 63, 387–396. [Google Scholar] [CrossRef]
- Griffths, P.J.; Ashley, C.C.; Bagni, M.A.; Maeda, Y.; Cecchi, G. Cross-bridge attachment and stiffness during isotonic shortening of intact single muscle fibers. Biophys. J. 1993, 64, 1150–1160. [Google Scholar] [CrossRef]
- Bordas, J.; Diakun, G.P.; Diaz, F.G.; Harries, J.E.; Lewis, R.A.; Lowy, J.; Mant, G.R.; Martin-Fernandez, M.L.; Towns-Andrews, E. 2-Dimensional time-resolved X-ray-diffraction studies of live isometrically contracting frog sartorius muscle. J. Muscle Res. Cell Motil. 1993, 14, 311–324. [Google Scholar] [CrossRef] [PubMed]
- Martin-Fernandez, M.L.; Bordas, J.; Diakun, G.; Harries, J.; Lowy, J.; Mant, G.R.; Svensson, A.; Towns-Andrews, E. Time-resolved X-ray diffraction studies of myosin head movements in live frog sartorius muscle during isometric and isotonic contractions. J. Muscle Res. Cell Motil. 1994, 15, 319–348. [Google Scholar] [CrossRef] [PubMed]
- Yagi, N.; Horiuti, K.; Takemori, S. A pre-active attached state of myosin heads in rat skeletal muscles. J. Muscle Res. Cell Motil. 1998, 19, 75–86. [Google Scholar] [PubMed]
- Kraft, T.; Xu, S.; Brenner, B.; Yu, L.C. The effect of thin filament activation on the attachment of weak binding cross-bridges: A two-dimensional X-ray diffraction study on single muscle fibers. Biophys. J. 1999, 76, 1494–1513. [Google Scholar] [CrossRef]
- Hoskins, B.K.; Ashley, C.C.; Rapp, G.; Griffths, P.J. Time-resolved X-ray diffraction by skinned skeletal muscle fibers during activation and shortening. Biophys. J. 2001, 80, 398–414. [Google Scholar] [CrossRef]
- Yagi, N. An X-ray diffraction study on early structural changes in skeletal muscle contraction. Biophys. J. 2003, 84, 1093–1102. [Google Scholar] [CrossRef]
- Squire, J.M. The Structural Basis of Muscular Contraction, 1st ed.; Plenum Press: New York, NY, USA, 1981. [Google Scholar]
- Harford, J.J.; Squire, J.M. Time-resolved diffraction studies of muscle using synchrotron radiation. Rep. Prog. Phys. 1997, 60, 1723–1787. [Google Scholar] [CrossRef]
- Squire, J.M.; Knupp, C. X-ray diffraction studies of muscle and the cross-bridge cycle. Adv. Protein Chem. 2005, 71, 195–255. [Google Scholar]
- Huxley, H.E.; Holmes, K.C. Development of Synchrotron Radiation as a High-Intensity Source for X-ray Diffraction. J. Synchrotron Radiat. 1997, 4, 366–379. [Google Scholar] [CrossRef] [PubMed]
- Irving, M.; Lombardi, V.; Piazzesi, P.; Ferenczi, M.A. Myosin head movements are synchronous with the elementary force-generating process in muscle. Nature 1992, 357, 156–158. [Google Scholar] [CrossRef] [PubMed]
- Lombardi, V.; Piazzesi, G.; Ferenczi, M.A.; Thirlwell, H.; Dobbie, I.; Irving, M. Elastic distortion of myosin heads and repriming of the working stroke in muscle. Nature 1995, 374, 553–555. [Google Scholar] [CrossRef] [PubMed]
- Dobbie, I.; Linari, M.; Piazzesi, G.; Reconditi, M.; Koubassova, N.; Ferenczi, M.A.; Lombardi, V.; Irving, M. Elastic bending and active tilting of myosin heads during muscle contraction. Nature 1998, 396, 383–387. [Google Scholar] [PubMed]
- Linari, M.; Piazzesi, G.; Dobbie, I.; Koubassova, N.; Reconditi, M.; Narayanan, T.; Diat, O.; Irving, M.; Lombardi, V. Interference fine structure and SL dependence of the axial X-ray pattern from active single muscle fibers. Proc. Natl. Acad. Sci. USA 2000, 97, 7226–7231. [Google Scholar] [CrossRef] [PubMed]
- Irving, M.; Piazzesi, G.; Lucii, L.; Sun, Y.B.; Harford, J.J.; Dobbie, I.M.; Ferenczi, M.A.; Reconditi, M.; Lombardi, V. Conformation of the myosin motor during force generation in skeletal muscle. Nat. Struct. Biol. 2000, 7, 482–485. [Google Scholar] [CrossRef] [PubMed]
- Bagni, M.A.; Colombini, B.; Amenitsch, H.; Bernstorff, S.; Ashley, C.C.; Rapp, G.; Griffiths, P.J. Frequency-dependent distortion of meridional intensity changes during sinusoidal length oscillations of activated skeletal muscle. Biophys. J. 2001, 80, 2809–2822. [Google Scholar] [CrossRef]
- Piazzesi, G.; Reconditi, M.; Linari, M.; Lucii, L.; Sun, Y.B.; Narayanan, T.; Boesecke, P.; Lombardi, V.; Irving, M. Mechanism of force generation by myosin heads in skeletal muscle. Nature 2002, 415, 659–662. [Google Scholar] [CrossRef] [PubMed]
- Piazzesi, G.; Reconditi, M.; Koubassova, N.; Decostre, V.; Linari, M.; Lucii, L.; Lombardi, V. Temperature dependence of the force-generating process in single fibres from frog skeletal muscle. J. Physiol. 2003, 549, 93–106. [Google Scholar] [CrossRef] [PubMed]
- Reconditi, M.; Linari, M.; Lucii, L.; Stewart, A.; Sun, Y.; Boesecke, P.; Narayanan, T.; Fischetti, R.F.; Irving, T.; Piazzesi, G.; et al. The myosin motor in muscle generates a smaller and slower working stroke at higher load. Nature 2004, 428, 578–581. [Google Scholar] [CrossRef] [PubMed]
- Ferenczi, M.A.; Bershitsky, S.Y.; Koubassova, N.; Siththanandan, V.B.; Helsby, W.I.; Panine, P.; Roessle, M.; Narayanan, T.; Tsaturyan, A.K. The “roll and lock” mechanism of force generation in muscle. Structure 2005, 13, 131–141. [Google Scholar] [CrossRef] [PubMed]
- Huxley, H.E.; Reconditi, M.; Stewart, A.; Irving, T. X-ray interference studies of cross-bridge action in muscle contraction: Evidence from quick releases. J. Mol. Biol. 2006, 363, 743–761. [Google Scholar] [CrossRef] [PubMed]
- Huxley, H.E.; Reconditi, M.; Stewart, A.; Irving, T. X-ray interference studies of cross-bridge action in muscle contraction: Evidence from muscles during steady shortening. J. Mol. Biol. 2006, 363, 762–772. [Google Scholar] [CrossRef] [PubMed]
- Brunello, E.; Bianco, P.; Piazzesi, G.; Linari, M.; Reconditi, M.; Panine, P.; Narayanan, T.; Helsby, W.I.; Irving, M.; Lombardi, V. Structural changes in the myosin filament and cross-bridges during active force development in single intact frog muscle fibres: Stiffness and X-ray diffraction measurements. J. Physiol. 2006, 577, 971–984. [Google Scholar] [CrossRef] [PubMed]
- Piazzesi, G.; Reconditi, M.; Linari, M.; Lucii, L.; Bianco, P.; Brunello, E.; Decostre, V.; Stewart, A.; Gore, D.B.; Irving, T.C.; et al. Skeletal muscle performance determined by modulation of number of myosin motors rather than motor force or stroke size. Cell 2007, 131, 784–795. [Google Scholar] [CrossRef] [PubMed]
- Knupp, C.; Offer, G.; Ranatunga, K.W.; Squire, J.M. Probing muscle myosin motor action: X-ray (M3 and M6) interference measurements report motor domain not lever arm movement. J. Mol. Biol. 2009, 390, 168–181. [Google Scholar] [CrossRef] [PubMed]
- Reedy, M.K. Ultrastructure of insect flight muscle: I. Screw sense and structural grouping in the rigor cross-bridge lattice. J. Mol. Biol. 1968, 31, 155–176. [Google Scholar] [CrossRef]
- Perz-Edwards, R.J.; Irving, T.C.; Baumann, B.A.J.; Gore, D.; Hutchinson, D.C.; Krzic, U.; Porter, R.L.; Ward, A.B.; Reedy, M.K. X-ray diffraction evidence for myosin-troponin connections and tropomyosin movement during stretch activation of insect flight muscle. Proc. Natl. Acad. Sci. USA 2011, 108, 120–125. [Google Scholar] [CrossRef] [PubMed]
- Harford, J.J.; Squire, J.M. Crystalline myosin cross-bridge array in relaxed bony fish muscle. Low-angle X-ray diffraction from Plaice fin muscle and its interpretation. Biophys. J. 1986, 50, 145–155. [Google Scholar] [CrossRef]
- Luther, P.K.; Squire, J.M.; Forey, P.L. Evolution of myosin filament arrangements in vertebrate skeletal muscle. J. Morphol. 1996, 229, 325–335. [Google Scholar] [CrossRef]
- Luther, P.K.; Squire, J.M. The intriguing dual lattices of the myosin filaments in vertebrate striated muscles: Evolution and advantage. Biology 2014, 3, 846–865. [Google Scholar] [CrossRef] [PubMed]
- Luther, P.K.; Squire, J.M. Three-dimensional structure of the vertebrate muscle A-band. II: The myosin filament superlattice. J. Mol. Biol. 1980, 141, 409–439. [Google Scholar] [CrossRef]
- Luther, P.K.; Munro, P.M.G.; Squire, J.M. Three-dimensional structure of the vertebrate muscle A-band. III: M-region structure and myosin filament symmetry. J. Mol. Biol. 1981, 151, 703–730. [Google Scholar] [CrossRef]
- Luther, P.K.; Munro, P.M.G.; Squire, J.M. Muscle ultrastructure in the teleost fish. Micron 1995, 26, 431–459. [Google Scholar] [CrossRef]
- Squire, J.M.; Harford, J.J. Time-resolved studies of cross-bridge movement: Why use X-rays? Why use fish muscle? In Mechanism of Myofilament Sliding in Muscle Contraction, 1st ed.; Sugi, H., Pollack, G.H., Eds.; Plenum Press: New York, NY, USA, 1993; Volume 332, pp. 435–450. [Google Scholar]
- Harford, J.J.; Squire, J.M. Static and time resolved X-ray diffraction studies of fish muscle. In Molecular Mechanisms in Muscular Contraction, 1st ed.; Squire, J., Ed.; Macmillan Press: London, UK, 1990; pp. 287–320. [Google Scholar]
- Squire, J.M.; Al-Khayat, H.A.; Harford, J.J.; Hudson, L.; Irving, T.C.; Knupp, C.; Mok, N.S.; Reedy, M.K. Myosin filament structure and myosin cross-bridge dynamics in fish and insect muscles. In Molecular and Cellular Aspects of Muscle Contraction, 1st ed.; Sugi, H., Ed.; Kluwer: New York, NY, USA, 2003; Volume 538, pp. 251–266. [Google Scholar]
- Gilly, W.F.; Aladjem, E. Physiological-properties of three muscle-fiber types controlling dorsal fin movements in a flatfish, citharichthys-sordidus. J. Muscle Res. Cell Motil. 1987, 8, 407–417. [Google Scholar] [CrossRef] [PubMed]
- Harford, J.J. Diffraction Analysis of Vertebrate Muscle Cross-bridge Arrangements. Ph.D. Thesis, Imperial College, London, UK, 1984. [Google Scholar]
- Cobb, J.L.S.; Fox, N.C.; Santer, R.M. A specific ringer solution for the Plaice. J. Fish Biol. 1973, 5, 587–591. [Google Scholar] [CrossRef]
- James, R.S.; Johnston, I.A. Influence of spawning on swimming performance and muscle contractile properties in the short-horn sculpin. J. Fish Biol. 1998, 53, 485–501. [Google Scholar] [CrossRef]
- James, R.S.; Cole, N.J.; Davies, M.L.F.; Johnston, I.A. Scaling of intrinsic contractile properties and myofibrillar protein composition of fast muscle in the fish Myoxocephalus scorpius L. J. Exp. Biol. 1998, 201, 901–912. [Google Scholar] [PubMed]
- Hudson, R.C. A Ringer solution for cottus (teleost) fast muscle fibres. Comp. Biochem. Physiol. 1968, 25, 719–725. [Google Scholar] [CrossRef]
- Elliott, G.F.; Lowy, J.; Worthington, C.R. An X-ray and light diffraction study of the filament lattice of striated muscle in the living state and in rigor. J. Mol. Biol. 1963, 6, 295–305. [Google Scholar] [CrossRef]
- Zite-Ferenczy, F.; Rudel, R. A diffractometer using a lateral effect photodiode for the rapid determination of SL changes in cross-striated muscle. Pflug. Arch. 1978, 374, 97–100. [Google Scholar] [CrossRef]
- Zite-Ferenczy, F.; Haberle, K.D.; Rudel, R.; Wilke, W. Correlation between the light diffraction pattern and the structure of a muscle fibre realized with Ewald’s construction. J. Muscle Res. Cell Motil. 1986, 7, 197–214. [Google Scholar] [CrossRef] [PubMed]
- Leung, A.F. Light diffractometry for determining the SL of striated muscle: An evaluation. J. Muscle Res. Cell Motil. 1983, 4, 473–484. [Google Scholar] [CrossRef] [PubMed]
- Ford, L.E.; Huxley, A.F.; Simmons, R.M. Tension responses to sudden length change in stimulated frog muscle fibres near slack length. J. Physiol. 1977, 269, 441–515. [Google Scholar] [CrossRef] [PubMed]
- Brenner, B.; Schoenberg, M.; Chalovich, J.M.; Greene, L.E.; Eisenberg, E. Evidence for cross-bridge attachment in relaxed muscle at low ionic strength. Proc. Natl. Acad. Sci. USA 1982, 79, 7288–7291. [Google Scholar] [CrossRef] [PubMed]
- Lecarpentier, Y.; Martin, J.L.; Claes, V.; Chambaret, J.P.; Migus, A.; Antonetti, A.; Hatt, P.Y. Real-time kinetics of sarcomere relaxation by laser diffraction. Circ. Res. 1985, 56, 331–339. [Google Scholar] [CrossRef] [PubMed]
- Paolini, P.J.; Roos, K.P. Length-dependent optical diffraction pattern changes in frog sartorius muscle. Physiol. Chem. Phys. 1975, 7, 235–254. [Google Scholar] [PubMed]
- Klimov, A.A.; Andreev, O.A. Accuracy of determining SLs in contracted muscle by laser diffraction method. Biofizika 1982, 27, 111–113. [Google Scholar] [PubMed]
- Burton, K.; Zagotta, W.N.; Baskin, R.J. SL behaviour along single frog muscle fibres at different lengths during isometric tetani. J. Muscle Res. Cell Motil. 1989, 10, 67–84. [Google Scholar] [CrossRef] [PubMed]
- Cecchi, G.; Griffths, P.J.; Bagni, M.A.; Ashley, C.C.; Maeda, Y. Time-resolved changes in equatorial X-ray diffraction and stiffness during rise of tetanic tension in intact length-clamped single muscle fibers. Biophys. J. 1991, 59, 1273–1283. [Google Scholar] [CrossRef]
- Lewis, R.A.; Fore, N.S.; Helsby, W.; Hall, C.; Jones, A.; Parker, B.; Sumner, I.; Worgan, J.S.; Budtzjorgensen, C. High counting rate gaseous X-ray-detectors for synchrotron radiation applications. Rev. Sci. Instrum. 1992, 63, 642–647. [Google Scholar] [CrossRef]
- Lewis, R.A.; Helsby, W.I.; Jones, A.O.; Hall, C.J.; Parker, B.; Sheldon, J.; Clifford, P.; Hillen, M.; Sumner, I.; Fore, N.S.; et al. The “rapid” high rate large area X-ray detector system. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 1997, 392, 32–41. [Google Scholar] [CrossRef]
- Rajkumar, G.; Al-Khayat, H.A.; Eakins, F.; He, A.; Knupp, C.; Squire, J.M. Fibrefix—A new integrated CCP13 software package. Fibre Diffr. Rev. 2005, 13, 11–18. [Google Scholar] [CrossRef]
- Rajkumar, G.; Al-Khayat, H.A.; Eakins, F.; Knupp, C.; Squire, J.M. The CCP13 Fibrefix program suite: Semi-automated analysis of diffraction patterns from non-crystalline materials. J. Appl. Crystallogr. 2007, 40, 178–184. [Google Scholar] [CrossRef] [PubMed]
- Ivanova, M.I.; Makowski, L. Iterative low-pass filtering for estimation of the background in fiber diffraction patterns. Acta Crystallogr. A 1998, 54, 626–631. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D., Jr.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Reconditi, M.; Brunello, E.; Linari, M.; Bianco, P.; Narayanan, T.; Panine, P.; Piazzesi, G.; Lombardi, V.; Irving, M. Motion of myosin head domains during activation and force development in skeletal muscle. Proc. Natl. Acad. Sci. USA 2011, 108, 7236–7240. [Google Scholar] [CrossRef] [PubMed]
- Yu, L.C.; Lymn, R.W.; Podolsky, R.J. Characterization of a non-indexible equatorial X-ray reflection from frog sartorius muscle. J. Mol. Biol. 1977, 115, 455–464. [Google Scholar] [CrossRef]
- Harford, J.J.; Luther, P.; Squire, J.M. Equatorial A-band and I-band X-ray-diffraction from relaxed and active fish muscle—Further details of myosin cross-bridge behavior. J. Mol. Biol. 1994, 239, 500–512. [Google Scholar] [CrossRef] [PubMed]
- Huxley, H.E. Structural difference between resting and rigor muscle; evidence from intensity changes in the low angle equatorial X-ray diagram. J. Mol. Biol. 1968, 37, 507–520. [Google Scholar] [CrossRef]
- Harford, J.J.; Chew, M.; Squire, J.M.; Towns-Andrews, E. Cross-bridge states in isometrically contracting fish muscle: Evidence for swinging of myosin heads on actin. Adv. Biophys. 1991, 27, 45–61. [Google Scholar] [CrossRef]
- Kress, M.; Huxley, H.E.; Faruqi, A.R.; Hendrix, J. Structural changes during activation of frog muscle studied by time-resolved X-ray diffraction. J. Mol. Biol. 1986, 188, 325–342. [Google Scholar] [CrossRef]
- Haselgrove, J.C.; Huxley, H.E. X-ray evidence for radial cross-bridge movement and for the sliding filament model in actively contracting skeletal muscle. J. Mol. Biol. 1973, 77, 549–568. [Google Scholar] [CrossRef]
- Yu, L.C.; Podolsky, R.J. Equatorial X-ray diffraction studies of single skinned muscle fibres. In Molecular Mechanisms in Muscular Contraction, 1st ed.; Squire, J., Ed.; Macmillan Press: London, UK, 1990; pp. 265–286. [Google Scholar]
- Malinchik, S.; Yu, L.C. Analysis of equatorial X-ray diffraction patterns from muscle fibers: Factors that affect the intensities. Biophys. J. 1995, 68, 2023–2031. [Google Scholar] [CrossRef]
- Cooke, R.; Franks, K. All myosin heads form bonds with actin in rigor rabbit skeletal muscle. Biochemistry 1980, 19, 2265–2269. [Google Scholar] [CrossRef] [PubMed]
- Lovell, S.J.; Knight, P.J.; Harrington, W.F. Fraction of myosin heads bound to thin filaments in rigor fibrils from insect flight and vertebrate muscles. Nature 1981, 293, 664–666. [Google Scholar] [CrossRef] [PubMed]
- Lymn, R.W. Myosin subfragment-1 attachment to actin. Expected effect on equatorial reflections. Biophys. J. 1978, 21, 93–98. [Google Scholar] [CrossRef]
- Squire, J.M.; Knupp, C. Studies of Muscle Contraction Using X-ray Diffraction. In Muscle Contraction and Cell Motility: Fundamentals and Developments, 1st ed.; Sugi, H., Ed.; Stanford Publishing: London, UK, 2016. [Google Scholar]
- Al-Khayat, H.A.; Kensler, R.W.; Squire, J.M.; Marston, S.B.; Morris, E.P. Atomic model of the human cardiac muscle myosin filament. Proc. Natl. Acad. Sci. USA 2013, 110, 318–323. [Google Scholar] [CrossRef] [PubMed]
- Shoenberg, M. Characterization of the myosin adenosine triphosphate (M-ATP) crossbridge in rabbit and frog skeletal muscle fibers. Biophys. J. 1988, 54, 135–148. [Google Scholar] [CrossRef]
- Wu, S.; Liu, J.; Reedy, M.C.; Tregear, R.T.; Winkler, H.; Franzini-Armstrong, C.; Sasaki, H.; Lucaveche, C.; Goldman, Y.E.; Reedy, M.K.; et al. Electron tomography of cryofixed, isometrically contracting insect flight muscle reveals novel actin-myosin interactions. PLoS ONE 2010, 5, e12643. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, H.; Kobayashi, T.; Amemiya, Y.; Wakabayashi, K. Time-resolved X-ray diffraction studies of frog skeletal muscle isometrically twitched by two successive stimuli using synchrotron radiation. Biophys. Chem. 1986, 25, 161–168. [Google Scholar] [CrossRef]



| Animal and Preparation Type | T (°C) | T1/2 Tension (ms) | T1/2I10 (ms) | T1/2I11 (ms) | Lead over Tension (ms) | Source |
|---|---|---|---|---|---|---|
| Frog | 5–6 | 38 ± 4 | 27 ± 5 | ~10 | Kress et al. [81] | |
| Intact muscle | ||||||
| Frog | 4 | 49.4 ± 11.4 | 33.2 ± 16.6 | 27.6 ± 12.1 | Of I10: 16 | Cecchi et al. [69] |
| Intact fibre, fixed end | Of I11: 22 | |||||
| Frog | 4 | 45.4 ± 16.1 | 27.0 ± 10.7 | 23.4 ± 11.5 | Of I10: 18 | Cecchi et al. [69] |
| Intact fibre, SL clamp | Of I11: 22 | |||||
| Turbot | 5–8 | 41 ± 3 | 35 ± 8 | 21 ± 4 | Of I10: 6 | Harford and Squire [15] |
| Whole muscle, fixed end | Of I11: 20 | |||||
| Plaice | 7–8 | 33.8 ± 0.6 | 25.0 ± 3.4 | 20.5 ± 2.6 | Of I10: 8.8 | Present study |
| Whole muscle, fixed end | Of I11: 13.3 | |||||
| Plaice | 7–8 | 22.5 ± 0.8 | 19.5 ± 2.0 | 17.0 ± 1.1 | Of I10: 3.0 | Present study |
| Whole muscle, SL controlled | Of I11: 5.5 |
| h | k | Cos(2π(h/3 + 2k/3)) | Sin(2π(h/3 + 2k/3) | Cos(2π(2h/3 + k/3)) | Sin(2π(2h/3 + k/3) | Sum of Cos Terms | Sum of Sin Terms | FA Factor |
|---|---|---|---|---|---|---|---|---|
| 1 | 0 | −0.50 | 0.87 | −0.50 | −0.87 | −1.00 | 0.00 | −1.00 |
| 1 | 1 | 1.00 | 0.00 | 1.00 | 0.00 | 2.00 | 0.00 | 2.00 |
| 2 | 0 | −0.50 | −0.87 | −0.50 | 0.87 | −1.00 | 0.00 | −1.00 |
| 2 | 1 | −0.50 | 0.87 | −0.50 | −0.87 | −1.00 | 0.00 | −1.00 |
| 3 | 0 | 1.00 | 0.00 | 1.00 | 0.00 | 2.00 | 0.00 | 2.00 |
| 3 | 1 | −0.50 | −0.87 | −0.50 | 0.87 | −1.00 | 0.00 | −1.00 |
| 4 | 0 | −0.50 | 0.87 | −0.50 | −0.87 | −1.00 | 0.00 | −1.00 |
| 3 | 2 | −0.50 | 0.87 | −0.50 | −0.87 | −1.00 | 0.00 | −1.00 |
| Equatorial Reflection | F(h, k, l) | Estimated Intensity Change | Observed Intensity Change |
|---|---|---|---|
| A(10) | FM − FA | Down | Down |
| A(11) | FM + 2FA | Up | Up |
| A(20) | FM − FA | Down | Down |
| A(21) | FM − FA | Down | Down |
| A(30) | FM + 2FA | Up | Up |
| A(31) | FM − FA | Down | Up |
| A(40) | FM − FA | Down | Up |
| A(32) | FM − FA | Down | Up |
| Model Figure 2b | Model | Parameter No. | Lowest Chi | Delay (ms) | k1 | r1 | k2 | r2 | k3 | r3 | k4 | r4 | k5 | r5 | Populations (%) | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Off | Weak | Strong | Reset | |||||||||||||||
| A | 2-state Free | 11 | 1457 | 10 | 34.0 | 67.9 | 67 | 33 | ||||||||||
| B | 2-state inc Rigor | 8 | 7802 | 19 | 107.0 | 52.7 | 32 | 68 | ||||||||||
| C | 3-state inc Rigor (Rigor20 free) | 19 | 1240 | 10 | 29.7 | 66.3 | 7.5 | 17.2 | 28.2 | 48 | 20 | 32 | ||||||
| D | 3-state Str Free | 23 | 1344 | 9 | 26.2 | 40.7 | 3.5 | 2.4 | 10.4 | 12.6 | 43 | 30 | 27 | |||||
| E | 4-state inc Rigor | 28 | 1270 | 10 | 30.0 | 61.8 | 3.0 | 7.4 | 2.2 | 0.2 | 29.1 | 9.3 | 52 | 24 | 7 | 17 | ||
| F | 4-state Str Free | 33 | 1298 | 9 | 23.6 | 47.9 | 5.3 | 2.4 | 0.4 | 4.0 | 5.0 | 4.7 | 40 | 20 | 20 | 20 | ||
| G | 4-state inc Rigor | 28 | 1220 | 10 | 26.3 | 69.7 | 7.4 | 1.3 | 9.2 | 3.9 | 23.0 | 5.9 | 52 | 19 | 20 | 19 | ||
| State | Model | Reflections | |||||||
|---|---|---|---|---|---|---|---|---|---|
| A(10) | A(11) | A(20) | A(21) | A(30) | A(31) | A(40) | A(32) | ||
| Rest | 10 | 5.1 | 2.79 | 2.13 | 1.76 | 0 | 0 | 0 | |
| Weak | 2-state Free | 5 | 16 | 1.3 | 1.3 | 3.3 | 4.5 | 3.4 | 3.8 |
| 3-state inc Rigor | 7.4 | 16 | 3.9 | 0 | 4.2 | 7.7 | 4.1 | 1.9 | |
| 3-state Free | 6.3 | 16.8 | 2.4 | 2.1 | 5 | 5 | 3 | 1.7 | |
| 4-state inc Rigor (A) | 6.4 | 18.3 | 2.3 | 0.9 | 4.6 | 5 | 1.5 | 2.7 | |
| 4-state inc Rigor (B) | 5 | 19.2 | 0.5 | 1.5 | 4.9 | 7.6 | 5 | 4.6 | |
| 4-state Free | 5 | 19.1 | 2.1 | 0.4 | 4.1 | 5.8 | 4.5 | 2 | |
| Average | 5.85 | 17.57 | 2.08 | 1.03 | 4.35 | 5.93 | 3.58 | 2.78 | |
| SD | 1.01 | 1.49 | 1.15 | 0.76 | 0.63 | 1.39 | 1.25 | 1.18 | |
| Middle | 4-state inc Rigor (B) | 7.8 | 6.8 | 0.0 | 0.0 | 0.10 | 0.20 | 0.60 | 3.70 |
| Strong | 2-state inc Rigor | 6.32 | 9.61 | 4.81 | 2.8 | 1.62 | 1.8 | 1.2 | 1.5 |
| 3-state Free | 7.7 | 5.8 | 1.2 | 1.1 | 0 | 0 | 0.4 | 3.3 | |
| 3-state inc Rigor | 6.32 | 9.61 | 4.81 | 2.8 | 1.62 | 1.1 | 1 | 5 | |
| 4-state Free | 8.1 | 11.4 | 1.3 | 0 | 1.6 | 1.5 | 0 | 1 | |
| 4-state inc Rigor (A) | 6.32 | 9.61 | 4.81 | 2.8 | 1.62 | 2 | 0.9 | 1.9 | |
| 4-state inc Rigor (B) | 6.32 | 9.61 | 4.81 | 2.8 | 1.62 | 0 | 0.4 | 0.5 | |
| Average | 6.85 | 9.27 | 3.62 | 2.05 | 1.35 | 1.07 | 0.65 | 2.20 | |
| SD | 0.83 | 1.85 | 1.84 | 1.21 | 0.66 | 0.88 | 0.45 | 1.67 | |
| Reset | 4-state inc Rigor (A) | 6.2 | 5.1 | 0 | 2.8 | 0 | 0.8 | 4.5 | 2.8 |
| 4-state Free | 8 | 2.5 | 1.8 | 4.7 | 1.4 | 0 | 0 | 4.3 | |
| Average | 7.1 | 3.8 | 0.9 | 3.75 | 0.7 | 0.4 | 2.25 | 3.55 | |
| SD | 1.27 | 1.44 | 0.87 | 1.49 | 0.57 | 0.41 | 2.04 | 1.12 | |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eakins, F.; Pinali, C.; Gleeson, A.; Knupp, C.; Squire, J.M. X-ray Diffraction Evidence for Low Force Actin-Attached and Rigor-Like Cross-Bridges in the Contractile Cycle. Biology 2016, 5, 41. https://doi.org/10.3390/biology5040041
Eakins F, Pinali C, Gleeson A, Knupp C, Squire JM. X-ray Diffraction Evidence for Low Force Actin-Attached and Rigor-Like Cross-Bridges in the Contractile Cycle. Biology. 2016; 5(4):41. https://doi.org/10.3390/biology5040041
Chicago/Turabian StyleEakins, Felicity, Christian Pinali, Anthony Gleeson, Carlo Knupp, and John M. Squire. 2016. "X-ray Diffraction Evidence for Low Force Actin-Attached and Rigor-Like Cross-Bridges in the Contractile Cycle" Biology 5, no. 4: 41. https://doi.org/10.3390/biology5040041
APA StyleEakins, F., Pinali, C., Gleeson, A., Knupp, C., & Squire, J. M. (2016). X-ray Diffraction Evidence for Low Force Actin-Attached and Rigor-Like Cross-Bridges in the Contractile Cycle. Biology, 5(4), 41. https://doi.org/10.3390/biology5040041





