Physics-Informed Neural Network-Based Inverse Framework for Time-Fractional Differential Equations for Rheology
Simple Summary
Abstract
1. Introduction
2. Problem Setup and Methodology
2.1. Fractional Derivatives
2.2. Anomalous Diffusion
2.3. Fractional Viscoelasticity
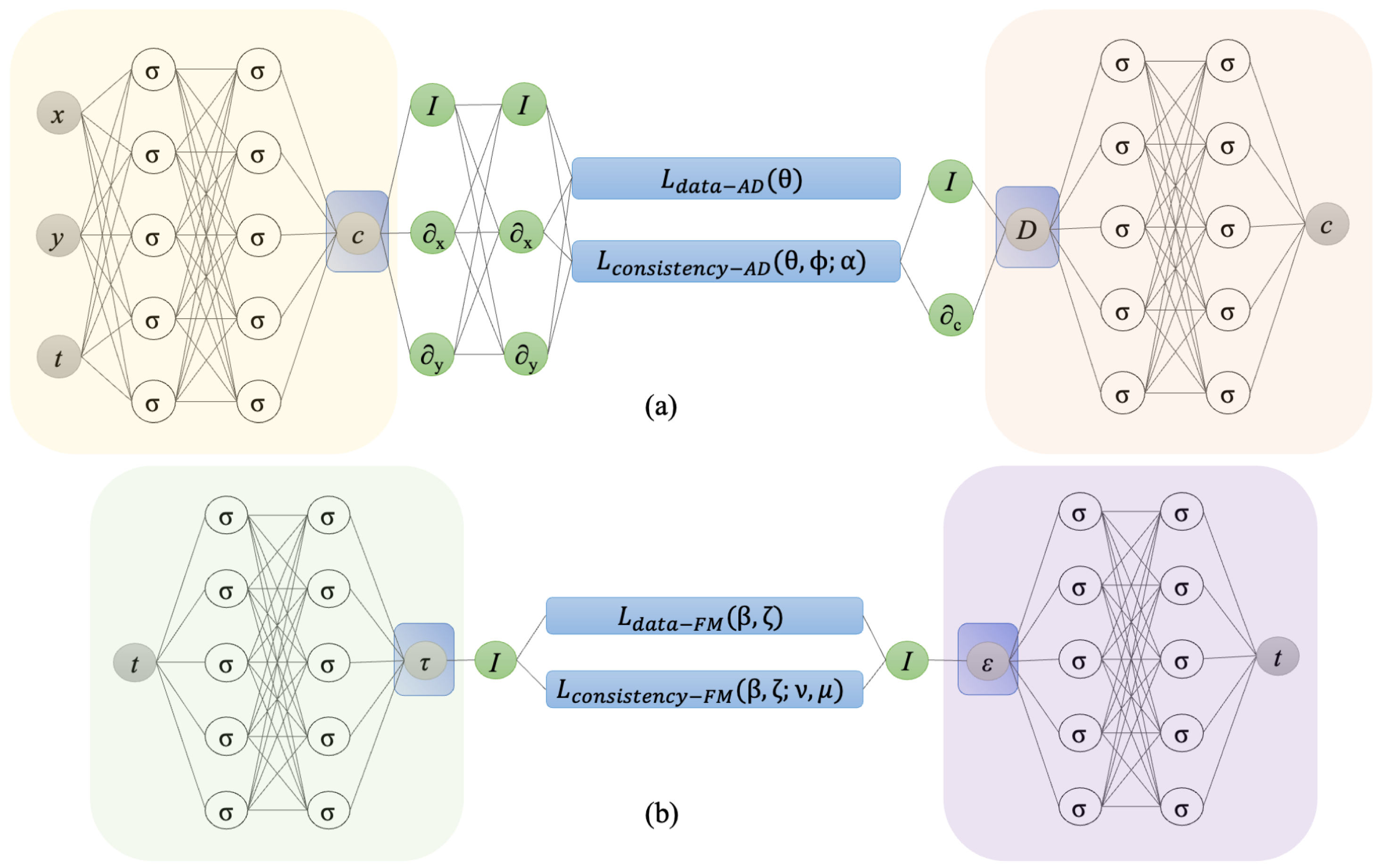
2.4. Physics-Informed Neural Networks
3. Results and Discussion
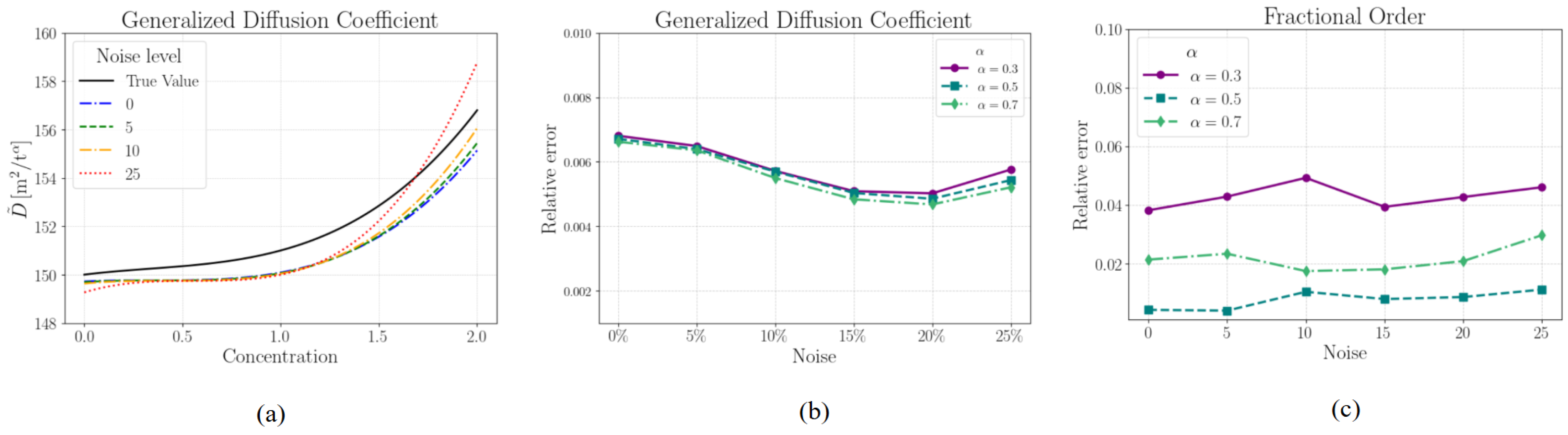
3.1. Numerical Dataset—Anomalous Diffusion
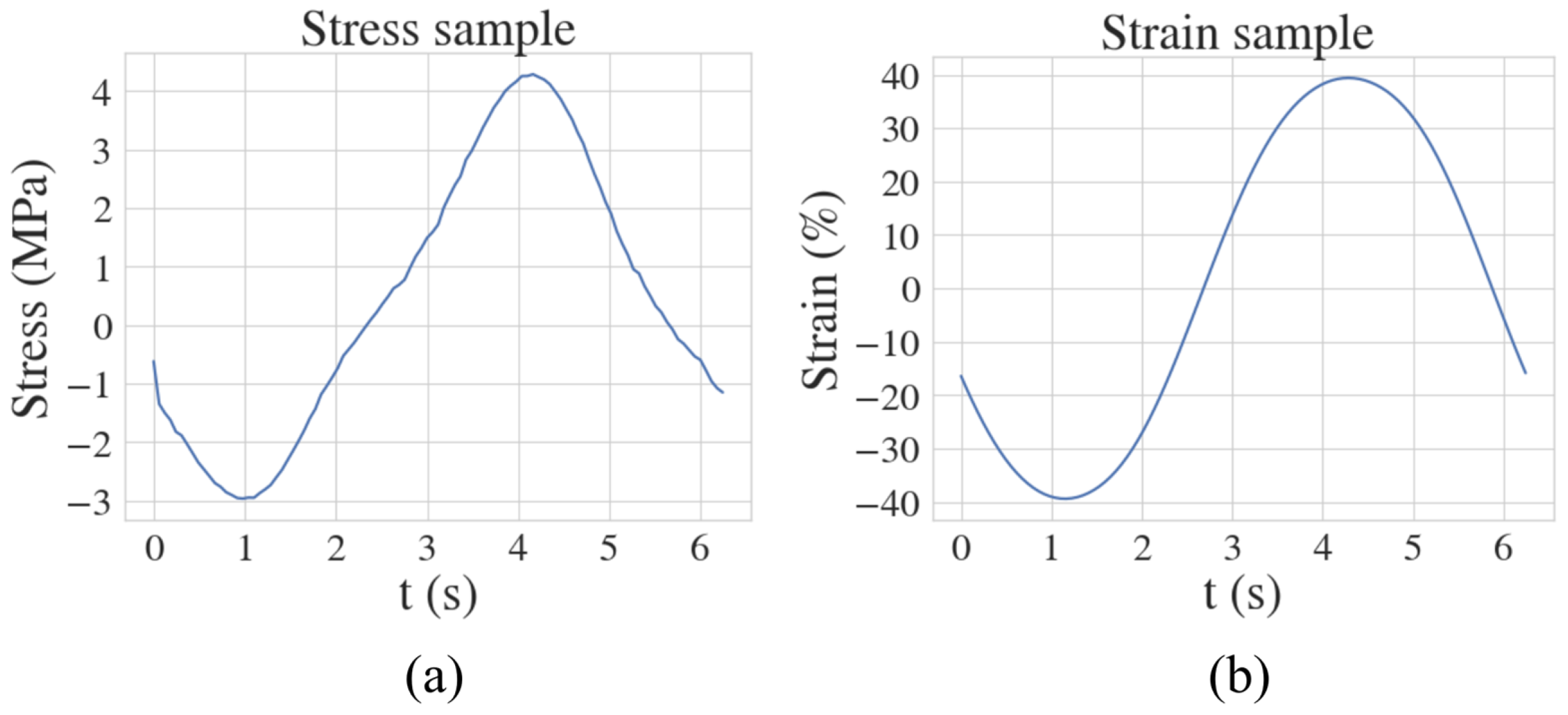
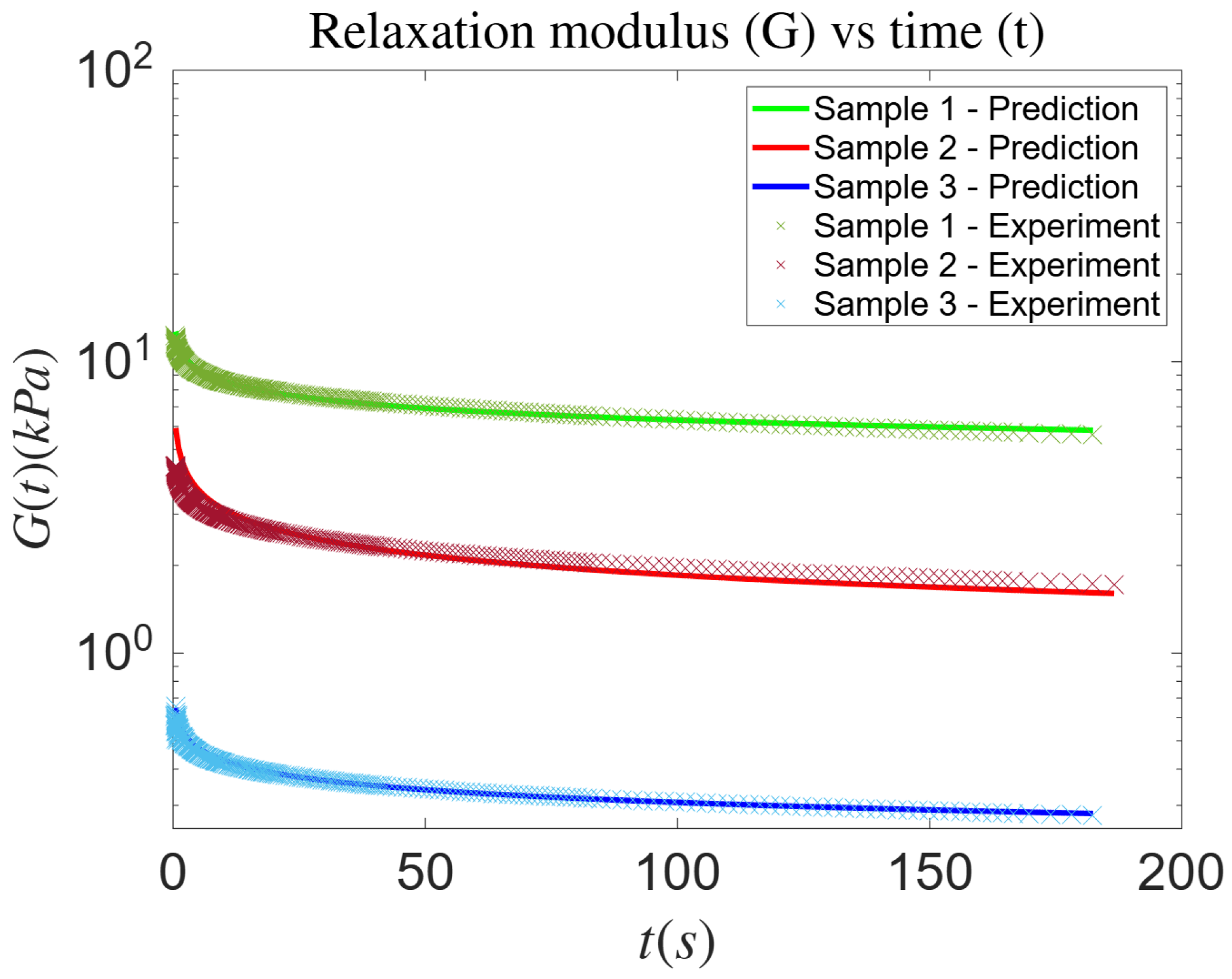
3.2. Experimental Dataset—Fractional Maxwell Model
4. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Engheta, N. On fractional calculus and fractional multipoles in electromagnetism. IEEE Trans. Antennas Propag. 1996, 44, 554–566. [Google Scholar] [CrossRef]
- Mainardi, F. Fractional Viscoelastic Models. In Fractional Calculus and Waves in Linear Viscoelasticity; World Scientific Publishing Europe Ltd.: London, UK, 2010; pp. 57–76. [Google Scholar]
- Bonfanti, A.; Kaplan, J.L.; Charras, G.; Kabla, A. Fractional viscoelastic models for power-law materials. Soft Matter 2020, 16, 6002–6020. [Google Scholar] [CrossRef] [PubMed]
- Odibat, Z.; Momani, S. The variational iteration method: An efficient scheme for handling fractional partial differential equations in fluid mechanics. Comput. Math. Appl. 2009, 58, 2199–2208. [Google Scholar] [CrossRef]
- Stankiewicz, A. Fractional Maxwell model of viscoelastic biological materials. BIO Web Conf. 2018, 10, 02032. [Google Scholar] [CrossRef]
- Jin, B.; Rundell, W. A tutorial on inverse problems for anomalous diffusion processes. Inverse Probl. 2015, 31, 035003. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Mainardi, F. Fractional relaxation-oscillation and fractional diffusion-wave phenomena. Chaos Solitons Fractals 1996, 7, 1461–1477. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional-order systems and PI/sup/spl lambda//D/sup/spl mu//-controllers. IEEE Trans. Autom. Control 1999, 44, 208–214. [Google Scholar] [CrossRef]
- Kilbas, A.; Rivero, M.; Rodriguez-Germa, L.; Trujillo, J. Caputo linear fractional differential equations. IFAC Proc. Vol. 2006, 39, 52–57. [Google Scholar] [CrossRef]
- Scher, H.; Montroll, E.W. Anomalous transit-time dispersion in amorphous solids. Phys. Rev. B 1975, 12, 2455. [Google Scholar] [CrossRef]
- Benson, D.A.; Wheatcraft, S.W.; Meerschaert, M.M. Application of a fractional advection-dispersion equation. Water Resour. Res. 2000, 36, 1403–1412. [Google Scholar] [CrossRef]
- Sokolov, I.M. Models of anomalous diffusion in crowded environments. Soft Matter 2012, 8, 9043–9052. [Google Scholar] [CrossRef]
- Magin, R.; Boregowda, S.; Deodhar, C. Modeling of pulsating peripheral bioheat transfer using fractional calculus and constructal theory. Int. J. Des. Nat. Ecodynamics 2006, 1, 18–33. [Google Scholar]
- Sun, H.; Zhang, Y.; Wei, S.; Zhu, J.; Chen, W. A space fractional constitutive equation model for non-Newtonian fluid flow. Commun. Nonlinear Sci. Numer. Simul. 2018, 62, 409–417. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Cai, S.; Mao, Z.; Wang, Z.; Yin, M.; Karniadakis, G.E. Physics-informed neural networks (PINNs) for fluid mechanics: A review. Acta Mech. Sin. Xuebao 2021, 37, 1727–1738. [Google Scholar] [CrossRef]
- Jin, X.; Cai, S.; Li, H.; Karniadakis, G.E. NSFnets (Navier-Stokes Flow nets): Physics-informed neural networks for the incompressible Navier-Stokes equations. J. Comput. Phys. 2021, 426, 109951. [Google Scholar] [CrossRef]
- Mahmoudabadbozchelou, M.; Karniadakis, G.E.; Jamali, S. nn-PINNs: Non-Newtonian physics-informed neural networks for complex fluid modeling. Soft Matter 2022, 18, 172–185. [Google Scholar] [CrossRef]
- Thakur, S.; Raissi, M.; Ardekani, A.M. ViscoelasticNet: A physics informed neural network framework for stress discovery and model selection. J. Non-Newton. Fluid Mech. 2024, 330, 105265. [Google Scholar] [CrossRef]
- Wang, J.; Peng, X.; Chen, Z.; Zhou, B.; Zhou, Y.; Zhou, N. Surrogate modeling for neutron diffusion problems based on conservative physics-informed neural networks with boundary conditions enforcement. Ann. Nucl. Energy 2022, 176, 109234. [Google Scholar] [CrossRef]
- Thakur, S.; Esmaili, E.; Libring, S.; Solorio, L.; Ardekani, A.M. Inverse resolution of spatially varying diffusion coefficient using Physics-Informed neural networks. Phys. Fluids 2024, 36, 081915. [Google Scholar] [CrossRef]
- Pang, G.; Lu, L.; Karniadakis, G.E. fPINNs: Fractional Physics-Informed Neural Networks. SIAM J. Sci. Comput. 2019, 41, A2603–A2626. [Google Scholar] [CrossRef]
- Mehta, P.P.; Pang, G.; Song, F.; Karniadakis, G.E. Discovering a universal variable-order fractional model for turbulent couette flow using a physics-informed neural network. Fract. Calc. Appl. Anal. 2019, 22, 1675–1688. [Google Scholar] [CrossRef]
- Kharazmi, E.; Cai, M.; Zheng, X.; Zhang, Z.; Lin, G.; Karniadakis, G.E. Identifiability and predictability of integer- and fractional-order epidemiological models using physics-informed neural networks. Nat. Comput. Sci. 2021, 1, 744–753. [Google Scholar] [CrossRef]
- Jin, B.; Lazarov, R.; Zhou, Z. An analysis of the L1 scheme for the subdiffusion equation with nonsmooth data. IMA J. Numer. Anal. 2014, 36, 197–221. [Google Scholar] [CrossRef]
- Lin, Y.; Xu, C. Finite difference/spectral approximations for the time-fractional diffusion equation. J. Comput. Phys. 2007, 225, 1533–1552. [Google Scholar] [CrossRef]
- Ahmadzadegan, A.; Zhang, J.; Ardekani, A.M.; Vlachos, P.P. Spatiotemporal measurement of concentration-dependent diffusion coefficient. Phys. Fluids 2022, 34, 051910. [Google Scholar] [CrossRef]
- Garrappa, R. Numerical evaluation of two and three parameter Mittag-Leffler functions. SIAM J. Numer. Anal. 2015, 53, 1350–1369. [Google Scholar] [CrossRef]
- Thakur, S.; Raissi, M.; Mitra, H.; Ardekani, A.M. Temporal consistency loss for physics-informed neural networks. Phys. Fluids 2024, 36, 077136. [Google Scholar] [CrossRef]
- Loshchilov, I.; Hutter, F. SGDR: Stochastic gradient descent with warm restarts. In Proceedings of the 5th International Conference on Learning Representations, ICLR 2017—Conference Track Proceedings, Toulon, France, 24–26 April 2017; pp. 1–16. [Google Scholar]
- Mitra, H.; Nonamaker, E.; Corder, R.D.; Solorio, L.; Ardekani, A.M. Rheological and lipid characterization of minipig and human skin tissue: A comparative study across different locations and depths. Ann. Biomed. Eng. 2024, 53, 420–440. [Google Scholar] [CrossRef]
| True | Noise | Noise | Noise | Noise | Noise | Noise |
|---|---|---|---|---|---|---|
| Samples | Sample 1 | Sample 2 | Sample 3 |
|---|---|---|---|
| Relative error |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thakur, S.; Mitra, H.; Ardekani, A.M. Physics-Informed Neural Network-Based Inverse Framework for Time-Fractional Differential Equations for Rheology. Biology 2025, 14, 779. https://doi.org/10.3390/biology14070779
Thakur S, Mitra H, Ardekani AM. Physics-Informed Neural Network-Based Inverse Framework for Time-Fractional Differential Equations for Rheology. Biology. 2025; 14(7):779. https://doi.org/10.3390/biology14070779
Chicago/Turabian StyleThakur, Sukirt, Harsa Mitra, and Arezoo M. Ardekani. 2025. "Physics-Informed Neural Network-Based Inverse Framework for Time-Fractional Differential Equations for Rheology" Biology 14, no. 7: 779. https://doi.org/10.3390/biology14070779
APA StyleThakur, S., Mitra, H., & Ardekani, A. M. (2025). Physics-Informed Neural Network-Based Inverse Framework for Time-Fractional Differential Equations for Rheology. Biology, 14(7), 779. https://doi.org/10.3390/biology14070779






