Biology-Informed Matrix Factorization: An AI-Driven Framework for Enhanced Drug Repositioning
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Datasets
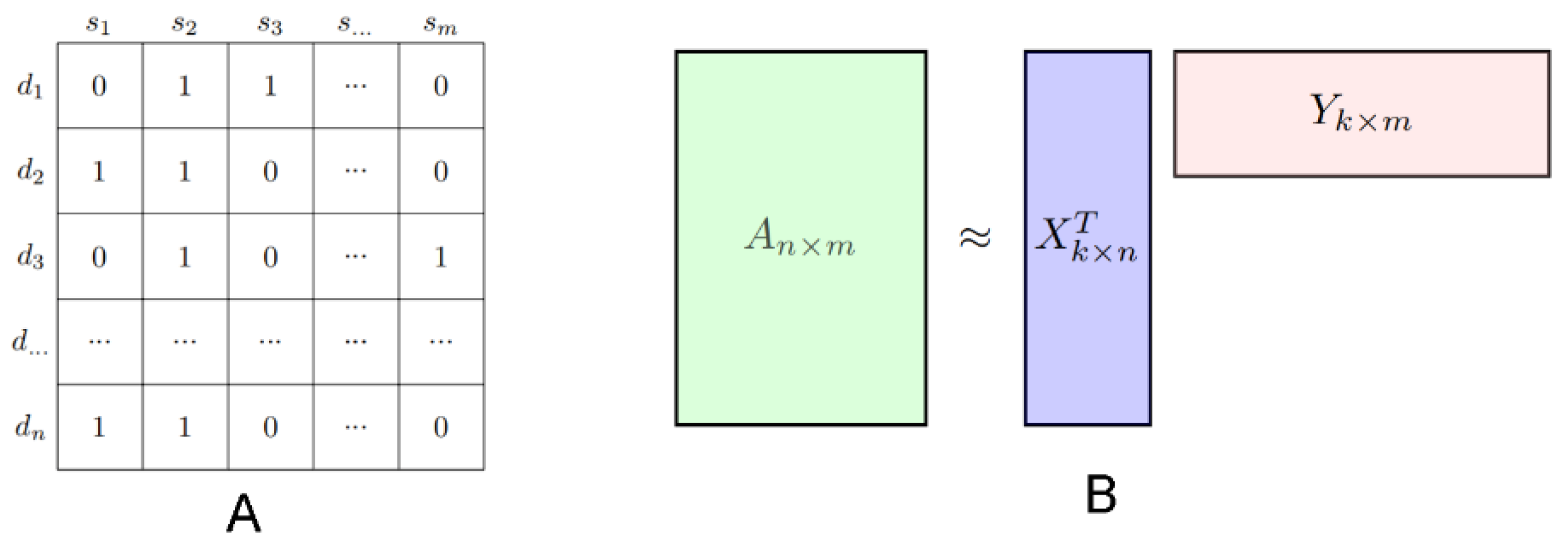
2.2. Standard NMF
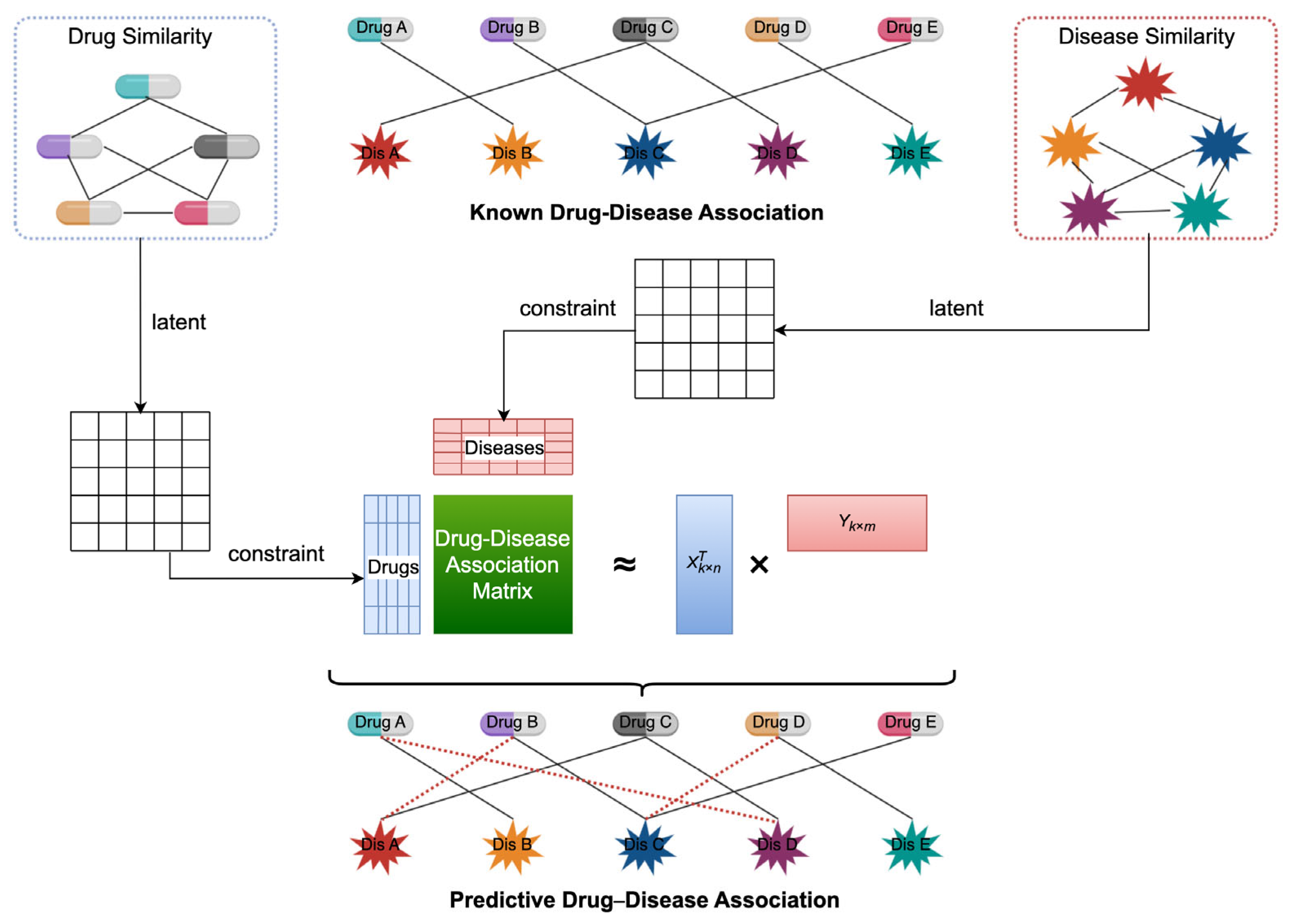
2.3. Proposed Model: NMFIBC
2.4. Optimization Algorithm
| Algorithm 1: Optimization algorithm for NMFIBC | |
| Input:; ; | |
| ; ; | |
| ; . ; ; ; while do ; ; ; end | |
| ; | |
2.5. Evaluation Metrics
3. Results
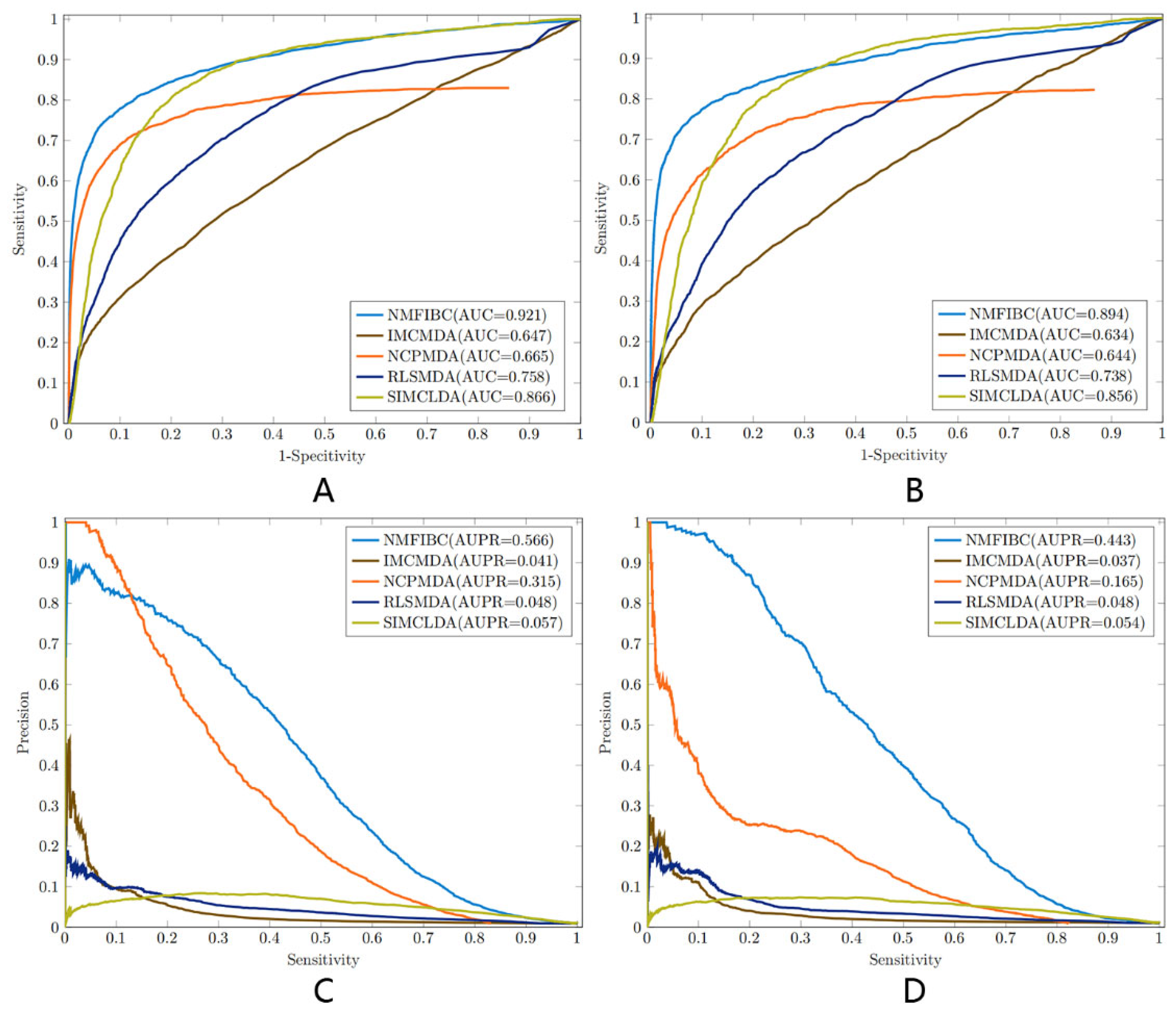
3.1. Performance Evaluation and Metric Analysis
3.2. Case Study Overview
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jourdan, J.-P.; Bureau, R.; Rochais, C.; Dallemagne, P. Drug repositioning: A brief overview. J. Pharm. Pharmacol. 2020, 72, 1145–1151. [Google Scholar] [CrossRef] [PubMed]
- Hua, Y.; Dai, X.; Xu, Y.; Xing, G.; Liu, H.; Lu, T.; Chen, Y.; Zhang, Y. Drug repositioning: Progress and challenges in drug discovery for various diseases. Eur. J. Med. Chem. 2022, 234, 114239. [Google Scholar] [CrossRef]
- Low, Z.Y.; Farouk, I.A.; Lal, S.K. Drug repositioning: New approaches and future prospects for life-debilitating diseases and the COVID-19 pandemic outbreak. Viruses 2020, 12, 1058. [Google Scholar] [CrossRef] [PubMed]
- Jarada, T.N.; Rokne, J.G.; Alhajj, R. A review of computational drug repositioning: Strategies, approaches, opportunities, challenges, and directions. J. Cheminform. 2020, 12, 46. [Google Scholar] [CrossRef]
- Yu, J.-L.; Dai, Q.-Q.; Li, G.-B. Deep learning in target prediction and drug repositioning: Recent advances and challenges. Drug Discov. Today 2022, 27, 1796–1814. [Google Scholar] [CrossRef] [PubMed]
- Sadeghi, S.; Lu, J.; Ngom, A. A network-based drug repurposing method via non-negative matrix factorization. Bioinformatics 2022, 38, 1369–1377. [Google Scholar] [CrossRef]
- Lee, D.D.; Seung, H.S. Learning the parts of objects by non-negative matrix factorization. Nature 1999, 401, 788–791. [Google Scholar] [CrossRef]
- Tang, Y.; Li, G.; Wu, Y.; Yi, D. Identifying potential miRNA-disease associations based on an improved manifold learning framework. IEEE Access 2020, 8, 33263–33275. [Google Scholar] [CrossRef]
- Wang, Y.Y.; Cui, C.; Qi, L.; Yan, H.; Zhao, X.M. DrPOCS: Drug Repositioning Based on Projection onto Convex Sets. IEEE/ACM Trans. Comput. Biol. Bioinform. 2019, 16, 154–162. [Google Scholar] [CrossRef]
- Liu, J.; Zuo, Z.; Wu, G. Link prediction only with interaction data and its application on drug repositioning. IEEE Trans. NanoBioscience 2020, 19, 547–555. [Google Scholar] [CrossRef]
- Luo, J.; Ding, P.; Liang, C.; Cao, B.; Chen, X. Collective prediction of disease-associated miRNAs based on transduction learning. IEEE/ACM Trans. Comput. Biol. Bioinform. 2016, 14, 1468–1475. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, X.; Chen, Y.; Wu, W.; Wang, W.; Li, X. Feature-derived graph regularized matrix factorization for predicting drug side effects. Neurocomputing 2018, 287, 154–162. [Google Scholar] [CrossRef]
- Zhang, W.; Yue, X.; Lin, W.; Wu, W.; Liu, R.; Huang, F.; Liu, F. Predicting drug-disease associations by using similarity constrained matrix factorization. BMC Bioinform. 2018, 19, 233. [Google Scholar] [CrossRef]
- Yang, M.; Luo, H.; Li, Y.; Wang, J. Drug repositioning based on bounded nuclear norm regularization. Bioinformatics 2019, 35, i455–i463. [Google Scholar] [CrossRef] [PubMed]
- Timilsina, M.; Tandan, M.; d’Aquin, M.; Yang, H. Discovering Links Between Side Effects and Drugs Using a Diffusion Based Method. Sci. Rep. 2019, 9, 10436. [Google Scholar] [CrossRef]
- Luo, H.; Wang, J.; Li, M.; Luo, J.; Peng, X.; Wu, F.X.; Pan, Y. Drug repositioning based on comprehensive similarity measures and Bi-Random walk algorithm. Bioinformatics 2016, 32, 2664–2671. [Google Scholar] [CrossRef] [PubMed]
- Gottlieb, A.; Stein, G.Y.; Ruppin, E.; Sharan, R. PREDICT: A method for inferring novel drug indications with application to personalized medicine. Mol. Syst. Biol. 2011, 7, 496. [Google Scholar] [CrossRef]
- Lee, D.; Seung, H.S. Algorithms for non-negative matrix factorization. In Proceedings of the Advances in Neural Information Processing Systems 13 (NIPS 2000), Denver, CO, USA, 1 January 2000. [Google Scholar]
- Guan, N.; Tao, D.; Luo, Z.; Yuan, B. Manifold regularized discriminative nonnegative matrix factorization with fast gradient descent. IEEE Trans. Image Process. 2011, 20, 2030–2048. [Google Scholar] [CrossRef]
- Yuan, L.; Zhu, L.; Guo, W.-L.; Zhou, X.; Zhang, Y.; Huang, Z.; Huang, D.-S. Nonconvex penalty based low-rank representation and sparse regression for eQTL mapping. IEEE/ACM Trans. Comput. Biol. Bioinfor-Matics 2016, 14, 1154–1164. [Google Scholar] [CrossRef]
- Cai, D.; He, X.; Han, J.; Huang, T.S. Graph regularized nonnegative matrix factorization for data representation. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 33, 1548–1560. [Google Scholar]
- Li, X.; Cui, G.; Dong, Y. Graph regularized non-negative low-rank matrix factorization for image clustering. IEEE Trans. Cybern. 2016, 47, 3840–3853. [Google Scholar] [CrossRef]
- Xiao, Q.; Luo, J.; Liang, C.; Cai, J.; Ding, P. A graph regularized non-negative matrix factorization method for identifying microRNA-disease associations. Bioinformatics 2017, 34, 239–248. [Google Scholar] [CrossRef] [PubMed]
- Facchinei, F.; Kanzow, C.; Sagratella, S. Solving quasi-variational inequalities via their KKT conditions. Math. Program. 2014, 144, 369–412. [Google Scholar] [CrossRef]
- Chen, X.; Wang, L.; Qu, J.; Guan, N.N.; Li, J.Q. Predicting miRNA-disease association based on inductive matrix completion. Bioinformatics 2018, 34, 4256–4265. [Google Scholar] [CrossRef] [PubMed]
- Gu, C.; Liao, B.; Li, X.; Li, K. Network Consistency Projection for Human miRNA-Disease Associations Inference. Sci. Rep. 2016, 6, 36054. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Yan, G.Y. Semi-supervised learning for potential human microRNA-disease associations inference. Sci. Rep. 2014, 4, 5501. [Google Scholar] [CrossRef] [PubMed]
- Lu, C.; Yang, M.; Luo, F.; Wu, F.X.; Li, M.; Pan, Y.; Li, Y.; Wang, J. Prediction of lncRNA-disease associations based on inductive matrix completion. Bioinformatics 2018, 34, 3357–3364. [Google Scholar] [CrossRef]
- Newson, J.M.; Santos, C.D.; Walters, B.L.; Todd, B.R. The Case of Flecainide Toxicity: What to Look for and How to Treat. J. Emerg. Med. 2020, 59, e43–e47. [Google Scholar] [CrossRef]
- Araujo, G.; Nascimento, M.; Arruda, P.; Moraes, L.F.; Carvalho, M.D.A.; Medeiros, D.; Sarinho, E. The importance of tacrolimus in the treatment of allergic keratoconjunctivitis. World Allergy Organ. J. 2015, 8 (Suppl. S1), A234. [Google Scholar] [CrossRef]
- Taniguchi, H.; Tokui, K.; Iwata, Y.; Abo, H.; Izumi, S. A case of severe bronchial asthma controlled with tacrolimus. J. Allergy 2011, 2011, 479129. [Google Scholar] [CrossRef]
- Gupta, A.; Dai, Y.; Vethanayagam, R.R.; Hebert, M.F.; Thummel, K.E.; Unadkat, J.D.; Ross, D.D.; Mao, Q. Cyclosporin A, tacrolimus and sirolimus are potent inhibitors of the human breast cancer resistance protein (ABCG2) and reverse resistance to mitoxantrone and topotecan. Cancer Chemother. Pharmacol. 2006, 58, 374–383. [Google Scholar] [CrossRef] [PubMed]
- Nakata, S.; Kakimoto, K.; Numa, K.; Kinoshita, N.; Kawasaki, Y.; Tatsumi, Y.; Tawa, H.; Koshiba, R.; Hirata, Y.; Ota, K.; et al. Risk Factors for Nephrotoxicity due to Tacrolimus Therapy for Ulcerative Colitis. Digestion 2022, 103, 339–346. [Google Scholar] [CrossRef] [PubMed]
- Molloy, S.; McKeith, I.G.; O’Brien, J.T.; Burn, D.J. The role of levodopa in the management of dementia with Lewy bodies. J. Neurol. Neurosurg. Psychiatry 2005, 76, 1200–1203. [Google Scholar] [CrossRef]
- Vaculova, A.; Kaminskyy, V.; Jalalvand, E.; Surova, O.; Zhivotovsky, B. Doxorubicin and etoposide sensitize small cell lung carcinoma cells expressing caspase-8 to TRAIL. Mol. Cancer 2010, 9, 87. [Google Scholar] [CrossRef] [PubMed]
- Manchun, S.; Dass, C.R.; Cheewatanakornkool, K.; Sriamornsak, P. Enhanced anti-tumor effect of pH-responsive dextrin nanogels delivering doxorubicin on colorectal cancer. Carbohydr. Polym. 2015, 126, 222–230. [Google Scholar] [CrossRef]
- Habas, K.; Anderson, D.; Brinkworth, M.H. Germ cell responses to doxorubicin exposure in vitro. Toxicol. Lett. 2017, 265, 70–76. [Google Scholar] [CrossRef] [PubMed]
- Dai, S.; Ye, Z.; Wang, F.; Yan, F.; Wang, L.; Fang, J.; Wang, Z.; Fu, Z. Doxorubicin-loaded poly(ε-caprolactone)-Pluronic micelle for targeted therapy of esophageal cancer. J. Cell. Biochem. 2018, 119, 9017–9027. [Google Scholar] [CrossRef]
- Evidente, V.G.H.; Adler, C.H.; Caviness, J.N.; Hentz, J.G.; Gwinn-Hardy, K. Amantadine is beneficial in restless legs syndrome. Mov. Disord. 2000, 15, 324–327. [Google Scholar] [CrossRef]
- Andrikopoulos, G.K.; Pastromas, S.; Tzeis, S. Flecainide: Current status and perspectives in arrhythmia management. World J. Cardiol. 2015, 7, 76–85. [Google Scholar] [CrossRef]
- Canzanello, V.J.; Textor, S.C.; Taler, S.J.; Schwartz, L.L.; Porayko, M.K.; Wiesner, R.H.; Krom, R.A. Late hypertension after liver transplantation: A comparison of cyclosporine and tacrolimus (FK 506). Liver Transplant. Surg. 1998, 4, 328–334. [Google Scholar] [CrossRef]
- Wishart, D.S.; Feunang, Y.D.; Guo, A.C.; Lo, E.J.; Marcu, A.; Grant, J.R.; Sajed, T.; Johnson, D.; Li, C.; Sayeeda, Z.; et al. DrugBank 5.0: A major update to the DrugBank database for 2018. Nucleic Acids Res. 2018, 46, 1074–1082. [Google Scholar] [CrossRef] [PubMed]
- Davis, A.P.; Wiegers, T.C.; Johnson, R.J.; Sciaky, D.; Wiegers, J.; Mattingly, C.J. Comparative Toxicogenomics Database (CTD): Update 2023. Nucleic Acids Res. 2023, 51, D1257–D1262. [Google Scholar] [CrossRef] [PubMed]
- Kanehisa, M.; Goto, S.; Sato, Y.; Kawashima, M.; Furumichi, M.; Tanabe, M. Data, information, knowledge and principle: Back to metabolism in KEGG. Nucleic Acids Res. 2014, 42, D199–D205. [Google Scholar] [CrossRef]

| Dataset | Drug Similarity Matrix | Disease Similarity Matrix | Known Associations |
|---|---|---|---|
| Cdataset | 663 × 663 | 409 × 409 | 409 × 663 |
| Fdataset | 593 × 593 | 313 × 313 | 313 × 593 |
| AUC | AUPR | Acc | Sen (Recall) | Spe | Pre | F1 | |
|---|---|---|---|---|---|---|---|
| NMFIBC | 0.921 | 0.566 | 0.993 | 0.504 | 0.997 | 0.633 | 0.561 |
| IMCMDA | 0.647 | 0.041 | 0.979 | 0.129 | 0.988 | 0.090 | 0.106 |
| NCPMDA | 0.665 | 0.315 | 0.989 | 0.333 | 0.995 | 0.395 | 0.362 |
| RLSMDA | 0.758 | 0.048 | 0.979 | 0.149 | 0.987 | 0.096 | 0.116 |
| SIMCLDA | 0.866 | 0.057 | 0.954 | 0.392 | 0.959 | 0.083 | 0.136 |
| AUC | AUPR | Acc | Sen (Recall) | Spe | Pre | F1 | |
|---|---|---|---|---|---|---|---|
| NMFIBC | 0.894 | 0.443 | 0.990 | 0.430 | 0.996 | 0.501 | 0.463 |
| IMCMDA | 0.634 | 0.037 | 0.982 | 0.100 | 0.992 | 0.111 | 0.105 |
| NCPMDA | 0.644 | 0.165 | 0.981 | 0.343 | 0.988 | 0.224 | 0.271 |
| RLSMDA | 0.738 | 0.048 | 0.982 | 0.121 | 0.991 | 0.121 | 0.121 |
| SIMCLDA | 0.856 | 0.054 | 0.941 | 0.408 | 0.946 | 0.074 | 0.125 |
| Drugs | Diseases (Existing Relations in Original Matrix) | Top Five Predicted Candidate Diseases (No Relation in Original Matrix) | Weight | Evidence |
|---|---|---|---|---|
| Levodopa (DB01235) | Paralysis agitans (168100) Parkinson disease (168600) Parkinson disease 2 (600116) Parkinson disease 7 (606324) Parkinson disease 15 (260300) | Dementia (125320) | 0.761 | DB/KEGG |
| Alzheimer disease 9 (608907) | 0.571 | DB/KEGG | ||
| Alzheimer disease (605055) | 0.568 | DB/KEGG | ||
| Alzheimer disease 2 (104310) | 0.560 | DB/KEGG | ||
| Alzheimer disease 5 (602096) | 0.536 | DB/KEGG | ||
| Doxorubicin (DB00997) | Mismatch repair cancer syndrome 1 (276300) Breast cancer (114480) Lymphoblastic leukemia (247640) Leukemia (601626) Lymphoma (236000) | Renal cell carcinoma (144700) | 0.734 | DB/KEGG |
| Testicular germ cell tumor (273300) | 0.692 | DB | ||
| Small cell cancer of the lung (182280) | 0.654 | DB | ||
| Leukemia (246470) | 0.651 | KEGG | ||
| Dohle bodies and leukemia (223350) | 0.649 | KEGG | ||
| Amantadine (DB00915) | Paralysis agitans (168100) Multiple sclerosis (126200) Popliteal pterygium syndrome (119500) | Parkinson’s disease 7 (606324) | 0.337 | DB/KEGG/CTD |
| Parkinson’s disease 15 (260300) | 0.325 | DB/KEGG/CTD | ||
| Schizophrenia (181500) | 0.322 | DB/KEGG | ||
| Parkinson’s disease (168600) | 0.318 | DB/KEGG/CTD | ||
| Parkinson’s disease 2 (600116) | 0.318 | DB/KEGG/CTD | ||
| Flecainide (DB01195) | Atrial fibrillation (607554) | Hypertension (608622) | 0.688 | [29] |
| Renal failure (161900) | 0.672 | [29] | ||
| Insensitivity to pain with hyperplastic Myelinopathy (147530) | 0.520 | Unknown | ||
| Raynaud disease (179600) | 0.413 | Unknown | ||
| Atrial fibrillation (608583) | 0.404 | DB/KEGG/CTD | ||
| Tacrolimus (DB00864) | Dermatitis (603165) Dermatitis (605805) Dermatitis (605804) Dermatitis (605844) | Allergic rhinitis (607154) | 0.625 | [30] |
| Asthma (208550) | 0.462 | [31] | ||
| Asthma (600807) | 0.438 | [31] | ||
| Breast cancer (114480) | 0.424 | [32] | ||
| Renal failure (161900) | 0.396 | [33] |
| Drugs | Diseases (Existing Relations in Original Matrix) | Top Five Predicted Candidate Diseases (No Relation in Original Matrix) | Weight | Evidence |
|---|---|---|---|---|
| Levodopa (DB01235) | Paralysis agitans (168100) Restless legs syndrome (102300) | Parkinson’s disease (168600) | 0.548 | DB/KEGG/CTD |
| Insensitivity to pain with hyperplastic Myelinopathy (147530) | 0.531 | Unknown | ||
| Dementia (125320) | 0.451 | DB/KEGG, [34] | ||
| Renal failure (161900) | 0.422 | Unknown | ||
| Attention deficit hyperactivity disorder (143465) | 0.382 | Unknown | ||
| Doxorubicin (DB00997) | Myeloma (254500) Breast cancer (114480) Neuroblastoma (256700) Leukemia (601626) Lymphoma (236000) | Small cell cancer of the lung (182280) | 0.577 | [35] |
| Colorectal cancer (114500) | 0.573 | [36] | ||
| Testicular germ cell tumor (273300) | 0.530 | [37] | ||
| Kaposi sarcoma (148000) | 0.518 | DB/KEGG | ||
| Esophageal cancer (133239) | 0.513 | [38] | ||
| Amantadine (DB00915) | Paralysis agitans (168100) Multiple sclerosis (126200) Popliteal pterygium syndrome (119500) | Dementia (125320) | 0.365 | DB/KEGG/CTD |
| Parkinson’s disease (168600) | 0.363 | DB/KEGG/CTD | ||
| Restless legs syndrome (102300) | 0.295 | [39] | ||
| Alzheimer’s disease (104300) | 0.227 | DB/KEGG/CTD | ||
| Alzheimer disease (605055) | 0.216 | DB/KEGG/CTD | ||
| Flecainide (DB01195) | Atrial fibrillation (607554) | Hypertension (608622) | 0.597 | [29] |
| Renal failure (161900) | 0.560 | [29] | ||
| Atrial fibrillation (608583) | 0.524 | DB/CTD, [29] | ||
| Insensitivity to pain with hyperplastic Myelinopathy (147530) | 0.463 | Unknown | ||
| Stroke (601367) | 0.335 | [40] | ||
| Tacrolimus (DB00864) | Dermatitis (603165) | Renal failure (161900) | 0.582 | [33] |
| Hypertension (608622) | 0.490 | [41] | ||
| Asthma (208550) | 0.381 | [31] | ||
| Insensitivity to pain with hyperplastic Myelinopathy (147530) | 0.376 | Unknown | ||
| Hypoparathyroidism (146255) | 0.374 | Unknown |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Wang, Y.; Hu, Y.; Wang, J. Biology-Informed Matrix Factorization: An AI-Driven Framework for Enhanced Drug Repositioning. Biology 2025, 14, 549. https://doi.org/10.3390/biology14050549
Wang Y, Wang Y, Hu Y, Wang J. Biology-Informed Matrix Factorization: An AI-Driven Framework for Enhanced Drug Repositioning. Biology. 2025; 14(5):549. https://doi.org/10.3390/biology14050549
Chicago/Turabian StyleWang, Yangyang, Yaping Wang, Ya Hu, and Jihan Wang. 2025. "Biology-Informed Matrix Factorization: An AI-Driven Framework for Enhanced Drug Repositioning" Biology 14, no. 5: 549. https://doi.org/10.3390/biology14050549
APA StyleWang, Y., Wang, Y., Hu, Y., & Wang, J. (2025). Biology-Informed Matrix Factorization: An AI-Driven Framework for Enhanced Drug Repositioning. Biology, 14(5), 549. https://doi.org/10.3390/biology14050549







