A Novel Ensemble Learning-Based Computational Method to Predict Protein-Protein Interactions from Protein Primary Sequences
Abstract
Simple Summary
Abstract
1. Introduction
2. Materials and Methodology
2.1. Protein Interaction Dataset
2.2. Encoding Amino Acid Sequence as Date Matrix
2.3. Discrete Hilbert Transform
2.4. Ensemble-Learning-Based Classifier
3. Results
3.1. Evaluation Measures
3.2. Prediction Performance on Three PPIs Datasets
3.3. Compared with Different Classifier Models
3.4. Evaluation of Prediction Ability on Four Independent Dataset
3.5. Compared with Existing Methods
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Izoré, T.; Cryle, M.J. The many faces and important roles of protein–protein interactions during non-ribosomal peptide synthesis. Nat. Prod. Rep. 2018, 35, 1120–1139. [Google Scholar] [CrossRef] [PubMed]
- Yakubu, R.R.; Nieves, E.; Weiss, L.M. The methods employed in mass spectrometric analysis of posttranslational modifications (PTMs) and protein–protein interactions (PPIs). In Advancements of Mass Spectrometry in Biomedical Research; Advances in Experimental Medicine and Biology book series; Springer: Berlin/Heidelberg, Germany, 2019; pp. 169–198. [Google Scholar]
- Carnes, R.M.; Kesterson, R.A.; Korf, B.R.; Mobley, J.A.; Wallis, D.J.G. Affinity purification of NF1 protein–protein interactors identifies keratins and neurofibromin itself as binding partners. Genes 2019, 10, 650. [Google Scholar] [CrossRef] [PubMed]
- Castel, P.; Holtz-Morris, A.; Kwon, Y.; Suter, B.P.; McCormick, F.J. DoMY-Seq: A yeast two-hybrid–based technique for precision mapping of protein–protein interaction motifs. J. Biol. Chem. 2021, 296, 100023. [Google Scholar] [CrossRef]
- Pan, J.; You, Z.-H.; Yu, C.-Q.; Li, L.-P.; Zhan, X.-K. Predicting Protein-Protein Interactions from Protein Sequence Information Using Dual-Tree Complex Wavelet Transform. In Proceedings of the International Conference on Intelligent Computing, Bari, Italy, 2–5 October 2020; pp. 132–142. [Google Scholar]
- Wang, L.; You, Z.-H.; Yan, X.; Xia, S.-X.; Liu, F.; Li, L.-P.; Zhang, W.; Zhou, Y.J. Using two-dimensional principal component analysis and rotation forest for prediction of protein-protein interactions. Sci. Rep. 2018, 8, 12874. [Google Scholar] [CrossRef] [PubMed]
- Romero-Molina, S.; Ruiz-Blanco, Y.B.; Harms, M.; Münch, J.; Sanchez-Garcia, E.J. PPI-detect: A support vector machine model for sequence-based prediction of protein–protein interactions. J. Comput. Chem. 2019, 40, 1233–1242. [Google Scholar] [CrossRef]
- Chakraborty, A.; Mitra, S.; De, D.; Pal, A.J.; Ghaemi, F.; Ahmadian, A.; Ferrara, M. Determining Protein–Protein Interaction Using Support Vector Machine: A Review. IEEE Access 2021, 9, 12473–12490. [Google Scholar] [CrossRef]
- Lin, X.; Chen, X.W. Heterogeneous data integration by tree-augmented naïve B ayes for protein–Protein interactions prediction. Proteomics 2013, 13, 261–268. [Google Scholar] [CrossRef]
- Huang, Y.-A.; You, Z.-H.; Gao, X.; Wong, L.; Wang, L. Using weighted sparse representation model combined with discrete cosine transformation to predict protein-protein interactions from protein sequence. BioMed Res. Int. 2015, 2015, 902198. [Google Scholar] [CrossRef]
- You, Z.-H.; Lei, Y.-K.; Zhu, L.; Xia, J.; Wang, B. Prediction of protein-protein interactions from amino acid sequences with ensemble extreme learning machines and principal component analysis. BMC Bioinform. 2013, 14, S10. [Google Scholar] [CrossRef]
- Li, J.-Q.; You, Z.-H.; Li, X.; Ming, Z.; Chen, X. PSPEL: In silico prediction of self-interacting proteins from amino acids sequences using ensemble learning. IEEE/ACM Trans. Comput. Biol. Bioinform. 2017, 14, 1165–1172. [Google Scholar] [CrossRef] [PubMed]
- Zeng, M.; Zhang, F.; Wu, F.-X.; Li, Y.; Wang, J.; Li, M. Protein–protein interaction site prediction through combining local and global features with deep neural networks. Bioinformatics 2020, 36, 1114–1120. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.-H.; You, Z.-H.; Li, L.-P.; Wang, Y.-B.; Wong, L.; Yi, H.-C. Prediction of self-interacting proteins from protein sequence information based on random projection model and fast Fourier transform. Int. J. Mol. Sci. 2019, 20, 930. [Google Scholar] [CrossRef] [PubMed]
- Pan, J.; Li, L.-P.; Yu, C.-Q.; You, Z.-H.; Ren, Z.-H.; Tang, J.-Y. FWHT-RF: A Novel Computational Approach to Predict Plant Protein-Protein Interactions via an Ensemble Learning Method. Sci. Program. 2021, 2021, 1607946. [Google Scholar] [CrossRef]
- Sun, T.; Zhou, B.; Lai, L.; Pei, J. Sequence-based prediction of protein protein interaction using a deep-learning algorithm. BMC Bioinform. 2017, 18, 277. [Google Scholar] [CrossRef]
- Zhang, L.; Yu, G.; Xia, D.; Wang, J. Protein–protein interactions prediction based on ensemble deep neural networks. Neurocomputing 2019, 324, 10–19. [Google Scholar] [CrossRef]
- Yao, Y.; Du, X.; Diao, Y.; Zhu, H. An integration of deep learning with feature embedding for protein–protein interaction prediction. PeerJ 2019, 7, e7126. [Google Scholar] [CrossRef]
- Hashemifar, S.; Neyshabur, B.; Khan, A.A.; Xu, J. Predicting protein–protein interactions through sequence-based deep learning. Bioinformatics 2018, 34, i802–i810. [Google Scholar] [CrossRef]
- Richoux, F.; Servantie, C.; Borès, C.; Téletchéa, S.J.A.P.A. Comparing two deep learning sequence-based models for protein-protein interaction prediction. arXiv 2019, arXiv:1901.06268. [Google Scholar]
- Pan, J.; You, Z.-H.; Li, L.-P.; Huang, W.-Z.; Guo, J.-X.; Yu, C.-Q.; Wang, L.-P.; Zhao, Z.-Y. DWPPI: A Deep Learning Approach for Predicting Protein–Protein Interactions in Plants Based on Multi-Source Information With a Large-Scale Biological Network. Front. Bioeng. Biotechnol. 2022, 10, 807522. [Google Scholar] [CrossRef]
- Salwinski, L.; Miller, C.S.; Smith, A.J.; Pettit, F.K.; Bowie, J.U.; Eisenberg, D. The database of interacting proteins: 2004 update. Nucleic Acids Res. 2004, 32, D449–D451. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Yu, L.; Wen, Z.; Li, M. Using support vector machine combined with auto covariance to predict protein–protein interactions from protein sequences. Nucleic Acids Res. 2008, 36, 3025–3030. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Jaroszewski, L.; Godzik, A. Clustering of highly homologous sequences to reduce the size of large protein databases. Bioinformatics 2001, 17, 282–283. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Godzik, A. Cd-hit: A fast program for clustering and comparing large sets of protein or nucleotide sequences. Bioinformatics 2006, 22, 1658–1659. [Google Scholar] [CrossRef] [PubMed]
- Keshava Prasad, T.; Goel, R.; Kandasamy, K.; Keerthikumar, S.; Kumar, S.; Mathivanan, S.; Telikicherla, D.; Raju, R.; Shafreen, B.; Venugopal, A. Human protein reference database—2009 update. Nucleic Acids Res. 2009, 37, D767–D772. [Google Scholar] [CrossRef] [PubMed]
- Gu, H.; Zhu, P.; Jiao, Y.; Meng, Y.; Chen, M. PRIN: A predicted rice interactome network. BMC Bioinform. 2011, 12, 161. [Google Scholar] [CrossRef]
- Gribskov, M.; McLachlan, A.D.; Eisenberg, D. Profile analysis: Detection of distantly related proteins. Proc. Natl. Acad. Sci. USA 1987, 84, 4355–4358. [Google Scholar] [CrossRef]
- Wang, Y.; Cheng, J.; Liu, Y.; Chen, Y. Prediction of protein secondary structure using support vector machine with PSSM profiles. In Proceedings of the 2016 IEEE Information Technology, Networking, Electronic and Automation Control Conference, Chongqing, China, 20–22 May 2016; pp. 502–505. [Google Scholar]
- Zhao, T.-H.; Jiang, M.; Huang, T.; Li, B.-Q.; Zhang, N.; Li, H.-P.; Cai, Y.-D. A novel method of predicting protein disordered regions based on sequence features. BioMed Res. Int. 2013, 2013, 414327. [Google Scholar] [CrossRef][Green Version]
- Gelfand, M.S. Prediction of function in DNA sequence analysis. J. Comput. Biol. 1995, 2, 87–115. [Google Scholar] [CrossRef]
- Cizek, V. Electroacoustics. Discrete hilbert transform. IEEE Trans. Audio Electroacoust. 1970, 18, 340–343. [Google Scholar] [CrossRef]
- Ponomareva, O.; Ponomarev, A.; Ponomarev, V. Evolution of forward and inverse discrete fourier transform. In Proceedings of the 2018 IEEE East-West Design & Test Symposium (EWDTS), Kazan, Russia, 14–17 September 2018; pp. 1–5. [Google Scholar]
- Read, R.R.; Treitel, S. The stabilization of two-dimensional recursive filters via the discrete Hilbert transform. IEEE Trans. Geosci. Electron. 1973, 11, 153–160. [Google Scholar] [CrossRef]
- Rodriguez, J.J.; Kuncheva, L.I.; Alonso, C.J. Rotation forest: A new classifier ensemble method. IEEE Trans Pattern Anal Mach Intell. 2006, 28, 1619–1630. [Google Scholar] [CrossRef] [PubMed]
- Good, R.P.; Kost, D.; Cherry, G.A. Introducing a unified PCA algorithm for model size reduction. IEEE Trans. Semicond. Manuf. 2010, 23, 201–209. [Google Scholar] [CrossRef]
- Ding, Y.; Tang, J.; Guo, F. Predicting protein-protein interactions via multivariate mutual information of protein sequences. BMC Bioinform. 2016, 17, 398. [Google Scholar] [CrossRef] [PubMed]
- Zhan, X.-K.; You, Z.-H.; Li, L.-P.; Li, Y.; Wang, Z.; Pan, J. Using Random Forest Model Combined with Gabor Feature to Predict Protein-Protein Interaction From Protein Sequence. Evol. Bioinform. 2020, 16, 1176934320934498. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.-B.; You, Z.-H.; Li, L.-P.; Huang, Y.-A.; Yi, H.-C. Detection of interactions between proteins by using legendre moments descriptor to extract discriminatory information embedded in pssm. Molecules 2017, 22, 1366. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Yang, S.; Li, Q.; Wuchty, S.; Zhang, Z.J.C. Prediction of human-virus protein-protein interactions through a sequence embedding-based machine learning method. Comput. Struct. Biotechnol. J. 2020, 18, 153–161. [Google Scholar] [CrossRef]
- Wang, X.; Yu, B.; Ma, A.; Chen, C.; Liu, B.; Ma, Q. Protein–protein interaction sites prediction by ensemble random forests with synthetic minority oversampling technique. Bioinformatics 2019, 35, 2395–2402. [Google Scholar] [CrossRef]
- Zhou, Y.Z.; Gao, Y.; Zheng, Y.Y. Prediction of protein-protein interactions using local description of amino acid sequence. In Advances in Computer Science and Education Applications; Springer: Berlin/Heidelberg, Germany, 2011; pp. 254–262. [Google Scholar]
- An, J.-Y.; Zhou, Y.; Zhao, Y.-J.; Yan, Z.-J. An efficient feature extraction technique based on local coding PSSM and multifeatures fusion for predicting protein-protein interactions. Evol. Bioinform. 2019, 15. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Z.; Li, L.-P.; You, Z.-H.; Huang, W.-Z.; Zhan, X.-K.; Wang, Y.-B. Robust and accurate prediction of protein–protein interactions by exploiting evolutionary information. Sci. Rep. 2021, 11, 16910. [Google Scholar] [CrossRef]
- Pan, X.-Y.; Zhang, Y.-N.; Shen, H.-B. Large-Scale prediction of human protein− protein interactions from amino acid sequence based on latent topic features. J. Proteome Res. 2010, 9, 4992–5001. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.-W.; You, Z.-H.; Chen, X.; Li, L.-P.; Huang, D.-S.; Yan, G.-Y.; Nie, R.; Huang, Y.-A. Accurate prediction of protein-protein interactions by integrating potential evolutionary information embedded in PSSM profile and discriminative vector machine classifier. Oncotarget 2017, 8, 23638. [Google Scholar] [CrossRef] [PubMed][Green Version]



| Dataset | ACC (%) | Sen. (%) | Spec. (%) | PR (%) | MCC (%) | AUC |
|---|---|---|---|---|---|---|
| 1 | 90.88 | 89.13 | 92.67 | 92.57 | 83.42 | 0.9562 |
| 2 | 91.55 | 90.31 | 92.79 | 92.55 | 84.52 | 0.9581 |
| 3 | 92.40 | 89.42 | 95.37 | 95.04 | 85.93 | 0.9581 |
| 4 | 92.49 | 90.90 | 94.15 | 94.20 | 86.10 | 0.9608 |
| 5 | 92.31 | 89.15 | 95.30 | 94.73 | 85.75 | 0.9599 |
| Average | 91.93 ± 0.69 | 89.78 ± 0.79 | 94.05 ± 1.30 | 93.82 ± 1.19 | 85.14 ± 1.15 | 0.9586 ± 0.0018 |
| Dataset | ACC (%) | Sen. (%) | Spec. (%) | PR (%) | MCC (%) | AUC |
|---|---|---|---|---|---|---|
| 1 | 96.20 | 95.23 | 97.08 | 96.72 | 92.67 | 0.9834 |
| 2 | 95.47 | 95.23 | 95.69 | 95.47 | 91.34 | 0.9808 |
| 3 | 96.94 | 97.10 | 96.78 | 96.62 | 94.06 | 0.9850 |
| 4 | 96.63 | 95.73 | 97.40 | 96.89 | 93.44 | 0.9817 |
| 5 | 96.51 | 95.53 | 97.41 | 97.14 | 93.24 | 0.9846 |
| Average | 96.35 ± 0.56 | 95.76 ± 0.78 | 96.87 ± 0.71 | 96.57 ± 0.64 | 92.95 ± 1.03 | 0.9831 ± 0.0018 |
| Dataset | ACC (%) | Sen. (%) | Spec. (%) | PR (%) | MCC (%) | AUC |
|---|---|---|---|---|---|---|
| 1 | 93.91 | 94.64 | 93.22 | 92.94 | 88.55 | 0.9635 |
| 2 | 94.38 | 94.64 | 94.13 | 93.83 | 89.38 | 0.9656 |
| 3 | 94.79 | 95.09 | 94.48 | 94.70 | 90.12 | 0.9674 |
| 4 | 94.22 | 95.28 | 93.17 | 93.22 | 89.10 | 0.9628 |
| 5 | 93.91 | 92.84 | 95.08 | 95.40 | 88.54 | 0.9689 |
| Average | 94.24 ± 0.37 | 94.50 ± 0.97 | 94.02 ± 0.82 | 94.02 ± 1.03 | 89.14 ± 0.66 | 0.9667 ± 0.0022 |
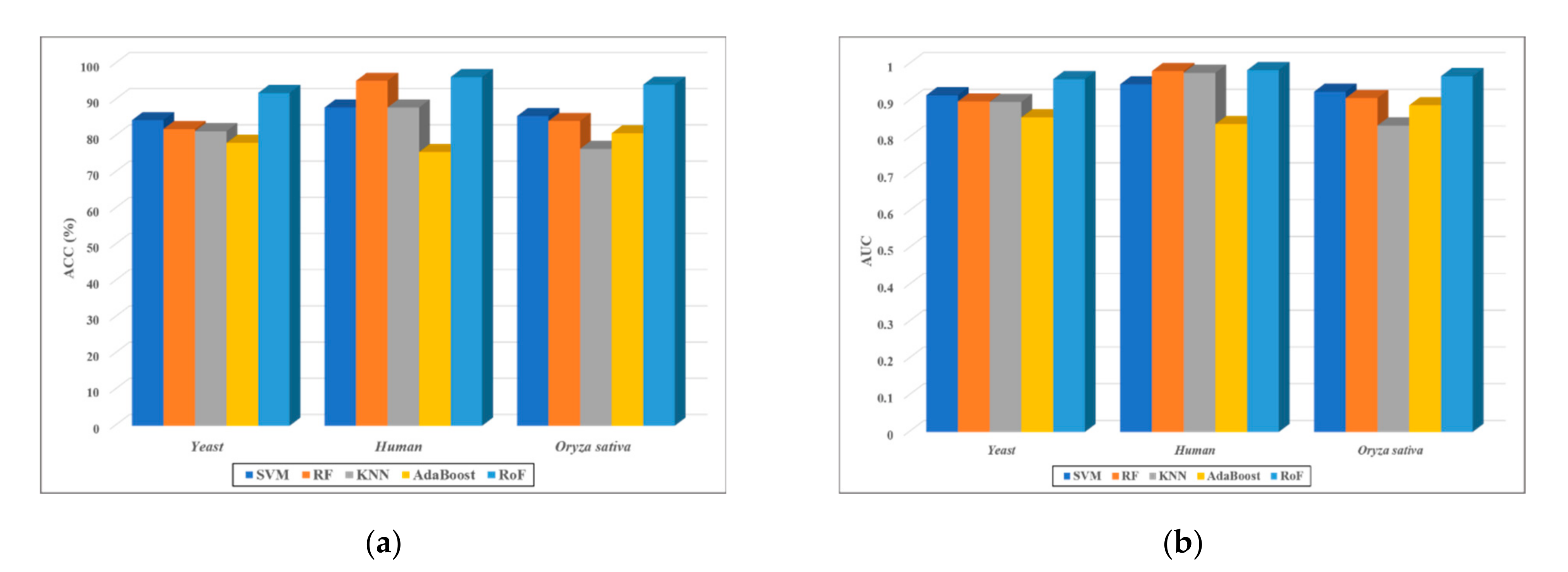
| Dataset | Method | ACC (%) | Sens. (%) | Spec. (%) | PR (%) | MCC (%) | AUC |
|---|---|---|---|---|---|---|---|
| Yeast | SVM | 84.44 ± 0.84 | 83.14 ± 1.01 | 85.77 ± 1.40 | 85.37 ± 1.68 | 73.71 ± 1.17 | 0.9149 ± 0.0061 |
| RF | 81.97 ± 0.41 | 80.26 ± 1.27 | 83.68 ± 0.48 | 83.09 ± 0.84 | 70.41 ± 0.55 | 0.8979 ± 0.0038 | |
| KNN | 81.39 ± 1.07 | 75.19 ± 2.16 | 87.63 ± 1.17 | 85.88 ± 1.21 | 69.47 ± 1.37 | 0.8967 ± 0.0057 | |
| AdaBoost | 78.15 ± 1.82 | 76.88 ± 1.90 | 79.45 ± 2.95 | 85.46 ± 2.85 | 65.87 ± 1.97 | 0.8546 ± 0.0120 | |
| RoF | 91.93 ± 0.69 | 89.78 ± 0.79 | 94.05 ± 1.30 | 93.82 ± 1.19 | 85.14 ± 1.15 | 0.9586 ± 0.0018 | |
| Human | SVM | 87.93 ± 0.86 | 85.78 ± 1.28 | 89.89 ± 1.37 | 88.59 ± 1.53 | 78.69 ± 1.31 | 0.9446 ± 0.0069 |
| RF | 95.32 ± 0.96 | 92.63 ± 1.93 | 97.82 ± 0.94 | 97.50 ± 1.03 | 91.04 ± 1.74 | 0.9804 ± 0.0016 | |
| KNN | 87.92 ± 1.19 | 76.67 ± 2.44 | 98.23 ± 0.49 | 97.51 ± 0.74 | 78.10 ± 1.96 | 0.9758 ± 0.0046 | |
| AdaBoost | 75.64 ± 1.69 | 71.36 ± 3.87 | 79.53 ± 3.04 | 76.19 ± 2.29 | 62.88 ± 1.83 | 0.8362 ± 0.0170 | |
| RoF | 96.35 ± 0.56 | 95.76 ± 0.78 | 96.87 ± 0.71 | 96.57 ± 0.64 | 92.95 ± 1.03 | 0.9831 ± 0.0018 | |
| Oryza sativa | SVM | 85.58 ± 1.27 | 84.06 ± 1.08 | 87.16 ± 2.46 | 86.73 ± 2.63 | 75.32 ± 1.78 | 0.9246 ± 0.0085 |
| RF | 84.19 ± 0.92 | 81.71 ± 1.23 | 86.68 ± 1.03 | 85.99 ± 0.85 | 73.34 ± 1.24 | 0.9070 ± 0.0096 | |
| KNN | 76.51 ± 0.70 | 85.19 ± 0.88 | 67.82 ± 0.91 | 72.58 ± 1.10 | 63.50 ± 0.77 | 0.8327 ± 0.0040 | |
| AdaBoost | 80.82 ± 1.37 | 81.50 ± 1.87 | 80.16 ± 1.61 | 80.40 ± 2.00 | 69.01 ± 1.67 | 0.8876 ± 0.0132 | |
| RoF | 94.24 ± 0.37 | 94.50 ± 0.97 | 94.02 ± 0.82 | 94.02 ± 1.03 | 89.14 ± 0.66 | 0.9667 ± 0.0022 |
| Species | Test Pair | Our Method | Ding et al. [37] | Huang et al. [10] | Zhan et al. [38] | Wang et al. [39] |
|---|---|---|---|---|---|---|
| H. sapiens | 1412 | 94.29% | 90.23% | 82.22% | 91.93% | 80.10% |
| H. pylori | 1420 | 91.67% | 90.34% | 82.18% | 91.34% | N/A |
| M. muscules | 313 | 93.12% | 91.37% | 79.87% | 94.89% | 89.14% |
| C. elegans | 4013 | 92.14% | 86.72% | 81.19% | 93.20% | 92.96% |
| Author | Method | ACC (%) | PR (%) | Sens. (%) | MCC (%) |
|---|---|---|---|---|---|
| Guo et al. [23] | ACC + SVM | 89.33 | 89.93 | 88.87 | N/A |
| Yang et al. [40] | LD + KNN | 86.15 | 90.24 | 81.30 | N/A |
| Wang et al. [41] | 3-MER + CNN | 90.26 | 91.65 | 88.14 | 82.38 |
| Zhou et al. [42] | LD + SVM | 88.56 | 89.50 | 87.37 | 77.15 |
| An et al. [43] | PSSMMF + SVM | 90.48 | 90.58 | 90.26 | 82.84 |
| You et al. [11] | PCA + ELLM | 87.00 | 87.59 | 86.15 | 77.36 |
| Our method | DHT + RoF | 91.93 | 93.82 | 89.78 | 85.14 |
| Author | Method | ACC (%) | PR (%) | Sens. (%) | MCC (%) |
|---|---|---|---|---|---|
| Ding et al. [37] | MMI + RF | 96.08 | 96.67 | 95.05 | 92.17 |
| Li et al. [44] | OLPP + RoF | 96.09 | 96.56 | 95.20 | 92.47 |
| Pan et al. [45] | LDA + SVM | 90.70 | N/A | 89.7 | 81.3 |
| Li et al. [46] | IWLD + SVM | 90.57 | 89.01 | 91.61 | 81.22 |
| Our method | DHT + RoF | 96.35 | 96.57 | 95.76 | 92.95 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, J.; Wang, S.; Yu, C.; Li, L.; You, Z.; Sun, Y. A Novel Ensemble Learning-Based Computational Method to Predict Protein-Protein Interactions from Protein Primary Sequences. Biology 2022, 11, 775. https://doi.org/10.3390/biology11050775
Pan J, Wang S, Yu C, Li L, You Z, Sun Y. A Novel Ensemble Learning-Based Computational Method to Predict Protein-Protein Interactions from Protein Primary Sequences. Biology. 2022; 11(5):775. https://doi.org/10.3390/biology11050775
Chicago/Turabian StylePan, Jie, Shiwei Wang, Changqing Yu, Liping Li, Zhuhong You, and Yanmei Sun. 2022. "A Novel Ensemble Learning-Based Computational Method to Predict Protein-Protein Interactions from Protein Primary Sequences" Biology 11, no. 5: 775. https://doi.org/10.3390/biology11050775
APA StylePan, J., Wang, S., Yu, C., Li, L., You, Z., & Sun, Y. (2022). A Novel Ensemble Learning-Based Computational Method to Predict Protein-Protein Interactions from Protein Primary Sequences. Biology, 11(5), 775. https://doi.org/10.3390/biology11050775






