Adult Skeletal Age-at-Death Estimation through Deep Random Neural Networks: A New Method and Its Computational Analysis
Abstract
:Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Dataset
2.1.1. Sampled Identified Skeletal Collections
2.1.2. Data Management and Processing
2.2. A Novel Technique for Macroscopic Age-At-Death Estimation
2.2.1. Cranial and Palatine Suture Scoring
2.2.2. Vertebrae Development and Degeneration Scoring
2.2.3. Joint and Musculoskeletal Degeneration Scoring
2.2.4. Clavicle Sternal and Acromial Ends Scoring
2.2.5. First Rib Costal Face and Tubercle Scoring
2.2.6. Pubic Symphysis Scoring
2.2.7. Sacral and Iliac Auricular Surfaces (Sacroiliac Joint) Scoring
2.2.8. Acetabulum Scoring
2.2.9. Scoring Reliability: Intra-Observer Error
2.3. Feature Analysis Via Sphering and Marginal Correlation Analysis
2.4. Randomized Neural Networks: Theory and Implementation
2.4.1. Efficient Training and Regularization in Randomized Neural Networks
2.4.2. From Shallow to Deep Randomized Neural Networks
2.4.3. Deep Random Neural Networks as Implicit Ensemble Models
2.5. Regression Uncertainty Modeling and Prediction Intervals
2.6. Computational Analysis: Design, Parameterization, Metrics, and Software
2.6.1. Experimental Design
- (A)
- The first experiment we conducted was designed to provide a baseline of the accuracy obtained by fitting DRNN models to blocks of traits that have standard or traditional analytical framing. For instance, we fitted models to different anatomical complexes or sets of traits that mimic existing aging standards, i.e., a model for the sutures or the pubis symphysis.
- (B)
- Our second computational experiment consisted of simulated different proportions of available traits from 90% to 10%. The objective of this experiment was to assess model performance in a more realistic scenario where the forensic anthropologist has skeletal traits available on a case-by-case basis.
2.6.2. Network Parameterization
2.6.3. Performance Metrics
2.6.4. Software
3. Results
3.1. Intra-Observer Scoring Error
3.2. Marginal Correlation Analysis
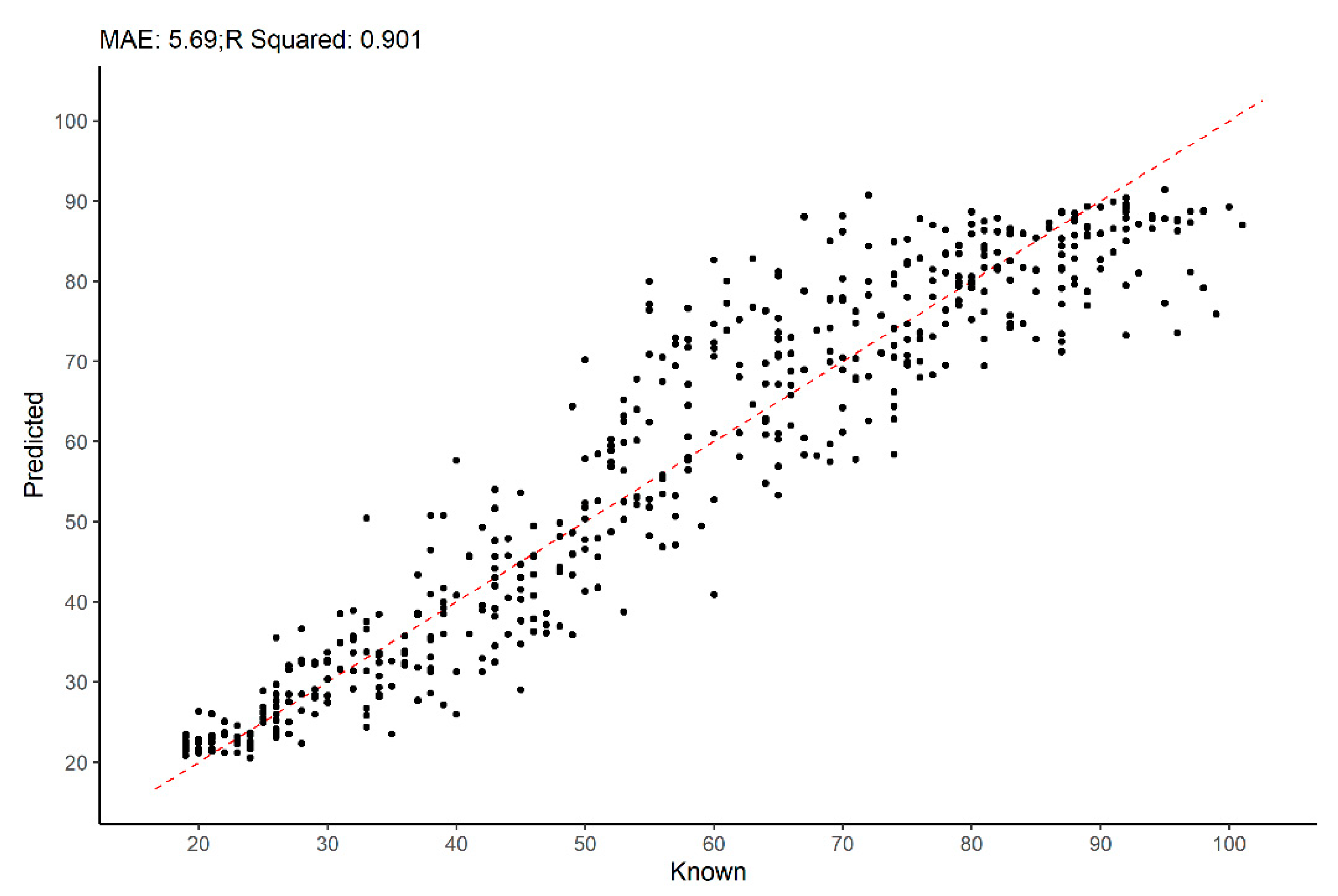
3.3. Computational Model Assessment
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dirkmaat, D.C.; Cabo, L.L.; Ousley, S.D.; Symes, S.A. New perspectives in forensic anthropology. Am. J. Phys. Anthropol. 2008, 137, 33–52. [Google Scholar] [CrossRef] [PubMed]
- Dirkmaat, D.C.; Cabo, L.L. Embracing the New Paradigm. In A Companion to Forensic Anthropology, 1st ed.; Dirkmaat, D.C., Ed.; Blackwell Publishing Ltd.: Hoboken, NJ, USA; pp. 1–40.
- Ritz-Timme, S.; Cattaneo, C.; Collins, M.; Waite, E.R.; Schütz, H.W.; Kaatsch, H.-J.; Borrman, H.I.M. Age estimation: The state of the art in relation to the specific demands of forensic practise. Int. J. Legal Med. 2000, 113, 129–136. [Google Scholar] [CrossRef] [PubMed]
- Ferrante, L.; Cameriere, R. Statistical methods to assess the reliability of measurements in the procedures for forensic age estimation. Int. J. Legal Med. 2009, 123, 277–283. [Google Scholar] [CrossRef] [PubMed]
- Garvin, H.M.; Passalacqua, N.V. Current Practices by Forensic Anthropologists in Adult Skeletal Age Estimation. J. Forensic Sci. 2011, 57, 427–433. [Google Scholar] [CrossRef] [PubMed]
- Franklin, D. Forensic age estimation in human skeletal remains: Current concepts and future directions. Leg. Med. 2010, 12, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Rösing, F.; Graw, M.; Marré, B.; Ritz-Timme, S.; Rothschild, M.; Rötzscher, K.; Schmeling, A.; Schröder, I.; Geserick, G. Recommendations for the forensic diagnosis of sex and age from skeletons. HOMO J. Comp. Hum. Biol. 2007, 58, 75–89. [Google Scholar] [CrossRef]
- Kimmerle, E.H.; Prince, D.A.; Berg, G.E. Inter-Observer Variation in Methodologies Involving the Pubic Symphysis, Sternal Ribs, and Teeth. J. Forensic Sci. 2008, 53, 594–600. [Google Scholar] [CrossRef]
- Martrille, L.; Ubelaker, D.H.; Cattaneo, C.; Seguret, F.; Tremblay, M.; Baccino, E. Comparison of Four Skeletal Methods for the Estimation of Age at Death on White and Black Adults. J. Forensic Sci. 2007, 52, 302–307. [Google Scholar] [CrossRef]
- Buckberry, J. The (mis)use of adult age estimates in osteology. Ann. Hum. Biol. 2015, 42, 323–331. [Google Scholar] [CrossRef] [Green Version]
- Bocquet-Appel, J.-P.; Masset, C. Farewell to paleodemography. J. Hum. Evol. 1982, 11, 321–333. [Google Scholar] [CrossRef]
- Samworth, R.; Gowland, R. Estimation of adult skeletal age-at-death: Statistical assumptions and applications. Int. J. Osteoarchaeol. 2006, 17, 174–188. [Google Scholar] [CrossRef] [Green Version]
- Kotěrová, A.; Navega, D.; Štepanovský, M.; Buk, Z.; Brůžek, J.; Cunha, E. Age estimation of adult human remains from hip bones using advanced methods. Forensic Sci. Int. 2018, 287, 163–175. [Google Scholar] [CrossRef] [PubMed]
- Navega, D.; Costa, E.; Cunha, E. Lost in the woods: The value of tree ensemble modelling for adult age-at-death estimation from skeletal degeneration. La Rev. Med. Légale 2017, 8, 181–182. [Google Scholar] [CrossRef]
- Navega, D.; Coelho, J.D.; Cunha, E.; Curate, F. DXAGE: A New Method for Age at Death Estimation Based on Femoral Bone Mineral Density and Artificial Neural Networks. J. Forensic Sci. 2017, 63, 497–503. [Google Scholar] [CrossRef]
- Konigsberg, L.W. Multivariate cumulative probit for age estimation using ordinal categorical data. Ann. Hum. Biol. 2015, 42, 368–378. [Google Scholar] [CrossRef]
- Lucy, D.; Aykroyd, R.G.; Pollard, A.M. Nonparametric calibration for age estimation. J. R. Stat. Soc. Ser. C (Appl. Stat.) 2002, 51, 183–196. [Google Scholar] [CrossRef]
- Konigsberg, L.; Frankenberg, S.R. Estimation of age structure in anthropological demography. Am. J. Phys. Anthropol. 1992, 89, 235–256. [Google Scholar] [CrossRef]
- Boldsen, J.L.; Milner, G.R.; Konigsberg, L.W.; Wood, J.W. Transition analysis: A new method for estimating age from the skeletons. In Paleodemography: Age Distributions from Skeletal Samples, 1st ed.; Hoppa, R.D., Vaupel, J.W., Eds.; Cambridge University Press: Cambridge, UK; pp. 73–106.
- Milner, G.R.; Boldsen, J.L. Transition analysis: A validation study with known-age modern American skeletons. Am. J. Phys. Anthropol. 2012, 148, 98–110. [Google Scholar] [CrossRef]
- Steadman, D.W.; Adams, B.J.; Konigsberg, L.W. Statistical basis for positive identification in forensic anthropology. Am. J. Phys. Anthropol. 2006, 131, 15–26. [Google Scholar] [CrossRef]
- Corsini, M.-M.; Schmitt, A.; Bruzek, J. Aging process variability on the human skeleton: Artificial network as an appropriate tool for age at death assessment. Forensic Sci. Int. 2005, 148, 163–167. [Google Scholar] [CrossRef]
- Martins, R.; Oliveira, P.E.; Schmitt, A. Estimation of age at death from the pubic symphysis and the auricular surface of the ilium using a smoothing procedure. Forensic Sci. Int. 2012, 219, 287.e1–287.e7. [Google Scholar] [CrossRef] [PubMed]
- Buk, Z.; Kordik, P.; Bruzek, J.; Schmitt, A.; Snorek, M. The age at death assessment in a multi-ethnic sample of pelvic bones using nature-inspired data mining methods. Forensic Sci. Int. 2012, 220, 294.e1–294.e9. [Google Scholar] [CrossRef] [PubMed]
- Baccino, E.; Ubelaker, D.H.; Hayek, L.-A.C.; Zerilli, A. Evaluation of Seven Methods of Estimating Age at Death from Mature Human Skeletal Remains. J. Forensic Sci. 1999, 44, 931–936. [Google Scholar] [CrossRef] [PubMed]
- Brooks, S.; Suchey, J.M. Skeletal age determination based on the os pubis: A comparison of the Acsádi-Nemeskéri and Suchey-Brooks methods. Hum. Evol. 1990, 5, 227–238. [Google Scholar] [CrossRef]
- Hanihara, K.; Suzuki, T. Estimation of age from the pubic symphysis by means of multiple regression analysis. Am. J. Phys. Anthropol. 1978, 48, 233–239. [Google Scholar] [CrossRef] [PubMed]
- Gilbert, B.M.; McKern, T.W. A method for aging the femaleOs pubis. Am. J. Phys. Anthropol. 1973, 38, 31–38. [Google Scholar] [CrossRef] [PubMed]
- McKern, T.W.; Stewart, T.D. Skeletal Age Changes in Young American Males, Analyzed from the Standpoint of Age Identification; Cambridge University Press: Natick, MA, USA, 1957. [Google Scholar]
- Todd, T.W. Age changes in the pubic bone. I. The male white pubis. Am. J. Phys. Anthropol. 1920, 3, 285–334. [Google Scholar] [CrossRef]
- Todd, T.W. Age changes in the pubic bone. Am. J. Phys. Anthropol. 1921, 4, 1–70. [Google Scholar] [CrossRef] [Green Version]
- Katz, D.; Suchey, J.M. Age determination of the male Os pubis. Am. J. Phys. Anthropol. 1986, 69, 427–435. [Google Scholar] [CrossRef]
- Stoyanova, D.; Algee-Hewitt, B.F.; Slice, D.E. An enhanced computational method for age-at-death estimation based on the pubic symphysis using 3D laser scans and thin plate splines. Am. J. Phys. Anthropol. 2015, 158, 431–440. [Google Scholar] [CrossRef]
- Slice, D.E.; Algee-Hewitt, B.F. Modeling Bone Surface Morphology: A Fully Quantitative Method for Age-at-Death Estimation Using the Pubic Symphysis. J. Forensic Sci. 2015, 60, 835–843. [Google Scholar] [CrossRef] [PubMed]
- Milner, G.R.; Boldsen, J.L. Skeletal Age Estimation: Where We Are and Where We Should Go. In A Companion to Forensic Anthropology, 1st ed.; Dirkmaat, D.C., Ed.; Blackwell Publishing Ltd.: Hoboken, NJ, USA, 2017; pp. 224–238. [Google Scholar]
- Milner, G.R.; Boldsen, J.L. Estimating Age and Sex from the Skeleton, a Paleopathological Perspective. In A Companion to Paleopathology, 1st ed.; Grauer, A.L., Ed.; Blackwell Publishing Ltd.: Hoboken, NJ, USA, 2008; pp. 268–284. [Google Scholar]
- Vilas-Boas, D.; Wasterlain, S.; d’Oliveira Coelho, J.; Navega, D.; Gonçalves, D. SPINNE: An app for human vertebral height estimation based on artificial neural networks. Forensic Sci. Int. 2019, 298, 121–130. [Google Scholar] [CrossRef] [PubMed]
- Scott, G.R.; Pilloud, M.A.; Navega, D.; Coelho, J.D.; Cunha, E.; Irish, J.D. rASUDAS: A New Web-Based Application for Estimating Ancestry from Tooth Morphology. Forensic Anthropol. 2018, 1, 18–31. [Google Scholar] [CrossRef] [Green Version]
- Navega, D.; Coelho, C.; Vicente, R.; Ferreira, M.T.; Wasterlain, S.; Cunha, E. AncesTrees: Ancestry estimation with randomized decision trees. Int. J. Leg. Med. 2014, 129, 1145–1153. [Google Scholar] [CrossRef]
- Damas, S.; Wilkinson, C.; Kahana, T.; Veselovskaya, E.; Abramov, A.; Jankauskas, R.; Jayaprakash, P.; Ruiz, E.; Navarro, F.; Huete, M.; et al. Study on the performance of different craniofacial superimposition approaches (II): Best practices proposal. Forensic Sci. Int. 2015, 257, 504–508. [Google Scholar] [CrossRef]
- Mesejo, P.; Martos, R.; Ibáñez; Novo, J.; Ortega, M. A Survey on Artificial Intelligence Techniques for Biomedical Image Analysis in Skeleton-Based Forensic Human Identification. Appl. Sci. 2020, 10, 4703. [Google Scholar] [CrossRef]
- Cunha, E.; Wasterlain, S. The Coimbra identified osteological collections. In Skeletal Series and Their Socio-Economic Context (Documenta Archaeobiologiae; Bd. 5), 1st ed.; Grupe, G., Peters, J., Eds.; Verlag Marie Leidorf GmbH, Rahden/Westf.: Rahden, Germany, 2013; pp. 23–34. [Google Scholar]
- Ferreira, M.T.; Vicente, R.; Navega, D.; Gonçalves, D.; Curate, F.; Cunha, E. A new forensic collection housed at the University of Coimbra, Portugal: The 21st century identified skeletal collection. Forensic Sci. Int. 2014, 245, 202.e1–202.e5. [Google Scholar] [CrossRef] [Green Version]
- Ferreira, M.T.; Coelho, C.; Makhoul, C.; Navega, D.; Gonçalves, D.; Cunha, E.; Curate, F. New data about the 21st Century Identified Skeletal Collection (University of Coimbra, Portugal). Int. J. Leg. Med. 2020, 135, 1087–1094. [Google Scholar] [CrossRef]
- Usher, B.M. Reference samples: The first step in linking biology and age in the human skeleton. In Paleodemography; Hoppa, R.D., Vaupel, J.W., Eds.; Cambridge University Press: Cambridge, UK, 2018; pp. 29–47. [Google Scholar]
- Beretta, L.; Santaniello, A. Nearest neighbor imputation algorithms: A critical evaluation. BMC Med. Inform. Decis. Mak. 2016, 16, 197–208. [Google Scholar] [CrossRef] [Green Version]
- Kemkes-Grottenthaler, A. Aging through the ages: Historical perspectives on age indicators methods. In Paleodemography: Age Distributions from Skeletal Samples, 1st ed.; Hoppa, R.D., Vaupel, J.W., Eds.; Cambridge University Press: Cambridge, UK, 2016; pp. 48–72. [Google Scholar]
- Shirley, N.R.; Montes, P.A.R. Age Estimation in Forensic Anthropology: Quantification of Observer Error in Phase versus Component-Based Methods. J. Forensic Sci. 2014, 60, 107–111. [Google Scholar] [CrossRef]
- Todd, T.W.; Lyon, D.W. Cranial Suture Closure, Its Progress and Age Relationship. Part I. Am. J. Phys. Anthropol. 1925, 8, 325–384. [Google Scholar]
- Todd, T.W.; Lyon, D.W. Cranial suture closure Part II. Am. J. Phys. Anthropol. 1925, 9, 23–44. [Google Scholar] [CrossRef]
- Meindl, R.S.; Lovejoy, O. Ectocranial suture closure: A revised method for the determination of skeletal age at death and blind tests of its accuracy. Am. J. Phys. Anthropol. 1985, 68, 57–66. [Google Scholar] [CrossRef] [PubMed]
- Perizonius, W.R.K. Closing and non-closing sutures in 256 crania of known age and sex from Amsterdam (a.d. 1883–1909). J. Hum. Evol. 1984, 13, 201–216. [Google Scholar] [CrossRef]
- Mann, R.W.; Jantz, R.L.; Bass, W.M.; Willey, P.S. Maxillary Suture Obliteration: A Visual Method for Estimating Skeletal Age. J. Forensic Sci. 1991, 36, 781–791. [Google Scholar] [CrossRef]
- Mann, R.W.; Symes, S.A.; Bass, W.M. Maxillary Suture Obliteration: Aging the Human Skeleton Based on Intact or Fragmentary Maxilla. J. Forensic Sci. 1987, 32, 148–157. [Google Scholar] [CrossRef]
- Acsadi, J.; Nemeskeri, G. History of Human Life Span and Mortality; Académiai Kiadó: Budapest, Hungary, 1970. [Google Scholar]
- Masset, C. Age estimation on the basis of cranial sutures. In Age Markers in the Human Skeleton; İşcan, M.Y., Ed.; Charles C Thomas: Springfield, IL, USA, 1989; pp. 71–103. [Google Scholar]
- Ríos, L.; Weisensee, K.; Rissech, C. Sacral fusion as an aid in age estimation. Forensic Sci. Int. 2008, 180, 111.e1–111.e7. [Google Scholar] [CrossRef] [Green Version]
- Belcastro, M.G.; Rastelli, E.; Mariotti, V. Variation of the degree of sacral vertebral body fusion in adulthood in two European modern skeletal collections. Am. J. Phys. Anthropol. 2007, 135, 149–160. [Google Scholar] [CrossRef]
- Passalacqua, N.V. Forensic Age-at-Death Estimation from the Human Sacrum. J. Forensic Sci. 2009, 54, 255–262. [Google Scholar] [CrossRef]
- Snodgrass, J.J. Sex Differences and Aging of the Vertebral Column. J. Forensic Sci. 2004, 49, 1–6. [Google Scholar] [CrossRef]
- Watanabe, S.; Terazawa, K. Age estimation from the degree of osteophyte formation of vertebral columns in Japanese. Leg. Med. 2006, 8, 156–160. [Google Scholar] [CrossRef] [PubMed]
- Albert, M.; Mulhern, D.; Torpey, M.A.; Boone, E. Age Estimation Using Thoracic and First Two Lumbar Vertebral Ring Epiphyseal Union. J. Forensic Sci. 2010, 55, 287–294. [Google Scholar] [CrossRef] [PubMed]
- Alves-Cardoso, F.; Assis, S. Can osteophytes be used as age at death estimators? Testing correlations in skeletonized human remains with known age-at-death. Forensic Sci. Int. 2018, 288, 59–66. [Google Scholar] [CrossRef] [PubMed]
- Milella, M.; Belcastro, M.G.; Mariotti, V.; Nikita, E. Estimation of adult age-at-death from entheseal robusticit.y: A test using an identified Italian skeletal collection. Am. J. Phys. Anthropol. 2020, 173, 190–199. [Google Scholar] [CrossRef]
- Milella, M.; Belcastro, M.G.; Zollikofer, C.P.; Mariotti, V. The effect of age, sex, and physical activity on entheseal morphology in a contemporary Italian skeletal collection. Am. J. Phys. Anthropol. 2012, 148, 379–388. [Google Scholar] [CrossRef]
- Winburn, A.P.; Stock, M.K. Reconsidering osteoarthritis as a skeletal indicator of age at death. Am. J. Phys. Anthropol. 2019, 170, 459–473. [Google Scholar] [CrossRef]
- Calce, S.E.; Kurki, H.K.; Weston, D.A.; Gould, L. Effects of osteoarthritis on age-at-death estimates from the human pelvis. Am. J. Phys. Anthropol. 2018, 167, 3–19. [Google Scholar] [CrossRef]
- Calce, S.E.; Kurki, H.K.; Weston, D.A.; Gould, L. Principal component analysis in the evaluation of osteoarthritis. Am. J. Phys. Anthropol. 2016, 162, 476–490. [Google Scholar] [CrossRef]
- Brennaman, A.L.; Love, K.R.; Bethard, J.D.; Pokines, J.T. A Bayesian Approach to Age-at-Death Estimation from Osteoarthritis of the Shoulder in Modern North Americans. J. Forensic Sci. 2016, 62, 573–584. [Google Scholar] [CrossRef]
- Calce, S.E.; Kurki, H.K.; Weston, D.A.; Gould, L. The relationship of age, activity, and body size on osteoarthritis in weight-bearing skeletal regions. Int. J. Paleopathol. 2018, 22, 45–53. [Google Scholar] [CrossRef]
- Buikstra, J.E.; Ubelaker, D.H. Standards for Data Collection from Human Skeletal Remains. Fayetteville 1995. [Google Scholar] [CrossRef]
- Henderson, C.Y.; Mariotti, V.; Pany-Kucera, D.; Villotte, S.; Wilczak, C. Recording Specific Entheseal Changes of Fibrocartilaginous Entheses: Initial Tests Using the Coimbra Method. Int. J. Osteoarchaeol. 2012, 23, 152–162. [Google Scholar] [CrossRef]
- Falys, C.G.; Prangle, D. Estimating age of mature adults from the degeneration of the sternal end of the clavicle. Am. J. Phys. Anthropol. 2014, 156, 203–214. [Google Scholar] [CrossRef] [Green Version]
- Langley-Shirley, N.; Jantz, R.L. A Bayesian Approach to Age Estimation in Modern Americans from the Clavicle. J. Forensic Sci. 2010, 55, 571–583. [Google Scholar] [CrossRef] [PubMed]
- Owings, W.P.A.; Myers, S.J.; Webb, P.A.O.; Suchey, J.M. Epiphyseal union of the anterior iliac crest and medial clavicle in a modern multiracial sample of American males and females. Am. J. Phys. Anthropol. 1985, 68, 457–466. [Google Scholar] [CrossRef]
- Cardoso, H.F.V. V Age estimation of adolescent and young adult male and female skeletons II, epiphyseal union at the upper limb and scapular girdle in a modern Portuguese skeletal sample. Am. J. Phys. Anthropol. 2008, 137, 97–105. [Google Scholar] [CrossRef] [Green Version]
- Can, M.Y.; Loth, S.R. Determination of age from the sternal rib in white males: A test of the phase method. J. Forensic Sci. 1986, 31, 122–132. [Google Scholar]
- İşcan, M.Y.; Loth, S.R.; Wright, R.K. Age Estimation from the Rib by Phase Analysis: White Males. J. Forensic Sci. 1984, 29, 1094–1104. [Google Scholar] [CrossRef]
- Can, M.Y.; Loth, S.R. Metamorphosis at the sternal rib end: A new method to estimate age at death in white males. Am. J. Phys. Anthropol. 1984, 65, 147–156. [Google Scholar]
- Işcan, M.Y.; Loth, S.R.; Wright, R.K. Racial Variation in the Sternal Extremity of the Rib and Its Effect on Age Determination. J. Forensic Sci. 1987, 32, 452–466. [Google Scholar] [CrossRef]
- Kunos, C.A.; Simpson, S.W.; Russell, K.F. Hershkovitz I First rib metamorphosis: Its possible utility for human age-at-death estimation. Am. J. Phys. Anthropol. 1999, 110, 303–323. [Google Scholar] [CrossRef]
- DiGangi, E.A.; Bethard, J.D.; Kimmerle, E.H.; Konigsberg, L.W. A new method for estimating age-at-death from the first rib. Am. J. Phys. Anthropol. 2009, 138, 164–176. [Google Scholar] [CrossRef] [PubMed]
- Sashin, D.A. Critical analysis pf the anatomy and the pathologic changes of the sacro-iliac joints. J. Bone Jt. Surg. 1992, 12, 891–910. [Google Scholar]
- Schunke, G.B. The anatomy and development of the sacro-iliac joint in man. Anat. Rec. 1938, 72, 313–331. [Google Scholar] [CrossRef]
- Lovejoy, C.O.; Meindl, R.S.; Pryzbeck, T.R.; Mensforth, R.P. Chronological metamorphosis of the auricular surface of the ilium: A new method for the determination of adult skeletal age at death. Am. J. Phys. Anthropol. 1985, 68, 15–28. [Google Scholar] [CrossRef]
- Buckberry, J.; Chamberlain, A. Age estimation from the auricular surface of the ilium: A revised method. Am. J. Phys. Anthropol. 2002, 119, 231–239. [Google Scholar] [CrossRef]
- San-Millán, M.; Rissech, C.; Turbón, D. New approach to age estimation of male and female adult skeletons based on the morphological characteristics of the acetabulum. Int. J. Leg. Med. 2016, 131, 501–525. [Google Scholar] [CrossRef]
- Winburn, A.P. Validation of the Acetabulum as a Skeletal Indicator of Age at Death in Modern European-Americans. J. Forensic Sci. 2018, 64, 989–1003. [Google Scholar] [CrossRef]
- Mays, S. A Test of a Recently Devised Method of Estimating Skeletal Age at Death using Features of the Adult Acetabulum. J. Forensic Sci. 2013, 59, 184–187. [Google Scholar] [CrossRef]
- Calce, S.E. A new method to estimate adult age-at-death using the acetabulum. Am. J. Phys. Anthropol. 2012, 148, 11–23. [Google Scholar] [CrossRef]
- Rissech, C.; Estabrook, G.F.; Cunha, E.; Malgosa, A. Using the Acetabulum to Estimate Age at Death of Adult Males. J. Forensic Sci. 2006, 51, 213–229. [Google Scholar] [CrossRef] [PubMed]
- Rissech, C.; Estabrook, G.F.; Cunha, E.; Malgosa, A.; Badalló, M.D.C.R. Estimation of Age-at-Death for Adult Males Using the Acetabulum, Applied to Four Western European Populations. J. Forensic Sci. 2007, 52, 774–778. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rougé-Maillart, C.; Vielle, B.; Jousset, N.; Chappard, D.; Telmon, N.; Cunha, E. Development of a method to estimate skeletal age at death in adults using the acetabulum and the auricular surface on a Portuguese population. Forensic Sci. Int. 2009, 188, 91–95. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rougé-Maillart, C.; Jousset, N.; Vielle, B.; Gaudin, A.; Telmon, N. Contribution of the study of acetabulum for the estimation of adult subjects. Forensic Sci. Int. 2007, 171, 103–110. [Google Scholar] [CrossRef] [PubMed]
- San-Millán, M.; Rissech, C.; Turbón, D. Application of the recent SanMillán–Rissech acetabular adult aging method in a North American sample. Int. J. Leg. Med. 2019, 133, 909–920. [Google Scholar] [CrossRef]
- Kendall, M.G.; Smith, B.B. The Problem of m Rankings. Ann. Math. Stat. 1939, 10, 275–287. [Google Scholar] [CrossRef]
- Zuber, V.; Strimmer, K. High-Dimensional Regression and Variable Selection Using CAR Scores. Stat. Appl. Genet. Mol. Biol. 2011, 10. [Google Scholar] [CrossRef] [Green Version]
- Kessy, A.; Lewin, A.; Strimmer, K. Optimal Whitening and Decorrelation. Am. Stat. 2018, 72, 309–314. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Scardapane, S.; Wang, D. Randomness in neural networks: An overview. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2017, 7, e1200. [Google Scholar] [CrossRef]
- Gallicchio, C.; Scardapane, S. Deep Randomized Neural Networks. Stud. Comput. Intell. 2020, 896, 43–68. [Google Scholar] [CrossRef]
- Schmidt, W.F.; Kraaijveld, M.A.; Duin, R.P.W. Feedforward neural networks with random weights. In Proceedings of the 11th IAPR International Conference on Pattern Recognition. Volume II. Conference B: Pattern Recognition Methodology and Systems, The Hague, The Netherlands, 30 August 1992; IEEE Comput. Soc. Press: Piscataway, NJ, USA, 1992; pp. 1–4. [Google Scholar]
- Pao, Y.-H.; Takefuji, Y. Functional-link net computing: Theory, system architecture, and functionalities. Computer (Long Beach Ca.) 1992, 25, 76–79. [Google Scholar] [CrossRef]
- Broomhead, D.S.; Lowe, D. Multivariable functional interpolation and adaptive networks. Complex Syst. 1988, 2, 321–355. [Google Scholar]
- Pao, Y.-H.; Park, G.-H.; Sobajic, D.J. Learning and generalization characteristics of the random vector functional-link net. Neurocomputing 1994, 6, 163–180. [Google Scholar] [CrossRef]
- Igelnik, B.; Pao, Y.-H. Stochastic choice of basis functions in adaptive function approximation and the functional-link net. IEEE Trans. Neural Netw. 1995, 6, 1320–1329. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, G.-B. What are Extreme Learning Machines? Filling the Gap between Frank Rosenblatt’s Dream and John von Neumann’s Puzzle. Cogn. Comput. 2015, 7, 263–278. [Google Scholar] [CrossRef]
- Huang, G.-B.; Zhu, Q.-Y.; Siew, C.-K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Huang, G.; Huang, G.; Bin Song, S.; You, K. Trends in extreme learning machines: A review. Neural Netw. 2015, 61, 32–48. [Google Scholar] [CrossRef]
- Huang, G.-B. An Insight into Extreme Learning Machines: Random Neurons, Random Features and Kernels. Cogn. Comput. 2014, 6, 376–390. [Google Scholar] [CrossRef]
- Wang, L.P.; Wan, C.R. Comments on “The Extreme Learning Machine. IEEE Trans. Neural Netw. 2008, 19, 1494–1495. [Google Scholar] [CrossRef] [Green Version]
- Shao, Z.; Er, M.J. Efficient Leave-One-Out Cross-Validation-based Regularized Extreme Learning Machine. Neurocomputing 2016, 194, 260–270. [Google Scholar] [CrossRef]
- Wang, D.; Wang, P.; Shi, J. A fast and efficient conformal regressor with regularized extreme learning machine. Neurocomputing 2018, 304, 1–11. [Google Scholar] [CrossRef]
- Tissera, M.D.; McDonnell, M. Deep extreme learning machines: Supervised autoencoding architecture for classification. Neurocomputing 2016, 174, 42–49. [Google Scholar] [CrossRef]
- Tang, J.; Deng, C.; Huang, G.-B. Extreme Learning Machine for Multilayer Perceptron. IEEE Trans. Neural Netw. Learn. Syst. 2015, 27, 809–821. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.; Huang, G.-B.; Lin, Z.; Wang, H.; Soh, Y.C. Stacked Extreme Learning Machines. IEEE Trans. Cybern. 2014, 45, 2013–2025. [Google Scholar] [CrossRef]
- Yu, W.; Zhuang, F.; He, Q.; Shi, Z. Learning deep representations via extreme learning machines. Neurocomputing 2015, 149, 308–315. [Google Scholar] [CrossRef]
- Shi, Q.; Katuwal, R.; Suganthan, P.; Tanveer, M. Random vector functional link neural network based ensemble deep learning. Pattern Recognit. 2021, 117, 107978. [Google Scholar] [CrossRef]
- Huang, G.-B.; Zhou, H.; Ding, X.; Zhang, R. Extreme Learning Machine for Regression and Multiclass Classification. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2012, 42, 513–529. [Google Scholar] [CrossRef] [Green Version]
- Hoerl, A.E.; Kennard, R.W. Ridge Regression: Biased Estimation for Nonorthogonal Problems. Technometrics 1970, 12, 55–67. [Google Scholar] [CrossRef]
- Bartlett, P.L. The sample complexity of pattern classification with neural networks: The size of the weights is more important than the size of the network. IEEE Trans. Inf. Theory 1998, 44, 525–536. [Google Scholar] [CrossRef] [Green Version]
- Bartlett, P.L. For valid generalization, the size of the weights is more important than the size of the network. Adv. Neural Inf. Processing Syst. 9 (NIPS 1996) 1996, 23, 35–39. [Google Scholar]
- Allen, D.M. The Relationship between Variable Selection and Data Agumentation and a Method for Prediction. Technometrics 1974, 16, 125. [Google Scholar] [CrossRef]
- Navega, D.; Cunha, E. Extreme learning machine neural networks for adult skeletal age-at-death estimation. In Statistics and Probability in Forensic Anthropology; Obertová, Z., Stewart, A., Cattaneo, C., Eds.; Elsevier: Amsterdam, The Netherlands, 2020; pp. 209–225. [Google Scholar]
- Milborrow, S. Variance Models in Earth. Available online: http://www.milbo.org/doc/earth-varmod.pdf (accessed on 18 March 2022).
- Geary, R.C. The Ratio of the Mean Deviation to the Standard Deviation as a Test of Normality. Biometrika 1935, 27, 310. [Google Scholar] [CrossRef]
- Konigsberg, L.W.; Herrmann, N.P.; Wescott, D.J.; Kimmerle, E.H. Estimation and Evidence in Forensic Anthropology: Age-at-Death. J. Forensic Sci. 2008, 53, 541–557. [Google Scholar] [CrossRef] [PubMed]
- Müller, H.-G.; Love, B.; Hoppa, R.D. Semiparametric method for estimating paleodemographic profiles from age indicator data. Am. J. Phys. Anthropol. 2001, 117, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Fieuws, S.; Willems, G.; Larsen-Tangmose, S.; Lynnerup, N.; Boldsen, J.; Thevissen, P. Obtaining appropriate interval estimates for age when multiple indicators are used: Evaluation of an ad-hoc procedure. Int. J. Leg. Med. 2015, 130, 489–499. [Google Scholar] [CrossRef]
- Papadopoulos, H.; Haralambous, H. Reliable prediction intervals with regression neural networks. Neural Netw. 2011, 24, 842–851. [Google Scholar] [CrossRef]
- Lappas, G. Estimating the Size of Neural Networks from the number of available training data. Neural Netw. 2007, 68–77. [Google Scholar] [CrossRef]
- Rougé-Maillart, C.; Telmon, N.; Rissech, C.; Malgosa, A.; Rougé, D. The determination of male adult age at death by central and posterior coxal analysis--a preliminary study. J. Forensic Sci. 2004, 49, 1–7. [Google Scholar] [CrossRef]
- Lovejoy, C.O.; Meindl, R.S.; Mensforth, R.P.; Barton, T.J. Multifactorial determination of skeletal age at death: A method and blind tests of its accuracy. Am. J. Phys. Anthropol. 1985, 68, 1–14. [Google Scholar] [CrossRef]
- Anderson, M.F.; Anderson, D.T.; Wescott, D.J. Estimation of adult skeletal age-at-death using the Sugeno fuzzy integral. Am. J. Phys. Anthropol. 2009, 142, 30–41. [Google Scholar] [CrossRef] [Green Version]
- Listi, G.A. The Use of Entheseal Changes in the Femur and Os Coxa for Age Assessment. J. Forensic Sci. 2015, 61, 12–18. [Google Scholar] [CrossRef] [PubMed]
- Listi, G.A.; Manhein, M.H. The Use of Vertebral Osteoarthritis and Osteophytosis in Age Estimation. J. Forensic Sci. 2012, 57, 1537–1540. [Google Scholar] [CrossRef] [PubMed]
- Jooste, N.; L’Abbé, E.N.; Pretorius, S.; Steyn, M. Validation of transition analysis as a method of adult age estimation in a modern South African sample. Forensic Sci. Int. 2016, 266, 580.e1–580.e7. [Google Scholar] [CrossRef] [PubMed]
- Baccino, E.; Sinfield, L.; Colomb, S.; Baum, T.P.; Martrille, L. Technical note: The two step procedure (TSP) for the determination of age at death of adult human remains in forensic cases. Forensic Sci. Int. 2014, 244, 247–251. [Google Scholar] [CrossRef]
- Miranker, M. A Comparison of Different Age Estimation Methods of the Adult Pelvis. J. Forensic Sci. 2016, 61, 1173–1179. [Google Scholar] [CrossRef]
- Merritt, C.E. Inaccuracy and bias in adult skeletal age estimation: Assessing the reliability of eight methods on individuals of varying body sizes. Forensic Sci. Int. 2017, 275, 315.e1–315.e11. [Google Scholar] [CrossRef]
- Hagelthorn, C.L.; Alblas, A.; Greyling, L. The accuracy of the Transition Analysis of aging on a heterogenic South African population. Forensic Sci. Int. 2019, 297, 370.e1–370.e5. [Google Scholar] [CrossRef]
- Valsecchi, A.; Olivares, J.I.; Mesejo, P. Age estimation in forensic anthropology: Methodological considerations about the validation studies of prediction models. Int. J. Leg. Med. 2019, 133, 1915–1924. [Google Scholar] [CrossRef] [Green Version]
- Burkart, N.; Huber, M.F. A Survey on the Explainability of Supervised Machine Learning. J. Artif. Intell. Res. 2021, 70, 245–317. [Google Scholar] [CrossRef]
- Jooste, N.; Pretorius, S.; Steyn, M. Performance of three mathematical models for estimating age-at-death from multiple indicators of the adult skeleton. Int. J. Leg. Med. 2021, 1–13. [Google Scholar] [CrossRef]
- Nikita, E.; Nikitas, P. Skeletal age-at-death estimation: Bayesian versus regression methods. Forensic Sci. Int. 2019, 297, 56–64. [Google Scholar] [CrossRef] [PubMed]
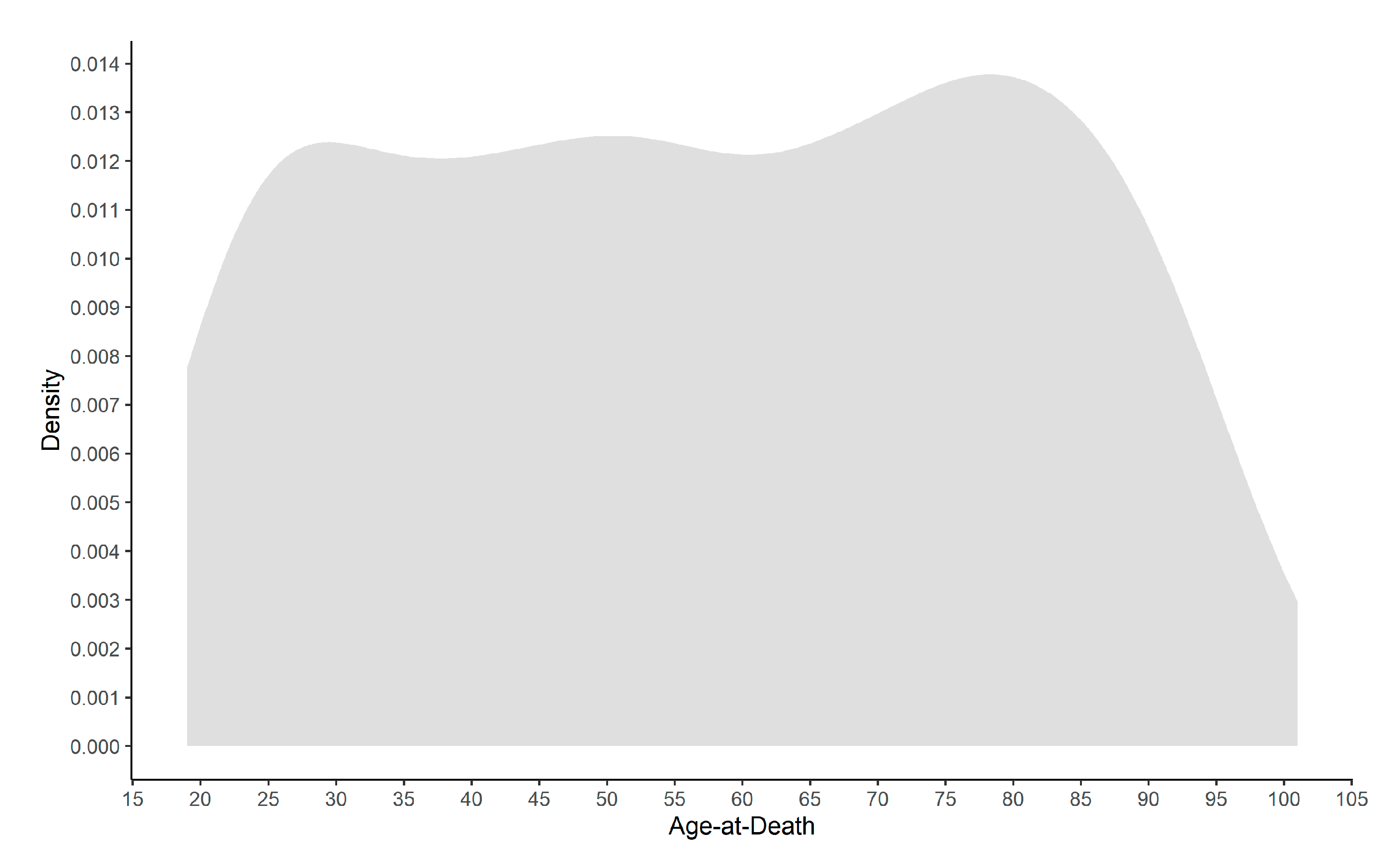






| CISC | XXI-ISC | Pooled Collections | Pooled Sex | |||||
|---|---|---|---|---|---|---|---|---|
| Female | Male | Female | Male | Female | Male | |||
| n | 168 | 166 | 82 | 84 | 250 | 250 | 500 | |
| Age-at-Death | Mean | 48.482 | 45.331 | 81.841 | 74.881 | 59.424 | 55.260 | 57.34 |
| (AGE) | Std. Dev. | 19.483 | 18.171 | 12.889 | 15.082 | 23.556 | 22.141 | 22.93 |
| Min. | 19 | 19 | 38 | 25 | 19 | 19 | 19 | |
| Max. | 95 | 96 | 101 | 96 | 101 | 96 | 101 | |
| Year of Birth | Mean | 1877.286 | 1879.994 | 1923.866 | 1930.560 | 1892.564 | 1896.984 | 1894.774 |
| (YOB) | Std. Dev. | 21.252 | 19.948 | 13.137 | 14.424 | 28.969 | 30.096 | 29.591 |
| Min. | 1830 | 1836 | 1904 | 1908 | 1830 | 1836 | 1830 | |
| Max. | 1911 | 1917 | 1970 | 1982 | 1970 | 1982 | 1982 | |
| Year of Death | Mean | 1925.768 | 1925.325 | 2005.707 | 2005.440 | 1951.988 | 1952.244 | 1952.116 |
| (YOD) | Std. Dev. | 6.597 | 7.343 | 3.707 | 3.919 | 38.051 | 38.452 | 38.214 |
| Min. | 1910 | 1910 | 2000 | 1995 | 1910 | 1910 | 1910 | |
| Max. | 1936 | 1936 | 2012 | 2011 | 2012 | 2011 | 2012 | |
| Accuracy | Bias | Validity | Efficiency | ||||
|---|---|---|---|---|---|---|---|
| Traits | MAE | PIW | PIW 95% CI | ||||
| Sutures | Median | 15.300 | 0.656 | 0.950 | 68.144 | 51.699 | 69.759 |
| (m = 9) | 95% CI | 13.586 | 0.590 | 0.900 | 66.054 | 46.361 | 68.312 |
| 17.206 | 0.732 | 0.990 | 69.741 | 55.776 | 70.963 | ||
| Axial | Median | 8.185 | 0.198 | 0.960 | 38.754 | 33.732 | 40.842 |
| (m = 16) | 95% CI | 7.365 | 0.137 | 0.920 | 37.102 | 32.272 | 39.215 |
| 9.139 | 0.260 | 0.990 | 40.091 | 35.029 | 42.191 | ||
| Appendicular | Median | 7.583 | 0.167 | 0.960 | 37.378 | 29.109 | 39.541 |
| (m = 23) | 95% CI | 6.678 | 0.103 | 0.910 | 35.412 | 27.613 | 38.014 |
| 8.523 | 0.231 | 0.990 | 39.079 | 30.399 | 41.061 | ||
| Clavicle | Median | 8.949 | 0.244 | 0.960 | 49.234 | 17.354 | 51.610 |
| (m = 2) | 95% CI | 7.798 | 0.169 | 0.920 | 39.064 | 15.981 | 49.962 |
| 10.192 | 0.307 | 0.990 | 52.688 | 18.617 | 53.098 | ||
| First Rib | Median | 9.500 | 0.277 | 0.950 | 48.936 | 24.334 | 49.637 |
| (m = 2) | 95% CI | 8.138 | 0.204 | 0.900 | 46.879 | 22.499 | 47.687 |
| 10.831 | 0.351 | 0.990 | 50.903 | 26.078 | 51.533 | ||
| Pubic symphysis | Median | 10.897 | 0.370 | 0.940 | 51.210 | 26.905 | 56.954 |
| (m = 3) | 95% CI | 9.371 | 0.280 | 0.870 | 48.688 | 24.520 | 54.799 |
| 12.542 | 0.459 | 0.980 | 55.558 | 29.058 | 58.802 | ||
| Sacroiliac complex | Median | 8.523 | 0.223 | 0.950 | 44.668 | 20.378 | 47.969 |
| (m = 6) | 95% CI | 7.380 | 0.145 | 0.890 | 39.350 | 18.596 | 46.017 |
| 9.742 | 0.288 | 0.990 | 47.547 | 21.915 | 49.720 | ||
| Acetabulum | Median | 8.886 | 0.229 | 0.970 | 42.978 | 31.727 | 45.742 |
| (m = 3) | 95% CI | 7.758 | 0.162 | 0.920 | 41.201 | 29.897 | 43.891 |
| 10.006 | 0.287 | 1.000 | 44.509 | 33.240 | 47.304 | ||
| Degenerative traits | Median | 6.962 | 0.147 | 0.970 | 33.732 | 28.882 | 35.122 |
| (m = 39) | 95% CI | 6.084 | 0.085 | 0.920 | 32.460 | 27.570 | 33.488 |
| 7.814 | 0.200 | 1.000 | 34.935 | 30.019 | 36.656 | ||
| Standard traits | Median | 6.609 | 0.147 | 0.950 | 34.245 | 12.927 | 41.087 |
| (m = 16) | 95% CI | 5.561 | 0.087 | 0.890 | 29.701 | 11.833 | 39.097 |
| 7.598 | 0.202 | 0.990 | 37.857 | 14.169 | 42.833 | ||
| All | Median | 5.925 | 0.117 | 0.950 | 30.010 | 15.631 | 36.081 |
| (m = 64) | 95% CI | 5.101 | 0.060 | 0.900 | 26.817 | 14.464 | 34.612 |
| 6.728 | 0.170 | 0.990 | 33.191 | 16.811 | 37.515 | ||
| Accuracy | Bias | Validity | Efficiency | ||||
|---|---|---|---|---|---|---|---|
| Traits | MAE | PIW | PIW 95% CI | ||||
| Sutures | Median | 15.245 | 0.655 | 0.953 | 68.120 | 51.782 | 69.796 |
| (m = 9) | 95% CI | 14.683 | 0.616 | 0.940 | 66.377 | 46.429 | 68.371 |
| 15.751 | 0.692 | 0.963 | 69.708 | 55.878 | 70.996 | ||
| Axial | Median | 8.156 | 0.200 | 0.960 | 38.825 | 33.594 | 40.881 |
| (m = 16) | 95% CI | 7.896 | 0.184 | 0.953 | 37.468 | 32.131 | 39.279 |
| 8.394 | 0.213 | 0.968 | 39.872 | 34.902 | 42.234 | ||
| Appendicular | Median | 7.557 | 0.169 | 0.960 | 37.534 | 29.035 | 39.599 |
| (m = 23) | 95% CI | 7.278 | 0.155 | 0.948 | 35.996 | 27.542 | 38.082 |
| 7.823 | 0.184 | 0.970 | 38.920 | 30.319 | 41.109 | ||
| Clavicle | Median | 8.943 | 0.245 | 0.963 | 49.216 | 17.336 | 51.768 |
| (m = 2) | 95% CI | 8.606 | 0.228 | 0.953 | 47.184 | 15.969 | 50.112 |
| 9.248 | 0.263 | 0.970 | 51.238 | 18.597 | 53.252 | ||
| First Rib | Median | 9.409 | 0.275 | 0.950 | 48.897 | 24.356 | 49.811 |
| (m = 2) | 95% CI | 9.067 | 0.255 | 0.938 | 47.036 | 22.502 | 47.862 |
| 9.751 | 0.296 | 0.960 | 50.829 | 26.102 | 51.724 | ||
| Pubic symphysis | Median | 10.898 | 0.370 | 0.932 | 51.113 | 27.029 | 57.040 |
| (m = 3) | 95% CI | 10.436 | 0.343 | 0.922 | 48.668 | 24.616 | 54.949 |
| 11.315 | 0.398 | 0.945 | 53.003 | 29.217 | 58.909 | ||
| Sacroiliac complex | Median | 8.438 | 0.220 | 0.950 | 44.765 | 20.350 | 48.037 |
| (m = 6) | 95% CI | 8.075 | 0.200 | 0.940 | 42.461 | 18.607 | 46.091 |
| 8.741 | 0.239 | 0.960 | 46.755 | 21.893 | 49.800 | ||
| Acetabulum | Median | 8.833 | 0.229 | 0.965 | 43.051 | 31.541 | 45.832 |
| (m = 3) | 95% CI | 8.490 | 0.210 | 0.955 | 41.302 | 29.726 | 43.995 |
| 9.116 | 0.247 | 0.975 | 44.535 | 33.054 | 47.395 | ||
| Degenerative traits | Median | 6.929 | 0.147 | 0.963 | 33.744 | 28.816 | 35.194 |
| (m = 39) | 95% CI | 6.694 | 0.133 | 0.953 | 32.530 | 27.499 | 33.566 |
| 7.154 | 0.157 | 0.973 | 34.829 | 29.946 | 36.715 | ||
| Standard traits | Median | 6.561 | 0.145 | 0.948 | 34.283 | 12.952 | 41.170 |
| (m = 16) | 95% CI | 6.277 | 0.132 | 0.935 | 32.464 | 11.853 | 39.222 |
| 6.855 | 0.157 | 0.960 | 36.027 | 14.122 | 42.921 | ||
| All | Median | 5.899 | 0.118 | 0.950 | 30.057 | 15.558 | 36.141 |
| (m = 64) | 95% CI | 5.677 | 0.110 | 0.940 | 28.758 | 14.403 | 34.644 |
| 6.121 | 0.127 | 0.963 | 31.485 | 16.668 | 37.620 | ||
| Accuracy | Bias | Validity | Efficiency | ||||
|---|---|---|---|---|---|---|---|
| Available Traits % | MAE | PIW | PIW 95% CI | ||||
| 90% | Median | 5.964 | 0.120 | 0.950 | 30.354 | 15.851 | 36.215 |
| (m ≈ 57) | 95% CI | 5.136 | 0.062 | 0.900 | 27.067 | 14.466 | 34.554 |
| 6.773 | 0.169 | 0.990 | 33.422 | 18.081 | 37.705 | ||
| 80% | Median | 6.026 | 0.121 | 0.950 | 30.498 | 16.004 | 36.261 |
| (m ≈ 51) | 95% CI | 5.211 | 0.061 | 0.900 | 27.183 | 14.213 | 34.498 |
| 6.851 | 0.172 | 0.990 | 33.584 | 18.492 | 37.902 | ||
| 70% | Median | 6.072 | 0.125 | 0.950 | 30.805 | 16.206 | 36.454 |
| (m ≈ 44) | 95% CI | 5.152 | 0.062 | 0.900 | 27.528 | 14.001 | 34.600 |
| 6.924 | 0.180 | 0.990 | 34.004 | 19.666 | 38.405 | ||
| 60% | Median | 6.131 | 0.125 | 0.950 | 30.964 | 16.352 | 36.649 |
| (m ≈ 38) | 95% CI | 5.316 | 0.065 | 0.900 | 27.513 | 13.893 | 34.672 |
| 7.049 | 0.179 | 0.990 | 34.320 | 20.532 | 38.692 | ||
| 50% | Median | 6.237 | 0.129 | 0.950 | 31.479 | 16.717 | 36.969 |
| (m ≈ 32) | 95% CI | 5.293 | 0.064 | 0.900 | 27.820 | 13.757 | 34.930 |
| 7.180 | 0.179 | 0.990 | 34.854 | 22.119 | 39.250 | ||
| 40% | Median | 6.360 | 0.134 | 0.950 | 32.125 | 17.165 | 37.429 |
| (m ≈ 25) | 95% CI | 5.441 | 0.074 | 0.900 | 28.500 | 13.910 | 35.075 |
| 7.380 | 0.193 | 0.990 | 35.636 | 23.292 | 40.166 | ||
| 30% | Median | 6.570 | 0.140 | 0.950 | 33.163 | 17.933 | 38.137 |
| (m ≈ 19) | 95% CI | 5.565 | 0.075 | 0.900 | 29.036 | 13.905 | 35.393 |
| 7.651 | 0.201 | 0.990 | 36.916 | 25.407 | 40.861 | ||
| 20% | Median | 6.951 | 0.153 | 0.950 | 35.263 | 19.946 | 39.694 |
| (m ≈ 12) | 95% CI | 5.857 | 0.086 | 0.900 | 31.082 | 14.074 | 36.427 |
| 8.139 | 0.218 | 0.990 | 39.625 | 28.892 | 43.619 | ||
| 10% | Median | 8.026 | 0.196 | 0.950 | 39.618 | 26.914 | 43.025 |
| (m ≈ 6) | 95% CI | 6.592 | 0.119 | 0.900 | 34.681 | 15.495 | 38.368 |
| 9.683 | 0.276 | 0.990 | 46.043 | 34.276 | 49.479 | ||
| Accuracy | Bias | Validity | Efficiency | ||||
|---|---|---|---|---|---|---|---|
| Available Traits % | MAE | PIW | PIW 95% CI | ||||
| 90% | Median | 5.942 | 0.121 | 0.953 | 30.276 | 15.745 | 36.278 |
| (m ≈ 57) | 95% CI | 5.699 | 0.110 | 0.940 | 28.748 | 14.339 | 34.599 |
| 6.198 | 0.131 | 0.965 | 31.797 | 18.048 | 37.772 | ||
| 80% | Median | 5.970 | 0.122 | 0.953 | 30.476 | 15.941 | 36.332 |
| (m ≈ 51) | 95% CI | 5.702 | 0.108 | 0.940 | 28.860 | 14.162 | 34.574 |
| 6.235 | 0.132 | 0.965 | 31.963 | 18.470 | 37.938 | ||
| 70% | Median | 6.028 | 0.124 | 0.953 | 30.711 | 16.182 | 36.518 |
| (m ≈ 44) | 95% CI | 5.737 | 0.108 | 0.938 | 28.960 | 14.013 | 34.697 |
| 6.376 | 0.137 | 0.965 | 32.583 | 19.643 | 38.435 | ||
| 60% | Median | 6.078 | 0.125 | 0.953 | 30.975 | 16.342 | 36.716 |
| (m ≈ 38) | 95% CI | 5.768 | 0.108 | 0.938 | 29.070 | 13.872 | 34.756 |
| 6.441 | 0.140 | 0.965 | 33.017 | 20.569 | 38.732 | ||
| 50% | Median | 6.173 | 0.128 | 0.953 | 31.502 | 16.684 | 37.040 |
| (m ≈ 32) | 95% CI | 5.819 | 0.111 | 0.938 | 29.410 | 13.724 | 34.989 |
| 6.648 | 0.146 | 0.968 | 33.900 | 22.110 | 39.305 | ||
| 40% | Median | 6.305 | 0.132 | 0.953 | 32.146 | 17.153 | 37.511 |
| (m ≈ 25) | 95% CI | 5.903 | 0.114 | 0.935 | 29.839 | 13.905 | 35.130 |
| 6.797 | 0.153 | 0.968 | 34.565 | 23.287 | 40.214 | ||
| 30% | Median | 6.501 | 0.138 | 0.953 | 33.097 | 17.923 | 38.203 |
| (m ≈ 19) | 95% CI | 6.046 | 0.118 | 0.935 | 30.583 | 13.899 | 35.468 |
| 7.096 | 0.163 | 0.965 | 35.986 | 25.377 | 40.943 | ||
| 20% | Median | 6.957 | 0.154 | 0.953 | 35.321 | 19.986 | 39.742 |
| (m ≈ 12) | 95% CI | 6.316 | 0.127 | 0.935 | 32.096 | 14.117 | 36.479 |
| 7.674 | 0.184 | 0.968 | 38.931 | 28.768 | 43.707 | ||
| 10% | Median | 7.952 | 0.192 | 0.955 | 39.733 | 26.846 | 43.076 |
| (m ≈ 6) | 95% CI | 6.968 | 0.154 | 0.940 | 35.229 | 15.515 | 38.419 |
| 9.214 | 0.256 | 0.973 | 46.437 | 34.087 | 49.551 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Navega, D.; Costa, E.; Cunha, E. Adult Skeletal Age-at-Death Estimation through Deep Random Neural Networks: A New Method and Its Computational Analysis. Biology 2022, 11, 532. https://doi.org/10.3390/biology11040532
Navega D, Costa E, Cunha E. Adult Skeletal Age-at-Death Estimation through Deep Random Neural Networks: A New Method and Its Computational Analysis. Biology. 2022; 11(4):532. https://doi.org/10.3390/biology11040532
Chicago/Turabian StyleNavega, David, Ernesto Costa, and Eugénia Cunha. 2022. "Adult Skeletal Age-at-Death Estimation through Deep Random Neural Networks: A New Method and Its Computational Analysis" Biology 11, no. 4: 532. https://doi.org/10.3390/biology11040532
APA StyleNavega, D., Costa, E., & Cunha, E. (2022). Adult Skeletal Age-at-Death Estimation through Deep Random Neural Networks: A New Method and Its Computational Analysis. Biology, 11(4), 532. https://doi.org/10.3390/biology11040532








