A Continuous Markov-Chain Model for the Simulation of COVID-19 Epidemic Dynamics
Abstract
:Simple Summary
Abstract
1. Introduction
2. Methods
2.1. Derivation of the Markov-Chain Model for COVID-19 Infection
2.1.1. Derivation of a Simplified Markov-Chain Model without Considering COVID-19 Mutation
2.1.2. Derivation of a Comprehensive Markov-Chain Model with Terms for Virus Mutation and Age Impact
2.2. Model Framework
3. Results
3.1. An Illustration of the Simplified Markov-Chain Model
3.2. The Prediction Capacity of the Markov-Chain Model Is Significantly Better Than That of the SIR Model
3.3. There Is No Simple Derivation Relationship between the Virus Basic Reproduction Number R0 and the Final Herd Immunity Threshold
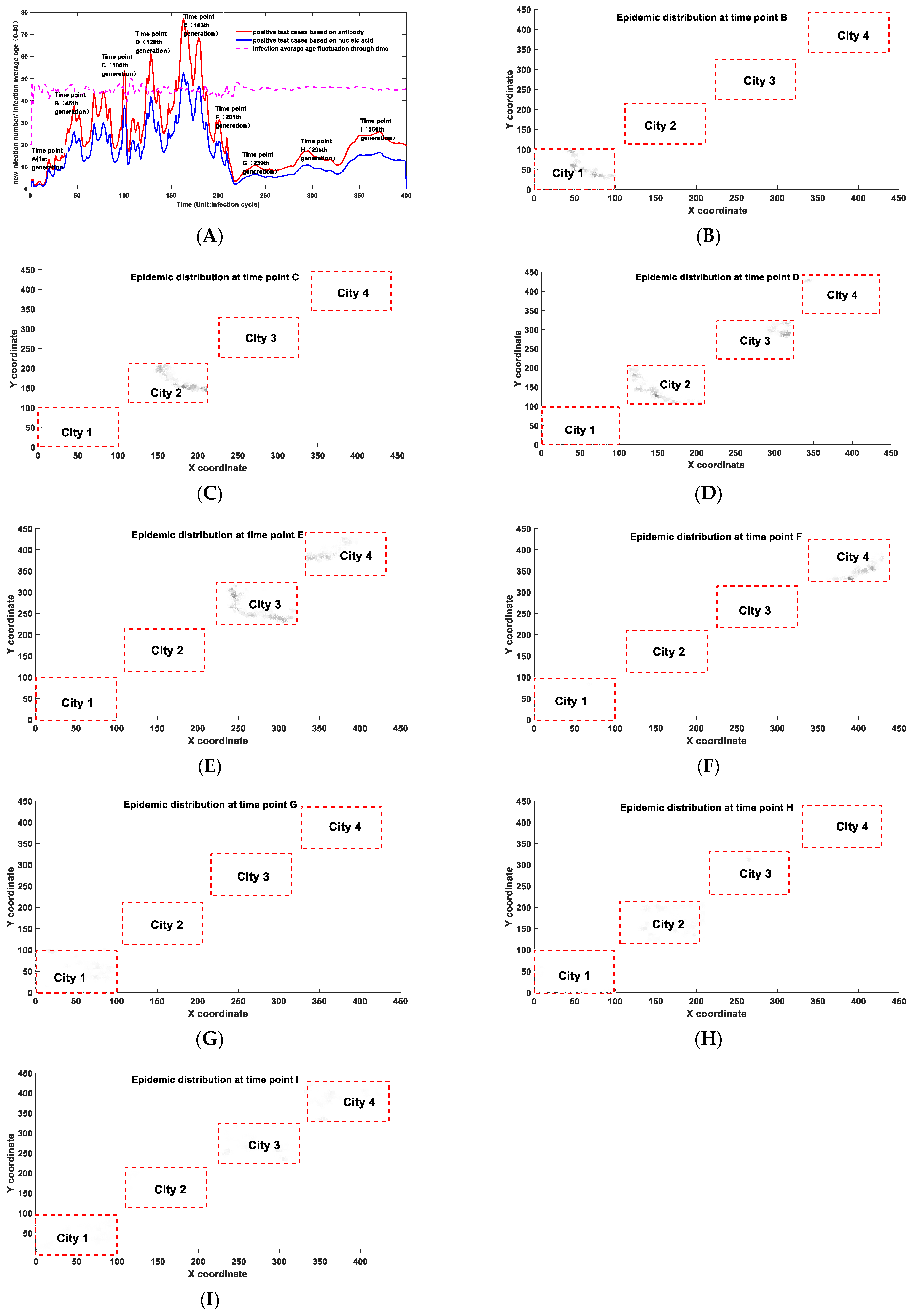
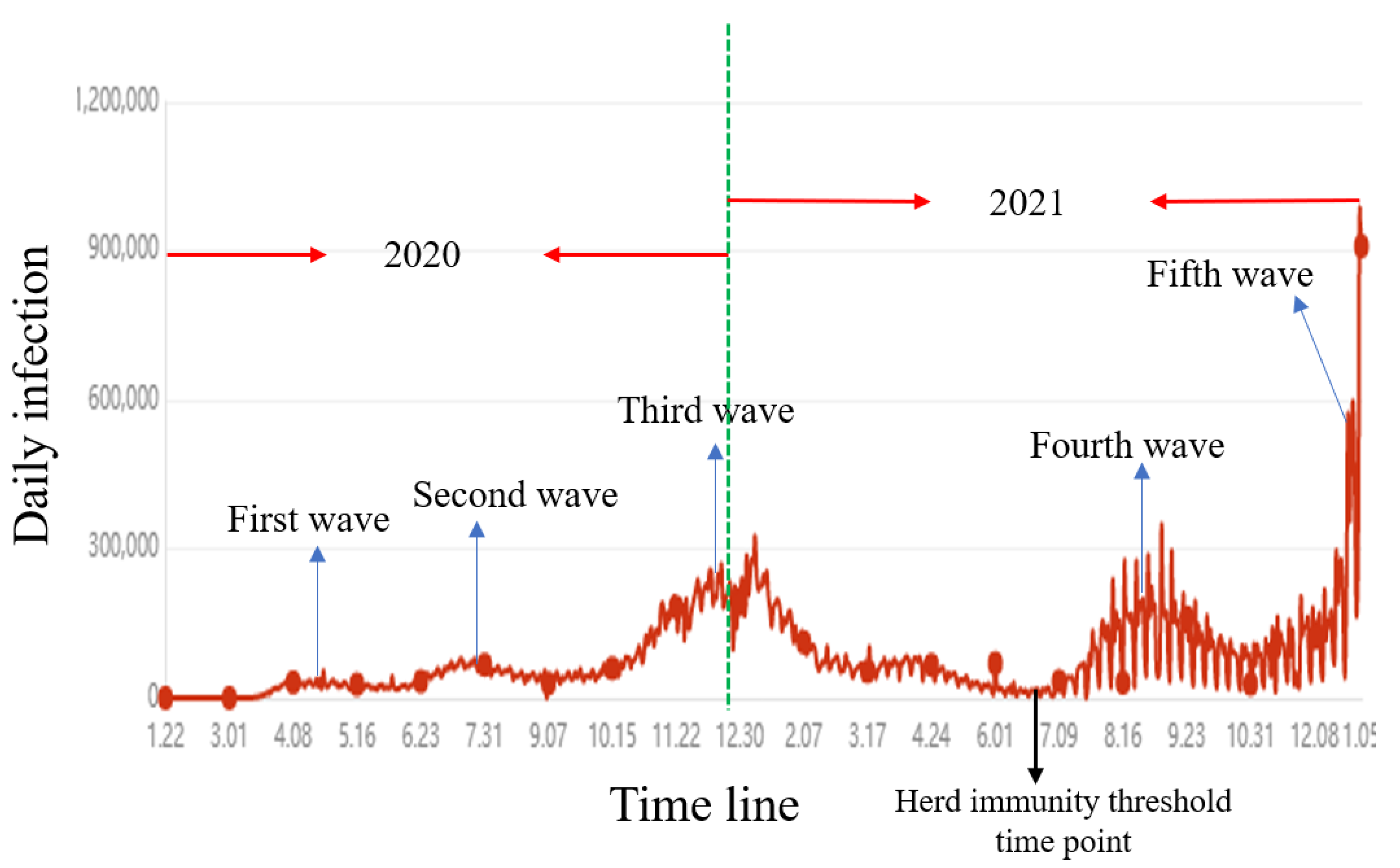
3.4. Simulation of the COVID-19 Epidemic Using a Complicated Markov-Chain Model
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Randolph, H.E.; Barreiro, L.B. Herd immunity: Understanding COVID-19. Immunity 2020, 52, 737–741. [Google Scholar] [CrossRef] [PubMed]
- Britton, T.; Ball, F.; Trapman, P. A mathematical model reveals the influence of population heterogeneity on herd immunity to SARS-CoV-2. Science 2020, 369, 846–849. [Google Scholar] [CrossRef] [PubMed]
- May, R.M. Infectious Diseases of Humans: Dynamics and Control; Oxford University Press: Oxford, UK, 1991. [Google Scholar]
- Diekmann, O.; Heesterbeek, A.P. Mathematical Epidemiology of Infectious Diseases: Model Building, Analysis and Interpretation; Wiley & Sons: New York, NY, USA, 2000. [Google Scholar]
- Hethcote, H.W. The mathematics of infectious diseases. SIAM Rev. 2000, 42, 599–653. [Google Scholar] [CrossRef] [Green Version]
- Banerjee, S.; Khajanchi, S.; Chaudhuri, S. A mathematical model to elucidate brain tumor abrogation by immunotherapy with T11 target structure. PLoS ONE 2015, 10, e0123611. [Google Scholar] [CrossRef] [Green Version]
- Kermack, W.O.; McKendrick, A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. London. Ser. A Contain. Pap. A Math. Phys. Character 1927, 115, 700–721. [Google Scholar]
- Chen, T.M.; Rui, J.; Wang, Q.-P.; Zhao, Z.-Y.; Cui, J.-A.; Yin, L. A mathematical model for simulating the phase-based transmissibility of a novel coronavirus. Infect. Dis. Poverty 2020, 9, 24. [Google Scholar] [CrossRef] [Green Version]
- Sarkar, K.; Khajanchi, S.; Nieto, J.J. Modeling and forecasting the COVID-19 pandemic in India. Chaos Solitons Fractals 2020, 139, 110049. [Google Scholar] [CrossRef]
- Khajanchi, S.; Sarkar, K.; Mondal, J.; Nisar, K.S.; Abdelwahab, S.F. Mathematical modeling of the COVID-19 pandemic with intervention strategies. Results Phys. 2021, 25, 104285. [Google Scholar] [CrossRef]
- Samui, P.; Mondal, J.; Khajanchi, S. A mathematical model for COVID-19 transmission dynamics with a case study of India. Chaos Solitons Fractals 2020, 140, 110173. [Google Scholar] [CrossRef]
- Diekmann, O.; Heesterbeek, A.P.; Metz, A. On the definition and the computation of the basic reproduction ratio R 0 in models for infectious diseases in heterogeneous populations. J. Math. Biol. 1990, 28, 365–382. [Google Scholar] [CrossRef] [Green Version]
- Van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Khajanchi, S.; Bera, S.; Roy, T.K. Mathematical analysis of the global dynamics of a HTLV-I infection model, considering the role of cytotoxic T-lymphocytes. Math. Comput. Simul. 2021, 180, 354–378. [Google Scholar] [CrossRef]
- Wu, Z.; McGoogan, M. Characteristics of and important lessons from the coronavirus disease 2019 (COVID-19) outbreak in China: Summary of a report of 72 314 cases from the Chinese Center for Disease Control and Prevention. JAMA 2020, 323, 1239–1242. [Google Scholar] [CrossRef] [PubMed]
- Khan, M.A.; Atangana, A. Modeling the dynamics of novel coronavirus (2019-nCov) with fractional derivative. Alex. Eng. J. 2020, 59, 2379–2389. [Google Scholar] [CrossRef]
- Das, D.K.; Khajanchi, S.; Kar, T.K. The impact of the media awareness and optimal strategy on the prevalence of tuberculosis. Appl. Math. Comput. 2020, 366, 124732. [Google Scholar] [CrossRef]
- Khan, M.A. Parameter estimation and fractional derivatives of dengue transmission model. AIMS Math. 2020, 5, 2758–2779. [Google Scholar]
- Khan, M.A.; Shah, S.W.; Ullah, S.; Gómez-Aguilar, J.F. A dynamical model of asymptomatic carrier zika virus with optimal control strategies. Nonlinear Anal. Real World Appl. 2019, 50, 144–170. [Google Scholar] [CrossRef]
- Calafiore, G.C.; Novara, C.; Possieri, C. A time-varying SIRD model for the COVID-19 contagion in Italy. Annu. Rev. Control 2020. [Google Scholar] [CrossRef]
- Fanelli, D.; Piazza, F. Analysis and forecast of COVID-19 spreading in China, Italy and France. Chaos Solitons Fractals 2020, 134, 109761. [Google Scholar] [CrossRef]
- Mohamadou, Y.; Halidou, A.; Kapen, P.T. A review of mathematical modeling, artificial intelligence and datasets used in the study, prediction and management of COVID-19. Appl. Intell. 2020, 50, 3913–3925. [Google Scholar] [CrossRef]
- Kucharski, A.; Russell, T.W.; Diamond, C.; Liu, Y.; Edmunds, J.; Funk, S.; Eggo, R.M. Early dynamics of transmission and control of COVID-19: A mathematical modelling study. Lancet Infect. Dis. 2020, 20, 553–558. [Google Scholar] [CrossRef] [Green Version]
- Omori, R.; Matsuyama, R.; Nakata, Y. The age distribution of mortality from novel coronavirus disease (COVID-19) suggests no large difference of susceptibility by age. Sci. Rep. 2020, 10, 16642. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Wei, F.; Hu, L.; Wen, L.; Chen, K. Epidemiology and clinical characteristics of COVID-19. Arch. Iran. Med. 2020, 23, 268–271. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Topîrceanu, A.; Precup, R.E. A novel geo-hierarchical population mobility model for spatial spreading of resurgent epidemics. Sci. Rep. 2021, 11, 14341. [Google Scholar] [CrossRef] [PubMed]
- Cacciapaglia, G.; Cot, C.; Sannino, F. Multiwave pandemic dynamics explained: How to tame the next wave of infectious diseases. Sci. Rep. 2021, 11, 6638. [Google Scholar] [CrossRef]
- Menda, K.R.; Laird, L.; Kochenderfer, M.J.; Caceres, R.S. Explaining COVID-19 Outbreaks with Reactive SEIRD Models. MedRxiv 2021. [Google Scholar] [CrossRef]
- Beira, M.; Sebastião, P. A differential equations model-fitting analysis of COVID-19 epidemiological data to explain multi-wave dynamics. Sci. Rep. 2021, 11, 16312. [Google Scholar] [CrossRef]
- Martsenyuk, V.; Bernas, M.; Klos-Witkowska, A. Two-Strain COVID-19 Model Using Delayed Dynamic System and Big Data. IEEE Access 2021, 9, 113866–113878. [Google Scholar] [CrossRef]
- Liu, X.; Zheng, X.; Balachandran, B. COVID-19: Data-driven dynamics, statistical and distributed delay models, and observations. Nonlinear Dyn. 2020, 101, 1527–1543. [Google Scholar] [CrossRef]
- Liao, Z.; Lan, P.; Fan, X.; Kelly, B.; Innes, A.; Liao, Z. SIRVD-DL: A COVID-19 deep learning prediction model based on time-dependent SIRVD. Comput. Biol. Med. 2021, 138, 104868. [Google Scholar] [CrossRef]
- Zeroual, A.; Harrou, F.; Dairi, A.; Sun, Y. Deep learning methods for forecasting COVID-19 time-Series data: A Comparative study. Chaos Solitons Fractals 2020, 140, 110121. [Google Scholar] [CrossRef] [PubMed]
- Devaraj, J.; Elavarasan, R.M.; Pugazhendhi, R.; Shafiullah, G.M.; Ganesan, S.; Jeysree, A.K.; Khan, I.A.; Hossain, E. Forecasting of COVID-19 cases using deep learning models: Is it reliable and practically significant? Results Phys. 2021, 21, 103817. [Google Scholar] [CrossRef] [PubMed]
- Wilensky, U.; Rand, W. An Introduction to Agent-Based Modeling Modeling Natural, Social, and Engineered Complex Systems with NetLogo; MIT Press: Cambridge, MA, USA, 2010. [Google Scholar]
- Banisch, S. Markov Chain Aggregation for Agent-Based Models; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Macal, C.M. Emergent structures from trust relationships in supply chains. In Proceedings of Agent 2004: Conference on Social Dynamics: Interaction, Reflexivity and Emergence, 7–9 October 2004; Macal, C., Sallach, D., North, M., Eds.; Argonne National Laboratory: Chicago, IL, USA, 2004; pp. 743–760. [Google Scholar]
- Kohler, T.A.; Gumerman, G.J.; Reynolds, R.G. Simulating ancient societies. Sci. Am. 2005, 293, 77–84. [Google Scholar] [CrossRef] [PubMed]
- Folcik, V.A.; An, G.C.; Orosz, C.G. The basic immune simulator: An agent-based model to study the interactions between innate and adaptive immunity. Theor. Biol. Med. Model. 2007, 4, 39. [Google Scholar] [CrossRef] [Green Version]
- Hoertel, N.; Blachier, M.; Blanco, C.; Olfson, M.; Massetti, M.; Rico, M.S.; Limosin, F.; Leleu, H. A stochastic agent-based model of the SARS-CoV-2 epidemic in France. Nat. Med. 2020, 26, 1417–1421. [Google Scholar] [CrossRef]
- Hinch, R.; Probert, W.J.M.; Nurtay, A.; Kendall, M.; Wymant, C.; Hall, M.; Lythgoe, K.; Cruz, A.B.; Zhao, L.; Stewart, A. OpenABM-Covid19—An agent-based model for non-pharmaceutical interventions against COVID-19 including contact tracing. PLoS Comput. Biol. 2021, 17, e1009146. [Google Scholar] [CrossRef]
- Cuevas, E. An agent-based model to evaluate the COVID-19 transmission risks in facilities. Comput. Biol. Med. 2020, 121, 103827. [Google Scholar] [CrossRef]
- Schelling, T.C. Dynamic models of segregation. Math. Sociol. 1971, 1, 143–186. [Google Scholar] [CrossRef]
- Sayama, H. Introduction to the Modeling and Analysis of Complex Systems; Open SUNY Textbooks, Milne Library: Oneonta, NY, USA, 2015. [Google Scholar]
- Privault, N. Understanding Markov Chains. Examples and Applications; Springer: Singapore, 2013; pp. 357–358. [Google Scholar]
- Meyn, S.P.; Tweedie, R.L. Markov Chains and Stochastic Stability; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Douc, R.; Moulines, E.; Priouret, P.; Soulier, P. Markov Chains; Springer International Publishing: Cham, Switzerland, 2018. [Google Scholar]
- Bernal, J.L.; Andrews, N.; Gower, C.; Eileen, G.; Ruth, S.; Simon, T.; Julia, S.; Elise, T.; Natalie, G.; Gavin, D.; et al. Effectiveness of COVID-19 vaccines against the B. 1.617. 2 variant. MedRxiv 2021. [Google Scholar] [CrossRef]
- Hansen, C.H.; Michlmayr, D.; Gubbels, S.M.; Mølbak, P.K.; Ethelberg, P.S. Assessment of protection against reinfection with SARS-CoV-2 among 4 million PCR-tested individuals in Denmark in 2020: A population-level observational study. Lancet 2021, 397, 1204–1212. [Google Scholar] [CrossRef]
- Sabino, E.C.; Buss, L.F.; Carvalho, M.P.S.; Prete, C.A.; Crispim, M.A.E.; Fraiji, N.A.; Pereira, R.H.M.; Parag, K.V.; da Silva Peixoto, P.; Kraemer, M.U.G. Resurgence of COVID-19 in Manaus, Brazil, despite high seroprevalence. Lancet 2021, 397, 452–455. [Google Scholar] [CrossRef]
- Poustchi, H.; Darvishian, M.; Mohammadi, Z.; Shayanrad, A.; Delavari, A.; Bahadorimonfared, A.; Eslami, S.; Javanmard, S.H.; Shakiba, E.; Somi, M.H.; et al. SARS-CoV-2 antibody seroprevalence in the general population and high-risk occupational groups across 18 cities in Iran: A population-based cross-sectional study. Lancet Infect. Dis. 2021, 21, 473–481. [Google Scholar] [CrossRef]
- Covid: More than 90% of Adults in England Have Some Protection against Coronavirus. Available online: https://www.itv.com/news/2021-07-21/covid-more-than-90-of-adults-in-england-have-some-protection-against-coronavirus-ons (accessed on 1 July 2021).
- Why Israel Fears a Third Wave Despite Vaccination. Available online: https://www.archyde.com/why-israel-fears-a-third-wave-despite-vaccination/ (accessed on 15 August 2021).
- Bendavid, E.; Mulaney, B.; Sood, N.; Shah, S.; Bromley-Dulfano, R.; Lai, C.; Weissberg, Z.; Saavedra-Walker, R.; Tedrow, J.; Bogan, A. Covid-19 antibody seroprevalence in Santa Clara county, california. Int. J. Epidemiol. 2021, 50, 410–419. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.E.; Jeong, H.S.; Yu, Y.; Shin, S.U.; Kim, S.; Oh, T.H.; Kim, U.J.; Kang, S.-J.; Jang, H.-C.; Jung, S.-I. Viral kinetics of SARS-CoV-2 in asymptomatic carriers and presymptomatic patients. Int. J. Infect. Dis. 2020, 95, 441–443. [Google Scholar] [CrossRef] [PubMed]
- Gorzalski, A.; Hartley, P.; Laverdure, C.; Kerwin, H.; Tillett, R.; Verma, S.; Rossetto, C.; Morzunov, S.; van Hooser, S.; Pandori, M.W. Characteristics of viral specimens collected from asymptomatic and fatal cases of COVID-19. J. Biomed. Res. 2020, 34, 431. [Google Scholar] [CrossRef]
- Yang, T.; Shen, K.; He, S.; Li, E.; Sun, P.; Chen, P.; Zuo, L.; Hu, J.; Mo, Y.; Zhang, W.; et al. CovidNet: To bring data transparency in the era of COVID-19. arXiv 2005, arXiv:2005.10948. [Google Scholar]
- China’s Latest COVID-19 Resurgence as a Challenge, But Controllable. Available online: http://www.china.org.cn/china/2021-08/10/content_77683411.htm (accessed on 15 August 2021).
- Zhang, X.; Ma, R.; Wang, L. Predicting turning point, duration and attack rate of COVID-19 outbreaks in major Western countries. Chaos Solitons Fractals 2020, 135, 109829. [Google Scholar] [CrossRef]
- Postnikov, E.B. Estimation of COVID-19 dynamics “on a back-of-envelope”: Does the simplest SIR model provide quantitative parameters and predictions? Chaos Solitons Fractals 2020, 135, 109841. [Google Scholar] [CrossRef]
- Mandal, M.; Jana, S.; Nandi, S.K.; Khatua, A.; Adak, S.; Kar, T.K. A model based study on the dynamics of COVID-19: Prediction and control. Chaos Solitons Fractals 2020, 136, 109889. [Google Scholar] [CrossRef]
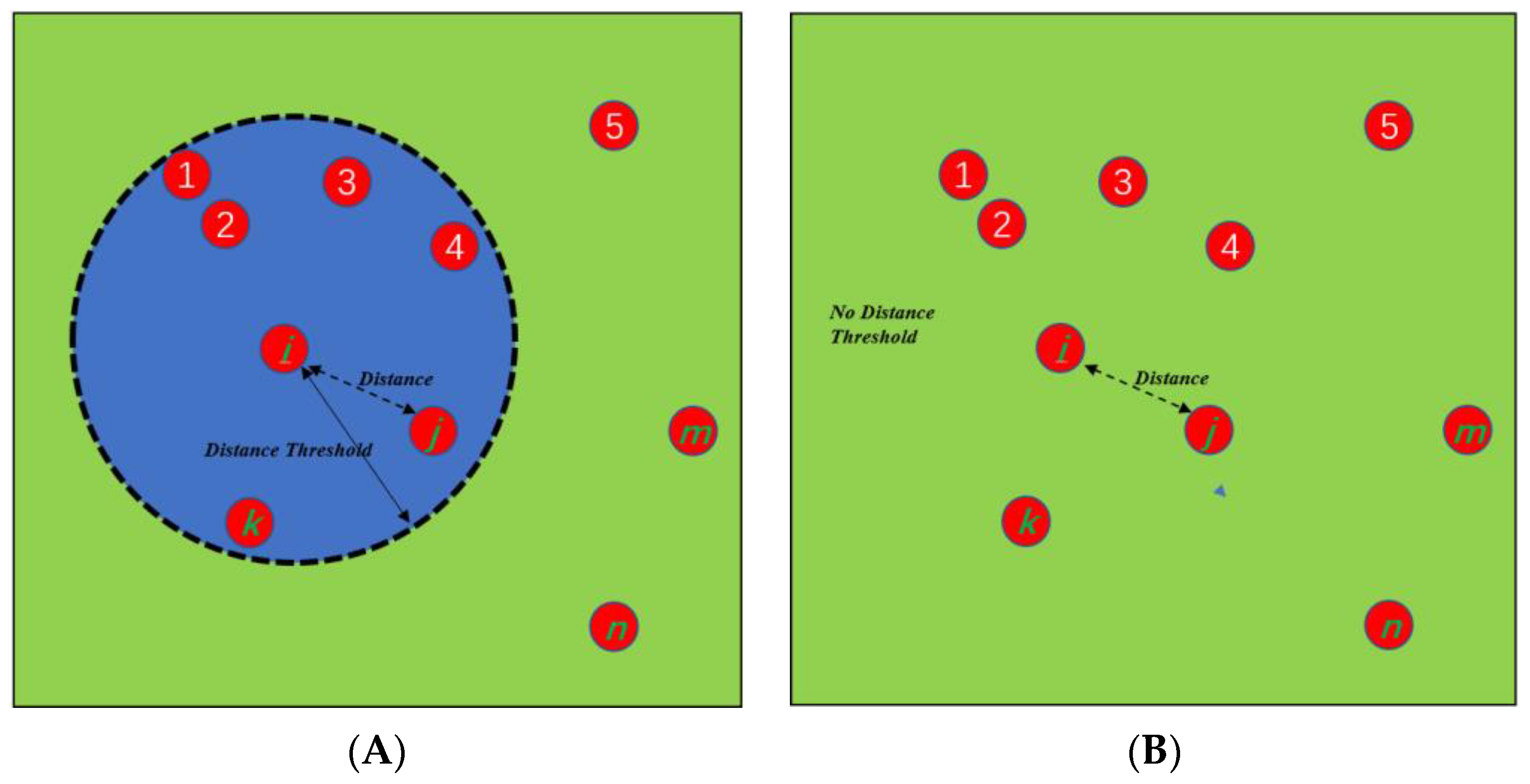
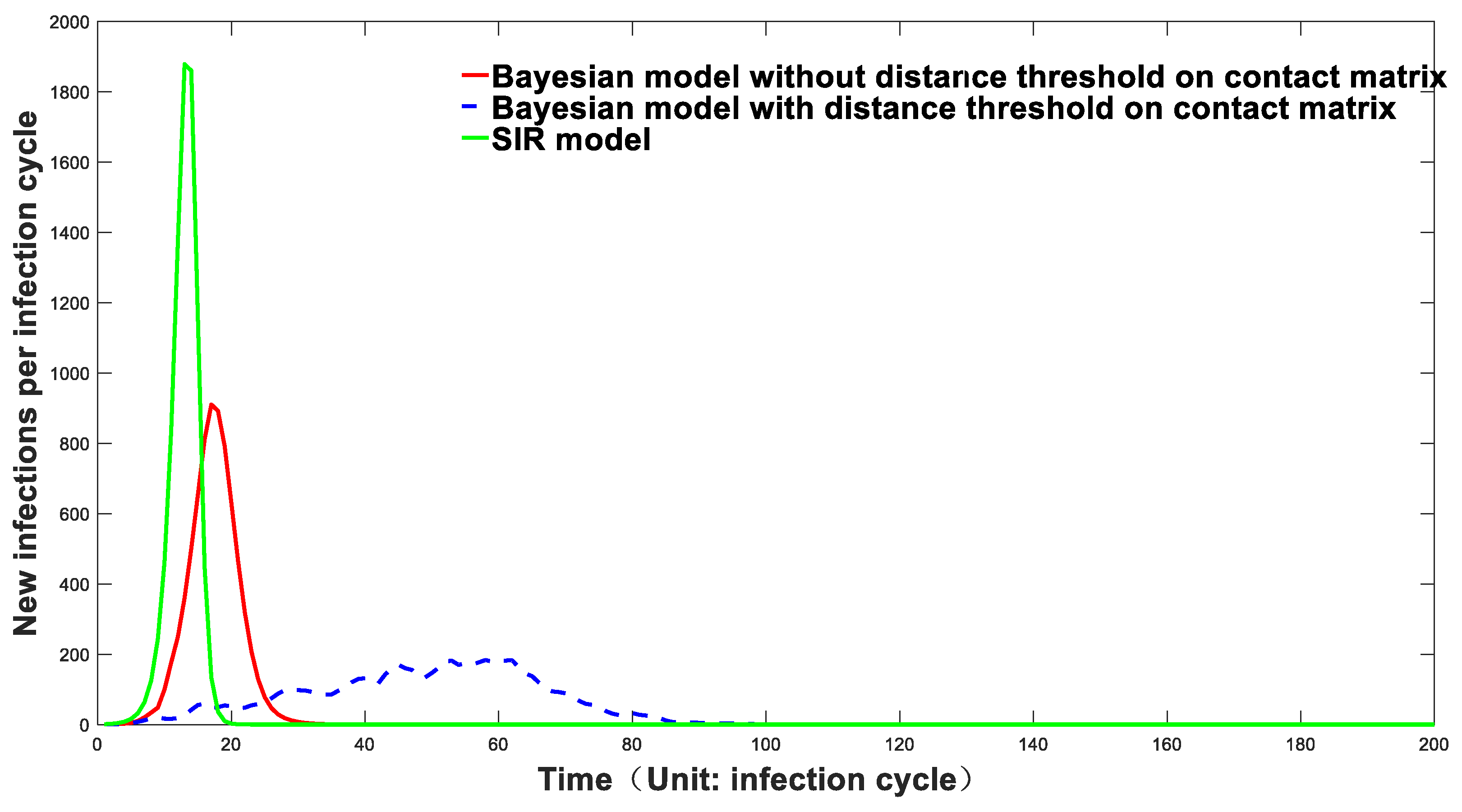
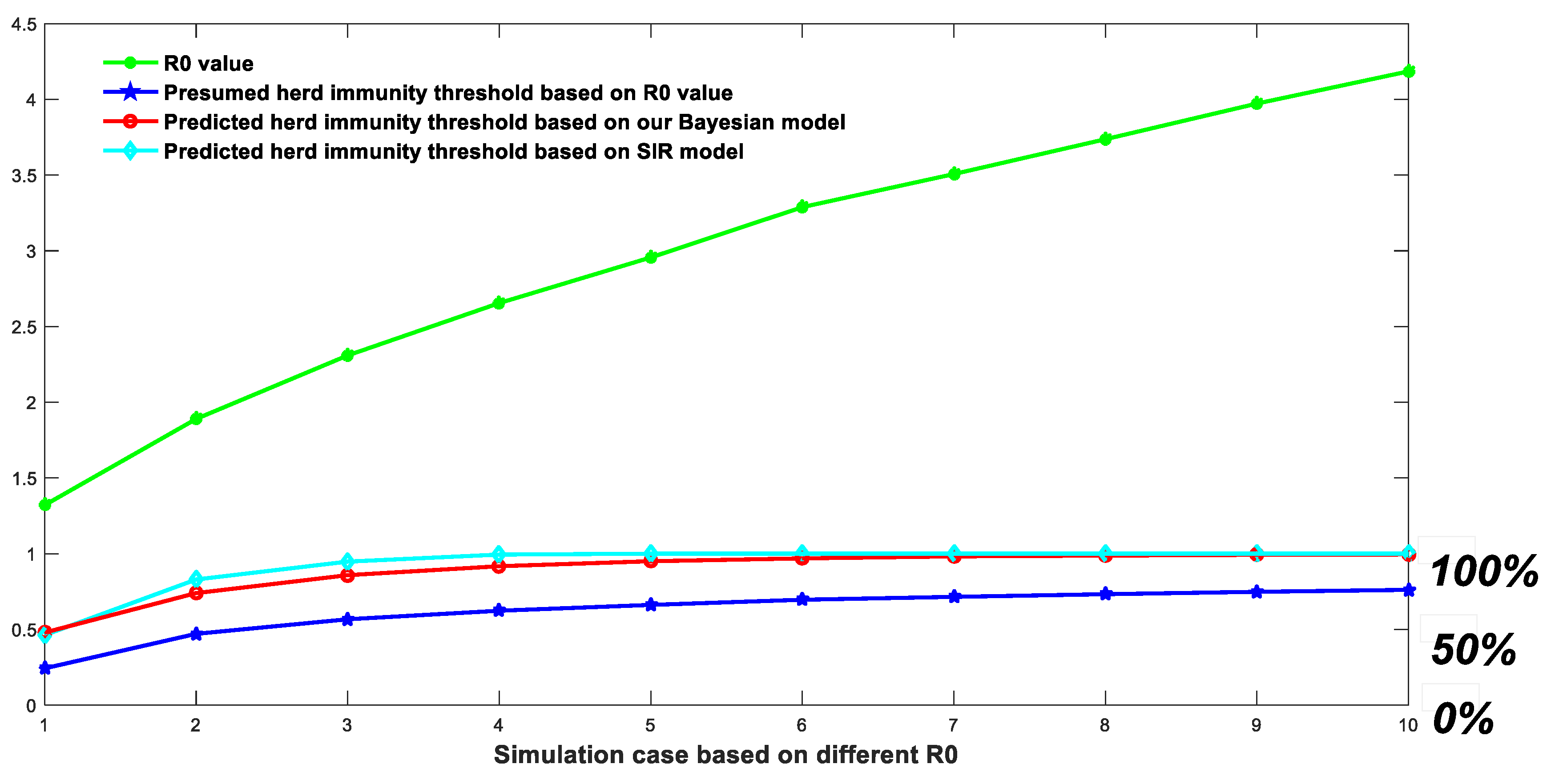
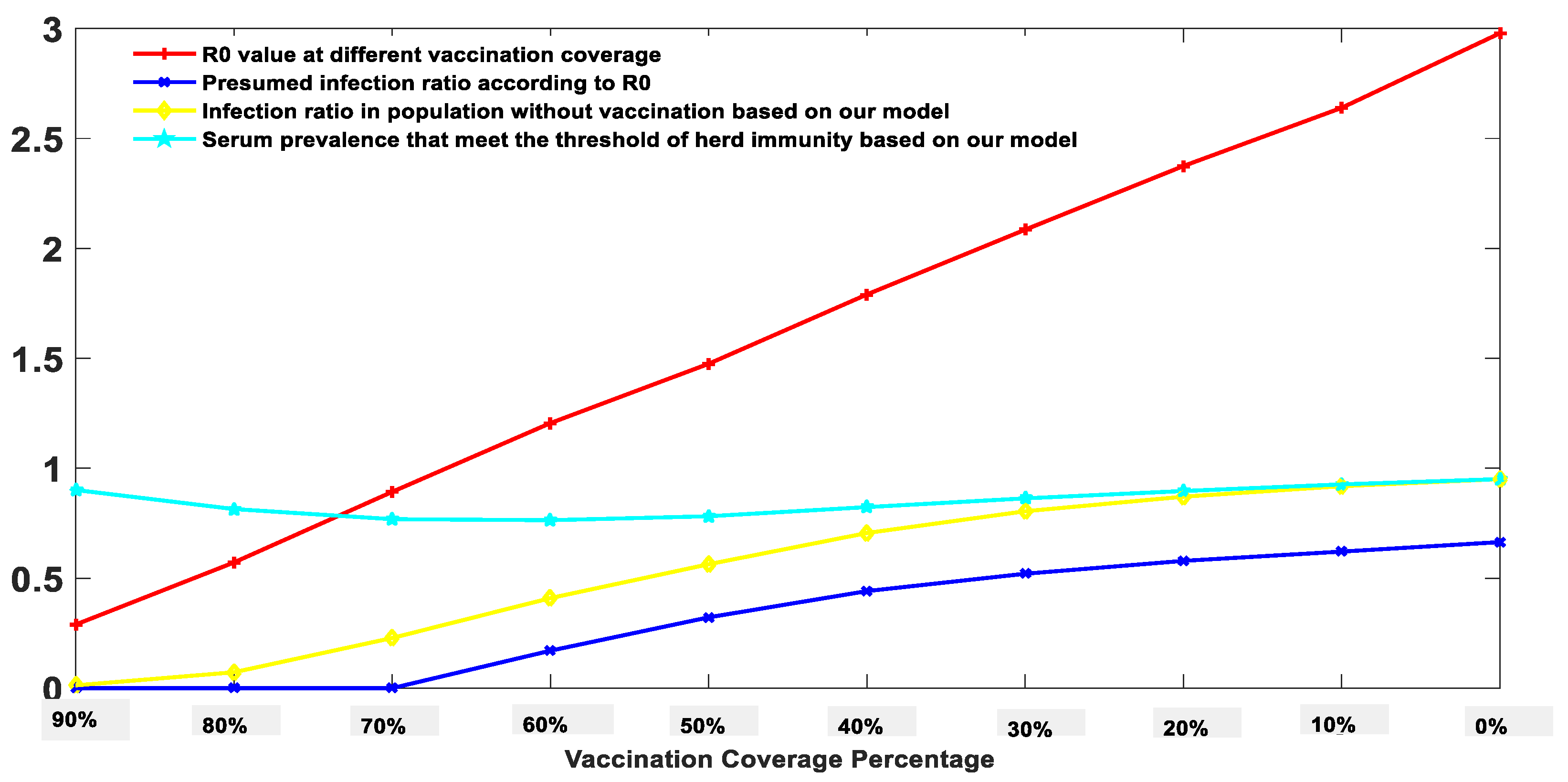
| Time Points | Infection Possibility | |
|---|---|---|
| 1 | 1 | |
| 2 | 1 − | |
| 3 | 1 − | |
| k |
| Time Points | Infection Possibility | |
|---|---|---|
| 1 | 1 | |
| 2 | 1 − | |
| 3 | 1 − | |
| k |
| Interaction Matrix | A | B | C |
|---|---|---|---|
| A | 0 | 0.8 | 0.5 |
| B | 0.8 | 0 | 0.6 |
| C | 0.5 | 0.6 | 0 |
| A | B | C | |
|---|---|---|---|
| 1st generation | 1 | 0 | 0 |
| 2nd generation | 0 | 0.8 | 0.5 |
| 3rd generation | 0 | 0.06 | 0.24 |
| 4th generation | 0 | 0.02016 | 0.00936 |
| Nth generation | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Z.; Zhang, H.; Huang, Z. A Continuous Markov-Chain Model for the Simulation of COVID-19 Epidemic Dynamics. Biology 2022, 11, 190. https://doi.org/10.3390/biology11020190
Xu Z, Zhang H, Huang Z. A Continuous Markov-Chain Model for the Simulation of COVID-19 Epidemic Dynamics. Biology. 2022; 11(2):190. https://doi.org/10.3390/biology11020190
Chicago/Turabian StyleXu, Zhaobin, Hongmei Zhang, and Zuyi Huang. 2022. "A Continuous Markov-Chain Model for the Simulation of COVID-19 Epidemic Dynamics" Biology 11, no. 2: 190. https://doi.org/10.3390/biology11020190
APA StyleXu, Z., Zhang, H., & Huang, Z. (2022). A Continuous Markov-Chain Model for the Simulation of COVID-19 Epidemic Dynamics. Biology, 11(2), 190. https://doi.org/10.3390/biology11020190






