Advanced Composite Retrofit of RC Columns and Frames with Prior Damages—Pseudodynamic Finite Element Analyses and Design Approaches
Abstract
:1. Introduction
2. Explicit Dynamics Finite Element Modelling
2.1. Concrete
2.2. Longitudinal Steel Bars and Steel Stirrups
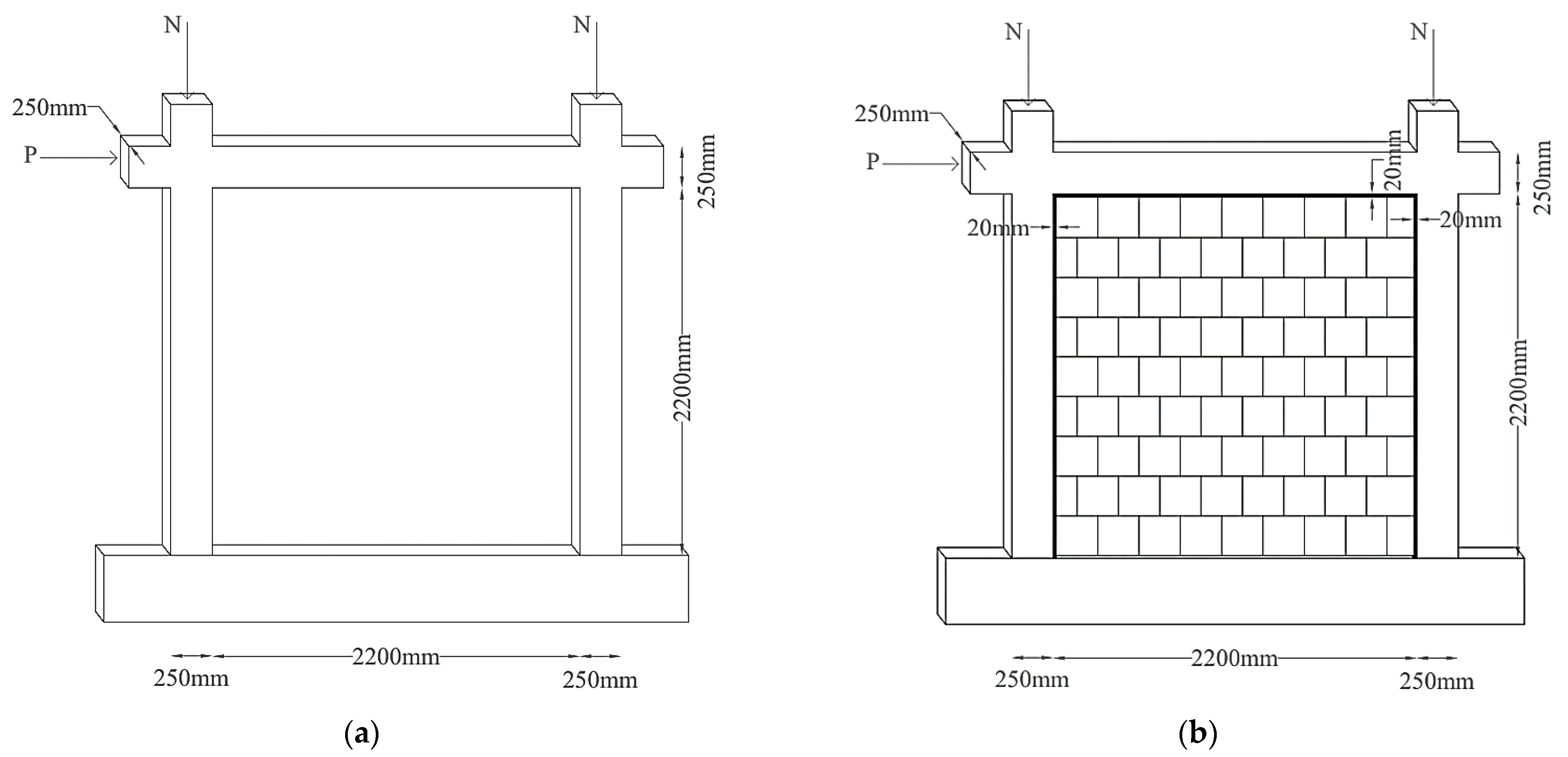
2.3. Brick Infill
2.4. Carbon Fiber Reinforced Polymers (CFRP)
2.5. Polyurethane Flexible Joints (PUFJ)
2.6. Element Types
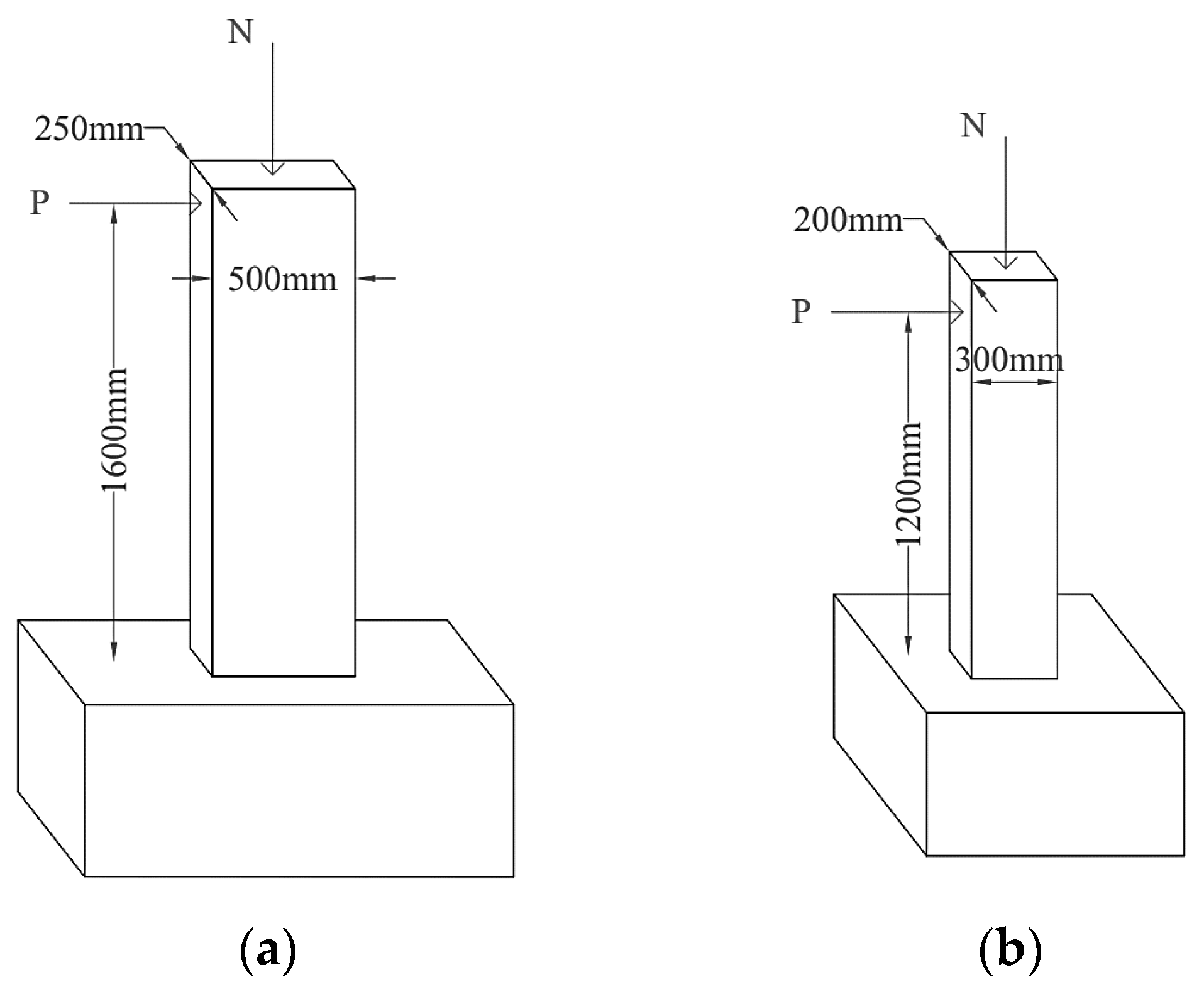
3. FE Models of Published RC Columns and Frames Tests
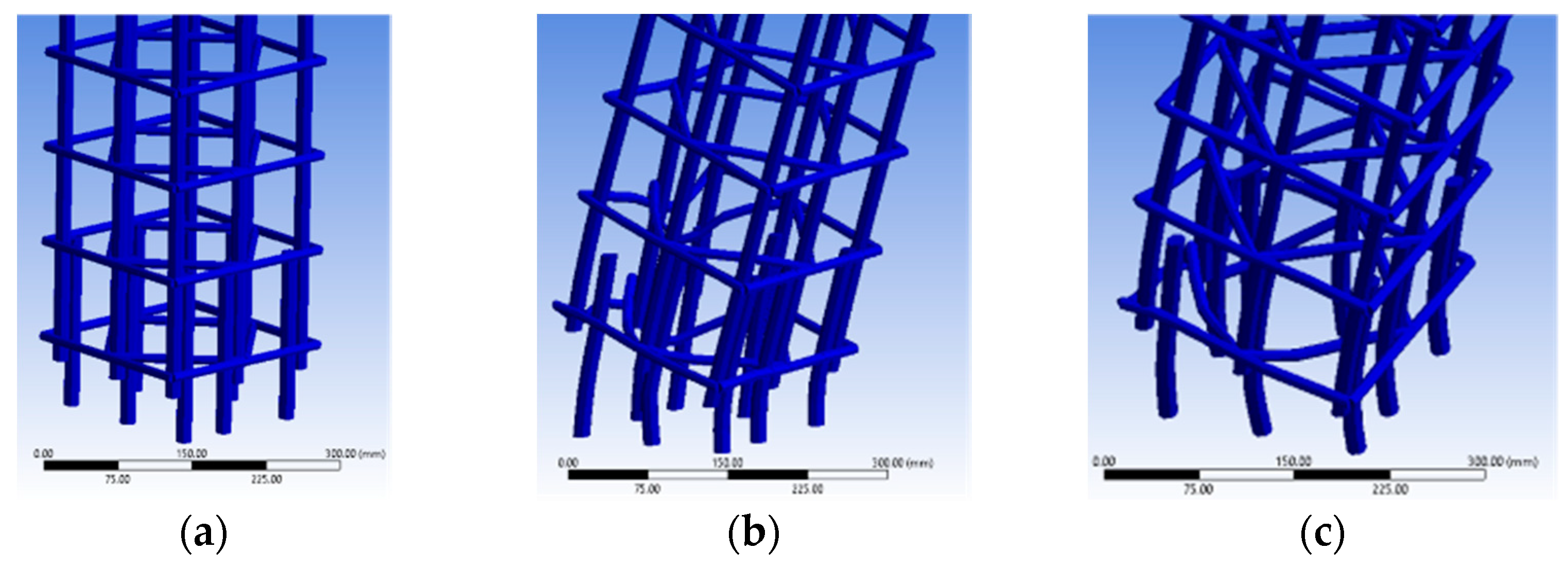
3.1. RC Columns with Lap Splices
3.2. RC Columns with Corroded Steel Reinforcement
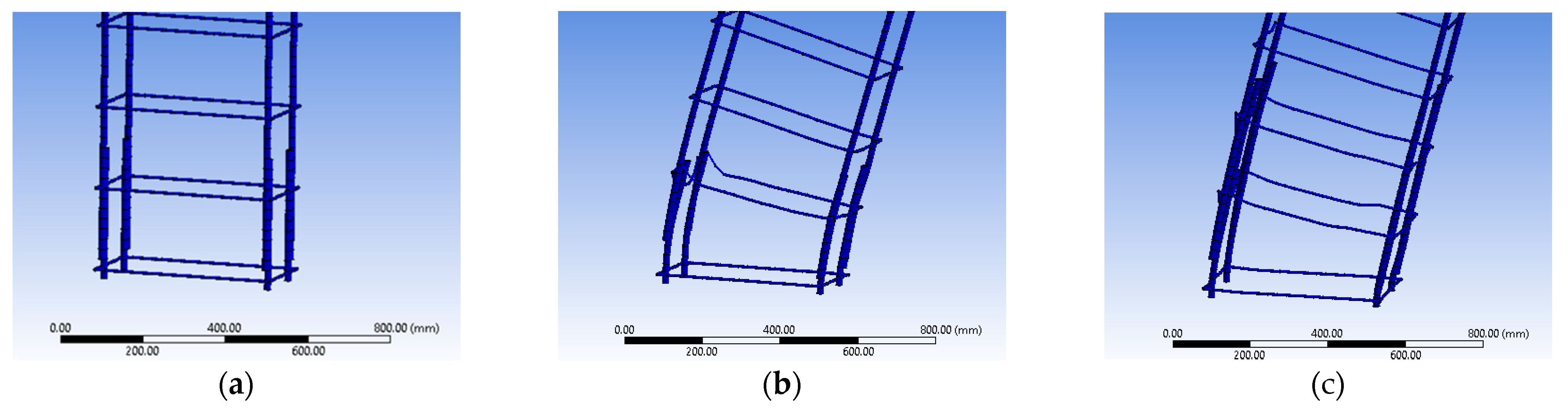
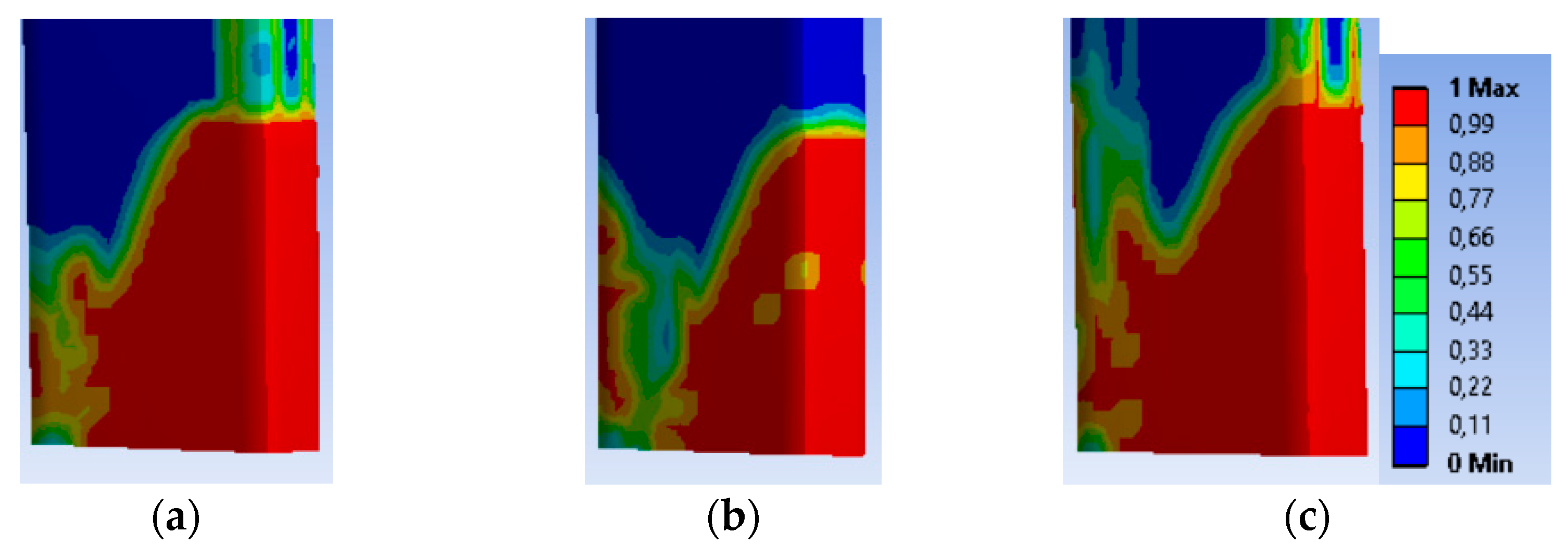
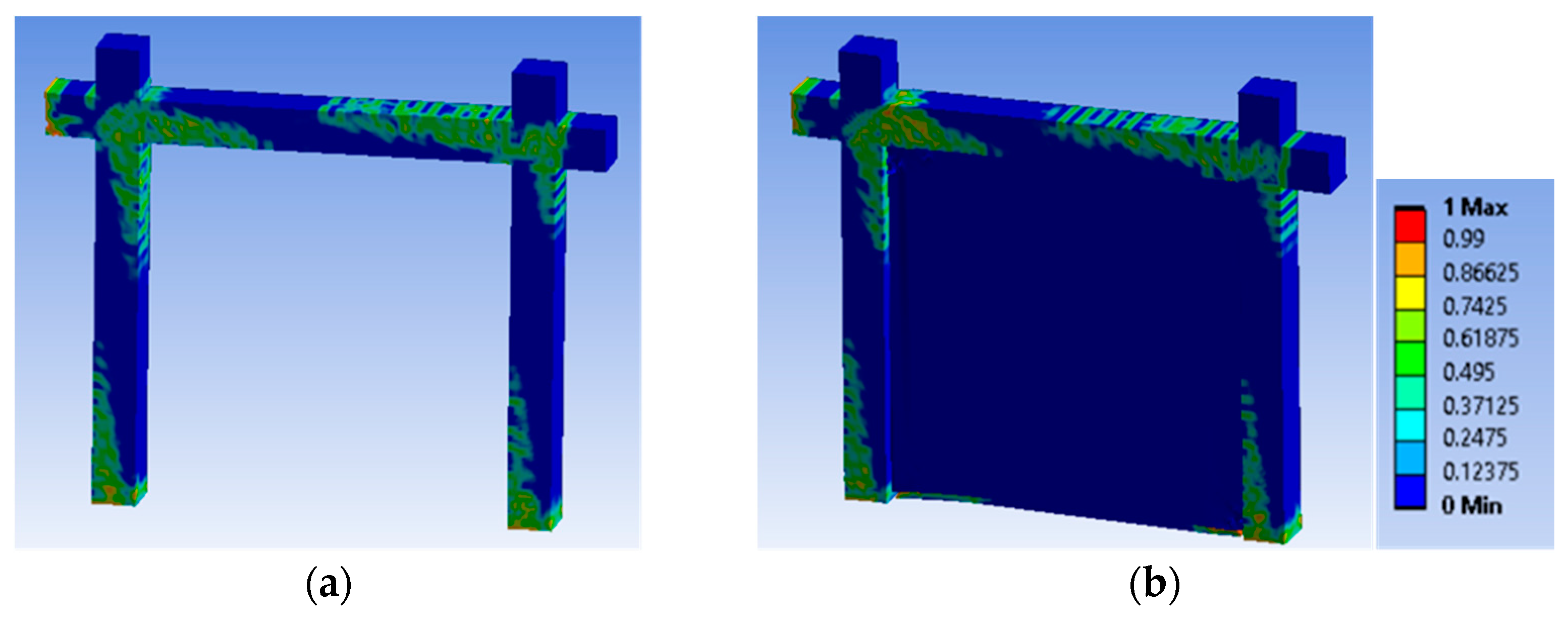
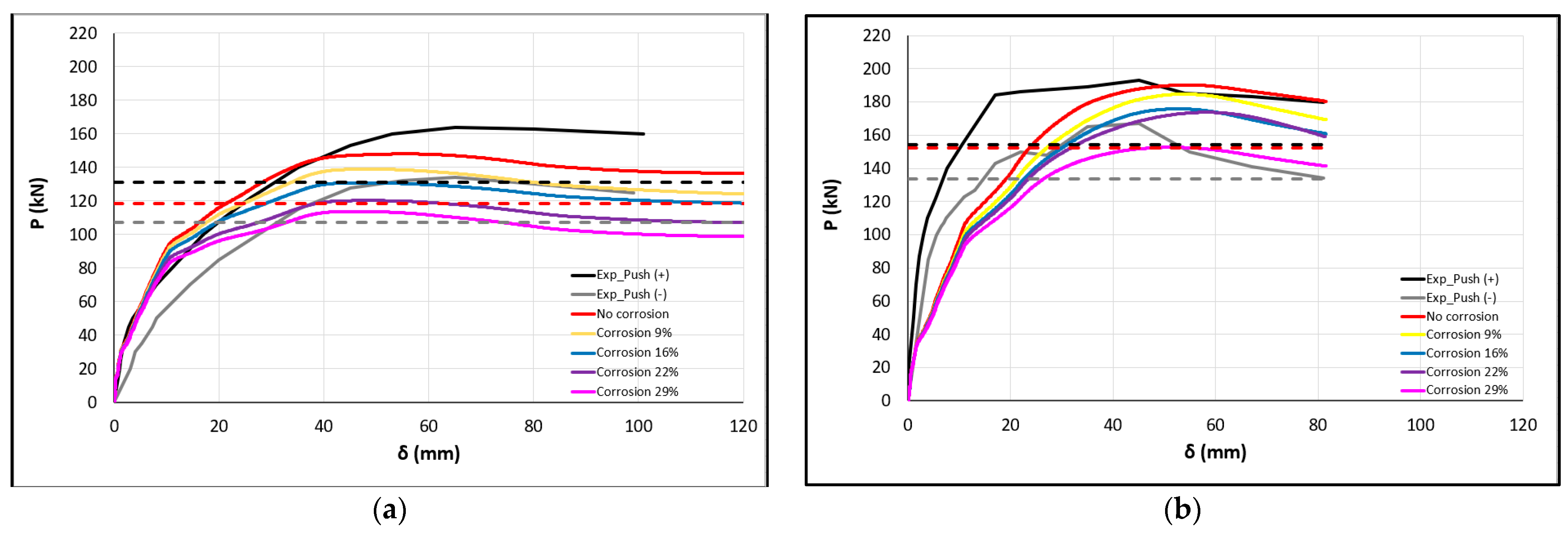
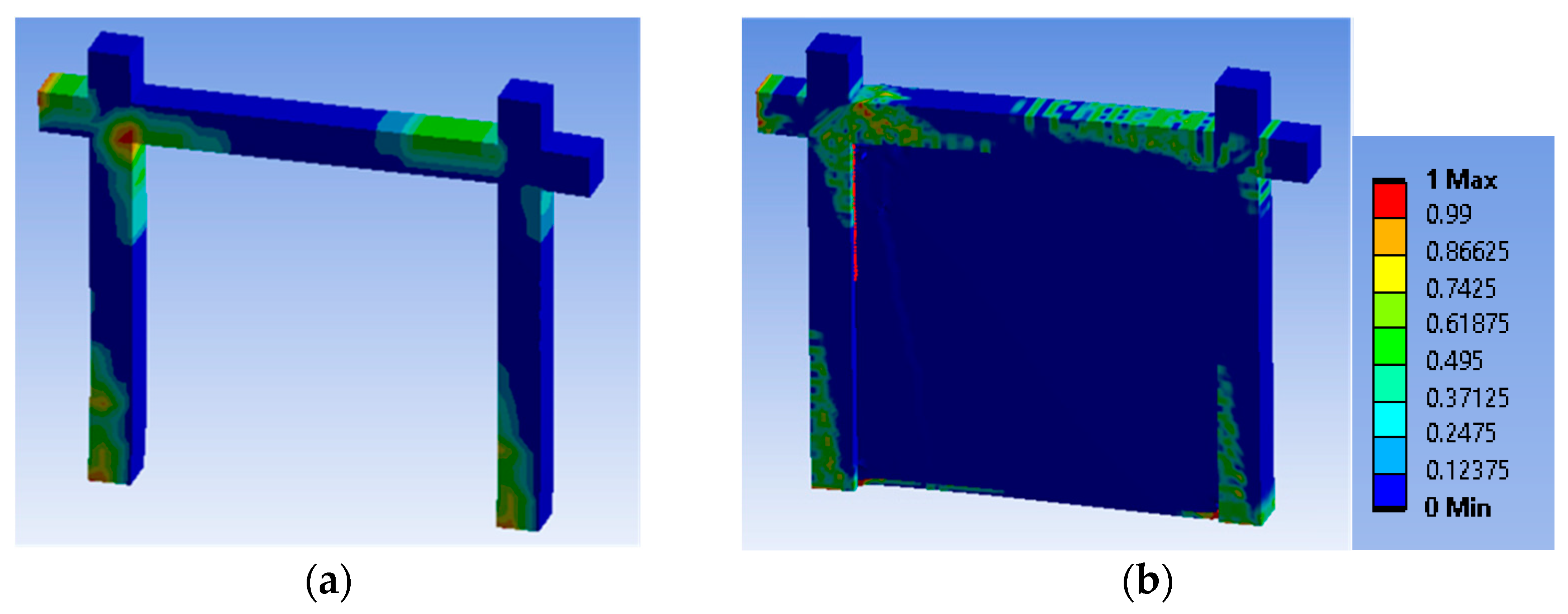
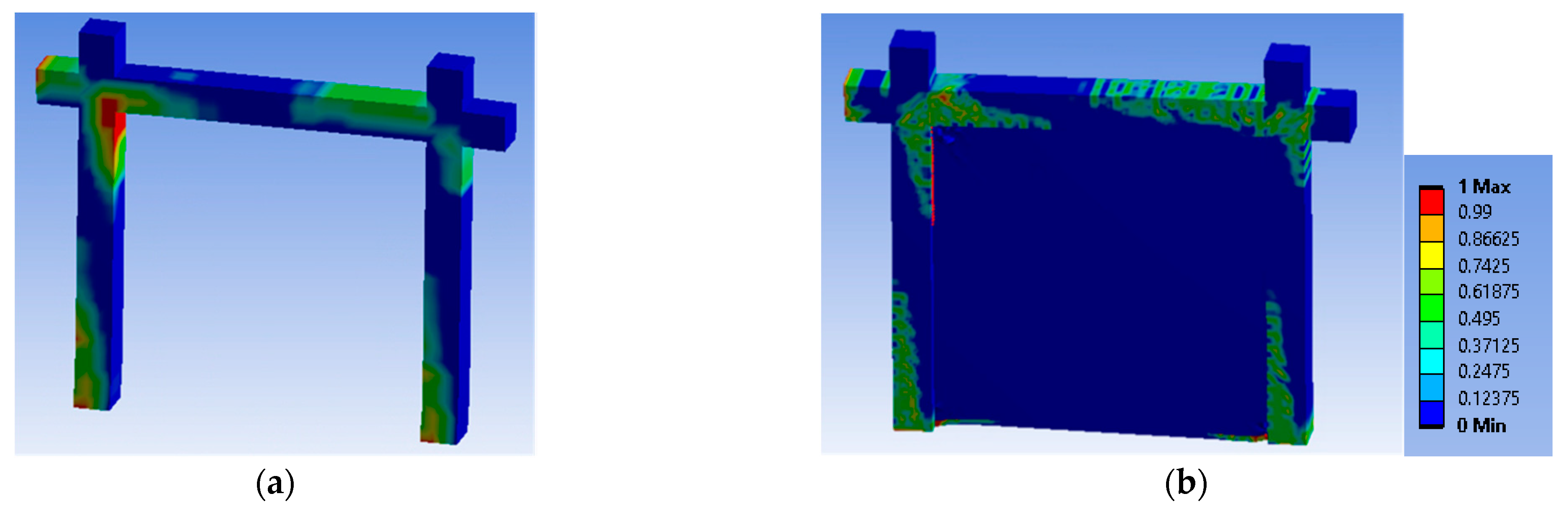
3.3. RC Frames
4. Parametric FE Analytical Investigation of Damaged RC Frames
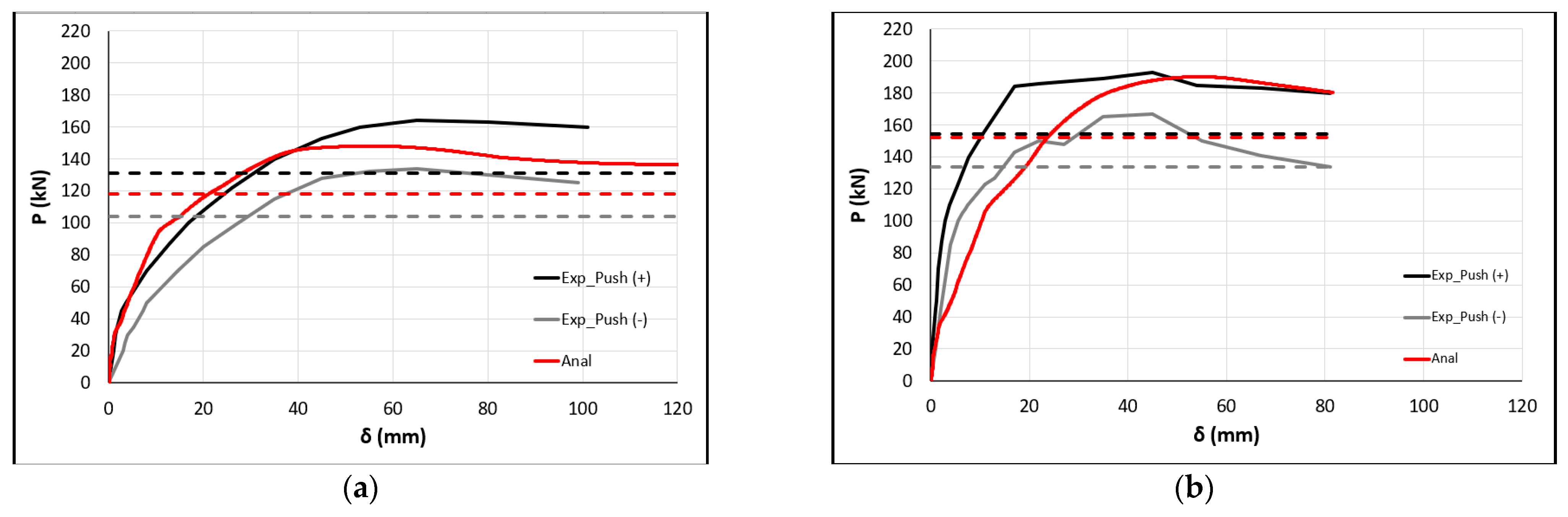
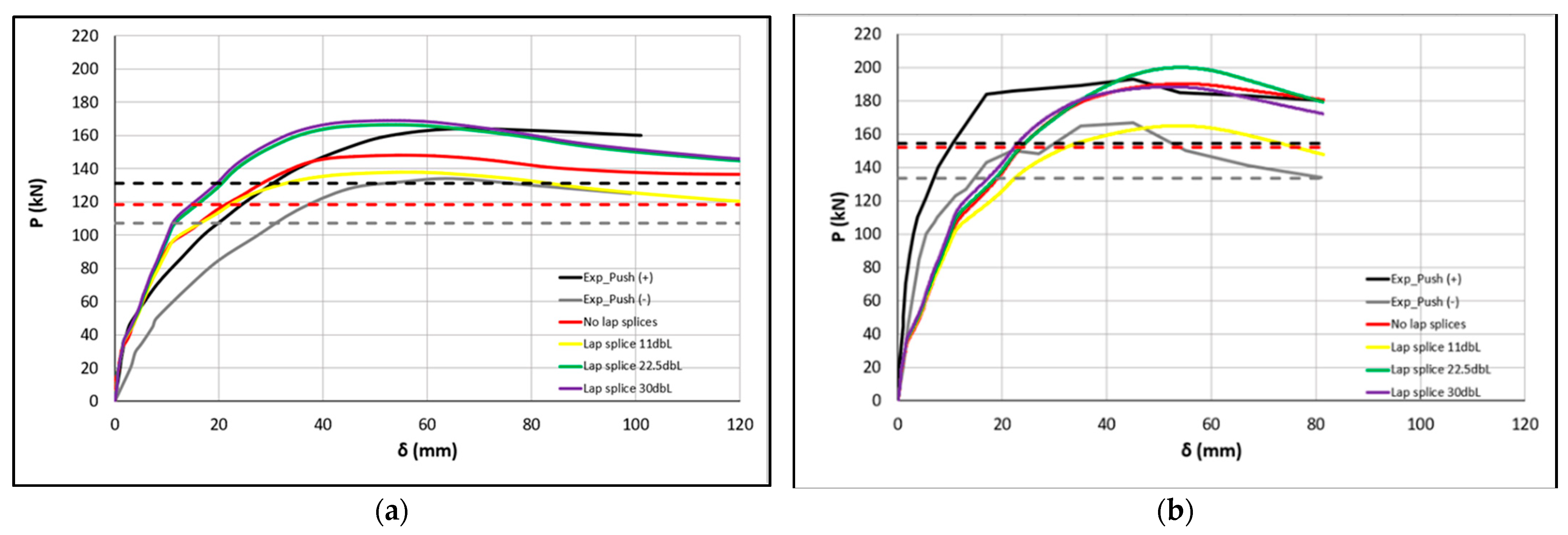
4.1. RC Frames with Lap-Spliced Longitudinal Bars
4.2. Corrosion of Steel Reinforcement
4.3. Performance of the Seismic Joint
5. Proposed Modifications of Existing Design Relations
5.1. Lap-Spliced Longitudinal Bars
- the thickness t of the diagonal strut;
- the width b of the diagonal strut (); and
- the mean compressive strength of the infill wall along the direction of the diagonal .
5.2. Corrosion of Steel Reinforcement
6. Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bousias, S.N.; Fardis, M.N.; Spathis, A.L.; Biskinis, D. Concrete or FRP jacketing of concrete columns for seismic retrofitting. In NATO Science Series: IV: Earth and Environmental Sciences; Wasti, S.T., Ozcebe, G., Eds.; Springer: Dordrecht, The Netherlands, 2006; Volume 66, pp. 33–46. [Google Scholar]
- Kalogeropoulos, G.I.; Tsonos, A.-D.G. Cyclic performance of RC Columns with inadequate lap splices strengthened with CFRP jackets. Fibers 2020, 8, 39. [Google Scholar] [CrossRef]
- Goksu, C.; Ilki, A. Seismic Behavior of Reinforced Concrete Columns with Corroded Deformed Reinforcing Bars. ACI Struct. J. 2016, 113, 1053–1064. [Google Scholar] [CrossRef]
- Rousakis, T.C.; Panagiotakis, G.D.; Archontaki, E.E.; Kostopoulos, A.K. Prismatic RC columns externally confined with FRP sheets and pre-tensioned basalt fiber ropes under cyclic axial load. Compos. Part B Eng. 2019, 163, 96–106. [Google Scholar] [CrossRef]
- Karantzikis, M.; Papanicolaou, C.G.; Antonopoulos, C.P.; Triantafillou, T.C. Experimental investigation of nonconventional confinement for concrete using FRP. J. Compos. Constr. 2005, 9, 480–487. [Google Scholar] [CrossRef]
- Triantafillou, T.C.; Papanicolaou, C.G.; Zissimopoulos, P.; Laourdekis, T. Concrete confinement with textile-reinforced mortar jackets. ACI Struct. J. 2006, 103, 28–37. [Google Scholar] [CrossRef]
- Ilki, A.; Peker, O.; Karamuk, E.; Demir, C.; Kumbasar, N. FRP retrofit of low and medium strength circular and rectangular reinforced concrete columns. J. Mater. Civ. Eng. 2008, 20, 169–188. [Google Scholar] [CrossRef]
- Yu, T.T.; Teng, J.G.; Wong, Y.L.; Dong, S.L. Finite element modeling of confined concrete-I: Drucker–Prager type plasticity model. Eng. Struct. 2010, 32, 665–679. [Google Scholar] [CrossRef]
- Ilki, A.; Kumbasar, N. Compressive behaviour of carbon fibre composite jacketed concrete with circular and non-circular cross-sections. J. Earthq. Eng. 2003, 7, 381–406. [Google Scholar] [CrossRef]
- Nistico, N.R.C. Square Sections Confined by FRP: A numerical procedure for predicting stress strain relationship. Compos. Part B 2014, 59, 238–247. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Wang, D.Y.; Smith, S.T.; Lu, D.G. CFRP-confined square RC columns. I: Experimental investigation. J. Compos. Constr. 2012, 16, 150–160. [Google Scholar] [CrossRef]
- Wu, Y.F.; Wei, Y.Y. Effect of cross-sectional aspect ratio on the strength of CFRP-confined rectangular concrete columns. Eng. Struct. 2010, 32, 32–45. [Google Scholar] [CrossRef]
- Triantafyllou, G.G.; Rousakis, T.C.; Karabinis, A.I. Corroded RC beams patch repaired and strengthened in flexure with fiber-reinforced polymer laminates. Compos. Part B Eng. 2017, 112, 125–136. [Google Scholar] [CrossRef]
- Triantafyllou, G.G.; Rousakis, T.C.; Karabinis, A.I. Analytical assessment of the bearing capacity of RC beams with corroded steel bars beyond concrete cover cracking. Compos. Part B Eng. 2017, 119, 132–140. [Google Scholar] [CrossRef]
- Triantafyllou, G.; Rousakis, T.; Karabinis, A. Corroded RC beams at service load before and after patch repair and strengthening with NSM CFRP strips. Buildings 2019, 9, 67. [Google Scholar] [CrossRef] [Green Version]
- Jiang, C.; Wu, Y.F.; Wu, G. Plastic hinge length of FRP-confined square RC columns. J. Compos. Constr. 2014, 18, 04014003. [Google Scholar] [CrossRef]
- Rousakis, T.C. Inherent seismic resilience of RC columns externally confined with nonbonded composite ropes. Compos. Part B Eng. 2018, 135, 142–148. [Google Scholar] [CrossRef]
- Belardi, V.G.; Fanelli, P.; Vivio, F. Structural analysis and optimization of anisogrid composite lattice cylindrical shells. Compos. Part B Eng. 2018, 139, 203–215. [Google Scholar] [CrossRef]
- Ye, G.; Bi, H.; Hu, Y. Compression behaviors of 3D printed pyramidal lattice truss composite structures. Compos. Struct. 2020, 233, 111706. [Google Scholar] [CrossRef]
- Chalioris, C.E.; Kytinou, V.K.; Voutetaki, M.E.; Karayannis, C.G. Flexural Damage Diagnosis in Reinforced Concrete Beams Using a Wireless Admittance Monitoring System—Tests and Finite Element Analysis. Sensors 2021, 21, 679. [Google Scholar] [CrossRef] [PubMed]
- Karayannis, C.G.; Golias, E. Full scale tests of RC joints with minor to moderate seismic damage repaired using C-FRP sheets. Earthq. Struct. 2018, 15, 617–627. [Google Scholar] [CrossRef]
- Katakalos, K.; Manos, G.; Papakonstantinou, C. Seismic retrofit of R/C T-beams with steel fiber polymers under cyclic loading conditions. Buildings 2019, 9, 101. [Google Scholar] [CrossRef] [Green Version]
- Triantafyllou, G.G.; Rousakis, T.C.; Karabinis, A.I. Effect of patch repair and strengthening with EBR and NSM CFRP laminates for RC beams with low, medium and heavy corrosion. Compos. Part B Eng. 2018, 133, 101–111. [Google Scholar] [CrossRef]
- Anagnostou, E.; Rousakis, T.C.; Karabinis, A.I. Seismic retrofitting of damaged RC columns with lap-spliced bars using FRP sheets. Compos. Part B Eng. 2019, 166, 598–612. [Google Scholar] [CrossRef]
- Kwiecień, A. Highly deformable polymers for repair and strengthening of cracked masonry structures. GSTF Int. J. Eng. Technol. (JET) 2013, 2, 182–196. [Google Scholar] [CrossRef]
- Akyildiz, A.; Kwiecień, A.; Zając, B.; Triller, P.; Bohinc, U.; Rousakis, T.; Viskovic, A. Preliminary in-plane shear test of infills protected by PUFJ interfaces. In Proceedings of the 17th International Brick and Block Masonry Conference from Historical to Sustainable Masonry (IB2MaC 2020), Krakow, Poland, 5–7 July 2020. [Google Scholar]
- Triller, P.; Kwiecien, A.; Bohinc, U.; Zajac, B.; Rousakis, T.; Viskovic, A. Preliminary in-plane shear test of damaged infill strengthened by FRPU. In Proceedings of the 10th International Conference on FRP Composites in Civil Engineering (CICE 2020/2021), Istanbul, Turkey, 8–10 December 2021. [Google Scholar]
- Rousakis, T.; Ilki, A.; Kwiecień, A.; Viskovic, A.; Triller, P.; Ghiassi, B.; Benedetti, A.; Gams, M.; Rakicevic, Z.; Halici, O.F.; et al. Quick Reparation of RC Infilled Frames after Seismic Damages—Experimental Tests on Shaking Table. In Proceedings of the 10th International Conference on FRP Composites in Civil Engineering (CICE 2020/2021), Istanbul, Turkey, 8–10 December 2021. [Google Scholar]
- Rousakis, T. Brick walls Interventions with FRPU or PUFJ and of RC columns with FR in Brick-Infilled RC Structures with the use of Pushover Beam-Column Element Analysis and Pseudo-Dynamic 3D Finite Element Analysis. In Proceedings of the 17th International Brick and Block Masonry Conference from Historical to Sustainable Masonry (IB2MaC 2020), Krakow, Poland, 5–7 July 2020. [Google Scholar]
- Rousakis, T.; Ilki, A.; Kwiecień, A.; Viskovic, A.; Gams, M.; Triller, P.; Ghiassi, B.; Benedetti, A.; Rakicevic, Z.; Colla, C.; et al. Deformable Polyurethane Joints and Fibre Grids for Resilient Seismic Performance of Reinforced Concrete Frames with Orthoblock Brick Infills. Polymers 2020, 12, 2869. [Google Scholar] [CrossRef] [PubMed]
- Rousakis, T.; Vanian, V.; Fanaradelli, T.; Anagnostou, E. 3D FEA of Infilled RC Framed Structures Protected by Seismic Joints and FRP Jackets. Appl. Sci. 2021, 11, 6403. [Google Scholar] [CrossRef]
- Zając, B.; Kwiecień, A. Thermal stress generated in masonries by stiff and flexible bonding materials. In Proceedings of the 9th International Masonry Conference (9th IMC), Guimarães, Portugal, 7–9 July 2014; Lourenço, P.B., Haseltine, B.A., Vasconcelos, G., Eds.; ISBN 978-972-8692-85-8. [Google Scholar]
- Koutas, L.; Triantafillou, T.C.; Bousias, S.N. Analytical modeling of masonry-infilled RC frames retrofitted with textile-reinforced mortar. J. Compos. Constr. 2014, 19, 04014082. [Google Scholar] [CrossRef]
- Rouka, D.; Kaloudaki, A.; Rousakis, T.; Fanaradelli, T.; Anagnostou, E.; Kwiecien, A.; Gams, M.; Viskovic, A.; Zajac, B. Response of RC buildings with Low-strength Infill Walls Retrofitted with FRP sheets with Highly Deformable Polymer—Effects of Infill Wall Strength. In Proceedings of the 25th International Conference on Composites/Nano Engineering (ICCE-25), Rome, Italy, 13–15 June 2012. [Google Scholar]
- Hany, N.F.; Hantouche, E.G.; Harajli, M.H. Finite element modeling of FRP-confined concrete using modified concrete damaged plasticity. Eng. Struct. 2016, 125, 1–14. [Google Scholar] [CrossRef]
- Youssf, O.; ElGawady, M.A.; Mills, J.E. Displacement and plastic hinge length of FRP confined circular reinforced concrete columns. Eng. Struct. 2015, 101, 465–476. [Google Scholar] [CrossRef]
- Yuan, F.; Wu, Y.F.; Li, C.Q. Modelling plastic hinge of FRP-confined RC columns. Eng. Struct. 2017, 131, 651–668. [Google Scholar] [CrossRef]
- Fanaradelli, T.D.; Rousakis, T.C. 3D Finite Element Pseudodynamic Analysis of Deficient RC Rectangular Columns Confined with Fiber Reinforced Polymers under Axial Compression. Polymers 2020, 12, 2546. [Google Scholar] [CrossRef] [PubMed]
- Anagnostou, E.; Rousakis, T.; Georgiadis, N. Finite element analysis of deficient RC columns with square and rectangular section under pseudoseismic load and comparison with retrofit code predictions. In Proceedings of the ICCE-26 Conference, Paris, France, 15–21 July 2018. [Google Scholar]
- Riedel, W. Beton unter Dynamischen Lasten: Meso- und makromechanische Modelle und ihre Parameter; Fraunhofer-Institut für Kurzzeitdynamik, Ernst-Mach-Institut EMI, Freiburg/Brsg., Eds.; Fraunhofer IRB Verlag: Stuttgart, Germany, 2004; ISBN 3-8167-6340-5. [Google Scholar]
- Riedel, W.; Thoma, K.; Hiermaier, S.; Schmolinske, E. Penetration of Reinforced Concrete by BETA-B-500, Numerical Analysis using a New Macroscopic Concrete Model for Hydrocodes. In Proceedings of the (CD-ROM) 9th Internationales Symposium, Interaction of the Effects of Munitions with Structures, Berlin Germany, 3–7 May 1999; pp. 315–322. [Google Scholar]
- Riedel, W.; Kawai, N.; Kondo, K. Numerical Assessment for Impact Strength Measurements in Concrete Materials. Int. J. Impact Eng. 2009, 36, 283–293. [Google Scholar] [CrossRef] [Green Version]
- ANSYS. Academic Research, Release 15.0; SAS IP, Inc.: Canonsburg, PA, USA, 2003. [Google Scholar]
- Bousias, S.N.; Triantafillou, T.C.; Fardis, M.N.; Spathis, L.; O’Regan, B.A. Fiber-reinforced polymer retrofitting of rectangular reinforced concrete columns with or without corrosion. Struct. J. 2004, 101, 512–520. [Google Scholar] [CrossRef]
- Meda, A.; Mostosi, S.; Rinaldi, Z.; Riva, P. Experimental evaluation of the corrosion influence on the cyclic behaviour of RC columns. Eng. Struct. 2014, 76, 112–123. [Google Scholar] [CrossRef]
- Code, P. Eurocode 8: Design of Structures for Earthquake Resistance—Part 3: Assessment and Retrofitting of Buildings; Incorporating corrigendum March 2010; European Committee for Standardization: Brussels, Belgium, 2005. [Google Scholar]
- Greek Retrofit Code (KANEPE), 2nd Revision. 2017. Available online: https://oasp.gr/node/92 (accessed on 25 May 2021).
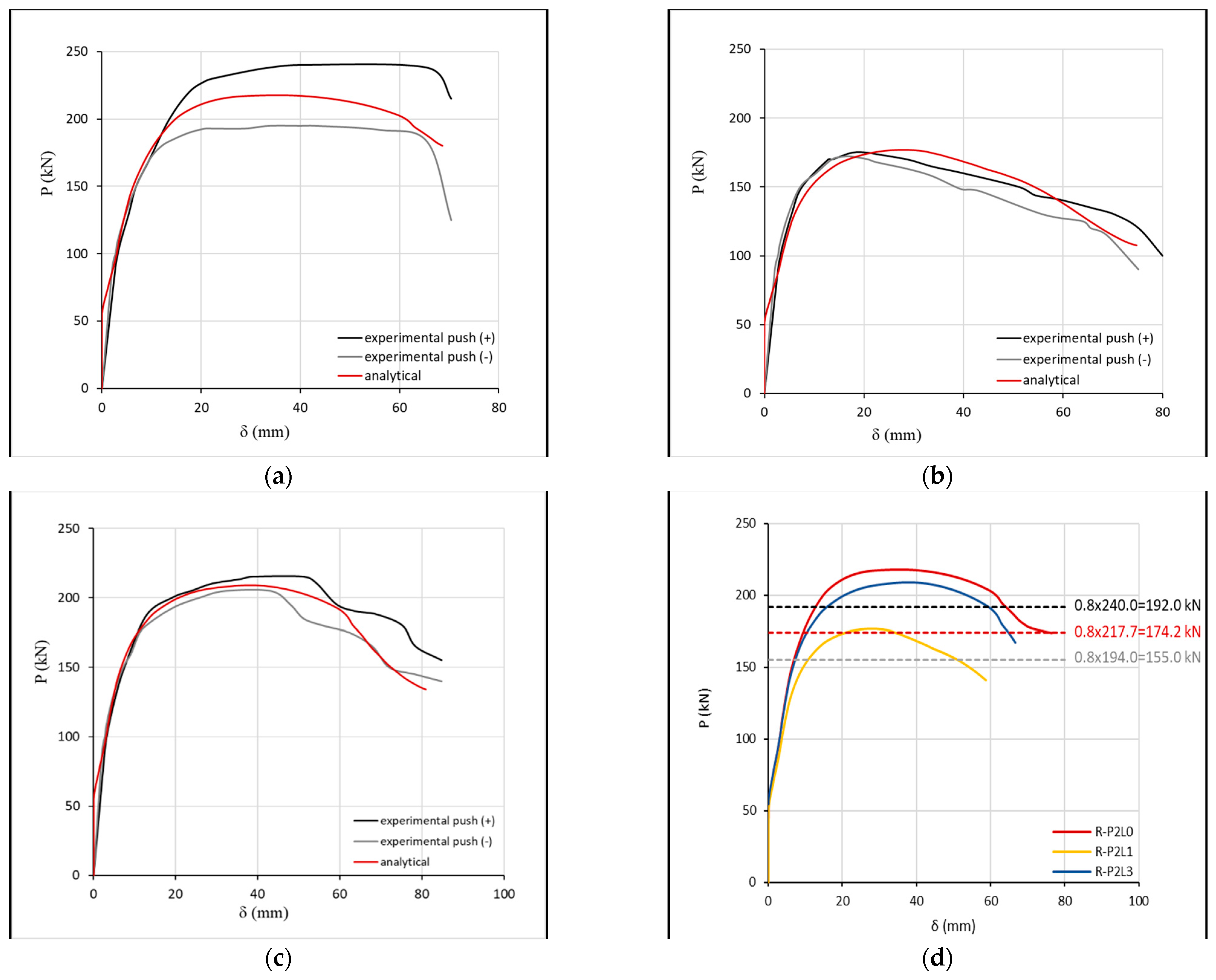
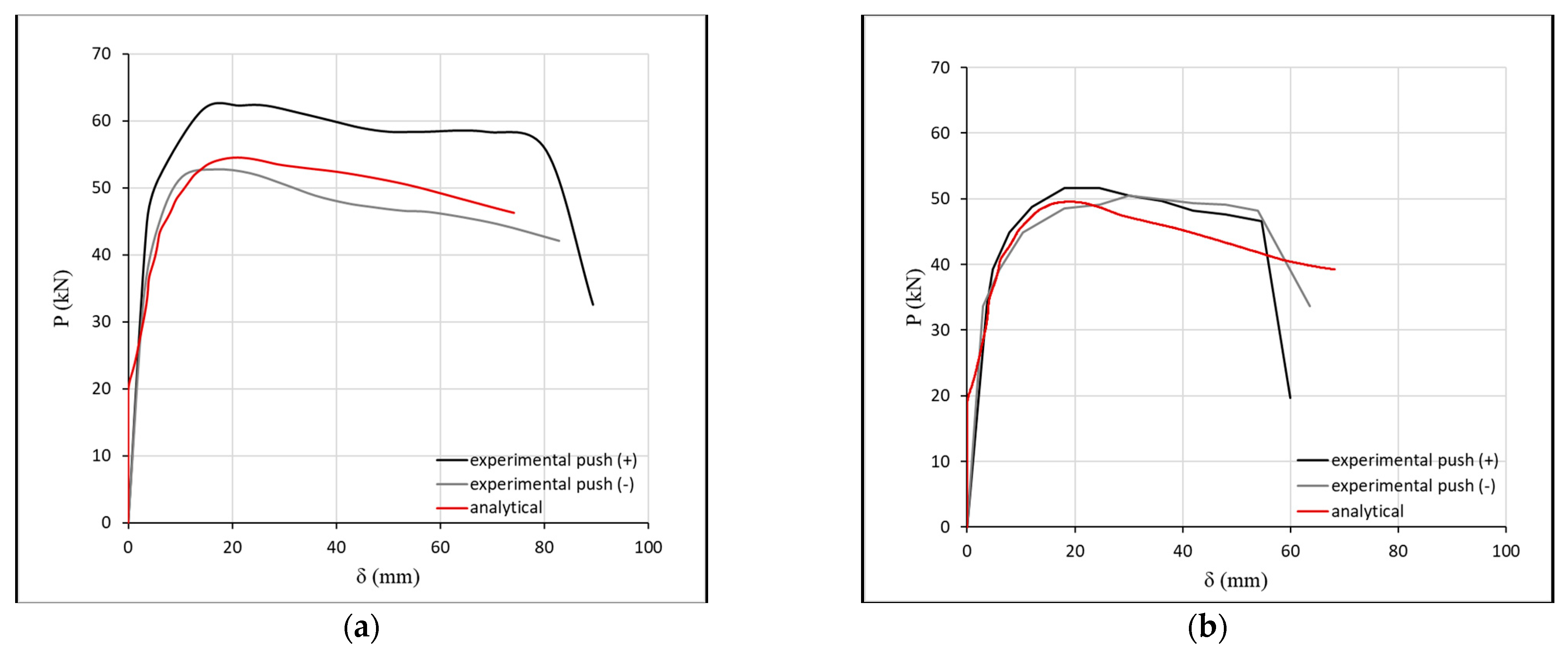
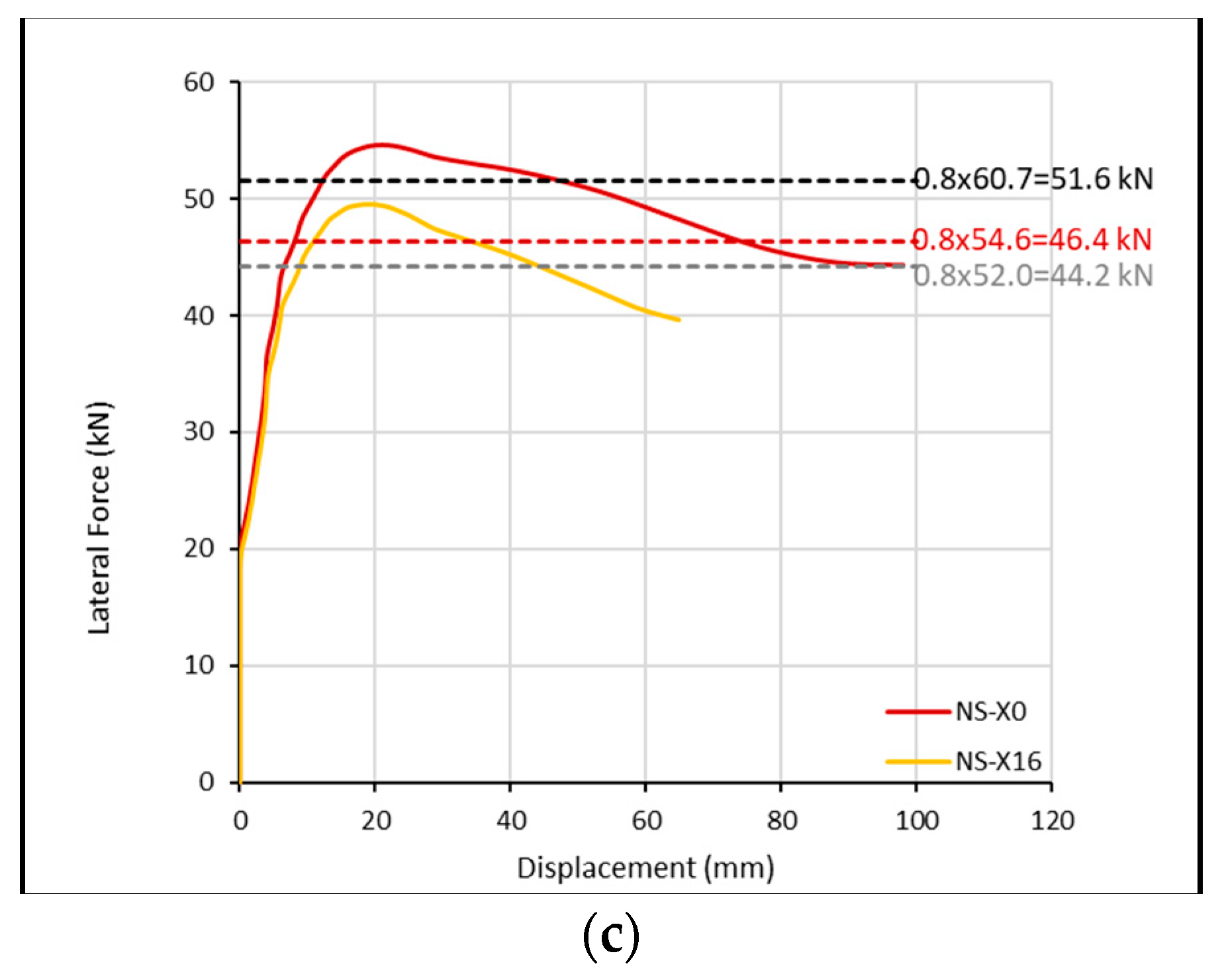

| R-P2L0 | R-P2L1 | R-P2L3 | Average AD (%) | ||||
|---|---|---|---|---|---|---|---|
| Exp | Anal | Exp | Anal | Exp | Anal | ||
| Pmax (+) (kN) | 240.00 | 217.73 | 175.00 | 176.86 | 215.00 | 209.11 | 4.36 |
| δPmax (+) (mm) | 48.50 | 34.84 | 19.50 | 27.77 | 48.50 | 38.13 | 30.65 |
| Pmax (−) (kN) | 194.00 | 217.73 | 168.00 | 176.86 | 208.00 | 209.11 | 6.01 |
| δPmax (−) (mm) | 38.50 | 34.84 | 19.00 | 27.77 | 34.50 | 38.13 | 22.06 |
| Pu (+) (kN) | 192.00 | 174.18 | 140.00 | 141.49 | 172.00 | 167.29 | 4.36 |
| δPu (+) (mm) | 70.40 | 75.37 | 54.40 | 58.46 | 75.20 | 66.85 | 8.54 |
| Pu (−) (kN) | 155.20 | 174.18 | 134.40 | 141.49 | 166.40 | 167.29 | 6.01 |
| δPu (−) (mm) | 64.00 | 75.37 | 50.00 | 58.46 | 65.00 | 66.85 | 12.51 |
| NS-X0 (without Corrosion) | NS-X16 (16% Corrosion) | CS-0 (10% Corrosion) | CS-C2 (10% Corrosion and FRP Jacket) | Average AD (%) | |||||
|---|---|---|---|---|---|---|---|---|---|
| Exp | Anal | Exp | Anal | Exp | Anal | Exp | Anal | ||
| Pmax (+) (kN) | 60.70 | 54.56 | 50.90 | 49.56 | 187.00 | 169.35 | 192.00 | 180.08 | 7.10 |
| δPmax (+) (mm) | 20.00 | 20.87 | 18.00 | 42.12 | 24.00 | 30.39 | 54.00 | 27.69 | 53.43 |
| Pmax (−) (kN) | 52.00 | 54.56 | 50.00 | 49.56 | 187.00 | 169.35 | 183.00 | 180.08 | 4.21 |
| δPmax (−) (mm) | 15.00 | 20.87 | 30.00 | 42.12 | 24.00 | 30.39 | 45.00 | 27.69 | 36.16 |
| Pu (+) (kN) | 51.60 | 46.38 | 43.27 | 42.13 | 149.60 | 135.48 | 153.60 | 161.89 | 6.90 |
| δPu (+) (mm) | 81.10 | 73.75 | 55.10 | 52.86 | 44.80 | 45.73 | 80.00 | 86.21 | 5.74 |
| Pu (−) (kN) | 44.20 | 46.38 | 42.50 | 42.13 | 149.60 | 135.48 | 146.40 | 161.89 | 6.46 |
| δPu (−) (mm) | 70.00 | 73.75 | 55.00 | 52.86 | 44.80 | 45.73 | 75.00 | 86.21 | 6.57 |
| Column Specimen | Lap Length (dbL) | Layers CFRP | θu,exp | θu,anal (Proposed) | AD (%) | VR,exp (kN) | VR,anal (kN) (Proposed) | AD(%) |
|---|---|---|---|---|---|---|---|---|
| R-P2L0 | 0 | 2 | 0.044 | 0.0419 | 4.8 | 217.0 | 200.9 | 7.4 |
| R-P2L1 | 15 | 2 | 0.034 | 0.0352 | 3.5 | 171.5 | 154.6 | 9.8 |
| R-P2L3 | 30 | 2 | 0.047 | 0.0442 | 5.9 | 211.5 | 205.2 | 3.0 |
| Average AD (%) | 4.73 | 6.73 |
| Column Specimen | Corrosion Degree (%) | θu,exp | θu,anal (Proposed) | AD (%) | VR,exp (kN) | VR,anal (kN) (Proposed) | AD (%) |
|---|---|---|---|---|---|---|---|
| NS-X0 | 0 | 0.0676 | 0.0455 | 32.6 | 60.7 | 55.3 | 8.8 |
| NS-X9 | 9 | 0.0804 | 0.0438 | 45.5 | 59.1 | 53.1 | 10.2 |
| NS-X16 | 16 | 0.0459 | 0.0425 | 7.4 | 50.9 | 51.2 | 0.6 |
| NS-X22 | 22 | 0.0462 | 0.0414 | 10.3 | 51.9 | 49.7 | 4.3 |
| NS-X54 | 54 | 0.0273 | 0.0355 | 29.9 | 44.3 | 41.2 | 7.0 |
| Average AD (%) | 25.14 | 6.18 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rousakis, T.; Anagnostou, E.; Fanaradelli, T. Advanced Composite Retrofit of RC Columns and Frames with Prior Damages—Pseudodynamic Finite Element Analyses and Design Approaches. Fibers 2021, 9, 56. https://doi.org/10.3390/fib9090056
Rousakis T, Anagnostou E, Fanaradelli T. Advanced Composite Retrofit of RC Columns and Frames with Prior Damages—Pseudodynamic Finite Element Analyses and Design Approaches. Fibers. 2021; 9(9):56. https://doi.org/10.3390/fib9090056
Chicago/Turabian StyleRousakis, Theodoros, Evgenia Anagnostou, and Theodora Fanaradelli. 2021. "Advanced Composite Retrofit of RC Columns and Frames with Prior Damages—Pseudodynamic Finite Element Analyses and Design Approaches" Fibers 9, no. 9: 56. https://doi.org/10.3390/fib9090056
APA StyleRousakis, T., Anagnostou, E., & Fanaradelli, T. (2021). Advanced Composite Retrofit of RC Columns and Frames with Prior Damages—Pseudodynamic Finite Element Analyses and Design Approaches. Fibers, 9(9), 56. https://doi.org/10.3390/fib9090056