Artificial Neural Networks to Predict the Mechanical Properties of Natural Fibre-Reinforced Compressed Earth Blocks (CEBs)
Abstract
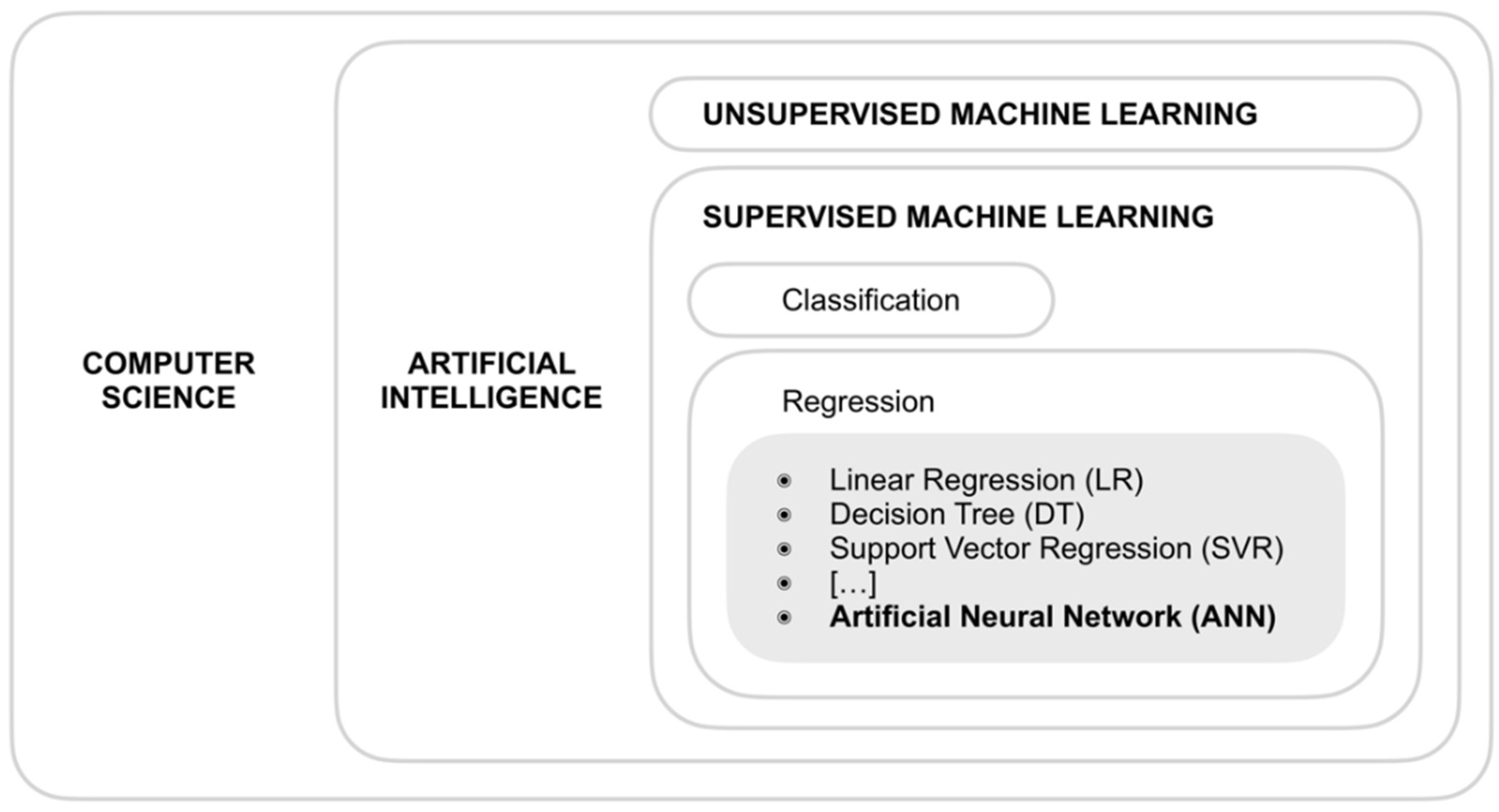
:1. Introduction
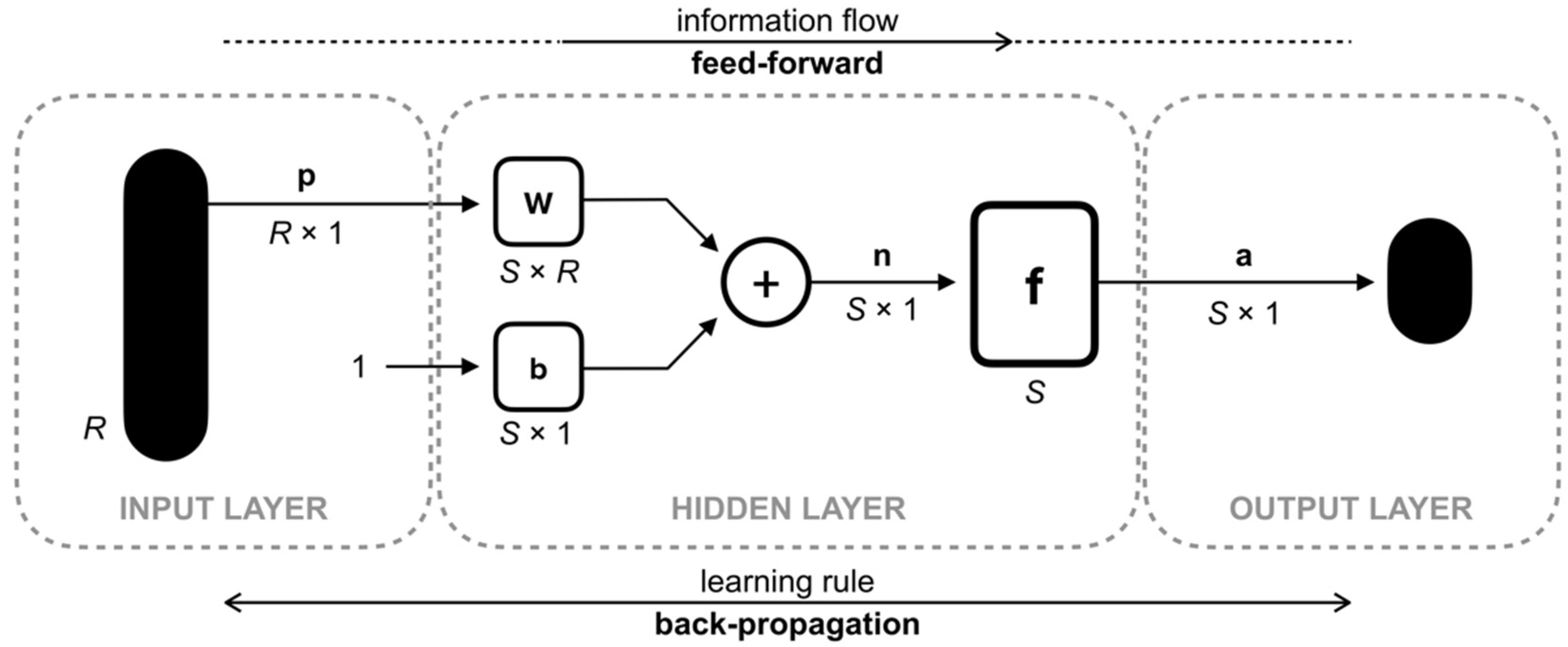
2. Artificial Neural Networks: Theoretical Background
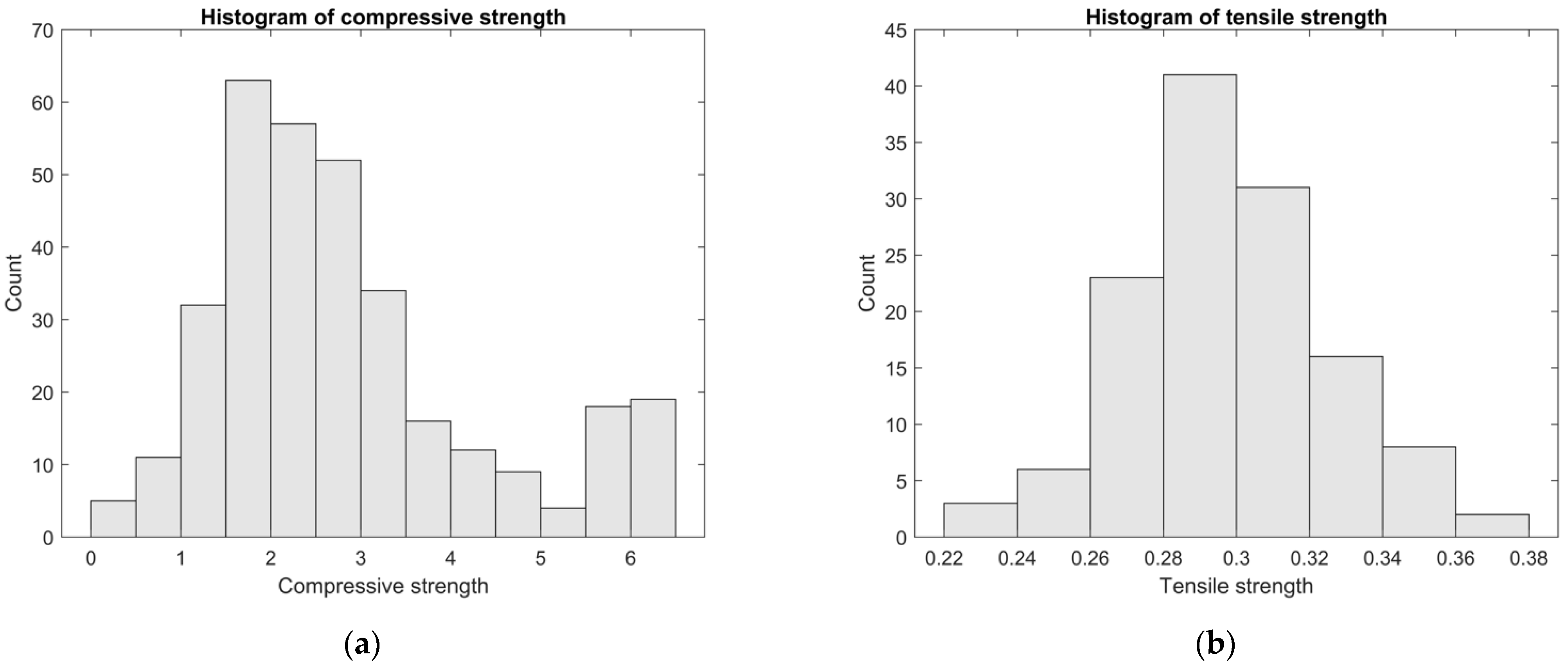
3. Data collection
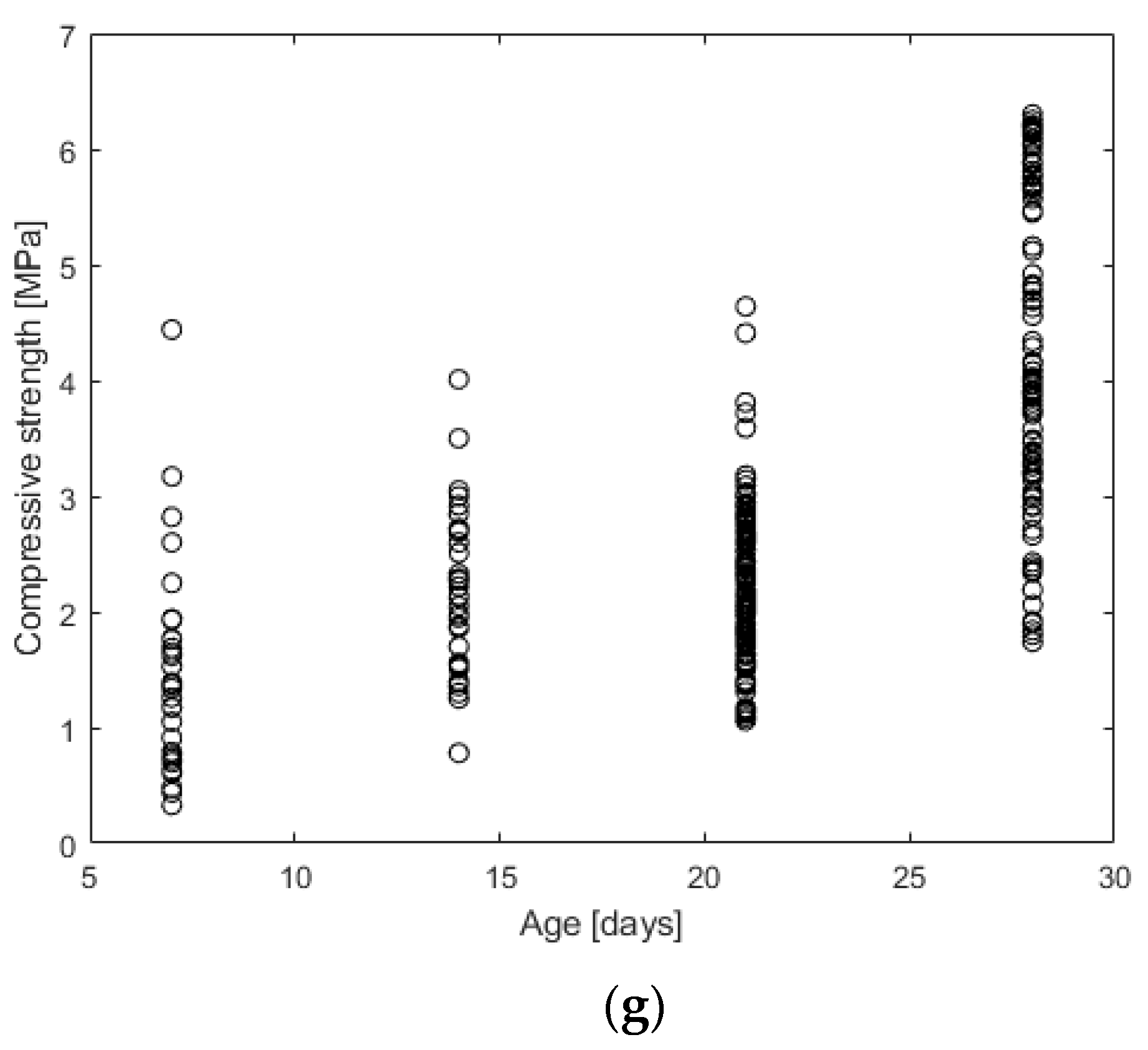
3.1. Database 1
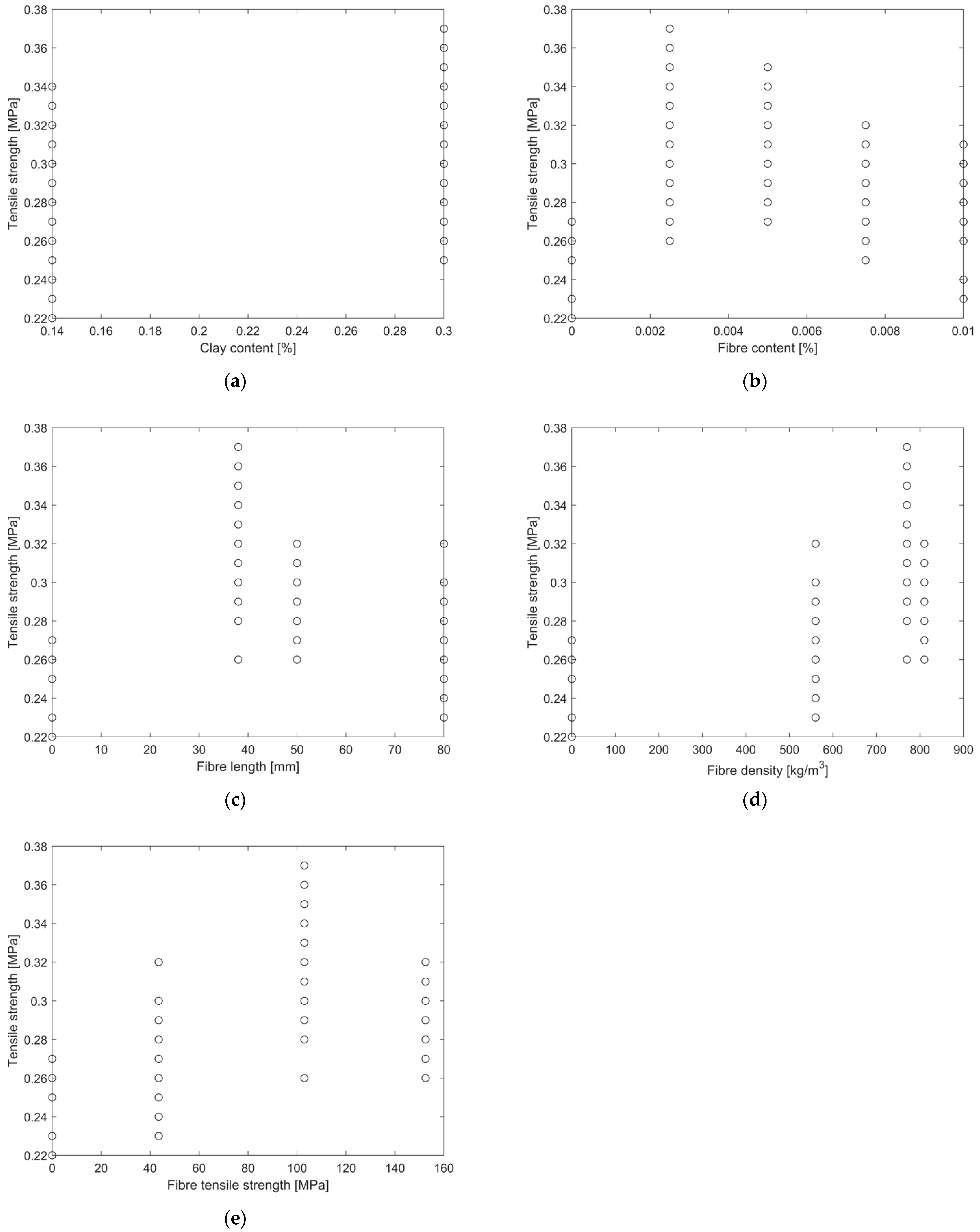
3.2. Database 2
4. Modelling of the ANNs
4.1. Data Processing
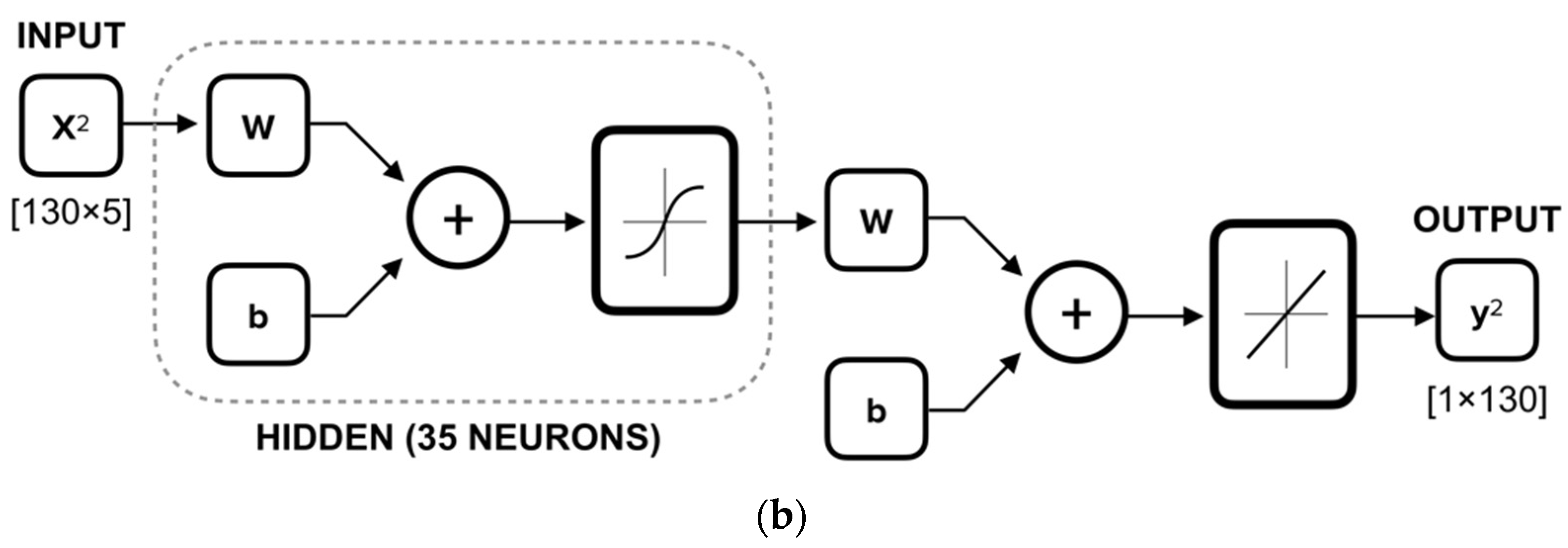
4.2. Definition of the Networks Architecture
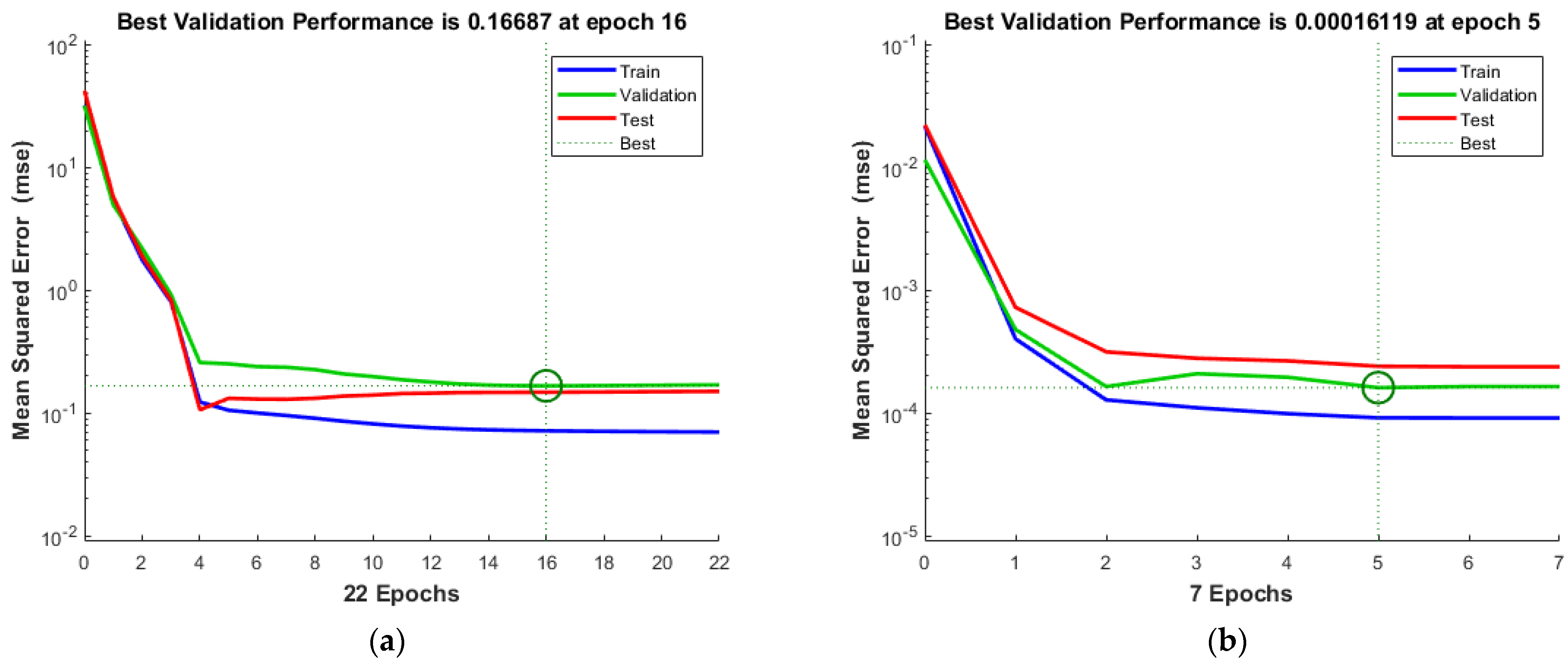
4.3. Training of the Networks
5. Evaluation of the Performance
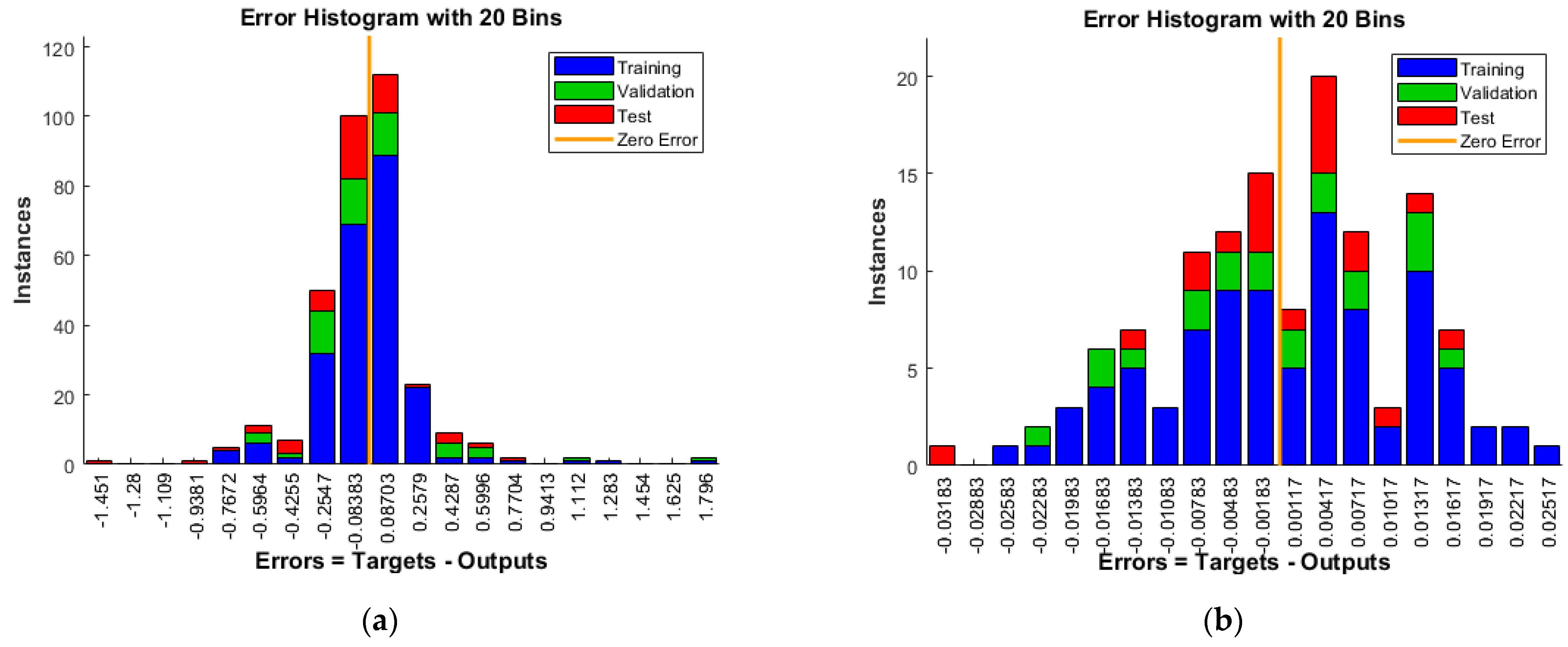
5.1. Error Trend
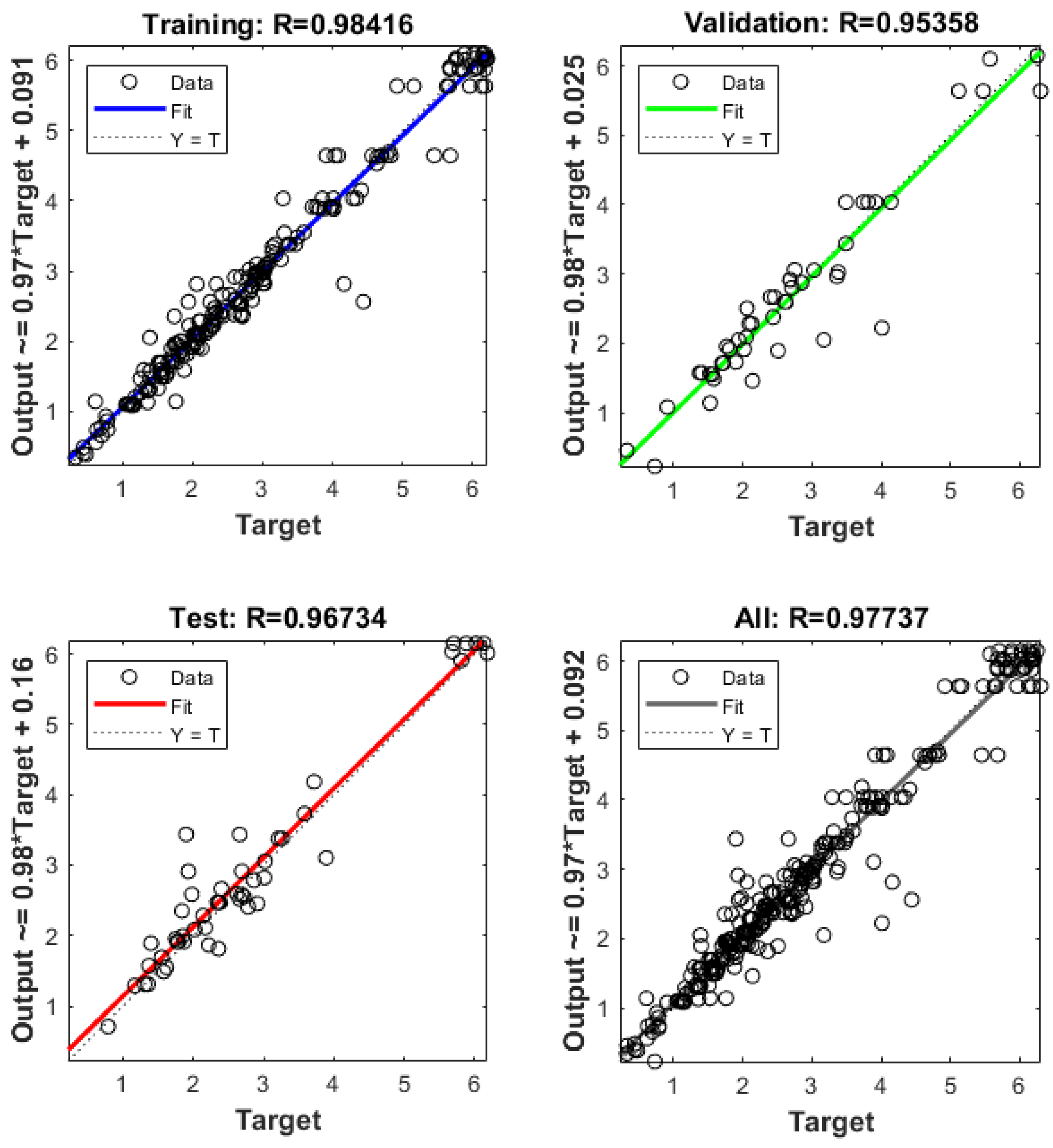
5.2. Prediction Accuracy of the Compressive Strength (ANN1)
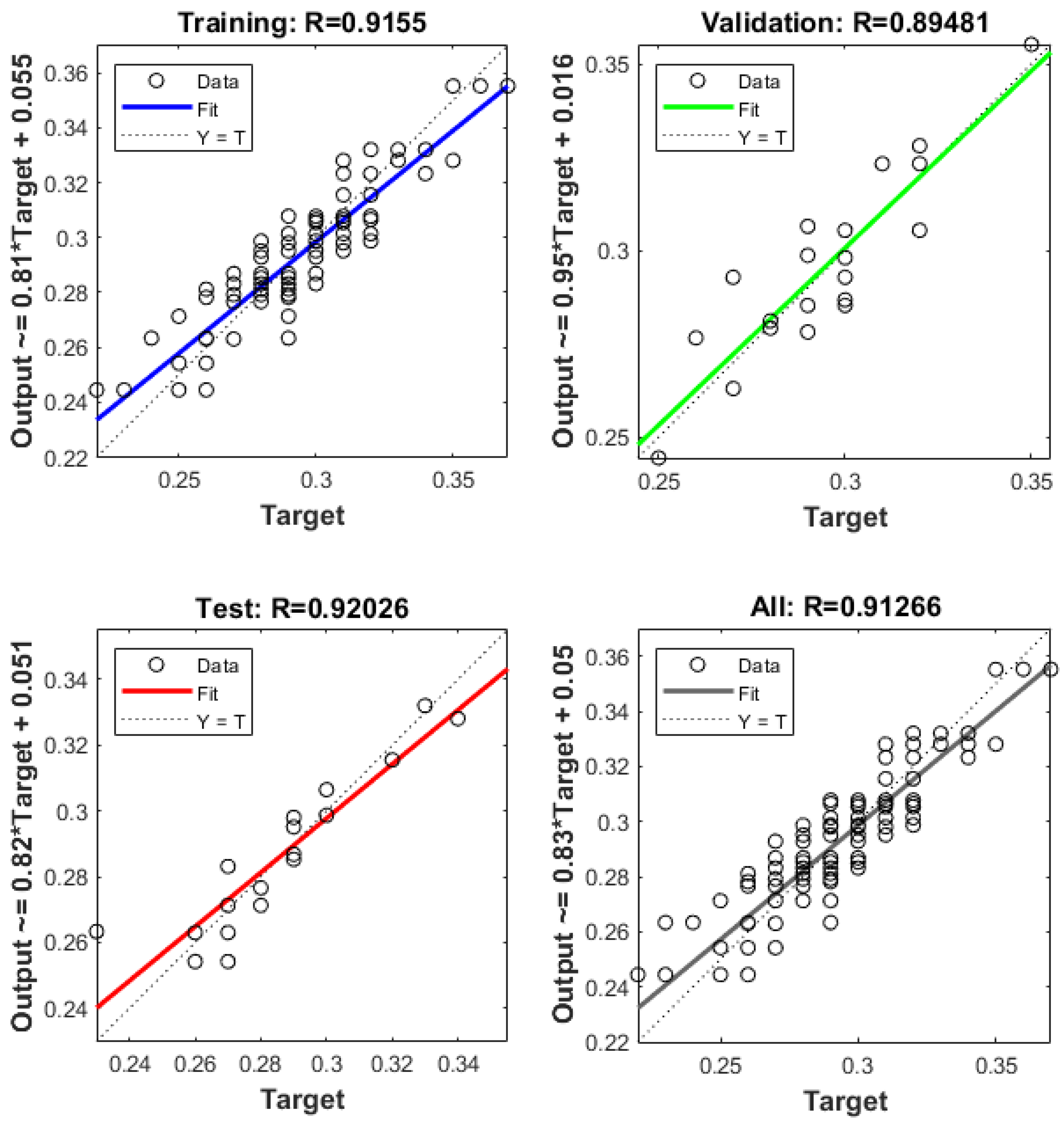
5.3. Prediction Accuracy of the Tensile Strength (ANN2)
6. Conclusions
- ANNs may be widely used within the scope of CEB optimisation to orient experimental campaigns and support numerical investigations. The possibility of executing many analyses in a short time represents valuable support to facilitate the development of a new durable and sustainable construction material, opening new opportunities for both researchers and practitioners.
- The database used covers a range of values that reproduce the most commonly obtained laboratory results. It does not classify the fibres on the basis of their original natural source (type of plants or animals) but on the basis of their physical and mechanical characterisation (density, length, tensile strength). This approach does not affect the predictive capabilities of the proposed model, as both the compressive and tensile strength of fibre-reinforced CEBs with type of fibres not included in the database can still be deduced from the ANNs as long as the characteristics entered fall within the available ranges.
- The prediction accuracy of the networks depends on the data sets used, and it would be advantageous to enhance and enrich it by providing new and increasingly variable data. To this end, a complete dataset should include mixture proportion (wt.%) comprising all components used (soil, as a composition of gravel, sand, silt and clay, cement, or other kinds of stabiliser, water, fibres, etc.), type of fibres, their length, tensile strength and chemical treatment, specimens’ size, age, etc. Such a list can be clearly extended with additional features according to the necessities.
- Future developments should be aimed at continuing the experimentation on blocks, collecting new data and further investigating the mechanisms that regulate the effect of fibres in the earth matrix. In this regard, it is essential to point out the importance of carefully and adequately designing experiments through, for example, the Design of the Experiments (DoE) methods. This would mitigate many problems related to uncertainty, and the approach to studying this promising construction technology would be better defined, allowing the scientific community to collaborate in creating an appropriate physical model.
- In addition to the mere prediction of the resistance values, ML algorithms can afterwards be used to optimise the design of the mixtures. In fact, it is well known that in the experiment-based approach, the user can rarely control all the variables, almost never reaching the optimal performing option. Especially in the case of new materials to be placed on the market, multi-objective optimisation problems are often faced, posing objectives that can also be in contrast with each other: compliance with regulatory standards, production costs, environmental impact, etc. To benefit from the support of AI, future studies should define variables, objectives, and constraints to ensure that the problem is correctly addressed.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rigassi, V. Compressed Earth Blocks: Manual of Production; GATE: Eschborn, Germany, 1985; Volume 1. [Google Scholar]
- Minke, G. Building with Earth: Design and Technology of a Sustainable Architecture, 2nd ed.; Birkhauser: Boston, MA, USA, 2009; pp. 30–32. [Google Scholar]
- Ben Mansour, M.; Jelidi, A.; Cherif, A.S.; Ben Jabrallah, S. Optimizing thermal and mechanical performance of compressed earth blocks (CEB). Constr. Build. Mater. 2016, 104, 44–51. [Google Scholar] [CrossRef]
- Teixeira, E.; Machado, G.; Junior, A.P.; Guarnier, C.; Fernandes, J.; Silva, S.; Mateus, R. Mechanical and Thermal Performance Characterisation of Compressed Earth Blocks. Energies 2020, 13, 2978. [Google Scholar] [CrossRef]
- Fernandes, J.; Peixoto, M.; Mateus, R.; Gervásio, H. Life cycle analysis of environmental impacts of earthen materials in the Portuguese context: Rammed earth and compressed earth blocks. J. Clean. Prod. 2019, 241, 118286. [Google Scholar] [CrossRef] [Green Version]
- Mateus, R.; Fernandes, J.; Teixeira, E.R. Environmental Life Cycle Analysis of Earthen Building Materials; Elsevier BV: Amsterdam, The Netherlands, 2020. [Google Scholar] [CrossRef] [Green Version]
- Jannat, N.; Hussien, A.; Abdullah, B.; Cotgrave, A. Application of agro and non-agro waste materials for unfired earth blocks construction: A review. Constr. Build. Mater. 2020, 254, 119346. [Google Scholar] [CrossRef]
- Laborel-Préneron, A.; Aubert, J.; Magniont, C.; Tribout, C.; Bertron, A. Plant aggregates and fibers in earth construction materials: A review. Constr. Build. Mater. 2016, 111, 719–734. [Google Scholar] [CrossRef]
- Danso, H.; Martinson, B.; Ali, M.; Mant, C. Performance characteristics of enhanced soil blocks: A quantitative review. Build. Res. Inf. 2014, 43, 253–262. [Google Scholar] [CrossRef] [Green Version]
- Pacheco-Torgal, F.; Jalali, S. Earth construction: Lessons from the past for future eco-efficient construction. Constr. Build. Mater. 2012, 29, 512–519. [Google Scholar] [CrossRef] [Green Version]
- Aymerich, F.; Fenu, L.; Francesconi, L.; Meloni, P. Fracture behaviour of a fibre reinforced earthen material under static and impact flexural loading. Constr. Build. Mater. 2016, 109, 109–119. [Google Scholar] [CrossRef]
- Salih, M.M.; Osofero, A.I.; Imbabi, M.S. Critical review of recent development in fiber reinforced adobe bricks for sustainable construction. Front. Struct. Civ. Eng. 2020, 14, 839–854. [Google Scholar] [CrossRef]
- Mohajerani, A.; Hui, S.-Q.; Mirzababaei, M.; Arulrajah, A.; Horpibulsuk, S.; Abdul Kadir, A.; Rahman, M.T.; Maghool, F. Amazing Types, Properties, and Applications of Fibres in Construction Materials. Materials 2019, 12, 2513. [Google Scholar] [CrossRef] [Green Version]
- Ramakrishnan, S.; Loganayagan, S.; Kowshika, G.; Ramprakash, C.; Aruneshwaran, M. Adobe blocks reinforced with natural fibres: A review. Mater. Today Proc. 2021, 45, 6493–6499. [Google Scholar] [CrossRef]
- Turco, C.; Junior, A.C.P.; Teixeira, E.R.; Mateus, R. Optimisation of Compressed Earth Blocks (CEBs) using natural origin materials: A systematic literature review. Constr. Build. Mater. 2021, 309, 125140. [Google Scholar] [CrossRef]
- Millogo, Y.; Aubert, J.-E.; Hamard, E.; Morel, J.-C. How Properties of Kenaf Fibers from Burkina Faso Contribute to the Reinforcement of Earth Blocks. Materials 2015, 8, 2332–2345. [Google Scholar] [CrossRef]
- Laibi, A.B.; Poullain, P.; Leklou, N.; Gomina, M.; Sohounhloué, D.K.C. Influence of the kenaf fiber length on the mechanical and thermal properties of Compressed Earth Blocks (CEB). KSCE J. Civ. Eng. 2017, 22, 785–793. [Google Scholar] [CrossRef]
- Danso, H.; Martinson, B.; Ali, M.; Williams, J. Physical, mechanical and durability properties of soil building blocks reinforced with natural fibres. Constr. Build. Mater. 2015, 101, 797–809. [Google Scholar] [CrossRef] [Green Version]
- Vodounon, N.A.; Kanali, C.; Mwero, J. Compressive and Flexural Strengths of Cement Stabilized Earth Bricks Reinforced with Treated and Untreated Pineapple Leaves Fibres. Open J. Compos. Mater. 2018, 8, 145–160. [Google Scholar] [CrossRef] [Green Version]
- Vincenzini, A.; Augarde, C.E.; Gioffrè, M. Experimental characterization of natural fibre–soil interaction: Lessons for earthen construction. Mater. Struct. 2021, 54, 110. [Google Scholar] [CrossRef]
- Danso, H.; Martinson, B.; Ali, M.; Williams, J. Effect of fibre aspect ratio on mechanical properties of soil building blocks. Constr. Build. Mater. 2015, 83, 314–319. [Google Scholar] [CrossRef] [Green Version]
- Mostafa, M.; Uddin, N. Effect of Banana Fibers on the Compressive and Flexural Strength of Compressed Earth Blocks. Buildings 2015, 5, 282–296. [Google Scholar] [CrossRef] [Green Version]
- Taallah, B.; Guettala, A. The mechanical and physical properties of compressed earth block stabilized with lime and filled with untreated and alkali-treated date palm fibers. Constr. Build. Mater. 2016, 104, 52–62. [Google Scholar] [CrossRef]
- Laborel-Préneron, A.; Aubert, J.-E.; Magniont, C.; Maillard, P.; Poirier, C. Effect of Plant Aggregates on Mechanical Properties of Earth Bricks. J. Mater. Civ. Eng. 2017, 29, 04017244. [Google Scholar] [CrossRef]
- Ajouguim, S.; Talibi, S.; Djelal-Dantec, C.; Hajjou, H.; Waqif, M.; Stefanidou, M.; Saadi, L. Effect of Alfa fibers on the mechanical and thermal properties of compacted earth bricks. Mater. Today Proc. 2021, 37, 4049–4057. [Google Scholar] [CrossRef]
- Hema, C.; Messan, A.; Lawane, A.; Soro, D.; Nshimiyimana, P.; van Moeseke, G. Improving the thermal comfort in hot region through the design of walls made of compressed earth blocks: An experimental investigation. J. Build. Eng. 2021, 38, 102148. [Google Scholar] [CrossRef]
- Nshimiyimana, P.; Hema, C.; Zoungrana, O.; Messan, A.; Courard, L. Courard, Thermophysical and mechanical properties of compressed earth blocks containing fibres: By-product of okra plant and polymer waste, WIT Trans. Built. Environ. 2020, 195, 149–161. [Google Scholar] [CrossRef]
- Velasco-Aquino, A.A.; Espuna-Mujica, J.A.; Perez-Sanchez, J.F.; Zuñiga-Leal, C.; Palacio-Perez, A.; Suarez-Dominguez, E.J. Compressed earth block reinforced with coconut fibers and stabilized with aloe vera and lime. J. Eng. Des. Technol. 2021, 19, 795–807. [Google Scholar] [CrossRef]
- Danso, H.; Martinson, B.; Ali, M.; Williams, J.B. Mechanisms by which the inclusion of natural fibres enhance the properties of soil blocks for construction. J. Compos. Mater. 2017, 51, 3835–3845. [Google Scholar] [CrossRef] [Green Version]
- Hagan, M.T.; Dcmuth, H.B.; Beale, M. Neural Network Design; PWS Publishing Co.: Boston, MA, USA, 1996. [Google Scholar]
- Lee, S.-C. Prediction of concrete strength using artificial neural networks. Eng. Struct. 2003, 25, 849–857. [Google Scholar] [CrossRef]
- Sarıdemir, M.; Topçu, I.B.; Özcan, F.; Severcan, M.H. Prediction of long-term effects of GGBFS on compressive strength of concrete by artificial neural networks and fuzzy logic. Constr. Build. Mater. 2009, 23, 1279–1286. [Google Scholar] [CrossRef]
- Topçu, İ.B.; Sarıdemir, M. Prediction of mechanical properties of recycled aggregate concretes containing silica fume using artificial neural networks and fuzzy logic. Comput. Mater. Sci. 2008, 42, 74–82. [Google Scholar] [CrossRef]
- Sitton, J.D.; Zeinali, Y.; Story, B.A. Rapid soil classification using artificial neural networks for use in constructing compressed earth blocks. Constr. Build. Mater. 2017, 138, 214–221. [Google Scholar] [CrossRef]
- Lan, G.; Wang, Y.; Zeng, G.; Zhang, J. Compressive strength of earth block masonry: Estimation based on neural networks and adaptive network-based fuzzy inference system. Compos. Struct. 2020, 235, 111731. [Google Scholar] [CrossRef]
- DeRousseau, M.; Kasprzyk, J.; Srubar, W. Computational design optimization of concrete mixtures: A review. Cem. Concr. Res. 2018, 109, 42–53. [Google Scholar] [CrossRef]
- Garzón-Roca, J.; Marco, C.O.; Adam, J.M. Compressive strength of masonry made of clay bricks and cement mortar: Estimation based on Neural Networks and Fuzzy Logic. Eng. Struct. 2013, 48, 21–27. [Google Scholar] [CrossRef]
- Zhou, Q.; Wang, F.; Zhu, F. Estimation of compressive strength of hollow concrete masonry prisms using artificial neural networks and adaptive neuro-fuzzy inference systems. Constr. Build. Mater. 2016, 125, 417–426. [Google Scholar] [CrossRef]
- Golafshani, E.M.; Behnood, A.; Arashpour, M. Predicting the compressive strength of normal and High-Performance Concretes using ANN and ANFIS hybridized with Grey Wolf Optimizer. Constr. Build. Mater. 2020, 232, 117266. [Google Scholar] [CrossRef]
- Azimi-Pour, M.; Eskandari-Naddaf, H. ANN and GEP prediction for simultaneous effect of nano and micro silica on the compressive and flexural strength of cement mortar. Constr. Build. Mater. 2018, 189, 978–992. [Google Scholar] [CrossRef]
- Güçlüer, K.; Özbeyaz, A.; Göymen, S.; Günaydın, O. A comparative investigation using machine learning methods for concrete compressive strength estimation. Mater. Today Commun. 2021, 27, 102278. [Google Scholar] [CrossRef]
- Teymen, A.; Mengüç, E.C. Comparative evaluation of different statistical tools for the prediction of uniaxial compressive strength of rocks. Int. J. Min. Sci. Technol. 2020, 30, 785–797. [Google Scholar] [CrossRef]
- Dantas, A.T.A.; Leite, M.B.; de Jesus Nagahama, K. Prediction of compressive strength of concrete containing construction and demolition waste using artificial neural networks. Constr. Build. Mater. 2013, 38, 717–722. [Google Scholar] [CrossRef]
- Duan, Z.; Kou, S.; Poon, C.S. Using artificial neural networks for predicting the elastic modulus of recycled aggregate concrete. Constr. Build. Mater. 2013, 44, 524–532. [Google Scholar] [CrossRef]
- Neeraja, D.; Swaroop, G. Prediction of Compressive Strength of Concrete using Artificial Neural Networks. Res. J. Pharm. Technol. 2017, 10, 35. [Google Scholar] [CrossRef]
- Topçu, I.B.; Sarıdemir, M. Prediction of compressive strength of concrete containing fly ash using artificial neural networks and fuzzy logic. Comput. Mater. Sci. 2008, 41, 305–311. [Google Scholar] [CrossRef]
- Ongpeng, J.M.C.; Gapuz, E.; Roxas, C.L.C. Optimization of mix proportions of compressed earth blocks with rice straw using artificial neural network. In Proceedings of the 2017 World Congress on Advances in Strucural Engineering and Mechanics (ASEM17), Seoul, Korea, 28 August–1 September 2017; pp. 1–14. [Google Scholar]
- Samuel, A.L. Some Studies in Machine Learning Using the Game of Checkers. IBM J. Res. Dev. 1959, 3, 210–229. [Google Scholar] [CrossRef]
- Marai, M.A.; Ahmed, M.A.; Mousa, S.E.-B. Neural networks for predicting compressive strength of structural light weight concrete. Constr. Build. Mater. 2009, 23, 2214–2219. [Google Scholar] [CrossRef]
- Kang, M.-C.; Yoo, D.-Y.; Gupta, R. Machine learning-based prediction for compressive and flexural strengths of steel fiber-reinforced concrete. Constr. Build. Mater. 2021, 266, 121117. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, J.; Ann, F.T.; Ma, G. Intelligent mixture design of steel fibre reinforced concrete using a support vector regression and firefly algorithm based multi-objective optimization model. Constr. Build. Mater. 2020, 260, 120457. [Google Scholar] [CrossRef]
- Young, B.A.; Hall, A.; Pilon, L.; Gupta, P.; Sant, G. Can the compressive strength of concrete be estimated from knowledge of the mixture proportions?: New insights from statistical analysis and machine learning methods. Cem. Concr. Res. 2019, 115, 379–388. [Google Scholar] [CrossRef]
- Danso, H. Use of Agricultural Waste Fibres as Enhancement of Soil Blocks for Low-Cost Housing in Ghana, University of Portsmouth. 2016. Available online: https://researchportal.port.ac.uk/en/studentTheses/use-of-agricultural-waste-fibres-as-enhancement-of-soil-blocks-fo (accessed on 27 September 2021).
- Mostafa, M.; Uddin, N. Experimental analysis of Compressed Earth Block (CEB) with banana fibers resisting flexural and compression forces. Case Stud. Constr. Mater. 2016, 5, 53–63. [Google Scholar] [CrossRef] [Green Version]
- Lejano, B.A.; Gabaldon, R.J.; Go, P.J.; Juan, C.G.; Wong, M. Compressed earth blocks with powdered green mussel shell as partial binder and pig hair as fiber reinforcement. Int. J. GEOMATE 2019, 16, 137–143. [Google Scholar] [CrossRef]
- Araya-Letelier, G.; Antico, F.C.; Urzua, J.; Bravo, R. Physical-mechanical characterization of fiber-reinforced mortar incorporating pig hair. In Proceedings of the 2nd International Conference on Bio-Based Building Materials & 1st Conference on ECOlogical Valorisation of GRAnular and FIbrous Materials, Clermont-Ferrand, France, 21–23 June 2017. [Google Scholar]
- Delgado, M.C.J.; Guerrero, I.C. The selection of soils for unstabilised earth building: A normative review. Constr. Build. Mater. 2007, 21, 237–251. [Google Scholar] [CrossRef]
- Day, R.W. Soil Testing Manual: Procedures, Classification Data, and Sampling Practices; McGraw Hill, Inc.: New York, NY, USA, 2001. [Google Scholar]
- Akhzouz, H.; El Minor, H.; Tatane, M.; Bendarma, A. Physical characterization of bio-composite CEB stabilized with Argan nut shell and cement. Mater. Today Proc. 2021, 36, 107–114. [Google Scholar] [CrossRef]







| Study Ref. | Type of Fibre Used | Dry Density | Water Absorption | Compressive Strength | Tensile Strength | Flexural Strength | Fibres Tensile Strength |
|---|---|---|---|---|---|---|---|
| [53] | Coconut coir | • | • | • | • | • | |
| Sugarcane bagasse | • | • | • | • | • | ||
| Oil palm fibres | • | • | • | • | • | ||
| [22] | Banana fibres | • | • | • | |||
| [54] | Banana fibres | • | • | • | • | ||
| [55] | Pig hair | • | |||||
| [19] | Pineapple leaves | • | • | • |
| Database 1 | Database 2 | |
|---|---|---|
| Features’ matrix | ||
| Target vector |
| Feature Vectors | U.M. | Mean | St. Dev. | Min. | Max. | |
|---|---|---|---|---|---|---|
| Clay content | % | 0.23 | 0.09 | 0.08 | 0.35 | |
| OMC | % | 0.20 | 0.08 | 0.10 | 0.31 | |
| Cement content | % | 0.03 | 0.03 | 0.00 | 0.07 | |
| Fibre content | % | 0.01 | 0.02 | 0.00 | 0.05 | |
| Fibre length | mm | 42.33 | 22.01 | 0.00 | 100.00 | |
| Fibre tensile strength | MPa | 218.16 | 227.73 | 0.00 | 751.95 | |
| Specimen’s age | Days | 20.96 | 6.51 | 7.00 | 28.00 | |
| Target vector | ||||||
| Compressive strength | MPa | 2.80 | 1.47 | 0.33 | 6.30 | |
| Feature Vectors | U.M. | Mean | St. Dev. | Min. | Max. | |
|---|---|---|---|---|---|---|
| Clay content | % | 0.22 | 0.08 | 0.14 | 0.30 | |
| Fibre content | % | 0.01 | 0.00 | 0.00 | 0.01 | |
| Fibre length | mm | 51.69 | 22.69 | 0.00 | 80.00 | |
| Fibre density | kg/m3 | 658.46 | 218.16 | 0.00 | 810.00 | |
| Fibre tensile strength | MPa | 92.00 | 50.58 | 0.00 | 152.50 | |
| Target vector | ||||||
| Tensile strength | MPa | 0.29 | 0.03 | 0.22 | 0.37 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Turco, C.; Funari, M.F.; Teixeira, E.; Mateus, R. Artificial Neural Networks to Predict the Mechanical Properties of Natural Fibre-Reinforced Compressed Earth Blocks (CEBs). Fibers 2021, 9, 78. https://doi.org/10.3390/fib9120078
Turco C, Funari MF, Teixeira E, Mateus R. Artificial Neural Networks to Predict the Mechanical Properties of Natural Fibre-Reinforced Compressed Earth Blocks (CEBs). Fibers. 2021; 9(12):78. https://doi.org/10.3390/fib9120078
Chicago/Turabian StyleTurco, Chiara, Marco Francesco Funari, Elisabete Teixeira, and Ricardo Mateus. 2021. "Artificial Neural Networks to Predict the Mechanical Properties of Natural Fibre-Reinforced Compressed Earth Blocks (CEBs)" Fibers 9, no. 12: 78. https://doi.org/10.3390/fib9120078
APA StyleTurco, C., Funari, M. F., Teixeira, E., & Mateus, R. (2021). Artificial Neural Networks to Predict the Mechanical Properties of Natural Fibre-Reinforced Compressed Earth Blocks (CEBs). Fibers, 9(12), 78. https://doi.org/10.3390/fib9120078









