Angle-Resolved Hollow-Core Fiber-Based Curvature Sensing Approach
Abstract
:1. Introduction
2. Materials and Methods
3. Results
3.1. The Fiber’s Bend-Dependent Response
3.2. Calibration of the Fiber Response
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Debord, B.; Amrani, F.; Vincetti, L.; Gérôme, F.; Benabid, F. Hollow-core fiber technology: The rising of ‘gas photonics’. Fibers 2019, 7, 16. [Google Scholar] [CrossRef] [Green Version]
- Gao, S.F.; Wang, Y.Y.; Ding, W.; Jiang, D.L.; Gu, S.; Zhang, X.; Wang, P. Hollow-core conjoined-tube negative-curvature fibre with ultralow loss. Nat. Commun. 2018, 19, 2828. [Google Scholar] [CrossRef] [Green Version]
- Amrani, F.; Osório, J.H.; Delahaye, F.; Giovanardi, F.; Vincetti, L.; Debord, B.; Gérôme, F.; Benabid, F. Low-loss single-mode hybrid-lattice hollow-core photonic-crystal fibre. Light Sci. Appl. 2021, 10, 7. [Google Scholar] [CrossRef]
- Sakr, H.; Chen, Y.; Jasion, G.T.; Bradley, T.D.; Hayes, J.R.; Mulvad, H.C.H.; Davidson, I.A.; Fokoua, E.N.; Poletti, F. Hollow core optical fibres with comparable attenuation to silica fibres between 600 and 1100 nm. Nat. Commun. 2020, 11, 6030. [Google Scholar] [CrossRef] [PubMed]
- Chafer, M.; Osório, J.H.; Amrani, F.; Delahaye, F.; Maurel, M.; Debord, B.; Gérôme, F. benabid, F. 1-km hollow-core fiber with loss at the silica Rayleigh limit in the green spectral range. IEEE Photon. Technol. Lett. 2019, 31, 685–688. [Google Scholar] [CrossRef]
- Gao, S.-F.; Wang, Y.-Y.; Ding, W.; Hong, Y.-F.; Wang, P. Conquering the Rayleigh scattering limit of silica glass fiber at visible wavelengths with a hollow-core fiber approach. Laser Photonics Rev. 2019, 14, 1900241. [Google Scholar]
- Osório, J.H.; Amrani, F.; Delahaye, F.; Dhaybi, A.; Vasko, K.; Tessier, G.; Giovanardi, F.; Vincetti, L.; Debord, B.; Gérôme, F.; et al. Hollow-core fiber with ultralow loss in the ultraviolet range and sub-thermodynamic equilibrium surface-roughness. arXiv 2021, arXiv:2105.11900. [Google Scholar]
- Cordier, M.; Delaye, P.; Gérôme, F.; Benabid, F.; Zaquine, I. Raman-free fibered photon-pair source. Sci. Rep. 2020, 10, 1650. [Google Scholar] [CrossRef]
- Okaba, S.; Yu, D.; Vincetti, L.; Benabid, F.; Katori, H. Superradiance from lattice-confined atoms inside hollow core fibre. Commun. Phys. 2019, 2, 136. [Google Scholar] [CrossRef] [Green Version]
- Chafer, M.; Osório, J.H.; Dhaybi, A.; Ravetta, F.; Amrani, F.; Delahaye, F.; Debord, B.; Caiteau-Fischbach, C.; Ancellet, G.; Gérôme, F.; et al. Near- and middle-ultraviolet reconfigurable Raman source using a record-low UV/visible transmission loss inhibited-coupling hollow-core fiber. arXiv 2021, arXiv:2108.11327. [Google Scholar]
- Ni, W.; Yang, C.; Luo, Y.; Xia, R.; Lu, P.; Hu, D.J.J.; Danto, S.; Shum, P.P.; Wei, L. Recent advancements of anti-resonant hollow-core fibers for sensing applications. Photonics 2021, 8, 128. [Google Scholar] [CrossRef]
- Yu, R.; Chen, Y.; Shui, L.; Xiao, L. Hollow-core photonic crystal fiber gas sensing. Sensors 2020, 20, 2996. [Google Scholar] [CrossRef] [PubMed]
- Cubillas, A.M.; Jiang, X.; Euser, T.G.; Taccardi, N.; Etzold, B.J.M.; Wasserscheid, P.; Russell, P.S. Photochemistry in a soft-glass single-ring hollow-core photonic crystal fiber. Analyst 2017, 142, 925–929. [Google Scholar] [CrossRef] [Green Version]
- Nissen, M.; Doherty, B.; Hamperl, J.; Kobelke, J.; Weber, K.; Henkel, T.; Schmidt, M.A. UV absorption spectroscopy in water-filled antiresonant hollow core fibers for pharmaceutical detection. Sensors 2018, 18, 478. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sardar, M.R.; Faisal, M.; Ahmed, K. Simple hollow core photonic crystal fiber for monitoring carbon dioxide gas with very high accuracy. Sens. Bio-Sens. Res. 2021, 31, 100401. [Google Scholar] [CrossRef]
- Arman, H.; Olyaee, S. Realization of low confinement loss acetylene gas sensor by using hollow-core photonic bandgap fiber. Opt. Quantum Electron. 2021, 53, 328. [Google Scholar] [CrossRef]
- Sardar, M.R.; Faisal, M.; Ahmed, K. Design and characterization of rectangular slotted porous core photonic crystal fiber for sensing CO2 gas. Sens. Bio-Sens. Res. 2021, 30, 100379. [Google Scholar] [CrossRef]
- Olyaee, S.; Arman, H.; Naraghi, A. Design, simulation, and optimization of acetylene gas sensor using hollow-core photonic bandgap fiber. Sens. Lett. 2015, 13, 387–392. [Google Scholar] [CrossRef]
- Ravaille, A.; Feugnet, G.; Debord, B.; Gérôme, F.; Benabid, F.; Bretenaker, F. Rotation measurements using a resonant fiber optic gyroscope based on Kagome fiber. Appl. Opt. 2019, 58, 2198–2204. [Google Scholar] [CrossRef] [PubMed]
- Sanders, G.A.; Taranta, A.A.; Narayanan, C.; Fokoua, E.N.; Mousavi, S.A.; Strandjord, L.K.; Smiciklas, M.; Bradley, T.D.; Hayes, J.; Jasion, G.T.; et al. Hollow-core resonator fiber optic gyroscope using nodeless anti-resonant fiber. Opt. Lett. 2021, 46, 46–49. [Google Scholar] [CrossRef]
- Yang, F.; Gyger, F.; Thévenaz, L. Intense Brillouing amplification in gas using hollow-core waveguides. Nat. Photonics. 2020, 14, 700–708. [Google Scholar] [CrossRef]
- Huang, X.; Zang, J.; Yoo, S. Multiple hollow-core anti-resonant fiber as a supermodal fiber interferometer. Sci. Rep. 2019, 9, 9342. [Google Scholar] [CrossRef] [PubMed]
- Cordeiro, C.M.B.; Osório, J.H.; Guimarães, W.M.; Franco, M.A.R. Azimuthally asymmetric tubular lattice hollow-core optical fiber. J. Opt. Soc. Am. B 2021, 38, F23–F28. [Google Scholar] [CrossRef]
- Wang, Y.; Rao, Y. A novel long period fiber grating sensor measuring and determining bend-direction simultaneously. IEEE Sens. J. 2005, 5, 839–843. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, C.; Webb, D.J.; Kalli, K.; Peng, G. Highly sensitive bend sensor based on Bragg grating in eccentric core polymer fiber. IEEE Photon. Technol. Lett. 2010, 22, 850–852. [Google Scholar] [CrossRef] [Green Version]
- Luo, H.; Su, L.; Zhang, J.; Yuan, W.; Liu, S.; Wang, Y.; Wang, C.; Wang, X. C-shape microfiber taper interferometer for simultaneous measurement of curvature and temperature. Optik 2017, 145, 181–187. [Google Scholar] [CrossRef]
- Gong, Y.; Zhao, T.; Rao, Y.; Wu, Y. All-fiber curvature sensor based on multimode interference. IEEE Photon. Technol. Lett. 2011, 23, 679–681. [Google Scholar] [CrossRef]
- Frazão, O.; Viegas, J.; Caldas, P.; Santos, J.L.; Araújo, F.M.; Ferreira, L.A.; Farahi, F. All-fiber Mach-Zehnder curvature sensor based on multimode interference combined with a long-period grating. Opt. Lett. 2007, 32, 3074–3076. [Google Scholar] [CrossRef] [PubMed]
- Tang, Z.; Lou, S.; Wang, X.; Zhang, W.; Yan, S.; Xing, Z. High-performance bending vector and strain sensor using a dual-tapered photonic crystal fiber Mach-Zehnder interferometer. IEEE Sens. J. 2019, 19, 4062–4068. [Google Scholar] [CrossRef]
- Frazão, O.; Baptista, J.M.; Santos, J.L.; Roy, P. Curvature sensor using a highly birefringent photonic crystal fiber with two asymmetric hole regions in a Sagnac interferometer. Appl. Opt. 2008, 47, 2520–2523. [Google Scholar] [CrossRef] [PubMed]
- Osório, J.H.; Oliveira, R.; Aristilde, S.; Chesini, G.; Franco, M.A.R.; Nogueira, R.N.; Cordeiro, C.M.B. Bragg gratings in surface-core fibers: Refractive index and directional curvature sensing. Opt. Fiber Technol. 2017, 34, 86–90. [Google Scholar] [CrossRef]
- Newkirk, A.V.; Antonio-Lopez, J.E.; Valazquez-Benitez, A.; Albert, J.; Amezcua-Correa, R.; Schülzgen, A. Bending sensor combining multicore fiber with a mode-selective photonic lantern. Opt. Lett. 2015, 40, 5188–5191. [Google Scholar] [CrossRef] [Green Version]
- Mousavi, S.A.; Sandoghchi, S.R.; Richardson, D.J.; Poletti, F. Broadband high birefringence and polarizing hollow core antiresonant fibers. Opt. Express. 2016, 24, 22943–22958. [Google Scholar] [CrossRef] [PubMed]
- Yerolatsitis, S.; Shurvinton, R.; Song, P.; Zhang, Y.; Francis-Jones, R.J.A.; Rusimova, K.R. Birefringent anti-resonant hollow-core fiber. J. Lightwave Technol. 2020, 38, 5157–5162. [Google Scholar] [CrossRef]
- Osório, J.H.; Chafer, M.; Debord, B.; Giovanardi, F.; Cordier, M.; Maurel, M.; Delahaye, F.; Amrani, F.; Vincetti, L.; Gérôme, F.; et al. Tailoring modal properties of inhibited-coupling guiding fibers by cladding modification. Sci. Rep. 2019, 9, 1376. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, C.; Yu, R.; Debord, B.; Gérôme, F.; Benabid, F.; Chiang, K.S.; Xiao, L. Ultralow-loss fusion splicing between negative curvature hollow-core fibers and conventional SMFs with a reverse-tapering method. Opt. Express. 2021, 29, 22470–22478. [Google Scholar] [CrossRef] [PubMed]
- Suslov, D.; Komanec, M.; Fokoua, E.R.N.; Dousek, D.; Zhong, A.; Zvánovec, S.; Bradley, T.D.; Poletti, F.; Richardson, D.J.; Slavík, R. Low loss and high performance interconnection between standard single-mode fiber and antiresonant hollow-core fiber. Sci. Rep. 2021, 11, 8799. [Google Scholar] [CrossRef]
- Yu, R.; Wang, C.; Benabid, F.; Chiang, K.S.; Xiao, L. Robust mode matching between structurally dissimilar optical fiber waveguides. ACS Photon. 2021, 8, 857–863. [Google Scholar] [CrossRef]
- Bradley, T.D.; Wang, Y.; Alharbi, M.; Debord, B.; Fourcade-Dutin, C.; Beaudou, B.; Gérôme, F.; Benabid, F. Optical properties of low loss (70dB/km) hypocycloid-core kagome hollow core photonic crystal fiber for Rb and Cs based optical applications. J. Light. Technol. 2013, 31, 2752–2755. [Google Scholar] [CrossRef]
- Couny, F.; Benabid, F.; Roberts, P.J.; Light, P.S.; Raymer, M.G. Generation and photonic guidance of multi-octave optical frequency combs. Science 2007, 318, 1118–1121. [Google Scholar] [CrossRef]
- Debord, B.; Amsanpally, A.; Chafer, M.; Baz, A.; Maurel, M.; Blondy, J.M.; Hugonnot, E.; Scol, F.; Vincetti, L.; Gérôme, F.; et al. Ultralow transmission loss in inhibited-coupling guiding hollow fibers. Optica 2017, 4, 209–217. [Google Scholar] [CrossRef] [Green Version]
- Malitson, I.H. Intraspecimen comparison of the refractive index of fused silica. J. Opt. Soc. Am. 1965, 55, 1205–1208. [Google Scholar] [CrossRef]
- Sakr, H.; Bradley, T.D.; Jasion, G.T.; Fokoua, E.N.; Sandoghchi, S.R.; Davidson, I.A.; Taranta, A.; Guerra, G.; Shere, W.; Chen, Y.; et al. Hollow core NANFs with five nested tubes and record low loss at 850, 1060, 1300 and 1625 nm. In Proceedings of the 2021 Optical Fiber Communications Conference and Exhibition (OFC), San Francisco, CA, USA, 6–10 June 2021. F3A.4. [Google Scholar]
- Wang, K.; Dong, X.; Köhler, M.H.; Kienle, P.; Bian, Q.; Jakobi, M.; Koch, A.W. Advances in optical fiber sensors based on multimode interference (MMI): A review. IEEE Sens. J. 2021, 21, 132–142. [Google Scholar] [CrossRef]
- Osório, J.H.; Guimarães, W.M.; Peng, L.; Franco, M.A.R.; Warren-Smith, S.C.; Ebendorff-Heidepriem, H.; Cordeiro, C.M.B. Exposed-core fiber multimode interference sensor. Results Opt. 2021, 5, 100125. [Google Scholar] [CrossRef]
- Setti, V.; Vincetti, L.; Argyros, A. Flexible tube lattice fibers for terahertz applications. Opt. Express. 2013, 21, 3388–3399. [Google Scholar] [CrossRef]
- Frosz, M.H.; Roth, P.; Günendi, M.C.; Russell, P.S. Analytical formulation for bending loss in single-ring hollow-core photonic crystal fibers. Photon. Res. 2017, 5, 88–91. [Google Scholar] [CrossRef] [Green Version]
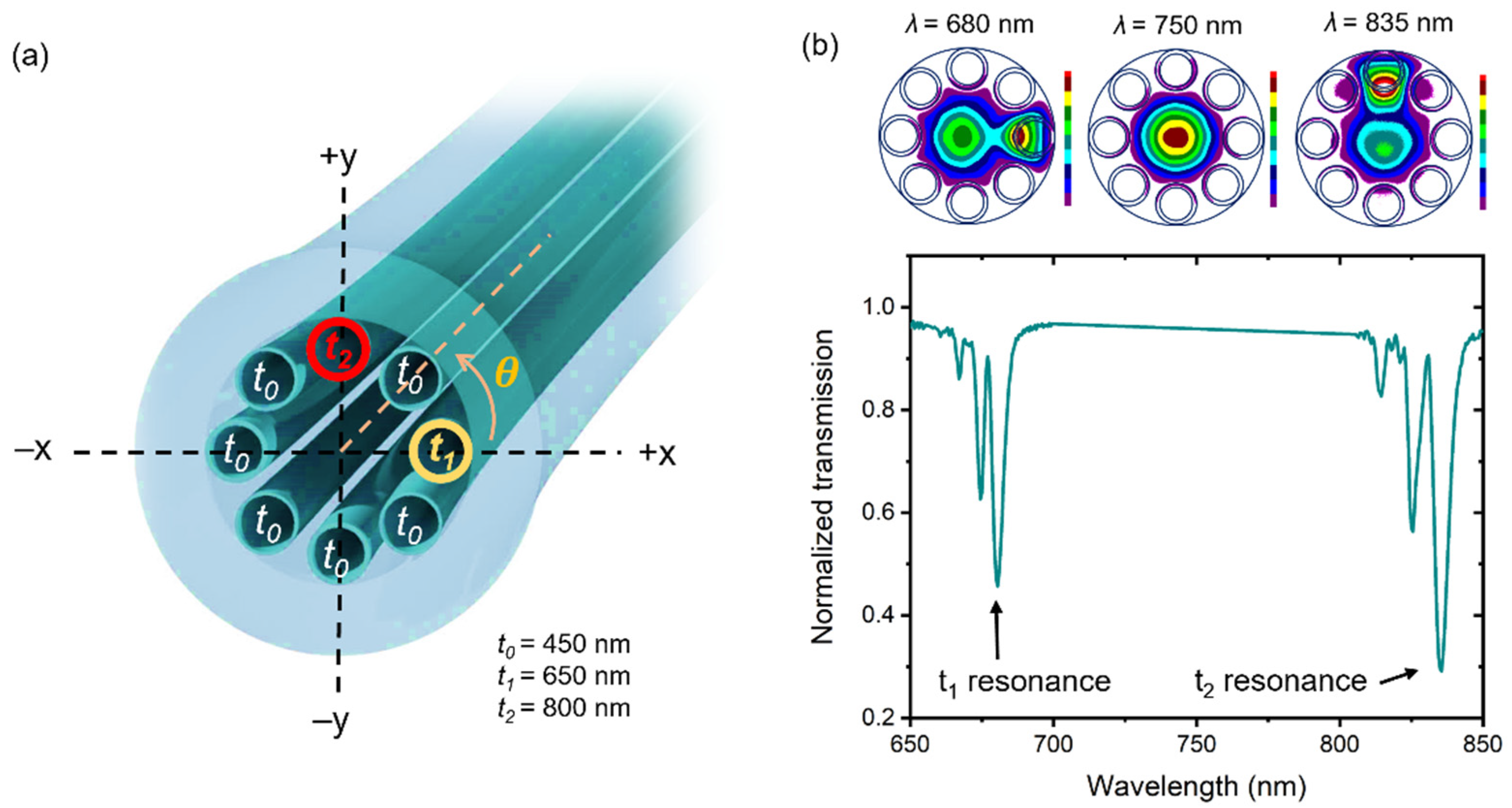
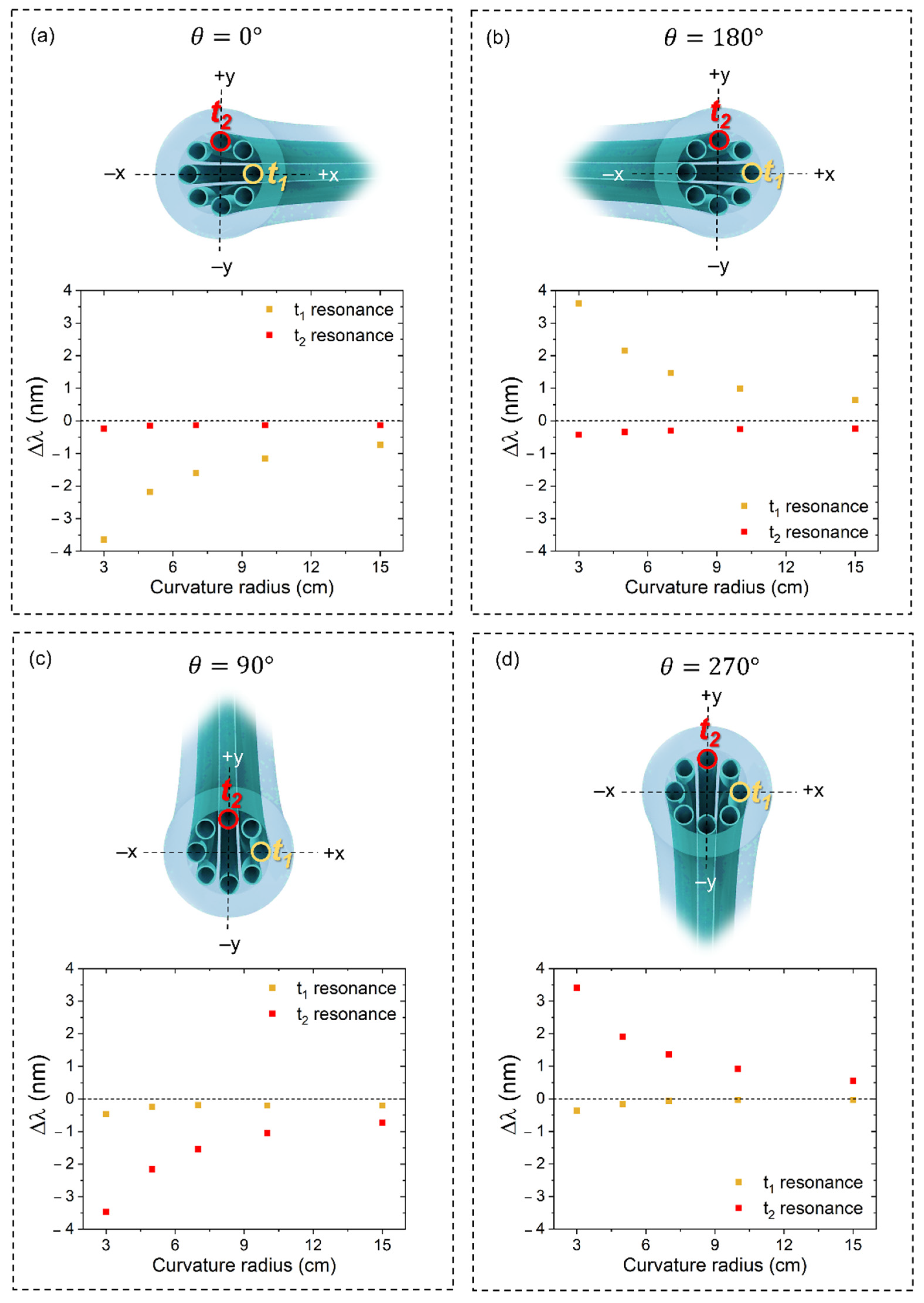
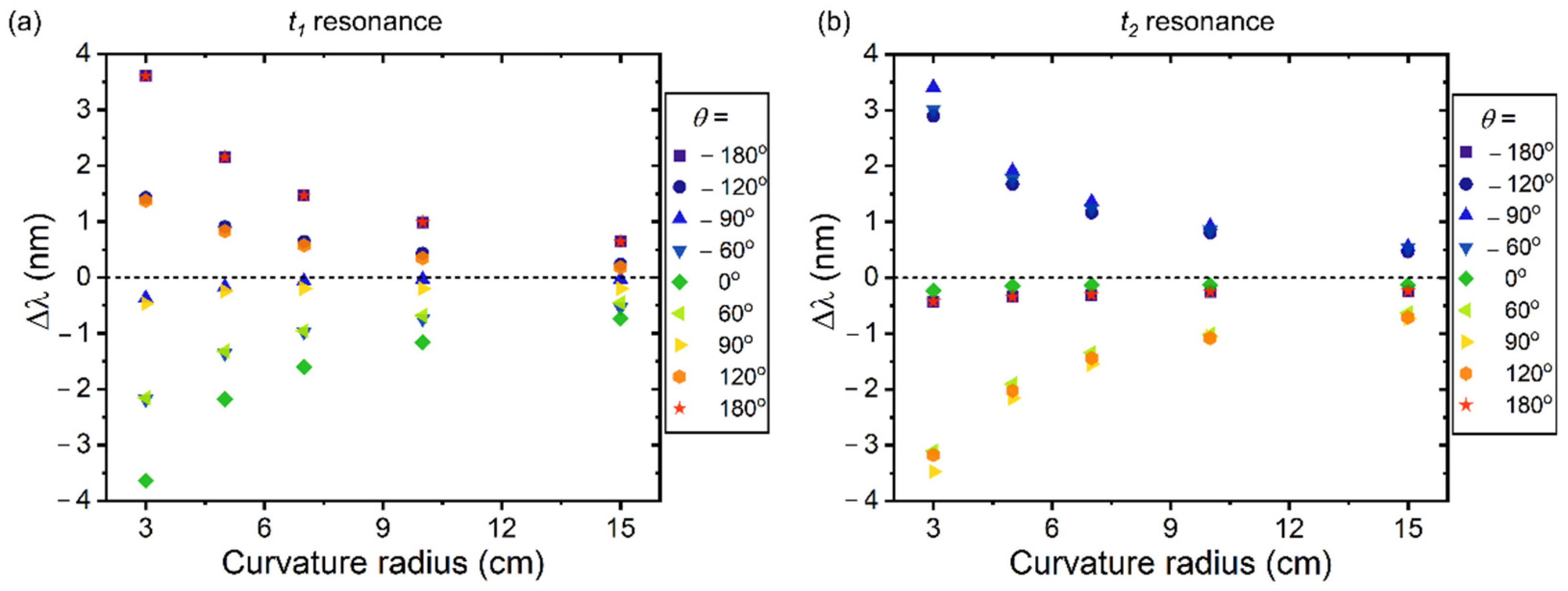
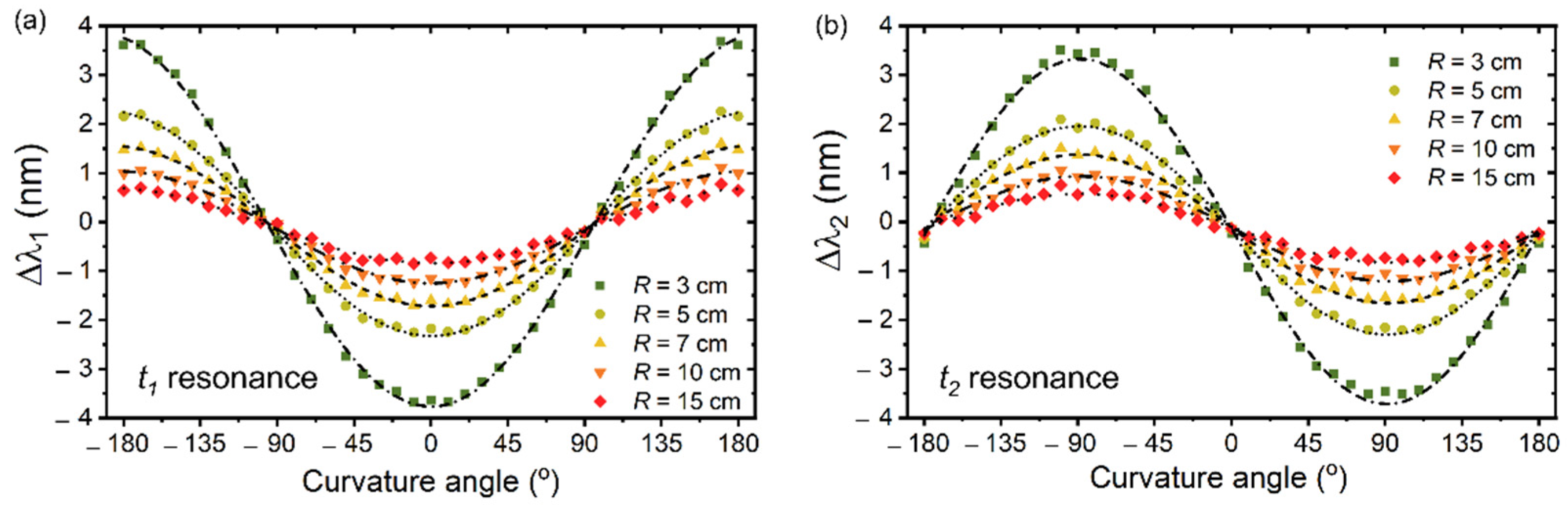
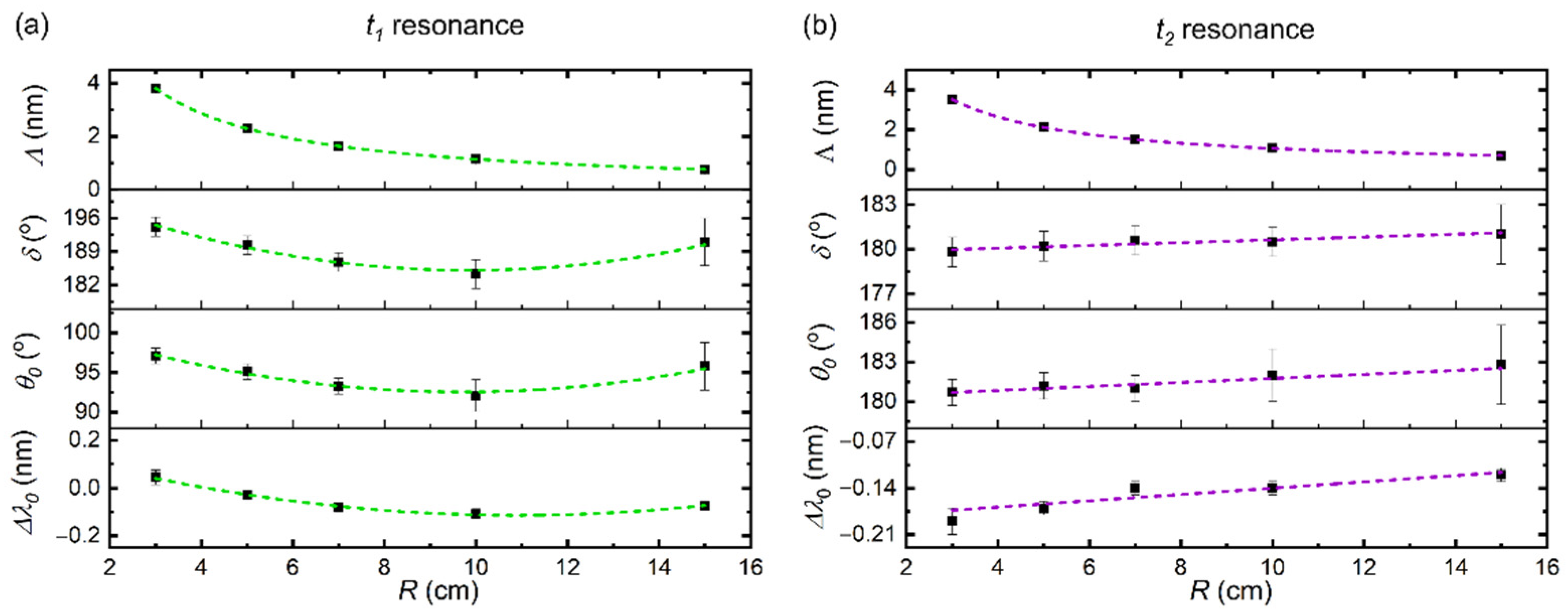
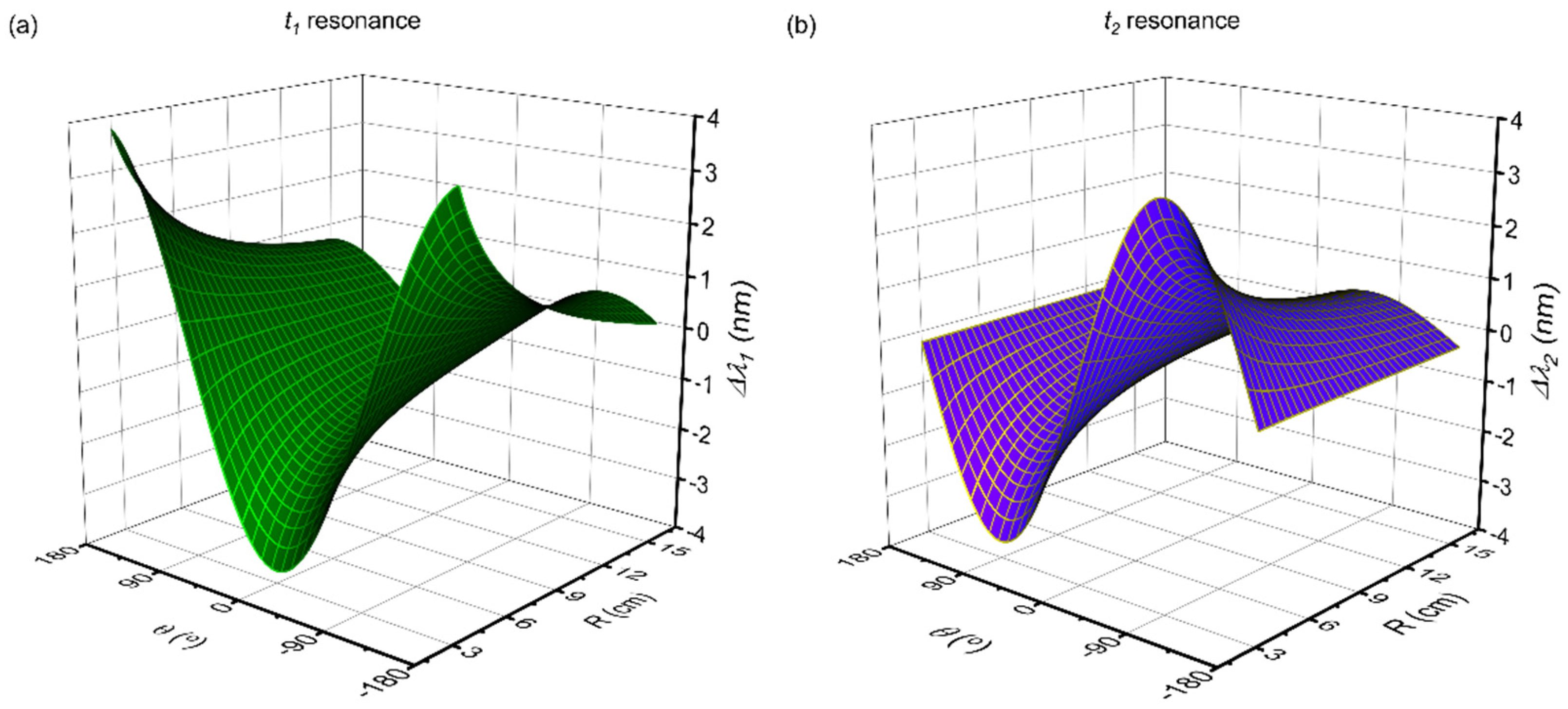
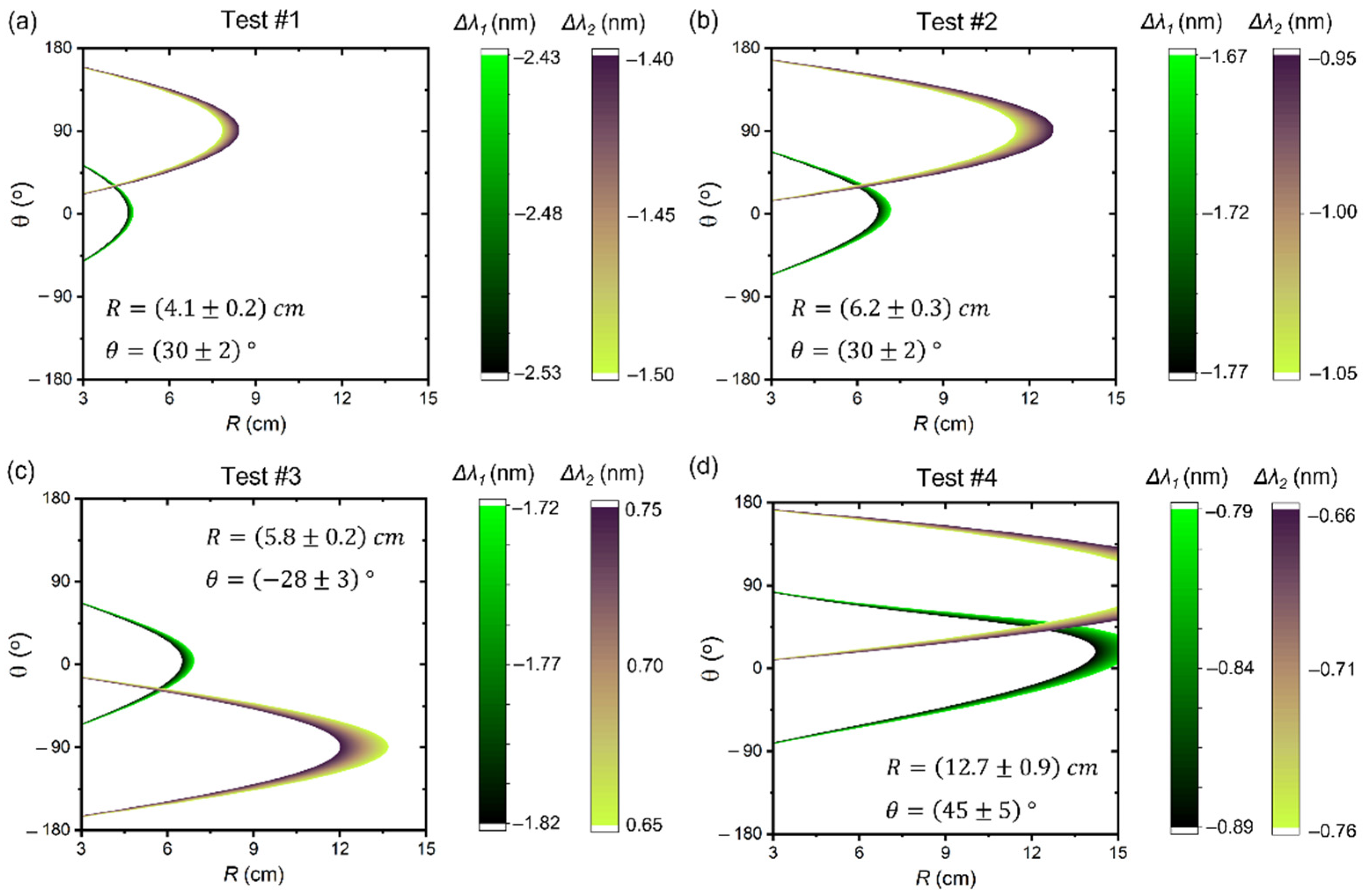
| Parameter | Fitting Function (t1 Resonance) | Fitting Function (t2 Resonance) |
|---|---|---|
| Λ | ||
| δ | ||
| θ0 | ||
| Δλ0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guimarães, W.M.; Cordeiro, C.M.B.; Franco, M.A.R.; Osório, J.H. Angle-Resolved Hollow-Core Fiber-Based Curvature Sensing Approach. Fibers 2021, 9, 72. https://doi.org/10.3390/fib9110072
Guimarães WM, Cordeiro CMB, Franco MAR, Osório JH. Angle-Resolved Hollow-Core Fiber-Based Curvature Sensing Approach. Fibers. 2021; 9(11):72. https://doi.org/10.3390/fib9110072
Chicago/Turabian StyleGuimarães, William M., Cristiano M. B. Cordeiro, Marcos A. R. Franco, and Jonas H. Osório. 2021. "Angle-Resolved Hollow-Core Fiber-Based Curvature Sensing Approach" Fibers 9, no. 11: 72. https://doi.org/10.3390/fib9110072
APA StyleGuimarães, W. M., Cordeiro, C. M. B., Franco, M. A. R., & Osório, J. H. (2021). Angle-Resolved Hollow-Core Fiber-Based Curvature Sensing Approach. Fibers, 9(11), 72. https://doi.org/10.3390/fib9110072






