MESO-Scale Modeling of CFRP-Confined Concrete: Microplane-Based Approach
Abstract
1. Introduction
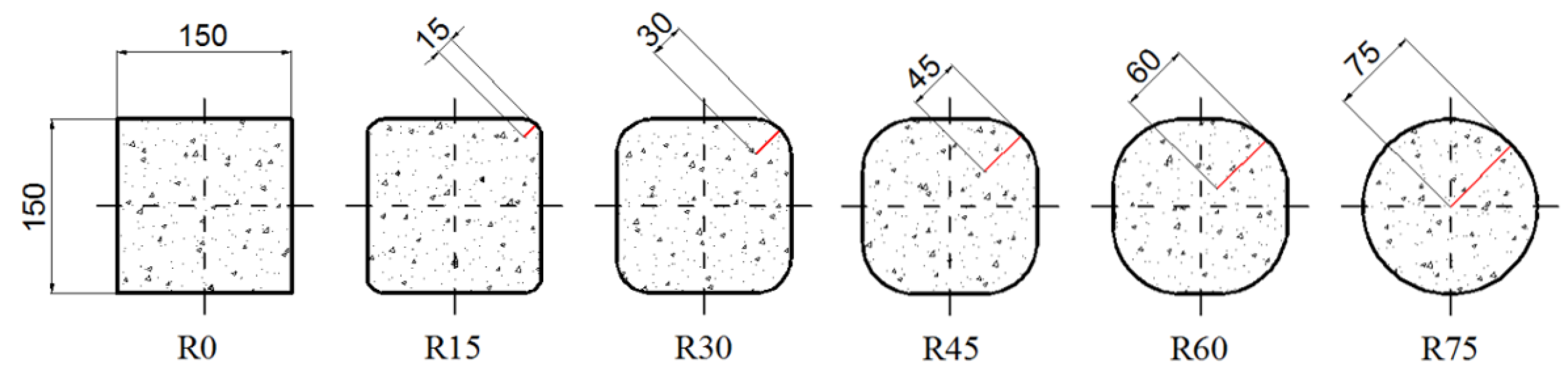
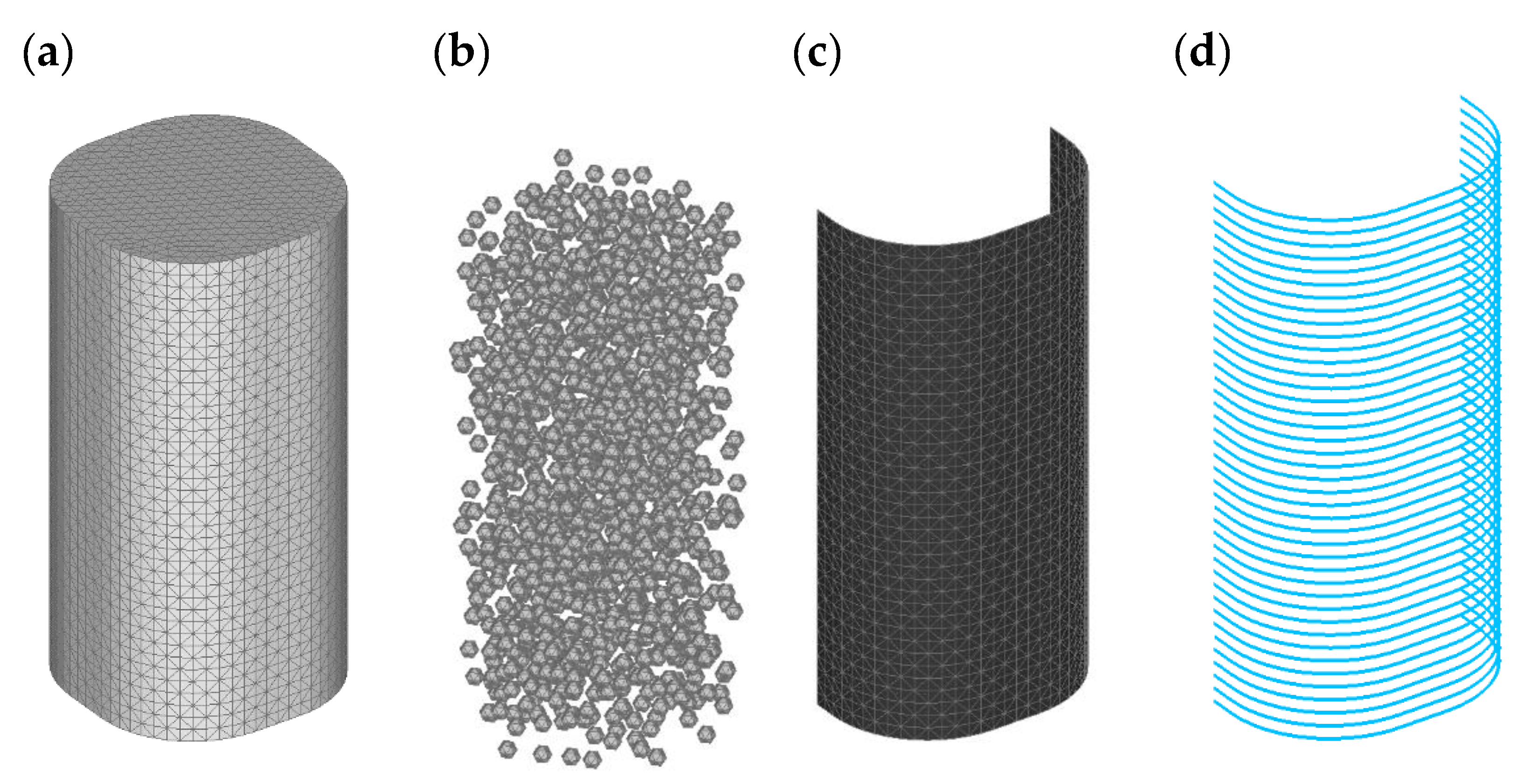
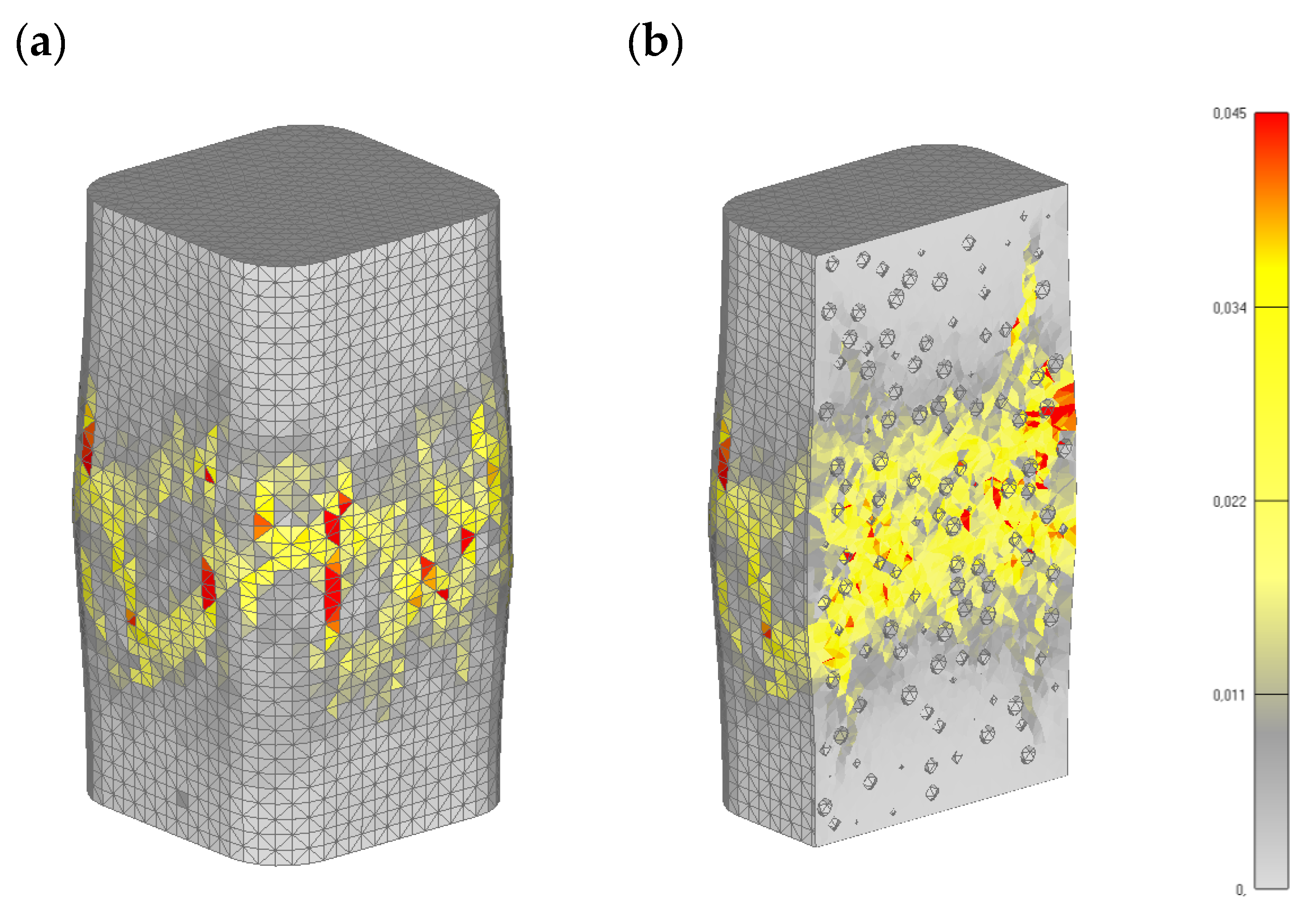
2. Random Aggregate Structure of Concrete
3. Materials and Method
4. Results and Discussion
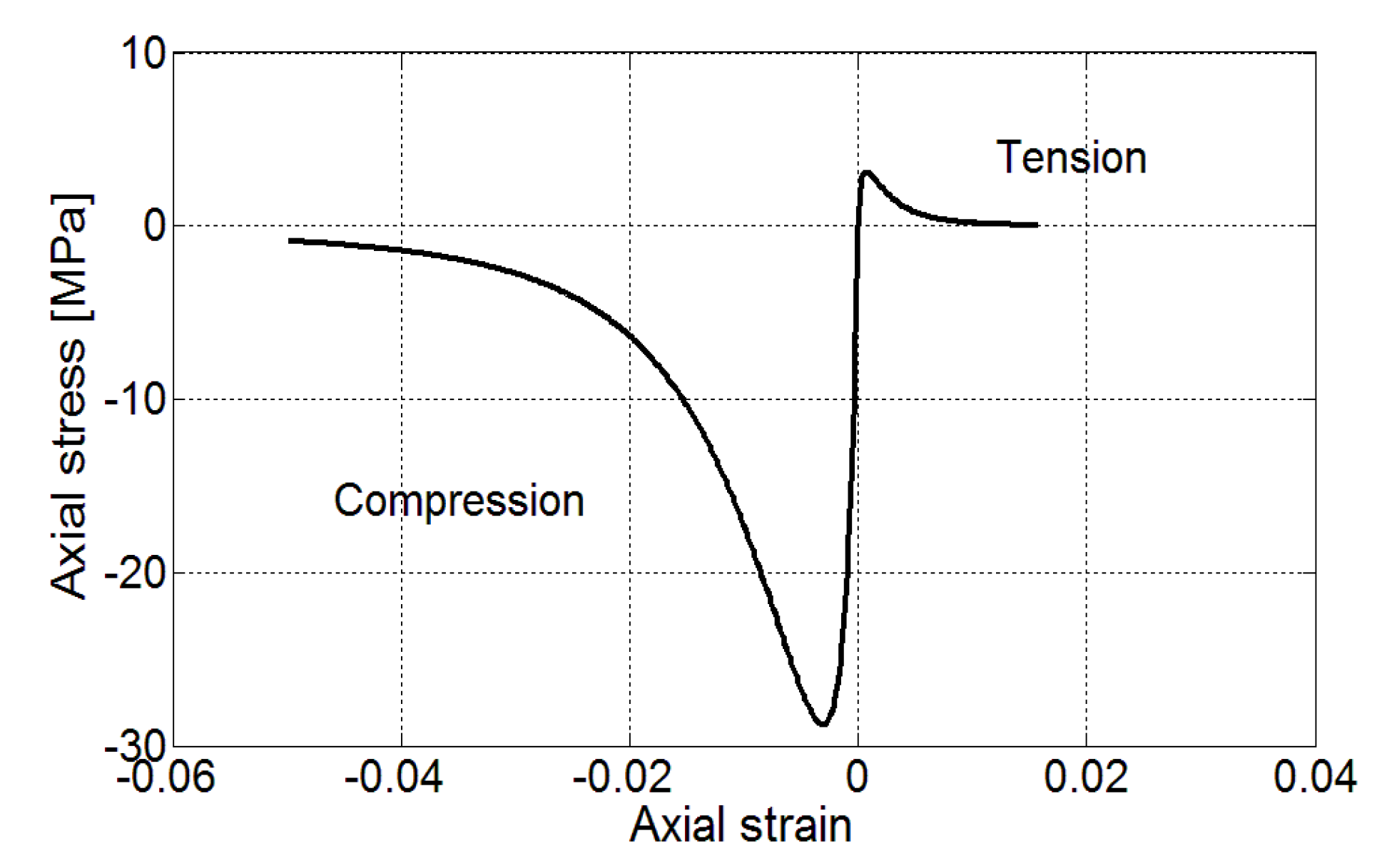
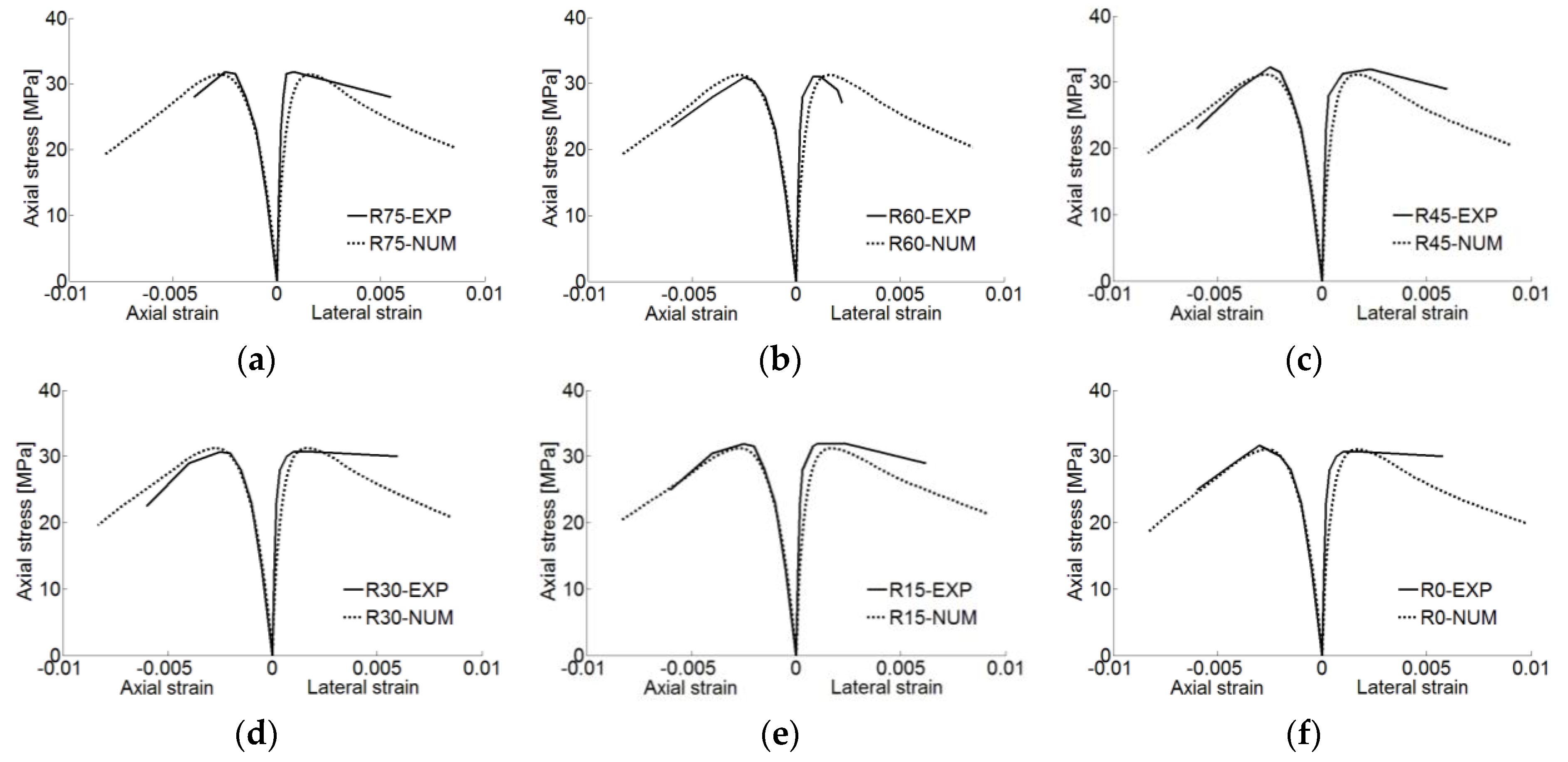
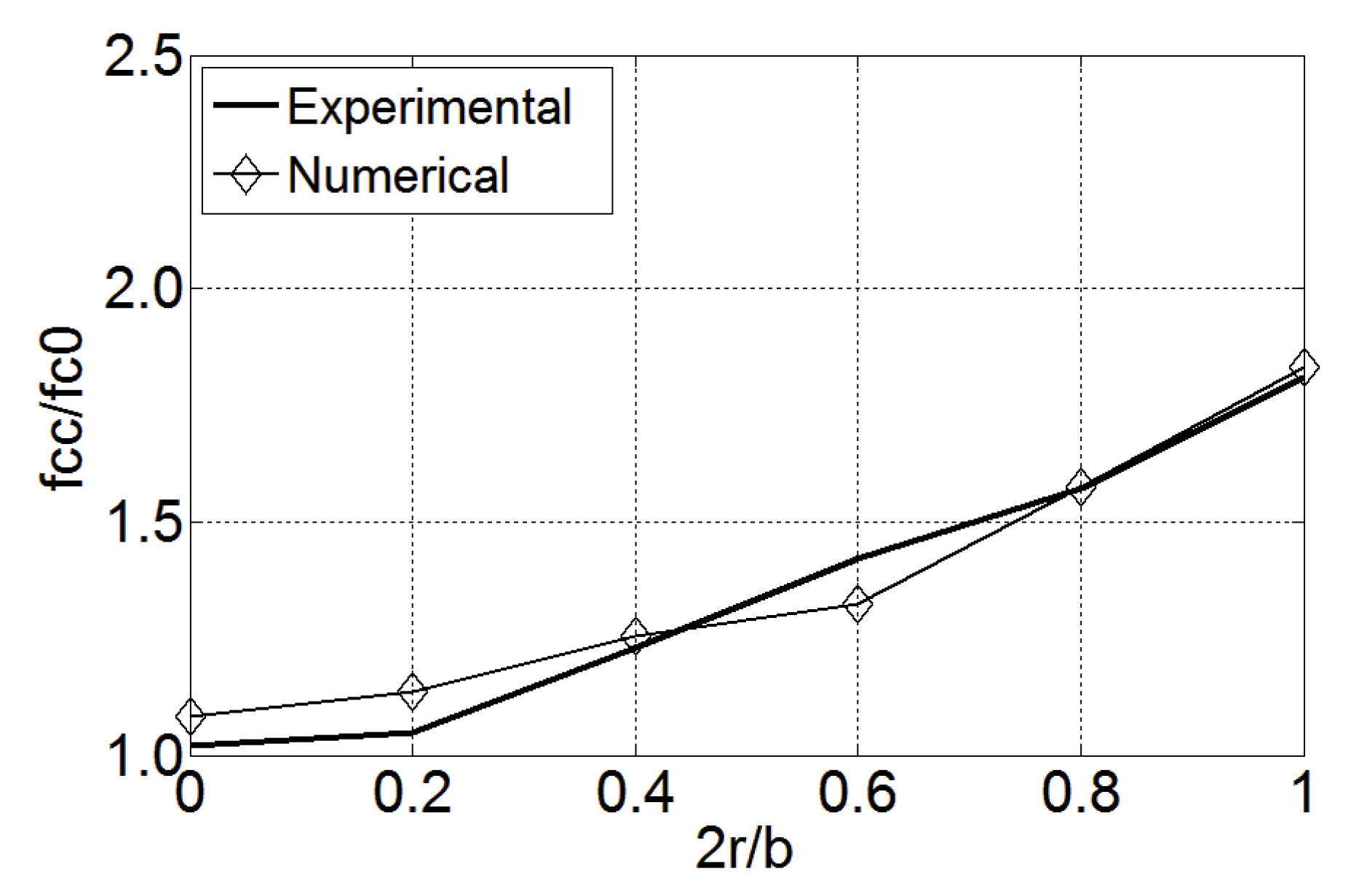
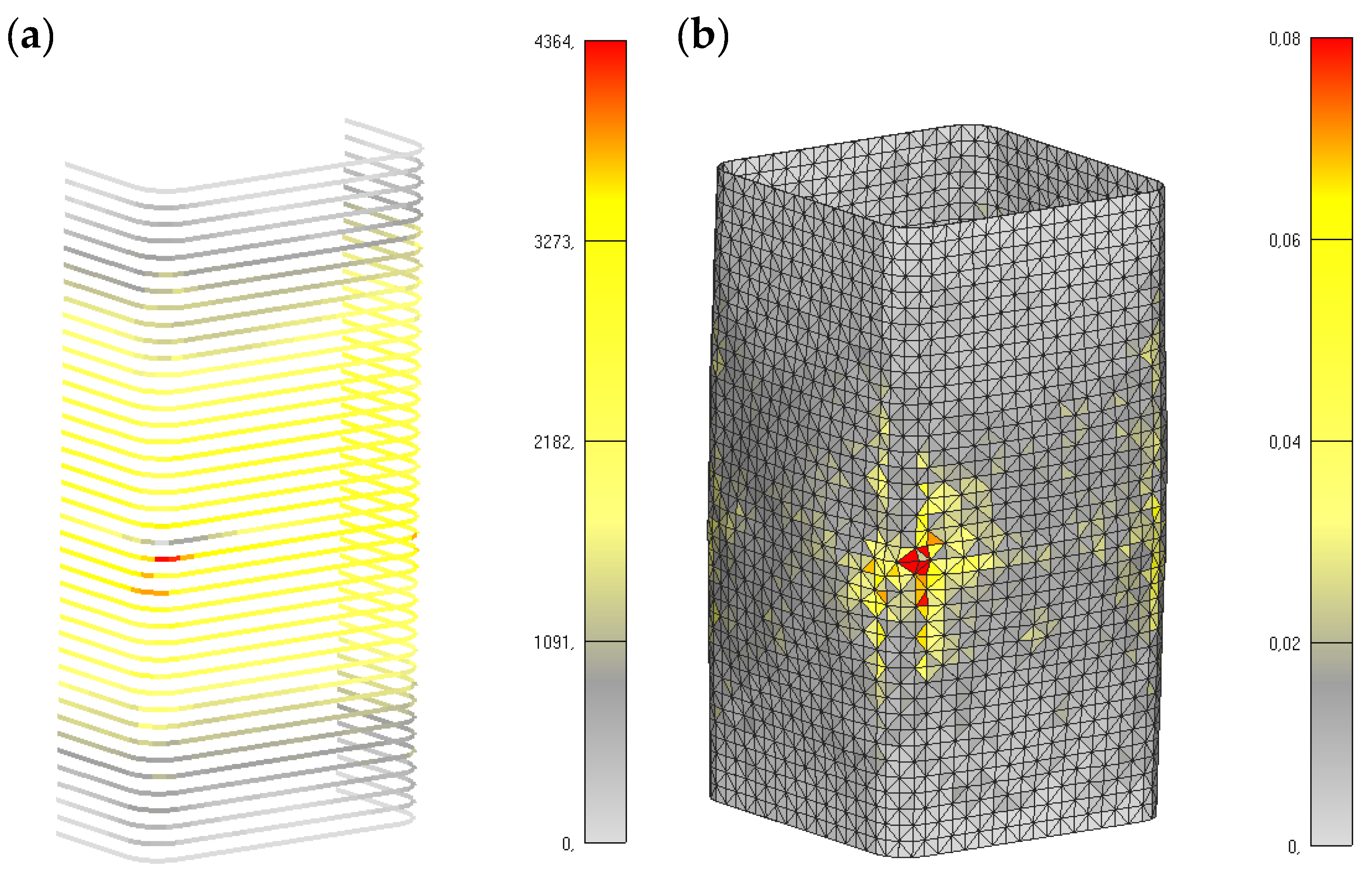
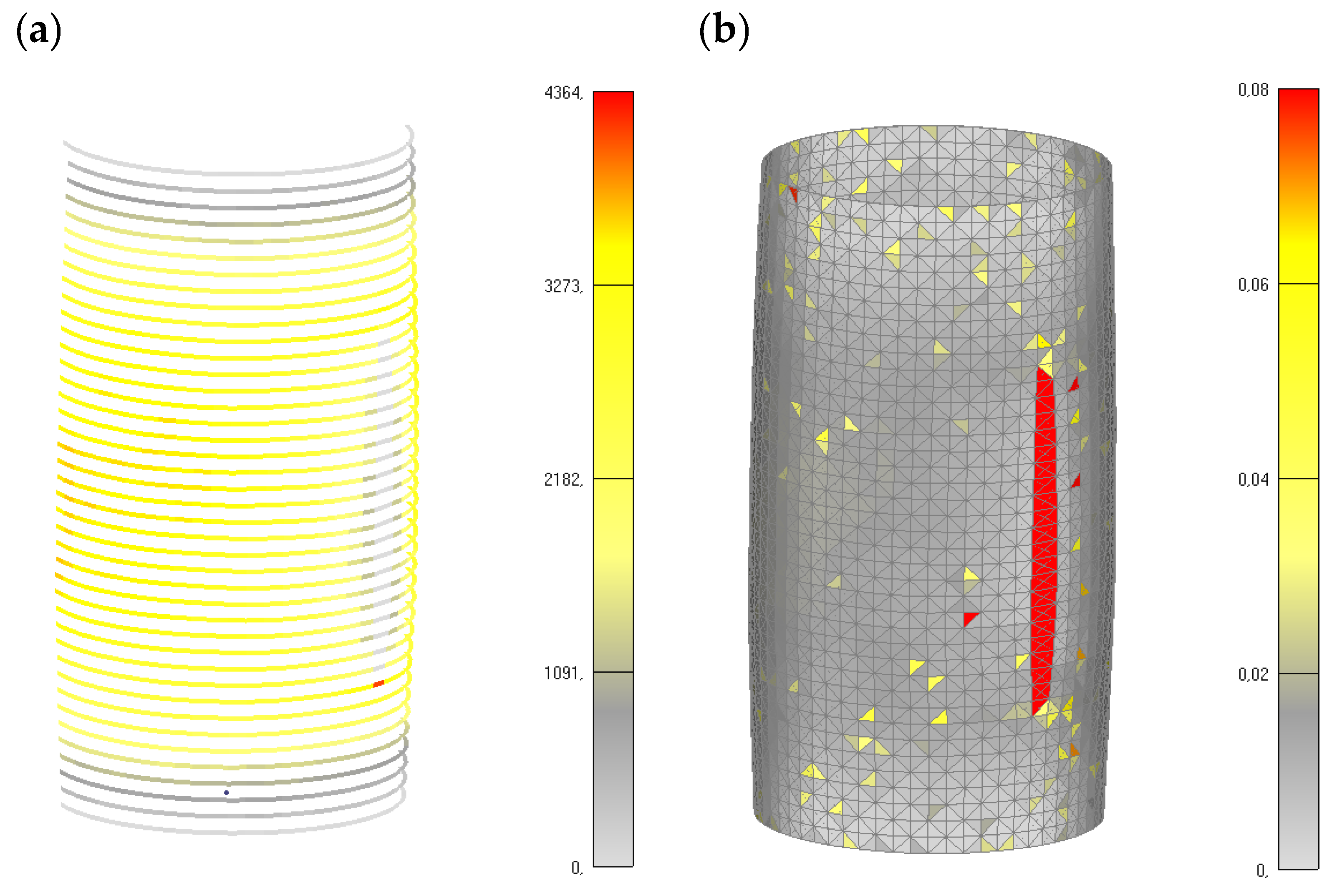
4.1. Plain Concrete (10% of Coarse Aggregate)
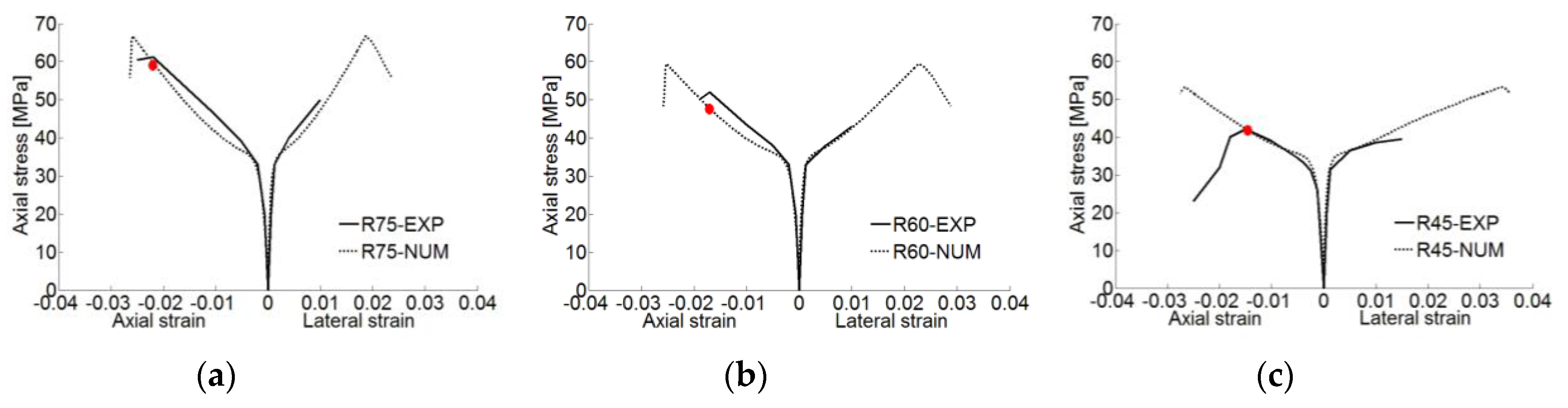
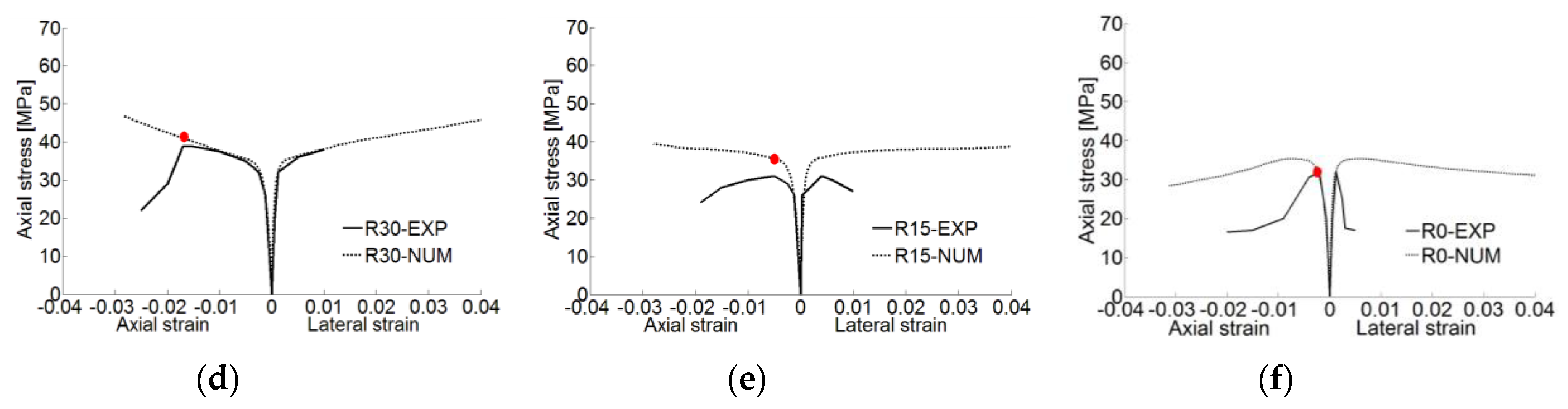
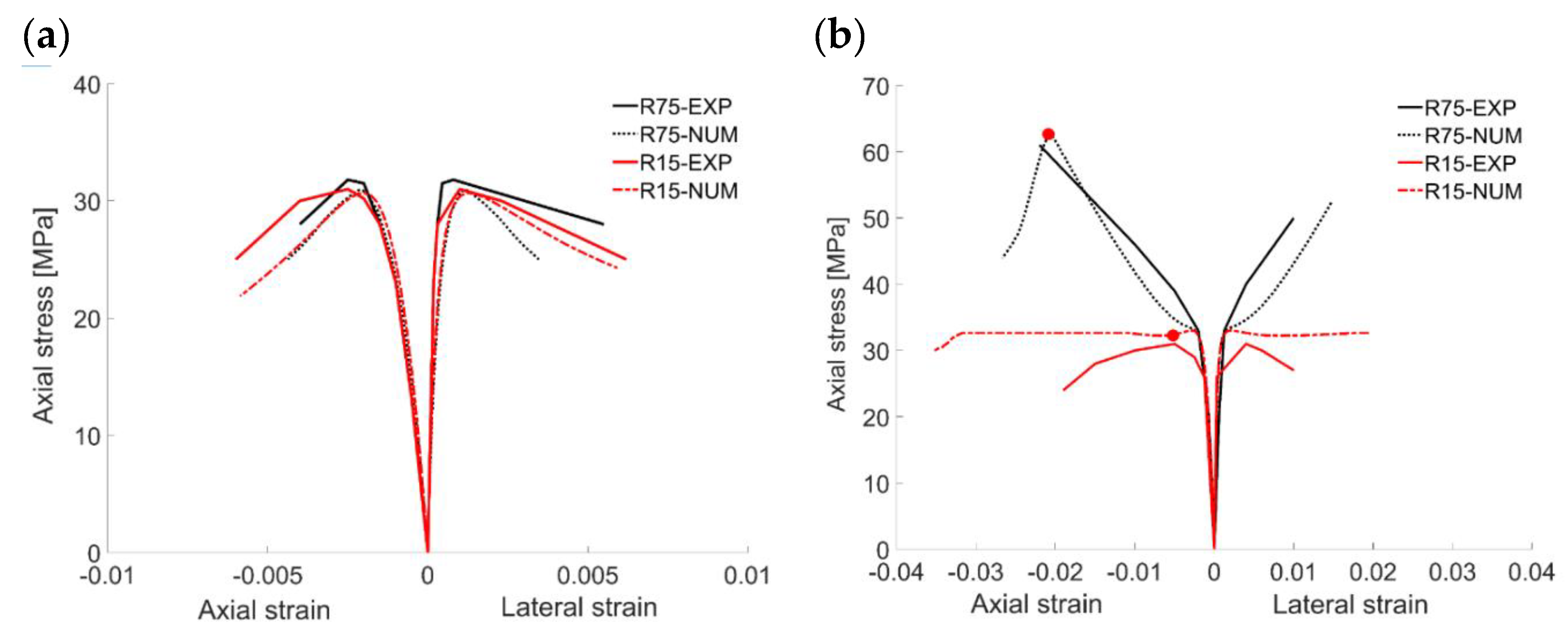
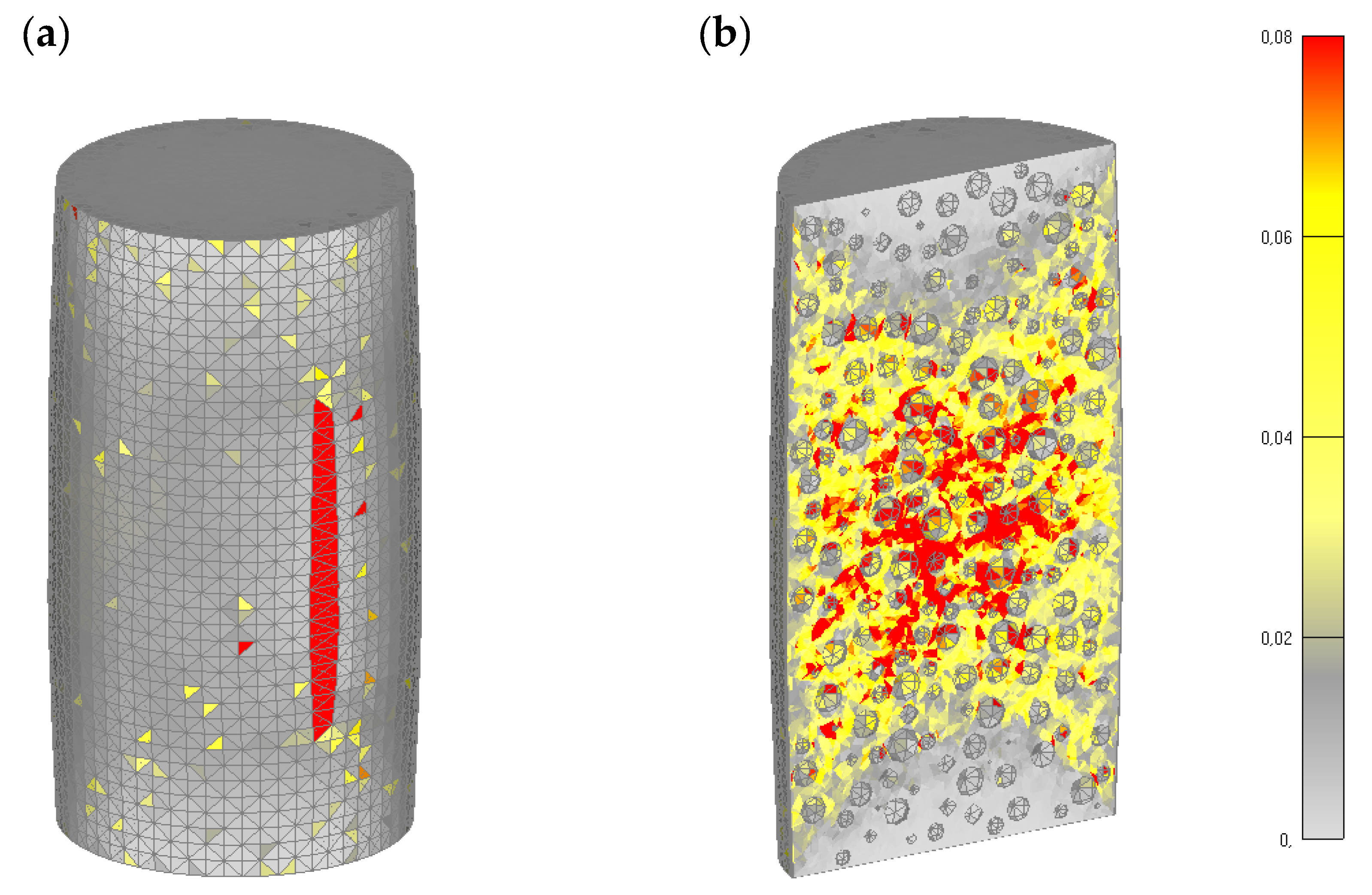
4.2. CFRP-Confined Concrete (10% of Coarse Aggregate)
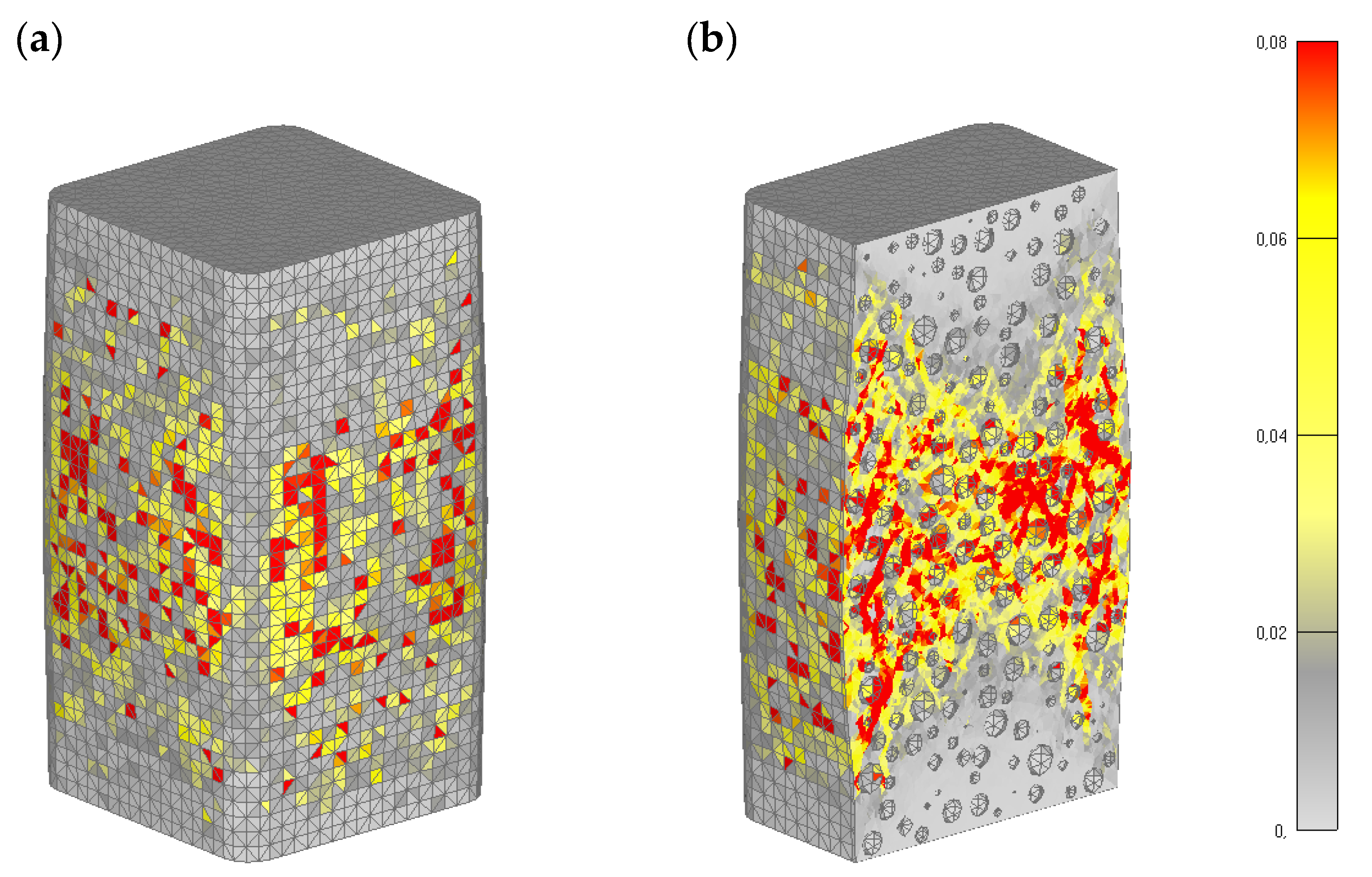
4.3. CFRP-Confined Concrete (30% of Coarse Aggregate)
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chalioris, C.E.; Kosmidou, P.-M.K.; Papadopoulos, N.A. Investigation of a new strengthening technique for RC deep beams using carbon FRP ropes as transverse reinforcements. Fibers 2018, 6, 52. [Google Scholar] [CrossRef]
- Bocciarelli, M.; Gambarelli, S.; Nisticò, N.; Pisani, M.A.; Poggi, C. Shear failure of RC elements strengthened with steel profiles and CFRP wraps. Compos. Part B 2014, 67, 9–21. [Google Scholar] [CrossRef]
- Chalioris, C.E.; Zapris, A.G.; Karayannis, C.G. U-jacketing applications of fiber-reinforced polymers in reinforced concrete T-beams against shear—Tests and design. Fibers 2020, 8, 13. [Google Scholar] [CrossRef]
- Wang, X.; Petru, M.; Ai, J.; Ou, S. Parametric Study of Flexural Strengthening of Concrete Beams with Prestressed Hybrid Reinforced Polymer. Materials 2019, 12, 3790. [Google Scholar] [CrossRef] [PubMed]
- Attari, N.; Amziane, S.; Chemrouk, M. Flexural strengthening of concrete beams using CFRP, GFRP and hybrid FRP sheets. Constr. Build. Mater. 2012, 37, 746–757. [Google Scholar] [CrossRef]
- Lewangamage, C.S.; Rankoth, C.K.; Jayasinghe, M.T.R. A Study on Reinforced Concrete Columns Partially Confined with Carbon Fibre Reinforced Polymer (CFRP). Engineer 2017, 4, 41–50. [Google Scholar] [CrossRef]
- Wang, L.-M.; Wu, Y.-F. Effects of corner radius on the performance of CFRP-confined square concrete columns. Test. Eng. Struct. 2008, 30, 493–505. [Google Scholar] [CrossRef]
- Lam, L.; Teng, J.G. Design-oriented stress-strain model for FRP-confined concrete. Constr. Build. Mater. 2003, 17, 471–489. [Google Scholar] [CrossRef]
- Realfonzo, R.; Napoli, A. Confining concrete members with FRP systems: Predictive vs design strain models. Compos. Struct. 2013, 104, 304–319. [Google Scholar] [CrossRef]
- Girgin, Z.C.; Girgin, K. A Design-Oriented Combined Model (7 MPa to 190 MPa) for FRP-Confined Circular Short Columns. Polymers 2015, 7, 1905–1917. [Google Scholar] [CrossRef]
- Jiang, T.; Teng, J.G. Analysis-oriented stress-strain models for FRP-confined concrete. Eng. Struct. 2007, 29, 2968–2986. [Google Scholar] [CrossRef]
- Lim, J.; Ozbakkaloglu, T. Unified Stress-Strain Model for FRP and Actively Confined Normal-Strength and High-Strength Concrete. J. Compos. Constr. 2015, 19, 04014072. [Google Scholar] [CrossRef]
- Cascardi, A.; Micelli, F.; Aiello, M.A. Unified model for hollow columns externally confined by FRP. Eng. Struct. 2016, 111, 119–130. [Google Scholar] [CrossRef]
- Rousakis, T.C.; Karabinis, A.I.; Kiousisb, P.D. FRP-confined concrete members: Axial compression experiments and plasticity modeling. Eng. Struct. 2007, 29, 1343–1353. [Google Scholar] [CrossRef]
- Karabinis, A.I.; Kiousis, P.D. Effects of confinement on concrete columns: Plasticity approach. ASCE J. Struct. Eng. 1994, 120, 2747–2767. [Google Scholar] [CrossRef]
- Karabinis, A.I.; Kiousis, P.D. Strength and ductility of rectangular concrete columns—A plasticity approach. ASCE J. Struct. Eng. 1996, 122, 267–274. [Google Scholar] [CrossRef]
- Rousakis, T.C.; Karabinis, A.I.; Kiousis, P.D.; Tepfers, R. Analytical modelling of plastic behavior of uniformly FRP confined concrete members. Compos. Part B 2008, 39, 1104–1113. [Google Scholar] [CrossRef]
- Karabinis, A.I.; Rousakis, T.C.; Manolitsi, G. 3D Finite Element Analysis of Substandard Columns Strengthened by Fiber Reinforced Polymer Sheets. ASCE J. Compos. Constr. 2008, 12, 531–540. [Google Scholar] [CrossRef]
- Yu, T.; Teng, J.G.; Wong, Y.L.; Dong, S.L. Finite element modeling of confined concrete-II: Plastic-damage model. Eng. Struct. 2010, 32, 680–691. [Google Scholar] [CrossRef]
- Wu, Y.F. Development of constitutive models for FRP-confined concrete structures. Compos. Part B-Eng. 2015, 1, 90. [Google Scholar]
- Lo, S.H.; Kwan, A.K.H.; Ouyang, Y.; Ho, J.C.M. Finite element analysis of axially loaded FRP-confined rectangular concrete columns. Eng. Struct. 2015, 100, 253–263. [Google Scholar] [CrossRef]
- Dong, C.X.; Kwan, A.K.H.; Ho, J.C.M. A constitutive model for predicting the lateral strain of confined concrete. Eng. Struct. 2015, 91, 155–166. [Google Scholar] [CrossRef]
- Menétrey, P.; Willam, K.J. Triaxial failure criterion for concrete and its generalization. ACI Struct. J. 1996, 92, 589–601. [Google Scholar]
- Hany, N.F.; Hantouche, E.G.; Harajli, M.H. Finite element modeling of FRP-confined concrete using modified concrete damaged plasticity. Eng. Struct. 2016, 125, 1–14. [Google Scholar] [CrossRef]
- Ceccato, C.; Pellegrino, C.; Cusatis, G. Simulation of concrete failure and fiber reinforced polymer fracture in confined columns with different cross sectional shape. Int. J. Solids Struct. 2017, 108, 216–229. [Google Scholar] [CrossRef]
- Ožbolt, J.; Li, Y.-J.; Kožar, I. Microplane model for concrete with relaxed kinematic constraint. Int. J. Solids Struct. 2001, 38, 2683–2711. [Google Scholar] [CrossRef]
- Gambarelli, S.; Nisticò, N.; Ožbolt, J. Microplane Model for Concrete: Part II—Applications on CFRP Confined Concrete Elements. In Applied Mechanics and Materials, Advances in Civil and Infrastructure Engineering II, Chapter II; Trans. Tech. Publications Ltd.: Zürich, Switzerland, 2016; Volume 847, pp. 106–120. [Google Scholar]
- Gambarelli, S.; Nisticò, N.; Ožbolt, J. Numerical analysis of compressed concrete columns confined with CFRP: Microplane-based approach. Compos. Part B 2014, 67, 303–312. [Google Scholar] [CrossRef]
- Gambarelli, S.; Nisticò, N.; Ožbolt, J. Mesoscale model for concrete: Microplane-based approach. In Proceedings of the 9th International Conference on Fracture Mechanics of Concrete and Concrete Structures (IA-FraMCoS), Berkeley, CA, USA, 22–25 May 2016. [Google Scholar]
- Ožbolt, J. MASA—Macroscopic Space Analysis; Internal Report; Institute für Werkstoffe im Bauwesen, Universität Stuttgart: Stuttgart, Germany, 1998. [Google Scholar]
- Bažant, Z.P.; Oh, B.H. Crack band theory for fracture of concrete. Mater. Struct. RILEM 1983, 16, 155–177. [Google Scholar] [CrossRef]
- Karabinis, A.I.; Rousakis, T.C. Carbon FRP confined concrete elements under axial load. In Proceedings of the International Conference on FRP Composites in Civil Engineering, Hong Kong, China, 12–15 December 2001; Teng, J.G., Ed.; 2001; pp. 309–316. [Google Scholar]

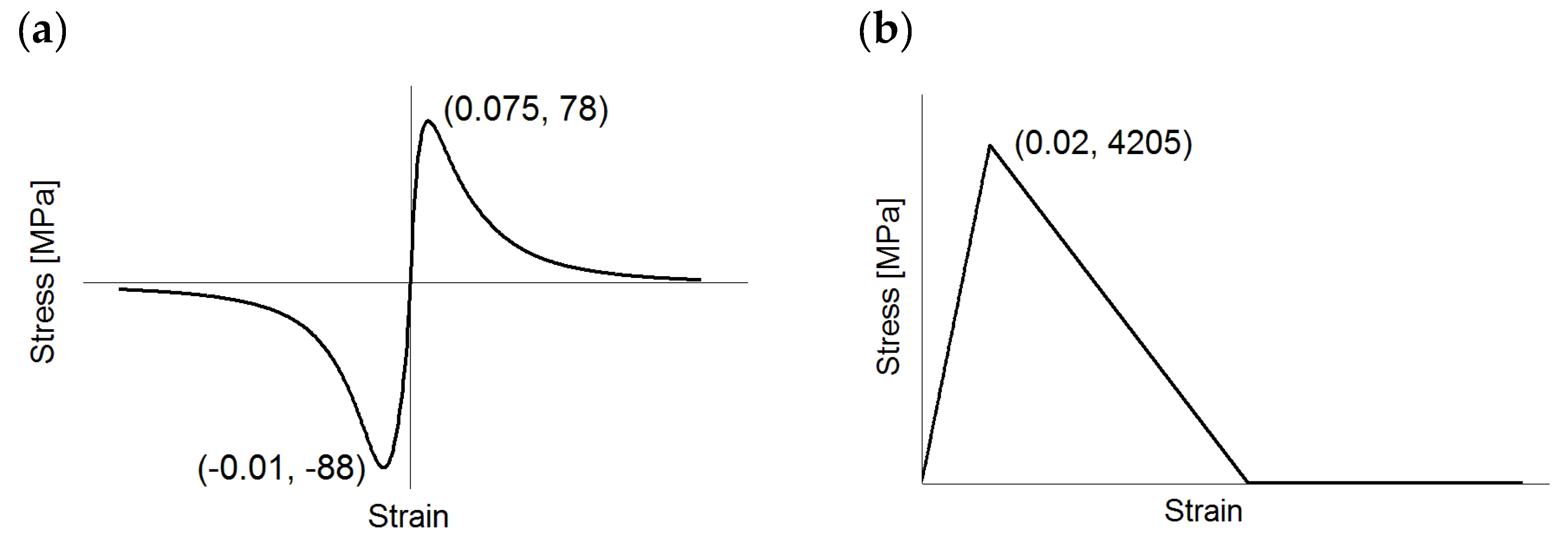
| Material Properties | Concrete | CFRP | ||
|---|---|---|---|---|
| Mortar | Aggregate | Carbon Fibers | Epoxy Resin | |
| [MPa] | 38,000 | 90,000 | 211,000 | 3000 |
| 0.2 | 0.2 | - | 0.25 | |
| [MPa] | 28 | - | - | 88.0 |
| [MPa] | 2.8 | - | 4205 | 78.0 |
| [J/m2] | 50 | - | - | - |
| 1ply CFRP | R75 | R60 | R45 | R30 | R15 | R0 |
|---|---|---|---|---|---|---|
| fc,c_num [MPa] | 58.6 | 50.39 | 42.33 | 40.15 | 36.37 | 34.67 |
| fc,c_exp [MPa] | 61.2 | 51.7 | 42.1 | 38.8 | 32 | 32 |
| error [%] | 4.25 | 2.53 | 0.54 | 3.49 | 13.67 | 8.33 |
| 1ply CFRP | R15 | R75 |
|---|---|---|
| fc,c_num [MPa] | 62.87 | 32.4 |
| fc,c_exp [MPa] | 61.2 | 32 |
| error [%] | 0.03 | 0.01 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gambarelli, S.; Ožbolt, J. MESO-Scale Modeling of CFRP-Confined Concrete: Microplane-Based Approach. Fibers 2020, 8, 38. https://doi.org/10.3390/fib8060038
Gambarelli S, Ožbolt J. MESO-Scale Modeling of CFRP-Confined Concrete: Microplane-Based Approach. Fibers. 2020; 8(6):38. https://doi.org/10.3390/fib8060038
Chicago/Turabian StyleGambarelli, Serena, and Joško Ožbolt. 2020. "MESO-Scale Modeling of CFRP-Confined Concrete: Microplane-Based Approach" Fibers 8, no. 6: 38. https://doi.org/10.3390/fib8060038
APA StyleGambarelli, S., & Ožbolt, J. (2020). MESO-Scale Modeling of CFRP-Confined Concrete: Microplane-Based Approach. Fibers, 8(6), 38. https://doi.org/10.3390/fib8060038




