Zero Stress Aging of Glass and Carbon Fibers in Water and Oil—Strength Reduction Explained by Dissolution Kinetics
Abstract
1. Introduction
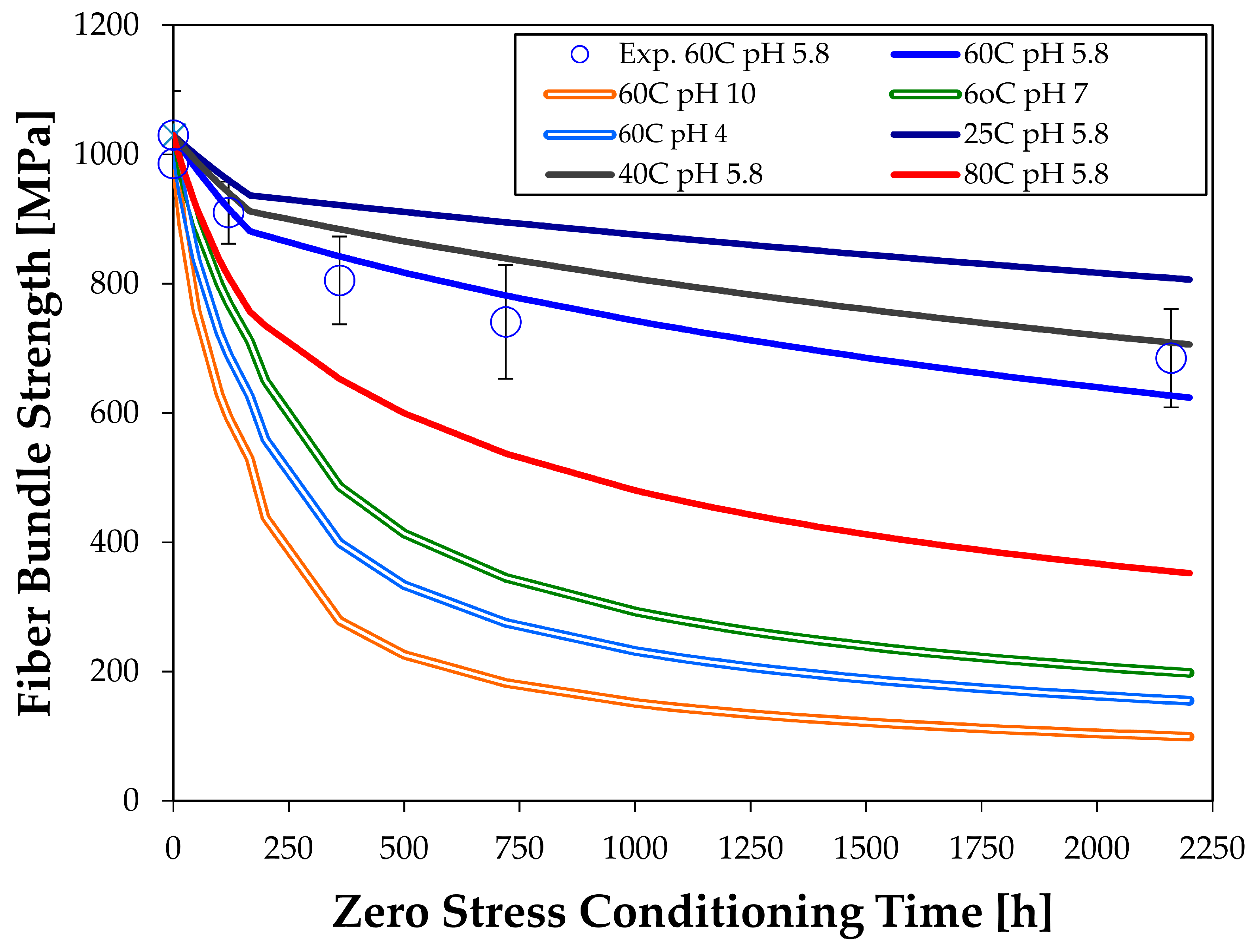
2. Modeling Strength Loss of Glass Fibers Due to the Environment
3. Materials and Methods
3.1. Fiber Bundles
3.2. Conditioning of Fiber Bundles
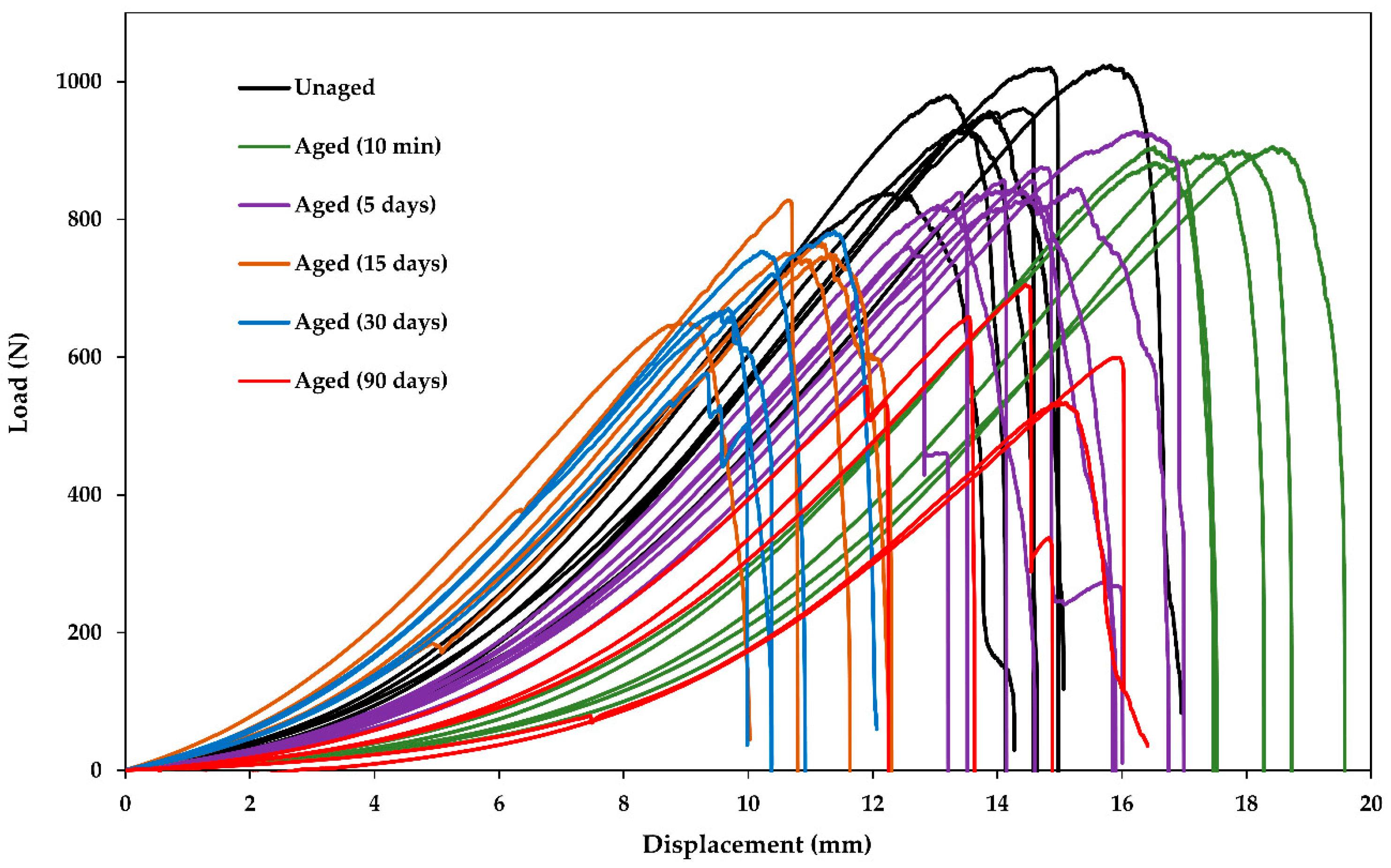
3.3. Fiber Bundle Tensile Tests
3.4. Fiber Strength and Bundle Strength
4. Results
4.1. Experimentally Measured Strengths
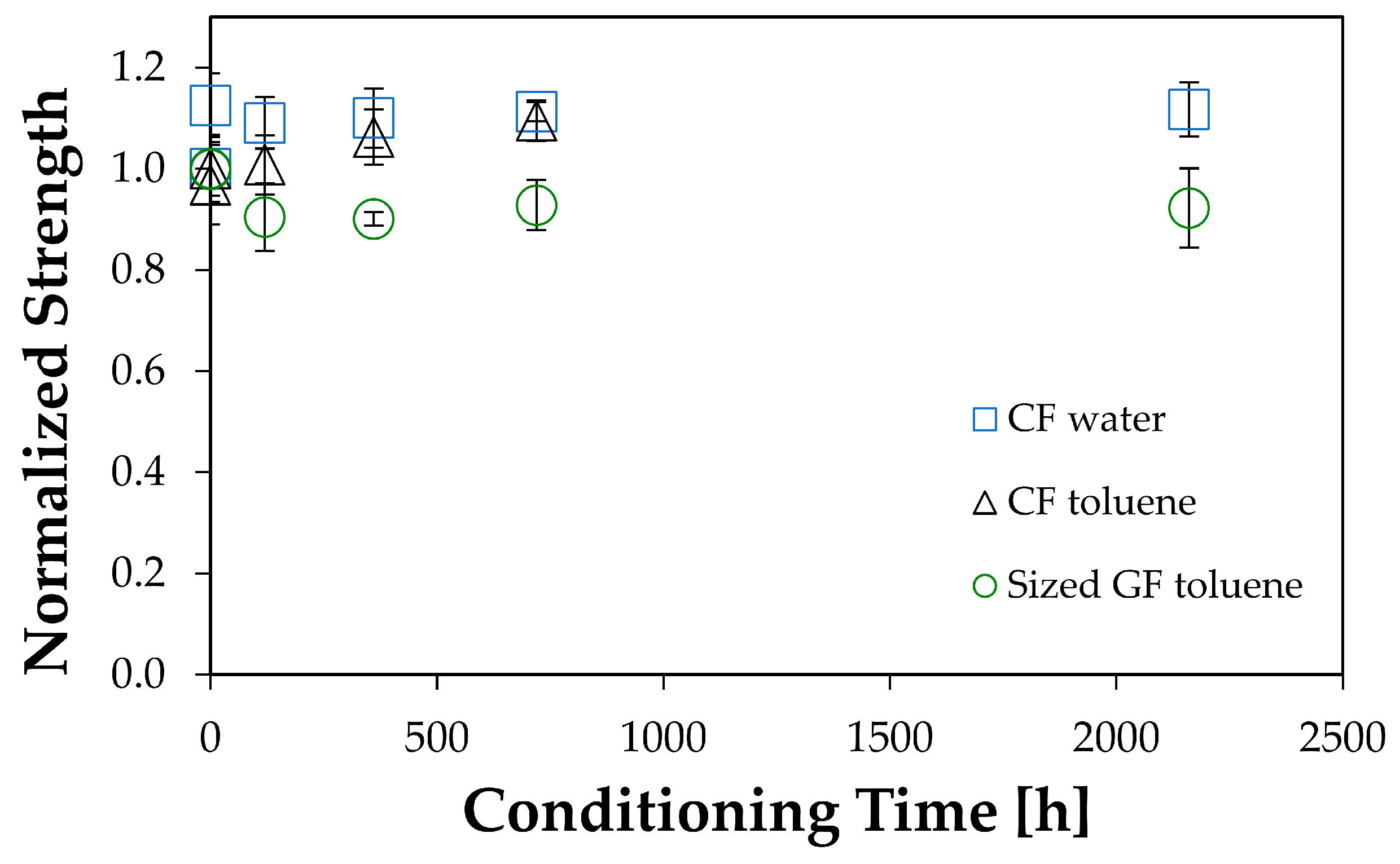
4.2. Strength Changes when Fibers Do Not Interact Chemically with the Environment
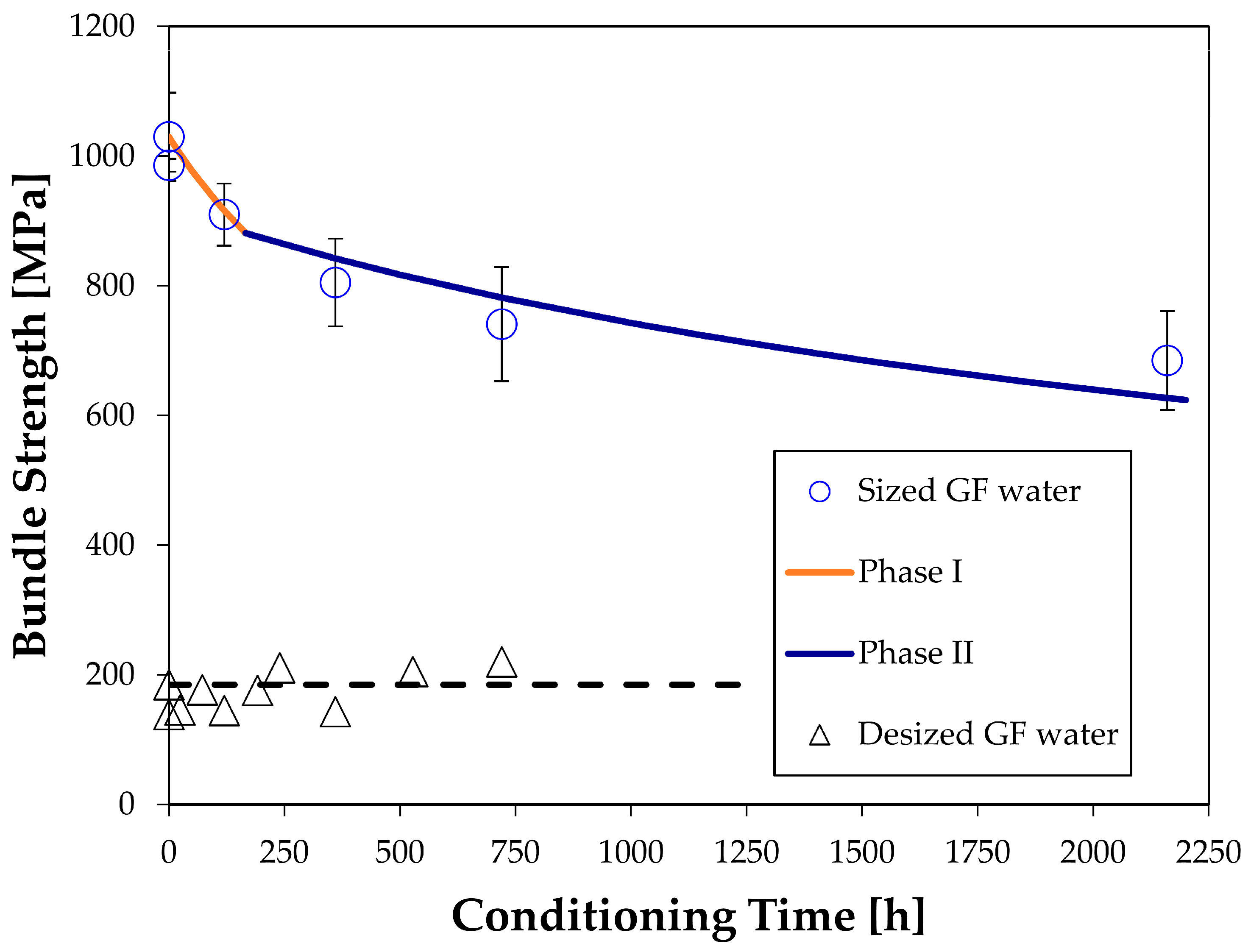
4.3. Strength Changes of Glass Fiber Bundles Interacting Chemically with Water
- sized fibers: a0 =
- desized fibers: a0 =
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Aging Time [h] | Sized GF Strength in Water [MPa] | Desized GF Strength in Water [MPa] | Sized GF Strength in Toluene [MPa] | CF Strength in Water [MPa] | CF Strength in Toluene [MPa] |
|---|---|---|---|---|---|
| 0 (unaged) | 1023, 901, 1001, 1101, 1098, 1054, 1033 | 185 | 1023, 901, 1001, 1101, 1098, 1054, 1033 | 2132, 2171, 1923, 2117 | 2132, 2171, 1923, 2117 |
| 0.17 (10 min) | 994, 984, 988, 970, 994 | 139 | 987, 1026, 1129, 974 | 2270, 2553, 2404, 2232, 2277 | 2203, 1994, 2273, 2445, 2184 |
| 24 (1 day) | - | 146 | - | - | - |
| 72 (3 days) | - | 177 | - | - | - |
| 120 (5 days) | 942, 920, 922, 817, 882, 907, 997, 902, 898 | 145 | 1035, 845, 916, 929, 938 | 2279, 2124, 2349, 2347 | 2139, 2203, 1966 |
| 192 (8 days) | - | 176 | - | - | - |
| 240 (10 days) | - | 211 | - | - | - |
| 360 (15 days) | 700, 805, 823, 809, 890 | 143 | 934, 906, 940, 924, 938 | 2327, 2287, 2450, 2337, 2076, 2294 | 2166, 2203, 2380, 2121 |
| 528 (22 days) | - | 205 | - | - | - |
| 720 (30 days) | 810, 721, 620, 711, 841 | 220 | 1039, 915, 958, 913, 954 | 2300, 2339, 2350, 2262, 2355 | 2188, 2332, 2248, 2374 |
| 2160 (90 days) | 702, 621, 730, 779, 595 | - | 1014, 1042, 948, 901, 846 | 2227, 2328, 2270, 2518, 2310 | - |
References
- ISO 527. Plastics—Determination of Tensile Properties; International Organization for Standardization: Geneva, Switzerland, 2019. [Google Scholar]
- ASTM. D3039 Standard Test Method for Tensile Properties of Polymer Matrix Composite Materials; ASTM International: West Conshohocken, PA, USA, 2017. [Google Scholar] [CrossRef]
- Lasn, K.; Klauson, A.; Echtermeyer, A.T. Back-calculation of ply elastic moduli for cross-ply laminates. Mech. Compos. Mater. 2014, 51, 55–68. [Google Scholar] [CrossRef]
- MIL-HDBK-17-1F. Polymer Matrix Composites, Volume 1: Guidelines for Characterization of Structural Materials; U.S. Department of Defense: Washington, DC, USA, 2002.
- Hart-Smith, L.J. Backing Out Equivalent Unidirectional Lamina Strengths from Tests on Cross-Plied Laminates. In Proceedings of the 37th International SAMPE Symposium, Anaheim, CA, USA, 9–12 March 1992; pp. 977–990. [Google Scholar]
- Griffith, A.A. The Phenomena of Rupture and Flow in Solids. Philos. Trans. R. Soc. A: Math. Phys. Eng. Sci. 1921, 221, 163–198. [Google Scholar] [CrossRef]
- Horstman, R.; Peters, K.; Enright, C.; Meltzer, R.; Vieth, M.B.; Bush, A. Stress Intensity Factors for Single-Edge-Crack Solid and Hollow Round Bars Loaded in Tension. J. Test. Eval. 1981, 9, 216–223. [Google Scholar] [CrossRef]
- Inglis, C.E. Stresses in a plate due to the presence of cracks and sharp corners. Proc. Inst. Naval. Archit. 1913, 60, 219–241. [Google Scholar]
- Orowan, E. Energy Criteria of Fracture. Weld. J. 1955, 34, 157–160. [Google Scholar]
- Charles, R.J. Static Fatigue of Glass. I. J. Appl. Phys. 1958, 29, 1549–1553. [Google Scholar] [CrossRef]
- Charles, R.J. Static Fatigue of Glass. II. J. Appl. Phys. 1958, 29, 1554–1560. [Google Scholar] [CrossRef]
- Wiederhorn, S.M.; Bolz, L.H. Stress Corrosion and Static Fatigue of Glass. J. Am. Ceram. Soc. 1970, 53, 543–548. [Google Scholar] [CrossRef]
- Freiman, S.W.; Wiederhorn, S.M.; Mecholsky, J.J.J. Environmentally Enhanced Fracture of Glass: A Historical Perspective. J. Am. Ceram. Soc. 2009, 92, 1371–1382. [Google Scholar] [CrossRef]
- Krauklis, A.E.; Echtermeyer, A.T. Dissolving Cylinder Zero-Order Kinetic Model for Predicting Hygrothermal Aging of Glass Fiber Bundles and Fiber-Reinforced Composites. In Proceedings of the 4th International Glass Fiber Symposium, Aachen, Germany, 29–30 October 2018; Gries, T., Pico, D., Lüking, A., Becker, T., Eds.; Verlag Mainz: Aachen, Germany, 2018; pp. 66–72, ISBN 978-3-95886-249-4. [Google Scholar]
- Krauklis, A.; Gagani, A.I.; Vegere, K.; Kalnina, I.; Klavins, M.; Echtermeyer, A.T. Dissolution Kinetics of R-Glass Fibres: Influence of Water Acidity, Temperature, and Stress Corrosion. Fibers 2019, 7, 22. [Google Scholar] [CrossRef]
- Krauklis, A.; Echtermeyer, A.T. Long-Term Dissolution of Glass Fibers in Water Described by Dissolving Cylinder Zero-Order Kinetic Model: Mass Loss and Radius Reduction. Open Chem. 2018, 16, 1189–1199. [Google Scholar] [CrossRef]
- Schultheisz, C.; McDonough, W.; Kondagunta, S.; Schutte, C.; Macturk, K.; McAuliffe, M.; Hunston, D. Effect of Moisture on E-Glass/Epoxy Interfacial and Fiber Strengths. In Composite Materials: Testing and Design, 13th ed.; Hooper, S., Ed.; ASTM International: West Conshohocken, PA, USA, 1997; pp. 257–286. [Google Scholar] [CrossRef]
- Armstrong, J.L.; Matthewson, M.J.; Juarez, M.G.; Chou, C.Y. Effect of diffusion rates in optical fiber polymer coatings on aging. In Proceedings of the Optical Fiber Reliability and Testing, Boston, MA, USA, 19–20 September 1999; Volume 3848. [Google Scholar] [CrossRef]
- Kennedy, M.T.; Cuellar, E.; Roberts, D.R. Stress-free aging of optical fibers in liquid water and humid environments: Part 1. In Proceedings of the Fiber Optic Components and Reliability, Boston, MA, USA, 3–6 September 1991; Volume 1580. [Google Scholar] [CrossRef]
- Hasløv, P.; Jensen, K.B.; Skovgaard, N.H. Degradation of Stressed Optical Fibers in Water: New Worst-case Lifetime Estimation Model. J. Am. Ceram. Soc. 1994, 77, 1531–1536. [Google Scholar] [CrossRef]
- Barbero, E.J.; Damiani, T.M. Phenomenological Prediction of Tensile Strength of E-Glass Composites from Available Aging and Stress Corrosion Data. J. Reinf. Plast. Compos. 2003, 22, 373–394. [Google Scholar] [CrossRef]
- Lara-Curzio, E. Oxidation Induced Stress-Rupture of Fiber Bundles. J. Eng. Mater. Technol. 1998, 120, 105–109. [Google Scholar] [CrossRef]
- 3B Fibreglass Technical Data Sheet; HiPer-tex W2020 Rovings; 3B: Herve, Belgium, 2012.
- Weibull, W. A Statistical Distribution Function of Wide Applicability. J. Appl. Mech. 1951, 18, 293–297. [Google Scholar]
- R’Mili, M.; Moevus, M.; Godin, N. Statistical fracture of E-glass fibres using a bundle tensile test and acoustic emission monitoring. Compos. Sci. Technol. 2009, 68, 1800–1808. [Google Scholar] [CrossRef]
- Chi, Z.; Chou, T.-W.; Shen, G. Determination of single fibre strength distribution from fibre bundle testings. J. Mater. Sci. 1984, 19, 3319–3324. [Google Scholar] [CrossRef]
- McCartney, L.N.; Smith, R.L. Statistical Theory of the Strength of Fiber Bundles. J. Appl. Mech. 1983, 50, 601–608. [Google Scholar] [CrossRef]
- Platt, M.M.; Klein, W.G.; Hamburger, W.J. Mechanics of Elastic Performance of Textile Materials: Part IX: Factors Affecting the Translation of Certain Mechanical Properties of Cordage Fibers into Cordage Yarn. Text. Res. J. 1952, 22, 641–667. [Google Scholar] [CrossRef]
- Hansen, A.; Hemmer, P.C.; Pradhan, S. The Fiber Bundle Model: Modeling Failure in Materials; Wiley-WCH: Weinheim, Germany, 2015; ISBN 978-3-527-67198-4. [Google Scholar]
- Torayca. T700S datasheet. In Technical Datasheet No. CFA-005; Torayca Carbon Fibers Inc.: Santa Ana, CA, USA, 2013. [Google Scholar]
- Wiederhorn, S.M. Fracture Surface Energy of Glass. In Proceedings of the 70th Annual Meeting, The American Ceramic Society, Chicago, IL, USA, 24 April 1968. [Google Scholar]
- Shand, E.B. Correlation of Strength of Glass with Fracture Flaws of Measured Size. In Proceedings of the Fall Meeting of the Glass Division, The American Ceramic Society, Bedford Springs, PA, USA, 14 October 1960. [Google Scholar]
- Lawn, B.R. Fracture of Brittle Solids, 2nd ed; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Champomier, F.P. Crack Propagation Measurements on Glass: A Comparison Between Double Torsion and Double Cantilever Beam Specimens. In Fracture Mechanics Applied to Brittle Materials; ASTM STP 678; Freiman, S.W., Ed.; American Society for Testing and Materials: West Conshohocken, PA, USA, 1979; pp. 60–72. [Google Scholar]
- Krauklis, A.E. Environmental Aging of Constituent Materials in Fiber-Reinforced Polymer Composites. Ph.D. Thesis, NTNU, Trondheim, Norway, 2019. [Google Scholar]

| Aging Time [h] | Sized GF Strength in Water [MPa] | Desized GF Strength in Water [MPa] | Sized GF Strength in Toluene [MPa] | CF Strength in Water [MPa] | CF Strength in Toluene [MPa] |
|---|---|---|---|---|---|
| 0 (unaged) | 1030 ± 68 | 185 | 1030 ± 68 | 2086 ± 111 | 2086 ± 111 |
| 0.17 (10 min) | 986 ± 10 | 139 | 1029 ± 70 | 2348 ± 132 | 2220 ± 163 |
| 24 (1 day) | - | 146 | - | - | - |
| 72 (3 days) | - | 177 | - | - | - |
| 120 (5 days) | 910 ± 48 | 145 | 932 ± 69 | 2275 ± 106 | 2102 ± 123 |
| 192 (8 days) | - | 176 | - | - | - |
| 240 (10 days) | - | 211 | - | - | - |
| 360 (15 days) | 805 ± 68 | 143 | 928 ± 14 | 2295 ± 122 | 2217 ± 114 |
| 528 (22 days) | - | 205 | - | - | - |
| 720 (30 days) | 741 ± 88 | 220 | 956 ± 51 | 2321 ± 39 | 2285 ± 84 |
| 2160 (90 days) | 685 ± 76 | - | 950 ± 81 | 2331 ± 112 | - |
| (1.82 ± 0.29) · 10−8 | (4.05 ± 0.29) · 10−9 | 166 | 0.165 |
| Initial Crack Length | Crack Sharpness Amplification Factor | Crack Speed Phase 1 | Crack Speed Phase 2 | |
|---|---|---|---|---|
| - | ||||
| Sized Fibers | 0.2 | 993 | 7.0 · 10−6 | 1.6 · 10−6 |
| Desized Fibers | 5.9 | 993 | 7.0 · 10−6 | 1.6 · 10−6 |
| T [°C] | 60 | 60 | 60 | 60 | 25 | 40 | 80 |
| pH | 5.8 | 10 | 7 | 4 | 5.8 | 5.8 | 5.8 |
| [g/m2·s] | 1.82 · 10−8 | 1.39 · 10−7 | 5.46 · 10−8 | 8.48 · 10−8 | 1.04 · 10−8 | 1.37 · 10−8 | 4.24 · 10−8 |
| [g/m2·s] | 4.05 · 10−9 | 1.11 · 10−7 | 4.85 · 10−8 | 6.24 · 10−8 | 1.42 · 10−9 | 2.72 · 10−9 | 1.47 · 10−8 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Echtermeyer, A.T.; Krauklis, A.E.; Gagani, A.I.; Sæter, E. Zero Stress Aging of Glass and Carbon Fibers in Water and Oil—Strength Reduction Explained by Dissolution Kinetics. Fibers 2019, 7, 107. https://doi.org/10.3390/fib7120107
Echtermeyer AT, Krauklis AE, Gagani AI, Sæter E. Zero Stress Aging of Glass and Carbon Fibers in Water and Oil—Strength Reduction Explained by Dissolution Kinetics. Fibers. 2019; 7(12):107. https://doi.org/10.3390/fib7120107
Chicago/Turabian StyleEchtermeyer, Andreas T., Andrey E. Krauklis, Abedin I. Gagani, and Erik Sæter. 2019. "Zero Stress Aging of Glass and Carbon Fibers in Water and Oil—Strength Reduction Explained by Dissolution Kinetics" Fibers 7, no. 12: 107. https://doi.org/10.3390/fib7120107
APA StyleEchtermeyer, A. T., Krauklis, A. E., Gagani, A. I., & Sæter, E. (2019). Zero Stress Aging of Glass and Carbon Fibers in Water and Oil—Strength Reduction Explained by Dissolution Kinetics. Fibers, 7(12), 107. https://doi.org/10.3390/fib7120107






