Temperature-Dependent Elastic and Damping Properties of Basalt- and Glass-Fabric-Reinforced Composites: A Comparative Study
Abstract
Highlights
- The newly developed and automated measurement setup allows for the easy, fast, and accurate identification of the orthotropic complex engineering constants of composite materials within a temperature interval between −20 °C and 60 °C;
- The complex engineering constants of bi-directionally glass-fiber-reinforced composites with an epoxy matrix and similar basalt-fiber-reinforced composites in a temperature interval between −20 °C and 60 °C have nearly the same values in a linearly loaded range.
- Within the limits of the described tests, glass or basalt reinforcement yields the same stiffness and damping properties as composite material parts;
- For a temperature above 60 °C and heavily loaded or pre-loaded construction parts, additional tests are required.
Abstract
1. Introduction
1.1. Glass-Fiber-Reinforced Polymer (GFRP) Composites
1.2. Basalt-Fiber-Reinforced Polymer (BFRP) Composites
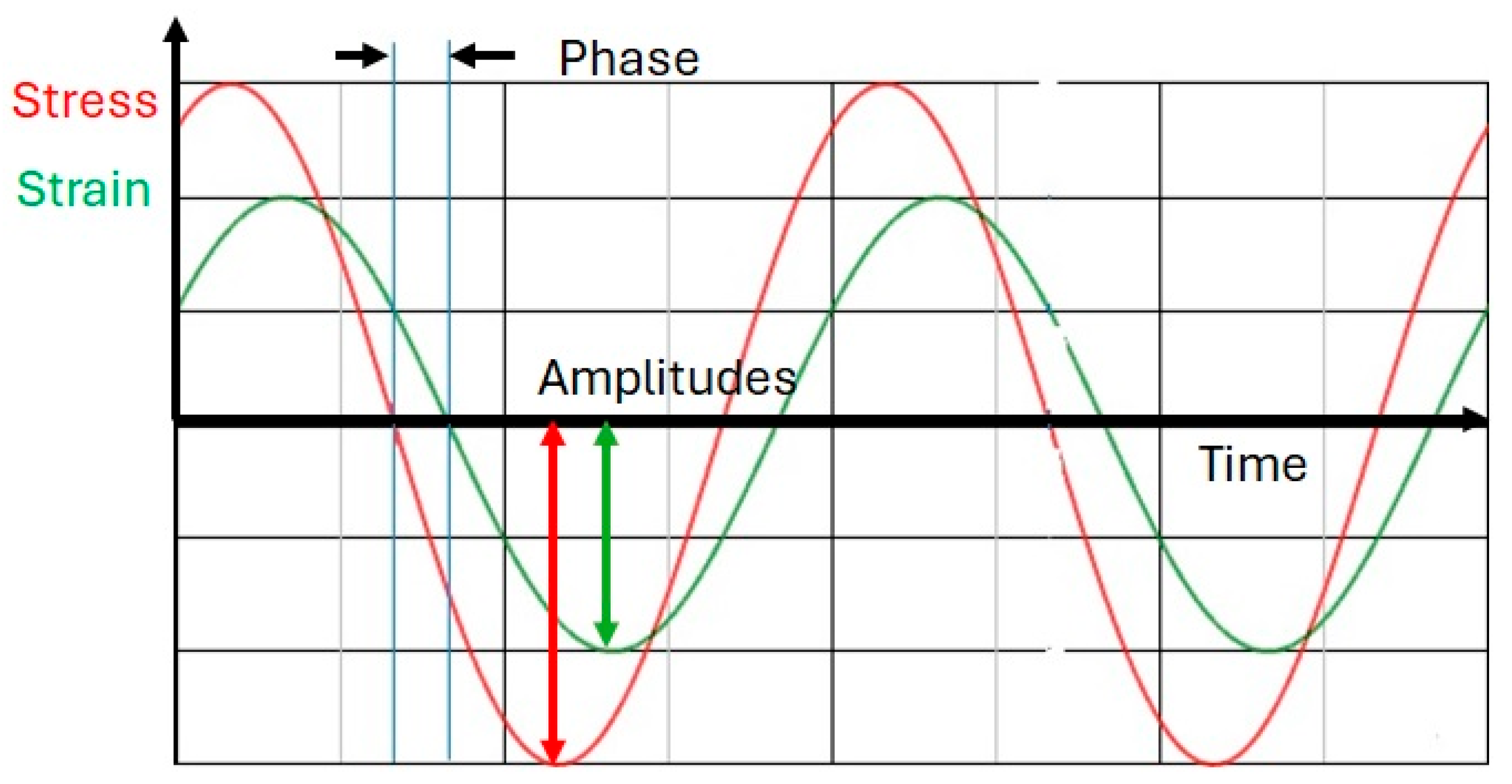
1.3. Elastic and Damping Properties of Composite Materials
1.4. A Novel Setup to Measure Orthotropic Engineering Constants
2. Measurement of Engineering Constants of Composite Materials
2.1. Static Measurement Methods
2.2. Dynamic Measurement Methods
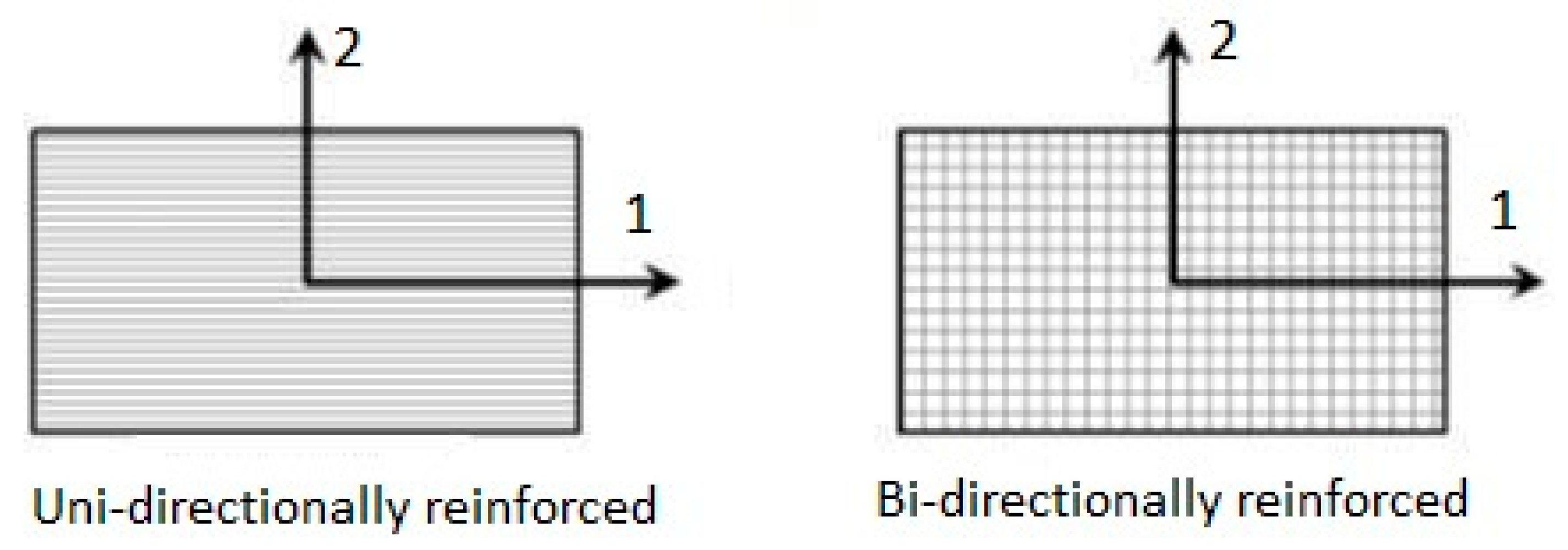
3. Tested Materials
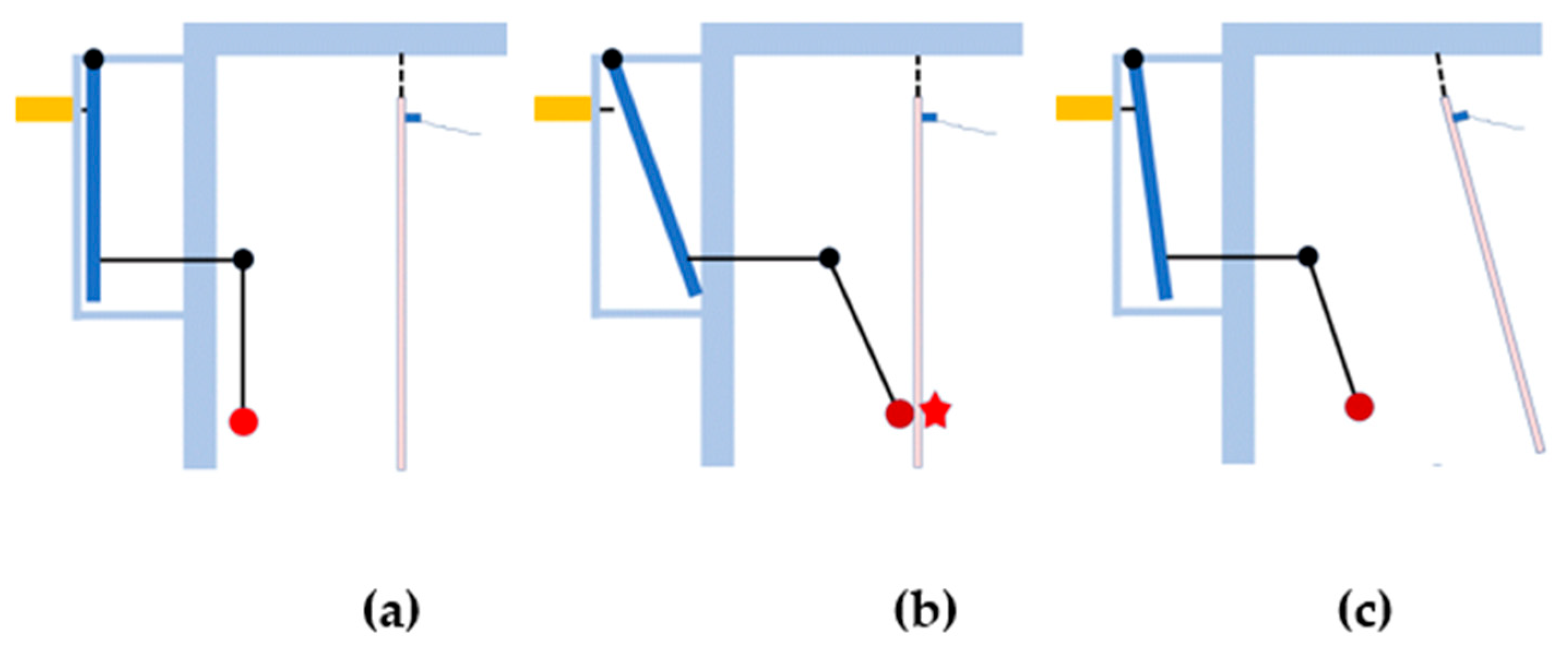
4. Measurement of Young’s Modulus by Three-Point Bending and IET
5. Automated Testing with the Extended Resonalyser Procedure
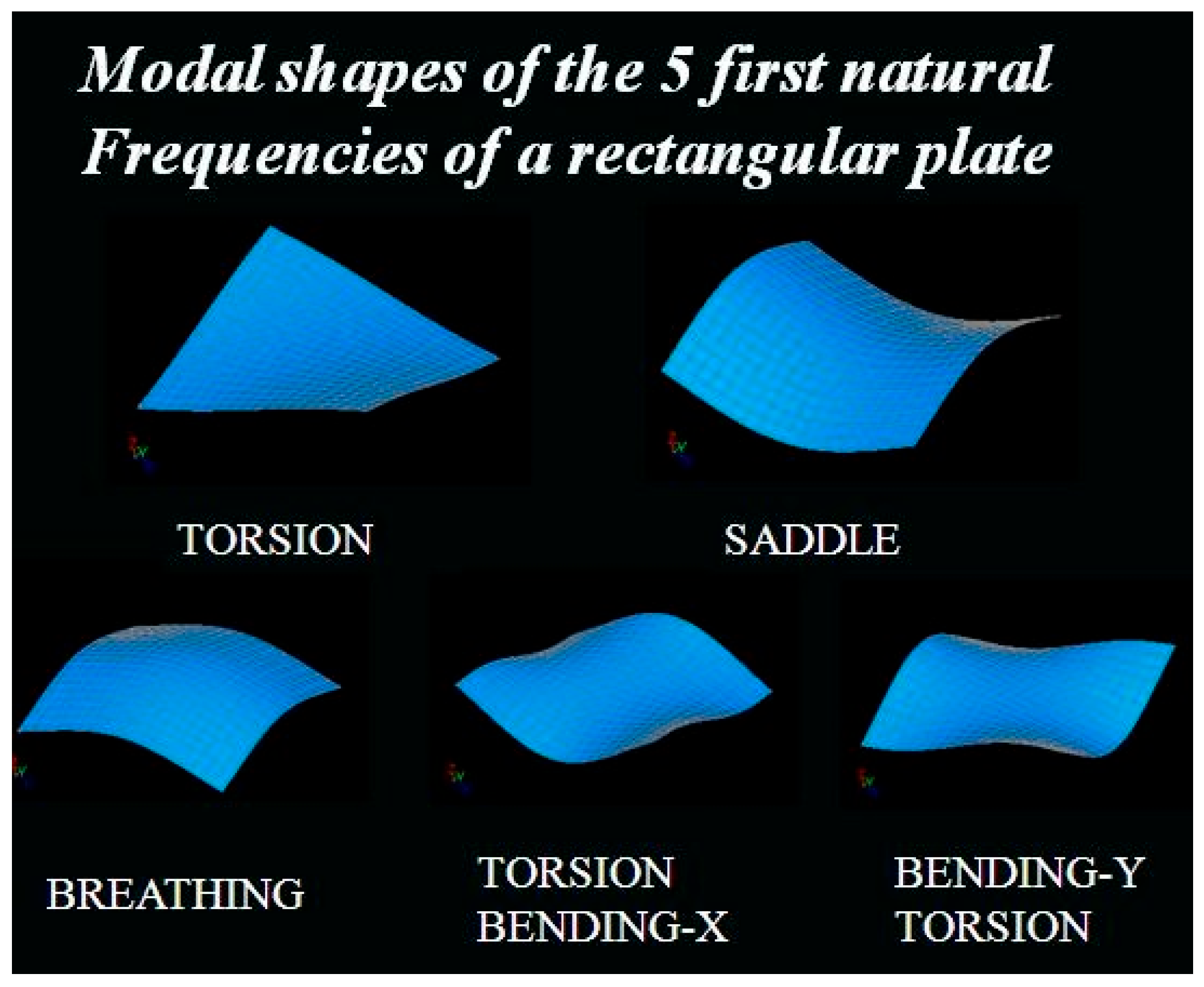
5.1. Measurement Results (Frequency and Damping Ratio Plots)
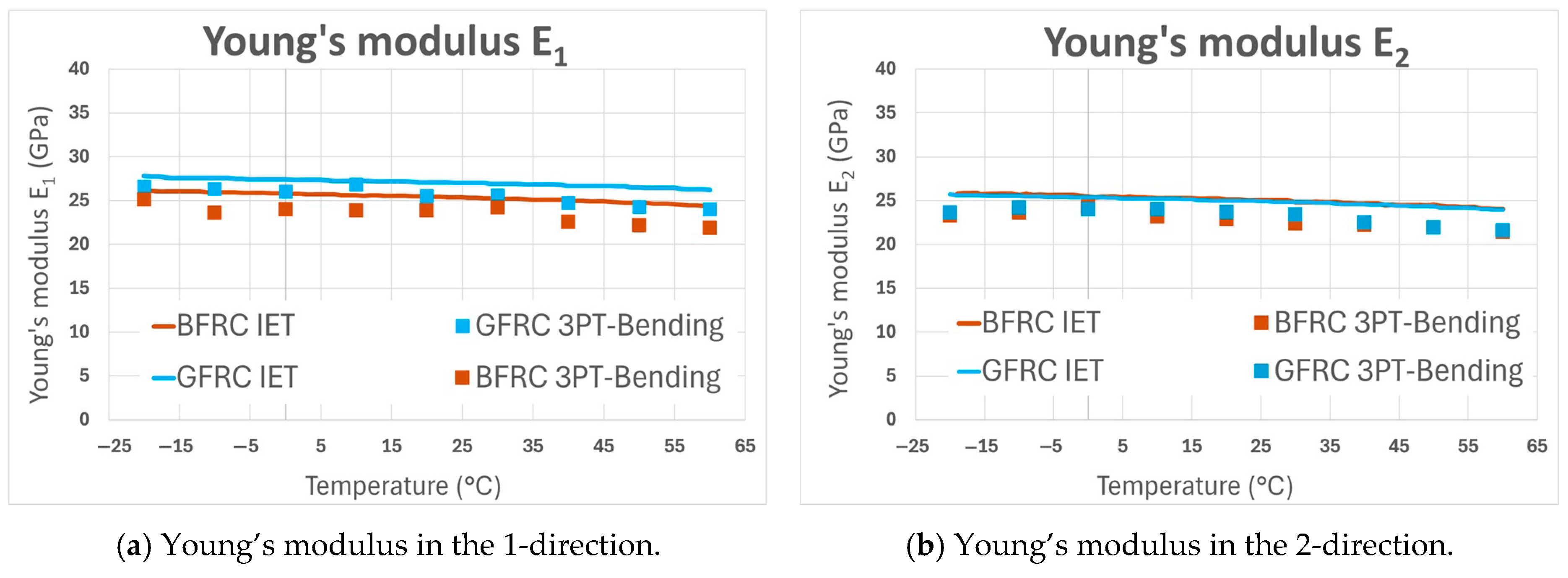
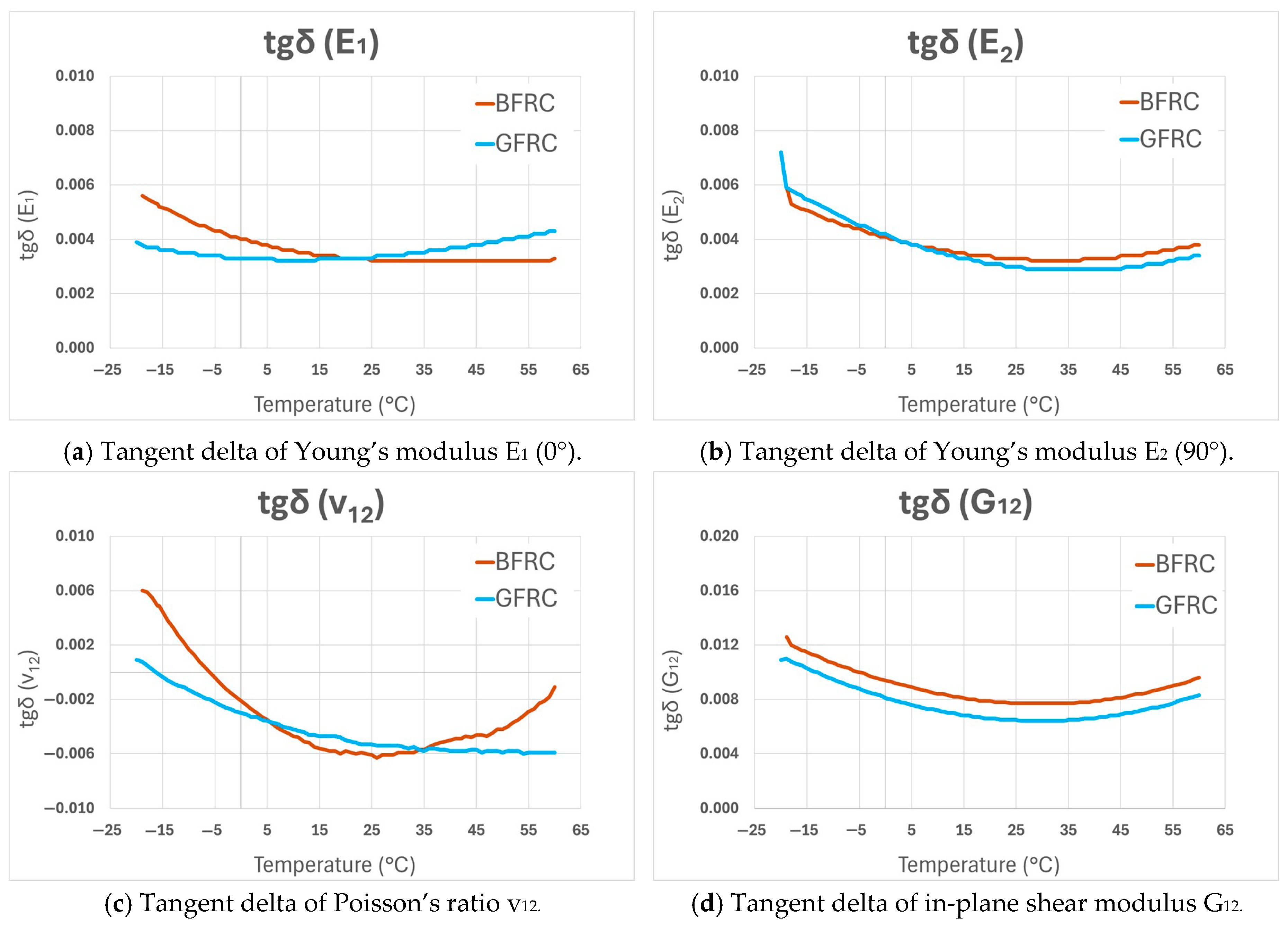
5.2. Identified Engineering Constants (Moduli and Tangents Delta)
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| IET | Impulse excitation technique |
| IRF | Impulse response function |
| DMA | Dynamic mechanical analysis |
| FE | Finite element |
| ASTM | American Standard Testing Materials |
| GF | Glass fiber |
| BF | Basalt fiber |
| GFRP | Glass fiber reinforced plastic |
| BFRP | Basalt fiber reinforced plastic |
References
- Sathishkumar, T.P.; Satheeshkumar, S.; Naveen, J. Glass fiber-reinforced polymer composites—A review. J. Reinf. Plast. Compos. 2014, 33, 1258–1275. [Google Scholar] [CrossRef]
- Singh, J.; Kumar, M.; Kumar, S.; Mohapatra, S.K. Properties of Glass Fiber Hybrid Composites: A Review. Polym.-Plast. Technol. Eng. 2017, 56, 455–469. [Google Scholar] [CrossRef]
- Pirzada, M.M. Recent Trends and Modifications in Glass Fibre Composites—A Review. Int. J. Mater. Chem. 2015, 5, 117–122. [Google Scholar]
- Jamshaid, H.; Mishra, R. A green material from rock: Basalt fiber—A review. J. Text. Inst. 2016, 107, 923–937. [Google Scholar] [CrossRef]
- Sbahieh, S.; Mckay, G.; Al-Ghamdi, S.G. A comparative life cycle assessment of fiber-reinforced polymers as a sustainable reinforcement option in concrete beams. Front. Built Environ. 2023, 9, 1194121. [Google Scholar] [CrossRef]
- Lapena, M.H.; Marinucci, G. Mechanical Characterization of Basalt and Glass Fiber Epoxy Composite Tube. Mater. Res. 2018, 21, e20170324. [Google Scholar] [CrossRef]
- Tavadi, A.R.; Naik, Y.; Kumaresan, K.; Jamadar, N.I.; Rajaravi, C. Basalt fiber and its composite manufacturing and applications: An overview. Int. J. Eng. Sci. Technol. 2021, 13, 50–56. [Google Scholar] [CrossRef]
- Christensen, R.M. Theory of Viscoelasticity an Introduction; Academic Press: Cambridge, MA, USA, 1971. [Google Scholar]
- Hashin, Z.V.I. Complex moduli of viscoelastic composites: General theory and application to particulate composites. Int. J. Solids Struct. 1970, 6, 539–552. [Google Scholar] [CrossRef]
- ASTM D3039; Standard Test Method for Tensile Properties of Polymer Matrix Composite Materials. ASTM: West Conshohocken, PA, USA, 2017; ASTM D3039/D3039M-17 from ASTM.org.
- ASTMD7264/D7264M-21; Standard Test Method for Flexural Properties of Polymer Matrix Composite Materials. ASTM: West Conshohocken, PA, USA, 2021. [CrossRef]
- Kostic, S.; Miljojkovic, J.; Simunovic, G.; Vukelic, D.; Tadic, B. Uncertainty in the determination of elastic modulus by tensile testing. Eng. Sci. Technol. Int. J. 2022, 25, 100998. [Google Scholar] [CrossRef]
- Lord, J.D.; Morrell, R.M. Elastic Modulus Measurement, Good Practice Guide No. 98; Elastic Modulus Measurement|NPL Publications; National Physical Laboratory: London, UK, 2006. [Google Scholar]
- ASTMC 1259–98; Standard Test Methods for Dynamic Young’s Modulus, Shear Modulus and Poisson’s Ratio for Advanced Ceramics by Impulse Excitation of Vibration. ASTM: West Conshohocken, PA, USA, 2022. [CrossRef]
- Schalnat, J.; Gómez, D.G.; Daelemans, L.; De Baere, I.; De Clerck, K.; Van Paepegem, W. Influencing parameters on measurement accuracy in dynamic mechanical analysis of thermoplastic polymers and their composites. Polym. Test. 2020, 91, 106799. [Google Scholar] [CrossRef]
- Ashok, R.B.; Srinivasa, C.V.; Basavaraju, B. Dynamic mechanical properties of natural fiber composites—A review. Adv. Compos. Hybrid Mater. 2019, 2, 586–607. [Google Scholar] [CrossRef]
- Heritage, K.; Frisby, C.; Wolfenden, A. Impulse excitation technique for dynamic flexural 740 measurements at moderate temperature. Rev. Sci. Instrum. 1988, 59, 973–974. [Google Scholar] [CrossRef]
- Brebels, A.; Bollen, B. Non-Destructive Evaluation of Material Properties as Function of Temperature by the Impulse Excitation Technique. e-J. Nondestruct. Test. 2015, 20, 6. [Google Scholar]
- Sol, H. Identification of Anisotropic Plate Rigidities Using Free Vibration Data. Ph.D. Thesis, Vrije Universiteit Brussel, Ixelles, Belgium, October 1986. [Google Scholar]
- Lauwagie, T.; Lambrinou, K.; Sol, H.; Heylen, W. Resonant-Based Identification of the Poisson’s Ratio of Orthotropic Materials. Exp. Mech. 2010, 50, 437–447. [Google Scholar] [CrossRef]
- Pierron, F.; Grediac, M. The Virtual Fields Method; Springer: Berlin/Heidelberg, Germany, 2012; ISBN 9781761418258. [Google Scholar]
- Sol, H.; Rahier, H.; Gu, J. Prediction and Measurement of the Damping Ratios of Laminated Polymer Composite Plates. Materials 2020, 13, 3370. [Google Scholar] [CrossRef]
- De Baer, I. Experimental and Numerical Study of Different Setups for Conducting and Monitoring Fatigue Experiments of Fibre-Reinforced Thermoplastics. Ph.D. Thesis, University Ghent, Ghent, Belgium, 2008. [Google Scholar]
- Lauwagie, T.; Sol, H.; Heylen, W. Handling uncertainties in mixed numerical-experimental techniques for vibration-based material identification. J. Sound Vib. 2006, 291, 723–739. [Google Scholar] [CrossRef]
- Lauwagie, T.; Sol, H.; Roebben, G.; Heylen, W.; Shi, Y. Validation of the Resonalyser method: An inverse method for material identification. In Proceedings of the ISMA 2002, International Conference on 734 Noise and Vibration Engineering, Leuven, Belgium, 16–18 September 2002; pp. 687–694. [Google Scholar]
- De Visscher, J.; Sol, H.; De Wilde, W.P.; Vantomme, J. Identification of the damping properties of orthotropic composite materials using a mixed numerical experimental method. Appl. Compos. Mater. 1997, 4, 13–33. [Google Scholar] [CrossRef]
- Bytec, B.V. Theoretical Background and Examples of the Resonalyser Procedure. Available online: www.resonalyser.com (accessed on 17 July 2025).
- Sol, H.; Gu, J.; Hernandez, G.M.; Nazerian, G.; Rahier, H. Thermo-Mechanical Identification of orthotropic engineering constants of composites using an extended non-destructive impulse excitation technique. Appl. Sci. 2025, 15, 3621. [Google Scholar] [CrossRef]
- Deobald, L.R.; Gibson, R.F. Determination of elastic constants of orthotropic plates by a modal 719 analysis/Rayleigh-Ritz technique. J. Sound Vib. 1988, 124, 269–283. [Google Scholar] [CrossRef]
- Pederson, P.; Frederiksen, P.S. Identification of orthotropic material moduli by a combined experimental/numerical approach. Measurement 1992, 10, 113–118. [Google Scholar] [CrossRef]
- Ayorinde, E.O.; Gibson, R.F. Elastic constants of orthotropic composite materials using plate resonance frequencies, classical lamination theory and an optimized three mode Rayleigh formulation. Compos. Eng. 1993, 3, 395–407. [Google Scholar] [CrossRef]
- Moussu, F.; Nivoit, M. Determination of the elastic constants of orthotropic plates by a modal analysis method of superposition. J. Sound Vib. 1993, 165, 149–163. [Google Scholar] [CrossRef]
- Frederiksen, P.S. Estimation of elastic moduli in thick composite plates by inversion of vibrational data. In Proceedings of the Second International Symposium on Inverse Problems, Paris, France, 2–4 November 1994; pp. 111–118. [Google Scholar]
- Ayorinde, E.O. Elastic constants of thick orthotropic composite plates. J. Compos. Mater. 1995, 29, 1025–1039. [Google Scholar] [CrossRef]
- Cunha, J. Application des Techniques de Recalage en Dynamique a L’identification des Constantes Elastiques des Materiaux Composites. Ph.D. Thesis, Université de Franche-Comté, Besançon, France, 1997. [Google Scholar]
- Qian, G.L.; Hoa, S.V.; Xiao, X. A vibration method for measuring mechanical properties of composite, theory and experiment. Compos. Struct. 1997, 39, 31–38. [Google Scholar] [CrossRef]
- Aguilo, M.A.; Swiler, L.P.; Urbina, A. An overview of inverse material identification within the frameworks of deterministic and stochastic parameter estimation. Int. J. Uncertain. Quantif. 2013, 3, 289–319. [Google Scholar] [CrossRef]
- Hwang, S.F.; Chang, C.S. Determination of elastic constants of materials by vibration testing. Compos. Struct. 2000, 49, 183–190. [Google Scholar] [CrossRef]
- Liu, G.R.; Lam, K.Y.; Han, X. Determination of elastic constants of anisotropic laminated plates using elastic waves and a progressive neural network. J. Sound Vib. 2002, 52, 239–259. [Google Scholar] [CrossRef]
- Muthurajan, K.G.; Sanakaranarayanasamy, K.; Rao, B.N. Nageswara Rao; Evaluation of elastic constants of specially orthotropic plates through vibration testing. J. Sound Vib. 2004, 272, 413–424. [Google Scholar] [CrossRef]
- Ayorinde, E.O.; Yu, L. On the elastic characterization of composite plates with vibration data. J. Sound Vib. 2005, 283, 243–262. [Google Scholar] [CrossRef]
- Alfano, M.; Pagnotta, L. Determining the elastic constants of isotropic materials by modal vibration testing of rectangular thin plates. J. Sound Vib. 2006, 293, 426–439. [Google Scholar] [CrossRef]
- Caillet, J.; Carmona, J.C.; Mazzoni, D. Estimation of plate elastic moduli through vibration testing. Appl. Acoust. 2007, 68, 334–349. [Google Scholar] [CrossRef]
- Bledzki, A.K.; Kessler, A.; Rikards, R.; Chate, A. Determination of elastic constants of glass/epoxy unidirectional laminates by the vibration testing of plates. Compos. Sci. Technol. 1999, 59, 2015–2024. [Google Scholar] [CrossRef]
- Cengel, Y. Heat Transfer, a Practical Approach; McGraw-Hill: Boston, MA, USA, 1998; ISBN 0-07-011505-2. [Google Scholar]
- ISO 527-5:2021; Plastics-Determination of Tensile Properties-Part 5: Test Conditions for Unidirectional Fibre Reinforced Plastic Composites. ISO: Geneva, Switzerland, 2021. Available online: https://www.iso.org/standard/80370.html (accessed on 24 July 2024).
- ISO 14125:1998; Fibre Reinforced Plastic Composites-Determination of Flexural Properties. ISO: Geneva, Switzerland, 1998. Available online: https://www.iso.org/standard/23637.html (accessed on 24 July 2024).



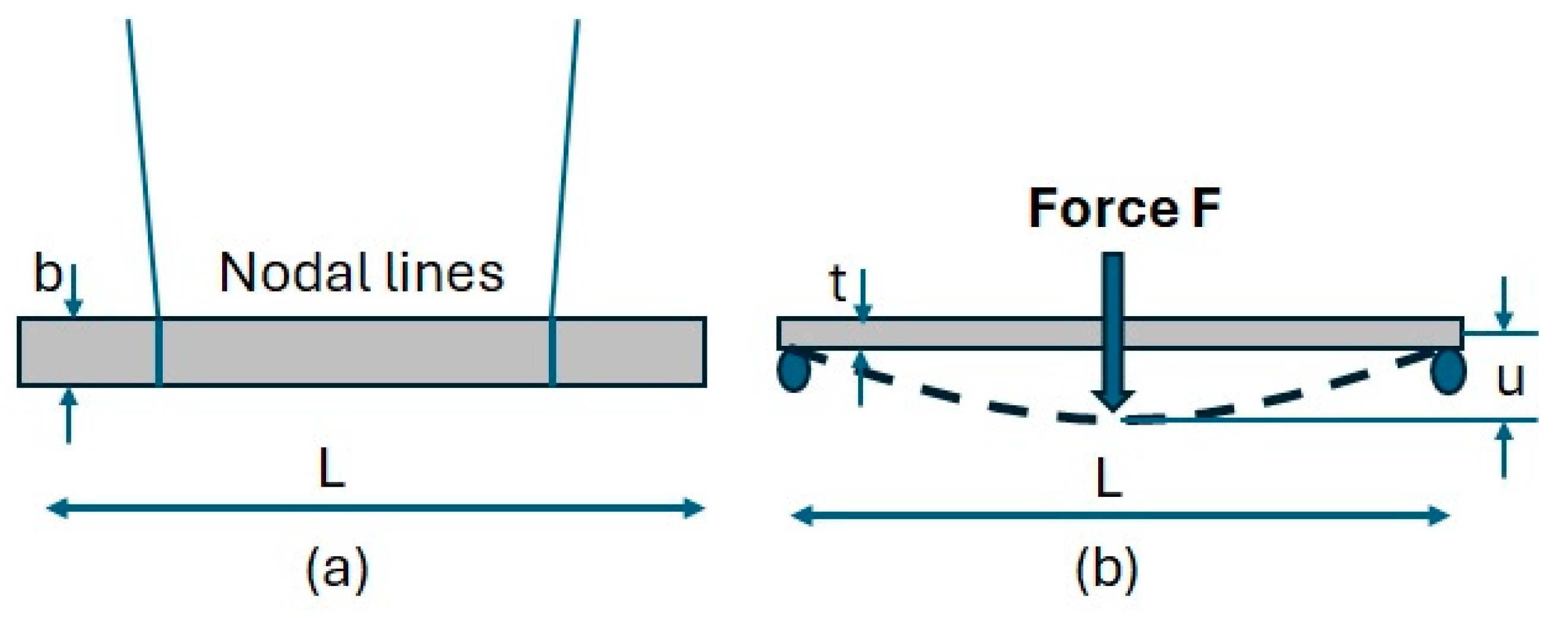
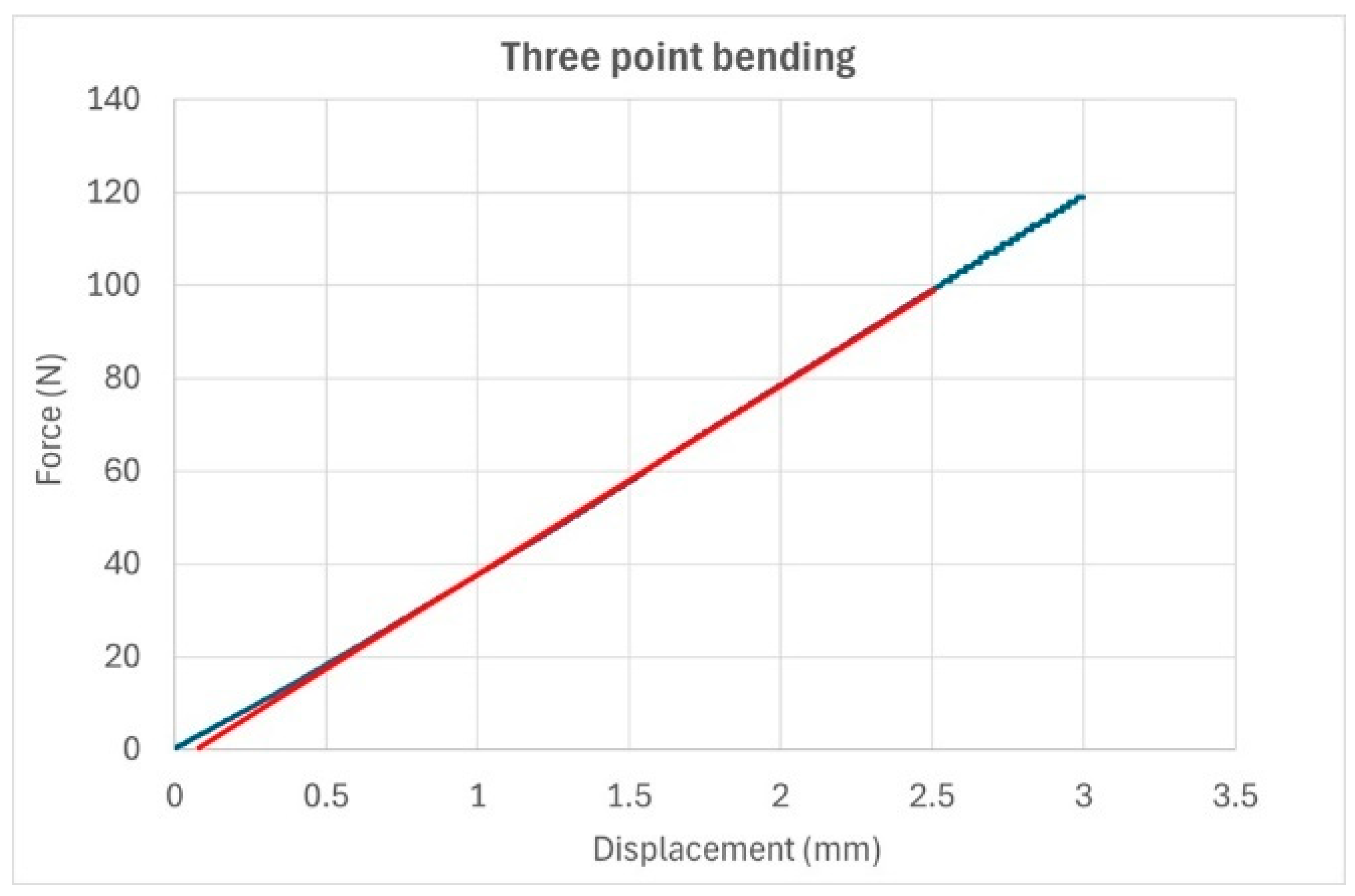



| Sample | Length [mm] | Width [mm] | Thickness [mm] | Mass [g] |
|---|---|---|---|---|
| GFRP Beam-1 (0°) | 255 | 25.9 | 2.00 | 24.9 |
| GFRP Beam-2 (90°) | 272 | 26.0 | 2.03 | 26.8 |
| GFRP plate | 243 | 234 | 2.03 | 217.0 |
| BFRP Beam-1 (0°) | 247 | 26.0 | 2.17 | 26.2 |
| BFRP Beam-2 (90°) | 273 | 26.0 | 2.17 | 28.9 |
| BFRP plate | 243 | 239 | 2.23 | 243.0 |
| Young’s Modulus E1 (0°) [GPa] | Young’s Modulus E2 (90°) [GPa] | |||||||
|---|---|---|---|---|---|---|---|---|
| Temperature [°C] | 3-pb * | Δ ** | IET | Δ ** | 3-pb * | Δ ** | IET | Δ ** |
| −20 | 26.6 | 0.8 | 27.8 | 0.5 | 23.6 | 0.7 | 25.7 | 0.5 |
| −10 | 26.3 | 0.8 | 27.6 | 0.5 | 24.2 | 0.7 | 25.5 | 0.5 |
| 0 | 26.0 | 0.8 | 27.4 | 0.5 | 24.0 | 0.7 | 25.4 | 0.5 |
| 10 | 26.8 | 0.8 | 27.2 | 0.5 | 24.0 | 0.7 | 25.2 | 0.5 |
| 20 | 25.5 | 0.7 | 27.1 | 0.5 | 23.7 | 0.7 | 25.0 | 0.5 |
| 30 | 25.6 | 0.7 | 26.9 | 0.4 | 23.4 | 0.7 | 24.8 | 0.5 |
| 40 | 24.7 | 0.7 | 26.7 | 0.4 | 22.5 | 0.6 | 24.6 | 0.5 |
| 50 | 24.3 | 0.7 | 26.5 | 0.4 | 21.9 | 0.6 | 24.4 | 0.5 |
| 60 | 24.0 | 0.7 | 26.2 | 0.4 | 21.6 | 0.6 | 24.0 | 0.5 |
| Young’s Modulus E1 (0°) [GPa] | Young’s Modulus E2 (90°) [GPa] | |||||||
|---|---|---|---|---|---|---|---|---|
| Temperature [°C] | 3-pb * | Δ ** | IET | Δ ** | 3-pb * | Δ ** | IET | Δ ** |
| −20 | 25.1 | 0.7 | 26.1 | 0.5 | 23.3 | 0.7 | 25.8 | 0.5 |
| −10 | 23.6 | 0.7 | 26.0 | 0.5 | 23.6 | 0.7 | 25.6 | 0.5 |
| 0 | 24.0 | 0.7 | 25.8 | 0.5 | 24.3 | 0.7 | 25.5 | 0.5 |
| 10 | 23.9 | 0.7 | 25.6 | 0.5 | 23.2 | 0.7 | 25.3 | 0.5 |
| 20 | 23.9 | 0.7 | 25.4 | 0.5 | 22.9 | 0.7 | 25.1 | 0.5 |
| 30 | 24.2 | 0.7 | 25.3 | 0.5 | 22.4 | 0.7 | 24.8 | 0.5 |
| 40 | 22.6 | 0.7 | 25.0 | 0.5 | 22.2 | 0.6 | 24.7 | 0.5 |
| 50 | 22.2 | 0.6 | 24.8 | 0.4 | 21.9 | 0.6 | 24.5 | 0.5 |
| 60 | 21.9 | 0.6 | 24.4 | 0.4 | 21.4 | 0.6 | 24.0 | 0.5 |
| Engineering Constant | Tensile Test [46] | Flexural Test [47] | ||
|---|---|---|---|---|
| Value | StDev | Value | StDev | |
| Young’s modulus E1 (0°) | 23.9 GPa | 0.1 | 25.2 GPa | 0.4 |
| Young’s modulus E2 (90°) | 22.6 GPa | 0.3 | 23.9 GPa | 0.4 |
| Poisson’s ratio V12 | 0.18 | - | 0.18 | - |
| Engineering Constant | Tensile Test [46] | Flexural Test [47] | ||
|---|---|---|---|---|
| Value | StDev | Value | StDev | |
| Young’s modulus E1 (0°) | 24.2 GPa | 0.3 | 22.4 GPa | 0.4 |
| Young’s modulus E2 (90°) | 23.2 GPa | 0.3 | 22.6 GPa | 0.4 |
| Poisson’s ratio V12 | 0.18 | - | 0.17 | - |
| Young’s Moduli | Resonalyser MPa | Three-Point Bending MPa | Flexural Test SDH MPa | Tensile Test SDH MPa |
|---|---|---|---|---|
| GFRC E1 (0°) | 27.1 | 25.5 | 23.9 | 25.2 |
| GFRC E2 (90°) | 25.0 | 23.7 | 22.6 | 23.9 |
| BFRC E1 (0°) | 25.4 | 23.9 | 24.2 | 22.4 |
| BFRC E2 (90°) | 25.1 | 22.9 | 23.2 | 22.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rahier, H.; Gu, J.; Hernandez, G.M.; Nazerian, G.; Sol, H. Temperature-Dependent Elastic and Damping Properties of Basalt- and Glass-Fabric-Reinforced Composites: A Comparative Study. Fibers 2025, 13, 99. https://doi.org/10.3390/fib13080099
Rahier H, Gu J, Hernandez GM, Nazerian G, Sol H. Temperature-Dependent Elastic and Damping Properties of Basalt- and Glass-Fabric-Reinforced Composites: A Comparative Study. Fibers. 2025; 13(8):99. https://doi.org/10.3390/fib13080099
Chicago/Turabian StyleRahier, Hubert, Jun Gu, Guillermo Meza Hernandez, Gulsen Nazerian, and Hugo Sol. 2025. "Temperature-Dependent Elastic and Damping Properties of Basalt- and Glass-Fabric-Reinforced Composites: A Comparative Study" Fibers 13, no. 8: 99. https://doi.org/10.3390/fib13080099
APA StyleRahier, H., Gu, J., Hernandez, G. M., Nazerian, G., & Sol, H. (2025). Temperature-Dependent Elastic and Damping Properties of Basalt- and Glass-Fabric-Reinforced Composites: A Comparative Study. Fibers, 13(8), 99. https://doi.org/10.3390/fib13080099







