Constitutive Model for Plain and Steel-Fibre-Reinforced Lightweight Aggregate Concrete Under Direct Tension and Pull-Out
Abstract
1. Background Review
1.1. Lightweight Aggregate Concrete
1.2. Steel Fibres
1.3. Tensile Behaviour and Limitations of Existing Research
2. Experimental Procedure
2.1. Material Properties
2.2. Properties of Mixes
2.3. Test Method for Pull-Out Test
3. Results and Discussion
3.1. Pull-Out Load–Slip Behaviour
3.1.1. Effect of Number of Bends nb
3.1.2. Effect of Fibre Aspect Ratio af
3.1.3. Effect of Fibre Length Lf
3.1.4. Effect of Fibre Dosage Vf
3.1.5. Effect of Compressive Strength flck
3.1.6. Effect of Embedded Length LE
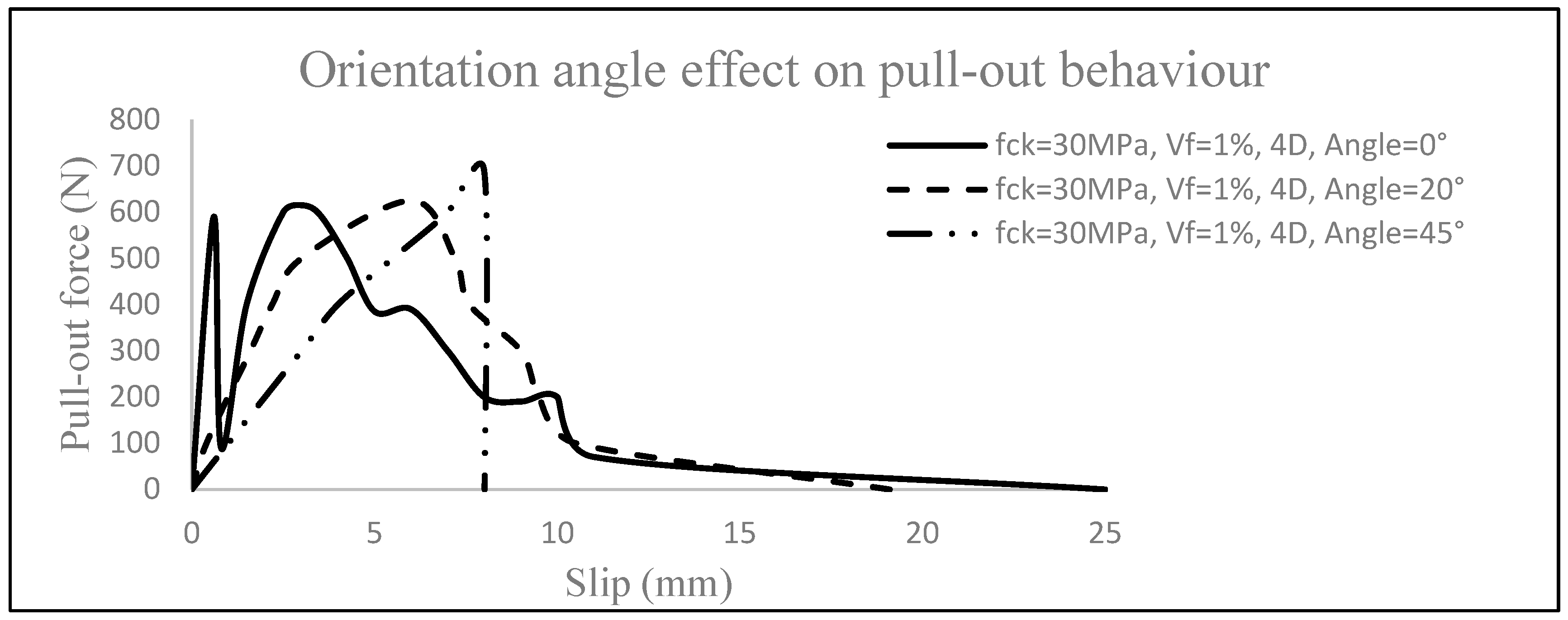
3.1.7. Effect of Fibre Inclination Angle ϴf
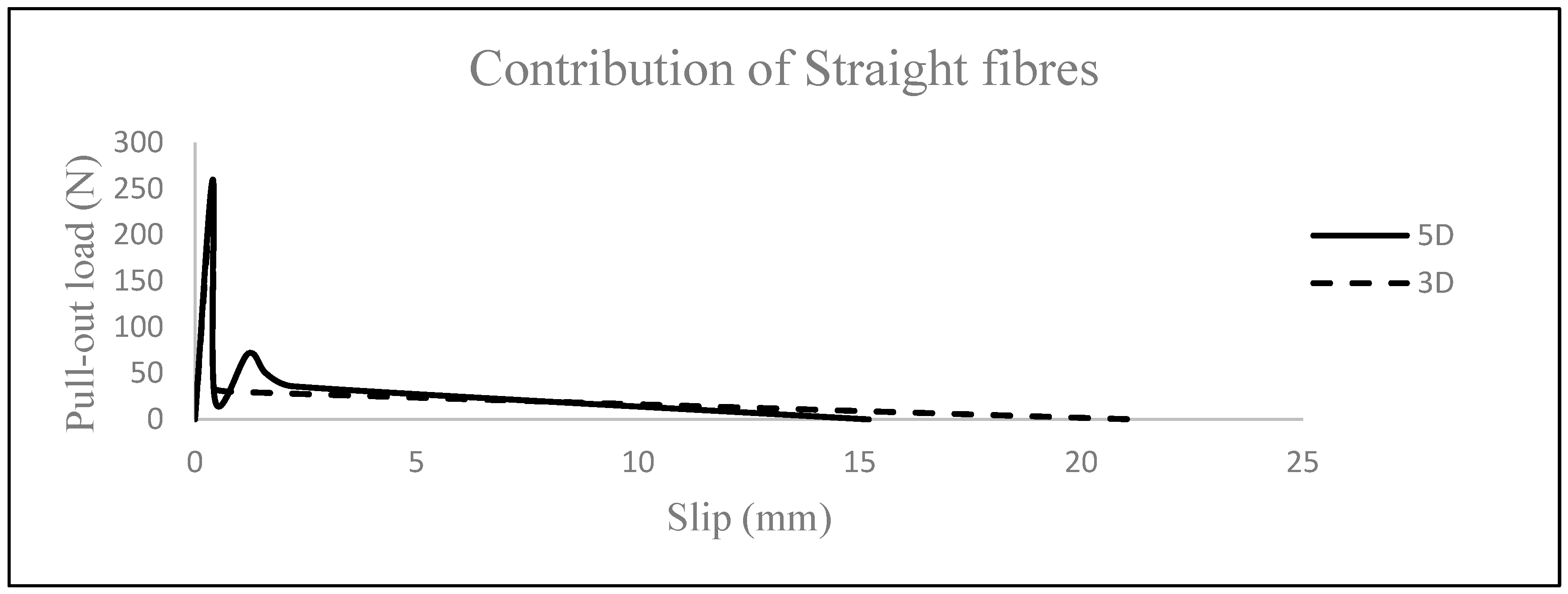
3.1.8. Adequacy of Smooth Fibres
3.2. Key Characteristics of the Uniaxial Tensile Behaviour of SFRLC
3.2.1. Maximum Uniaxial Tensile Stress flctm,m
3.2.2. Pull-Out Work
3.2.3. Bond Strength
3.3. Fibre Optimisation
3.3.1. Fibre Stress Efficiency
3.3.2. Fibre Energy and Bond Indices
3.3.3. Fibre Plasticity Study
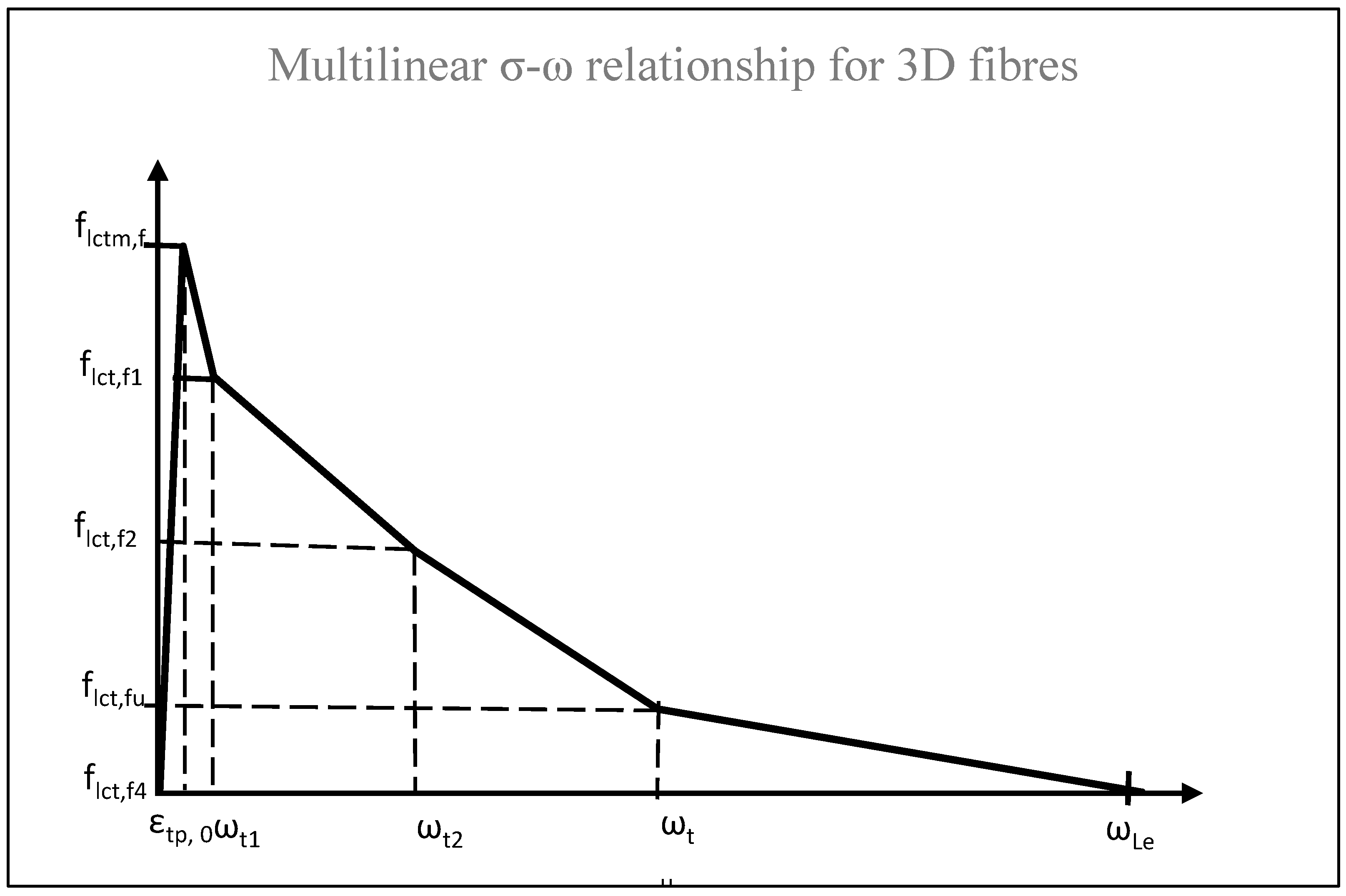
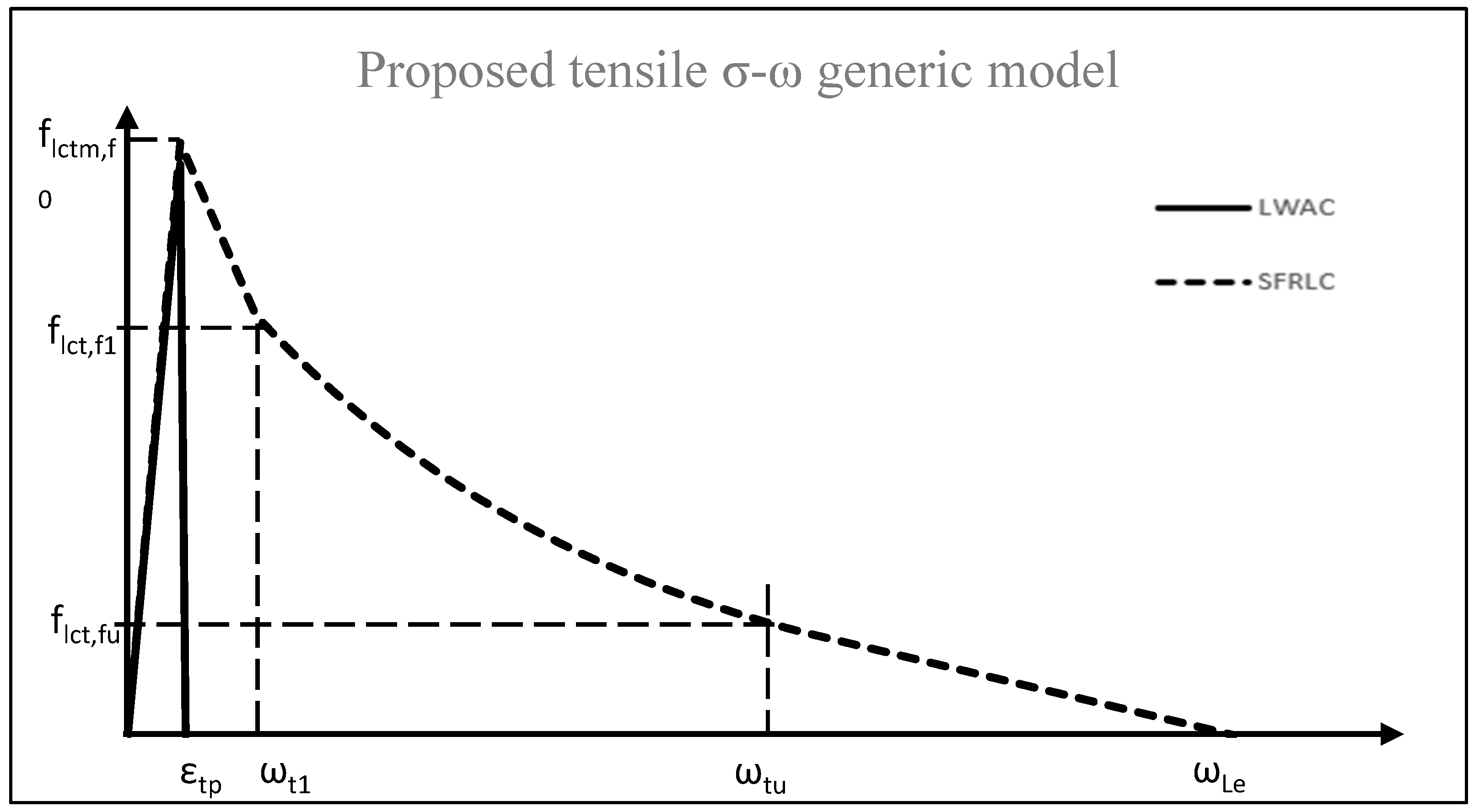
3.4. Proposed Constitutive Tensile σ-ω Model
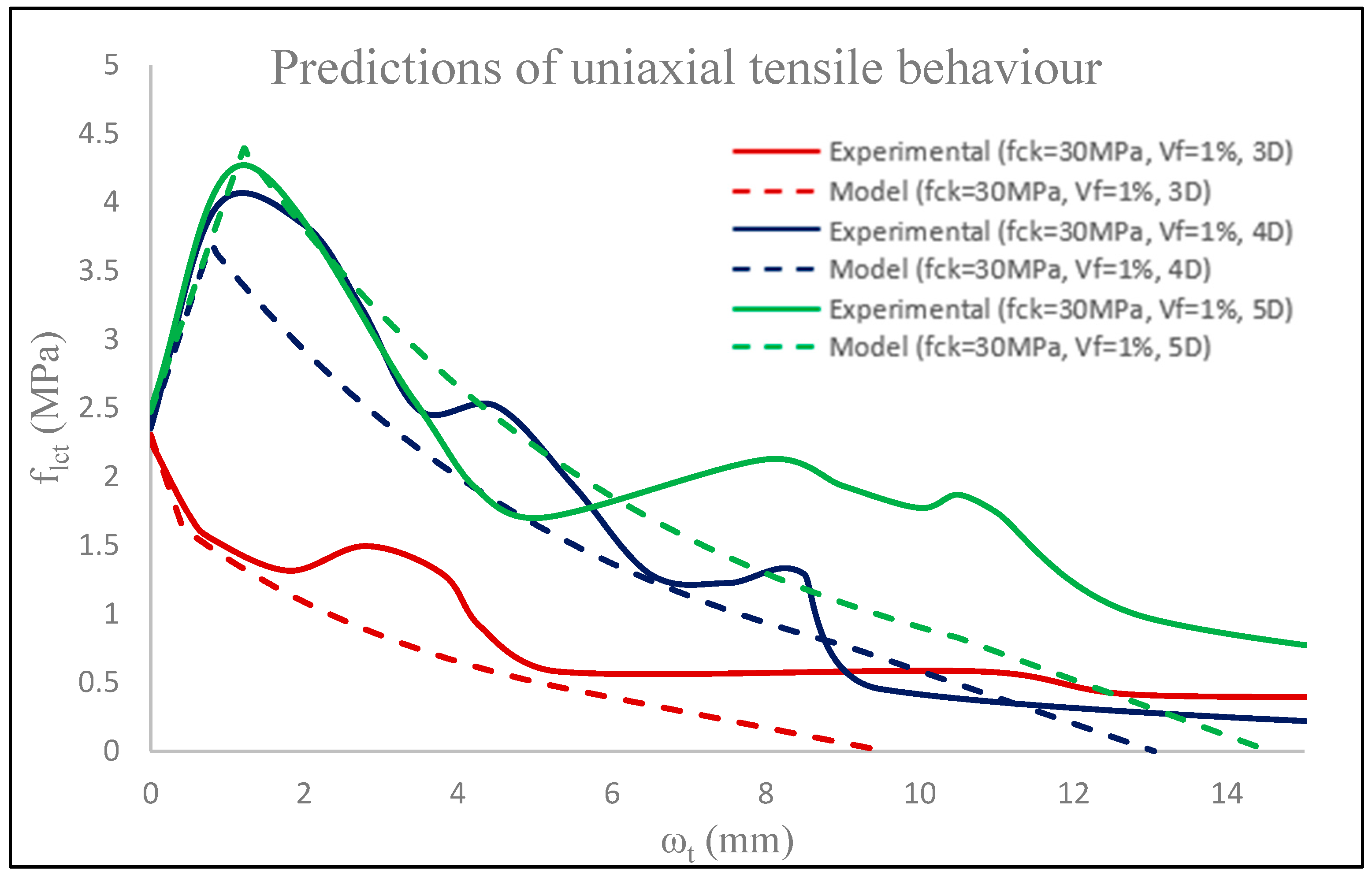
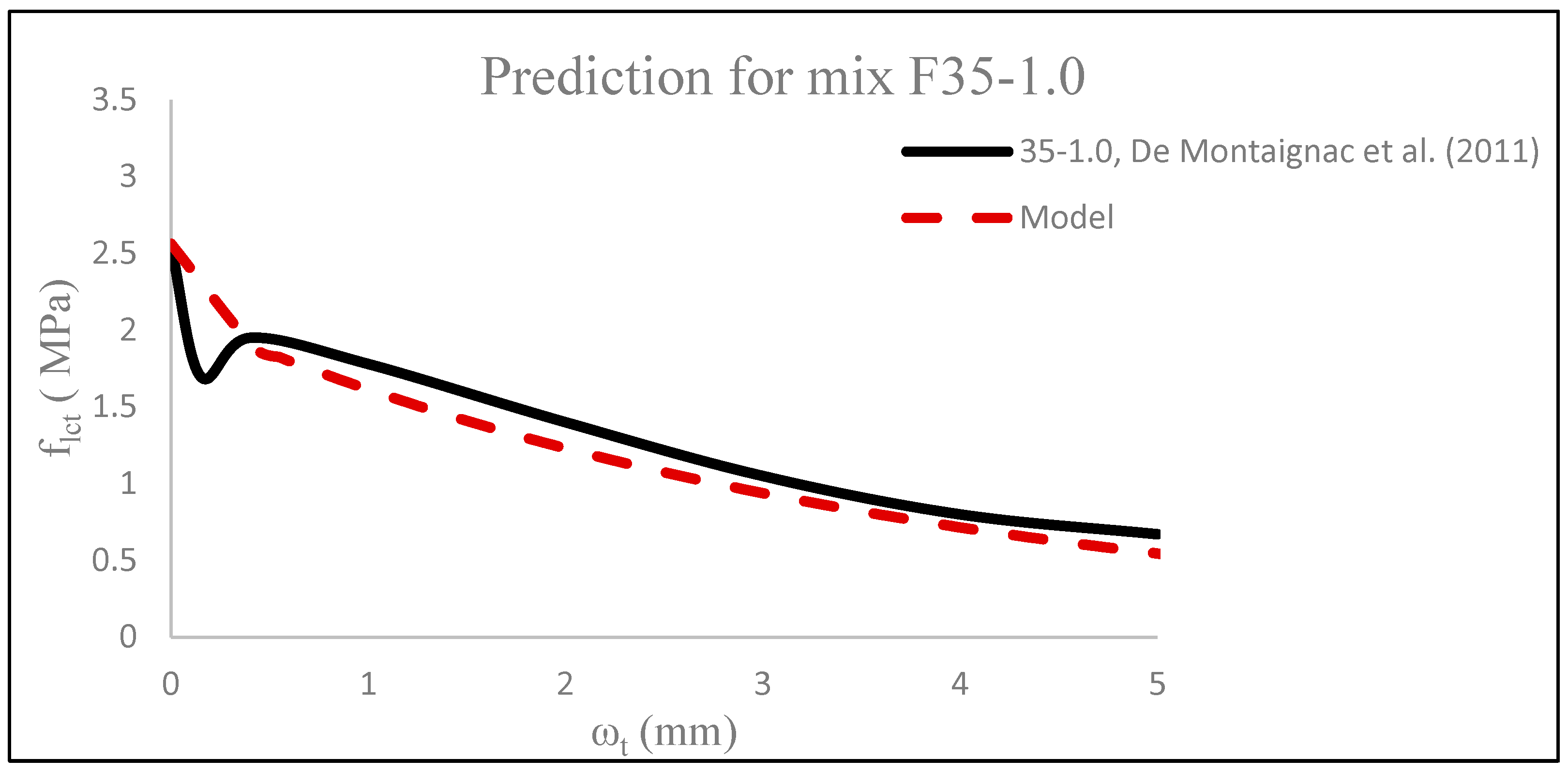
3.5. Validation of Tensile σ-ω Model
3.6. Fracture Energy Gf
3.7. Conclusions
- The designed pull-out test showed a truer representation of a tensile crack being bridged by fibres on the macro level in a structural member. Also, using the area of the notch in which the fibre(s) was embedded, it was possible to regard the pull-out test as a uniaxial tensile test of plain and fibrous lightweight concrete.
- Due to the absence of a natural tension-stiffening mechanism, plain lightweight concrete was found to fail in a sudden brittle manner once it reached its peak tensile strength. The addition of fibres to lightweight concrete was seen to drastically enhance both the tensile strength and ductility, including work and fracture energy, once the main tensile crack was initiated. Before the latter took place, a negligible increase in strength was seen. The higher the number of fibre bends nb and the higher the fibre aspect ratio af, fibre length Lf, fibre dosage Vf and plain concrete compressive strength flck, the higher the post-cracking tensile strength and ductility of the fibrous composite. The embedded length LE was found to only enhance the ductility of SFRLC. It was found that a minimum value of LE = Lh +5df is required for hooked-end fibres to bond adequately and achieve a maximum pull-out load Pmax. Also, although the increase in the fibre inclination angle ϴf was found to increase the post-cracking tensile strength as compared to ϴf = 0°, in some instances where ϴf = 45°, the concrete fractured. An inclination angle of about 20° was found to add tensile strength without compromising ductility. It was found that smooth fibres were ineffective at increasing the strength of SFRLC and merely enhanced ductility via frictional pull-out.
- A new ultimate bond strength equation to quantify the behaviour of hooked-end steel fibres in lightweight concrete was suggested based on the pull-out tests. It was found that 4D fibres showed the highest bond strength, while 3D** fibres showed the lowest bond strength. Also, the maximum uniaxial tensile stress for SFRLC specimens was determined while taking into consideration the random distribution of fibres in a practical situation.
- A fibre optimisation study was carried out, and it was concluded that incorporating multiple-bend fibres such as 5D fibres, which also have a high tensile strength of 2300 MPa, with a concrete of strength of 30 MPa can cause local fracturing of a lightweight concrete matrix. This is attributed to the difficulty of concrete to allow plastic hinge formation and straightening of the fibre during the pull-out process. Hence, it is advised that 5D fibres should not be employed as reinforcements for concrete of low grade. Also, 3D* and 4D fibres appeared to be the most efficient and optimum fibres for reinforcing lightweight concrete with tested strengths of 30–45 MPa, with the aspect ratio af playing a significant role in bond strength efficiency and the number of bends nb having a greater impact on the energy dissipation efficiency.
- A semi-empirical constitutive tensile stress–crack width (σ-ω) model for fibrous lightweight concrete based on experimental testing was derived. The equations defining the residual tensile strengths flct,f1 and crack widths ωt1 were based on a regression analysis. The model showed its success in predicting the uniaxial tensile behaviour of SFRLC specimens. Since the model relies on the fibre reinforcing factor ρf (which is based on the fibre geometry and fibre volume fraction) and plain compressive or tensile strength, the model was also capable of validating the uniaxial tensile behaviour of steel-fibre-reinforced normal weight concrete from previous studies in the literature.
- The benefits of steel fibres in addressing the brittleness of lightweight concrete is of particular interest to designers and practitioners. This is in addition to the construction time savings from using fibres (which are simply added to the mix as opposed to steel laying). Using recycled-waste-based aggregates alongside fibres also adds to these practical benefits. The proposed constitutive model will allow designers to carry out more detailed analysis and design simulations in order to better understand the structural responses.
- In terms of future work, more research on SFRLC needs to be carried out at the structural level to include a comprehensive experimental testing programme of structural beams of different boundary and loading conditions, cross-sections, spans, and shear configurations. Numerical modelling can also be performed using the proposed material model. Some structural testing and finite-element analyses have been already undertaken, which will be reported in follow-up articles. The long-term behaviour of fibrous concrete remains largely unquantified by current standards, so this will benefit from further examination.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Notation
| flck,cube | characteristic cube compressive stress |
| flck | characteristic cylinder compressive stress |
| flc | cylinder compressive stress |
| flcm | mean compressive cylinder stress |
| flcm,p | mean compressive cylinder stress of plain concrete |
| flcm,cube | mean cube compressive stress |
| flctm,m | maximum uniaxial tensile stress |
| Af | area of a single fibre |
| df | fibre diameter |
| Elcm | mean value of Young’s modulus of elasticity |
| Elcm,f | peak elastic modulus of SFRLC |
| nb | number of bends |
| df | diameter of fibre |
| Le | effective fibre anchorage length |
| LE | embedded length of fibre |
| Lf | length of fibre |
| κ | fibre material factor |
| ρf | fibre reinforcing factor |
| δ | fibre shape factor |
| Pmax | maximum pull-out strength for a single fibre |
| Vf | fibre volume fraction |
| Wp | total work performed by fibre |
| μlc | Poisson’s ratio |
| ε | strain |
| εlc1 | strain at peak compressive stress of LWAC |
| εlcf | strain at peak compressive stress of SFRLC |
| εt1 | strain at post-cracking first residual tensile stress |
| εlcu | strain at ultimate compressive stress of LWAC |
| εlcf,ult | strain at ultimate compressive stress of SFRLC |
| η0 | fibre orientation factor |
| σf | fibre stress |
| τav | fibre–matrix interfacial bond shear stress |
| τult | ultimate bond strength of SFRLC matrix |
| σ | stress |
| σav,f | average stress of fibre |
| σc | average stress of concrete |
| σy | fibre yield stress |
| σu | fibre ultimate stress |
| Ef | Young’s modulus of elasticity fibre |
| SFRLC | steel-fibre-reinforced lightweight concrete |
| LWAC | lightweight aggregate concrete |
References
- Al-Khaiat, H.; Haque, Μ.Ν. Effect of initial curing on early strength and physical properties of lightweight concrete. Cem. Concr. Res. 1998, 28, 859–866. [Google Scholar] [CrossRef]
- Gerritse, A. Design considerations for reinforced lightweight concrete. Int. J. Cem. Compos. Lightweight Concr. 1981, 3, 57–69. [Google Scholar] [CrossRef]
- Lyag. Technical Manual; Lytag Ltd.: London, UK, 2011. [Google Scholar]
- Lytag. Ramboll Frame Comparison Study. 2014. Available online: https://www.aggregate.com/our-businesses/lytag (accessed on 31 December 2019).
- Chandra, S.; Berntsson, L. Lightweight Aggregate Concrete Science; Technology and Applications; Standard Publishers Distributors: Delhi, India, 2003; ISBN 81-8014-052-0. [Google Scholar]
- Ahn, Y.B.; Jang, J.G.; Lee, H.K. Mechanical properties of lightweight concrete made with coal ashes after exposure to elevated temperatures. Cem. Concr. Compos. 2016, 72, 27–38. [Google Scholar] [CrossRef]
- Libre, N.A.; Shekarchi, M.; Mahoutian, M.; Soroushian, P. Mechanical properties of hybrid fiber reinforced lightweight aggregate concrete made with natural pumice. Constr. Build. Mater. 2011, 25, 2458–2464. [Google Scholar] [CrossRef]
- Campione, G. Flexural and Shear Resistance of Steel Fiber–Reinforced Lightweight Concrete Beams. J. Struct. Eng. 2014, 140, 04013103. [Google Scholar] [CrossRef]
- Dias-da-Costa, D.; Carmo, R.N.F.; Graça-e-Costa, R.; Valença, J.; Alfaiate, J. Longitudinal reinforcement ratio in lightweight aggregate concrete beams. Eng. Struct. 2014, 81, 219–229. [Google Scholar] [CrossRef]
- Mo, K.M.; Goh, S.; Alengaram, U.; Visintin, P.; Jumaat, M. Mechanical, toughness, bond and durability-related properties of lightweight concrete reinforced with steel fibres. Mater. Struct. 2017, 50, 46. [Google Scholar] [CrossRef]
- Lim, W.; Mansur, K. Flexural behavior of reinforced lightweight aggregate concrete beams. In Asia-Pacific Structural Engineering and Construction Conference; APSEC: Kuala Lumpur, Malaysia, 2006; pp. 68–82. [Google Scholar]
- Chen, H.; Huang, C.; Tang, C. Dynamic Properties of Lightweight Concrete Beams Made by Sedimentary Lightweight Aggregate. J. Mater. Civ. Eng. 2010, 22, 599–606. [Google Scholar] [CrossRef]
- Wu, C.; Kan, Y.; Huang, C.; Yen, T.; Chen, L. Flexural behavior and size effect of full scale reinforced lightweight concrete beam. J. Mar. Sci. Technol. 2011, 19, 132–140. [Google Scholar] [CrossRef]
- Badogiannis, E.; Kotsovos, M. Monotonic and cyclic flexural tests on lightweight aggregate concrete beams. Earthq. Struct. 2014, 6, 317–334. [Google Scholar] [CrossRef]
- Lambert, G. Properties and Behaviour of Structural Lightweight (Lytag—Sand) Concrete. Ph.D. Thesis, University of Sheffield, Sheffield, UK, 1982. [Google Scholar]
- Lo, T.Y.; Cui, H.; Memon, S.A.; Noguchi, T. Manufacturing of sintered lightweight aggregate using high-carbon fly ash and its effect on the mechanical properties and microstructure of concrete. J. Clean. Prod. 2016, 112, 753–762. [Google Scholar] [CrossRef]
- Bilodeau, A.; Kodur, V.; Hoff, G. Optimization of the type and amount of polypropylene fibres for preventing the spalling of lightweight concrete subjected to hydrocarbon fire. Cem. Concr. Compos. 2004, 26, 163–174. [Google Scholar] [CrossRef]
- Collins, R.; Sherwood, P. Use of Waste and Recycled Materials as Aggregates; H.M.S.O.: London, UK, 1995.
- Gao, J.; Sun, W.; Morino, K. Mechanical properties of steel fiber-reinforced, high-strength, lightweight concrete. Cem. Concr. Compos. 1997, 19, 307–313. [Google Scholar] [CrossRef]
- Campione, G.; La Mendola, L. Behavior in compression of lightweight fiber reinforced concrete confined with transverse steel reinforcement. Cem. Concr. Compos. 2004, 26, 645–656. [Google Scholar] [CrossRef]
- Abbas, A.A.; Syed Mohsin, S.M.; Cotsovos, D.M. Seismic response of steel fibre reinforced concrete beam–column joints. Eng. Struct. 2014, 59, 261–283. [Google Scholar] [CrossRef]
- Di Prisco, M.; Colombo, M.; Dozio, D. Fibre-reinforced concrete in fib Model Code 2010: Principles, models and test validation. Struct. Concr. 2013, 14, 342–361. [Google Scholar] [CrossRef]
- Grabois, T.M.; Cordeiro, G.C.; Filho, R.D.T. Fresh and hardened-state properties of self-compacting lightweight concrete reinforced with steel fibers. Constr. Build. Mater. 2016, 104, 284–292. [Google Scholar] [CrossRef]
- Abbas, A.A.; Syed Mohsin, S.M.; Cotsovos, D.M.; Ruiz-Teran, A.M. Shear behaviour of SFRC simply-supported beams, ICE Proc. Struct. Build. 2014, 167, 544–558. [Google Scholar] [CrossRef]
- Ritchie, A.; Kayali, O. The effects of fiber reinforcement on lightweight aggregate concrete. In Proceedings of RILEM Symposium on Fiber Reinforced Cement and Concrete; Neville, A., Ed.; The Construction Press Ltd.: Hong Kong, China, 1975; pp. 247–256. [Google Scholar]
- Swamy, N.; Jones, R.; Chiam, A. Influence of Steel fibers on the Shear Resistance of Lightweight Concrete I-Beams. ACI Struct. J. 1993, 90, 103–114. [Google Scholar]
- Kang, T.; Kim, W. Shear Strength of Steel Fiber-Reinforced Lightweight Concrete Beams; Korea Concrete Institute: Oklahoma, TX, USA, 2010; pp. 1386–1392. [Google Scholar]
- Iqbal, S.; Ali, A.; Holschemacher, K.; Bier, T. Mechanical properties of steel fiber reinforced high strength lightweight self-compacting concrete (SHLSCC). Constr. Build. Mater. 2015, 98, 325–333. [Google Scholar] [CrossRef]
- IEA. World Energy Outlook 2019; IEA: Paris, France, 2019; Available online: https://www.iea.org/reports/world-energy-outlook-2019/coal#abstract (accessed on 1 October 2020).
- Al-Naimi, H. Structural Behaviour of Steel Fibre Reinforced Lightweight Concrete. Ph.D. Thesis, Univeraity of East London, London, UK, 2020. [Google Scholar]
- Al-Naimi, H.K.; Abbas, A.A. Constitutive model for plain and steel-fibre-reinforced lightweight concrete under compression. Struct. Concr. 2023, 24, 7625–7647. [Google Scholar] [CrossRef]
- Kotsovos, M.D.; Pavlović, M.N. Structural Concrete, Finite-Element Analysis for Limit-State Design; Thomas Telford: London, UK, 1995. [Google Scholar]
- Löfgren, I. Fibre-reinforced Concrete for Industrial Construction: A fracture mechanics approach to material testing and structural analysis. Ph.D. Thesis, Chalmers University Of Technology, Göteborg, Sweden, 2005. [Google Scholar]
- Lee, S.-C.; Cho, J.-Y.; Vecchio, F.J. Diverse Embedment Model for Steel Fiber-Reinforced Concrete in Tension: Model Development. ACI Mater. J. 2011, 108, 516–525. [Google Scholar]
- Kayali, O.; Haque, M.; Zhu, B. Some characteristics of high strength fiber reinforced lightweight aggregate concrete. Cem. Concr. Compos. 2003, 25, 207–213. [Google Scholar] [CrossRef]
- Zhao, M.; Zhao, M.; Chen, M.; Li, J.; Law, D. An experimental study on strength and toughness of steel fiber reinforced expanded-shale lightweight concrete. Constr. Build. Mater. 2018, 183, 493–501. [Google Scholar] [CrossRef]
- Badogiannis, E.G.; Christidis, Κ.I.; Tzanetatos, G.E. Evaluation of the mechanical behavior of pumice lightweight concrete reinforced with steel and polypropylene fibers. Constr. Build. Mater. 2019, 196, 443–456. [Google Scholar] [CrossRef]
- Liu, X.; Wu, T.; Liu, Y. Stress-strain relationship for plain and fibre-reinforced lightweight aggregate concrete. Constr. Build. Mater. 2019, 225, 256–272. [Google Scholar] [CrossRef]
- Mo, K.M.; Yap, K.K.Q.; Alengaram, U.J.; Jumaat, M.Z. The effect of steel fibres on the enhancement of flexural and compressive toughness and fracture characteristics of oil palm shell concrete. Constr. Build. Mater. 2014, 55, 20–28. [Google Scholar] [CrossRef]
- ASTM D638-10; Standard Test Method for Tensile Properties of Plastics. ASTM International: West Conshohocken, PA, USA, 2014.
- RILEM TC 162-TDF: Test and Design Methods for Steel Fibre Reinforced Concrete. Recommendations for uni-axial tension test. Mater. Struct. 2001, 34, 3–6. [CrossRef]
- Abdallah, S.; Rees, D.W.A.; Hamidreza, S.; Fan, M. Understanding the effects of hooked-end steel fibre geometry on the uniaxial tensile behaviour of self-compacting concrete. Constr. Build. Mater. 2018, 178, 484–494. [Google Scholar] [CrossRef]
- Abdallah, S.; Fan, M.; Zhou, X. Effect of Hooked-End Steel Fibres Geometry on Pull-Out Behaviour of Ultra-High Performance Concrete. Int. J. Civ. Environ. Struct. Constr. Archit. Eng. 2016, 10, 1594–1599. [Google Scholar]
- Bekaert. 2020. Available online: https://www.bekaert.com/en/ (accessed on 20 June 2020).
- Robins, P.; Austin, S.; Jones, P. Pull-out Behaviour of Hooked Steel Fibres. Mater. Struct. 2002, 35, 434–442. [Google Scholar] [CrossRef]
- Alwan, J.; Naaman, A.; Guerrero, P. Effect of mechanical clamping on the pull-out response of hooked steel fibers embedded in cementitious matrices. Concr. Sci. Eng. 1999, 1, 15–25. [Google Scholar]
- Abdallah, S.; Fan, M.; Rees, D.W.A. Analysis and modelling of mechanical anchorage of 4D/5D hooked end steel fibres. Mater. Des. 2016, 112, 539–552. [Google Scholar] [CrossRef]
- Abdallah, S.; Fan, M.; Zhou, X. Pull-Out Behaviour of Hooked End Steel Fibres Embedded in Ultra-high Performance Mortar with Various W/B Ratios. Int. J. Concr. Struct. Mater. 2017, 11, 301–313. [Google Scholar] [CrossRef]
- Romualdi, J.P.; Mandel, J.A. Tensile Strength of Concrete Affected by Uniformly Distributed and Closely Spaced Short Length of Wire Reinforcement. ACI J. Proc. 1964, 61, 657–671. [Google Scholar]
- Krenchel, H. Fibre Spacing and Specific Fibre Surface. In Testing and Test Methods of Fibre Cement Composites; Proceedings of the RILEM Symposium; Construction Press Ltd.: Lancaster, UK, 1978; pp. 69–79. [Google Scholar]
- Soroushian, P.; Lee, C.-D. Tensile Strength of Steel Fiber Reinforced Concrete: Correlation with Some Measures of Fiber Spacing. ACI Mater. J. 1990, 87, 541–546. [Google Scholar]
- Wille, K.; Naaman, A.E. Pullout behavior of highstrength steel fibers embedded in ultra-high-performance concrete. ACI Mater. J. 2012, 109, 479–588. [Google Scholar]
- Wille, K.; Naaman, A.E. Effect of ultra-high-performance concrete on pullout behavior of high-strength brass-coated straight steel fibers. ACI Mater. J. 2013, 110, 451–462. [Google Scholar]
- Cao, Y.Y.Y.; Yu, Q.L. Effect on inclination angle on hooked end steel fiber pull out behavior in ultra-high performance concrete. Compos. Struct. 2018, 201, 151–160. [Google Scholar] [CrossRef]
- Qi, J.; Wu, Z.; Ma, Z.J.; Wang, J. Pullout behaviour of straight and hooked-end steel fibers in UHPC matrix with various embedded angles. Constr. Build. Mater. 2018, 191, 764–774. [Google Scholar] [CrossRef]
- Barragán, B.E.; Gettu, R.; Martín, M.A.; Zerbino, R.L. Uniaxial tension test for steel fibre reinforced concrete––A parametric study. Cem. Concr. Compos 2003, 25, 767–777. [Google Scholar] [CrossRef]
- Abdallah, S.; Rees, D.W.A. Comparisons Between Pull-Out Behaviour of Various Hooked-End Fibres in Normal–High Strength Concretes. Int. J. Concr. Struct. Mater. 2019, 13, 27. [Google Scholar] [CrossRef]
- Lim, T.Y.; Paramasivam, P.; Lee, S.L. Analytical Model for Tensile Behaviour of Steel-Fibre Concrete. ACI Mater. J. Tech. Pap. 1987, 84, 286–298. [Google Scholar]
- Lok, T.; Xiao, J. Tensile behaviour and moment–curvature relationship of steel fibre reinforced concrete. Mag. Concr. Res. 1998, 50, 359–368. [Google Scholar] [CrossRef]
- Lok, T.-S.; Xiao, J.R. Flexural Strength Assessment of Steel Fiber Reinforced Concrete. J. Mater. Civ. Eng. 1999, 11, 188–196. [Google Scholar] [CrossRef]
- Hannant, D.J. Fibre Cements and Fibre Concrètes; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 1978. [Google Scholar]
- Joo Kim, D. Strain Rate Effect on High Performance Fiber Reinforced Cementitious Composites Using Slip Hardening High Strength Deformed Steel Fibers; University of Michigan: Ann Arbor, MI, USA, 2009. [Google Scholar]
- Naaman, A.E.; Namur, G.G.; Alwan, J.M.; Najm, H. Fiber pull-out and bond slip, Part I: Analytical study. ASCE J. Struct. Eng. 1991, 117, 2769–2790. [Google Scholar] [CrossRef]
- De Montaignac, R.; Massicotte, B.; Charron, J.-P.; Nour, A. Design of SFRC structural elements: Post-cracking tensile strength measurement. Mater. Struct. 2011, 45, 609–622. [Google Scholar] [CrossRef]
- Fédération Internationale du béton. fib Model Code for Concrete Structures 2010; Ernst and Sohn: Berlin, Germany, 2013; pp. 147–150. [Google Scholar]
- BS EN 1992:1:1; Eurocode 2: Design of Concrete Structures—Part 1: General Rules and Rules for Buildings. Comité Européen De Normalisation: Bruxelles, Belgium, 2004.



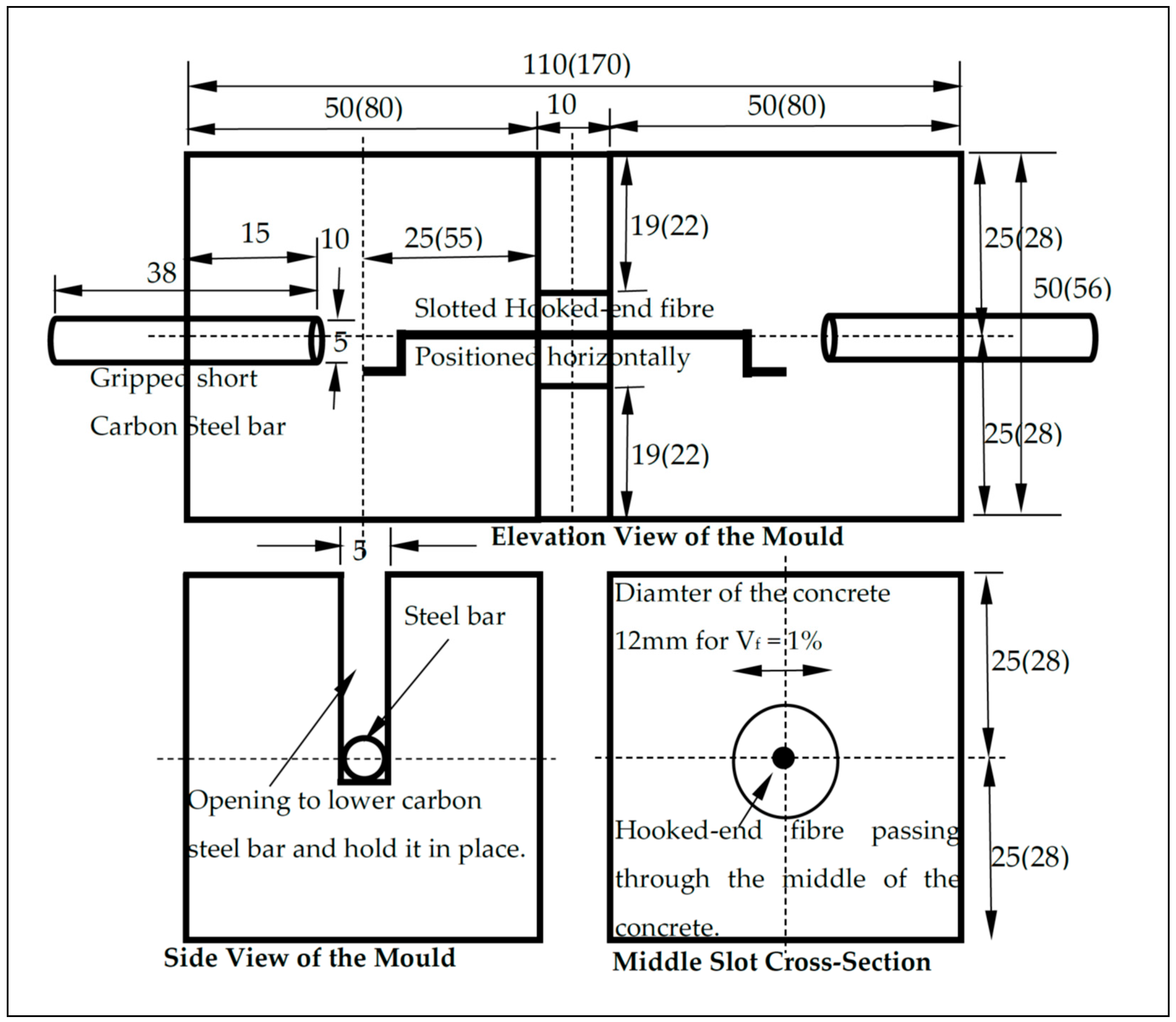







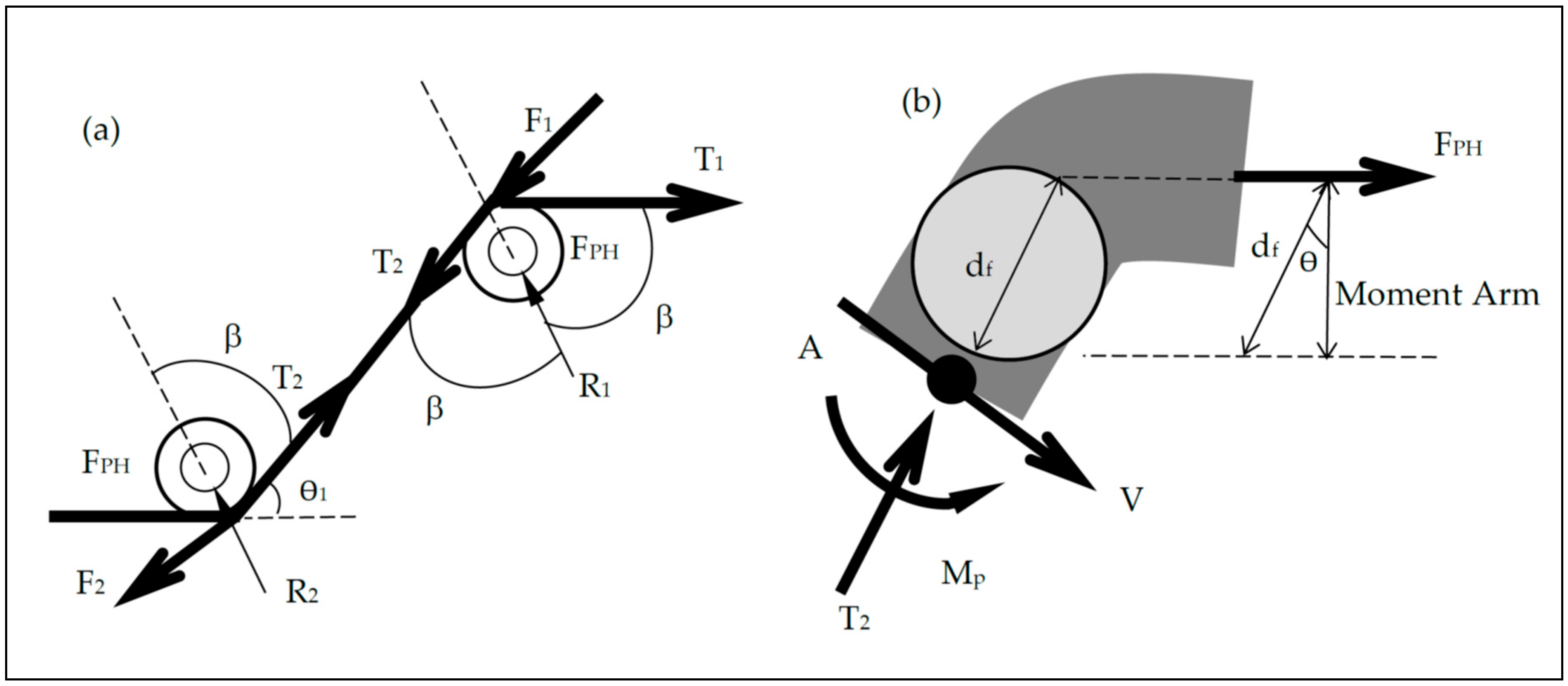
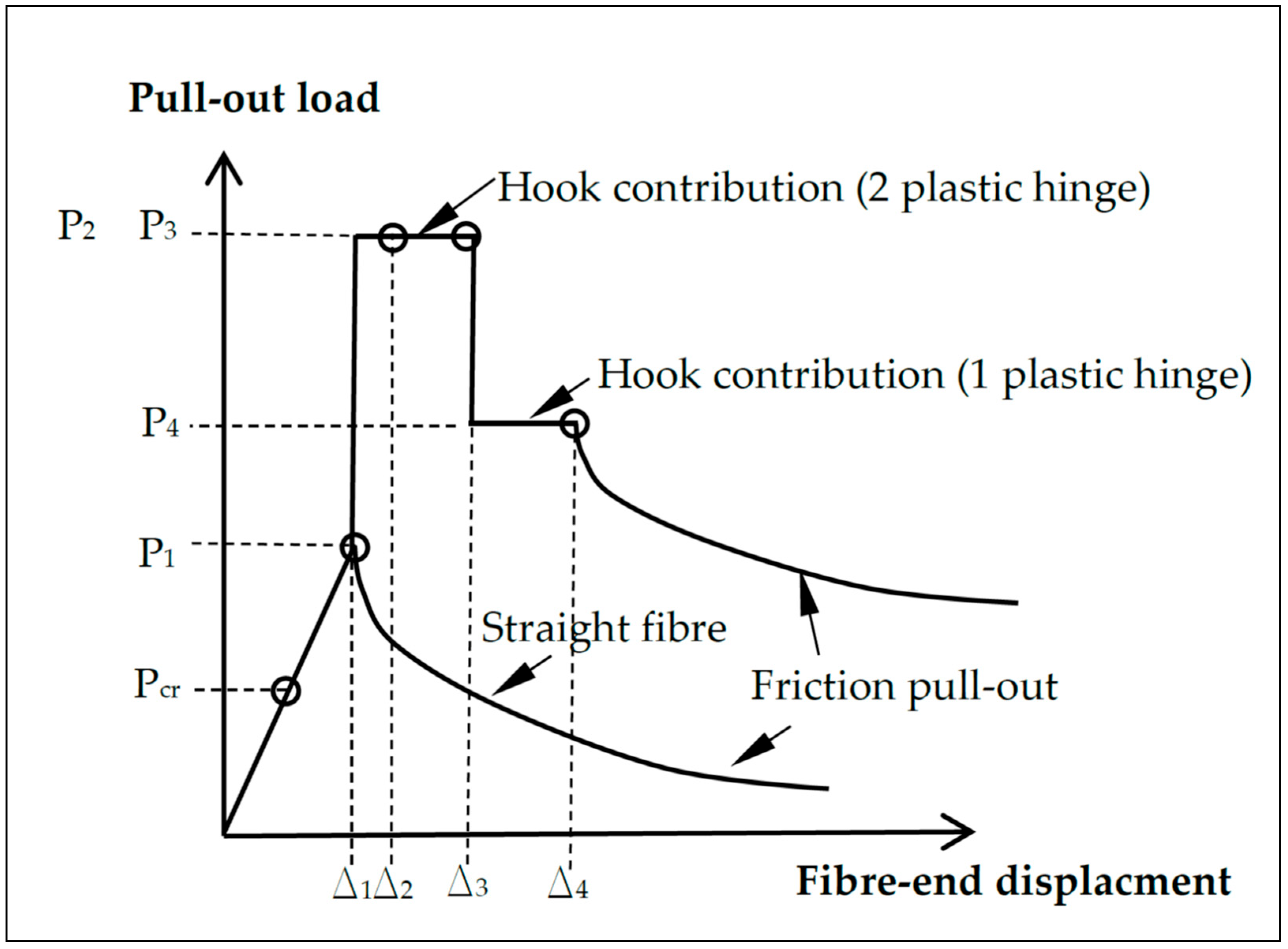
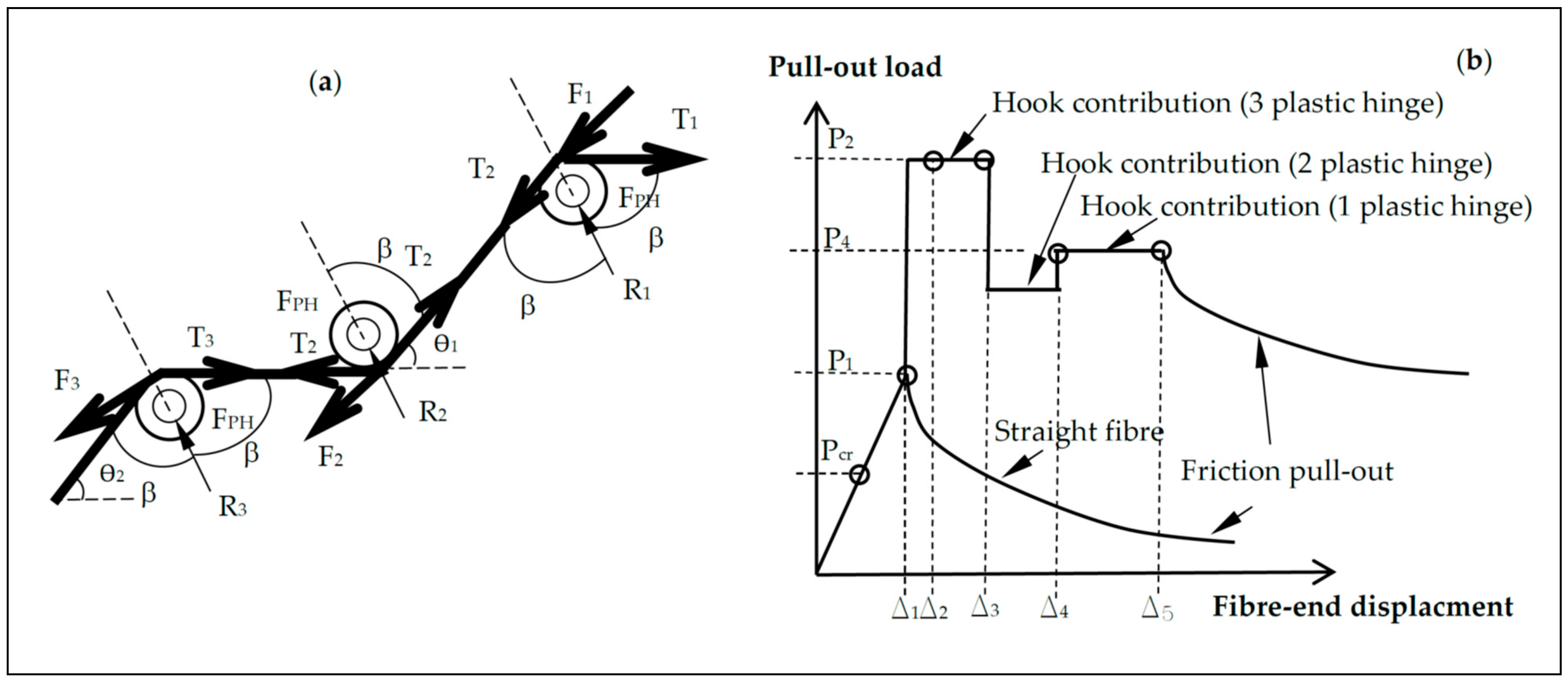
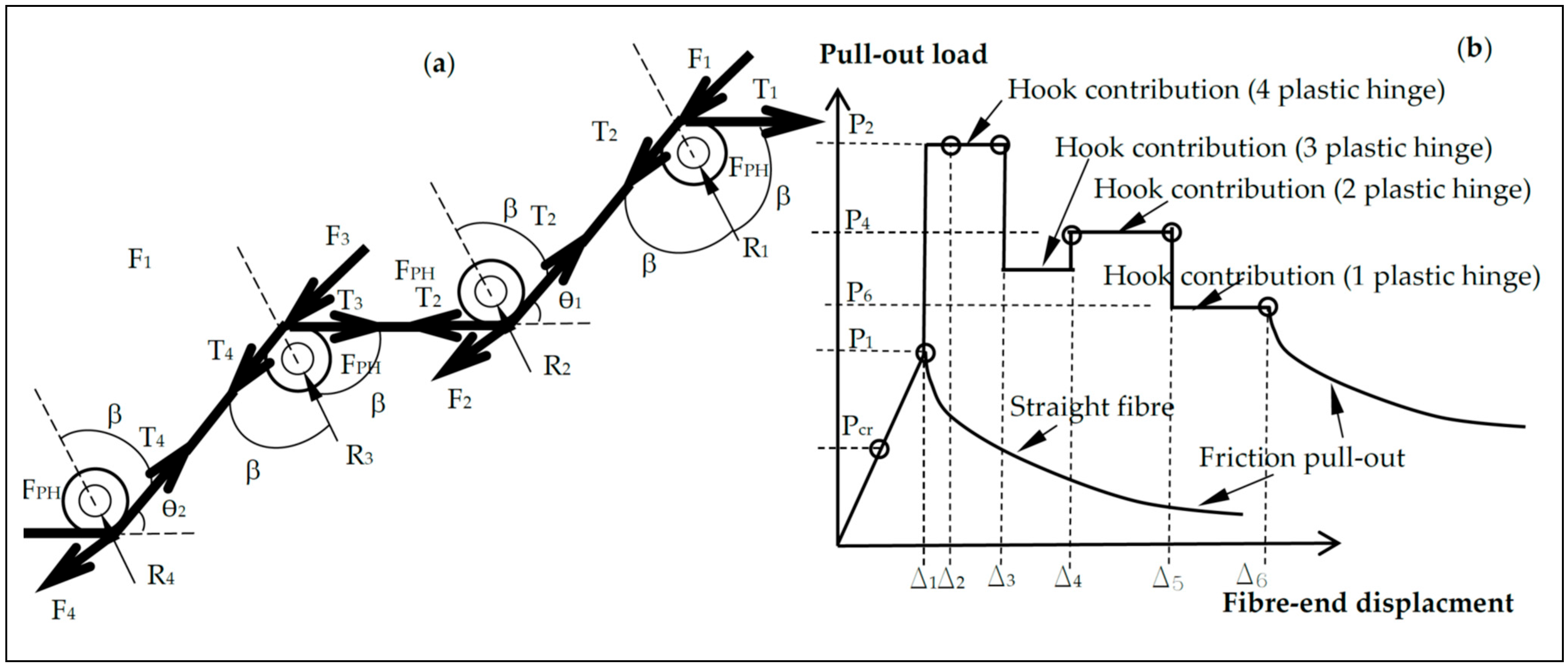

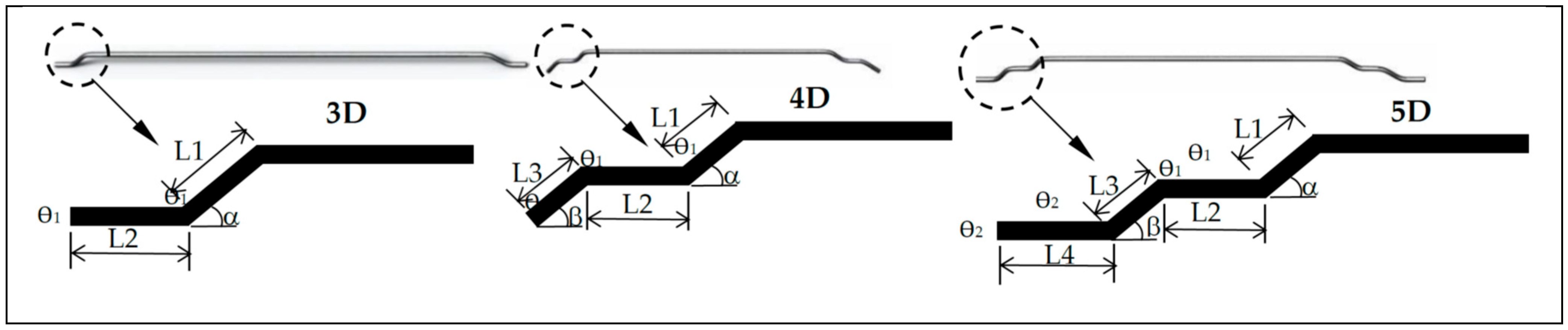
| Fibre Type | σu (MPa) | eu (%) | E (GPa) | σy (MPa) | Lf (mm) | df (mm) | L1 (mm) | L2 (mm) | L3 (mm) | L4 (mm) | ϴ1 (°) | ϴ2 (°) | β (°) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3D | 1160 | 0.8 | 210 | 775–985 | 60 | 0.9 | 2.12 | 2.95 | - | - | 45.7 | - | 67.5 |
| 3D* | 1225 | 0.8 | 210 | 775–985 | 60 | 0.75 | - | - | - | - | - | - | - |
| 3D** | 1345 | 0.8 | 210 | 775–985 | 35 | 0.55 | 2.55 | 2.22 | - | - | 38.3 | - | 70.9 |
| 4D | 1500 | 0.8 | 210 | 1020–1166 | 60 | 0.9 | 2.98 | 2.62 | 3.05 | - | 30.1 | 30.8 | 75 |
| 5D | 2300 | 6 | 210 | 1177–1455 | 60 | 0.9 | 2.57 | 2.38 | 2.57 | 2.56 | 27.9 | 28.2 | 76 |
| Mix | Vf (%) | Fibre | flck/flck,cube | Cement (kg/m3) | Sand (kg/m3) | PFA-Based Aggregates (kg/m3) | Effective Water (kg/m3) |
|---|---|---|---|---|---|---|---|
| 1-3D | 1–2 (80–160 kg/m3) | 3D | LC30/33 | 370 | 592 | 635.6 | 175 |
| 1-3D* | 3D* | ||||||
| 1-3D** | 3D** | ||||||
| 1-4D | 4D | ||||||
| 2 | 3D | LC35/38 | 420 | 546 | |||
| 3 | 5D | LC40/44 | 480 | 485 |
| Mix | flck (MPa) | Fibre | Slump (mm) | Density (kg/m3) | flcm,cube (MPa) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Plain | Vf = 1% | Vf = 2% | Plain | Vf = 1% | Vf = 2% | Plain | Vf = 1% | Vf = 2% | |||
| 1-3D | 30 | 3D | 91 (7.6) | 66 (3.1) | 32 (5.2) | 1981 (124) *1723 (159) | 1992 (182) | 1979 (133) | 37 (3.1) | 37 (4.1) | 38 (3.2) |
| 1-3D* | 30 | 3D* | 96 (8.1) | 57 (3.1) | 31 (2.8) | 1968 (144) *1693 (163) | 1963 (161) | 1979 (189) | 39 (2.2) | 41 (3.8) | 40 (3.1) |
| 1-3D** | 30 | 3D** | 103 (10.2) | 87 (4.4) | 42 (4.6) | 2001 (137) *1731 (122) | 1991 (149) | 1986 (173) | 37 (5.1) | 38 (2.9) | 37 (6.3) |
| 1-4D | 30 | 4D | 98 (11.2) | 49 (3.3) | 26 (4.1) | 1998 (166) *1777 (172) | 1962 (171) | 1951 (111) | 36 (4.3) | 37 (3.8) | 34 (4.2) |
| 2 | 35 | 3D | 86 (7.2) | 46 (6.1) | 28 (2.1) | 2000 (178) *1786 (153) | 1988 (182) | 1963 (121) | 45 (5.6) | 42 (3.8) | 44 (3.2) |
| 3 | 40 | 5D | 88 (4.9) | 42 (1.3) | 20 (2.6) | 1954 (121) *1712 (142) | 1936 (168) | 1917 (167) | 50 (6.8) | 49 (4.2) | 51 (3.1) |
| flcm (MPa) | Vf (%) | Fibre Type | LE (mm) | Pmax (N) | Δmax 6 (mm) | Contribution of Fibre [Interval] (mm) | Δu 7 (mm) | |
|---|---|---|---|---|---|---|---|---|
| Hook | Pull-Out | |||||||
| 30.1 | 0 | 244 | 0.8 | 0.8 | ||||
| 36.5 | 0 | 267 | 0.73 | 0.73 | ||||
| 44.1 | 0 | 320 | 0.68 | 0.68 | ||||
| 33.3 | 1 | 3D | 18.41 | 265 | 1.6 | [1, 6] | [6, 19.2] | 19.2 |
| 32.8 | 1 | 3D | 23.5 | 266 | 1.2 | [0.6, 6.6] | [6.6, 24] | 24 |
| 35.0 | 2 | 3D | 24 | 570 | 1.6 | 24.5 | ||
| 34.9 | 1 | 4D | 24.4 | 615 | 3.1 | [0.6, 9.3] | [9.3, 25] | 25 |
| 34.6 | 2 | 4D | 23.4 | 1020 | 3.4 | 23.8 | ||
| 34.3 | 1 | 4D 1 | 18.7 | 625 | 6 | [0.42, 9.2] | [9.2, 19.1] | 19.1 |
| 34.1 | 1 | 4D 2 | 19 | 690 | 8.1 | [1.1, 8.1] | 8.1 | |
| 36.2 | 1 | 3D | 12.9 | 326 | 1.8 | [1.4, 6.4] | [6.4, 13.9] | 13.9 |
| 34.6 | 1 | 5D | 25 | 662 | 4.5 | [2.5, 12.5] | [12.5, 26] | 26 |
| 44.1 | 1 | 5D | 14.45 | 705 | 2.8 | [1.1, 11.1] | [11.1, 15.1] | 15 |
| 44.1 | 1 | 5D 3 | 11 | 520 | 3.2 | [1, 5] | 12 | |
| 31.5 | 0.7 | 3D* | 21.7 | 316 | 1.6 | [1.35, 6.3] | [6.3, 23] | 23 |
| 31.0 | 0.4 | 3D** | 14 | 92 | 9.4 | [7.2, 12.4] | [12.4, 14.4] | 14.4 |
| 38.2 | 1.2 | 3D** | 13.6 | 236 | 2.2 | 14 | ||
| 32.4 | 1 | 5D 4 | 14.8 | 30–56 | 1.2 | [0.4, 15.2] | 15.2 | |
| 32.4 | 1 | 3D 5 | 20.8 | 34–52 | 0.42 | [0.4, 23] | 21.4 | |
| flcm (MPa) | Vf % | Fibre Type | flctm,m 1 (MPa) | Wtotal 2 (N.mm) | τav 3 (MPa) | τeq 4 (MPa) | τult 5 (MPa) | ξ 6 |
|---|---|---|---|---|---|---|---|---|
| 30.1 (3.8) | 0 | 2.16 (0.13) | ||||||
| 36.5 (4.2) | 0 | 2.36 (0.17) | ||||||
| 44.1 (5.7) | 0 | 2.83 (0.37) | ||||||
| 33.3 (4.1) | 1 | 3D | 4.17 (0.39) | 1801.6 | 5.1 | 3.8 | 9.83 | 0.36 |
| 32.8 (3.3) | 1 | 3D | 4.18 (0.41) | 2167.8 | 4.01 | 2.8 | 9.85 | 0.36 |
| 35.0 (4.4) | 2 | 3D | 8.96 (0.72) | 4655.1 | ||||
| 34.9 (4.1) | 1 | 4D | 9.67 (1.02) | 4085.8 | 8.9 | 4.9 | 16.6 | 0.65 |
| 34.6 (3.2) | 2 | 4D | 16.03 (1.38) | 6073 | ||||
| 34.3 (4.7) | 1 | 4D | 9.82 (1.11) | 4547.5 | 0.65 | |||
| 34.1 (4.1) | 1 | 4D | 10.85 (0.82) | 2898.5 | 0.72 | |||
| 36.2 (6.2) | 1 | 3D | 5.12 (0.35) | 1551.2 | 6.93 | 6.6 | 12.1 | 0.44 |
| 34.6 (4.9) | 1 | 5D | 10.41 (1.33) | 6170.5 | 9.37 | 7 | 16.1 | 0.45 |
| 44.1 (5.9) | 1 | 5D | 8.17 (0.37) | 2216 | 0.36 | |||
| 44.1 (6.7) | 1 | 5D | 11.08 (1.21) | 3257.8 | 17.3 | 11.04 | 17.1 | 0.48 |
| 31.5 (2.1) | 0.7 | 3D* | 5.01 (0.59) | 1812.8 | 6.2 | 3.3 | 15.2 | 0.58 |
| 31.0 (8.1) | 0.4 | 3D** | 1.55 (0.13) | 667.8 | 3.8 | 3.9 | 6.8 | 0.29 |
| 38.2 (4.9) | 1.2 | 3D** | 3.97 (0.41) | 903.7 | ||||
| 32.4 (2.1) | 1 | 5D | 0.49 (0.08) | 325 | 1.7 | 1.05 | 1.26 | 0.08 |
| 32.4 (6.2) | 1 | 3D | 0.53 (0.04) | 318 | 0.6 | 0.5 | 0.48 | 0.04 |
| Type of Fibre | FPH,test (N) | FPH,theoretical (N) Alwan et al. (1999) | FPH,theoretical (N) Proposed |
|---|---|---|---|
| 3D | 73.8 | 117.6 | 72.1 |
| 3D** | 31.5 | 42.8 | 31.1 |
| 4D | 131.2 | 214.2 | 129.7 |
| 5D | 90.5 | 265.4 | 166.7 |
| Fibre Type | Vf | GF (N/mm) |
|---|---|---|
| 3D | 1% | 5393 |
| 2% | 13,253 | |
| 4D | 1% | 17,433 |
| 2% | 44,892 | |
| 5D | 1% | 23,563 |
| 2% | 60,589 | |
| 3D* | 1% | 9389 |
| 2% | 22,045 | |
| 3D** | 1% | 4872 |
| 2% | 11,654 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Naimi, H.K.; Abbas, A.A. Constitutive Model for Plain and Steel-Fibre-Reinforced Lightweight Aggregate Concrete Under Direct Tension and Pull-Out. Fibers 2025, 13, 84. https://doi.org/10.3390/fib13070084
Al-Naimi HK, Abbas AA. Constitutive Model for Plain and Steel-Fibre-Reinforced Lightweight Aggregate Concrete Under Direct Tension and Pull-Out. Fibers. 2025; 13(7):84. https://doi.org/10.3390/fib13070084
Chicago/Turabian StyleAl-Naimi, Hasanain K., and Ali A. Abbas. 2025. "Constitutive Model for Plain and Steel-Fibre-Reinforced Lightweight Aggregate Concrete Under Direct Tension and Pull-Out" Fibers 13, no. 7: 84. https://doi.org/10.3390/fib13070084
APA StyleAl-Naimi, H. K., & Abbas, A. A. (2025). Constitutive Model for Plain and Steel-Fibre-Reinforced Lightweight Aggregate Concrete Under Direct Tension and Pull-Out. Fibers, 13(7), 84. https://doi.org/10.3390/fib13070084